Arabic numerals are the ten symbols most commonly used to write decimal numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. They are also used for writing numbers in other systems such as octal, and for writing identifiers such as computer symbols, trademarks, or license plates. The term often implies a decimal number, in particular when contrasted with Roman numerals.
They are also called Western Arabic numerals, Ghubār numerals, Hindu-Arabic numerals,[1] Western digits, Latin digits, or European digits.[2] The Oxford English Dictionary differentiates them with the fully capitalized Arabic Numerals to refer to the Eastern digits.[3] The term numbers or numerals or digits often implies only these symbols, however this can only be inferred from context.
Europeans learned of Arabic numerals about the 10th century, though their spread was a gradual process. Two centuries later, in the Algerian city of Béjaïa, the Italian scholar Fibonacci first encountered the numerals; his work was crucial in making them known throughout Europe. European trade, books, and colonialism helped popularize the adoption of Arabic numerals around the world. The numerals have found worldwide use significantly beyond the contemporary spread of the Latin alphabet, and have become common in the writing systems where other numeral systems existed previously, such as Chinese and Japanese numerals.
History[edit]
Origin[edit]
Evolution of Indian numerals into Arabic numerals and their adoption in Europe
The reason the digits are more commonly known as «Arabic numerals» in Europe and the Americas is that they were introduced to Europe in the 10th century by Arabic speakers of Spain and North Africa, who were then using the digits from Libya to Morocco. In the eastern part of Arabic Peninsula, Arabs were using the Eastern Arabic numerals or «Mashriki» numerals: ٠ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ ٩[a][4]
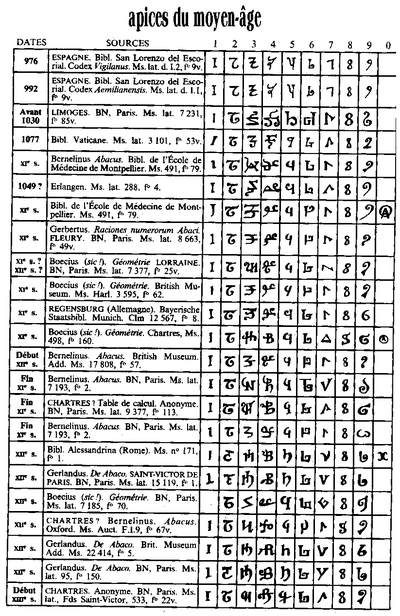
Al-Nasawi wrote in the early 11th century that mathematicians had not agreed on the form of the numerals, but most of them had agreed to train themselves with the forms now known as Eastern Arabic numerals.[5] The oldest specimens of the written numerals available are from Egypt and date to 873–874 CE. They show three forms of the numeral «2» and two forms of the numeral «3», and these variations indicate the divergence between what later became known as the Eastern Arabic numerals and the Western Arabic numerals.[6] The Western Arabic numerals came to be used in the Maghreb and Al-Andalus from the 10th century onward.[7] Some amount of consistency in the Western Arabic numeral forms endured from the 10th century, found in a Latin manuscript of Isidore of Seville’s Etymologiae from 976 and the Gerbertian abacus, into the 12th and 13th centuries, in early manuscripts of translations from the city of Toledo.[4]
Calculations were originally performed using a dust board (takht, Latin: tabula), which involved writing symbols with a stylus and erasing them. The use of the dust board appears to have introduced a divergence in terminology as well: whereas the Hindu reckoning was called ḥisāb al-hindī in the east, it was called ḥisāb al-ghubār in the west (literally, «calculation with dust»).[8] The numerals themselves were referred to in the west as ashkāl al‐ghubār («dust figures») or qalam al-ghubår («dust letters»).[9] Al-Uqlidisi later invented a system of calculations with ink and paper «without board and erasing» (bi-ghayr takht wa-lā maḥw bal bi-dawāt wa-qirṭās).[10]
A popular myth claims that the symbols were designed to indicate their numeric value through the number of angles they contained, but no evidence exists of this, and the myth is difficult to reconcile with any digits past 4.[11]
Adoption and spread[edit]
The first mentions of the numerals from 1 to 9 in the West are found in the Codex Vigilanus of 976, an illuminated collection of various historical documents covering a period from antiquity to the 10th century in Hispania.[12] Other texts show that numbers from 1 to 9 were occasionally supplemented by a placeholder known as sipos, represented as a circle or wheel, reminiscent of the eventual symbol for zero. The Arabic term for zero is sifr (صفر), transliterated into Latin as cifra, and the origin of the English word cipher.
From the 980s, Gerbert of Aurillac (later, Pope Sylvester II) used his position to spread knowledge of the numerals in Europe. Gerbert studied in Barcelona in his youth. He was known to have requested mathematical treatises concerning the astrolabe from Lupitus of Barcelona after he had returned to France.[12]
The reception of Arabic numerals in the West was gradual and lukewarm, as other numeral systems circulated in addition to the older Roman numbers. As a discipline, the first to adopt Arabic numerals as part of their own writings were astronomers and astrologists, evidenced from manuscripts surviving from mid-12th-century Bavaria. Reinher of Paderborn (1140–1190) used the numerals in his calendrical tables to calculate the dates of Easter more easily in his text Compotus emendatus.[13]
Italy[edit]
A page of the Liber Abaci. The list on the right shows the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. The 2, 8, and 9 resemble Arabic numerals more than Eastern Arabic numerals or Indian numerals
Fibonacci, a mathematician from the Republic of Pisa who had studied in Béjaïa (Bugia), Algeria, promoted the Hindu-Arabic numeral system in Europe with his 1202 book Liber Abaci:
When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians’ nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.
The Liber Abaci introduced the huge advantages of a positional numeric system, and was widely influential. As Fibonacci used the symbols from Béjaïa for the digits, these symbols were also introduced in the same instruction, ultimately leading to their widespread adoption.[14]
Fibonacci’s introduction coincided with Europe’s commercial revolution of the 12th and 13th centuries, centered in Italy. Positional notation could be used for quicker and more complex mathematical operations (such as currency conversion) than Roman and other numeric systems could. They could also handle larger numbers, did not require a separate reckoning tool, and allowed the user to check a calculation without repeating the entire procedure.[14] Although positional notation opened possibilities that were hampered by previous systems, late medieval Italian merchants did not stop using Roman numerals (or other reckoning tools). Rather, Arabic numerals became an additional tool that could be used alongside others.[14]
Europe[edit]
A German manuscript page teaching use of Arabic numerals (Talhoffer Thott, 1459). At this time, knowledge of the numerals was still widely seen as esoteric, and Talhoffer presents them with the Hebrew alphabet and astrology.
In the late 14th century only a few texts using Arabic numerals appeared outside of Italy. This suggests that the use of Arabic numerals in commercial practice, and the significant advantage they conferred, remained a virtual Italian monopoly until the late 15th century.[14] This may in part have been due to language – although Fibonacci’s Liber Abaci was written in Latin, the Italian abacus traditions was predominantly written in Italian vernaculars that circulated in the private collections of abacus schools or individuals. It was likely difficult for non-Italian merchant bankers to access comprehensive information.
The European acceptance of the numerals was accelerated by the invention of the printing press, and they became widely known during the 15th century. Their use grew steadily in other centers of finance and trade such as Lyon.[15] Early evidence of their use in Britain includes: an equal hour horary quadrant from 1396,[16] in England, a 1445 inscription on the tower of Heathfield Church, Sussex; a 1448 inscription on a wooden lych-gate of Bray Church, Berkshire; and a 1487 inscription on the belfry door at Piddletrenthide church, Dorset; and in Scotland a 1470 inscription on the tomb of the first Earl of Huntly in Elgin Cathedral.[17] In central Europe, the King of Hungary Ladislaus the Posthumous, started the use of Arabic numerals, which appear for the first time in a royal document of 1456.[18]
By the mid-16th century, they were in common use in most of Europe. Roman numerals remained in use mostly for the notation of Anno Domini years, and for numbers on clock faces.[citation needed] Other digits (such as Eastern Arabic) were virtually unknown.[citation needed]
Russia[edit]
Prior to the introduction of Arabic numerals, Cyrillic numerals, derived from the Cyrillic alphabet, were used by South and East Slavic peoples. The system was used in Russia as late as the early 18th century, although it was formally replaced in official use by Peter the Great in 1699.[19] Reasons for Peter’s switch from the alphanumerical system are believed to go beyond his desire to imitate the West. Historian Peter Brown makes arguments for sociological, militaristic, and pedagogical reasons for the change. At a broad, societal level, Russian merchants, soldiers, and officials increasingly came into contact with counterparts from the West and became familiar with the communal use of Arabic numerals. Peter the Great also travelled incognito throughout Northern Europe from 1697 to 1698 during his Grand Embassy and was likely exposed to Western mathematics, if informally, during this time.[20] The Cyrillic numeric system was also inferior in terms of calculating properties of objects in motions, such as the trajectories and parabolic flight patterns of artillery. It was unable to keep pace with Arabic numerals in the growing science of ballistics, whereas Western mathematicians such as John Napier had been publishing on the topic since 1614.[21]
China[edit]
Chinese numeral systems that used positional notation (such as the counting rod system and Suzhou numerals) were in use in China preior to the introduction of Arabic numerals,[22][23] and some were introduced to medieval China by the Muslim Hui people. In the early 17th century, European-style Arabic numerals were introduced by Spanish and Portuguese Jesuits.[24][25][26]
Encoding[edit]
The ten Arabic numerals are encoded in virtually every character set designed for electric, radio, and digital communication, such as Morse code.
They are encoded in ASCII at positions 0x30 to 0x39. Masking to the lower four binary bits (or taking the last hexadecimal digit) gives the value of the digit, a great help in converting text to numbers on early computers. These positions were inherited in Unicode.[27] EBCDIC used different values, but also had the lower 4 bits equal to the digit value.
| ASCII Binary | ASCII Octal | ASCII Decimal | ASCII Hex | Unicode | EBCDIC Hex |
|
|---|---|---|---|---|---|---|
| 0 | 0011 0000 | 060 | 48 | 30 | U+0030 DIGIT ZERO | F0 |
| 1 | 0011 0001 | 061 | 49 | 31 | U+0031 DIGIT ONE | F1 |
| 2 | 0011 0010 | 062 | 50 | 32 | U+0032 DIGIT TWO | F2 |
| 3 | 0011 0011 | 063 | 51 | 33 | U+0033 DIGIT THREE | F3 |
| 4 | 0011 0100 | 064 | 52 | 34 | U+0034 DIGIT FOUR | F4 |
| 5 | 0011 0101 | 065 | 53 | 35 | U+0035 DIGIT FIVE | F5 |
| 6 | 0011 0110 | 066 | 54 | 36 | U+0036 DIGIT SIX | F6 |
| 7 | 0011 0111 | 067 | 55 | 37 | U+0037 DIGIT SEVEN | F7 |
| 8 | 0011 1000 | 070 | 56 | 38 | U+0038 DIGIT EIGHT | F8 |
| 9 | 0011 1001 | 071 | 57 | 39 | U+0039 DIGIT NINE | F9 |
Comparison with other digits[edit]
| Symbol | Used with scripts | Numerals | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | many | Arabic numerals |
| 𑁦 | 𑁧 | 𑁨 | 𑁩 | 𑁪 | 𑁫 | 𑁬 | 𑁭 | 𑁮 | 𑁯 | Brahmi | Brahmi numerals |
| ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | Devanagari | Devanagari numerals |
| ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ | Bengali–Assamese | Bengali numerals |
| ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | Gurmukhi | Gurmukhi numerals |
| ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | Gujarati | Gujarati numerals |
| ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ | Odia | Odia numerals |
| ᱐ | ᱑ | ᱒ | ᱓ | ᱔ | ᱕ | ᱖ | ᱗ | ᱘ | ᱙ | Santali | Santali numerals |
| 𑇐 | 𑇑 | 𑇒 | 𑇓 | 𑇔 | 𑇕 | 𑇖 | 𑇗 | 𑇘 | 𑇙 | Sharada | Sharada numerals |
| ௦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ | Tamil | Tamil numerals |
| ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ | Telugu | Telugu script § Numerals |
| ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ | Kannada | Kannada script § Numerals |
| ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ | Malayalam | Malayalam numerals |
| ෦ | ෧ | ෨ | ෩ | ෪ | ෫ | ෬ | ෭ | ෮ | ෯ | Sinhala | Sinhala numerals |
| ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ | Burmese | Burmese numerals |
| ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ | Tibetan | Tibetan numerals |
| ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | ᠖ | ᠗ | ᠘ | ᠙ | Mongolian | Mongolian numerals |
| ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ | Khmer | Khmer numerals |
| ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ | Thai | Thai numerals |
| ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ | Lao | Lao script § Numerals |
| ᮰ | ᮱ | ᮲ | ᮳ | ᮴ | ᮵ | ᮶ | ᮷ | ᮸ | ᮹ | Sundanese | Sundanese numerals |
| ꧐ | ꧑ | ꧒ | ꧓ | ꧔ | ꧕ | ꧖ | ꧗ | ꧘ | ꧙ | Javanese | Javanese numerals |
| ᭐ | ᭑ | ᭒ | ᭓ | ᭔ | ᭕ | ᭖ | ᭗ | ᭘ | ᭙ | Balinese | Balinese numerals |
| ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | Arabic | Eastern Arabic numerals |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Persian / Dari / Pashto | |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Urdu / Shahmukhi | |
| — | ፩ | ፪ | ፫ | ፬ | ፭ | ፮ | ፯ | ፰ | ፱ | Ethio-Semitic | Ge’ez numerals |
| 〇 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | East Asia | Chinese numerals |
See also[edit]
- Arabic numeral variations
- Regional variations in modern handwritten Arabic numerals
- Seven-segment display
- Text figures
Explanatory notes[edit]
- ^ Shown right-to-left, zero is on the right, nine on the left.
Citations[edit]
- ^ «Arabic numeral». American Heritage Dictionary. Houghton Mifflin Harcourt Publishing Company. 2020. Archived from the original on 21 November 2021. Retrieved 21 November 2021.
- ^ Terminology for Digits Archived 26 October 2021 at the Wayback Machine. Unicode Consortium.
- ^ «Arabic», Oxford English Dictionary, 2nd edition
- ^ a b Burnett, Charles (2002). Dold-Samplonius, Yvonne; Van Dalen, Benno; Dauben, Joseph; Folkerts, Menso (eds.). From China to Paris: 2000 Years Transmission of Mathematical Ideas. Franz Steiner Verlag. pp. 237–288. ISBN 978-3-515-08223-5. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Kunitzsch 2003, p. 7: «Les personnes qui se sont occupées de la science du calcul n’ont pas été d’accord sur une partie des formes de ces neuf signes; mais la plupart d’entre elles sont convenues de les former comme il suit.»
- ^ Kunitzsch 2003, p. 5.
- ^ Kunitzsch 2003, pp. 12–13: «While specimens of Western Arabic numerals from the early period—the tenth to thirteenth centuries—are still not available, we know at least that Hindu reckoning (called ḥisāb al-ghubār) was known in the West from the 10th century onward…»
- ^ Kunitzsch 2003, p. 8.
- ^ Kunitzsch 2003, p. 10.
- ^ Kunitzsch 2003, pp. 7–8.
- ^ Ifrah, Georges (1998). The universal history of numbers: from prehistory to the invention of the computer. Translated by David Bellos (from the French). London: Harvill Press. pp. 356–357. ISBN 9781860463242.
- ^ a b Nothaft, C. Philipp E. (3 May 2020). «Medieval Europe’s satanic ciphers: on the genesis of a modern myth». British Journal for the History of Mathematics. 35 (2): 107–136. doi:10.1080/26375451.2020.1726050. ISSN 2637-5451. S2CID 213113566.
- ^ Herold, Werner (2005). «Der «computus emendatus» des Reinher von Paderborn». ixtheo.de (in German). Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ a b c d Danna, Raffaele (12 July 2021). The Spread of Hindu-Arabic Numerals in the European Tradition of Practical Arithmetic: a Socio-Economic Perspective (13th–16th centuries) (Doctoral thesis). University of Cambridge. doi:10.17863/cam.72497. Archived from the original on 27 July 2021. Retrieved 29 July 2022.
- ^ Danna, Raffaele; Iori, Martina; Mina, Andrea (22 June 2022). «A Numerical Revolution: The Diffusion of Practical Mathematics and the Growth of Pre-modern European Economies». SSRN 4143442.
- ^ «14th century timepiece unearthed in Qld farm shed». ABC News. Archived from the original on 29 February 2012. Retrieved 10 November 2011.
- ^ See G. F. Hill, The Development of Arabic Numerals in Europe, for more examples.
- ^ Erdélyi: Magyar művelődéstörténet 1-2. kötet. Kolozsvár, 1913, 1918.
- ^ Conatser Segura, Sylvia (26 May 2020). Orthographic Reform and Language Planning in Russian History (Honors thesis). Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Brown, Peter B. (2012). «Muscovite Arithmetic in Seventeenth-Century Russian Civilization: Is It Not Time to Discard the «Backwardness» Label?». Russian History. 39 (4): 393–459. doi:10.1163/48763316-03904001. ISSN 0094-288X. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Lockwood, E. H. (October 1978). «Mathematical discoveries 1600-1750, by P. L. Griffiths. Pp 121. £2·75. 1977. ISBN 0 7223 1006 4 (Stockwell)». The Mathematical Gazette. 62 (421): 219. doi:10.2307/3616704. ISSN 0025-5572. JSTOR 3616704. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Shell-Gellasch, Amy (2015). Algebra in context : introductory algebra from origins to applications. J. B. Thoo. Baltimore. ISBN 978-1-4214-1728-8. OCLC 907657424.
- ^ Uy, Frederick L. (January 2003). «The Chinese Numeration System and Place Value». Teaching Children Mathematics. 9 (5): 243–247. doi:10.5951/tcm.9.5.0243. ISSN 1073-5836. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Helaine Selin, ed. (1997). Encyclopaedia of the history of science, technology, and medicine in non-western cultures. Springer. p. 198. ISBN 978-0-7923-4066-9. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ Meuleman, Johan H. (2002). Islam in the era of globalization: Muslim attitudes towards modernity and identity. Psychology Press. p. 272. ISBN 978-0-7007-1691-3. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ Peng Yoke Ho (2000). Li, Qi and Shu: An Introduction to Science and Civilization in China. Mineola, New York: Courier Dover Publications. p. 106. ISBN 978-0-486-41445-4. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ «The Unicode Standard, Version 13.0» (PDF). unicode.org. Archived (PDF) from the original on 2 June 2001. Retrieved 1 September 2021.
General and cited sources[edit]
- Kunitzsch, Paul (2003). «The Transmission of Hindu-Arabic Numerals Reconsidered». In J. P. Hogendijk; A. I. Sabra (eds.). The Enterprise of Science in Islam: New Perspectives. MIT Press. pp. 3–22. ISBN 978-0-262-19482-2.
Further reading[edit]
- Burnett, Charles (2006). «The Semantics of Indian Numerals in Arabic, Greek and Latin». Journal of Indian Philosophy. Springer-Netherlands. 34 (1–2): 15–30. doi:10.1007/s10781-005-8153-z. S2CID 170783929.
- Hayashi, Takao (1995). The Bakhshālī Manuscript: An Ancient Indian Mathematical Treatise. Groningen, Netherlands: Egbert Forsten. ISBN 906980087X.
- Ifrah, Georges (2000). A Universal History of Numbers: From Prehistory to Computers. New York: Wiley. ISBN 0471393401.
- Katz, Victor J., ed. (20 July 2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton, New Jersey: Princeton University Press. ISBN 978-0691114859.
- «Mathematics in South Asia». Nature. 189 (4761): 273. 1961. Bibcode:1961Natur.189S.273.. doi:10.1038/189273c0. S2CID 4288165.
- Ore, Oystein (1988). «Hindu-Arabic numerals». Number Theory and Its History. Dover. pp. 19–24. ISBN 0486656209.
External links[edit]
- Lam Lay Yong, «Development of Hindu Arabic and Traditional Chinese Arithmetic», Chinese Science 13 (1996): 35–54.
- «Counting Systems and Numerals», Historyworld. Retrieved 11 December 2005.
- The Evolution of Numbers. 16 April 2005.
- O’Connor, J. J., and E. F. Robertson, Indian numerals Archived 6 July 2015 at the Wayback Machine. November 2000.
- History of the numerals
- Arabic numerals
- Hindu-Arabic numerals
- Numeral & Numbers’ history and curiosities
- Gerbert d’Aurillac’s early use of Hindu-Arabic numerals at Convergence
Arabic numerals are the ten symbols most commonly used to write decimal numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. They are also used for writing numbers in other systems such as octal, and for writing identifiers such as computer symbols, trademarks, or license plates. The term often implies a decimal number, in particular when contrasted with Roman numerals.
They are also called Western Arabic numerals, Ghubār numerals, Hindu-Arabic numerals,[1] Western digits, Latin digits, or European digits.[2] The Oxford English Dictionary differentiates them with the fully capitalized Arabic Numerals to refer to the Eastern digits.[3] The term numbers or numerals or digits often implies only these symbols, however this can only be inferred from context.
Europeans learned of Arabic numerals about the 10th century, though their spread was a gradual process. Two centuries later, in the Algerian city of Béjaïa, the Italian scholar Fibonacci first encountered the numerals; his work was crucial in making them known throughout Europe. European trade, books, and colonialism helped popularize the adoption of Arabic numerals around the world. The numerals have found worldwide use significantly beyond the contemporary spread of the Latin alphabet, and have become common in the writing systems where other numeral systems existed previously, such as Chinese and Japanese numerals.
History[edit]
Origin[edit]
Evolution of Indian numerals into Arabic numerals and their adoption in Europe
The reason the digits are more commonly known as «Arabic numerals» in Europe and the Americas is that they were introduced to Europe in the 10th century by Arabic speakers of Spain and North Africa, who were then using the digits from Libya to Morocco. In the eastern part of Arabic Peninsula, Arabs were using the Eastern Arabic numerals or «Mashriki» numerals: ٠ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ ٩[a][4]
Al-Nasawi wrote in the early 11th century that mathematicians had not agreed on the form of the numerals, but most of them had agreed to train themselves with the forms now known as Eastern Arabic numerals.[5] The oldest specimens of the written numerals available are from Egypt and date to 873–874 CE. They show three forms of the numeral «2» and two forms of the numeral «3», and these variations indicate the divergence between what later became known as the Eastern Arabic numerals and the Western Arabic numerals.[6] The Western Arabic numerals came to be used in the Maghreb and Al-Andalus from the 10th century onward.[7] Some amount of consistency in the Western Arabic numeral forms endured from the 10th century, found in a Latin manuscript of Isidore of Seville’s Etymologiae from 976 and the Gerbertian abacus, into the 12th and 13th centuries, in early manuscripts of translations from the city of Toledo.[4]
Calculations were originally performed using a dust board (takht, Latin: tabula), which involved writing symbols with a stylus and erasing them. The use of the dust board appears to have introduced a divergence in terminology as well: whereas the Hindu reckoning was called ḥisāb al-hindī in the east, it was called ḥisāb al-ghubār in the west (literally, «calculation with dust»).[8] The numerals themselves were referred to in the west as ashkāl al‐ghubār («dust figures») or qalam al-ghubår («dust letters»).[9] Al-Uqlidisi later invented a system of calculations with ink and paper «without board and erasing» (bi-ghayr takht wa-lā maḥw bal bi-dawāt wa-qirṭās).[10]
A popular myth claims that the symbols were designed to indicate their numeric value through the number of angles they contained, but no evidence exists of this, and the myth is difficult to reconcile with any digits past 4.[11]
Adoption and spread[edit]
The first mentions of the numerals from 1 to 9 in the West are found in the Codex Vigilanus of 976, an illuminated collection of various historical documents covering a period from antiquity to the 10th century in Hispania.[12] Other texts show that numbers from 1 to 9 were occasionally supplemented by a placeholder known as sipos, represented as a circle or wheel, reminiscent of the eventual symbol for zero. The Arabic term for zero is sifr (صفر), transliterated into Latin as cifra, and the origin of the English word cipher.
From the 980s, Gerbert of Aurillac (later, Pope Sylvester II) used his position to spread knowledge of the numerals in Europe. Gerbert studied in Barcelona in his youth. He was known to have requested mathematical treatises concerning the astrolabe from Lupitus of Barcelona after he had returned to France.[12]
The reception of Arabic numerals in the West was gradual and lukewarm, as other numeral systems circulated in addition to the older Roman numbers. As a discipline, the first to adopt Arabic numerals as part of their own writings were astronomers and astrologists, evidenced from manuscripts surviving from mid-12th-century Bavaria. Reinher of Paderborn (1140–1190) used the numerals in his calendrical tables to calculate the dates of Easter more easily in his text Compotus emendatus.[13]
Italy[edit]
A page of the Liber Abaci. The list on the right shows the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. The 2, 8, and 9 resemble Arabic numerals more than Eastern Arabic numerals or Indian numerals
Fibonacci, a mathematician from the Republic of Pisa who had studied in Béjaïa (Bugia), Algeria, promoted the Hindu-Arabic numeral system in Europe with his 1202 book Liber Abaci:
When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians’ nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.
The Liber Abaci introduced the huge advantages of a positional numeric system, and was widely influential. As Fibonacci used the symbols from Béjaïa for the digits, these symbols were also introduced in the same instruction, ultimately leading to their widespread adoption.[14]
Fibonacci’s introduction coincided with Europe’s commercial revolution of the 12th and 13th centuries, centered in Italy. Positional notation could be used for quicker and more complex mathematical operations (such as currency conversion) than Roman and other numeric systems could. They could also handle larger numbers, did not require a separate reckoning tool, and allowed the user to check a calculation without repeating the entire procedure.[14] Although positional notation opened possibilities that were hampered by previous systems, late medieval Italian merchants did not stop using Roman numerals (or other reckoning tools). Rather, Arabic numerals became an additional tool that could be used alongside others.[14]
Europe[edit]
A German manuscript page teaching use of Arabic numerals (Talhoffer Thott, 1459). At this time, knowledge of the numerals was still widely seen as esoteric, and Talhoffer presents them with the Hebrew alphabet and astrology.
In the late 14th century only a few texts using Arabic numerals appeared outside of Italy. This suggests that the use of Arabic numerals in commercial practice, and the significant advantage they conferred, remained a virtual Italian monopoly until the late 15th century.[14] This may in part have been due to language – although Fibonacci’s Liber Abaci was written in Latin, the Italian abacus traditions was predominantly written in Italian vernaculars that circulated in the private collections of abacus schools or individuals. It was likely difficult for non-Italian merchant bankers to access comprehensive information.
The European acceptance of the numerals was accelerated by the invention of the printing press, and they became widely known during the 15th century. Their use grew steadily in other centers of finance and trade such as Lyon.[15] Early evidence of their use in Britain includes: an equal hour horary quadrant from 1396,[16] in England, a 1445 inscription on the tower of Heathfield Church, Sussex; a 1448 inscription on a wooden lych-gate of Bray Church, Berkshire; and a 1487 inscription on the belfry door at Piddletrenthide church, Dorset; and in Scotland a 1470 inscription on the tomb of the first Earl of Huntly in Elgin Cathedral.[17] In central Europe, the King of Hungary Ladislaus the Posthumous, started the use of Arabic numerals, which appear for the first time in a royal document of 1456.[18]
By the mid-16th century, they were in common use in most of Europe. Roman numerals remained in use mostly for the notation of Anno Domini years, and for numbers on clock faces.[citation needed] Other digits (such as Eastern Arabic) were virtually unknown.[citation needed]
Russia[edit]
Prior to the introduction of Arabic numerals, Cyrillic numerals, derived from the Cyrillic alphabet, were used by South and East Slavic peoples. The system was used in Russia as late as the early 18th century, although it was formally replaced in official use by Peter the Great in 1699.[19] Reasons for Peter’s switch from the alphanumerical system are believed to go beyond his desire to imitate the West. Historian Peter Brown makes arguments for sociological, militaristic, and pedagogical reasons for the change. At a broad, societal level, Russian merchants, soldiers, and officials increasingly came into contact with counterparts from the West and became familiar with the communal use of Arabic numerals. Peter the Great also travelled incognito throughout Northern Europe from 1697 to 1698 during his Grand Embassy and was likely exposed to Western mathematics, if informally, during this time.[20] The Cyrillic numeric system was also inferior in terms of calculating properties of objects in motions, such as the trajectories and parabolic flight patterns of artillery. It was unable to keep pace with Arabic numerals in the growing science of ballistics, whereas Western mathematicians such as John Napier had been publishing on the topic since 1614.[21]
China[edit]
Chinese numeral systems that used positional notation (such as the counting rod system and Suzhou numerals) were in use in China preior to the introduction of Arabic numerals,[22][23] and some were introduced to medieval China by the Muslim Hui people. In the early 17th century, European-style Arabic numerals were introduced by Spanish and Portuguese Jesuits.[24][25][26]
Encoding[edit]
The ten Arabic numerals are encoded in virtually every character set designed for electric, radio, and digital communication, such as Morse code.
They are encoded in ASCII at positions 0x30 to 0x39. Masking to the lower four binary bits (or taking the last hexadecimal digit) gives the value of the digit, a great help in converting text to numbers on early computers. These positions were inherited in Unicode.[27] EBCDIC used different values, but also had the lower 4 bits equal to the digit value.
| ASCII Binary | ASCII Octal | ASCII Decimal | ASCII Hex | Unicode | EBCDIC Hex |
|
|---|---|---|---|---|---|---|
| 0 | 0011 0000 | 060 | 48 | 30 | U+0030 DIGIT ZERO | F0 |
| 1 | 0011 0001 | 061 | 49 | 31 | U+0031 DIGIT ONE | F1 |
| 2 | 0011 0010 | 062 | 50 | 32 | U+0032 DIGIT TWO | F2 |
| 3 | 0011 0011 | 063 | 51 | 33 | U+0033 DIGIT THREE | F3 |
| 4 | 0011 0100 | 064 | 52 | 34 | U+0034 DIGIT FOUR | F4 |
| 5 | 0011 0101 | 065 | 53 | 35 | U+0035 DIGIT FIVE | F5 |
| 6 | 0011 0110 | 066 | 54 | 36 | U+0036 DIGIT SIX | F6 |
| 7 | 0011 0111 | 067 | 55 | 37 | U+0037 DIGIT SEVEN | F7 |
| 8 | 0011 1000 | 070 | 56 | 38 | U+0038 DIGIT EIGHT | F8 |
| 9 | 0011 1001 | 071 | 57 | 39 | U+0039 DIGIT NINE | F9 |
Comparison with other digits[edit]
| Symbol | Used with scripts | Numerals | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | many | Arabic numerals |
| 𑁦 | 𑁧 | 𑁨 | 𑁩 | 𑁪 | 𑁫 | 𑁬 | 𑁭 | 𑁮 | 𑁯 | Brahmi | Brahmi numerals |
| ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | Devanagari | Devanagari numerals |
| ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ | Bengali–Assamese | Bengali numerals |
| ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | Gurmukhi | Gurmukhi numerals |
| ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | Gujarati | Gujarati numerals |
| ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ | Odia | Odia numerals |
| ᱐ | ᱑ | ᱒ | ᱓ | ᱔ | ᱕ | ᱖ | ᱗ | ᱘ | ᱙ | Santali | Santali numerals |
| 𑇐 | 𑇑 | 𑇒 | 𑇓 | 𑇔 | 𑇕 | 𑇖 | 𑇗 | 𑇘 | 𑇙 | Sharada | Sharada numerals |
| ௦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ | Tamil | Tamil numerals |
| ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ | Telugu | Telugu script § Numerals |
| ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ | Kannada | Kannada script § Numerals |
| ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ | Malayalam | Malayalam numerals |
| ෦ | ෧ | ෨ | ෩ | ෪ | ෫ | ෬ | ෭ | ෮ | ෯ | Sinhala | Sinhala numerals |
| ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ | Burmese | Burmese numerals |
| ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ | Tibetan | Tibetan numerals |
| ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | ᠖ | ᠗ | ᠘ | ᠙ | Mongolian | Mongolian numerals |
| ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ | Khmer | Khmer numerals |
| ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ | Thai | Thai numerals |
| ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ | Lao | Lao script § Numerals |
| ᮰ | ᮱ | ᮲ | ᮳ | ᮴ | ᮵ | ᮶ | ᮷ | ᮸ | ᮹ | Sundanese | Sundanese numerals |
| ꧐ | ꧑ | ꧒ | ꧓ | ꧔ | ꧕ | ꧖ | ꧗ | ꧘ | ꧙ | Javanese | Javanese numerals |
| ᭐ | ᭑ | ᭒ | ᭓ | ᭔ | ᭕ | ᭖ | ᭗ | ᭘ | ᭙ | Balinese | Balinese numerals |
| ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | Arabic | Eastern Arabic numerals |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Persian / Dari / Pashto | |
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | Urdu / Shahmukhi | |
| — | ፩ | ፪ | ፫ | ፬ | ፭ | ፮ | ፯ | ፰ | ፱ | Ethio-Semitic | Ge’ez numerals |
| 〇 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | East Asia | Chinese numerals |
See also[edit]
- Arabic numeral variations
- Regional variations in modern handwritten Arabic numerals
- Seven-segment display
- Text figures
Explanatory notes[edit]
- ^ Shown right-to-left, zero is on the right, nine on the left.
Citations[edit]
- ^ «Arabic numeral». American Heritage Dictionary. Houghton Mifflin Harcourt Publishing Company. 2020. Archived from the original on 21 November 2021. Retrieved 21 November 2021.
- ^ Terminology for Digits Archived 26 October 2021 at the Wayback Machine. Unicode Consortium.
- ^ «Arabic», Oxford English Dictionary, 2nd edition
- ^ a b Burnett, Charles (2002). Dold-Samplonius, Yvonne; Van Dalen, Benno; Dauben, Joseph; Folkerts, Menso (eds.). From China to Paris: 2000 Years Transmission of Mathematical Ideas. Franz Steiner Verlag. pp. 237–288. ISBN 978-3-515-08223-5. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Kunitzsch 2003, p. 7: «Les personnes qui se sont occupées de la science du calcul n’ont pas été d’accord sur une partie des formes de ces neuf signes; mais la plupart d’entre elles sont convenues de les former comme il suit.»
- ^ Kunitzsch 2003, p. 5.
- ^ Kunitzsch 2003, pp. 12–13: «While specimens of Western Arabic numerals from the early period—the tenth to thirteenth centuries—are still not available, we know at least that Hindu reckoning (called ḥisāb al-ghubār) was known in the West from the 10th century onward…»
- ^ Kunitzsch 2003, p. 8.
- ^ Kunitzsch 2003, p. 10.
- ^ Kunitzsch 2003, pp. 7–8.
- ^ Ifrah, Georges (1998). The universal history of numbers: from prehistory to the invention of the computer. Translated by David Bellos (from the French). London: Harvill Press. pp. 356–357. ISBN 9781860463242.
- ^ a b Nothaft, C. Philipp E. (3 May 2020). «Medieval Europe’s satanic ciphers: on the genesis of a modern myth». British Journal for the History of Mathematics. 35 (2): 107–136. doi:10.1080/26375451.2020.1726050. ISSN 2637-5451. S2CID 213113566.
- ^ Herold, Werner (2005). «Der «computus emendatus» des Reinher von Paderborn». ixtheo.de (in German). Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ a b c d Danna, Raffaele (12 July 2021). The Spread of Hindu-Arabic Numerals in the European Tradition of Practical Arithmetic: a Socio-Economic Perspective (13th–16th centuries) (Doctoral thesis). University of Cambridge. doi:10.17863/cam.72497. Archived from the original on 27 July 2021. Retrieved 29 July 2022.
- ^ Danna, Raffaele; Iori, Martina; Mina, Andrea (22 June 2022). «A Numerical Revolution: The Diffusion of Practical Mathematics and the Growth of Pre-modern European Economies». SSRN 4143442.
- ^ «14th century timepiece unearthed in Qld farm shed». ABC News. Archived from the original on 29 February 2012. Retrieved 10 November 2011.
- ^ See G. F. Hill, The Development of Arabic Numerals in Europe, for more examples.
- ^ Erdélyi: Magyar művelődéstörténet 1-2. kötet. Kolozsvár, 1913, 1918.
- ^ Conatser Segura, Sylvia (26 May 2020). Orthographic Reform and Language Planning in Russian History (Honors thesis). Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Brown, Peter B. (2012). «Muscovite Arithmetic in Seventeenth-Century Russian Civilization: Is It Not Time to Discard the «Backwardness» Label?». Russian History. 39 (4): 393–459. doi:10.1163/48763316-03904001. ISSN 0094-288X. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Lockwood, E. H. (October 1978). «Mathematical discoveries 1600-1750, by P. L. Griffiths. Pp 121. £2·75. 1977. ISBN 0 7223 1006 4 (Stockwell)». The Mathematical Gazette. 62 (421): 219. doi:10.2307/3616704. ISSN 0025-5572. JSTOR 3616704. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Shell-Gellasch, Amy (2015). Algebra in context : introductory algebra from origins to applications. J. B. Thoo. Baltimore. ISBN 978-1-4214-1728-8. OCLC 907657424.
- ^ Uy, Frederick L. (January 2003). «The Chinese Numeration System and Place Value». Teaching Children Mathematics. 9 (5): 243–247. doi:10.5951/tcm.9.5.0243. ISSN 1073-5836. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
- ^ Helaine Selin, ed. (1997). Encyclopaedia of the history of science, technology, and medicine in non-western cultures. Springer. p. 198. ISBN 978-0-7923-4066-9. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ Meuleman, Johan H. (2002). Islam in the era of globalization: Muslim attitudes towards modernity and identity. Psychology Press. p. 272. ISBN 978-0-7007-1691-3. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ Peng Yoke Ho (2000). Li, Qi and Shu: An Introduction to Science and Civilization in China. Mineola, New York: Courier Dover Publications. p. 106. ISBN 978-0-486-41445-4. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
- ^ «The Unicode Standard, Version 13.0» (PDF). unicode.org. Archived (PDF) from the original on 2 June 2001. Retrieved 1 September 2021.
General and cited sources[edit]
- Kunitzsch, Paul (2003). «The Transmission of Hindu-Arabic Numerals Reconsidered». In J. P. Hogendijk; A. I. Sabra (eds.). The Enterprise of Science in Islam: New Perspectives. MIT Press. pp. 3–22. ISBN 978-0-262-19482-2.
Further reading[edit]
- Burnett, Charles (2006). «The Semantics of Indian Numerals in Arabic, Greek and Latin». Journal of Indian Philosophy. Springer-Netherlands. 34 (1–2): 15–30. doi:10.1007/s10781-005-8153-z. S2CID 170783929.
- Hayashi, Takao (1995). The Bakhshālī Manuscript: An Ancient Indian Mathematical Treatise. Groningen, Netherlands: Egbert Forsten. ISBN 906980087X.
- Ifrah, Georges (2000). A Universal History of Numbers: From Prehistory to Computers. New York: Wiley. ISBN 0471393401.
- Katz, Victor J., ed. (20 July 2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton, New Jersey: Princeton University Press. ISBN 978-0691114859.
- «Mathematics in South Asia». Nature. 189 (4761): 273. 1961. Bibcode:1961Natur.189S.273.. doi:10.1038/189273c0. S2CID 4288165.
- Ore, Oystein (1988). «Hindu-Arabic numerals». Number Theory and Its History. Dover. pp. 19–24. ISBN 0486656209.
External links[edit]
- Lam Lay Yong, «Development of Hindu Arabic and Traditional Chinese Arithmetic», Chinese Science 13 (1996): 35–54.
- «Counting Systems and Numerals», Historyworld. Retrieved 11 December 2005.
- The Evolution of Numbers. 16 April 2005.
- O’Connor, J. J., and E. F. Robertson, Indian numerals Archived 6 July 2015 at the Wayback Machine. November 2000.
- History of the numerals
- Arabic numerals
- Hindu-Arabic numerals
- Numeral & Numbers’ history and curiosities
- Gerbert d’Aurillac’s early use of Hindu-Arabic numerals at Convergence
Арабские цифры (шрифт без засечек)
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская |
Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая |
Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этруская Римская |
Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления |
Арабские цифры — традиционное название набора из десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; ныне использующегося в большинстве стран для записи чисел в десятичной системе счисления.
История
Арабские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — арабский, справа — персидский.
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел.
Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму[1].
Индийскую систему записи широко популяризировал учёный ал-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра».
Арабские цифры стали известны европейцам в X веке. Благодаря тесным связям христианской Барселоны (Барселонское графство) и мусульманской Кордовы (Кордовский халифат), Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими цифрами и начал всячески пропагандировать их внедрение в европейскую науку.
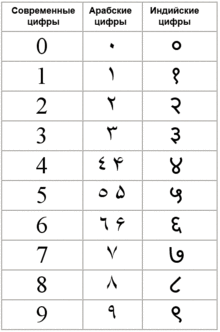
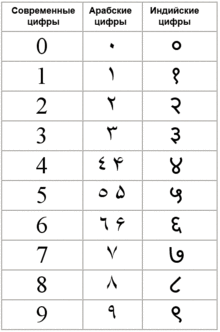
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидские цифры | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Цифры в письме гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Цифры в письме гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Цифры в письме лимбу (Limbu) | ᥆ | ᥇ | ᥈ | ᥉ | ᥊ | ᥋ | ᥌ | ᥍ | ᥎ | ᥏ |
| Цифры в бенгальском письме | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Цифры в письме ория | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Цифры в письме телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Цифры в письме каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Цифры в письме малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Цифры в тамильском письме | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Цифры в тибетском письме | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Цифры в бирманском письме | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Цифры в тайском письме | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Цифры в кхмерском письме | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Цифры в лаосском письме | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
Одна из легенд происхождения начертания современных арабских цифр[2]. Количество углов соответствует числовому значению цифры.
|
|
|
Название «арабские цифры» образовалось исторически, из-за того что именно арабы распространяли десятичную позиционную систему счисления. Цифры, которые используют в арабских странах, по начертанию сильно отличаются от используемых в европейских странах.
Примечания
- ↑ وجهات النظر حول أصل الأرقام ا&# … (ар.)
- ↑ Florian Cajori A History of Mathematical Notations. — Cosimo, Inc., 2007. — Vol. I. — P. 64-66. — ISBN 9781602066847
Ссылки
- Арабские цифры // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- «Арабские цифры» в Большой советской энциклопедии
- Титло — переводчик национальных начертаний арабских и других чисел
- Арабские цифры, использующиеся при датировке ковров
У этого термина существуют и другие значения, см. Цифра (значения).
Арабские цифры (шрифт без засечек)
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская |
Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая |
Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская |
Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) |
Ара́бские ци́фры (называемые также индийскими или индо-арабскими)[1] — традиционное название набора из десяти знаков (цифр), используемых в большинстве стран для записи чисел в десятичной позиционной системе счисления:
-
0123456789
Название «арабские цифры» образовалось исторически, из-за того, что в Европу десятичная позиционная система счисления попала через арабские страны[2]. Тем не менее цифры, используемые в арабских странах Азии и в Египте (называемые арабами «индийскими цифрами»), по начертанию сильно отличаются от используемых в европейских странах.
История[править | править код]
-
Халифат Аббасидов — территория распространения индо-арабских и персидских цифр
-
Халифат Альмохадов — территория, откуда арабские цифры попали в Европу
Первое обнаруженное появление нуля — IX век, Индия
1) «Современные цифры» — обычные арабские цифры. «Арабские цифры» — индо-арабские и персидские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — индо-арабский, справа — персидский. «Индийские цифры» — цифры деванагари современной Индии.
Индо-арабские цифры возникли в Индии не позднее V века[3]. Эта цифровая система была основана на принципах, проверенных всей предыдущей историей развития цифр — десятеричного, позиционного, принципа представления числовых значений и на использовании знака «ноль» для обозначения отсутствия цифры[4].
Первая дошедшая до наших дней запись в десятичной позиционной системе относится к 595 году н. э. Отдельного знака для нуля сначала у индийцев не было, вместо него оставляли пустое место. Символ нуля (шунья) окончательно оформился в IX веке[5].
Преимущества индийской системы записи для арифметических расчётов вскоре оценили персы и арабы. Индийские цифры активно популяризировал в IX веке при дворе халифа аль-Мансура в Багдаде хорезмиец Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». Аль-Хорезми написал книгу «Об индийском счёте», которая способствовала популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до мусульманской Испании[6].
Сохранились трактат математика Ас-Сиджизи, датированный 969 годом, и копия трактата астронома Аль-Бируни, датированная 1082 годом, содержащие индийские цифры[7].
В современных арабских странах Азии, а также в Египте, Иране, Пакистане и Афганистане, в основном, используются цифры, мало отличающиеся от имеющихся в труде аль-Бируни. Арабы называют их «ар-кам хиндия» (أَرْقَام هِنْدِيَّة) — «индийские цифры», но европейцы чаще называют их «индо-арабскими» и «персидскими», так как в языках народов современной Индии цифры эволюционировали и теперь сильно отличаются от средневековых индийских цифр. Позднее их начертания продолжали изменяться, и в трактате западноафриканского математика Ибн аль-Банна аль-Марракуши (XIII век) уже все цифры походили на нынешние европейские (хотя четвёрка и пятёрка были повёрнуты на 90 градусов)[7]. В современных арабских странах Африки (кроме Египта) используются те же цифры, что и в Европе.
Арабские цифры стали известны европейцам в X веке[6]. Первое их описание содержит «Вигиланский кодекс» (Испания, X век), причём ноль ещё не упоминается[8]. В других странах Западной Европы история индоарабских цифр начинается с XII века, а их широкое применение в Западной Европе — с XIII—XIV веков[9].
В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена Робертом Честерским на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении арабских цифр[10].
После отвоевания Испании контакты европейцев с арабами ослабли и многие европейцы по-прежнему использовали римские цифры. Итальянский математик Фибоначчи, изучавший в 1192—1200 годах математику в Алжире и других арабских странах, снова привлёк внимание европейцев к арабским цифрам, написав «Книгу абака»[11]. В эпоху Возрождения возрос интерес к арабской науке, итальянские математики привозили в Европу арабские рукописи. Ко времени распространения книгопечатания в западноевропейской науке укоренилось западно-арабское начертание цифр.
В России арабские цифры появились в XIV—XV вв., широкое распространение получили с XVII в., а после введения гражданской азбуки в XVIII в. вытеснили из гражданской печати славяно-кирилловские цифры[4].
Преимущества индо-арабских цифр[править | править код]
Реализованная с помощью индо-арабских цифр десятичная позиционная система счисления постепенно вытеснила римские цифры и другие непозиционные системы нумерации благодаря множеству несомненных преимуществ[12].
- Индийская запись чисел компактнее римской и позволяет быстро сравнивать разные числа по величине.
- При расчётах на абаке можно одновременно записывать числа и проводить расчёты.
- Вычисления стало возможно проводить без абака, на бумаге. Появились новые, более простые методы умножения и деления, специально рассчитанные на индоарабские цифры.
- Вычислительная математика и математика вообще получили мощный импульс к развитию. Например, трудно представить изобретение логарифмов без индоарабских цифр.
- Благодаря им появилась возможность создания счётных машин.
Версии написания цифр[править | править код]
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидские цифры | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Цифры в письме гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Цифры в письме гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Цифры в бенгальском письме | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Цифры в письме ория | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Цифры в письме телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Цифры в письме каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Цифры в письме малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Цифры в тамильском письме | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Цифры в тибетском письме | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Цифры в монгольском письме | ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | ᠖ | ᠗ | ᠘ | ᠙ |
| Цифры в бирманском письме | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Цифры в тайском письме | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Цифры в кхмерском письме | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Цифры в лаосском письме | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
| Китайские иероглифы, соответствующие цифрам | 零〇 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 |
|
|
|
Галерея[править | править код]
-
Современная арабская телефонная клавиатура с двумя формами арабских цифр: западные арабские/европейские цифры слева и восточно-арабские цифры справа
-
Заимствование индийских цифр через арабов по Европе
-
На немецкой странице рукописи, использующей арабские цифры (Talhoffer Thott, 1459). В это время знание цифр всё ещё широко рассматривалось как эзотерическое, и Тальхоффер представляет еврейский алфавит и астрологию.
-
Французский революционный «десятичный» циферблат XVIII века.
Примечания[править | править код]
- ↑ Цифры // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 826—827.
- ↑ Андронов И. К. Арифметика. Развитие понятия числа и действий над числами. — Учпедгиз, 1959. — С. 28—30. — 361 с.
- ↑ Bulliet, Richard. The Earth and Its Peoples: A Global History, Volume 1 / Richard Bulliet, Pamela Crossley, Daniel Headrick … []. — Cengage Learning, 2010. — P. 192. — «Indian mathematicians invented the concept of zero and developed the «Arabic» numerals and system of place-value notation used in most parts of the world today». — ISBN 1439084742.
- ↑ 1 2 Истрин В.А. Развитие письма / Ред. Вентцель Т.В.. — М.: АН СССР, 1961. — С. 330—331.
- ↑ История математики, том I, 1970, с. 182—183.
- ↑ 1 2 Меннингер, 2011, с. 476—477.
- ↑ 1 2 J. J. O’Connor and E. F. Robertson. The Arabic numeral system. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Arabic_numerals.html
- ↑ Florian Cajori. A history of mathematical notations. — 1993. — P. 50. — 385 p. — ISBN 0486677664.
- ↑ История математики, том I, 1970, с. 256—257.
- ↑ Юшкевич А. П. История математики в средние века. — М.: Гос. изд-во физико-математической литературы, 1961. — С. 156, 191, 331.
- ↑ Меннингер, 2011, с. 493—494.
- ↑ Меннингер, 2011, с. 508—515.
Литература[править | править код]
- «Арабские цифры» в Большой советской энциклопедии
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — 352 с.
- Меннингер К. История цифр. Числа, символы, слова. — М.: ЗАО Центрполиграф, 2011. — 543 с. — ISBN 9785952449787.
Ссылки[править | править код]
- Арабские цифры, использующиеся при датировке ковров
- O’Connor J. J., Robertson E. F. Indian numerals. MacTutor.
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 2 | |
|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ٢ |
| Персидские цифры | ۰ | ۲ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | २ |
| Цифры в письме гуджарати | ૦ | ૨ |
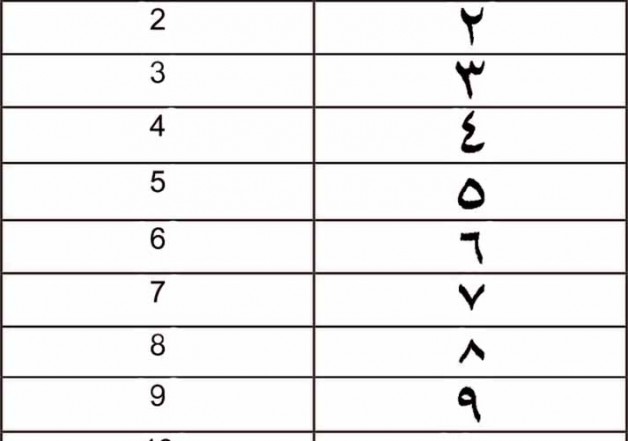
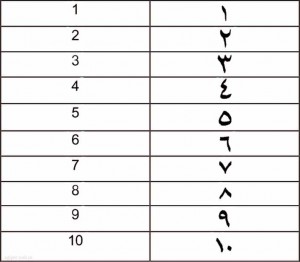
Как пишутся арабские цифры от 1 до 10?
Цифры от 1 до 10 на арабском языке
| Русский | Арабский (прописью) | Арабский (число) |
|---|---|---|
| один | وَاحِد | ١ |
| два | اثْنَان | ٢ |
| три | ثَلاثَة | ٣ |
| четыре | أَرْبَعَة | ٤ |
Как пишутся арабские цифры до 20?
Числительные в арабском языке
| Числа | ||
|---|---|---|
| 20- двадцать | Эшрин | ٢٠ |
| 30- тридцать | Талятин | ٣٠ |
| 40- сорок | Арбаин | ٤٠ |
| 50- пятьдесят | Хамсин | ٥٠ |
Почему арабские цифры пишутся именно так?
Наши цифры называются арабскими, потому, что европейцы узнали про них от арабов. Европу с ними познакомил в 13 веке итальянский математик Леонардо Фибоначчи. Однако, сами арабы называли эти цифры индийскими или индусским счётом, так как позаимствовали их в Индии.
Как пишется арабская цифра 1?
Таблица Римских цифр от 1 до 100
| Арабские цифры | Римские цифры |
|---|---|
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
Как пишется римские цифры от 1 до 20?
Малая таблица римских цифр от 1 до 20
| Арабские цифры | Римские цифры |
|---|---|
| 17 | XVII |
| 18 | XVIII |
| 19 | XIX |
| 20 | XX |
Как читать цифры в Египте?
В Египте цифры пишутся и читаются слева направо, так же как и у нас. Автомобильные номера в Египте с настоящими арабскими цифрами. На дорожных указателях и в названиях улиц часто используется и арабский и латинский шрифт.
Какие цифры бывают римские и еще какие?
Основные римские числа
- 1 = I. 2 = II. 3 = III. 4 = IV. 5 = V. 6 = VI. 7 = VII. 8 = VIII. 9 = IX. 10 = X. 20 = XX. …
- 100 = C. 200 = CC. 300 = CCC. 400 = CD. 500 = D. 600 = DC. 700 = DCC. 800 = DCCC. 900 = CM. 1 000 = M. …
- 10 000 = X. 20 000 = XX. 30 000 = XXX. 40 000 = XL. 50 000 = L. 60 000 = LX. 70 000 = LXX. 80 000 = LXXX. 90 000 = XC. 100 000 = C.
4 окт. 2019 г.
Какие бывают арабские цифры?
Арабские цифры — традиционное название набора из десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; ныне использующегося в большинстве стран для записи чисел в десятичной системе счисления.
Как считать до десяти на арабском?
Количество просмотров этой статьи: 29 658. Арабский язык является одним из самых распространенных языков в мире.
…
Количественные числа до десяти:
- 1 — Уахид
- 2 — Итнан
- 3 Талата
- 4 — Арба-а
- 5 — Хамиза
- 6 — Ситта
- 7 — Саба-а
- 8 — Таманиа
Какой народ придумал арабские цифры?
Арабские цифры, как совершенно точно известно, изобрели арабы. Вернее, индусы. Но арабы жили неподалеку. Как войдешь в Индию, то на север и за углом.
Почему арабы не пользуются арабскими цифрами?
Почему в Объединенных арабских эмиратах не пользуются арабскими цифрами Арабские цифры – это математические знаки, количество которых равно десяти. … Свое название они получили из-за того, что именно арабский народ распространил данную систему исчисления.
Какие цифры есть?
Цифры
- римские цифры: I V X L C D M.
- шестнадцатеричные цифры: 0 1 2 3 4 5 6 7 8 9 A B C D E F.
- цифры майя: от 0 до 19.
- в некоторых языках, например, в церковнославянском, древнегреческом, иврите и др., существует система записи чисел буквами
Почему цифры 0 1 2 3 так далее называют арабскими?
0 1 2 3 4 5 6 7 8 9. Название «арабские цифры» образовалось исторически, из-за того, что в Европу десятичная позиционная система счисления попала через арабские страны.
Как пишется римская цифра 1?
Римская цифра 1 латинскими буквами пишется так — I. Для та во чтобы посмотреть как выглядят остальные римские цифры. Запишите в форму то число которое хотите посмотреть в римских.
Какая это цифра LX?
Большая таблица Римских цифр от 1 до 1000
| Арабские цифры | Римские цифры |
|---|---|
| 57 | LVII |
| 58 | LVIII |
| 59 | LIX |
| 60 | LX |
Учим цифры на арабском языке. Арабские числа.
| Арабские цифры | Цифры на арабском языке |
|---|---|
| 0 | صفر |
| 1 | واحد |
| 2 | اثنان |
| 3 | ثلاثة |
| 4 | أربعة |
| 5 | خمسة |
| 6 | ستة |
| 7 | سبعة |
| 8 | ثمانية |
| 9 | تسعة |
| 10 | عشرة |
| 11 | أحد عشر |
| 12 | اثنا عشر |
| 13 | ثلاثة عشر |
| 14 | أربعة عشرة |
| 15 | خمسة عشر |
| 16 | ست عشرة |
| 17 | سبعة عشر |
| 18 | ثمانية عشر |
| 19 | تسعة عشر |
| 20 | عشرون |
| 30 | ثلاثون |
| 40 | أربعون |
| 50 | خمسون |
| 60 | ستون |
| 70 | سبعون |
| 80 | ثمانون |
| 90 | تسعون |
| 100 | مائة |
| 200 | مائتان |
| 300 | ثلاثمائة |
| 400 | أربعة |
| 500 | خمسمائة |
| 600 | ستة |
| 700 | سبعمائة |
| 800 | ثمانمائة |
| 900 | تسعة |
| 1000 | ألف |
| 2000 | ألفي |
| 3000 | ثلاثة آلاف |
| 4000 | أربعة آلاف |
| 5000 | خمسة آلاف |
| 6000 | ستة آلاف |
| 7000 | سبعة آلاف |
| 8000 | ثمانية آلاف |
| 9000 | تسعة آلاف |
| 10000 | عشرة آلاف |
| 1000000 | مليون |
| 1000000000 | المليار |
| 1000000000000 | تريليون |
Содержание
- Арабские цифры и полезные фразы
- Арабские цифры и числительные в египетском языке
- Числительные, арабские цифры — египетский (каирский) диалект
- Количественные числительные
- Десятки
- Сотни
- Тысячи
- Правила числительных
- Числительные сотен:
- Формы порядковых числительных
- Порядковые числительные применяются в качестве вводных слов:
- § 36. Количественные числительные أَسْمَاءُ العَدَدِ الأَصْلِيَّة
Арабские цифры и полезные фразы
Эту статью я подготовила для любознательных. Здесь не будет фотографий и лирики, только информация, которая может пригодиться.
В сувенирных магазинах Египта цены чаще всего пишут «нашими» цифрами. Здесь все понятно. Но на рынках, маленьких магазинчиках и лавочках, они скорее всего будут написаны на арабском. И вполне возможен вариант, что вы спросите «сколько это стоит», а владелец вместо 10 фунтов скажет 20, улыбаясь во все 28 зубов. Поэтому я решила написать статью об арабских цифрах – о том, как они пишутся, и как они звучат.
К тому же, египтяне более сговорчивы в плане цен как в магазинах, так и в такси, если их называть на арабском. Если ты знаешь язык, значит ты «местный» — живешь здесь или часто летаешь. И облапошить тебя будет не просто. У меня эта схема работала почти всегда. Вы можете либо выучить несколько цифр, либо выписать их себе на листочек. Либо просто почитать.
С написанием двузначных чисел все просто, как и обычных числах – чтобы написать «10», мы «ставим рядом» 1 и 0. С произношением – посложнее.
15 – ١٥ — хамустАшер
17 – ١٧ — сабаатОшэр
18 – ١٨ — тамантОшэр
Чтобы произнести числа 21, 22, 34 и так далее, мы «составляем» их задом наперед таким образом: 21=1+20 (1-вахед, 20 – ашэрин), добавляя посередине слог «ва»
21 – ٢١ – вАхед ва ашэрИн
34 – ٣٤ – арбА ва талатин
150 – ١٥٠ — мЭя ви хамсИн (100+50)
И так далее до бесконечности. Слово «с половиной» звучит как «унОс». 3,5 будет «телета унос».
| Добрый день | мехрабА |
| Добрый вечер | сабАк эльхрИр |
| До свидания | мЭа ас салЯма |
| Как дела? | кОли тамАм |
| Хорошо, слава Богу | тамАм, хамдюлЯ |
| Как тебя зовут? | эсмАк/эсмИк э? |
| Меня зовут Елена | Ана эсмИк Елена |
| Спасибо/Пожалуйста | шукрАн/афуАн |
| Что ты хочешь? | айз/Айза э? |
| Я хочу воды | Ана айз/айза майя |
| Я не хочу | миш айз/айза |
| Я не понимаю | Ана миш Фахма |
| Чуть-чуть (немного) | швАя-швАя |
| Окей | меш |
| Да | Айва |
| Нет | ля |
| Нет, спасибо | ля, шукрАн |
| Сколько это стоит? | бикЕм (бикЕм ди) |
| Что это такое? | Эда? |
| Давай!/Скорее!/Поехали! | Ялла |
| Остановите (автобус)! | алЕ гам |
В арабском языке, как и в русском, различается женский и мужской род. Например, обращение на ты/вы к мужчине будет «Энта», а к женщине – «Энти».
Прожив какое-то время в Египте, я поймала себя на мысли, что зачастую, даже если я не могу многое сказать, то прекрасно понимаю, о чем идет разговор. Как бы «страшно» не звучали арабские слова на первый взгляд, на деле язык запоминается довольно легко.
Шукран, дорогие читатели, что уделили внимание этой статье. Удачных путешествий!
Источник
Арабские цифры и числительные в египетском языке
Числительные в арабский язык пришли из Индии, хотя цифрами привычного нам вида (1, 2, 3 и т.д.) пользуется весь мир, при этом почему-то называя их арабскими. В отличие от слов, пишущихся «справа налево» арабские цифры пишутся наоборот — «слева направо», что является лучшим доказательством заимствованности системы счёта от чуждой арабам культуры, а заодно и выдаёт тайну истоков происхождения цивилизации «серой подрасы» из Индии. При этом весь неарабский мир продолжает упорно не замечать факт чуждости для планеты Земля самой арабской цивилизации, отличающейся не только письменностью, но также устройством общества и семьи, религией, жизненными ценностями, принципами жизни и отношением к другим народам.
Фактов хватает, об этом будет написана отдельная статья, а пока, так как мы продолжаем ездить отдыхать на Красное море, придётся учить арабские цифры и числа на арабском языке.
Числительные, арабские цифры — египетский (каирский) диалект
Арабские цифры от 1 до 10
Количественные числительные
Единица в сочетании с именем мужского рода звучит «ва’хид», в сочетании с именем женского рода — «ва’хида». Остальные количественные числительные применяются без изменений, независимо от рода.
Числительные от 11 до 19 применяются с исчисляемым именем в единственном числе, по родам не изменяются.
Десятки
Сотни
Тысячи
Множественное число для миллиона — «мильуи’нин».
Чаще говорят «этн’ийн мильуи’нин», «таля’та мильуи’нин», т.е. «два миллионов, три …». Хотя граматически правильно нужно говорить «этни’йн мильу’н».
Правила числительных
Числительные от 21 содержат связующий элемент «уау», встречается произношение «ва», «уи», «уа», «у»:
Числительные сотен:
В сложных комбинациях после второй сотни происходит перенос связующего предлога-элемента «уау», «ва», «уи», «уа» и последующего числительного единиц-десятков за пределы числительного сотен-тысяч:
355 — ту’льту ме’йя хамса ва хамси’н
2216 — альфе’йн мите’йн уау ситта’шар
4555 — арба’а тале’ф хомсуме’йя ха’мса уау хамси’н
5555 — хамс тале’ф хомсуме’йя ха’мса ва хамси’н
6890 — сит тале’ф то’му ми’йя уау тисъаи’н
Формы порядковых числительных
Дальнейшие числительные по аналогичной схеме.
В десятках женского рода окончание не меняется, изменяются только единицы:
Примечание:
Порядковое числительное «сатиса» — «шестая» может произноситься как «сатса», «тамина» «восьмая» — как «тамна», то есть происходит упущение гласного звука.
Порядковые числительные применяются в качестве вводных слов:
Для полноты обзора арабских цифр и египетских числительных назову ещё дробные:
Ну и конечно же важнейшая арабская цифра 0 — ноль — цифр, пишется как наша точка.
Создатель блога Египет web, Олег.
Видеоролик для арабских детей: Арабские цифры от 1 до 10.
Источник
§ 36. Количественные числительные أَسْمَاءُ العَدَدِ الأَصْلِيَّة
мужской род: женский род:
وَاحِدٌ один وَاحِدَةٌ одна
اِثْنَانِ два اِثْنَتَانِ две
ثَلاَثٌ три ثَلاَثَةٌ три
أَرْبَعٌ четыре أَرْبَعَةٌ четыре
خَمْسٌ пять خَمْسَةٌ пять
سِتٌّ шесть سِتَّةٌ шесть
سَبْعٌ семь سَبْعَةٌ семь
ثَمَانٍ восемь ثَمَانِيَة ٌ восемь
تِسْعٌ девять تِسْعَة ٌ девять
عَشْرٌ десять عَشَرَةٌ десять
Числительные وَاحِدٌ «один» и اِثْنَانِ «два» ( وَاحِدةٌ «одна» اِثْنَتَانِ «две») ставятся после исчисляемого и, подобно прилагательным, полностью согласуются с ним:
جَاءَ طَالِبٌ وَاحِدٌ Пришел один студент
جَاءَتْ طَالِبَةٌ وَاحِدَةٌ Пришла одна студентка
رَأَيْتُ طَالِباً وَاحِداً Я видел одного студента
رَأَيْتُ طَالِبَةً وَاحِدَةً Я видел одну студентку
أَخَذْتُ الكِتَابَ مِنْ طَالِبٍ وَاحِدٍ Я взял книгу у одного студента
أَخَذْتُ الكِتَابَ مِنْ طَالِبَةٍ وَاحِدَةٍ Я взял книгу у одной студентки
جَاءَ طَالِبَانِ اِثْنَانِ Пришли два студента
جَاءَتْ طَالِبَتَانِ اِثْنَتَانِ Пришли две студентки
رَأَيْتُ طَالِبيْنِ اِثْنَيْنِ Я видел двух студентов
رَأَيْتُ طَالِبَتَيْنِ اِثْنَتَيْنِ Я видел двух студенток
أَخَذْتُ الكِتَابَ مِنْ طَالِبَيْنِ اِثْنَيْنِ Я взял книгу у двух студентов
أَخَذْتُ الكِتَابَ مِنْ طَالِبَتَيْنِ اِثْنَتَيْنِ Я взял книгу у двух студенток
Числительные от 3 до 10 образуют со своими исчисляемыми изафетное сочетание. Они склоняются по падежам и ставятся в роде, противоположном роду исчисляемого в единственном числе, а их исчисляемое ставится во множественном числе родительного падежа неопределенного состояния:
عِنْدِي ثَلاَثََةُ كُتُبٍ У меня три книги
قَرَأْتُ ثَلاَثَةَ كُتُبٍ Я прочитал три книги
وَجَدْتُ هَذَا فِي ثَلاَثَةِ كُتُبٍ Я нашел это в трех книгах
عِنْدِي ثَلاَثُ وَرَقَاتٍ У меня три бумаги
أَخَذْتُ ثَلاَثَ وَرَقَاتٍ Я взял три бумаги
وَجَدْتُ هَذَا فِي ثَلاَثِ وَرَقَاتٍ Я нашел это в трех бумагах
Упражнения для закрепления
1) Переведите следующие словосочетания на русский язык:
رَجُلٌ وَاحِدٌ ___________________________ ثَلاَثَةُ بُيُوتٍ ____________________________
رِجْلٌ وَاحِدَةٌ __________________________ ثَلاَثُ بَنَاتٍ __________________________
جَرِيدَةٌ وَاحِدَةٌ _________________________ أَرْبَعَةُ طُلاَّبٍ __________________________
دَفْتَرَانِ اثْنَانِ __________________________ أَرْبَعُ نِسَاءٍ __________________________
بِنْتَانِ اثْنَتَانِ ___________________________ خَمْسَةُ رِجَالٍ ___________________________
خَمْسُ مَدَارِسَ _________________________ سِتَّةُ مَسَاجِدَ ___________________________
سِتُّ قَبَائِلَ ___________________________ سَبْعَةُ حُرُوفٍ ____________________________
سَبْعُ جَرَائِدَ ____________________________ ثَمَانِي طَالِبَاتٍ ___________________________
ثَمَانِيَةُ جِبَالٍ __________________________ تِسْعُ أُمَّهَاتٍ ____________________________
تِسْعَةُ آبَاءٍ ____________________________ عَشْرُ سُوَرٍ ___________________________
عَشْرُ تِلْمِيذَاتٍ _________________________ عَشَرَةُ مَفَاتِيحَ ____________________________
2 ) Переведите следующие словосочетания на арабский язык:
два дома _________________________ два класса ______________________________
два студента ______________________ два глаза _______________________________
две горы __________________________ две реки ______________________________
три мальчика _______________________ три девочки ___________________________
четыре книги ______________________ четыре газеты ___________________________
пять столов ________________________ пять слов _______________________________
шесть ручек _______________________ шесть студенток _________________________
семь учеников ______________________ семь учительниц _________________________
восемь инженеров __________________ восемь сестер ___________________________
девять братьев _____________________ девять кошек ____________________________
десять собак ________________________ десять университетов ____________________
3) Переведите предложения на русский язык:
جَاءَ رَجُلٌ وَاحِدٌ وَثَلاَثُ نِسَاءٍ
قَتَلَ حَمْزَةُ أَسَدَيْنِ اثْنَيْنِ
دَرَسَ عَلِيٌّ اللُّغَةَ العَرَبِيَّةَ فِي ثَلاَثِ جَامِعَاتٍ
زُرْتُ فِي سُورِيَا خَمْسَ مَدَارِسَ وَثَلاَثَةَ مَسَاجِدَ
تَكَلَّمْتُ أَمْسِ مَعَ ثَلاَثَةِ مُهَنْدِسِينَ وَأَرْبَعِ مُدَرِّسَاتٍ
سَمِعْتُ هَذَا الْخَبَرَ مِنْ عَشْرِ طَالِبَاتٍ
حَفِظَتْ أُخْتُكَ ثَمَانِيَ سُوَرٍ وَحَفِظَ أَخُوكَ تِسْعَ سُوَرٍ
قَرَأْتُ هَذَا الْكِتَابَ عَشْرَ سَاعَاتٍ
4) Завершите перевод предложений на арабский язык:
Мы купили один дом и два сада ___________________________________________ اِشْتَرَيْنَا
Ахмад просмотрел три книги и шесть журналов ________________________ اِطَّلَعَ أَحْمَدُ عَلَى
У моего дяди три сына и три дочери __________________________________________ لِعَمِّي
Больного посетили три студента и три учительницы ________________________ عَادَ الْمَرِيضَ
Количественные числительные от 11 до 19 (кроме 12) являются несклоняемыми по флексии (см. § 33) и огласуются фатхой без танвина в конце единиц и десяток:
мужской род: женский род:
одиннадцать أَحَدَ عَشَرَ إِحْدَى عَشْرَةَ
двенадцать اِثْنا عَشَرَ اِثْنَتَا عَشْرَةَ
тринадцать ثَلاثَةَ عَشَرَ ثَلاثَ عَشْرَةَ
четырнадцать أَرْبَعَةَ عَشَرَ أَرْبَعَ عَشْرَةَ
пятнадцать خَمْسَةَ عَشَرَ خَمْسَ عَشْرَةَ
шестнадцать سِتَّةَ عَشَرَ سِتَّ عَشْرَةَ
семнадцать سَبْعَةَ عَشَرَ سَبْعَ عَشْرَةَ
восемнадцать ثَمَانِيَةَ عَشَر َ ثَمَانِيَ عَشْرَةَ
девятнадцать تِسْعَةَ عَشَرَ تِسْعَ عَشْرَةَ
جَاءَ خَمْسَةَ عَشَرَ طَالِباً Пришли 15 студентов
رَأَيْتُ خَمْسَةَ عَشَرَ طَالِباً Я видел 15 студентов
أَخَذْتُ الكُتُبَ مِنْ خَمْسَةَ عَشَرَ طَالِباً Я взял книги у 15 студентов
جَاءَ خَمْسَ عَشْرَةَ طَالِبَةً Пришли 15 студенток
رَأَيْتُ خَمْسَ عَشْرَةَ طَالِبَةً Я видел 15 студенток
أَخَذْتُ الكُتُبَ مِنْ خَمْسَ عَشْرَةََ طَالِبَةً Я взял книги у 15 студенток
В числительных 11 и 12 и единицы, и десятки ставятся в роде, соответствующем роду исчисляемого. Единицы числительного 12 изменяются по падежам подобно имени двойственного числа, являющемуся первым членом идафы:
جَاءَ أَحَدَ عَشَرَ طَالِباً Пришли 11 студентов
جَاءَ إِحْدَى عَشْرَةَ طَالِبَة Пришли 11 студенток
رَأَيْتُ أَحَدَ عَشَرَ طَالِباً Я видел 11 студентов
رَأَيْتُ اِِحْدَى عَشْرَةَ طَالِبَةً Я видел 11 студенток
أَخَذْتُ الكُتُبَ مِنْ أَحَدَ عَشَرَ طَالِباً Я взял книги у 11 студентов
أَخَذْتُ الكُتُبَ مِنْ اِحَدَى عَشْرَةَ طَالِبَةً Я взял книги у 11 студенток
جَاءَ اِثْنَا عَشَرَ طَالِباً Пришли 12 студентов
جَاءَ اَثْنَتَا عَشْرَةَ طَالِبَة Пришли 12 студенток
رَأَيْتُ اِثْنَتَيْ عَشَرَ طَالِباً Я видел 12 студентов
رَأَيْتُ اِِثْنَتَىْ عَشْرَةَ طَالِبَةً Я видел 12 студенток
أَخَذْتُ الكُتُبَ مِنْ اِثْنَيْ عَشَرَ طَالِباً Я взял книги у 12 студентов
أَخَذْتُ الكُتُبَ مِنْ اِثْنَتَيْ عَشْرَةَ طَالِبَةً Я взял книги у 12 студенток
Упражнения для закрепления
1) Переведите следующие словосочетания на русский язык:
أَحَدَ عَشَرَ وَلَدًا ___________________
اِثْنَا عَشَرَ رَجُلاً ___________________
ثَلاَثَةَ عَشَرَ طَائِرًا ___________________
أَرْبَعَةَ عَشَرَ جُنْدِيًّا ___________________
خَمْسَةَ عَشَرَ أَسَدًا ___________________
سِتَّةَ عَشَرَ أُسْتَاذًا ___________________
سَبْعَةَ عَشَرَ كِتَابًا ___________________
ثَمَانِيَةَ عَشَرَ جَمَلاً ___________________
تِسْعَةَ عَشَرَ ذِئْبًا ___________________
إِحْدَى عَشْرَةَ بِنْتًا ___________________
اِثْنَتَا عَشْرَةَ امْرَأَةً ___________________
ثَلاَثَ عَشْرَةَ تِلْمِيذَةً ___________________
أَرْبَعَ عَشْرَةَ مُدَرِّسَةً ___________________
خَمْسَ عَشْرَةَ زَهْرَةً ___________________
سِتَّ عَشْرَةَ مُمَرِّضَةً ___________________
سَبْعَ عَشْرَةَ مَدْرَسَةً ___________________
ثَمَانِيَ عَشْرَةَ نَاقَةً ___________________
تِسْعَ عَشْرَةَ بَطَّةً ___________________
2) Переведите слова на арабский язык:
одиннадцать студентов ________________
двенадцать мужчин ____________________
тринадцать стран ______________________
четырнадцать мечетей __________________
пятнадцать домов ______________________
шестнадцать мальчиков _________________
семнадцать ослов ______________________
восемнадцать тетрадей __________________
девятнадцать братьев ___________________
одиннадцать студенток _________________
двенадцать женщин ____________________
тринадцать городов ____________________
четырнадцать школ ____________________
пятнадцать деревьев ____________________
шестнадцать девочек ___________________
семнадцать кур ________________________
восемнадцать рук ______________________
девятнадцать сестёр ____________________
3) Переведите предложения на русский язык:
حَفِظَ السُّورَةَ أَحَدَ عَشَرَ تِلْمِيذًا
قَرَأَتْ هَذَا الْكِتَابَ اِثْنَتَا عَشْرَةَ طَالِبَةً
بَاتَ فِي هَذَا الْفُنْدُقِ ثَلاَثَةَ عَشَرَ سَائِحًا
قَتَلَ الصَّائِدُ أَرْبَعَةَ عَشَرَ ذِئْبًا
سَمِعْتُ هَذَا الْقَوْلَ مِنْ خَمْسَ عَشْرَةَ مُدَرِّسَةً
كَتَبَ هَذِهِ الرِّسَالَةَ سِتَّةَ عَشَرَ رَجُلاً
اِشْتَرَكَتْ فِي الْمُبَارَاةِ سَبْعَ عَشْرَةَ بِنْتًا
أَقْرَضْتُ لِحَسَنٍ ثَمَانِيَةَ عَشَرَ دُولاَرًا
أَكَلَ الأَسَدُ تِسْعَ عَشْرَةَ شَاةً
4) Завершите перевод предложений на арабский язык:
Эту статью подготовили одиннадцать учителей أَعَدَّ هَذِهِ الْمَقَالَةَ
У Ахмада двенадцать кур и двенадцать петухов لِأَحْمَدَ
Эту суру выучили четырнадцать студентов حَفِظَ هَذِهِ السُّورَةَ
Я просмотрел сегодня пятнадцать газет اِطَّلَعْتُ الْيَوْمَ عَلَى
На столе шестнадцать книг عَلَى الْمَكْتَبِ
В этой деревне семнадцать машин فِي هَذِهِ الْقَرْيَةِ
В этом городе восемнадцать домов فِي هَذِهِ الْمَدِينَةِ
В этом упражнении девятнадцать новых слов فِي هَذَا التَّمْرِينِ كَلِمَةً جَدِيدَةً
3. Числительные, обозначающие круглые десятки (20, 30, 40, 50, 60, 70, 80, 90) имеют одну и ту же форму для обоих родов:
Эти числительные склоняются как имена целого множественного числа мужского
рода ( جَمْعُ المُذَكَّرِ السَّالِم ) (см. гл. II § 31), а их исчисляемое ставится в винительном падеже единственного числа неопределённого состояния:
جَاءَ ثَلاَثُونَ طَالِباً ( الرَّفْعُ ) Пришли тридцать студентов (именительный падеж)
أَخَذْتُ الكُتُبَ مِنْ ثَلاَثِينَ طَالِباً ( الْجَرُّ ) Я взял книги у тридцати студентов (родительный падеж)
رَأَيْتُ ثَلاثِينَ طَالِباً ( النَّصْبُ ) Я видел тридцать студентов (винительный падеж)
Единицы этих числительных (от 3 до 9) ставятся в роде, противоположном роду имени исчисляемого и склоняются по падежам:
мужской род женский род:
وَاحِدٌ وَعِشْرُونَ двадцать один وَاحِدَةٌ وَعِشْرُونَ двадцать одна
اِثْنَانِ وَعِشْرُونَ двадцать два اِثْنَتَانِ وَعِشْرُونَ двадцать две
ثَلاَثَةٌ وَعِشْرُونَ двадцать три ثَلاَثٌ وَعِشْرُونَ двадцать три
أَرْبَعَةٌ وَعِشْرُونَ двадцать четыре أَرْبَعٌ وَعِشْرُونَ двадцать четыре
خَمْسَةٌ وَعِشْرُونَ двадцать пять خَمْسٌ وَعِشْرُونَ двадцать пять
سِتَّةٌ وَعِشْرُونَ двадцать шесть سِتٌّ وَعِشْرُونَ двадцать шесть
سَبْعَةٌ وَعِشْرُونَ двадцать семь سَبْعٌ وَعِشْرُونَ двадцать семь
ثَمَانِيَةٌ وَعِشْرُونَ двадцать восемь ثَمَانٍ وَعِشْرُونَ двадцать восемь
تِسْعَةٌ وَعِشْرُونَ двадцать девять تِسْعٌ وَعِشْرُونَ двадцать девять
ثَلاَثُونَ тридцать ثَلاَثُونَ тридцать
Их исчисляемое также ставится в винительном падеже единственного числа неопределённого состояния:
جَاءَ خَمْسَةٌ وعِشْرُونَ رَجُلاً Пришли 25 мужчин
رَأَيْتُ خَمْسَةً وَعِشْرِينَ رَجُلاً Я видел 25 мужчин
أَخَذْتُ الكُتُبَ مِنْ خَمْسَةٍ وَعِشْرِينَ رَجُلاً Я взял книги у 25 мужчин
جَاءَتْ خَمْسٌ وعِشْرُونَ اِمْرأَةً Пришли 25 женщин
أَخَذْتُ الكُتُبَ مِنْ خَمْسٍ وَعِشْرِينَ اِمْرَأَةً Я взял книги у 25 женщин
رَأَيْتُ خَمْساً وَعِشْرِينَ اِمْرَأَةً Я видел 25 женщин
Упражнения для закрепления
1) Переведите следующие словосочетания на русский язык:
عِشْرُونَ مُسَدَّسًا ________________________
ثَلاَثُونَ لاَعِبًا ________________________
أَرْبَعُونَ سَيْفًا ________________________
خَمْسُونَ جُنْدِيًّا ________________________
سِتُّونَ أَسَدًا ________________________
سَبْعُونَ أُسْتَاذًا ________________________
ثَمَانُونَ رُمْحًا ________________________
تِسْعُونَ جَمَلاً ________________________
عِشْرُونَ وَرَقَةً ________________________
ثَلاَثُونَ دَبَّابَةً ________________________
أَرْبَعُونَ امْرَأَةً ________________________
خَمْسُونَ تِلْمِيذَةً ________________________
سِتُّونَ مُدَرِّسَةً ________________________
سَبْعُونَ زَهْرَةً ________________________
ثَمَانُونَ خَرْطُوشَةً ________________________
تِسْعُونَ مَدِينَةً ________________________
2) Переведите следующие словосочетания на арабский язык:
двадцать один студент _________________
тридцать два мужчины __________________
сорок три страны ______________________
пятьдесят четыре мечети _____________
шестьдесят пять домов ________________
семьдесят шесть мальчиков ____________
восемьдесят семь ослов _________________
девяноста восемь тетрадей _____________
двадцать одна студентка ________________
тридцать две женщины _________________
сорок три города ____________________
пятьдесят четыре школы _______________
шестьдесят пять деревьев_______________
семдесят шесть девочек ________________
восемьдесят семь кур ___________________
девяноста восемь рук ___________________
3) Переведите предложения на русский язык:
حَفِظَ الشِّعْرَ عِشْرُونَ تِلْمِيذًا
قَرَأَتْ هَذَا الْحَدِيثَ اِثْنَتَانِ وَعِشْرُونَ طَالِبَةً
أَقَامَ فِي هَذَا الْفُنْدُقِ ثَلاَثَةٌ وَثَلاَثُونَ سَائِحًا
قَتَلَ الصَّائِدُ عِشْرِينَ أَرْنَبًا
سَمِعْتُ هَذَا الْخَبَرَ مِنْ خَمْسَةٍ وَأَرْبَعِينَ رَجُلاً
رَأَى هَذِهِ الرِّسَالَةَ سِتَّةٌ وَخَمْسُونَ شَخْصاً
اِشْتَرَكَتْ فِي الْمُسَابَقَةِ سَبْعٌ وَسَبْعُونَ فَتَاةً
أَعْطَيْتُ حَسَنًا ثَمَانِيَةً وَثَمَانِينَ دُولاَرًا
أَكَلَ الثَّعْلَبُ تِسْعًا وَتِسْعِينَ دَجَاجَةً
4) Завершите перевод предложений на арабский язык:
Эту проект подготовил двадцать один ученый أَعَدَّ هَذَا الْمَشْرُوعَ
У Ахмада тридцать две курицы и сорок три петуха لِأَحْمَدَ
Этот хадис выучили пятьдесят четыре студента حَفِظَ هَذِهِ الْحَدِيثَ
Я просмотрел сегодня шестьдесят пять газет اِطَّلَعْتُ الْيَوْمَ عَلَى
На столе семьдесят шесть рублей عَلَى الْمَكْتَبِ
В этой деревне восемьдесят семь машин فِي هَذِهِ الْقَرْيَةِ
В этом городе девяносто восемь мечетей فِي هَذِهِ الْمَدِينَةِ
В этом тексте девяносто девять новых слов فِي هَذَا الْمَتْنِ كَلِمَةً جَدِيدَةً
مِئَةُ رَجُلٍ وَمِئَةُ امْرَأَةٍ 100 мужчин и 100 женщин
مِئَتَا رَجُلٍ وَ مِئَتَا امْرَأَةٍ 200 мужчин и 200 женщин
ثَلاَثُمِئَةِ رَجُلٍ وَ ثَلاَثُمِئَةِ امْرَأَةٍ 300 мужчин и 300 женщин
أَرْبَعُمِئَةِ رَجُلٍ وَ أَرْبَعُمِئَةِ امْرَأَةٍ 400 мужчин и 400 женщин
خَمْسُمِئَةِ رَجُلٍ وَ خَمْسُمِئَةِ امْرَأَةٍ 500 мужчин и 500 женщин
سِتُّمِئَةِ رَجُلٍ وَ سِتُّمِئَةِ امْرَأَةٍ 600 мужчин и 600 женщин
سَبْعُمِئَةِ رَجُل وَ سَبْعُمِئَةِ امْرَأَةٍ ٍ 700 мужчин и 700 женщин
ثَمَانِيمِئَةِ رَجُلٍ وَ ثَمَانِيمِئَةِ امْرَأَةٍ 800 мужчин и 800 женщин
تِسْعُمِئَةِ رَجُلٍ وَ تِسْعُمِئَةِ امْرَأَةٍ 900 мужчин и 900 женщин
أَلْفُ رَجُلٍ وَ أَلْفُ امْرَأَةٍ 1000 мужчин и 1000 женщин
أَلْفَا رَجُلٍ وَ أَلْفَا امْرَأَةٍ 2000 мужчин и 2000 женщин
ثَلاَثَةُ آلاَفِ رَجُلٍ وَ ثَلاَثَةُ آلاَفِ امْرَأَةٍ 3000 мужчин и 3000 женщин
أَرْبَعَةُ آلاَفِ رَجُلٍ وَ أَرْبَعَةُ آلاَفِ اِمْرَأَةٍ 4000 мужчин и 4000 женщин
خَمْسَةُ آلاَفِ رَجُلِ وَ خَمْسَةُ آلاَفِ اِمْرَأَةٍ 5000 мужчин и 5000 женщин
В сложных числительных после 100 имя исчисляемого предмета ставится в соответствии с последним произносимым числительным. Числительные произносятся в порядке убывания, однако единицы опережают десятки. Например:
أَلْفٌ وَتِسْعُمِئَةٍ وَخَمْسَةٌ وَأَرْبَعُونَ رُوبْلاً 1.945 рублей
أَلْفَانِ وَخَمْسُمِئَةٍ وَسِتُّونَ صَفْحَةٍ 2.560 страниц
أَرْبَعَةُ آلاَفٍ ومِئَةٌ وَسَبْعَةُ كُتُبٍ 4.107 книг
خَمْسَةُ آلاَفٍ وَخَمْسُمِئَةٍ وَأَرْبَعٌ وَثَلاَثُونَ طَالِبَةً 5.534 студенток
مِلْيُونٌ وَمِئَتَانِ وَثَلاَثَةُ رِجَالٍ 1.000.203 человек
مِلْيَارٌ وَثَلاَثَةُ مَلاَيِينَ وَتِسْعُمِئَةِ أَلْفٍ وَثَمَانِيمِئَةٍ وَسِتَّةٌ وَسَبْعُونَ دُولاَرًا 1. 003.900.876 долларов
Упражнения для закрепления
1) Переведите следующие словосочетания:
مِئَةُ دَفْتَرٍ _____________________ مِئَةُ وَرَقَةٍ _____________________
مِئَتَا مُسَدَّسٍ _____________________ مِئَتَا دَبَّابَةٍ _____________________
ثَلاَثُمِئَةِ عُصْفُورٍ _____________________ ثَلاَثُمِئَةِ شَجَرَةٍ _____________________
أَرْبَعُمِئَة ِذِئْبٍ _____________________ أَرْبَعُمِئَةِ دَجَاجَةٍ _____________________
خَمْسُمِئَةِ دِيكٍ _____________________ خَمْسُمِئَةِ بَقَرَةٍ _____________________
سِتُّمِئَةِ تِلْفَازٍ _____________________ سِتُّمِئَةِ سَلَّةٍ _____________________
سَبْعُمِئَةِ حَدِيثٍ _____________________ سَبْعُمِئَةِ آيَةٍ _____________________
ثَمَانِيمِئَةِ دَلْوٍ _____________________ ثَمَانِيمِئَةِ سُنْبُلَةٍ _____________________
تِسْعُمِئَةِ رِيَالٍ _____________________ تِسْعُمِئَةِ طَائِرَةٍ _____________________
أَلْفُ خَرُوفٍ _____________________ أَلْفُ ثَوْرٍ _____________________
أَلْفَا جُنْدِيٍّ _____________________ أَلْفَا سَمَكَةٍ _____________________
أَرْبَعَةُ آلاَفِ أَسِيرٍ ________________ ثَلاَثَةُ آلاَفِ طَبِيبَةٍ _____________________
تِسْعَةُ آلاَفِ صِينِيٍّ ________________ خَمْسَةُ آلاَفِ أَمْرِيكِيٍّ _____________________
مِلْيُونُ مَرِيضٍ ________________ مِلْيُونُ خِرِّيجٍ _____________________
2) Переведите следующие предложения:
عَمَلٌ وَاحِدٌ خَيْرٌ مِنْ مِئَةِ كَلِمَةٍ
تَكَلَّمْتُ الْيَوْمَ مَعَ مِئَتَيْ عَامِلٍ
اِشْتَرَتْ زَوْجَتِي هَذَا الْقَمِيصَ بِثَلاَثِمِئَةِ رُوبْلٍ
كَانَ عَدَدُ الْجَيْشِ سِتَّمِئَةٍ وَأَرْبَعِينَ
وُلِدَتْ أُمِّي سَنَةَ أَلْفٍ وَتِسْعِمِئَةٍ وَخَمْسِينَ
ثَمَنُ هَذِهِ السَّيَّارَةِ عَشَرَةُ آلاَفِ دُولاَرٍ
عَدَدُ سُكَّانِ رُوسِيَا مِئَةٌ وَثَمَانِيَةٌ وَ أَرْبَعُونَ مِلْيُونَ نَفَرٍ أَوْ أَقَلُّ مِنْ ذَلِكَ
عَدَدُ الْمُسْلِمِينَ فِي الْعَالَمِ مِلْيَارٌ وَاحِدٌ وَثَلاَثُمِئَةِ مِلْيُونٍ تَقْرِيبًا
فِي السَّنَةِ الْوَاحِدَةِ ثَلاَثُمِئَةٍ وَخَمْسَةٌ وَسِتُّونَ يَوْمًا
أَكْثَرُ مِنْ أَرْبَعِينَ مِلْيُونَ نَفَرٍ ذَهَبُوا ضَحِيَّةً فِي الْحَرْبِ الْعَالَمِيَّةِ الثَّانِيَّةِ
الْمَسَافَةُ بَيْنَ الأَرْضِ وَالْقَمَرِ تُسَاوِي ثَلاَثَمِئَةٍ وَأَرْبَعَةً وَثَمَانِينَ أَلْفًا وَأَرْبَعَمِئَةِ كِيلُومِتْرٍ
سُرْعَةُ دَوَرَانِ الأَرْضِ حَوْلَ الشَّمْسِ ثَلاَثُونَ كِيلُومِتْرًا فِي الثَّانِيَةِ
كَسَرَ مُحَمَّدٌ (ص) يَوْمَ فَتْحِ مَكَّةَ ثَلاَثَمِئَةٍ وَسِتِّينَ صَنَمًا أَوْ أَكْثَرَ
عَدَدُ الصِّينِيِّينَ يَزيدُ عَلَى مِلْيَارٍ وَأَرْبَعِينَ مِلْيُونًا
3) Скажите по-арабски:
100 собак ______________________________
200 куриц _____________________________
300 мечей _____________________________
400 слов ______________________________
500 домов _____________________________
600 учениц ____________________________
700 учителей __________________________
800 городов ___________________________
900 мечетей ___________________________
1000 самолетов _________________________
2000 деревьев __________________________
3000 арабов ____________________________
4) Переведите предложения на арабский язык:
Я родилась в 1984 году
Вес этого быка 246 килограммов
В этой книге 874 страницы
Численность японцев превышает 120 миллионов
Численность китайцев в России 10 миллионов
Расстояние от моего дома до мечети 135 метров
Источник
Арабские цифры как пишутся и читаются
Когда я впервые попала в Египет, мое внимание привлекли номера на машинах, обозначенные какими-то странными цифрами.
Несмотря на то, что в большей части земного шара люди пользуются арабским десятичным исчислением и арабскими цифрами, в Египте используются индийские цифры. Уж не знаю, каким образом вышло это недоразумение, но советы типа запоминайте номер такси, когда садитесь в него, абсолютно бесполезны, если Вы не знаете этих самых арабско-индийских цифр и арабских букв.

А вот с произношением чисел все наоборот. Особенно с числами от 21 до 99. Они не говорят, как мы, двадцать один. Араб скажет: один и два десятка, 35 будет – пять и три десятка и т.д. То есть, если Вы захотите сказать 5 689 374, то в дословном переводе с арабского это будет звучать: пять миллионов, шесть сотен, девять и восемьдесят тысяч, три сотни, четыре и семьдесят. Нужно просто привыкнуть к такой перестановке чисел. Кстати, сдачу при оплате чего-либо дают от меньшего к большему. Например, с 200-фунтовой купюры ваша сдача ожидается 173 фунта. В этом случае вы получите сначала 3 фунта, потом 20, потом 50 и потом 100.
Запомнить арабские числа меня побудила вполне прозаическая ситуация. Однажды я приехала в Хургаду и остановилась не в гостинице, а в съемной квартире. Около дома был магазинчик, где можно было купить все необходимое. Но цены, естественно, были указаны по-арабски. Очень неприятно ощущать себя неграмотной. Ведь хозяин мог озвучить мне совершенно другую цену, нежели ту, что стояла на ценнике. А разве трудно запомнить десять цифр? В тот же приезд мы отправились в путешествие по Нилу, жили в египетских семьях, и арабские дети помогли мне запомнить цифры.
Также, как они мне объясняли, попробую объяснить вам их и я.
С единицей всё просто. Это такая же палочка, как у нас. Слово «вахед» я запоминала через слово «выход». Ведь арабы очень невнимательно относятся к гласным звукам. Поэтому можно себе позволить вот такую вольность. По арабски бы всё равно записали ВХД.
К единице добавляется маленький хвостик и получается двойка. Он может быть закругленным, а может быть прямым.
Если к закругленному хвостику двойки добавить ещё один хвостик, то получится тройка.
Если хвостики от двойки станут один на другой, то получится четвёрка. А само слово легко запомнить: у арбы 4 колеса.
То, что похоже на наш ноль, это пятерка. Словом хамса также называется вот этот амулет. Если Вы присмотритесь к нему повнимательнее, то увидите маленьких рыбок. Скорее всего это Камса (чтобы легче было запомнить).
Слово ситта мне напоминает сито. Пишется шестёрка почти также как двойка с прямым хвостиком, но смотрит в другую сторону.
Семёрка пишется так же, как римская пятёрка. Для тех, кто понимает английский, вероятно поможет ассоциация «seven see in heaven». Моя ассоциация была сАбаа-ка.
Причём здесь Аня? Восьмёрка очень похожа на семёрку, только перевёрнутую и называется там-анья.
Девятка такая же как у нас. Я запоминала ее через «из необТЕССАнного бревна можно девять досок наТЕССАть ».
Ноль это просто точка. Конец счёту. А само слово «сфр» очень напоминает наше слово «цифра». Скорее всего оно пришло к нам из арабского.
Ашера напомнило мне название самой дорогой кошачьей породы в мире. А Вам?
Это короткое видео с детской песенкой-считалкой поможет Вам легко запомнить все цифры и научиться их правильно произносить.
Проверьте себя, всё ли Вы запомнили и поняли правильно? Какие номера телефонов указаны на вывеске?
Вот видите, запомнить цифры совсем не сложно. Повторяя за носителями Вы научились правильному произношению. Научиться читать тоже можно достаточно просто, если всё объяснено на примере русского языка и запоминать с помощью ассоциаций – так же как объясняют детям.
Источник статьи: http://www.speakland.net/kak-legko-i-prosto-zapomnit-arabskie-tsifry.html
Арабские цифры и числительные в египетском языке
Числительные в арабский язык пришли из Индии, хотя цифрами привычного нам вида (1, 2, 3 и т.д.) пользуется весь мир, при этом почему-то называя их арабскими. В отличие от слов, пишущихся «справа налево» арабские цифры пишутся наоборот — «слева направо», что является лучшим доказательством заимствованности системы счёта от чуждой арабам культуры, а заодно и выдаёт тайну истоков происхождения цивилизации «серой подрасы» из Индии. При этом весь неарабский мир продолжает упорно не замечать факт чуждости для планеты Земля самой арабской цивилизации, отличающейся не только письменностью, но также устройством общества и семьи, религией, жизненными ценностями, принципами жизни и отношением к другим народам.
Фактов хватает, об этом будет написана отдельная статья, а пока, так как мы продолжаем ездить отдыхать на Красное море, придётся учить арабские цифры и числа на арабском языке.
Числительные, арабские цифры — египетский (каирский) диалект
Арабские цифры от 1 до 10
В египетском языке существуют количественные и порядковые числительные. Количественные числительные свободно употребляются вместо порядковых. Существуют некоторые диалектические вариации произношения, не имеющие принципиального значения и понятные всем арабам (примерно как разница между произношениями украинского и русского языков: одын, один, одыныця, единица) . Для полного раскрытия темы здесь указаны и вариации.
Знак «’» обозначает ударение.
Количественные числительные
- 1 — ва’хид, уа’хид
- 2 — итни’н, этни’н, этни’йн
- 3 — тале’та, таля’та
- 4 — арба’а
- 5 — ха’мса
- 6 — сы’тта, си’тта
- 7 — са’баа
- 8 — тама’ния, тамэ’ния
- 9 — ты’сса, ти’съа
- 10 — а’шара, а’шэра, а’шра
Единица в сочетании с именем мужского рода звучит «ва’хид», в сочетании с именем женского рода — «ва’хида». Остальные количественные числительные применяются без изменений, независимо от рода.
Числительные от 11 до 19 применяются с исчисляемым именем в единственном числе, по родам не изменяются.
- 11 — хэда’шар, хада’шр, хидаа’шар
- 12 — итна’шар, итна’шр, итнаа’шар
- 13 — талята’шар, талята’шр, тляттаа’шар
- 14 — арбаата’шар, арбаата’шр
- 15 — хамста’шар, хамаста’шр, хамастаа’шар
- 16 — ситта’шар, ситта’шр, ситтаа’шар
- 17 — сабаата’шар, сабаата’шр, сабаата’шар
- 18 — таманта’шар, таманта’шр, тмантаа’шар
- 19 — тиссата’шар, тисъата’шр, тэсаата’шар, тсаата’шар
Десятки
- 20 — ашри’н, эшри’н
- 30 — таляти’н, талети’н
- 40 — арбаи’н
- 50 — хамси’н
- 60 — сытти’н, ситти’н
- 70 — сабаи’н
- 80 — тамэни’н, тамани’н
- 90 — тиссаи’н, тисъаи’н
Сотни
- 100 — ми’йя, ме’йа
- 200 — митти’н, мите’йн
- 300 — ту’льта ми’йя, ту’льта ме’йа
- 400 — арба’ ми’йя, арба’ ме’йа, урба’ ми’йя
- 500 — хо’мсу ми’йя, хо’мсу ме’йа
- 600 — си’та ми’йя, си’та ме’йа
- 700 — са’баа ми’йя, са’баа ме’йа
- 800 — то’му ми’йя, то’мму ме’йа
- 900 — ты’сса ми’йя, ти’съа ме’йа
Тысячи
- 1 000 — альф
- 2 000 — альфе’йн, альфе’йин, итне’йн альф
- 3 000 — тале’т тале’ф, таля’т тале’ф, таляталя’ф
- 4 000 — арба’а тале’ф, арбааталя’ф
- 5 000 — ха’мса тале’ф, хамс тале’ф, хама’сталяф
- 6 000 — сит тале’ф, си’тталяф
- 7 000 — са’баа тале’ф, са’бааталяф
- 8 000 — тама’н тале’ф, тама’нияталяф
- 9 000 — ты’сса тале’ф, та’съа тале’ф, ти’сааталяф
- 10 000 — ашр тале’ф, а’шараталяф
- 11 000 — хэда’шр альф, хада’шр альф
- 12 000 — итна’шр альф
- 13 000 — талята’шр альф
- 14 000 — арбата’шр альф
- 15 000 — хамаста’шр альф, хамста’шр альф
- 16 000 — ситта’шр альф
- 17 000 — сабата’шр альф
- 18 000 — таманта’шр альф
- 19 000 — тыссата’шр альф, тисъата’шр альф
- 20 000 — ашри’ин альф, а’шрин альф
- 30 000 — таляти’н альф, т’лятин альф
- 40 000 — арбаи’н альф
- 50 000 — хамси’н альф
- 60 000 — ситти’н альф
- 70 000 — сабаи’н альф
- 80 000 — тамани’н альф
- 90 000 — тыссаи’н альф, тисъаи’н альф
- 100 000 — мит альф
- 200 000 — мите’йн альф
- 300 000 — ту’льту мит альф
- 400 000 — ро’бу мит альф
- 500 000 — хо’мсу мит альф
- 600 000 — си’ту мит альф
- 700 000 — со’бу мит альф
- 800 000 — то’му мит альф
- 900 000 — ты’сса мит альф, ти’съа мит альф
- 1 000 000 — мильу’н, мильё’н
- 2 000 000 — итни’ин мильу’н
- …
- 1 000 000 000 — милиа’р
Множественное число для миллиона — «мильуи’нин».
Чаще говорят «этн’ийн мильуи’нин», «таля’та мильуи’нин», т.е. «два миллионов, три …». Хотя граматически правильно нужно говорить «этни’йн мильу’н».
Правила числительных
Числительные от 21 содержат связующий элемент «уау», встречается произношение «ва», «уи», «уа», «у»:
- 21 — ва’хид ва ашри’н, уа’хид уау (уи) ашри’н, ва’хед у ашри’н
- 22 — этни’н ва ашри’н, этни’йн уау (уи) ашри’н, итнэ’йн у ашри’н
- 23 — тале’та ва ашри’н, таля’та уау (уи) ашри’н
- 24 — арба’ ва ашри’н, арба’ уи (уи) ашри’н
- 25 — ха’мса ва ашри’н, ха’мса уау (уи) ашри’н
- 26 — сы’тта ва ашри’н, си’тта уау (уи) ашри’н
- 27 — са’баа ва ашри’н, са’баа уау (уи) ашри’н
- 28 — тамэ’ния ва ашри’н, тама’ния уау (уи) ашрин
- 29 — ты’сса ва ашри’н, ти’съа уау (уи) ашри’н
- 30 — талети’н, таляти’н
- 31 — ва’хид ва таляти’н, уахид уау (уи) талети’н
- 32 — этни’н ва таляти’н, этнийн уау (уи) талети’н
- …
Числительные сотен:
- 101 — ми’йя у ва’хид, ми’йя ва ва’хид, ме’йя уи уа’хид
- 102 — ми’йя ва итни’н, ме’йя уи этни’йн
- 103 — ми’йя ва тале’та, ме’йя уи таля’та
- 104 — ми’йя ва арба’а, ме’йя уи арба’а
- 105 — ми’йя ва ха’мса, ме’йя уи ха’мса
- 106 — ми’йя ва сы’тта, ме’йя уи си’тта
- 107 — ми’йя ва са’баа, ме’йя уи са’баа
- 108 — ми’йя ва тамэ’ния, ме’йя уи тама’ния
- 109 — ми’йя ва ты’сса, ме’йя уи ти’съа
- 110 — ми’йя ва а’шэра, мейя уи ашра
- 120 — ми’йя ва эшри’н, мейя уи ашрин
- 130 — ми’йя ва талети’н, мейя уи талятин
- 140 — ми’йя ва арбаи’н, мейя уи арбаи’н
- 150 — ми’йя ва хамси’н, мейя уи хамсин
- 160 — ми’йя ва сытти’н, мейя уи ситтин
- 170 — ми’йя ва сабаи’н, мейя уи сабаи’н
- 180 — ми’йя ва тамэни’н, мейя уи тамани’н
- 190 — ми’йя ва тиссаи’н, мейя уи тисъаи’н
- 200 — митти’н, мите’йн
- 201 — митти’н ва ва’хид, мите’йн уи уахид
- 202 — митти’н ва итни’н, мите’йн уи этни’йн
- …
В сложных комбинациях после второй сотни происходит перенос связующего предлога-элемента «уау», «ва», «уи», «уа» и последующего числительного единиц-десятков за пределы числительного сотен-тысяч:
355 — ту’льту ме’йя хамса ва хамси’н
2216 — альфе’йн мите’йн уау ситта’шар
4555 — арба’а тале’ф хомсуме’йя ха’мса уау хамси’н
5555 — хамс тале’ф хомсуме’йя ха’мса ва хамси’н
6890 — сит тале’ф то’му ми’йя уау тисъаи’н
Формы порядковых числительных
- первый — авва’ль, ауа’ль
- первая — у’ля
- второй — та’ни, тэ’ни
- вторая — та’ния
- третий — та’лит
- третья — та’льта
- четвертый — ра’би
- четвертая — ра’биа
- пятый — ха’мис
- пятая — ха’миса
- шестой — са’тис, са’дис
- шестая — са’тса, са’дса, са’диса
- седьмой — са’би
- седьмая — са’биа
- восьмой — та’мин
- восьмая — та’мина, та’мна
- девятый — та’съи, та’си
- девятая — та’съиа, та’сиа
- десятый — а’шир
- десятая — а’шира
- 11-й — ха’ди ашир
- 11-я — ха’дия а’шира
- 12-й — та’ни а’шир
- 12-я — та’ния а’шира
- 13-й — та’лят а’шир, та’лит а’шир
- 13-я — та’лята а’шира, та’лита а’шира
- 14-й — ра’би а’шир
- 14-я — ра’биа а’шира
- 15-й — ха’мис а’шир
- 15-я — ха’миса а’шира
- 16-й — са’тис а’шир, са’дис а’шир
- 16-я — са’тиса а’шира, са’диса а’шира
- 17-й — са’би а’шир
- 17-я — са’биа а’шира
- 18-й — та’мин а’шир
- 18-я — та’мина а’шира
- 19-й — та’съи а’шир, та’си а’шир
- 19-я — та’съиа а’шира, та’сиа а’шира
- …
Дальнейшие числительные по аналогичной схеме.
В десятках женского рода окончание не меняется, изменяются только единицы:
- 21-й — ха’ди уи ашри’н, та’ни у ашри’н
- 21-я — ха’дия уи ашри’н, та’ния у ашри’н
- 22-й — та’ни уи ашри’н, та’ни у ашри’н
- 22-я — та’ниа уи ашри’н, та’ния у ашри’н
- 23-й — та’лит уи ашри’н, та’лит у ашри’н
- 23-я — та’лита уи ашри’н, та’лита у ашри’н
- …
Примечание:
Порядковое числительное «сатиса» — «шестая» может произноситься как «сатса», «тамина» «восьмая» — как «тамна», то есть происходит упущение гласного звука.
Порядковые числительные применяются в качестве вводных слов:
- во-первых — а’вваллян, а’уаллян
- во-вторых — тани’ян
- в-третьих — тали’тян
- в-четвертых — раби’ан
- в-пятых — хамси’ан
- в-шестых — сади’сан, сати’сан
- в-седьмых — саби’ан
- в–восьмых — тами’нан
- в девятых — таси’ан, тисъан
- в-десятых — аши’ран
- в-одиннадцатых — ха’дия аши’ран
Для полноты обзора арабских цифр и египетских числительных назову ещё дробные:
Ну и конечно же важнейшая арабская цифра 0 — ноль — цифр, пишется как наша точка.
Видеоролик для арабских детей: Арабские цифры от 1 до 10.
Источник статьи: http://egipet-web.ru/egipet/arabskij_yazyk/arabskie_cifry_chislitelnye.html
Один мой приятель после посещения Египта передал мне свой диалог с другим российским туристом во время экскурсии к пирамидам. Люди, бывавшие там, знают как это выглядит: арабы, бегающие со свистками и прогоняющие любителей полазить по пирамидам. После непродолжительного созерцания этого цирка попутчик спросил его «Ты веришь, что ЭТИ могли построить такое? Я — нет». Приятель с ним согласился.
Тем не менее каждый раз, когда я позволяю себе нелицеприятные высказывания об арабах, находится человек, который напоминает мне, что позиционную систему исчисления, которой мы пользуемся, придумали арабы и именно поэтому цифры называются «арабскими», в отличие от, например, от римских.
Однако арабскими эти числа назвали европейцы, которые позаимствовали их у арабов.
В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении индо-арабских цифр. (источник)
А вот на арабском они называются «ар ракм аль хинди», что означает «индийский счёт». Индийскими называют их и в Иране: «шумаре ха йе хенди» на фарси означает «индийские цифры». Мы не можем знать наверняка, построили ли арабы пирамиды, но то, что они не имеют никакого отношения к созданию так называемых «арабских» чисел — это достоверный и общепризнанный факт.
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел. Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму. Индийскую систему записи широко популяризировал учёный Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». (источник)
Но представим, что у нас нет доступа к интернету и книгам или мы не верим написанному в википедии. О том, что арабы просто воспользовались результатом, можно легко догадаться даже не зная про «индийские цифры». Как известно, арабы пишут справа налево. Но при этом написание цифр происходит как у большинства белых народов, слева направо. Поэтому, если при письме арабу надо написать число, ему приходится отступать влево, прикидывая сколько места оно займёт, вписывать число слева направо и потом возвращаться обратно к письму справа налево. Возьмите лист бумаги и попытайтесь писать текст справа налево, а цифры — как обычно, и вы поймёте, что имеется в виду. Если писать приходится быстро, то можно второпях недооценить необходимое для числа место, и тогда оно будет сплющенное к концу.
Надпись по-арабски «Получена сумма в размере 25976000 реалов». Последние три нуля не уместились в отступ и их пришлось дописывать мелким шрифтом сверху.
Более образованный оппонент сразу скажет, что мол достижение арабов не столько в создании системы позиционного исчисления, сколько в создании алгебры, прародителем которой считают выдающегося арабского (об этом чуть ниже) математика Аль-Хорезми. Cоздателем алгебры его считают конечно же не за «арабские» числа, а за упомянутый выше труд, книгу «Китаб аль-джебр ва-ль-мукабала». Слово «аль-джебр» в названии означает «перенос», а слово «ва-ль-мукбала» означает «приведение». Перенос членов и приведение подобных — это одни из основных действий при решении уравнений. Кстати, слово «алгоритм» происходит как раз от имени Аль-Хорезми — латинский перевод его книги начинался словами «Dixit Algorizmi» (сказал Алгоризми).
Мухаммад Аль-Хорезми, (предположительно) персидский математик, трудившийся под арабской оккупацией. Реального изображения конечно же не сохранилось и автор по какой-то причине решил нарисовать учёному арабский клювообразный нос. (фото отсюда)
Википедия сообщает нам, что Аль-Хорезми ввёл некую классификацию для линейных и квадратных уравнений и описал правила их решения. Методы решения квадратных уравнений — это вне всякого сомнения достижение для того времени. Но только они были известны уже до него
Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.); Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду (источник)
Как можно понять из имени, Брахмагупта принадлежал к индийской касте брахманов (то есть был арийцем, а не индусом; подробнее тут и тут ).
«Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы», или «Пересмотр системы Брахмы») — самый известный труд Брахмагупты, посвящённый математике и астрономии. Трактат написан стихами и содержит только результаты без доказательств. Труд состоит из 25 глав (в других источниках говорится о 24 главах и приложении с таблицами). 18-я глава, «Распылитель», имеет прямое отношение к алгебре, но поскольку такого термина ещё не существовало, названа по первой задаче, рассматриваемой в главе. (источник)
Может быть Аль-Хорезми не был знаком с трудами Брахмагупты и переоткрыл способы решения квадратных уравнений?
Во второй половине VIII века, когда багдадский халиф из династии Аббасидов Абу-ль-Аббас Абд-Аллах аль-Мамун (712—775) был с посольством в Индии, пригласил в Багдад учёного из Удджайна по имени Канках, который преподавал индийскую систему астрономии на основе «Брахма-спхута-сиддханта». Халиф заказал письменный перевод книги на арабский язык, который был осуществлён математиком и философом Ибрахимом аль-Фазари в 771 году. Перевод, выполненный в виде таблиц — зиджа — с необходимыми пояснениями и рекомендациями, получил название «Большой Синдхинд». Известно, что этой работой пользовался ал-Хорезми для написания своих трудов по астрономии («Зидж ал-Хорезми») и арифметике («Книга об индийском счёте»). (источник)
Как видим, Аль-Хорезми был хорошо знаком с книгой Брахмагупты. Да, он был несомненно крупным учёным своего времени, но никак не основоположником алгебры. И если бы европейская математика получала знания напрямую из Индии, а не через Багдад, то алгебра сейчас называлась бы какой-нибудь «брахмаспхутой».
Скорее всего не был Аль-Хорезми и арабом. Почему? Помните, мы упоминали о том, что в арабской системе письма (справа налево) запись цифр слева направо выглядит весьма неестественно? Неужели крупный математик своего времени не мог догадаться, что можно писать цифры и справа налево? Наверняка мог. Даже не с целью скрыть факт заимствования, а просто из соображений удобства. Но не сделал. Почему? Вполне возможно намеренно, чтобы оставить очевидным факт того, что это чужая система, не арабская. Это как послание из глубины веков, мол смотрите люди, арабы не имеют никакого отношения к числам. Нашу догадку частично подтверждает википедия
Сведений о жизни учёного сохранилось крайне мало. Родился предположительно в Хиве в 783 году. В некоторых источниках аль-Хорезми называют «аль-маджуси», то есть маг, из этого делается вывод, что он происходил из рода зороастрийских жрецов, позже принявших ислам. (источник)
Зороастризм, который упоминает википедия, — это не этническая принадлежность, а религиозная. Понятно, что если семья Аль-Хорезми исповедовала зороастризм, то арабом он быть никак не мог. Но кем тогда? Зороастризм исповедовали в основном персы, то есть скорее всего он был персом.
Ещё более искушённый оппонент возможно скажет, что мол выше упоминалось, что багдадский халиф аль-Мамун заказал перевод книги Брахмагупты, а значит поддерживал развитие науки. Чтобы у читателя не осталось ложных ощущений на этот счёт, посмотрим на историю Хорезма, родины Аль-Хорезми.
В 712 году происходит завоевание Хорезма арабским полководцем Кутейбой ибн Муслимом, учинившим жестокую расправу над хорезмийской аристократией. Особенно жестокие репрессии Кутейба обрушил на учёных Хорезма. Как пишет в «Хрониках минувших поколений» аль-Бируни, «и всеми способами рассеял и уничтожил Кутейба всех, кто знал письменность хорезмийцев, кто хранил их предания, всех учёных, что были среди них, так что покрылось всё это мраком и нет истинных знаний о том, что было известно из их истории во время пришествия к ним ислама». (источник)
Вот что представляло собой нашествие арабов на просвещенный мир — вырезать всех учёных, а для нескольких оставшихся построить библиотеку в Багдаде.
Аль-Хорезми родился предположительно в 783 году, то есть спустя примерно 60 лет после прихода арабов. Представьте, что вашу родину захватило племя кочевников и ваши деды вечерами рассказывают истории, как захватчики вырезали ваших родственников. Видимо тихо ненавидел Аль-Хорезми мусульманских оккупантов, вот и оставил направление записи чисел как у индусов. Мол пусть арабские животные хоть так помучаются, записывая тексты то справа налево, то слева направо.
Что имеем в сухом остатке? Арабские цифры — вовсе не арабские, а индийские, а гордость арабского мира, якобы основоположник алгебры математик Аль-Хорезми, алгебру не создавал и скорее всего даже не был арабом.

↓ СОДЕРЖАНИЕ СТАТЬИ: ↓
- Цифры от 1 до 10 на арабском языке
- Количественные числительные от 11 до 19
- Числительные круглых десятков
- Числительные круглых сотен
- Числительные круглых тысяч
- Числительные круглых десятков тысяч
- Числительные круглых сотен тысяч
- Египетский фунт — названия бумажных денег и монет
Слова в арабском языке пишутся справа налево, а вот числа — как и привычно нам — слева направо.
Цифры от 1 до 10 на арабском языке
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| один | وَاحِد | ١ | уахид |
| два | اثْنَان | ٢ | итнин |
| три | ثَلاثَة | ٣ | талята |
| четыре | أَرْبَعَة | ٤ | эрба |
| пять | خَمْسَة | ٥ | хэмса |
| шесть | سِتَّة | ٦ | ситта |
| семь | سَبْعة | ٧ | сааба |
| восемь | ثَمانِيَة | ٨ | самания |
| девять | تِسْعَة | ٩ | тыса |
| десять | عَشَرَة | ١٠ | ашара |
Количественные числительные от 11 до 19
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| одиннадцать | أَحَدَ عَشَرَ | ١١ | ахда ашер |
| двенадцать | اِثْنا عَشَرَ | ١٢ | итнин ашер |
| тринадцать | ثَلاثَ عَشْرَة | ١٣ | талята ашер |
| четырнадцать | أَرْبَعَ عَشْرَة | ١٤ | эрба ашер |
| пятнадцать | خ َمْسَ عَشْرَة |
١٥ | хэмса ашер |
| шестнадцать | سِتَّ عَشْرَة | ١٦ | ситта ашер |
| семнадцать | سَبْع عَشْرَة | ١٧ | сааба ашер |
| восемнадцать | ثَمانِيَ عَشْرَة | ١٨ | самания ашер |
| девятнадцать | تِسْعَ عَشْرَة | ١٩ | тыса ашер |
Числительные круглых десятков
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| десять | عَشَرَة | ١٠ | ашара |
| двадцать | اعِشْرُون | ٢٠ | ашрин |
| тридцать | ثلاثون | ٣٠ | талятин |
| сорок | أَرْبَعُون | ٤٠ | арбаин |
| пятьдесят | خَمْسُون | ٥٠ | хамсин |
| шестьдесят | ستون | ٦٠ | ситтин |
| семьдесят | سَبْعُونَ | ٧٠ | сабаин |
| восемьдесят | ثَمَانُونَ | ٨٠ | саманин |
| девяносто | تِسْعُونَ | ٩٠ | тысин |
Числительные круглых сотен
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| сто | مِائَة | ١٠٠ | ми’а |
| двести | مِائَتَيْنْ | ٢٠٠ | ми’атейн |
| триста (три сотни) | ثَلاثْ مِائَة | ٣٠٠ | саляс ми’а |
| четыреста (четыре сотни) | ﺁﺭﺒﻤﻴﺔ | ٤٠٠ | эрба ми’а |
| пятьсот (пять сотен) | ﺨﻤﺴﻤﻴﺔ | ٥٠٠ | хэмса ми’а |
| шестьсот (шесть сотен) | ﺴﺘﻤﻴﺔ | ٦٠٠ | ситта ми’а |
| семьсот (семь сотен) | ﺴﺒﻌﻤﻴﺔ | ٧٠٠ | сабаа ми’а |
| восемьсот (восемь сотен) | ﺘﻤﻨﻤﻴﺔ | ٨٠٠ | томму ми’а |
| девятьсот (девять сотен) | ﺘﺴﻌﻤﻴﺔ | ٩٠٠ | тыс’а ми’а |
Числительные круглых тысяч
| Число | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| 1 000 | ﺁﻟﻒ | ١٠٠٠ | альф |
| 2 000 | ﺁﻟﻓﻴﻦ | ٢٠٠٠ | альфейн |
| 3 000 | ﺘﻟﺘﻼﻒ | ٣٠٠٠ | талет талеф |
| 4 000 | ﺁﺮﺒﻌﺘﻼﻒ | ٤٠٠٠ | арбаа талеф |
| 5 000 | ﺨﻤﺴﺘﻼﻒ | ٥٠٠٠ | хамса талеф |
| 6 000 | ﺴﺘﻼﻒ | ٦٠٠٠ | сит талеф |
| 7 000 | ﺴﺒﻌﻼﻒ | ٧٠٠٠ | сабаа талеф |
| 8 000 | ﺘﻤﻨﺘﻼﻒ | ٨٠٠٠ | таман талеф |
| 9 000 | ﺘﺴﻌﺘﻼﻒ | ٩٠٠٠ | тысса талеф |
Числительные круглых десятков тысяч
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| 10 000 | ﻋﺸﺮﺘﻼﻒ | ١٠٠٠٠ | ашр талеф |
| 11 000 | ﺤﺪﺍﺸﺭﺁﻠﻑ | ١١٠٠٠ | хэдашр альф |
| 12 000 | ﺍﺘﻨﺎﺸﺭﺁﻠﻑ | ١٢٠٠٠ | итнашр альф |
| 13 000 | ﺘﻠﺘﺎﺸﺭﺁﻠﻑ | ١٣٠٠٠ | таляташр альф |
| 14 000 | ﺁﺭﺒﻌﺘﺎﺸﺭﺁﻠﻑ | ١٤٠٠٠ | арбаташр альф |
| 15 000 | ﺤﻤﺴﺘﺎﺸﺭﺁﻠﻑ | ١٥٠٠٠ | хамасташр альф |
| 16 000 | ﺴﺘﺎﺸﺭﺁﻠﻑ | ١٦٠٠٠ | ситташр альф |
| 17 000 | ﺴﺒﻌﺘﺎﺸﺭﺁﻠﻑ | ١٧٠٠٠ | сабаташр альф |
| 18 000 | ﺘﻤﻨﺘﺎﺸﺭﺁﻠﻑ | ١٨٠٠٠ | таманташр альф |
| 19 000 | ﺘﺴﻌﺘﺎﺸﺭﺁﻠﻑ | ١٩٠٠٠ | тыссаташр альф |
| 20 000 | ﻋﺸﺭﻴﻦﺁﻠﻑ | ٢٠٠٠٠ | ашриин альф |
| 30 000 | ﺘﻼﺘﻴﻦﺁﻠﻑ | ٣٠٠٠٠ | талятин альф |
| 40 000 | ﺁﺭﺒﻌﻴﻦﺁﻠﻑ | ٤٠٠٠٠ | арбаин альф |
| 50 000 | ﺤﻤﺴﻴﻦﺁﻠﻑ | ٥٠٠٠٠ | хамсин альф |
| 60 000 | ﺴﺘﻴﻦ ﺁﻠﻑ | ٦٠٠٠٠ | ситтин альф |
| 70 000 | ﺴﺒﻴﻦﺁﻠﻑ | ٧٠٠٠٠ | сабаин альф |
| 80 000 | ﺘﻤﻨﻴﻦ ﺁﻠﻑ | ٨٠٠٠٠ | таманин альф |
| 90 000 | ﺘﺴﻌﻴﻦ ﺁﻠﻑ | ٩٠٠٠٠ | тыссаин альф |
Числительные круглых сотен тысяч
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
| 100 000 | ﻤﻴﺖ ﺁﻠﻑ | ١٠٠٠٠٠ | мит альф |
| 200 000 | ﻤﺘﻴﻦ ﺁﻠﻑ | ٢٠٠٠٠٠ | митейн альф |
| 300 000 | ﺘﻟﺘﻤﻴﺖ ﺁﻠﻑ | ٣٠٠٠٠٠ | тульту мит альф |
| 400 000 | ﺭﺒﻌﻤﻴﺖ ﺁﻠﻑ | ٤٠٠٠٠٠ | робу мит альф |
| 500 000 | ﺤﻤﺴﻤﻴﺖ ﺁﻠﻑ | ٥٠٠٠٠٠ | хомсу мит альф |
| 600 000 | ﺴﺘﻤﻴﺖ ﺁﻠﻑ | ٦٠٠٠٠٠ | ситу мит альф |
| 700 000 | ﺴﺒﻤﻴﺖ ﺁﻠﻑ | ٧٠٠٠٠٠ | собу мит альф |
| 800 000 | ﺘﻤﻭﻤﻴﺖ ﺁﻠﻑ | ٨٠٠٠٠٠ | тому мит альф |
| 900 000 | ﺘﺴﻌﻤﻴﺖ ﺁﻠﻑ | ٩٠٠٠٠٠ | тысса мит альф |
Египетский фунт — названия бумажных денег и монет
Подробная статья про египетские деньги с фотографиями здесь: Деньги Египта.
| Русский | Арабский (число) | Как произносить (масри) |
|---|---|---|
| 200 фунтов | ٢٠٠ | ми’атейн гине |
| 100 фунтов | ١٠٠ | ми’а гине |
| 50 фунтов | ٥٠ | хамсин гине |
| 20 фунтов | ٢٠ | ашрин гине |
| 10 фунтов | ١٠ | ашер гине |
| 5 фунтов | ٥ | хэмса гине |
| 1 фунт | ١ | уахид гине |
| 50 пиастров | ٥٠ | нысф гине (хамсин эрш) |
| 25 пиастров | ٢٥ | хэмс-ашрин эрш |
| 75 пиастров | ٧٥ | хэмс-саабаин эрш |
| 1 фунт 25 пиастров | гине уа хэмс-ашрин эрш |