The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a power ratio of 101/10 (approximately 1.26) or root-power ratio of 101⁄20 (approximately 1.12).[1][2]
The unit expresses a relative change or an absolute value. In the latter case, the numeric value expresses the ratio of a value to a fixed reference value; when used in this way, the unit symbol is often suffixed with letter codes that indicate the reference value. For example, for the reference value of 1 volt, a common suffix is «V» (e.g., «20 dBV»).[3][4]
Two principal types of scaling of the decibel are in common use. When expressing a power ratio, it is defined as ten times the logarithm in base 10.[5] That is, a change in power by a factor of 10 corresponds to a 10 dB change in level. When expressing root-power quantities, a change in amplitude by a factor of 10 corresponds to a 20 dB change in level. The decibel scales differ by a factor of two, so that the related power and root-power levels change by the same value in linear systems, where power is proportional to the square of amplitude.
The definition of the decibel originated in the measurement of transmission loss and power in telephony of the early 20th century in the Bell System in the United States. The bel was named in honor of Alexander Graham Bell, but the bel is seldom used. Instead, the decibel is used for a wide variety of measurements in science and engineering, most prominently in acoustics, electronics, and control theory. In electronics, the gains of amplifiers, attenuation of signals, and signal-to-noise ratios are often expressed in decibels.
| dB | Power ratio | Amplitude ratio | ||
|---|---|---|---|---|
| 100 | 10000000000 | 100000 | ||
| 90 | 1000000000 | 31623 | ||
| 80 | 100000000 | 10000 | ||
| 70 | 10000000 | 3162 | ||
| 60 | 1000000 | 1000 | ||
| 50 | 100000 | 316 | .2 | |
| 40 | 10000 | 100 | ||
| 30 | 1000 | 31 | .62 | |
| 20 | 100 | 10 | ||
| 10 | 10 | 3 | .162 | |
| 6 | 3 | .981 ≈ 4 | 1 | .995 ≈ 2 |
| 3 | 1 | .995 ≈ 2 | 1 | .413 ≈ √2 |
| 1 | 1 | .259 | 1 | .122 |
| 0 | 1 | 1 | ||
| −1 | 0 | .794 | 0 | .891 |
| −3 | 0 | .501 ≈ 1⁄2 | 0 | .708 ≈ √1⁄2 |
| −6 | 0 | .251 ≈ 1⁄4 | 0 | .501 ≈ 1⁄2 |
| −10 | 0 | .1 | 0 | .3162 |
| −20 | 0 | .01 | 0 | .1 |
| −30 | 0 | .001 | 0 | .03162 |
| −40 | 0 | .0001 | 0 | .01 |
| −50 | 0 | .00001 | 0 | .003162 |
| −60 | 0 | .000001 | 0 | .001 |
| −70 | 0 | .0000001 | 0 | .0003162 |
| −80 | 0 | .00000001 | 0 | .0001 |
| −90 | 0 | .000000001 | 0 | .00003162 |
| −100 | 0 | .0000000001 | 0 | .00001 |
| An example scale showing power ratios x, amplitude ratios √x, and dB equivalents 10 log10 x. |
History[edit]
The decibel originates from methods used to quantify signal loss in telegraph and telephone circuits. Until the mid-1920s, the unit for loss was Miles of Standard Cable (MSC). 1 MSC corresponded to the loss of power over one mile (approximately 1.6 km) of standard telephone cable at a frequency of 5000 radians per second (795.8 Hz), and matched closely the smallest attenuation detectable to a listener. A standard telephone cable was «a cable having uniformly distributed resistance of 88 ohms per loop-mile and uniformly distributed shunt capacitance of 0.054 microfarads per mile» (approximately corresponding to 19 gauge wire).[6]
In 1924, Bell Telephone Laboratories received favorable response to a new unit definition among members of the International Advisory Committee on Long Distance Telephony in Europe and replaced the MSC with the Transmission Unit (TU). 1 TU was defined such that the number of TUs was ten times the base-10 logarithm of the ratio of measured power to a reference power.[7]
The definition was conveniently chosen such that 1 TU approximated 1 MSC; specifically, 1 MSC was 1.056 TU. In 1928, the Bell system renamed the TU into the decibel,[8] being one tenth of a newly defined unit for the base-10 logarithm of the power ratio. It was named the bel, in honor of the telecommunications pioneer Alexander Graham Bell.[9]
The bel is seldom used, as the decibel was the proposed working unit.[10]
The naming and early definition of the decibel is described in the NBS Standard’s Yearbook of 1931:[11]
Since the earliest days of the telephone, the need for a unit in which to measure the transmission efficiency of telephone facilities has been recognized. The introduction of cable in 1896 afforded a stable basis for a convenient unit and the «mile of standard» cable came into general use shortly thereafter. This unit was employed up to 1923 when a new unit was adopted as being more suitable for modern telephone work. The new transmission unit is widely used among the foreign telephone organizations and recently it was termed the «decibel» at the suggestion of the International Advisory Committee on Long Distance Telephony.
The decibel may be defined by the statement that two amounts of power differ by 1 decibel when they are in the ratio of 100.1 and any two amounts of power differ by N decibels when they are in the ratio of 10N(0.1). The number of transmission units expressing the ratio of any two powers is therefore ten times the common logarithm of that ratio. This method of designating the gain or loss of power in telephone circuits permits direct addition or subtraction of the units expressing the efficiency of different parts of the circuit …
In 1954, J. W. Horton argued that the use of the decibel as a unit for quantities other than transmission loss led to confusion, and suggested the name logit for «standard magnitudes which combine by multiplication», to contrast with the name unit for «standard magnitudes which combine by addition».[12][clarification needed]
In April 2003, the International Committee for Weights and Measures (CIPM) considered a recommendation for the inclusion of the decibel in the International System of Units (SI), but decided against the proposal.[13] However, the decibel is recognized by other international bodies such as the International Electrotechnical Commission (IEC) and International Organization for Standardization (ISO).[14] The IEC permits the use of the decibel with root-power quantities as well as power and this recommendation is followed by many national standards bodies, such as NIST, which justifies the use of the decibel for voltage ratios.[15] In spite of their widespread use, suffixes (such as in dBA or dBV) are not recognized by the IEC or ISO.
Definition[edit]
ISO 80000-3 describes definitions for quantities and units of space and time.
The IEC Standard 60027-3:2002 defines the following quantities. The decibel (dB) is one-tenth of a bel: 1 dB = 0.1 B. The bel (B) is 1⁄2 ln(10) nepers: 1 B = 1⁄2 ln(10) Np. The neper is the change in the level of a root-power quantity when the root-power quantity changes by a factor of e, that is 1 Np = ln(e) = 1, thereby relating all of the units as nondimensional natural log of root-power-quantity ratios, 1 dB = 0.115 13… Np = 0.115 13…. Finally, the level of a quantity is the logarithm of the ratio of the value of that quantity to a reference value of the same kind of quantity.
Therefore, the bel represents the logarithm of a ratio between two power quantities of 10:1, or the logarithm of a ratio between two root-power quantities of √10:1.[16]
Two signals whose levels differ by one decibel have a power ratio of 101/10, which is approximately 1.25893, and an amplitude (root-power quantity) ratio of 101⁄20 (1.12202).[17][18]
The bel is rarely used either without a prefix or with SI unit prefixes other than deci; it is preferred, for example, to use hundredths of a decibel rather than millibels. Thus, five one-thousandths of a bel would normally be written 0.05 dB, and not 5 mB.[19]
The method of expressing a ratio as a level in decibels depends on whether the measured property is a power quantity or a root-power quantity; see Power, root-power, and field quantities for details.
Power quantities[edit]
When referring to measurements of power quantities, a ratio can be expressed as a level in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to reference value. Thus, the ratio of P (measured power) to P0 (reference power) is represented by LP, that ratio expressed in decibels,[20] which is calculated using the formula:[21]
The base-10 logarithm of the ratio of the two power quantities is the number of bels. The number of decibels is ten times the number of bels (equivalently, a decibel is one-tenth of a bel). P and P0 must measure the same type of quantity, and have the same units before calculating the ratio. If P = P0 in the above equation, then LP = 0. If P is greater than P0 then LP is positive; if P is less than P0 then LP is negative.
Rearranging the above equation gives the following formula for P in terms of P0 and LP:
Root-power (field) quantities[edit]
When referring to measurements of root-power quantities, it is usual to consider the ratio of the squares of F (measured) and F0 (reference). This is because the definitions were originally formulated to give the same value for relative ratios for both power and root-power quantities. Thus, the following definition is used:
The formula may be rearranged to give
Similarly, in electrical circuits, dissipated power is typically proportional to the square of voltage or current when the impedance is constant. Taking voltage as an example, this leads to the equation for power gain level LG:
where Vout is the root-mean-square (rms) output voltage, Vin is the rms input voltage. A similar formula holds for current.
The term root-power quantity is introduced by ISO Standard 80000-1:2009 as a substitute of field quantity. The term field quantity is deprecated by that standard and root-power is used throughout this article.
Relationship between power and root-power levels[edit]
Although power and root-power quantities are different quantities, their respective levels are historically measured in the same units, typically decibels. A factor of 2 is introduced to make changes in the respective levels match under restricted conditions such as when the medium is linear and the same waveform is under consideration with changes in amplitude, or the medium impedance is linear and independent of both frequency and time. This relies on the relationship
holding.[22] In a nonlinear system, this relationship does not hold by the definition of linearity. However, even in a linear system in which the power quantity is the product of two linearly related quantities (e.g. voltage and current), if the impedance is frequency- or time-dependent, this relationship does not hold in general, for example if the energy spectrum of the waveform changes.
For differences in level, the required relationship is relaxed from that above to one of proportionality (i.e., the reference quantities P0 and F0 need not be related), or equivalently,
must hold to allow the power level difference to be equal to the root-power level difference from power P1 and F1 to P2 and F2. An example might be an amplifier with unity voltage gain independent of load and frequency driving a load with a frequency-dependent impedance: the relative voltage gain of the amplifier is always 0 dB, but the power gain depends on the changing spectral composition of the waveform being amplified. Frequency-dependent impedances may be analyzed by considering the quantities power spectral density and the associated root-power quantities via the Fourier transform, which allows elimination of the frequency dependence in the analysis by analyzing the system at each frequency independently.
Conversions[edit]
Since logarithm differences measured in these units often represent power ratios and root-power ratios, values for both are shown below. The bel is traditionally used as a unit of logarithmic power ratio, while the neper is used for logarithmic root-power (amplitude) ratio.
| Unit | In decibels | In bels | In nepers | Power ratio | Root-power ratio |
|---|---|---|---|---|---|
| 1 dB | 1 dB | 0.1 B | 0.11513 Np | 101⁄10 ≈ 1.25893 | 101⁄20 ≈ 1.12202 |
| 1 Np | 8.68589 dB | 0.868589 B | 1 Np | e2 ≈ 7.38906 | e ≈ 2.71828 |
| 1 B | 10 dB | 1 B | 1.151 3 Np | 10 | 101⁄2 ≈ 3.162 28 |
Examples[edit]
The unit dBW is often used to denote a ratio for which the reference is 1 W, and similarly dBm for a 1 mW reference point.
- Calculating the ratio in decibels of 1 kW (one kilowatt, or 1000 watts) to 1 W yields:
- The ratio in decibels of √1000 V ≈ 31.62 V to 1 V is
(31.62 V / 1 V)2 ≈ 1 kW / 1 W, illustrating the consequence from the definitions above that LG has the same value, 30 dB, regardless of whether it is obtained from powers or from amplitudes, provided that in the specific system being considered power ratios are equal to amplitude ratios squared.
- The ratio in decibels of 10 W to 1 mW (one milliwatt) is obtained with the formula
- The power ratio corresponding to a 3 dB change in level is given by
A change in power ratio by a factor of 10 corresponds to a change in level of 10 dB. A change in power ratio by a factor of 2 or 1⁄2 is approximately a change of 3 dB. More precisely, the change is ±3.0103 dB, but this is almost universally rounded to 3 dB in technical writing. This implies an increase in voltage by a factor of √2 ≈ 1.4142. Likewise, a doubling or halving of the voltage, and quadrupling or quartering of the power, is commonly described as 6 dB rather than ±6.0206 dB.
Should it be necessary to make the distinction, the number of decibels is written with additional significant figures. 3.000 dB corresponds to a power ratio of 103⁄10, or 1.9953, about 0.24% different from exactly 2, and a voltage ratio of 1.4125, 0.12% different from exactly √2. Similarly, an increase of 6.000 dB corresponds to the power ratio is 106⁄10 ≈ 3.9811, about 0.5% different from 4.
Properties[edit]
The decibel is useful for representing large ratios and for simplifying representation of multiplicative effects, such as attenuation from multiple sources along a signal chain. Its application in systems with additive effects is less intuitive, such as in the combined sound pressure level of two machines operating together. Care is also necessary with decibels directly in fractions and with the units of multiplicative operations.
Reporting large ratios[edit]
The logarithmic scale nature of the decibel means that a very large range of ratios can be represented by a convenient number, in a manner similar to scientific notation. This allows one to clearly visualize huge changes of some quantity. See Bode plot and Semi-log plot. For example, 120 dB SPL may be clearer than «a trillion times more intense than the threshold of hearing».[citation needed]
Representation of multiplication operations[edit]
Level values in decibels can be added instead of multiplying the underlying power values, which means that the overall gain of a multi-component system, such as a series of amplifier stages, can be calculated by summing the gains in decibels of the individual components, rather than multiply the amplification factors; that is, log(A × B × C) = log(A) + log(B) + log(C). Practically, this means that, armed only with the knowledge that 1 dB is a power gain of approximately 26%, 3 dB is approximately 2× power gain, and 10 dB is 10× power gain, it is possible to determine the power ratio of a system from the gain in dB with only simple addition and multiplication. For example:
- A system consists of 3 amplifiers in series, with gains (ratio of power out to in) of 10 dB, 8 dB, and 7 dB respectively, for a total gain of 25 dB. Broken into combinations of 10, 3, and 1 dB, this is:
25 dB = 10 dB + 10 dB + 3 dB + 1 dB + 1 dB
With an input of 1 watt, the output is approximately
1 W × 10 × 10 × 2 × 1.26 × 1.26 ≈ 317.5 W
Calculated precisely, the output is 1 W × 1025⁄10 ≈ 316.2 W. The approximate value has an error of only +0.4% with respect to the actual value, which is negligible given the precision of the values supplied and the accuracy of most measurement instrumentation.
However, according to its critics, the decibel creates confusion, obscures reasoning, is more related to the era of slide rules than to modern digital processing, and is cumbersome and difficult to interpret.[23][24]
Quantities in decibels are not necessarily additive,[25][26] thus being «of unacceptable form for use in dimensional analysis».[27]
Thus, units require special care in decibel operations. Take, for example, carrier-to-noise-density ratio C/N0 (in hertz), involving carrier power C (in watts) and noise power spectral density N0 (in W/Hz). Expressed in decibels, this ratio would be a subtraction (C/N0)dB = CdB − N0dB. However, the linear-scale units still simplify in the implied fraction, so that the results would be expressed in dB-Hz.
Representation of addition operations[edit]
According to Mitschke,[28] «The advantage of using a logarithmic measure is that in a transmission chain, there are many elements concatenated, and each has its own gain or attenuation. To obtain the total, addition of decibel values is much more convenient than multiplication of the individual factors.» However, for the same reason that humans excel at additive operation over multiplication, decibels are awkward in inherently additive operations:[29]
if two machines each individually produce a sound pressure level of, say, 90 dB at a certain point, then when both are operating together we should expect the combined sound pressure level to increase to 93 dB, but certainly not to 180 dB!; suppose that the noise from a machine is measured (including the contribution of background noise) and found to be 87 dBA but when the machine is switched off the background noise alone is measured as 83 dBA. […] the machine noise [level (alone)] may be obtained by ‘subtracting’ the 83 dBA background noise from the combined level of 87 dBA; i.e., 84.8 dBA.; in order to find a representative value of the sound level in a room a number of measurements are taken at different positions within the room, and an average value is calculated. […] Compare the logarithmic and arithmetic averages of […] 70 dB and 90 dB: logarithmic average = 87 dB; arithmetic average = 80 dB.
Addition on a logarithmic scale is called logarithmic addition, and can be defined by taking exponentials to convert to a linear scale, adding there, and then taking logarithms to return. For example, where operations on decibels are logarithmic addition/subtraction and logarithmic multiplication/division, while operations on the linear scale are the usual operations:
Note that the logarithmic mean is obtained from the logarithmic sum by subtracting 
Fractions[edit]
Attenuation constants, in topics such as optical fiber communication and radio propagation path loss, are often expressed as a fraction or ratio to distance of transmission. In this case, dB/m represents decibel per meter, dB/mi represents decibel per mile, for example. These quantities are to be manipulated obeying the rules of dimensional analysis, e.g., a 100-meter run with a 3.5 dB/km fiber yields a loss of 0.35 dB = 3.5 dB/km × 0.1 km.
Uses[edit]
Perception[edit]
The human perception of the intensity of sound and light more nearly approximates the logarithm of intensity rather than a linear relationship (see Weber–Fechner law), making the dB scale a useful measure.[30][31][32][33][34][35]
Acoustics[edit]
Examples of sound levels in decibels from various sound sources and activities, taken from the «How loud is too loud» screen of the NIOSH Sound Level Meter app
The decibel is commonly used in acoustics as a unit of sound pressure level. The reference pressure for sound in air is set at the typical threshold of perception of an average human and there are common comparisons used to illustrate different levels of sound pressure. As sound pressure is a root-power quantity, the appropriate version of the unit definition is used:
where prms is the root mean square of the measured sound pressure and pref is the standard reference sound pressure of 20 micropascals in air or 1 micropascal in water.[36]
Use of the decibel in underwater acoustics leads to confusion, in part because of this difference in reference value.[37]
Sound intensity is proportional to the square of sound pressure. Therefore the sound intensity level can also be defined as:
The human ear has a large dynamic range in sound reception. The ratio of the sound intensity that causes permanent damage during short exposure to that of the quietest sound that the ear can hear is equal to or greater than 1 trillion (1012).[38] Such large measurement ranges are conveniently expressed in logarithmic scale: the base-10 logarithm of 1012 is 12, which is expressed as a sound intensity level of 120 dB re 1 pW/m2. The reference values of I and p in air have been chosen such that this also corresponds to a sound pressure level of 120 dB re 20 μPa.
Since the human ear is not equally sensitive to all sound frequencies, the acoustic power spectrum is modified by frequency weighting (A-weighting being the most common standard) to get the weighted acoustic power before converting to a sound level or noise level in decibels.[39]
Telephony[edit]
The decibel is used in telephony and audio. Similarly to the use in acoustics, a frequency weighted power is often used. For audio noise measurements in electrical circuits, the weightings are called psophometric weightings.[40]
Electronics[edit]
In electronics, the decibel is often used to express power or amplitude ratios (as for gains) in preference to arithmetic ratios or percentages. One advantage is that the total decibel gain of a series of components (such as amplifiers and attenuators) can be calculated simply by summing the decibel gains of the individual components. Similarly, in telecommunications, decibels denote signal gain or loss from a transmitter to a receiver through some medium (free space, waveguide, coaxial cable, fiber optics, etc.) using a link budget.
The decibel unit can also be combined with a reference level, often indicated via a suffix, to create an absolute unit of electric power. For example, it can be combined with «m» for «milliwatt» to produce the «dBm». A power level of 0 dBm corresponds to one milliwatt, and 1 dBm is one decibel greater (about 1.259 mW).
In professional audio specifications, a popular unit is the dBu. This is relative to the root mean square voltage which delivers 1 mW (0 dBm) into a 600-ohm resistor, or √1 mW×600 Ω ≈ 0.775 VRMS. When used in a 600-ohm circuit (historically, the standard reference impedance in telephone circuits), dBu and dBm are identical.
Optics[edit]
In an optical link, if a known amount of optical power, in dBm (referenced to 1 mW), is launched into a fiber, and the losses, in dB (decibels), of each component (e.g., connectors, splices, and lengths of fiber) are known, the overall link loss may be quickly calculated by addition and subtraction of decibel quantities.[41]
In spectrometry and optics, the blocking unit used to measure optical density is equivalent to −1 B.
Video and digital imaging[edit]
In connection with video and digital image sensors, decibels generally represent ratios of video voltages or digitized light intensities, using 20 log of the ratio, even when the represented intensity (optical power) is directly proportional to the voltage generated by the sensor, not to its square, as in a CCD imager where response voltage is linear in intensity.[42]
Thus, a camera signal-to-noise ratio or dynamic range quoted as 40 dB represents a ratio of 100:1 between optical signal intensity and optical-equivalent dark-noise intensity, not a 10,000:1 intensity (power) ratio as 40 dB might suggest.[43]
Sometimes the 20 log ratio definition is applied to electron counts or photon counts directly, which are proportional to sensor signal amplitude without the need to consider whether the voltage response to intensity is linear.[44]
However, as mentioned above, the 10 log intensity convention prevails more generally in physical optics, including fiber optics, so the terminology can become murky between the conventions of digital photographic technology and physics. Most commonly, quantities called «dynamic range» or «signal-to-noise» (of the camera) would be specified in 20 log dB, but in related contexts (e.g. attenuation, gain, intensifier SNR, or rejection ratio) the term should be interpreted cautiously, as confusion of the two units can result in very large misunderstandings of the value.
Photographers typically use an alternative base-2 log unit, the stop, to describe light intensity ratios or dynamic range.
Suffixes and reference values[edit]
Suffixes are commonly attached to the basic dB unit in order to indicate the reference value by which the ratio is calculated. For example, dBm indicates power measurement relative to 1 milliwatt.
In cases where the unit value of the reference is stated, the decibel value is known as «absolute». If the unit value of the reference is not explicitly stated, as in the dB gain of an amplifier, then the decibel value is considered relative.
This form of attaching suffixes to dB is widespread in practice, albeit being against the rules promulgated by standards bodies (ISO and IEC),[15] given the «unacceptability of attaching information to units»[a] and the «unacceptability of mixing information with units»[b]. The IEC 60027-3 standard recommends the following format:[14] Lx (re xref) or as Lx/xref, where x is the quantity symbol and xref is the value of the reference quantity, e.g., LE (re 1 μV/m) = 20 dB or LE/(1 μV/m)= 20 dB for the electric field strength E relative to 1 μV/m reference value.
If the measurement result 20 dB is presented separately, it can be specified using the information in parentheses, which is then part of the surrounding text and not a part of the unit: 20 dB (re: 1 μV/m) or 20 dB (1 μV/m).
Outside of documents adhering to SI units, the practice is very common as illustrated by the following examples. There is no general rule, with various discipline-specific practices. Sometimes the suffix is a unit symbol («W»,»K»,»m»), sometimes it is a transliteration of a unit symbol («uV» instead of μV for microvolt), sometimes it is an acronym for the unit’s name («sm» for square meter, «m» for milliwatt), other times it is a mnemonic for the type of quantity being calculated («i» for antenna gain with respect to an isotropic antenna, «λ» for anything normalized by the EM wavelength), or otherwise a general attribute or identifier about the nature of the quantity («A» for A-weighted sound pressure level). The suffix is often connected with a hyphen, as in «dB‑Hz», or with a space, as in «dB HL», or enclosed in parentheses, as in «dB(sm)», or with no intervening character, as in «dBm» (which is non-compliant with international standards).
Voltage[edit]
Since the decibel is defined with respect to power, not amplitude, conversions of voltage ratios to decibels must square the amplitude, or use the factor of 20 instead of 10, as discussed above.
- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.[3] This is used to measure microphone sensitivity, and also to specify the consumer line-level of −10 dBV, in order to reduce manufacturing costs relative to equipment using a +4 dBu line-level signal.[45]
- dBu or dBv
- RMS voltage relative to
(i.e. the voltage that would dissipate 1 mW into a 600 Ω load). An RMS voltage of 1 V therefore corresponds to
[3] Originally dBv, it was changed to dBu to avoid confusion with dBV.[46] The v comes from volt, while u comes from the volume unit used in the VU meter.[47]dBu can be used as a measure of voltage, regardless of impedance, but is derived from a 600 Ω load dissipating 0 dBm (1 mW). The reference voltage comes from the computation
where
is the resistance and
is the power. In professional audio, equipment may be calibrated to indicate a «0» on the VU meters some finite time after a signal has been applied at an amplitude of +4 dBu. Consumer equipment typically uses a lower «nominal» signal level of −10 dBV.[48] Therefore, many devices offer dual voltage operation (with different gain or «trim» settings) for interoperability reasons. A switch or adjustment that covers at least the range between +4 dBu and −10 dBV is common in professional equipment.
- dBm0s
- Defined by Recommendation ITU-R V.574.; dBmV: dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.[49] Widely used in cable television networks, where the nominal strength of a single TV signal at the receiver terminals is about 0 dBmV. Cable TV uses 75 Ω coaxial cable, so 0 dBmV corresponds to −78.75 dBW (−48.75 dBm) or approximately 13 nW.
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt. Widely used in television and aerial amplifier specifications. 60 dBμV = 0 dBmV.
Acoustics[edit]
Probably the most common usage of «decibels» in reference to sound level is dB SPL, sound pressure level referenced to the nominal threshold of human hearing:[50] The measures of pressure (a root-power quantity) use the factor of 20, and the measures of power (e.g. dB SIL and dB SWL) use the factor of 10.
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 micropascals (μPa), or 2×10−5 Pa, approximately the quietest sound a human can hear. For sound in water and other liquids, a reference pressure of 1 μPa is used.[51] An RMS sound pressure of one pascal corresponds to a level of 94 dB SPL.
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2, which is roughly the threshold of human hearing in air.
- dB SWL
- dB sound power level – relative to 10−12 W.
- dBA, dBB, and dBC
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dB(A). According to standards from the International Electro-technical Committee (IEC 61672-2013)[52] and the American National Standards Institute, ANSI S1.4,[53] the preferred usage is to write LA = x dB. Nevertheless, the units dBA and dB(A) are still commonly used as a shorthand for A‑weighted measurements. Compare dBc, used in telecommunications.
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss. The reference level varies with frequency according to a minimum audibility curve as defined in ANSI and other standards, such that the resulting audiogram shows deviation from what is regarded as ‘normal’ hearing.[citation needed]
- dB Q
- sometimes used to denote weighted noise level, commonly using the ITU-R 468 noise weighting[citation needed]
- dBpp
- relative to the peak to peak sound pressure.[54]
- dBG
- G‑weighted spectrum[55]
Audio electronics[edit]
See also dBV and dBu above.
- dBm
- dB(mW) – power relative to 1 milliwatt. In audio and telephony, dBm is typically referenced relative to a 600 Ω impedance,[56] which corresponds to a voltage level of 0.775 volts or 775 millivolts.
- dBm0
- Power in dBm (described above) measured at a zero transmission level point.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBVU
- dB volume unit[57]
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.[58] In digital systems, 0 dBTP would equal the highest level (number) the processor is capable of representing. Measured values are always negative or zero, since they are less than or equal to full-scale.
Radar[edit]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3:[59] energy of reflectivity (weather radar), related to the amount of transmitted power returned to the radar receiver. Values above 20 dBZ usually indicate falling precipitation.[60]
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the radar cross section (RCS) of a target. The power reflected by the target is proportional to its RCS. «Stealth» aircraft and insects have negative RCS measured in dBsm, large flat plates or non-stealthy aircraft have positive values.[61]
Radio power, energy, and field strength[edit]
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power. Compare dBC, used in acoustics.
- dBpp
- relative to the maximum value of the peak power.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBm
- dB(mW) – power relative to 1 milliwatt. In the radio field, dBm is usually referenced to a 50 Ω load, with the resultant voltage being 0.224 volts.[62]
- dBμV/m, dBuV/m, or dBμ
- [63] dB(μV/m) – electric field strength relative to 1 microvolt per meter. The unit is often used to specify the signal strength of a television broadcast at a receiving site (the signal measured at the antenna output is reported in dBμV).
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBW
- dB(W) – power relative to 1 watt.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBe
- dB electrical.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in a system that is thermal noise limited.[64]
Antenna measurements[edit]
- dBi
- dB(isotropic) – the gain of an antenna compared with the gain of a theoretical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBd
- dB(dipole) – the gain of an antenna compared with the gain a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBiC
- dB(isotropic circular) – the gain of an antenna compared to the gain of a theoretical circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBq
- dB(quarterwave) – the gain of an antenna compared to the gain of a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the antenna effective area.[65]
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
Other measurements[edit]
- dB‑Hz
- dB(Hz) – bandwidth relative to one hertz. E.g., 20 dB‑Hz corresponds to a bandwidth of 100 Hz. Commonly used in link budget calculations. Also used in carrier-to-noise-density ratio (not to be confused with carrier-to-noise ratio, in dB).
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs. Similar to dBFS, but also applicable to analog systems. According to ITU-T Rec. G.100.1 the level in dBov of a digital system is defined as:
,
- with the maximum signal power
, for a rectangular signal with the maximum amplitude
. The level of a tone with a digital amplitude (peak value) of
is therefore
.[66]
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to a -90 dBm reference level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America. The Psophometric filter is used for this purpose on international circuits. See Psophometric weighting to see a comparison of frequency response curves for the C-message weighting and Psophometric weighting filters.[67]
- dBK
- dB(K) – decibels relative to 1 K; used to express noise temperature.[68]
- dB/K
- dB(K−1) – decibels relative to 1 K−1.[69] — not decibels per kelvin: Used for the G/T factor, a figure of merit utilized in satellite communications, relating the antenna gain G to the receiver system noise equivalent temperature T.[70][71]
List of suffixes in alphabetical order[edit]
Unpunctuated suffixes[edit]
- dBA
- see dB(A).
- dBa
- see dBrn adjusted.
- dBB
- see dB(B).
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power.
- dBC
- see dB(C).
- dBD
- see dB(D).
- dBd
- dB(dipole) – the forward gain of an antenna compared with a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBe
- dB electrical.
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBG
- G-weighted spectrum
- dBi
- dB(isotropic) – the forward gain of an antenna compared with the hypothetical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBiC
- dB(isotropic circular) – the forward gain of an antenna compared to a circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBK
- dB(K) – decibels relative to kelvin: Used to express noise temperature.
- dBm
- dB(mW) – power relative to 1 milliwatt.
- dBm0
- Power in dBm measured at a zero transmission level point.
- dBm0s
- Defined by Recommendation ITU-R V.574.
- dBmV
- dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in system that is thermal noise limited.
- dBO
- see dBov
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs.
- dBpp
- relative to the peak to peak sound pressure.
- dBpp
- relative to the maximum value of the peak power.
- dBq
- dB(quarterwave) – the forward gain of an antenna compared to a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to the circuit noise level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America.
- dBsm
- dB(m2) – decibel relative to one square meter
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.
- dBu or dBv
- RMS voltage relative to
.
- dBu0s
- Defined by Recommendation ITU-R V.574.
- dBuV
- see dBμV
- dBuV/m
- see dBμV/m
- dBv
- see dBu
- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.
- dBVU
- dB volume unit
- dBW
- dB(W) – power relative to 1 watt.
- dBW·m−2·Hz−1
- spectral density relative to 1 W·m−2·Hz−1[72]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3
- dBμ
- see dBμV/m
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt.
- dBμV/m, dBuV/m, or dBμ
- dB(μV/m) – electric field strength relative to 1 microvolt per meter.
Suffixes preceded by a space[edit]
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss.
- dB Q
- sometimes used to denote weighted noise level
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 μPa in air or 1 μPa in water
- dB SWL
- dB sound power level – relative to 10−12 W.
Suffixes within parentheses[edit]
- dB(A), dB(B), dB(C), dB(D), dB(G), and dB(Z)
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dBA.
Other suffixes[edit]
- dB-Hz
- dB(Hz) – bandwidth relative to one hertz.
- dB/K
- dB(K−1) – decibels relative to reciprocal of kelvin
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
[edit]
- mBm
- mB(mW) – power relative to 1 milliwatt, in millibels (one hundredth of a decibel). 100 mBm = 1 dBm. This unit is in the Wi-Fi drivers of the Linux kernel[73] and the regulatory domain sections.[74]
See also[edit]
- Apparent magnitude
- Cent (music)
- dB drag racing
- Decade (log scale)
- Loudness
- One-third octave § Base 10
- pH
- Phon
- Richter magnitude scale
- Sone
Notes[edit]
- ^ «When one gives the value of a quantity, it is incorrect to attach letters or other symbols to the unit in order to provide information about the quantity or its conditions of measurement. Instead, the letters or other symbols should be attached to the quantity.»[15]: 16
- ^ «When one gives the value of a quantity, any information concerning the quantity or its conditions of measurement must be presented in such a way as not to be associated with the unit. This means that quantities must be defined so that they can be expressed solely in acceptable units…»[15]: 17
References[edit]
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ a b c Utilities : VRMS / dBm / dBu / dBV calculator, Analog Devices, retrieved 16 September 2016
- ^ Thompson and Taylor 2008, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811 Archived 2016-06-03 at the Wayback Machine.
- ^ IEEE Standard 100: a dictionary of IEEE standards and terms (7th ed.). New York: The Institute of Electrical and Electronics Engineering. 2000. p. 288. ISBN 978-0-7381-2601-2.
- ^ Johnson, Kenneth Simonds (1944). Transmission Circuits for Telephonic Communication: Methods of analysis and design. New York: D. Van Nostrand Co. p. 10.
- ^ Davis, Don; Davis, Carolyn (1997). Sound system engineering (2nd ed.). Focal Press. p. 35. ISBN 978-0-240-80305-0.
- ^ Hartley, R. V. L. (December 1928). «‘TU’ becomes ‘Decibel’«. Bell Laboratories Record. AT&T. 7 (4): 137–139.
- ^ Martin, W. H. (January 1929). «DeciBel—The New Name for the Transmission Unit». Bell System Technical Journal. 8 (1).
- ^ 100 Years of Telephone Switching, p. 276, at Google Books, Robert J. Chapuis, Amos E. Joel, 2003
- ^ Harrison, William H. (1931). «Standards for Transmission of Speech». Standards Yearbook. National Bureau of Standards, U. S. Govt. Printing Office. 119.
- ^ Horton, J. W. (1954). «The bewildering decibel». Electrical Engineering. 73 (6): 550–555. doi:10.1109/EE.1954.6438830. S2CID 51654766.
- ^ «Meeting minutes» (PDF). Consultative Committee for Units. Section 3. Archived (PDF) from the original on 6 October 2014.
- ^ a b «Letter symbols to be used in electrical technology». International Electrotechnical Commission. 19 July 2002. Part 3: Logarithmic and related quantities, and their units. IEC 60027-3, Ed. 3.0.
- ^ a b c d Thompson, A. and Taylor, B. N. sec 8.7, «Logarithmic quantities and units: level, neper, bel», Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF
- ^ «Letter symbols to be used in electrical technology». International Standard CEI-IEC 27-3. International Electrotechnical Commission. Part 3: Logarithmic quantities and units.
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ Fedor Mitschke, Fiber Optics: Physics and Technology, Springer, 2010 ISBN 3642037038.
- ^ Pozar, David M. (2005). Microwave Engineering (3rd ed.). Wiley. p. 63. ISBN 978-0-471-44878-5.
- ^ IEC 60027-3:2002
- ^ I M Mills; B N Taylor; A J Thor (2001), «Definitions of the units radian, neper, bel and decibel», Metrologia, 38 (4): 353, Bibcode:2001Metro..38..353M, doi:10.1088/0026-1394/38/4/8, S2CID 250827251
- ^ R. Hickling (1999), Noise Control and SI Units, J Acoust Soc Am 106, 3048
- ^ Hickling, R. (2006). Decibels and octaves, who needs them?. Journal of sound and vibration, 291(3-5), 1202-1207.
- ^ Nicholas P. Cheremisinoff (1996) Noise Control in Industry: A Practical Guide, Elsevier, 203 pp, p. 7
- ^ Andrew Clennel Palmer (2008), Dimensional Analysis and Intelligent Experimentation, World Scientific, 154 pp, p.13
- ^ J. C. Gibbings, Dimensional Analysis, p.37, Springer, 2011 ISBN 1849963177.
- ^ Fiber Optics. Springer. 2010.
- ^ R. J. Peters, Acoustics and Noise Control, Routledge, 12 November 2013, 400 pages, p. 13
- ^ Sensation and Perception, p. 268, at Google Books
- ^ Introduction to Understandable Physics, Volume 2, p. SA19-PA9, at Google Books
- ^ Visual Perception: Physiology, Psychology, and Ecology, p. 356, at Google Books
- ^ Exercise Psychology, p. 407, at Google Books
- ^ Foundations of Perception, p. 83, at Google Books
- ^ Fitting The Task To The Human, p. 304, at Google Books
- ^ ISO 1683:2015
- ^ C. S. Clay (1999), Underwater sound transmission and SI units, J Acoust Soc Am 106, 3047
- ^ «Loud Noise Can Cause Hearing Loss». cdc.gov. Centers for Disease Control and Prevention. 7 October 2019. Retrieved 30 July 2020.
- ^ Richard L. St. Pierre, Jr. and Daniel J. Maguire (July 2004), The Impact of A-weighting Sound Pressure Level Measurements during the Evaluation of Noise Exposure (PDF), archived (PDF) from the original on 22 December 2015, retrieved 13 September 2011
- ^ Reeve, William D. (1992). Subscriber Loop Signaling and Transmission Handbook – Analog (1st ed.). IEEE Press. ISBN 0-87942-274-2.
- ^
Chomycz, Bob (2000). Fiber optic installer’s field manual. McGraw-Hill Professional. pp. 123–126. ISBN 978-0-07-135604-6. - ^
Stephen J. Sangwine and Robin E. N. Horne (1998). The Colour Image Processing Handbook. Springer. pp. 127–130. ISBN 978-0-412-80620-9. - ^
Francis T. S. Yu and Xiangyang Yang (1997). Introduction to optical engineering. Cambridge University Press. pp. 102–103. ISBN 978-0-521-57493-8. - ^
Junichi Nakamura (2006). «Basics of Image Sensors». In Junichi Nakamura (ed.). Image sensors and signal processing for digital still cameras. CRC Press. pp. 79–83. ISBN 978-0-8493-3545-7. - ^ Winer, Ethan (2013). The Audio Expert: Everything You Need to Know About Audio. Focal Press. p. 107. ISBN 978-0-240-82100-9.
- ^ Stas Bekman. «3.3 – What is the difference between dBv, dBu, dBV, dBm, dB SPL, and plain old dB? Why not just use regular voltage and power measurements?». stason.org.
- ^ Rupert Neve, Creation of the dBu standard level reference, archived from the original on 30 October 2021
- ^ deltamedia.com. «DB or Not DB». Deltamedia.com. Retrieved 16 September 2013.
- ^ The IEEE Standard Dictionary of Electrical and Electronics terms (6th ed.). IEEE. 1996 [1941]. ISBN 978-1-55937-833-8.
- ^ Jay Rose (2002). Audio postproduction for digital video. Focal Press. p. 25. ISBN 978-1-57820-116-7.
- ^ Morfey, C. L. (2001). Dictionary of Acoustics. Academic Press, San Diego.
- ^ IEC 61672-1:2013 Electroacoustics — Sound Level meters — Part 1: Specifications. Geneva: International Electrotechnical Committee. 2013.
- ^ ANSI S1.4-19823 Specification for Sound Level Meters, 2.3 Sound Level, p. 2–3.
- ^ Zimmer, Walter MX, Mark P. Johnson, Peter T. Madsen, and Peter L. Tyack. «Echolocation clicks of free-ranging Cuvier’s beaked whales (Ziphius cavirostris).» The Journal of the Acoustical Society of America 117, no. 6 (2005): 3919–3927.
- ^ «Turbine Sound Measurements». Archived from the original on 12 December 2010.
- ^ Bigelow, Stephen (2001). Understanding Telephone Electronics. Newnes. p. 16. ISBN 978-0750671750.
- ^ Tharr, D. (1998). Case Studies: Transient Sounds Through Communication Headsets. Applied Occupational and Environmental Hygiene, 13(10), 691–697.
- ^ ITU-R BS.1770
- ^ «Glossary: D’s». National Weather Service. Archived from the original on 8 August 2019. Retrieved 25 April 2013.
- ^ «RIDGE Radar Frequently Asked Questions». Archived from the original on 31 March 2019. Retrieved 8 August 2019.
- ^ «Definition at Everything2». Archived from the original on 10 June 2019. Retrieved 8 August 2019.
- ^ Carr, Joseph (2002). RF Components and Circuits. Newnes. pp. 45–46. ISBN 978-0750648448.
- ^ «The dBµ vs. dBu Mystery: Signal Strength vs. Field Strength?». radio-timetraveller.blogspot.com. 24 February 2015. Retrieved 13 October 2016.
- ^ Chand, N., Magill, P. D., Swaminathan, S. V., & Daugherty, T. H. (1999). Delivery of digital video and other multimedia services (> 1 Gb/s bandwidth) in passband above the 155 Mb/s baseband services on a FTTx full service access network. Journal of lightwave technology, 17(12), 2449–2460.
- ^ David Adamy. EW 102: A Second Course in Electronic Warfare. Retrieved 16 September 2013.
- ^ ITU-T Rec. G.100.1 The use of the decibel and of relative levels in speechband telecommunications https://www.itu.int/rec/dologin_pub.asp?lang=e&id=T-REC-G.100.1-201506-I!!PDF-E&type=items
- ^ dBrnC is defined on page 230 in «Engineering and Operations in the Bell System,» (2ed), R.F. Rey (technical editor), copyright 1983, AT&T Bell Laboratories, Murray Hill, NJ, ISBN 0-932764-04-5
- ^ K. N. Raja Rao (31 January 2013). Satellite Communication: Concepts And Applications. Retrieved 16 September 2013.
- ^ Ali Akbar Arabi. Comprehensive Glossary of Telecom Abbreviations and Acronyms. Retrieved 16 September 2013.
- ^ Mark E. Long. The Digital Satellite TV Handbook. Retrieved 16 September 2013.
- ^ Mac E. Van Valkenburg (19 October 2001). Reference Data for Engineers: Radio, Electronics, Computers and Communications. Retrieved 16 September 2013.
- ^ «Archived copy». Archived from the original on 3 March 2016. Retrieved 24 August 2013.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ «en:users:documentation:iw [Linux Wireless]». wireless.kernel.org.
- ^ «Is your WiFi AP Missing Channels 12 & 13?». wordpress.com. 16 May 2013.
Further reading[edit]
- Tuffentsammer, Karl (1956). «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [The decilog, a bridge between logarithms, decibel, neper and preferred numbers]. VDI-Zeitschrift (in German). 98: 267–274.
- Paulin, Eugen (1 September 2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon — natürlich verwandt! [Logarithms, preferred numbers, decibel, neper, phon — naturally related!] (PDF) (in German). Archived (PDF) from the original on 18 December 2016. Retrieved 18 December 2016.
External links[edit]
- What is a decibel? With sound files and animations
- Conversion of sound level units: dBSPL or dBA to sound pressure p and sound intensity J
- OSHA Regulations on Occupational Noise Exposure
- Working with Decibels (RF signal and field strengths)
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a power ratio of 101/10 (approximately 1.26) or root-power ratio of 101⁄20 (approximately 1.12).[1][2]
The unit expresses a relative change or an absolute value. In the latter case, the numeric value expresses the ratio of a value to a fixed reference value; when used in this way, the unit symbol is often suffixed with letter codes that indicate the reference value. For example, for the reference value of 1 volt, a common suffix is «V» (e.g., «20 dBV»).[3][4]
Two principal types of scaling of the decibel are in common use. When expressing a power ratio, it is defined as ten times the logarithm in base 10.[5] That is, a change in power by a factor of 10 corresponds to a 10 dB change in level. When expressing root-power quantities, a change in amplitude by a factor of 10 corresponds to a 20 dB change in level. The decibel scales differ by a factor of two, so that the related power and root-power levels change by the same value in linear systems, where power is proportional to the square of amplitude.
The definition of the decibel originated in the measurement of transmission loss and power in telephony of the early 20th century in the Bell System in the United States. The bel was named in honor of Alexander Graham Bell, but the bel is seldom used. Instead, the decibel is used for a wide variety of measurements in science and engineering, most prominently in acoustics, electronics, and control theory. In electronics, the gains of amplifiers, attenuation of signals, and signal-to-noise ratios are often expressed in decibels.
| dB | Power ratio | Amplitude ratio | ||
|---|---|---|---|---|
| 100 | 10000000000 | 100000 | ||
| 90 | 1000000000 | 31623 | ||
| 80 | 100000000 | 10000 | ||
| 70 | 10000000 | 3162 | ||
| 60 | 1000000 | 1000 | ||
| 50 | 100000 | 316 | .2 | |
| 40 | 10000 | 100 | ||
| 30 | 1000 | 31 | .62 | |
| 20 | 100 | 10 | ||
| 10 | 10 | 3 | .162 | |
| 6 | 3 | .981 ≈ 4 | 1 | .995 ≈ 2 |
| 3 | 1 | .995 ≈ 2 | 1 | .413 ≈ √2 |
| 1 | 1 | .259 | 1 | .122 |
| 0 | 1 | 1 | ||
| −1 | 0 | .794 | 0 | .891 |
| −3 | 0 | .501 ≈ 1⁄2 | 0 | .708 ≈ √1⁄2 |
| −6 | 0 | .251 ≈ 1⁄4 | 0 | .501 ≈ 1⁄2 |
| −10 | 0 | .1 | 0 | .3162 |
| −20 | 0 | .01 | 0 | .1 |
| −30 | 0 | .001 | 0 | .03162 |
| −40 | 0 | .0001 | 0 | .01 |
| −50 | 0 | .00001 | 0 | .003162 |
| −60 | 0 | .000001 | 0 | .001 |
| −70 | 0 | .0000001 | 0 | .0003162 |
| −80 | 0 | .00000001 | 0 | .0001 |
| −90 | 0 | .000000001 | 0 | .00003162 |
| −100 | 0 | .0000000001 | 0 | .00001 |
| An example scale showing power ratios x, amplitude ratios √x, and dB equivalents 10 log10 x. |
History[edit]
The decibel originates from methods used to quantify signal loss in telegraph and telephone circuits. Until the mid-1920s, the unit for loss was Miles of Standard Cable (MSC). 1 MSC corresponded to the loss of power over one mile (approximately 1.6 km) of standard telephone cable at a frequency of 5000 radians per second (795.8 Hz), and matched closely the smallest attenuation detectable to a listener. A standard telephone cable was «a cable having uniformly distributed resistance of 88 ohms per loop-mile and uniformly distributed shunt capacitance of 0.054 microfarads per mile» (approximately corresponding to 19 gauge wire).[6]
In 1924, Bell Telephone Laboratories received favorable response to a new unit definition among members of the International Advisory Committee on Long Distance Telephony in Europe and replaced the MSC with the Transmission Unit (TU). 1 TU was defined such that the number of TUs was ten times the base-10 logarithm of the ratio of measured power to a reference power.[7]
The definition was conveniently chosen such that 1 TU approximated 1 MSC; specifically, 1 MSC was 1.056 TU. In 1928, the Bell system renamed the TU into the decibel,[8] being one tenth of a newly defined unit for the base-10 logarithm of the power ratio. It was named the bel, in honor of the telecommunications pioneer Alexander Graham Bell.[9]
The bel is seldom used, as the decibel was the proposed working unit.[10]
The naming and early definition of the decibel is described in the NBS Standard’s Yearbook of 1931:[11]
Since the earliest days of the telephone, the need for a unit in which to measure the transmission efficiency of telephone facilities has been recognized. The introduction of cable in 1896 afforded a stable basis for a convenient unit and the «mile of standard» cable came into general use shortly thereafter. This unit was employed up to 1923 when a new unit was adopted as being more suitable for modern telephone work. The new transmission unit is widely used among the foreign telephone organizations and recently it was termed the «decibel» at the suggestion of the International Advisory Committee on Long Distance Telephony.
The decibel may be defined by the statement that two amounts of power differ by 1 decibel when they are in the ratio of 100.1 and any two amounts of power differ by N decibels when they are in the ratio of 10N(0.1). The number of transmission units expressing the ratio of any two powers is therefore ten times the common logarithm of that ratio. This method of designating the gain or loss of power in telephone circuits permits direct addition or subtraction of the units expressing the efficiency of different parts of the circuit …
In 1954, J. W. Horton argued that the use of the decibel as a unit for quantities other than transmission loss led to confusion, and suggested the name logit for «standard magnitudes which combine by multiplication», to contrast with the name unit for «standard magnitudes which combine by addition».[12][clarification needed]
In April 2003, the International Committee for Weights and Measures (CIPM) considered a recommendation for the inclusion of the decibel in the International System of Units (SI), but decided against the proposal.[13] However, the decibel is recognized by other international bodies such as the International Electrotechnical Commission (IEC) and International Organization for Standardization (ISO).[14] The IEC permits the use of the decibel with root-power quantities as well as power and this recommendation is followed by many national standards bodies, such as NIST, which justifies the use of the decibel for voltage ratios.[15] In spite of their widespread use, suffixes (such as in dBA or dBV) are not recognized by the IEC or ISO.
Definition[edit]
ISO 80000-3 describes definitions for quantities and units of space and time.
The IEC Standard 60027-3:2002 defines the following quantities. The decibel (dB) is one-tenth of a bel: 1 dB = 0.1 B. The bel (B) is 1⁄2 ln(10) nepers: 1 B = 1⁄2 ln(10) Np. The neper is the change in the level of a root-power quantity when the root-power quantity changes by a factor of e, that is 1 Np = ln(e) = 1, thereby relating all of the units as nondimensional natural log of root-power-quantity ratios, 1 dB = 0.115 13… Np = 0.115 13…. Finally, the level of a quantity is the logarithm of the ratio of the value of that quantity to a reference value of the same kind of quantity.
Therefore, the bel represents the logarithm of a ratio between two power quantities of 10:1, or the logarithm of a ratio between two root-power quantities of √10:1.[16]
Two signals whose levels differ by one decibel have a power ratio of 101/10, which is approximately 1.25893, and an amplitude (root-power quantity) ratio of 101⁄20 (1.12202).[17][18]
The bel is rarely used either without a prefix or with SI unit prefixes other than deci; it is preferred, for example, to use hundredths of a decibel rather than millibels. Thus, five one-thousandths of a bel would normally be written 0.05 dB, and not 5 mB.[19]
The method of expressing a ratio as a level in decibels depends on whether the measured property is a power quantity or a root-power quantity; see Power, root-power, and field quantities for details.
Power quantities[edit]
When referring to measurements of power quantities, a ratio can be expressed as a level in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to reference value. Thus, the ratio of P (measured power) to P0 (reference power) is represented by LP, that ratio expressed in decibels,[20] which is calculated using the formula:[21]
The base-10 logarithm of the ratio of the two power quantities is the number of bels. The number of decibels is ten times the number of bels (equivalently, a decibel is one-tenth of a bel). P and P0 must measure the same type of quantity, and have the same units before calculating the ratio. If P = P0 in the above equation, then LP = 0. If P is greater than P0 then LP is positive; if P is less than P0 then LP is negative.
Rearranging the above equation gives the following formula for P in terms of P0 and LP:
Root-power (field) quantities[edit]
When referring to measurements of root-power quantities, it is usual to consider the ratio of the squares of F (measured) and F0 (reference). This is because the definitions were originally formulated to give the same value for relative ratios for both power and root-power quantities. Thus, the following definition is used:
The formula may be rearranged to give
Similarly, in electrical circuits, dissipated power is typically proportional to the square of voltage or current when the impedance is constant. Taking voltage as an example, this leads to the equation for power gain level LG:
where Vout is the root-mean-square (rms) output voltage, Vin is the rms input voltage. A similar formula holds for current.
The term root-power quantity is introduced by ISO Standard 80000-1:2009 as a substitute of field quantity. The term field quantity is deprecated by that standard and root-power is used throughout this article.
Relationship between power and root-power levels[edit]
Although power and root-power quantities are different quantities, their respective levels are historically measured in the same units, typically decibels. A factor of 2 is introduced to make changes in the respective levels match under restricted conditions such as when the medium is linear and the same waveform is under consideration with changes in amplitude, or the medium impedance is linear and independent of both frequency and time. This relies on the relationship
holding.[22] In a nonlinear system, this relationship does not hold by the definition of linearity. However, even in a linear system in which the power quantity is the product of two linearly related quantities (e.g. voltage and current), if the impedance is frequency- or time-dependent, this relationship does not hold in general, for example if the energy spectrum of the waveform changes.
For differences in level, the required relationship is relaxed from that above to one of proportionality (i.e., the reference quantities P0 and F0 need not be related), or equivalently,
must hold to allow the power level difference to be equal to the root-power level difference from power P1 and F1 to P2 and F2. An example might be an amplifier with unity voltage gain independent of load and frequency driving a load with a frequency-dependent impedance: the relative voltage gain of the amplifier is always 0 dB, but the power gain depends on the changing spectral composition of the waveform being amplified. Frequency-dependent impedances may be analyzed by considering the quantities power spectral density and the associated root-power quantities via the Fourier transform, which allows elimination of the frequency dependence in the analysis by analyzing the system at each frequency independently.
Conversions[edit]
Since logarithm differences measured in these units often represent power ratios and root-power ratios, values for both are shown below. The bel is traditionally used as a unit of logarithmic power ratio, while the neper is used for logarithmic root-power (amplitude) ratio.
| Unit | In decibels | In bels | In nepers | Power ratio | Root-power ratio |
|---|---|---|---|---|---|
| 1 dB | 1 dB | 0.1 B | 0.11513 Np | 101⁄10 ≈ 1.25893 | 101⁄20 ≈ 1.12202 |
| 1 Np | 8.68589 dB | 0.868589 B | 1 Np | e2 ≈ 7.38906 | e ≈ 2.71828 |
| 1 B | 10 dB | 1 B | 1.151 3 Np | 10 | 101⁄2 ≈ 3.162 28 |
Examples[edit]
The unit dBW is often used to denote a ratio for which the reference is 1 W, and similarly dBm for a 1 mW reference point.
- Calculating the ratio in decibels of 1 kW (one kilowatt, or 1000 watts) to 1 W yields:
- The ratio in decibels of √1000 V ≈ 31.62 V to 1 V is
(31.62 V / 1 V)2 ≈ 1 kW / 1 W, illustrating the consequence from the definitions above that LG has the same value, 30 dB, regardless of whether it is obtained from powers or from amplitudes, provided that in the specific system being considered power ratios are equal to amplitude ratios squared.
- The ratio in decibels of 10 W to 1 mW (one milliwatt) is obtained with the formula
- The power ratio corresponding to a 3 dB change in level is given by
A change in power ratio by a factor of 10 corresponds to a change in level of 10 dB. A change in power ratio by a factor of 2 or 1⁄2 is approximately a change of 3 dB. More precisely, the change is ±3.0103 dB, but this is almost universally rounded to 3 dB in technical writing. This implies an increase in voltage by a factor of √2 ≈ 1.4142. Likewise, a doubling or halving of the voltage, and quadrupling or quartering of the power, is commonly described as 6 dB rather than ±6.0206 dB.
Should it be necessary to make the distinction, the number of decibels is written with additional significant figures. 3.000 dB corresponds to a power ratio of 103⁄10, or 1.9953, about 0.24% different from exactly 2, and a voltage ratio of 1.4125, 0.12% different from exactly √2. Similarly, an increase of 6.000 dB corresponds to the power ratio is 106⁄10 ≈ 3.9811, about 0.5% different from 4.
Properties[edit]
The decibel is useful for representing large ratios and for simplifying representation of multiplicative effects, such as attenuation from multiple sources along a signal chain. Its application in systems with additive effects is less intuitive, such as in the combined sound pressure level of two machines operating together. Care is also necessary with decibels directly in fractions and with the units of multiplicative operations.
Reporting large ratios[edit]
The logarithmic scale nature of the decibel means that a very large range of ratios can be represented by a convenient number, in a manner similar to scientific notation. This allows one to clearly visualize huge changes of some quantity. See Bode plot and Semi-log plot. For example, 120 dB SPL may be clearer than «a trillion times more intense than the threshold of hearing».[citation needed]
Representation of multiplication operations[edit]
Level values in decibels can be added instead of multiplying the underlying power values, which means that the overall gain of a multi-component system, such as a series of amplifier stages, can be calculated by summing the gains in decibels of the individual components, rather than multiply the amplification factors; that is, log(A × B × C) = log(A) + log(B) + log(C). Practically, this means that, armed only with the knowledge that 1 dB is a power gain of approximately 26%, 3 dB is approximately 2× power gain, and 10 dB is 10× power gain, it is possible to determine the power ratio of a system from the gain in dB with only simple addition and multiplication. For example:
- A system consists of 3 amplifiers in series, with gains (ratio of power out to in) of 10 dB, 8 dB, and 7 dB respectively, for a total gain of 25 dB. Broken into combinations of 10, 3, and 1 dB, this is:
25 dB = 10 dB + 10 dB + 3 dB + 1 dB + 1 dB
With an input of 1 watt, the output is approximately
1 W × 10 × 10 × 2 × 1.26 × 1.26 ≈ 317.5 W
Calculated precisely, the output is 1 W × 1025⁄10 ≈ 316.2 W. The approximate value has an error of only +0.4% with respect to the actual value, which is negligible given the precision of the values supplied and the accuracy of most measurement instrumentation.
However, according to its critics, the decibel creates confusion, obscures reasoning, is more related to the era of slide rules than to modern digital processing, and is cumbersome and difficult to interpret.[23][24]
Quantities in decibels are not necessarily additive,[25][26] thus being «of unacceptable form for use in dimensional analysis».[27]
Thus, units require special care in decibel operations. Take, for example, carrier-to-noise-density ratio C/N0 (in hertz), involving carrier power C (in watts) and noise power spectral density N0 (in W/Hz). Expressed in decibels, this ratio would be a subtraction (C/N0)dB = CdB − N0dB. However, the linear-scale units still simplify in the implied fraction, so that the results would be expressed in dB-Hz.
Representation of addition operations[edit]
According to Mitschke,[28] «The advantage of using a logarithmic measure is that in a transmission chain, there are many elements concatenated, and each has its own gain or attenuation. To obtain the total, addition of decibel values is much more convenient than multiplication of the individual factors.» However, for the same reason that humans excel at additive operation over multiplication, decibels are awkward in inherently additive operations:[29]
if two machines each individually produce a sound pressure level of, say, 90 dB at a certain point, then when both are operating together we should expect the combined sound pressure level to increase to 93 dB, but certainly not to 180 dB!; suppose that the noise from a machine is measured (including the contribution of background noise) and found to be 87 dBA but when the machine is switched off the background noise alone is measured as 83 dBA. […] the machine noise [level (alone)] may be obtained by ‘subtracting’ the 83 dBA background noise from the combined level of 87 dBA; i.e., 84.8 dBA.; in order to find a representative value of the sound level in a room a number of measurements are taken at different positions within the room, and an average value is calculated. […] Compare the logarithmic and arithmetic averages of […] 70 dB and 90 dB: logarithmic average = 87 dB; arithmetic average = 80 dB.
Addition on a logarithmic scale is called logarithmic addition, and can be defined by taking exponentials to convert to a linear scale, adding there, and then taking logarithms to return. For example, where operations on decibels are logarithmic addition/subtraction and logarithmic multiplication/division, while operations on the linear scale are the usual operations:
Note that the logarithmic mean is obtained from the logarithmic sum by subtracting 
Fractions[edit]
Attenuation constants, in topics such as optical fiber communication and radio propagation path loss, are often expressed as a fraction or ratio to distance of transmission. In this case, dB/m represents decibel per meter, dB/mi represents decibel per mile, for example. These quantities are to be manipulated obeying the rules of dimensional analysis, e.g., a 100-meter run with a 3.5 dB/km fiber yields a loss of 0.35 dB = 3.5 dB/km × 0.1 km.
Uses[edit]
Perception[edit]
The human perception of the intensity of sound and light more nearly approximates the logarithm of intensity rather than a linear relationship (see Weber–Fechner law), making the dB scale a useful measure.[30][31][32][33][34][35]
Acoustics[edit]
Examples of sound levels in decibels from various sound sources and activities, taken from the «How loud is too loud» screen of the NIOSH Sound Level Meter app
The decibel is commonly used in acoustics as a unit of sound pressure level. The reference pressure for sound in air is set at the typical threshold of perception of an average human and there are common comparisons used to illustrate different levels of sound pressure. As sound pressure is a root-power quantity, the appropriate version of the unit definition is used:
where prms is the root mean square of the measured sound pressure and pref is the standard reference sound pressure of 20 micropascals in air or 1 micropascal in water.[36]
Use of the decibel in underwater acoustics leads to confusion, in part because of this difference in reference value.[37]
Sound intensity is proportional to the square of sound pressure. Therefore the sound intensity level can also be defined as:
The human ear has a large dynamic range in sound reception. The ratio of the sound intensity that causes permanent damage during short exposure to that of the quietest sound that the ear can hear is equal to or greater than 1 trillion (1012).[38] Such large measurement ranges are conveniently expressed in logarithmic scale: the base-10 logarithm of 1012 is 12, which is expressed as a sound intensity level of 120 dB re 1 pW/m2. The reference values of I and p in air have been chosen such that this also corresponds to a sound pressure level of 120 dB re 20 μPa.
Since the human ear is not equally sensitive to all sound frequencies, the acoustic power spectrum is modified by frequency weighting (A-weighting being the most common standard) to get the weighted acoustic power before converting to a sound level or noise level in decibels.[39]
Telephony[edit]
The decibel is used in telephony and audio. Similarly to the use in acoustics, a frequency weighted power is often used. For audio noise measurements in electrical circuits, the weightings are called psophometric weightings.[40]
Electronics[edit]
In electronics, the decibel is often used to express power or amplitude ratios (as for gains) in preference to arithmetic ratios or percentages. One advantage is that the total decibel gain of a series of components (such as amplifiers and attenuators) can be calculated simply by summing the decibel gains of the individual components. Similarly, in telecommunications, decibels denote signal gain or loss from a transmitter to a receiver through some medium (free space, waveguide, coaxial cable, fiber optics, etc.) using a link budget.
The decibel unit can also be combined with a reference level, often indicated via a suffix, to create an absolute unit of electric power. For example, it can be combined with «m» for «milliwatt» to produce the «dBm». A power level of 0 dBm corresponds to one milliwatt, and 1 dBm is one decibel greater (about 1.259 mW).
In professional audio specifications, a popular unit is the dBu. This is relative to the root mean square voltage which delivers 1 mW (0 dBm) into a 600-ohm resistor, or √1 mW×600 Ω ≈ 0.775 VRMS. When used in a 600-ohm circuit (historically, the standard reference impedance in telephone circuits), dBu and dBm are identical.
Optics[edit]
In an optical link, if a known amount of optical power, in dBm (referenced to 1 mW), is launched into a fiber, and the losses, in dB (decibels), of each component (e.g., connectors, splices, and lengths of fiber) are known, the overall link loss may be quickly calculated by addition and subtraction of decibel quantities.[41]
In spectrometry and optics, the blocking unit used to measure optical density is equivalent to −1 B.
Video and digital imaging[edit]
In connection with video and digital image sensors, decibels generally represent ratios of video voltages or digitized light intensities, using 20 log of the ratio, even when the represented intensity (optical power) is directly proportional to the voltage generated by the sensor, not to its square, as in a CCD imager where response voltage is linear in intensity.[42]
Thus, a camera signal-to-noise ratio or dynamic range quoted as 40 dB represents a ratio of 100:1 between optical signal intensity and optical-equivalent dark-noise intensity, not a 10,000:1 intensity (power) ratio as 40 dB might suggest.[43]
Sometimes the 20 log ratio definition is applied to electron counts or photon counts directly, which are proportional to sensor signal amplitude without the need to consider whether the voltage response to intensity is linear.[44]
However, as mentioned above, the 10 log intensity convention prevails more generally in physical optics, including fiber optics, so the terminology can become murky between the conventions of digital photographic technology and physics. Most commonly, quantities called «dynamic range» or «signal-to-noise» (of the camera) would be specified in 20 log dB, but in related contexts (e.g. attenuation, gain, intensifier SNR, or rejection ratio) the term should be interpreted cautiously, as confusion of the two units can result in very large misunderstandings of the value.
Photographers typically use an alternative base-2 log unit, the stop, to describe light intensity ratios or dynamic range.
Suffixes and reference values[edit]
Suffixes are commonly attached to the basic dB unit in order to indicate the reference value by which the ratio is calculated. For example, dBm indicates power measurement relative to 1 milliwatt.
In cases where the unit value of the reference is stated, the decibel value is known as «absolute». If the unit value of the reference is not explicitly stated, as in the dB gain of an amplifier, then the decibel value is considered relative.
This form of attaching suffixes to dB is widespread in practice, albeit being against the rules promulgated by standards bodies (ISO and IEC),[15] given the «unacceptability of attaching information to units»[a] and the «unacceptability of mixing information with units»[b]. The IEC 60027-3 standard recommends the following format:[14] Lx (re xref) or as Lx/xref, where x is the quantity symbol and xref is the value of the reference quantity, e.g., LE (re 1 μV/m) = 20 dB or LE/(1 μV/m)= 20 dB for the electric field strength E relative to 1 μV/m reference value.
If the measurement result 20 dB is presented separately, it can be specified using the information in parentheses, which is then part of the surrounding text and not a part of the unit: 20 dB (re: 1 μV/m) or 20 dB (1 μV/m).
Outside of documents adhering to SI units, the practice is very common as illustrated by the following examples. There is no general rule, with various discipline-specific practices. Sometimes the suffix is a unit symbol («W»,»K»,»m»), sometimes it is a transliteration of a unit symbol («uV» instead of μV for microvolt), sometimes it is an acronym for the unit’s name («sm» for square meter, «m» for milliwatt), other times it is a mnemonic for the type of quantity being calculated («i» for antenna gain with respect to an isotropic antenna, «λ» for anything normalized by the EM wavelength), or otherwise a general attribute or identifier about the nature of the quantity («A» for A-weighted sound pressure level). The suffix is often connected with a hyphen, as in «dB‑Hz», or with a space, as in «dB HL», or enclosed in parentheses, as in «dB(sm)», or with no intervening character, as in «dBm» (which is non-compliant with international standards).
Voltage[edit]
Since the decibel is defined with respect to power, not amplitude, conversions of voltage ratios to decibels must square the amplitude, or use the factor of 20 instead of 10, as discussed above.
- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.[3] This is used to measure microphone sensitivity, and also to specify the consumer line-level of −10 dBV, in order to reduce manufacturing costs relative to equipment using a +4 dBu line-level signal.[45]
- dBu or dBv
- RMS voltage relative to
(i.e. the voltage that would dissipate 1 mW into a 600 Ω load). An RMS voltage of 1 V therefore corresponds to
[3] Originally dBv, it was changed to dBu to avoid confusion with dBV.[46] The v comes from volt, while u comes from the volume unit used in the VU meter.[47]dBu can be used as a measure of voltage, regardless of impedance, but is derived from a 600 Ω load dissipating 0 dBm (1 mW). The reference voltage comes from the computation
where
is the resistance and
is the power. In professional audio, equipment may be calibrated to indicate a «0» on the VU meters some finite time after a signal has been applied at an amplitude of +4 dBu. Consumer equipment typically uses a lower «nominal» signal level of −10 dBV.[48] Therefore, many devices offer dual voltage operation (with different gain or «trim» settings) for interoperability reasons. A switch or adjustment that covers at least the range between +4 dBu and −10 dBV is common in professional equipment.
- dBm0s
- Defined by Recommendation ITU-R V.574.; dBmV: dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.[49] Widely used in cable television networks, where the nominal strength of a single TV signal at the receiver terminals is about 0 dBmV. Cable TV uses 75 Ω coaxial cable, so 0 dBmV corresponds to −78.75 dBW (−48.75 dBm) or approximately 13 nW.
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt. Widely used in television and aerial amplifier specifications. 60 dBμV = 0 dBmV.
Acoustics[edit]
Probably the most common usage of «decibels» in reference to sound level is dB SPL, sound pressure level referenced to the nominal threshold of human hearing:[50] The measures of pressure (a root-power quantity) use the factor of 20, and the measures of power (e.g. dB SIL and dB SWL) use the factor of 10.
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 micropascals (μPa), or 2×10−5 Pa, approximately the quietest sound a human can hear. For sound in water and other liquids, a reference pressure of 1 μPa is used.[51] An RMS sound pressure of one pascal corresponds to a level of 94 dB SPL.
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2, which is roughly the threshold of human hearing in air.
- dB SWL
- dB sound power level – relative to 10−12 W.
- dBA, dBB, and dBC
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dB(A). According to standards from the International Electro-technical Committee (IEC 61672-2013)[52] and the American National Standards Institute, ANSI S1.4,[53] the preferred usage is to write LA = x dB. Nevertheless, the units dBA and dB(A) are still commonly used as a shorthand for A‑weighted measurements. Compare dBc, used in telecommunications.
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss. The reference level varies with frequency according to a minimum audibility curve as defined in ANSI and other standards, such that the resulting audiogram shows deviation from what is regarded as ‘normal’ hearing.[citation needed]
- dB Q
- sometimes used to denote weighted noise level, commonly using the ITU-R 468 noise weighting[citation needed]
- dBpp
- relative to the peak to peak sound pressure.[54]
- dBG
- G‑weighted spectrum[55]
Audio electronics[edit]
See also dBV and dBu above.
- dBm
- dB(mW) – power relative to 1 milliwatt. In audio and telephony, dBm is typically referenced relative to a 600 Ω impedance,[56] which corresponds to a voltage level of 0.775 volts or 775 millivolts.
- dBm0
- Power in dBm (described above) measured at a zero transmission level point.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBVU
- dB volume unit[57]
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.[58] In digital systems, 0 dBTP would equal the highest level (number) the processor is capable of representing. Measured values are always negative or zero, since they are less than or equal to full-scale.
Radar[edit]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3:[59] energy of reflectivity (weather radar), related to the amount of transmitted power returned to the radar receiver. Values above 20 dBZ usually indicate falling precipitation.[60]
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the radar cross section (RCS) of a target. The power reflected by the target is proportional to its RCS. «Stealth» aircraft and insects have negative RCS measured in dBsm, large flat plates or non-stealthy aircraft have positive values.[61]
Radio power, energy, and field strength[edit]
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power. Compare dBC, used in acoustics.
- dBpp
- relative to the maximum value of the peak power.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBm
- dB(mW) – power relative to 1 milliwatt. In the radio field, dBm is usually referenced to a 50 Ω load, with the resultant voltage being 0.224 volts.[62]
- dBμV/m, dBuV/m, or dBμ
- [63] dB(μV/m) – electric field strength relative to 1 microvolt per meter. The unit is often used to specify the signal strength of a television broadcast at a receiving site (the signal measured at the antenna output is reported in dBμV).
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBW
- dB(W) – power relative to 1 watt.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBe
- dB electrical.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in a system that is thermal noise limited.[64]
Antenna measurements[edit]
- dBi
- dB(isotropic) – the gain of an antenna compared with the gain of a theoretical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBd
- dB(dipole) – the gain of an antenna compared with the gain a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBiC
- dB(isotropic circular) – the gain of an antenna compared to the gain of a theoretical circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBq
- dB(quarterwave) – the gain of an antenna compared to the gain of a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBsm
- dB(m2) – decibel relative to one square meter: measure of the antenna effective area.[65]
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
Other measurements[edit]
- dB‑Hz
- dB(Hz) – bandwidth relative to one hertz. E.g., 20 dB‑Hz corresponds to a bandwidth of 100 Hz. Commonly used in link budget calculations. Also used in carrier-to-noise-density ratio (not to be confused with carrier-to-noise ratio, in dB).
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs. Similar to dBFS, but also applicable to analog systems. According to ITU-T Rec. G.100.1 the level in dBov of a digital system is defined as:
,
- with the maximum signal power
, for a rectangular signal with the maximum amplitude
. The level of a tone with a digital amplitude (peak value) of
is therefore
.[66]
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to a -90 dBm reference level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America. The Psophometric filter is used for this purpose on international circuits. See Psophometric weighting to see a comparison of frequency response curves for the C-message weighting and Psophometric weighting filters.[67]
- dBK
- dB(K) – decibels relative to 1 K; used to express noise temperature.[68]
- dB/K
- dB(K−1) – decibels relative to 1 K−1.[69] — not decibels per kelvin: Used for the G/T factor, a figure of merit utilized in satellite communications, relating the antenna gain G to the receiver system noise equivalent temperature T.[70][71]
List of suffixes in alphabetical order[edit]
Unpunctuated suffixes[edit]
- dBA
- see dB(A).
- dBa
- see dBrn adjusted.
- dBB
- see dB(B).
- dBc
- relative to carrier – in telecommunications, this indicates the relative levels of noise or sideband power, compared with the carrier power.
- dBC
- see dB(C).
- dBD
- see dB(D).
- dBd
- dB(dipole) – the forward gain of an antenna compared with a half-wave dipole antenna. 0 dBd = 2.15 dBi
- dBe
- dB electrical.
- dBf
- dB(fW) – power relative to 1 femtowatt.
- dBFS
- dB(full scale) – the amplitude of a signal compared with the maximum which a device can handle before clipping occurs. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale square wave. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBG
- G-weighted spectrum
- dBi
- dB(isotropic) – the forward gain of an antenna compared with the hypothetical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBiC
- dB(isotropic circular) – the forward gain of an antenna compared to a circularly polarized isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBJ
- energy relative to 1 joule. 1 joule = 1 watt second = 1 watt per hertz, so power spectral density can be expressed in dBJ.
- dBk
- dB(kW) – power relative to 1 kilowatt.
- dBK
- dB(K) – decibels relative to kelvin: Used to express noise temperature.
- dBm
- dB(mW) – power relative to 1 milliwatt.
- dBm0
- Power in dBm measured at a zero transmission level point.
- dBm0s
- Defined by Recommendation ITU-R V.574.
- dBmV
- dB(mVRMS) – voltage relative to 1 millivolt across 75 Ω.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in system that is thermal noise limited.
- dBO
- see dBov
- dBov or dBO
- dB(overload) – the amplitude of a signal (usually audio) compared with the maximum which a device can handle before clipping occurs.
- dBpp
- relative to the peak to peak sound pressure.
- dBpp
- relative to the maximum value of the peak power.
- dBq
- dB(quarterwave) – the forward gain of an antenna compared to a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- dBrn
- dB above reference noise. See also dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to the circuit noise level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America.
- dBsm
- dB(m2) – decibel relative to one square meter
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.
- dBu or dBv
- RMS voltage relative to
.
- dBu0s
- Defined by Recommendation ITU-R V.574.
- dBuV
- see dBμV
- dBuV/m
- see dBμV/m
- dBv
- see dBu
- dBV
- dB(VRMS) – voltage relative to 1 volt, regardless of impedance.
- dBVU
- dB volume unit
- dBW
- dB(W) – power relative to 1 watt.
- dBW·m−2·Hz−1
- spectral density relative to 1 W·m−2·Hz−1[72]
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3
- dBμ
- see dBμV/m
- dBμV or dBuV
- dB(μVRMS) – voltage relative to 1 microvolt.
- dBμV/m, dBuV/m, or dBμ
- dB(μV/m) – electric field strength relative to 1 microvolt per meter.
Suffixes preceded by a space[edit]
- dB HL
- dB hearing level is used in audiograms as a measure of hearing loss.
- dB Q
- sometimes used to denote weighted noise level
- dB SIL
- dB sound intensity level – relative to 10−12 W/m2
- dB SPL
- dB SPL (sound pressure level) – for sound in air and other gases, relative to 20 μPa in air or 1 μPa in water
- dB SWL
- dB sound power level – relative to 10−12 W.
Suffixes within parentheses[edit]
- dB(A), dB(B), dB(C), dB(D), dB(G), and dB(Z)
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s response to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBA or dBA.
Other suffixes[edit]
- dB-Hz
- dB(Hz) – bandwidth relative to one hertz.
- dB/K
- dB(K−1) – decibels relative to reciprocal of kelvin
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
[edit]
- mBm
- mB(mW) – power relative to 1 milliwatt, in millibels (one hundredth of a decibel). 100 mBm = 1 dBm. This unit is in the Wi-Fi drivers of the Linux kernel[73] and the regulatory domain sections.[74]
See also[edit]
- Apparent magnitude
- Cent (music)
- dB drag racing
- Decade (log scale)
- Loudness
- One-third octave § Base 10
- pH
- Phon
- Richter magnitude scale
- Sone
Notes[edit]
- ^ «When one gives the value of a quantity, it is incorrect to attach letters or other symbols to the unit in order to provide information about the quantity or its conditions of measurement. Instead, the letters or other symbols should be attached to the quantity.»[15]: 16
- ^ «When one gives the value of a quantity, any information concerning the quantity or its conditions of measurement must be presented in such a way as not to be associated with the unit. This means that quantities must be defined so that they can be expressed solely in acceptable units…»[15]: 17
References[edit]
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ a b c Utilities : VRMS / dBm / dBu / dBV calculator, Analog Devices, retrieved 16 September 2016
- ^ Thompson and Taylor 2008, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811 Archived 2016-06-03 at the Wayback Machine.
- ^ IEEE Standard 100: a dictionary of IEEE standards and terms (7th ed.). New York: The Institute of Electrical and Electronics Engineering. 2000. p. 288. ISBN 978-0-7381-2601-2.
- ^ Johnson, Kenneth Simonds (1944). Transmission Circuits for Telephonic Communication: Methods of analysis and design. New York: D. Van Nostrand Co. p. 10.
- ^ Davis, Don; Davis, Carolyn (1997). Sound system engineering (2nd ed.). Focal Press. p. 35. ISBN 978-0-240-80305-0.
- ^ Hartley, R. V. L. (December 1928). «‘TU’ becomes ‘Decibel’«. Bell Laboratories Record. AT&T. 7 (4): 137–139.
- ^ Martin, W. H. (January 1929). «DeciBel—The New Name for the Transmission Unit». Bell System Technical Journal. 8 (1).
- ^ 100 Years of Telephone Switching, p. 276, at Google Books, Robert J. Chapuis, Amos E. Joel, 2003
- ^ Harrison, William H. (1931). «Standards for Transmission of Speech». Standards Yearbook. National Bureau of Standards, U. S. Govt. Printing Office. 119.
- ^ Horton, J. W. (1954). «The bewildering decibel». Electrical Engineering. 73 (6): 550–555. doi:10.1109/EE.1954.6438830. S2CID 51654766.
- ^ «Meeting minutes» (PDF). Consultative Committee for Units. Section 3. Archived (PDF) from the original on 6 October 2014.
- ^ a b «Letter symbols to be used in electrical technology». International Electrotechnical Commission. 19 July 2002. Part 3: Logarithmic and related quantities, and their units. IEC 60027-3, Ed. 3.0.
- ^ a b c d Thompson, A. and Taylor, B. N. sec 8.7, «Logarithmic quantities and units: level, neper, bel», Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF
- ^ «Letter symbols to be used in electrical technology». International Standard CEI-IEC 27-3. International Electrotechnical Commission. Part 3: Logarithmic quantities and units.
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. p. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Second ed.). Holt, Rinehart and Winston. p. 206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ Fedor Mitschke, Fiber Optics: Physics and Technology, Springer, 2010 ISBN 3642037038.
- ^ Pozar, David M. (2005). Microwave Engineering (3rd ed.). Wiley. p. 63. ISBN 978-0-471-44878-5.
- ^ IEC 60027-3:2002
- ^ I M Mills; B N Taylor; A J Thor (2001), «Definitions of the units radian, neper, bel and decibel», Metrologia, 38 (4): 353, Bibcode:2001Metro..38..353M, doi:10.1088/0026-1394/38/4/8, S2CID 250827251
- ^ R. Hickling (1999), Noise Control and SI Units, J Acoust Soc Am 106, 3048
- ^ Hickling, R. (2006). Decibels and octaves, who needs them?. Journal of sound and vibration, 291(3-5), 1202-1207.
- ^ Nicholas P. Cheremisinoff (1996) Noise Control in Industry: A Practical Guide, Elsevier, 203 pp, p. 7
- ^ Andrew Clennel Palmer (2008), Dimensional Analysis and Intelligent Experimentation, World Scientific, 154 pp, p.13
- ^ J. C. Gibbings, Dimensional Analysis, p.37, Springer, 2011 ISBN 1849963177.
- ^ Fiber Optics. Springer. 2010.
- ^ R. J. Peters, Acoustics and Noise Control, Routledge, 12 November 2013, 400 pages, p. 13
- ^ Sensation and Perception, p. 268, at Google Books
- ^ Introduction to Understandable Physics, Volume 2, p. SA19-PA9, at Google Books
- ^ Visual Perception: Physiology, Psychology, and Ecology, p. 356, at Google Books
- ^ Exercise Psychology, p. 407, at Google Books
- ^ Foundations of Perception, p. 83, at Google Books
- ^ Fitting The Task To The Human, p. 304, at Google Books
- ^ ISO 1683:2015
- ^ C. S. Clay (1999), Underwater sound transmission and SI units, J Acoust Soc Am 106, 3047
- ^ «Loud Noise Can Cause Hearing Loss». cdc.gov. Centers for Disease Control and Prevention. 7 October 2019. Retrieved 30 July 2020.
- ^ Richard L. St. Pierre, Jr. and Daniel J. Maguire (July 2004), The Impact of A-weighting Sound Pressure Level Measurements during the Evaluation of Noise Exposure (PDF), archived (PDF) from the original on 22 December 2015, retrieved 13 September 2011
- ^ Reeve, William D. (1992). Subscriber Loop Signaling and Transmission Handbook – Analog (1st ed.). IEEE Press. ISBN 0-87942-274-2.
- ^
Chomycz, Bob (2000). Fiber optic installer’s field manual. McGraw-Hill Professional. pp. 123–126. ISBN 978-0-07-135604-6. - ^
Stephen J. Sangwine and Robin E. N. Horne (1998). The Colour Image Processing Handbook. Springer. pp. 127–130. ISBN 978-0-412-80620-9. - ^
Francis T. S. Yu and Xiangyang Yang (1997). Introduction to optical engineering. Cambridge University Press. pp. 102–103. ISBN 978-0-521-57493-8. - ^
Junichi Nakamura (2006). «Basics of Image Sensors». In Junichi Nakamura (ed.). Image sensors and signal processing for digital still cameras. CRC Press. pp. 79–83. ISBN 978-0-8493-3545-7. - ^ Winer, Ethan (2013). The Audio Expert: Everything You Need to Know About Audio. Focal Press. p. 107. ISBN 978-0-240-82100-9.
- ^ Stas Bekman. «3.3 – What is the difference between dBv, dBu, dBV, dBm, dB SPL, and plain old dB? Why not just use regular voltage and power measurements?». stason.org.
- ^ Rupert Neve, Creation of the dBu standard level reference, archived from the original on 30 October 2021
- ^ deltamedia.com. «DB or Not DB». Deltamedia.com. Retrieved 16 September 2013.
- ^ The IEEE Standard Dictionary of Electrical and Electronics terms (6th ed.). IEEE. 1996 [1941]. ISBN 978-1-55937-833-8.
- ^ Jay Rose (2002). Audio postproduction for digital video. Focal Press. p. 25. ISBN 978-1-57820-116-7.
- ^ Morfey, C. L. (2001). Dictionary of Acoustics. Academic Press, San Diego.
- ^ IEC 61672-1:2013 Electroacoustics — Sound Level meters — Part 1: Specifications. Geneva: International Electrotechnical Committee. 2013.
- ^ ANSI S1.4-19823 Specification for Sound Level Meters, 2.3 Sound Level, p. 2–3.
- ^ Zimmer, Walter MX, Mark P. Johnson, Peter T. Madsen, and Peter L. Tyack. «Echolocation clicks of free-ranging Cuvier’s beaked whales (Ziphius cavirostris).» The Journal of the Acoustical Society of America 117, no. 6 (2005): 3919–3927.
- ^ «Turbine Sound Measurements». Archived from the original on 12 December 2010.
- ^ Bigelow, Stephen (2001). Understanding Telephone Electronics. Newnes. p. 16. ISBN 978-0750671750.
- ^ Tharr, D. (1998). Case Studies: Transient Sounds Through Communication Headsets. Applied Occupational and Environmental Hygiene, 13(10), 691–697.
- ^ ITU-R BS.1770
- ^ «Glossary: D’s». National Weather Service. Archived from the original on 8 August 2019. Retrieved 25 April 2013.
- ^ «RIDGE Radar Frequently Asked Questions». Archived from the original on 31 March 2019. Retrieved 8 August 2019.
- ^ «Definition at Everything2». Archived from the original on 10 June 2019. Retrieved 8 August 2019.
- ^ Carr, Joseph (2002). RF Components and Circuits. Newnes. pp. 45–46. ISBN 978-0750648448.
- ^ «The dBµ vs. dBu Mystery: Signal Strength vs. Field Strength?». radio-timetraveller.blogspot.com. 24 February 2015. Retrieved 13 October 2016.
- ^ Chand, N., Magill, P. D., Swaminathan, S. V., & Daugherty, T. H. (1999). Delivery of digital video and other multimedia services (> 1 Gb/s bandwidth) in passband above the 155 Mb/s baseband services on a FTTx full service access network. Journal of lightwave technology, 17(12), 2449–2460.
- ^ David Adamy. EW 102: A Second Course in Electronic Warfare. Retrieved 16 September 2013.
- ^ ITU-T Rec. G.100.1 The use of the decibel and of relative levels in speechband telecommunications https://www.itu.int/rec/dologin_pub.asp?lang=e&id=T-REC-G.100.1-201506-I!!PDF-E&type=items
- ^ dBrnC is defined on page 230 in «Engineering and Operations in the Bell System,» (2ed), R.F. Rey (technical editor), copyright 1983, AT&T Bell Laboratories, Murray Hill, NJ, ISBN 0-932764-04-5
- ^ K. N. Raja Rao (31 January 2013). Satellite Communication: Concepts And Applications. Retrieved 16 September 2013.
- ^ Ali Akbar Arabi. Comprehensive Glossary of Telecom Abbreviations and Acronyms. Retrieved 16 September 2013.
- ^ Mark E. Long. The Digital Satellite TV Handbook. Retrieved 16 September 2013.
- ^ Mac E. Van Valkenburg (19 October 2001). Reference Data for Engineers: Radio, Electronics, Computers and Communications. Retrieved 16 September 2013.
- ^ «Archived copy». Archived from the original on 3 March 2016. Retrieved 24 August 2013.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ «en:users:documentation:iw [Linux Wireless]». wireless.kernel.org.
- ^ «Is your WiFi AP Missing Channels 12 & 13?». wordpress.com. 16 May 2013.
Further reading[edit]
- Tuffentsammer, Karl (1956). «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [The decilog, a bridge between logarithms, decibel, neper and preferred numbers]. VDI-Zeitschrift (in German). 98: 267–274.
- Paulin, Eugen (1 September 2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon — natürlich verwandt! [Logarithms, preferred numbers, decibel, neper, phon — naturally related!] (PDF) (in German). Archived (PDF) from the original on 18 December 2016. Retrieved 18 December 2016.
External links[edit]
- What is a decibel? With sound files and animations
- Conversion of sound level units: dBSPL or dBA to sound pressure p and sound intensity J
- OSHA Regulations on Occupational Noise Exposure
- Working with Decibels (RF signal and field strengths)
Запрос «Дб» перенаправляется сюда; см. также другие значения.
Децибе́л — логарифмическая единица уровней, затуханий и усилений.[1]
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять:
где AdB — величина в децибелах, A — измеренная физическая величина, A0 — величина, принятая за базис.
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трёхкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причём к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB»[2] (неправильно: дб, Дб).
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международное бюро мер и весов рекомендовала включить его в эту систему.
Содержание
- 1 Сравнение с другими логарифмическими единицами
- 2 Области применения
- 3 Переход к децибелам
- 3.1 Измерение «энергетических» величин
- 3.2 Измерение «неэнергетических» величин
- 3.3 Децибелы «по мощности», «по напряжению» и «по току»
- 4 Примеры вычислений
- 4.1 Переход к дБ
- 4.2 Переход от дБ к «разам»
- 4.3 Переход от дБ к мощности
- 4.4 Переход от дБ к напряжению (току)
- 4.5 Рекомендации
- 5 Причины использования децибелов
- 6 Условные обозначения
- 7 Опорный уровень
- 8 См. также
- 9 Примечания
- 10 Ссылки
Сравнение с другими логарифмическими единицами
| название | сокращение | соответствует изменению в … раз |
пересчёт в … | |||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | Xm | |||
| децибел | дБ, dB | ≈1,26 (![sqrt[10]{10}](https://dic.academic.ru/dic.nsf/ruwiki/40f2d8715e2f4e13e16fa33cea40c1d6.png) ) ) |
1 | 0,1 | ≈0,115 | −0,25 |
| бел | Б, B | 10 | 10 | 1 | ≈1,15 | −2,5 |
| непер | Нп, Np | ≈2,72 (e) | ≈8,686 | ≈0,8686 | 1 | ≈−1,086 |
| звёздная величина |
Xm | ≈0,398 (![sqrt[5]{0,01}](https://dic.academic.ru/dic.nsf/ruwiki/2cdc2c2548f0dfac37d83483d5da6ef1.png) ) ) |
−4 | −0,4 | ≈−0,921 | 1 |
Области применения
Децибелы широко применяются в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибелы используются не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). В децибелах можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
Переход к децибелам
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P ~ U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические.[источник не указан 153 дня]
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:
,
где x — величина, измеряемая в дБ; P1/P0 — отношение значений двух мощностей: измеряемой P1 к так называемой опорной P0, то есть базовой, взятой за нулевой уровень (имеется в виду нулевой уровень в единицах дБ, поскольку в случае равенства мощностей P1 = P0 логарифм их отношения lg(P1/P0) = 0).
Соответственно, переход от дБ к отношению мощностей осуществляется по формуле:
,
где x — величина, измеряемая в дБ. Мощность P1 может быть найдена при известной опорной мощности P0 по выражению
.
Измерение «неэнергетических» величин
Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца 


В общем случае напряжения U1 и U0 могут регистрироваться на различных по величине сопротивлениях (R1 не равно R0). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае
- величина в децибелах =
.
Только в частном (весьма распространенном) случае, если оба напряжения U1 и U0 измерялись на одном и том же сопротивлении (R1 = R0), можно пользоваться кратким выражением
- величина в децибелах =
.
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
- дБ по напряжению =
;
- дБ по току =
.
Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
- при регистрации мощности изменению на +1 дБ (+1 дБ «по мощности») соответствует приращение мощности в ≈1,259 раза, изменению на −3,01 дБ — снижение мощности в два раза, в то время как
- при регистрации напряжения (силы тока) изменению на +1 дБ (+1 дБ «по напряжению», «по току») будет соответствовать приращение напряжения (силы тока) в ≈1,122 раза, при изменении на −3,01 дБ напряжение (сила тока) снизятся и составят
≈ 0,707 от своего исходного значения.
Примеры вычислений
Переход к дБ
Пусть значение мощности P1 стало в 2 раза больше исходного значения мощности P0, тогда
- 10 lg(P1/P0) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,
то есть рост мощности на 3 дБ означает её увеличение в 2 раза.
Пусть значение мощности P1 стало в 2 раза меньше исходного значения мощности P0, то есть P1 = 0,5 P0. Тогда
- 10 lg(P1/P0) = 10 lg(0,5) ≈ −3 дБ,
то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:
- рост мощности в 10 раз: 10 lg(P1/P0) = 10 lg(10) = 10 дБ, снижение в 10 раз: 10 lg(P1/P0) = 10 lg(0,1)= −10 дБ;
- рост в 1 млн раз: 10 lg(P1/P0) = 10 lg(1 000 000) = 60 дБ, снижение в 1 млн раз: 10 lg(P1/P0) = 10 lg(0,000001) = −60 дБ.
Переход от дБ к «разам»
Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:
 |
10000 | 100 | 10 | ≈ 4 | ≈ 2 | ≈ 1.26 | 1 | ≈ 0.79 | ≈ 0.5 | ≈ 0.25 | 0.1 | 0.01 | 0.0001 |
 |
40 дБ | 20 дБ | 10 дБ | 6 дБ | 3 дБ | 1 дБ | 0 дБ | −1 дБ | −3 дБ | −6 дБ | −10 дБ | −20 дБ | −40 дБ |
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:
Вт.
Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:
≈ 4 В.
Рекомендации
Операции с децибелами можно выполнять в уме: вместо умножения, деления, возведения в степень и извлечения корня применяется сложение и вычитание децибельных единиц. Для этого можно использовать таблицы соотношений (первые 2 — приближённые):
- 1 дБ → в 1,25 раза,
- 3 дБ → в 2 раза,
- 10 дБ → в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
- 6 дБ = 3 дБ + 3 дБ → в 2·2 = в 4 раза,
- 9 дБ = 3 дБ + 3 дБ + 3 дБ → в 2·2·2 = в 8 раз,
- 12 дБ = 4 · (3 дБ) → в 24 = в 16 раз
и т. п., а также:
- 13 дБ = 10 дБ + 3 дБ → в 10·2 = в 20 раз,
- 20 дБ = 10 дБ + 10 дБ → в 10·10 = в 100 раз,
- 30 дБ = 3 · (10 дБ) → в 10³ = в 1000 раз
и т. п.
Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:
- уменьшение мощности в 40 раз → это в 4·10 раз или на −(6 дБ + 10 дБ) = −16 дБ;
- увеличение мощности в 128 раз это 27 или на 7·(3 дБ) = 21 дБ;
- снижение напряжения в 4 раза эквивалентно снижению мощности (величины второго порядка) в 4² = 16 раз; и то и другое при R1 = R0 эквивалентно снижению на 4·(−3 дБ) = −12 дБ.
Причины использования децибелов
Для применения децибелов и оперирования логарифмами вместо процентов или долей есть ряд причин:
- Характер отображения в органах чувств человека и животных изменений течения многих физических и биологических процессов пропорционален не амплитуде входного воздействия, а логарифму входного воздействия (живая природа живёт по логарифму[3]). Поэтому вполне естественно шкалы приборов и вообще шкалы единиц устанавливать именно в логарифмические, в том числе, используя децибелы. Например музыкальная равномерно темперированная шкала частот является одной из таких логарифмических шкал.
- Удобство логарифмической шкалы в тех случаях, когда в одной задаче приходится оперировать одновременно величинами, различающимися не во втором знаке после запятой, а в разы и, тем более, различающимися на много порядков (примеры: задача выбора графического отображения уровней сигнала, частотных диапазонов радиоприемников и др. звуковоспроизводящих устройств, расчет частот для настройки клавиатуры фортепьяно, расчеты спектров при синтезе и обработке музыкальных и других гармонических звуковых, световых волн, графические отображения скоростей в космонавтике, авиации, в скоростном транспорте, графическое отображения других переменных величин, изменения которых в широком диапазоне величин являются критически важными).
- Удобство отображения и анализа величины, изменяющейся в очень широких пределах (примеры — диаграмма направленности антенны, амплитудно-частотная характеристика электрического фильтра).
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например дБВ (децибел относительно вольта) или дБмкВ (децибел относительно микровольта), дБВт (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину её значение помещают в скобках за обозначением логарифмической величины, например, для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Опорный уровень
Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0 дБ).
Строго говоря, должно быть однозначно определено, какая именно физическая величина и какое именно её значение используются в качестве опорного уровня. Опорный уровень указывается в виде добавки, следующей за символами «дБ» (например, дБм), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).
На практике распространены следующие опорные уровни и специальные обозначения для них:
- dBm (русское дБм) — опорный уровень — это мощность в 1 мВт. Мощность обычно определяется на номинальной нагрузке (для профессиональной техники — обычно 10 кОм для частот менее 10 МГц, для радиочастотной техники — 50 Ом или 75 Ом). Например, «выходная мощность усилительного каскада составляет 13 дБм» (то есть мощность, выделяющаяся на номинальной для этого усилительного каскада нагрузке, составляет 20 мВт).
- dBV (русское дБВ) — опорное напряжение 1 В на номинальной нагрузке (для бытовой техники — обычно 47 кОм); например, стандартизованный уровень сигнала для бытового аудиооборудования составляет −10 дБВ, то есть 0,316 В на нагрузке 47 кОм.
- dBuV (русское дБмкВ) — опорное напряжение 1 мкВ; например, «чувствительность радиоприёмника, измеренная на антенном входе — −10 дБмкВ … номинальное сопротивление антенны — 50 Ом».
Связь напряжения в dBu с вольтами, ваттами и дБм. Падение напряжения в 0,775 В (среднеквадратическое значение) на нагрузке с сопротивлением 600 Ом приводит к рассеянию на этой нагрузке средней мощности в 1 мВт (0 дБм). Говорят, что в этом случае уровень сигнала — 0 dBu
- dBu — опорное напряжение 0.775 В, соответствующее мощности 1 мВт на нагрузке 600 Ом; например, стандартизованный уровень сигнала для профессионального аудиооборудования составляет +4 dBu, то есть 1,23 В.
- dBm0 (русское дБм0) — опорная мощность в дБм в точке нулевого относительного уровня. «Абсолютный уровень мощности относительно 1 мВт в точке линии передачи с нулевым уровнем»[1]
- dBrn — опорное напряжение соответствует тепловому шуму идеального резистора сопротивлением 50Ω при комнатной температуре в полосе 1Гц:
. Например, «уровень шума усилителя составляет 6dBrn».
- dBFS (англ. Full Scale — «полная шкала») — опорное напряжение соответствует полной шкале прибора; например, «уровень записи составляет −6dBfs». Для линейного цифрового кода каждый разряд соответствует 6дБ, и максимально возможный уровень записи равен 0dBFS.
- dBSPL (англ. Sound Pressure Level — «уровень звукового давления») — опорное звуковое давление 20мкПа, соответствующее порогу слышимости; например, «громкость 100dBSPL».
- dBPa — опорное звуковое давление 1Па или 94дБ звуковой шкалы громкости dBSPL; например, «для громкости 6dBPa микшером установили +4dBu, а регулятором записи −3dBFS, искажения при этом составили −70dBc».
- dBA, dBB, dBC, dBD — опорные уровни выбраны в соответствии с частотными характеристиками «весовых фильтров» в соответствии с кривыми равной громкости (см.: Фон (единица измерения)).
- dBc (русское дБн) — опорным является уровень излучения на частоте несущей (англ. carrier) или уровень основной гармоники в спектре сигнала. Примеры использования: «уровень побочного излучения радиопередатчика на частоте второй гармоники составляет −60 дБн» (то есть мощность этого побочного излучения в 1 млн раз меньше мощности несущей) или «уровень искажений составляет −60 дБн».
- dBi (русское дБи) — изотропный децибел (децибел относительно изотропного излучателя). Характеризует коэффициент направленного действия (а также коэффициент усиления) антенны относительно коэффициента направленного действия изотропного излучателя. Как правило, если не оговорено специально, характеристики усиления реальных антенн даются именно относительно усиления изотропного излучателя. То есть, когда вам говорят, что коэффициент усиления какой-то антенны равен 12 децибел, подразумевается 12 дБи.
- dBd (русское дБд) — децибел относительно полуволнового вибратора («относительно диполя»). Характеризует коэффициент направленного действия (а также коэффициент усиления) антенны относительно коэффициента направленного действия полуволнового вибратора, размещенного в свободном пространстве. Поскольку коэффициент направленного действия указанного полуволнового вибратора приближённо равен 2,15 дБи, то коэффициент направленного действия, измеряемый в дБд, всегда меньше коэффициента направленного действия, измеряемого в дБи, на фиксированную величину, равную 2,15 дБ.
- dBsm — децибел относительно одного квадратного метра. Характеризует эффективную поверхность рассеяния рассеивателя в радиолокации.
По аналогии образуются составные единицы измерений. Например, уровень спектральной плотности мощности дБВт/Гц — «децибельный» аналог единицы измерения Вт/Гц (мощность, выделяющаяся на номинальной нагрузке в полосе частот шириной в 1 Гц с центром на указанной частоте). Опорным уровнем в данном примере является 1 Вт/Гц, то есть физическая величина «спектральная плотность мощности», её размерность «Вт/Гц» и значение «1». Так, запись «-120 дБВт/Гц» полностью эквивалентна записи «10−12 Вт/Гц».
В случае затруднения во избежание путаницы достаточно указать опорный уровень явно. Например, запись −20 дБ (относительно 0,775 B на нагрузке 50 Ом) исключает двойное толкование.
Справедливы следующие правила (следствие правил действий с размерными величинами):
- перемножать или делить «децибельные» значения нельзя (это бессмысленно);
- суммирование «децибельных» значений соответствует умножению абсолютных значений, вычитание «децибельных» значений — делению абсолютных значений;
- суммирование или вычитание «децибельных» значений может выполняться независимо от их «исходной» размерности. Например, равенство 10 дБм + 13 дБ = 23 дБм является корректным, полностью эквивалентно равенству 10 мВт · 20 = 200 мВт и может трактоваться как «усилитель с коэффициентом усиления 13 дБ увеличивает мощность сигнала с 10 дБм до 23 дБм».
При пересчёте уровней мощностей (дБВт, дБм) в уровни напряжений (дБВ, дБмкВ) и обратно необходимо учитывать сопротивление, на котором определяется мощность и напряжение:
Для 50 Ом:
- Мощность в напряжение:
- дБмкВ = дБм + 107
- дБмкВ = дБВт + 137
- дБВ = дБм — 13
- дБВ = дБВт + 17
- Напряжение в мощность:
- дБм = дБмкВ — 107
- дБм = дБВ + 13
- дБВт = дБмкВ — 137
- дБВт = дБВ — 17
Для 75 Ом:
- Мощность в напряжение:
- дБмкВ = дБм + 108,75
- дБмкВ = дБВт + 138,75
- дБВ = дБм — 11,25
- дБВ = дБВт + 18,75
- Напряжение в мощность:
- дБм = дБмкВ — 108,75
- дБм = дБВ + 11,25
- дБВт = дБмкВ — 138,75
- дБВт = дБВ — 18,75
См. также
- Аттенюатор
Примечания
- ↑ 1 2 ОСТ 45.159-2000. Отраслевая система обеспечения единства измерений. Термины и определения
- ↑ ГОСТ 8.417-2002
- ↑ Закон Вебера — Фехнера
Ссылки
- Что такое децибел?
- Таблица перехода от децибелов
- Конвертер мощности в дБм и обратно
- Таблица dBu — V, с шагом 0,1 db диапазона 0,0 db / −60,0 db
- Таблица dBu — V, с шагом 0,1 db диапазона 0,0 db / +40,0 db
- Таблицы dBu — V, с шагом 0,01 db диапазона 0,0 db / −60,0 db
- Таблицы dBu — V, с шагом 0,01 db диапазона 0,0 db / +40,0 db
- Таблицы dBu — V, с шагом 0,001 db диапазона 0,0 db / −60,0 db
- Таблицы dBu — V, с шагом 0,001 db диапазона 0,0 db / +40,0 db
- Постановление Правительства РФ от 31 октября 2009 г. N 879 Об утверждении положения о единицах величин, допускаемых к применению в Российской Федерации
- Сравнительные шкалы процентов и децибелов для расчёта уровня цифрового звука
Отношение
D
P
{displaystyle D_{P}}
двух значений энергетической величины
P
{displaystyle P}
, такой как мощность, энергия, плотность энергии и т. п., выраженное в децибелах, определяется по формуле:
D
P
=
10
lg
P
1
P
0
.
{displaystyle D_{P}=10lg {frac {P_{1}}{P_{0}}}.}
Отсюда следует, что увеличение энергетической величины на 1 дБ означает её увеличение в
10
0
,
1
{displaystyle 10^{0,1}}
≈ 1,259 раза.
Энергетические величины пропорциональны квадратам силовых величин (или величин поля, как принято в международных документах), таких как звуковое давление, электрическое напряжение, сила электрического тока и т. п., поэтому отношение
D
F
{displaystyle D_{F}}
двух значений силовой величины
F
{displaystyle F}
, выраженное в децибелах, определяется по формуле:
D
F
=
20
lg
F
1
F
0
.
{displaystyle D_{F}=20lg {frac {F_{1}}{F_{0}}}.}
Отсюда следует, что увеличение силовой величины на 1 дБ означает её увеличение в
10
0
,
05
{displaystyle 10^{0,05}}
≈ 1,122 раза.
Децибел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.
дБ, дБм, дБВт, дБн Основы: в чем разница между ними?
Date:2020/10/26 12:18:09 Hits:
В ВЧ- и СВЧ-измерениях обычно используются такие единицы, как дБ, дБм, дБн и дБВт. Эти термины могут показаться запутанными, но на самом деле они довольно хороши. легко понять.
В этой короткой статье мы рассмотрим разницу между этими терминами и навсегда разрешите эту путаницу!
1. дБ или децибел — функция, работающая на безразмерном параметр
Короче говоря, дБ — это отношение двух величин. Поскольку это соотношение, в нем нет единицы. Обычно мы говорим о соотношении двух уровней мощности, хотя в некоторых В случаях мы также используем соотношение уровней напряжения. Вот что такое дБ.
Итак, вот уравнение, о котором нужно помнить:
дБ = 10 log (Power2 / Power1) (Power2 / Power1 безразмерно! )
Это относительное значение между двумя уровнями мощности.
В: Без единиц! Что в этом хорошего! ?
О: Многие значения безразмерны, например, отношения и коэффициенты.

Подождите минуту! Мы видели такие утверждения, как:

Мощность не безразмерная (но ватт — это единица измерения?) !!
Правда! Но посмотрите, как выражается сила; не в дБ,но в дБм или дБВт.
В: Что означает дБм или дБВт?
A: Это своего рода уловка!
2. дБм или децибел относительно уровня мощности 1 мВт
дБм — это просто мощность, измеренная относительно 1 милливатта. Итак, если мы заменим Power1 с 1 мВт в предыдущем уравнении, результат измерения в дБм.
Это абсолютное значение (поскольку оно измеряется относительно фиксированного ссылка).
дБ = 10 log (мощность2 / 1 мВт)
Мощность в РЧ-измерениях обычно выражается в дБмВт.
Так какая же мощность в дБм при 1 мВт? Конечно 0 дБм!
Допустим, у нас есть мощность P. Мы можем выразить P в дБм илидБВт как:
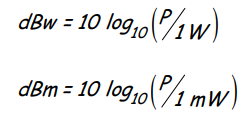
Следовательно, dBw и dBm выражают Prelative как 1 Вт и 1 мВт соответственно!
Примечание: Аргументом функции log10 является коэффициент (т. Е. Безразмерный).
Например,
20 дБм означает 100 x 1 мВт = 100 мВт
3 дБВт означает 2 x 1 Вт = 2 Вт
Будьте осторожны при вычислениях с децибелами!
Стандартные значения в дБ
Обратите внимание, что 10 log10 (10) = 10.
Поэтому говорят, что усилитель с коэффициентом усиления G = 10 имеетусиление 10 дБ.
3. дБВт или децибел относительно уровня мощности 1 Вт.
дБВт не сильно отличается от дБм с той лишь разницей, что мы просто используйте 1 Вт в качестве эталона вместо 1 мВт в дБмВт.
дБ = 10 log (мощность2 / 1 Вт)
Это абсолютная величина.
4. дБн или децибел относительно уровня мощности несущей
дБн — мощность, измеренная относительно уровня мощности несущей.
Обычно это используется для указания таких параметров, как SFDR (Spurious Free Dynamic Range), гармоники и т. Д., Которые имеют большее значение, когда мощность основной несущей в перспективе
В заключение:
0 дБм = 1 мВт = -30 дБВт
+30 дБм = 1 Вт = 0 дБВт
Я считаю, что вы, ребята, можете отличить дБ, дБм, дБВт, дБн.
Итак, чЕсть несколько небольших тестов для вас:
Q1. Подайте 10 мВт на РЧ-усилитель, и измеренная мощность составит 150 мВт. Каков коэффициент усиления в дБ этого усилителя?
Q2. Коэффициент усиления ВЧ усилителя составляет 18 дБ, если измеренная выходная мощность составляет 230 мВт, то какова входная мощность?
Q3. Насколько 12 дБ больше 30 дБмВт?

Ответ 1
Поскольку Pin = 10 мВт и Pout = 150 мВт
Усиление (дБ) = 10log (150/10) = 11.8 дБ
Ответ 2
* Поскольку Pout = 230 мВт и усиление = 18 дБ
* 10log (230 / Pin) = 18 дБ
* Журнал (230 / контактный) = (18/10) = 1.8
* 101.8 = 230 / контактный
*Therefore, Pin=230/(101.8)=230/63.1=3.65 mW
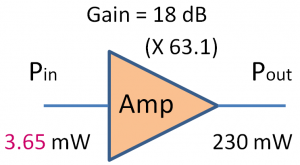
Ответ3.
12 дБ более 30 дБм — это 42 дБм.
И мы можем удобно сказать,
30 дБм (1 Вт) + 12 дБ (x 16) = 42 дБм (16 Вт)
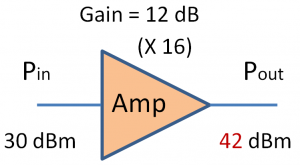
Правильно ли вы поняли your Жду вашего комментария!
Оставить сообщение
Список сообщений
Эта статья про логарифмическую единицу. Для использования в других целях см. Децибел (значения).
В децибел (символ: дБ) является родственником единица измерения соответствует одной десятой Bel (B). Он используется для выражения отношения одного значения power или root-power количество к другому, на логарифмическая шкала. Логарифмическая величина в децибелах называется уровень. Два сигнала, уровни которых отличаются на один децибел, имеют коэффициент мощности 101/10 (приблизительно 1,25893) или (иногда эквивалентно) отношение амплитуд (величины поля) 101⁄20 (примерно 1,12202).[1][2]
Децибелы могут использоваться для выражения изменения значения (например, +1 дБ или -1 дБ) или абсолютного значения. В последнем случае количество децибел выражает отношение значения к фиксированному эталонному значению; при использовании таким образом к символу децибел часто добавляется суффикс, указывающий на эталонное значение. Например, если эталонное значение равно 1вольт, то суффикс «V «(например,» 20 дБВ «), и если эталонное значение равно единице милливатт, то суффикс «м «(например,» 20 дБм «) согласно NIST.[3][4]
Для выражения отношения в децибелах используются разные определения, в зависимости от природы величин: степень и корень-степень. При выражении отношения мощности число децибел в десять раз больше логарифм по основанию 10.[5] То есть изменение мощность в 10 раз соответствует изменению уровня на 10 дБ. При выражении величин корневой степени изменение амплитуда в 10 раз соответствует изменению уровня на 20 дБ. Шкалы децибел различаются в два раза, так что соответствующие уровни мощности и корня мощности изменяются на одинаковое количество децибел в линейных системах, где мощность пропорциональна квадрату амплитуды.
Определение децибела возникло при измерении мощности в телефония начала 20 века в Bell System В Соединенных Штатах. Один децибел равен одной десятой (деци- ) одного Bel, названный в честь Александр Грэхем Белл; однако пояс используется редко. Сегодня децибел используется для самых разных измерений в науке и инженерное дело, наиболее заметно в акустика, электроника, и теория управления. В электронике прибыль усилителей, затухание сигналов, и отношения сигнал / шум часто выражаются в децибелах.
в Международная система количеств, децибел определяется как единица измерения величин типа уровень или разность уровней, которые определяются как логарифм отношения степенных или корневых степенных величин.[6]
| дБ | Коэффициент мощности | Соотношение амплитуд | ||
|---|---|---|---|---|
| 100 | 10000000000 | 100000 | ||
| 90 | 1000000000 | 31623 | ||
| 80 | 100000000 | 10000 | ||
| 70 | 10000000 | 3162 | ||
| 60 | 1000000 | 1000 | ||
| 50 | 100000 | 316 | .2 | |
| 40 | 10000 | 100 | ||
| 30 | 1000 | 31 | .62 | |
| 20 | 100 | 10 | ||
| 10 | 10 | 3 | .162 | |
| 6 | 3 | .981 ≈ 4 | 1 | .995 ≈ 2 |
| 3 | 1 | .995 ≈ 2 | 1 | .413 ≈ √2 |
| 1 | 1 | .259 | 1 | .122 |
| 0 | 1 | 1 | ||
| −1 | 0 | .794 | 0 | .891 |
| −3 | 0 | .501 ≈ 1⁄2 | 0 | .708 ≈ √1⁄2 |
| −6 | 0 | .251 ≈ 1⁄4 | 0 | .501 ≈ 1⁄2 |
| −10 | 0 | .1 | 0 | .3162 |
| −20 | 0 | .01 | 0 | .1 |
| −30 | 0 | .001 | 0 | .03162 |
| −40 | 0 | .0001 | 0 | .01 |
| −50 | 0 | .00001 | 0 | .003162 |
| −60 | 0 | .000001 | 0 | .001 |
| −70 | 0 | .0000001 | 0 | .0003162 |
| −80 | 0 | .00000001 | 0 | .0001 |
| −90 | 0 | .000000001 | 0 | .00003162 |
| −100 | 0 | .0000000001 | 0 | .00001 |
| Пример шкалы, показывающей отношения мощностей Икс, отношения амплитуд √Икс, а эквивалент в дБ 10 log10 Икс. |
История
Децибел возник из методов, используемых для количественной оценки потерь сигнала в телеграфных и телефонных сетях. Единица измерения потерь изначально была Мили стандартного кабеля (МСК). 1 MSC соответствовал потере мощности более 1миля (примерно 1,6 км) длина стандартного телефонного кабеля на частоте 5000радианы в секунду (795,8 Гц) и близко соответствует наименьшему ослаблению, обнаруживаемому средним слушателем. Под стандартным телефонным кабелем подразумевается «кабель, имеющий равномерно распределенное сопротивление 88 Ом на петлевую милю и равномерно распределенный. шунт емкость 0,054микрофарады за милю «(приблизительно соответствует 19измерять провод).[7]
В 1924 г. Bell Telephone Laboratories получил положительный отклик на новое определение единицы среди членов Международный консультативный комитет по междугородной телефонии в Европе и заменил MSC на Блок трансмиссии (ВТ). 1 ТУ был определен таким образом, что количество БПД десять раз по основанию 10 логарифм отношения измеренной мощности к эталонной мощности.[8]Определение было удобно выбрано так, что 1 TU приблизительно соответствовал 1 MSC; в частности, 1 MSC был 1.056 TU. В 1928 году система Bell переименовала TU в децибел,[9] составляющая одну десятую вновь определенной единицы для десятичного логарифма отношения мощностей. Он был назван Bel, в честь пионера телекоммуникаций Александр Грэхем Белл.[10]Бел редко используется, так как децибел был предложенной рабочей единицей.[11]
Именование и раннее определение децибела описано в NBS Ежегодник Standard за 1931 год:[12]
С первых дней существования телефона была признана необходимость в устройстве для измерения эффективности передачи телефонных средств. Внедрение кабеля в 1896 году обеспечило прочную основу для удобного устройства, и вскоре после этого «миля стандартного» кабеля стала широко использоваться. Это устройство использовалось до 1923 года, когда было принято новое устройство, более подходящее для современной телефонной работы. Новое устройство передачи широко используется среди иностранных телефонных организаций, и недавно оно было названо «децибелом» по предложению Международного консультативного комитета по междугородной телефонии.
Децибел может быть определен утверждением, что два количества мощности отличаются на 1 децибел, когда они находятся в соотношении 100.1 и любые два уровня мощности отличаются на N децибел, когда они находятся в соотношении 10N(0.1). Количество единиц передачи, выражающих отношение любых двух степеней, поэтому в десять раз больше десятичного логарифма этого отношения. Этот метод обозначения усиления или потери мощности в телефонных цепях позволяет прямое сложение или вычитание единиц, выражающих эффективность различных частей цепи …
В 1954 году Дж. У. Хортон утверждал, что использование децибела в качестве единицы для величин, отличных от потерь передачи, привело к путанице, и предложил название логит для «стандартных величин, которые складываются путем умножения», чтобы контрастировать с названием единица измерения для «стандартных величин, которые складываются путем сложения».[13][требуется разъяснение ]
В апреле 2003 г. Международный комитет мер и весов (CIPM) рассмотрел рекомендацию о включении децибела в Международная система единиц (SI), но отказался от предложения.[14] Однако децибел признан другими международными организациями, такими как Международная электротехническая комиссия (IEC) и Международная организация по стандартизации (ISO).[15] МЭК разрешает использовать децибелы для значений основной мощности, а также мощности, и этой рекомендации следуют многие национальные органы по стандартизации, такие как NIST, что оправдывает использование децибел для отношений напряжений.[16] Несмотря на широкое распространение, суффиксы (например, в дБА или дБВ) не признаются IEC или ISO.
Определение
ISO 80000-3 описывает определения количеств и единиц пространства и времени.
Стандарт ISO 80000-3:2006 определяет следующие величины. Децибел (дБ) составляет одну десятую бела: 1 дБ = 0,1 Б. Bel (B) — это1⁄2 пер (10) неперс: 1 В =1⁄2 ln (10) Np. Непер — это изменение уровень величины корневой мощности, когда ее количество изменяется в е, то есть 1 Np = ln (e) = 1, тем самым связывая все единицы как безразмерный натуральный логарифм отношений корня-степени-количества, 1 дБ = 0,11513… Np = 0,11513…. Наконец, уровень количества — это логарифм отношения значения этого количества к контрольному значению того же вида количества.
Следовательно, бел представляет собой логарифм отношения между двумя величинами мощности 10: 1 или логарифм отношения между двумя величинами корня степени мощности √10:1.[17]
Два сигнала, уровни которых отличаются на один децибел, имеют коэффициент мощности 101/10, что приблизительно равно 1,25893, а отношение амплитуды (величина корня к мощности) равно 101⁄20 (1.12202).[18][19]
Ремень редко используется без приставки или с Префиксы единиц СИ Кроме как деци; предпочтительно, например, использовать сотые доли децибела скорее, чем миллибелы. Таким образом, пять тысячных бела обычно записываются как «0,05 дБ», а не «5 мБ».[20]
Метод выражения отношения в виде уровня в децибелах зависит от того, является ли измеренное свойство количество мощности или величина корневой мощности; видеть Мощность, корневая степень и величина поля для подробностей.
Величины мощности
Что касается измерений мощность количествах, соотношение может быть выражено как уровень в децибелах, оценив в десять раз больше логарифм по основанию 10 отношения измеренной величины к контрольной величине. Таким образом, соотношение п (измеренная мощность) до п0 (эталонная мощность) представлена Lп, это соотношение выражается в децибелах,[21] который рассчитывается по формуле:[22]
Логарифм по основанию 10 отношения двух величин мощности — это количество бел. Количество децибел в десять раз превышает количество бел (эквивалентно, децибел составляет одну десятую бела). п и п0 должны измерять один и тот же тип количества и иметь те же единицы перед вычислением отношения. Если п = п0 в приведенном выше уравнении, тогда Lп = 0. Если п больше, чем п0 тогда Lп положительный; если п меньше чем п0 тогда Lп отрицательный.
Преобразование приведенного выше уравнения дает следующую формулу для п с точки зрения п0 и Lп:
Корнево-степенные (полевые) величины
Обращаясь к измерениям величин корневой степени, обычно принимают во внимание отношение квадратов F (измерено) и F0 (ссылка). Это связано с тем, что определения были первоначально сформулированы так, чтобы дать одно и то же значение для относительных отношений как для степенных, так и для корневых величин. Таким образом, используется следующее определение:
Формулу можно изменить, чтобы получить
Аналогичным образом в электрические схемы, рассеиваемая мощность обычно пропорциональна квадрату Напряжение или же Текущий когда сопротивление постоянно. На примере напряжения это приводит к уравнению для уровня усиления мощности Lграмм:
куда Vиз это среднеквадратичный (действующее значение) выходное напряжение, Vв это действующее значение входного напряжения. Аналогичная формула верна для тока.
Период, термин величина корневой мощности введен стандартом ISO 80000-1:2009 как замена количество полей. Период, термин количество полей устарел этим стандартом и корневая сила используется в этой статье.
Взаимосвязь между уровнем власти и корневым уровнем власти
Несмотря на то, что мощность и основная мощность являются разными величинами, их соответствующие уровни исторически измеряются в одних и тех же единицах, обычно децибелах. Коэффициент 2 вводится, чтобы сделать изменения на соответствующих уровнях совпадают в ограниченных условиях, например, когда среда является линейной и одно и тоже форма волны рассматривается с изменениями амплитуды, или сопротивление среды линейно и не зависит как от частоты, так и от времени. Это зависит от отношений
держа.[23] В нелинейной системе это соотношение не выполняется по определению линейности. Однако даже в линейная система в котором количество мощности является произведением двух линейно связанных величин (например, Напряжение и Текущий ), если сопротивление зависит от частоты или времени, это соотношение в общем случае не выполняется, например, если изменяется энергетический спектр формы волны.
Для различий в уровнях требуемое соотношение ослаблено от приведенного выше до отношения пропорциональности (т. Е. Контрольные величины п0 и F0 не обязательно связаны), или, что то же самое,
должен удерживаться, чтобы позволить разнице уровней мощности быть равной разнице корневого уровня мощности от мощности п1 и V1 к п2 и V2. Примером может быть усилитель с единичным коэффициентом усиления по напряжению, независимый от нагрузки и частоты, управляющий нагрузкой с частотно-зависимым импедансом: относительное усиление по напряжению усилителя всегда равно 0 дБ, но коэффициент усиления по мощности зависит от меняющегося спектрального состава формы волны. усиливается. Частотно-зависимые импедансы могут быть проанализированы с учетом величин спектральная плотность мощности и соответствующие величины корневой мощности через преобразование Фурье, что позволяет исключить частотную зависимость при анализе, анализируя систему на каждой частоте независимо.
Конверсии
Поскольку разности логарифмов, измеренные в этих единицах, часто представляют собой отношения мощностей и отношения корневой мощности, значения для обоих значений показаны ниже. Бел традиционно используется как единица логарифмического отношения мощности, а непер используется для логарифмического отношения корня к мощности (амплитуде).
| Единица измерения | В децибелах | В поясах | В неперс | Коэффициент мощности | Соотношение корневой мощности |
|---|---|---|---|---|---|
| 1 дБ | 1 дБ | 0,1 млрд | 0,11513 Np | 101⁄10 ≈ 1.25893 | 101⁄20 ≈ 1.12202 |
| 1 нп | 8,68589 дБ | 0,868589 В | 1 нп | е2 ≈ 7.38906 | е ≈ 2.71828 |
| 1 млрд | 10 дБ | 1 млрд | 1.1513 Np | 10 | 101⁄2 ≈ 3.16228 |
Примеры
Единица дБВт часто используется для обозначения отношения, для которого эталонное значение составляет 1 Вт, и аналогично дБм для 1 мВт ориентир.
- Расчет отношения в децибелах 1 кВт (один киловатт или 1000 ватт) до 1 Вт дает:
- Соотношение в децибелах √1000 V ≈ 31,62 В к 1 В является
(31,62 В / 1 В)2 ≈ 1 кВт / 1 Вт, иллюстрируя следствие из приведенных выше определений, что Lграмм имеет одинаковое значение, 30 дБ, независимо от того, получено оно из мощностей или из амплитуд, при условии, что в конкретной рассматриваемой системе отношения мощностей равны отношениям амплитуд в квадрате.
- Соотношение в децибелах 1 мВт (один милливатт) до 10 Вт получается по формуле
- Коэффициент мощности, соответствующий 3 дБ изменение уровня определяется
Изменение коэффициента мощности в 10 раз соответствует изменению уровня 10 дБ. Изменение коэффициента мощности в 2 или более раз.1⁄2 примерно изменение на 3 дБ. Точнее, изменение составляет ± 3,0103 дБ, но это почти всегда округляется до «3 дБ» в технической документации. Это означает увеличение напряжения в 1 раз. √2 ≈ 1.4142. Аналогично, удвоение или уменьшение наполовину напряжения, а также учетверение или деление мощности на четверть обычно описывается как «6 дБ», а не ± 6,0206 дБ.
Если необходимо провести различие, количество децибел записывается с дополнительными значимые фигуры. 3.000 дБ соответствует коэффициенту мощности 103⁄10, или 1,9953, что примерно на 0,24% отличается от ровно 2, а отношение напряжений 1,4125, что на 0,12% отличается от точно √2. Аналогичным образом увеличение на 6.000 дБ соответствует коэффициенту мощности 106⁄10 ≈ 3.9811, примерно на 0,5% отличается от 4.
Характеристики
Децибел полезен для представления больших отношений и для упрощения представления умноженных эффектов, таких как затухание от нескольких источников в цепи сигнала. Его применение в системах с аддитивными эффектами менее интуитивно понятно.
Отчетность о больших коэффициентах
В логарифмическая шкала природа децибела означает, что очень большой диапазон соотношений может быть представлен удобным числом, аналогично научная нотация. Это позволяет четко визуализировать огромные изменения некоторого количества. Видеть Сюжет Боде и Полубревенчатый сюжет. Например, 120 дБ SPL может быть более четким, чем «в триллион раз более интенсивным, чем порог слышимости».
Представление операций умножения
Значения уровня в децибелах могут быть добавлены вместо умножения основных значений мощности, что означает, что общий коэффициент усиления многокомпонентной системы, такой как серия усилитель мощности каскадов, можно рассчитать путем суммирования коэффициентов усиления в децибелах отдельных компонентов, а не умножения коэффициентов усиления; то есть, бревно(А × B × C) = журнал (А) + журнал (B) + журнал (C). На практике это означает, что, обладая только информацией о том, что 1 дБ составляет примерно 26% прирост мощности, 3 дБ составляет примерно 2-кратное усиление мощности и 10 дБ составляет 10-кратное усиление мощности, можно определить коэффициент мощности система с усилением в дБ с простым сложением и умножением. Например:
-
- Система состоит из 3 последовательно соединенных усилителей с коэффициентами усиления (отношение выходной мощности к входной) 10 дБ, 8 дБ и 7 дБ соответственно, что дает общий коэффициент усиления 25 дБ. В разбивке на комбинации 10, 3 и 1 дБ это:
- 25 дБ = 10 дБ + 10 дБ + 3 дБ + 1 дБ + 1 дБ
- При потребляемой мощности 1 Вт выходная мощность составляет примерно
- 1 Вт × 10 × 10 × 2 × 1,26 × 1,26 ≈ 317,5 Вт
- При точном расчете мощность составляет 1 Вт × 1025⁄10 ≈ 316,2 Вт. Приблизительное значение имеет погрешность всего + 0,4% по отношению к фактическому значению, что незначительно с учетом точности предоставленных значений и точности большинства измерительных приборов.
- Система состоит из 3 последовательно соединенных усилителей с коэффициентами усиления (отношение выходной мощности к входной) 10 дБ, 8 дБ и 7 дБ соответственно, что дает общий коэффициент усиления 25 дБ. В разбивке на комбинации 10, 3 и 1 дБ это:
Однако, по мнению его критиков, децибел создает путаницу, затемняет рассуждения, больше относится к эпохе правила слайдов чем современная цифровая обработка, громоздка и трудна для интерпретации.[24][25]
Представление операций сложения
По словам Митшке,[26] «Преимущество использования логарифмической меры состоит в том, что в цепи передачи много элементов сцеплены, и каждый имеет собственное усиление или затухание. Для получения итоговых значений сложение значений в децибелах намного удобнее, чем умножение отдельных факторов. » Однако по той же причине, по которой люди преуспевают в аддитивных операциях над умножением, децибелы неудобны в изначально аддитивных операциях:[27] «если две машины по отдельности производят звуковое давление уровень, скажем, 90 дБ в определенный момент, тогда, когда оба работают вместе, мы должны ожидать, что общий уровень звукового давления увеличится до 93 дБ, но уж точно не до 180 дБ! «;» предположим, что шум от машины измеренный (включая вклад фонового шума), он составил 87 дБА, но когда машина выключена, только фоновый шум измеряется как 83 дБА. […] машинный шум [уровень (только)] может быть получен путем «вычитания» фонового шума 83 дБА из комбинированного уровня 87 дБА; т. е. 84,8 дБА. «;», чтобы найти репрезентативное значение уровня звука в комнате, выполняется ряд измерений в разных точках комнаты, и вычисляется среднее значение. […] Сравните логарифмические и средние арифметические […] 70 дБ и 90 дБ: логарифмическое среднее = 87 дБ; среднее арифметическое = 80 дБ «.
Сложение в логарифмической шкале называется логарифмическое сложение, и его можно определить, взяв экспоненты для преобразования в линейную шкалу, сложив их, а затем взяв логарифмы для возврата. Например, где операции с децибелами — это логарифмическое сложение / вычитание и логарифмическое умножение / деление, а операции с линейной шкалой — это обычные операции:
Обратите внимание, что среднее логарифмическое значение получается из логарифмической суммы путем вычитания 
Величины в децибелах не обязательно добавка,[28][29] таким образом будучи «неприемлемой формы для использования в размерный анализ «.[30]
Использует
Восприятие
Человеческое восприятие интенсивности звука и света больше приближается к логарифму интенсивности, чем к линейной зависимости (см. Закон Вебера – Фехнера ), что делает шкалу дБ полезным показателем.[31][32][33][34][35][36]
Акустика
Примеры уровней звука в децибелах от различных источников звука и действий, взятые с экрана «Как громко это слишком громко» приложения NIOSH Sound Level Meter
Децибел обычно используется в акустика как единица уровень звукового давления. Эталонное давление звука в воздухе установлено на типичном пороге восприятия среднего человека, и есть общие сравнения, используемые для иллюстрации различных уровней звукового давления. Поскольку звуковое давление является величиной основной мощности, используется соответствующая версия определения единицы:
куда псреднеквадратичное значение это среднеквадратичное значение измеренного звукового давления и пссылка стандартное эталонное звуковое давление 20 микропаскали в воздухе или 1 микропаскаль в воде.[37]
Использование децибел в подводной акустике приводит к путанице, отчасти из-за этой разницы в эталонных значениях.[38]
Человеческое ухо имеет большой динамический диапазон в звуковом приеме. Отношение интенсивности звука, вызывающего необратимое повреждение во время короткого воздействия, к интенсивности самого тихого звука, который может слышать ухо, больше или равно 1 триллиону (1012).[39] Такие большие диапазоны измерений удобно выражать в логарифмическая шкала: десятичный логарифм 1012 равно 12, что выражается как уровень звукового давления 120 дБ относительно 20мкПа.
Поскольку человеческое ухо не одинаково чувствительно ко всем звуковым частотам, спектр акустической мощности изменяется: частотное взвешивание (А-взвешивание является наиболее распространенным стандартом), чтобы получить взвешенную акустическую мощность перед преобразованием в уровень звука или уровень шума в децибелах.[40]
Телефония
Децибел используется в телефония и аудио. Как и в акустике, часто используется частотно-взвешенная мощность. Для измерения звукового шума в электрических цепях взвешивания называются псофометрические веса.[41]
Электроника
В электронике децибел часто используется для выражения отношения мощности или амплитуды (как для прибыль ) вместо арифметика соотношения или проценты. Одним из преимуществ является то, что общее усиление в децибелах ряда компонентов (таких как усилители и аттенюаторы ) можно рассчитать простым суммированием усиления децибел отдельных компонентов. Точно так же в телекоммуникациях децибелы обозначают усиление или потерю сигнала от передатчика к приемнику через некоторую среду (свободное место, волновод, коаксиальный кабель, волоконная оптика и т. д.) с помощью бюджет ссылки.
Единицу децибела можно также комбинировать с эталонным уровнем, часто обозначаемым суффиксом, чтобы создать абсолютную единицу электроэнергии. Например, его можно комбинировать с «m» для «милливатта» для получения «дБм «. Уровень мощности 0 дБм соответствует одному милливатту, а 1 дБм — одному децибелу больше (около 1,259 мВт).
В профессиональных спецификациях звука популярным устройством является дБу. Это относительно среднеквадратичное значение напряжение, которое выдает 1 мВт (0 дБмВт) на резистор 600 Ом, или √1 мВт × 600 Ом ≈ 0,775 ВRMS. При использовании в цепи на 600 Ом (исторически это стандартное эталонное сопротивление в телефонных цепях), дБн и дБм равны идентичный.
Оптика
В оптическая связь, если известное количество оптический мощность, в дБм (относительно 1 мВт), запускается в волокно, а потери в дБ (децибелах) каждого компонента (например, соединителей, сращиваний и длины волокна) известны, общие потери в канале связи можно быстро вычислить путем сложения и вычитания величин в децибелах.[42]
В спектрометрии и оптике блокирующий блок используется для измерения оптическая плотность эквивалентно −1 B.
Видео и цифровые изображения
В связи с видео и цифровыми датчики изображения, децибелы обычно представляют собой отношения видеонапряжения или оцифрованной интенсивности света с использованием 20 log отношения, даже когда представленная интенсивность (оптическая мощность) прямо пропорциональна напряжению, генерируемому датчиком, а не его квадрату, как в ПЗС-камера где напряжение срабатывания линейно по интенсивности.[43]Таким образом, камера соотношение сигнал шум или же динамический диапазон Указанный как 40 дБ представляет собой отношение 100: 1 между интенсивностью оптического сигнала и оптически эквивалентной интенсивностью темнового шума, а не отношение интенсивности (мощности) 10 000: 1, как можно было бы предположить в 40 дБ.[44]Иногда определение 20 логарифмического отношения применяется непосредственно к счетам электронов или фотонов, которые пропорциональны амплитуде сигнала датчика без необходимости учитывать, является ли реакция напряжения на интенсивность линейной.[45]
Однако, как упоминалось выше, в физической оптике, в том числе в волоконной оптике, в более общем плане преобладает правило 10 log интенсивности, поэтому терминология между соглашениями цифровой фотографической технологии и физикой может стать нечеткой. Чаще всего величины, называемые «динамический диапазон» или «отношение сигнал / шум» (камеры), указываются в 20 log дБ, но в связанных контекстах (например, затухание, усиление, SNR усилителя или коэффициент подавления) следует использовать термин следует интерпретировать с осторожностью, так как смешение двух единиц может привести к очень серьезному недопониманию значения.
Фотографы обычно используют альтернативный лог-блок base-2, остановка, чтобы описать отношения интенсивности света или динамический диапазон.
Суффиксы и справочные значения
Суффиксы обычно присоединены к основному блоку дБ для указания опорного значения, с помощью которого вычисляется отношение. Например, дБм означает измерение мощности относительно 1 милливатта.
В тех случаях, когда указывается единичное значение эталона, значение в децибелах называется «абсолютным». Если единичное значение эталона не указано явно, как, например, усиление усилителя в дБ, то значение в децибелах считается относительным.
SI не разрешает добавлять квалификаторы к единицам, будь то суффикс или префикс, кроме стандартных. Префиксы SI. Следовательно, даже если децибел принят для использования вместе с Единицы СИ, практика добавления суффикса к базовой единице дБ, образуя составные единицы, такие как дБм, дБн, дБА и т. д., не является.[16] Правильный способ, согласно IEC 60027-3,[15] либо как LИкс (повторно Иксссылка) или как LИкс/Иксссылка, куда Икс это символ количества и Иксссылка — значение контрольной величины, например, LE (re 1 мкВ / м) = LE/ (1 мкВ / м) для напряженность электрического поля E относительно эталонного значения 1 мкВ / м.
Помимо документов, использующих единицы СИ, эта практика очень распространена, что иллюстрируется следующими примерами. Не существует общего правила с различными практиками, ориентированными на конкретные дисциплины. Иногда суффикс представляет собой символ единицы («W», «K», «m»), иногда это транслитерация символа единицы («мкВ» вместо мкВ для микровольт), иногда это аббревиатура названия единицы. («см» — квадратный метр, «м» — милливатт), в других случаях это мнемоника для типа вычисляемой величины («i» — коэффициент усиления антенны по отношению к изотропной антенне, «λ» — все, что нормализовано Длина волны ЭМ), или иным образом общий атрибут или идентификатор, относящийся к природе величины («A» для A-взвешенный уровень звукового давления). Суффикс часто связан с дефис, как в «дБ ‑ Гц», или с пробелом, как в «дБ HL», или без промежуточного символа, как в «дБм», или заключенный в круглые скобки, как в «дБ (см)».
Напряжение
Поскольку децибел определяется по мощности, а не по амплитуде, при преобразовании отношений напряжения в децибелы необходимо возводить в квадрат амплитуду или использовать коэффициент 20 вместо 10, как обсуждалось выше.
- дБВ
- дБ (ВRMS) – Напряжение относительно 1 В независимо от импеданса.[3] Это используется для измерения чувствительности микрофона, а также для указания потребителя. линейный уровень из −10 дБВ, чтобы снизить производственные затраты относительно оборудования, использующего +4 дБн линейный сигнал.[46]
- дБу или дБв
- RMS Напряжение относительно
(т. е. напряжение, которое рассеивает 1 мВт на нагрузку 600 Ом). An RMS напряжение 1 В, следовательно, соответствует
[3] Первоначально dBv, он был изменен на dBu, чтобы избежать путаницы с dBV.[47] «V» происходит от «вольт», а «u» — от громкости. единица измерения используется в VU метр.[48]dBu может использоваться как мера напряжения независимо от импеданса, но рассчитывается исходя из нагрузки 600 Ом, рассеивающей 0 дБмВт (1 мВт). Опорное напряжение происходит от вычисления
. В профессиональное аудио оборудование может быть откалибровано так, чтобы показывать «0» на измерителях VU через некоторое конечное время после подачи сигнала с амплитудой +4 дБн. Потребительское оборудование обычно использует более низкий «номинальный» уровень сигнала −10 дБВ.[49] Поэтому многие устройства предлагают работу с двумя напряжениями (с разными настройками усиления или «подстройки») по причинам совместимости. Переключатель или регулировка, охватывающая как минимум диапазон между +4 дБн и −10 дБВ распространено в профессиональном оборудовании.
- дБм0 с
- Определено Рекомендацией МСЭ-R V.574 .; дБмВ: дБ (мВRMS) – Напряжение относительно 1 милливольта на 75 Ом.[50] Широко используется в кабельное телевидение сети, в которых номинальная мощность одиночного ТВ-сигнала на терминалах приемника составляет около 0 дБмВ. Для кабельного телевидения используется коаксиальный кабель 75 Ом, поэтому 0 дБмВ соответствует −78,75 дБВт (−48,75 дБмВт) или приблизительно 13 нВт.
- дБмкВ или дБуВ
- дБ (мкВRMS) – Напряжение относительно 1 мкВ. Широко используется в телевизионных и антенных усилителях. 60 дБмкВ = 0 дБмВ.
Акустика
Вероятно, наиболее распространенное использование «децибел» в отношении уровня звука — это дБ SPL, уровень звукового давления относительно номинального порога человеческого слуха:[51] Меры давления (величина коренной мощности) используют коэффициент 20, а меры мощности (например, дБ SIL и дБ SWL) используют коэффициент 10.
- дБ SPL
- дБ SPL (уровень звукового давления ) — для звука в воздухе и других газах, относительно 20 микропаскалей (мкПа), или 2×10−5 Па, примерно самый тихий звук, который может слышать человек. За звук в воде и других жидкостей используется эталонное давление 1 мкПа.[52] Среднеквадратичное звуковое давление в один паскаль соответствует уровню 94 дБ SPL.
- дБ SIL
- дБ уровень интенсивности звука — относительно 10−12 Вт / м², что примерно соответствует порог человеческого слуха в воздухе.
- дБ SWL
- дБ уровень звуковой мощности — относительно 10−12 W.
- дБА, дББ и дБВ
- Эти символы часто используются для обозначения использования различных взвешивающие фильтры, используется для аппроксимации человеческого уха отклик на звук, хотя измерения все еще производятся в дБ (SPL). Эти измерения обычно относятся к шуму и его воздействию на людей и других животных, и они широко используются в промышленности при обсуждении вопросов контроля шума, нормативных требований и экологических стандартов. Другие возможные вариации: дБА или же дБ (А). Согласно стандартам Международного электротехнического комитета (МЭК 61672-2013 )[53] и Американский национальный институт стандартов, ANSI S1.4,[54] предпочтительное использование — написать LА = x дБ. Тем не менее, единицы дБА и дБ (А) по-прежнему обычно используются в качестве сокращений для измерений, взвешенных по шкале А. Сравнивать дБн, используется в телекоммуникациях.
- дБ HL
- уровень слышимости дБ используется в аудиограммы как мера потери слуха. Контрольный уровень зависит от частоты в зависимости от кривая минимальной слышимости как определено в ANSI и других стандартах, так что полученная аудиограмма показывает отклонение от того, что считается «нормальным» слухом.[нужна цитата ]
- дБ Q
- иногда используется для обозначения взвешенного уровня шума, обычно с помощью ITU-R 468 взвешивание шума[нужна цитата ]
- дБпп
- относительно размаха звукового давления.[55]
- дБГ
- G-взвешенный спектр[56]
Аудио электроника
См. Также dBV и dBu выше.
- дБм
- дБ (мВт) — мощность относительно 1милливатт. В аудио и телефонии дБм обычно указывается относительно импеданса 600 Ом,[57] что соответствует уровню напряжения 0,775 вольт или 775 милливольт.
- дБм0
- Мощность в дБм (описана выше), измеренная при точка нулевого уровня передачи.
- дБFS
- дБ (полная шкала ) — амплитуда сигнала по сравнению с максимумом, который устройство может обработать до вырезка происходит. Полномасштабный можно определить как уровень мощности натурного синусоида или альтернативно полномасштабный прямоугольная волна. Сигнал, измеренный относительно полномасштабной синусоидальной волны, кажется на 3 дБ слабее по сравнению с полномасштабной прямоугольной волной, таким образом: 0 dBFS (полномасштабная синусоида) = -3 dBFS (полноразмерная прямоугольная волна).
- дБВУ
- единица громкости дБ[58]
- дБТП
- дБ (истинный пик) — пиковая амплитуда сигнала по сравнению с максимумом, который устройство может обработать до того, как произойдет ограничение.[59] В цифровых системах 0 dBTP будет равняться наивысшему уровню (номеру), который процессор способен представить. Измеренные значения всегда отрицательны или равны нулю, так как они меньше или равны полной шкале.
Радар
- дБЗ
- дБ (Z) — децибел относительно Z = 1 мм6⋅m−3:[60] энергия отражательной способности (метеорологический радар), связанная с количеством переданной мощности, возвращаемой приемнику радара. Значения выше 20 дБз обычно указывают на выпадающие осадки.[61]
- дБсм
- дБ (м²) — децибел на один квадратный метр: мера радиолокационный разрез (RCS) цели. Мощность, отраженная целью, пропорциональна ее RCS. Самолеты-невидимки и насекомые имеют отрицательную RCS, измеренную в дБсм, большие плоские пластины или незаметные самолеты имеют положительные значения.[62]
Мощность радио, энергия и напряженность поля
- дБн
- относительно перевозчика — в телекоммуникации, это указывает относительные уровни шума или мощности боковой полосы по сравнению с мощностью несущей. Сравните dBC, используемые в акустике.
- дБпп
- относительно максимального значения пиковой мощности.
- дБдж
- энергия относительно 1джоуль. 1 джоуль = 1 ватт-секунда = 1 ватт на герц, поэтому спектральная плотность мощности может быть выражено в дБдж.
- дБм
- дБ (мВт) — мощность относительно 1милливатт. In the radio field, dBm is usually referenced to a 50 Ω load, with the resultant voltage being 0.224 volts.[63]
- dBμV/m, dBuV/m, or dBμ
- [64] dB(μV/m) – напряженность электрического поля relative to 1 microvolt на метр. The unit is often used to specify the signal strength of a телевидение транслировать at a receiving site (the signal measured at the antenna output is reported in dBμV).
- дБф
- dB(fW) – power relative to 1 femtowatt.
- dBW
- dB(W) – power relative to 1 ватт.
- dBk
- dB(kW) – power relative to 1 киловатт.
- dBe
- dB electrical.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in a system that is thermal noise limited.[65]
Antenna measurements
- dBi
- dB(isotropic) – the forward gain of an antenna compared with the hypothetical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBd
- dB(dipole) – the forward gain of an антенна compared with a half-wave дипольная антенна. 0 dBd = 2.15 dBi
- dBiC
- dB(isotropic circular) – the forward gain of an antenna compared to a циркулярно поляризованный isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- дБк
- dB(quarterwave) – the forward gain of an antenna compared to a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBsm
- dB(m²) – decibel relative to one square meter: measure of the antenna effective area.[66]
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
Прочие измерения
- dB‑Hz
- dB(Hz) – bandwidth relative to one hertz. E.g., 20 dB‑Hz corresponds to a bandwidth of 100 Hz. Commonly used in link budget расчеты. Also used in отношение несущей к плотности шума (не путать с отношение несущая / шум, in dB).
- dBov or dBO
- dB(overload) – the амплитуда of a signal (usually audio) compared with the maximum which a device can handle before вырезка происходит. Similar to dBFS, but also applicable to analog systems. According to ITU-T Rec. G.100.1 the level in dBov of a digital system is defined as:
,
- with the maximum signal power
, for a rectangular signal with the maximum amplitude
. The level of a tone with a digital amplitude (peak value) of
is therefore
.[67]
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- дБн
- dB above reference noise. Смотрите также dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to a -90 dBm reference level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America. The Psophometric filter is used for this purpose on international circuits. Видеть Psophometric weighting to see a comparison of frequency response curves for the C-message weighting and Psophometric weighting filters.[68]
- dBK
- dB(K) – decibels relative to 1 K; используется для выражения шумовая температура.[69]
- dB/K
- dB(K−1) – decibels relative to 1 K−1.[70] — нет decibels per kelvin: Used for the G / T factor, a добродетель utilized in спутниковая связь, relating the antenna gain грамм к приемник system noise equivalent temperature Т.[71][72]
List of suffixes in alphabetical order
Unpunctuated suffixes
- дБА
- see dB(A).
- dBB
- see dB(B).
- dBc
- relative to carrier – in телекоммуникации, this indicates the relative levels of noise or sideband power, compared with the carrier power.
- dBC
- see dB(C).
- dBd
- dB(dipole) – the forward gain of an антенна compared with a half-wave дипольная антенна. 0 dBd = 2.15 dBi
- dBe
- dB electrical.
- дБф
- dB(fW) – power relative to 1 femtowatt.
- dBFS
- dB(полная шкала ) – the амплитуда of a signal compared with the maximum which a device can handle before вырезка происходит. Full-scale may be defined as the power level of a full-scale sinusoid or alternatively a full-scale прямоугольная волна. A signal measured with reference to a full-scale sine-wave appears 3 dB weaker when referenced to a full-scale square wave, thus: 0 dBFS(fullscale sine wave) = −3 dBFS(fullscale square wave).
- dBG
- G-weighted spectrum
- dBi
- dB(isotropic) – the forward gain of an antenna compared with the hypothetical isotropic antenna, which uniformly distributes energy in all directions. Linear polarization of the EM field is assumed unless noted otherwise.
- dBiC
- dB(isotropic circular) – the forward gain of an antenna compared to a циркулярно поляризованный isotropic antenna. There is no fixed conversion rule between dBiC and dBi, as it depends on the receiving antenna and the field polarization.
- dBJ
- energy relative to 1 джоуль. 1 joule = 1 watt second = 1 watt per hertz, so спектральная плотность мощности can be expressed in dBJ.
- dBk
- dB(kW) – power relative to 1 киловатт.
- dBK
- dB(K) – decibels relative to кельвин: Used to express шумовая температура.
- dBm
- dB(mW) – power relative to 1 milliwatt.
- dBm0
- Power in dBm measured at a zero transmission level point.
- dBm0s
- Defined by Recommendation ITU-R V.574.
- dBmV
- dB(mVRMS) – Напряжение relative to 1 millivolt across 75 Ω.
- dBo
- dB optical. A change of 1 dBo in optical power can result in a change of up to 2 dBe in electrical signal power in system that is thermal noise limited.
- dBO
- see dBov
- dBov or dBO
- dB(overload) – the амплитуда of a signal (usually audio) compared with the maximum which a device can handle before вырезка происходит.
- dBpp
- relative to the peak to peak sound pressure.
- dBpp
- relative to the maximum value of the peak power.
- дБк
- dB(quarterwave) – the forward gain of an antenna compared to a quarter wavelength whip. Rarely used, except in some marketing material. 0 dBq = −0.85 dBi
- dBr
- dB(relative) – simply a relative difference from something else, which is made apparent in context. The difference of a filter’s response to nominal levels, for instance.
- дБн
- dB above reference noise. Смотрите также dBrnC
- dBrnC
- dBrnC represents an audio level measurement, typically in a telephone circuit, relative to the circuit noise level, with the measurement of this level frequency-weighted by a standard C-message weighting filter. The C-message weighting filter was chiefly used in North America.
- dBsm
- dB(m²) – decibel relative to one square meter
- dBTP
- dB(true peak) – peak amplitude of a signal compared with the maximum which a device can handle before clipping occurs.
- dBu or dBv
- RMS Напряжение относительно
.
- dBu0s
- Defined by Recommendation ITU-R V.574.
- dBuV
- see dBμV
- dBuV/m
- see dBμV/m
- дБв
- see dBu
- dBV
- dB(VRMS) – Напряжение relative to 1 volt, regardless of impedance.
- dBVU
- dB volume unit
- dBW
- dB(W) – power relative to 1 ватт.
- dBZ
- dB(Z) – decibel relative to Z = 1 mm6⋅m−3
- dBμ
- see dBμV/m
- dBμV or dBuV
- dB(μVRMS) – Напряжение relative to 1 microvolt.
- dBμV/m, dBuV/m, or dBμ
- dB(μV/m) – напряженность электрического поля relative to 1 microvolt на метр.
Suffixes preceded by a space
- dB HL
- dB hearing level is used in аудиограммы as a measure of hearing loss.
- dB Q
- sometimes used to denote weighted noise level
- dB SIL
- дБ sound intensity level – relative to 10−12 W/m²
- dB SPL
- dB SPL (уровень звукового давления ) – for sound in air and other gases, relative to 20 μPa in air or 1 μPa in water
- dB SWL
- дБ sound power level – relative to 10−12 W.
Suffixes within parentheses
- dB(A), dB(B), and dB(C)
- These symbols are often used to denote the use of different weighting filters, used to approximate the human ear’s отклик to sound, although the measurement is still in dB (SPL). These measurements usually refer to noise and its effects on humans and other animals, and they are widely used in industry while discussing noise control issues, regulations and environmental standards. Other variations that may be seen are dBА или же дБА.
Другие суффиксы
- дБ-Гц
- dB(Hz) – bandwidth relative to one hertz.
- dB/K
- dB(K−1) – decibels relative to взаимный из кельвин
- dBm−1
- dB(m−1) – decibel relative to reciprocal of meter: measure of the antenna factor.
- mBm
- mB(mW) – power relative to 1 milliwatt, in millibels (one hundredth of a decibel). 100 mBm = 1 dBm. This unit is in the Wi-Fi drivers of the Linux ядро[73] and the regulatory domain sections.[74]
- Np
- Another closely related unit is the непер (Np). Like the decibel, the neper is a unit of уровень.[6]
Фракции
Затухание constants, in topics such as оптоволокно communication and radio propagation потеря пути, are often expressed as a дробная часть or ratio to distance of transmission. dB/m represents decibel per meter, dB/mi represents decibel per mile, for example. These quantities are to be manipulated obeying the rules of dimensional analysis, e.g., a 100-meter run with a 3.5 dB/km fiber yields a loss of 0.35 dB = 3.5 dB/km × 0.1 km.
Смотрите также
- Видимая величина
- Cent (музыка)
- dB drag racing
- Decade (log scale)
- Громкость
- One-third octave § Base 10
- pH
- Телефон
- Шкала звездных величин Рихтера
- Sone
Рекомендации
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. п. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Второе изд.). Холт, Райнхарт и Уинстон. п.206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ а б c Utilities : VRMS / dBm / dBu / dBV calculator, Analog Devices, получено 16 сентября 2016
- ^ Thompson and Taylor 2008, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811 В архиве 2016-06-03 в Wayback Machine.
- ^ IEEE Standard 100: a dictionary of IEEE standards and terms (7-е изд.). New York: The Institute of Electrical and Electronics Engineering. 2000. p. 288. ISBN 978-0-7381-2601-2.
- ^ а б «ISO 80000-3:2006». Международная организация по стандартизации. Получено 20 июля 2013.
- ^ Johnson, Kenneth Simonds (1944). Transmission Circuits for Telephonic Communication: Methods of analysis and design. Нью-Йорк: D. Van Nostrand Co. п. 10.
- ^ Davis, Don; Davis, Carolyn (1997). Sound system engineering (2-е изд.). Focal Press. п. 35. ISBN 978-0-240-80305-0.
- ^ Hartley, R. V. L. (December 1928). «‘TU’ becomes ‘Decibel‘«. Bell Laboratories Record. AT&T. 7 (4): 137–139.
- ^ Martin, W. H. (January 1929). «DeciBel—The New Name for the Transmission Unit». Технический журнал Bell System. 8 (1).
- ^ 100 Years of Telephone Switching, п. 276, в Google Книги, Robert J. Chapuis, Amos E. Joel, 2003
- ^ Harrison, William H. (1931). «Standards for Transmission of Speech». Standards Yearbook. National Bureau of Standards, U. S. Govt. Типография. 119.
- ^ Horton, J. W. (1954). «The bewildering decibel». Электротехника. 73 (6): 550–555. Дои:10.1109/EE.1954.6438830. S2CID 51654766.
- ^ «Протокол заседаний» (PDF). Consultative Committee for Units. Section 3.
- ^ а б «Letter symbols to be used in electrical technology». International Electrotechnical Commission. 19 July 2002. Part 3: Logarithmic and related quantities, and their units. IEC 60027-3, Ed. 3.0.
- ^ а б Thompson, A. and Taylor, B. N. sec 8.7, «Logarithmic quantities and units: level, neper, bel», Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF
- ^ «Letter symbols to be used in electrical technology». International Standard CEI-IEC 27-3. International Electrotechnical Commission. Part 3: Logarithmic quantities and units.
- ^ Mark, James E. (2007). Physical Properties of Polymers Handbook. Springer. п. 1025. Bibcode:2007ppph.book…..M.
[…] the decibel represents a reduction in power of 1.258 times […]
- ^ Yost, William (1985). Fundamentals of Hearing: An Introduction (Второе изд.). Холт, Райнхарт и Уинстон. п.206. ISBN 978-0-12-772690-8.
[…] a pressure ratio of 1.122 equals + 1.0 dB […]
- ^ Fedor Mitschke, Fiber Optics: Physics and Technology, Springer, 2010 ISBN 3642037038.
- ^ Pozar, David M. (2005). Microwave Engineering (3-е изд.). Вайли. п. 63. ISBN 978-0-471-44878-5.
- ^ IEC 60027-3:2002
- ^ I M Mills; B N Taylor; A J Thor (2001), «Definitions of the units radian, neper, bel and decibel», Метрология, 38 (4): 353, Bibcode:2001Metro..38..353M, Дои:10.1088/0026-1394/38/4/8
- ^ R. Hickling (1999), Noise Control and SI Units, J Acoust Soc Am 106, 3048
- ^ Hickling, R. (2006). Decibels and octaves, who needs them?. Journal of sound and vibration, 291(3-5), 1202-1207.
- ^ Fiber Optics. Springer. 2010 г.
- ^ R. J. Peters, Acoustics and Noise Control, Routledge, 12 November 2013, 400 pages, p. 13
- ^ Nicholas P. Cheremisinoff (1996) Noise Control in Industry: A Practical Guide, Elsevier, 203 pp, p. 7
- ^ Andrew Clennel Palmer (2008), Dimensional Analysis and Intelligent Experimentation, World Scientific, 154 pp, p.13
- ^ J. C. Gibbings, Dimensional Analysis, стр.37, Springer, 2011 г. ISBN 1849963177.
- ^ Ощущение и восприятие, п. 268, в Google Книги
- ^ Introduction to Understandable Physics, Volume 2, п. SA19-PA9, at Google Книги
- ^ Visual Perception: Physiology, Psychology, and Ecology, п. 356, at Google Книги
- ^ Exercise Psychology, п. 407, в Google Книги
- ^ Foundations of Perception, п. 83, at Google Книги
- ^ Fitting The Task To The Human, п. 304, at Google Книги
- ^ ISO 1683:2015
- ^ C. S. Clay (1999), Underwater sound transmission and SI units, J Acoust Soc Am 106, 3047
- ^ «Loud Noise Can Cause Hearing Loss». cdc.gov. Центры по контролю и профилактике заболеваний. Получено 30 июля 2020.
- ^ Richard L. St. Pierre, Jr. and Daniel J. Maguire (July 2004), The Impact of A-weighting Sound Pressure Level Measurements during the Evaluation of Noise Exposure (PDF), получено 13 сентября 2011
- ^ Reeve, William D. (1992). Subscriber Loop Signaling and Transmission Handbook – Analog (1-е изд.). IEEE Press. ISBN 0-87942-274-2.
- ^ Chomycz, Bob (2000). Fiber optic installer’s field manual. McGraw-Hill Professional. С. 123–126. ISBN 978-0-07-135604-6.
- ^ Stephen J. Sangwine and Robin E. N. Horne (1998). The Colour Image Processing Handbook. Springer. pp. 127–130. ISBN 978-0-412-80620-9.
- ^ Francis T. S. Yu and Xiangyang Yang (1997). Introduction to optical engineering. Издательство Кембриджского университета. С. 102–103. ISBN 978-0-521-57493-8.
- ^ Junichi Nakamura (2006). «Basics of Image Sensors». In Junichi Nakamura (ed.). Image sensors and signal processing for digital still cameras. CRC Press. pp. 79–83. ISBN 978-0-8493-3545-7.
- ^ Winer, Ethan (2013). The Audio Expert: Everything You Need to Know About Audio. Focal Press. п. 107. ISBN 978-0-240-82100-9.
- ^ stason.org, Stas Bekman: stas (at). «3.3 – What is the difference between dBv, dBu, dBV, dBm, dB SPL, and plain old dB? Why not just use regular voltage and power measurements?». stason.org.
- ^ Руперт Нев, Creation of the dBu standard level reference
- ^ deltamedia.com. «DB or Not DB». Deltamedia.com. Получено 16 сентября 2013.
- ^ The IEEE Standard Dictionary of Electrical and Electronics terms (6-е изд.). IEEE. 1996 [1941]. ISBN 978-1-55937-833-8.
- ^ Jay Rose (2002). Audio postproduction for digital video. Focal Press. п. 25. ISBN 978-1-57820-116-7.
- ^ Morfey, C. L. (2001). Dictionary of Acoustics. Academic Press, Сан-Диего.
- ^ IEC 61672-1:2013 Electroacoustics — Sound Level meters — Part 1: Specifications. Geneva: International Electrotechnical Committee. 2013.
- ^ ANSI S1.4-19823 Specification for Sound Level Meters, 2.3 Sound Level, p. 2–3.
- ^ Zimmer, Walter MX, Mark P. Johnson, Peter T. Madsen, and Peter L. Tyack. «Echolocation clicks of free-ranging Cuvier’s beaked whales (Ziphius cavirostris).» The Journal of the Acoustical Society of America 117, no. 6 (2005): 3919–3927.
- ^ http://oto2.wustl.edu/cochlea/wt4.html
- ^ Bigelow, Stephen (2001). Understanding Telephone Electronics. Newnes. п.16. ISBN 978-0750671750.
- ^ Tharr, D. (1998). Case Studies: Transient Sounds Through Communication Headsets. Applied Occupational and Environmental Hygiene, 13(10), 691–697.
- ^ МСЭ-R BS.1770
- ^ «Glossary: D’s». Национальная служба погоды. В архиве с оригинала 8 августа 2019 г.. Получено 25 апреля 2013.
- ^ «RIDGE Radar Frequently Asked Questions». В архиве from the original on 31 March 2019. Получено 8 августа 2019.
- ^ «Definition at Everything2». В архиве с оригинала 10 июня 2019 г.. Получено 8 августа 2019.
- ^ Carr, Joseph (2002). Радиочастотные компоненты и схемы. Newnes. С. 45–46. ISBN 978-0750648448.
- ^ «The dBµ vs. dBu Mystery: Signal Strength vs. Field Strength?». radio-timetraveller.blogspot.com. 24 февраля 2015 г.. Получено 13 октября 2016.
- ^ Chand, N., Magill, P. D., Swaminathan, S. V., & Daugherty, T. H. (1999). Delivery of digital video and other multimedia services (> 1 Gb/s bandwidth) in passband above the 155 Mb/s baseband services on a FTTx full service access network. Journal of lightwave technology, 17(12), 2449–2460.
- ^ David Adamy. EW 102: A Second Course in Electronic Warfare. Получено 16 сентября 2013.
- ^ Рек. МСЭ-Т. G.100.1 The use of the decibel and of relative levels in speechband telecommunications https://www.itu.int/rec/dologin_pub.asp?lang=e&id=T-REC-G.100.1-201506-I!!PDF-E&type=items
- ^ dBrnC is defined on page 230 in «Engineering and Operations in the Bell System,» (2ed), R.F. Rey (technical editor), copyright 1983, AT&T Bell Laboratories, Murray Hill, NJ, ISBN 0-932764-04-5
- ^ K. N. Raja Rao (31 January 2013). Satellite Communication: Concepts And Applications. Получено 16 сентября 2013.
- ^ Ali Akbar Arabi. Comprehensive Glossary of Telecom Abbreviations and Acronyms. Получено 16 сентября 2013.
- ^ Mark E. Long. The Digital Satellite TV Handbook. Получено 16 сентября 2013.
- ^ Mac E. Van Valkenburg (19 October 2001). Reference Data for Engineers: Radio, Electronics, Computers and Communications. Получено 16 сентября 2013.
- ^ «en:users:documentation:iw [Linux Wireless]». wireless.kernel.org.
- ^ «Is your WiFi AP Missing Channels 12 & 13?». wordpress.com. 16 мая 2013 г.
дальнейшее чтение
- Tuffentsammer, Karl (1956). «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [The decilog, a bridge between logarithms, decibel, neper and preferred numbers]. VDI-Zeitschrift (на немецком). 98: 267–274.
- Paulin, Eugen (1 September 2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon — natürlich verwandt! [Logarithms, preferred numbers, decibel, neper, phon — naturally related!] (PDF) (на немецком). В архиве (PDF) from the original on 18 December 2016. Получено 18 декабря 2016.
внешняя ссылка
- What is a decibel? With sound files and animations
- Conversion of sound level units: dBSPL or dBA to sound pressure p and sound intensity J
- OSHA Regulations on Occupational Noise Exposure
- Working with Decibels (RF signal and field strengths)
Мы часто встречаем уровни звука, указанные в децибелах — дБ или dBu и привыкли считать что это единица измерения шума, звука. А вот и нет. Это совсем не так. Децибел — это не единица измерения вообще. Это относительная характеристика, которая может отражать напряжение, мощность, силу тока и т.д. Что-то типа процентов, долей, но в логарифмической зависимости. Сначала понять, что такое децибел, непросто, но затем оказывается, что это очень удобно.
Содержание статьи
- 1 Понятие децибела
- 1.1 Что значит бел и децибел
- 1.2 Почему используют децибелы, а не прямые величины
- 1.3 Что такое dBm, dBv, dBA (дБм, дБв, дБА)
- 2 Как считают децибелы
- 3 Децибелы в акустике
- 3.1 Таблица уровней шумов
- 4 Перевод децибелов в разы
Понятие децибела
Мы хорошо воспринимаем измерение каких-либо параметров в прямых величинах. Например, напряжение измеряется в вольтах, сила тока — в амперах, сопротивление — в омах и т.д. Когда говорим об этом, все ясно и понятно. Когда говорим об увеличении или снижении в этих прямых единицах измерения тоже все понятно. Например, напряжение с 220 вольт снизилось до 150 вольт. Все понятно. Выражение «мощность возросла на 50 ватт» тоже вопросов не вызывает.
Как понять что такое децибел и что он означает
Но иногда говорят об увеличении или уменьшении того же напряжения или мощности на 2 децибела. Как это понять? Что измеряется в децибелах? Ведь мощность меряем в ваттах? Как соотнести децибелы с ваттами или вольтами, амперами и другими величинами. Ведь так описывают многие параметры. Тут надо разбираться. Не очень просто сначала понять, но потом все становится очевидным.
Что значит бел и децибел
Сразу стоит уяснить, что бел и децибел — это не единицы измерения чего-либо. Это не результат измерений. Децибел — это величина, которая показывает насколько/во сколько раз изменился тот или иной параметр. То есть бел или децибел — это относительная величина, которая высчитывается при сравнении двух измерений одного и того же параметра.
Например, на рисунке дан график, который построили по результатам измерения напряжение на выходе прибора при изменении подаваемой на вход частоты (АЧХ). Сняты были характеристики при уровне сигнала 1 V (график 1) и 100 мV (график 2). Если смотреть на графики прямых измерений, понять что-то сложно. На втором рисунке график построен в децибелах. На этом графике очевидно, что реакция прибора одинаковая, изменился только уровень сигнала на выходе, что и понятно.
Два графика измерений. Левый — прямая зависимость (напряжения от частоты), правый — изменение напряжения в дБ при изменении частоты
Первоначально стали использовать единицу Бел. Международное обозначение бела — B, российское — Б (например, 10Б или 10B). Но более удобным оказалось применение одной ее десятой доли — децибела или дБ в российском обозначении и dBu в международном. То есть один децибел — это 0,1 Бела.
Дальше, к сожалению, без математики не обойтись. Придется вспомнить что такое десятичный логарифм. Десятичный логарифм показывает, в какую степень надо возвести число 10 чтобы получить требуемую цифру. На рисунке вы видите соотношение, возможно будет понятнее в таком виде.
Несколько значений десятичных логарифмов
Теперь, собственно о Белах и децибелах. Если говорить об определениях, то Бел — это десятичный логарифм отношения двух величин. Любых двух величин. Мощностей, напряжения, силы звука, частоты и т.д. Давайте на примере. Надо понять, что выдает прибор на выходе при изменении параметров на входе. Выбирают какую-то точку отсчета — базу. Затем изменяют параметр, проводят измерение результата, делят его на «базу» и берут десятичный логарифм. Получают результат измерения в децибелах. Так измеряют параметры, пересчитывают в децибелы и строят зависимости.
Формула, которая поясняет что такое дБ (децибел) и как их считают
На рисунке даны две формулы — для вычисления энергетических величин (по мощности) и амплитудных (по напряжению). Как видите, они отличаются только коэффициентом. U1 тут — это результат измерений, а Uo — базовая величина, с который сравнивают измерений.
Почему используют децибелы, а не прямые величины
Использование логарифмических зависимостей часто более понятно и несет больше информации, чем прямые измерения. Это видно на примере построения графиков амплитудно-частотной характеристики. И такой случай не единичный, многие зависимости более информативны в логарифмической зависимости.
Кроме того, децибелы используют в тех областях, где параметры изменяются в очень широком диапазоне. Более понятна нам ситуация со звуками. Человек в состоянии воспринимать частоты от 20 Гц до 20 000 Гц. Ничего себе разброс! В тысячу раз.
Интенсивность звука и его соответствие в дБА
С уровнем звука еще круче. Нижний предел восприятия — 10-12 Вт/м, а уровень, при котором возникает боль — 10 Вт/м. То есть, диапазон измерения значений — 13 порядков. Это 10 000 000 000 000 раз. Оперировать такими цифрами, как минимум неудобно. С использованием относительных величин — децибел — цифры получаются значительно меньше, работать, воспринимать и запоминать их легче. Несколько примеров:
- Если показатель увеличился в 10 раз, говорят, что он увеличился на 1 Бел.
- Если тот же показатель увеличился в 100 раз, то говорят об увеличении на 2 Бела.
- Увеличение в 100 000 тысяч раз — всего на 5 Бел.
Заметили разницу? Показатель увеличился в 100 раз, а в белах увеличился на 2 Б. Это удобнее. Согласитесь, проще оперировать единицами, чем сотнями тысяч. Важно просто понимать смысл сказанного. При возрастании прямых величин их надо умножать на то число, на которое параметр увеличился. При оперировании децибелами их складывают. Согласитесь, это проще.
Что такое dBm, dBv, dBA (дБм, дБв, дБА)
Как вы уже поняли, децибел — это относительная величина и отражать она может что угодно. Надо только выбрать точку отсчета, базу, эталон, с которым сравнивают все последующие изменения. База для сравнения может быть взята произвольно. Но тогда непонятно как соотносить разные измерения. В таком случае, обычно, указывают относительно чего считался логарифм. То есть, что подставляли в знаменатель (в формуле выше это Uo).
Для электротехники и мощностей были выбраны базовые точки отсчета — две величины напряжения, с которыми сравнивают большую часть измерений электрических величин.
- Основная база — это мощность в один милливатт (1 мВт) при нагрузке 600 Ом. Если пересчитать, то напряжение получаем 0,775 Вольта. Именно эти значения и являются той базой, относительно которой высчитывают логарифмы. Это принято и в международных измерениях, и в отечественных. Именно при использовании такой базы ставят обозначение dBu или дБ в русском варианте. Реже встречается обозначение dBm. Это тоже, что dBu.
- Иногда выходное напряжение сравнивают с 1 В. В этом случае результат подписывают как dBv или дБв.
На что влияет точка отсчета? Просто на уровень, на котором строится зависимость. Если же по данным построить график, он будет иметь ту же форму.
При описании звуков и шумов употребляют дБА (dBA) или акустические децибелы. При таком исчислении за точку отсчета берут нижний порог слышимости или частоты, которую различает человеческое ухо. Это 2·10-5 Па и относительно нее вычисляют отношение.
Как считают децибелы
Больше в ходу не Белы, а их десятая часть — децибелы (обозначение dB или дБ). Ведь чаще увеличение не в сотни и тысячи раз, а чуть поскромнее. Так что обычно говорят об увеличении того или иного показания или характеристики на 5 дБ или на 10 дБ.
Пример соответствия децибел и «раз»
Но важно помнить, что описанная выше прямая зависимость характерна только для энергетических величин (это если мощность возросла в 10 раз, то она увеличилась на 10 дБ). Для других зависимость тоже логарифмическая, но вычисляется по другой формуле. И это надо помнить.
| Децибелы | Соотношение мощностей | Соотношение амплитуд |
|---|---|---|
| -3 | 0,5 | 0,7 |
| -6 | 0,25 | 0,5 |
| -10 | 0,1 | 0,3 |
| -20 | 1,01 | 0,1 |
| -25 | 0,03 | 0,05 |
| -40 | 0,01 | 0,0001 |
| -60 | 0,001 | 0,000001 |
Возможно, поможет понять что такое децибел следующие сравнение. Представим, что мощность изменяется литрами. Соотношение между 0,5 литра и 1 литром такое же как и между 1 литром и 2 литрами. Это 0,5 и равно оно 6 дБ. Но если сравнивать 0,5 и 0,75 литра, то они относятся как 0,66(6) что в децибелах около 3,6 дБ. Примерно так.
Децибелы в акустике
Вы, возможно, удивитесь, но для акустики децибелы подходят просто идеально. Собственно, Александр Белл ввел понятие Бел при исследовании порога слышимости. Он определил, что «громкость» мы воспринимаем не по реальной мощности сигнала, а по десятичному логарифму от этой мощности. Как так? Давайте рассмотрим пример.
Имеется усилитель, который выдает сигнал мощностью 1 Вт. Чтобы увеличить его в 1,1 раза, добавить надо только 0,1 Вт. А если на выходе у нас 100 Вт, то чтобы увеличить мощность в 1,1 раза надо поднять мощность на 10 Вт. Увеличение громкости в обоих случаях будет «для уха» одинаковым, а увеличение мощности имеет явно нелинейный характер.
Мы воспринимаем не реальный уровень сигнала, а логарифмическую зависимость
На основании вот этого явления Белл и вывел то самое логарифмическое отношение. В его честь и названа эта относительная единица измерений. Что еще это нам дает? А вот такие факты:
- 1 дБ — это минимальный уровень слышимости сигнала. Звуки с более низкой мощностью (о дБ и ниже) большинство людей не замечают и определяют как «абсолютную тишину».
- Если говорят о том, что мощность сигнала/звука возросла на 3 дБ, то значит она возросла в два раза. Не путайте с громкостью.
- При увеличении мощности звука на 10 дБ, громкость увеличивается в 2 раза.
- Увеличение напряжения в два раза — это 6 дБ.
Принять децибелы не так легко. Но наверное, вы уже поняли, что в децибелах громкость звука/шума не измеряется. Эта цифра показывает насколько изменился сигнал относительно «нулевой» точки восприятия. Примерно так можно это сформулировать.
Таблица уровней шумов
Ну, а чтобы было понятнее, приведем таблицу сравнений привычных, знакомых звуков и их среднего уровня.
| дБ | С чем можно сравнить | дБ | С чем можно сравнить |
|---|---|---|---|
| 0 дБ | Полная тишина | 90 дБ | Звук работающего фена, мотоцикла, поезда |
| 1 дБ | Самый нижний порог слышимости | 100-105 дБ | Ремонт и рок-концерт |
| 10-24 дБ | Шелест листвы | 110 дБ | Музыка в ночном клубе |
| 20 дБ | Шепот | 120 дБ | Автомобильный гудок |
| 40 дБ | Так звучит дождь | 130-135 дБ | Звук работающей дрели |
| 45 дБ | Тихий разговор | 140 дБ | Шум турбин самолета |
| 60 дБ | Громкий разговор | 160 дБ | Звук выстрела возле уха |
| 80-90 дБ | Шоссе с интенсивным движением | 200 дБ | Смертельный уровень шума |
Каждый шум или звук имеет определенный уровень мощности, но проще его описывать в децибелах
Факты, которые позволят оценить важность акустики и децибелов:
- Комфортным уровнем шума считается 50-55 дБ. Как видите, эту величину можно сравнить с разговором обычной «громкости». Именно этот уровень по СНиПу определен как приемлемый для дневного времени.
- Уровень 70-90 дБ относится к «терпимым», но длительное воздействие может привести к заболеваниям нервной системы.
- Длительное воздействие шума в 100 дБ приводит к снижению слуха и глухоте.
- Звуки мощностью 130 дБ вызывают болевые ощущения.
- Мощность звука в 200 дБ может быть смертельной.
Вообще, постоянное нахождение в шумном помещении сильно снижает способность воспринимать звуки. Мало того, оно приводит к расстройствам психики, сна, что негативно сказывается и на общем самочувствии. Поэтому шумные производства — зона риска. Чтобы хорошо себя чувствовать, просто необходимо время от времени находится если не при полной тишине, то при низком уровне шума.
Перевод децибелов в разы
Давайте попробуем сформулировать что такое децибел по-другому. Децибел — это логарифм соотношения двух величин. Эта относительная величина, которая показывает во сколько одно значение больше или меньше другого (базового). «Во сколько раз» это нам понятно. Поэтому часто приходится переводить децибелы в разы и наоборот. Можно, конечно, посчитать, но проще пользоваться таблицей.
| дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы | дБ | Увеличение напряжения (силы тока) в разы | Увеличение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 28 | 25,12 | 631 |
| 1 | 1,12 | 1,26 | 29 | 28,17 | 794 |
| 2 | 1,26 | 1,59 | 30 | 31,64 | 1000 |
| 3 | 1,41 | 2 | 31 | 35,46 | 1257 |
| 4 | 1,59 | 2,51 | 32 | 39,84 | 1587 |
| 5 | 1,78 | 3,16 | 33 | 44,64 | 1993 |
| 6 | 2 | 2,98 | 34 | 48,08 | 2312 |
| 7 | 2,24 | 5,01 | 35 | 56,82 | 3165 |
| 8 | 2,51 | 6,31 | 36 | 63,29 | 4006 |
| 9 | 2,82 | 7,94 | 37 | 70,92 | 5030 |
| 10 | 3,16 | 10 | 38 | 79,36 | 6298 |
| 11 | 3,55 | 12,59 | 39 | 89,29 | 7973 |
| 12 | 3,98 | 15,85 | 40 | 100 | 10000 |
| 13 | 4,47 | 19,96 | 41 | 112,23 | 12596 |
| 14 | 5,01 | 25,12 | 42 | 125,94 | 15861 |
| 15 | 5,62 | 31,65 | 43 | 141,24 | 19949 |
| 16 | 6,31 | 39,84 | 44 | 158,48 | 25116 |
| 17 | 7,08 | 48,08 | 45 | 177,94 | 31663 |
| 18 | 7,94 | 63,59 | 46 | 199,60 | 39840 |
| 19 | 8,91 | 79,36 | 47 | 223,71 | 50046 |
| 20 | 10 | 100 | 48 | 251,26 | 63132 |
| 21 | 11,22 | 125,94 | 49 | 281,69 | 79349 |
| 22 | 12,59 | 158,48 | 50 | 316,5 | 100 000 |
| 23 | 14,12 | 199,60 | 60 | 1 000 | 1 000 000 |
| 24 | 15,85 | 251,26 | 70 | 3165 | 10 000 000 |
| 25 | 17,79 | 316,50 | 80 | 10 000 | 100 000 000 |
| 26 | 19,96 | 398,4 | 90 | 31650 | 1 000 000 000 |
| 27 | 22,37 | 500,42 | 100 | 100 000 | 10 000 000 000 |
Как видите, чтобы напряжение увеличилось в три раза, мощность необходимо поднять в 10 раз. Впечатляющая разница. Эта таблица позволяет точно понять связь между этими величинами.
Но сигналы и величины не только увеличиваются, они могут и снижаться. Следующая таблица дана для падения значений относительно эталона.
| дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы | дБ | Снижение напряжения (силы тока) в разы | Снижение мощности (энергетической составляющей) в разы |
|---|---|---|---|---|---|
| 0 | 1 | 1 | -8,0 | 0,398 | 0,159 |
| -0,1 | 0,989 | 0,977 | -9,0 | 0,355 | 0,126 |
| -0,2 | 0,977 | 0,955 | -10 | 0,316 | 0,1 |
| -0,3 | 0,966 | 0,933 | -11 | 0,282 | 0,0794 |
| -0,4 | 0,955 | 0,912 | -12 | 0,251 | 0,0631 |
| -0,5 | 0,944 | 0,891 | -13 | 0,224 | 0,0501 |
| -0,6 | 0,933 | 0,871 | -14 | 0,2 | 0,0398 |
| -0,8 | 0,912 | 0,832 | -15 | 0,178 | 0,0316 |
| -1,0 | 0,891 | 0,794 | -16 | 0,159 | 0,0251 |
| -1,5 | 0,841 | 0,708 | -18 | 0,126 | 0,0159 |
| -2,0 | 0,794 | 0,631 | -20 | 0,1 | 0,01 |
| -2,5 | 0,750 | 0,562 | -30 | 0,0316 | 0,001 |
| -3,0 | 0,668 | 0,501 | -40 | 0,01 | 0,0001 |
| -3,5 | 0,631 | 0,447 | -50 | 0,00316 | 0,00001 |
| -4,0 | 0,596 | 0,398 | -60 | 0,001 | 0,000001 |
| -4,5 | 0,562 | 0,355 | -70 | 0,000316 | 0,0000001 |
| -5,0 | 0,501 | 0,316 | -80 | 0,0001 | 0,00000001 |
| -6,0 | 0,501 | 0,251 | -90 | 0,0000316 | 0,000000001 |
| -7,0 | 0,447 | 0,2 | -100 | 0,00001 | 0,0000000001 |
Ослабление того или иного сигнала проще описывать в децибелах. Простые цифры легче запоминаются. Но иногда надо знать и реальный уровень мощности. Для этого используют таблицы (перевод дБ в мкВ)
Перевод ослабления сигнала в дБ в микровольты мкВ
15.06.2010
Что такое Децибел (dB)?
Децибе́л — Логарифмическая единица уровней, затуханий и усилений .
Децибел — десятая часть бела, то есть десятая часть логарифма безразмерного отношения физической величины к одноименной физической величине, принимаемой за исходную
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трехкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причем к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB» (неправильно: дб, Дб). Децибел аналогичен единицам бел (Б, B) и непер (Нп, Np) и прямо пропорционален им.
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
Области применения
Децибел широко применяется в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибел используется не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). С помощью децибела можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
В настоящее время рекомендуется употреблять децибелы только для измерения уровня мощности и некоторых других связанных с мощностью величин.
Как перейти к децибелам?
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P ~ U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические.
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:
где P1/P0 — отношение значений двух мощностей: измеряемой P1 к так называемой опорной P0, то есть базовой, взятой за нулевой уровень (имеется ввиду нулевой уровень в единицах дБ, поскольку в случае равенства мощностей P1 = P0 логарифм их отношения lg(P1/P0) = 0).
Соответственно, переход от дБ к отношению мощностей осуществляется по формуле
P1/P0 = 10(0.1 · величина в дБ),
а мощность P1 может быть найдена при известной опорной мощности P0 по выражению
P1 = P0 · 10(0.1 · величина в дБ).
Измерение «неэнергетических» величин
Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца P = U²/R или P = I² R.
Следовательно,

, где R1 — сопротивление, на котором определяется изменяемое напряжение U1, а R0 — сопротивление, на котором было определено опорное напряжение U0.
В общем случае напряжения U1 и U0 могут регистрироваться на различных по величине сопротивлениях (R1 не равно R0). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае
величина в децибелах =
Только в частном (весьма распространенном) случае, если оба напряжения U1 и U0 измерялись на одном и том же сопротивлении (R1 = R0), можно пользоваться кратким выражением
величина в децибелах = .
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
дБ по напряжению =
дБ по току =
Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует четко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
при регистрации мощности изменению на +1 дБ (+1 дБ «по мощности») соответствует приращение мощности в ≈1.259 раза, изменению на −3.01 дБ — снижение мощности в два раза, в то время как
Переход от дБ к «разам»
Чтобы вычислить изменение «в разах» по известному изменению в дБ («dB» в формулах ниже), нужно:
для мощности:
для напряжения (силы тока):
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:
Вт.

Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:
≈ 4 В.
Рекомендации
При некотором навыке операции с децибелами вполне реально выполнять в уме. Более того, нередко это очень удобно: вместо умножения, деления, возведения в степень и извлечения корня удается обходиться сложением и вычитанием «децибельных» единиц.
Для этого полезно помнить и научиться применять несложную таблицу:
1 дБ — в 1.25 раза,
3 дБ — в 2 раза,
10 дБ — в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ — в 2·2 = в 4 раза,
9 дБ = 3 дБ + 3 дБ + 3 дБ — в 2·2·2 = в 8 раз,
12 дБ = 4 · (3 дБ) — в 24 = в 16 раз
и т. п., а также:
13 дБ = 10 дБ + 3 дБ — в 10·2 = в 20 раз,
20 дБ = 10 дБ + 10 дБ — в 10·10 = в 100 раз,
30 дБ = 3 · (10 дБ) — в 10³ = в 1000 раз
и т. п.
Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:
уменьшение мощности в 40 раз — это в 4·10 раз или на −(6 дБ + 10 дБ) = −16 дБ;
увеличение мощности в 128 раз это 27 или на 7·(3 дБ) = 21 дБ;
снижение напряжения в 4 раза эквивалентно снижению мощности (величины второго порядка) в 4² = 16 раз; и то и другое при R1 = R0 эквивалентно снижению на 4·(−3 дБ) = −12 дБ.
Зачем использовать децибелы?
Зачем вообще применять децибелы и оперировать логарифмами, если для решения задачи в принципе можно обойтись более привычными процентами или долями? Тому есть ряд причин:
Характер отображения в органах чувств человека и животных изменений течения многих физических и биологических процессов пропорционален не амплитуде входного воздействия, а логарифму входного воздействия (живая природа живет по логарифму[3]). Поэтому вполне естественно шкалы приборов и вообще шкалы единц устанавливать именно в логарифмические, в том числе, используя децибелы. Например музыкальная равномерно темперированная шкала частот является одной из таких логарифмических шкал.
Удобство логарифмической шкалы в тех случаях, когда в одной задаче приходится оперировать одновременно величинами, различающимися не во втором знаке после запятой, а в разы и, тем более, различающимися на много порядков (примеры: задача выбора графического отображения уровней сигнала, частотных диапазонов радиоприемников и др. звуковоспроизводящих устройств, расчет частот для настройки клавиатуры фортепьяно, расчеты спектров при синтезе и обработке музыкальных и других гармонических звуковых, световых волн, графические отображения скоростей в космонавтике, авиации, в скоростном транспорте, графическое отображения других переменных величин, изменения которых в широком диапазоне величин являются критически важными …).
Удобство отображения и анализа величины, изменяющейся в очень широких пределах (пример — диаграмма направленности антенны, график движений курса валют за год,…).
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например «дБВ» (децибел относительно вольта) или «дБмкВ» (децибел относительно микровольта), «дБВт» (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину ее значение помещают в скобках за обозначением логарифмической величины, например для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Опорный уровень
Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0 дБ).
Строго говоря, должно быть однозначно определено, какая именно физическая величина и какое именно ее значение используются в качестве опорного уровня. Опорный уровень указывается в виде «добавки», следующей за символами «дБ» (например, «дБм»), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).
На практике распространены следующие опорные уровни и специальные обозначения для них:
dBm (русское дБм) — опорный уровень — это мощность в 1 мВт. Мощность обычно определяется на номинальной нагрузке (для профессиональной техники — обычно 10 кОм для частот менее 10 МГц, для радиочастотной техники — 50 Ом или 75 Ом). Например, «выходная мощность усилительного каскада составляет 13 дБм» (то есть мощность, выделяющаяся на номинальной для этого усилительного каскада нагрузке, составляет 20 мВт).[4].
dBV (русское дБВ) — опорное напряжение 1 В на номинальной нагрузке (для бытовой техники — обычно 47 кОм); например, стандартизованный уровень сигнала для бытового аудиооборудования составляет −10 дБВ, то есть 0.316 В на нагрузке 47 кОм.
dBuV (русское дБмкВ) — опорное напряжение 1 мкВ; например, «чувствительность радиоприёмника, измеренная на антенном входе — −10 дБмкВ … номинальное сопротивление антенны — 50 Ом».
dBu — опорное напряжение 0,775В, соответствующее мощности 1мВт на нагрузке 600Ω; например, стандартизованный уровень сигнала для профессионального аудиооборудования составляет +4dBu, то есть 1.23В.
dBm0 (русское дБм0) — опорная мощность в дБм в точке нулевого относительного уровня. «Абсолютный уровень мощности относительно 1 мВт в точке линии передачи с нулевым уровнем»[1]
dBFS (англ. Full Scale — «полная шкала») — опорное напряжение соответствует полной шкале прибора; например, «уровень записи составляет −6dBfs». Для линейного цифрового кода каждый разряд соответствует 6дБ, и максимально возможный уровень записи равен 0dBFS.
dBSPL (англ. Sound Pressure Level — «уровень звукового давления») — опорное звуковое давление 20мкПа, соответствующее порогу слышимости; например, «громкость 100dBSPL».
dBPa — опорное звуковое давление 1Па или 94дБ звуковой шкалы громкости dBSPL; например, «для громкости 6dBPa микшером установили +4dBu, а регулятором записи −3dBFS, искажения при этом составили −70dBc».
dBA, dBB, dBC, dBD — опорные уровни выбраны в соответствии с частотными характеристиками «весовых фильтров» в соответствии с кривыми равной громкости (см. Фон).
dBc (русское дБн) — опорным является уровень излучения на частоте несущей (англ. carrier) или уровень основной гармоники в спектре сигнала. Примеры использования: «уровень побочного излучения радиопередатчика на частоте второй гармоники составляет −60 дБн» (то есть мощность этого побочного излучения в 1 млн раз меньше мощности несущей) или «уровень искажений составляет −60 дБн».
dBi (русское дБи) — изотропный децибел (децибел относительно изотропного излучателя). Характеризует коэффициент направленного действия (а также коэффициент усиления) антенны относительно коэффициента направленного действия изотропного излучателя. Как правило, если не оговорено специально, характеристики усиления реальных антенн даются именно относительно усиления изотропного излучателя. То есть, когда вам говорят, что коэффициент усиления какой-то антенны равен 12 децибел, подразумевается 12 дБи.
dBd (русское дБд) — децибел относительно полуволнового вибратора («относительно диполя»). Характеризует коэффициент направленного действия (а также коэффициент усиления) антенны относительно коэффициента направленного действия полуволнового вибратора, размещенного в свободном пространстве. Поскольку коэффициент направленного действия указанного полуволнового вибратора приближенно равен 2.15 дБи, то 1 дБд = 2.15 дБи.
По аналогии образуются составные единицы измерений. Например, уровень спектральной плотности мощности дБВт/Гц — «децибельный» аналог единицы измерения Вт/Гц (мощность, выделяющаяся на номинальной нагрузке в полосе частот шириной в 1 Гц с центром на указанной частоте). Опорным уровнем в данном примере является 1 Вт/Гц, то есть физическая величина «спектральная плотность мощности», ее размерность «Вт/Гц» и значение «1». Так, запись «-120 дБВт/Гц» полностью эквивалентна записи «10−12 Вт/Гц».
В случае затруднения во избежание путаницы достаточно указать опорный уровень явно. Например, запись −20 дБ (относительно 0.775 B на нагрузке 50 Ом) исключает двойное толкование.
Справедливы следующие правила (следствие правил действий с размерными величинами):
перемножать или делить «децибельные» значения нельзя (это бессмысленно);
суммирование «децибельных» значений соответствует умножению абсолютных значений, вычитание «децибельных» значений — делению абсолютных значений;
суммирование или вычитание «децибельных» значений может выполняться независимо от их «исходной» размерности. Например, равенство 10 дБм + 13 дБ = 23 дБм является корректным, полностью эквивалентно равенству 10 мВт · 20 = 200 мВт и может трактоваться как «усилитель с коэффициентом усиления 13 дБ увеличивает мощность сигнала с 10 дБм до 23 дБм».
Следует аккуратно использовать знак «минус», поскольку цена ошибки со знаком в операциях с децибелами — не «в два раза», а «на много порядков». Например, из записи «входной уровень — 10 дБм» не ясно, идёт ли речь о «+10 дБм» или же о «минус 10 дБм». В зависимости от ситуации лучше писать: «входной уровень +10 дБм», «входной уровень: 10 дБм», «входной уровень минус 10 дБм».
Громкость звука. Уровень шума и его источники
Физическая характеристика громкости звука — уровень звукового давления, в децибелах (дБ). «Шум» — это беспорядочное смешение звуков.
Звуки с низкой и высокой частотой кажутся тише, чем среднечастотные той же интенсивности. С учётом этого, неравномерную чувствительность
человеческого уха к звукам разных частот модулируют с помощью специального электронного частотного фильтра, получая, в результате нормирования
измерений, так называемый эквивалентный (по энергии, «взвешенный») уровень звука с размерностью дБА (дБ(А), то есть — с фильтром «А»).
Человек может слышать звуки громкостью от 10-15 дБ и выше. Максимальный диапазон частот для человеческого уха — от 20 до 20 000 Гц. Лучше
слышен звук с частотой 3-4 КГц (обычен в телефонах и по радио на СВ и ДВ диапазонах). С возрастом, воспринимаемый на слух звуковой диапозон
сужается, особенно для высокочастотных звуков, уменьшаясь до 18 килогерц и менее.
В случае отсутствия на стенах помещений звукопоглощающих материалов (ковров, специальных покрытий), звук будет громче из-за многократного
отражения (реверберации, то есть — эха от стен, потолка и мебели), что увеличит уровень шума на несколько децибел.
Шкала шумов (уровни звука, децибел):
0 Ничего не слышно
5 Почти не слышно
10 Почти не слышно тихий шелест листьев
15 Едва слышно шелест листвы
20 Едва слышно шепот человека (1м).
25 Тихо шепот человека (1м)
30 Тихо шепот, тиканье настенных часов.
Норма для жилых помещений ночью, с 23 до 7 ч.
35 Довольно слышно приглушенный разговор
40 Довольно слышно обычная речь.
Норма для жилых помещений, с 7 до 23 ч.
45 Довольно слышно обычный разговор
50 Отчётливо слышно разговор, пишущая машинка
55 Отчётливо слышно Норма для офисных помещений класса А (по европейским нормам)
60 Шумно Норма для контор
65 Шумно громкий разговор (1м)
70 Шумно громкие разговоры (1м)
75 Шумно крик, смех (1м)
80 Очень шумно крик, мотоцикл с глушителем.
85 Очень шумно громкий крик, мотоцикл с глушителем
90 Очень шумно громкие крики, грузовой железнодорожный вагон (в семи метрах)
95 Очень шумно вагон метро (7м)
100 Крайне шумно оркестр, вагон метро (прерывисто), раскаты грома
Максимально допустимое звуковое давление для наушников плеера (по европейским нормам)
105 Крайне шумно в самолёте (до 80-х годов ХХ столетия)
110 Крайне шумно вертолёт
115 Крайне шумно пескоструйный аппарат (1м)
120 Почти невыносимо отбойный молоток (1м)
125 Почти невыносимо
130 Болевой порог самолёт на старте
135 Контузия
140 Контузия звук взлетающего реактивного самолета
145 Контузия старт ракеты
150 Контузия, травмы
155 Контузия, травмы
160 Шок, травмы ударная волна от сверхзвукового самолёта
При уровнях звука свыше 160 дБ возможен разрыв барабанных перепонок и лёгких, больше 200 — смерть
Максимально допустимые уровни звука (LАмакс, дБА) — больше «нормальных» на 15 децибел. Например, для жилых комнат квартир допустимый
постоянный уровень звука в дневное время — 40 децибелов, а временный максимальный — 55.
Неслышный шум — звуки с частотами менее 16-20 Гц (инфразвук) и более 20 КГц (ультразвук). Низкочастотные колебания в 5-10 герц могут вызывать
резонанс внутренних органов и влиять на работу мозга. Низкочастотные акустические колебания усиливают ноющие боли в костях и суставах у
больных. Источники инфразвука: автомобили, вагоны, гром от молнии и т.д. Высокочастотные колебания вызывают нагрев тканей. Эффект зависит от
силы звука, расположения и свойств его источников.
На рабочих местах предельно допустимые эквивалентные уровни звука для прерывистого шума: максимальный уровень звука не должен превышать 110
дБА, а для импульсного шума — 125 дБАI. Запрещается даже кратковременное пребывание в зонах с уровнями звукового давления свыше 135 дБ в любой
октавной полосе.
Шум, издаваемый компьютером, принтером и факсом в комнате без звукопоглощающих материалов — может превышать уровень 70 db. Поэтому не
рекомендуется размещать много оргтехники в одном помещении. Слишком шумное оборудование должно выноситься за пределы помещения, где
располагаются рабочие места.
Снизить уровень шума можно, если использовать шумопоглощающие материалы в качестве отделки помещения и занавески из плотной ткани. Помогут и
противошумные бируши для ушей.
При возведении зданий и сооружений, в соответствии с современными, более жесткими требованиями звукоизоляции, должны применяться технологии и
материалы, способные обеспечить надёжную защиту от шума.
Для пожарной сигнализации: уровень звукового давления полезного аудиосигнала, обеспечиваемый оповещателем, должен быть не менее 75 дБА на
расстоянии 3 м от оповещателя и не более 120 dba в любой точке защищаемого помещения (п.3.14 НПБ 104-03).
Сирена большой мощности и корабельный ревун — давит больше 120-130 децибел.
Спецсигналы (сирены и «крякалки» — Air Horn), устанавливаемые на служебном транспорте, регламентируются ГОСТ Р 50574 — 2002. Уровень звукового
давления сигнального устройства при подаче специального звук. сигнала, на расстоянии 2 метра по оси рупора, должен быть не ниже:
116 дБ(А) — при установке излучателя звука на крыше транспортного средства;
122 дБА — при установке излуч-ля в подкапотное пространство автотранспорта.
Изменения основной частоты должны быть от 150 до 2000 Гц. Продолжительность цикла — от 0,5 до 6,0 с.
Клаксон гражданского автомобиля, согласно ГОСТ Р 41.28-99 и Правил ЕЭК ООН №28, должен издавать непрерывный и монотонный звук с уровнем
акустического давления не более 118 децибел. Такого порядка максимально допустимые значения — и для автосигнализации.
Если городской житель, привыкший к постоянному шуму, окажется на некоторое время в полной тишине (в сухой пещере, например, где уровень шума —
менее 20 db), то он вполне может испытать депрессивные состояния вместо отдыха.
Прибор шумометр для измерения уровня звука, шума
Для измерения уровня шума применяется прибор шумомер (на фото), который производят в разных модификациях: бытовые (ориентировочная цена — 3-4
т.р, диапазоны измерения: 30-130 дБ, 31,5 Гц — 8 кГц, фильтры А и С), промышленные (интегрирующие и т.д.) Наиболее распространённые модели:
SL, октава, svan. Для измерений инфразвуковых и ультразвуковых шумов применяются широкодиапазонные шумометры.
Как сохранить свой слух
Длительное воздействие шума с уровнем более 80-90 децибелл может привести к частичной или полной потере слуха. Так же, могут произойти
патологические изменения в сердечно-сосудистой и нервной системе. Безопасны только звуки громкостью до 35 дБ.
Реакцией на длительное и сильное шумовое воздействие является «тиннитус» — звон в ушах, «шум в голове», который может перерасти в
прогрессирующее снижение слуха. Характерно для возрастов старше 30 лет, при ослабленном организме, стрессах, злоупотреблении алкоголем и курении. В простейшем случае, причиной ушного шума или тугоухости может быть серная пробка в ухе, которая легко удаляется врачём-специалистом
(промыванием или извлечением). Если воспалён слуховой нерв — это лечится, тоже сравнительно легко, и без медиков. Пульсирующий шум — более
тяжёлый случай (сужение кровенослых сосудов при атеросклерозе или опухолях, а так же — при подвывихе шейных позвонков).
Чтобы уберечь слух:
• не увеличивать громкость звука в наушниках плеера, пытаясь заглушить внешний шум (в метро или на улице). При этом увеличивается и
электромагнитное излучение на мозг от динамика наушника;
• в шумном месте использовать противошумные мягкие «беруши» или наушники-вкладыши. Их надо «подгонять» индивидуально под ухо;
• в помещениях применять шумоизолирующие экологичные материалы для снижения шума;
• при подводном погружении, чтобы не произошёл разрыв барабанной перепонки — вовремя продуваться (проводить продувание ушей зажав нос или
глотательным движением). Сразу после дайвинга — нельзя на самолёт. Прыгая с парашютом — так же надо своевременно выравнивать давление, чтобы
не получить баротравму. Последствия баротравмы: шум и звон в ушах (субъективный «тиннитус»), снижение слуха, боль в ухе, тошнота и
головокружение, в тяжёлых случаях — потеря сознания.
• с простудой и насморком, когда заложен нос и гайморовы пазухи, недопустимы резкие перепады давления: ныряние (гидростатическое давл-е – 1
атмосфера на 10 метров глубины погружения в воду, то есть: две — на десяти, три — на 20 м. и т.д.), парашютные прыжки (0,01 атм. на 100 м.
высоты, быстро увеличивается);
• давать своим ушам отдыхать
Приёмы выравнивания давления с обеих сторон барабанной перепонки уха: глотание, зевание, продувание с закрытым носом. Артиллеристы, производя
выстрел — открывают рот или закрывают уши ладонями рук.
Частые причины снижения слуха: попадание в уши воды, инфекции (в том числе и органов дыхания), травмы и опухоли, образование серной пробки и
её набухание при контакте с водой, длительное пребывание в шумной обстановке, баротравма при резком перепаде давления, воспаление среднего уха
— отит (скопление жидкости за барабанной перепонкой).
ДЕЦИБЕЛ
(дБ, dB), дольная ед. от бела — ед. логарифмич. относит. величины; 1 дБ=0,1 Б. В акустике — ед. уровня звук. давления; 1 дБ — уровень звук. давления р, для к-рого выполняется соотношение 201g(p/p0)=1, где p0 — пороговое звук. давление, принимаемое равным 2 •10-5 Па.
Физический энциклопедический словарь. — М.: Советская энциклопедия..1983.
Синонимы:
единица
ДЖОЗЕФСОНА ЭФФЕКТ →← ДЕЦИ
Синонимы слова «ДЕЦИБЕЛ»:
ЕДИНИЦА
Смотреть что такое ДЕЦИБЕЛ в других словарях:
ДЕЦИБЕЛ
(от Деци… и Бел) дольная единица от бела — единицы логарифмической относительной величины (десятичного логарифма отношения двух одноимённых фи… смотреть
ДЕЦИБЕЛ
ДЕЦИБЕЛ, -а, род. мн. децибелов и при счете преимущ. децибел, м.(спец.). Единица величины (уровня звукового давления, усиления, ослабления).
ДЕЦИБЕЛ
децибел м. Логарифмическая единица для сопоставления значений физических величин (уровней звуковой мощности, коэффициента усиления электронных приборов и т.п.), равная одной десятой доле бела.<br><br><br>… смотреть
ДЕЦИБЕЛ
децибел
сущ., кол-во синонимов: 1
• единица (830)
Словарь синонимов ASIS.В.Н. Тришин.2013.
.
Синонимы:
единица
ДЕЦИБЕЛ
ДЕЦИБЕЛ (от деци… и бел),
дольная
единица от бела — единицы логарифмической относит, величины (десятичного
логарифма отношения двух одноимённых фи… смотреть
ДЕЦИБЕЛ
децибе́л
(см. деци…) десятая часть бела; сокращ. обозначения: дб, db.
Новый словарь иностранных слов.- by EdwART, ,2009.
децибел
[фр. decibel] – ед… смотреть
ДЕЦИБЕЛ
ДЕЦИБЕЛ (англ. decibel, dB) — психофизическая единица интенсивности стимулов, одна десятая бела: 1 бел = lg (I / Iпор ), где I — интенсивность данного стимула (напр., физическая яркость света или сила звука), Iпор — интенсивность порогового стимула (величина абсолютного порога). С одной стороны, шкала Д. позволяет более адекватно судить о субъективной силе разных стимулов (в соответствии с законом Фехнера); с др. стороны, зная свойства логарифмов, нетрудно оценить соотношение физических характеристик. Шкала Д. также позволяет более непосредственно проводить кросс-модальные сопоставления интенсивности стимулов (напр., как сила звука, так и яркость света, равные 130-140 дБ являются запредельными и физически опасными для органов чувств, тогда как 60-70 дБ — это уровень средних по громкости и яркости раздражителей). Ср. Слух, Фон. (Б. М.)<br><br><br>… смотреть
ДЕЦИБЕЛ
(англ. decibel, dB) — психофизическая единица интенсивности стимулов, одна десятая бела: 1 бел = lg (I / Iпор ), где I — интенсивность данного стимула (напр., физическая яркость света или сила звука), Iпор — интенсивность порогового стимула (величина абсолютного порога). С одной стороны, шкала Д. позволяет более адекватно судить о субъективной силе разных стимулов (в соответствии с законом Фехнера); с др. стороны, зная свойства логарифмов, нетрудно оценить соотношение физических характеристик. Шкала Д. также позволяет более непосредственно проводить кросс-модальные сопоставления интенсивности стимулов (напр., как сила звука, так и яркость света, равные 130-140 дБ являются запредельными и физически опасными для органов чувств, тогда как 60-70 дБ — это уровень средних по громкости и яркости раздражителей). Ср. Слух, Фон. (Б. М.)… смотреть
ДЕЦИБЕЛ
ДЕЦИБЕ́Л, а, ч., спец.Логарифмічна одиниця відношень енергій, потужностей у фізиці, радіотехніці, електротехніці, акустиці, яка дорівнює одній десятій … смотреть
ДЕЦИБЕЛ
1) Орфографическая запись слова: децибел2) Ударение в слове: дециб`ел3) Деление слова на слоги (перенос слова): децибел4) Фонетическая транскрипция сло… смотреть
ДЕЦИБЕЛ
ДЕЦИБЕЛ (обозначение дБ), логарифмическая единица, одна десятая бела, служащая для сопоставления двух уровней энергии. Децибелами часто пользуются для … смотреть
ДЕЦИБЕЛ
децибе/л, -а, род. мн. децибе/л и децибе/лов
Синонимы: единица
ДЕЦИБЕЛ
Децибел
мера шумового загрязнения.
EdwART.Словарь экологических терминов и определений,2010
Синонимы: единица
ДЕЦИБЕЛ
[лат. decem десять + бел (по имени американского изобретателя A.G. Bell, 1847—1922)] — одна десятая часть бела — логарифмической единицы измерения, пре… смотреть
ДЕЦИБЕЛ
корень — ДЕЦИ; корень — БЕЛ; нулевое окончание;Основа слова: ДЕЦИБЕЛВычисленный способ образования слова: Бессуфиксальный или другой∩ — ДЕЦИ; ∩ — БЕЛ; … смотреть
ДЕЦИБЕЛ
децибел [ ат. decem десять + бел (по имени амер. изобретателя A. G. Bell, 1847-1922)] — одна десятая часть бела — логарифмической единицы измерения, представляющей собой десятичный логарифм отношения двух одноименных физических величин; в медицине в Д. выражается количественная характеристика интенсивности звука по отношению к пороговой (0,0002 дин/см<sup>2</sup>). <br><br><br>… смотреть
ДЕЦИБЕЛ
единица изменения шумового загрязнения, интенсивности (мощности, звукового давления) звука. Условное обозначение дБ. Интервал комфорта не выше 30–40 дБ, болевой порог – 120 дБ. Шкала силы звука строится на логарифмах отношения данной величины звука к порогу слышимости, принимаемому за ноль. Интенсивность звука в 10 дБ превышает порог слышимости в 10 раз, в 20 дБ – в 100 раз. … смотреть
ДЕЦИБЕЛ
(от лат. decem — десять; десятая часть бела; сокращенное обозначение — дБ, dB) — логарифмическая единица измерения интенсивности потока энергии (колебаний) относительно условно принятого исходного уровня отсчета. В Д. может измеряться также отношение двух каких-либо физических величин (напр., коэффициент усиления или затухания сигнала, коэффициент поглощения и т. д.)…. смотреть
ДЕЦИБЕЛ
( ат. decem десять + бел (по имени амер. изобретателя A. G. Bell, 1847-1922)) одна десятая часть бела — логарифмической единицы измерения, представляющей собой десятичный логарифм отношения двух одноименных физических величин; в медицине в Д. выражается количественная характеристика интенсивности звука по отношению к пороговой (0,0002 дин/см2)…. смотреть
ДЕЦИБЕЛ
(2 м); мн. децибе/лы, Р. децибе/лов и при обозначении количества децибе/лСинонимы: единица
ДЕЦИБЕЛ
Rzeczownik децибел m Fizyczny decybel m
ДЕЦИБЕЛ
дециб’ел, -а, род. п. мн. ч. -ов, счетн. ф. -б’елСинонимы: единица
ДЕЦИБЕЛ
децибе́л,
децибе́лы,
децибе́ла,
децибе́лов,
децибе́л,
децибе́лу,
децибе́лам,
децибе́л,
децибе́лы,
децибе́лом,
децибе́лами,
децибе́ле,
децибе́лах
(Источник: «Полная акцентуированная парадигма по А. А. Зализняку»)
.
Синонимы:
единица… смотреть
ДЕЦИБЕЛ
1. Логарифмическая единица уровней, затуханий и усилений Употребляется в документе:
ОСТ 45.159-2000 Отраслевая система обеспечения единства измерений. Термины и определения
Телекоммуникационный словарь.2013.
Синонимы:
единица… смотреть
ДЕЦИБЕЛ
децибе́л, -а; р. мн. -ов, счётн.ф. децибе́л [дэ]Синонимы: единица
ДЕЦИБЕЛ
сущ. муж. родамуз., спец.децибел
ДЕЦИБЕЛ
(от деци… и бел) — допускаемая к применению внесистемная дольная ед. логарифмич. величины (уровня звукового давления, усиления, ослабления и т. п.). … смотреть
ДЕЦИБЕЛ
Ударение в слове: дециб`елУдарение падает на букву: еБезударные гласные в слове: дециб`ел
ДЕЦИБЕЛ
допускаемая к применению внесистемная дольная единица логарифмической величины (уровня звукового давления, усиления, ослабления и т. П.); 10-я часть бела. Обозначение дб…. смотреть
ДЕЦИБЕЛ
імен. чол. родуспец.децибел
ДЕЦИБЕЛ
-а, ч. Одиниця виміру гучності звуку; десята частина бела.
ДЕЦИБЕЛ
децибел, дециб′ел, -а, род. п. мн. ч. ~ов и при счёте преимущ. ~, м. (спец.). Единица величины (уровня звукового давления, усиления, ослабления).
ДЕЦИБЕЛ
децибе́л
(від деци… та бел)
логарифмічна одиниця відношень енергій, потужностей у радіотехніці, електротехніці, акустиці; 1 дб дорівнює 0,1 бела.
ДЕЦИБЕЛ
децибел; ч.
(деци… та бел)
логарифмічна одиниця відношень енергій, потужностей у радіотехніці, електротехніці, акустиці; 1 дб дорівнює 0,1 бела.
ДЕЦИБЕЛ
децибел — decibel — Dezibel — логарифмічна одиниця відношень енергій, потужностей у радіотехніці, електротехніці, акустиці; 1 дб дорівнює 0,1 бела.
ДЕЦИБЕЛ
decibel* * *децибе́л м.decibel, dBСинонимы: единица
ДЕЦИБЕЛ
децибе’л, децибе’лы, децибе’ла, децибе’лов, децибе’л, децибе’лу, децибе’лам, децибе’л, децибе’лы, децибе’лом, децибе’лами, децибе’ле, децибе’лах
ДЕЦИБЕЛ
ДЕЦИБЕЛ, -а, род. мн. децибелов и при счёте преимущ. децибел, м. (спец.). Единица величины (уровня звукового давления, усиления, ослабления).
ДЕЦИБЕЛ
〔名词〕 分贝 〈复二〉 -ов 或(表示计量时多用)-бел〔阳〕〈理〉分贝. Синонимы: единица
ДЕЦИБЕЛ
Дольная единица логарифмической величины, равная 0,1 Б.Синонимы: единица
ДЕЦИБЕЛ
м.(акустическая единица) decibel
ДЕЦИБЕЛ
м.décibel mСинонимы: единица
ДЕЦИБЕЛ
десятая часть бела, обозначается дБ. Синонимы: единица
ДЕЦИБЕЛ
– единица измерения уровня громкости шума.Синонимы: единица
ДЕЦИБЕЛ
decibel– децибел на декадуСинонимы: единица
ДЕЦИБЕЛ
Начальная форма — Децибел, винительный падеж, единственное число, мужской род, неодушевленное
ДЕЦИБЕЛ
децибел м Dezibel n 1dСинонимы: единица
ДЕЦИБЕЛ
децибел [см. деци…] — десятая часть бела; сокращ. обозначения: дб, db.
ДЕЦИБЕЛ
Децибе́лdesibeli (-), kipimo cha mrindimo (vi-)
ДЕЦИБЕЛ
-а, ч. Одиниця виміру гучності звуку; десята частина бела.
ДЕЦИБЕЛ
м. спец.
decibel
Итальяно-русский словарь.2003.
Синонимы:
единица
ДЕЦИБЕЛ
Дели Делец Делиец Децибел Елец Лед Белец Биде Леди Блиц Еле Дебил
ДЕЦИБЕЛ
децибел дециб`ел, -а, р. мн. -ов, счетн. ф. -б`ел
ДЕЦИБЕЛ
ДЕЦИБЕЛ, десятая часть бела, обозначается дБ.
ДЕЦИБЕЛ
(дБ) одиниця, рівна 0,1 Б (Бела).
ДЕЦИБЕЛ
ДЕЦИБЕЛ — десятая часть бела, обозначается дБ.
ДЕЦИБЕЛ
ДЕЦИБЕЛ , десятая часть бела, обозначается дБ.
ДЕЦИБЕЛ
ДЕЦИБЕЛ, десятая часть бела, обозначается дБ.
ДЕЦИБЕЛ
— десятая часть бела, обозначается дБ.
ДЕЦИБЕЛ
физ.
децибе́л
Синонимы:
единица
ДЕЦИБЕЛ
децибе́л
іменник чоловічого роду
ДЕЦИБЕЛ
(дБ) одиниця, рівна 0,1 Б (Бела).
ДЕЦИБЕЛ
(единица силы звука) decibel
Слово «децибел» состоит из двух частей: приставки «деци» и корня «бел». «Деци» дословно означает «десятая часть», т.е. десятая часть «бэла». Значит, чтобы понять что такое децибел надо понять, что такое бел и всё станет на свои места.
Давным давно Александр Белл выяснил, что человек перестает слышать звук, если мощность источника этого звука меньше, чем 10-12 Вт/м2, а если она превышает 10 Вт/м2, то готовьте ваши ушки к неприятной боли — это болевой порог.
Как видно разница между 10-12 Вт/м2 и 10 Вт/м2 целых 13 порядков. Белл поделил расстояние между порогом слышимости и болевым порогом на 13 ступеней: от 0 (10-12 Вт/м2) до 13 (10 Вт/м2). Таким образом он определил шкалу звуковой мощности.
Тут можно сказать: «О, всё понятно!», — хорошо! Но дальше ещё интересней.
Ближе к делу
Мы выяснили, что децибел равен 1/10 бела, но как это применять в жизни? Приведу такой пример:
- 0 Дб — ничего не слышно
- 15 Дб — едва слышно (шелест листвы)
- 50 Дб — Отчётливо слышно
- 60 Дб — Шумно
Да зачем это надо, если можно, к примеру, сказать: «уровень звуковой мощности 0.1 Вт/м2«. Дело в том, что экспериментально установлено, что человек ощущает изменение яркости, громкости и т.д. тогда, когда они изменяются логарифмически. Вот так:
Что в белах выражается как отношение уровня измеряемого сигнала к некоторому эталонному. 1 Бэл = lg(P1/P0), где P0 — это звуковая мощность порога слышимости, ну а чтобы получить децибел надо всего-то умножить на 10: 1 Дб = 10*lg(P1/P0)
Таким образом децибел показывает логарифм отношения уровня одного сигнала к другому и используется для сравнения двух сигналов. Из формулы, кстати, видно, что децибелах можно сравнивать любые сигналы (и не только звуковую мощность), так как децибел величина безразмерная.
Особенности
Путаница с децибелами возникает из-за того, что существует несколько их «видов». Они условно называются амплитудными и мощностными (энергетическими).
Формула 1 Дб = 10*lg(P1/P0) — сравнивает в децибелах две энергетические величины. В данном случае мощность. А формула 1 Дб = 20*lg(A1/A0) — сравнивает две амплитудные величины. К примеру, напряжение, ток и т.д.
Перейти от амплитудных децибелов к энергетическим и обратно очень просто. Требуется просто «неэнергетические» величины преобразовать в энергетические. Покажу это на примере тока и напряжения.
Из определения мощности P = UI = U2 / R = I2 * R. Подставим в 10*lg(P1/P0) и после преобразования получим 20*lg(A1/A0) — всё просто.
Таким же образом будут проводится преобразования для других амплитудных значений. Подробнее как всегда можно прочитать в учебниках и справочниках.
Зачем надо было всё усложнять?
Понимаешь, две величины могут отличаться в миллионы раз. Таким образом простое отношение (P1/P0) может давать как очень большие, так и очень маленькие значения. Согласись, что это не очень удобно в практической деятельности. Может быть это также одна из причин такой распространенности децибел (наряду со следствием из закона Вебера-Фехнера)
Таким образом децибел позволяет от исчисления в «попугаях», т.е. в разах перейти к более конкретным и небольшим величинам. Которые можно быстро складывать и вычитать в уме. А если все же хочется оценить отношение в попугаях по известному значению в децибелах, то достаточно запомнить простое мнемоническое правило (подсмотрел у Ревича):
— Если отношение величин больше единицы, то это будет положительный Дб (+3 Дб), а если меньше — отрицательный (-3 Дб). Таким образом:
- 3 Дб означает увеличение/уменьшение сигнала на треть
- 6 Дб означает увеличение/уменьшение в 2 раза
- 10 Дб соответствует изменение величины в 3 раза
- 20 Дб соответствует изменению в 10 раз
А теперь на примере. Пусть нам сказали, что сигнал усиливается на 50 Дб. А 50 Дб = 10 Дб + 20 Дб + 20 Дб = 3 * 10 * 10 = 300 раз. Т.е. сигнал усилился в 300 раз.
Так что децибел всего лишь удобное инженерное соглашение, которое введено в результате некоторых практических измерений, а также выгоды от практического использования.
Что еще почитать по теме:
- Децибелы — МРБ 0805. Зельдин Е.А.
- Шум — Р.Tэйлор.
/blog/chto-takoe-detsibel/
Краткий рассказ о самой непонятной величине для начинающих любителей электроники! Ты узнаешь, что значит 0 Дб, 15 Дб или 60 Дб и будешь понимать зачем была придумана такая странная величина!
2015-08-28
2016-03-22























![{displaystyle L_{text{ov}}=10log _{10}left({frac {P}{P_{0}}}right) [{text{dBov}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62c0e3bffad47446013fc2c871778c67c03741bb)





 ,
, ,
, .
. .
. .
. ;
; .
. ≈ 0,707 от своего исходного значения.
≈ 0,707 от своего исходного значения.![{P_1} = {left( {sqrt[10]{10^{dB}}} right) } {P_0} = {left( {sqrt[10]{10^{20}}} right) } {0,001}=0,1](https://dic.academic.ru/dic.nsf/ruwiki/93169ccb4cb7d0408a150de6e86c1764.png) Вт.
Вт.![{U_1} = {left( {sqrt[20]{10^{dB}}} right) } {U_0} = {left( {sqrt[20]{10^{6}}} right) } {2}](https://dic.academic.ru/dic.nsf/ruwiki/38c7e62143f3795d2122e167fe6bbc58.png) ≈ 4 В.
≈ 4 В.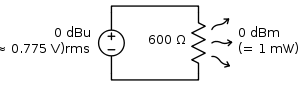
![V_{noise}=sqrt{4k_{B}TR}=9cdot 10^{-4}left[ mu text{V} right]=-61text{ dBuV}=-168text{ dBm}](https://dic.academic.ru/dic.nsf/ruwiki/ab219aba27ec307f16caf0d2560191b7.png) . Например, «уровень шума усилителя составляет 6dBrn».
. Например, «уровень шума усилителя составляет 6dBrn».