∈ Принадлежит
Нажмите, чтобы скопировать и вставить символ
Значение символа
Принадлежит. Математические операторы.
Символ «Принадлежит» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| bmg | 220B |
| Композиционное исключение | Нет |
| Изменение регистра | 2208 |
| Простое изменение регистра | 2208 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 88 88 | 226 136 136 | 14846088 | 11100010 10001000 10001000 |
| UTF-16BE | 22 08 | 34 8 | 8712 | 00100010 00001000 |
| UTF-16LE | 08 22 | 8 34 | 2082 | 00001000 00100010 |
| UTF-32BE | 00 00 22 08 | 0 0 34 8 | 8712 | 00000000 00000000 00100010 00001000 |
| UTF-32LE | 08 22 00 00 | 8 34 0 0 | 136445952 | 00001000 00100010 00000000 00000000 |
Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Знак (символ, сокращение) |
Пояснения (расшифровка, легенда) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
т.о. |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
ЧТД QED |
Конец доказательства = «Что и требовалось доказать» = quod erat demonstrandum | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
= |
Равенство | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
Записывается a |
|||||||||||||||||||||||
|
|
По определению логически эквивалентно | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Неравенство | |||||||||||||||||||||||
|
|
Меньше | |||||||||||||||||||||||
|
|
Больше | |||||||||||||||||||||||
|
|
Много меньше | |||||||||||||||||||||||
|
|
Много больше | |||||||||||||||||||||||
|
<= |
Меньше или равно | |||||||||||||||||||||||
|
>= |
Больше или равно | |||||||||||||||||||||||
|
|
Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Разделить | |||||||||||||||||||||||
|
|
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G
Если X — множество с заданным на нем отношением эквивалентности |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Минус плюс — имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
P(A|B) — вероятность события А, при условии, что событие B уже произошло
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f
A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. |
|||||||||||||||||||||||
|
|
a||b — параллельные прямые a и b
Если X — множество с отношением частичного порядка ≤, а a и b — его элементы, то a||b — a и b несравнимы, если про них невозможно сказать ни a≤b, ни b≤a
|
|||||||||||||||||||||||
|
|
n# — произведение простых чисел, не превышающих n |
|||||||||||||||||||||||
|
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
|||||||||||||||||||||||
|
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
|||||||||||||||||||||||
|
|
мощность континуума — теория множеств |
|||||||||||||||||||||||
|
: |
E:K значит, что E — это расширение поля K
|
|||||||||||||||||||||||
|
! |
n!=1*2*3…..*(n-1)*n читается n-факториал
!A=1, если А=0, !А=0, если А=1, читается не А. |
|||||||||||||||||||||||
|
|
сплетение групп в теории групп (Также обозначается как АwrВ) | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Антисоединение отношений (Antijoin) — операция реляционной алгебры, которая оставляет только те кортежи первого отношения, для которых не найдется кортежей второго отношения, совпадающих с ними по общему атрибуту. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Естественное соединение отношений (Natural Join)- операция реляционной алгебры, результатом которой является набор всех возможных комбинаций кортежей исходных отношений, то есть комбинаций тех кортежей, у которых совпадают общие атрибуты |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
импликация (материальная) логика |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
исключающее ИЛИ (только в логике) |
|||||||||||||||||||||||
|
|
обозначение понятия — любой, читается как — «для любого», «для всех», «для каждого» |
|||||||||||||||||||||||
|
|
обозначение понятия — существует, читается как «найдется», «существует», «существуют»… |
|||||||||||||||||||||||
|
|
обозначение понятия — существует единственный, читается как «найдется ровно один «, «существует один и только один «, «существует единственный «… |
|||||||||||||||||||||||
|
|
внутри скобок записываются элементы множества |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок принадлежности к множеству — читается «принадлежит…» |
|||||||||||||||||||||||
|
|
значок не принадлежности к множеству — читается «не принадлежит…» |
|||||||||||||||||||||||
|
|
Знак подмножества. А |
|||||||||||||||||||||||
|
|
Знак собственного (строгого = истинного ) подмножества. А |
|||||||||||||||||||||||
|
|
Знак надмножества. А |
|||||||||||||||||||||||
|
|
Знак строгого = истинного надмножества. А |
|||||||||||||||||||||||
|
|
В теории множеств-объединение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — пересечение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — симметрическая разность множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — разность множеств (или относительное дополнение одного множества до другого). С= А |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Стрелка, определяющая отображение (функцию) f. Запись f: a Наример, f: x |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Множество натуральных чисел. В зависимости от контекста и области применения этого обозначения за  обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. |
|||||||||||||||||||||||
|
|
Множество целых чисел.
Также можно написать |
|||||||||||||||||||||||
|
|
Множество положительных целых чисел. Т.е. множество {1, 2, 3, …} | |||||||||||||||||||||||
|
|
Множество неотрицательных целых чисел. Т.е. множество {0, 1, 2, …} | |||||||||||||||||||||||
|
Z/(n)Z Z/(n) |
Кольцо вычетов по модулю n. Стоит понимать, что вместо n может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Множество p-адических чисел вида Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Проективное пространство. В частности,  n n-мерное проективное пространство. n n-мерное проективное пространство. |
|||||||||||||||||||||||
|
P(X) Pr(X) P[X] Pr[X] |
В теории вероятности — вероятность. |
|||||||||||||||||||||||
|
|
Множество рациональных чисел.
|
|||||||||||||||||||||||
|
|
Множество действительных чисел | |||||||||||||||||||||||
|
|
Множество комплексных чисел.
|
|||||||||||||||||||||||
|
|
Множество кватернионов (кватернионов Гамильтона).
Другими словами, a — это рациональное число, а b i +c j +d k — это вектор трехмерного пространства с координатами {b, c, d}. |
|||||||||||||||||||||||
|
O |
O-большое в исследовании ассимптотического поведения функций. Описывает ассимптотическое поведение функции, когда ее аргумент стремится к числу или к бесконечности. Запись f(x)=O(g(x)) при x |
|||||||||||||||||||||||
|
|
Бесконечность. Элемент расширенной числовой прямой, который больше любого числа. Чаще всего употребляется, когда речь идет о пределах. | |||||||||||||||||||||||
|
|
Огругление числа до целого в меньшую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до целого в большую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до ближайшего целого к нему. Например, |
|||||||||||||||||||||||
|
|
[E:K] — это по определению размерность векторного пространства E над K. Например, [
|
|||||||||||||||||||||||
|
|
Например, [2=3]=0; [4<5]=1.
Иными словами, f[X]={f(x) | x∈X} |
|||||||||||||||||||||||
|
|
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы.
|
|||||||||||||||||||||||
|
|
Смешанное произведение векторов. | |||||||||||||||||||||||
|
|
f(x) — образ x при применении f.
Иными словами, f(X)={f(x) | x∈X}
|
|||||||||||||||||||||||
| (( )) |
Количество мультимножеств -число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
|||||||||||||||||||||||
|
|
(a, b)=НОД(a, b) — наибольший общий делитель чисел a и b.
(a,b)={x∈
|
|||||||||||||||||||||||
|
|
Интервал (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
<S> — среднее значение элементов множества S.
Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S, т.е. прересечение всех подпространств линейного пространства L, содержащих в себе множество S.
Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S, т.е. минимальная подгруппа G, содержащая S. |
|||||||||||||||||||||||
|
|
Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an.
Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an, т.е. минимальная подгруппа G, содержащая в себе элементы a1, a2…,an.
|
|||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
В обозначениях Дирака — кет-вектор. |φ> — вектор φ некоторого гильбертого пространства | |||||||||||||||||||||||
|
|
В обозначениях Дирака — бра-вектор из пространства, сопряженного некоторому гильбертовому пространству. <φ| — бра вектор, соответствующий кет-вектору |φ> (говорят, даже, совпадающий с кет-фектором |φ>), задающий линейный функционал, ставящий в соответствие каждому кет-вектору |ψ> скалярное произведение <φ|ψ>. | |||||||||||||||||||||||
|
|
число советаний из r элементов, выбранных из n элементов | |||||||||||||||||||||||
|
|
Сумма, ряд.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
В теории категорий — копроизведение (категорная сумма) | |||||||||||||||||||||||
|
|
Производная. f'(x) — значение производной функции f в точке x (Тангенс угла наклона касательно к функции f в точке x). | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Интеграл по контуру (поверхности — знак интеграла удваивается, объему-знак интеграла утраивается). | |||||||||||||||||||||||
|
|
Если вектор
Если вектор где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то |
|||||||||||||||||||||||
|
|
Если M — некоторое множество, то
Если f — многочлен, то |
|||||||||||||||||||||||
|
|
Оператор Лапласа ставит функции от n переменных в соответствие ее дифференциал второго порядка.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Операция, которая из заданного отношения (таблицы) выбирает подмножество, которое получается выбором нескольких из имеющихся атрибутов и (если потребуется) вычеркиванием повторяющихся кортежей. Результатом перации Например: Если в изначальной таблице ЛЮДИ атрибутами являются рост, вес, пол, то результатом операции
Математическая константа, равная отношению длины окружности к ее диаметру. |
|||||||||||||||||||||||
|
|
В реляционной алгебре — выборка Операция |
|||||||||||||||||||||||
|
|
В теории порядка — покрытие (понятие, определяющее смежность вершин диаграммы Хассе некоторого частично-упорядоченного множества). Если X — множество с отношением частичного порядка ≤ , а отношение < на этом множестве задается следующим образом : a<b, если a≤b и а ≠ b, то элемент y покрывает элемент x и пишется x x<z<y. Если a |
|||||||||||||||||||||||
|
|
В теории типов — подтип (подкласс, дочерний тип(класс)). Часто используется в объектно-ориентированном программировании. S  T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. Например, Круги  Фигуры. Фигуры.S  T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. |
|||||||||||||||||||||||
|
|
Эрмитово-сопряженная (комплексно-сопряженная) матрица. A† — матрица, полученная из матрицы A транспонированием и заменой каждого элемента матрицы A комплексно-сопряженным ему. Чаще всего такая матрица обозначается A*, а также встречаются обозначения A*T, AT*, |
|||||||||||||||||||||||
|
|
Транспонирование матрицы. AT — матрица, в которой в качестве строк записаны столбцы матрицы А. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
x⊥y значит, что векторы (прямые) x и y перпендикулярны, или, в более общем случае, ортогональны.
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W, т.е. множество векторов пространства V, перпендикулярных каждому из векторов подпространства W.
a⊥b значит, что наибольший общий делитель чисел a и b равен единице. Часто записывается как (a, b)=1
A⊥B значит, что случайные события A и B независимы, т.е. наступление одного из них не влияет на вероятность наступления другого.
⊥ — наименьший (нижний) элемент решетки
⊥ — тип, у которого нет подтипов
x⊥y значит, что элементы x и y частично упорядоченного множества сравнимы, т.е. про них известно, что x≤y или y≤x |
|||||||||||||||||||||||
|
|
Импликация (логическое следование) — в теории моделей A |
|||||||||||||||||||||||
|
|
Вывод — в логике высказываний (предикатов). A |
|||||||||||||||||||||||
|
|
Тензорное произведение (модулей) — в линейной алгебре. Если A и B — линейные пространства, то Если а A и b
a Если A и B — модули над коммутативным кольцом R, то A |
|||||||||||||||||||||||
|
|
a
где f, g — функции, определенные и интегрируемые относительно меры Лебега на пространстве Rd
z* — число, комплексно-сопряженное к z. Если z=a+bi, то z*=a-bi
R* — группа обратимых элементов кольца R
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. Вместо R можно использовать также другие множества, например, N*.
Линейный оператор из пространства p-векторов в пространства (n-p)-форм. Если вектор v — поливектор степени p, то *v — дифференциальная форма степени n-p. |
|||||||||||||||||||||||
|
|
Если S — некоторое подмножество топологического пространства, то |
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Легенда (пояснение, расшифровка) |
Символ (знак, сокращение) |
|||
| Следовательно, таким образом, поэтому |
1. 2. т.о. 3. |
|||
| Потому что, из-за того что, вследствие того что, поскольку, в результате того, что |
|
|||
| Конец доказательства, что и требовалось доказать |
1. ЧТД, QED (Что и требовалось доказать, quod erat demonstrandum) 2. 3. 4. |
|||
| Таких что, так что, такие что |
1. A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. 2. :
|
|||
| Материальная эквивалентность, равносильность, тогда и только тогда |
1. 2. |
|||
| Любой, для любого | ||||
| Существует, найдется | ||||
| Существует единственный | ||||
| Или | ||||
| Бесконечность |  |
|||
| Приращение, изменение |  |
|||
| Стремится |  |
|||
| Равно | = | |||
| По определению равно | 1. 2. 3. 4. 5. 6. |
|||
| По определению эквивалентно | ||||
| Равно по модулю |
Записывается a |
|||
| Не равно | ||||
| Приблизительно равно | ||||
| Сложение, ряд |
1. 2.
|
|||
| Вычитание | ||||
| Умножение, произведение |
1. 2. 3. * 4.
|
|||
| Деление, разделить |
1. : 2. 3. |
|||
| Квадратный корень (действительный, мнимый) | ||||
| Возведение в степень |
2^3 = 23 |
|||
| Факториал |
! n!=1*2*3…..*(n-1)*n читается n-факториал |
|||
| Модуль числа |
1. |a| — модуль а 2. Abs(a) |
|||
| Плюс-минус, минус-плюс |
1. 2. имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||
| Больше | ||||
| Больше или равно |
1. 2. >= |
|||
| Меньше | ||||
| Меньше или равно |
1. 2. <= |
|||
| Много больше | ||||
| Много меньше | ||||
| Числа одного порядка | ||||
| Приоритет операций | ( ) | |||
| Число сочетаний из n по r |
1. 2. |
|||
| Количество мультимножеств, число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
(( )) |
|||
| Число Пи |  |
|||
| Кортеж , упорядоченный набор (список) некоторых величин, или горизонтальный вектор |
1. 2. |
|||
| Среднее значение, усреднение |
1. 2. |
|||
| Множество, знак множества |
1. 2. 3. |
|||
| Пустое множество |
1. 2. 3. |
|||
| Знак принадлежности множеству, принадлежит | ||||
| Знак «не принадлежит множеству» |  |
|||
| Множество натуральных чисел |
|
|||
| Множество целых чисел |
1. 2. 3. |
|||
| Множество рациональных чисел |
|
|||
| Множество действительных чисел |
|
|||
| Множество комплексных чисел |
|
|||
| Множество кватернионов |
|
|||
| Множество p-адических чисел |
Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||
| Множество гипердействительных чисел |
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. |
|||
| Мощность множества, кардинальное число, количество элементов |
1. 2. |
|||
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
||||
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
||||
|
Континуум, мощность континуума |
||||
| Знак подмножества |
1. А 2. А |
|||
| Знак надмножества |
1. А 2. А |
|||
| Объединение (множеств) |  |
|||
| Пересечение (множеств) |  |
|||
| Симметрическая разность (множеств) |
1. 2. |
|||
| Разность множеств |
1. 2. — (редко) |
|||
| Прямое (декартово) произведение множеств | 1. 
2. |
|||
| Прямая сумма | ||||
| Несвязное объединение, несвязная сумма, дизъюнктное объединение | ||||
| Логическое отрицание |
1. 2. 3. ! |
|||
| Логическая конъюнкция |
1. 2. & |
|||
| Логическая дизъюнкция | ||||
| Исключающее или | ||||
| Импликация (логическое следование) |
1. 2. 3. 4. |
|||
| Вывод в логике высказываний |  |
|||
| Нотация Айверсона, или скобка Айверсона. Сопоставляет некоторому утверждению 1 или 0, в зависимости от того, истинно или ложно данное утверждение. |  |
|||
| Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
1. 2. |
|||
| Делитель, делит/ не делит нацело |
1. 2. |
|||
| Точный делитель (при разложении числа в произведение степеней простых чисел — простое число в максимальной степени, делящее исходное) | ||||
| Взаимно простые числа |  |
|||
| Примориал или праймориал | ||||
| Наибольший общий делитель |
1. 2. НОД |
|||
| Окргугление числа до целого |
1. 2. 3. 4. 5. 6. Round(x) — до ближайшего целого 7. Nint(x) — до ближайшего целого |
|||
| Сопряжение комплексных чисел |
1. z* — число, комплексно-сопряженное к z 2.
|
|||
| Пропорциональность | ||||
| Отрезок |  |
|||
| Интервал |
1. 2. |
|||
| Полуинтервал |
1. 2. 3. 4. |
|||
| Норма, длина вектора |
1. 2. |
|||
| Обозначения Дирака: кет-вектор |  |
|||
| Обозначения Дирака: бра-вектор |  |
|||
| Скалярное произведение |
1. 2. 3. 4. 5. |
|||
| Векторное произведение векторов |
1. 2. |
|||
| Смешанное произведение векоторов |  |
|||
| Ортогональность (перпендикулярность) |  |
|||
| Параллельность | ||||
| Эквивалентность матриц | ||||
| Скалярное произведение матриц | : | |||
| Определитель матрицы |
1. 2. det(A), где А — матрица 3. |
|||
| Транспонирование матрицы |
АТ — транспонированная матрица А |
|||
| Эрмитово-сопряженная (комплексно-сопряженная) матрица к матрице А |
1. A† 2.A* 3.А*T 4. AT* 5. 6. |
|||
| Произведение Адамара двух матриц одинакового размера | ||||
| Определение функции, область определения и область значений функции |
Запись f : X |
|||
| Определение функции (отображения) , задание функции |
Запись f: a |
|||
| Образ элемента/множества |
1. f(x) — образ элемента x; f(X) — образ множества X 2. f[X] — образ множества X |
|||
| Ограничение функции на множестве, сужение области определения функции |
|
|||
| Определение функции, область определения и область значений функции |
Запись f : X |
|||
| Определение функции (отображения) , задание функции |
Запись f: a |
|||
| Образ элемента/множества |
1. f(x) — образ элемента x; f(X) — образ множества X 2. f[X] — образ множества X |
|||
| Ограничение функции на множестве, сужение области определения функции |
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f |
|||
| Композиция функций | ||||
| Производная |
1. 2.
3. |
|||
| Интеграл, первообразная |
1. 2. 3. 4. |
|||
| Свертка функция |
|
|||
| Градиент |
|
|||
| Дивергенция |
|
|||
| Ротор |
|
|||
| Эквивалентность функций при определенной базе | ||||
| Производная |
1. 2.
3. |
|||
| Интеграл, первообразная |
1. 2. 3. 4. |
|||
| Свертка функция |
|
|||
| Градиент |
|
|||
| Дивергенция |
|
|||
| Ротор |
|
|||
| Эквивалентность функций при определенной базе | ||||
| О-большое | O | |||
| Степень многочлена |
1.
2. deg f |
|||
| Лапласиан, оператор Лапласа |  |
|||
| Кольцо вычетов по модулю n | 1. 
2. 3. Z/(n)Z 4. Z/(n) |
|||
| Проективное пространство |
1. 2. |
|||
| Изоморфизм |
1. 2. |
|||
| Конгруэнтность | ||||
| Коммутатор |
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы |
|||
| Группа, порожденная подмножеством/элементом группы |
1. Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S 2. Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an |
|||
| Линейная оболочка подмножества/векторов линейного пространства |
1. Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S 2. Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an. |
|||
| Ортогональное дополнение подпространства |
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W |
|||
| Тензорное произведение |  |
|||
| Нормальная (инвариантная) подгруппа | ||||
| Идеал кольца | ||||
| Индекс подгруппы |
Если H — подгруппа группы G, то [G:H] — индекс подгруппы H |
|||
| Расширение поля |
: E:K значит, что E — это расширение поля K |
|||
| Степень расширения поля |
[E:K] — это степень расширения поля E:K, где E — это расширение поля K. |
|||
| Факторгруппа |
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G |
|||
| Фактормножество |
Если X — множество с заданным на нем отношением эквивалентности |
|||
| Сплетение групп |
1. 2. АwrВ |
|||
| Граница множества |
Если M — некоторое множество, |
|||
| Группа единиц (обратимых элементов) кольца |
1. R* 2. Rx 3. U(R) |
|||
| Звезда Ходжа |  |
|||
| Замыкание (алгебраическое, топологическое) |  |
|||
| Полупрямое произведение групп | ||||
| Копроизведение (категорная сумма) |  |
|||
| Антисоединение отношений (Antijoin) — реляционная алгебра | ||||
| Полусоединение отношений (Semijoin) — реляционная алгебра | ||||
| Естественное соединение отношений (Natural Join) — реляционная алгебра | ||||
| Проекция — реляционная алгебра |
|
|||
| Выборка — реляционная алгебра |
|
|||
| Отношение эквивалентности, принадлежность одному классу эквивалентности | ||||
| Класс эквивалентности |
[a] — это множество элементов, эквивалентных a. Более точная запись — [a]R означает класс эквивалентности, порожденный элементом a относительно отношения эквивалентности R |
|||
| Вероятность события X |
1. 2. 3. P(X) 4. Pr(X) 5. P[X] 6. Pr[X] |
|||
| Условная вероятность |
P(A|B) — вероятность события А, при условии, что событие B уже произошло |
|||
| Независимость случайных событий |  |
|||
| Распределение вероятности случайной величины | ||||
| Несравнимость в теории порядка | ||||
| Сравнимость в теории порядка |  |
|||
| Покрытие в теории порядка |
x |
|||
| Наибольший (верхний )элемент решетки в теории порядка |  |
|||
| Наименьший (нижний) элемент решетки |  |
|||
| Подтип, подкласс, дочерний класс в теории типов |
S |
|||
| Высший (универсальный) тип в теории типов |  |
|||
| Нижайший тип (универсальный подтип) в теории типов |  |
|||
| Дельта-функция |
|
|||
| Символ Кронекера, индикатор равенства переменных |
|
- Сортировка знак / легенда
- Сортировка легенда / знак
Обозначения и символика
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
5. Углы обозначаются:
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3. n:
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
Источник
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, … , L, М, N, …
1,2,3,4,…,12,13,14,…
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, … , l, m, n, …
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ,…,ζ,η,ν,…
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d1 d2gα) — поверхность β определяется направляющими d1 и d2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
Например:
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π1 и π2,
где π1 — горизонтальная плоскость проекций;
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А’, В’, С’, D’, … , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a’ , b’ , c’ , d’ , … , l’, m’ , n’ , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α’, β’, γ’, δ’,…,ζ’,η’,ν’,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0α — горизонтальный след плоскости (поверхности) α;
f0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3,…, n:
А1, А2, А3,…,Аn;
a1, a2, a3,…,an;
α1, α2, α3,…,αn;
Ф1, Ф2, Ф3,…,Фn и т. д.
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, …
Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0:
А0, В0, С0, D0, …
10, 20, 30, 40, …
a0, b0, c0, d0, …
α0, β0, γ0, δ0, …
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
А1 0, В1 0, С1 0, D1 0, …
11 0, 21 0, 31 0, 41 0, …
a1 0, b1 0, c1 0, d1 0, …
α1 0, β1 0, γ1 0, δ1 0, …
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 |  |
Скрещиваются | с  d — прямые с и d скрещиваются d — прямые с и d скрещиваются |
| 7 |  |
Касательные | t  l — прямая t является касательной к линии l. l — прямая t является касательной к линии l. β  α — плоскость β касательная к поверхности α α — плоскость β касательная к поверхности α |
| 8 | → | Отображаются | Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | рsα Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| № по пор. | Обозначение | Содержание | Пример символической записи | Пример символической записи в геометрии |
|---|---|---|---|---|
| 1 | M,N | Множества | — | — |
| 2 | A,B,C,… | Элементы множества |
— | — |
| 3 | { … } | Состоит из … | Ф{A, B, C,… } | Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, … |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов ) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а ) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5} |
ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD] |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀( ΔАВС)(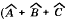 = 180°) Для всякого (для любого) треугольника сумма величин его углов = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | а b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | Отрицание знака | [AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b |




 f означает, что z(x)=g(f(x)).
f означает, что z(x)=g(f(x)). — матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц
— матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц 





 , где m≥0; ak — целые числа, а p — простое число.
, где m≥0; ak — целые числа, а p — простое число.









 x
x — это наибольшее целое число, меньшее или равное х.
— это наибольшее целое число, меньшее или равное х.
 x
x -это наименьшее целое число, большее или равное х.
-это наименьшее целое число, большее или равное х.

























 =vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то
=vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то




 — граница множества M (другими словами, множество всех граничных точек множества M)
— граница множества M (другими словами, множество всех граничных точек множества M) — степень многочлена f. Чаще встречается обозначение deg f.
— степень многочлена f. Чаще встречается обозначение deg f.





 ,
,  .
.



 — топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
— топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
 — строгое, истинное подмножество
— строгое, истинное подмножество


