The addition x + a on the number line. All numbers greater than x and less than x + a fall within that open interval.
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in between. Other examples of intervals are the set of numbers such that 0 < x < 1, the set of all real numbers 
Real intervals play an important role in the theory of integration, because they are the simplest sets whose «length» (or «measure» or «size») is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure.
Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Intervals are likewise defined on an arbitrary totally ordered set, such as integers or rational numbers. The notation of integer intervals is considered in the special section below.
Terminology[edit]
An open interval does not include its endpoints, and is indicated with parentheses.[1] For example, (0, 1) means greater than 0 and less than 1. This means (0, 1) = {x | 0 < x < 1}.
This interval can also be denoted by ]0, 1[, see below.
A closed interval is an interval which includes all its limit points, and is denoted with square brackets.[1] For example, [0, 1] means greater than or equal to 0 and less than or equal to 1.
A half-open interval includes only one of its endpoints, and is denoted by mixing the notations for open and closed intervals.[2] For example, (0, 1] means greater than 0 and less than or equal to 1, while [0, 1) means greater than or equal to 0 and less than 1.
A degenerate interval is any set consisting of a single real number (i.e., an interval of the form [a, a]).[2] Some authors include the empty set in this definition. A real interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded, if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded, if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, range, or size of the interval. The size of unbounded intervals is usually defined as +∞, and the size of the empty interval may be defined as 0 (or left undefined).
The centre (midpoint) of a bounded interval with endpoints a and b is (a + b)/2, and its radius is the half-length |a − b|/2. These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it contains no minimum (an element that is smaller than all other elements); right-open if it contains no maximum; and open if it contains neither. The interval [0, 1) = {x | 0 ≤ x < 1}, for example, is left-closed and right-open. The empty set and the set of all reals are both open and closed intervals, while the set of non-negative reals, is a closed interval that is right-open but not left-open. The open intervals are open sets of the real line in its standard topology, and form a base of the open sets.
An interval is said to be left-closed if it has a minimum element or is left-unbounded, right-closed if it has a maximum or is right unbounded; it is simply closed if it is both left-closed and right closed. So, the closed intervals coincide with the closed sets in that topology.
The interior of an interval I is the largest open interval that is contained in I; it is also the set of points in I which are not endpoints of I. The closure of I is the smallest closed interval that contains I; which is also the set I augmented with its finite endpoints.
For any set X of real numbers, the interval enclosure or interval span of X is the unique interval that contains X, and does not properly contain any other interval that also contains X.
An interval I is subinterval of interval J if I is a subset of J. An interval I is a proper subinterval of J if I is a proper subset of J.
Note on conflicting terminology[edit]
The terms segment and interval have been employed in the literature in two essentially opposite ways, resulting in ambiguity when these terms are used. The Encyclopedia of Mathematics[3] defines interval (without a qualifier) to exclude both endpoints (i.e., open interval) and segment to include both endpoints (i.e., closed interval), while Rudin’s Principles of Mathematical Analysis[4] calls sets of the form [a, b] intervals and sets of the form (a, b) segments throughout. These terms tend to appear in older works; modern texts increasingly favor the term interval (qualified by open, closed, or half-open), regardless of whether endpoints are included.
Notations for intervals[edit]
The interval of numbers between a and b, including a and b, is often denoted [a, b]. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon may be used as a separator to avoid ambiguity.
Including or excluding endpoints[edit]
To indicate that one of the endpoints is to be excluded from the set, the corresponding square bracket can be either replaced with a parenthesis, or reversed. Both notations are described in International standard ISO 31-11. Thus, in set builder notation,
Each interval (a, a), [a, a), and (a, a] represents the empty set, whereas [a, a] denotes the singleton set {a}. When a > b, all four notations are usually taken to represent the empty set.
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation (a, b) is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. That is why Bourbaki introduced the notation ]a, b[ to denote the open interval.[5] The notation [a, b] too is occasionally used for ordered pairs, especially in computer science.
Some authors such as Yves Tillé use ]a, b[ to denote the complement of the interval (a, b); namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
Infinite endpoints[edit]
In some contexts, an interval may be defined as a subset of the extended real numbers, the set of all real numbers augmented with −∞ and +∞.
In this interpretation, the notations [−∞, b] , (−∞, b] , [a, +∞] , and [a, +∞) are all meaningful and distinct. In particular, (−∞, +∞) denotes the set of all ordinary real numbers, while [−∞, +∞] denotes the extended reals.
Even in the context of the ordinary reals, one may use an infinite endpoint to indicate that there is no bound in that direction. For example, (0, +∞) is the set of positive real numbers, also written as 

Integer intervals[edit]
When a and b are integers, the notation ⟦a, b⟧, or [a .. b] or {a .. b} or just a .. b, is sometimes used to indicate the interval of all integers between a and b included. The notation [a .. b] is used in some programming languages; in Pascal, for example, it is used to formally define a subrange type, most frequently used to specify lower and upper bounds of valid indices of an array.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing a .. b − 1 , a + 1 .. b , or a + 1 .. b − 1. Alternate-bracket notations like [a .. b) or [a .. b[ are rarely used for integer intervals.[citation needed]
Classification of intervals[edit]
The intervals of real numbers can be classified into the eleven different types listed below[citation needed], where a and b are real numbers, and 
Properties of intervals[edit]
The intervals are precisely the connected subsets of 
The intervals are also the convex subsets of 


The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other – e.g., ![(a,b)cup [b,c]=(a,c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20dd7d6ce8ba23bfb9de0d90487008656b91eb94)
If 
Any element x of an interval I defines a partition of I into three disjoint intervals I1, I2, I3: respectively, the elements of I that are less than x, the singleton ![[x,x]={x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08cd03413513401836efbed8ca64419d73d3f481)
Dyadic intervals[edit]
A dyadic interval is a bounded real interval whose endpoints are 



Dyadic intervals have the following properties:
- The length of a dyadic interval is always an integer power of two.
- Each dyadic interval is contained in exactly one dyadic interval of twice the length.
- Each dyadic interval is spanned by two dyadic intervals of half the length.
- If two open dyadic intervals overlap, then one of them is a subset of the other.
The dyadic intervals consequently have a structure that reflects that of an infinite binary tree.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinement, multigrid methods and wavelet analysis. Another way to represent such a structure is p-adic analysis (for p = 2).[6]
Generalizations[edit]
Multi-dimensional intervals[edit]
In many contexts, an 



For 

In higher dimensions, the Cartesian product of 
A facet of such an interval 






Complex intervals[edit]
Intervals of complex numbers can be defined as regions of the complex plane, either rectangular or circular.[7]
Topological algebra[edit]
Intervals can be associated with points of the plane, and hence regions of intervals can be associated with regions of the plane. Generally, an interval in mathematics corresponds to an ordered pair (x,y) taken from the direct product R × R of real numbers with itself, where it is often assumed that y > x. For purposes of mathematical structure, this restriction is discarded,[8] and «reversed intervals» where y − x < 0 are allowed. Then, the collection of all intervals [x,y] can be identified with the topological ring formed by the direct sum of R with itself, where addition and multiplication are defined component-wise.
The direct sum algebra 
Every interval can be considered a symmetric interval around its midpoint. In a reconfiguration published in 1956 by M Warmus, the axis of «balanced intervals» [x, −x] is used along with the axis of intervals [x,x] that reduce to a point. Instead of the direct sum 
- z = (x + y)/2 + j (x − y)/2.
This linear mapping of the plane, which amounts of a ring isomorphism, provides the plane with a multiplicative structure having some analogies to ordinary complex arithmetic, such as polar decomposition.
See also[edit]
- Arc (geometry)
- Inequality
- Interval graph
- Interval finite element
- Interval (statistics)
- Line segment
- Partition of an interval
- Unit interval
References[edit]
- ^ a b «Intervals». www.mathsisfun.com. Retrieved 2020-08-23.
- ^ a b Weisstein, Eric W. «Interval». mathworld.wolfram.com. Retrieved 2020-08-23.
- ^ «Interval and segment — Encyclopedia of Mathematics». encyclopediaofmath.org. Archived from the original on 2014-12-26. Retrieved 2016-11-12.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 31. ISBN 0-07-054235-X.
- ^ «Why is American and French notation different for open intervals (x, y) vs. ]x, y[?». hsm.stackexchange.com. Retrieved 28 April 2018.
- ^ Kozyrev, Sergey (2002). «Wavelet theory as p-adic spectral analysis». Izvestiya RAN. Ser. Mat. 66 (2): 149–158. arXiv:math-ph/0012019. Bibcode:2002IzMat..66..367K. doi:10.1070/IM2002v066n02ABEH000381. S2CID 16796699. Retrieved 2012-04-05.
- ^ Complex interval arithmetic and its applications, Miodrag Petković, Ljiljana Petković, Wiley-VCH, 1998, ISBN 978-3-527-40134-5
- ^ Kaj Madsen (1979) Review of «Interval analysis in the extended interval space» by Edgar Kaucher[permanent dead link] from Mathematical Reviews
- ^ D. H. Lehmer (1956) Review of «Calculus of Approximations»[permanent dead link] from Mathematical Reviews
Bibliography[edit]
- T. Sunaga, «Theory of interval algebra and its application to numerical analysis» Archived 2012-03-09 at the Wayback Machine, In: Research Association of Applied Geometry (RAAG) Memoirs, Ggujutsu Bunken Fukuy-kai. Tokyo, Japan, 1958, Vol. 2, pp. 29–46 (547-564); reprinted in Japan Journal on Industrial and Applied Mathematics, 2009, Vol. 26, No. 2-3, pp. 126–143.
External links[edit]
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval computations website Archived 2006-03-02 at the Wayback Machine
- Interval computations research centers Archived 2007-02-03 at the Wayback Machine
- Interval Notation by George Beck, Wolfram Demonstrations Project.
- Weisstein, Eric W. «Interval». MathWorld.
The addition x + a on the number line. All numbers greater than x and less than x + a fall within that open interval.
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in between. Other examples of intervals are the set of numbers such that 0 < x < 1, the set of all real numbers 
Real intervals play an important role in the theory of integration, because they are the simplest sets whose «length» (or «measure» or «size») is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure.
Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Intervals are likewise defined on an arbitrary totally ordered set, such as integers or rational numbers. The notation of integer intervals is considered in the special section below.
Terminology[edit]
An open interval does not include its endpoints, and is indicated with parentheses.[1] For example, (0, 1) means greater than 0 and less than 1. This means (0, 1) = {x | 0 < x < 1}.
This interval can also be denoted by ]0, 1[, see below.
A closed interval is an interval which includes all its limit points, and is denoted with square brackets.[1] For example, [0, 1] means greater than or equal to 0 and less than or equal to 1.
A half-open interval includes only one of its endpoints, and is denoted by mixing the notations for open and closed intervals.[2] For example, (0, 1] means greater than 0 and less than or equal to 1, while [0, 1) means greater than or equal to 0 and less than 1.
A degenerate interval is any set consisting of a single real number (i.e., an interval of the form [a, a]).[2] Some authors include the empty set in this definition. A real interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded, if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded, if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, range, or size of the interval. The size of unbounded intervals is usually defined as +∞, and the size of the empty interval may be defined as 0 (or left undefined).
The centre (midpoint) of a bounded interval with endpoints a and b is (a + b)/2, and its radius is the half-length |a − b|/2. These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it contains no minimum (an element that is smaller than all other elements); right-open if it contains no maximum; and open if it contains neither. The interval [0, 1) = {x | 0 ≤ x < 1}, for example, is left-closed and right-open. The empty set and the set of all reals are both open and closed intervals, while the set of non-negative reals, is a closed interval that is right-open but not left-open. The open intervals are open sets of the real line in its standard topology, and form a base of the open sets.
An interval is said to be left-closed if it has a minimum element or is left-unbounded, right-closed if it has a maximum or is right unbounded; it is simply closed if it is both left-closed and right closed. So, the closed intervals coincide with the closed sets in that topology.
The interior of an interval I is the largest open interval that is contained in I; it is also the set of points in I which are not endpoints of I. The closure of I is the smallest closed interval that contains I; which is also the set I augmented with its finite endpoints.
For any set X of real numbers, the interval enclosure or interval span of X is the unique interval that contains X, and does not properly contain any other interval that also contains X.
An interval I is subinterval of interval J if I is a subset of J. An interval I is a proper subinterval of J if I is a proper subset of J.
Note on conflicting terminology[edit]
The terms segment and interval have been employed in the literature in two essentially opposite ways, resulting in ambiguity when these terms are used. The Encyclopedia of Mathematics[3] defines interval (without a qualifier) to exclude both endpoints (i.e., open interval) and segment to include both endpoints (i.e., closed interval), while Rudin’s Principles of Mathematical Analysis[4] calls sets of the form [a, b] intervals and sets of the form (a, b) segments throughout. These terms tend to appear in older works; modern texts increasingly favor the term interval (qualified by open, closed, or half-open), regardless of whether endpoints are included.
Notations for intervals[edit]
The interval of numbers between a and b, including a and b, is often denoted [a, b]. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon may be used as a separator to avoid ambiguity.
Including or excluding endpoints[edit]
To indicate that one of the endpoints is to be excluded from the set, the corresponding square bracket can be either replaced with a parenthesis, or reversed. Both notations are described in International standard ISO 31-11. Thus, in set builder notation,
Each interval (a, a), [a, a), and (a, a] represents the empty set, whereas [a, a] denotes the singleton set {a}. When a > b, all four notations are usually taken to represent the empty set.
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation (a, b) is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. That is why Bourbaki introduced the notation ]a, b[ to denote the open interval.[5] The notation [a, b] too is occasionally used for ordered pairs, especially in computer science.
Some authors such as Yves Tillé use ]a, b[ to denote the complement of the interval (a, b); namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
Infinite endpoints[edit]
In some contexts, an interval may be defined as a subset of the extended real numbers, the set of all real numbers augmented with −∞ and +∞.
In this interpretation, the notations [−∞, b] , (−∞, b] , [a, +∞] , and [a, +∞) are all meaningful and distinct. In particular, (−∞, +∞) denotes the set of all ordinary real numbers, while [−∞, +∞] denotes the extended reals.
Even in the context of the ordinary reals, one may use an infinite endpoint to indicate that there is no bound in that direction. For example, (0, +∞) is the set of positive real numbers, also written as 

Integer intervals[edit]
When a and b are integers, the notation ⟦a, b⟧, or [a .. b] or {a .. b} or just a .. b, is sometimes used to indicate the interval of all integers between a and b included. The notation [a .. b] is used in some programming languages; in Pascal, for example, it is used to formally define a subrange type, most frequently used to specify lower and upper bounds of valid indices of an array.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing a .. b − 1 , a + 1 .. b , or a + 1 .. b − 1. Alternate-bracket notations like [a .. b) or [a .. b[ are rarely used for integer intervals.[citation needed]
Classification of intervals[edit]
The intervals of real numbers can be classified into the eleven different types listed below[citation needed], where a and b are real numbers, and 
Properties of intervals[edit]
The intervals are precisely the connected subsets of 
The intervals are also the convex subsets of 


The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other – e.g., ![(a,b)cup [b,c]=(a,c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20dd7d6ce8ba23bfb9de0d90487008656b91eb94)
If 
Any element x of an interval I defines a partition of I into three disjoint intervals I1, I2, I3: respectively, the elements of I that are less than x, the singleton ![[x,x]={x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08cd03413513401836efbed8ca64419d73d3f481)
Dyadic intervals[edit]
A dyadic interval is a bounded real interval whose endpoints are 



Dyadic intervals have the following properties:
- The length of a dyadic interval is always an integer power of two.
- Each dyadic interval is contained in exactly one dyadic interval of twice the length.
- Each dyadic interval is spanned by two dyadic intervals of half the length.
- If two open dyadic intervals overlap, then one of them is a subset of the other.
The dyadic intervals consequently have a structure that reflects that of an infinite binary tree.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinement, multigrid methods and wavelet analysis. Another way to represent such a structure is p-adic analysis (for p = 2).[6]
Generalizations[edit]
Multi-dimensional intervals[edit]
In many contexts, an 



For 

In higher dimensions, the Cartesian product of 
A facet of such an interval 






Complex intervals[edit]
Intervals of complex numbers can be defined as regions of the complex plane, either rectangular or circular.[7]
Topological algebra[edit]
Intervals can be associated with points of the plane, and hence regions of intervals can be associated with regions of the plane. Generally, an interval in mathematics corresponds to an ordered pair (x,y) taken from the direct product R × R of real numbers with itself, where it is often assumed that y > x. For purposes of mathematical structure, this restriction is discarded,[8] and «reversed intervals» where y − x < 0 are allowed. Then, the collection of all intervals [x,y] can be identified with the topological ring formed by the direct sum of R with itself, where addition and multiplication are defined component-wise.
The direct sum algebra 
Every interval can be considered a symmetric interval around its midpoint. In a reconfiguration published in 1956 by M Warmus, the axis of «balanced intervals» [x, −x] is used along with the axis of intervals [x,x] that reduce to a point. Instead of the direct sum 
- z = (x + y)/2 + j (x − y)/2.
This linear mapping of the plane, which amounts of a ring isomorphism, provides the plane with a multiplicative structure having some analogies to ordinary complex arithmetic, such as polar decomposition.
See also[edit]
- Arc (geometry)
- Inequality
- Interval graph
- Interval finite element
- Interval (statistics)
- Line segment
- Partition of an interval
- Unit interval
References[edit]
- ^ a b «Intervals». www.mathsisfun.com. Retrieved 2020-08-23.
- ^ a b Weisstein, Eric W. «Interval». mathworld.wolfram.com. Retrieved 2020-08-23.
- ^ «Interval and segment — Encyclopedia of Mathematics». encyclopediaofmath.org. Archived from the original on 2014-12-26. Retrieved 2016-11-12.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 31. ISBN 0-07-054235-X.
- ^ «Why is American and French notation different for open intervals (x, y) vs. ]x, y[?». hsm.stackexchange.com. Retrieved 28 April 2018.
- ^ Kozyrev, Sergey (2002). «Wavelet theory as p-adic spectral analysis». Izvestiya RAN. Ser. Mat. 66 (2): 149–158. arXiv:math-ph/0012019. Bibcode:2002IzMat..66..367K. doi:10.1070/IM2002v066n02ABEH000381. S2CID 16796699. Retrieved 2012-04-05.
- ^ Complex interval arithmetic and its applications, Miodrag Petković, Ljiljana Petković, Wiley-VCH, 1998, ISBN 978-3-527-40134-5
- ^ Kaj Madsen (1979) Review of «Interval analysis in the extended interval space» by Edgar Kaucher[permanent dead link] from Mathematical Reviews
- ^ D. H. Lehmer (1956) Review of «Calculus of Approximations»[permanent dead link] from Mathematical Reviews
Bibliography[edit]
- T. Sunaga, «Theory of interval algebra and its application to numerical analysis» Archived 2012-03-09 at the Wayback Machine, In: Research Association of Applied Geometry (RAAG) Memoirs, Ggujutsu Bunken Fukuy-kai. Tokyo, Japan, 1958, Vol. 2, pp. 29–46 (547-564); reprinted in Japan Journal on Industrial and Applied Mathematics, 2009, Vol. 26, No. 2-3, pp. 126–143.
External links[edit]
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval computations website Archived 2006-03-02 at the Wayback Machine
- Interval computations research centers Archived 2007-02-03 at the Wayback Machine
- Interval Notation by George Beck, Wolfram Demonstrations Project.
- Weisstein, Eric W. «Interval». MathWorld.
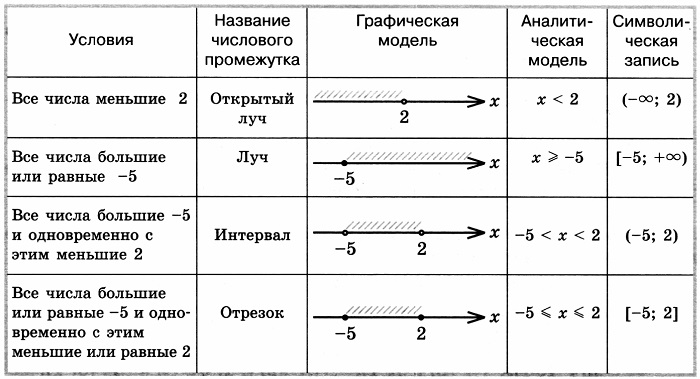
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
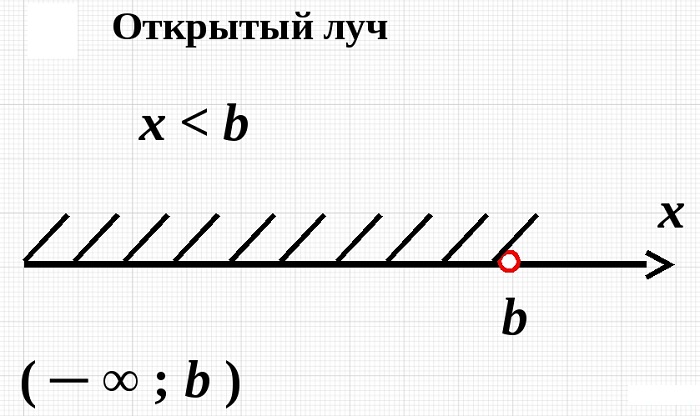
- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a — (x<a) или больше a — (x>a).
Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается виде промежутка (−∞, a), а для x>a, как (a, +∞).
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Рассмотрим несколько примеров.
При заданном строгом неравенстве x>−3 задается открытый луч. Эту запись можно представить в виде координат (−3, ∞) . То есть это все точки, лежащие правее, чем -3.
Если имеем неравенство вида x<2,3, то запись (−∞, 2,3) является аналогичной при задании открытого числового луча.
- Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.
Его задание идет с помощью нестрогих неравенств вида x≤a или x≥a. Для такого вида приняты специальные обозначения вида (−∞, a] и [a, +∞), причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.
Для наглядного примера зададим числовой луч.
Неравенство вида x≥5 соответствует записи [5, +∞), тогда получаем луч такого вида:
- Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a<x<b, где а и b являются некоторыми действительными числами, где a меньше b, а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a, но меньше b. Обозначение такого интервала принято записывать в виде (a, b). Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.
Рассмотрим рисунок, приведенный ниже.
Пример интервала −1<x<3,5 говорит о том, что его можно записать в виде интервала (−1, 3,5). Изобразим на координатной прямой и рассмотрим.
- Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a≤x≤b. Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [a, b], значит, что точки включаются во множество и изображаются закрашенными.
Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2≤x≤3, которое изображаем в виде 2, 3. На координатной прямой данный точки будут включены в решение и закрашены.
- Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a<x≤b или a≤b<c, где (a, b] и [a, b). Изобразим на координатной прямой.
Если имеется полуинтервал (1, 3], тогда его обозначение можно в виде двойного неравенства 1<x≤3, при чем на координатной прямой изобразится с точками 1 и 3, где 1 будет исключена, то есть выколота на прямой.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
- открытого числового луча;
- числового луча;
- интервала;
- числового отрезка;
- полуинтервала.
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Интервал (математика)
- Интервал (математика)
-
Промежуток, открытый промежуток, интервал — множество точек числовой прямой, заключённых между двумя данными числами a и b, то есть множество чисел x, удовлетворяющих условию: a < x < b. Промежуток не включает концов и обозначается (a,b) (иногда ]a,b[), в отличие от отрезка [a,b] (замкнутого промежутка), включающего концы, то есть состоящего из точек
.
В записи (a,b), числа a и b называют концами промежутка. Промежуток
включает все вещественные числа, промежуток
— все числа меньшие a и промежуток
— все числа большие a.
Термин промежуток используется в составе сложных терминов:
- при интегрировании — промежуток интегрирования,
- при уточнении корней уравнения — промежуток изоляции
- при определении сходимости степенных рядов — промежуток сходимости степенного ряда.
Кстати, в английском языке словом interval называется отрезок. А для обозначения понятия интервала используется термин open interval.
Литература
- Выгодский М. Я. Справочник по высшей математике. М.: «Астрель», «АСТ», 2002
См. также
- Отрезок
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Интервал (математика)» в других словарях:
-
Промежуток (математика) — Промежуток, или более точно, промежуток числовой прямой множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними[1]. С использованием логических символов, это определение… … Википедия
-
Портал:Математика — Начинающим · Сообщество · Порталы · Награды · Проекты · Запросы · Оценивание География · История · Общество · Персоналии · Религия · Спорт · Техника · Наука · Искусство · Философия … Википедия
-
Регрессия (математика) — У этого термина существуют и другие значения, см. регрессия. Регрессия (лат. regressio обратное движение, отход), в теории вероятностей и математической статистике, зависимость среднего значения какой либо величины от некоторой другой… … Википедия
-
Промежутки (математика) — Промежуток, открытый промежуток, интервал множество точек числовой прямой, заключённых между двумя данными числами a и b, то есть множество чисел x, удовлетворяющих условию: a < x < b. Промежуток не включает концов и обозначается (a,b)… … Википедия
-
Апории Зенона — … Википедия
-
Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м … Словарь-справочник терминов нормативно-технической документации
-
«Новая хронология» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
-
Критика естественно-научных методов в «Новой хронологии» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
-
Критика естественно-научных методов в «Новой хронологии» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
-
Новая Хронология — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
Числовые промежутки
- Виды числовых промежутков
- Открытый и замкнутый луч
- Отрезок
- Интервал и полуинтервал
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности
.
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:
Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности
и числовой луч от минус бесконечности до двух
. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх
.
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх
.
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3
, и полуинтервал от минус двух до трёх, включая минус два
.
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
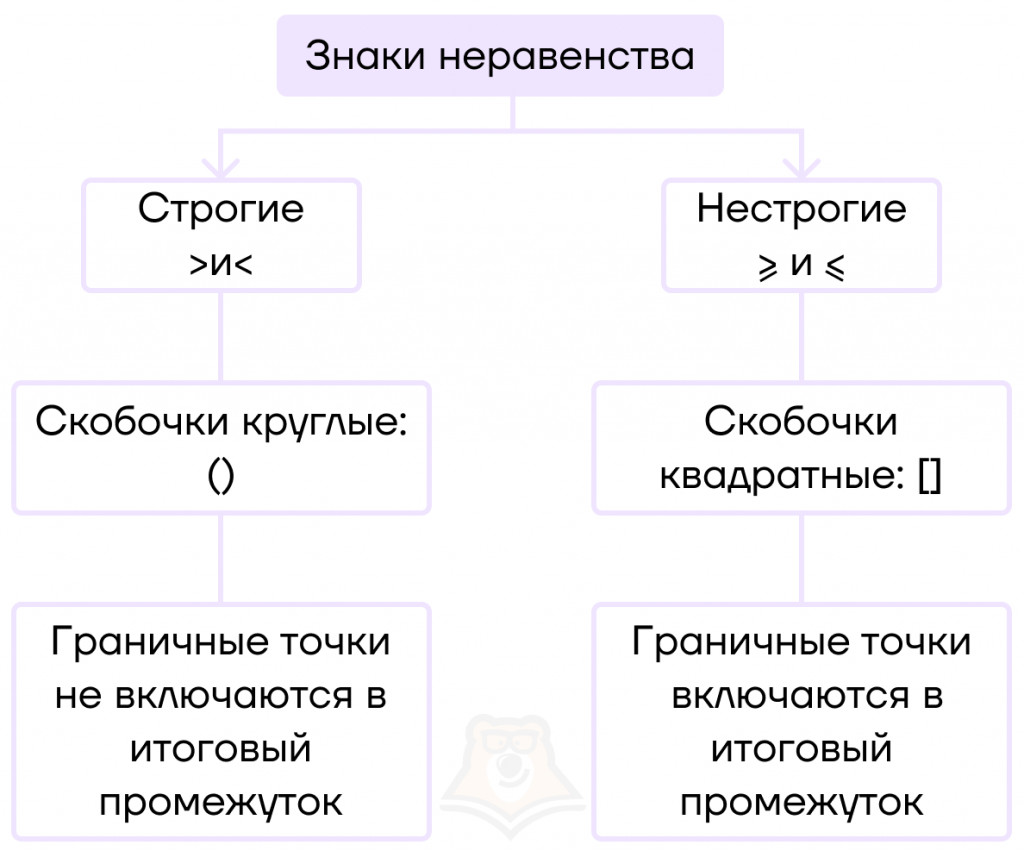
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
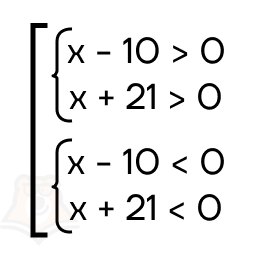
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
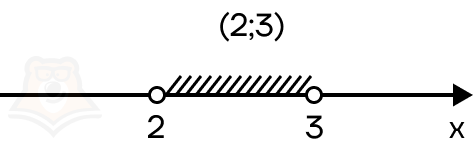
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
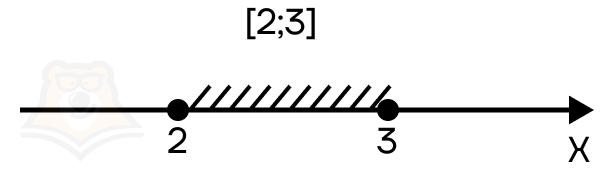
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
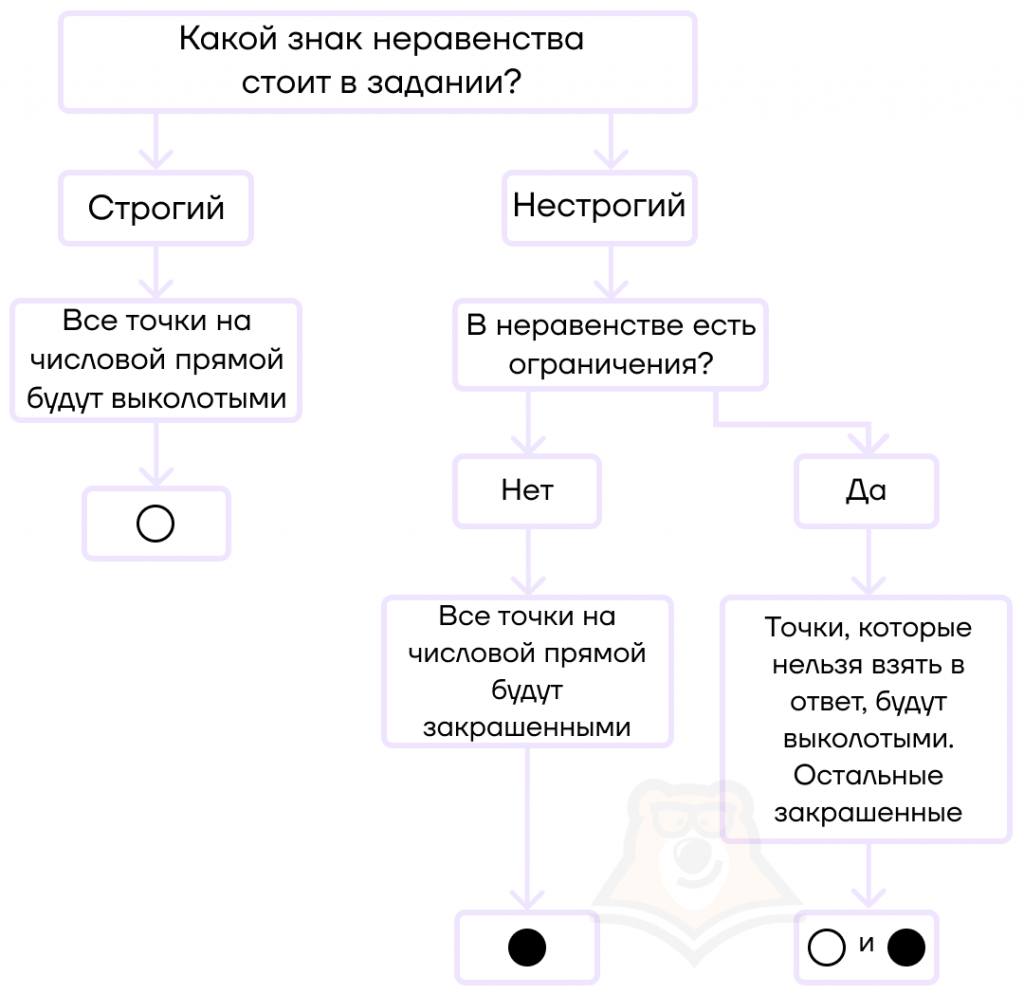
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
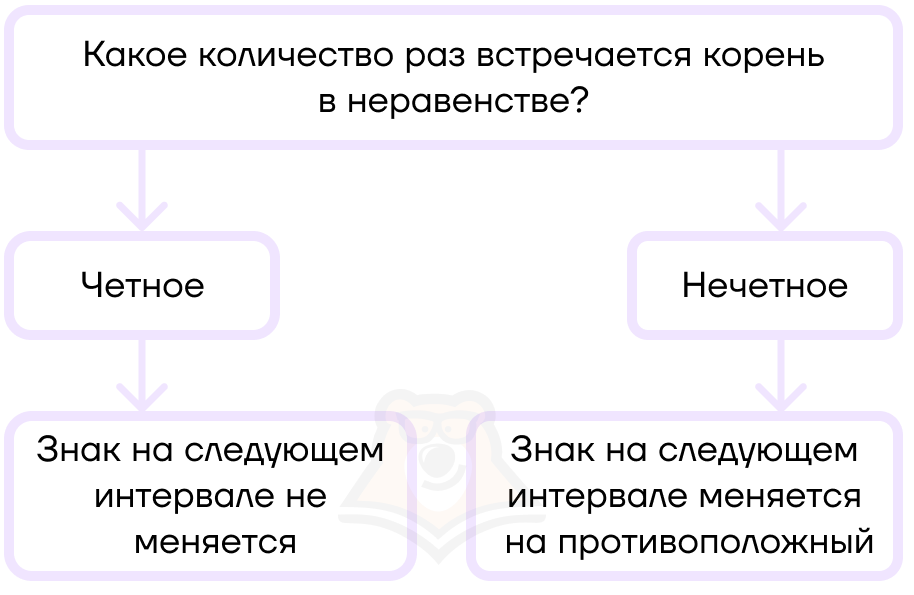
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
2. Находим корни уравнения, получаем х = 3 и х = -11.
3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
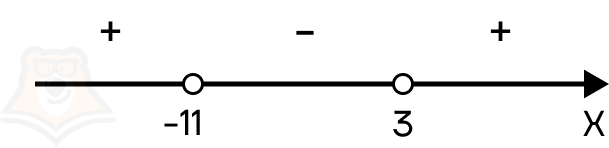
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
В математике — набор действительных чисел, содержащий все числа, лежащие между любыми двумя числами в наборе. 
В математике (вещественный ) интервал равен набор из вещественных чисел, который содержит все действительные числа, лежащие между любыми двумя числами набора. Например, набор чисел x, удовлетворяющих 0 ≤ x ≤ 1, представляет собой интервал, содержащий 0, 1 и все числа между ними. Другими примерами интервалов являются такие числа, как 0 < x < 1, the set of all real numbers R { displaystyle mathbb {R}}
Реальные интервалы играют важную роль в теории интегрирования, поскольку они представляют собой простейшие множества, «размер» (или «меру» или «длину») которых легко определить. Затем понятие меры может быть расширено на более сложные наборы действительных чисел, что приведет к мере Бореля и, в конечном итоге, к мере Лебега.
Интервалы являются центральным элементом интервальной арифметики, общий метод числовых вычислений, который автоматически обеспечивает гарантированные вложения для произвольных формул, даже при наличии неопределенностей, математических приближений и арифметического округления.
Интервалы аналогичным образом определяются для произвольных полностью упорядоченный набор, например целые числа или рациональные числа. Обозначение целочисленных интервалов рассматривается в специальном разделе ниже.
Содержание
- 1 Терминология
- 1.1 Примечание о противоречивой терминологии
- 2 Обозначения для интервалов
- 2.1 Включение или исключение конечных точек
- 2.2 Бесконечные конечные точки
- 2.3 Целочисленные интервалы
- 3 Классификация интервалов
- 4 Свойства интервалов
- 5 Диадические интервалы
- 6 Обобщения
- 6.1 Многомерные интервалы
- 6.2 Сложные интервалы
- 7 Топологическая алгебра
- 8 См. Также
- 9 Ссылки
- 10 Библиография
- 11 Внешние ссылки
Терминология
открытый интервал не включает его конечные точки, и обозначается круглыми скобками. Например, (0,1) означает больше 0 и меньше 1. Это означает (0,1) = {x | 0 < x < 1}.
A закрытый интервал — это интервал, который включает все его предельные точки, и обозначается квадратными скобками. Например, [0,1] означает больше или равно 0 и меньше или равно 1.
A полуоткрытый интервал включает только одну из его конечных точек и обозначается смешением обозначений для открытого и закрытые интервалы. Например, (0,1] означает больше 0 и меньше или равно 1, а [0,1) означает больше или равно 0 и меньше 1.
A вырожденный интервал — любое набор, состоящий из одного действительного числа (т. е. интервал вида [a, a] { displaystyle [a, a]}![{ displaystyle [ a, a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baa9fb386c1c5d50012bddea7ec7d51cd3782eb9)
Интервал называется ограниченным слева или ограниченным справа, если существует какое-то действительное число, которое, соответственно, меньше или больше всех его элементы. Интервал называется ограниченным, если он ограничен как слева, так и справа; и называется неограниченным в противном случае. Интервалы, ограниченные только на одном конце, называются полуограниченными . Пустое множество ограничено, а набор всех вещественных чисел — единственный интервал, неограниченный с обоих концов. Ограниченные интервалы также широко известны как конечные интервалы .
Ограниченные интервалы — это ограниченные множества в том смысле, что их диаметр (который равен абсолютной разности между конечными точками) конечно. Диаметр может называться длиной, шириной, размером, диапазоном или размером интервала. Размер неограниченных интервалов обычно определяется как + ∞, а размер пустого интервала может быть определен как 0 (или оставлен неопределенным).
Центр центр (средняя точка ) ограниченного интервала с конечными точками a и b равен (a + b) / 2, а его радиус равен полудлина | a — b | / 2. Эти концепции не определены для пустых или неограниченных интервалов.
Интервал называется левым открытым тогда и только тогда, когда он не содержит минимум (элемент, который меньше всех других элементов); открывается вправо, если он не содержит максимум ; и открыть, если у него есть оба свойства. Интервал [0,1) = {x | 0 ≤ x < 1}, for example, is left-closed and right-open. The empty set and the set of all reals are open intervals, while the set of non-negative reals, is a right-open but not left-open interval. The open intervals are открытые наборы реальной линии в его стандартной топологии и образуют базу открытых множеств.
Интервал называется закрытым влево, если он имеет минимальный элемент, закрытым вправо, если он имеет максимум, и просто закрытым если есть и то, и другое. Эти определения обычно расширяются, чтобы включать пустое множество и (слева или справа) неограниченные интервалы, так что закрытые интервалы совпадают с замкнутыми множествами в этой топологии.
внутренний интервала I — это самый большой открытый интервал, содержащийся в I; это также множество точек в I, которые не являются конечными точками I. Замыкание I — это наименьший замкнутый интервал, содержащий I; которое также является множеством, которое я дополнил своими конечными точками.
Для любого набора X действительных чисел интервал или интервал X является уникальным интервалом, который содержит X и не содержит никаких других интервалов. который также содержит X.
Интервал I { displaystyle I}







Примечание о противоречивой терминологии
Термины сегмент и интервал используются в литературе двумя по существу противоположными способами, что приводит к двусмысленности при использовании этих терминов. Энциклопедия математики определяет интервал (без квалификатора) для исключения обеих конечных точек (т. Е. Открытый интервал) и сегмент, включающий обе конечные точки (т. Е. Закрытый интервал), в то время как в Принципах математического анализа Рудина называются наборы формы [a, b] интервалы и множества формы (а, б) отрезки на всем протяжении. Эти термины, как правило, встречаются в более старых работах; современные тексты все больше отдают предпочтение термину интервал (квалифицируемый как открытый, закрытый или полуоткрытый), независимо от того, включены ли конечные точки.
Обозначения для интервалов
Интервал чисел между a и b, включая a и b, часто обозначается [a, b]. Эти два числа называются конечными точками интервала. В странах, где числа записываются с помощью десятичной запятой , точка с запятой может использоваться в качестве разделителя во избежание двусмысленности.
Включение или исключение конечных точек
Чтобы указать, что одна из конечных точек должна быть исключена из набора, соответствующую квадратную скобку можно заменить скобкой или перевернуть. Обе записи описаны в международном стандарте ISO 31-11. Таким образом, в задайте обозначение построителя,
- (a, b) =] a, b [= {x ∈ R ∣ a < x < b }, [ a, b) = [ a, b [ = { x ∈ R ∣ a ≤ x < b }, ( a, b ] = ] a, b ] = { x ∈ R ∣ a < x ≤ b }, [ a, b ] = [ a, b ] = { x ∈ R ∣ a ≤ x ≤ b }. {displaystyle {begin{aligned}{color {Maroon}(}a,b{color {Maroon})}={mathopen {color {Maroon}]}}a,b{mathclose {color {Maroon}[}}={xin mathbb {R} mid a{color {Maroon}<}x{color {Maroon}<}b},\{}{color {DarkGreen}[}a,b{color {Maroon})}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {Maroon}[}}={xin mathbb {R} mid a{color {DarkGreen}leq }x{color {Maroon}<}b},\{}{color {Maroon}(}a,b{color {DarkGreen}]}={mathopen {color {Maroon}]}}a,b{mathclose {color {DarkGreen}]}}={xin mathbb {R} mid a{color {Maroon}<}x{color {DarkGreen}leq }b},\{}{color {DarkGreen}[}a,b{color {DarkGreen}]}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {DarkGreen}]}}={xin mathbb {R} mid a{color {DarkGreen}leq }x{color {DarkGreen}leq }b}.end{aligned}}}
Каждый интервал (a, a), [a, a) и (a, a] представляет пустой набор, тогда как [a, a] обозначает одноэлементный набор {a}. Когда a>b, все четыре обозначения обычно используются для представления пустого набора.
Обе нотации могут перекрываться с другими случаями использования круглых и квадратных скобок в математике. Например, нотация (a, b) часто используется для обозначения упорядоченной пары в теории множеств, координаты точки или вектора в аналитической геометрии и линейной алгебре, или (иногда) комплексное число в алгебре. Вот почему Бурбаки ввел обозначение] a, b [для обозначения открытого интервала. Обозначение [a, b] также иногда используется для упорядоченных пар, особенно в информатика.
Некоторые авторы используют] a, b [для обозначения дополнения интервала (a, b), а именно, набора всех действительных чисел, которые либо меньше, либо равны a, либо больше эр, чем или равно b.
Бесконечные конечные точки
В некоторых контекстах интервал может быть определен как подмножество расширенных действительных чисел, набора всех действительных чисел, дополненных −∞ и + ∞.
В этой интерпретации обозначения [−∞, b], (−∞, b], [a, + ∞] и [a, + ∞) все значимы и различны. В частности, (−∞, + ∞) обозначает множество всех обычных действительных чисел, а [−∞, + ∞] обозначает расширенные действительные числа.
Даже в контексте обычных вещественных чисел можно использовать бесконечную конечную точку, чтобы указать, что в этом направлении нет привязки. Например, (0, + ∞) — это набор положительных действительных чисел, также записываемых как R + { displaystyle mathbb {R} _ {+}}

Целочисленные интервалы
Когда a и b являются целыми числами, обозначение ⟦a, b⟧, или [a.. b], или {a.. b}, или просто a.. b, иногда используется для обозначения интервала всех включенных целых чисел от a до b. Обозначение [a.. b] используется в некоторых языках программирования ; в Pascal, например, он используется для формального определения типа поддиапазона, наиболее часто используемого для определения нижней и верхней границ допустимых индексов массива .
целочисленный интервал, имеющий конечную нижнюю или верхнюю конечную точку, всегда включает эту конечную точку. Следовательно, исключение конечных точек может быть явно обозначено записью a.. b — 1, a + 1.. b или a + 1.. b — 1. Обозначения с альтернативными скобками, например [a.. b) или [a.. b [редко используются для целочисленных интервалов.
Классификация интервалов
Интервалы действительных чисел можно разделить на одиннадцать различных типов, перечисленных ниже, где a и b — действительные числа, и a < b {displaystyle a
- Пусто: [b, a] = (b, a) = [b, a) = (b, a] = (a, a) = [a, a) = (a, a] = {} = ∅ { Displaystyle [b, a] = (b, a) = [b, a) = (b, a] = (a, a) = [a, a) = (a, a] = {} = emptyset}
- Вырожденный: [a, a] = {a} { displaystyle [a, a] = {a }}
- Правильный и ограниченный:
- Открыто: (a, b) = {x ∣ a < x < b } {displaystyle (a,b)={xmid a
- Закрыто: [a, b] = {x ∣ a ≤ x ≤ b} { displaystyle [a, b] = {x mid a leq x leq b }}
- Закрыто слева, открыто справа: [a, b) = {x ∣ a ≤ x < b } {displaystyle [a,b)={xmid aleq x
- Открыто слева, справа- закрыто: (a, b] = {x ∣ a < x ≤ b } {displaystyle (a,b]={xmid a
- Открыто: (a, b) = {x ∣ a < x < b } {displaystyle (a,b)={xmid a
- Ограничено слева и неограничено справа:
- Открыто слева: (a, + ∞) = {x ∣ x>а} { di splaystyle (a, + infty) = {x mid x>a }}
- Закрыто влево: [a, + ∞) = {x ∣ x ≥ a} { displaystyle [a, + infty) = {x mid x geq a }}
- Открыто слева: (a, + ∞) = {x ∣ x>а} { di splaystyle (a, + infty) = {x mid x>a }}
- Неограниченное слева и ограничение справа:
- Открытие справа: (- ∞, b) знак равно {Икс ∣ Икс < b } {displaystyle (-infty,b)={xmid x
- Закрыто вправо: (- ∞, b] = {x ∣ x ≤ b} { displaystyle (- infty, b] = {x mid x leq b }}
- Открытие справа: (- ∞, b) знак равно {Икс ∣ Икс < b } {displaystyle (-infty,b)={xmid x
- Неограниченный на обоих концах (одновременно открытый и закрытый): (- ∞, + ∞) = R { displaystyle (- infty, + infty) = mathbb {R}}
:
Свойства интервалов
Интервалы — это в точности связанные подмножества R { displaystyle mathbb {R}}
. Интервалы также являются выпуклыми подмножествами в R { displaystyle mathbb {R}}


Пересечение любого набора интервалов всегда является интервалом. Объединение двух интервалов является интервалом тогда и только тогда, когда они имеют непустое пересечение или открытая конечная точка одного интервала является закрытой конечной точкой другого (например, (a, b) ∪ [ b, c] = (a, c] { displaystyle (a, b) cup [b, c] = (a, c]}![(a, b) cup [b, c] = (a, c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20dd7d6ce8ba23bfb9de0d90487008656b91eb94)
Если R { displaystyle mathbb {R}}
Любой элемент x интервала I определяет разбиение I на три непересекающихся интервала I 1, I 2, I 3 : соответственно, элементы I, которые меньше x, одноэлемент [x, x] = {x} { displaystyle [x, x] = {x }}![[x, x] = {x }](https://wikimedia.org/api/rest_v1/media/math/render/svg/08cd03413513401836efbed8ca64419d73d3f481)
Диадический интервал als
Диадический интервал — это ограниченный действительный интервал, конечными точками которого являются j 2 n { textstyle { frac {j} {2 ^ {n}}}}



Диадические интервалы обладают следующими свойствами:
- Длина диадического интервала всегда является целой степенью двойки.
- Каждый диадический интервал содержится ровно в одном диадическом интервале, вдвое большей длины.
- Каждый диадический интервал охватывает два диадических интервала половинной длины.
- Если два открытых диадических интервала перекрываются, то один из них является подмножеством другого.
Диадический следовательно, интервалы имеют структуру, отражающую структуру бесконечного двоичного дерева.
Диадические интервалы актуальны для нескольких областей численного анализа, включая адаптивное уточнение сетки, многосеточные методы и вейвлет-анализ. Другой способ представления такой структуры — p-адический анализ (для p = 2).
Обобщения
Многомерные интервалы
Во многих контекстах n { displaystyle n}



Для n = 2 { displaystyle n = 2}


A фасет такого интервала I { displaystyle I}






Комплексные интервалы
Интервалы комплексных чисел могут быть определены как области комплексной плоскости, либо прямоугольной, либо круговая.
Топологическая алгебра
Интервалы могут быть связаны с точками плоскости, и, следовательно, области интервалов могут быть связаны с областями плоскости. Обычно интервал в математике соответствует упорядоченной паре (x, y), взятой из прямого произведения R × R действительных чисел с самим собой, где часто предполагается, что y>x. Для целей математической структуры это ограничение отбрасывается, и «инвертированные интервалы», где y — x < 0 are allowed. Then, the collection of all intervals [x,y] can be identified with the топологическое кольцо образовано прямой суммой R с самим собой, где сложение и умножение определяются покомпонентно.
Алгебра прямой суммы (R ⊕ R, +, ×) { displaystyle (R oplus R, +, times)}
Каждый интервал можно рассматривать как симметричный интервал вокруг его средней точки. В реконфигурации, опубликованной в 1956 г. М. Вармусом, ось «сбалансированных интервалов» [x, −x] используется вместе с осью интервалов [x, x], которые сводятся к точке. Вместо прямой суммы R ⊕ R { displaystyle R oplus R}
- z = (x + y) / 2 + j (x — y) / 2.
Это линейное отображение плоскости, которое составляет изоморфизм кольца , обеспечивает плоскость мультипликативной структурой, имеющей некоторые аналогии с обычной комплексной арифметикой, такой как полярное разложение.
См. Также
- Неравенство
- График интервалов
- Интервальный конечный элемент
- Интервал (статистика)
- Отрезок линии
- Разделение интервала
- Единичный интервал
Ссылки
Библиография
- T. Сунага, «Теория интервальной алгебры и ее применение к численному анализу», В: Мемуары Исследовательской ассоциации прикладной геометрии (RAAG), Ггудзюцу Бункен Фукуй-кай. Токио, Япония, 1958, т. 2. С. 29–46 (547–564); перепечатано в Japan Journal on Industrial and Applied Mathematics, 2009, Vol. 26, No. 2-3, pp. 126–143.
Внешние ссылки
- Прозрачный интервал Брайана Хейса: статья американского ученого содержит введение.
- Веб-сайт интервальных вычислений
- Исследовательские центры интервальных вычислений
- Интервальная нотация Джорджа Бека, Демонстрационный проект Wolfram.
- Вайсштейн, Эрик У. «Интервал». MathWorld.
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
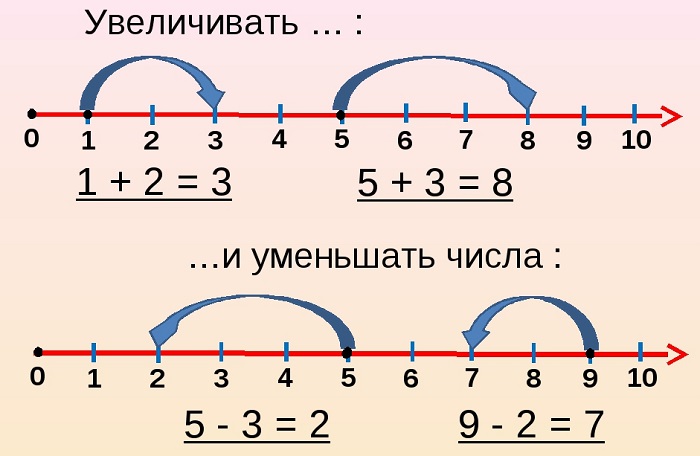
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
-
(-∞; А);
-
(А; +∞).
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
-
х < А;
-
х > А.
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.
Также ему соответствует условие:
-
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
-
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».
Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».
Таблица числовых промежутков
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.
Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.

![{displaystyle {begin{aligned}{color {Maroon}(}a,b{color {Maroon})}={mathopen {color {Maroon}]}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {Maroon}{}<{}}b},\{}{color {DarkGreen}[}a,b{color {Maroon})}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {Maroon}{}<{}}b},\{}{color {Maroon}(}a,b{color {DarkGreen}]}={mathopen {color {Maroon}]}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {DarkGreen}{}leq {}}b},\{}{color {DarkGreen}[}a,b{color {DarkGreen}]}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {DarkGreen}{}leq {}}b}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0410c727e5c09b33b3074d6f7cfa99a624883079)











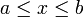 .
.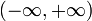 включает все вещественные числа, промежуток
включает все вещественные числа, промежуток 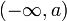 — все числа меньшие
— все числа меньшие 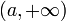 — все числа большие
— все числа большие 






![{ displaystyle { begin {align} { color {Maroon} (} a, b { color {Maroon})} = { mathopen { color {Maroon}]}} a, b { mathclose { color {Maroon} [}} = {x in mathbb {R} mid a { color {Maroon} <} x { color {Maroon} <} b }, \ {} { color {DarkGreen} [ } a, b { color {Maroon})} = { mathopen { color {DarkGreen} [}} a, b { mathclose { color {Maroon} [}} = {x in mathbb { R} mid a { color {DarkGreen} leq} x { color {Maroon} <} b }, \ {} { color {Maroon} (} a, b { color {DarkGreen}]} = { mathopen { color {Maroon}]}} a, b { mathclose { color {DarkGreen}]}} = {x in mathbb {R} mid a { color {Maroon} <} x { color {DarkGreen} leq} b }, \ {} { color {DarkGreen} [} a, b { color {DarkGreen}]} = { mathopen { color {DarkGreen} [} } a, b { mathclose { color {DarkGreen}]}} = {x in mathbb {R} mid a { color {DarkGreen} leq} x { color {DarkGreen} leq} б }. конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a0a3c093d4274b5090fbc118d5ceb5048980c12)
![{ displaystyle [b, a] = (b, a) = [b, a) = (b, a] = (a, a) = [a, a) = (a, a] = {} = emptyset}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f774c450e62dd5b31905618849e5e1b384f0c7ab)
![[a, a] = {a }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5fc662e432a951ab083a879223c7446790c03b)

![{ displaystyle [a, b] = {x mid a leq x leq b }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81bcee67611d05fd8e6fbda35f3c0b33827a8e59)

![{ displaystyle (a, b] = {x mid a <x leq b }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b49d87cec713117b07c85a42de9646056caafd48)



![{ displaystyle (- infty, b] = {x mid x leq b }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45361d3546a56cae970d5b62c5d835b5c3873e3)
 :
: