как в калькуляторе обозначается модуль
Вы искали как в калькуляторе обозначается модуль? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как модуль обозначается в калькуляторе, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «как в калькуляторе обозначается модуль».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как в калькуляторе обозначается модуль,как модуль обозначается в калькуляторе,как обозначается модуль в калькуляторе,калькулятор модулей онлайн,калькулятор онлайн модули,калькулятор онлайн модуль,калькулятор с модулем,калькулятор с модулем онлайн,калькулятор с модулями онлайн,онлайн калькулятор модуль,онлайн калькулятор с модулем. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как в калькуляторе обозначается модуль. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как обозначается модуль в калькуляторе).
Где можно решить любую задачу по математике, а так же как в калькуляторе обозначается модуль Онлайн?
Решить задачу как в калькуляторе обозначается модуль вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Ввод чисел:
Целые числа вводятся обычным способом, например:
4; 18; 56
Для ввода отрицательного числа необходимо поставить знак минус:
-19; -45; -90
Рациональные числа вводятся с использованием символа
/, например:
3/4;-5/3;5/(-19)
Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей:
4.5;-0.4
Ввод переменных и констант:
Переменные и константы вводятся латинскими буквами, например:
x; y; z; a; b.
Константы
π
и
e
вводятся как pi и e — соответственно.
Символ бесконечности
∞
вводится двумя маленькими латинскими буквами oo или словом
inf.
Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.
Сумма и разность:
Сумма и разность задаются при помощи знаков
+
и
—
соответственно, например:
3+a;
x+y;
5—4+t;
a—b+4;
ВНИМАНИЕ!
Никаких пробелов между операндами быть не должно, например ввод:
x + a
—
неправильный,
правильно
вводить так:
x+a
— без пробелов.
Умножение:
Умножение задается знаком
*,
например:
3*t;
x*y;
-5*x.
ВНИМАНИЕ!
Ввод знака
*
необходим всегда, т.е. запись типа:
2x —
недопустима
.
Следует всегда использовать знак
*
, т.е
правильная
запись:
3*x.
Деление:
Деление задается знаком
/,
например:
15/a;
y/x;.
Степень:
Степень задается знаком
^,
например:
x^2;
4^2;
y^(-1/2).
Приоритет операций:
Для указания (или изменения) приоритета операций необходимо использовать скобки (), например:
(a+b)/4
— тут вначале будет произведено сложение a+b, а потом сумма разделится на 4, тогда как без скобок:
— сначала b разделится на 4 и к полученному прибавится a.
ВНИМАНИЕ! В непонятных случаях лучше всегда использовать скобки для получения нужного
результата, например: 2^4^3
— неясно как будет вычислено это выражение: cначала 2^4, а затем результат в степень
3, или сначала 4^3=64,
а затем 2^64? Поэтому, в данном случае, необходимо использовать скобки:
(2^4)^3 или
2^(4^3) — смотря что нужно.
Также распространенной ошибкой является запись вида: x^3/4 —
непонятно: вы хотите возвести x в куб и полученное выражение
разделить на 4, или хотите возвести x в степень
3/4?
В последнем случае необходимо использовать скобки:
x^(3/4).
Ввод функций:
Функции вводятся с использованием маленьких латинских букв:
sin; cos;
tan; log.
ВНИМАНИЕ! Аргумент функции всегда берется в скобки (), например:
sin(4);
cos(x);
log(4+y).
Запись типа:
sin 4;
cos x;
log 4+y
— недопустима. Правильная запись:
sin(4);
cos(x);
log(4+y).
Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так:
(sin(x))^2.
Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x^2), тогда это выглядит вот так:
sin(x^2). Запись типа:
sin^2 x — недопустима.
| Функция | Описание | Пример ввода | Примечания |
|---|---|---|---|
|
x
|
квадратный корень | sqrt(x) или x^(1/2) | — |
| nx | корень n-ой степени | x^(1/n) | — |
|
log(x) или ln(x) |
натуральный логарифм | log(x) или ln(x) | — |
|
log10(x) или lg(x) |
десятичный логарифм | lg(x) | — |
| loga(b) | произвольный логарифм | lg(b)/lg(a) | — |
| ex | экспонента | exp(x) | — |
| sin(x) | синус | sin(x) | — |
| cos(x) | косинус | cos(x) | — |
|
tan(x) или tg(x) |
тангенс | tan(x) или tg(x) | — |
|
cot(x) или ctg(x) |
котангенс | cot(x) или ctg(x) | — |
| sec(x) | секанс | sec(x) | sec(x)=1/cos(x) |
|
csc(x) или cosec(x) |
косеканс | csc(x) или cosec(x) | csc(x)=1/sin(x) |
|
sin−1(x) или arcsin(x) |
арксинус | arcsin(x) или asin(x) | — |
|
cos−1(x) или arccos(x) |
арккосинус | arccos(x) или acos(x) | — |
|
tan−1(x) или arctan(x) |
арктангенс | arctg(x) или atan(x) | — |
|
cot−1(x) или arcctg(x) |
арккотангенс | arcctg(x) или acot(x) | — |
|
sec−1(x) или arcsec(x) |
арксеканс | arcsec(x) или asec(x) | arcsec(x)=arccos(1/x) |
|
csc−1(x) или arccosec(x) |
арккосеканс | arccosec(x) или acsc(x) | arcsec(x)=arcsin(1/x) |
| sinh(x) | гиперболический синус | sinh(x) | sinh(x)=(exp(x)-exp(-x))/2 |
| cosh(x) | гиперболический косинус | cosh(x) | cosh(x)=(exp(x)+exp(-x))/2 |
| tanh(x) | гиперболический тангенс | tanh(x) | tanh(x)=sinh(x)/cosh(x) |
| coth(x) | гиперболический котангенс | coth(x) | coth(x)=cosh(x)/sinh(x) |
| sech(x) | гиперболический секанс | sech(x) | sech(x)=1/cosh(x) |
| csch(x) | гиперболический косеканс | cosech(x) или csch(x) | csch(x)=1/sinh(x) |
|
sinh−1(x) или arcsinh(x) |
гиперболический арксинус | arcsinh(x) или asinh(x) | — |
|
cosh−1(x) или arccosh(x) |
гиперболический арккосинус | arccosh(x) или acosh(x) | — |
|
tanh−1(x) или arctanh(x) |
гиперболический арктангенс | arctanh(x) или atanh(x) | — |
|
coth−1(x) или arccoth(x) |
гиперболический арккотангенс | arccoth(x) или acoth(x) | — |
|
sech−1(x) или arcsech(x) |
гиперболический арксеканс | arcsech(x) или asech(x) | arcsech(x)=arccosh(1/x) |
|
csch−1(x) или arccsch(x) |
гиперболический арккосеканс | arccsch(x) или acsch(x) | arccsch(x)=arcsinh(1/x) |
| Что ввели | Что получится |
|---|---|
| x^4 | x4 |
| (5-2*x)^(1/3) | 52×13 |
| (5/2+x)^4/2 | 52×42 |
| sin(3*x+4)^5 | sin53x4 |
| 1/sqrt(3*x^2+2) |
13×22
|
| (sqrt(x)-2*(x^3)+6)/x | x2x36x |
| e^(3*x)*cos(x)^2 | e3xcos2x |
| ((ln(x-7))^5)/(x-7) | ln5x7x7 |
| 1/(arcsin(x)^2*sqrt(1-x^2)) | 1arcsin2x1x2 |
| 2*x*arccos(3*x^2) | 2xarccos3x2 |
| (5+(x/3)^3)/(8*(x+y)^(1/2)) | 5x338xy |

Ввод данных, наверное, это самое главное, что необходимо усвоить при работе с математическими калькуляторами по решению задач. Не важно какие сервисы вы используете, будь то сайт, десктопная программа или мобильное приложение, ведь именно с корректного ввода данных начинается постановка задачи для вычислительной системы.
Как правило у каждого подобного сервиса свой синтаксис. Но какими бы ни были современные математические калькуляторы (программы), в любом случае все они базируются на принципах обработки, которые появились еще в прошлом веке. Отличаются лишь методы обработки (парсинг математических выражений), но математические формулы от этого, разумеется, не меняются.
Стоит отметить, что калькуляторы на Math24.biz куда более «умнее», или, иными словами, менее требовательны, чем ряд других аналогичных калькуляторов на просторах интернета.
Итак, начнем. Самые элементарные правила как вводить данные касаются записи чисел и скобок.
Скобки используются круглые. Но даже если вы введете [, ], { или }, то они преобразуются в соответствующие круглые. Кстати, это небольшое наше преимущество в отличие от других калькуляторов.
Что касается натуральных или дробных чисел, то тут все очевидно — «Как вижу, так и пишу!».
Обратим внимание на записи десятичных чисел и некоторых математических констант. В десятичной записи числа необходимо использовать точку, а не запятую.
Примеры ввода десятичных чисел
1.78, 87.001, 0.99 и так далее.
Такое правило ввода данных оправдывается тем, что запятая используется в функциях, например, логарифмических, в которых разделены через запятую основание логарифма и число, от которого берется логарифм. И таких функций множество, включая функции нескольких переменных.
Примеры обозначений математических констант
pi — Число Пи
e — Экспонента (основание натурального логарифма)
i — Мнимая единица, i2 = -1
Корень квадратный от числа записывается как sqr или sqrt.
Примеры записи квадратного корня
sqrt(2) — корень квадратный из числа 2
sqrt(3/4) — корень квадратный из дробного числа ¾
Наверняка многие сейчас подумали, что квадратный корень из 2 можно записать как 2^(1/2) или 2^(0.5). Но в данном случае мы хотим лишь сказать, что sqrt есть обозначение квадратного корня, которое используется во многих программах.
Примите это на заметку, если ранее не встречались с этим обозначением!
Далее быстро пройдемся по математическим операциям и правилам их ввода, потому что здесь всё проще-простого.
+ Операция сложения (суммирование)
− Операция вычитания (разность)
* Операция умножения
Кстати, если два множителя записать через пробел, то калькулятор воспримет это за знак умножения. Например, x y равносильно x*y
/ Операция деления
^ Возведение в степень
Чуть сложнее для визуального восприятия, но никак не для понимания, это правило записи дробных выражений. Как вводить данные от таких выражений мы покажем на примерах с применением различных цветов.
Это позволит лучше и быстрее освоить необходимые навыки юным ученикам. Хотя, поверьте нам, старшеклассники и студенты очень часто сталкиваются с проблемой ввода сложных формул.
Примеры ввода дробных выражений
Для лучшего визуального восприятия мы специально добавили пробелы, чтобы выделить отдельные операции.
( x^2 — 1 ) / ( x^2 + 1 )
( Sin(x) * Cos(y) ) / ( x^5 — y + 7 )
( (z-1) (t+1) ) / ( (x-1) / (y+1) )
Как вы могли заметить, одним из базовых правил при вводе данных является использование букв только латинского алфавита!
Ниже перечислим наиболее часто встречающиеся функции при изучении школьной математики и математических дисциплин начальных курсов ВУЗов и других учебных заведений.
Если возникнут вопросы, пожалуйста, обращайтесь к нам на почту info@math24.biz
 |
Математический образовательный портал. «Математика это просто!» — посетите наш сайт и убедитесь в этом. |
- Калькуляторы
- Справочник
Правила ввода функций в онлайн калькуляторах.
На данной странице описаны правила ввода функций, которых следует придерживаться в онлайн калькуляторах, созданных на базе виждетов WolframAlpha Mathematica.
Не забывайте проверять правильность написания формул. Неточность и ошибки в написании, приводят к невернному ответу и ситуациям при которых калькулятор отказывается проводить вычисления.
|
Оператор |
Описание |
|
Простейшие математические операции |
|
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * — необязателен: выражение 2sin(3 x ) еквивалентно 2*sin(3* x ). |
|
0.5 |
Десятичные дроби записываются через точку:
|
|
Элементарные функции |
|
|
x ^ n |
Возведение в степень:
xn , например x ^2 значит x 2 |
|
sqrt( x ) |
Квадратный корень: √
x . Эквивалентно root(x ,2) или x ^(1/2) |
|
cbrt( x ) |
Кубический корень: 3√
x . Эквивалентно root(x ,3) или x ^(1/3) |
|
root( x , n ) |
Корень
n -той степени из x . Эквивалентно x ^(1/ n ) |
|
log( a , x ) |
Логарифм от
x по основанию a |
|
ln( x ) |
Натуральный логарифм (логарифм c основанием
e ) |
|
lg( x ) |
Десятичный логарифм (логарифм по основанию 10) |
|
exp( x ) |
Экспоненциальная функция, эквивалентно
e ^ x |
|
Тригонометрические функции |
|
|
sin( x ) |
Синус от
x |
|
cos( x ) |
Косинус от
x |
|
tg( x ) |
Тангенс от
x . Можно вводить tg( x ) или tan( x ) |
|
ctg( x ) |
Котангенс от
x . Можно вводить ctg( x ) или cot( x ) |
|
sec( x ) |
Секанс от
x , определяется как 1/cos( x ) |
|
csc( x ) |
Косеканс от
x , определяется как 1/sin( x ) |
|
arcsin( x ) |
Арксинус от
x . Можно вводить arcsin( x ) или asin( x ) |
|
arccos( x ) |
Арккосинус от
x . Можно вводить arccos( x ) или acos( x ) |
|
atan( x ) |
Арктангенс от
x . Можно вводить arctg( x ) или atan( x ) |
|
arcctg( x ) |
Арккотангенс от
x . Можно вводить arcctg( x ) или acot( x ) |
|
asec( x ) |
Арксеканс от
x |
|
acsc( x ) |
Арккосеканс от
x |
|
Некоторые константы |
|
|
e |
Число Эйлера
e = 2.718281828459045… |
|
pi |
Число
π = 3.141592653589793… |
| © 2013-2023 Довжик Михаил Копирование материала запрещено. |
СЕРВИСЫ
Онлайн калькуляторы |
O-Math.com
О проекте |
Как взять число по модулю
Абсолютное значение числа — модуль — показывает, насколько отличается это число от нуля. Брать по модулю можно любые величины — от бесконечности в отрицательной части шкалы, до бесконечности в положительной, но результат этой операции всегда будет положителен, если исходное значение отличается от нуля. Определение модуля числа — очень простая задача, а вызвать вопросы может только ее реализация каким-то конкретным способом.
Инструкция
Если требуется «в уме» определить модуль вещественного числа, просто отбросьте его отрицательный знак, если такой есть. Например, модуль числа -257 равен 257, а модуль 747 равен самому этому числу. Записываются эти два примера так: |-257| = 257 и |747| = 747.
При необходимости взять модуль числа в калькуляторе отрицательную величину умножайте на минус один, а положительную оставляйте без изменений. Если вы используете программный калькулятор Windows в его «инженерном» интерфейсе, можно обойтись без умножения — воспользуйтесь кнопкой смены знака. Она помещена во второй ряд второй справа колонки кнопок и помечена символом ±.
Чтобы применять модуль числа в формулах табличного редактора Microsoft Office Excel задействуйте его встроенную функцию ABS. Например, если требуется просто отобразить в ячейке B3 модуль значения из ячейки A1 без каких-то других изменений, содержимое B3 должно выглядеть так: =ABS(A1).
Программно реализовать вычисление модуля можно с использованием условного оператора ветвления if/then — эта конструкция существует практически в любом языке программирования. Например, чтобы значение, содержащееся в переменной с названием $someNum, заменить его модулем на языке php код строки должен выглядеть так:
if($someNum Pascal эту же операцию можно записать так:
if(someNum
Это очень простая и часто используемая математическая операция, поэтому во всех языках программирования есть встроенная функция, которая позволяет обойтись без условного оператора. Как и в Excel, в большинстве программных языков этой функции присвоено название abs, но есть и исключения — в Си она названа fabs. Синтаксис имеет больше различий и подчиняется правилам конкретного языка. Например, описанный выше пример на языке php можно заменить таким применением функции:
$someNum = abs($someNum);
Это очень простая и часто используемая математическая операция, поэтому во всех языках программирования есть встроенная функция, которая позволяет обойтись без условного оператора. Как и в Excel, в большинстве программных языков этой функции присвоено название abs, но есть и исключения — в Си она названа fabs. Синтаксис имеет больше различий и подчиняется правилам конкретного языка. Например, описанный выше пример на языке php можно заменить таким применением функции:
$someNum = abs($someNum);
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Кто знает игру на калькуляторах?
другой человек должен набрать число и нажать знак «=» ,так чтобы получилось 1, если набрано число больше загаданного, то высвечивается результат больше 1, если меньше то меньше 1, до тех пор пока на будет 1.
Затем меняются кто отгадывал число, тот загадывает.
Побеждает тот кому потребовалось меньше попыток.
Если имеются ввиду непрограммируемые калькуляторы, то практически на всех калькуляторах есть операция повторения делителя (после завершения операции деления на число, можно набрать новое число и нажать «=», получим результат деления на это же число)
Игры на советском калькуляторе МК-90
В этой статье я хочу рассказать о своём опыте работы с микрокалькулятором «Электроника МК-90».
Будет рассмотрено несколько вариантов работы с модулем памяти калькулятора, а также несколько игр на нём.
Данный калькулятор по своей сути это «портативная электронно-вычислительная машина на основе оригинального энергоэффективного асинхронного микропроцессорного набора серии 588, которая имеет встроенный интерпретатор языка Бейсик».
Мой образец был выпущен в апреле 1990 года и имел цену 1500 рублей.
Под одной из крышек устанавливаются четыре батарейки формата АА.
Под другой — два модуля оперативной памяти.
▍ Ознакомление с ОЗУ
Промышленность выпускала сменные модули памяти объёмом 10 Кбайт. Литиевый источник питания формата CR2016 обеспечивал сохранность данных около 1 года.
Конечно, в настоящее время информация на данном модуле была утеряна.
В интернете удалось найти сборник ПО для данного микрокалькулятора, в том числе и игры.
Человеком развившим тему общения модуля памяти с ПК был поляк Piotr Piatek. В своём блоге он вдоль и поперёк препарировал МК-90.
▍ Варианты записи информации на модуль памяти
Самый первый вариант программатора предложил сам Piotr Piatek. Это была довольно простая схема с использованием LPT-порта.
Так как на моём (а скорее всего и на большинстве современных) ПК нет данного порта, от этой схемы я отказался.
Второй вариант я подсмотрел у Ильи Данилова в его блоге.
Данная схема общается с ПК через USB порт и требует наличия программатора, так как построена на микроконтроллере ATmega8-16PU.
Весь необходимый софт Илья написал сам, за что ему респект. Однако блог давно уже не обновлялся. Надеюсь, что у него всё в порядке 🙂
После сборки схемы и прошивки микроконтроллера через программатор Тритон меня постигла неудача:
Выглядит похоже на авторскую плату, но не работает 🙁
При подключении данной схемы мой ПК находил новое устройство, однако идентификаторы были нулевые, несмотря на все мои танцы с бубном.
Третий вариант также нашёлся в интернете и не потребовал наличия программатора.
Пользователи walhi и Radon17 на форуме zx-pk.ru предложили использовать два программатора USB ASP.
Суть такова: сначала через первый программатор мы прошиваем второй. После данной процедуры мы можем общаться с модулем памяти МК-90, используя второй программатор.
Идея простая и рабочая. Остаётся лишь к шлейфу припаять разъём для подключения модуля памяти. Необходимые драйвера и софт также доступны на вышеуказанном форуме.

▍ Пробная запись и запуск игр
Следует отметить, что используя ПО для записи информации на модули, имеется возможность лишь записи и чтения. Режим «стирание» не предусмотрен. Поэтому для экспериментов с разными играми приходилось извлекать литиевую батарейку из модуля.
Вот небольшой перечень игр, которые корректно запустились на калькуляторе. Большинство игр занимают по 10 Кбайт, лишь игра «шахматы» занимает 20 Кбайт и требует соответственно два модуля памяти.
- Бокс
- Головоломка
- Змейка
- Космос
- Пакман
- Теннис
- Ханойская башня
- Ночная разборка (Сергей Сургутский)
- Робокоп (Сергей Сургутский)
- Терминатор 2 (Сергей Сургутский)
- «Весёлая Птичка» (2019) от Azya
Запуск всех игр смонтировал в небольшой ролик:
В интернете также нашёл альтернативные игры, написанные для эмулятора. Запустить их на «живом» калькуляторе не представилось возможным. Образ записывался корректно, однако при запуске отображалась ошибка.
▍ Заключение и благодарности
Надеюсь вам было интересно окунуться в мир старой компьютерной техники, благодарю за внимание!
Гениальные математические игры с калькулятором
Наши старушки калькуляторов школе, институту или университету сегодня есть что сказать; и благодаря им мы можем удивить наших друзей и семью всевозможные игры с калькулятором , друг гениальный. Теперь мы хотим предложить вам окончательные советы по математике и расчетам , 8 способов удивить местных и иностранцев гениальные цифровые головоломки которые мы можем использовать, чтобы сделать встречи с нашими людьми более приятными. Кроме того, мы предлагаем вам небольшой дополнительный совет на калькуляторе iPhone , то, что вы, вероятно, не знаете, хотя вы пользователь iOS . Ensuite, лучшие математические приемы с калькулятором .
Лучшие советы по математике с калькулятором
Тайна числа 73
- Напишите число 73 на листе бумаги. никому не показывая, сложите и отдайте кому-нибудь.
- Попросите этого человека придумать четырехзначное число и дважды подряд ввести его в калькулятор (например, 12341234).
- Скажите ему разделить число на 137.
- Теперь скажите ему, что он может разделить результат на его исходное четырехзначное число; Попросите его проверить сложенную бумагу (73).
- Калькулятор и бумага отобразят число 73.
Цикл 421
- Выберите число и введите его в калькулятор.
- Если он четный, разделите его на 2, если он нечетный, умножьте на 3 и прибавьте 1.
- Повторяйте этот процесс снова и снова с разными числами.
- Результатом всегда будет 4, 2 или 1, нечетные или четные числа.
Математический фокус
На этот раз мы будем играть с числом 37037:
- Умножьте число 37037 на 3, кратное 27.
- Результат всегда будет возвращать цифры с их шестью цифрами, равными (например, 111111, если мы умножим исходное число на 3).
Прогноз на 10
Выполните следующие действия, чтобы удивить своих друзей предсказаниями с числом ангела 10 в результате:
- Скажите кому-нибудь дать вам любой номер.
- Добавьте 5.
- Вычтите 2.
- Добавьте 6.
- Вычтите исходное число.
- Добавьте 1.
- Результат всегда… 10!
Угадай день рождения
Теперь вы можете угадать день рождения своих друзей (если вы еще этого не знаете) с помощью хитрого математического трюка с вашим калькулятором; Дайте калькулятор человеку, которого хотите удивить, и попросите его выполнить следующие действия:
- Введите цифру 7.
- Умножьте его на число месяца рождения (например, 3 марта).
- Вычтите 1.
- Умножьте результат на 13.
- Добавьте число дня вашего рождения (числовой день в календаре).
- Добавьте 3.
- Умножьте результат на 11.
- Вычтите месяц вашего рождения.
- Вычтите день своего рождения.
- Разделите результат на 10.
- Добавьте 11.
- И, наконец, разделите результат на 100.
Таким образом, на экране калькулятора появится число, которое будет соответствовать дню рождения человека, которого нужно удивить; Так, если он родился 2 марта, появится число 3.02, или что то же самое, 3 (март), 02 (день месяца).
Предсказать невезение
- Попросите кого-нибудь ввести трехзначное число дважды в калькулятор без вашего ведома (например, 123123).
- Скажите ему, что это число делится на 11; Попросите его провести операцию.
- Теперь скажите ему, что это число также делится на 13; Попросите его повторить операцию.
- Скажите ему разделить результат на исходное трехзначное число.
- Скажите ему, что результат 7.
- Если вы хотите предсказать неудачу, попросите его разделить число из третьего шага на 7.
- Результатом будет 13 — число неудач.
Бесконечная петля
- Попросите кого-нибудь выбрать число от 1 до 9.
- Попросите человека, выбравшего это число, умножить его на 9, а результат на 12345679 (пропустив 8 в последовательности) с помощью калькулятора.
- Попросите человека, который производил вычисления с помощью калькулятора, сообщить вам результат.
- Скажите ему номер, который вы выбрали изначально.
- В результате всегда будет отображаться исходный номер, повторяющийся в порядке XXXXXXXXX.
Таинственный цикл 6174
Теперь мы собираемся попытать счастья с числом 6174, чем-то, что удивит всех и на самом деле не дает четкой картины. Джоуэр!
- Введите в калькулятор четырехзначное число (не кратное 1111).
- Введите их сначала в порядке возрастания.
- Затем проделайте то же самое сверху вниз.
- Вычтите маленькое число из большого числа.
- Повторите шаги 2, 3 и 4 для разных результатов.
- Он всегда будет возвращать 6174!
Бонусный совет: удаляйте числа на калькуляторе iPhone!
Калькулятор iPhone не позволяет вам вычеркивать независимо числа, введенные в калькулятор с помощью клавиш сенсорного экрана; Если мы допустили ошибку в операции, нам придется стереть все числа и попробовать еще раз. Так было до сих пор! И это то, что пользователь обнаружил (и поделился через сети, становится вирусным ) что если мы касаемся или проводим пальцем по цифровому экрану калькулятор iPhone, приложение удаляет последний введенный номер , которого нет в официальных инструкциях к iPhone. Очень полезный совет, что многие Пользователи iOS делают не знать.
Контакты
E-mail: info@semestr.ru
❉: 594-797-934
Skype: newsemestr
ВКонтакте Youtube
Полезные советы
- Чтобы не вводить много данных, можно использовать вставку из Excel и Word
- Если решение не доступно, убедитесь, что в браузере отключен блокиратор (например Adblock).
- Если в Word вместо формулы отображается Ошибка, уменьшите шрифт формулы.
- Остальные советы можно найти в руководстве.
На главной странице находятся лишь некоторые виды онлайн-калькуляторов. Для доступа к другим разделам воспользуйтесь каталогом Калькуляторы по направлениям или функцией Поиск.
Принцип работы
- Решение
- Видео решение

Принятые обозначения
- Число π ≡ pi.
- Число e ≡ exp(1).
- Степень числа x2 ≡ x^2, x^(n-1).
- Функции: sin(x), cos(x), tan(x), atan(x).
- Корень квадратный √¯ ≡ sqrt().
- Степень корня ≡ x^(2/3), (x-1)^(1/3).
- Логарифм log5(x) ≡ log(x,5).
Автоматизация расчетов
Наиболее популярные средства расчетов:
- MS Excel
- WolframAlpha, Desmos
- Mathcad, Maple
- Statistica
Классификация онлайн — калькуляторов
По типу получения информации:
- Платные.
- Бесплатные (данный калькулятор).
По способу отображения результатов:
- Чистый html.
- html + javascript.
- html + javascript + Word (данный калькулятор).
Калькуляторы по направлениям
- Высшая математика
- Методы решения СЛАУ
- Аналитическая геометрия
- Матричный калькулятор
- Теория вероятностей
- Эконометрика онлайн
- Статистика онлайн
- Сетевая модель
- Информатика онлайн
- Математические методы в психологии
- Вычислительная математика
- Методы оптимизации
- Динамическое программирование
- Линейное программирование
- Исследование операций
- Системы массового обслуживания
- Теория игр онлайн
- Теория автоматического управления
Инструкция пользования онлайн-калькулятора
Оформление результатов в формате Word
По умолчанию все вычисления оформляются в файле формата MS Word. Однако следует учесть, что такая возможность имеется только для браузеров, поддерживающих javascript. Если javascript отключены, необходимо включить их (в настройках браузера). В остальных случаях всегда доступен просмотр решения в формате html (т.е. непосредственно в браузере).
Решение в Word не доступно чаще всего в этих случаях:
- В браузере установлен блокиратор AdBlock (AdFender, AdMuncher, Adguard). Если установлены антивирусы Kaspersky, DrWeb или Avast), то необходимо временно отключить этот фильтр или добавить сайт в список исключений (Подробнее).
- Если Вы ранее пользовались калькулятором, то необходимо очистить кэш вашего браузера и перезагрузить страницу.
- Загрузились не все javascript на предыдущем шаге. Необходимо вернуться на предыдущий шаг, обновить страницу и дождаться загрузки всех скриптов javascript.
- Если ни один из вышеуказанных пунктов не подходит, просто обновите страницу (F5).
Ввод цифровых данных и математических выражений
В вещественных числах в качестве разделителя используйте точку. Например, 1.2, 6.34.
Дробные числа: 1/3, 45/78.
Математические функции: exp(), log(), sqrt(), sin(), cos(), tan(), atan(), acos(), asin(), cot(), asec(), acsc(), acot(), cosh(), sinh(), tanh(), sech(), csch(), coth(), acosh(), asinh(), atanh(), acoth().
Знак корень
√¯ вводится как sqrt(), e ≡ exp(1); π ≡ pi; ∞ ≡ infinity.
Степень числа или функции: x^2, x^(1/2), (x-1)^(2/3), sin(x)^2
Работа с формулами WORD
Для редактирования формул в MS Word 2003 используйте Shift+F9 или двойной щелчок мышью для запуска редактора формул Equation 3.0.
Частые вопросы и ответы
- Использовал ваш метод ветвей и границ, но рисунки не подгружаются.
Если количество рисунков на странице решения больше 15, то многие из них сразу не будут отображены. Для их отображение нажмите на правую кнопку мыши и выполните команду Перезагрузить изображение. - Картинки в калькуляторе Графический метод все равно не отображаются.
Проверьте формат входных данных. Например, положительные числа записываются без знака +. Правильно: 3,6,11. Неправильно: +3,+5. - Не получается решить задачу методом ветвей и границ с тремя переменными
На данный момент сервис учитывает только две переменные. - Как сохранить решение в Word?. Выдается надпись
В вашем браузере установлены плагины, которые блокируют формирование решения в Word
Как правило, проблема в установленных блокираторах скриптов типа AdBlock. Необходимо отключить этот фильтр. Вторая проблема — старый кэш вашего браузера. Необходимо его очистить и перезагрузить страницу. - Хотелось бы узнать, как поставить степень корня в калькуляторе?
числитель записывается как (1+sin(x))^(1/5)-1
- Не могу скачать решение в Word
Файл в Word необходимо скачать в течение 20 минут после получения решения. - В полученном решении формата Word в тексте встречаются слова Ошибка.
Возможно в двух случаях.
1. Это особенности отображения формул при большом размере шрифта. Необходимо выделить формулу Ошибка и выбрать меньший размер шрифта. Если формула находится в таблице, можно увеличить ширину столбца.2. Зависит от региональных настроек интерфейса программы MS Word. А именно, какой символ используется в качестве разделителя списков. Подробнее.
Автозаполнение данных в браузере
Чтобы не заполнять ранее введенные данные, нажмите кнопку Backspace на клавиатуре.
Часто на ней просто нарисована стрелка, направленная влево.
Или можно нажать кнопку Назад в меню браузера.
Правила ввода математических выражений
Ввод чисел:
Целые числа вводятся обычным способом, например: 4 ; 18 ; 56
Для ввода отрицательного числа необходимо поставить знак минус: -19 ; -45 ; -90
Рациональные числа вводятся с использованием символа / , например: 3 / 4 ; -5 / 3 ; 5 / (-19)
Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей: 4.5 ; -0.4
Ввод переменных и констант:
Переменные и константы вводятся латинскими буквами, например: x ; y ; z ; a ; b .
Константы π и e вводятся как pi и e — соответственно.
Символ бесконечности ∞ вводится двумя маленькими латинскими буквами oo или словом inf .
Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.
Сумма и разность:
Сумма и разность задаются при помощи знаков + и — соответственно, например: 3 + a ; x + y ; 5 — 4 + t ; a — b + 4 ; ВНИМАНИЕ! Никаких пробелов между операндами быть не должно, например ввод: x + a — неправильный , правильно вводить так: x + a — без пробелов.
Умножение:
Умножение задается знаком * , например: 3 * t ; x * y ; -5 * x .
ВНИМАНИЕ! Ввод знака * необходим всегда, т.е. запись типа: 2 x — недопустима . Следует всегда использовать знак * , т.е правильная запись: 3 * x .
Деление:
Деление задается знаком / , например: 15 / a ; y / x ;.
Степень:
Степень задается знаком ^ , например: x ^ 2 ; 4 ^ 2 ; y ^ (-1 / 2) .
Приоритет операций:
Для указания (или изменения) приоритета операций необходимо использовать скобки () , например: ( a + b ) / 4 — тут вначале будет произведено сложение a + b , а потом сумма разделится на 4 , тогда как без скобок: — сначала b разделится на 4 и к полученному прибавится a . ВНИМАНИЕ! В непонятных случаях лучше всегда использовать скобки для получения нужного результата, например: 2 ^ 4 ^ 3 — неясно как будет вычислено это выражение: cначала 2 ^ 4 , а затем результат в степень 3 , или сначала 4 ^ 3 = 64 , а затем 2 ^ 64 ? Поэтому, в данном случае, необходимо использовать скобки: (2 ^ 4) ^ 3 или 2 ^ (4 ^ 3) — смотря что нужно.
Также распространенной ошибкой является запись вида: x ^ 3 / 4 — непонятно: вы хотите возвести x в куб и полученное выражение разделить на 4 , или хотите возвести x в степень 3 / 4 ? В последнем случае необходимо использовать скобки: x ^ (3 / 4) .
Ввод функций:
Функции вводятся с использованием маленьких латинских букв: sin ; cos ; tan ; log .
ВНИМАНИЕ! Аргумент функции всегда берется в скобки () , например: sin( 4 ) ; cos( x ) ; log( 4 + y ) .
Запись типа: sin 4 ; cos x ; log 4 + y — недопустима . Правильная запись: sin( 4 ) ; cos( x ) ; log( 4 + y ) .
Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так: (sin( x )) ^ 2 . Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x ^ 2 ), тогда это выглядит вот так: sin( x ^ 2) . Запись типа: sin ^ 2 x — недопустима .
Системы уравнений по-шагам
Результат
Примеры систем уравнений
- Метод Гаусса
- Метод Крамера
- Прямой метод
- Система нелинейных уравнений
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Задача для решения системы произвольных уравнений. Описание.
Знак умножения нужно вводить только между числами, во всех остальных случаях его можно не вводить.
| Функция | Описание | Пример ввода | Результат ввода |
|---|---|---|---|
| pi | Число (pi) | pi | $$ pi $$ |
| e | Число (e) | e | $$ e $$ |
| e^x | Степень числа (e) | e^(2x) | $$ e^ <2x>$$ |
| exp(x) | Степень числа (e) | exp(1/3) | $$ sqrt[3] $$ |
| |x| abs(x) |
Модуль (абсолютное значение) числа (x) | |x-1| abs(cos(x)) |
( |x-1| ) ( |cos(x)| ) |
| sin(x) | Синус | sin(x-1) | $$ sin(x-1) $$ |
| cos(x) | Косинус | 1/(cos(x))^2 | $$ frac<1> $$ |
| tg(x) | Тангенс | x*tg(x) | $$ x cdot tg(x) $$ |
| ctg(x) | Котангенс | 3ctg(1/x) | $$ 3 ctg left( frac<1> right) $$ |
| arcsin(x) | Арксинус | arcsin(x) | $$ arcsin(x) $$ |
| arccos(x) | Арккосинус | arccos(x) | $$ arccos(x) $$ |
| arctg(x) | Арктангенс | arctg(x) | $$ arctg(x) $$ |
| arcctg(x) | Арккотангенс | arcctg(x) | $$ arcctg(x) $$ |
| sqrt(x) | Квадратный корень | sqrt(1/x) | $$ sqrt<frac<1>> $$ |
| root(n,x) | Корень степени n root(2,x) эквивалентно sqrt(x) |
root(4,exp(x)) | $$ sqrt[4] < e^> $$ |
| x^(1/n) | Корень степени n x^(1/2) эквивалентно sqrt(x) |
(cos(x))^(1/3) | $$ sqrt[Large 3 normalsize] $$ |
| ln(x) log(x) log(e,x) |
Натуральный логарифм (основание — число e ) |
1/ln(3-x) | $$ frac<1> $$ |
| log(10,x) | Десятичный логарифм числа x | log(10,x^2+x) | $$ log_<10>(x^2+x) $$ |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
Почему решение на английском языке?
При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли. Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях. Единственное неудобство — на английском языке, но это не большая цена за качество.
Некоторые пояснения по выводу решения.
| Вывод | Перевод, пояснение |
|---|---|
| (log(x)) | Натуральный логарифм, основание — число e. У нас пишут (ln(x)) |
| (arccos(x)) или (cos^<-1>(x)) | Арккосинус. У нас пишут ( arccos(x) ) |
| (arcsin(x)) или (sin^<-1>(x)) | Арксинус. У нас пишут ( arcsin(x) ) |
| (tan(x)) | Тангенс. У нас пишут (tg(x) = frac) |
| (arctan(x)) или (tan^<-1>(x)) | Арктангенс. У нас пишут (arctg(x)) |
| (cot(x)) | Котангенс. У нас пишут (ctg(x) = frac) |
| (arccot(x)) или (cot^<-1>(x)) | Арккотангенс. У нас пишут (arcctg(x)) |
| (sec(x)) | Секанс. У нас пишут также (sec(x) = frac<1>) |
| (csc(x)) | Косеканс. У нас пишут (cosec(x) = frac<1>) |
| (cosh(x)) | Гиперболический косинус. У нас пишут (ch(x) = frac> <2>) |
| (sinh(x)) | Гиперболический синус. У нас пишут (sh(x) = frac> <2>) |
| (tanh(x)) | Гиперболический тангенс. У нас пишут (th(x) = frac>> ) |
| (coth(x)) | Гиперболический котангенс. У нас пишут (cth(x) = frac<1>) |
Если вам что-то осталось не понятно обязательно напишите об этом в Обратной связи и мы дополним эту таблицу.
источники:
http://mrexam.ru/systemofequations
http://www.math-solution.ru/math-task/systems-info














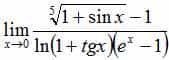 числитель записывается как (1+sin(x))^(1/5)-1
числитель записывается как (1+sin(x))^(1/5)-1