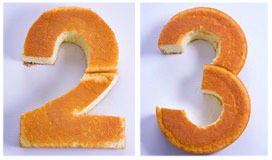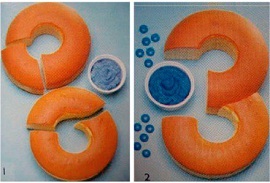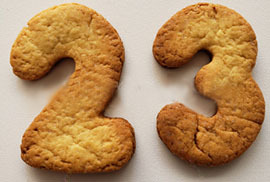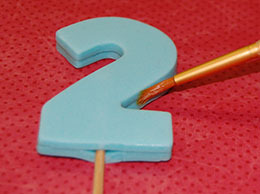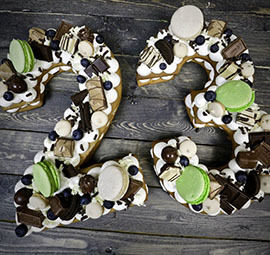«100 million» redirects here. For the song by Birdman, see 100 Million.
| 100000000 | |
|---|---|
← 100 101 102 103 104 105 106 107 108 109 |
|
| Cardinal | One hundred million |
| Ordinal | 100000000th (one hundred millionth) |
| Factorization | 28 × 58 |
| Greek numeral |  |
| Roman numeral | C |
| Binary | 1011111010111100001000000002 |
| Ternary | 202220111120122013 |
| Senary | 135312025446 |
| Octal | 5753604008 |
| Duodecimal | 295A645412 |
| Hexadecimal | 5F5E10016 |
100,000,000 (one hundred million) is the natural number following 99,999,999 and preceding 100,000,001.
In scientific notation, it is written as 108.
East Asian languages treat 100,000,000 as a counting unit, significant as the square of a myriad, also a counting unit. In Chinese, Korean, and Japanese respectively it is yi (simplified Chinese: 亿; traditional Chinese: 億; pinyin: yì) (or Chinese: 萬萬; pinyin: wànwàn in ancient texts), eok (억/億) and oku (億). These languages do not have single words for a thousand to the second, third, fifth powers, etc.
100,000,000 is also the fourth power of 100 and also the square of 10000.
Selected 9-digit numbers (100,000,001–999,999,999)[edit]
100,000,001 to 199,999,999[edit]
- 100,000,007 = smallest nine digit prime[1]
- 100,005,153 = smallest triangular number with 9 digits and the 14,142nd triangular number
- 100,020,001 = 100012, palindromic square
- 100,544,625 = 4653, the smallest 9-digit cube
- 102,030,201 = 101012, palindromic square
- 102,334,155 = Fibonacci number
- 102,400,000 = 405
- 104,060,401 = 102012 = 1014, palindromic square
- 105,413,504 = 147
- 107,890,609 = Wedderburn-Etherington number[2]
- 111,111,111 = repunit, square root of 12345678987654321
- 111,111,113 = Chen prime, Sophie Germain prime, cousin prime.
- 113,379,904 = 106482 = 4843 = 226
- 115,856,201 = 415
- 119,481,296 = logarithmic number[3]
- 121,242,121 = 110112, palindromic square
- 123,454,321 = 111112, palindromic square
- 123,456,789 = smallest zeroless base 10 pandigital number
- 125,686,521 = 112112, palindromic square
- 126,491,971 = Leonardo prime
- 129,140,163 = 317
- 129,145,076 = Leyland number
- 129,644,790 = Catalan number[4]
- 130,691,232 = 425
- 134,217,728 = 5123 = 89 = 227
- 134,218,457 = Leyland number
- 136,048,896 = 116642 = 1084
- 139,854,276 = 118262, the smallest zeroless base 10 pandigital square
- 142,547,559 = Motzkin number[5]
- 147,008,443 = 435
- 148,035,889 = 121672 = 5293 = 236
- 157,115,917 – number of parallelogram polyominoes with 24 cells.[6]
- 157,351,936 = 125442 = 1124
- 164,916,224 = 445
- 165,580,141 = Fibonacci number
- 167,444,795 = cyclic number in base 6
- 170,859,375 = 157
- 177,264,449 = Leyland number
- 179,424,673 = 10,000,000th prime number
- 184,528,125 = 455
- 188,378,402 = number of ways to partition {1,2,…,11} and then partition each cell (block) into subcells.[7]
- 190,899,322 = Bell number[8]
- 191,102,976 = 138242 = 5763 = 246
- 192,622,052 = number of free 18-ominoes
- 199,960,004 = number of surface-points of a tetrahedron with edge-length 9999[9]
200,000,000 to 299,999,999[edit]
- 200,000,002 = number of surface-points of a tetrahedron with edge-length 10000[10]
- 205,962,976 = 465
- 210,295,326 = Fine number
- 212,890,625 = 1-automorphic number[11]
- 214,358,881 = 146412 = 1214 = 118
- 222,222,222 = repdigit
- 222,222,227 = safe prime
- 223,092,870 = the product of the first nine prime numbers, thus the ninth primorial
- 225,058,681 = Pell number[12]
- 225,331,713 = self-descriptive number in base 9
- 229,345,007 = 475
- 232,792,560 = superior highly composite number;[13] colossally abundant number;[14] the smallest number divisible by all the numbers 1 through 22
- 244,140,625 = 156252 = 1253 = 256 = 512
- 244,389,457 = Leyland number
- 244,330,711 = n such that n | (3n + 5)[15]
- 253,450,711 = Wedderburn-Etherington prime[2]
- 254,803,968 = 485
- 267,914,296 = Fibonacci number
- 268,435,456 = 163842 = 1284 = 167 = 414 = 228
- 268,436,240 = Leyland number
- 268,473,872 = Leyland number
- 272,400,600 = the number of terms of the harmonic series required to pass 20
- 275,305,224 = the number of magic squares of order 5, excluding rotations and reflections
- 282,475,249 = 168072 = 495 = 710
- 292,475,249 = Leyland number
300,000,000 to 399,999,999[edit]
- 308,915,776 = 175762 = 6763 = 266
- 312,500,000 = 505
- 321,534,781 = Markov prime
- 331,160,281 = Leonardo prime
- 333,333,333 = repdigit
- 345,025,251 = 515
- 362,802,072 – number of parallelogram polyominoes with 25 cells.[16]
- 364,568,617 = Leyland number
- 365,496,202 = n such that n | (3n + 5)[17]
- 367,567,200 = colossally abundant number,[18] superior highly composite number[19]
- 380,204,032 = 525
- 381,654,729 = the only polydivisible number that is also a zeroless pandigital number
- 387,420,489 = 196832 = 7293 = 276 = 99 = 318 and in tetration notation 29
- 387,426,321 = Leyland number
400,000,000 to 499,999,999[edit]
- 400,080,004 = 200022, palindromic square
- 400,763,223 = Motzkin number[5]
- 404,090,404 = 201022, palindromic square
- 405,071,317 = 11 + 22 + 33 + 44 + 55 + 66 + 77 + 88 + 99
- 410,338,673 = 177
- 418,195,493 = 535
- 429,981,696 = 207362 = 1444 = 128 = 100,000,00012 AKA a gross-great-great-gross (10012 great-great-grosses)
- 433,494,437 = Fibonacci prime, Markov prime
- 442,386,619 = alternating factorial[20]
- 444,101,658 = number of (unordered, unlabeled) rooted trimmed trees with 27 nodes[21]
- 444,444,444 = repdigit
- 455,052,511 = number of primes under 1010
- 459,165,024 = 545
- 467,871,369 = number of triangle-free graphs on 14 vertices[22]
- 477,638,700 = Catalan number[4]
- 479,001,599 = factorial prime[23]
- 479,001,600 = 12!
- 481,890,304 = 219522 = 7843 = 286
- 499,999,751 = Sophie Germain prime
500,000,000 to 599,999,999[edit]
- 503,284,375 = 555
- 522,808,225 = 228652, palindromic square
- 535,828,591 = Leonardo prime
- 536,870,911 = third composite Mersenne number with a prime exponent
- 536,870,912 = 229
- 536,871,753 = Leyland number
- 542,474,231 = k such that the sum of the squares of the first k primes is divisible by k.[24]
- 543,339,720 = Pell number[12]
- 550,731,776 = 565
- 554,999,445 = a Kaprekar constant for digit length 9 in base 10
- 555,555,555 = repdigit
- 574,304,985 = 19 + 29 + 39 + 49 + 59 + 69 + 79 + 89 + 99 [25]
- 575,023,344 = 14-th derivative of xx at x=1[26]
- 594,823,321 = 243892 = 8413 = 296
- 596,572,387 = Wedderburn-Etherington prime[2]
600,000,000 to 699,999,999[edit]
- 601,692,057 = 575
- 612,220,032 = 187
- 617,323,716 = 248462, palindromic square
- 644,972,544 = 8643, 3-smooth number
- 656,356,768 = 585
- 666,666,666 = repdigit
- 670,617,279 = highest stopping time integer under 109 for the Collatz conjecture
700,000,000 to 799,999,999[edit]
- 701,408,733 = Fibonacci number
- 714,924,299 = 595
- 715,827,883 = Wagstaff prime,[27] Jacobsthal prime
- 729,000,000 = 270002 = 9003 = 306
- 742,624,232 = number of free 19-ominoes
- 774,840,978 = Leyland number
- 777,600,000 = 605
- 777,777,777 = repdigit
- 778,483,932 = Fine number
- 780,291,637 = Markov prime
- 787,109,376 = 1-automorphic number[11]
800,000,000 to 899,999,999[edit]
- 801,765,089 = 9293
- 804,357,000 = 9303
- 806,954,491 = 9313
- 809,557,568 = 9323
- 812,166,237 = 9333
- 814,780,504 = 9343
- 815,730,721 = 138
- 815,730,721 = 1694
- 817,400,375 = 9353
- 820,025,856 = 9363
- 822,656,953 = 9373
- 825,293,672 = 9383
- 827,936,019 = 9393
- 830,584,000 = 9403
- 833,237,621 = 9413
- 835,210,000 = 1704
- 835,896,888 = 9423
- 837,759,792 – number of parallelogram polyominoes with 26 cells.[28]
- 838,561,807 = 9433
- 841,232,384 = 9443
- 843,908,625 = 9453
- 844,596,301 = 615
- 846,590,536 = 9463
- 849,278,123 = 9473
- 851,971,392 = 9483
- 854,670,349 = 9493
- 855,036,081 = 1714
- 857,375,000 = 9503
- 860,085,351 = 9513
- 862,801,408 = 9523
- 865,523,177 = 9533
- 868,250,664 = 9543
- 870,983,875 = 9553
- 873,722,816 = 9563
- 875,213,056 = 1724
- 876,467,493 = 9573
- 879,217,912 = 9583
- 881,974,079 = 9593
- 884,736,000 = 9603
- 887,503,681 = 316
- 887,503,681 = 9613
- 888,888,888 – repdigit
- 890,277,128 = 9623
- 893,056,347 = 9633
- 893,554,688 = 2-automorphic number[29]
- 893,871,739 = 197
- 895,745,041 = 1734
900,000,000 to 999,999,999[edit]
- 906,150,257 = smallest counterexample to the Polya conjecture
- 916,132,832 = 625
- 923,187,456 = 303842, the largest zeroless pandigital square
- 942,060,249 = 306932, palindromic square
- 987,654,321 = largest zeroless pandigital number
- 992,436,543 = 635
- 997,002,999 = 9993, the largest 9-digit cube
- 999,950,884 = 316222, the largest 9-digit square
- 999,961,560 = highest triangular number with 9 digits and the 44,720th triangular number
- 999,999,937 = largest 9-digit prime number
- 999,999,999 = repdigit
References[edit]
- ^ Sloane, N. J. A. (ed.). «Sequence A003617 (Smallest n-digit prime)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 7 September 2017.
- ^ a b c Sloane, N. J. A. (ed.). «Sequence A001190 (Wedderburn-Etherington numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A002104 (Logarithmic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A000108 (Catalan numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A001006 (Motzkin numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A000258 (Expansion of e.g.f. exp(exp(exp(x)-1)-1))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A000110 : Bell or exponential numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A003226 (Automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-04-06.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A000129 (Pell numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A005165 : Alternating factorials». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A002955 (Number of (unordered, unlabeled) rooted trimmed trees with n nodes)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A006785 (Number of triangle-free graphs on n vertices)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A088054 : Factorial primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-02.
- ^ Sloane, N. J. A. (ed.). «Sequence A031971». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A005727». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A000979 : Wagstaff primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A030984 (2-automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2021-09-01.
«100 million» redirects here. For the song by Birdman, see 100 Million.
| 100000000 | |
|---|---|
← 100 101 102 103 104 105 106 107 108 109 |
|
| Cardinal | One hundred million |
| Ordinal | 100000000th (one hundred millionth) |
| Factorization | 28 × 58 |
| Greek numeral |  |
| Roman numeral | C |
| Binary | 1011111010111100001000000002 |
| Ternary | 202220111120122013 |
| Senary | 135312025446 |
| Octal | 5753604008 |
| Duodecimal | 295A645412 |
| Hexadecimal | 5F5E10016 |
100,000,000 (one hundred million) is the natural number following 99,999,999 and preceding 100,000,001.
In scientific notation, it is written as 108.
East Asian languages treat 100,000,000 as a counting unit, significant as the square of a myriad, also a counting unit. In Chinese, Korean, and Japanese respectively it is yi (simplified Chinese: 亿; traditional Chinese: 億; pinyin: yì) (or Chinese: 萬萬; pinyin: wànwàn in ancient texts), eok (억/億) and oku (億). These languages do not have single words for a thousand to the second, third, fifth powers, etc.
100,000,000 is also the fourth power of 100 and also the square of 10000.
Selected 9-digit numbers (100,000,001–999,999,999)[edit]
100,000,001 to 199,999,999[edit]
- 100,000,007 = smallest nine digit prime[1]
- 100,005,153 = smallest triangular number with 9 digits and the 14,142nd triangular number
- 100,020,001 = 100012, palindromic square
- 100,544,625 = 4653, the smallest 9-digit cube
- 102,030,201 = 101012, palindromic square
- 102,334,155 = Fibonacci number
- 102,400,000 = 405
- 104,060,401 = 102012 = 1014, palindromic square
- 105,413,504 = 147
- 107,890,609 = Wedderburn-Etherington number[2]
- 111,111,111 = repunit, square root of 12345678987654321
- 111,111,113 = Chen prime, Sophie Germain prime, cousin prime.
- 113,379,904 = 106482 = 4843 = 226
- 115,856,201 = 415
- 119,481,296 = logarithmic number[3]
- 121,242,121 = 110112, palindromic square
- 123,454,321 = 111112, palindromic square
- 123,456,789 = smallest zeroless base 10 pandigital number
- 125,686,521 = 112112, palindromic square
- 126,491,971 = Leonardo prime
- 129,140,163 = 317
- 129,145,076 = Leyland number
- 129,644,790 = Catalan number[4]
- 130,691,232 = 425
- 134,217,728 = 5123 = 89 = 227
- 134,218,457 = Leyland number
- 136,048,896 = 116642 = 1084
- 139,854,276 = 118262, the smallest zeroless base 10 pandigital square
- 142,547,559 = Motzkin number[5]
- 147,008,443 = 435
- 148,035,889 = 121672 = 5293 = 236
- 157,115,917 – number of parallelogram polyominoes with 24 cells.[6]
- 157,351,936 = 125442 = 1124
- 164,916,224 = 445
- 165,580,141 = Fibonacci number
- 167,444,795 = cyclic number in base 6
- 170,859,375 = 157
- 177,264,449 = Leyland number
- 179,424,673 = 10,000,000th prime number
- 184,528,125 = 455
- 188,378,402 = number of ways to partition {1,2,…,11} and then partition each cell (block) into subcells.[7]
- 190,899,322 = Bell number[8]
- 191,102,976 = 138242 = 5763 = 246
- 192,622,052 = number of free 18-ominoes
- 199,960,004 = number of surface-points of a tetrahedron with edge-length 9999[9]
200,000,000 to 299,999,999[edit]
- 200,000,002 = number of surface-points of a tetrahedron with edge-length 10000[10]
- 205,962,976 = 465
- 210,295,326 = Fine number
- 212,890,625 = 1-automorphic number[11]
- 214,358,881 = 146412 = 1214 = 118
- 222,222,222 = repdigit
- 222,222,227 = safe prime
- 223,092,870 = the product of the first nine prime numbers, thus the ninth primorial
- 225,058,681 = Pell number[12]
- 225,331,713 = self-descriptive number in base 9
- 229,345,007 = 475
- 232,792,560 = superior highly composite number;[13] colossally abundant number;[14] the smallest number divisible by all the numbers 1 through 22
- 244,140,625 = 156252 = 1253 = 256 = 512
- 244,389,457 = Leyland number
- 244,330,711 = n such that n | (3n + 5)[15]
- 253,450,711 = Wedderburn-Etherington prime[2]
- 254,803,968 = 485
- 267,914,296 = Fibonacci number
- 268,435,456 = 163842 = 1284 = 167 = 414 = 228
- 268,436,240 = Leyland number
- 268,473,872 = Leyland number
- 272,400,600 = the number of terms of the harmonic series required to pass 20
- 275,305,224 = the number of magic squares of order 5, excluding rotations and reflections
- 282,475,249 = 168072 = 495 = 710
- 292,475,249 = Leyland number
300,000,000 to 399,999,999[edit]
- 308,915,776 = 175762 = 6763 = 266
- 312,500,000 = 505
- 321,534,781 = Markov prime
- 331,160,281 = Leonardo prime
- 333,333,333 = repdigit
- 345,025,251 = 515
- 362,802,072 – number of parallelogram polyominoes with 25 cells.[16]
- 364,568,617 = Leyland number
- 365,496,202 = n such that n | (3n + 5)[17]
- 367,567,200 = colossally abundant number,[18] superior highly composite number[19]
- 380,204,032 = 525
- 381,654,729 = the only polydivisible number that is also a zeroless pandigital number
- 387,420,489 = 196832 = 7293 = 276 = 99 = 318 and in tetration notation 29
- 387,426,321 = Leyland number
400,000,000 to 499,999,999[edit]
- 400,080,004 = 200022, palindromic square
- 400,763,223 = Motzkin number[5]
- 404,090,404 = 201022, palindromic square
- 405,071,317 = 11 + 22 + 33 + 44 + 55 + 66 + 77 + 88 + 99
- 410,338,673 = 177
- 418,195,493 = 535
- 429,981,696 = 207362 = 1444 = 128 = 100,000,00012 AKA a gross-great-great-gross (10012 great-great-grosses)
- 433,494,437 = Fibonacci prime, Markov prime
- 442,386,619 = alternating factorial[20]
- 444,101,658 = number of (unordered, unlabeled) rooted trimmed trees with 27 nodes[21]
- 444,444,444 = repdigit
- 455,052,511 = number of primes under 1010
- 459,165,024 = 545
- 467,871,369 = number of triangle-free graphs on 14 vertices[22]
- 477,638,700 = Catalan number[4]
- 479,001,599 = factorial prime[23]
- 479,001,600 = 12!
- 481,890,304 = 219522 = 7843 = 286
- 499,999,751 = Sophie Germain prime
500,000,000 to 599,999,999[edit]
- 503,284,375 = 555
- 522,808,225 = 228652, palindromic square
- 535,828,591 = Leonardo prime
- 536,870,911 = third composite Mersenne number with a prime exponent
- 536,870,912 = 229
- 536,871,753 = Leyland number
- 542,474,231 = k such that the sum of the squares of the first k primes is divisible by k.[24]
- 543,339,720 = Pell number[12]
- 550,731,776 = 565
- 554,999,445 = a Kaprekar constant for digit length 9 in base 10
- 555,555,555 = repdigit
- 574,304,985 = 19 + 29 + 39 + 49 + 59 + 69 + 79 + 89 + 99 [25]
- 575,023,344 = 14-th derivative of xx at x=1[26]
- 594,823,321 = 243892 = 8413 = 296
- 596,572,387 = Wedderburn-Etherington prime[2]
600,000,000 to 699,999,999[edit]
- 601,692,057 = 575
- 612,220,032 = 187
- 617,323,716 = 248462, palindromic square
- 644,972,544 = 8643, 3-smooth number
- 656,356,768 = 585
- 666,666,666 = repdigit
- 670,617,279 = highest stopping time integer under 109 for the Collatz conjecture
700,000,000 to 799,999,999[edit]
- 701,408,733 = Fibonacci number
- 714,924,299 = 595
- 715,827,883 = Wagstaff prime,[27] Jacobsthal prime
- 729,000,000 = 270002 = 9003 = 306
- 742,624,232 = number of free 19-ominoes
- 774,840,978 = Leyland number
- 777,600,000 = 605
- 777,777,777 = repdigit
- 778,483,932 = Fine number
- 780,291,637 = Markov prime
- 787,109,376 = 1-automorphic number[11]
800,000,000 to 899,999,999[edit]
- 801,765,089 = 9293
- 804,357,000 = 9303
- 806,954,491 = 9313
- 809,557,568 = 9323
- 812,166,237 = 9333
- 814,780,504 = 9343
- 815,730,721 = 138
- 815,730,721 = 1694
- 817,400,375 = 9353
- 820,025,856 = 9363
- 822,656,953 = 9373
- 825,293,672 = 9383
- 827,936,019 = 9393
- 830,584,000 = 9403
- 833,237,621 = 9413
- 835,210,000 = 1704
- 835,896,888 = 9423
- 837,759,792 – number of parallelogram polyominoes with 26 cells.[28]
- 838,561,807 = 9433
- 841,232,384 = 9443
- 843,908,625 = 9453
- 844,596,301 = 615
- 846,590,536 = 9463
- 849,278,123 = 9473
- 851,971,392 = 9483
- 854,670,349 = 9493
- 855,036,081 = 1714
- 857,375,000 = 9503
- 860,085,351 = 9513
- 862,801,408 = 9523
- 865,523,177 = 9533
- 868,250,664 = 9543
- 870,983,875 = 9553
- 873,722,816 = 9563
- 875,213,056 = 1724
- 876,467,493 = 9573
- 879,217,912 = 9583
- 881,974,079 = 9593
- 884,736,000 = 9603
- 887,503,681 = 316
- 887,503,681 = 9613
- 888,888,888 – repdigit
- 890,277,128 = 9623
- 893,056,347 = 9633
- 893,554,688 = 2-automorphic number[29]
- 893,871,739 = 197
- 895,745,041 = 1734
900,000,000 to 999,999,999[edit]
- 906,150,257 = smallest counterexample to the Polya conjecture
- 916,132,832 = 625
- 923,187,456 = 303842, the largest zeroless pandigital square
- 942,060,249 = 306932, palindromic square
- 987,654,321 = largest zeroless pandigital number
- 992,436,543 = 635
- 997,002,999 = 9993, the largest 9-digit cube
- 999,950,884 = 316222, the largest 9-digit square
- 999,961,560 = highest triangular number with 9 digits and the 44,720th triangular number
- 999,999,937 = largest 9-digit prime number
- 999,999,999 = repdigit
References[edit]
- ^ Sloane, N. J. A. (ed.). «Sequence A003617 (Smallest n-digit prime)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 7 September 2017.
- ^ a b c Sloane, N. J. A. (ed.). «Sequence A001190 (Wedderburn-Etherington numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A002104 (Logarithmic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A000108 (Catalan numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A001006 (Motzkin numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A000258 (Expansion of e.g.f. exp(exp(exp(x)-1)-1))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A000110 : Bell or exponential numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A003226 (Automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-04-06.
- ^ a b Sloane, N. J. A. (ed.). «Sequence A000129 (Pell numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ «Sloane’s A005165 : Alternating factorials». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A002955 (Number of (unordered, unlabeled) rooted trimmed trees with n nodes)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A006785 (Number of triangle-free graphs on n vertices)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A088054 : Factorial primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-02.
- ^ Sloane, N. J. A. (ed.). «Sequence A031971». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A005727». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ «Sloane’s A000979 : Wagstaff primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
- ^ Sloane, N. J. A. (ed.). «Sequence A006958 (Number of parallelogram polyominoes with n cells (also called staircase polyominoes, although that term is overused))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). «Sequence A030984 (2-automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2021-09-01.
Идеи для поздравления мужчин на 23 февраля бывают самыми разными. Для сладкого подарка своими руками пригодятся съедобные цифры «23». Получить презент с циферным украшением весело, забавно, интересно. Такое поздравление, также, актуально для именинника, для даты торжественного события и т. д.
Седобные цифры могут быть плоскими, — например, чтобы оформить для подачи на стол салата и закусок, а также, — объемными.
С плоскими цифрами все просто: без всякого шаблона или схем, их можно «нарисовать» из продуктов на поверхности угощений. Например, выложить из мелко порезанной отварной моркови плюс оливок цифры «23» в победной георгиевской расцветке, как у ленточки. Также, закуски можно оформить плоскими цифрами из сыра, кусочков колбасной нарезки, из овощей. Очень легко выдавить из пакетика майонезную цифру «23» для салата, а сладкие цифры — из джема, айсинга, повидла, крема, мастики и т. д.
С объемными цифрами все не так просто. Надо уметь моделировать, фантазировать, найти шаблоны.
Так, с выпечкой, понадобится разрезать корж, чтобы сделать из него торт-цифры или украсить такой торт.
Бисквит может быть выпеченным самостоятельно, либо, также, какая угодно приобретенная выпечка из магазина.
Как сделать бисквитные цифры, как обрезать корж? — здесь схемы:
Украшение «бисквитной тройки» для торта конфетами:
Еще выпеченные объемные цифры можно сделать своими руками из готового слоеного теста. Очень красивыми получаются тарты с пышным кремом и украшением из ягод в виде праздничных цифр.
Одно из простых решений — взять несколько кексов, выложить из них на блюде — «23», украсить взбитым кремом, присыпать ягодами и угощение-украшение готово!
Пышный крем для кексов может быть из взбитого творога или сливочного сыра, масляный крем, крем из сливок, шоколадный и т. д.
Присыпать можно тертым шоколадом, кондитерской посыпкой или «sprinkle», кокосовой стружкой, кусочками ягод и т. д.
Очень милый и приятный подарок!
По любому рецепту для имбирного или медового печенья можно сделать печенье из цифр «23», как самостоятельное угощение или украшение выпечки:
Объемные цифры для выпчки легко сделать из мастики. Мастику для цифр можно приобрести в готовом виде, а далее только вырезать цифры по шаблону и вдавить в выпечку при помощи зубочистки.
Кроме мастики, можно сделать объемные цифры из меренги, из слоеного или дрожжевого теста и т. д.
Подходят шаблоны, вырубки и готовые формы для цифр.
Торт из цифр «23» бисквитный с кремом и фруктами (рецепт бисквита есть в ролике по ссылке):
Здесь очень красивые торты из бисквита с украшением из мастики. Особенно празднично и стильно сделать, украсив мастикой с акцентом на мужской праздник. Например, с оттенком «под камуфляж» или цвета «тельняшки» для ВМФ:
Украшение торта «23» кремом в расцветке «милитари» и «флаг России»:
Здесь тоже для декора использовали украшение мастикой с акцентом на день Защитника Отечества — «флаг России», «погоны», «звезды» из мастики для выпечки из цифр в стиле «23»:
Очень красивые тарты, слоеные торты и пирожные в тренде, со стильном оформлением под цифру «23» с рецептом, с кремоми и украшением плюс декор ягодами, сладостями типа зефира, макаронсов:
Хороших идей!
Прекрасного праздника!
Можно другие съедобные цифра сделать, например, «8», «9» и др. Здесь — торт из цифры «8», торт для романтического праздника из цифр.
Хороших идей!
Прекрасного торжества!