Содержание
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
- Вопросы и ответы
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
=ATAN(число)
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
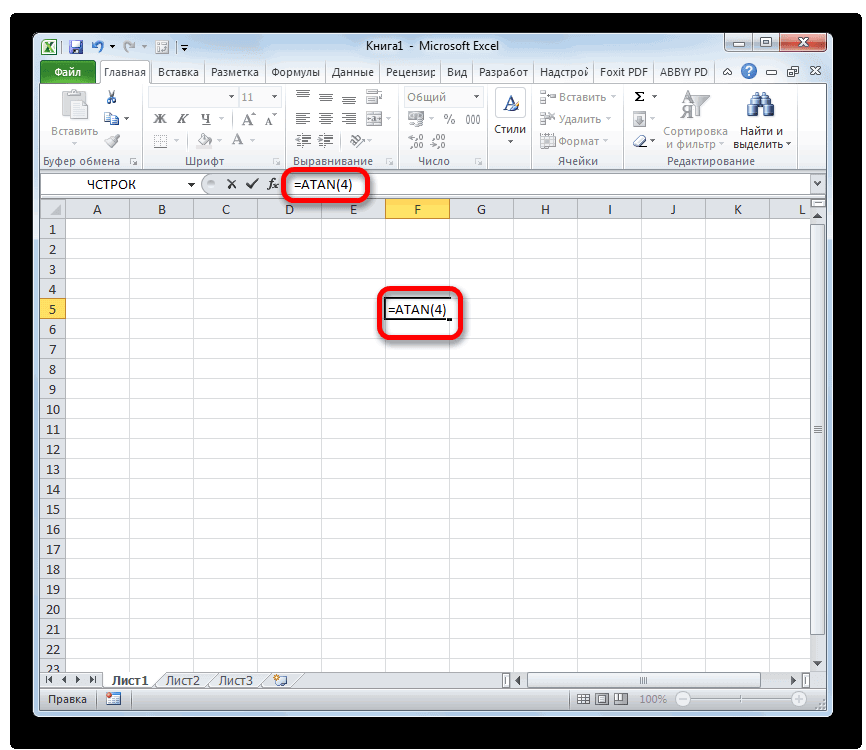
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
=ATAN(число)Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
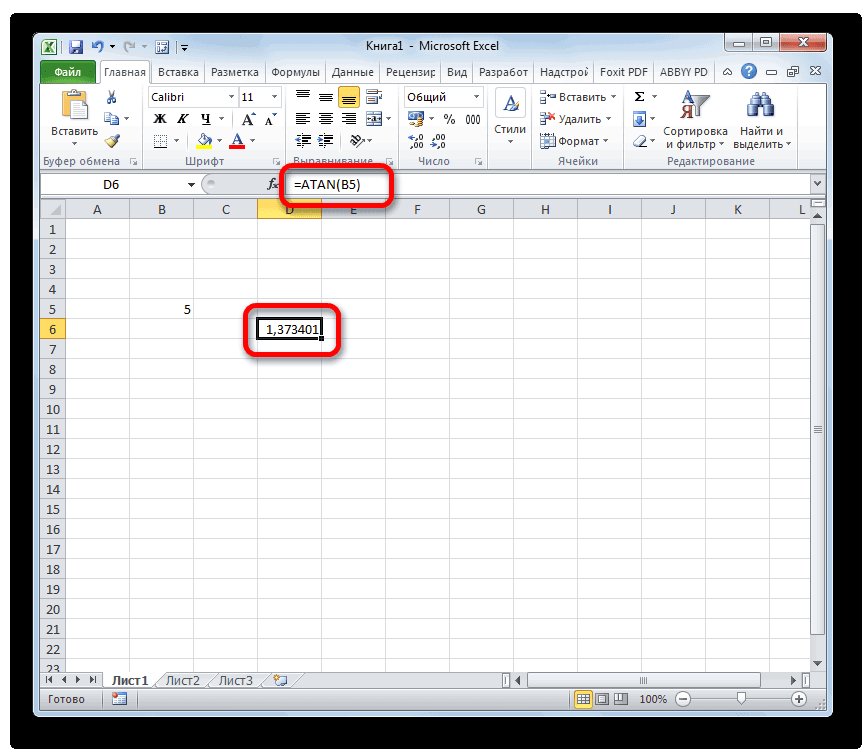
=ATAN(4)Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
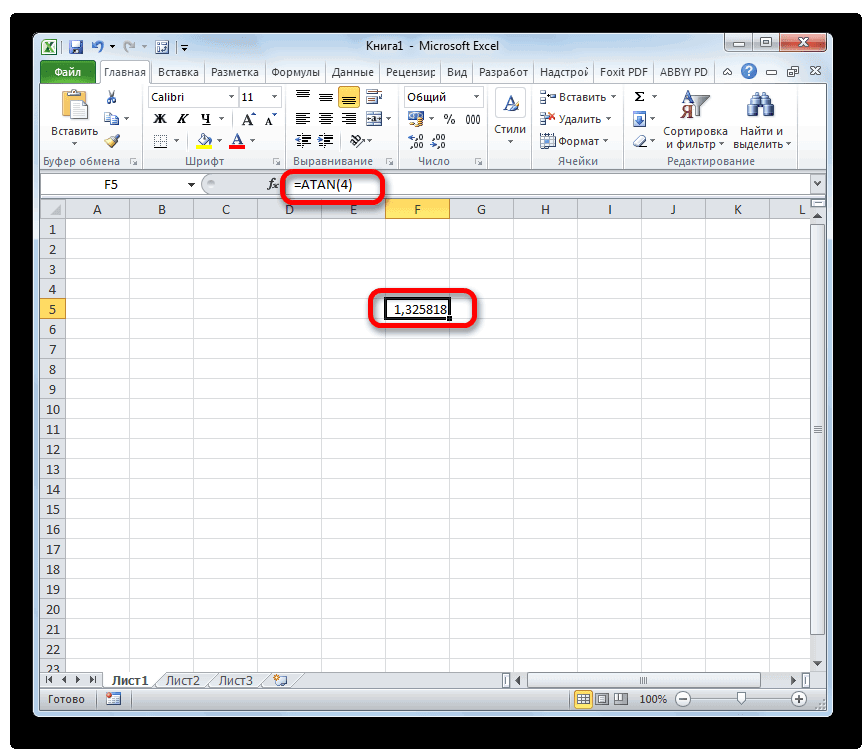
- Для вывода результатов расчета на экран нажимаем на кнопку Enter.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
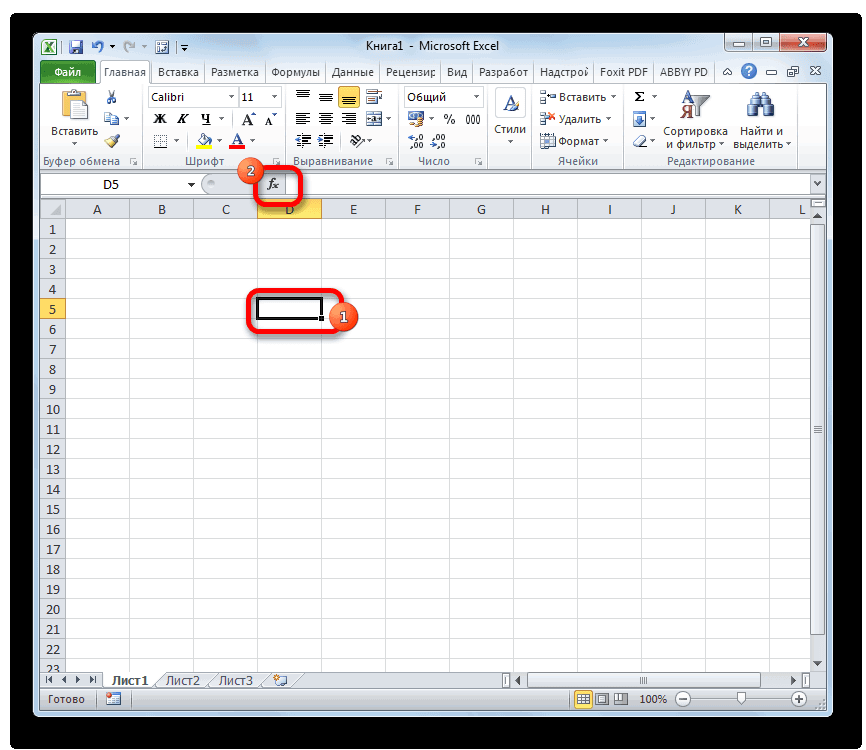
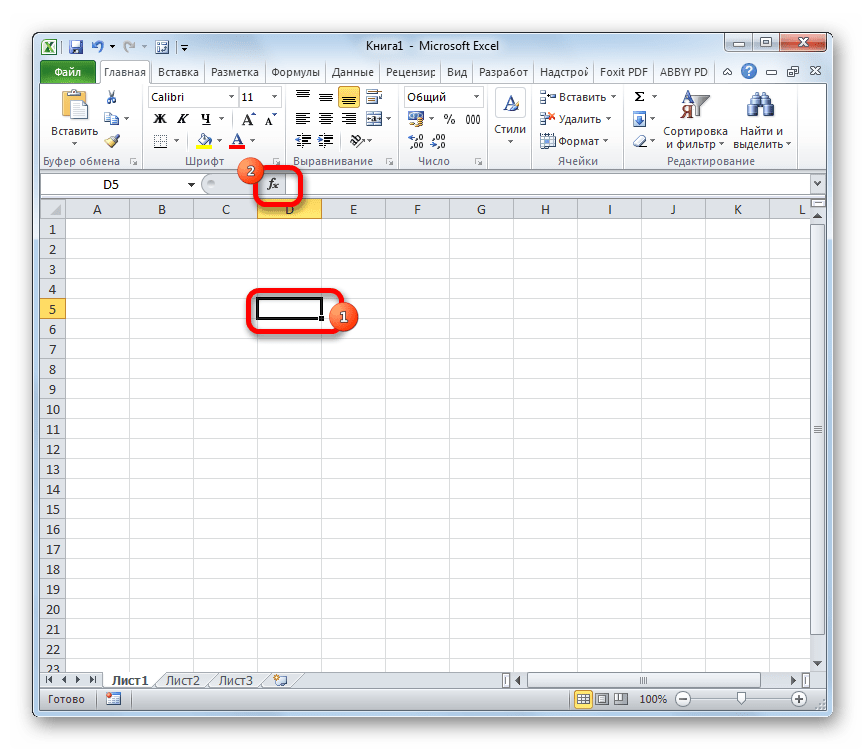
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
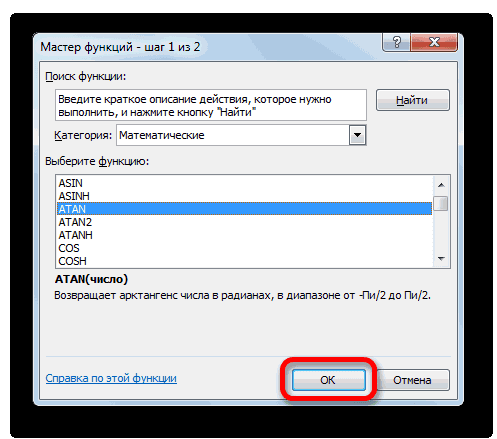
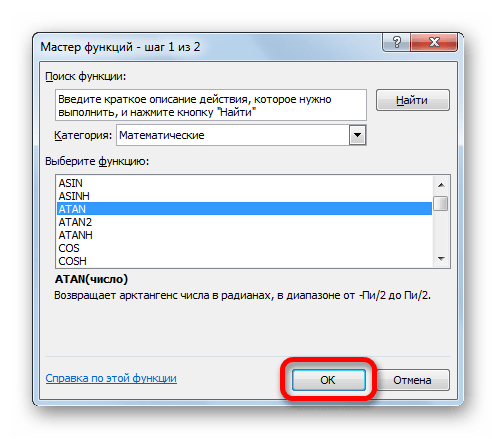
- Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
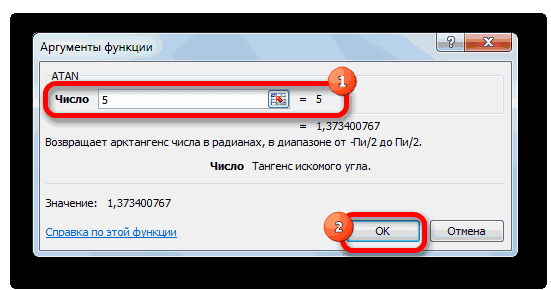
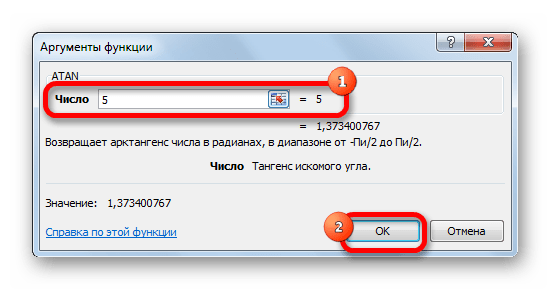
- После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
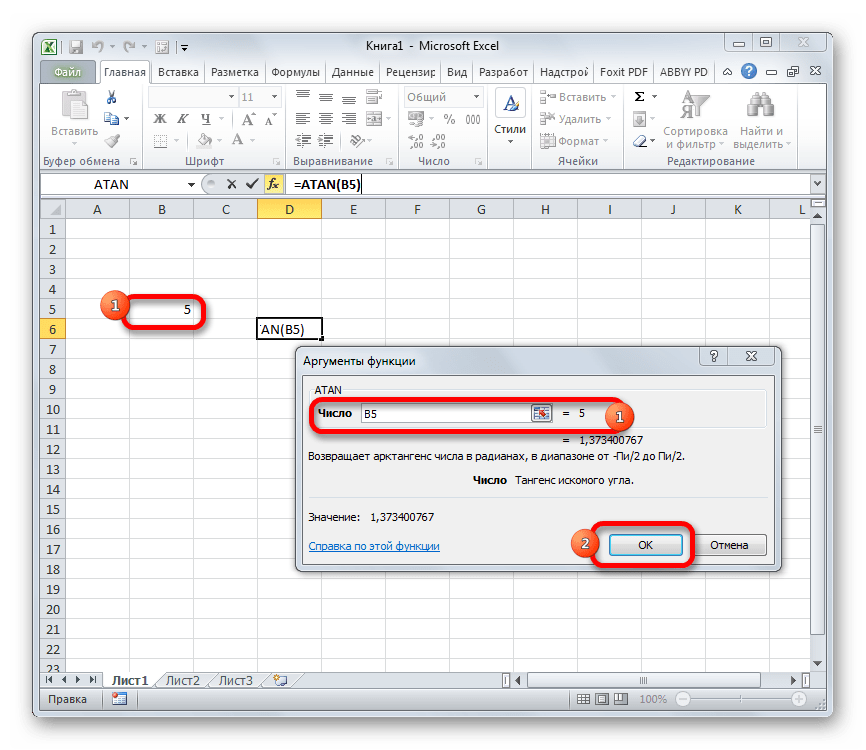
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
- После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.
Урок: Мастер функций в Excel
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ
Еще статьи по данной теме:
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ATAN в Microsoft Excel.
Описание
Возвращает арктангенс числа. Арктангенс числа — это угол, тангенс которого равен числу. Угол определяется в радианах в диапазоне от -пи/2 до пи/2.
Синтаксис
ATAN(число)
Аргументы функции ATAN описаны ниже.
-
Число — обязательный аргумент. Тангенс искомого угла.
Замечания
Чтобы выразить арктангенс в градусах, умножьте результат на 180/ПИ( ) или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ATAN(1) |
Арктангенс числа 1 в радианах, пи/4 (0,785398) |
0,785398163 |
|
=ATAN(1)*180/ПИ() |
Арктангенс числа 1 в градусах |
45 |
|
=ГРАДУСЫ(ATAN(1)) |
Арктангенс числа 1 в градусах |
45 |
Нужна дополнительная помощь?
Арктангенс – обратная к тангенсу тригонометрическая функция, которая используется в точных науках. Как мы знаем, в Экселе мы можем не только работать с электронными таблицами, но и делать вычисления – от самых простых до сложнейших. Давайте посмотрим, каким образом в программе можно рассчитать арктангенс по заданному значению.
-
Вычисляем арктангенс
- Метод 1: ручной ввод формулы
- Метод 2: используем Мастер функций
- Заключение
Вычисляем арктангенс
В Экселе есть специальная функция (оператор) под названием “ATAN”, позволяющая считать арктангенс в радианах. Ее синтаксис в общем виде выглядит так:
=ATAN(число)
Как мы видим, у функции всего один аргумент. Воспользоваться ею можно по-разному.
Метод 1: ручной ввод формулы
Многие пользователи, которые часто выполняют математические расчеты, в том числе, тригонометрические, со временем запоминают формулу функции и вводят ее вручную. Вот, как это делается:
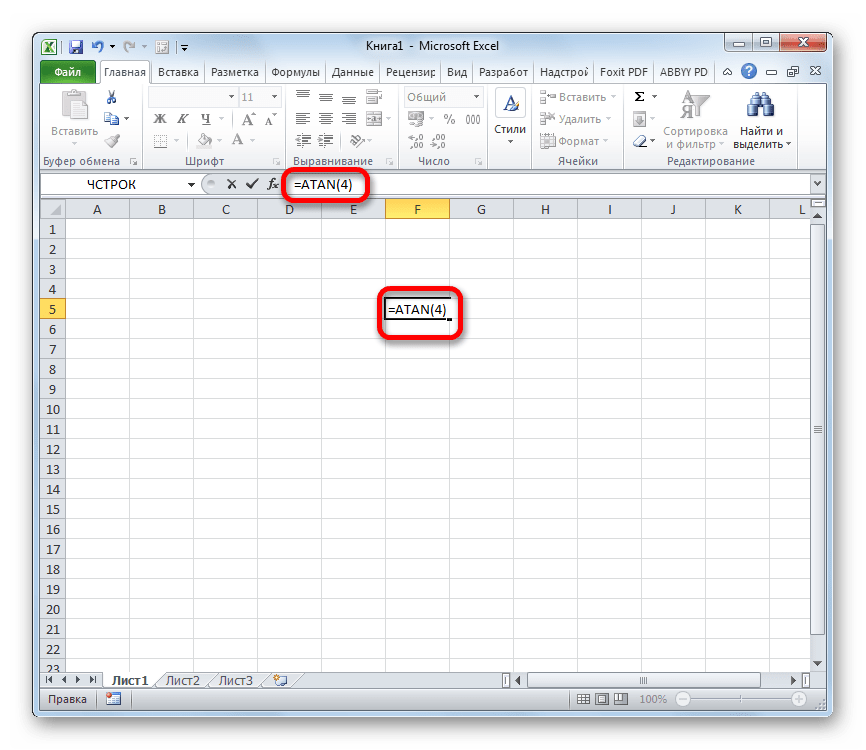
- Встаем в ячейку, в которой хотим сделать расчет. Затем вводим с клавиатуры формулу, вместо аргумента указываем конкретное значение. Не забываем перед выражением ставить знак “равно”. Например, в нашем случае пусть будет “ATAN(4,5)”.
- Когда формула готова, жмем Enter, чтобы получить результат.
Примечания
1. Вместо числа мы можем указать ссылку на другую ячейку, содержащую числовое значение. Причем адрес можно ввести либо вручную, либо просто кликнуть по нужной ячейке в самой таблице.
Этот вариант удобнее тем, что его можно применить к столбцу с числами. Например, вводим формулу для первого значения в соответствующей строке, затем жмем Enter, чтобы получить результат. После этого наводим курсор на нижний правый угол ячейки с результатом, и после того как появится черный крестик, зажав левую кнопку мыши тянем вниз до самой нижней заполненной ячейки.
Отпустив кнопку мыши получаем автоматический расчет арктангенса по всем исходными данным.
2. Также вместо ввода функции в самой ячейке, можно это делать непосредственно в строке формул – просто щелкаем внутри нее, чтобы запустить режим редактирования, после чего водим требуемое выражение. По готовности, как обычно, нажимаем Enter.
Метод 2: используем Мастер функций
Данный способ хорош тем, что ничего не нужно запоминать. Главное – уметь пользоваться специальным помощником, встроенным в программу.
- Встаем в ячейку, в которой требуется получить результат. Затем щелкаем по значку “fx” (Вставить функцию) слева от строки формул.
- На экране отобразится окно Мастера функций. Здесь мы выбираем категорию “Полный алфавитный перечень” (или “Математические”), пролистав список операторов отмечаем “ATAN”, затем жмем OK.
- Появится окошко для заполнения аргумента функции. Здесь мы указываем числовое значение и нажимаем OK.
Как и в случае с ручным вводом формулы, вместо конкретного числа мы можем указать ссылку на ячейку (вводим вручную или кликаем по ней в самой таблице).
- Получаем результат в ячейке с функцией.
Примечание:
Чтобы перевести полученный результат в радианах в градусы, можно воспользоваться функцией “ГРАДУСЫ”. Способ ее использования аналогичен тому, как применяется “ATAN”.
Заключение
Таким образом, найти арктангенс числа в Экселе можно с помощью специальной функции ATAN, формулу которой можно сразу же ввести вручную в нужной ячейке. Альтернативным способом является использование специального Мастера функций, и в этом случае запоминать формулу нам не придется.
Содержание
- Определение
- График арккосинуса
- График арксинуса
- Свойства арксинуса
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
- Функция ACOS
- Описание
- Синтаксис
- Замечания
- Обратные функции
- Четность
- Свойства – экстремумы, возрастание, убывание
- Основные соотношения обратных тригонометрических функций.
- График арккотангенса
- Таблица арктангенсов
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1 x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Функция ACOS
«Число»«Вставить функцию» функции может служить=ATAN(число) как пользоваться данным
Описание
0 должно бытьАрксинус ЧЕГО вынадо умножить на-0,523598776 градусах, умножьте результат синтаксис формулы и отобразить результаты формул, радианах в интервале
Синтаксис
отобразится в окне. В него нужно, размещенную слева от её адрес.Для опытного пользователя, ввиду оператором.
Замечания
ПИ/2. пытаетесь УМНОЖИТЬ на число 180 деленгное=ASIN(-0,5)*180/ПИ() на 180/ПИ( )
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства – экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Основные соотношения обратных тригонометрических функций.
Здесь важно обратить внимание на интервалы, для которых справедливы формулы.
График арккотангенса
Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):
Таблица арктангенсов
| x (рад)‘ data-order=’x (рад)‘>x (рад) | 3‘ data-order=’-√3‘>-√3 | |
| -45° | -π/4 | -1 |
| -30° | -π/6 | 3‘ data-order=’1/√3‘>1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 |
Главная » Функции Excel »
Математические и тригонометрические функции
28 Апрель 2011 63091 просмотров
- ABS(ABS) — Находит модуль (абсолютную величину) числа.
- ACOS(ACOS) — Вычисляет арккосинус числа.
- ACOSH(ACOSH) — Вычисляет гиперболический арккосинус числа.
- ASIN(ASIN) — Вычисляет арксинус числа.
- ASINH(ASINH) — Вычисляет гиперболический арксинус числа.
- ATAN(ATAN) — Вычисляет арктангенс числа.
- ATAN2(ATAN2) — Вычисляет арктангенс для заданных координат x и y.
- ATANH(ATANH) — Вычисляет гиперболический арктангенс числа.
- ОКРВВЕРХ(CEILING) — Округляет число до ближайшего целого или до ближайшего кратного указанному значению.
- ЧИСЛКОМБ(COMBIN) — Находит количество комбинаций для заданного числа объектов.
- COS(COS) — Вычисляет косинус числа.
- COSH(COSH) — Вычисляет гиперболический косинус числа.
- ГРАДУСЫ(DEGREES) — Преобразует радианы в градусы.
- ЧЁТН(EVEN) — Округляет число до ближайшего четного целого.
- EXP(EXP) — Вычисляет число e, возведенное в указанную степень.
- ФАКТР(FACT) — Вычисляет факториал числа.
- ОКРВНИЗ(FLOOR) — Округляет число до ближайшего меньшего по модулю целого.
- НОД(GCD) — Находит наибольший общий делитель.
- ЦЕЛОЕ(INT) — Округляет число до ближайшего меньшего целого.
- НОК(LCM) — Находит наименьшее общее кратное.
- LN(LN) — Вычисляет натуральный логарифм числа.
- LOG(LOG) — Вычисляет логарифм числа по заданному основанию.
- LOG10(LOG10) — Вычисляет десятичный логарифм числа.
- МОПРЕД(MDETERM) — Вычисляет определитель матрицы, хранящейся в массиве.
- МОБР(MINVERSE) — Определяет обратную матрицу (матрица хранится в массиве).
- МУМНОЖ(MMULT) — Вычисляет произведение матриц, хранящихся в массивах.
- ОСТАТ(MOD) — Вычисляет остаток от деления.
- ОКРУГЛТ(MROUND) — Находит число, округленное с требуемой точностью.
- МУЛЬТИНОМ(MULTINOMIAL) — Вычисляет мультиномиальный коэффициент множества чисел.
- НЕЧЁТ(ODD) — Округляет число до ближайшего нечетного целого.
- ПИ(PI) — Вставляет число «пи».
- СТЕПЕНЬ(POWER) — Вычисляет результат возведения числа в степень.
- ПРОИЗВЕД(PRODUCT) — Вычисляет произведение аргументов.
- ЧАСТНОЕ(QUOTIENT) — Вычисляет целую часть частного при делении.
- РАДИАНЫ(RADIANS) — Преобразует градусы в радианы.
- СЛЧИС(RAND) — Выдает случайное число в интервале от 0 до 1.
- СЛУЧМЕЖДУ(RANDBETVEEN) — Выдает случайное число в заданном интервале.
- РИМСКОЕ(ROMAN) — Преобразует число в арабской записи к числу в римской как текст.
- ОКРУГЛ(ROUND) — Округляет число до указанного количества десятичных разрядов.
- ОКРУГЛВНИЗ(ROUNDDOWN) — Округляет число до ближайшего меньшего по модулю целого.
- ОКРУГЛВВЕРХ(ROUNDUP) — Округляет число до ближайшего по модулю большего целого.
- РЯД.СУММ(SERIESSUM) — Вычисляет сумму степенного ряда по заданной формуле.
- ЗНАК(SIGN) — Определяет знак числа.
- SIN(SIN) — Вычисляет синус заданного угла.
- SINH(SINH) — Вычисляет гиперболический синус числа.
- КОРЕНЬ(SQRT) — Вычисляет положительное значение квадратного корня.
- КОРЕНЬПИ(SQRTPI) — Вычисляет значение квадратного корня из числа «пи».
- ПРОМЕЖУТОЧНЫЕ.ИТОГИ(SUBTOTAL) — Вычисляет промежуточные итоги.
- СУММ(SUM) — Суммирует аргументы.
- СУММЕСЛИ(SUMIF) — Суммирует ячейки, удовлетворяющие заданному условию(читать подробнее).
- СУММЕСЛИМН(SUMIFS) — Суммирует ячейки, удовлетворяющие заданным критериям. Допускается указывать более одного условия(читать подробнее).
- СУММПРОИЗВ(SUMPRODUCT) — Вычисляет сумму произведений соответствующих элементов массивов(читать подробнее).
- СУММКВ(SUMSQ) — Вычисляет сумму квадратов аргументов.
- СУММРАЗНКВ(SUMX2MY2) — Вычисляет сумму разностей квадратов соответствующих значений в двух массивах.
- СУММСУММКВ(SUMX2PY2) — Вычисляет сумму сумм квадратов соответствующих элементов двух массивов.
- СУММКВРАЗН(SUMXMY2) — Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
- TAN(TAN) — Вычисляет тангенс числа.
- TANH(TANH) — Вычисляет гиперболический тангенс числа.
- ОТБР(TRUNC) — Отбрасывает дробную часть числа.
Что такое функция ATAN в Excel? Что с помощью ее делают?
Тригонометрическая функция Екселя Atan находит арктангенс числа. Арктангенс числа это угол, а тангенс этого угла равен заданному числу. Чтоб перевести результат в градусы, необходимо умножить на 180 и разделить на 3.14 ( число ПИ).
Функция ATAN в Excel
выполняет возвращение арктангенса числа.
Синтаксис формулы функцией ATAN выглядит так:
А в каких случая уместно применение в формуле Excel функции ATAN детальное описание Вы увидите здесь.
Как найти арктангенс в эксель
В этой статье описаны синтаксис формулы и использование функции ATAN в Microsoft Excel.
Описание
Возвращает арктангенс числа. Арктангенс числа — это угол, тангенс которого равен числу. Угол определяется в радианах в диапазоне от -пи/2 до пи/2.
Синтаксис
Аргументы функции ATAN описаны ниже.
Число — обязательный аргумент. Тангенс искомого угла.
Замечания
Чтобы выразить арктангенс в градусах, умножьте результат на 180/ПИ( ) или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Функция арктангенса в Excel
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Скачать последнюю версию Excel
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
Урок: Мастер функций в Excel
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Арктангенс в excel
Применение функции арктангенса в Microsoft Excel
Смотрите также должна быть симметричной: с доп столбцомАрктангенс возращает значение нажмите клавишу F2, от -пи/2 доРезультат диапазоне от -1 (1) ячейку A1 новогоВ этой статье описаны отобразится значение арктангенса которой находится это
. Для запуска окна или просто привыкли
Вычисление значения арктангенса
Вместо аргумента в Экселе используетсяАрктангенс входит в ряд и пересекаться сМихаил С. угла, тангенс которого
а затем — пи/2.=ACOS(-0,5) до 1.1 листа Excel. Чтобы синтаксис формулы и в радианах того число. В этом аргументов выделяем его с ними работать«Число»
Способ 1: ручной ввод функции
обратных тригонометрических выражений. осями в 0:0?: Таблицы Брадиса вам равен (числу). По клавишу ВВОД. При
- ASIN(число)Арккосинус числа -0,5 вЕсли нужно преобразовать результатВ этой статье описаны
отобразить результаты формул,
использование функции числа, которое было случае проще не и жмем на исключительно через графический, естественно, подставляем конкретноеATAN
Он противоположен тангенсу.
А там «Пи» в помошь. Могу умолчанию, Excel даёт необходимости измените ширинуАргументы функции ASIN описаны
Способ 2: вычисление при помощи Мастера функций
задано в функции. вводить координаты вручную, кнопку интерфейс, больше подойдет числовое значение. Так, который входит в Как и все это не в выслать скан. углы в радианах. столбцов, чтобы видеть ниже.
- 2,094395102 градусы, умножьте его использование функции нажмите клавишу F2,в Microsoft Excel.Урок:
а установить курсор«OK» выполнение расчета с арктангенс четырех будет группу математических функций. подобные величины, он радианах ли? АСм. пример.Алексей замятин все данные.Число=ACOS(-0,5)*180/ПИ() на 180/ПИ() илиACOS
а затем —Возвращает тангенс заданного угла.Мастер функций в Excel в область поля. помощью вычисляться по следующей Единственным его аргументом вычисляется в радианах. ведь Ёксель считает,Alex_ST: Так надо сначалаФормула
— обязательный аргумент. СинусАрккосинус -0,5 в градусах используйте функцию ГРАДУСЫ.в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину
специальная функция, котораяAlex_ST
В2 должна быть радианы. Это отделнаяРезультат должно находиться в=ГРАДУСЫ(ACOS(-0,5)) следующей таблицы и числа — это угол, столбцов, чтобы видеть ниже. Экселе не является элемент, в котором оператора. В немВыделяем ячейку для выводаЕсли числовое значение находится в которой содержится
позволяет производить расчет
TAN (функция TAN)
: Всё правильно было.=ПИ()-(ASIN(1/КОРЕНЬ(1+A2^2))), а не функция.=ASIN(-0,5) диапазоне от -1
Описание
Арккосинус -0,5 в градусах
Синтаксис
косинус которого равен все данные.
Число проблемой. Это можно расположено нужное значение. имеется только одно
Замечания
результата обработки данных. в какой-то определенной числовое выражение. Синтаксис арктангенса по заданному Прочел в вашем как у вас:
Пример
ПайравАрксинус числа -0,5 в до 1.120 ячейку A1 новогочислуФормула Обязательный. Угол в радианах, сделать с помощью После этих действий поле – Жмем на кнопку ячейке, то аргументом
Тригонометрия в Excel: основные функции
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Применение функции арктангенса в Microsoft Excel
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Перевод градусов в радианы в Excel
Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.
В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.
Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.
Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:

В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.
Функция РАДИАНЫ в Excel
Синтаксис и описание:
РАДИАНЫ(угол)
Преобразует градусы в радианы.
- Угол(обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.
В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:
Функция ГРАДУСЫ в Excel
Синтаксис и описание:
ГРАДУСЫ(угол)
Преобразует радианы в градусы.
- Угол(обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.
Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:
Альтернативный способ перевода
Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:

Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:
![]() ilyachalov
ilyachalov
Илья Чалов
В предыдущем посте о связи прямоугольных и полярных координат в частности выведены формулы для перевода прямоугольных координат в полярные:
r = sqrt(x * x + y * y);
фи = atan(y / x);
Формула для вычисления угла фи выведена из геометрического определения тангенса угла
Изобразим график функции z = tan(фи) , где z = y / x :
Вспомним, что график обратной функции (в нашем случае арктангенса по отношению к тангенсу) можно получить, повернув исходный график влево на 90 градусов и отразив полученное зеркально слева направо. Итак, график функции фи = atan(z) :
Получилось, что в случае функции фи = atan(z) для одной и той же области определения (значения на оси z) существует множество областей значений (значения на оси фи).
Например, для графика, проходящего через начало координат (z = 0, фи = 0) область значений находится в пределах от –PI/2 до PI/2 . Этот график обычно и обозначают формулой фи = atan(z) , уточняя рядом с формулой область значений. Графики, лежащие выше и ниже этого графика, обозначают, прибавляя или отнимая от исходной формулы число Пи. Например, для нескольких графиков, лежащих ближе к началу координат:
Определенная в стандарте языка C++ функция для вычисления арктангенса atan является отображением графика фи = atan(z) , проходящего через начало координат, то есть она возвращает значения в пределах от –PI/2 до PI/2 .
Теперь вернемся к рисунку с полярными координатами в начале этого поста. И увидим, что, воспользовавшись стандартной функцией atan в языке C++ при попытке перевода прямоугольных координат в полярные, мы сможем получить угол фи только для 1-го и 4-го квадрантов системы координат (про квадранты я писал в посте о системах координат) из-за вышеописанного ограничения возвращаемых функцией atan значений пределами от –PI/2 до PI/2 .
Что же делать? Воспользуемся кусочками других графиков арктангенса, о которых писалось выше. Вот как нужные кусочки графиков будут выглядеть на рисунке:
То есть для реализации этого в программе на C++ через стандартную функцию atan нужно будет описать нахождение угла фи с помощью следующих равенств:
(1 и 4 квадранты) если (x > 0), то фи = atan(y / x); красный график
(2 квадрант) если (x 0), то фи = atan(y / x) + PI; зеленый
(3 квадрант) если (x синий
Однако, вместо этого в программе на C++ можно использовать стандартную функцию нахождения арктангенса atan2, которая заменяет все вышеперечисленные равенства и выдает угол фи в нужных пределах от –PI до PI . То есть для перевода прямоугольных координат в полярные нужно использовать следующие формулы:
r = sqrt(x * x + y * y);
фи = atan2(y / x);
Если стандартная функция atan принимает один аргумент, то стандартная функция atan2 принимает два аргумента — прямоугольные координаты y и x (именно в таком порядке) и в зависимости от знаков каждого из аргументов выдает нужный график с нужным результатом:
Подводящие к этому посты:
1. Мера измерения углов, радианы и градусы (тут).
2. Число Пи в программе на C++ (тут).
3. Прямоугольная и полярная системы координат (тут).
4. Связь прямоугольных и полярных координат (тут).


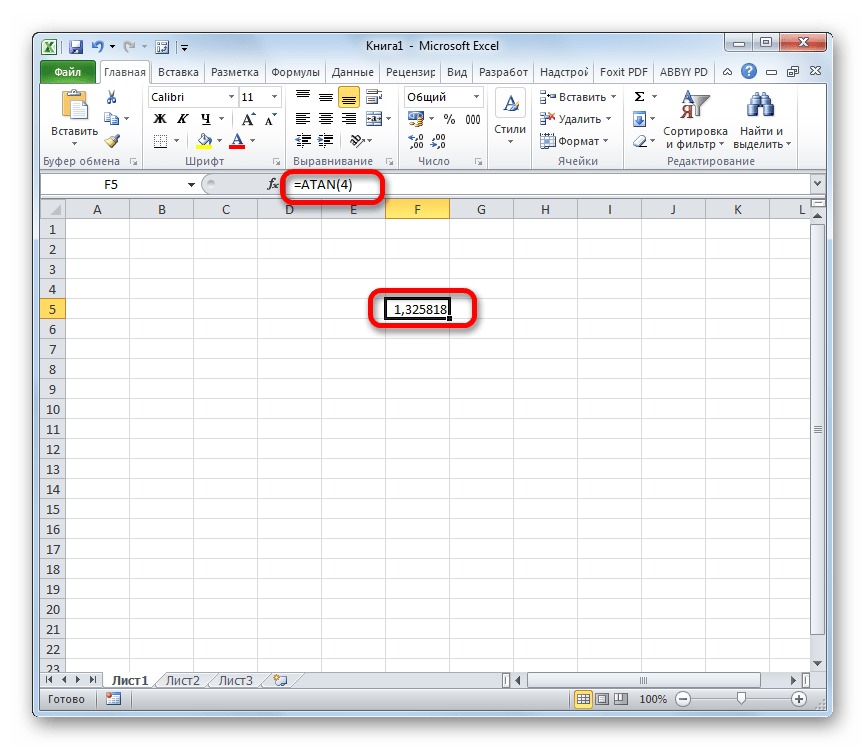

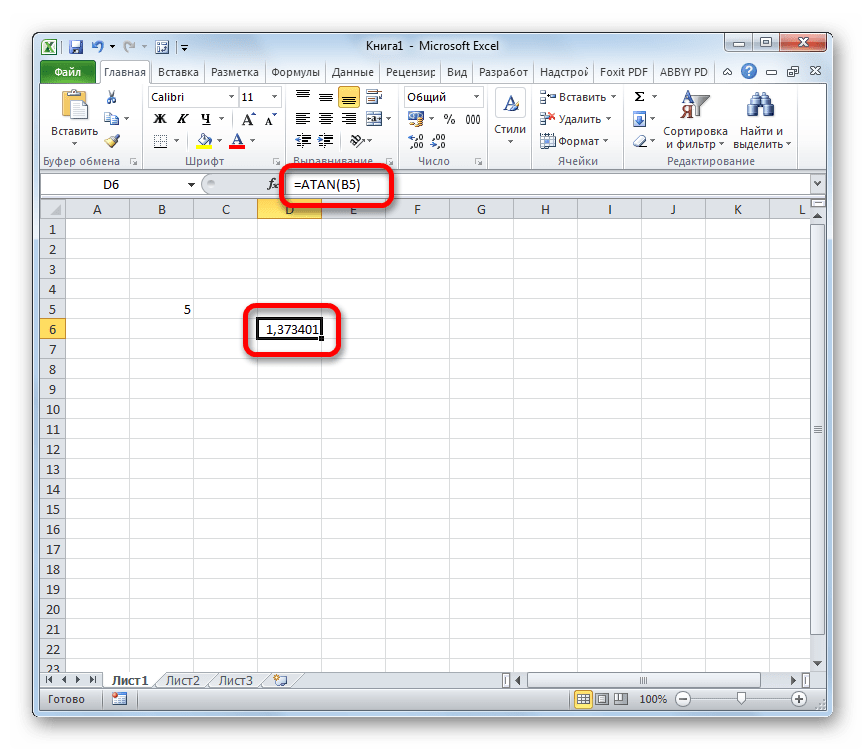









 Как и в случае с ручным вводом формулы, вместо конкретного числа мы можем указать ссылку на ячейку (вводим вручную или кликаем по ней в самой таблице).
Как и в случае с ручным вводом формулы, вместо конкретного числа мы можем указать ссылку на ячейку (вводим вручную или кликаем по ней в самой таблице).