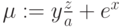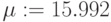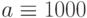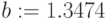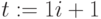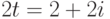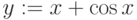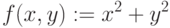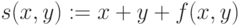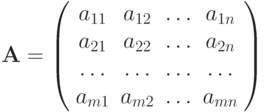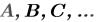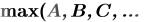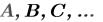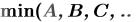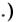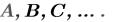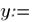MathCAD. MatLab
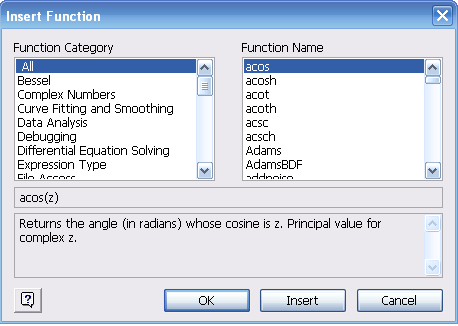
— Арктангенса нет на панелях инструментов, поэтому его нужно найти в специальном списке функций. Вызвать этот список можно либо сочетанием [Ctrl]+[E], либо выполнив команду Insert / Function (Вставка/Функция), либо при помощи специальной кнопки панели Standard (Стандартная). В открывшемся окне есть список категорий функций (Function Category), список самих функций выбранной категории (Function Name), а также окно информации о выбранной функции. По умолчанию определена категория All (Все) и в окне Function Name находится полный список всех встроенных функций MathCAD.
Очевидно, что арктангенс нужно искать в категории Trigonometric (Тригонометрические). Среди множества всевозможных тригонометрических функций находится 2 вида арктангенса (Atan и Atan2).
Для того чтобы определить, какой из них следует выбрать, прочитаем описание для каждого:
Atan(Z). »Returns the angle (in radians) whose tangent is z. Principal value for complex z.» »Возвращает угол (в радианах), для которого тангенс — это Z. Главное значение для комплексного Z».
Atan2(x,y). »Returns the angle (in radians) from the x-axis to a line containing the origin (0, 0) and the point (x, y). Both x and y must be real.» » Возвращает угол (в радианах) между осью x и линией, содержащей точку начала координат и точку (x,y). X и Y должны быть действительными».
Очевидно, нужно использовать первую функцию. Выбираем ее и нажимаем Ok.
2) Выражение введено, но параметры его вида, установленные по умолчанию, зачастую могут не удовлетворить пользователя. Для того чтобы отредактировать вид выражения, нужно при помощи команды Format/Equation (Формат/Уравнение) вызвать соответствующее меню.
Здесь вы можете определить цвет шрифта формул (Default equation color), выбрать стиль (Style name). При помощи кнопки Modify (Модифицировать) вы можете изменить стиль текста формул: выбрать тип, размер, начертание шрифта. Чтобы поменять параметры самой математической области, выполните правый щелчок мышью по любой точке редактируемой формулы и в открывшемся контекстном меню выберите пункт Properties (Свойства).
Как записать арктангенс в маткаде
Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.
1.2.1 Тригонометрические функции
sin (z) — синус . cos (z) — косинус
tan (z) — тангенс . sec (z) — секанс
csc (z) — косеканс . cot (z) — котангенс
1.2.2 Гиперболические функции
sinh (z) — гиперболический синус
cosh(z) — гиперболический косинус
tanh(z) — гиперболический тангенс
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс
coth(z) — гиперболический котангенс
1.2.3 Обратные тригонометрические функции
asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс
1.2.3 Обратные тригонометрические функции
asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс
1.2.4 Обратные гиперболические функции
asinh (z) — обратный гиперболический синус
acosh(z) — обратный гиперболический косинус
atanh(z) — обратный гиперболический тангенс
1.2.5 Показательные и логарифмические функции
exp (z) — экспоненциальная функция
ln (z) — натуральный логарифм
log (z) — десятичный логарифм
1.2.6 Функции с условиями сравнения
ceil (x) — наименьшее целое, большее или равное х
floor(x) — наибольшее целое, меньшее или равное х
mod(x,y) — остаток отделения х/у со знаком х
angle(x,y) — положительный угол с осью х для точки с координатами (х,у)
Как ввести arctg в mathcad
Как правильно записать Arcctg()

Как правильно записать F(x) чтоб реализовать метод простой итерации

Записываю интеграл как есть ,а он выдаёт странное решение,помогите, как правильно записать?

не могу записать фор-лу,постоянно что-то горит красным..
Основные средства программы MathCAD
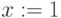
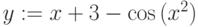
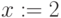
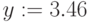
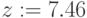
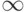



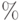
- Набираемая формула всегда заключена в рамку. Не выходите из рамки, пока не закончили набор формулы!
- Для набора формул пользуйтесь «Калькулятором» из «Математической палитры»
При наборе формул возможно появление ошибок набора. Кнопка 
Встроенные функции MathCAD
Создаются матрицы при помощи кнопки 

|
Имя |
Значение |
Применение |
|||
|
по |
|||||
|
умолчанию |
|||||
|
Определяет |
точность |
сходимости |
|||
|
некоторых функций, таких как интеграл, |
|||||
|
производная, |
и |
. |
|||
|
Определяет, насколько точно должно |
|||||
|
выполняться |
ограничение |
в блоке |
|||
|
решения, чтобы решение считалось |
|||||
|
приемлемым при использовании функций |
|||||
|
и |
|||||
Примечание: Значения указанных выше системных переменных можно изменять в указанной ниже вкладки:
Переменные-диапазоны
Переменные-диапазоны – это последовательности значений, определенные с использованием оператора диапазона(..):
Здесь переменная-диапазон 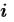
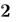
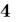
Размер шага можно изменить, задав второе значение последовательности:
11
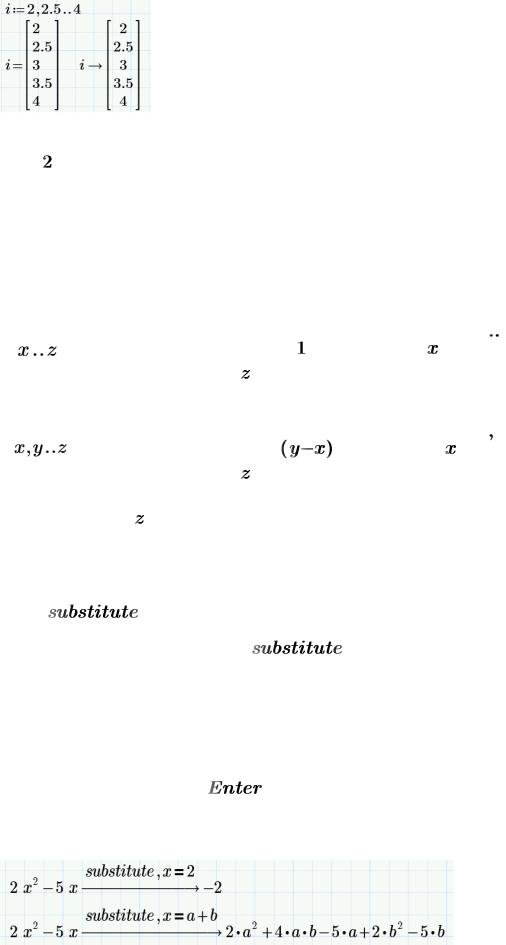
Здесь размер шага переменной-диапазона 
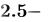
Операторы диапазона:
|
Оператор |
Описание |
Сочетание |
|||
|
клавиш |
|||||
|
Возвращает |
последовательность |
||||
|
значений с |
шагом |
, начиная с |
и |
||
|
заканчивая на . |
Две точки |
||||
|
Возвращает |
последовательность |
||||
|
значений с шагом |
, начиная с |
и |
|||
|
заканчивая на |
Запятая |
||||
Операнды 
Подстановка переменных:
1. Поместите курсор в конец выражения, вставьте ключевое слово из вкладки Математика/ Символьные операции.
|
2. После ключевого слова |
введите запятую и переменную, |
|
которую требуется заменить. |
3.Вставьте логический оператор равенства (
Математика/ Операторы/Сравнение, а затем введите число,
переменную или выражение, которые требуется подставить.
|
4. Нажмите клавишу |
или щелкните место вне области. Mathcad |
заменит в результате все вхождения переменной ее значением. Примеры:
12
1.2. Операторы и функции. Вычисление значений выражений
Для составления различных выражений и нахождения их значения при различных данных используются: переменные, различные операторы, символы, константы, символьные операции, встроенные функции Mathcad Prime, а также создаваемые пользователем функции (функция пользователя). Рассмотрим наиболее часто используемые из них.
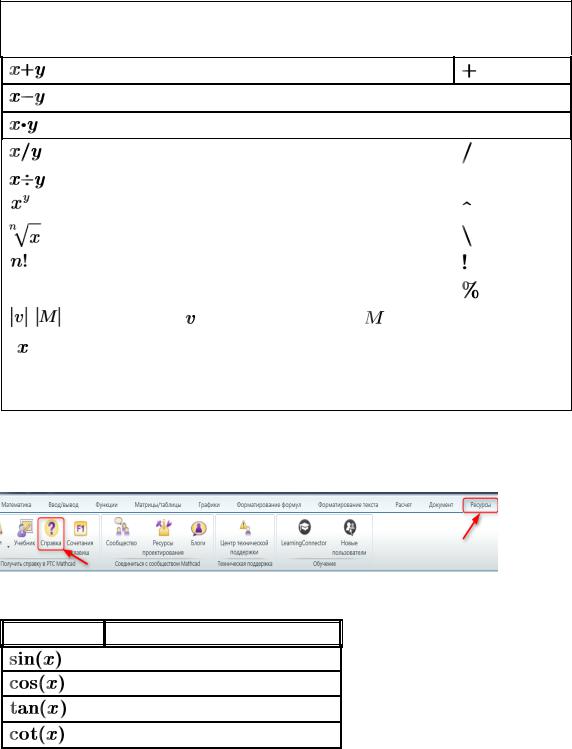
Алгебраические операторы:
|
Оператор |
Описание |
Сочетание |
|
клавиш |



|
Деление |
|||
|
Деление в строку |
|||
|
Возведение в степень |
|||
|
Квадратный и n — ый корень |
|||
|
Факториал |
|||
|
% |
Процент |
||
|
, |
Модуль |
или определитель |
|
|
( ) |
Согласованная пара круглых скобок |
( |
|
|
, |
Запятая, |
разделяющая аргументы |
, |
|
функции |
Запятая |
Примечание: Более подробное изложение о назначениях операторов и функции смотрите в справочнике на русском языке, который встроен в
Mathcd Prime:
Прямые и обратные тригонометрические функции:
Функция Описание




13









Где, – скалярное значение в радианах или вектор скалярных значений,
– скалярное значение или вектор скалярных значений.
Экспоненциальные и логарифмические функции:

возвращает логарифм z по основанию b. Если
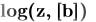
возвращает натуральный логарифм (по
основанию e) числа z.
возвращает натуральный логарифм (по
основанию e) числа z, но возвращает –1×10307 при z = 0.
Где, — безразмерное скалярное значение (вещественное, комплексное или мнимое) или вектор скалярных значений. Для функций 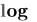
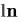


Скаляр (от лат. scalaris – ступенчатый) – величина, каждое значение которой может быть выражено одним числом. В математике под
14

«числами» могут подразумеваться элементы произвольного поля, тогда как в физике имеются ввиду действительные или комплексные числа. Скаляр описывается одним числом, а вектор двумя или более числами.
Некоторые числовые функции:
наибольший общий делитель (НОД), являющийся
наибольшим целым числом, на которое делятся нацело все значения в
наименьшее общее кратное (НОК), являющееся
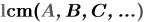
|
возвращает остаток от деления |
на . Знак |
|
результата совпадает со знаком . |
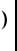



|
Для функции |
и |
аргументы |
могут быть массивами, |
|
|
скалярами или строками, для |
и |
– целые числа или массивы, |
элементы которых являются целыми числами. Параметры и y являются
|
вещественными скалярными величинами и |
, |
и |
— целые числа, |
|||
|
большие или равные |
, причем |
|||||
|
Примечание: Функцию |
часто используют для установления |
|||||
|
факта четности или нечетности. Например: если |
( |
)=0 , то – |
||||
|
четное, а если |
( |
) , то |
– нечетное. |
15
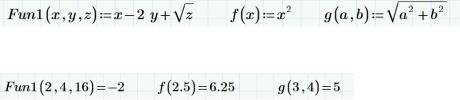
В PTC Mathcad содержится более 700 встроенных функций. Встроенные функции обозначаются именем функции, за которым следует один или несколько операндов, заключенных в круглые скобки. Операнды функций называются аргументами, и каждый аргумент определяется выражением. Результат функции рассчитывается посредством применения действия функции к аргументам.
Примечание: Имена встроенных функций зависят от регистра клавиатуры. Все функции PTC Mathcad (встроенные и определяемые пользователем) принимают максимум 16 аргументов. Многие общие операции представляются соответствующими математическими обозначениями и считаются операторами, которые описываются отдельно.
Кроме встроенных функции Mathcad Prime позволяет определять свои функции (функция пользователя) и использовать их в дальнейших вычислениях.
Для определения функции пользователя:
1.Введите в документ имя определяемой функции.
2.Введите открывающуюся скобку. Появятся местозаполнитель и закрывающие скобки.
3.Введите в местозаполнитель список аргументов, разделенных запятыми. Аргументы должны быть именами. Они не могут быть более сложными выражениями.
4.Вставьте оператор присваивания :=. Появится второй местозаполнитель.
5.Введите в местозаполнитель выражение или строку. Переменные справа должны быть либо ранее определены, либо входить в список аргументов. Неопределенные переменные обводятся красным цветом.
Примеры определения функции пользователя:
Примеры использования этих функции пользователя:
16
Mathcad Prime вычисляет математические выражения в порядке слева направо, сверху вниз. При изменении математического выражения его результат автоматически обновляется. Все связанные математические области, находящиеся справа или снизу от измененных выражений, соответственно обновляются. Если отключить расчет области, результаты не будут обновляться:
Для набора различных математических выражении (формул) и нахождения их значений для различных исходных данных, используют в основном следующие вкладки:
17
Примечание: Функции можно набирать и с помощью клавиатуры.
Чтобы вычислить значение выражения, нужно ввести необходимое выражение, предварительно присвоив начальные значения переменным и поставить обычный знак равенства «=» – оператор вычисления:
Если мы запишем выражение 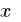
значение 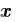

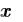
или, после, в любом месте документа, с помощью оператора глобального присваивания (вкладка Математика/Операторы), так:
Оператор глобального присваивания , сохраняет назначенное значение во всем документе. Попытка присвоить глобальной переменной новое значение приведет к неудаче.
Еще один символ 
служит для запуска в действие символьных операций:
При вычислении функции с использованием оператора аналитического преобразования 
18

В режиме программирования используется еще один вид присваивания 
Оператор сравнения (жирный знак равенства 
Упрощение выражений производится при помощи команды из вкладки Математика/Символьные вычисления. Ключевое слово 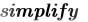
упрощает квадратные корни и степени. Примеры:
Разложение на множители производится при помощи команды из вкладки Математика/Символьные вычисления. Эта операция позволяет разложить полиномы на произведение более простых полиномов, а целые числа — на простые сомножители. Примеры:
19

Приведение подобных слагаемых производится при помощи команды 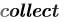
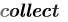
Разложение на простые дроби производится при помощи команды из вкладки Математика/Символьные вычисления.Пример:
Примеры вычисления суммы и произведения:
Операторы суммы и произведения:
|
Оператор |
Описание |
||
|
Возвращает сумму всех элементов вектора . |
|||
|
Возвращает сумму по выражения . |
|||
|
Возвращает сумму выражения |
для всех от до |
||
|
. |
|||
|
Возвращает произведение по |
выражения . |
||
|
Возвращает произведение выражения для всех |
|||
|
от |
до . |
||
20
1.5. Некоторые стандартные функции MathCAD
Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:
M – квадратная матрица;
V – вектор (матрица из одного столбца);
A – произвольная матрица;
S – симметричная матрица;
G – произвольная матрица или число;
X – вектор или число;
Z – комплексная матрица или число;
z – комплексное число;
прочие символы – скалярные величины.
Экспоненциальные и логарифмические функции
exp(X) – экспонента от X;
ln(X) – натуральный логарифм от X;
log(X) – десятичный логарифм от X;
log(X,b) – логарифм от X по основанию b.
Гиперболические и тригонометрические (прямые и обратные) функции
sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;
sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;
asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.
Функции для работы с комплексными числами
Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;
arg(z) – аргумент комплексного числа z (в радианах).
Матричные функции
length(V) – возвращает число элементов вектора V;
cols(A) – возвращает число столбцов матрицы A;
rows(A) – возвращает число строк матрицы A;
matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;
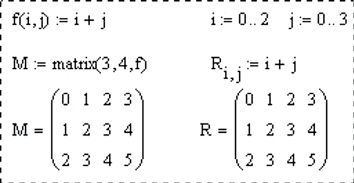
identity(n) – единичная матрица n×n;
tr(M) – след матрицы M (сумма элементов главной диагонали);
rank(A) – ранг матрицы M;
norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;
eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;
eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;
cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;
lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.
Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.

Элементы статистического анализа данных
gmean(G1,G2,G3…) – среднее геометрическое аргументов;
mean(G1,G2,G3…) – среднее арифметическое аргументов;
var(G1,G2,G3…) – дисперсия;
stdev(G1,G2,G3…) – среднеквадратичное отклонение.
Дискретные преобразования
fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;
cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;
wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.
Аппроксимация, интерполяция и экстраполяция
Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.
Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).
Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).
Применяются следующие функции MathCAD:
regress(VX,VY,k) – возвращает вектор данных, используемый для поиска интерполирующего полинома (a0 + a1x + a2x2 + … + akxk) порядка k. Полином должен описывать данные, состоящие из упорядоченных значений аргумента (VX) и соответствующих значений неизвестной функции (VY), то есть график полинома должен проходить через все точки, заданные координатами (VX, VY), или максимально близко к этим точкам;
interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.
Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.
Примеры интерполяции и экстраполяции:
1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.
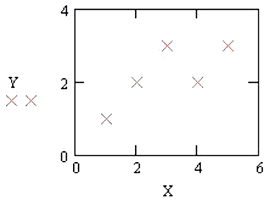
1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.
Решения показаны на рис. 19.
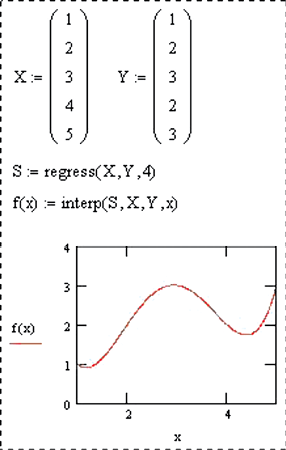
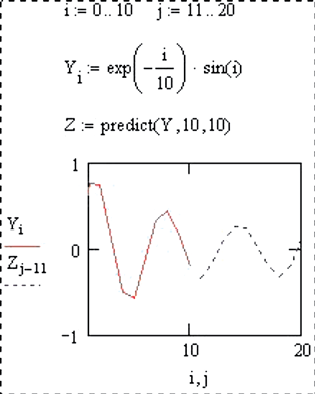
а б
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач
Нахождение корней полинома
polyroots(V) – возвращает вектор, содержащий все корни полинома a0 + a1x + a2x2 + … + akxk, заданного вектором-столбцом коэффициентов
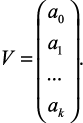
Прочие функции
max(G1,G2,…) – максимальное значение среди аргументов;
min(G1,G2,…) – минимальное значение среди аргументов;
if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;
sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.
На рис. 20 показан пример применения функции if.
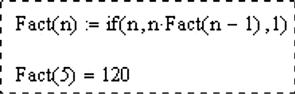
Рис. 20. Функция, вычисляющая факториал