Содержание
- 1 Что такое амплитуда
- 2 Что такое период
- 3 Что такое частота
- 4 Что такое циклическая частота
- 5 Что такое начальная фаза и как определить ее по графику колебаний
- 5.1 Как вычислить начальный угол по интервалу смещения
- 6 Что такое фаза колебаний
- 6.1 Различия между фазой и начальной фазой
- 6.2 Как на графике колебаний отметить фазу
- 6.3 Как определить фазу с помощью формулы
- 7 Что такое разность фаз
- 8 Как связаны характеристики колебаний — формулы
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
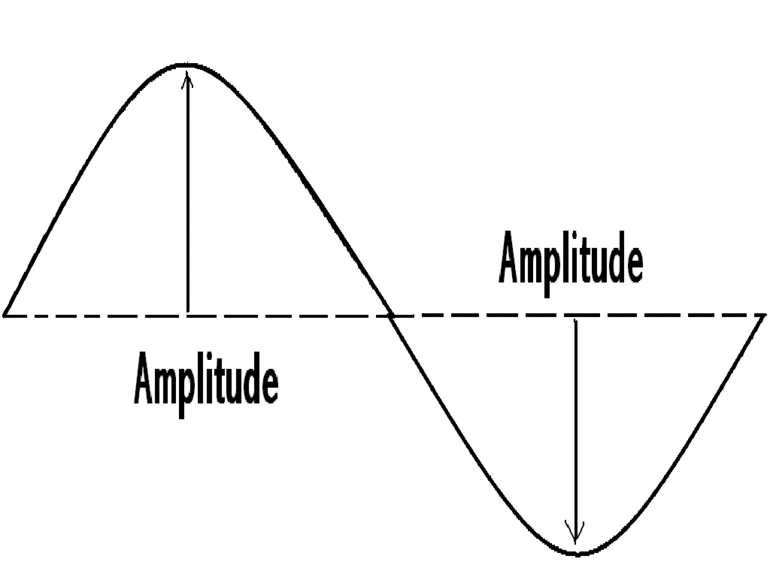
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
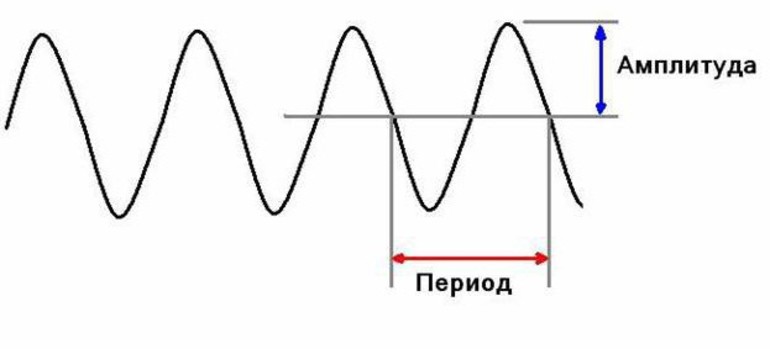
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
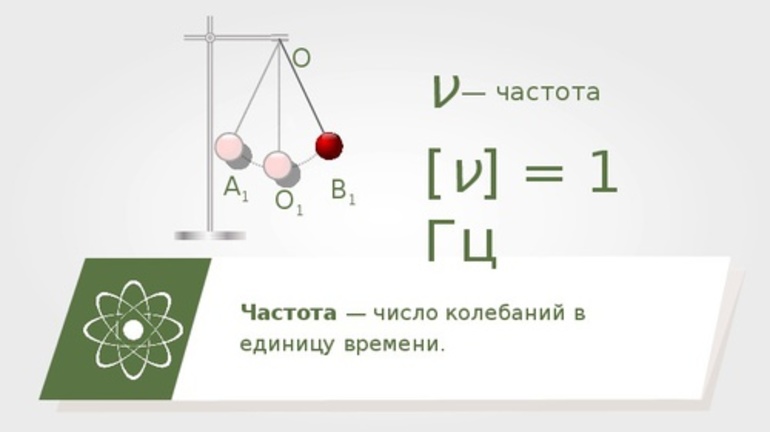
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
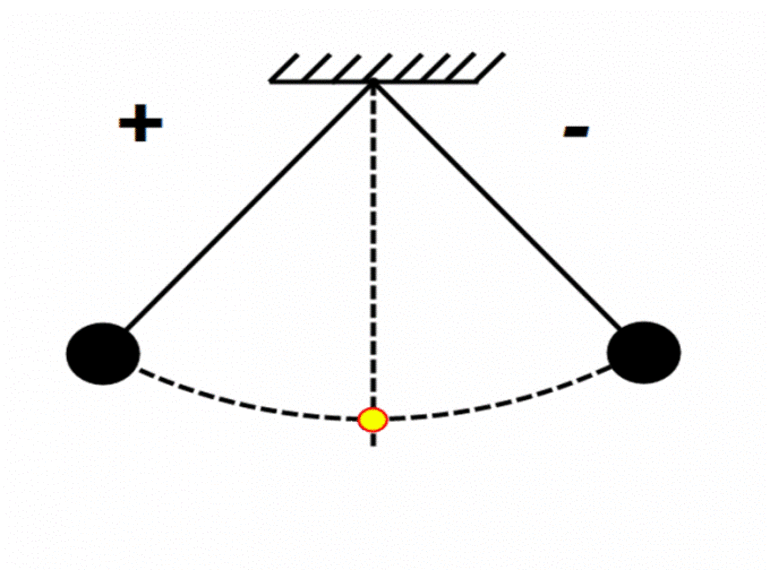
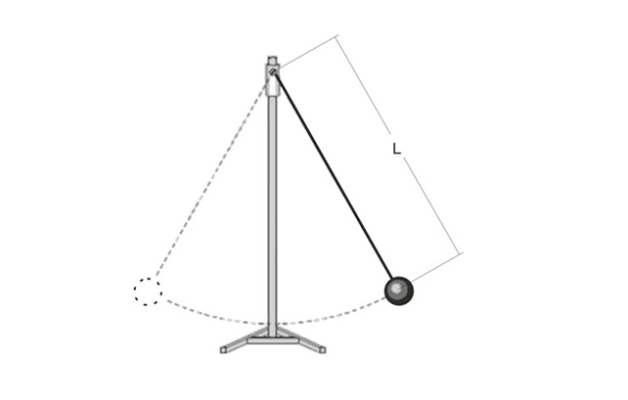
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Частота в физике, теория и онлайн калькуляторы
Частота
Определение частоты
Определение
Частотой называют физическую величину, характеризующую периодический процесс.
Она равна числу повторений или реализации событий за единицу времени. Обозначают частоту $nu ,$ могут встречаться другие варианты обозначений частоты, например $f$ или $F$.
Частота (наряду со временем) — это наиболее точно измеряемая величина.
Частота колебаний
Частота служит одним из основных параметров, характеризующих колебания.
Определение
Частота — это физическая величина обратная периоду колебаний (T). Частота — это число полных колебаний, которые совершаются за
единицу времени.
[nu =frac{1}{T}left(1right).]
В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:
[left[nu right]=с^{-1}=Гц.]
Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(2right).]
Другой характеристикой колебаний является циклическая частота, которая равна:
[{omega }_0=2pi nu left(3right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
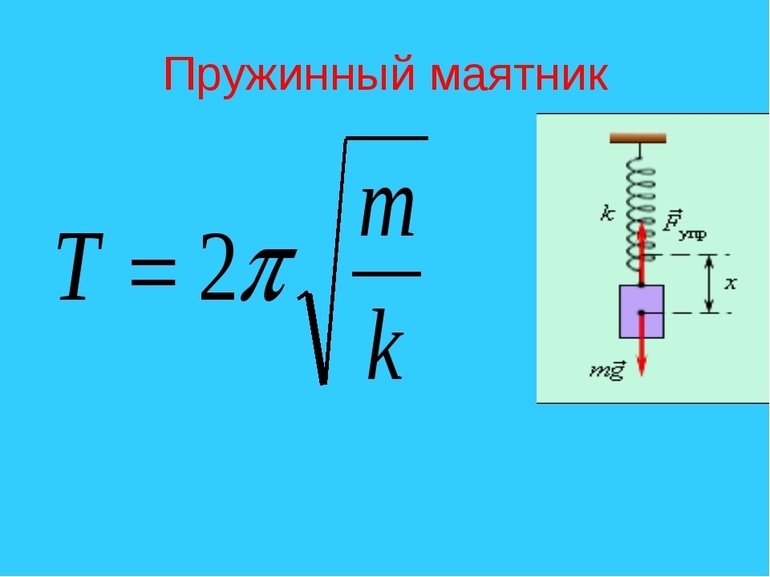
Частота колебаний тела, массой$ m,$ подвешенного на пружине с жесткостью $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(4right).]
Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.
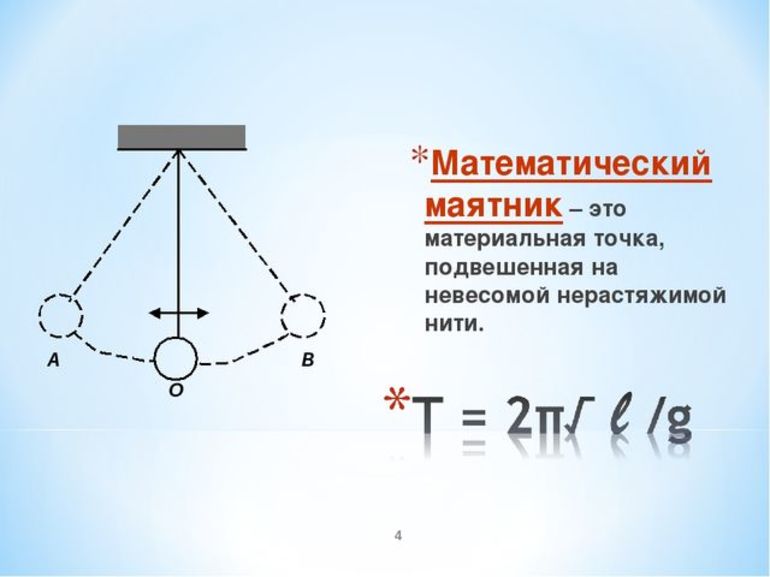
Частота колебаний математического маятника, длина нити которого $l$:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(5right),]
где $g$ — ускорение свободного падения.
Частота колебаний физического маятника:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(6right),]
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее результаты дают эти формулы.
Частота дискретных событий, частота вращения
Определение
Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(7right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(8right).]
Примеры задач с решением
Пример 1
Задание. Частица совершает гармонические колебания, которые описывает следующий закон: $x=6{sin left(frac{pi }{4}t+frac{pi }{3}right) }(м)$. Какова частота этих колебаний?
Решение. Рассмотрим уравнение движения частицы:
[x=6{sin left(frac{pi }{4}t+frac{pi }{3}right)left(1.1right). }]
Из этого уравнения мы видим, что амплитуда колебаний точки равна: $x_m=6 left(мright);;$ циклическая частота колебаний равна ${omega }_0=frac{pi }{4}(frac{рад}{с})$; начальная фаза колебаний: ${varphi }_0=frac{pi }{3}(рад)$. Частоту найдем, используя формулу:
[{omega }_0=2pi nu left(1.2right),]
из которой имеем:
[nu =frac{{omega }_0}{2pi }left(1.3right).]
Подставим значение циклической частоты, полученное из уравнения (1.1) в формулу (1.3), получаем:
[nu =frac{frac{pi }{4}}{2pi }=frac{1}{8} left(Гцright).]
Ответ. $nu =frac{1}{8}Гц$
Пример 2
Задание. К упругой пружине прикрепили маленький груз, при этом она растянулась на $Delta x$ (м). Какой будет частота колебаний грузика, если он будет совершать свободные колебания? Затуханием колебаний пренебречь.
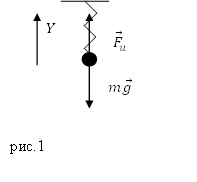
Решение. Сделаем рисунок.
В нашей задаче мы имеем колебания пружинного маятника, частоту которого можно найти как:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(2.1right).]
Рассмотрим состояние равновесия тела, которое прикреплено к пружине (рис.1). Запишем второй закон Ньютона для сил, действующих на это тело в состоянии равновесия:
[moverline{g}+{overline{F}}_u=0 left(2.2right).]
Запишем проекцию уравнения (2.2) на ось Y:
[F_u=mgleft(2.3right).]
Так как колебания груза на пружине малые, то выполняется закон Гука и мы можем считать, что:
[F_u=kDelta x left(2.4right).]
Из (2.3) и (2.4) найдем отношение ${m}/{k}:$
[mg=kDelta x to {m}/{k}={Delta x}/{g}left(2.5right).]
Подставим полученный в (2.5) результат в (1.1), частота колебаний тела на пружине равна:
[nu =frac{1}{2pi sqrt{{Delta x}/{g}}}.]
Ответ. $nu =frac{1}{2pi sqrt{{Delta x}/{g}}}$
Читать дальше: эффект Доплера.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
| Frequency | |
|---|---|

A pendulum making 25 complete oscillations in 60 s, a frequency of 0.416 Hz |
|
|
Common symbols |
f, ν |
| SI unit | hertz (Hz) |
|
Other units |
|
| In SI base units | s−1 |
|
Derivations from |
|
| Dimension |  |
Frequency is the number of occurrences of a repeating event per unit of time.[1] It is also occasionally referred to as temporal frequency for clarity, and is distinct from angular frequency. Frequency is measured in hertz (Hz) which is equal to one event per second. The period is the interval of time between events, so the period is the reciprocal of the frequency.[2]
For example, if a heart beats at a frequency of 120 times a minute (2 hertz), the period, T—the interval at which the beats repeat—is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light.
Definitions and units[edit]
A pendulum with a period of 2.8 s and a frequency of 0.36 Hz
For cyclical phenomena such as oscillations, waves, or for examples of simple harmonic motion, the term frequency is defined as the number of cycles or vibrations per unit of time. The conventional symbol for frequency is f; the Greek letter ν (nu) is also used.[3] The period T is the time taken to complete one cycle of an oscillation or rotation. The relation between the frequency and the period is given by the equation[4]
The term temporal frequency is used to emphasise that the frequency is characterised by the number of occurrences of a repeating event per unit time.
The SI unit of frequency is the hertz (Hz),[4] named after the German physicist Heinrich Hertz by the International Electrotechnical Commission in 1930. It was adopted by the CGPM (Conférence générale des poids et mesures) in 1960, officially replacing the previous name, cycle per second (cps). The SI unit for the period, as for all measurements of time, is the second.[5] A traditional unit of frequency used with rotating mechanical devices, where it is termed rotational frequency, is revolution per minute, abbreviated r/min or rpm.[6] 60 rpm is equivalent to one hertz.[7]
Period versus frequency[edit]
As a matter of convenience, longer and slower waves, such as ocean surface waves, are more typically described by wave period rather than frequency.[8] Short and fast waves, like audio and radio, are usually described by their frequency. Some commonly used conversions are listed below:
| Frequency | Period |
|---|---|
| 1 mHz (10−3 Hz) | 1 ks (103 s) |
| 1 Hz (100 Hz) | 1 s (100 s) |
| 1 kHz (103 Hz) | 1 ms (10−3 s) |
| 1 MHz (106 Hz) | 1 μs (10−6 s) |
| 1 GHz (109 Hz) | 1 ns (10−9 s) |
| 1 THz (1012 Hz) | 1 ps (10−12 s) |
[edit]
Diagram of the relationship between the different types of frequency and other wave properties.
- Angular frequency, usually denoted by the Greek letter ω (omega), is defined as the rate of change of angular displacement (during rotation), θ (theta), or the rate of change of the phase of a sinusoidal waveform (notably in oscillations and waves), or as the rate of change of the argument to the sine function:
The unit of angular frequency is the radian per second (rad/s) but, for discrete-time signals, can also be expressed as radians per sampling interval, which is a dimensionless quantity. Angular frequency is frequency multiplied by 2π.
- Spatial frequency, denoted here by ξ, is analogous to temporal frequency, but with a spatial measurement replacing time measurement,[note 1] e.g.:
In wave propagation [edit]
For periodic waves in nondispersive media (that is, media in which the wave speed is independent of frequency), frequency has an inverse relationship to the wavelength, λ (lambda). Even in dispersive media, the frequency f of a sinusoidal wave is equal to the phase velocity v of the wave divided by the wavelength λ of the wave:
In the special case of electromagnetic waves in vacuum, then v = c, where c is the speed of light in vacuum, and this expression becomes
When monochromatic waves travel from one medium to another, their frequency remains the same—only their wavelength and speed change.
Measurement[edit]
Measurement of frequency can be done in the following ways:
Counting[edit]
Calculating the frequency of a repeating event is accomplished by counting the number of times that event occurs within a specific time period, then dividing the count by the period. For example, if 71 events occur within 15 seconds the frequency is:
If the number of counts is not very large, it is more accurate to measure the time interval for a predetermined number of occurrences, rather than the number of occurrences within a specified time.[10] The latter method introduces a random error into the count of between zero and one count, so on average half a count. This is called gating error and causes an average error in the calculated frequency of 



A resonant-reed frequency meter, an obsolete device used from about 1900 to the 1940s for measuring the frequency of alternating current. It consists of a strip of metal with reeds of graduated lengths, vibrated by an electromagnet. When the unknown frequency is applied to the electromagnet, the reed which is resonant at that frequency will vibrate with large amplitude, visible next to the scale.
Stroboscope[edit]
An old method of measuring the frequency of rotating or vibrating objects is to use a stroboscope. This is an intense repetitively flashing light (strobe light) whose frequency can be adjusted with a calibrated timing circuit. The strobe light is pointed at the rotating object and the frequency adjusted up and down. When the frequency of the strobe equals the frequency of the rotating or vibrating object, the object completes one cycle of oscillation and returns to its original position between the flashes of light, so when illuminated by the strobe the object appears stationary. Then the frequency can be read from the calibrated readout on the stroboscope. A downside of this method is that an object rotating at an integer multiple of the strobing frequency will also appear stationary.
Frequency counter[edit]
Higher frequencies are usually measured with a frequency counter. This is an electronic instrument which measures the frequency of an applied repetitive electronic signal and displays the result in hertz on a digital display. It uses digital logic to count the number of cycles during a time interval established by a precision quartz time base. Cyclic processes that are not electrical, such as the rotation rate of a shaft, mechanical vibrations, or sound waves, can be converted to a repetitive electronic signal by transducers and the signal applied to a frequency counter. As of 2018, frequency counters can cover the range up to about 100 GHz. This represents the limit of direct counting methods; frequencies above this must be measured by indirect methods.
Heterodyne methods[edit]
Above the range of frequency counters, frequencies of electromagnetic signals are often measured indirectly utilizing heterodyning (frequency conversion). A reference signal of a known frequency near the unknown frequency is mixed with the unknown frequency in a nonlinear mixing device such as a diode. This creates a heterodyne or «beat» signal at the difference between the two frequencies. If the two signals are close together in frequency the heterodyne is low enough to be measured by a frequency counter. This process only measures the difference between the unknown frequency and the reference frequency. To reach higher frequencies, several stages of heterodyning can be used. Current research is extending this method to infrared and light frequencies (optical heterodyne detection).
Examples[edit]
Light[edit]
Visible light is an electromagnetic wave, consisting of oscillating electric and magnetic fields traveling through space. The frequency of the wave determines its color: 400 THz (4×1014 Hz) is red light, 800 THz (8×1014 Hz) is violet light, and between these (in the range 400–800 THz) are all the other colors of the visible spectrum. An electromagnetic wave with a frequency less than 4×1014 Hz will be invisible to the human eye; such waves are called infrared (IR) radiation. At even lower frequency, the wave is called a microwave, and at still lower frequencies it is called a radio wave. Likewise, an electromagnetic wave with a frequency higher than 8×1014 Hz will also be invisible to the human eye; such waves are called ultraviolet (UV) radiation. Even higher-frequency waves are called X-rays, and higher still are gamma rays.
All of these waves, from the lowest-frequency radio waves to the highest-frequency gamma rays, are fundamentally the same, and they are all called electromagnetic radiation. They all travel through vacuum at the same speed (the speed of light), giving them wavelengths inversely proportional to their frequencies.
where c is the speed of light (c in vacuum or less in other media), f is the frequency and λ is the wavelength.
In dispersive media, such as glass, the speed depends somewhat on frequency, so the wavelength is not quite inversely proportional to frequency.
Sound[edit]
The sound wave spectrum, with rough guide of some applications
Sound propagates as mechanical vibration waves of pressure and displacement, in air or other substances.[11] In general, frequency components of a sound determine its «color», its timbre. When speaking about the frequency (in singular) of a sound, it means the property that most determines its pitch.[12]
The frequencies an ear can hear are limited to a specific range of frequencies. The audible frequency range for humans is typically given as being between about 20 Hz and 20,000 Hz (20 kHz), though the high frequency limit usually reduces with age. Other species have different hearing ranges. For example, some dog breeds can perceive vibrations up to 60,000 Hz.[13]
In many media, such as air, the speed of sound is approximately independent of frequency, so the wavelength of the sound waves (distance between repetitions) is approximately inversely proportional to frequency.
Line current[edit]
In Europe, Africa, Australia, southern South America, most of Asia, and Russia, the frequency of the alternating current in household electrical outlets is 50 Hz (close to the tone G), whereas in North America and northern South America, the frequency of the alternating current in household electrical outlets is 60 Hz (between the tones B♭ and B; that is, a minor third above the European frequency). The frequency of the ‘hum’ in an audio recording can show where the recording was made, in countries using a European, or an American, grid frequency.
Aperiodic frequency[edit]
Aperiodic frequency is the rate of incidence or occurrence of non-cyclic phenomena, including random processes such as radioactive decay. It is expressed with the unit of reciprocal second (s−1)[14] or, in the case of radioactivity, becquerels.[15]
It is defined as a ratio, f = N/T, involving the number of times an event happened (N) during a given time duration (T); it is a physical quantity of type temporal rate.
See also[edit]
- Audio frequency
- Bandwidth (signal processing)
- Cutoff frequency
- Downsampling
- Electronic filter
- Fourier analysis
- Frequency band
- Frequency converter
- Frequency domain
- Frequency distribution
- Frequency extender
- Frequency grid
- Frequency modulation
- Frequency spectrum
- Interaction frequency
- Least-squares spectral analysis
- Natural frequency
- Negative frequency
- Periodicity (disambiguation)
- Pink noise
- Preselector
- Radar signal characteristics
- Signaling (telecommunications)
- Spread spectrum
- Spectral component
- Transverter
- Upsampling
- Orders of magnitude (frequency)
Notes[edit]
- ^ The term spatial period, sometimes used in place of wavelength, analogously corresponds to the (temporal) period.[9]
References[edit]
- ^ «Definition of FREQUENCY». Retrieved 3 October 2016.
- ^ «Definition of PERIOD». Retrieved 3 October 2016.
- ^ Serway & Faughn 1989, p. 346.
- ^ a b Serway & Faughn 1989, p. 354.
- ^ «Resolution 12 of the 11th CGPM (1960)». BIPM (International Bureau of Weights and Measures). Archived from the original on 8 April 2020. Retrieved 21 January 2021.
- ^ «Special Publication 811: NIST Guide to the SI, Chapter 8». Nist. 28 January 2016. Retrieved 2022-11-08.
- ^ Davies 1997, p. 275.
- ^ Young 1999, p. 7.
- ^ Boreman, Glenn D. «Spatial Frequency». SPIE. Retrieved 22 January 2021.
- ^ Bakshi, K.A.; A.V. Bakshi; U.A. Bakshi (2008). Electronic Measurement Systems. US: Technical Publications. pp. 4–14. ISBN 978-81-8431-206-5.
- ^ «Definition of SOUND». Retrieved 3 October 2016.
- ^ Pilhofer, Michael (2007). Music Theory for Dummies. For Dummies. p. 97. ISBN 978-0-470-16794-6.
- ^ Condon, Tim (2003). Elert, Glenn (ed.). «Frequency range of dog hearing». The Physics Factbook. Retrieved 2008-10-22.
- ^ Lombardi, Michael A. (2007). «Fundamentals of Time and Frequency». In Bishop, Robert H. (ed.). Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling. Austin: CRC Press. ISBN 9781420009002.
- ^ Bureau international des poids et mesures, Le Système international d’unités (SI) / The International System of Units (SI), 9th ed.[permanent dead link] (Sèvres: 2019), ISBN 978‑92‑822‑2272‑0, sub§2.3.4, Table 4.
Sources[edit]
- Davies, A. (1997). Handbook of Condition Monitoring: Techniques and Methodology. New York: Springer. ISBN 978-0-412-61320-3.
- Serway, Raymond A.; Faughn, Jerry S. (1989). College Physics. London: Thomson/Brooks-Cole. ISBN 978-05344-0-814-5.
- Young, Ian R. (1999). Wind Generated Ocean Waves. Elsevere Ocean Engineering. Vol. 2. Oxford: Elsevier. ISBN 978-0-08-043317-2.
Further reading[edit]
- Giancoli, D.C. (1988). Physics for Scientists and Engineers (2nd ed.). Prentice Hall. ISBN 978-0-13-669201-0.
External links[edit]
- Keyboard frequencies = naming of notes – The English and American system versus the German system
- A frequency generator with sound, useful for hearing tests
| Frequency | |
|---|---|

A pendulum making 25 complete oscillations in 60 s, a frequency of 0.416 Hz |
|
|
Common symbols |
f, ν |
| SI unit | hertz (Hz) |
|
Other units |
|
| In SI base units | s−1 |
|
Derivations from |
|
| Dimension |  |
Frequency is the number of occurrences of a repeating event per unit of time.[1] It is also occasionally referred to as temporal frequency for clarity, and is distinct from angular frequency. Frequency is measured in hertz (Hz) which is equal to one event per second. The period is the interval of time between events, so the period is the reciprocal of the frequency.[2]
For example, if a heart beats at a frequency of 120 times a minute (2 hertz), the period, T—the interval at which the beats repeat—is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light.
Definitions and units[edit]
A pendulum with a period of 2.8 s and a frequency of 0.36 Hz
For cyclical phenomena such as oscillations, waves, or for examples of simple harmonic motion, the term frequency is defined as the number of cycles or vibrations per unit of time. The conventional symbol for frequency is f; the Greek letter ν (nu) is also used.[3] The period T is the time taken to complete one cycle of an oscillation or rotation. The relation between the frequency and the period is given by the equation[4]
The term temporal frequency is used to emphasise that the frequency is characterised by the number of occurrences of a repeating event per unit time.
The SI unit of frequency is the hertz (Hz),[4] named after the German physicist Heinrich Hertz by the International Electrotechnical Commission in 1930. It was adopted by the CGPM (Conférence générale des poids et mesures) in 1960, officially replacing the previous name, cycle per second (cps). The SI unit for the period, as for all measurements of time, is the second.[5] A traditional unit of frequency used with rotating mechanical devices, where it is termed rotational frequency, is revolution per minute, abbreviated r/min or rpm.[6] 60 rpm is equivalent to one hertz.[7]
Period versus frequency[edit]
As a matter of convenience, longer and slower waves, such as ocean surface waves, are more typically described by wave period rather than frequency.[8] Short and fast waves, like audio and radio, are usually described by their frequency. Some commonly used conversions are listed below:
| Frequency | Period |
|---|---|
| 1 mHz (10−3 Hz) | 1 ks (103 s) |
| 1 Hz (100 Hz) | 1 s (100 s) |
| 1 kHz (103 Hz) | 1 ms (10−3 s) |
| 1 MHz (106 Hz) | 1 μs (10−6 s) |
| 1 GHz (109 Hz) | 1 ns (10−9 s) |
| 1 THz (1012 Hz) | 1 ps (10−12 s) |
[edit]
Diagram of the relationship between the different types of frequency and other wave properties.
- Angular frequency, usually denoted by the Greek letter ω (omega), is defined as the rate of change of angular displacement (during rotation), θ (theta), or the rate of change of the phase of a sinusoidal waveform (notably in oscillations and waves), or as the rate of change of the argument to the sine function:
The unit of angular frequency is the radian per second (rad/s) but, for discrete-time signals, can also be expressed as radians per sampling interval, which is a dimensionless quantity. Angular frequency is frequency multiplied by 2π.
- Spatial frequency, denoted here by ξ, is analogous to temporal frequency, but with a spatial measurement replacing time measurement,[note 1] e.g.:
In wave propagation [edit]
For periodic waves in nondispersive media (that is, media in which the wave speed is independent of frequency), frequency has an inverse relationship to the wavelength, λ (lambda). Even in dispersive media, the frequency f of a sinusoidal wave is equal to the phase velocity v of the wave divided by the wavelength λ of the wave:
In the special case of electromagnetic waves in vacuum, then v = c, where c is the speed of light in vacuum, and this expression becomes
When monochromatic waves travel from one medium to another, their frequency remains the same—only their wavelength and speed change.
Measurement[edit]
Measurement of frequency can be done in the following ways:
Counting[edit]
Calculating the frequency of a repeating event is accomplished by counting the number of times that event occurs within a specific time period, then dividing the count by the period. For example, if 71 events occur within 15 seconds the frequency is:
If the number of counts is not very large, it is more accurate to measure the time interval for a predetermined number of occurrences, rather than the number of occurrences within a specified time.[10] The latter method introduces a random error into the count of between zero and one count, so on average half a count. This is called gating error and causes an average error in the calculated frequency of 



A resonant-reed frequency meter, an obsolete device used from about 1900 to the 1940s for measuring the frequency of alternating current. It consists of a strip of metal with reeds of graduated lengths, vibrated by an electromagnet. When the unknown frequency is applied to the electromagnet, the reed which is resonant at that frequency will vibrate with large amplitude, visible next to the scale.
Stroboscope[edit]
An old method of measuring the frequency of rotating or vibrating objects is to use a stroboscope. This is an intense repetitively flashing light (strobe light) whose frequency can be adjusted with a calibrated timing circuit. The strobe light is pointed at the rotating object and the frequency adjusted up and down. When the frequency of the strobe equals the frequency of the rotating or vibrating object, the object completes one cycle of oscillation and returns to its original position between the flashes of light, so when illuminated by the strobe the object appears stationary. Then the frequency can be read from the calibrated readout on the stroboscope. A downside of this method is that an object rotating at an integer multiple of the strobing frequency will also appear stationary.
Frequency counter[edit]
Higher frequencies are usually measured with a frequency counter. This is an electronic instrument which measures the frequency of an applied repetitive electronic signal and displays the result in hertz on a digital display. It uses digital logic to count the number of cycles during a time interval established by a precision quartz time base. Cyclic processes that are not electrical, such as the rotation rate of a shaft, mechanical vibrations, or sound waves, can be converted to a repetitive electronic signal by transducers and the signal applied to a frequency counter. As of 2018, frequency counters can cover the range up to about 100 GHz. This represents the limit of direct counting methods; frequencies above this must be measured by indirect methods.
Heterodyne methods[edit]
Above the range of frequency counters, frequencies of electromagnetic signals are often measured indirectly utilizing heterodyning (frequency conversion). A reference signal of a known frequency near the unknown frequency is mixed with the unknown frequency in a nonlinear mixing device such as a diode. This creates a heterodyne or «beat» signal at the difference between the two frequencies. If the two signals are close together in frequency the heterodyne is low enough to be measured by a frequency counter. This process only measures the difference between the unknown frequency and the reference frequency. To reach higher frequencies, several stages of heterodyning can be used. Current research is extending this method to infrared and light frequencies (optical heterodyne detection).
Examples[edit]
Light[edit]
Visible light is an electromagnetic wave, consisting of oscillating electric and magnetic fields traveling through space. The frequency of the wave determines its color: 400 THz (4×1014 Hz) is red light, 800 THz (8×1014 Hz) is violet light, and between these (in the range 400–800 THz) are all the other colors of the visible spectrum. An electromagnetic wave with a frequency less than 4×1014 Hz will be invisible to the human eye; such waves are called infrared (IR) radiation. At even lower frequency, the wave is called a microwave, and at still lower frequencies it is called a radio wave. Likewise, an electromagnetic wave with a frequency higher than 8×1014 Hz will also be invisible to the human eye; such waves are called ultraviolet (UV) radiation. Even higher-frequency waves are called X-rays, and higher still are gamma rays.
All of these waves, from the lowest-frequency radio waves to the highest-frequency gamma rays, are fundamentally the same, and they are all called electromagnetic radiation. They all travel through vacuum at the same speed (the speed of light), giving them wavelengths inversely proportional to their frequencies.
where c is the speed of light (c in vacuum or less in other media), f is the frequency and λ is the wavelength.
In dispersive media, such as glass, the speed depends somewhat on frequency, so the wavelength is not quite inversely proportional to frequency.
Sound[edit]
The sound wave spectrum, with rough guide of some applications
Sound propagates as mechanical vibration waves of pressure and displacement, in air or other substances.[11] In general, frequency components of a sound determine its «color», its timbre. When speaking about the frequency (in singular) of a sound, it means the property that most determines its pitch.[12]
The frequencies an ear can hear are limited to a specific range of frequencies. The audible frequency range for humans is typically given as being between about 20 Hz and 20,000 Hz (20 kHz), though the high frequency limit usually reduces with age. Other species have different hearing ranges. For example, some dog breeds can perceive vibrations up to 60,000 Hz.[13]
In many media, such as air, the speed of sound is approximately independent of frequency, so the wavelength of the sound waves (distance between repetitions) is approximately inversely proportional to frequency.
Line current[edit]
In Europe, Africa, Australia, southern South America, most of Asia, and Russia, the frequency of the alternating current in household electrical outlets is 50 Hz (close to the tone G), whereas in North America and northern South America, the frequency of the alternating current in household electrical outlets is 60 Hz (between the tones B♭ and B; that is, a minor third above the European frequency). The frequency of the ‘hum’ in an audio recording can show where the recording was made, in countries using a European, or an American, grid frequency.
Aperiodic frequency[edit]
Aperiodic frequency is the rate of incidence or occurrence of non-cyclic phenomena, including random processes such as radioactive decay. It is expressed with the unit of reciprocal second (s−1)[14] or, in the case of radioactivity, becquerels.[15]
It is defined as a ratio, f = N/T, involving the number of times an event happened (N) during a given time duration (T); it is a physical quantity of type temporal rate.
See also[edit]
- Audio frequency
- Bandwidth (signal processing)
- Cutoff frequency
- Downsampling
- Electronic filter
- Fourier analysis
- Frequency band
- Frequency converter
- Frequency domain
- Frequency distribution
- Frequency extender
- Frequency grid
- Frequency modulation
- Frequency spectrum
- Interaction frequency
- Least-squares spectral analysis
- Natural frequency
- Negative frequency
- Periodicity (disambiguation)
- Pink noise
- Preselector
- Radar signal characteristics
- Signaling (telecommunications)
- Spread spectrum
- Spectral component
- Transverter
- Upsampling
- Orders of magnitude (frequency)
Notes[edit]
- ^ The term spatial period, sometimes used in place of wavelength, analogously corresponds to the (temporal) period.[9]
References[edit]
- ^ «Definition of FREQUENCY». Retrieved 3 October 2016.
- ^ «Definition of PERIOD». Retrieved 3 October 2016.
- ^ Serway & Faughn 1989, p. 346.
- ^ a b Serway & Faughn 1989, p. 354.
- ^ «Resolution 12 of the 11th CGPM (1960)». BIPM (International Bureau of Weights and Measures). Archived from the original on 8 April 2020. Retrieved 21 January 2021.
- ^ «Special Publication 811: NIST Guide to the SI, Chapter 8». Nist. 28 January 2016. Retrieved 2022-11-08.
- ^ Davies 1997, p. 275.
- ^ Young 1999, p. 7.
- ^ Boreman, Glenn D. «Spatial Frequency». SPIE. Retrieved 22 January 2021.
- ^ Bakshi, K.A.; A.V. Bakshi; U.A. Bakshi (2008). Electronic Measurement Systems. US: Technical Publications. pp. 4–14. ISBN 978-81-8431-206-5.
- ^ «Definition of SOUND». Retrieved 3 October 2016.
- ^ Pilhofer, Michael (2007). Music Theory for Dummies. For Dummies. p. 97. ISBN 978-0-470-16794-6.
- ^ Condon, Tim (2003). Elert, Glenn (ed.). «Frequency range of dog hearing». The Physics Factbook. Retrieved 2008-10-22.
- ^ Lombardi, Michael A. (2007). «Fundamentals of Time and Frequency». In Bishop, Robert H. (ed.). Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling. Austin: CRC Press. ISBN 9781420009002.
- ^ Bureau international des poids et mesures, Le Système international d’unités (SI) / The International System of Units (SI), 9th ed.[permanent dead link] (Sèvres: 2019), ISBN 978‑92‑822‑2272‑0, sub§2.3.4, Table 4.
Sources[edit]
- Davies, A. (1997). Handbook of Condition Monitoring: Techniques and Methodology. New York: Springer. ISBN 978-0-412-61320-3.
- Serway, Raymond A.; Faughn, Jerry S. (1989). College Physics. London: Thomson/Brooks-Cole. ISBN 978-05344-0-814-5.
- Young, Ian R. (1999). Wind Generated Ocean Waves. Elsevere Ocean Engineering. Vol. 2. Oxford: Elsevier. ISBN 978-0-08-043317-2.
Further reading[edit]
- Giancoli, D.C. (1988). Physics for Scientists and Engineers (2nd ed.). Prentice Hall. ISBN 978-0-13-669201-0.
External links[edit]
- Keyboard frequencies = naming of notes – The English and American system versus the German system
- A frequency generator with sound, useful for hearing tests
Примеры движения
Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.
В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:
- тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
- груза на нитке;
- электрического контура и других.
Амплитуда, период и частота
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:
- Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
- Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
- Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
- Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.
Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.
Математический маятник
Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.
Также нить должна быть невесомой и нерастяжимой.
Груз в этом случае считается материальной точкой.
При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:
α=x/l.
На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.
Период: T=2π /ω T=2π*sqrt (g/l)
Это формула Галилея, которая описывает движение математического маятника.
Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.
Пружинный маятник
Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.
Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:
F=-kx.
Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.
По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.
После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.
Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.
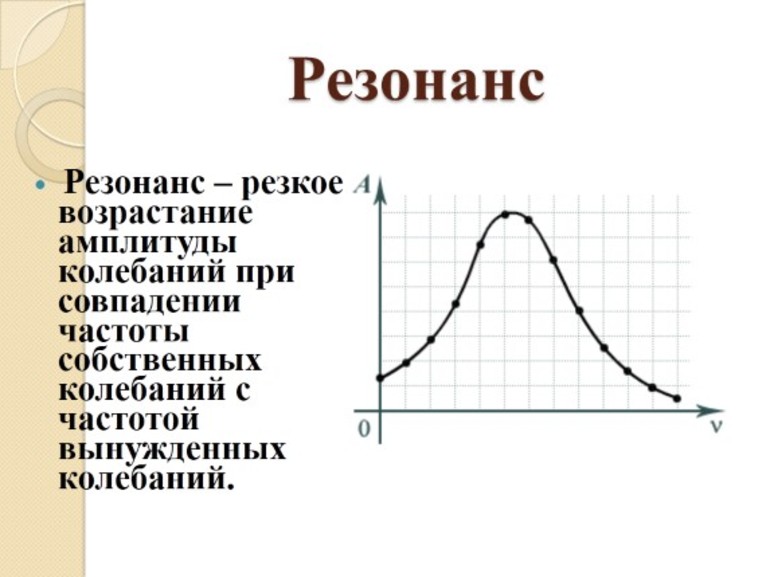
Явление резонанса
Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.
Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.
В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.
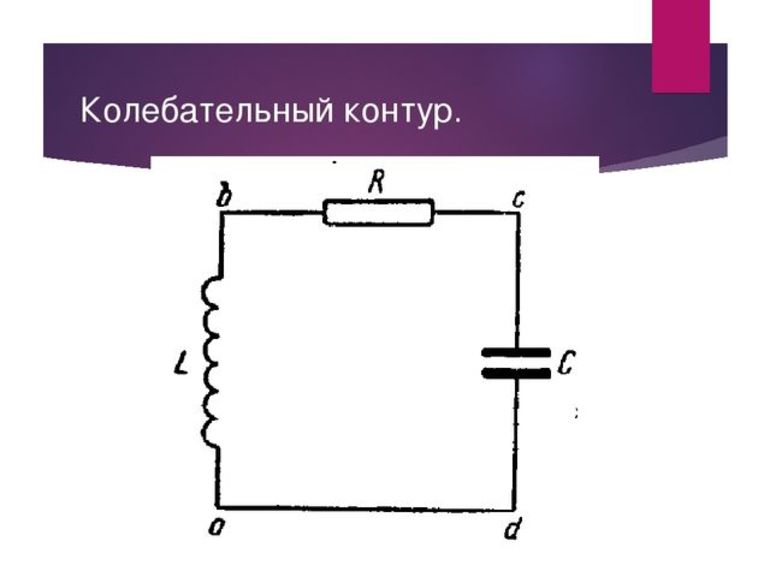
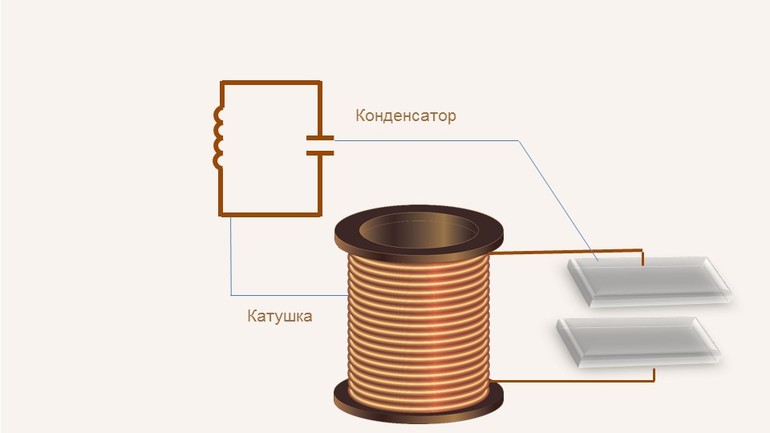
Колебательный контур
Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.
В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.
Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.
Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.
Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.
Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.
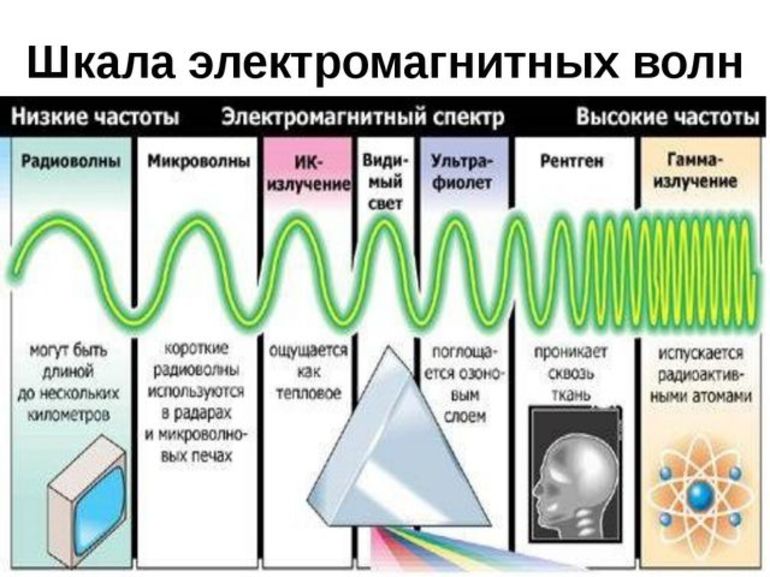
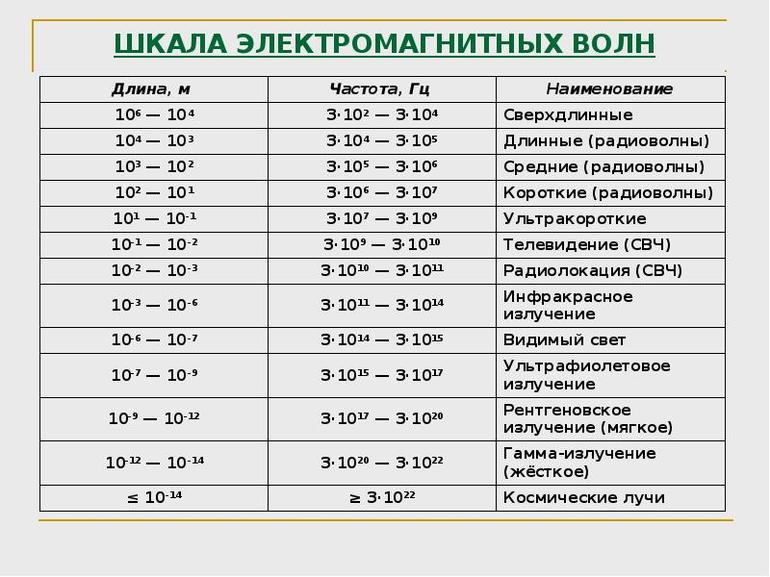
Звук и электромагнитные волны
Понятие частоты вводится и для звуковых и электромагнитных волн. Первые представляют собой колебания плотности среды. Вторые — изменение со временем напряженности магнитного и электрического полей.
От частоты звука зависит его тональность. Этим свойством пользуются для стандартизации описания музыки и создания музыкальных инструментов — каждой ноте соответствует своя частота.
До 16 Гц человеческое ухо не воспринимает, так же как и выше 20 КГЦ. Более высокие частоты используются в эхолокации, ультразвуковой диагностике.
Частота электромагнитных волн также определяет их способность взаимодействовать с человеческим организмом. Рентгеновское излучение проходит насквозь, при этом взаимодействуя с молекулами, вызывая их ионизацию. Ультразвук провоцирует процессы загара, фотосинтеза. Радиоволновое излучение практически не оказывает прямого воздействия, но хорошо подходит для передачи информации. В видимом диапазоне частота определяет цвет.
Есть также такая характеристика, как частота колебаний молекул. Она зависит от температуры тела и определяет его агрегатное состояние.
Таким образом, частота колебаний описывает большое количество процессов и оказывает воздействие на их характеристики.
Частота колебаний

4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
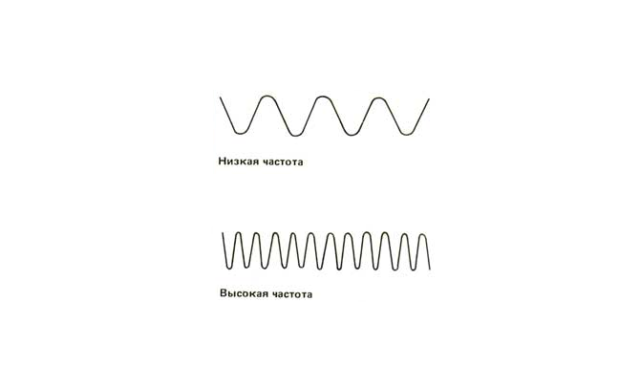
Частота колебаний – это один из параметров, описывающих колебательные процессы в природе. Многие явления зависят от частоты, и происходят по-разному при ее изменении. Рассмотрим это понятие подробнее.
Колебания в природе
Колебания различных величин очень широко распространены в природе. Явление колебаний заключается в том, что измеряемый параметр меняет свое значение вокруг некоторого среднего.
Колебания могут быть периодическими (маятник), а могут быть непериодическими (флаг на ветру). Поскольку любое непериодическое колебание может быть представлено в виде бесконечной суммы периодических, то в первую очередь изучаются периодические колебания. График таких колебаний представляет собой синусоиду, которая хорошо изучена в математике.
Маятник
Для рассмотрения базовых понятий колебательных процессов в качестве примера удобно взять маятник – подвешенную на тонкой легкой нити небольшую массу. Если ее качнуть, она начнет совершать равномерные движения.
Каждое движение маятника, начинающееся от крайней точки, и заканчивающееся в ней же, называется колебанием.
Частота колебаний
Если взять несколько маятников разной длины, можно убедиться, что они будут совершать колебания «с разной скоростью» (хотя линейная скорость груза при этом может быть одинаковой). То есть «скорость колебаний» и скорость движения груза маятника – это не одно и то же.
Для характеристики «скорости колебаний» используют специальное понятие – частоту колебаний.
Число колебаний, которое совершается за единицу времени, называется частотой колебаний. Для обозначения используется греческая буква $nu$ («ню»).
Единица частоты колебаний в системе СИ – Герц (Гц). Один Герц – это число колебаний, происходящих в одну секунду.
Для измерения частоты колебаний подсчитывают число колебаний за некоторый отрезок времени, и делят его на длительность отрезка:
$$nu={Nover t},$$
где:
- N – число колебаний;
- t – время, за которое эти колебания были совершены (сек).
В данной формуле величина колебаний не имеет значения, важно только число этих колебаний.
Величины частот колебаний, непосредственно воспринимаемые человеком, лежат в пределах от значений порядка $10^{-9}$ Гц (частота обращения планет вокруг Солнца) до 20 кГц (самый высокий звук). В хозяйстве и технике встречаются частоты до $10^{25}$ Гц (жесткое гамма-излучение).
Что мы узнали?
Колебание – это изменение измеряемой величины от начальной точки до точки максимального отклонения и дальнейшее возвращение в исходную точку. Число колебаний, происходящих в единицу времени, называется частотой колебаний.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Егор Князев
4/5
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
А какая ваша оценка?
ЧАСТОТА КОЛЕБАНИЙ
- ЧАСТОТА КОЛЕБАНИЙ
-
- ЧАСТОТА КОЛЕБАНИЙ
-
величина, обратная периоду колебаний T(f=1/Т), т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени. Обычно Ч. к. измеряется в герцах: 1 Гц соответствует одному колебанию в секунду. Часто используется также величина w=2pf, наз. циклической или круговой частотой. В случае гармонич. волновых процессов
u(x, t)=Acos(wt± kx),
где А — амплитуда колебаний, t — время, х — координата. Круговая Ч. к. связана с волновым числом k и фазовой скоростью v соотношением w=kv.
Физический энциклопедический словарь. — М.: Советская энциклопедия.
.
1983.
.
Смотреть что такое «ЧАСТОТА КОЛЕБАНИЙ» в других словарях:
-
частота колебаний — число колебаний в 1 с. Обозначается f или ν. Если Т период колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ω = 2πf = 2π/T рад/с. * * * ЧАСТОТА КОЛЕБАНИЙ ЧАСТОТА КОЛЕБАНИЙ, число колебаний в 1 с. Обозначается f или n.… … Энциклопедический словарь
-
частота колебаний — (f[v]) Величина, обратная периоду колебаний. [ГОСТ 7601 78] частота колебаний Число колебаний в единицу времени [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] частота колебаний частота Количество периодов… … Справочник технического переводчика
-
ЧАСТОТА КОЛЕБАНИЙ — число колебаний в 1 с. Обозначается f или ?. Если T период от колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ??= 2?f = 2?/T рад/с … Большой Энциклопедический словарь
-
Частота колебаний — 14. Частота колебаний v Средняя частота спектра лазерного излучения в пределах интервала частот линии спонтанного излучения Источник: ГОСТ 24453 80: Измерения пара … Словарь-справочник терминов нормативно-технической документации
-
частота колебаний — svyravimų dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillation, f … Automatikos terminų žodynas
-
частота колебаний — virpesių dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillations, f … Automatikos terminų žodynas
-
частота колебаний — svyravimų dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Svyruojamojo judesio dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f ryšiai:… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
-
частота колебаний — virpesių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikros sistemos virpėjimo dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
-
частота колебаний — virpesių dažnis statusas T sritis chemija apibrėžtis Virpesių skaičius per 1 sekundę. atitikmenys: angl. oscillation frequency rus. частота колебаний … Chemijos terminų aiškinamasis žodynas
-
частота колебаний — svyravimų dažnis statusas T sritis fizika atitikmenys: angl. oscillation frequency vok. Schwingfrequenz, f; Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f … Fizikos terminų žodynas