Какое на свете самое больше число, которое что–то означает? В этой статье я попытаюсь рассказать о цифровом монстре, называемом число Грэма,

Пишет sly2m.livejournal.com
Если долго всматриваться в бездну, можно неплохо провести время.
Инженер Механических Душ
Число Грэма на пальцах™
Как только ребенок (а это происходит где то года в три-четыре) понимает, что все числа делятся на три группы «один, два и много», он тут же пытается выяснить: насколько много бывает много, чем много отличается от очень много, и может ли оказаться так много, что больше не бывает. Наверняка вы играли с родителями в интересную (для того возраста) игру, кто назовет самое большее число, и если предок был не глупее пятиклассника, то он всегда выигрывал, на каждый «миллион» отвечая «два миллиона», а на «миллиард» — «два миллиарда» или «миллиард плюс один».
Уже к первому классу школы каждый знает — чисел бесконечное множество, они никогда не заканчиваются и самого большого числа не бывает. К любому миллиону триллионов миллиардов всегда можно сказать «плюс один» и остаться в выигрыше. А чуточку позже приходит (должно прийти!) понимание, что длинные строки цифр сами по себе ничего не значат. Все эти триллионы миллиардов только тогда имеют смысл, когда служат представлением какого — то количества предметов или же описывают некое явление. Выдумать длиннющее число, которое ничего из себя не представляет, кроме набора долго звучащих цифр, нет никакого труда, их итак бесконечное количество. Наука, в какой — то образной мере, занимается тем, что выискивает в этой необозримой бездне совершенно конкретные комбинации цифр, присовокупляя к некому физическому явлению, например скорости света, числу Авогадро или постоянной Планка.
И сразу же возникает вопрос, а какое на свете самое больше число, которое что–то означает? В этой статье я попытаюсь рассказать о цифровом монстре, называемом число Грэма, хотя строго говоря, науке известны числа и побольше. Число Грэма самое распиаренное, можно сказать «на слуху» у широкой публики, потому что оно довольно просто в объяснении и все же достаточно велико, чтобы вскружить голову. Вообще, тут необходимо объявить небольшой disclaimer (рус. предостережение). Пусть прозвучит как шутка, но я нифига не шучу. Говорю вполне серьезно — дотошное ковыряние в подобных математических глубинах в совокупности с безудержным расширением границ восприятия может оказать (и окажет) серьезное влияние на мироощущение, на позиционирование личности в обществе, и, в конечном итоге, на общее психологическое состояние ковыряющего, или, будем называть вещи своими именами — открывает дорогу к шизе. Не нужно чересчур внимательно вчитываться в нижеследующий текст, не стоит слишком ярко и живо представлять описываемые в нем вещи. И не говорите потом, что вас не предупреждали!
Пальцы:
Прежде чем переходить к числам–монстрам, потренируемся для начала на кошках. Напомню, что для описания больших чисел (не монстров, а просто больших чисел) удобно пользоваться научным или т.н. экспоненциальным способом записи.
Когда говорят, скажем, о количестве звезд во Вселенной (в Обозримой Вселенной), никакой идиот не лезет вычислять сколько их там в буквальном смысле с точностью до последней звезды. Считается, что примерно 10²¹ штук. И это оценка снизу. Значит общее количество звезд можно выразить числом, у которого после единицы стоит 21 ноль, т.е. «1 000 000 000 000 000 000 000».
Так выглядит небольшая часть из них (около 100 000) в шаровом скоплении Омега Центавра.

Естественно, когда речь идет о подобных масштабах, действительные цифры в числе существенного значения не играют, все ведь весьма условно и примерно. Может быть на самом деле число звезд во Вселенной «1 564 861 615 140 168 357 973», а может «9 384 684 643 798 468 483 745». А то и «3 333 333 333 333 333 333 333», почему нет, хотя маловероятно, конечно. В космологии, науке о свойствах Вселенной в целом, такими мелочами не морочатся. Главное представлять, что примерно это число состоит из 22 цифр, от чего удобней считать его единицей с 21 нулем, и записывать как 10²¹. Правило общее и весьма простое. Какая цифра или число стоят на месте степени (напечатаны мелким шрифтом сверху над 10), столько нолей после единицы будет в этом числе, если расписать его по–простецки, знаками подряд, а не по–научному. У некоторых чисел существуют «человеческие названия», например 10³ мы называем «тысяча», 10⁶ — «миллион», а 10⁹ — «миллиард», а у некоторых нет. Скажем у 10⁵⁹ нет общепринятого названия. А у 10²¹, кстати, есть — это «секстиллион».
Все, что идет до миллиона, практически любому человеку понятно интуитивно, ведь кто не хочет стать миллионером? Дальше у некоторых начинаются проблемы. Хотя миллиард (10⁹) тоже знают почти все. До миллиарда даже можно досчитать. Если только родившись, буквально в момент появления на свет начать считать раз в секунду «один, два, три, четыре…» и не спать, не пить, не есть, а только считать–считать–считать без устали днем и ночью, то когда стукнет 32 года можно досчитать до миллиарда, потому что 32 оборота Земли вокруг Солнца занимают примерно миллиард секунд.
7 миллиардов — количество людей на планете. Исходя из вышеизложенного, посчитать их всех по порядку в течение человеческой жизни совершенно невозможно, придется прожить больше двухсот лет.
100 миллиардов (10¹¹) — столько или около того людей жило на планете за всю ее историю. 100 миллиардов гамбургеров продал Макдональдс к 1998 году за 50 лет своего существования. 100 миллиардов звезд (ну, чуть больше) находится в нашей галактике Млечный Путь, и Солнце — одна из них. Такое же количество галактик содержится в обозримой Вселенной. 100 миллиардов нейронов находится в головном мозге человека. И столько же анаэробных бактерий проживают у каждого читающего эти строки в слепой кишке.
Триллион (10¹²) — число, которым редко пользуются. До триллиона досчитать невозможно, на это уйдет 32 тысячи лет. Триллион секунд назад люди жили в пещерах и охотились с копьями на мамонтов. Да, триллион секунд назад на Земле жили мамонты. В океанах планеты примерно триллион рыб. В соседней с нами галактике Андромеды около триллиона звезд. Человек состоит из 10 триллионов клеток. ВВП России в 2013м году составил 66 триллионов рублей (в рублях 2013го года). От Земли до Сатурна 100 триллионов сантиметров и столько же букв в целом было отпечатано во всех когда–либо опубликованных книгах.
Квадриллион (10¹⁵, миллион миллиардов) — столько всего муравьев на планете. Это слово нормальные люди вслух не произносят, ну, признайтесь, когда вы последний раз в разговоре слышали «квадриллион чего–то»?
Квинтиллион (10¹⁸, миллиард миллиардов) — столько существует возможных конфигураций при сборке кубика Рубика 3х3х3. Так же количество кубометров воды в мировом океане.
Секстиллион (10²¹) — это число нам уже встречалось. Количество звезд в Обозримой Вселенной. Количество песчинок всех пустынь Земли. Количество транзисторов во всех существующих электронных устройствах человечества, если Intel нам не врал.
10 секстиллионов (10²²) — количество молекул в грамме воды.
10²⁴ — масса Земли в килограммах.
10²⁶ — диаметр Обозримой Вселенной в метрах, но в метрах считать не очень удобно, общепринятые границы Обозримой Вселенной 93 миллиарда световых лет.
Размерами, большими чем Обозримая Вселенная, наука не оперирует. Мы знаем наверняка, что Обозримая Вселенная это не вся–вся–вся Вселенная. Это та часть, что мы, хотя бы теоретически, можем видеть и наблюдать. Или могли видеть в прошлом. Или сможем увидеть когда–нибудь в отдаленном будущем, оставаясь в рамках современной науки. От остальных частей Вселенной даже со скоростью света сигналы не смогут до нас добраться, от чего этих мест с нашей точки зрения как бы не существует. Насколько велика та большая Вселенная на самом деле никто не знает. Может быть в миллион раз больше, чем Обозримая. А может в миллиард. А может и вообще бесконечная. Говорю же, это уже не наука, а гадание на кофейной гуще. У ученых есть кое–какие догадки, но это больше фантазии, чем реальность.
Для визуализации космических масштабов полезно изучить эту картинку, раскрыв ее на весь экран.
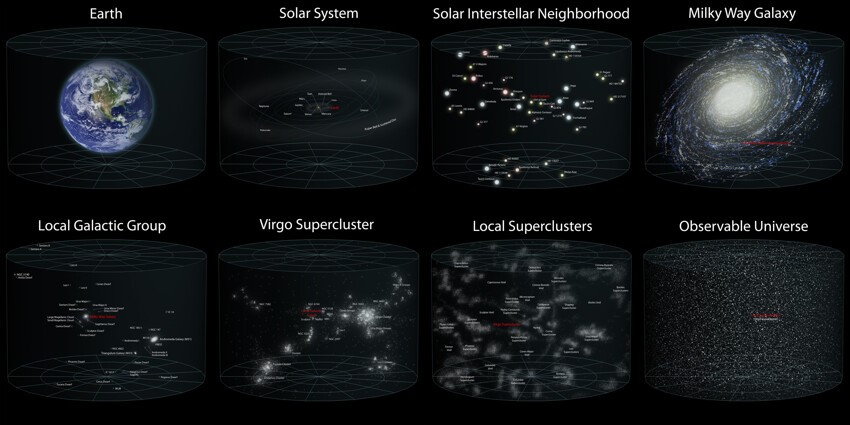
Источник:
Однако даже в Обозримую Вселенную можно напихать гораздо больше чего–то другого, чем метры.
10⁵¹ атомов составляют планету Земля.
10⁸⁰ примерное количество элементарных частиц в Обозримой Вселенной.
10⁹⁰ примерное количество фотонов в Обозримой Вселенной. Их почти в 10 миллиардов раз больше, чем элементарных частиц, электронов и протонов.
10¹⁰⁰ — гугол. Это число ничего физически не значит, просто круглое и красивое. Компания, которая поставила себе целью индексировать гугол ссылок (шутка, конечно, это же больше, чем число элементарных частиц во Вселенной!) в 1998 году взяла себе название Google.
10¹²² протонов понадобится, чтобы набить Обозримую Вселенную под завязку, плотненько так, протончик к протончику, впритык.
10¹⁸⁵ планковских объемов занимает Обозримая Вселенная. Меньших величин, чем планковский объем (кубик размеров планковской длины 10⁻³⁵ метра) наша наука не знает. Наверняка, как и со Вселенной, там есть что–то еще более мелкое, но вменяемых формул для подобных мелочей ученые еще не придумали, одни сплошные спекуляции.
Получается, что 10¹⁸⁵ или около того — наибольшее число, которое в принципе может что–то значить в современной науке. В науке, которая может пощупать и измерить. Это то, что существует или могло бы существовать, если так случилось, что мы узнали о Вселенной все, что можно было узнать. Число состоит из 186 цифр, вот оно:
100 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Наука здесь, конечно же, не заканчивается, но дальше уже идут вольные теории, догадки, а то и просто околонаучный чес и гон. Например, вы наверняка слышали про инфляционную теорию, согласно которой, возможно, наша Вселенная лишь часть более общей Мультивселенной, в которой этих вселенных как пузырей в океане шампанского.

Или слышали о теории струн, согласно которой может существовать около 10⁵⁰⁰ конфигураций колебаний струн, а значит такое же количество потенциальных вселенных, каждая со своими законами.
Чем дальше в лес, тем меньше теоретической физики и вообще науки остается в набирающих объемы числах, и за колонками нулей начинает проглядывать все более чистая, ничем не замутненная царица наук. Математика это ведь не физика, тут ограничений нет и стыдиться нечего, гуляй душа, пиши нули в формулах хоть до упаду.
Упомяну лишь известный многим гуголплекс. Число у которого гугол цифр, десять в степени гугол или десять в степени десять в степени сто

10¹⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰ ⁰⁰⁰
Не буду записывать его цифрами. Гуголплекс не значит абсолютно ничего. Человек не может представить себе гуголплекс чего бы то ни было, это физически невозможно. Чтобы записать такое число понадобится вся Обозримая Вселенная, если писать «нано–ручкой» прямо по вакууму фактически в планковские ячейки космоса. Переведем всю материю на чернила и заполним Вселенную одними сплошными цифрами, тогда получим гуголплекс. Но математики (страшные люди!) гуголпрексом только разминаются, это нижайшая планка, с которой для них стартуют настоящие ништяки. И если вы думаете, что гуголплекс в степени гуголплекс это то, о чем пойдет речь, вы даже не представляете, НАСКОЛЬКО ошибаетесь.
За гуголплексом идут много интересных чисел, имеющих ту или иную роль в математических доказательствах, долго ли коротко, перейдем сразу к числу Грэма, названному так в честь (ну, естественно) математика Рональда Грэма. Сначала расскажу, что это такое и для чего нужно, после чего образно и на пальцах™ опишу, каково оно по величине, а затем уже напишу само число. Точнее попытаюсь объяснить, что же я написал.
Число Грэма появилось в работе, посвященной решению одной из задач в теории Рамсея, причем «рамсея» тут не деепричастие несовершенного вида, а фамилия другого математика, Франка Рамсея. Задача конечно же довольно надуманная с обывательской точки зрения, хоть и не сильно замороченная, даже легко понятная.
Представьте себе куб, все вершины которого соединены линиями–отрезками двух цветов, красного или синего. Соединены и раскрашены в случайном порядке. Кое–кто уже догадался, что речь пойдет о разделе математики под названием комбинаторика.
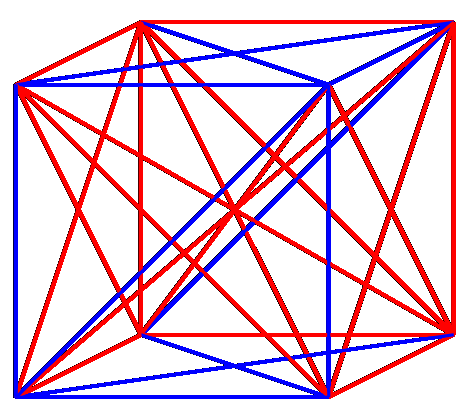
Сможем ли мы исхитриться и так подобрать конфигурацию цветов (а их всего два — красный и синий), чтобы при раскраске этих отрезков у нас НЕ ВЫШЛО, что все отрезки одного цвета, соединяющие четыре вершины, лежат в одной плоскости? В данном случае, НЕ представляют из себя такую фигуру:
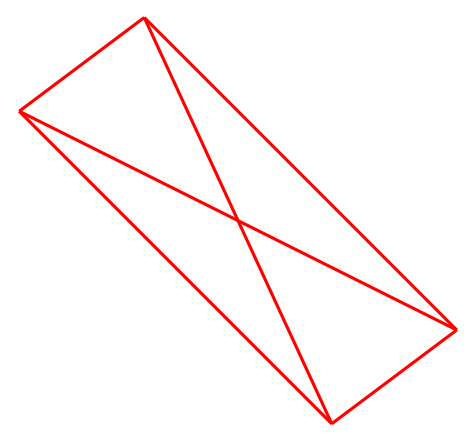
Можете сами покумекать, покрутить куб в воображении перед глазами, сделать подобное не так уж и сложно. Цвета два, вершин (углов) у куба 8, значит отрезков их соединяющих — 28. Можно так подобрать конфигурацию раскраски, что мы нигде не получим вышеуказанной фигуры, во всех возможных плоскостях будут разноцветные линии.
А что, если у нас больше измерений? Что, если мы возьмем не куб, а четырехмерный куб, т.е. тессеракт? Сможем ли мы провернуть тот же фокус, что и с трехмерным?
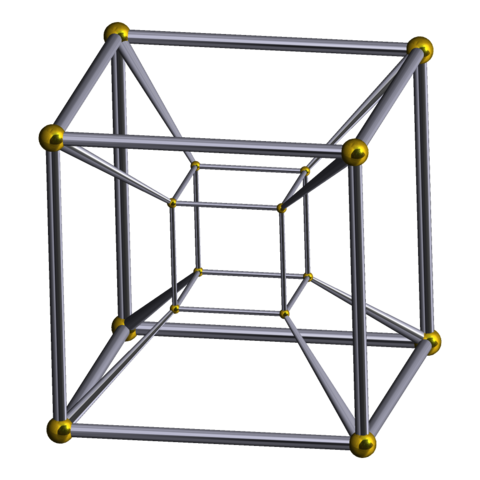
Даже не стану объяснять, что такое четырехмерный куб, все знают? У четырехмерного куба 16 вершин. И не нужно пыжить мозг и пытаться представить четырехмерный куб. Это же чистая математика. Посмотрел на количество измерений, подставил в формулу, получил количество вершин, ребер, граней и так далее. Ну, или в Википедии подглядел, если формулы не помнишь. Итак у четырехмерного куба 16 вершин и 120 отрезков их соединяющих. Количество комбинаций раскраски в четырехмерном случае гораздо больше, чем в трехмерном, но и тут не сильно сложно посчитать, разделить, сократить и тому подобное. Короче выяснить, что в четырехмерном пространстве тоже можно так исхитриться с раскраской отрезков у гиперкуба, что все линии одного цвета, соединяющие 4 вершины, не будут лежать в одной плоскости.
В пятимерном? И в пятимерном, там где куб называется пентерактом или пентакубом, тоже можно.
И в шестимерном.
А дальше уже сложности. Грэм не смог математически доказать, что у семимерного гиперкуба удастся провернуть такую операцию. И у восьмимерного и у девятимерного и так далее. Но данное «и так далее», оказалось, не уходит в бесконечность, а заканчивается неким очень большим числом, которое и назвали «числом Грэма».
То есть существует какая–то минимальная размерность гиперкуба, при котором условие нарушается, и уже невозможно избежать комбинации раскраски отрезков, что четыре точки одного цвета будут лежать в одной плоскости. И эта минимальная размерность точно больше шести и точно меньше числа Грэма, в этом и заключается математическое доказательство ученого.
А теперь определение того, что я выше расписал на несколько абзацев, сухим и скучным (зато емким) языком математики. Понимать не надо, но не привести его я не могу.
Рассмотрим n–мерный гиперкуб и соединим все пары вершин для получения полного графа с 2n вершинами. Раскрасим каждое ребро этого графа либо в красный, либо в синий цвет. При каком наименьшем значении n каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, все из которых лежат в одной плоскости?
В 1971м году Грэм доказал, что указанная проблема имеет решение, и что это решение (количество размерности) лежит между числом 6 и неким большим числом, которое позже (не самим автором) было названо в его честь. В 2008м году доказательство улучшили, нижнюю границу подняли, теперь искомое количество размерностей лежит уже между числом 13 и числом Грэма. Математики не спят, работа идет, прицел сужается.
С 70х годов прошло немало лет, были найдены математические задачи в которых проявляются числа и побольше грэмова, но это первое число–монстр так поразило современников, понимавших о каких масштабах идет речь, что в 1980м году его включили в книгу рекордов Гиннесса, как «самое большое число, когда–либо участвовавшее в строгом математическом доказательстве» на тот момент.
Давайте попытаемся разобраться, насколько оно велико. Самое большое число, могущее иметь какой–то физический смысл 10¹⁸⁵, а если всю Обозримую Вселенную заполнить кажущимся бесконечным набором мизерных циферок, получим что–то соизмеримое с гуголплексом.
Представляете себе эту громаду? Вперед, назад, вверх, вниз, насколько хватает глаз и насколько хватает телескопа Хаббл, и даже насколько не хватает, до самых далеких галактик и заглядывая за них — цифры, цифры, цифры размером много меньше протона. Существовать такая Вселенная, конечно, долго не сможет, тут же в черную дыру схлопнется. Припоминаете, сколько информации можно теоретически уместить во Вселенную?
Число действительно огромно, рвет мозг. Оно не совсем точно равно гуголплексу, и у него нет названия, потому буду называть его «дохулион». Только что придумал, почему бы и нет. Количество планковских ячеек в Обозримой Вселенной, и в каждой ячейке записана цифра. Число содержит 10¹⁸⁵ цифр, его можно изобразить как
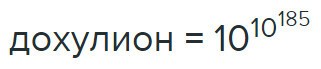
Раскроем двери восприятия чуть пошире. Помните инфляционную теорию? Что наша Вселенная лишь одна из многих пузырьков Мультивселенной. А если представить дохулион таких пузырьков? Возьмем число, длиною со все сущее и представим себе Мультивселенную с подобным количеством вселенных, каждая из которых под завязку исписана цифрами — получим дохулион дохулионов. Представляете себе такое? Как плывешь в небытии скалярного поля, а кругом вселенные–вселенные и в них цифры–цифры–цифры… Надеюсь, подобный кошмар (хотя, почему кошмар?) не будет мучить (и почему мучить?) излишне впечатлительного читателя по ночам.
Для удобства назовем подобную операцию «флип». Такое несерьезное междометие, как будто взяли Вселенную и вывернули наизнанку, то она была внутри в цифрах, а теперь наоборот у нас снаружи столько вселенных, сколько было цифр, и каждая полным–полна коробочка, сама вся в цифрах. Как гранат чистишь, корочку так отгибаешь, изнутри выворачиваются зернышки, а в зернышках снова гранаты. Тоже на ходу придумалось, почему бы и нет, с дохулионом ведь прокатило.
К чему я клоню? Стоит ли тормозить? Давайте, хоба, и еще один флип! И вот у нас столько вселенных, сколько было цифр во вселенных, количество которых было равно дохулиону цифр, заполнявших нашу Вселенную. И сразу, не останавливаясь, еще раз флип. И четвертый, и пятый. Десятый, тысячный. Успеваете за мыслью, все еще представляете себе картину?
Не будем мелочиться, распускаем крылья воображения, разгоняемся по полной и флипаем флип флипов. Столько раз выворачиваем каждую вселенную наизнанку, сколько дохулионов вселенных было в предыдущем флипе, который флипал из позапрошлого, который… эээ… ну, вы следите? Где–то так. Пусть теперь наше число станет, предположим, «дохулиард».
дохулиард = флип флипов
Не останавливаемся и продолжаем флипать дохулионы дохулиардов до тех пор пока есть силы. Пока в глазах не темнеет, пока не захочется кричать. Тут каждый сам себе отважный Буратина, стоп–слово будет «брынза».
Так вот. Это все о чем? Огромные и бесконечные дохулионы флипов и дохулиарды вселенных полных цифр не идут ни в какое сравнение с числом Грэма. Даже не скребут по поверхности. Если число Грэма представить в виде палки, растянутой по традиции во всю Обозримую Вселенную, то, что мы тут с вами нафлипали окажется засечкой толщины… ну… как бы это так, помягче выразить… недостойной упоминания. Вот, смягчал, как мог.
Теперь давайте немного отвлечемся, передохнем. Мы читали, мы считали, наши глазоньки устали. Забудем про число Грэма, до него еще ползти и ползти, расфокусируем взгляд, расслабимся, помедитируем на гораздо меньшее, прямо–таки миниатюрнейшее число, которое назовем g₁, и запишем всего шестью знаками:
g₁ = 3↑↑↑↑3
Число g₁ равно «три, четыре стрелочки, три». Что это значит? Так выглядит способ записи, называемый стрелочная нотация Кнута.
Для подробностей и деталей можно почитать статью в Википедии, но там формулы, я коротенько перескажу ее простыми словами.
Одна стрелочка означает обыкновенное возведение в степень.
2↑2 = 2² = 4
3↑3 = 3³ = 27
4↑4 = 4⁴ = 256
10↑10 = 10¹⁰ = 10 000 000 000
Две стрелочки означают, что понятно, возведение в степень степени.

Короче говоря, «число стрелочка стрелочка другое число» показывает, какая высота степеней (математики говорят «башня») выстраивается из первого числа. Например 5↑↑8 означает башню из восьми пятерок и настолько велико, что не может быть рассчитано ни на каком суперкомпьютере, даже на всех компьютерах планеты одновременно.

Переходим к трем стрелочкам. Если двойная стрелочка показывала высоту башни степеней, то тройная, казалось бы, укажет «высоту башни высоты башни»? Какой–там! В случае тройки мы имеем высоту башни высоты башни высоты башни (в математике такого понятия нет, я решил назвать его «безбашней»). Как–то так:
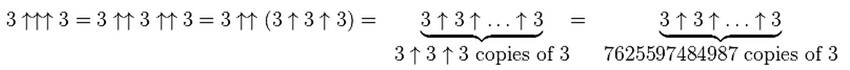
То есть 3↑↑↑3 образует безбашню из троек, высотой в 7 триллионов штук. Что такое 7 триллионов троек, поставленные друг на друга и именуемые «безбашней»? Если вы внимательно читали этот текст и не уснули в самом начале, вероятно помните, что от Земли до Сатурна 100 триллионов сантиметров. Тройка, показанная на экране двенадцатым шрифтом, вот эта — 3 — высотой миллиметров пять. Значит безбашня из троек протянется от вашего экрана… ну, не до Сатурна, конечно. Даже до Солнца не дотянется, всего четверть астрономической единицы, примерно как от Земли до Марса в хорошую погоду. Обращаю внимание (не спать!), что безбашня это не число длиной от Земли до Марса, это башня степеней такой высоты. Мы помним, что пять троек в этой башне покрывают гуголплекс, вычисление первого дециметра троек сжигает все предохранители компьютеров планеты, а остальные миллионы километров степеней уже как бы и ни к чему, они просто в открытую насмехаются над читателем, считать их бесполезно.

Теперь понятно, что 3↑↑↑4 = 3↑↑3↑↑3↑↑3 = 3↑↑3↑↑7 625 597 484 987 = 3↑↑безбашня, (не 3 в степени безбашни, а «три стрелочка стрелочка безбашня»(!)), она же безбашня безбашни не влезет ни по длине ни по высоте в Обозримую Вселенную, и даже не поместится в предполагаемую Мультивселенную.
На 3↑↑↑5 = 3↑↑3↑↑3↑↑3↑↑3 заканчиваются слова, а на 3↑↑↑6 = 3↑↑3↑↑3↑↑3↑↑3↑↑3 кончаются междометия, но можете потренироваться, коль есть интерес.
Переходим к четырем стрелочкам. Как вы уже догадались, тут безбашня на безбашне сидит, безбашней погоняет, и хоть с башней, что без башни — все равно. Просто молча приведу картинку, раскрывающую схему вычисления четырех стрелочек, когда каждое следующее число башни степеней определяет высоту башни степеней, определяющую высоту башни степеней, определяющую высоту башни степеней… и так до самозабвения.
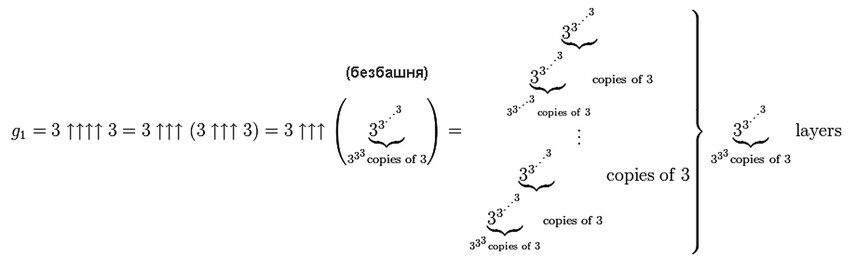
Рассчитывать его бесполезно, да и не получится. Количество степеней здесь не поддается осмысленному учету. Это число невозможно представить, его невозможно описать. Никакие аналогии на пальцах™ неприменимы, число просто не с чем сравнивать. Можно говорить, что оно огромно, что грандиозно, что монументально и заглядывает за горизонт событий. То есть придать ему какие–то словесные эпитеты. Но визуализация, даже вольная и образная — невозможна. Если с тремя стрелочками еще хоть что–то удавалось сказать, нарисовать безбашню от Земли до Марса, как–то с чем–то сопоставить, то тут аналогий быть просто не может. Попробуйте вообразить себе тонкую башню из троек от Земли до Марса, рядом еще одну почти такую же и еще одну, и еще… Бескрайнее поле башень уходит вдаль, в бесконечность, башни повсюду, башни везде. И, что самое обидное, эти башни даже отношения к числу не имеют, они лишь определяют высоту других башен, которые нужно построить, чтобы получить высоту башень, чтобы получить высоту башень… чтобы через невообразимое количество времени и итераций получить само число.
Вот, что такое g₁, вот что такое 3↑↑↑↑3.
Передохнули? Теперь от g₁ с новыми силами возвращаемся к штурму числа Грэма. Заметили, как нарастает эскалация от стрелочки к стрелочке?
3↑3 = 27
3↑↑3 = 7 625 597 484 987
3↑↑↑3 = башня, высотой от Земли до Марса.
3↑↑↑↑3 = число, которое невозможно ни представить ни описать.
А вообразите какой цифровой кошмар творится, когда стрелок окажется пять? Когда их шесть? Можете представить число, когда стрелок будет сто? Если можете, позвольте предложить вашему вниманию число g₂, в котором количество этих стрелок оказывается равно g₁. Помните, что такое g₁, да?
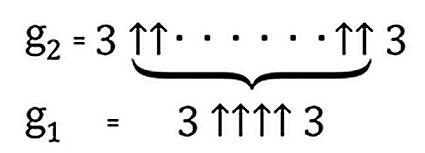
Все, что было написано до сих пор, все эти расчеты, степени и башни не помещающиеся в мультивселенные мультивселенных нужны были только для одного. Чтобы показать КОЛИЧЕСТВО СТРЕЛОК в числе g₂. Тут уже не нужно ничего считать, можно просто рассмеяться и махнуть рукой.
Не буду скрывать, есть еще g₃, в котором содержится g₂ стрелок. Кстати, все еще понятно, что g₃, это не g₂ «в степени» g₂, а количество безбашен, определяющих высоту безбашен, определяющих высоту… и так по всей цепочке вниз до тепловой смерти Вселенной? Здесь можно начинать плакать.
Почему плакать? Потому что совершенно верно. Есть еще число g₄, в котором содержится g₃ стрелочек между тройками. Есть так же g₅, есть g₆ и g₇ и g₁₇ и g₄₃…
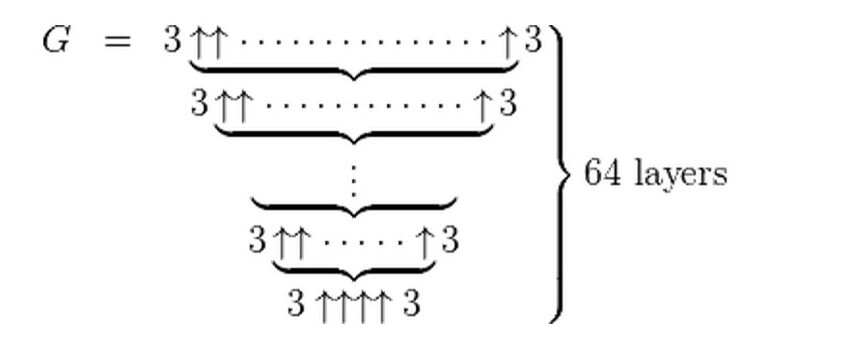
Короче их 64 штуки этих g. Каждое предыдущее численно равно количеству стрелок в следующем. Последнее g₆₄ и есть число Грэма, с которого все так вроде бы невинно начиналось. Это число размерностей гиперкуба, которого точно будет достаточно, чтобы правильно раскрасить отрезки красным и синим цветами. Может и меньше, это, так сказать, верхняя граница. Его записывают следующим образом:
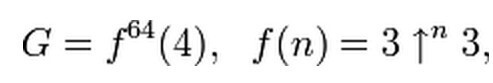
Все, теперь можно расслабиться по–честному. Нет больше необходимости ничего представлять и рассчитывать. Если вы дочитали до этого места, уже как бы все должно встать на свои места. Или не встать. Или не на свои.
Да, опытный читатель с прокачанными предохранителями, не нужно упреков, вы абсолютно правы. Число Грэма — надуманная и высосанная из пальца фигня. Все эти безразмерные гиперкубы и абстрактные плоскости, дьявол их раздери, кому они нужны? Где килограммы, где электроны, где то, что можно измерить? Что за пустые разглагольствования ни о чем? Соглашусь. Можно сказать, что сегодняшний пост на пальцах™ максимально, на сколько это было возможно, далек от реальной науки, почти весь целиком парит в каких–то заумных математических фантазиях, в то время как ученым не хватает денег на приборы, не решена мировая энергетическая проблема, а у кого–то все еще туалет во дворе. А у кого и в поле.
Но знаете, есть такая теория, тоже весьма эфемерная и философская, может слышали — все, что человек мог себе представить или вообразить обязательно когда–нибудь воплотится. Потому что развитие цивилизации определяется по тому, насколько она смогла воплотить в реальность фантазии прошлого.
Истории человеческой цивилизации 10 000 лет. Задумайтесь, человечеству всего 10 000 лет! Хотя отдельному человеку в виде прямоходящей обезьяны без хвоста дают 4 миллиона. Все эти 4 миллиона лет спустившаяся с деревьев обезьяна училась держать палку и добывать огонь. Только десять тысяч лет назад появилось какое–то первое подобие общества, человек вышел из пещер и начал строить дома и деревни. Герой того времени (уже довольно цивилизованный по современным меркам) не мог посчитать дальше сотни тысяч (а просто нечего было считать больше такого количества), не имел понятия о среднем арифметическом и не знал суммы квадратов катетов. Этого великого открытия нужно было дожидаться много веков, не одну тысячу лет. 4000 лет назад человек был уверен, что молнии в небе происходят лично от Зевса, 2000 лет назад считал, что можно развести руками воды моря, стоит только заручиться поддержкой влиятельной особы, тогда как родственные узы дадут возможность ходить по воде. 500 лет назад человек доказал, что Земля круглая, 400 — что вертится вокруг Солнца, 200 лет назад узнал о свойствах пара приводить в движение мертвый металл, а около 100 лет назад был уверен, что полеты на аппаратах тяжелее воздуха невозможны. 70 лет назад человечество догадалось, как расщепить атом, 60 лет назад вышло в космос, а еще через 15 открыло для себя число Грэма. 20 лет назад мы увидели самую далекую, одну из самых первых сформировавшихся после Большого Взрыва галактик и тогда же примерно запустили общемировую информационную сеть, выведя цивилизацию на следующий качественный уровень развития. Десять лет назад к этой сети подключилась половина населения планеты.
Никто не знает, что ждет нас в будущем. У человеческой цивилизации есть тысячи способов закончиться: ядерные войны, экологические катастрофы, смертоносные пандемии, астероид какой может прилететь, динозавры не дадут соврать. Развитие человечества может остановиться само собой, вдруг есть такой закон, что по достижению определенного уровня развитие просто прекращается и все. Или прилетят представители межгалактического союза и остановят это развитие силой.
Но есть все–таки, и не маленький, шанс, что развитие человечества продолжится без остановки. Пусть даже не такое головокружительно быстрое, как в последние 100 лет, главное, что движение вперед, главное, что поступательное.
У природы есть один незыблемый закон, известный нам с самой давней древности. Как бы ни было, что бы ни случилось, что бы мы себе ни думали, но время никуда не денется, оно пройдет. Хотим мы этого или не хотим, с нами или без — пройдут и тысяча и 10 тысяч лет.
200 лет назад ковер–самолет (обычный самолет), волшебное зеркало (скайп видео) или тридевятое царство (поверхность планеты Марс) казались несбыточной сказкой, 2000 лет назад полагались только богам, 20 000 лет такого вообще представить не могли, способностей воображения не хватало. Вы можете сказать, что будет доступно человеку через 200 лет? Через 2000, через 20000 лет?
Выживет ли человечество, будет ли это вообще человечество с приставкой «чело–», а может к тому времени и этап Искусственного Интеллекта закончится, порождая какие–то эфирные энергетические субстанции особой категории осознанности? Может да, может нет.
А если пройдет миллион лет? А ведь он пройдет, куда денется. Число Грэма, и вообще все, о чем человек способен задуматься, представить, вытащить из небытия и сделать пусть не осязаемой, но хотя бы имеющей какой–то смысл сущностью — обязательно рано или поздно воплотится. Просто потому, что сегодня у нас хватило сил развиться до способности осознания подобного.
Сегодня, завтра, когда будет возможность — запрокиньте голову в ночное небо. Помните этот момент ощущения собственной ничтожности? Чувствуете, какой человек крошечный? Пылинка, атом по сравнению с безбрежной Вселенной, которая звезд полна, коим числа нет, ну, и бездна, соответственно, тоже не маленькая.
В следующий раз попробуйте ощутить, какая Вселенная песчинка по сравнению с тем, что происходит в голове. Какая пучина открывается, какие неизмеримые концепции рождаются, какие миры строятся, как Вселенная флипается наизнанку одним только движением мысли, как и насколько живая, разумная материя отличается от мертвой и неразумной.
Я верю, что через какое–то время человек дотянется до числа Грэма, дотронется до него рукой, или что у него к тому времени будет вместо руки. Это не обоснованная, научно доказанная мысль, это действительно всего лишь надежда, то, что меня вдохновляет. Не Вера с большой буквы, не религиозный экстаз, не учение и не духовная практика. Это то, чего я жду от человечества. В чем стремлюсь, в меру сил, помочь. Хоть и продолжаю из осторожности причислять себя к агностикам.
This article is about the very large number named after Ronald Graham. For the investing term named after Benjamin Graham, see Graham number.
Graham’s number is an immense number that arose as an upper bound on the answer of a problem in the mathematical field of Ramsey theory. It is much larger than many other large numbers such as Skewes’s number and Moser’s number, both of which are in turn much larger than a googolplex. As with these, it is so large that the observable universe is far too small to contain an ordinary digital representation of Graham’s number, assuming that each digit occupies one Planck volume, possibly the smallest measurable space. But even the number of digits in this digital representation of Graham’s number would itself be a number so large that its digital representation cannot be represented in the observable universe. Nor even can the number of digits of that number—and so forth, for a number of times far exceeding the total number of Planck volumes in the observable universe. Thus Graham’s number cannot be expressed even by physical universe-scale power towers of the form 
However, Graham’s number can be explicitly given by computable recursive formulas using Knuth’s up-arrow notation or equivalent, as was done by Ronald Graham, the number’s namesake. As there is a recursive formula to define it, it is much smaller than typical busy beaver numbers. Though too large to be computed in full, the sequence of digits of Graham’s number can be computed explicitly via simple algorithms; the last 13 digits are …7262464195387. With Knuth’s up-arrow notation, Graham’s number is 
Graham’s number was used by Graham in conversations with popular science writer Martin Gardner as a simplified explanation of the upper bounds of the problem he was working on. In 1977, Gardner described the number in Scientific American, introducing it to the general public. At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof. The number was described in the 1980 Guinness Book of World Records, adding to its popular interest. Other specific integers (such as TREE(3)) known to be far larger than Graham’s number have since appeared in many serious mathematical proofs, for example in connection with Harvey Friedman’s various finite forms of Kruskal’s theorem. Additionally, smaller upper bounds on the Ramsey theory problem from which Graham’s number derived have since been proven to be valid.
Context[edit]
Example of a 2-colored 3-dimensional cube containing one single-coloured 4-vertex coplanar complete subgraph. The subgraph is shown below the cube. Note that this cube would contain no such subgraph if, for example, the bottom edge in the present subgraph were replaced by a blue edge – thus proving by counterexample that N* > 3.
Graham’s number is connected to the following problem in Ramsey theory:
Connect each pair of geometric vertices of an n-dimensional hypercube to obtain a complete graph on 2n vertices. Colour each of the edges of this graph either red or blue. What is the smallest value of n for which every such colouring contains at least one single-coloured complete subgraph on four coplanar vertices?
In 1971, Graham and Rothschild proved the Graham–Rothschild theorem on the Ramsey theory of parameter words, a special case of which shows that this problem has a solution N*. They bounded the value of N* by 6 ≤ N* ≤ N, with N being a large but explicitly defined number
where 
which contains three tetrations.[2] In 2019 this was further improved to:[3]
The lower bound of 6 was later improved to 11 by Geoffrey Exoo in 2003,[4] and to 13 by Jerome Barkley in 2008.[5] Thus, the best known bounds for N* are 13 ≤ N* ≤ N».
Graham’s number, G, is much larger than N: 

Publication[edit]
The number gained a degree of popular attention when Martin Gardner described it in the «Mathematical Games» section of Scientific American in November 1977, writing that Graham had recently established, in an unpublished proof, «a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof.» The 1980 Guinness Book of World Records repeated Gardner’s claim, adding to the popular interest in this number. According to physicist John Baez, Graham invented the quantity now known as Graham’s number in conversation with Gardner. While Graham was trying to explain a result in Ramsey theory which he had derived with his collaborator Bruce Lee Rothschild, Graham found that the said quantity was easier to explain than the actual number appearing in the proof. Because the number which Graham described to Gardner is larger than the number in the paper itself, both are valid upper bounds for the solution to the problem studied by Graham and Rothschild.[7]
Definition[edit]
Using Knuth’s up-arrow notation, Graham’s number G (as defined in Gardner’s Scientific American article) is
where the number of arrows in each subsequent layer is specified by the value of the next layer below it; that is,
where 
and where a superscript on an up-arrow indicates how many arrows there are. In other words, G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3s; the second step is to calculate g2 with g1 up-arrows between 3s; the third step is to calculate g3 with g2 up-arrows between 3s; and so on, until finally calculating G = g64 with g63 up-arrows between 3s.
Equivalently,
and the superscript on f indicates an iteration of the function, e.g., 




Magnitude[edit]
To convey the difficulty of appreciating the enormous size of Graham’s number, it may be helpful to express—in terms of exponentiation alone—just the first term (g1) of the rapidly growing 64-term sequence. First, in terms of tetration (
where the number of 3s in the expression on the right is
Now each tetration (

where there are X 3s.
Thus,
becomes, solely in terms of repeated «exponentiation towers»,
and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.
In other words, g1 is computed by first calculating the number of towers, 

1st tower: 3
2nd tower: 3↑3↑3 (number of 3s is 3) = 7625597484987
3rd tower: 3↑3↑3↑3↑...↑3 (number of 3s is 7625597484987) = …
⋮
g1 = nth tower: 3↑3↑3↑3↑3↑3↑3↑...↑3 (number of 3s is given by the n-1th tower)
where the number of 3s in each successive tower is given by the tower just before it. Note that the result of calculating the third tower is the value of n, the number of towers for g1.
The magnitude of this first term, g1, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volumes (roughly 10185 of them) into which one can imagine subdividing the observable universe. And after this first term, still another 63 terms remain in the rapidly growing g sequence before Graham’s number G = g64 is reached. To illustrate just how fast this sequence grows, while g1 is equal to 
Rightmost decimal digits[edit]
Graham’s number is a «power tower» of the form 3↑↑n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost «3» in the tower; i.e., the topmost «3» can be changed to any other non-negative integer without affecting the d rightmost digits.
The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10d of them) does not occur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table:
| Number of digits (d) | 3↑x | 3↑3↑x | 3↑3↑3↑x | 3↑3↑3↑3↑x | 3↑3↑3↑3↑3↑x |
|---|---|---|---|---|---|
| 1 | 4 (1,3,9,7) |
2 (3,7) |
1 (7) |
1 (7) |
1 (7) |
| 2 | 20 (01,03,…,87,…,67) |
4 (03,27,83,87) |
2 (27,87) |
1 (87) |
1 (87) |
| 3 | 100 (001,003,…,387,…,667) |
20 (003,027,…387,…,587) |
4 (027,987,227,387) |
2 (987,387) |
1 (387) |
The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3
A simple algorithm[8] for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment x = 3x mod 10d. Except for omitting any leading 0s, the final value assigned to x (as a base-ten numeral) is then composed of the d rightmost decimal digits of 3↑↑n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)
Let k be the numerousness of these stable digits, which satisfy the congruence relation G(mod 10k)≡[GG](mod 10k).
k=t-1, where G(t):=3↑↑t.[9] It follows that, g63 ≪ k ≪ g64.
The algorithm above produces the following 500 rightmost decimal digits of Graham’s number (OEIS: A133613):
...02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387
References[edit]
- ^ «Graham’s number records». Iteror.org. Archived from the original on 2013-10-19. Retrieved 2014-04-09.
- ^ Lavrov, Mikhail; Lee, Mitchell; Mackey, John (2014). «Improved upper and lower bounds on a geometric Ramsey problem». European Journal of Combinatorics. 42: 135–144. doi:10.1016/j.ejc.2014.06.003.
- ^ Lipka, Eryk (2019). «Further improving of upper bound on a geometric Ramsey problem». arXiv:1905.05617 [math.CO].
- ^ Exoo, Geoffrey (2003). «A Euclidean Ramsey Problem». Discrete & Computational Geometry. 29 (2): 223–227. doi:10.1007/s00454-002-0780-5. Exoo refers to the Graham & Rothschild upper bound N by the term «Graham’s number». This is not the «Graham’s number» G published by Martin Gardner.
- ^ Barkley, Jerome (2008). «Improved lower bound on an Euclidean Ramsey problem». arXiv:0811.1055 [math.CO].
- ^ Martin Gardner (1977) «In which joining sets of points leads into diverse (and diverting) paths» Archived 2013-10-19 at the Wayback Machine. Scientific American, November 1977
- ^ John Baez (2013). «A while back I told you about Graham’s number…» Archived from the original on 2013-11-13. Retrieved 2013-01-11.
- ^ «The Math Forum @ Drexel («Last Eight Digits of Z»)». Mathforum.org. Retrieved 2014-04-09.
- ^ Ripà, Marco (2011). La strana coda della serie n^n^…^n (in Italian). UNI Service. ISBN 978-88-6178-789-6.
Bibliography[edit]
- Gardner, Martin (November 1977). «Mathematical Games» (PDF). Scientific American. 237 (5): 18–28. Bibcode:1977SciAm.237e..18G. doi:10.1038/scientificamerican1177-18.; reprinted (revised) in Gardner (2001), cited below.
- Gardner, Martin (1989). Penrose Tiles to Trapdoor Ciphers. Washington, D.C.: Mathematical Association of America. ISBN 978-0-88385-521-8.
- Gardner, Martin (2001). The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. New York, NY: Norton. ISBN 978-0-393-02023-6.
- Graham, R. L.; Rothschild, B. L. (1971). «Ramsey’s Theorem for n-Parameter Sets» (PDF). Transactions of the American Mathematical Society. 159: 257–292. doi:10.2307/1996010. JSTOR 1996010. The explicit formula for N appears on p. 290. This is not the «Graham’s number» G published by Martin Gardner.
- Graham, R. L.; Rothschild, B. L. (1978). «Ramsey Theory». In Rota, G-C (ed.). Studies in Combinatorics (MAA Studies in Mathematics). Vol. 17. Mathematical Association of America. pp. 80–99. ISBN 978-0-88385-117-3. On p. 90, in stating «the best available estimate» for the solution, the explicit formula for N is repeated from the 1971 paper.
External links[edit]
- OEIS sequence A133613 (Graham’s number)
- Sbiis Saibian’s article on Graham’s number
- «A Ramsey Problem on Hypercubes» by Geoff Exoo
- Mathworld article on Graham’s number
- How to calculate Graham’s number
- Conceptualizing Graham’s number
- Some Ramsey results for the n-cube prepublication mentions Graham’s number
- Padilla, Tony; Parker, Matt. «Graham’s Number». Numberphile. Brady Haran. Archived from the original on 2014-05-27. Retrieved 2013-04-08.
- Archived at Ghostarchive and the Wayback Machine: Ron Graham. «What is Graham’s Number? (feat Ron Graham)» (video). Numberphile. Brady Haran.
- Archived at Ghostarchive and the Wayback Machine: Ron Graham. «How Big is Graham’s Number? (feat Ron Graham)» (video). Numberphile. Brady Haran.
- The last 16 million digits of Graham’s number by the Darkside communication group
This article is about the very large number named after Ronald Graham. For the investing term named after Benjamin Graham, see Graham number.
Graham’s number is an immense number that arose as an upper bound on the answer of a problem in the mathematical field of Ramsey theory. It is much larger than many other large numbers such as Skewes’s number and Moser’s number, both of which are in turn much larger than a googolplex. As with these, it is so large that the observable universe is far too small to contain an ordinary digital representation of Graham’s number, assuming that each digit occupies one Planck volume, possibly the smallest measurable space. But even the number of digits in this digital representation of Graham’s number would itself be a number so large that its digital representation cannot be represented in the observable universe. Nor even can the number of digits of that number—and so forth, for a number of times far exceeding the total number of Planck volumes in the observable universe. Thus Graham’s number cannot be expressed even by physical universe-scale power towers of the form 
However, Graham’s number can be explicitly given by computable recursive formulas using Knuth’s up-arrow notation or equivalent, as was done by Ronald Graham, the number’s namesake. As there is a recursive formula to define it, it is much smaller than typical busy beaver numbers. Though too large to be computed in full, the sequence of digits of Graham’s number can be computed explicitly via simple algorithms; the last 13 digits are …7262464195387. With Knuth’s up-arrow notation, Graham’s number is 
Graham’s number was used by Graham in conversations with popular science writer Martin Gardner as a simplified explanation of the upper bounds of the problem he was working on. In 1977, Gardner described the number in Scientific American, introducing it to the general public. At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof. The number was described in the 1980 Guinness Book of World Records, adding to its popular interest. Other specific integers (such as TREE(3)) known to be far larger than Graham’s number have since appeared in many serious mathematical proofs, for example in connection with Harvey Friedman’s various finite forms of Kruskal’s theorem. Additionally, smaller upper bounds on the Ramsey theory problem from which Graham’s number derived have since been proven to be valid.
Context[edit]
Example of a 2-colored 3-dimensional cube containing one single-coloured 4-vertex coplanar complete subgraph. The subgraph is shown below the cube. Note that this cube would contain no such subgraph if, for example, the bottom edge in the present subgraph were replaced by a blue edge – thus proving by counterexample that N* > 3.
Graham’s number is connected to the following problem in Ramsey theory:
Connect each pair of geometric vertices of an n-dimensional hypercube to obtain a complete graph on 2n vertices. Colour each of the edges of this graph either red or blue. What is the smallest value of n for which every such colouring contains at least one single-coloured complete subgraph on four coplanar vertices?
In 1971, Graham and Rothschild proved the Graham–Rothschild theorem on the Ramsey theory of parameter words, a special case of which shows that this problem has a solution N*. They bounded the value of N* by 6 ≤ N* ≤ N, with N being a large but explicitly defined number
where 
which contains three tetrations.[2] In 2019 this was further improved to:[3]
The lower bound of 6 was later improved to 11 by Geoffrey Exoo in 2003,[4] and to 13 by Jerome Barkley in 2008.[5] Thus, the best known bounds for N* are 13 ≤ N* ≤ N».
Graham’s number, G, is much larger than N: 

Publication[edit]
The number gained a degree of popular attention when Martin Gardner described it in the «Mathematical Games» section of Scientific American in November 1977, writing that Graham had recently established, in an unpublished proof, «a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof.» The 1980 Guinness Book of World Records repeated Gardner’s claim, adding to the popular interest in this number. According to physicist John Baez, Graham invented the quantity now known as Graham’s number in conversation with Gardner. While Graham was trying to explain a result in Ramsey theory which he had derived with his collaborator Bruce Lee Rothschild, Graham found that the said quantity was easier to explain than the actual number appearing in the proof. Because the number which Graham described to Gardner is larger than the number in the paper itself, both are valid upper bounds for the solution to the problem studied by Graham and Rothschild.[7]
Definition[edit]
Using Knuth’s up-arrow notation, Graham’s number G (as defined in Gardner’s Scientific American article) is
where the number of arrows in each subsequent layer is specified by the value of the next layer below it; that is,
where 
and where a superscript on an up-arrow indicates how many arrows there are. In other words, G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3s; the second step is to calculate g2 with g1 up-arrows between 3s; the third step is to calculate g3 with g2 up-arrows between 3s; and so on, until finally calculating G = g64 with g63 up-arrows between 3s.
Equivalently,
and the superscript on f indicates an iteration of the function, e.g., 




Magnitude[edit]
To convey the difficulty of appreciating the enormous size of Graham’s number, it may be helpful to express—in terms of exponentiation alone—just the first term (g1) of the rapidly growing 64-term sequence. First, in terms of tetration (
where the number of 3s in the expression on the right is
Now each tetration (

where there are X 3s.
Thus,
becomes, solely in terms of repeated «exponentiation towers»,
and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.
In other words, g1 is computed by first calculating the number of towers, 

1st tower: 3
2nd tower: 3↑3↑3 (number of 3s is 3) = 7625597484987
3rd tower: 3↑3↑3↑3↑...↑3 (number of 3s is 7625597484987) = …
⋮
g1 = nth tower: 3↑3↑3↑3↑3↑3↑3↑...↑3 (number of 3s is given by the n-1th tower)
where the number of 3s in each successive tower is given by the tower just before it. Note that the result of calculating the third tower is the value of n, the number of towers for g1.
The magnitude of this first term, g1, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volumes (roughly 10185 of them) into which one can imagine subdividing the observable universe. And after this first term, still another 63 terms remain in the rapidly growing g sequence before Graham’s number G = g64 is reached. To illustrate just how fast this sequence grows, while g1 is equal to 
Rightmost decimal digits[edit]
Graham’s number is a «power tower» of the form 3↑↑n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost «3» in the tower; i.e., the topmost «3» can be changed to any other non-negative integer without affecting the d rightmost digits.
The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10d of them) does not occur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table:
| Number of digits (d) | 3↑x | 3↑3↑x | 3↑3↑3↑x | 3↑3↑3↑3↑x | 3↑3↑3↑3↑3↑x |
|---|---|---|---|---|---|
| 1 | 4 (1,3,9,7) |
2 (3,7) |
1 (7) |
1 (7) |
1 (7) |
| 2 | 20 (01,03,…,87,…,67) |
4 (03,27,83,87) |
2 (27,87) |
1 (87) |
1 (87) |
| 3 | 100 (001,003,…,387,…,667) |
20 (003,027,…387,…,587) |
4 (027,987,227,387) |
2 (987,387) |
1 (387) |
The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3
A simple algorithm[8] for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment x = 3x mod 10d. Except for omitting any leading 0s, the final value assigned to x (as a base-ten numeral) is then composed of the d rightmost decimal digits of 3↑↑n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)
Let k be the numerousness of these stable digits, which satisfy the congruence relation G(mod 10k)≡[GG](mod 10k).
k=t-1, where G(t):=3↑↑t.[9] It follows that, g63 ≪ k ≪ g64.
The algorithm above produces the following 500 rightmost decimal digits of Graham’s number (OEIS: A133613):
...02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387
References[edit]
- ^ «Graham’s number records». Iteror.org. Archived from the original on 2013-10-19. Retrieved 2014-04-09.
- ^ Lavrov, Mikhail; Lee, Mitchell; Mackey, John (2014). «Improved upper and lower bounds on a geometric Ramsey problem». European Journal of Combinatorics. 42: 135–144. doi:10.1016/j.ejc.2014.06.003.
- ^ Lipka, Eryk (2019). «Further improving of upper bound on a geometric Ramsey problem». arXiv:1905.05617 [math.CO].
- ^ Exoo, Geoffrey (2003). «A Euclidean Ramsey Problem». Discrete & Computational Geometry. 29 (2): 223–227. doi:10.1007/s00454-002-0780-5. Exoo refers to the Graham & Rothschild upper bound N by the term «Graham’s number». This is not the «Graham’s number» G published by Martin Gardner.
- ^ Barkley, Jerome (2008). «Improved lower bound on an Euclidean Ramsey problem». arXiv:0811.1055 [math.CO].
- ^ Martin Gardner (1977) «In which joining sets of points leads into diverse (and diverting) paths» Archived 2013-10-19 at the Wayback Machine. Scientific American, November 1977
- ^ John Baez (2013). «A while back I told you about Graham’s number…» Archived from the original on 2013-11-13. Retrieved 2013-01-11.
- ^ «The Math Forum @ Drexel («Last Eight Digits of Z»)». Mathforum.org. Retrieved 2014-04-09.
- ^ Ripà, Marco (2011). La strana coda della serie n^n^…^n (in Italian). UNI Service. ISBN 978-88-6178-789-6.
Bibliography[edit]
- Gardner, Martin (November 1977). «Mathematical Games» (PDF). Scientific American. 237 (5): 18–28. Bibcode:1977SciAm.237e..18G. doi:10.1038/scientificamerican1177-18.; reprinted (revised) in Gardner (2001), cited below.
- Gardner, Martin (1989). Penrose Tiles to Trapdoor Ciphers. Washington, D.C.: Mathematical Association of America. ISBN 978-0-88385-521-8.
- Gardner, Martin (2001). The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. New York, NY: Norton. ISBN 978-0-393-02023-6.
- Graham, R. L.; Rothschild, B. L. (1971). «Ramsey’s Theorem for n-Parameter Sets» (PDF). Transactions of the American Mathematical Society. 159: 257–292. doi:10.2307/1996010. JSTOR 1996010. The explicit formula for N appears on p. 290. This is not the «Graham’s number» G published by Martin Gardner.
- Graham, R. L.; Rothschild, B. L. (1978). «Ramsey Theory». In Rota, G-C (ed.). Studies in Combinatorics (MAA Studies in Mathematics). Vol. 17. Mathematical Association of America. pp. 80–99. ISBN 978-0-88385-117-3. On p. 90, in stating «the best available estimate» for the solution, the explicit formula for N is repeated from the 1971 paper.
External links[edit]
- OEIS sequence A133613 (Graham’s number)
- Sbiis Saibian’s article on Graham’s number
- «A Ramsey Problem on Hypercubes» by Geoff Exoo
- Mathworld article on Graham’s number
- How to calculate Graham’s number
- Conceptualizing Graham’s number
- Some Ramsey results for the n-cube prepublication mentions Graham’s number
- Padilla, Tony; Parker, Matt. «Graham’s Number». Numberphile. Brady Haran. Archived from the original on 2014-05-27. Retrieved 2013-04-08.
- Archived at Ghostarchive and the Wayback Machine: Ron Graham. «What is Graham’s Number? (feat Ron Graham)» (video). Numberphile. Brady Haran.
- Archived at Ghostarchive and the Wayback Machine: Ron Graham. «How Big is Graham’s Number? (feat Ron Graham)» (video). Numberphile. Brady Haran.
- The last 16 million digits of Graham’s number by the Darkside communication group
|
Если долго всматриваться в бездну, бездна начнёт всматриваться в тебя. |
| Ницше |
Число Грэма (число Грехема, англ. Graham’s number) — ебически огромное число, которое вывел внезапно Рональд Грэм как верхний предел в хуй никому не упёршейся проблемы с раскрашенными гиперкубами из теории Рамсея. То есть, предупреждая вопросы отдельных личностей «почему именно столько, а не столько плюс адын» — это не просто взятая от балды величина, это решение конкретной задачи.
Суть[править]
Снизу — то, как не должно быть
Проблема с кубами в теории Рамсея состоит в том, что это никакая не проблема, а одна из задач в комбинаторике, где любят переставлять или красить мелкие части одного большого множества и смотреть, что интересного может получиться. В нашем случае предлагается взять n-мерный кубик, соединить его вершины линиями, и каждое получившееся ребро покрасить одним цветом из двух — либо синим, либо красным. Суть в том, чтобы понять, до какого значения n можно, по-разному закрашивая рёбра, избежать ситуации, когда одна плоскость в кубе закрашена одним цветом. То есть, мы не хотим, чтобы получался одноцветный конвертик, как на картинке. Математики посидели-позакрашивали — видят, что в обычном кубике это сделать легче лёгкого. Добавили ещё измерение (получился тессеракт), снова позакрашивали — получилось, избежать конвертика можно. Добавили пятое, шестое, седьмое — всё отлично! Но тут пришёл Грэм и сказал, что они занимаются хуитой, и он-де сразу сейчас посчитает, при каком количестве измерений одноцветный конвертик будет получаться по-любому. ИЧСХ, посчитал-таки, однако искомым решением это назвать нельзя.
Дело в том, что теорема предлагает найти наименьшее количество измерений с нарушением условия появления одноцветной плоскости. Но хитрый Грэм подумал и решил, что считать по порядку никакого терпения не хватит. Он подозревал, что количество измерений будет большим, но не бесконечным, поэтому, применив специальное кунг-фу из комбинаторики, посчитал сразу максимальное количество этих самых измерений. Этим приёмом он не нашёл решения теоремы, но обозначил верхнюю границу поисков. То есть, если вдруг начнёте решать эту задачу с гиперкубами, то размерности больше числа Грэма можете не брать. И на сегодняшний день та самая минимальная размерность гиперкуба лежит между 13-ю измерениями и, собственно, числом Грэма. Таким образом, число Грэма — это верхний предел количества измерений гиперкуба, при котором точно невозможно избежать подграфа, закрашенного одним цветом.
Популярность[править]
Хотя ныне в математике используются числа, которые в 100500 раз больше, чем число Грэма, все они не настолько известны по ряду причин. Во-первых, на число Грэма обратил внимание широкой публики такой популяризатор матана, как Мартин Гарднер, написав колонку в научном журнале, где сказал, что Грэм совсем охуел придумывать такие числа. А в 1980 году число и вовсе попало в книгу рекордов Гиннесса, где ему был приписан рекорд как самому большому числу, когда-либо использовавшемуся в математическом доказательстве. В довесок ко всему, сам «способ» вычисления этой величины довольно понятен простому смертному (это просто перемноженные по несложному алгоритму тройки). После этого все мало-мальски знакомые с матаном стали фапать на это число, пытаясь как-то представить себе и объяснить другим масштаб этого числа. Но не тут-то было…
Формальная запись для самых любознательных
Эпичность[править]
…, ведь число риальнэ БОЛЬШОЕ. Нет, правда. На самом деле, оно больше любых самых смелых фантазий. Представьте себе цифру, написанную самым мелким шрифтом. Таким мелким, что на атоме можно нарисовать миллионы таких цифр. Представьте себе пространство, заполненное этими цифрами во всех трёх измерениях, вплотную друг к другу. Так вот, места, чтобы вместить десятичную запись числа Грэма, потребуется гораздо больше всей наблюдаемой Вселенной. Мало того, оно не вместится даже в количество Вселенных, равное количеству цифр, помещённых в нашу Вселенную. И так далее… ну ты понел. Продолжать можно, пока клавиатура не сотрётся. А когда сотрётся, сходить за новой и убить тоже. Кстати, до сих пор мы говорили только о количестве цифр, из которых состоит число Грэма, а не о самом числе (например, миллиард секунд — это почти 32 года, но в самом числе «миллиард» всего 10 цифр, которые можно пересчитать за 10 секунд)! Никакие гуголы с гуголплексами тут даже рядом не стояли.
Но все эти эпитеты и аналогии всё равно не отражают масштаба трагедии. По-настоящему заклинить свой МНУ ты можешь, попытавшись вникнуть в принцип вычисления этого числа. А чтобы не пугать честной норот простынёй непонятных знаков, мы положим его под половицу.
Глубока ли кроличья нора?
Чтобы хоть как-то представить себе масштаб числа, разберём его запись поподробнее.
1. Итак, в математике существует понятие «гипероператор» для определения уровня арифметических действий. Так, сложение — это гипероператор первого уровня, а гипероператор второго уровня — умножение, которое суть повторяющееся сложение. То есть множитель — это число, которое говорит нам, сколько раз надо сложить умножаемую величину. Например: 3 · 3 = 3 + 3 + 3 = 9. Следующий гипероператор — возведение в степень, xn = х^n, что по сути является повторяющимся умножением. Пример: 33 = 3 · 3 · 3 = 27. Запись 33 в нотации Кнута будет выглядеть как 3↑3.
Здесь для ясности следует сказать, что первая цифра в выражении 3↑3 — это значение, с которым мы и производим действие, а количество стрелочек между цифрами — это арифметическое действие; в данном случае одна стрелочка означает возведение в степень. Вторая цифра означает то, в какую степень надо возвести первую цифру (сколько раз перемножить на себя). Соответственно, выражение 7↑4 означает семь в четвёртой степени. Иначе говоря, 7 нужно умножить на 7 четыре раза.
2. Гипероператор четвёртого уровня — тетрация, повторяющееся возведение в степень. В записи Кнута — две стрелки между цифрами. Пример: 3↑↑3 = 33 = 333 = 327 = 7 625 597 484 987. То есть вторая цифра при наличии двух стрелок означает, что столько раз нужно возвести в степень самого себя первое число. Другими словами, показывает нам высоту степенной башни из первой цифры. Например, запись 5↑↑8 означает башню из восьми пятёрок, нагромождённых друг на друга, как кубики.
Тем, чей мозг совсем заплыл жиром или занят лишь мыслями о том, как найти тян, вкачать своего эльфа или избавиться от прыщей, следует запомнить, что в тетрации выражения высчитываются сверху вниз, или справа налево. Проще говоря, 333 равняется нихуя не 273, а как раз-таки 327. Теперь ты видишь, мой маленький мохнатый друг, что тетрация — уже довольно мощный способ записи, позволяющий коротеньким выражением записывать числа в 100500 раз бо́льшие, чем само 100500. Но это ещё не всё, ибо она является недостаточно мощным гипероператором для вычисления числа Грэма.
3. Идём дальше: гипероператор пятого уровня — пентация (повторяющаяся тетрация). Три стрелочки между цифрами. Вот здесь-то и начинается пиздец, от которого люди, не являющиеся профессиональными математиками, плюют на всю эту лабуду и больше не пытаются её понять. Но ведь ты не такой, как они? Если ты подумал, что пентация числа 3 раскладывается на 3 в степени 7 625 597 484 987, то ты ошибаешься. Ты даже не представляешь, НАСКОЛЬКО ошибаешься. Ибо 3 в степени 7 625 597 484 987 — это всего лишь 3↑↑4.
А пентация — это 3↑↑↑3 = 3↑↑(3↑↑3) = 3↑↑(7 625 597 484 987) = 3↑3…(количество возведений в степень — 7 625 597 484 987 раз)…↑3. То есть, степенная башня из троек получается высотой в более чем семь с половиной триллионов этажей! Иначе говоря, вторая цифра при наличии трёх стрелочек означает, какой высоты будет башня тетраций первой цифры. Для большей наглядности: 3↑↑↑4 можно записать как 3333, либо 3 ↑↑ (3 ↑↑ (3 ↑↑ 3)). И здесь главное — понять, что эта башня из тетраций не есть башня из степеней, тут эскалация намного стремительнее. 3↑↑↑4 = 3333 = 7 625 597 484 98733.
Понял, наконец, сука?! 3↑↑↑4 равняется 3 в тетрации числа, которое получается в результате вычисления степенной башни из цифры 3 высотой в 7 625 597 484 987 этажей. Соответственно, если 3↑↑↑4 записать как степенную башню из троек, то количество этажей в этой башне будет равняться числу, которое получится при вычислении степенной башни высотой в 7 625 597 484 987 этажей. Представил? Не представил, конечно, такие величины с наскоку не осмыслить.
Если ты всё-таки начал потихоньку не понимать, что за херня здесь происходит, то заново перечитай пункт 2.
4. И последний нужный нам гипероператор — гексация. Как вы уже догадались, четыре стрелочки между тройками. Это, соответственно, повторяющаяся пентация. Вторая цифра при наличии четырёх стрелочек означает, какой высоты будет уже «пентационная» башня. 3↑↑↑↑3 = 3↑↑↑(3↑↑↑3) = 3↑↑3↑↑3…3↑↑3, где количество тетраций — результат вычисления пентации 3↑↑↑3. Если опять ничего не понял, то заново прочитай пункты 3 и 2.
Если мы переместимся в самый конец этой немыслимой цепочки тетраций и начнём её вычислять, то уже вторая с конца тройка будет в тетрации равна 7 625 597 484 987. А результатом тетрации третьей тройки с конца будет число, полученное пентацией тройки в предыдущем пункте. А перед нами — ещё гуголплексы и гуголплексы повторяющихся тетраций цифры 3. Тут уже бесполезно что-то пытаться осмыслить, как-то охватить результат… И тут вы, возможно, спросите: «Неужели это число Грэма? Надо же, насколько громадное!» Но нет, это не число Грэма. Это была только математическая присказка, и она ничтожно, неизмеримо мала по сравнению с числом Грэма.
Стало быть, гексация — это всего лишь добавление к пентации одной ссаной стрелочки, но результат оказывается больше в невообразимое количество порядков. А теперь, собственно, вычисление числа Грэма. Цифра три в примерах была использована не просто так, ибо число Грэма по сути и есть перемноженные тройки. Итак, назовём результат нашей гексации (3↑↑↑↑3) G1. Это какбэ был первый шаг вычислений. Только первый. А следующий шаг ускоряет прогрессию так, что добавление одной, десяти, МИЛЛИОНА стрелок между цифрами — топтание на месте. Шаг второй — вычисление G2: теперь мы берём результат нашей гексации тройки и пишем выражение, где число стрелочек сверхстепени будет равно этому результату. G2 = 3↑↑↑↑↑↑↑↑↑↑↑↑↑↑…(количество стрелочек сверхстепени — G1)…↑↑↑↑↑↑↑3. Интересно, как называется гипероператор ТАКОГО уровня?..
Запись не то что результата, но даже этого гипероператора уже невозможна без сокращения. А число, получившееся при его вычислении (если, конечно, его возможно было бы вычислить), заполнило бы своими цифрами и Вселенную, и параллельные миры, и подпространство, и всяческий другой астрал. И не забываем, что в G1 количество стрелочек было равно четырём — и это уже число, недоступное для вычисления и записи обычным способом! А в G2 это число — только количество сверхстепеней. Вот так-то. Прогрессия невероятно стремительная. И это только начало. Следующим шагом идёт вычисление числа G3, где количество стрелочек сверхстепени будет равно G2! Подобным образом после этого следует ещё 62 шага вычислений, где результат каждого шага будет лишь количеством стрелок сверхстепени следующего шага, и число Грэма есть G64!
Ваистену, матан иногда штырит похлеще любых наркотиков.
Мякотка числа также в том, что, несмотря на невозможность записать число полностью, вполне возможно вычислить его последние цифры. Нерды от матана, сперва немного охуев от масштаба числа, взяли себя в руки и высчитали более 500 цифр с конца этого числа. Вот десять самых последних: …2464195387. А какая цифра первая? Ну, калькулятор вам в руки, только имейте в виду, что тепловая смерть Вселенной прервёт ваши вычисления в самом начале.
Moar[править]
Литлвуд первым расставляет точки
Но время идёт, математики не сидят сложа руки, и невозможное для осознания число Грэма больше не является чем-то особенным. В настоящее время самым большим числом является величина под названием «Число Райо» (Rayo’s number). У него даже есть формула и алгоритм вычисления, только вот посчитать как-то не удаётся: мощностей не хватает (и вряд ли когда-нибудь хватит). Поэтому, чтобы хоть как-то его определять, для него придумали следующую языковую конструкцию: «Самое маленькое число, большее, чем любое конечное число, определённое выражением на языке теории множеств с использованием гугола символов или меньше». Аплодисменты.
Видеота[править]
|
Годное видео про сабж. Видеоряд доставляет… |
О сабже с 18-й минуты |
Интересные факты[править]
- Онотоле знает все цифры этого числа. Но вам не скажет.
- Результат степенной башни из гуголплексов в гуголплекс этажей неизмеримо меньше числа Грэма.
См. также[править]
- Четвёртое измерение
- Квадратура круга
Ссылки[править]
- Подробнейшее описание, написанное доставляющим языком
- Число Райо — победитель конкурса в MIT
- Джон Литлвуд о записи самых больших чисел (п. 15), 1948 год
- Ещё одна попытка объяснить вычисление числа Грэма
| Науки | Высшая математика • Евгеника • Матан • Российская • Сопромат • Философия (Детерминизм) |
| Достижения | TeX • Атомная бомба • Биореактор • Большой адронный коллайдер • ГМО • Двести двадцать • Корчеватель • Кубик Рубика • Нанотехнологии • Палата мер и весов • Резонатор Гельмгольца • Роботы • Термоядерный синтез • Чернобыль • Экзоскелет • Фукусима |
| Теории и открытия | Геометрия Лобачевского • Звездчатый многоугольник • Квантовая механика • Когнитивная психология • Популяционная теория Мальтуса • Радиация • Тёмная энергия • Теория большого взрыва (сериал) • Теория относительности • Теория разбитых окон • Теория струн • Четвёртое измерение • Чёрная дыра • Эволюция • Элементарные частицы • Энтропия |
| Мемы | 265 • xkcd • Бритва Оккама • Деление на ноль (Яценюк) • Дигидрогена монооксид • Задача Льва Толстого • Задача Эйнштейна • Закон Мерфи • Закон Парето • Квадратно-гнездовой способ мышления • Квадратура круга • Коробочка фотонов • Кот Шрёдингера • Матановая капча • Критерий Поппера • Метод научного тыка • Пик нефти • Поймать льва в пустыне • Простые числа • Рекурсия • Сферический конь в вакууме • Теорема Абеля — Галуа • Теорема Ферма • Число Грэма • Число Эрдёша |
| Люди и организации | Организации (ИТМО • МФТИ • НМУ) • Байрон • Белоненко • Березовский • Вассерман • Вербицкий • да Винчи • Декарт • Докинз • Инженер • Кэрролл • Лаборатория • Лейбниц • Луговский (цитатник) • Паскаль • Перельманы (Григорий • Яков) • Переслегин • Пятисемиты • Саган • Тейлор • Тесла • Технофашисты • Фейнман • Хайям • Хокинг • Эшер |
| Паранаука | Science freaks/Научное фричество • Scorcher.ru • Артефакт • Великая тайна воды • Вечный двигатель • Гомеопатия • ГСМ • Информационное поле Вселенной • Квадратно-гнездовой способ мышления • Научный креационизм (аргументы) • НЛП • Принцип Арнольда • Соционика • Телегония • Торсионные поля • ХУЯС • Электронный голосовой феномен |
| Фрики и шарлатаны | Sherak • Британские учёные • Бронников • Гаряев • Жданов • Катющик • Лотов • Лысенко • Малахов • Мулдашев • Мухин • Никонов • Олег Т. • Петрик • Протопопов • РАЕН • Скляров • Стерлигов • Фоменко • Чащихин • Чернобров • Чудинов • Чурляев • Чуров |
| Срачи | Бесполезная наука • Взлетит или не взлетит? • Дети индиго • Луносрач • Наука vs религия • Пирамидосрач • Плутоносрач • Физики vs лирики • Шмель летать не должен |
| Числа и цифры | +1 • 1.0 • 2.0 • π • 3,5 • 3,62 • 8/64 • 13 • 14/88 • 16 • 19 • 20 • 25 • 28 • 34 • 38 • 40 • 42 • 51 • 57 • 63 • 77 • 80 • 101 • 121 • 128 • 220 • 228 • 265 • 282 • 314 • 322 • 359 • 404 • 410 • 502 • 640 • 646 • 666 • 1111 • 1138 • 1200+ε • 1337 • 1500 • 1812 • 2000 • 2300 • 3310 • 3605 • 3730 • 9000 • 9600 • 12309 • 40 000 • 100500 • 260602 • 13 000 000 • 1 000 000 000 (Сталинский • Золотой) • 1 208 925 819 614 629 174 706 176 • G64 • ∞ |
| Проценты | 90% женщин • 95% населения • Инфа 100% • 146% |
| Время | 3 секунды • 5 секунд • Полшестого • 7:40 • 10:10 • 1917 год • 1980-е (1984 год) • 1990-е • 2000-е (2000 год) • 2010-е (2012 год) |
| Прочее | 1 Guy 1 Jar • 2 Girls 1 Cup • ⑨ • Sweet home • 2 в 1 • 3 Guys 1 Hammer • 58 видов геев • Автомобильные номера • Гет • ДЕЕ1991ГР • Деление на ноль • Закон Парето • Код • Матан • Матановая капча • Натуральные числа • Простые числа • Вещественные числа • Рулетка • Сотни нефти • Теорема Ферма • Теория относительности • Чуть более, чем наполовину • Семь чудес света • Квадратура круга • Три обезьяны • Monkey dust |
Число Грэма (Грехема, англ. Graham’s number) — большое число, которое является верхней границей для решения определённой проблемы в теории Рамсея. Названо в честь Рональда Грэма (англ.).
Оно стало известно широкой публике после того, как Мартин Гарднер описал его в своей колонке «Математические игры» в журнале Scientific American в ноябре 1977 года, где было сказано: «В неопубликованном доказательстве Грэм недавно установил … границу настолько большую, что ей принадлежит рекорд как наибольшему числу, когда-либо использовавшемуся в серьёзном математическом доказательстве».
В 1980 году Книга рекордов Гиннесса повторила утверждения Гарднера, ещё больше подогрев интерес публики к этому числу. Число Грехема в невообразимое количество раз больше, чем другие хорошо известные большие числа, такие, как гугол, гуголплекс и даже больше, чем число Скьюза и число Мозера. На самом деле, вся наблюдаемая вселенная слишком мала для того, чтобы вместить в себя обыкновенную десятичную запись числа Грехема, предполагая, что запись каждой цифры занимает по меньшей мере объём Планка. Даже степенные башни вида 
В современных математических доказательствах иногда встречаются числа, ещё много бо́льшие, чем число Грехема, например, в работе с конечной формой Фридмана в теореме Краскала.
Содержание
- 1 Проблема Грехема
- 2 Определение числа Грехема
- 2.1 Масштаб числа Грехема
- 3 См. также
- 4 Литература
- 5 Ссылки
Проблема Грехема
Число Грехема связано со следующей проблемой в теории Рамсея:
- Рассмотрим n-мерный гиперкуб и соединим все пары вершин для получения полного графа с
вершинами. Раскрасим каждое ребро этого графа либо в красный, либо в чёрный цвет. При каком наименьшем значении n каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, все из которых лежат в одной плоскости?
Грехем и Ротшильд в 1971 году доказали, что эта проблема имеет решение, N*, и показали что 6 ≤ N* ≤ N, где N — конкретное, точно определённое, очень большое число. На языке стрелочной нотации Кнута оно может быть записано как 

Нижняя граница была улучшена Экзу в 2003 году и Баркли в 2008 году, который показал, что N* должно быть не меньше 13. Таким образом, 13 ≤ N* ≤ N.
Предметом настоящей статьи является верхняя граница G, которая много слабее (то есть больше), чем N; а именно 

Определение числа Грехема
Используя стрелочную нотацию Кнута, число Грехема G может быть записано как
где количество стрелок в каждом слое, начиная с верхнего, определяется числом в следующем слое, то есть
и где верхний индекс у стрелки показывает общее количество стрелок. Другими словами, G вычисляется в 64 шага: на первом шаге мы вычисляем g1 с четырьмя стрелками между тройками, на втором — g2 с g1 стрелок между тройками, на третьем — g3 с g2 стрелок между тройками и так далее, в конце мы вычисляем G = g64 с g63 стрелок между тройками.
Это может быть записано как
где верхний индекс у f означает итерации функций. Функция f является частным случаем гипероператоров, 

Масштаб числа Грехема
Для того, чтобы осознать невероятный размер числа Грехема, полезно попробовать представить через возведение в степень хотя бы первый член (g1) стремительно растущей 64-членной последовательности. На языке тетраций 
где число троек в выражении справа
Теперь каждая тетрация (
, где X — количество 3-ек.
Таким образом,
, где количество троек —
записанное на языке степеней
, где число башен —
и где количество троек в каждой башне, начиная слева, указывается предыдущей башней.
Другими словами, g1 вычисляется путём вычисления количества башен, n = 

1ая башня: 3
2ая башня: 3↑3↑3 (количество троек — 3) = 7625597484987
3я башня: 3↑3↑3↑3↑...↑3 (количество троек — 7625597484987) = ...
.
.
.
g1 = nая башня: 3↑3↑3↑3↑3↑3↑3↑...↑3 (количество троек задаётся результатом вычисления n-1ой башни)
Масштаб первого члена, g1, настолько велик, что его практически невозможно осознать, хотя запись выше относительно проста для понимания. Хотя n это всего лишь количество башен в этой формуле для g1, уже это число много больше количества объёмов Планка, которые содержатся в наблюдаемой вселенной (примерно 8.5*10185). После первого члена нас ожидает ещё 63 члена стремительно растущей последовательности.
См. также
- теорема Краскала
- функция Аккермана
Литература
- Graham, R. L.; Rothschild, B. L. (1971). «Ramsey’s Theorem for n-Parameter Sets». Transactions of the American Mathematical Society 159: 257-292. DOI:10.2307/1996010. The explicit formula for N appears on p. 290.
- Graham, R. L.; Rothschild, B.L. (1978). «Ramsey Theory», Studies in Combinatorics, Rota, G.-G., ed., Mathematical Association of America, 17:80-99. On p. 90, in stating «the best available estimate» for the solution, the explicit formula for N is repeated from the 1971 paper.
- Gardner, Martin (November 1977). «Mathematical Games». Scientific American 237: 18-28.; reprinted (revised 2001) in the following book:
- Gardner Martin The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. — New York, NY: Norton, 2001. — ISBN 0393020231
- Gardner Martin Penrose Tiles to Trapdoor Ciphers. — Washington, D.C.: Mathematical Association of America, 1989. — ISBN 0-88385-521-6
- Exoo, Geoffrey (2003). «A Euclidean Ramsey Problem». Discrete Computational Geometry 29: 223-227. DOI:10.1007/s00454-002-0780-5.
Ссылки
- «Проблема Рамсей о гиперкубах». Geoff Exoo (англ.)
- Weisstein, Eric W. Graham’s number (англ.) на сайте Wolfram MathWorld.
- Как вычислить число Грэма (англ.)
- Numeropedia — the Special Encyclopedia of Numbers (англ.)
| |
|
|---|---|
| Вещественные | Пи • Золотое сечение • Серебряное сечение • e (число Эйлера) • Постоянная Эйлера — Маскерони • Постоянные Фейгенбаума • Постоянная Гельфонда • Константа Бруна • Постоянная Каталана • Постоянная Апери |
| Натуральные | Чёртова дюжина • Число зверя • Число Рамануджана — Харди • Число Грэма • Число Скьюза • Число Мозера |
| Степени десяти | Мириада • Гугол • Асанкхейя • Гуголплекс |
| Степени тысячи | Тысяча • Миллион • Миллиард • Биллион • Триллион • Квадриллион • … • Центиллион |
| Степени двенадцати | Дюжина • Гросс • Масса |





















 вершинами. Раскрасим каждое ребро этого графа либо в красный, либо в чёрный цвет. При каком наименьшем значении n каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, все из которых лежат в одной плоскости?
вершинами. Раскрасим каждое ребро этого графа либо в красный, либо в чёрный цвет. При каком наименьшем значении n каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, все из которых лежат в одной плоскости?





 , где X — количество 3-ек.
, где X — количество 3-ек. , где количество троек —
, где количество троек — 
 , где число башен —
, где число башен — 