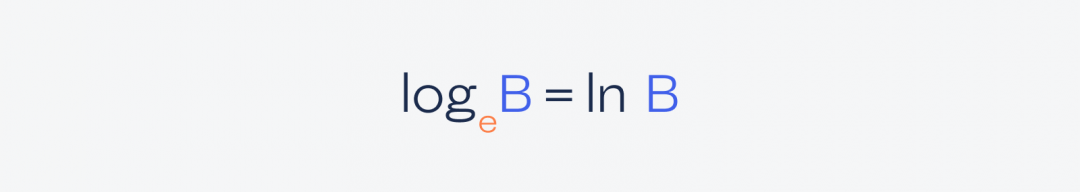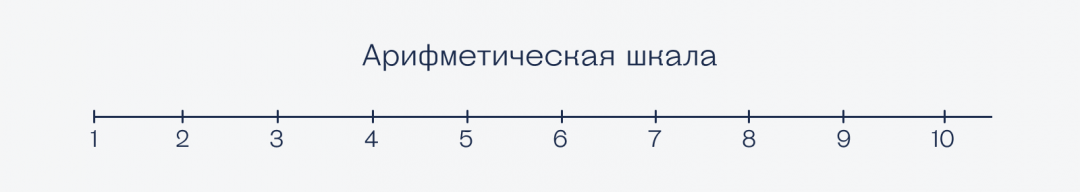Как пишется десятичный логарифм - Граматика и образование на Pisanino.ru

Результатом вычисления логарифма числа является показатель степени, в которую необходимо возвести одно число для получения другого.

Определение десятичного логарифма
Свойства десятичного логарифма
Таблица десятичных логарифмов
График десятичного логарифма

Определение десятичного логарифма

Десятичный логарифм — это логарифм, основанием которого является число 10. Обозначается как lg и пишется следующим образом:

lg y = log₁₀ y = x, при y>0

lg y является решением уравнения y = 10^x. Другими словами, в какую степень (x) необходимо возвести число 10, чтобы получить y.

Связь с натуральным логарифмом

lg x ≈ 0,43429 ln x

Данное соотношение получено путем перехода к новому основанию:

т.к. ln 10 ≈ 2,30259.

Свойства десятичного логарифма

Таблица десятичных логарифмов


x	lg x	x	lg x	x	lg x	x	lg x
1	0	26	1,41497	51	1,70757	76	1,88081
2	0,30103	27	1,43136	52	1,716	77	1,88649
3	0,47712	28	1,44716	53	1,72428	78	1,89209
4	0,60206	29	1,4624	54	1,73239	79	1,89763
5	0,69897	30	1,47712	55	1,74036	80	1,90309
6	0,77815	31	1,49136	56	1,74819	81	1,90849
7	0,8451	32	1,50515	57	1,75587	82	1,91381
8	0,90309	33	1,51851	58	1,76343	83	1,91908
9	0,95424	34	1,53148	59	1,77085	84	1,92428
10	1	35	1,54407	60	1,77815	85	1,92942
11	1,04139	36	1,5563	61	1,78533	86	1,9345
12	1,07918	37	1,5682	62	1,79239	87	1,93952
13	1,11394	38	1,57978	63	1,79934	88	1,94448
14	1,14613	39	1,59106	64	1,80618	89	1,94939
15	1,17609	40	1,60206	65	1,81291	90	1,95424
16	1,20412	41	1,61278	66	1,81954	91	1,95904
17	1,23045	42	1,62325	67	1,82607	92	1,96379
18	1,25527	43	1,63347	68	1,83251	93	1,96848
19	1,27875	44	1,64345	69	1,83885	94	1,97313
20	1,30103	45	1,65321	70	1,8451	95	1,97772
21	1,32222	46	1,66276	71	1,85126	96	1,98227
22	1,34242	47	1,6721	72	1,85733	97	1,98677
23	1,36173	48	1,68124	73	1,86332	98	1,99123
24	1,38021	49	1,6902	74	1,86923	99	1,99564
25	1,39794	50	1,69897	75	1,87506	100	2

microexcel.ru


lg x	1	2	3	4	5	6	7	8	9	10
x	10	10²	10³	10⁴	10⁵	10⁶	10⁷	10⁸	10⁹	10¹⁰

microexcel.ru

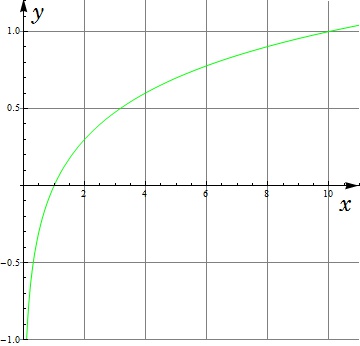
График десятичного логарифма

Функция десятичного логарифма задается как y = lg x. Существует только при неотрицательных значениях переменной x. График выглядит так:

Источник

Десятичный логарифм

Навигация по странице:

Определение
Калькулятор
Свойства
Примеры

Определение. Логарифмом числа b по основанию a, где a > 0, a ≠ 1, b > 0, называется показатель степени, в которую нужно возвести основание a, чтоб получить число b.

Определение. Десятичный логарифм — логарифм по основанию 10.

Другими словами, десятичный логарифм числа b является решением уравнения 10^x = b.

Обозначение. Десятичный логарифм обозначается lg x или log x.

Калькулятор десятичных логарифмов

lg 2

Свойства десятичного логарифмов

Для любых x > 0 и y > 0 выполняются следующие свойства десятичных логарифмов.

lg x = log₁₀ x — так как основание десятичного логарифма равно 10.
10^{lg b} = b.
lg 1 = 0
lg 10 = 1
lg 10ⁿ = n
lg(x · y) = lg x + lg y
lg xy = lg x — lg y
lg xⁿ = n lg x
График функции y = lg x
(lg x)′ = 1x ln 10
∫ lg x dx = x lg x — xln 10 + C

Пример 1. Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.

lg 100 = lg 10² = 2

lg 1000 = lg 10³ = 3

lg 0.1 = lg 10^-1 = -1

lg 0.01 = lg 10^-2 = -2

lg 0.001 = lg 10^-3 = -3

Пример 2.

Доказать равенство: a ^{lg b} = b ^{lg a}.

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10^{lg b · lg a} = 10^{lg a · lg b}

(10^{lg b})^{lg a} = (10^{lg a})^{lg b}

b^{lg a} = a^{lg b}

Равенство доказано.

Пример 3.

Зная, что lg 2 = a, lg 3 = b, lg 5 = c, выразить lg 6; lg 30; lg 16 через a, b, c.

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;

lg 16 = lg 2⁴= 4 · lg 2 = 4a.

Пример 4.

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5lg 9 · lg 27lg 25

Используем свойство логарифма степени lg xⁿ = n lg x:

lg 5lg 9 · lg 27lg 25 = lg 5lg 3² · lg 3³lg 5² = lg 52 lg 3 · 3 lg 32 lg 5 = 34

Пример 5.

Вычислить log₃₀ 8, если lg 5 = a, lg 3 = b.

Перейдем к основе 10:

log ₃₀ 8 = lg 8lg 30 = lg 2³lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 105:

= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 — lg 5)lg 3 + 1 = 3(1 — lg 5)lg 3 + 1 =

Подставим lg 5 = a, lg 3 = b:

= 3(1 — a)b + 1

Ответ:

log₃₀ 8 = 3(1 — a)b + 1

Источник

Понятия и термины

Впервые упоминание о логарифмах встречается в XIX веке в астрономических вычислениях. Сам же термин ввёл в обиход математик Спейдел. В 1893 году обозначать натуральный логарифм буквами ln предложил немецкий учёный Прингсхейм. Но лишь только в книге «Введение в анализ бесконечности» Эйлер дал определения логарифмам и описал их свойства, выделив при этом выражение с основанием равным десяти.

Существует несколько определений логарифмов. Для того чтобы разобраться в сущности термина нужно представить себе любое простое уравнение, содержащее степень. Например, 3^x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.

Теперь можно рассмотреть другое уравнение: 3^x= 7. Если попробовать его решить, то можно обнаружить, что подобрать неизвестное значение будет довольно сложно. Интуитивно можно понять, что ответ будет располагаться между числом три в степени один и три в степени два. Искомое число и было решено назвать логарифмом. Записывается он как x = log3 7. Читается же формула как икс равный логарифму семи по основанию три.

Цифра, стоящая в нижнем регистре записи, называется основанием, а в верхней части аргументом. То есть любое выражение вида c^x = k можно записать как x = logc k. Эта запись очень удобна для обозначения иррациональных чисел.

Логарифм можно записать только при выполнении условия: logp K = b, где pb = k, p > 0, k > 0, p ≠ 0. Существует три вида логарифма:

Обыкновенный. Им называют выражение определённого числа по основанию.
Десятичный. Определение логарифма связано с указаннім основанием равным десяти.
Натуральный. Это логарифм, у которого в основании иррациональная постоянная составляет 2,72, то есть является экспонентной.

Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна, так как используя определение, запись можно переписать в виде: 10² = 100. Для того чтобы научиться решать задачи по нахождению логарифмов нужно знать их свойства, формулы сокращённого умножения и правила вычисления степеней.

Свойства и формулы

Формулы сокращённого умножения изучают в средней школе на уроках алгебры. Учащимся предлагается выучить семь основных выражений, собранных в таблицу. С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:

g²− l²= (g − l) * (g + l).
(g + l)²= g² + 2gl + l².
(g − l)²= g² − 2gl + l².
(g + l) ³= g³+ 3g²l + 3gl²+ l³.
(g − l) ³= g³− 3g²l + 3gl²− l³.
g³+ l³= (g + l) * (g² − gl + l²).
g³− l³= (g − l) * (g² + gl + l²).

На этих формулах основаны свойства десятичных логарифмов. Большинство задач можно решить, зная только эти закономерности. Первое свойство вытекает из самого определения выражения: logp p^v = v. Для доказательства этого свойства можно использовать рассуждение, что если logі p = v, то i^v = p. Тогда отношение logk p / logk I будет равняться: logk i^v / logk I = v * logk i / logk I = v = logі p. Что и требовалось доказать.

Второе и третье свойство помогает определить сумму логарифмов и посчитать их разницу. Согласно ему сумма выражений с одинаковым основанием равняется их произведению: logp i + logp c = logp (i * c). А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.

Четвёртое свойство позволяет при необходимости степень выносить за знак логарифма: logk i^v = n * logk i. Пятое правило гласит, что если в основании логарифма стоит степень, то её можно переместить за знак функции: logkⁿ i = 1/ n * logk i. В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.

Следующее свойство сообщает, что если основание и аргумент имеют степень, то эти показатели можно вынести за знак выражения как дробь: logkⁿ * i^m = (m/n) * logki. При этом если степени совпадают по своему значению, это правило можно записать как log k n i n = log k i. Седьмое свойство помогает решать логарифмы с разным основанием. Так, любой логарифм можно записать в виде равенства: log k i = log c i / log c k.

Эти свойства применимы к любым видам логарифмов. При этом существует ещё одно позволяющее поменять местами основание и аргумент. Для этого нужно просто единицу разделить на логарифм: log k b = 1 / log k b.

Дифференцирование и функция

Производная десятичного логарифма определяется, как отношение в числителе которого стоит единица, а в знаменателе показатель. Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.

Её график определён при p больше нуля. Нужно найти производную по переменной p. По определению производной она ограничивается лимитом: t’ = lim t * ((p + Δ p) – t(p)) / (Δp) = = lim t ( log (p + Δ p) – log p / (Δp)). Используя свойства логарифмов это выражение можно преобразовать до вида: (1/p) * logc (1+ Δp / p)^p/Δp.

Воспользовавшись свойством формулу можно упростить и записать: t’ = 1/t * logc p = (1/t) * (1/ln p) = 1 / t * ln p. То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.

Интеграл функции можно записать выражением: ∫ ln x dx = x * ln x – x + C. Находят его способом интегрирования по частям. Этим методом выражение сводится к более простому виду.

Функцию десятичного логарифма можно записать как y = lg x. График имеет вид плавной возрастающей кривой, которую ещё называют логарифмикой. К основным характеристикам функции относят:

Неупорядоченность.
Область определения, лежащую в интервале от нуля до плюс бесконечности.
Множество значений, принадлежащих области от минус бесконечности до плюс.
Пересечение графика с осью абсцисс в точке (1; 0).
Возрастание кривой на всей области определения.
Отсутствие минимума и максимума.
Знакопостоянство промежутков для значений ординаты больше нуля, принадлежащих области от единицы до плюс бесконечности и для ординаты меньше нуля от нуля до единицы.

Функция монотонная, то есть всё время она не убывает и не возрастает. Иными словами, она всегда неотрицательная или неположительная, но при этом всюду дифференцируемая. Производная для выражения находится с помощью формулы: (d/dx) lg x = lg e / x. Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.

Примеры решения задач

При решении задач на сложение или вычитание логарифмов для быстрого вычисления нужно использовать знания, что десятичное выражение единицы всегда равняется нулю. А также то, что десятичный логарифм десятков, сотен, тысяч и подобных чисел будет иметь столько положительных единиц, сколько нулей содержит число. Например, lg 1000 = 3, lg 1 00000 = 5. В то же время логарифм дробных выражений наподобие 1/10, 1/100, то есть с нулями после единицы в делителе, в ответе будет иметь столько отрицательных цифр, сколько нулей содержится в знаменателе. Например, lg 0,001 = -3.

При решении тождеств, содержащих тригонометрические функции, поможет и сборник таблиц Брадиса. Это пособие, в котором собраны ответы для чаще всего встречающихся типовых выражений.

Следующие типы примеров наиболее часто предлагаются в школе для самостоятельного решения:

Нужно преобразовать заданное выражение до удобного вида и вычислить ответ. Пусть дано отношение: (2* lg 40 – lg 16) / (lg 50 – ½ * (lg 25). Для упрощения этого выражения нужно использовать свойство произведений и степеней. Исходную формулу можно привести к виду: (2 * (lg 4 + lg 10) — lg 4²) / lg 5 + lg 10 — (1/2) * lg 5². После нужно раскрыть скобки и выделить подобные слагаемые, при этом учесть, что lg10 = 1. Таким образом, выражение примет вид: (2 * lg 4 + 2 – 2 * lg 4) / lg 5 + 1 – 1/2 * (2 * lg 5) = 2 / ( lg 5 + 1 – lg 5) = 1 / 2 = 2. То есть сложная дробь превратилась в простую натуральную цифру.
Доказать справедливость или ошибочность линейного неравенства: 3 * lg 0,09 – 2 * lg 27 > -3. Левую часть уравнения можно представить в виде степенного многочлена: 3 * lg 0,09 – 2 * lg 27 = 3 * lg (9/10²) – 2 * lg 27 = 3 * lg (3/10)² – 2 * lg 3³ = 3 * 2 * lg (3/10) – 2 * 3 * lg 3 = 6 * lg (3/10) – 6 * lg 3. Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно.
Найти корень уравнения: lg (4x² — 16x + 144) = lg 2 x + lg(2 x+ 6). Используя свойства знак логарифма можно вынести за скобки: lg (4x² — 16x + 144) = lg (4x² + 12x). В правой и левой части стоит одинаковое действие – логарифмирование. Поэтому на него можно сократить. В итоге получится: 4x² — 16x + 144 = 4x² + 12x. После объединения подобных членов уравнение примет вид двоичного: -4x +144 = 0 или x = 144 / 4 = 36.

Но бывает так, что самостоятельно решить задачу довольно сложно из-за громоздкости записи уравнения. При этом не так сложно провести вычисления, как правильно выбрать алгоритм решения. Поэтому в таких случаях используют так называемые онлайн-калькуляторы.

Использование онлайн-калькулятора

Использовать сервисы предлагающие услуги по вычислению десятичного логарифма, довольно удобно. Всё, что требуется от пользователя, — это интернет-канал и браузер с поддержкой флеш-технологии. Доступ к онлайн-калькуляторам предоставляется бесплатно, при этом даже нет необходимости в регистрации или указании каких-либо данных.

Онлайн-расчётчики позволяют не только получить быстрый и правильный ответ вычисления выражения любой сложности, но и предоставляют подробное решение с пояснениями. Кроме того, на страницах таких сервисов содержится краткая теория с примерами. Так что проблем с понятием, откуда взялся ответ возникнуть не должно.

Программы, используемые для расчётов, написаны на Java и включают в свой алгоритм все необходимые формулы. Пользователь, загрузив сервис должен ввести условие задачи в специально предложенную формулу и нажать кнопку «Решение» или «Вычислить». После чего буквально через две три секунды появится ответ с поэтапным решением.

Такие сервисы будут полезны не только учащимся для проверки своих знаний, но и даже инженерам, проводящим сложные вычисления. Ведь самостоятельный расчёт требует повышенного внимания и скрупулёзности. При этом любая незначительная ошибка приведёт к неправильному ответу. В то же время появление ошибки при вычислении на онлайн-калькуляторе практически невозможно.

По мнению пользователей, из нескольких десятков существующих сайтов можно выделить тройку лидеров:

Kontrolnaya-rabota.
Umath.
Allcalc.
Nauchniestati.
Allworks.

Приведённые онлайн-калькуляторы для десятичного логарифма имеют интуитивно понятный интерфейс. Используемые программы написаны российскими программистами и не содержат рекламного и вредоносного кода. Решив несколько задач с помощью этих порталов, пользователь научится самостоятельно вычислять любые логарифмические уравнения. То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.

Источник

Что такое логарифм

11 июля 2011

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

2¹	2²	2³	2⁴	2⁵	2⁶
2	4	8	16	32	64

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение: log_a x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 2³ = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2³ = 8). С тем же успехом log₂ 64 = 6, поскольку 2⁶ = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

2¹	2²	2³	2⁴	2⁵	2⁶
2	4	8	16	32	64
log₂ 2 = 1	log₂ 4 = 2	log₂ 8 = 3	log₂ 16 = 4	log₂ 32 = 5	log₂ 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log₂ 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 2² < 5 < 2³, а чем больше степень двойки, тем больше получится число.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log₂ 5 = 2,32192809…
log₃ 8 = 1,89278926…
log₅ 100 = 2,86135311…

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log₂ 5, log₃ 8, log₅ 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log_a x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log₂ 0,5 = −1, т.к. 0,5 = 2⁻¹.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной b уравнение: x = a^b;
Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log₅ 25

Представим основание и аргумент как степень пятерки: 5 = 5¹; 25 = 5²;
Составим и решим уравнение:
log₅ 25 = b ⇒ (5¹)^b = 5² ⇒ 5^b = 5² ⇒ b = 2;
Получили ответ: 2.

Задача. Вычислите логарифм:

Представим основание и аргумент как степень тройки: 3 = 3¹; 1/81 = 81⁻¹ = (3⁴)⁻¹ = 3⁻⁴;
Составим и решим уравнение:
Получили ответ: −4.

Задача. Вычислите логарифм: log₄ 64

Представим основание и аргумент как степень двойки: 4 = 2²; 64 = 2⁶;
Составим и решим уравнение:
log₄ 64 = b ⇒ (2²)^b = 2⁶ ⇒ 2^2b = 2⁶ ⇒ 2b = 6 ⇒ b = 3;
Получили ответ: 3.

Задача. Вычислите логарифм: log₁₆ 1

Представим основание и аргумент как степень двойки: 16 = 2⁴; 1 = 2⁰;
Составим и решим уравнение:
log₁₆ 1 = b ⇒ (2⁴)^b = 2⁰ ⇒ 2^4b = 2⁰ ⇒ 4b = 0 ⇒ b = 0;
Получили ответ: 0.

Задача. Вычислите логарифм: log₇ 14

Представим основание и аргумент как степень семерки: 7 = 7¹; 14 в виде степени семерки не представляется, поскольку 7¹ < 14 < 7²;
Из предыдущего пункта следует, что логарифм не считается;
Ответ — без изменений: log₇ 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2³ — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2⁴ — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3⁴ — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log₁₀ x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x. Обозначение: ln x.

Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459…

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log_e x

Таким образом, ln e = 1; ln e² = 2; ln e¹⁶ = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Смотрите также:

Тест к параграфу «Что такое логарифм» (легкий)
Тест к уроку «Что такое логарифм» (средний)
Десятичные дроби
Центральные и вписанные углы в задании 6
Задача B5: вычисление площади методом обводки
Задачи B4: перевозка груза тремя фирмами

Источник

A graph of the common logarithm of numbers from 0.1 to 100

In mathematics, the common logarithm is the logarithm with base 10.^[1] It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered its use, as well as standard logarithm. Historically, it was known as logarithmus decimalis^[2] or logarithmus decadis.^[3] It is indicated by log(x),^[4] log₁₀ (x),^[5] or sometimes Log(x) with a capital L (however, this notation is ambiguous, since it can also mean the complex natural logarithmic multi-valued function). On calculators, it is printed as «log», but mathematicians usually mean natural logarithm (logarithm with base e ≈ 2.71828) rather than common logarithm when they write «log». To mitigate this ambiguity, the ISO 80000 specification recommends that log₁₀ (x) should be written lg(x), and log_e (x) should be ln(x).

Page from a table of common logarithms. This page shows the logarithms for numbers from 1000 to 1500 to five decimal places. The complete table covers values up to 9999.

Before the early 1970s, handheld electronic calculators were not available, and mechanical calculators capable of multiplication were bulky, expensive and not widely available. Instead, tables of base-10 logarithms were used in science, engineering and navigation—when calculations required greater accuracy than could be achieved with a slide rule. By turning multiplication and division to addition and subtraction, use of logarithms avoided laborious and error-prone paper-and-pencil multiplications and divisions.^[1] Because logarithms were so useful, tables of base-10 logarithms were given in appendices of many textbooks. Mathematical and navigation handbooks included tables of the logarithms of trigonometric functions as well.^[6] For the history of such tables, see log table.

Mantissa and characteristic[edit]

An important property of base-10 logarithms, which makes them so useful in calculations, is that the logarithm of numbers greater than 1 that differ by a factor of a power of 10 all have the same fractional part. The fractional part is known as the mantissa.^{[note 1]} Thus, log tables need only show the fractional part. Tables of common logarithms typically listed the mantissa, to four or five decimal places or more, of each number in a range, e.g. 1000 to 9999.

The integer part, called the characteristic, can be computed by simply counting how many places the decimal point must be moved, so that it is just to the right of the first significant digit. For example, the logarithm of 120 is given by the following calculation:

${displaystyle log _{10}(120)=log _{10}left(10^{2}times 1.2right)=2+log _{10}(1.2)approx 2+0.07918.}$

The last number (0.07918)—the fractional part or the mantissa of the common logarithm of 120—can be found in the table shown. The location of the decimal point in 120 tells us that the integer part of the common logarithm of 120, the characteristic, is 2.

Negative logarithms[edit]

Positive numbers less than 1 have negative logarithms. For example,

${displaystyle log _{10}(0.012)=log _{10}left(10^{-2}times 1.2right)=-2+log _{10}(1.2)approx -2+0.07918=-1.92082.}$

To avoid the need for separate tables to convert positive and negative logarithms back to their original numbers, one can express a negative logarithm as a negative integer characteristic plus a positive mantissa. To facilitate this, a special notation, called bar notation, is used:

${displaystyle log _{10}(0.012)approx {bar {2}}+0.07918=-1.92082.}$

The bar over the characteristic indicates that it is negative, while the mantissa remains positive. When reading a number in bar notation out loud, the symbol is read as «bar n«, so that is read as «bar 2 point 07918…». An alternative convention is to express the logarithm modulo 10, in which case

${displaystyle log _{10}(0.012)approx 8.07918{bmod {1}}0,}$

with the actual value of the result of a calculation determined by knowledge of the reasonable range of the result.^{[note 2]}

The following example uses the bar notation to calculate 0.012 × 0.85 = 0.0102:

${displaystyle {begin{array}{rll}{text{As found above,}}&log _{10}(0.012)approx {bar {2}}.07918\{text{Since}};;log _{10}(0.85)&=log _{10}left(10^{-1}times 8.5right)=-1+log _{10}(8.5)&approx -1+0.92942={bar {1}}.92942\log _{10}(0.012times 0.85)&=log _{10}(0.012)+log _{10}(0.85)&approx {bar {2}}.07918+{bar {1}}.92942\&=(-2+0.07918)+(-1+0.92942)&=-(2+1)+(0.07918+0.92942)\&=-3+1.00860&=-2+0.00860;^{*}\&approx log _{10}left(10^{-2}right)+log _{10}(1.02)&=log _{10}(0.01times 1.02)\&=log _{10}(0.0102).end{array}}}$

* This step makes the mantissa between 0 and 1, so that its antilog (10^mantissa) can be looked up.

The following table shows how the same mantissa can be used for a range of numbers differing by powers of ten:

Common logarithm, characteristic, and mantissa of powers of 10 times a number

Number	Logarithm	Characteristic	Mantissa	Combined form
n = 5 × 10ⁱ	log₁₀(n)	i = floor(log₁₀(n))	log₁₀(n) − i
5 000 000	6.698 970…	6	0.698 970…	6.698 970…
50	1.698 970…	1	0.698 970…	1.698 970…
5	0.698 970…	0	0.698 970…	0.698 970…
0.5	−0.301 029…	−1	0.698 970…	1.698 970…
0.000 005	−5.301 029…	−6	0.698 970…	6.698 970…

Note that the mantissa is common to all of the 5 × 10ⁱ. This holds for any positive real number because

${displaystyle log _{10}left(xtimes 10^{i}right)=log _{10}(x)+log _{10}left(10^{i}right)=log _{10}(x)+i.}$

Since i is a constant, the mantissa comes from $log _{{10}}(x)$ , which is constant for given . This allows a table of logarithms to include only one entry for each mantissa. In the example of 5 × 10ⁱ, 0.698 970 (004 336 018 …) will be listed once indexed by 5 (or 0.5, or 500, etc.).

Numbers are placed on slide rule scales at distances proportional to the differences between their logarithms. By mechanically adding the distance from 1 to 2 on the lower scale to the distance from 1 to 3 on the upper scale, one can quickly determine that 2 × 3 = 6.

History[edit]

Common logarithms are sometimes also called «Briggsian logarithms» after Henry Briggs, a 17th century British mathematician. In 1616 and 1617, Briggs visited John Napier at Edinburgh, the inventor of what are now called natural (base-e) logarithms, in order to suggest a change to Napier’s logarithms. During these conferences, the alteration proposed by Briggs was agreed upon; and after his return from his second visit, he published the first chiliad of his logarithms.

Because base-10 logarithms were most useful for computations, engineers generally simply wrote «log(x)» when they meant log₁₀ (x). Mathematicians, on the other hand, wrote «log(x)» when they meant log_e (x) for the natural logarithm. Today, both notations are found. Since hand-held electronic calculators are designed by engineers rather than mathematicians, it became customary that they follow engineers’ notation. So the notation, according to which one writes «ln(x)» when the natural logarithm is intended, may have been further popularized by the very invention that made the use of «common logarithms» far less common, electronic calculators.

Numeric value[edit]

The logarithm keys (log for base-10 and ln for base-e) on a typical scientific calculator. The advent of hand-held calculators largely eliminated the use of common logarithms as an aid to computation.

The numerical value for logarithm to the base 10 can be calculated with the following identities:^[5]

${displaystyle log _{10}(x)={frac {ln(x)}{ln(10)}}quad }$

or ${displaystyle quad log _{10}(x)={frac {log _{2}(x)}{log _{2}(10)}}quad }$

or ${displaystyle quad log _{10}(x)={frac {log _{B}(x)}{log _{B}(10)}}quad }$

using logarithms of any available base

as procedures exist for determining the numerical value for logarithm base e (see Natural logarithm § Efficient computation) and logarithm base 2 (see Algorithms for computing binary logarithms).

Derivative[edit]

The derivative of a logarithm with a base b is such that

${displaystyle {d over dx}log _{b}(x)={1 over xln(b)}}$ , so ${displaystyle {d over dx}log _{10}(x)={1 over xln(10)}}$ .^[7]

Notes[edit]

^ This use of the word mantissa stems from an older, non-numerical, meaning: a minor addition or supplement, e.g., to a text. Nowadays, the word mantissa is generally used to describe the fractional part of a floating-point number on computers, though the recommended term is significand.
^ For example, Bessel, F. W. (1825). «Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermessungen». Astronomische Nachrichten. 331 (8): 852–861. arXiv:0908.1823. Bibcode:1825AN……4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
gives (beginning of section ,
.
From the context, it is understood that
${displaystyle b=10^{6.51335464}}$ , the minor radius of the earth ellipsoid
in toise (a large number), whereas
${displaystyle e=10^{8.9054355-10}}$ , the eccentricity of the earth ellipsoid
(a small number).

References[edit]

^ ^a ^b Hall, Arthur Graham; Frink, Fred Goodrich (1909). «Chapter IV. Logarithms [23] Common logarithms». Trigonometry. Vol. Part I: Plane Trigonometry. New York: Henry Holt and Company. p. 31.
^ Euler, Leonhard; Speiser, Andreas; du Pasquier, Louis Gustave; Brandt, Heinrich; Trost, Ernst (1945) [1748]. Speiser, Andreas (ed.). Introductio in Analysin Infinitorum (Part 2). Opera Omnia, Opera Mathematica. 1 (in Latin). Vol. 9. B.G. Teubner.
^ Scherffer, P. Carolo (1772). Institutionum Analyticarum Pars Secunda de Calculo Infinitesimali Liber Secundus de Calculo Integrali (in Latin). Vol. 2. Joannis Thomæ Nob. De Trattnern. p. 198.
^ «Introduction to Logarithms». www.mathsisfun.com. Retrieved 2020-08-29.
^ ^a ^b Weisstein, Eric W. «Common Logarithm». mathworld.wolfram.com. Retrieved 2020-08-29.
^ Hedrick, Earle Raymond (1913). Logarithmic and Trigonometric Tables. New York, USA: Macmillan.
^ «Derivatives of Logarithmic Functions». Math24. 2021-04-14. Archived from the original on 2020-10-01.

Bibliography[edit]

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Möser, Michael (2009). Engineering Acoustics: An Introduction to Noise Control. Springer. p. 448. ISBN 978-3-540-92722-8.
Poliyanin, Andrei Dmitrievich; Manzhirov, Alexander Vladimirovich (2007) [2006-11-27]. Handbook of mathematics for engineers and scientists. CRC Press. p. 9. ISBN 978-1-58488-502-3.

Источник

A graph of the common logarithm of numbers from 0.1 to 100

Page from a table of common logarithms. This page shows the logarithms for numbers from 1000 to 1500 to five decimal places. The complete table covers values up to 9999.

Mantissa and characteristic[edit]

${displaystyle log _{10}(120)=log _{10}left(10^{2}times 1.2right)=2+log _{10}(1.2)approx 2+0.07918.}$

Negative logarithms[edit]

Positive numbers less than 1 have negative logarithms. For example,

${displaystyle log _{10}(0.012)=log _{10}left(10^{-2}times 1.2right)=-2+log _{10}(1.2)approx -2+0.07918=-1.92082.}$

${displaystyle log _{10}(0.012)approx {bar {2}}+0.07918=-1.92082.}$

${displaystyle log _{10}(0.012)approx 8.07918{bmod {1}}0,}$

with the actual value of the result of a calculation determined by knowledge of the reasonable range of the result.^{[note 2]}

The following example uses the bar notation to calculate 0.012 × 0.85 = 0.0102:

* This step makes the mantissa between 0 and 1, so that its antilog (10^mantissa) can be looked up.

The following table shows how the same mantissa can be used for a range of numbers differing by powers of ten:

Common logarithm, characteristic, and mantissa of powers of 10 times a number

Number	Logarithm	Characteristic	Mantissa	Combined form
n = 5 × 10ⁱ	log₁₀(n)	i = floor(log₁₀(n))	log₁₀(n) − i
5 000 000	6.698 970…	6	0.698 970…	6.698 970…
50	1.698 970…	1	0.698 970…	1.698 970…
5	0.698 970…	0	0.698 970…	0.698 970…
0.5	−0.301 029…	−1	0.698 970…	1.698 970…
0.000 005	−5.301 029…	−6	0.698 970…	6.698 970…

Note that the mantissa is common to all of the 5 × 10ⁱ. This holds for any positive real number because

${displaystyle log _{10}left(xtimes 10^{i}right)=log _{10}(x)+log _{10}left(10^{i}right)=log _{10}(x)+i.}$

History[edit]

Numeric value[edit]

The numerical value for logarithm to the base 10 can be calculated with the following identities:^[5]

${displaystyle log _{10}(x)={frac {ln(x)}{ln(10)}}quad }$

or ${displaystyle quad log _{10}(x)={frac {log _{2}(x)}{log _{2}(10)}}quad }$

or ${displaystyle quad log _{10}(x)={frac {log _{B}(x)}{log _{B}(10)}}quad }$

using logarithms of any available base

as procedures exist for determining the numerical value for logarithm base e (see Natural logarithm § Efficient computation) and logarithm base 2 (see Algorithms for computing binary logarithms).

Derivative[edit]

The derivative of a logarithm with a base b is such that

${displaystyle {d over dx}log _{b}(x)={1 over xln(b)}}$ , so ${displaystyle {d over dx}log _{10}(x)={1 over xln(10)}}$ .^[7]

Notes[edit]

^ This use of the word mantissa stems from an older, non-numerical, meaning: a minor addition or supplement, e.g., to a text. Nowadays, the word mantissa is generally used to describe the fractional part of a floating-point number on computers, though the recommended term is significand.
^ For example, Bessel, F. W. (1825). «Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermessungen». Astronomische Nachrichten. 331 (8): 852–861. arXiv:0908.1823. Bibcode:1825AN……4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
gives (beginning of section ,
.
From the context, it is understood that
${displaystyle b=10^{6.51335464}}$ , the minor radius of the earth ellipsoid
in toise (a large number), whereas
${displaystyle e=10^{8.9054355-10}}$ , the eccentricity of the earth ellipsoid
(a small number).

References[edit]

^ ^a ^b Hall, Arthur Graham; Frink, Fred Goodrich (1909). «Chapter IV. Logarithms [23] Common logarithms». Trigonometry. Vol. Part I: Plane Trigonometry. New York: Henry Holt and Company. p. 31.
^ Euler, Leonhard; Speiser, Andreas; du Pasquier, Louis Gustave; Brandt, Heinrich; Trost, Ernst (1945) [1748]. Speiser, Andreas (ed.). Introductio in Analysin Infinitorum (Part 2). Opera Omnia, Opera Mathematica. 1 (in Latin). Vol. 9. B.G. Teubner.
^ Scherffer, P. Carolo (1772). Institutionum Analyticarum Pars Secunda de Calculo Infinitesimali Liber Secundus de Calculo Integrali (in Latin). Vol. 2. Joannis Thomæ Nob. De Trattnern. p. 198.
^ «Introduction to Logarithms». www.mathsisfun.com. Retrieved 2020-08-29.
^ ^a ^b Weisstein, Eric W. «Common Logarithm». mathworld.wolfram.com. Retrieved 2020-08-29.
^ Hedrick, Earle Raymond (1913). Logarithmic and Trigonometric Tables. New York, USA: Macmillan.
^ «Derivatives of Logarithmic Functions». Math24. 2021-04-14. Archived from the original on 2020-10-01.

Bibliography[edit]

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Möser, Michael (2009). Engineering Acoustics: An Introduction to Noise Control. Springer. p. 448. ISBN 978-3-540-92722-8.
Poliyanin, Andrei Dmitrievich; Manzhirov, Alexander Vladimirovich (2007) [2006-11-27]. Handbook of mathematics for engineers and scientists. CRC Press. p. 9. ISBN 978-1-58488-502-3.

Источник

Для многих логарифм — это самая странная часть в математике: непонятно, как их считать, где применять и как они могут пригодиться в жизни. Сегодня ответим на все эти вопросы.

Что такое логарифм

Задача логарифма — ответить на такой вопрос:

В какую степень нужно возвести одно число, чтобы получилось другое?

На языке математики это будет выглядеть вот так:

Теперь сделаем то же самое, но уже с числами. Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.

Десятичный, натуральный и другие логарифмы

Число A, которое возводят в какую-то степень, называется основанием логарифма. Самые популярные у математиков логарифмы — десятичный и натуральный.

Десятичный логарифм — это когда в основании логарифма стоит число 10. Наша задача в этом случае — найти, в какую степень нужно возвести 10, чтобы получить желаемое число. Обозначается так — lg:

Натуральный логарифм устроен похоже, только вместо десятки в основании логарифма стоит число e, которое примерно равно 2,71828 и называется числом Эйлера. В математике число e играет такую же важную роль, как в геометрии — число пи, поэтому логарифм по основанию e часто встречается во многих математических выкладках и доказательствах.

Обозначается натуральный логарифм так — ln:

Логарифмическая шкала

Если мы возьмём линию и отметим на ней точки через каждый сантиметр, то мы получим арифметическую шкалу. Арифметическую — потому что каждая новая отметка считается арифметическим действием — сложением шага и предыдущего значения:

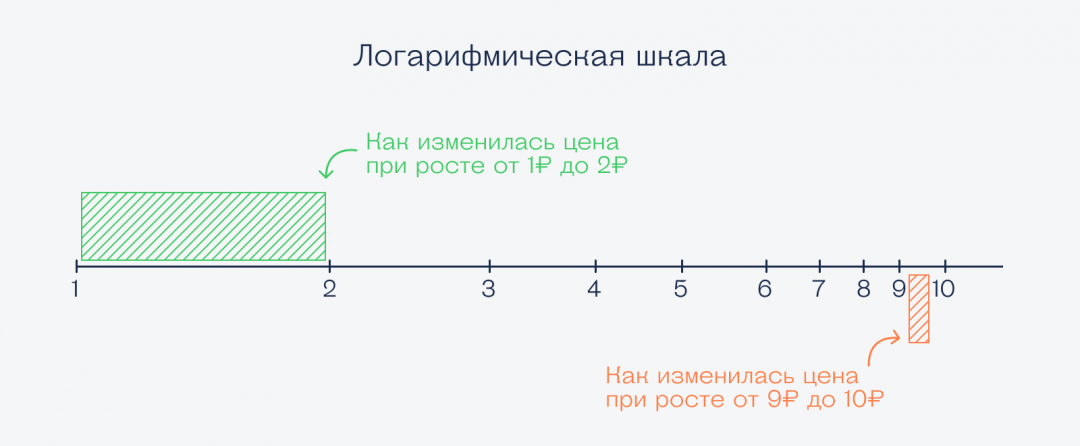
Но если мы вместо сложения возьмём логарифм, например, по основанию 10, то каждая новая отметка будет зависеть от значения десятичного логарифма:

Это выглядит странно, но логарифмическая шкала постоянно применяется в экономике и маркетинге, когда нужно оценить рост или падение стоимости товара. Если взять обычную арифметическую шкалу, то разница между парами (1, 2) и (9, 10) будет одной и той же — 1 пункт.

Но при этом в первом случае цена выросла в 2 раза, с 1 до 2, а во втором случае — всего лишь на 10%. С логарифмической шкалой рост цены будет выглядеть логичнее:

Зачем нужны логарифмы в жизни

Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется. Вот несколько примеров.

Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.

В химии активность водородных ионов тоже считается по логарифмической шкале.

Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.

В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.

Логарифмы в природе

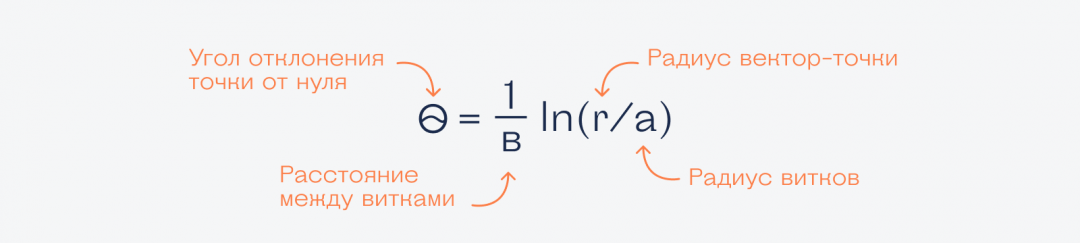
Больше всего логарифмов можно встретить в природе в виде логарифмической спирали. Математическая формула спирали выглядит так:

Если мы захотим построить график этого уравнения, то он будет выглядеть так:

Логарифмическая спираль в математике.

А вот логарифмическая спираль в природе — в ракушках, подсолнечнике и капусте. С капустой ещё связана другая интересная тема — фракталы, но про них поговорим в другой раз.

Даже рога у горных козлов закручиваются по логарифмической спирали:

Что дальше

Теперь мы знаем про логарифмы достаточно, чтобы понять, как они работают. В следующей статье напишем простую программу из двух циклов, которая посчитает нам практически любой логарифм по любому основанию.

Вёрстка:

Кирилл Климентьев

Источник

Определение десятичного логарифма

Свойства десятичного логарифма

Таблица десятичных логарифмов

График десятичного логарифма

Десятичный логарифм

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

Понятия и термины

Свойства и формулы

Дифференцирование и функция

Примеры решения задач

Использование онлайн-калькулятора

Что такое логарифм

Как считать логарифмы

Десятичный логарифм

Натуральный логарифм

Mantissa and characteristic[edit]

Negative logarithms[edit]

History[edit]

Numeric value[edit]

Derivative[edit]

See also[edit]

Notes[edit]

References[edit]

Bibliography[edit]

Mantissa and characteristic[edit]

Negative logarithms[edit]

History[edit]

Numeric value[edit]

Derivative[edit]

See also[edit]

Notes[edit]

References[edit]

Bibliography[edit]

Что такое логарифм

Десятичный, натуральный и другие логарифмы

Логарифмическая шкала

Зачем нужны логарифмы в жизни

Логарифмы в природе

Что дальше