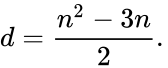The diagonals of a cube with side length 1. AC’ (shown in blue) is a space diagonal with length 

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios,[1] «from angle to angle» (from διά- dia-, «through», «across» and γωνία gonia, «angle», related to gony «knee»); it was used by both Strabo[2] and Euclid[3] to refer to a line connecting two vertices of a rhombus or cuboid,[4] and later adopted into Latin as diagonus («slanting line»).
In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner.
There are also other, non-mathematical uses.
Non-mathematical uses[edit]
A stand of basic scaffolding on a house construction site, with diagonal braces to maintain its structure
In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliers are wire-cutting pliers defined by the cutting edges of the jaws intersects the joint rivet at an angle or «on a diagonal», hence the name.
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.
Polygons[edit]
As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any n-sided polygon (n ≥ 3), convex or concave, has 
|
|
|
|
|
Regions formed by diagonals[edit]
In a convex polygon, if no three diagonals are concurrent at a single point in the interior, the number of regions that the diagonals divide the interior into is given by
For n-gons with n=3, 4, … the number of regions is[5]
- 1, 4, 11, 25, 50, 91, 154, 246…
This is OEIS sequence A006522.[6]
Intersections of diagonals[edit]
If no three diagonals of a convex polygon are concurrent at a point in the interior, the number of interior intersections of diagonals is given by 
Regular polygons[edit]
There exist separate formulae for calculating the length of the longest diagonal in regular polygons with an even or odd number of sides.
In an even-sided regular polygon with n sides and side length a, the length of the longest diagonal is equivalent to the diameter of its circumcircle because the long diagonals all intersect each other at the polygon’s center. This is given by the following formula.
The length of the longest diagonal of any odd-sided regular n-sided polygon (n ≥ 5) with side length a is given by the following formula.[9]
The length of a polygon’s shortest diagonal can also be calculated for all polygons (n ≥ 4) with the following formula.[10] As the number of sides approaches infinity, the shortest diagonal approaches 2a.
These are not applicable for a triangle which has no diagonals.
Special cases include:
A square has two diagonals of equal length, which intersect at the center of the square. The ratio of a diagonal to a side is 
A regular pentagon has five diagonals all of the same length. The ratio of a diagonal to a side is the golden ratio, 
A regular hexagon has nine diagonals: the six shorter ones are equal to each other in length; the three longer ones are equal to each other in length and intersect each other at the center of the hexagon. The ratio of a long diagonal to a side is 2, and the ratio of a short diagonal to a side is 
A regular heptagon has 14 diagonals. The seven shorter ones equal each other, and the seven longer ones equal each other. The reciprocal of the side equals the sum of the reciprocals of a short and a long diagonal.
In general a regular n-gon has 
Polyhedrons[edit]
A polyhedron (a solid object in three-dimensional space, bounded by two-dimensional faces) may have two different types of diagonals: face diagonals on the various faces, connecting non-adjacent vertices on the same face; and space diagonals, entirely in the interior of the polyhedron (except for the endpoints on the vertices).
Just as a triangle has no diagonals, so also a tetrahedron (with four triangular faces) has no face diagonals and no space diagonals.
A cuboid has two diagonals on each of the six faces and four space diagonals.
Matrices[edit]
For a square matrix, the diagonal (or main diagonal or principal diagonal) is the diagonal line of entries running from the top-left corner to the bottom-right corner.[11][12][13] For a matrix 




The top-right to bottom-left diagonal is sometimes described as the minor diagonal or antidiagonal.
The off-diagonal entries are those not on the main diagonal. A diagonal matrix is one whose off-diagonal entries are all zero.[14][15]
A superdiagonal entry is one that is directly above and to the right of the main diagonal.[16][17] Just as diagonal entries are those 


Likewise, a subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry 








Geometry[edit]
By analogy, the subset of the Cartesian product X×X of any set X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the equality relation on X or equivalently the graph of the identity function from X to X. This plays an important part in geometry; for example, the fixed points of a mapping F from X to itself may be obtained by intersecting the graph of F with the diagonal.
In geometric studies, the idea of intersecting the diagonal with itself is common, not directly, but by perturbing it within an equivalence class. This is related at a deep level with the Euler characteristic and the zeros of vector fields. For example, the circle S1 has Betti numbers 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-torus S1xS1 and observe that it can move off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed-point theorem; the self-intersection of the diagonal is the special case of the identity function.
See also[edit]
- Jordan normal form
- Main diagonal
- Diagonal functor
Notes[edit]
- ^ Online Etymology Dictionary
- ^ Strabo, Geography 2.1.36–37
- ^ Euclid, Elements book 11, proposition 28
- ^ Euclid, Elements book 11, proposition 38
- ^ Weisstein, Eric W. «Polygon Diagonal.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonDiagonal.html
- ^ Sloane, N. J. A. (ed.). «Sequence A006522». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Poonen, Bjorn; Rubinstein, Michael. «The number of intersection points made by the diagonals of a regular polygon». SIAM J. Discrete Math. 11 (1998), no. 1, 135–156; link to a version on Poonen’s website
- ^ [1], beginning at 2:10
- ^ «Murderous Maths: The LOngest Diagonal Formula!».
- ^ «Length of Diagonal of a n-sided regular polygon». 2 January 2019.
- ^ Bronson (1970, p. 2)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Bronson (1970, pp. 203, 205)
- ^ Herstein (1964, p. 239)
- ^ Cullen (1966, p. 114)
References[edit]
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
External links[edit]
Look up diagonal in Wiktionary, the free dictionary.
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld.
- Diagonal of a matrix from MathWorld.
The diagonals of a cube with side length 1. AC’ (shown in blue) is a space diagonal with length 

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios,[1] «from angle to angle» (from διά- dia-, «through», «across» and γωνία gonia, «angle», related to gony «knee»); it was used by both Strabo[2] and Euclid[3] to refer to a line connecting two vertices of a rhombus or cuboid,[4] and later adopted into Latin as diagonus («slanting line»).
In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner.
There are also other, non-mathematical uses.
Non-mathematical uses[edit]
A stand of basic scaffolding on a house construction site, with diagonal braces to maintain its structure
In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliers are wire-cutting pliers defined by the cutting edges of the jaws intersects the joint rivet at an angle or «on a diagonal», hence the name.
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.
Polygons[edit]
As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any n-sided polygon (n ≥ 3), convex or concave, has 
|
|
|
|
|
Regions formed by diagonals[edit]
In a convex polygon, if no three diagonals are concurrent at a single point in the interior, the number of regions that the diagonals divide the interior into is given by
For n-gons with n=3, 4, … the number of regions is[5]
- 1, 4, 11, 25, 50, 91, 154, 246…
This is OEIS sequence A006522.[6]
Intersections of diagonals[edit]
If no three diagonals of a convex polygon are concurrent at a point in the interior, the number of interior intersections of diagonals is given by 
Regular polygons[edit]
There exist separate formulae for calculating the length of the longest diagonal in regular polygons with an even or odd number of sides.
In an even-sided regular polygon with n sides and side length a, the length of the longest diagonal is equivalent to the diameter of its circumcircle because the long diagonals all intersect each other at the polygon’s center. This is given by the following formula.
The length of the longest diagonal of any odd-sided regular n-sided polygon (n ≥ 5) with side length a is given by the following formula.[9]
The length of a polygon’s shortest diagonal can also be calculated for all polygons (n ≥ 4) with the following formula.[10] As the number of sides approaches infinity, the shortest diagonal approaches 2a.
These are not applicable for a triangle which has no diagonals.
Special cases include:
A square has two diagonals of equal length, which intersect at the center of the square. The ratio of a diagonal to a side is 
A regular pentagon has five diagonals all of the same length. The ratio of a diagonal to a side is the golden ratio, 
A regular hexagon has nine diagonals: the six shorter ones are equal to each other in length; the three longer ones are equal to each other in length and intersect each other at the center of the hexagon. The ratio of a long diagonal to a side is 2, and the ratio of a short diagonal to a side is 
A regular heptagon has 14 diagonals. The seven shorter ones equal each other, and the seven longer ones equal each other. The reciprocal of the side equals the sum of the reciprocals of a short and a long diagonal.
In general a regular n-gon has 
Polyhedrons[edit]
A polyhedron (a solid object in three-dimensional space, bounded by two-dimensional faces) may have two different types of diagonals: face diagonals on the various faces, connecting non-adjacent vertices on the same face; and space diagonals, entirely in the interior of the polyhedron (except for the endpoints on the vertices).
Just as a triangle has no diagonals, so also a tetrahedron (with four triangular faces) has no face diagonals and no space diagonals.
A cuboid has two diagonals on each of the six faces and four space diagonals.
Matrices[edit]
For a square matrix, the diagonal (or main diagonal or principal diagonal) is the diagonal line of entries running from the top-left corner to the bottom-right corner.[11][12][13] For a matrix 




The top-right to bottom-left diagonal is sometimes described as the minor diagonal or antidiagonal.
The off-diagonal entries are those not on the main diagonal. A diagonal matrix is one whose off-diagonal entries are all zero.[14][15]
A superdiagonal entry is one that is directly above and to the right of the main diagonal.[16][17] Just as diagonal entries are those 


Likewise, a subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry 








Geometry[edit]
By analogy, the subset of the Cartesian product X×X of any set X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the equality relation on X or equivalently the graph of the identity function from X to X. This plays an important part in geometry; for example, the fixed points of a mapping F from X to itself may be obtained by intersecting the graph of F with the diagonal.
In geometric studies, the idea of intersecting the diagonal with itself is common, not directly, but by perturbing it within an equivalence class. This is related at a deep level with the Euler characteristic and the zeros of vector fields. For example, the circle S1 has Betti numbers 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-torus S1xS1 and observe that it can move off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed-point theorem; the self-intersection of the diagonal is the special case of the identity function.
See also[edit]
- Jordan normal form
- Main diagonal
- Diagonal functor
Notes[edit]
- ^ Online Etymology Dictionary
- ^ Strabo, Geography 2.1.36–37
- ^ Euclid, Elements book 11, proposition 28
- ^ Euclid, Elements book 11, proposition 38
- ^ Weisstein, Eric W. «Polygon Diagonal.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonDiagonal.html
- ^ Sloane, N. J. A. (ed.). «Sequence A006522». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Poonen, Bjorn; Rubinstein, Michael. «The number of intersection points made by the diagonals of a regular polygon». SIAM J. Discrete Math. 11 (1998), no. 1, 135–156; link to a version on Poonen’s website
- ^ [1], beginning at 2:10
- ^ «Murderous Maths: The LOngest Diagonal Formula!».
- ^ «Length of Diagonal of a n-sided regular polygon». 2 January 2019.
- ^ Bronson (1970, p. 2)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Bronson (1970, pp. 203, 205)
- ^ Herstein (1964, p. 239)
- ^ Cullen (1966, p. 114)
References[edit]
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
External links[edit]
Look up diagonal in Wiktionary, the free dictionary.
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld.
- Diagonal of a matrix from MathWorld.
Диагональ (греч. διαγώνιος от δια- «через» и γώνια «угол») в математике имеет геометрический смысл, а также используется при описании квадратных матриц.
Шестиугольник с диагоналями
Многоугольники и многогранники
Для многоугольников, диагональ это отрезок, соединяющий две вершины, не лежащие на одной стороне. Так, четырёхугольник имеет две диагонали, соединяющие противолежащие вершины. У выпуклого многоугольника диагонали проходят внутри него. Многоугольник выпуклый тогда и только тогда, когда его диагонали лежат внутри.
Пусть 


,
однако, мы посчитали каждую диагональ дважды (по разу для каждого конца) — отсюда,
Диагональю многогранника называется отрезок, соединяющий две его вершины, не принадлежащие одной грани. Так, на изображении куба отмечена диагональ 

Аналогично можно определить диагональ и для многогранников в пространствах бо́льших размерностей.
Матрицы
В случае с квадратными матрицами, главная диагональ является диагональной линией элементов, которая проходит с северо-запада на юго-восток. Например, единичная матрица может быть описана, как матрица, имеющая единицы на главной диагонали и нули вне её. Диагональ с юго-запада на северо-восток часто называется побочной диагональю. Наддиагональными элементами называются такие, что лежат выше и правее главной диагонали. Поддиагональными — те, что ниже и левее. Диагональная матрица — такая матрица, у которой все элементы вне главной диагонали равны нулю.
Теория множеств
По аналогии, подмножество декартового произведения X×X произвольного множества X на само себя, состоящее из пар элементов (x, x), называется диагональю множества. Это — единичное отношение, оно играет важную роль в геометрии: например, константные элементы отображения F с X в X могут быть получены сечением F с диагональю множества X.
Внешние ссылки
- Диагонали многоугольника с интерактивными анимациями
- Диагонали многоугольника с MathWorld.
- Диагонали матриц от MathWorld.

3 { dis playstyle { sqrt {3}}}

2 { displaystyle { sqrt {2}} }

В геометрии диагональ — это отрезок линии, соединяющий две вершины многоугольника или многогранник, когда эти вершины не находятся на одном ребре . Неформально любую наклонную линию называют диагональной. Слово «диагональ» происходит от древнегреческого διαγώνιος diagonios, «от угла к углу» (от διά- dia-, «через», «поперек» и γωνία gonia, «угол», относящегося к коленному суставу). «); он использовался как Страбон, так и Евклидом для обозначения линии, соединяющей две вершины ромба или кубоида, а позже был принят в Латинское как диагонус («косая линия»).
В матричной алгебре диагональ квадратной матрицы представляет собой набор элементов, простирающихся от одного угла до самого дальнего угла.
Есть и другие нематематические применения.
Содержание
- 1 Нематематическое использование
- 2 Многоугольники
- 2.1 Области, образованные диагоналями
- 2.2 Пересечения диагоналей
- 2.3 Правильные многоугольники
- 3 Многогранники
- 4 Матрицы
- 5 Геометрия
- 6 См. Также
- 7 Примечания
- 8 Ссылки
- 9 Внешние ссылки
Нематематические применения

В инженерии диагональная скоба — это балка, используемая для крепления прямоугольной конструкции (такой как строительные леса ), чтобы выдерживать сильные силы, проталкивающие ее; хотя диагональные скобы называются диагональными, из практических соображений они часто не соединяются с углами прямоугольника.
Диагональные плоскогубцы — это кусачки, режущие кромки челюстей которых пересекают соединительную заклепку под углом или «по диагонали», отсюда и название.
A диагональная найтовка — это тип найтовки, используемой для связывания лонжеронов или стоек вместе, применяемых таким образом, чтобы найтовы пересекали стойки под углом.
В ассоциативном футболе система управления по диагонали — это метод, который судьи и помощники судьи используют для позиционирования себя в одном из четырех квадрантов поля.

Многоугольники
Применительно к многоугольнику диагональ — это линейный сегмент, соединяющий любые две непоследовательные вершины. Следовательно, четырехугольник имеет две диагонали, соединяющие противоположные пары вершин. Для любого выпуклого многоугольника все диагонали находятся внутри многоугольника, но для повторно входящих многоугольников некоторые диагонали находятся за пределами многоугольника.
Любой n-сторонний многоугольник (n ≥ 3), выпуклый или вогнутый, имеет n (n — 3) 2 { displaystyle { tfrac {n (n-3)} {2}}}
|
|
|
|
|
Области, образованные диагоналями
В выпуклом многоугольнике, если никакие три диагонали не параллельны в одной точке внутри, количество областей, в которых диагонали разделить внутреннее пространство на:
- (n 4) + (n — 1 2) = (n — 1) (n — 2) (n 2 — 3 n + 12) 24. { Displaystyle { binom {n} {4}} + { binom {n-1} {2}} = { frac {(n-1) (n-2) (n ^ {2} -3n + 12)} {24}}.}
Для n-угольников с n = 3, 4,… количество регионов
- 1, 4, 11, 25, 50, 91, 154, 246…
Это последовательность OEIS A006522.
Пересечение диагоналей
Если никакие три диагонали выпуклого многоугольника не совпадают в точке во внутренней части, количество внутренних пересечений диагоналей равно (n 4) { displaystyle { binom {n} {4}}}
Правильные многоугольники
A треугольник не имеет диагоналей.
A квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне 2 ≈ 1,414. { displaystyle { sqrt {2}} приблизительно 1,414.}
A правильный пятиугольник имеет пять диагоналей одинаковой длины. Отношение диагонали к стороне — это золотое сечение, 1 + 5 2 ≈ 1,618. { displaystyle { frac {1 + { sqrt {5}}} {2}} около 1,618.}
У правильного шестиугольника девять диагоналей: шесть более коротких равны каждой другие по длине; три более длинных равны друг другу по длине и пересекают друг друга в центре шестиугольника. Отношение длинной диагонали к стороне равно 2, а отношение короткой диагонали к стороне составляет 3 { displaystyle { sqrt {3}}}
Правильный семиугольник имеет 14 диагоналей. Семь более коротких равны друг другу, а семь более длинных равны друг другу. Обратная сторона равна сумме обратных величин короткой и длинной диагонали.
В любом правильном n-угольнике с четным n все длинные диагонали пересекаются друг с другом в центре многоугольника.
Многогранники
A многогранник (твердый объект в трехмерном пространстве, ограниченный двухмерным грани ) могут иметь два разных типа диагоналей: диагонали граней на разных гранях, соединяющие несмежные вершины на одной грани; и пробел диагонали, полностью внутри многогранника (за исключением концов на вершинах).
Так же, как треугольник не имеет диагоналей, так и тетраэдр (с четырьмя треугольными гранями) не имеет диагоналей граней и диагоналей пространства.
A Кубоид имеет две диагонали на каждой из шести граней и четыре диагонали пространства.
Матрицы
В случае квадратной матрицы главная или главная диагональ — это диагональная линия записей, идущая от верхнего левого угла к нижнему правому угол. Для матрицы A { displaystyle A}




- (1 0 0 0 1 0 0 0 1) { displaystyle { begin {pmatrix } 1 0 0 \ 0 1 0 \ 0 0 1 end {pmatrix}}}
Диагональ от верхнего правого до нижнего левого угла иногда описывается как меньшая диагональ или антидиагональ. Недиагональные записи — это те, которые не находятся на главной диагонали. Диагональная матрица — это матрица, все недиагональные элементы которой равны нулю.
Супердиагональная матрица — это матрица, которая находится непосредственно над и справа от главной диагонали. Так же, как диагональные записи — это те A ij { displaystyle A_ {ij}}


- (0 2 0 0 0 3 0 0 0) { displaystyle { begin {pmatrix} 0 2 0 \ 0 0 3 \ 0 0 0 end {pmatrix}}}
Аналогично, поддиагональная запись — это запись, которая находится непосредственно под и слева от главной диагонали, то есть запись A ij { displaystyle A_ {ij}}








Геометрия
По аналогии, подмножество в декартовом произведении X × X любого набора X сам с собой, состоящий из всех пар (x, x), называется диагональю и является графиком отношения равенства отношения на X или, что эквивалентно, график функции тождества от X до x. Это играет важную роль в геометрии; например, неподвижные точки отображения F из X в себя могут быть получены путем пересечения графика F с диагональю.
В геометрических исследованиях распространена идея пересечения диагонали с самой собой, причем не напрямую, а путем нарушения ее в рамках класса эквивалентности. Это связано на глубоком уровне с характеристикой Эйлера и нулями векторных полей. Например, круг S имеет числа Бетти 1, 1, 0, 0, 0 и, следовательно, характеристику Эйлера 0. Геометрический способ выразить это — посмотреть на диагональ на два- тор SxS и заметим, что он может отодвинуться от себя небольшим движением (θ, θ) к (θ, θ + ε). В общем, число пересечений графика функции с диагональю может быть вычислено с использованием гомологии с помощью теоремы Лефшеца о неподвижной точке ; самопересечение диагонали является частным случаем тождественной функции.
См. Также
- нормальная форма Джордана
- Основная диагональ
- Диагональный функтор
Примечания
Ссылки
- Ричард Бронсон (1970), Матричные методы: введение, Нью-Йорк: Academic Press, LCCN 70097490
- Каллен, Чарльз Г. (1966), Матрицы и линейные преобразования, Литература: Addison-Wesley, LCCN 66021267
- Herstein, IN (1964), Topics In Algebra, Waltham:, ISBN 978-1114541016
- Неринг, Эвар D. (1970), Линейная алгебра и теория матриц (2-е изд.), Нью-Йорк: Wiley, LCCN 76091646
Внешние ссылки
| Искать диагональ в Викисловаре, бесплатный словарь. |
- Диагонали многоугольника с интерактивной анимацией
- Диагональ многоугольника из MathWorld.
- Диагональ матрицы из MathWorld.
В математике, диагональ имеет геометрический смысл, а также используется в терминах квадратных матриц.
Файл:Diagonals.svg Шестиугольник с диагоналями
Многоугольники
Для многоугольников, диагональ это отрезок, соединяющий две вершины, не лежащие на одной стороне. Так, четырёхугольник имеет две диагонали, соединяющие противолежащие вершины. У выпуклого многоугольника диагонали проходят внутри него. Это не выполняется для самопересекающихся многоугольников. Многоугольник выпуклый тогда и только тогда, когда его диагонали лежат внутри.
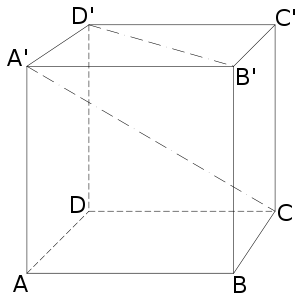
Пусть n — число вершин многоугольника, вычислим d — число возможных разных диагоналей. Каждая вершина соединена диагоналями со всеми другими вершинами, кроме двух соседних и, естественно, себя самой. Таким образом, из одной вершины можно провести n-3 диагонали; перемножим это на число вершин
- (n − 3) × n,
однако, мы посчитали каждую диагональ дважды (по разу для каждого конца) — отсюда,
Матрицы
В случае с квадратными матрицами, главная диагональ является диагональной линией элементов, которая проходит с северо-запада на юго-восток. Например, единичная матрица может быть описана, как матрица, имеющая единицы на главной диагонали и нули вне её. Диагональ с юго-запада на северо-восток часто называется побочная диагональ. Наддиагональными элементами называются такие, что лежат выше и правее главной диагонали. Поддиагональными — те, что ниже и левее. Диагональная матрица — такая матрица, у которой все элементы вне главной диагонали равны нулю.
Формула расчета диагонали квадрата — дополнить статью…
Теория множеств
По аналогии, подмножество декартового произведения X×X произвольного множества X на само себя, состоящее из пар элементов (x, x), называется диагональю множества. Это — единичное отношение, оно играет важную роль в геометрии: например, константные элементы отображения F с X в X могут быть получены сечением F с диагональю множества X.
Внешние ссылки.
- Диагонали многоугольникка с интерактивными анимациями
- Диагонали многоугольника с MathWorld.
- Диагонали матриц от MathWorld.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Диагональ. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .








 ,
,