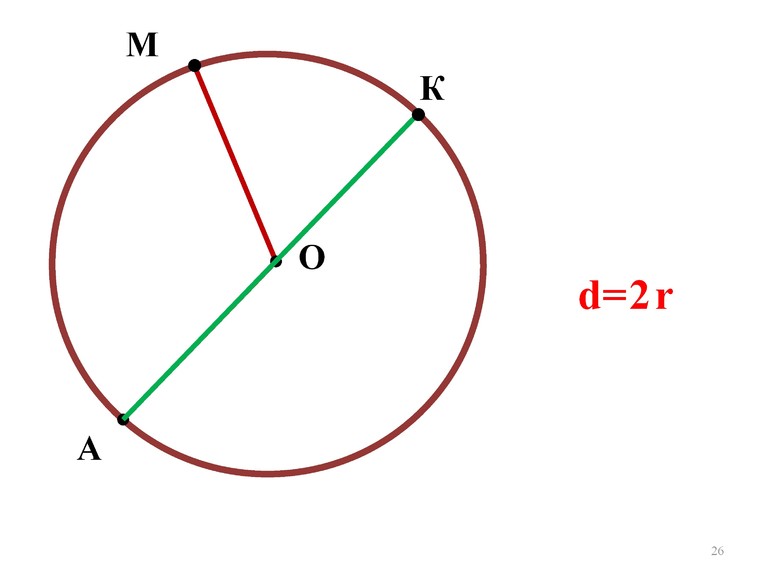
Circle with
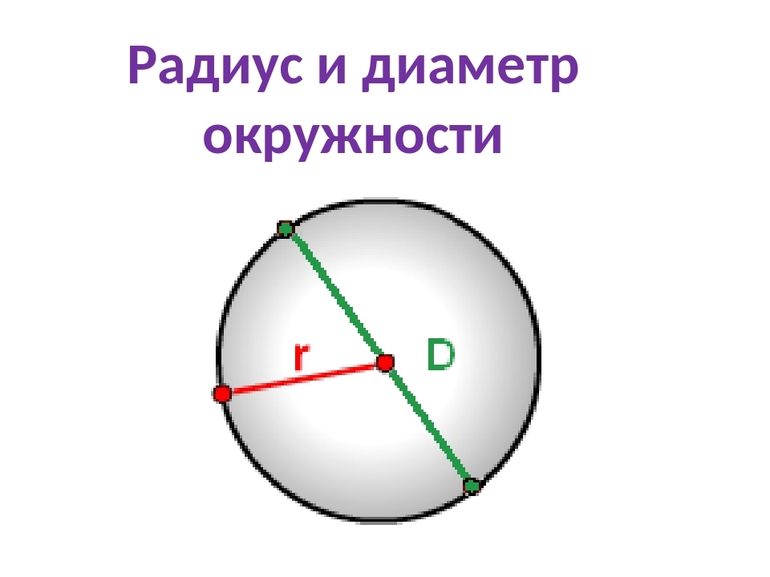
diameter D
radius R
center or origin O
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length 

For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the width is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers.[1] For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.
For an ellipse, the standard terminology is different. A diameter of an ellipse is any chord passing through the centre of the ellipse.[2] For example, conjugate diameters have the property that a tangent line to the ellipse at the endpoint of one diameter is parallel to the conjugate diameter. The longest diameter is called the major axis.
The word «diameter» is derived from Ancient Greek: διάμετρος (diametros), «diameter of a circle», from διά (dia), «across, through» and μέτρον (metron), «measure».[3] It is often abbreviated 

Generalizations[edit]
The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of 


If the metric 





For any solid object or set of scattered points in 
In differential geometry, the diameter is an important global Riemannian invariant.
In planar geometry, a diameter of a conic section is typically defined as any chord which passes through the conic’s centre; such diameters are not necessarily of uniform length, except in the case of the circle, which has eccentricity 
Symbol[edit]
Sign ⌀ in a technical drawing
Sign U+2205 ∅ EMPTY SET from an AutoCAD drawing in dim.shx font with an angle 16°. This font does not contain U+2300 ⌀ DIAMETER SIGN.
Not to be confused with the Scandinavian letter «Ø», the empty set symbol «∅«, the slashed zero, or the greek letter phi (Φ).
The symbol or variable for diameter, ⌀, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. «⌀ 55 mm»), indicating that it represents diameter. For example, photographic filter thread sizes are often denoted in this way.
In German, the diameter symbol (German Durchmesserzeichen) is also used as an average symbol (Durchschnittszeichen).
Similar symbols[edit]
The Latin small letter o with stroke ø is similar in size and design to this. The diameter symbol ⌀ is distinct from the empty set symbol ∅, from an (italic) uppercase phi Φ, and from the Nordic vowel Ø (Latin capital letter O with stroke).[5] See also slashed zero.
Encodings[edit]
The symbol has a Unicode code point at U+2300 ⌀ DIAMETER SIGN, in the Miscellaneous Technical set. On an Apple Macintosh, the diameter symbol can be entered via the character palette (this is opened by pressing ⌥ Opt⌘ CmdT in most applications), where it can be found in the Technical Symbols category. In Unix/Linux/ChromeOS systems, it is generated using Ctrl+⇧ Shift+U 2300space. It can be obtained in Unix-like operating systems using a Compose key by pressing, in sequence, Composedi.[6] In Windows, it can be entered in most programs with Alt code 8960.
The character will sometimes not display correctly, however, since many fonts do not include it. In many situations, the Nordic letter ø at Unicode U+00F8 ø LATIN SMALL LETTER O WITH STROKE (ø) is an acceptable substitute. It can be entered on a Macintosh by pressing ⌥ OptO (the letter o, not the number 0). In Unix/Linux/ChromeOS systems, it is generated using Ctrl+⇧ Shift+U F8space or Composeo/. AutoCAD uses U+2205 ∅ EMPTY SET available as a shortcut string %%c.
In Microsoft Word, the diameter symbol can be acquired by typing 2300 and then pressing Alt+X.
In LaTeX, the diameter symbol can be obtained with the command diameter from the «wasysym» package.[7]
Diameter vs. radius[edit]
The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in the Euclidean metric. The page on Jung’s theorem discusses some more general inequalities relating the diameter to the radius.
See also[edit]
- Angular diameter – How large a sphere or circle appears
- Caliper, micrometer, tools for measuring diameters
- Conjugate diameters – Perpendicular diameters of a circle or hyperbolic-orthogonal diameters of a hyperbola
- Diameter (group theory), a concept in group theory
- Eratosthenes, who calculated the diameter of the Earth around 240 BC.
- Graph or network diameter – Length of shortest path between two nodes of a graph
- Hydraulic diameter
- Inside diameter* Semidiameter – Term in geometry; half of a shape’s diameter
- Sauter mean diameter
- Tangent lines to circles – Line which touches a circle at exactly one point
- The diameters of a screwthread
- Ø (disambiguation)
References[edit]
- ^ Toussaint, Godfried T. (1983). «Solving geometric problems with the rotating calipers». Proc. MELECON ’83, Athens. CiteSeerX 10.1.1.155.5671.
- ^ Bogomolny, Alexander. «Conjugate Diameters in Ellipse». www.cut-the-knot.org.
- ^ «diameter — Origin and meaning of diameter by Online Etymology Dictionary». www.etymonline.com.
- ^ «Re: diameter of an empty set». at.yorku.ca.
- ^ Korpela, Jukka K. (2006), Unicode Explained, O’Reilly Media, Inc., pp. 23–24, ISBN 978-0-596-10121-3.
- ^ Monniaux, David. «UTF-8 (Unicode) compose sequence». Retrieved 2018-07-13.
- ^ «wasysym – LaTeX support for the wasy fonts». Comprehensive TeX Archive Network. Retrieved 2022-03-11.
Look up diameter in Wiktionary, the free dictionary.
Circle with
diameter D
radius R
center or origin O
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length 

For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the width is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers.[1] For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.
For an ellipse, the standard terminology is different. A diameter of an ellipse is any chord passing through the centre of the ellipse.[2] For example, conjugate diameters have the property that a tangent line to the ellipse at the endpoint of one diameter is parallel to the conjugate diameter. The longest diameter is called the major axis.
The word «diameter» is derived from Ancient Greek: διάμετρος (diametros), «diameter of a circle», from διά (dia), «across, through» and μέτρον (metron), «measure».[3] It is often abbreviated 

Generalizations[edit]
The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of 


If the metric 





For any solid object or set of scattered points in 
In differential geometry, the diameter is an important global Riemannian invariant.
In planar geometry, a diameter of a conic section is typically defined as any chord which passes through the conic’s centre; such diameters are not necessarily of uniform length, except in the case of the circle, which has eccentricity 
Symbol[edit]
Sign ⌀ in a technical drawing
Sign U+2205 ∅ EMPTY SET from an AutoCAD drawing in dim.shx font with an angle 16°. This font does not contain U+2300 ⌀ DIAMETER SIGN.
Not to be confused with the Scandinavian letter «Ø», the empty set symbol «∅«, the slashed zero, or the greek letter phi (Φ).
The symbol or variable for diameter, ⌀, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. «⌀ 55 mm»), indicating that it represents diameter. For example, photographic filter thread sizes are often denoted in this way.
In German, the diameter symbol (German Durchmesserzeichen) is also used as an average symbol (Durchschnittszeichen).
Similar symbols[edit]
The Latin small letter o with stroke ø is similar in size and design to this. The diameter symbol ⌀ is distinct from the empty set symbol ∅, from an (italic) uppercase phi Φ, and from the Nordic vowel Ø (Latin capital letter O with stroke).[5] See also slashed zero.
Encodings[edit]
The symbol has a Unicode code point at U+2300 ⌀ DIAMETER SIGN, in the Miscellaneous Technical set. On an Apple Macintosh, the diameter symbol can be entered via the character palette (this is opened by pressing ⌥ Opt⌘ CmdT in most applications), where it can be found in the Technical Symbols category. In Unix/Linux/ChromeOS systems, it is generated using Ctrl+⇧ Shift+U 2300space. It can be obtained in Unix-like operating systems using a Compose key by pressing, in sequence, Composedi.[6] In Windows, it can be entered in most programs with Alt code 8960.
The character will sometimes not display correctly, however, since many fonts do not include it. In many situations, the Nordic letter ø at Unicode U+00F8 ø LATIN SMALL LETTER O WITH STROKE (ø) is an acceptable substitute. It can be entered on a Macintosh by pressing ⌥ OptO (the letter o, not the number 0). In Unix/Linux/ChromeOS systems, it is generated using Ctrl+⇧ Shift+U F8space or Composeo/. AutoCAD uses U+2205 ∅ EMPTY SET available as a shortcut string %%c.
In Microsoft Word, the diameter symbol can be acquired by typing 2300 and then pressing Alt+X.
In LaTeX, the diameter symbol can be obtained with the command diameter from the «wasysym» package.[7]
Diameter vs. radius[edit]
The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in the Euclidean metric. The page on Jung’s theorem discusses some more general inequalities relating the diameter to the radius.
See also[edit]
- Angular diameter – How large a sphere or circle appears
- Caliper, micrometer, tools for measuring diameters
- Conjugate diameters – Perpendicular diameters of a circle or hyperbolic-orthogonal diameters of a hyperbola
- Diameter (group theory), a concept in group theory
- Eratosthenes, who calculated the diameter of the Earth around 240 BC.
- Graph or network diameter – Length of shortest path between two nodes of a graph
- Hydraulic diameter
- Inside diameter* Semidiameter – Term in geometry; half of a shape’s diameter
- Sauter mean diameter
- Tangent lines to circles – Line which touches a circle at exactly one point
- The diameters of a screwthread
- Ø (disambiguation)
References[edit]
- ^ Toussaint, Godfried T. (1983). «Solving geometric problems with the rotating calipers». Proc. MELECON ’83, Athens. CiteSeerX 10.1.1.155.5671.
- ^ Bogomolny, Alexander. «Conjugate Diameters in Ellipse». www.cut-the-knot.org.
- ^ «diameter — Origin and meaning of diameter by Online Etymology Dictionary». www.etymonline.com.
- ^ «Re: diameter of an empty set». at.yorku.ca.
- ^ Korpela, Jukka K. (2006), Unicode Explained, O’Reilly Media, Inc., pp. 23–24, ISBN 978-0-596-10121-3.
- ^ Monniaux, David. «UTF-8 (Unicode) compose sequence». Retrieved 2018-07-13.
- ^ «wasysym – LaTeX support for the wasy fonts». Comprehensive TeX Archive Network. Retrieved 2022-03-11.
Look up diameter in Wiktionary, the free dictionary.
Знак диаметра
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией «Ø». Этот символ наносят перед размерным числом.
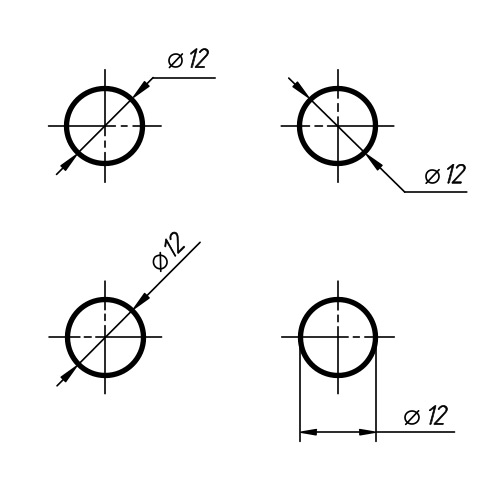
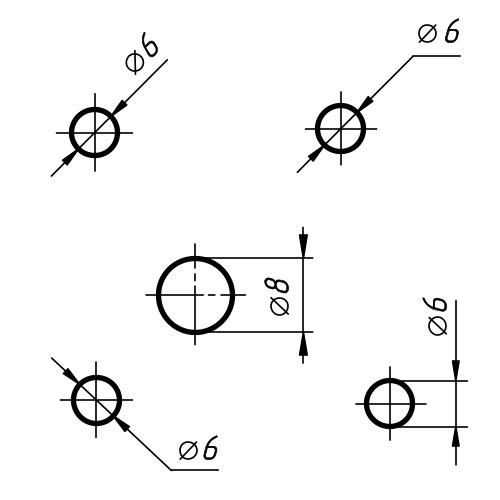
Примеры использования знака диаметра:
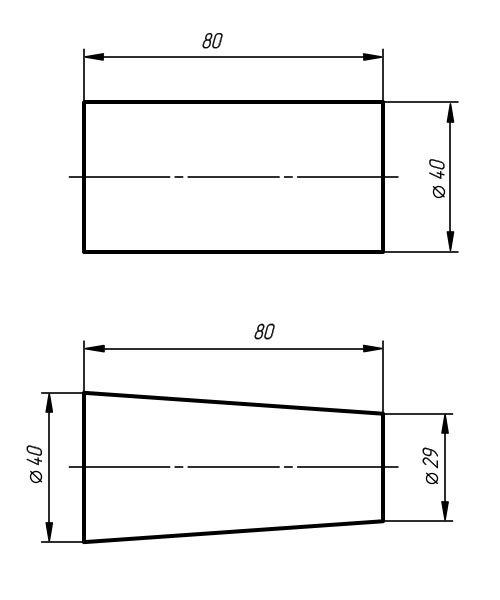
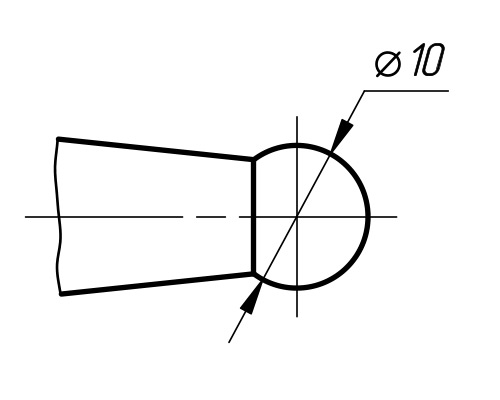
Знаки диаметра на деталях вращения цилиндрической и конической формы
Размеры наносимые при недостатке места
на размерной линии
Обозначение размеров при недостатке места
для стрелок
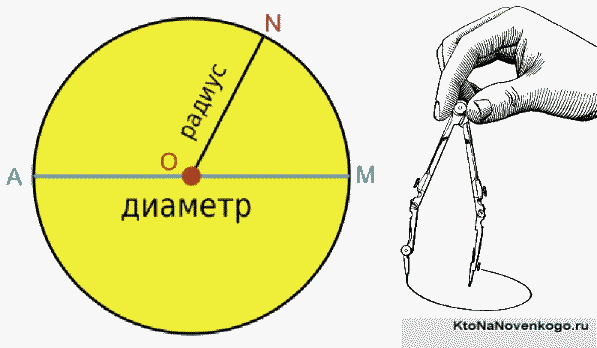
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «D» или знаком «Ø». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
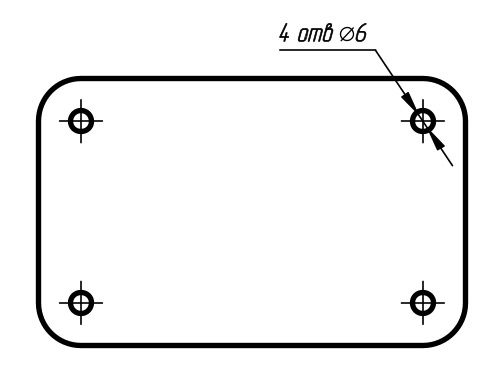
Пример обозначения четырёх отверстий
с указанием диаметра
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности «Ø». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: «D» – больший диаметр, «d» – меньший диаметр, «L» – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «Ø» а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы. Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки «Ø».
Пример нанесения знака диаметра
на сферической поверхности
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «d» меньший диаметр, «D» большой диаметр, «L» длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак «Ø».
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин. При обозначении на технических чертежах знак диаметра должен сопровождаться обозначением оси штрихпунктирной линией, что указывает на круглое сечение участка детали.
Диаметр в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Содержание
- 1 Диаметр геометрических фигур
- 1.1 Диаметр окружности, круга, сферы, шара
- 2 Символ диаметра
- 3 Вариации и обобщения
- 4 См. также
- 5 Литература
Диаметр геометрических фигур
Диаметр окружности, круга, сферы, шара
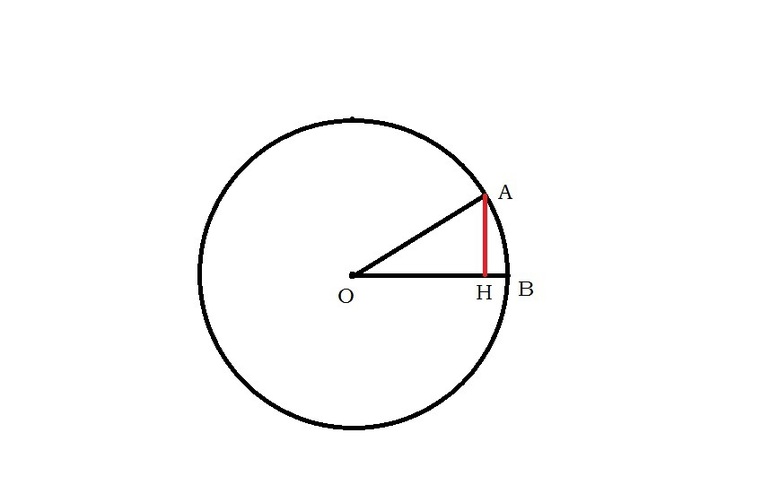
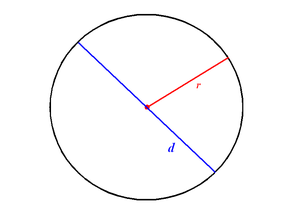
Радиус (r) и диаметр (d) окружности
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
Символ диаметра
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов Юникода» (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализорованные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Следует отличать символ диаметра «⌀» от других похожих на него символов:
- «ø» — строчная перечёркнутая латинская буква O (используется в датском, норвежском и фарерском алфавитах);
- «∅» и «
» — символы пустого множества, в свою очередь похожие на «Ø» (заглавную перечёркнутую латинскую букву O) или на перечёркнутый ноль;
- «Φ» — греческая заглавная буква «фи», кириллическая буква «эф»;
- «Ѳ» и «ѳ» — русская буква «фита» (использовалась до орфографической реформы 1918 года).
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
.
См. также
- Радиус
- Пи
- При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
- Теорема Бибербаха о максимальном свойстве шара
- Угловой диаметр астрономических объектов.
- Диаметр циркуляции
Литература
- Диаметр // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Диаметр — это золотое сечение окружности
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такое ДИАМЕТР. Это одно из базовых понятий в математике, которое начинают изучать еще в 3-м классе.
Но и повседневной жизни он встречается настолько часто, что знать его просто необходимо.
Диаметр — это…
Диаметр – это в первую очередь, хорда. Так называют отрезок (что это?) прямой, который соединяет две определенные точки. В нашем случае эти точки располагаются на максимально отдаленном друг от друга расстоянии на окружности, благодаря чему хорда проходит через ее центр.
В то же время диаметром еще называют и длину это самой хорды. Кстати, аналогичные определения применимы не только к окружностям, но и к другим геометрическим фигурам, таким как шар или сфера.
Графически это выглядит вот так:
Само слово «диаметр», как и многие термины в нашем языке, пришло из Древней Греции. Ведь именно в этой стране жили прославленные математики, такие как Евклид, Пифагор, Архимед, Платон. Так вот, греческое слово можно перевести как «поперечник».
Интересно, что во многих современных языках есть также похожие слова. Например, на латыни это «diametrus». А в русском языке мы нередко употребляем слово «диаметральный».
Например, говорим «диаметральные взгляды» или «диаметральные точки зрения», подразумевая совершенно противоположное отношение к чему-либо. Ну, точно как противоположные точки на окружности, разделенные диаметром.
Обозначения и символ диаметра
Диаметр имеет несколько сокращенных обозначений.
Например, если речь идет о математике, то в ней чаще всего употребляется латинская буква «D». Причем допускается как прописное написание этой буквы, так и строчное – «d». Второй вариант даже чаще встречается в задачках.
Например, это может выглядеть так:
d = 12 см или D = 12 см
А вот если говорить о бытовом понятии «диаметра», то тут уже чаще используется другой символ. Это – перечеркнутая буква «О».
Именно такой знак вы наверняка увидите, когда речь идет о трубах, о размере сверла и так далее. И записываются они так:
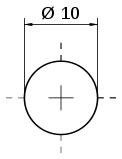
Ø6, Ø8, Ø12, Ø15, Ø20, Ø100
По умолчанию считается, что подобные обозначения всегда считаются в миллиметрах.
Стоит сказать, что символа «Ø» нет на обычной раскладке клавиатуры. И чтобы напечатать его в тексте, нужно или открыть специальный раздел «дополнительные символы» в программе Word, или просто скопировать откуда-нибудь, а потом вставить.
Радиус и другие величины, связанные с диаметром
Главной величиной, которая неизменно связана с диаметром, является радиус.
Радиус – это расстояние от центра окружности до любой точки на дуге окружности. Соответственно, радиусом также называют и длину этого отрезка.
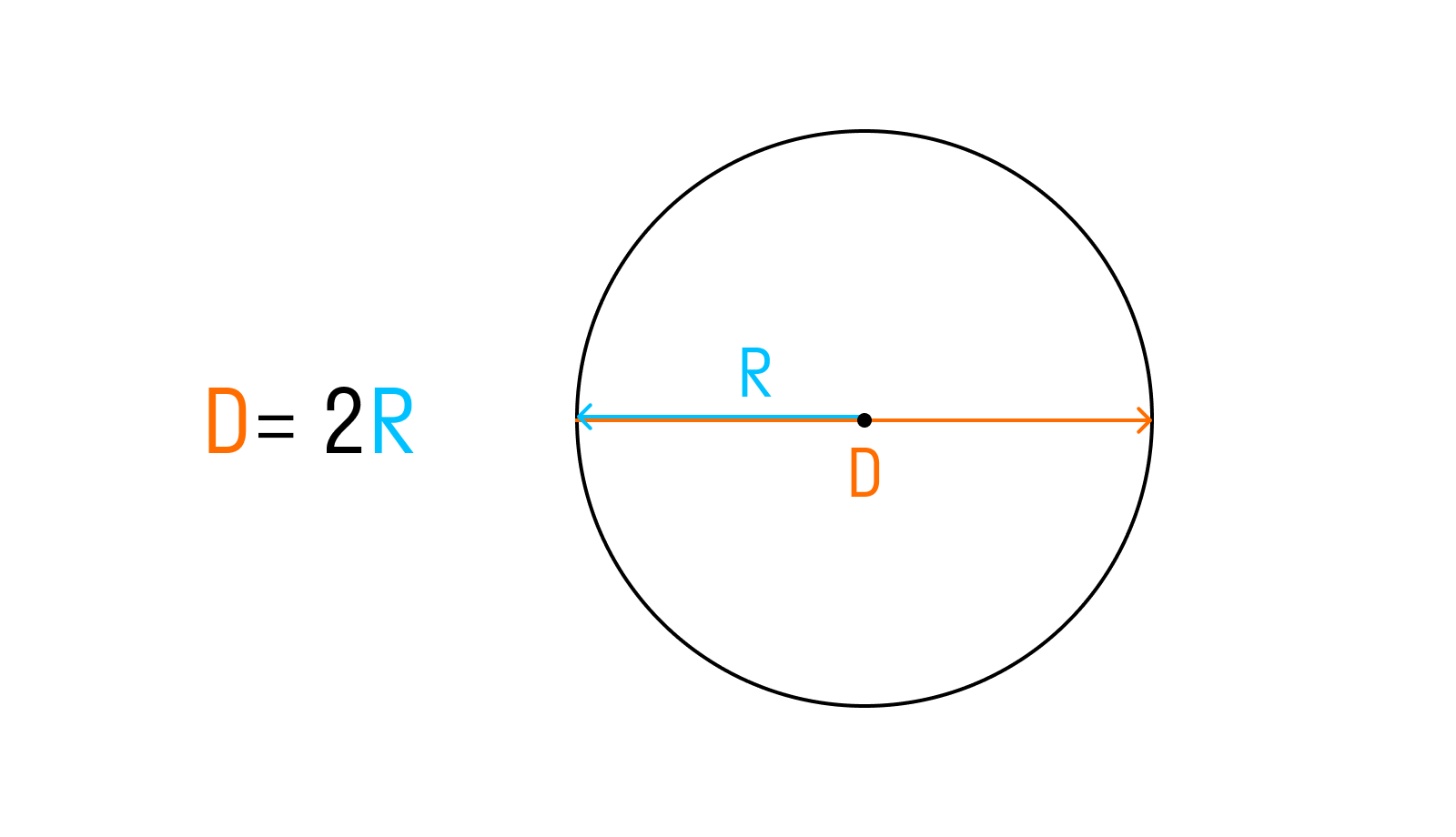
Радиус обозначается буквой «R» или «r». И он всегда равен половине диаметра. В математике это уравнение записывают как:
D = 2R или R = D/2
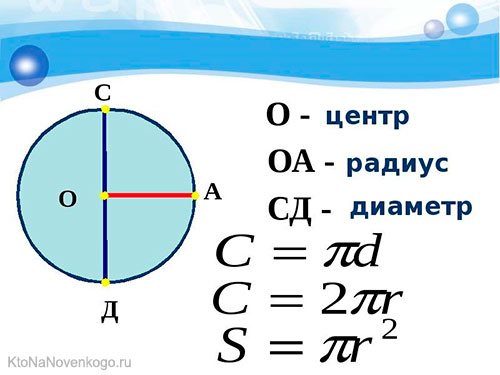
Еще одна важная величина – длина окружности. Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:
С = 2πR или С = πD
Где «π», как многие знают, это математическая константа. И считать ее принято как 3,14, хотя после запятой там бесконечное количество знаков.
И наконец, еще одна величина – площадь окружности (круга). Это размер всего, что находится внутри ее границ. Обозначается она буквой «S». И чтобы ее вычислить, опять же надо воспользоваться определенной формулой:
S=πR²
Соответственно, эти формулы можно и перевернуть. То есть, зная длину или площадь окружности, всегда можно высчитать ее диаметр.
Интересные факты о диаметре
Первое документальное упоминание слова «диаметр» в России относится к 1720 году. И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.
Диаметр Земли составляет 12 543 километра. Это огромное расстояние. Но и оно кажется маленьким, если сравнить, например, с Солнцем. А у него диаметр составляет 1 390 000 километров, что в 109 раз больше земного.
Диаметр 10-копеечных монет в нашей стране не менялись на протяжении сотни лет. Он составляет 17,5 миллиметров. Таким он был еще при Николае II, таким же и в советское время, таким же остался и сейчас.
Вот и все, что мы хотели рассказать о таком понятии, как диаметр. До новых встреч на страницах нашего блога.
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Записывайтесь на онлайн-курсы по математике для детей и подростков!
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
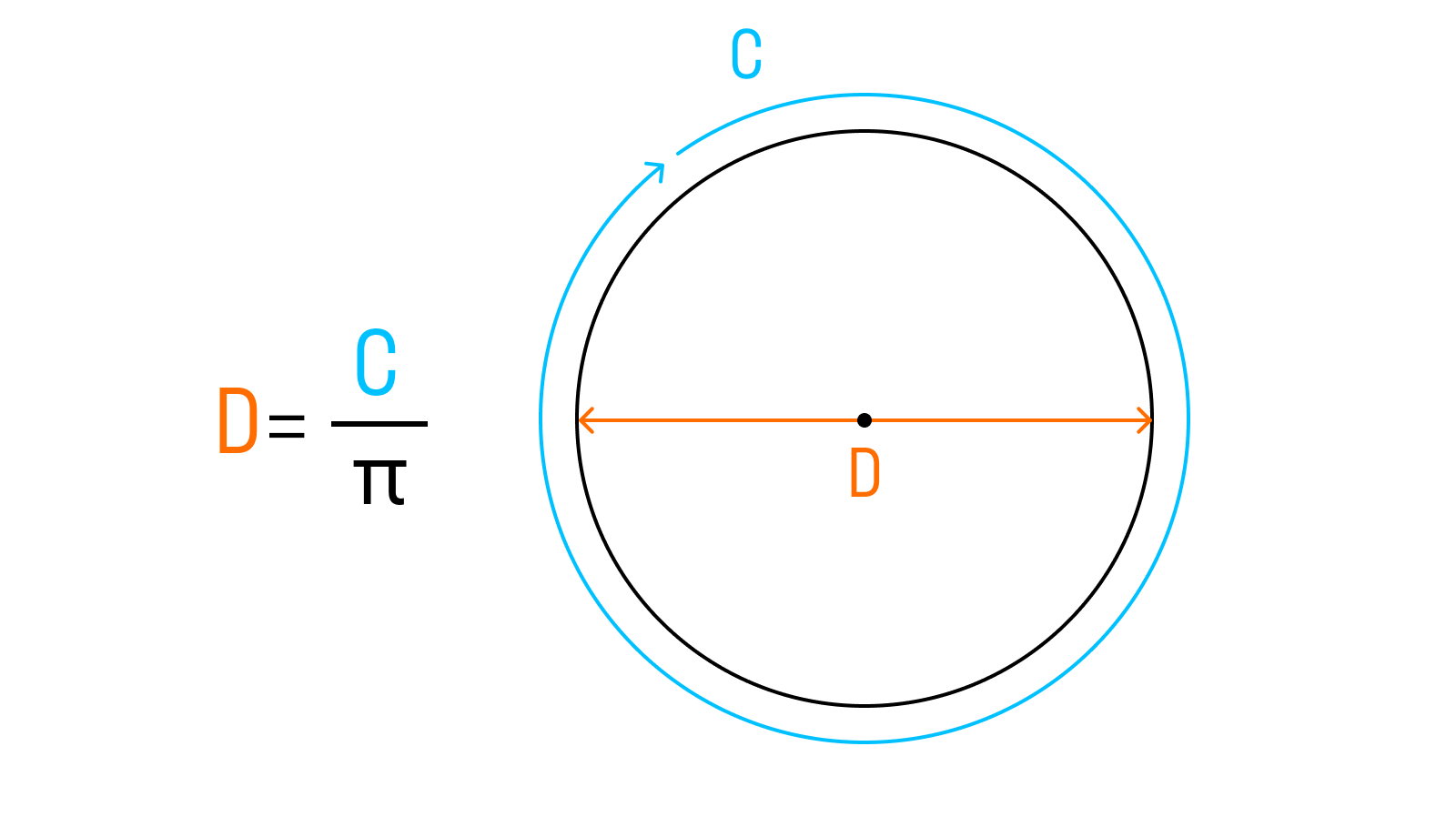
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
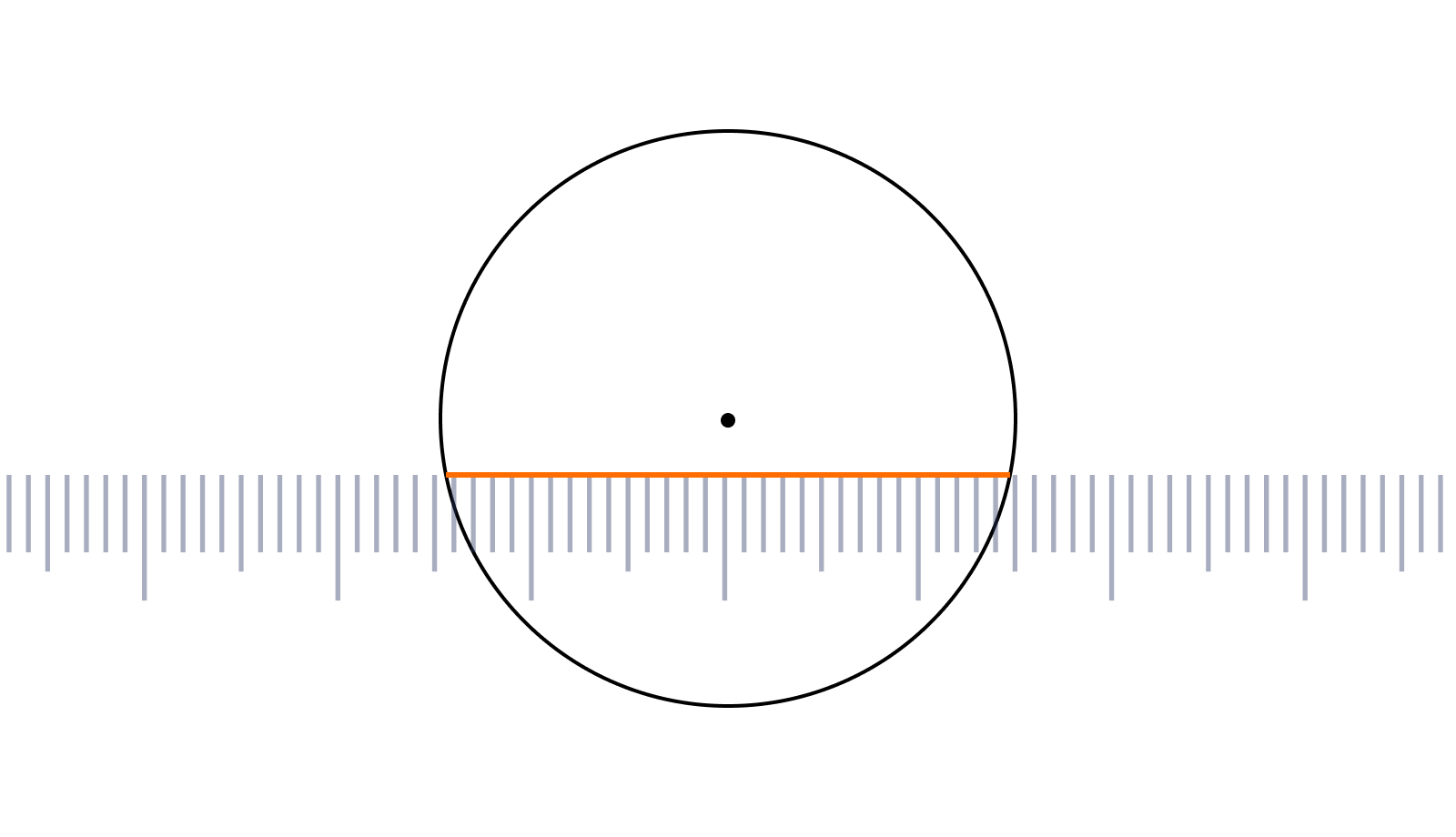
3. Если есть чертеж окружности
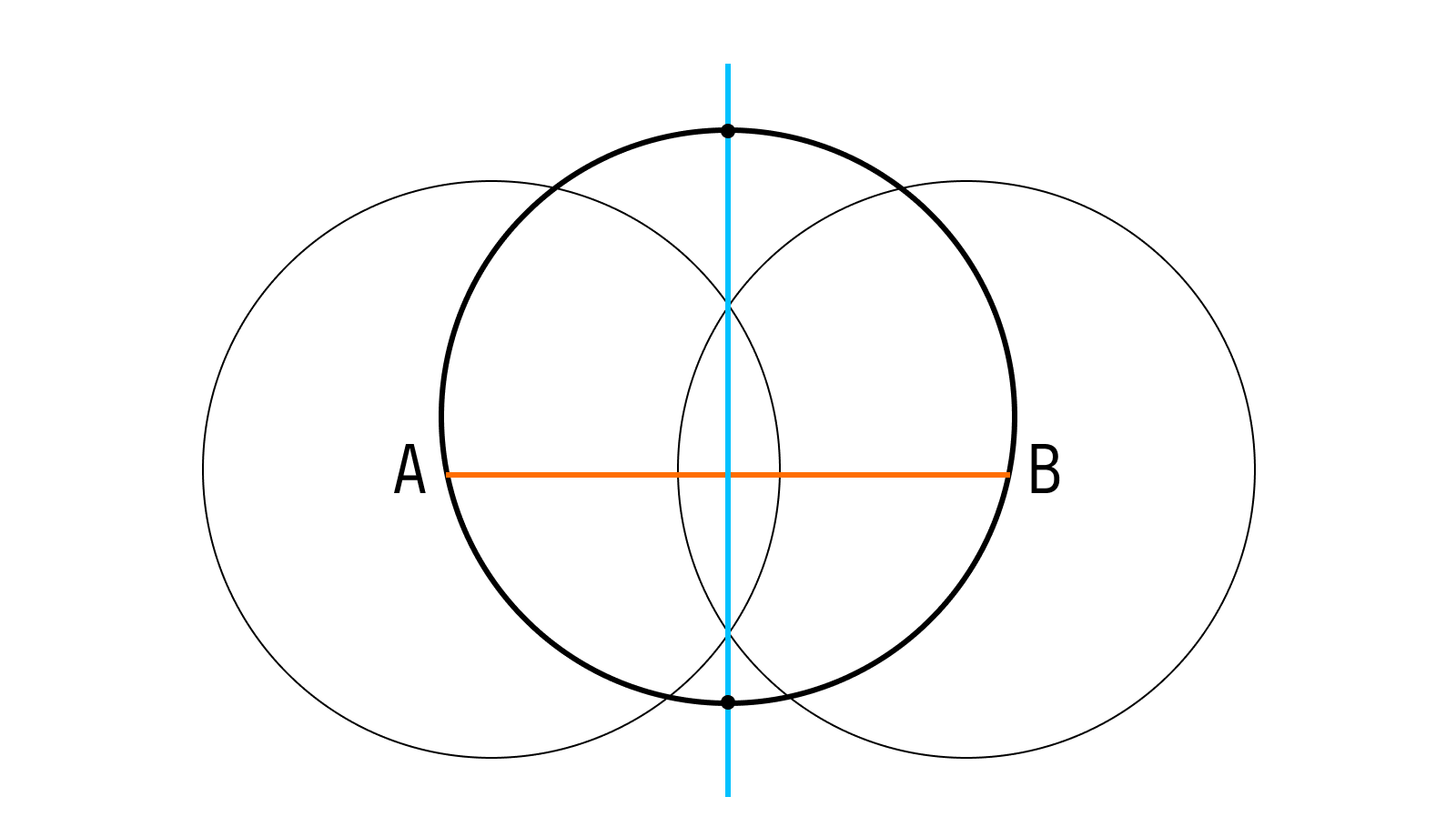
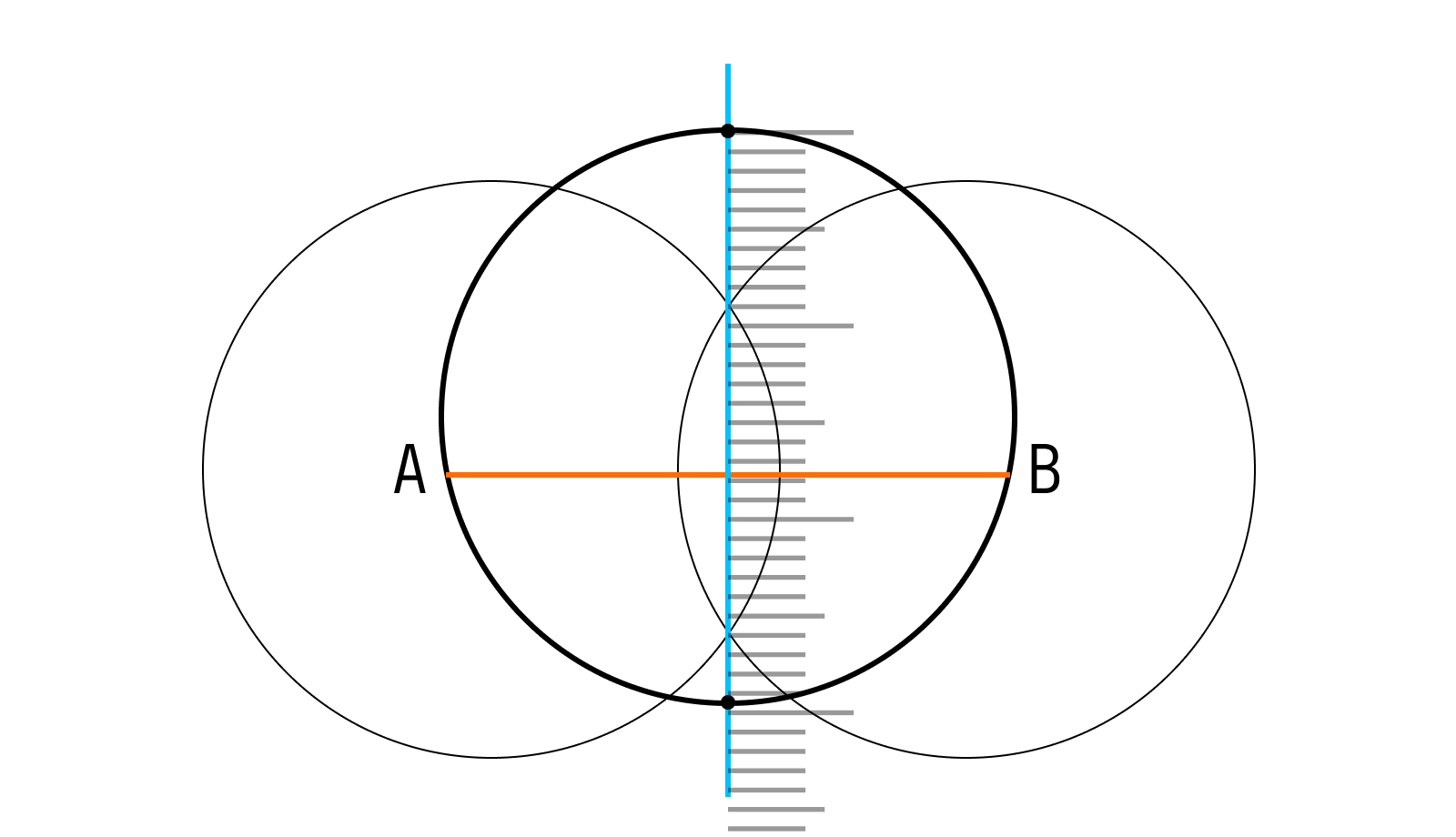
-
Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
-
Отметить точки пересечения прямой и окружности.
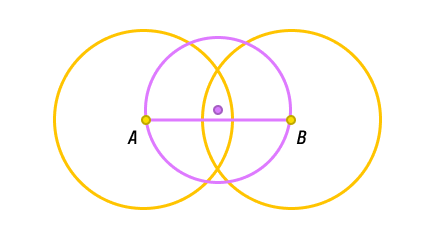
-
Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
-
Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
-
Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
Диаметр в изначальном значении — это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка.
Диаметр равен двум радиусам: D = 2R.
Радиус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра.
Диаметр геометрических фигур (окружности, круга, сферы, шара)
Диаметр — это хорда (отрезок, соединяющий две точки на окружности (сфере, поверхности шара) и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через центр этой окружности; такая хорда имеет максимальную длину.
В круге все диаметры равны и делят круг и все перпендикулярные хорды пополам. В эллипсе лишь два диаметра: самый большой и самый малый, перпендикулярные между собой, они делят эллипс пополам. В шаре, сфероиде, эллипсоиде и подобным геометрическим фигурам, диаметр = плоскость, проходит через центр и делит все перпендикулярные плоскости пополам.
Символ диаметра
Символ диаметра «Ø» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀).
Символ диаметра не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства, например, приложение «Таблица символов» в Windows, программу «Таблица символов Юникода» (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т.д. Специализорованные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты, например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Допускается обозначать диаметр буквой D.
Следует отличать символ диаметра «Ø» от других похожих на него символов:
- «ø» — строчная перечёркнутая латинская буква O (используется в датском, норвежском и фарерском алфавитах);
- «∅» — символы пустого множества, в свою очередь похожие на «Ø» (заглавную перечёркнутую латинскую букву O) или на перечёркнутый ноль;
- «Φ» — греческая заглавная буква «фи», кириллическая буква «эф».
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты:
- Под диаметром конического сечения понимается прямая, проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга;
- диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
Источники информации:
- Диаметр — Википедия;
- Диаметр — «Энциклопедический словарь Брокгауза и Ефрона» в 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Окружность — геометрическое место точек плоскости, в котором длина от точек к центру одинаковая. По-другому можно описать определение, что это замкнутая кривая, в которой править будут равные отрезки, проведенные от центра до краев фигуры. Круг — часть плоскости, которая ограничена окружностью.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Первый раз о термине заговорили в 1569 году, и примерно через 100 лет он стал общепринятым. И не удивительно, так как в обиходе люди часто говорят, к примеру, «пожар в радиусе 10 км уничтожил все», «в радиусе 5 м нет видимости» и так далее.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
- см;
- дм;
- м;
- км.
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Дополнительные сведения
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.
Если в точке пересечения радиуса с поверхностью =начертить касательную, то обе линии будут перпендикулярными по отношению друг к другу. Если провести к хорде так, чтобы между ними образовался угол 900, то в точке пересечения хорда будет разделена на 2 части. Если с хордой пересекается диаметр под углом 900, то хорда и дуга будут разделены на две равные части.
⌀ Знак диаметра
Нажмите, чтобы скопировать и вставить символ
Значение символа
Диаметр – отрезок (хорда), соединяющий две точки на окружности и проходящий через её центр. Но, обычно, под диаметром подразумевают длину этого отрезка. Равняется двум радиусам. В формулах обозначается латинской буквой «D». Слово «диаметр» происходит от греческого «diametros» (поперечник).
Символ диаметра представляет собой окружность перечёркнутую вышеупомянутым отрезком. Правда, для наглядности, концы отрезка выходят за пределы окружности, что строго говоря неверно. Символ диаметра похож на «о с диагональным штрихом», используемую в некоторых основанных на латинице алфавитах. Кроме того, часто похожим образом пишут цифру «ноль», перечёркивая её, чтобы отличить от буквы «о».
Обычно, знак диаметра используется на чертежах деталей. Символ наносят перед числом на размерной линии: «⌀ 40 см». Диаметр можно указывать, как для цилиндрических деталей, так и для конических. Пример детали с цилиндрической поверхностью – вал. Конической – переходная втулка.
Символ «Знак диаметра» был утвержден как часть Юникода версии 1.1 в 1993 г.
Этот текст также доступен на следующих языках:
English;
Свойства
| Версия | 1.1 |
| Блок | Разнообразные технические символы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2300 |
| Простое изменение регистра | 2300 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8C 80 | 226 140 128 | 14847104 | 11100010 10001100 10000000 |
| UTF-16BE | 23 00 | 35 0 | 8960 | 00100011 00000000 |
| UTF-16LE | 00 23 | 0 35 | 35 | 00000000 00100011 |
| UTF-32BE | 00 00 23 00 | 0 0 35 0 | 8960 | 00000000 00000000 00100011 00000000 |
| UTF-32LE | 00 23 00 00 | 0 35 0 0 | 2293760 | 00000000 00100011 00000000 00000000 |




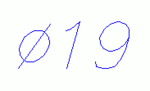
 » — символы пустого множества, в свою очередь похожие на «Ø» (заглавную перечёркнутую латинскую букву O) или на перечёркнутый ноль;
» — символы пустого множества, в свою очередь похожие на «Ø» (заглавную перечёркнутую латинскую букву O) или на перечёркнутый ноль; .
.