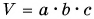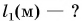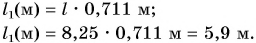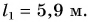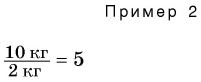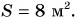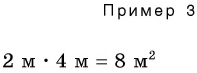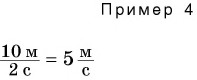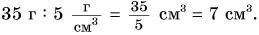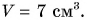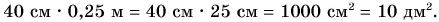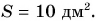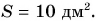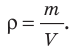Практически каждый раз при решении задач по математике, физике или другим дисциплинам приходится выбирать обозначения тех или иных величин. Среди них следует различать обозначения общепринятые (или даже устанавливаемые нормативными документами) и обозначения, выбор которых обычно выполняется самостоятельно, в зависимости от индивидуальных предпочтений. Есть также величины, обозначения которых в разных дисциплинах приняты свои. Есть обозначения международные, а есть – принятые различными в разных странах.
Как обозначается длина, ширина, высота, толщина, глубина
Обозначение длины в математике обычно зависит от того, какой объект в данном случае рассматривается: одномерный, двумерный или трехмерный. Если речь идёт об обозначении длины одномерного объекта (нити, проволоки и т.п.) или обозначении длины куска сортового проката (трубы, швеллера, двутавра и т.п.), то длина обычно обозначается буквой l (написанной курсивом, т.е. с наклоном, чтобы не было похоже на «единицу») или L. Если же речь идёт о двумерном объекте, в котором нужно обозначить не только длину, но и ширину, то обычно принимают одну из таких пар обозначений: a и b (а – длина, b — ширина), l и b (l – длина, b — ширина), l и h (l – длина, h — высота). Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов. Если же речь идёт о длине волны, то она обозначается строчной греческой буквой «лямбда».
Высота обозначается обычно буквой h (читается: [аш]). В технической литературе для обозначения высоты также используют букву Н (читается: [аш]). Этими же буквами (h, реже Н) обозначается глубина.
Толщина в физике обозначается либо строчной (маленькой) буквой s, либо греческой строчной буквой «дельта», с использованием (при необходимости) нижних индексов (обычно – числовых, соответствующих номеру слоя, т.е. 1, 2, 3, 4 и т.д.).
Вопросы «как в математике пишется длина», «как в математике пишется периметр», «как в математике пишется площадь» некорректны. Здесь уместно вместо слова «пишется» употребить слово «обозначается».
Как обозначается периметр
При решении задач по геометрии часто возникает необходимость обозначить периметр. Периметр в математике обозначается заглавной (т.е. большой) буквой Р (читается: [пэ]).
Как обозначается площадь
Обозначение площади в научно-технической литературе можно встретить различные. Поэтому и возникают вопросы «Как обозначается площадь в математике», «Как обозначается площадь в физике» и т.п. Ответ на вопрос о том, какой буквой обозначается площадь, зависит от конкретной дисциплины, о которой в данный момент идёт речь. В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.п.). Если нужно в одной задаче обозначить площадь нескольких фигур, то используются нижние индексы. В качестве индекса могут быть использованы числа (1, 2, 3 и т.д.), т.е. площади обозначаются как S1, S2, S3 и т.д., а могут быть использованы сокращения от названия фигур (Sтр, Sпр, Sкв, Sр и т.п.). При необходимости обозначения в одной задаче площадей нескольких треугольников чаще в качестве нижнего индекса принимают обозначения этих треугольников (например, SABC, SMNP, SLPH со значком треугольника перед буквами ABC, MNP, LPH). В физике обозначается площадь поперечного сечения той же буквой S, при необходимости – с добавлением нижнего индекса (например, S1, S2, S3 и т.д.). Однако, в сопромате и в строительной механике буквой S (с добавлением индекса) обозначается не площадь, а статический момент площади относительно оси, а для обозначения площади в этих дисциплинах обычно используются буквы F (читается: [эф]) и A (читается: [а]).
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- ru.wikipedia.org – список обозначений в физике
| Length | |
|---|---|
The metric length of one kilometre is equivalent to the imperial measurement of 0.62137 miles. |
|
|
Common symbols |
l |
| SI unit | metre (m) |
|
Other units |
see unit of length |
| Extensive? | yes |
| Dimension | L |
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre.
Length is commonly understood to mean the most extended dimension of a fixed object.[1] However, this is not always the case and may depend on the position the object is in.
Various terms for the length of a fixed object are used, and these include height, which is vertical length or vertical extent, and width, breadth or depth. Height is used when there is a base from which vertical measurements can be taken. Width or breadth usually refer to a shorter dimension when length is the longest one. Depth is used for the third dimension of a three dimensional object.[2]
Length is the measure of one spatial dimension, whereas area is a measure of two dimensions (length squared) and volume is a measure of three dimensions (length cubed).
History[edit]
Measurement has been important ever since humans settled from nomadic lifestyles and started using building materials, occupying land and trading with neighbours. As trade between different places increased, the need for standard units of length increased. And later, as society has become more technologically oriented, much higher accuracy of measurement is required in an increasingly diverse set of fields, from micro-electronics to interplanetary ranging.[3]
Under Einstein’s special relativity, length can no longer be thought of as being constant in all reference frames. Thus a ruler that is one metre long in one frame of reference will not be one metre long in a reference frame that is moving relative to the first frame. This means the length of an object varies depending on the speed of the observer.
Use in mathematics[edit]
Euclidean geometry[edit]
In Euclidean geometry, length is measured along straight lines unless otherwise specified and refers to segments on them. Pythagoras’s theorem relating the length of the sides of a right triangle is one of many applications in Euclidean geometry. Length may also be measured along other types of curves and is referred to as arclength.
In a triangle, the length of an altitude, a line segment drawn from a vertex perpendicular to the side not passing through the vertex (referred to as a base of the triangle), is called the height of the triangle.
The area of a rectangle is defined to be length × width of the rectangle. If a long thin rectangle is stood up on its short side then its area could also be described as its height × width.
The volume of a solid rectangular box (such as a plank of wood) is often described as length × height × depth.
The perimeter of a polygon is the sum of the lengths of its sides.
The circumference of a circular disk is the length of the boundary (a circle) of that disk.
Other geometries[edit]
In other geometries, length may be measured along possibly curved paths, called geodesics. The Riemannian geometry used in general relativity is an example of such a geometry. In spherical geometry, length is measured along the great circles on the sphere and the distance between two points on the sphere is the shorter of the two lengths on the great circle, which is determined by the plane through the two points and the center of the sphere.
Graph theory[edit]
In an unweighted graph, the length of a cycle, path, or walk is the number of edges it uses.[4] In a weighted graph, it may instead be the sum of the weights of the edges that it uses.[5]
Length is used to define the shortest path, girth (shortest cycle length), and longest path between two vertices in a graph.
Measure theory[edit]
In measure theory, length is most often generalized to general sets of 
so that the Lebesgue outer measure 

Units[edit]
In the physical sciences and engineering, when one speaks of units of length, the word length is synonymous with distance. There are several units that are used to measure length. Historically, units of length may have been derived from the lengths of human body parts, the distance traveled in a number of paces, the distance between landmarks or places on the Earth, or arbitrarily on the length of some common object.
In the International System of Units (SI), the base unit of length is the metre (symbol, m) and is now defined in terms of the speed of light (about 300 million metres per second). The millimetre (mm), centimetre (cm) and the kilometre (km), derived from the metre, are also commonly used units. In U.S. customary units, English or Imperial system of units, commonly used units of length are the inch (in), the foot (ft), the yard (yd), and the mile (mi). A unit of length used in navigation is the nautical mile (nmi).[7]
Units used to denote distances in the vastness of space, as in astronomy, are much longer than those typically used on Earth (metre or centimetre) and include the astronomical unit (au), the light-year, and the parsec (pc).
Units used to denote sub-atomic distances, as in nuclear physics, are much smaller than the centimetre. Examples include the fermi.
See also[edit]
- Arc length
- Conversion of units
- Humorous units of length
- Length measurement
- Metric system
- Metric units
- Orders of magnitude (length)
- Reciprocal length
References[edit]
Wikimedia Commons has media related to Length.
- ^ «WordNet Search — 3.1». wordnetweb.princeton.edu. Archived from the original on 25 September 2016. Retrieved 15 March 2020.
- ^ «Measurement: Length, width, height, depth | Think Math!». thinkmath.edc.org. Archived from the original on 24 February 2020. Retrieved 15 March 2020.
- ^ History of Length Measurement, National Physical Laboratory Archived 2013-11-26 at the Wayback Machine
- ^ Caldwell, Chris K. (1995). «Graph Theory Glossary».
- ^ Cheung, Shun Yan. «Weighted graphs and path length».
- ^ Le, Dung. «Lebesgue Measure» (PDF). Archived (PDF) from the original on 2010-11-30.
- ^ Cardarelli, François (2003). Encyclopaedia of Scientific Units, Weights, and Measures: Their SI Equivalences and Origins. Springer. ISBN 9781852336820.
| Length | |
|---|---|
The metric length of one kilometre is equivalent to the imperial measurement of 0.62137 miles. |
|
|
Common symbols |
l |
| SI unit | metre (m) |
|
Other units |
see unit of length |
| Extensive? | yes |
| Dimension | L |
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre.
Length is commonly understood to mean the most extended dimension of a fixed object.[1] However, this is not always the case and may depend on the position the object is in.
Various terms for the length of a fixed object are used, and these include height, which is vertical length or vertical extent, and width, breadth or depth. Height is used when there is a base from which vertical measurements can be taken. Width or breadth usually refer to a shorter dimension when length is the longest one. Depth is used for the third dimension of a three dimensional object.[2]
Length is the measure of one spatial dimension, whereas area is a measure of two dimensions (length squared) and volume is a measure of three dimensions (length cubed).
History[edit]
Measurement has been important ever since humans settled from nomadic lifestyles and started using building materials, occupying land and trading with neighbours. As trade between different places increased, the need for standard units of length increased. And later, as society has become more technologically oriented, much higher accuracy of measurement is required in an increasingly diverse set of fields, from micro-electronics to interplanetary ranging.[3]
Under Einstein’s special relativity, length can no longer be thought of as being constant in all reference frames. Thus a ruler that is one metre long in one frame of reference will not be one metre long in a reference frame that is moving relative to the first frame. This means the length of an object varies depending on the speed of the observer.
Use in mathematics[edit]
Euclidean geometry[edit]
In Euclidean geometry, length is measured along straight lines unless otherwise specified and refers to segments on them. Pythagoras’s theorem relating the length of the sides of a right triangle is one of many applications in Euclidean geometry. Length may also be measured along other types of curves and is referred to as arclength.
In a triangle, the length of an altitude, a line segment drawn from a vertex perpendicular to the side not passing through the vertex (referred to as a base of the triangle), is called the height of the triangle.
The area of a rectangle is defined to be length × width of the rectangle. If a long thin rectangle is stood up on its short side then its area could also be described as its height × width.
The volume of a solid rectangular box (such as a plank of wood) is often described as length × height × depth.
The perimeter of a polygon is the sum of the lengths of its sides.
The circumference of a circular disk is the length of the boundary (a circle) of that disk.
Other geometries[edit]
In other geometries, length may be measured along possibly curved paths, called geodesics. The Riemannian geometry used in general relativity is an example of such a geometry. In spherical geometry, length is measured along the great circles on the sphere and the distance between two points on the sphere is the shorter of the two lengths on the great circle, which is determined by the plane through the two points and the center of the sphere.
Graph theory[edit]
In an unweighted graph, the length of a cycle, path, or walk is the number of edges it uses.[4] In a weighted graph, it may instead be the sum of the weights of the edges that it uses.[5]
Length is used to define the shortest path, girth (shortest cycle length), and longest path between two vertices in a graph.
Measure theory[edit]
In measure theory, length is most often generalized to general sets of 
so that the Lebesgue outer measure 

Units[edit]
In the physical sciences and engineering, when one speaks of units of length, the word length is synonymous with distance. There are several units that are used to measure length. Historically, units of length may have been derived from the lengths of human body parts, the distance traveled in a number of paces, the distance between landmarks or places on the Earth, or arbitrarily on the length of some common object.
In the International System of Units (SI), the base unit of length is the metre (symbol, m) and is now defined in terms of the speed of light (about 300 million metres per second). The millimetre (mm), centimetre (cm) and the kilometre (km), derived from the metre, are also commonly used units. In U.S. customary units, English or Imperial system of units, commonly used units of length are the inch (in), the foot (ft), the yard (yd), and the mile (mi). A unit of length used in navigation is the nautical mile (nmi).[7]
Units used to denote distances in the vastness of space, as in astronomy, are much longer than those typically used on Earth (metre or centimetre) and include the astronomical unit (au), the light-year, and the parsec (pc).
Units used to denote sub-atomic distances, as in nuclear physics, are much smaller than the centimetre. Examples include the fermi.
See also[edit]
- Arc length
- Conversion of units
- Humorous units of length
- Length measurement
- Metric system
- Metric units
- Orders of magnitude (length)
- Reciprocal length
References[edit]
Wikimedia Commons has media related to Length.
- ^ «WordNet Search — 3.1». wordnetweb.princeton.edu. Archived from the original on 25 September 2016. Retrieved 15 March 2020.
- ^ «Measurement: Length, width, height, depth | Think Math!». thinkmath.edc.org. Archived from the original on 24 February 2020. Retrieved 15 March 2020.
- ^ History of Length Measurement, National Physical Laboratory Archived 2013-11-26 at the Wayback Machine
- ^ Caldwell, Chris K. (1995). «Graph Theory Glossary».
- ^ Cheung, Shun Yan. «Weighted graphs and path length».
- ^ Le, Dung. «Lebesgue Measure» (PDF). Archived (PDF) from the original on 2010-11-30.
- ^ Cardarelli, François (2003). Encyclopaedia of Scientific Units, Weights, and Measures: Their SI Equivalences and Origins. Springer. ISBN 9781852336820.
Каждое измерение — это сравнение измеряемой величины с другой, однородной с ней величиной, которую считают единичной. Теоретически единицы для всех величин в физике можно выбрать независимыми друг от друга. Но это крайне неудобно, так как для каждой величины следовало бы ввести свой эталон. Кроме этого во всех физических уравнениях, которые отображают связь между разными величинами, возникли бы числовые коэффициенты.
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения «Пространство и время»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Длина |
l, s, d |
метр |
м |
Протяжённость объекта в одном измерении. |
|
|
Площадь |
S |
квадратный метр |
м2 |
Протяженность объекта в двух измерениях. |
|
|
Объем, вместимость |
V |
кубический метр |
м3 |
Протяжённость объекта в трёх измерениях. |
экстенсивная величина |
|
Время |
t |
секунда |
с |
Продолжительность события. |
|
|
Плоский угол |
α, φ |
радиан |
рад |
Величина изменения направления. |
|
|
Телесный угол |
α, β, γ |
стерадиан |
ср |
Часть пространства |
|
|
Линейная скорость |
v |
метр в секунду |
м/с |
Быстрота изменения координат тела. |
вектор |
|
Линейное ускорение |
a, w |
метр в секунду в квадрате |
м/с2 |
Быстрота изменения скорости объекта. |
вектор |
|
Угловая скорость |
ω |
радиан в секунду |
рад/с = (с−1) |
Скорость изменения угла. |
|
|
Угловое ускорение |
ε |
радиан на секунду в квадрате |
рад/с2 = (с−2) |
Быстрота изменения угловой скорости |
Таблица единиц измерения «Механика»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Масса |
m |
килограмм |
кг |
Величина, определяющая инерционные и гравитационные свойства тел. |
экстенсивная величина |
|
Плотность |
ρ |
килограмм на кубический метр |
кг/м3 |
Масса на единицу объёма. |
интенсивная величина |
|
Поверхностная плотность |
ρA |
Масса на единицу площади. |
кг/м2 |
Отношение массы тела к площади его поверхности |
|
|
Линейная плотность |
ρl |
Масса на единицу длины. |
кг/м |
Отношение массы тела к его линейному параметру |
|
|
Удельный объем |
v |
кубический метр на килограмм |
м3/кг |
Объём, занимаемый единицей массы вещества |
|
|
Массовый расход |
Qm |
килограмм в секунду |
кг/с |
Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени |
|
|
Объемный расход |
Qv |
кубический метр в секунду |
м3/с |
Объёмный расход жидкости или газа |
|
|
Импульс |
P |
килограмм-метр в секунду |
кг•м/с |
Произведение массы и скорости тела. |
экстенсивная, сохраняющаяся величина |
|
Момент импульса |
L |
килограмм-метр в квадрате в секунду |
кг•м2/с |
Мера вращения объекта. |
сохраняющаяся величина |
|
Момент инерции |
J |
килограмм-метр в квадрате |
кг•м2 |
Мера инертности объекта при вращении. |
тензорная величина |
|
Сила, вес |
F, Q |
ньютон |
Н |
Действующая на объект внешняя причина ускорения. |
вектор |
|
Момент силы |
M |
ньютон-метр |
Н•м = (кг·м2/с2) |
Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. |
вектор |
|
Импульс силы |
I |
ньютон-секунда |
Н•с |
Произведение силы на время её действия |
вектор |
|
Давление, механическое напряжение |
p, σ |
паскаль |
Па = (кг/(м·с2)) |
Сила, приходящаяся на единицу площади. |
интенсивная величина |
|
Работа |
A |
джоуль |
Дж = (кг·м2/с2) |
Скалярное произведение силы и перемещения. |
скаляр |
|
Энергия |
E, U |
джоуль |
Дж = (кг·м2/с2) |
Способность тела или системы совершать работу. |
экстенсивная, сохраняющаяся величина, скаляр |
|
Мощность |
N |
ватт |
Вт = (кг·м2/с3) |
Скорость изменения энергии. |
Таблица единиц измерения «Периодические явления, колебания и волны»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Период |
T |
секунда |
с |
Промежуток времени, за который система совершает одно полное колебание |
|
|
Частота периодического процесса |
v, f |
герц |
Гц = (с−1) |
Число повторений события за единицу времени. |
|
|
Циклическая (круговая) частота |
ω |
радиан в секунду |
рад/с |
Циклическая частота электромагнитных колебаний в колебательном контуре. |
|
|
Частота вращения |
n |
секунда в минус первой степени |
с-1 |
Периодический процесс, равный числу полных циклов, совершённых за единицу времени. |
|
|
Длина волны |
λ |
метр |
м |
Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. |
|
|
Волновое число |
k |
метр в минус первой степени |
м-1 |
Пространственная частота волны |
Таблица единиц измерения «Тепловые явления»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Температура |
T |
кельвин |
К |
Средняя кинетическая энергия частиц объекта. |
Интенсивная величина |
|
Температурный коэффициент |
α |
кельвин в минус первой степени |
К-1 |
Зависимость электрического сопротивления от температуры |
|
|
Температурный градиент |
gradT |
кельвин на метр |
К/м |
Изменение температуры на единицу длины в направлении распространения теплоты. |
|
|
Теплота (количество теплоты) |
Q |
джоуль |
Дж = (кг·м2/с2) |
Энергия, передаваемая от одного тела к другому немеханическим путём |
|
|
Удельная теплота |
q |
джоуль на килограмм |
Дж/кг |
Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его. |
|
|
Теплоемкость |
C |
джоуль на кельвин |
Дж/К |
Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания. |
|
|
Удельная теплоемкость |
c |
джоуль на килограмм-кельвин |
Дж/(кг•К) |
Теплоёмкость единичной массы вещества. |
|
|
Энтропия |
S |
джоуль на килограмм |
Дж/кг |
Мера необратимого рассеивания энергии или бесполезности энергии. |
Таблица единиц измерения «Молекулярная физика»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Количество вещества |
v, n |
моль |
моль |
Количество однотипных структурных единиц, из которых состоит вещество. |
Экстенсивная величина |
|
Молярная масса |
M, μ |
килограмм на моль |
кг/моль |
Отношение массы вещества к количеству молей этого вещества. |
|
|
Молярная энергия |
Hмол |
джоуль на моль |
Дж/моль |
Энергия термодинамической системы. |
|
|
Молярная теплоемкость |
смол |
джоуль на моль-кельвин |
Дж/(моль•К) |
Теплоёмкость одного моля вещества. |
|
|
Концентрация молекул |
c, n |
метр в минус третьей степени |
м-3 |
Число молекул, содержащихся в единице объема. |
|
|
Массовая концентрация |
ρ |
килограмм на кубический метр |
кг/м3 |
Отношение массы компонента, содержащегося в смеси, к объёму смеси. |
|
|
Молярная концентрация |
смол |
моль на кубический метр |
моль/м3 |
Содержание компонента относительно всей смеси. |
|
|
Подвижность ионов |
В, μ |
квадратный метр на вольт-секунду |
м2/(В•с) |
Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем. |
Таблица единиц измерения «Электричество и магнетизм»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Сила тока |
I |
ампер |
А |
Протекающий в единицу времени заряд. |
|
|
Плотность тока |
j |
ампер на квадратный метр |
А/м2 |
Сила электрического тока, протекающего через элемент поверхности единичной площади. |
Векторная величина |
|
Электрический заряд |
Q, q |
кулон |
Кл = (А·с) |
Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. |
экстенсивная, сохраняющаяся величина |
|
Электрический дипольный момент |
p |
кулон-метр |
Кл•м |
Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей. |
|
|
Поляризованность |
P |
кулон на квадратный метр |
Кл/м2 |
Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве. |
|
|
Напряжение |
U |
вольт |
В |
Изменение потенциальной энергии, приходящееся на единицу заряда. |
скаляр |
|
Потенциал, ЭДС |
φ, σ |
вольт |
В |
Работа сторонних сил (некулоновских) по перемещению заряда. |
|
|
Напряженность электрического поля |
E |
вольт на метр |
В/м |
Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q |
|
|
Электрическая емкость |
C |
фарад |
Ф |
Мера способности проводника накапливать электрический заряд |
|
|
Электрическое сопротивление |
R, r |
ом |
Ом = (м2·кг/(с3·А2)) |
сопротивление объекта прохождению электрического тока |
|
|
Удельное электрическое сопротивление |
ρ |
ом-метр |
Ом•м |
Способность материала препятствовать прохождению электрического тока |
|
|
Электрическая проводимость |
G |
сименс |
См |
Способность тела (среды) проводить электрический ток |
|
|
Магнитная индукция |
B |
тесла |
Тл |
Векторная величина, являющаяся силовой характеристикой магнитного поля |
Векторная величина |
|
Магнитный поток |
Ф |
вебер |
Вб = (кг/(с2·А)) |
Величина, учитывающая интенсивность магнитного поля и занимаемую им область. |
|
|
Напряженность магнитного поля |
H |
ампер на метр |
А/м |
Разность вектора магнитной индукции B и вектора намагниченности M |
Векторная величина |
|
Магнитный момент |
pm |
ампер-квадратный метр |
А•м2 |
Величина, характеризующая магнитные свойства вещества |
|
|
Намагниченность |
J |
ампер на метр |
А/м |
Величина, характеризующая магнитное состояние макроскопического физического тела. |
векторная величина |
|
Индуктивность |
L |
генри |
Гн |
Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком |
|
|
Электромагнитная энергия |
N |
джоуль |
Дж = (кг·м2/с2) |
Энергия, заключенная в электромагнитном поле |
|
|
Объемная плотность энергии |
w |
джоуль на кубический метр |
Дж/м3 |
Энергия электрического поля конденсатора |
|
|
Активная мощность |
P |
ватт |
Вт |
Мощность в цепи переменного тока |
|
|
Реактивная мощность |
Q |
вар |
вар |
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока |
|
|
Полная мощность |
S |
ватт-ампер |
Вт•А |
Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической |
Таблица единиц измерения «Оптика, электромагнитное излучение»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Сила света |
J, I |
кандела |
кд |
Количество световой энергии, излучаемой в заданном направлении в единицу времени. |
Световая, экстенсивная величина |
|
Световой поток |
Ф |
люмен |
лм |
Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения |
|
|
Световая энергия |
Q |
люмен-секунда |
лм•с |
Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения |
|
|
Освещенность |
E |
люкс |
лк |
Отношение светового потока, падающего на малый участок поверхности, к его площади. |
|
|
Светимость |
M |
люмен на квадратный метр |
лм/м2 |
Световая величина, представляющая собой световой поток |
|
|
Яркость |
L, B |
кандела на квадратный метр |
кд/м2 |
Сила света, излучаемая единицей площади поверхности в определенном направлении |
|
|
Энергия излучения |
E, W |
джоуль |
Дж = (кг·м2/с2) |
Энергия, переносимая оптическим излучением |
Таблица единиц измерения «Акустика»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Звуковое давление |
p |
паскаль |
Па |
Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны |
|
|
Объемная скорость |
c, V |
кубический метр в секунду |
м3/с |
Отношение объема сырья, подаваемого в реактор в час к объему катализатора |
|
|
Скорость звука |
v, u |
метр в секунду |
м/с |
Скорость распространения упругих волн в среде |
|
|
Интенсивность звука |
l |
ватт на квадратный метр |
Вт/м2 |
Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения |
скалярная физическая величина |
|
Акустическое сопротивление |
Za, Ra |
паскаль-секунда на кубический метр |
Па•с/м3 |
Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны |
|
|
Механическое сопротивление |
Rm |
ньютон-секунда на метр |
Н•с/м |
Указывает силу, необходимую для движения тела при каждой частоте |
Таблица единиц измерения «Атомная и ядерная физика. Радиоактивность»
|
Физическая величина |
Символ |
Единица измерения физической величины |
Ед. изм. физ. вел. |
Описание |
Примечания |
|
Масса (масса покоя) |
m |
килограмм |
кг |
Масса объекта, находящегося в состоянии покоя. |
|
|
Дефект массы |
Δ |
килограмм |
кг |
Величина, выражающая влияние внутренних взаимодействий на массу составной частицы |
|
|
Элементарный электрический заряд |
e |
кулон |
Кл |
Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц |
|
|
Энергия связи |
Eсв |
джоуль |
Дж = (кг·м2/с2) |
Разность между энергией состояния, в котором составляющие части системы бесконечно удалены |
|
|
Период полураспада, среднее время жизни |
T, τ |
секунда |
с |
Время, в течение которого система распадается в примерном отношении 1/2 |
|
|
Эффективное сечение |
σ |
квадратный метр |
м2 |
Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей |
|
|
Активность нуклида |
A |
беккерель |
Бк |
Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада |
|
|
Энергия ионизирующего излучения |
E,W |
джоуль |
Дж = (кг·м2/с2) |
Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц |
|
|
Поглощенная доза ионизирующего излучения |
Д |
грей |
Гр |
Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул |
|
|
Эквивалентная доза ионизирующего излучения |
H, Дэк |
зиверт |
Зв |
Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества |
|
|
Экспозиционная доза рентгеновского и гамма-излучения |
Х |
кулон на килограмм |
Кл/кг |
отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения |
Обозначения в физике с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как
. Дифференциал обозначается малой буквой
перед названием величины, например
.
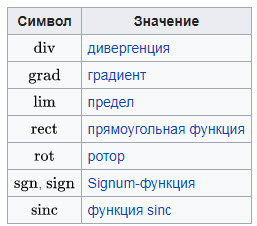
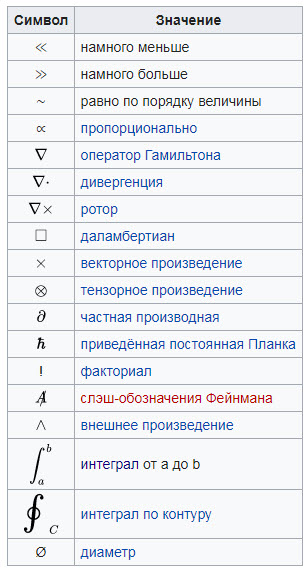
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
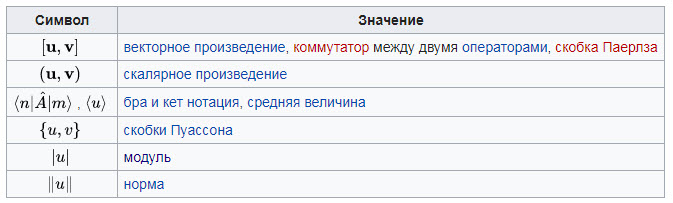
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
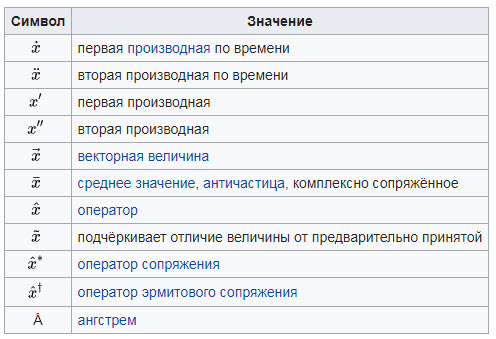
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
Длина — расстояние от точки до точки, измерение кривой: для отрезка прямой длина — расстояние между его концами, для ломаной — сумма длин ее звеньев, для других кривых — верхняя граница длины ломаной линии, вписанной в эту кривую.
В физике длина обозначается в основном буквами L или l (от англ. Length). Единицей измерения длины в системе СИ является метр, в системе СГС — сантиметр.
Содержание
- 1 Линейные размеры тела
- 2 Единицы измерения
- 3 Длина в специальной теории относительности
- 4 См. также
- 5 Источники
Линейные размеры тела[править]
Термин длина употребляется также для обозначения одного из линейных размеров тела. Если тело имеет форму параллелепипеда, то стороны этого параллелепипеда обычно называют длиной, шириной и толщиной. Наибольшая (самая длинная) из сторон — длина. Учитывая ориентацию предмета относительно поверхности Земли, его стороны можно назвать высотой, длиной и толщиной (или шириной). В этом случае длина — большая из горизонтальных сторон. Реки имеют длину русла, ширину и глубину.
Единицы измерения[править]
Стандартной единицей длины в международной системе единиц СИ является метр и его кратные и частные производные: сантиметр, километр, миллиметр, микрометр, нанометр и др. В некоторых странах (США, Великобритания) и профессиях (полиграфия, морское дело) принято использовать традиционные единицы длины, такие как мили или ярды.
Длина в специальной теории относительности[править]
Согласно специальной теории относительности, длина любого тела движущегося выглядит меньше по направлению движения этого тела по сравнению с длиной в собственной системе отсчета этого тела. Если длина тела в собственной системе отсчета равна [math]displaystyle{ l_0 }[/math], то его длина в движущейся системе сокращается до[1]
- [math]displaystyle{ l = l_0 sqrt{1 — frac{v^2}{c^2}} }[/math],
где v — скорость подвижной системы, c — скорость света. Это явление называется лоренцовым сокращением длины.
См. также[править]
- Планковская длина
Источники[править]
- ↑ Жданов В. І. Вступ до теорії відносності. — К.: ВПЦ «Київський університет», 2008. — 290 с. (укр.)
Содержание:
Явления природы и свойства тел в физике описывают с помощью терминов, например: движение, траектория, состояние спокойствия. Описывая движение (рис. 4.1), можно указать, куда движется тело (вперед, назад или вверх), большое оно или маленькое; движется по пря-мой или поворачивает (влево или вправо), а может, вообще не движется. Такая характеристика движения является качественной.
Нас интересуют и количественные характеристики: с какой скоростью двигался автомобиль, какое расстояние он проехал. Количественной характеристикой тела или явления является физическая величина. Физическая величина описывает определенное свойство тела или явления. Она характеризуется числовым значением и единицей измерения. Например: автомобиль проехал путь в 30 километров. Сокращенно можно записать S = 30 км.
Каждая физическая величина имеет свое на-звание и символ, которым она обозначается.
Чтобы описать явление падения определенного тела, можно применить такие физические величины, как масса тела, высота, время падения. Физические величины обычно обозначают латинскими или греческими буквами. Массу тела обозначают буквой «m», высоту – буквой «h», время – буквой «t». Например, если тело массой 2 килограмма упало с высоты 5 метров за одну секунду, то пишут: m = 2 кг, h = 5 м, t = 1 с, употребляя общепринятые сокращения: кг – килограмм, м – метр, с – секунда.
Если нас интересует единица измерения физической величины, а не ее числовое значение, то эту величину пишут в квадратных скобках. Например, диаметр трубы составляет d = 3,2 см, а название единицы измерения (размерность): [d] =см.
Почему нужно измерять:
Начертите на листе бумаги горизонтальный отрезок. Потом проведите от середины этого отрезка перпендикулярный к нему отрезок такой же длины «на глаз». Измерьте длину отрезков линейкой, и вы убедитесь, что вертикальный отрезок короче. Вот почему нужно проводить измерения.
Средства измерения
Прямые измерения физических величин осуществляют с помощью приборов. Длину измеряют линейкой, время – с помощью часов, массу – на весах. Для определения размеров очень малых тел или больших расстояний используют более сложные приборы. Измерить физическую величину – значит сравнить ее с определенной мерой, которая является копией общепринятого образца-эталона. Эталонов немного, и хранятся они в специальных метрологических лабораториях.
История:
Для измерения времени использовали вытекание или капанье воды в сосуд с делениями или пересыпание песка – водяные или песочные часы (рис. 4.2). Движение Солнца по небу давало возможность измерять время с помощью солнечных часов (рис. 4.3). Такими часами люди пользовались несколько тысячелетий, однако они имели существенный недостаток – были довольно неточными.
Рис. 4.3. Солнечные часы
В настоящее время появились очень точные кварцевые часы, которые отсчитывают время в на-ручных часах, мобильном телефоне или компьютере. Для потребностей навигации и науки используют атомные часы, которые «ходят» настолько точно, что допускают ошибку в одну секунду за 500 000 лет!
Для измерения длины надо иметь образец, дли-на которого соответствует общепринятым единицам измерения. Сейчас это 1 м. Эталон (образец) метра хранится в метрологических лабораториях, главная из которых находится в г. Севре (Франция). Измерить длину можно еще и в других единицах измерения – канцелярскими скрепками, например, или спичками и сказать: мой рост составляет 80 скрепок или 36 спичечных коробков. Однако у других людей скрепки или спички могут оказаться другого размера, что усложнит обмен информацией. В давние времена так и было: пользовались футами (длина ступни – 30 см), дюймами (длина последней фаланги большого пальца, приблизительно 2,5 см), ярдами, пядями, саженями, локтями.
Инициаторами перехода на метрическую систему единиц были французы. Согласно договоренности, один метр определили как одну сорокамиллионную часть длины меридиана, который проходит через Париж. Для определения длины меридиана достаточно было измерять его часть, которая простирается от юга Испании до севера Норвегии. Начался этот процесс во время Великой французской революции. Днем рождения метрической системы мер считают 10 декабря 1799 г.
На территории нашей страны метрическая система мер была введена специальным декретом 14 сентября в 1918 г. Переход на новые стандарты измерений связан с изменением привычек, необходимостью переиздания справочников, переоборудования метрических лабораторий, с переподготовкой персонала и тому подобным. Все это стоит довольно дорого. США, например, переход на новые стандарты обошелся в 11 млрд. долларов.
Международная система единиц измерения – СИ
В связи с потребностью международного сотрудничества в 1960 году большинство стран мира подписали соглашение о единой Международной системе еди-ниц измерения SI – Systeme International (на русском языке – СИ).
Рис. 4.4. Эталон метра хранится в Международном бюро мер и весов в Париже
Рис. 4.5. Эталон килограмма
В СИ есть 7 основных единицы измерения, которые обеспечены соответствующими эталонами. Остальные единицы измерения могут быть выражены через основные единицы. Для начала нам понадобятся три основные единицы: метр, килограмм и секунда.
Эталон метра изображен на рис. 4.4. Это рельс определенного профиля, длина которого составляет одну сорокамиллионную часть меридиана, проходящего через Париж. Первый эталон метра был изготовлен во Франции в 1795 году.
В 1983 году эталон длины был изменен: теперь метр определен как расстояние, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Эталон килограмма – цилиндр из платиново-иридиевого сплава, высота которого равна его диаметру и составляет 39 мм (рис. 4.5).
С эталоном секунды вы ознакомитесь в 11 классе.
Таблица 4.1
| Величина | Символ | Размерность | |
| рус. | междунар. | ||
| Длина | l | м | m |
| Масса | m | кг | kg |
| Время | t | с | s |
| Площадь | S, | м2 | m2 |
| Объем | V | м3 | m3 |
| Скорость | v | м/с | m/s |
Площадь в СИ измеряют в м2 (квадратные метры), объем – в м3 (кубические метры).
В таблице 4.1 единицы площади, объема и скорости являются производны-ми единицами, их размерности происходят от основных единиц измерения.
В расчетах используют также кратные и дольные единицы.
Кратные единицы – это единицы, которые больше основных единиц в 10, 100, 1000 и больше раз. Например: 1 дм = 10 см = 101 см, 1 м = 100 см = 102 см, 1 км = 1000 м = 103 м, 1 кг = 1000 г = 103 г.
Дольные единицы – это единицы, которые меньше основных единиц в 10, 100, 1000 и больше раз: 1 см = 0,01 м = 10–2 м, 1 мм = 0,1 см = 10–1 см.
С единицами времени несколько иначе: 1 мин. = 60 с, 1 час = 3600 с. Дольными являются лишь 1 мс (миллисекунда) = 0,001 с = 10–3 с и 1 мкс (микросекунда)= = 0,000001 с = 10–6 с.
Для обозначения кратных и дольных единиц используют приставки (табл. 4.2).
Таблица 4.2 Приставки для обозначения кратных и дольных единиц
| Кратность | Приставка | Обозначение | Пример | ||
| русское | международное | русское | международное | ||
| 102 | гекто | hecto | г | h | 5 гПа (гектопаскаль) = = 500 Па |
| 103 | кило | kilo | к | k | 6 кг (килограмм) = 6000 г |
| 106 | мега | mega | М | M | 2 МДж (мегаджоуль) = = 2 000 000 Дж |
| 109 | гига | giga | Г | G | 1 ГГц (гигагерц) = = 1 000 000 000 Гц |
| Дольность | |||||
| 10–1 | деци | deci | д | d | дм – дециметр |
| 10–2 | санти | centi | с | c | см – сантиметр |
| 10–3 | милли | milli | м | м | мл – миллилитр |
| 10–6 | микро | micro | мк | µ | мкм – микрометр, микрон |
| 10–9 | нано | nano | н | n | нм – нанометр |
Итоги
- Физические величины количественно описывают свойства тел и явлений.
- Физические величины характеризуются названием, символом, числовым значением и единицей измерения.
- В международной системе единиц измерения (СИ) основные механические единицы измерения физических величин – метр, килограмм и секунда.
- Измерить физическую величину – значит сравнить ее с мерой-эталоном.
Физические величины
Физические тела и явления характеризуют физическими величинами. Некоторые из них вам уже знакомы из курса природоведения: это длина, площадь, объем, масса, сила. Рассмотрим их подробнее.
В науке используют единицы физических величин, определенные Международной системой единиц, которую сокращенно называют1 SI — от английских слов System International, что означает «международная система».
Длина, Площадь, Объем
Длиной характеризуют физические тела и, например, путь, пройденный телом за время его движения. За единицу длины в SI принят2 I метр (м).
На линейках и мерных лентах (рулетках) нанесены деления, обозначающие сотые и тысячные доли метра — сантиметры и миллиметры (рис. 3.1).
Единицы площади и объема определяют с помощью единицы длины: единицей площади является I м2 (площадь квадрата со стороной I м), а единицей объема — I м3 (объем куба с ребром I м).
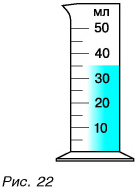
Объем жидкости измеряют с помощью измерительных цилиндров, называемых часто мензурками (рис. 3.2). Длину, площадь и объем задают их числовыми значениями. Физические величины, которые задают только числовыми значениями, называют скалярными.
Время
Всякое физическое явление длится в течение определённого промежутка времени. За единицу времени в S1 принята 1 секунда (с), 60 с составляют 1 минуту (мун), а 60 минут — 1 час (ч).
Время измеряют часами (рис. 3.3). Они представляют собой обычно устройства, в которых повторяется определенный процесс. Например, в маятниковых часах повторяются колебания маятника. Сегодня чаще используют кварцевые часы, в которых колеблются крошечные кристаллы кварца.
Перемещение и скорость
При движении тело изменяет свое положение в пространстве.
Перемещением тела называют направленный отрезок, проведенный из начального положения тела в его конечное положение.
Перемещение задают числовым значением (длиной указанного отрезка) и направлением. Физические величины, которые характеризуют числовым значением и направлением, называют векторными:
Значение векторной величины называют ее модулем.
Векторную величину обозначают буквой со стрелкой, а модуль — той же буквой без стрелки. Так, перемещение обычно обозначают 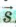

Скоростью тела называют физическую величину, равную отношению перемещения тела к промежутку времени, в течение которого произошло это перемещение.
Скорость, как и перемещение, является векторной величиной, то есть ее характеризуют модулем и направлением. Например, скорости двух встречных автомобилей могут быть равными по модулю, но направлены они противоположно. Скорость обозначают обычно 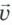
Единицей скорости в SI является 1 метр в секунду (м/с). Тело, которое движется с такой скоростью, за 1 с перемещается на 1 м, — это скорость прогулки. Рекорд скорости в беге — чуть больше 10 м/с.
Скорость современных реактивных самолетов достигает почти километра в секунду (км/с), а космических кораблей — даже больше 10 км/с. Но ни одно тело не может двигаться со скоростью, превышающей скорость света в вакууме, которая равна примерно 300 000 км/с.
Для измерения скорости автомобилей и мотоциклов используют спидометры1 (рис. 3.4-3.6). Они показывают обычно скорость в километрах в час (км/ч). Вы, наверное, замечали, что во время движения автомобиля стрелка спидомстра обычно «покачивается». Дело в том, что скорость автомобиля при движении обычно изменяется.
Масса
Каждое физическое тело имеет определенную массу. Массы двух тел можно сравнить, измерив, как изменяются их скорости при взаимодействии друг с другом: скорость тела большей массы изменяется меньше, чем скорость тела меньшей массы.
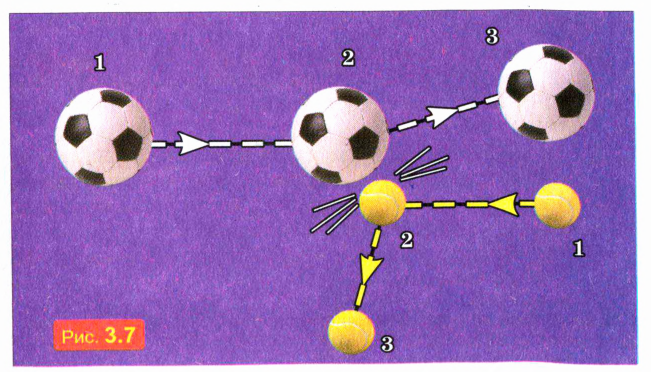
Например, на рис. 3.7 схематически показано столкновение, футбольного и теннисного мячей (цифры обозначают положение мячей в три последовательных момента времени). Мы видим, что при столкновении скорость футбольного мяча изменилась намного меньше, чем скорость теннисного. Значит, масса футбольного мяча намного больше массы теннисного мяча.
Далее мы расскажем о намного более простом способе измерения массы тел, который обычно и используют на практике.
Единицей массы в S1 является 1 килограмм (кг). Это примерно масса одного литра воды. Международный эталон килограмма представляет собой металлический цилиндр из специального сплава.
Сила
Мерой взаимодействия тел является сила: чем больше сила, действующая на тело, тем больше изменяется скорость этого тела за 1 с. Сила является векторной величиной: ее задают числовым значением и направлением. На рисунках силу обозначают стрелкой, начало которой находится в точке приложения силы.
Единицу силы в честь Ньютона назвали ньютоном (Н)1. Сила в 1 Н, приложенная к движущемуся телу массой 1 кг в направлении движения тела, увеличивает его скорость за каждую секунду на 1 м/с,
Чтобы вы представили себе, что такое сила в 1 Н, приведем пример: когда вы держите полное ведро воды, то прикладываете к нему силу, равную примерно 100 Н. При этом приложенная вами сила уравновешивает силу, с которой Земля притягивает то же самое ведро с водой.
Силу, с которой Земля притягивает предметы, называют силой тяжести. В многочисленных опытах было установлено, что сила тяжести, действующая на тело, пропорциональна его массе.
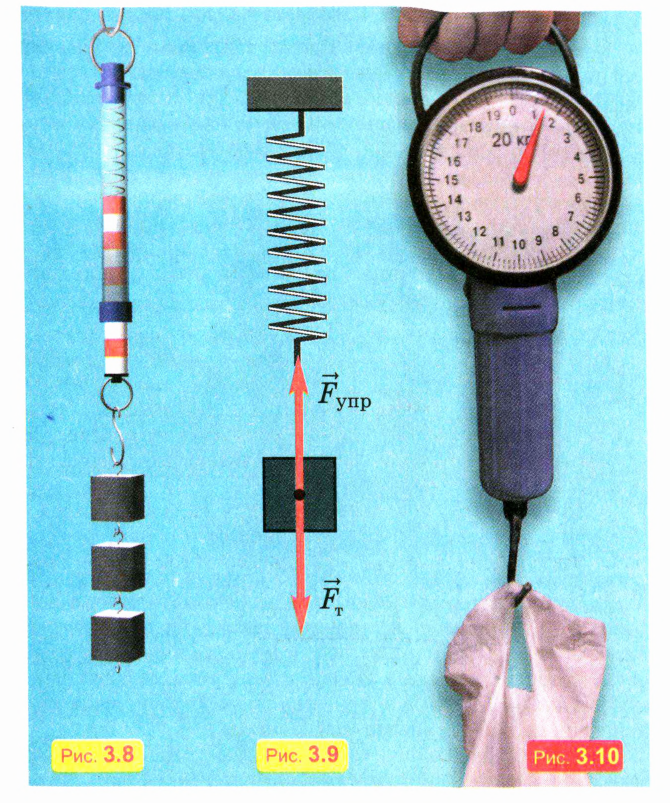
Силу измеряют динамометром2. На рис. 3.8 показан пружинный динамометр, действие которого основано на том, что удлинение пружины пропорционально значению растягивающей ее силы.
На рис. 3.9 схематически изображены силы, действующие на тело, подвешенное к динамометру: это сила тяжести со стороны Земли и сила упругости со стороны пружины. Если тело находится в покое, сила упругости уравновешивает силу тяжести, то есть направлена противоположно ей и равна ей по модулю.
Значит, по удлинению пружины в этом случае можно найти значение силы тяжести. А это, в свою очередь, позволяет рассчитать массу тела, поскольку сила тяжести пропорциональна массе тела.
Таким образом, массу тела можно найти с помощью взвешивания. Пружинные весы (рис. 3.10) — это динамометр, шкала которого размечена (проградуирована) так, что она показывает массу подвешенного груза.
Что называется физической величиной
Издавна люди для более точного описания каких-нибудь событий, явлений, свойств тел и веществ используют их характеристики. Например, сравнивая тела, которые нас окружают, мы говорим, что книга меньше, чем книжный шкаф, а конь больше кошки. Это означает, что объем коня больше объема кошки, а объем книги меньше объема шкафа.
Объем — пример физической величины, которая характеризует общее свойство тел занимать ту или иную часть пространства (рис. 1.15, а). При этом числовое значение объема каждого из тел индивидуально.
Рис. 1.15. Для характеристики свойства тел занимать ту или иную часть пространства мы используем физическую величину объем (а, б), для характеристики движения — скорость (б, в)
Общая характеристика многих материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Еще одним примером физической величины может служить известное вам понятие «скорость*. Все движущиеся тела изменяют свое положение в пространстве с течением времени, однако быстрота этого изменения для каждого тела различна (рис. 1.15, б, в). Так, самолет за 1 с полета успевает изменить свое положение в пространстве на 250 м, автомобиль — на 25 м, человек — на 1 м, а черепаха — всего на несколько сантиметров. Поэтому физики и говорят, что скорость — это физическая величина, которая характеризует быстроту движения.
Нетрудно догадаться, что объем и скорость,— это далеко не все физические величины, которыми оперирует физика. Масса, плотность, сила, температура, давление, напряжение, освещенность — это лишь малая часть тех физических величин, с которыми вы познакомитесь, изучая физику.
Что означает измерить физическую величину
Для того чтобы количественно описать свойства какого-либо материального объекта или физического явления, необходимо установить значение физической величины, которая характеризует данный объект или явление.
Значение физических величин получают путем измерений (рис. 1.16— 1.19) или вычислений.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Приведем пример из художественной литературы: «Пройдя шагов триста по берегу реки, маленький отряд вступил под своды дремучего леса, извилистыми тропами которого им надо было странствовать на протяжении десяти дней*. (Ж. Верн «Пятнадцатилетний капитан*)
Герои романа Ж. Верна измеряли пройденный путь, сравнивая его с шагом, то есть единицей измерения служил шаг. Таких шагов оказалось триста. В результате измерения было получено числовое значение (триста) физической величины (пути) в избранных единицах (шагах).
Рис. 1.20. Если бабушка и внук будут измерять расстояние в шагах. то они всегда будут получать разные результаты
Очевидно, что выбор такой единицы не позволяет сравнивать результаты измерений, полученные разными людьми, поскольку длина шага у всех разная (рис. 1.20). Поэтому ради удобства и точности люди давным-давно начали договариваться о том, чтобы измерять одну и ту же физическую величину одинаковыми единицами. Ныне в большинстве стран мира действует принятая в I960 году Международная система единиц измерения, которая носит название «Система Интернациональная* (СИ) (рис. 1.21).
В этой системе единицей длины является метр (м), времени — секунда (с); объем измеряется в метрах кубических (м3), а скорость — в метрах в секунду (м/с). Об остальных единицах СИ вы узнаете позже.
Кратные и дольные единицы
Из курса математики вы знаете, что для сокращения записи больших и малых значений разных величин пользуются кратными и дольными единицами.
Кратные единицы — это единицы, которые больше основных единиц в 10, 100, 1000 и более раз.
Дольные единицы — это единицы, которые меньше основных в 10, 100, 1000 и более раз.
Для записи кратных и дольных единиц используют приставки. Например, единицы
Рис. 1.21. Основные единицы Международной системы (СИ)
длины, кратные одному метру,— это километр (1000 м), декаметр (10 м). Единицы длины, дольные одному метру,— это дециметр (0,1 м), сантиметр (0,01 м), микрометр (0,000001 м) и так далее.
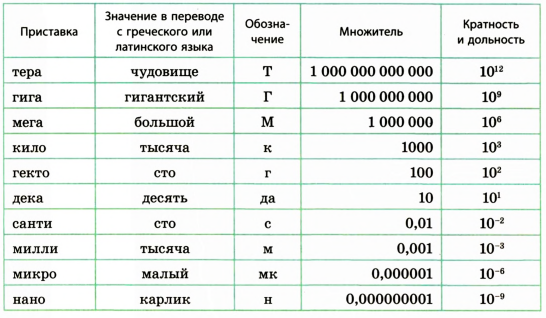
В таблице приведены наиболее часто употребляемые приставки.
Приставки, служащие для образования кратных и дольных единиц
Измерительные приборы
Измерение физических величин ученые проводят с помощью измерительных приборов. Простейшие из них — линейка, рулетка — служат для измерения расстояния и линейных размеров тела. Вам также хорошо известны такие измерительные приборы, как часы — прибор для измерения времени, транспортир — прибор для измерения углов на плоскости, термометр — прибор для измерения температуры и некоторые другие (рис. 1.22, с. 20). Со многими измерительными приборами вам еще предстоит познакомиться.
Большинство измерительных приборов имеют шкалу, которая обеспечивает возможность измерения. Кроме шкалы, на приборе указывают единицы, в которых выражается измеренная данным прибором величина*.
По шкале можно установить две наиболее важные характеристики прибора: пределы измерения и цену деления.
Пределы измерения — это наибольшее и наименьшее значения физической величины, которые можно измерить данным прибором.

————————————————
Цена деления — это значение наименьшего деления шкалы измерительного прибора.
Например, верхний предел измерений медицинского термометра (рис. 1.23) равен 42 °С, нижний — 34 °С, а цена деления шкалы этого термометра составляет 0,1 °С.
Напоминаем: чтобы определить цену деления шкалы любого прибора, необходимо разность двух любых значений величин, указанных на шкале, разделить на количество делений между ними.
Итоги:
Общая характеристика материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
В результате измерений мы получаем значение физических величин.
Говоря о значении физической величины, следует указать ее числовое значение и единицу.
Для измерения физических величин пользуются измерительными приборами.
Для сокращения записи числовых значений больших и малых физических величин используют кратные и дольные единицы. Они образуются с помощью приставок.
Точность измерений
Теперь вы знаете, что означает измерить физическую величину. И в повсе дневной жизни вам уже приходилось выполнять множество простейших измерений. Но насколько точными были ваши измерения? Можно ли получить абсолютно точное значение физической величины?
Попробуем разобраться в этих непростых вопросах.
Оцениваем размеры и проверяем результат:
Начнем с проверки вашего глазомера.
Оцените на глаз длину иглы, изображенной на рис 1.24. А теперь давайте проверим, насколько результат вашей оценки соответствует действительности, то есть измерим длину той же иглы с помощью линейки. Для этого:
- — приложим линейку к игле так, чтобы «ноль» на ее шкале совпал с одним концом иглы (рис. 1.25);
- — определим значение деления шкалы, напротив которого расположен ее другой конец.
Мы видим, что он расположен возле отметки 5 см. Отсюда делаем вывод, что длина иглы около 5 см. Если результат вашей предварительной оценки совпадает с этим значением, то у вас хороший глазомер. Определить на глаз размер более точно нам не удастся.
Результат измерений:
Если нам нужен более точный результат, придется обратить внимание на то, что кончик иглы немного более чем на два миллиметра выступает за отметку 5 см. Итак, более точная длина иглы — 5,2 см, или 52 мм.
Вы можете возразить, что это тоже неточно.
Да, неточно! Именно поэтому принято всегда указывать точность, с которой выполнено измерение.
В первом случае наше измерение выполнено с точностью до 1 см, а во втором — с точностью до 0,1 см.
Чтобы произвести еще более точное измерение, необходимо учесть длину той части иглы, которая выступает за отметку 52 мм, и тогда точность повысится до 0,01 см. Но для этого нам придется использовать измерительный прибор с еще меньшей ценой деления, то есть более точный, но даже тогда мы не можем утверждать, что измерили иглу совершенно точно.
Причин для этого достаточно: это и несовершенство конструкции прибора, и погрешности, которые возникают при проведении опыта (например, начало иглы невозможно абсолютно точно совместить с «нулем» линейки). Таким образом, даже если измерение проводится более тщательно и с помощью более совершенного прибора, точность возрастает, но погрешностей все равно не избежать.
Чтобы уменьшить погрешность, измерение можно выполнить несколько раз, а затем вычислить среднее значение всех полученных результатов (наити их среднее арифметическое).
Точность измерений
Однако не следует думать, что чем точнее измерение, тем лучше: излишняя точность не всегда целесообразна.
Предположим, что вместо длины иглы вам необходимо измерить длину крышки стола. В этом случае нет необходимости учитывать десятые и сотые доли миллиметра, поскольку, измеряя длину стола в разных местах, мы получим величины, отличающиеся на несколько миллиметров. Поэтому долями миллиметра в этом случае можно пренебречь. Также нет смысла измерять длину стены с точностью до одного миллиметра (рис. 1.26).
Из этого можно сделать вывод, что необходимую точность измерения определяет цель эксперимента.
Чаще всего важно не значение погрешности, а то, какую часть от всей измеренной величины составляет возможная погрешность.
Если портной, выкраивая брюки, ошибется на 1 мм, вы этого даже не заметите. А вот если, втягивая нить в ушко иглы, он всякий раз будет ошибаться на 1 мм (рис. 1.27), то едва ли брюки вообще когда-либо будут сшиты.
Роль измерений в физике. Прямые и косвенные измерения
Наука начинается с тех пор, как начинают измерять… Д. И. Менделеев
Вдумайтесь в слова известного ученого. Из них ясна роль измерений в любой науке, особенно в физике. Но, кроме того, измерения важны в практической жизни. Можете ли вы представить свою жизнь без измерений времени, массы, длины, скорости движения, расхода электроэнергии и т. д.?
Как измерить физическую величину? Для этой цели используются измерительные приборы. Некоторые из них вам уже известны. Это разного вида линейки, часы, термометры, весы, транспортиры и др.
Измерительные приборы бывают цифровые и шкальные. В цифровых приборах результат измерений определяется цифрами. Это электронные приборы — часы, термометр, счетчик электроэнергии (рис. 19) и др.
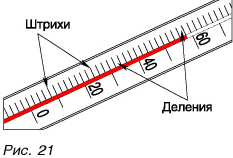
Линейка, стрелочные часы, термометр бытовой, весы, транспортир (рис. 20) — это шкальные приборы. Они имеют шкалу. По ней определяется результат измерений. Вся шкала расчерчена штрихами на деления (рис. 21). Одно деление это не один штрих, как иногда ошибочно считают некоторые учащиеся, а промежуток между двумя ближайшими штрихами. На рисунке 22 на шкале мензурки от значения 10 мл до значения 20 мл два деления, но три штриха. Приборы, которые мы будем использовать в лабораторных работах, в основном шкальные.
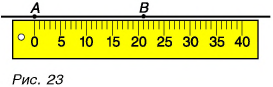
Что значит измерить физическую величину? Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу. Например, чтобы измерить длину отрезка прямой между точками A и В, нужно приложить линейку и по ее шкале (рис. 23) определить, сколько миллиметров укладывается между точками А и В. Однородной величиной, с которой проводилось сравнение длины отрезка АВ, в данном случае была длина, равная 1 мм.
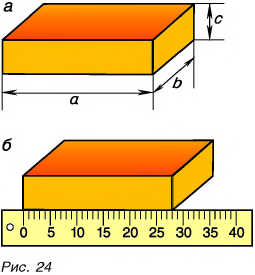
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямым. Например, приложив линейку к разным ребрам бруска, мы определим его длину а, ширину b и высоту с (рис. 24, а). Значение длины, ширины и высоты мы определили непосредственно, сняв данные со шкалы линейки. Из рисунка 24, б следует: a = 28 мм. Это прямое измерение.
А как определить объем бруска? Надо провести прямые измерения его длины а, ширины b и высоты с, а затем по формуле
вычислить объем бруска.
В этом случае мы говорим, что объем бруска определили по формуле, т. е. косвенно, и измерение объема называется косвенным измерением.
В физике измерения физических величин чаще всего косвенные. В дальнейшем вы убедитесь в этом сами.
Главные выводы:
- Измерительные приборы бывают цифровые и шкальные.
- При прямых измерениях физическая величина определяется непосредственно по шкале прибора.
- При косвенных измерениях физическая величина определяется по формуле.
Для любознательных:
Изучая строение человеческого тела и работу его органов, ученые проводят множество измерений. Оказывается, в человеке массой примерно 70 кг около 6 л крови. Сердце человека в спокойном состоянии сокращается 60—80 раз в минуту. За одно сокращение оно выбрасывает в среднем 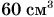
В течение суток кровь человека около 360 раз проходит через почки, очищаясь там от вредных веществ. Общая протяженность почечных кровеносных сосудов составляет приблизительно 18 км. Ведя здоровый образ жизни, мы помогаем нашему организму работать без сбоев!
Единицы измерения физических величин
Чтобы решить, как быстрее доехать до вокзала — на трамвае или на такси, сравнивают скорости движения этих транспортных средств. Скорость — физическая величина. Она количественно описывает физическое явление — движение. Если скорость автомобиля 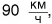
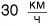
В физике для описания физических явлений и свойств используется множество физических величин: длина, сила, давление и др. Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения. Например, длина бруска 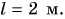
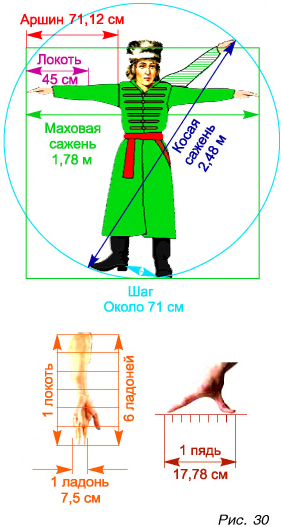
Исторически сложилось так, что у разных народов и государств единицы измерения одних и тех же физических величин различались. Часто это были единицы, соответствующие размерам частей тела человека, массе семени бобов и т. д. Пользоваться такими единицами было неудобно, особенно в торговле между разными государствами.
Например, в Англии для измерения длины использовался фут (1 фут = 30,5 см), а на Руси — аршин (1 аршин = 71,1 см) (рис. 30). Нужно было упорядочить систему единиц, сделать ее удобной в использовании всеми странами. В 1960 г. ввели единую Международную систему единиц (сокращенно СИ — Систему Интернациональную). Ею пользуется большинство стран. Основными единицами в СИ являются: метр (м) — для длины, килограмм (кг) — для массы, секунда (с) — для промежутка времени, Кельвин (К) — для температуры.
Но всегда ли удобно измерять время в секундах, а длину — в метрах? Оказывается, нет. Например, время движения поезда из Минска в Москву измеряют в часах (ч), а путь — в километрах (км). Единицы 1 ч и 1 км — это неосновные (кратные) единицы СИ. Между основными и неосновными единицами существует связь. Так, 1 км = 1000 м, 1 ч = 3600 с.
Основные единицы измерения имеют эталоны. Эталоны хранятся в г. Севре (Франция) в Международном бюро мер и весов. На рисунке 31 приведен эталон килограмма — цилиндр из плати но-иридиевого сплава. По эталону делают копии, которыми пользуются разные страны. Позже вы познакомитесь с эталонами других единиц измерения.
Для любознательных
Эталонная база страны обеспечивает единство измерений и является частью национального достояния. В Беларуси, как и в других странах, ведется работа по исследованию и созданию эталонных комплексов. В Белорусском государственном институте метрологии созданы эталоны массы, времени (см. рис.), температуры и др.
Главные выводы
- Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения.
- Основными единицами СИ являются: метр, килограмм, секунда, Кельвин и др.
- Основные единицы измерения имеют свои эталоны.
Пример №1
В одной из книг немецкого путешественника XVII в. есть такие строки: «Шелковая материя, привозимая с Востока, называется русскими «китайкой», и каждый кусок содержит ни больше ни меньше как восемь с четвертью аршин». Сколько метров в куске материи?
Дано:
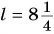
1 аршин = 71,1 см = 0,711 м
Решение
Так как 1 аршин = 71,1 см = 0,711 м, то длина восьми с четвертью аршин в метрах будет равна:
Ответ:
- Заказать решение задач по физике
Действия над физическими величинами
В математике можно складывать, вычитать и сравнивать любые числа. А какие действия можно производить над физическими величинами?
Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.
Мы можем складывать длину с длиной, вычитать из массы массу, сравнивать промежуток времени с промежутком времени (пример 1). Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг. А вот умножать и делить можно как однородные, так и разные физические величины.
В примере 2 делятся не только числовые значения (10 : 2 = 5), но и единицы физических величин (кг : кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
В примере 3 умножаются числовые значения 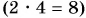
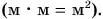
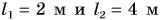
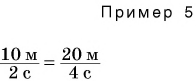
В примере 4 в результате деления двух разных физических величин — длины 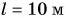
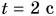
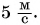
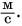
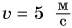
В примере 5 знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 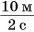
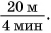
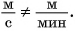
Для любознательных:
Большие единицы времени — год и сутки — дала нам сама природа. Но час, минута и секунда появились благодаря человеку.
Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятеричная система счисления. Поскольку 60 делится без остатка на 12, сутки у вавилонян состояли из 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, — наследие шестидесятеричной системы счисления Вавилона.
Главные выводы:
- Складывать, вычитать и сравнивать можно только однородные физические величины.
- Умножение и деление разнородных величин приводит к появлению новой физической величины.
Пример №2
Выберите значения физических величин, которые можно складывать: 120 г, 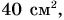
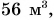
Решение
Однородными физическими величинами в данном случае являются массы тел: 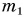
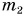
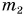
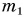
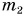
Следовательно, m = 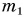
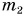
Ответ: результатом сложения является масса m = 168 г.
Пример №3
Определите физические величины, получившиеся в результате
выполнения следующих действий: 1) 35 г : 5 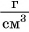
Решение
1) Найдем отношение двух физических величин, разделив их числовые значения и единицы:
Мы получили физическую величину — объем
2) Чтобы умножить две однородные физические величины, необходимо выразить их в одних единицах, например в сантиметрах (см):
Мы получили физическую величину — площадь
Ответ: 1) в результате деления двух физических величин разного рода (массы и плотности) получена третья физическая величина — объем 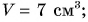
физические величины и их измерение
Чем отличается язык физики (и любой другой точной науки) от обычного? язык физики интернационален: он создавался лучшими умами человечества, его однозначно понимают в любом уголке нашей планеты. язык физики объективен: каждое его понятие однозначно, оно имеет один смысл, который может измениться (чаще всего — расшириться) только благодаря опытам. Как и методы научного познания, язык физики родился из практики.
Что такое физическое исследование и каковы его методы
Вспомним, с чего начинается исследовательская работа ученых. Прежде всего — это наблюдение за определенным явлением (телом или материалом) и размышления над его сущностью.
Наблюдение — это восприятие природы с целью получения первичных данных для последующего анализа. Далеко не всегда наблюдения приводят к правильным выводам. Поэтому, чтобы опровергнуть или подтвердить собственные выводы, ученые проводят физические исследования.
Физическое исследование — это целенаправленное изучение явлений и свойств природы средствами физики.
| Методы физических исследований | |
|---|---|
| экспериментальный | теоретический |
| Эксперимент — исследование физического явления в условиях, находящихся под контролем исследователя. В своей основе физика является экспериментальной наукой: большинство ее законов основаны на фактах, установленных опытным путем. | Анализ данных, полученных в результате экспериментов, формулирование законов природы, объяснение конкретных явлений и свойств на основе этих законов, а главное — предвидение и теоретическое обоснование (с широким использованием математики) еще не известных явлений и свойств. |
Какие наблюдения, теоретические и экспериментальные исследования вы провели бы, чтобы исследовать свечение обычной лампы накаливания?
Теоретические исследования проводят не с конкретным физическим телом, а с его идеализированным аналогом — физической моделью, которая должна учитывать только некоторые основные свойства исследуемого тела. Так, изучая движение автомобиля, мы иногда используем его физическую модель — материальную точку (рис. 2.1, а).
Эту модель используют, если размеры тела не существенны для теоретического описания, то есть в модели «материальная точка» учитывается только масса тела, а его форма и размеры во внимание не принимаются. А вот если нужно выяснить, как на движение автомобиля влияет сопротивление воздуха, целесообразно применить уже другую физическую модель — она должна учитывать и форму, и размеры автомобиля (рис. 2.1, б), но может не учитывать, например, размещение пассажиров в салоне. Чем больше выбрано соответствующих параметров для исследования физической системы «автомобиль», тем точнее можно предвидеть «поведение» этой системы.
Рис. 2.1. Определяя скорость и время движения автомобиля, можно применять физическую модель «материальная точка» (а); выясняя аэродинамические свойства автомобиля, эту физическую модель применять нельзя (б)
Целесообразно ли использовать физическую модель «материальная точка», если инженеры должны рассчитать устойчивость автомобиля?
Как измерить физическую величину
Описывая, например, движение автомобиля, мы используем определенные количественные характеристики: скорость, ускорение, время движения, силу тяги, мощность и т. п.
Из предыдущего курса физики вы знаете, что количественную меру свойства тела, физического процесса или явления называют физической величиной. Значение физической величины устанавливают в ходе измерений, которые, в свою очередь, бывают прямые и косвенные. При прямых измерениях величину сравнивают с ее единицей (метром, секундой, килограммом, ампером и т. п.) с помощью измерительного прибора, проградуированного в соответствующих единицах (рис. 2.2).
Рис. 2.2. Современные приборы для прямого измерения температуры (а); массы (б); скорости движения (в)
Назовите несколько физических величин, значения которых вы находили с помощью прямых измерений. В каких единицах измеряют эти величины? какими приборами? При косвенных измерениях величину вычисляют по результатам прямых измерений других величин, связанных с измеряемой величиной некоторой функциональной зависимостью. Так, чтобы найти среднюю плотность ρ тела, нужно с помощью весов измерить массу m тела, с помощью, например, мензурки измерить его объем V, а затем массу разделить на объем:
Построение системы единиц
В конце XVIII в., после Великой французской революции, перед французскими учеными была поставлена задача создать систему единиц на научной основе. В результате появилась метрическая система единиц. В 1960 г. была создана Международная система единиц CИ, которая со временем стала в мире доминирующей.
Основные единицы СИ
- килограмм (1 кг, 1 kg) единица массы
- метр (1 м, 1 m) единица длины
- секунда (1 с, 1 s) единица времени
- ампер (1 А, 1 А) единица силы тока
- моль (1 моль, 1 mol) единица количества вещества
- кельвин (1 К, 1 K) единица температуры
- кандела (1 кд, 1 kd) единица силы света
Исторически единицы физических величин связывали с определенными телами или природными процессами. Так, 1 метр был связан с размерами планеты Земля, 1 килограмм — с определенным объемом воды, 1 секунда — с суточным вращением Земли. Позже для каждой единицы был создан эталон — средство (или комплекс средств) для воспроизведения и хранения единицы физической величины. Основные эталоны хранились (и хранятся сейчас) в Международном бюро мер и весов (г. Севр, Франция).
Сейчас все большее распространение получают методы построения системы единиц, основанные на особенностях излучения и распространения электромагнитных волн, а также на фундаментальных физических константах. Рассмотрим основные этапы создания системы единиц на примерах метра и килограмма.
Напомним, что для удобства записи больших и малых значений физических величин используют кратные и дольные единицы. Кратные единицы больше основных единиц в 10, 100, 1000 и более раз. Дольные единицы меньше основных единиц в 10, 100, 1000 и более раз.
Названия кратных и дольных единиц включают в себя специальные префиксы. Например, километр (1000 м, или 103 м) — кратная единица длины, миллиметр (0,001 м, или 10–3 м) — дольная единица длины (см. табл. 1).
Таблица 1. Префиксы для образования названий кратных и дольных единиц
| Префикс | Символ | Множитель |
| атто- | а | 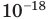 |
| фемто- | ф | 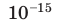 |
| пико- | п | 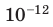 |
| нано- | н | 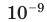 |
| микро- | мк | 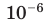 |
| милли- | м | 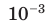 |
| санти- | с | 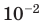 |
| кило- | к | 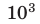 |
| мега- | М | 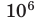 |
| гига- | Г | 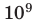 |
| тера- | Т | 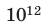 |
| пета | п | 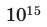 |
| экса | е | 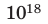 |
Погрешности измерений
При измерении любой физической величины обычно выполняют три последовательные операции: 1) выбор, проверка и установка прибора (приборов); 2) снятие показаний прибора (приборов); 3) вычисление искомой величины по результатам измерений (при косвенных измерениях); 4) оценка погрешности.
Например, нужно измерить на местности расстояние около 5 м. Разумеется, что для этого не следует брать ученическую линейку, — удобнее воспользоваться рулеткой. Все приборы имеют определенную точность. Расстояние в 5 м, как правило, не требуется определять с точностью до миллиметра, поэтому шкала рулетки может и не содержать соответствующих делений.
Рис. 2.3. Штангенциркуль. Точность измерения изображенным прибором — сотые доли миллиметра
А вот если для ремонта лабораторного крана необходимо определить размер шайбы, целесообразно воспользоваться штангенциркулем (см. рис. 2.3). Однако даже с помощью сверхточного прибора нельзя выполнить измерения абсолютно точно. Всегда есть погрешности измерений — отклонение значения измеренной величины от ее истинного значения. Модуль разности между измеренным (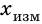
Отношение абсолютной погрешности к измеренному значению измеряемой величины называют относительной погрешностью измерения 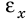
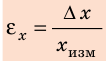
Погрешности при измерениях бывают случайные и систематические.
Случайные погрешности
Случайные погрешности связаны с процессом измерения: измеряя расстояние рулеткой, невозможно проложить ее идеально ровно; отсчитывая секундомером время, прибор невозможно мгновенно включить и выключить и т. д. Чтобы результаты были более точными, измерения проводят несколько раз и определяют среднее значение измеряемой величины:
где 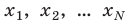
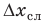
Если измерение проводилось один раз, будем считать, что случайная погрешность равна половине цены деления шкалы прибора.
Систематические погрешности
Систематические погрешности связаны прежде всего с выбором прибора: невозможно найти рулетку с идеально точной шкалой, идеально равноплечие рычаги и т. п. Систематические погрешности определяются классом точности прибора, поэтому их часто называют погрешностями прибора. В процессе эксплуатации точность приборов может снижаться, поэтому их необходимо периодически калибровать при помощи специального оборудования. Абсолютные погрешности некоторых приборов, используемых в школе, приведены в табл. 2. Если используются другие приборы, будем считать, что абсолютная погрешность прибора равна половине цены деления его шкалы.
Абсолютная погрешность прямого измерения (∆x) учитывает как систематическую погрешность, связанную с прибором (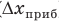
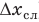
Обратите внимание! Приведенные формулы очень упрощены. Ученые используют более сложные методы расчетов погрешностей.
Таблица 2. Абсолютные погрешности некоторых физических приборов
| Физический прибор | Цена деления шкалы прибора | Абсолютная погрешность прибора |
| Линейка ученическая | 1 мм | ±1 мм |
| Лента измерительная | 0,5 см | ±0,5 см |
| Штангенциркуль | 0,1 мм | ±0,05 мм |
| Цилиндр измерительный | 1 мл | ±1 мл |
| Секундомер | 0,2 с | ±1 с за 30 мин |
| Динамометр учебный | 0,1 Н | ±0,05 Н |
| Термометр лабораторный | 1 °С | ±1 °С |
Как определить погрешности косвенных измерений
Многие физические величины невозможно измерить непосредственно. Их косвенное измерение включает два этапа: 1) методом прямых измерений находят значения определенных величин, например x, y; 2) по соответствующей формуле вычисляют искомую величину f. Как в таком случае определить абсолютную ∆f и относительную 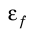
- Относительную погрешность определяют по специальным формулам (см. табл. 3).
- Абсолютную погрешность определяют по относительной погрешности:
- Если эксперимент проводят, чтобы выяснить, выполняется ли некое равенство (например, X Y= ), то относительную погрешность экспериментальной проверки равенства X Y= можно оценить по формуле:
Таблица 3. Некоторые формулы для определения относительной погрешности
| Функциональная зависимость | Относительная погрешность |
|---|---|
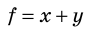 |
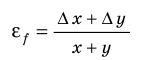 |
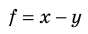 |
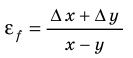 |
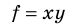 |
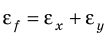 |
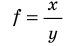 |
|
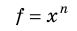 |
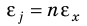 |
Как правильно записать результаты
Абсолютная погрешность эксперимента определяет точность, с которой имеет смысл вычислять измеряемую величину. Абсолютную погрешность ∆x обычно округляют до одной значащей цифры с завышением, а результат измерения xизм — до величины разряда, оставшегося после округления в абсолютной погрешности. Окончательный результат х записывают в виде:
Абсолютная погрешность — положительная величина, поэтому 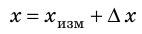
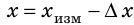
Рис. 2.4. Абсолютная погрешность измерения определяет интервал, в котором находится истинное значение измеряемой величины
Пример. Пусть измеряли ускорение свободного падения (g). После обработки экспериментальных данных получили: 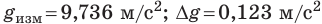
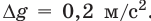
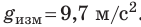
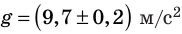
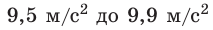
Рис. 2.5. Табличное значение: 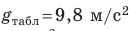
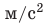
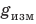
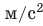
- Точность измерений и погрешности
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Что изучает физика
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс