Как пишется дуга в геометрии

Окружность

Построение окружности циркулем
Радиус, хорда и диаметр
Дуга

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Построение окружности циркулем

Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

D = 2r.

Дуга

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

Источник

A circular sector is shaded in green. Its curved boundary of length L is a circular arc.

A circular arc is the arc of a circle between a pair of distinct points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the centre of the circle that is less than π radians (180 degrees); and the other arc, the major arc, subtends an angle greater than π radians. The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that connects the two ends of the arc is known as a chord of a circle. If the length of an arc is exactly half of the circle, it is known as a semicircular arc.

Length[edit]

The length (more precisely, arc length) of an arc of a circle with radius r and subtending an angle θ (measured in radians) with the circle center — i.e., the central angle — is

This is because

${displaystyle {frac {L}{mathrm {circumference} }}={frac {theta }{2pi }}.}$

Substituting in the circumference

${displaystyle {frac {L}{2pi r}}={frac {theta }{2pi }},}$

and, with α being the same angle measured in degrees, since θ = α/180π, the arc length equals

${displaystyle L={frac {alpha pi r}{180}}.}$

A practical way to determine the length of an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle, measure the angle where the two lines meet the center, then solve for L by cross-multiplying the statement:

measure of angle in degrees/360° = L/circumference.

For example, if the measure of the angle is 60 degrees and the circumference is 24 inches, then

${displaystyle {begin{aligned}{frac {60}{360}}&={frac {L}{24}}\[6pt]360L&=1440\[6pt]L&=4.end{aligned}}}$

This is so because the circumference of a circle and the degrees of a circle, of which there are always 360, are directly proportional.

The upper half of a circle can be parameterized as

${displaystyle y={sqrt {r^{2}-x^{2}}}.}$

Then the arc length from x=a to is

${displaystyle L=r{Big [}arcsin left({frac {x}{r}}right){Big ]}_{a}^{b}.}$

Sector area[edit]

The area of the sector formed by an arc and the center of a circle (bounded by the arc and the two radii drawn to its endpoints) is

${displaystyle A={frac {r^{2}theta }{2}}.}$

The area A has the same proportion to the circle area as the angle θ to a full circle:

$frac{A}{pi r^2}=frac{theta}{2pi}.$

We can cancel π on both sides:

$frac{A}{r^2}=frac{theta}{2}.$

By multiplying both sides by r², we get the final result:

$A=frac{1}{2} r^2 theta.$

Using the conversion described above, we find that the area of the sector for a central angle measured in degrees is

$A=frac{alpha}{360} pi r^2.$

Segment area[edit]

The area of the shape bounded by the arc and the straight line between its two end points is

${displaystyle {frac {1}{2}}r^{2}(theta -sin theta ).}$

To get the area of the arc segment, we need to subtract the area of the triangle, determined by the circle’s center and the two end points of the arc, from the area . See Circular segment for details.

Radius[edit]

The product of the line segments AP and PB equals the product of the line segments CP and PD. If the arc has a width AB and height CP, then the circle’s diameter ${displaystyle CD={frac {APcdot PB}{CP}}+CP}$

Using the intersecting chords theorem (also known as power of a point or secant tangent theorem) it is possible to calculate the radius r of a circle given the height H and the width W of an arc:

Consider the chord with the same endpoints as the arc. Its perpendicular bisector is another chord, which is a diameter of the circle. The length of the first chord is W, and it is divided by the bisector into two equal halves, each with length W/2. The total length of the diameter is 2r, and it is divided into two parts by the first chord. The length of one part is the sagitta of the arc, H, and the other part is the remainder of the diameter, with length 2r − H. Applying the intersecting chords theorem to these two chords produces

${displaystyle H(2r-H)=left({frac {W}{2}}right)^{2},}$

whence

${displaystyle 2r-H={frac {W^{2}}{4H}},}$

${displaystyle r={frac {W^{2}}{8H}}+{frac {H}{2}}.}$

External links[edit]

Table of contents for Math Open Reference Circle pages
Math Open Reference page on circular arcs With interactive animation
Math Open Reference page on Radius of a circular arc or segment With interactive animation
Weisstein, Eric W. «Arc». MathWorld.

Источник

A circular sector is shaded in green. Its curved boundary of length L is a circular arc.

Length[edit]

The length (more precisely, arc length) of an arc of a circle with radius r and subtending an angle θ (measured in radians) with the circle center — i.e., the central angle — is

This is because

${displaystyle {frac {L}{mathrm {circumference} }}={frac {theta }{2pi }}.}$

Substituting in the circumference

${displaystyle {frac {L}{2pi r}}={frac {theta }{2pi }},}$

and, with α being the same angle measured in degrees, since θ = α/180π, the arc length equals

${displaystyle L={frac {alpha pi r}{180}}.}$

measure of angle in degrees/360° = L/circumference.

For example, if the measure of the angle is 60 degrees and the circumference is 24 inches, then

${displaystyle {begin{aligned}{frac {60}{360}}&={frac {L}{24}}\[6pt]360L&=1440\[6pt]L&=4.end{aligned}}}$

This is so because the circumference of a circle and the degrees of a circle, of which there are always 360, are directly proportional.

The upper half of a circle can be parameterized as

${displaystyle y={sqrt {r^{2}-x^{2}}}.}$

Then the arc length from x=a to is

${displaystyle L=r{Big [}arcsin left({frac {x}{r}}right){Big ]}_{a}^{b}.}$

Sector area[edit]

The area of the sector formed by an arc and the center of a circle (bounded by the arc and the two radii drawn to its endpoints) is

${displaystyle A={frac {r^{2}theta }{2}}.}$

The area A has the same proportion to the circle area as the angle θ to a full circle:

$frac{A}{pi r^2}=frac{theta}{2pi}.$

We can cancel π on both sides:

$frac{A}{r^2}=frac{theta}{2}.$

By multiplying both sides by r², we get the final result:

$A=frac{1}{2} r^2 theta.$

Using the conversion described above, we find that the area of the sector for a central angle measured in degrees is

$A=frac{alpha}{360} pi r^2.$

Segment area[edit]

The area of the shape bounded by the arc and the straight line between its two end points is

${displaystyle {frac {1}{2}}r^{2}(theta -sin theta ).}$

Radius[edit]

Using the intersecting chords theorem (also known as power of a point or secant tangent theorem) it is possible to calculate the radius r of a circle given the height H and the width W of an arc:

${displaystyle H(2r-H)=left({frac {W}{2}}right)^{2},}$

whence

${displaystyle 2r-H={frac {W^{2}}{4H}},}$

${displaystyle r={frac {W^{2}}{8H}}+{frac {H}{2}}.}$

External links[edit]

Table of contents for Math Open Reference Circle pages
Math Open Reference page on circular arcs With interactive animation
Math Open Reference page on Radius of a circular arc or segment With interactive animation
Weisstein, Eric W. «Arc». MathWorld.

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности.

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

M N – диаметр.

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

∪ A B = ∪ C D = α

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

l = 2 π R

Длина дуги окружности, на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Замкнутый сегмент дифференцируемой кривой A круговой сектор закрашено зеленым. Его криволинейная граница длиной L представляет собой дугу окружности.

В евклидовой геометрии дуга (символ: ⌒ ) представляет собой соединенный подмножество дифференцируемой кривой. Дуги линий называются сегментами или лучами, в зависимости от того, ограничены они или нет. Распространенный пример изогнутой кривой — это дуга окружности, называемая дугой окружности . В сфере (или сфероида ) дуга большого круга (или большого эллипса ) называется большая дуга .

Каждая пара различных точек на окружности определяет две дуги. Если две точки не находятся прямо напротив друг друга, одна из этих дуг, вспомогательная дуга, будет соединить угол в центре окружности, который меньше π радианы (180 градусов), а другая дуга, большая дуга, будет составлять угол больше, чем π радиан.

Содержание

1 Дуги окружности
- 1.1 Длина дуги окружности
- 1.2 Площадь сектора дуги
- 1.3 Площадь сегмента дуги
- 1.4 Радиус дуги
2 Параболические дуги
3 См. Также
4 Ссылки
5 Внешние ссылки

Дуги окружности

Длина дуги окружности

Длина (точнее, длина дуги ) дуги окружности радиусом r, соединяющей угол θ (измеренный в радианах) с центром окружности, т. Е. Центральный угол , составляет

L = θ r. { displaystyle L = theta r.}

Это потому, что

L c i r c u m f e r e n c e = θ 2 π. { displaystyle { frac {L} { mathrm {окружность}}} = { frac { theta} {2 pi}}.} ${ displaystyle { frac {L} { mathrm {окружность}}} = { frac { theta} {2 pi}}.}$

Подставляем в окружность

L 2 π r = θ 2 π, { displaystyle { frac {L} {2 pi r}} = { frac { theta} {2 pi}},} ${ displaystyle { frac {L} {2 pi r}} = { frac { theta} {2 pi}},}$

и, где α — тот же угол, измеренный в градусах, поскольку θ = α / 180π, длина дуги равна

L = α π r 180. { displaystyle L = { frac { alpha pi r} {180}}.} ${ displaystyle L = { frac { alpha pi r} {180}}.}$

Практический способ определить длину дуги в окружности — построить две линии от ее концов до центра окружности, измерьте угол, под которым две прямые пересекаются с центром, затем решите для L, перемножив выражение:

мера угла в градусах / 360 ° = L / окружность.

Например, если угол составляет 60 градусов, а длина окружности — 24 дюйма, то

60 360 = L 24 360 L = 1440 L = 4. { displaystyle { begin {align} { frac {60 } {360}} = { frac {L} {24}} \ 360L = 1440 \ L = 4. End {align}}} ${ displaystyle { begin {align} { frac {60} {360}} = { frac {L} {24}} \ 360L = 1440 \ L = 4. end {align}}}$

Это так, потому что длина окружности и градусы круга, которых всегда 360, прямо пропорциональны.

Верхняя половина круга может быть параметризована как

y = r 2 — x 2. { displaystyle y = { sqrt {r ^ {2} -x ^ {2}}}.} ${ displaystyle y = { sqrt {r ^ {2} -x ^ {2}}}.}$

Тогда длина дуги из x = a { displaystyle x = a} x = a до x = b { displaystyle x = b}равно

L = r [arcsin ⁡ (xr)] ab. { displaystyle L = r { Big [} arcsin left ({ frac {x} {r}} right) { Big]} _ {a} ^ {b}.} ${ displaystyle L = r { Big [} arcsin left ({ frac {x} {r}} right) { Big]} _ {a} ^ {b}.}$

Площадь сектора дуги

Площадь сектора, образованного дугой и центром круга (ограниченного дугой и двумя радиусами, проведенными к ее конечным точкам), составляет

A = r 2 θ 2. { displaystyle A = { frac {r ^ {2} theta} {2}}.} ${ displaystyle A = { frac {r ^ {2} theta} {2}}.}$

Область A имеет ту же пропорцию к площади круга , что и угол θ до полного круг:

A π r 2 = θ 2 π. { displaystyle { frac {A} { pi r ^ {2}}} = { frac { theta} {2 pi}}.} $frac {A} { pi r ^ 2} = frac { theta} {2 pi}.$

Мы можем сократить π с обеих сторон:

A г 2 = θ 2. { displaystyle { frac {A} {r ^ {2}}} = { frac { theta} {2}}.} $frac {A} {r ^ 2} = frac { theta} {2}.$

Умножая обе стороны на r, мы получаем окончательный результат:

А = 1 2 г 2 θ. { displaystyle A = { frac {1} {2}} r ^ {2} theta.} $A = frac {1} {2} r ^ 2 theta.$

Используя преобразование, описанное выше, мы находим, что площадь сектора для центрального угла, измеренная в градусах, равна

А = α 360 π r 2. { displaystyle A = { frac { alpha} {360}} pi r ^ {2}.} $A = frac { alpha} {360} pi r ^ 2.$

Площадь сегмента дуги

Площадь фигуры, ограниченная дугой и прямой линией между двумя его конечными точками находится

1 2 r 2 (θ — sin ⁡ θ). { displaystyle { frac {1} {2}} r ^ {2} left ( theta — sin { theta} right).} ${ displaystyle { frac {1} {2}} r ^ {2} left ( theta - sin { theta} right).}$

Чтобы получить площадь дугового сегмента , нам нужно вычесть площадь треугольника, определяемую центром круга и двумя конечными точками дуги, из площади A { displaystyle A}. Подробнее см. Круглый сегмент.

Радиус дуги

Произведение отрезков отрезков AP и PB равно произведению отрезков CP и PD. Если дуга имеет ширину AB и высоту CP, тогда диаметр круга

CD = AP ⋅ PBCP + CP { displaystyle CD = { frac {AP cdot PB} {CP}} + CP}

${ displaystyle CD = { frac {AP cdot PB} {CP}} + CP}$

Использование теорема о пересечении хорд (также известная как степень точки или теорема о секущем касательном) позволяет вычислить радиус r окружности с учетом высоты H и ширины W arc:

Рассмотрим хорду с теми же конечными точками, что и дуга. Его серединный перпендикуляр — это еще одна хорда, которая равна диаметру окружности. Длина первой хорды равна W, и она делится биссектрисой на две равные половины, каждая длиной W / 2. Общая длина диаметра составляет 2r, и он делится на две части первой хордой. Длина одной части — это стрела дуги, H, а другая часть — это остаток диаметра, длиной 2r — H. Применение теоремы о пересечении хорд к этим двум хордам дает

H (2 r — H) = (W 2) 2, { displaystyle H (2r-H) = left ({ frac {W} {2}} right) ^ {2},} ${ displaystyle H (2r-H) = left ({ frac {W} {2}} right) ^ {2},}$

откуда

2 r — H = W 2 4 H, { displaystyle 2r-H = { frac {W ^ {2}} {4H}},} ${ displaystyle 2r-H = { frac {W ^ {2}} {4H}},}$

поэтому

r = W 2 8 H + H 2. { displaystyle r = { frac {W ^ {2}} {8H}} + { frac {H} {2}}.} ${ displaystyle r = { frac {W ^ {2}} {8H}} + { frac {H} { 2}}.}$

Параболические дуги

См. также

Biarc
Круговой граф
Меридианная дуга
Окружность
Периметр

Ссылки

Внешние ссылки

Оглавление для страниц Math Open Reference Circle
Math Open Reference page на дугах окружности С интерактивной анимацией
Math Открыть справочную страницу по радиусу дуги окружности или сегмента С интерактивной анимацией
Вайсштейн, Эрик У. «Арк». MathWorld.

Источник

Г Л А В А I.

ОСНОВНЫЕ ПОНЯТИЯ.

§ 12. ОКРУЖНОСТЬ. КРУГ.

1. Радиус. Хорда. Диаметр.

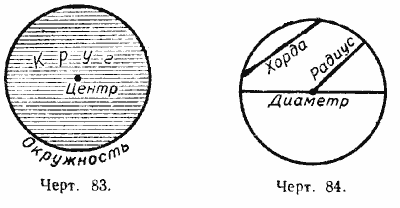
Если мы раскроем циркуль и укрепим конец одной ножки в какой-нибудь точке плоскости, а другую ножку будем вращать, не меняя раствора циркуля, так, чтобы её конец двигался по плоскости (черт. 82), то этот конец опишет кривую линию, все точки которой находятся на равном расстоянии от одной и той же точки. Если вращение продолжать до тех пор, пока кривая окажется замкнутой, то получим о к р у ж н о с т ь.

Окружностью называется кривая замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки; эта точка называется центром окружности.

Часть плоскости, ограниченная окружностью, называется кругом (черт. 83).

Отрезок прямой, соединяющий точку окружности с её центром, называется радиусом (черт. 84).

Так как все точки окружности находятся от центра на одном и том же расстоянии, то все радиусы одной и той же окружности равны между собой. Радиус обыкновенно обозначается буквой R или r.

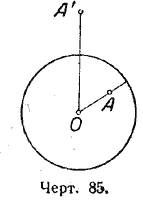
Точка, взятая внутри окружности, находится от её центра на расстоянии, меньшем радиуса. В этом легко убедиться, если через данную точку провести радиус (черт. 85).

Точка, взятая вне окружности, находится от её центра на расстоянии, большем радиуса. В этом легко убедиться, если соединить данную точку с центром окружности (черт. 85).

Отрезок прямой, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр, называется диаметром (черт. 84). Диаметр обыкновенно обозначается буквой D. Диаметр равен двум радиусам:

D = 2r.

Так как все радиусы одного и того же круга равны между собой, то и все диаметры данного круга равны между собой.

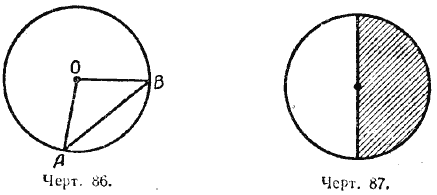
Теорема. Хорда, не проходящая через центр круга, меньше диаметра, проведённого в том же круге.

В самом деле, если проведём какую-нибудь хорду, например АВ, и соединим её концы с центром О (черт. 86), то увидим, что хорда АВ меньше ломаной линии АО + ОВ, т. е. АВ < 2r, а так как 2r = D, то АВ < D.

Если круг перегнуть по диаметру (черт. 87), то обе части круга и окружности совместятся. Диаметр делит круг и окружность на две равные части.

Два круга (две окружности) называются равными, если их можно наложить друг на друга так, чтобы они совместились.

Поэтому два круга (две окружности) с равными радиусами равны.

2. Дуга окружности.

Часть окружности называется дугой.

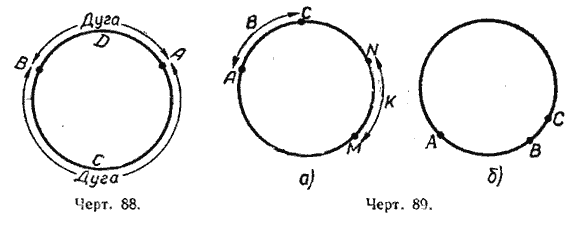
Слово «дуга» иногда заменяется знаком . Дуга обозначается двумя или тремя буквами, из которых две ставятся на концах дуги, а третья — у какой-нибудь точки дуги. На чертеже 88 обозначены две дуги: АСВ и ADB.

В том случае, когда дуга меньше полуокружности, она обычно обозначается двумя буквами. Так, дугу АDВ можно обозначить АВ (черт. 88). О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Если передвинуть дугу АС (черт. 89, а) так, чтобы она скользила поданной окружности, и если при этом она совпадает с дугой МN, то АС = NM.

На чертеже 89, б дуги АС и АВ не равны между собой. Начинаются обе дуги в точке А, но одна дуга ( АВ) составляет только часть другой дуги (AС).
Поэтому АС > АВ; АВ < АС.

Упражнения.

1. Сформулируйте определения, которые приведены в данном параграфе.

2. Сформулируйте теоремы, которые доказаны в данном параграфе.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Окружность
Градусная мера дуги окружности

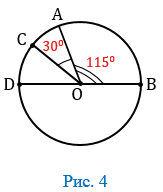
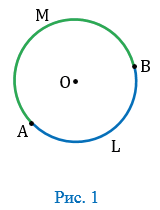
На рисунке 1 две точки А и В разделяют окружность на две дуги. На каждой дуге отмечают промежуточную точку, например L и М, для того, чтобы различать эти дуги. Обозначают дуги так: АLB и АМВ. Если в задаче ясно, о какой из двух дуг идет речь, то используют обозначение без промежуточной точки: АВ.

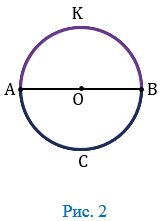
Если отрезок, соединяющий концы дуги является диаметром то, такая дуга называется полуокружностью. На рисунке 2 изображена окружность с центром О, концы диаметра АВ разделяют данную окружность на две полуокружности: АКB и АСВ.

Центральный угол — угол с вершиной в центре окружности. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В. Центральному углу АОВ соответствуют две дуги с концами А и В.

Измерение дуги окружности

Дугу окружности можно измерять в градусах.

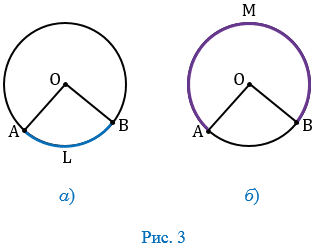
Если дуга АВ окружности с центром О меньше полуокружности (Рис. 3, а) или является полуокружностью (Рис. 2), то ее градусная мера считается равной градусной мере центрального угла АОВ.
Если дуга АВ окружности с центром О больше полуокружности (Рис. 3, б), то ее градусная мера считается равной 360⁰ — АОВ.

Сумма градусных мер двух дуг окружности с общими концами равна 360⁰.

Градусная мера дуги АВ (дуги АLВ), как и сама дуга, обозначается символом АВ ( АLВ). На рисунке 4 градусная мера дуги САВ равна 145⁰. Обычно говорят кратко: «Дуга САВ равна 145⁰» и пишут: САВ = 145⁰. Также на рисунке 4 АDВ = 360⁰ — 115⁰ = 245⁰, СDВ = 360⁰ — 145⁰ = 215⁰, DВ = 180⁰.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Взаимное расположение прямой и окружности

Касательная к окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Свойства серединного перпендикуляра к отрезку

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Окружность

Правило встречается в следующих упражнениях:

7 класс

Задание 651,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 652,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 704,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 705,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 26,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 716,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 726,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 884,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1180,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1289,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Окружность

Построение окружности циркулем

Радиус, хорда и диаметр

Дуга

Length[edit]

Sector area[edit]

Segment area[edit]

Radius[edit]

See also[edit]

External links[edit]

Length[edit]

Sector area[edit]

Segment area[edit]

Radius[edit]

See also[edit]

External links[edit]

Определение окружности

Отрезки в окружности

Дуга в окружности

Углы в окружности

Длина окружности, длина дуги

Площадь круга и его частей

Теорема синусов

Примеры решений заданий из ОГЭ

Содержание

Дуги окружности

Длина дуги окружности

Площадь сектора дуги

Площадь сегмента дуги

Радиус дуги

Параболические дуги

См. также

Ссылки

Внешние ссылки

Измерение дуги окружности

Советуем посмотреть:

Правило встречается в следующих упражнениях: