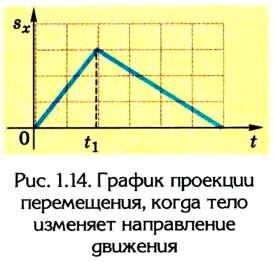
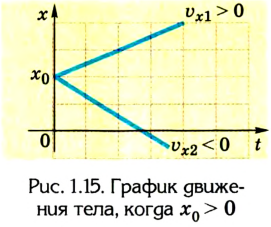
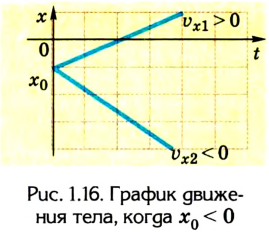
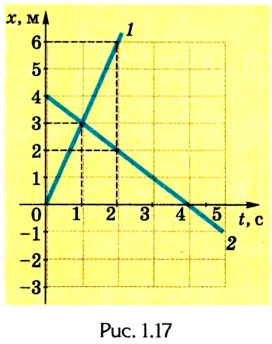
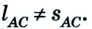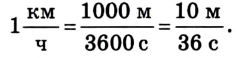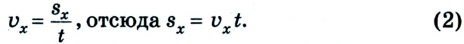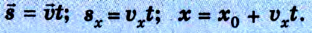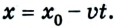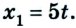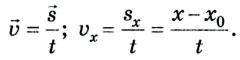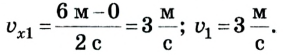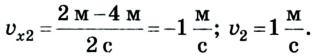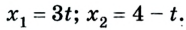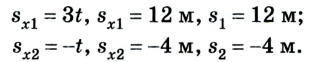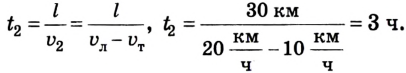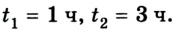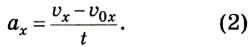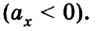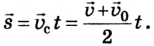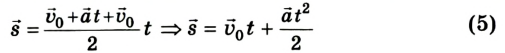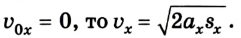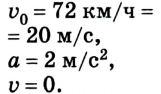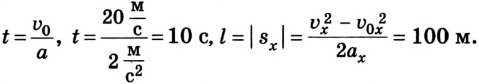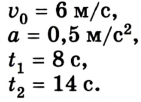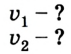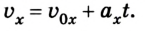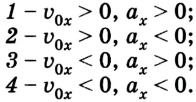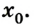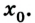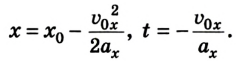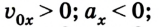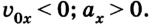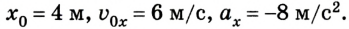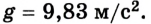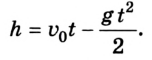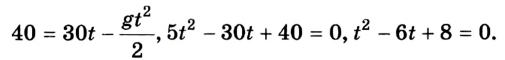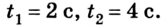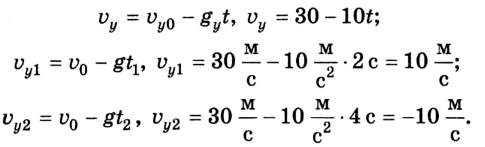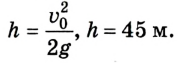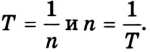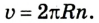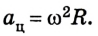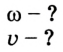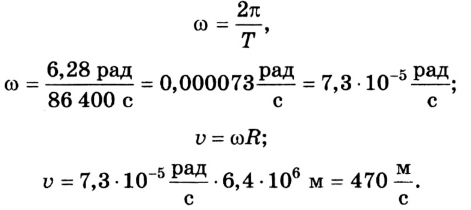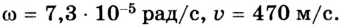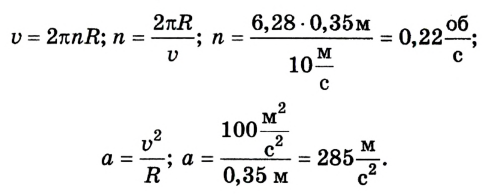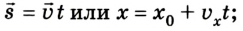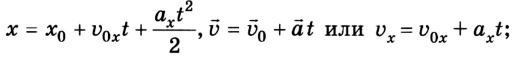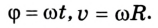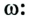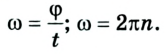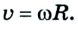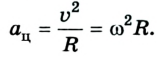A motorcyclist doing a wheelie, representing motion
In physics, motion is the phenomenon in which an object changes its position with respect to time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed and frame of reference to an observer and measuring the change in position of the body relative to that frame with change in time. The branch of physics describing the motion of objects without reference to its cause is called kinematics, while the branch studying forces and their effect on motion is called dynamics.
If an object is not changing relative to a given frame of reference, the object is said to be at rest, motionless, immobile, stationary, or to have a constant or time-invariant position with reference to its surroundings. Modern physics holds that, as there is no absolute frame of reference, Newton’s concept of absolute motion cannot be determined.[1] As such, everything in the universe can be considered to be in motion.[2]: 20–21
Motion applies to various physical systems: objects, bodies, matter particles, matter fields, radiation, radiation fields, radiation particles, curvature, and space-time. One can also speak on the motion of images, shapes, and boundaries. In general, the term motion signifies a continuous change in the positions or configuration of a physical system in space. For example, one can talk about the motion of a wave or the motion of a quantum particle, where the configuration consists of probabilities of the wave or particle occupying specific positions.
Equations of motion[edit]
Laws of motion[edit]
In physics, the motion of massive bodies is described through two related sets of laws of mechanics. Classical mechanics for super atomic (larger than an atom) objects (such as cars, projectiles, planets, cells, and humans) and quantum mechanics for atomic and sub-atomic objects (such as helium, protons, and electrons). Historically, Newton and Euler formulated three laws of classical mechanics:
Classical mechanics[edit]
Classical mechanics is used for describing the motion of macroscopic objects moving at speeds significantly slower than the speed of light, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. It produces very accurate results within these domains and is one of the oldest and largest scientific descriptions in science, engineering, and technology.
Classical mechanics is fundamentally based on Newton’s laws of motion. These laws describe the relationship between the forces acting on a body and the motion of that body. They were first compiled by Sir Isaac Newton in his work Philosophiæ Naturalis Principia Mathematica, which was first published on July 5, 1687. Newton’s three laws are:
- A body at rest will remain at rest, and a body in motion will remain in motion unless it is acted upon by an external force. (This is known as the law of inertia.)
- Force (
) is equal to the change in momentum per change in time (
). For a constant mass, force equals mass times acceleration (
).
- For every action, there is an equal and opposite reaction. (In other words, whenever one body exerts a force
onto a second body, (in some cases, which is standing still) the second body exerts the force
back onto the first body.
and
are equal in magnitude and opposite in direction. So, the body which exerts
will be pushed backward.)[5]
Newton’s three laws of motion were the first to accurately provide a mathematical model for understanding orbiting bodies in outer space. This explanation unified the motion of celestial bodies and the motion of objects on Earth.
Relativistic mechanics[edit]
Modern kinematics developed with study of electromagnetism and refers all velocities 



Quantum mechanics[edit]
Quantum mechanics is a set of principles describing physical reality at the atomic level of matter (molecules and atoms) and the subatomic particles (electrons, protons, neutrons, and even smaller elementary particles such as quarks). These descriptions include the simultaneous wave-like and particle-like behavior of both matter and radiation energy as described in the wave–particle duality.[6]
In classical mechanics, accurate measurements and predictions of the state of objects can be calculated, such as location and velocity. In quantum mechanics, due to the Heisenberg uncertainty principle, the complete state of a subatomic particle, such as its location and velocity, cannot be simultaneously determined.[7]
In addition to describing the motion of atomic level phenomena, quantum mechanics is useful in understanding some large-scale phenomena such as superfluidity, superconductivity, and biological systems, including the function of smell receptors and the structures of protein.[8]
Orders of magnitude[edit]
Humans, like all known things in the universe, are in constant motion;[2]: 8–9 however, aside from obvious movements of the various external body parts and locomotion, humans are in motion in a variety of ways which are more difficult to perceive. Many of these «imperceptible motions» are only perceivable with the help of special tools and careful observation. The larger scales of imperceptible motions are difficult for humans to perceive for two reasons: Newton’s laws of motion (particularly the third) which prevents the feeling of motion on a mass to which the observer is connected, and the lack of an obvious frame of reference which would allow individuals to easily see that they are moving.[9] The smaller scales of these motions are too small to be detected conventionally with human senses.
Universe[edit]
Spacetime (the fabric of the universe) is expanding, meaning everything in the universe is stretching, like a rubber band. This motion is the most obscure as it is not physical motion, but rather a change in the very nature of the universe. The primary source of verification of this expansion was provided by Edwin Hubble who demonstrated that all galaxies and distant astronomical objects were moving away from Earth, known as Hubble’s law, predicted by a universal expansion.[10]
Galaxy[edit]
The Milky Way Galaxy is moving through space and many astronomers believe the velocity of this motion to be approximately 600 kilometres per second (1,340,000 mph) relative to the observed locations of other nearby galaxies. Another reference frame is provided by the Cosmic microwave background. This frame of reference indicates that the Milky Way is moving at around 582 kilometres per second (1,300,000 mph).[11][failed verification]
Sun and Solar System[edit]
The Milky Way is rotating around its dense Galactic Center, thus the Sun is moving in a circle within the galaxy’s gravity. Away from the central bulge, or outer rim, the typical stellar velocity is between 210 and 240 kilometres per second (470,000 and 540,000 mph).[12] All planets and their moons move with the Sun. Thus, the Solar System is in motion.
Earth[edit]
The Earth is rotating or spinning around its axis. This is evidenced by day and night, at the equator the earth has an eastward velocity of 0.4651 kilometres per second (1,040 mph).[13] The Earth is also orbiting around the Sun in an orbital revolution. A complete orbit around the sun takes one year, or about 365 days; it averages a speed of about 30 kilometres per second (67,000 mph).[14]
Continents[edit]
The Theory of Plate tectonics tells us that the continents are drifting on convection currents within the mantle, causing them to move across the surface of the planet at the slow speed of approximately 2.54 centimetres (1 in) per year.[15][16] However, the velocities of plates range widely. The fastest-moving plates are the oceanic plates, with the Cocos Plate advancing at a rate of 75 millimetres (3.0 in) per year[17] and the Pacific Plate moving 52–69 millimetres (2.0–2.7 in) per year. At the other extreme, the slowest-moving plate is the Eurasian Plate, progressing at a typical rate of about 21 millimetres (0.83 in) per year.
Internal body[edit]
The human heart is constantly contracting to move blood throughout the body. Through larger veins and arteries in the body, blood has been found to travel at approximately 0.33 m/s. Though considerable variation exists, and peak flows in the venae cavae have been found between 0.1 and 0.45 metres per second (0.33 and 1.48 ft/s).[18] additionally, the smooth muscles of hollow internal organs are moving. The most familiar would be the occurrence of peristalsis which is where digested food is forced throughout the digestive tract. Though different foods travel through the body at different rates, an average speed through the human small intestine is 3.48 kilometres per hour (2.16 mph).[19] The human lymphatic system is also constantly causing movements of excess fluids, lipids, and immune system related products around the body. The lymph fluid has been found to move through a lymph capillary of the skin at approximately 0.0000097 m/s.[20]
Cells[edit]
The cells of the human body have many structures and organelles which move throughout them. Cytoplasmic streaming is a way in which cells move molecular substances throughout the cytoplasm,[21] various motor proteins work as molecular motors within a cell and move along the surface of various cellular substrates such as microtubules, and motor proteins are typically powered by the hydrolysis of adenosine triphosphate (ATP), and convert chemical energy into mechanical work.[22] Vesicles propelled by motor proteins have been found to have a velocity of approximately 0.00000152 m/s.[23]
Particles[edit]
According to the laws of thermodynamics, all particles of matter are in constant random motion as long as the temperature is above absolute zero. Thus the molecules and atoms which make up the human body are vibrating, colliding, and moving. This motion can be detected as temperature; higher temperatures, which represent greater kinetic energy in the particles, feel warm to humans who sense the thermal energy transferring from the object being touched to their nerves. Similarly, when lower temperature objects are touched, the senses perceive the transfer of heat away from the body as a feeling of cold.[24]
Subatomic particles[edit]
Within the standard atomic orbital model, electrons exist in a region around the nucleus of each atom. This region is called the electron cloud. According to Bohr’s model of the atom, electrons have a high velocity, and the larger the nucleus they are orbiting the faster they would need to move. If electrons were to move about the electron cloud in strict paths the same way planets orbit the sun, then electrons would be required to do so at speeds which would far exceed the speed of light. However, there is no reason that one must confine oneself to this strict conceptualization (that electrons move in paths the same way macroscopic objects do), rather one can conceptualize electrons to be ‘particles’ that capriciously exist within the bounds of the electron cloud.[25] Inside the atomic nucleus, the protons and neutrons are also probably moving around due to the electrical repulsion of the protons and the presence of angular momentum of both particles.[26]
Light[edit]
Light moves at a speed of 299,792,458 m/s, or 299,792.458 kilometres per second (186,282.397 mi/s), in a vacuum. The speed of light in vacuum (or 
In addition, the speed of light is an invariant quantity: it has the same value, irrespective of the position or speed of the observer. This property makes the speed of light c a natural measurement unit for speed and a fundamental constant of nature.
In 2011, the speed of light was redefined alongside all seven SI base units using what it calls «the explicit-constant formulation», where each «unit is defined indirectly by specifying explicitly an exact value for a well-recognized fundamental constant», as was done for the speed of light. A new, but completely equivalent, wording of the metre’s definition was proposed: «The metre, symbol m, is the unit of length; its magnitude is set by fixing the numerical value of the speed of light in vacuum to be equal to exactly 299792458 when it is expressed in the SI unit m s−1.»[27] This implicit change to the speed of light was one of the changes that was incorporated in the 2019 redefinition of the SI base units, also termed the New SI.Cite error: A <ref> tag is missing the closing </ref> (see the help page). This occurs owing to how motion is often calculated at long distances; oftentimes calculations fail to account for the fact that the speed of light is finite. When measuring the movement of distant objects across the sky, there is a large time delay between what has been observed and what has occurred, due to the large distance the light from the distant object has to travel to reach us. The error in the above naive calculation comes from the fact that when an object has a component of velocity directed towards the Earth, as the object moves closer to the Earth that time delay becomes smaller. This means that the apparent speed as calculated above is greater than the actual speed. Correspondingly, if the object is moving away from the Earth, the above calculation underestimates the actual speed.[28]
Types of motion[edit]
- Brownian motion (i.e. the random movement of particles)
- Circular motion
- Rotatory motion – a motion about a fixed point. (e.g. Ferris wheel).
- Curvilinear motion – It is defined as the motion along a curved path that may be planar or in three dimensions.
- Rolling motion – (as of the wheel of a bicycle)
- Oscillatory – (swinging from side to side)
- Vibratory motion
- Combination (or simultaneous) motions – Combination of two or more above listed motions
- Projectile motion – uniform horizontal motion + vertical accelerated motion
- Linear motion
- Circular motion
- Oscillation
Fundamental motions[edit]
- Wave
- Relative motion
- Fundamental motions
- Deflection (physics)
- Kinematics – Branch of physics describing the motion of objects without considering forces
- Simple machines
See also[edit]
- Kinematic chain – Mathematical model for a mechanical system
- Power – Rate at which energy is transferred, used, or transformed to do work at a given interval of time
- Machine
- Microswimmer
- Motion (geometry) – Transformation of a geometric space preserving structure
- Motion capture – Process of recording the movement of objects or people
- Displacement
- Translatory motion
References[edit]
- ^ Wahlin, Lars (1997). «9.1 Relative and absolute motion» (PDF). The Deadbeat Universe. Boulder, CO: Coultron Research. pp. 121–129. ISBN 978-0-933407-03-9. Archived (PDF) from the original on 2016-03-04. Retrieved 25 January 2013.
- ^ a b Tyson, Neil de Grasse; Charles Tsun-Chu Liu; Robert Irion (2000). One Universe : at home in the cosmos. Washington, DC: National Academy Press. ISBN 978-0-309-06488-0.
- ^ Encyclopaedia of Physics (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ^ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- ^ Newton’s «Axioms or Laws of Motion» can be found in the «Principia» on p. 19 of volume 1 of the 1729 translation Archived 2015-09-28 at the Wayback Machine.
- ^ «The Feynman Lectures on Physics Vol. I Ch. 38: The Relation of Wave and Particle Viewpoints». Archived from the original on 2022-08-14. Retrieved 2022-05-03.
- ^ «Understanding the Heisenberg Uncertainty Principle». ThoughtCo. Archived from the original on 2022-05-10. Retrieved 2022-05-10.
- ^ Folger, Tim (October 23, 2018). «How Quantum Mechanics Lets Us See, Smell and Touch: How the science of the super small affects our everyday lives». Discovery Magazine. Archived from the original on January 26, 2021. Retrieved October 24, 2021.
- ^ Safkan, Yasar. «Question: If the term ‘absolute motion’ has no meaning, then why do we say that the earth moves around the sun and not vice versa?». Ask the Experts. PhysLink.com. Archived from the original on 3 November 2013. Retrieved 25 January 2014.
- ^ Hubble, Edwin (1929-03-15). «A relation between distance and radial velocity among extra-galactic nebulae». Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS…15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
- ^ Kogut, A.; Lineweaver, C.; Smoot, G.F.; Bennett, C.L.; Banday, A.; Boggess, N.W.; Cheng, E.S.; de Amici, G.; Fixsen, D.J.; Hinshaw, G.; Jackson, P.D.; Janssen, M.; Keegstra, P.; Loewenstein, K.; Lubin, P.; Mather, J.C.; Tenorio, L.; Weiss, R.; Wilkinson, D.T.; Wright, E.L. (1993). «Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps». Astrophysical Journal. 419: 1. arXiv:astro-ph/9312056. Bibcode:1993ApJ…419….1K. doi:10.1086/173453. S2CID 209835274.
- ^ Imamura, Jim (August 10, 2006). «Mass of the Milky Way Galaxy». University of Oregon. Archived from the original on 2007-03-01. Retrieved 2007-05-10.
- ^ Ask an Astrophysicist Archived 2009-03-11 at the Wayback Machine. NASA Goodard Space Flight Center.
- ^ Williams, David R. (September 1, 2004). «Earth Fact Sheet». NASA. Archived from the original on 2013-05-08. Retrieved 2007-03-17.
- ^ Staff. «GPS Time Series». NASA JPL. Archived from the original on 2011-07-21. Retrieved 2007-04-02.
- ^ Huang, Zhen Shao (2001). Elert, Glenn (ed.). «Speed of the Continental Plates». The Physics Factbook. Archived from the original on 2020-06-19. Retrieved 2020-06-20.
- ^ Meschede, M.; Udo Barckhausen, U. (November 20, 2000). «Plate Tectonic Evolution of the Cocos-Nazca Spreading Center». Proceedings of the Ocean Drilling Program. Texas A&M University. Archived from the original on 2011-08-08. Retrieved 2007-04-02.
- ^ Wexler, L.; D H Bergel; I T Gabe; G S Makin; C J Mills (1 September 1968). «Velocity of Blood Flow in Normal Human Venae Cavae». Circulation Research. 23 (3): 349–359. doi:10.1161/01.RES.23.3.349. PMID 5676450.
- ^ Bowen, R (27 May 2006). «Gastrointestinal Transit: How Long Does It Take?». Pathophysiology of the digestive system. Colorado State University. Archived from the original on 3 April 2015. Retrieved 25 January 2014.
- ^ M. Fischer; U.K. Franzeck; I. Herrig; U. Costanzo; S. Wen; M. Schiesser; U. Hoffmann; A. Bollinger (1 January 1996). «Flow velocity of single lymphatic capillaries in human skin». Am J Physiol Heart Circ Physiol. 270 (1): H358–H363. doi:10.1152/ajpheart.1996.270.1.H358. PMID 8769772.
- ^ «cytoplasmic streaming – biology». Encyclopædia Britannica. Archived from the original on 2008-06-11. Retrieved 2022-06-23.
- ^ «Microtubule Motors». rpi.edu. Archived from the original on 2007-11-30.
- ^ Hill, David; Holzwarth, George; Bonin, Keith (2002). «Velocity and Drag Forces on motor-protein-driven Vesicles in Cells». APS Southeastern Section Meeting Abstracts. 69: EA.002. Bibcode:2002APS..SES.EA002H.
- ^ Temperature and BEC. Archived 2007-11-10 at the Wayback Machine Physics 2000: Colorado State University Physics Department
- ^ «Classroom Resources». anl.gov. Argonne National Laboratory. Archived from the original on 2010-06-08. Retrieved 2009-03-09.
- ^ «Chapter 2, Nuclear Science- A guide to the nuclear science wall chart. Berkley National Laboratory» (PDF). Archived (PDF) from the original on 2009-03-04. Retrieved 2009-03-09.
- ^ «The «explicit-constant» formulation». BIPM. 2011. Archived from the original on 11 August 2014.
- ^ Meyer, Eileen (June 2018). «Detection of an Optical/UV Jet/Counterjet and Multiple Spectral Components in M84». The Astrophysical Journal. 680 (1): 9. arXiv:1804.05122. Bibcode:2018ApJ…860….9M. doi:10.3847/1538-4357/aabf39. S2CID 67822924.
Further reading[edit]
- Conover, Emily (2 November 2016). «Units of measure are getting a fundamental upgrade». Science News
- Knotts, Sandra; Mohr, Peter J.; Phillips, William D. (January 2017) «An Introduction to the New SI», The Physics Teacher 55 (1): 16–21. Bibcode:2017PhTea..55…16K. doi:10.1119/1.4972491 ISSN 0031-921X. S2CID 117581000.
- «SI Redefinition», National Institute of Standards and Technology 11 May 2018
External links[edit]
Wikiquote has quotations related to Motion.
- Feynman’s lecture on motion
Media related to Motion at Wikimedia Commons
A motorcyclist doing a wheelie, representing motion
In physics, motion is the phenomenon in which an object changes its position with respect to time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed and frame of reference to an observer and measuring the change in position of the body relative to that frame with change in time. The branch of physics describing the motion of objects without reference to its cause is called kinematics, while the branch studying forces and their effect on motion is called dynamics.
If an object is not changing relative to a given frame of reference, the object is said to be at rest, motionless, immobile, stationary, or to have a constant or time-invariant position with reference to its surroundings. Modern physics holds that, as there is no absolute frame of reference, Newton’s concept of absolute motion cannot be determined.[1] As such, everything in the universe can be considered to be in motion.[2]: 20–21
Motion applies to various physical systems: objects, bodies, matter particles, matter fields, radiation, radiation fields, radiation particles, curvature, and space-time. One can also speak on the motion of images, shapes, and boundaries. In general, the term motion signifies a continuous change in the positions or configuration of a physical system in space. For example, one can talk about the motion of a wave or the motion of a quantum particle, where the configuration consists of probabilities of the wave or particle occupying specific positions.
Equations of motion[edit]
Laws of motion[edit]
In physics, the motion of massive bodies is described through two related sets of laws of mechanics. Classical mechanics for super atomic (larger than an atom) objects (such as cars, projectiles, planets, cells, and humans) and quantum mechanics for atomic and sub-atomic objects (such as helium, protons, and electrons). Historically, Newton and Euler formulated three laws of classical mechanics:
Classical mechanics[edit]
Classical mechanics is used for describing the motion of macroscopic objects moving at speeds significantly slower than the speed of light, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. It produces very accurate results within these domains and is one of the oldest and largest scientific descriptions in science, engineering, and technology.
Classical mechanics is fundamentally based on Newton’s laws of motion. These laws describe the relationship between the forces acting on a body and the motion of that body. They were first compiled by Sir Isaac Newton in his work Philosophiæ Naturalis Principia Mathematica, which was first published on July 5, 1687. Newton’s three laws are:
- A body at rest will remain at rest, and a body in motion will remain in motion unless it is acted upon by an external force. (This is known as the law of inertia.)
- Force (
) is equal to the change in momentum per change in time (
). For a constant mass, force equals mass times acceleration (
).
- For every action, there is an equal and opposite reaction. (In other words, whenever one body exerts a force
onto a second body, (in some cases, which is standing still) the second body exerts the force
back onto the first body.
and
are equal in magnitude and opposite in direction. So, the body which exerts
will be pushed backward.)[5]
Newton’s three laws of motion were the first to accurately provide a mathematical model for understanding orbiting bodies in outer space. This explanation unified the motion of celestial bodies and the motion of objects on Earth.
Relativistic mechanics[edit]
Modern kinematics developed with study of electromagnetism and refers all velocities 



Quantum mechanics[edit]
Quantum mechanics is a set of principles describing physical reality at the atomic level of matter (molecules and atoms) and the subatomic particles (electrons, protons, neutrons, and even smaller elementary particles such as quarks). These descriptions include the simultaneous wave-like and particle-like behavior of both matter and radiation energy as described in the wave–particle duality.[6]
In classical mechanics, accurate measurements and predictions of the state of objects can be calculated, such as location and velocity. In quantum mechanics, due to the Heisenberg uncertainty principle, the complete state of a subatomic particle, such as its location and velocity, cannot be simultaneously determined.[7]
In addition to describing the motion of atomic level phenomena, quantum mechanics is useful in understanding some large-scale phenomena such as superfluidity, superconductivity, and biological systems, including the function of smell receptors and the structures of protein.[8]
Orders of magnitude[edit]
Humans, like all known things in the universe, are in constant motion;[2]: 8–9 however, aside from obvious movements of the various external body parts and locomotion, humans are in motion in a variety of ways which are more difficult to perceive. Many of these «imperceptible motions» are only perceivable with the help of special tools and careful observation. The larger scales of imperceptible motions are difficult for humans to perceive for two reasons: Newton’s laws of motion (particularly the third) which prevents the feeling of motion on a mass to which the observer is connected, and the lack of an obvious frame of reference which would allow individuals to easily see that they are moving.[9] The smaller scales of these motions are too small to be detected conventionally with human senses.
Universe[edit]
Spacetime (the fabric of the universe) is expanding, meaning everything in the universe is stretching, like a rubber band. This motion is the most obscure as it is not physical motion, but rather a change in the very nature of the universe. The primary source of verification of this expansion was provided by Edwin Hubble who demonstrated that all galaxies and distant astronomical objects were moving away from Earth, known as Hubble’s law, predicted by a universal expansion.[10]
Galaxy[edit]
The Milky Way Galaxy is moving through space and many astronomers believe the velocity of this motion to be approximately 600 kilometres per second (1,340,000 mph) relative to the observed locations of other nearby galaxies. Another reference frame is provided by the Cosmic microwave background. This frame of reference indicates that the Milky Way is moving at around 582 kilometres per second (1,300,000 mph).[11][failed verification]
Sun and Solar System[edit]
The Milky Way is rotating around its dense Galactic Center, thus the Sun is moving in a circle within the galaxy’s gravity. Away from the central bulge, or outer rim, the typical stellar velocity is between 210 and 240 kilometres per second (470,000 and 540,000 mph).[12] All planets and their moons move with the Sun. Thus, the Solar System is in motion.
Earth[edit]
The Earth is rotating or spinning around its axis. This is evidenced by day and night, at the equator the earth has an eastward velocity of 0.4651 kilometres per second (1,040 mph).[13] The Earth is also orbiting around the Sun in an orbital revolution. A complete orbit around the sun takes one year, or about 365 days; it averages a speed of about 30 kilometres per second (67,000 mph).[14]
Continents[edit]
The Theory of Plate tectonics tells us that the continents are drifting on convection currents within the mantle, causing them to move across the surface of the planet at the slow speed of approximately 2.54 centimetres (1 in) per year.[15][16] However, the velocities of plates range widely. The fastest-moving plates are the oceanic plates, with the Cocos Plate advancing at a rate of 75 millimetres (3.0 in) per year[17] and the Pacific Plate moving 52–69 millimetres (2.0–2.7 in) per year. At the other extreme, the slowest-moving plate is the Eurasian Plate, progressing at a typical rate of about 21 millimetres (0.83 in) per year.
Internal body[edit]
The human heart is constantly contracting to move blood throughout the body. Through larger veins and arteries in the body, blood has been found to travel at approximately 0.33 m/s. Though considerable variation exists, and peak flows in the venae cavae have been found between 0.1 and 0.45 metres per second (0.33 and 1.48 ft/s).[18] additionally, the smooth muscles of hollow internal organs are moving. The most familiar would be the occurrence of peristalsis which is where digested food is forced throughout the digestive tract. Though different foods travel through the body at different rates, an average speed through the human small intestine is 3.48 kilometres per hour (2.16 mph).[19] The human lymphatic system is also constantly causing movements of excess fluids, lipids, and immune system related products around the body. The lymph fluid has been found to move through a lymph capillary of the skin at approximately 0.0000097 m/s.[20]
Cells[edit]
The cells of the human body have many structures and organelles which move throughout them. Cytoplasmic streaming is a way in which cells move molecular substances throughout the cytoplasm,[21] various motor proteins work as molecular motors within a cell and move along the surface of various cellular substrates such as microtubules, and motor proteins are typically powered by the hydrolysis of adenosine triphosphate (ATP), and convert chemical energy into mechanical work.[22] Vesicles propelled by motor proteins have been found to have a velocity of approximately 0.00000152 m/s.[23]
Particles[edit]
According to the laws of thermodynamics, all particles of matter are in constant random motion as long as the temperature is above absolute zero. Thus the molecules and atoms which make up the human body are vibrating, colliding, and moving. This motion can be detected as temperature; higher temperatures, which represent greater kinetic energy in the particles, feel warm to humans who sense the thermal energy transferring from the object being touched to their nerves. Similarly, when lower temperature objects are touched, the senses perceive the transfer of heat away from the body as a feeling of cold.[24]
Subatomic particles[edit]
Within the standard atomic orbital model, electrons exist in a region around the nucleus of each atom. This region is called the electron cloud. According to Bohr’s model of the atom, electrons have a high velocity, and the larger the nucleus they are orbiting the faster they would need to move. If electrons were to move about the electron cloud in strict paths the same way planets orbit the sun, then electrons would be required to do so at speeds which would far exceed the speed of light. However, there is no reason that one must confine oneself to this strict conceptualization (that electrons move in paths the same way macroscopic objects do), rather one can conceptualize electrons to be ‘particles’ that capriciously exist within the bounds of the electron cloud.[25] Inside the atomic nucleus, the protons and neutrons are also probably moving around due to the electrical repulsion of the protons and the presence of angular momentum of both particles.[26]
Light[edit]
Light moves at a speed of 299,792,458 m/s, or 299,792.458 kilometres per second (186,282.397 mi/s), in a vacuum. The speed of light in vacuum (or 
In addition, the speed of light is an invariant quantity: it has the same value, irrespective of the position or speed of the observer. This property makes the speed of light c a natural measurement unit for speed and a fundamental constant of nature.
In 2011, the speed of light was redefined alongside all seven SI base units using what it calls «the explicit-constant formulation», where each «unit is defined indirectly by specifying explicitly an exact value for a well-recognized fundamental constant», as was done for the speed of light. A new, but completely equivalent, wording of the metre’s definition was proposed: «The metre, symbol m, is the unit of length; its magnitude is set by fixing the numerical value of the speed of light in vacuum to be equal to exactly 299792458 when it is expressed in the SI unit m s−1.»[27] This implicit change to the speed of light was one of the changes that was incorporated in the 2019 redefinition of the SI base units, also termed the New SI.Cite error: A <ref> tag is missing the closing </ref> (see the help page). This occurs owing to how motion is often calculated at long distances; oftentimes calculations fail to account for the fact that the speed of light is finite. When measuring the movement of distant objects across the sky, there is a large time delay between what has been observed and what has occurred, due to the large distance the light from the distant object has to travel to reach us. The error in the above naive calculation comes from the fact that when an object has a component of velocity directed towards the Earth, as the object moves closer to the Earth that time delay becomes smaller. This means that the apparent speed as calculated above is greater than the actual speed. Correspondingly, if the object is moving away from the Earth, the above calculation underestimates the actual speed.[28]
Types of motion[edit]
- Brownian motion (i.e. the random movement of particles)
- Circular motion
- Rotatory motion – a motion about a fixed point. (e.g. Ferris wheel).
- Curvilinear motion – It is defined as the motion along a curved path that may be planar or in three dimensions.
- Rolling motion – (as of the wheel of a bicycle)
- Oscillatory – (swinging from side to side)
- Vibratory motion
- Combination (or simultaneous) motions – Combination of two or more above listed motions
- Projectile motion – uniform horizontal motion + vertical accelerated motion
- Linear motion
- Circular motion
- Oscillation
Fundamental motions[edit]
- Wave
- Relative motion
- Fundamental motions
- Deflection (physics)
- Kinematics – Branch of physics describing the motion of objects without considering forces
- Simple machines
See also[edit]
- Kinematic chain – Mathematical model for a mechanical system
- Power – Rate at which energy is transferred, used, or transformed to do work at a given interval of time
- Machine
- Microswimmer
- Motion (geometry) – Transformation of a geometric space preserving structure
- Motion capture – Process of recording the movement of objects or people
- Displacement
- Translatory motion
References[edit]
- ^ Wahlin, Lars (1997). «9.1 Relative and absolute motion» (PDF). The Deadbeat Universe. Boulder, CO: Coultron Research. pp. 121–129. ISBN 978-0-933407-03-9. Archived (PDF) from the original on 2016-03-04. Retrieved 25 January 2013.
- ^ a b Tyson, Neil de Grasse; Charles Tsun-Chu Liu; Robert Irion (2000). One Universe : at home in the cosmos. Washington, DC: National Academy Press. ISBN 978-0-309-06488-0.
- ^ Encyclopaedia of Physics (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ^ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- ^ Newton’s «Axioms or Laws of Motion» can be found in the «Principia» on p. 19 of volume 1 of the 1729 translation Archived 2015-09-28 at the Wayback Machine.
- ^ «The Feynman Lectures on Physics Vol. I Ch. 38: The Relation of Wave and Particle Viewpoints». Archived from the original on 2022-08-14. Retrieved 2022-05-03.
- ^ «Understanding the Heisenberg Uncertainty Principle». ThoughtCo. Archived from the original on 2022-05-10. Retrieved 2022-05-10.
- ^ Folger, Tim (October 23, 2018). «How Quantum Mechanics Lets Us See, Smell and Touch: How the science of the super small affects our everyday lives». Discovery Magazine. Archived from the original on January 26, 2021. Retrieved October 24, 2021.
- ^ Safkan, Yasar. «Question: If the term ‘absolute motion’ has no meaning, then why do we say that the earth moves around the sun and not vice versa?». Ask the Experts. PhysLink.com. Archived from the original on 3 November 2013. Retrieved 25 January 2014.
- ^ Hubble, Edwin (1929-03-15). «A relation between distance and radial velocity among extra-galactic nebulae». Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS…15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
- ^ Kogut, A.; Lineweaver, C.; Smoot, G.F.; Bennett, C.L.; Banday, A.; Boggess, N.W.; Cheng, E.S.; de Amici, G.; Fixsen, D.J.; Hinshaw, G.; Jackson, P.D.; Janssen, M.; Keegstra, P.; Loewenstein, K.; Lubin, P.; Mather, J.C.; Tenorio, L.; Weiss, R.; Wilkinson, D.T.; Wright, E.L. (1993). «Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps». Astrophysical Journal. 419: 1. arXiv:astro-ph/9312056. Bibcode:1993ApJ…419….1K. doi:10.1086/173453. S2CID 209835274.
- ^ Imamura, Jim (August 10, 2006). «Mass of the Milky Way Galaxy». University of Oregon. Archived from the original on 2007-03-01. Retrieved 2007-05-10.
- ^ Ask an Astrophysicist Archived 2009-03-11 at the Wayback Machine. NASA Goodard Space Flight Center.
- ^ Williams, David R. (September 1, 2004). «Earth Fact Sheet». NASA. Archived from the original on 2013-05-08. Retrieved 2007-03-17.
- ^ Staff. «GPS Time Series». NASA JPL. Archived from the original on 2011-07-21. Retrieved 2007-04-02.
- ^ Huang, Zhen Shao (2001). Elert, Glenn (ed.). «Speed of the Continental Plates». The Physics Factbook. Archived from the original on 2020-06-19. Retrieved 2020-06-20.
- ^ Meschede, M.; Udo Barckhausen, U. (November 20, 2000). «Plate Tectonic Evolution of the Cocos-Nazca Spreading Center». Proceedings of the Ocean Drilling Program. Texas A&M University. Archived from the original on 2011-08-08. Retrieved 2007-04-02.
- ^ Wexler, L.; D H Bergel; I T Gabe; G S Makin; C J Mills (1 September 1968). «Velocity of Blood Flow in Normal Human Venae Cavae». Circulation Research. 23 (3): 349–359. doi:10.1161/01.RES.23.3.349. PMID 5676450.
- ^ Bowen, R (27 May 2006). «Gastrointestinal Transit: How Long Does It Take?». Pathophysiology of the digestive system. Colorado State University. Archived from the original on 3 April 2015. Retrieved 25 January 2014.
- ^ M. Fischer; U.K. Franzeck; I. Herrig; U. Costanzo; S. Wen; M. Schiesser; U. Hoffmann; A. Bollinger (1 January 1996). «Flow velocity of single lymphatic capillaries in human skin». Am J Physiol Heart Circ Physiol. 270 (1): H358–H363. doi:10.1152/ajpheart.1996.270.1.H358. PMID 8769772.
- ^ «cytoplasmic streaming – biology». Encyclopædia Britannica. Archived from the original on 2008-06-11. Retrieved 2022-06-23.
- ^ «Microtubule Motors». rpi.edu. Archived from the original on 2007-11-30.
- ^ Hill, David; Holzwarth, George; Bonin, Keith (2002). «Velocity and Drag Forces on motor-protein-driven Vesicles in Cells». APS Southeastern Section Meeting Abstracts. 69: EA.002. Bibcode:2002APS..SES.EA002H.
- ^ Temperature and BEC. Archived 2007-11-10 at the Wayback Machine Physics 2000: Colorado State University Physics Department
- ^ «Classroom Resources». anl.gov. Argonne National Laboratory. Archived from the original on 2010-06-08. Retrieved 2009-03-09.
- ^ «Chapter 2, Nuclear Science- A guide to the nuclear science wall chart. Berkley National Laboratory» (PDF). Archived (PDF) from the original on 2009-03-04. Retrieved 2009-03-09.
- ^ «The «explicit-constant» formulation». BIPM. 2011. Archived from the original on 11 August 2014.
- ^ Meyer, Eileen (June 2018). «Detection of an Optical/UV Jet/Counterjet and Multiple Spectral Components in M84». The Astrophysical Journal. 680 (1): 9. arXiv:1804.05122. Bibcode:2018ApJ…860….9M. doi:10.3847/1538-4357/aabf39. S2CID 67822924.
Further reading[edit]
- Conover, Emily (2 November 2016). «Units of measure are getting a fundamental upgrade». Science News
- Knotts, Sandra; Mohr, Peter J.; Phillips, William D. (January 2017) «An Introduction to the New SI», The Physics Teacher 55 (1): 16–21. Bibcode:2017PhTea..55…16K. doi:10.1119/1.4972491 ISSN 0031-921X. S2CID 117581000.
- «SI Redefinition», National Institute of Standards and Technology 11 May 2018
External links[edit]
Wikiquote has quotations related to Motion.
- Feynman’s lecture on motion
Media related to Motion at Wikimedia Commons
Уравнение движения тела. Все виды уравнений движения
Понятие «движение» определить не так уж просто, как это может показаться. С житейской точки зрения, это состояние является полной противоположностью покоя, но современная физика считает, что это не совсем так. В философии под движением подразумеваются любые изменения, происходящие с материей. Аристотель полагал, что данное явление равносильно самой жизни. А для математика любое перемещение тела выражается уравнением движения, записанным при помощи переменных и цифр.
Материальная точка
В физике перемещение различных тел в пространстве изучает раздел механики, именуемый кинематикой. Если размеры некоего объекта слишком малы в сравнении с расстоянием, которое ему приходится преодолевать вследствие его движения, то он рассматривается здесь как материальная точка. Примером тому может служить автомобиль, едущий по дороге из одного города в другой, птица, летящая в небе, а также многое другое. Подобная упрощенная модель удобна при написании уравнения движения точки, за которую принимается определённое тело.
Бывают и другие ситуации. Представим, что тот же автомобиль хозяин решил переместить с одного конца гаража в другой. Здесь изменение местоположения сравнимо с размерами объекта. Поэтому каждая из точек автомобиля будет иметь разные координаты, а сам он рассматривается как объёмное тело в пространстве.
Основные понятия
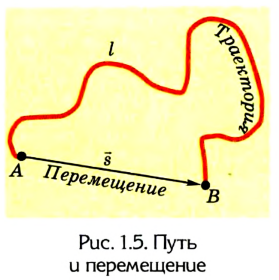
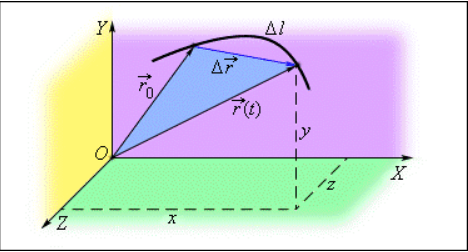
Следует учитывать, что для физика путь, пройденный определённым объектом, и перемещение – совсем не одно и то же, а эти слова не являются синонимами. Уяснить разницу между данными понятиями можно, рассмотрев движение самолёта в небе.
След, который он оставляет, наглядно показывает его траекторию, то есть линию. При этом путь представляет собой её длину и выражается в определённых единицах (к примеру, в метрах). А перемещение – это вектор, соединяющий лишь точки начала и конца движения.
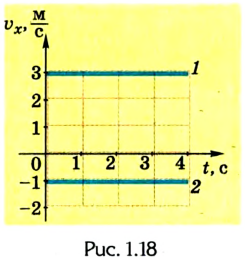
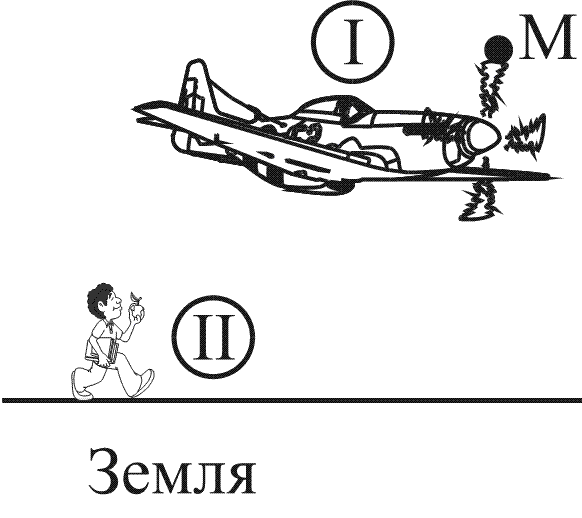
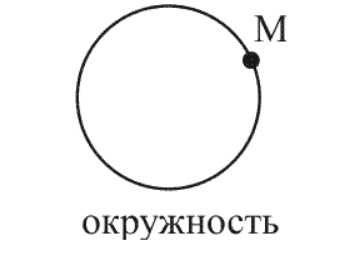
Подобное можно увидеть на рисунке, приведённом ниже, который демонстрирует маршрут машины, едущей по извилистой дороге, и вертолёта, летящего по прямой. Векторы перемещения для этих объектов будут одинаковые, а пути и траектории – разными.
Равномерное движение по прямой
Теперь рассмотрим различные виды уравнений движения. И начнём с самого простого случая, когда некий объект перемещается по прямой с одинаковой скоростью. Это значит, что по истечении равных промежутков времени путь, который он проходит за данный период, не меняется по величине.
Что нам потребуется для описания данного движения тела, вернее, материальной точки, как уже было условлено его называть? Важно выбрать систему координат. Для простоты предположим, что перемещение происходит вдоль некоей оси 0Х.
Тогда уравнение движения: x = х0 + vхt. Оно и будет описывать процесс в общем виде.
Важным понятием при изменении местоположения тела является скорость. В физике она является векторной величиной, поэтому принимает положительное и отрицательное значение. Здесь всё зависит от направления, ведь тело может перемещаться по выбранной оси с возрастающей координатой и в противоположную сторону.
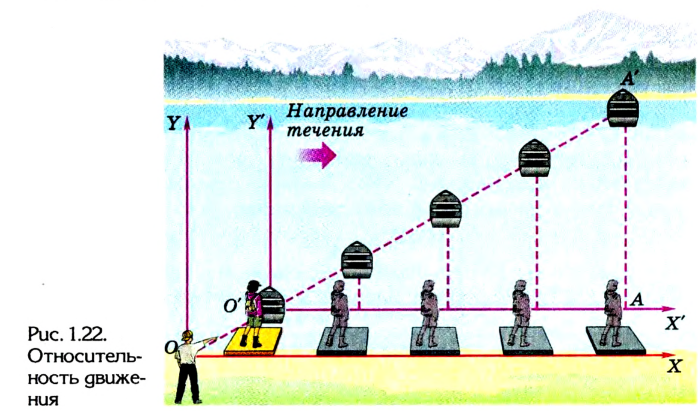
Относительность движения
Почему так важно выбрать систему координат, а также точку отсчёта для описания указанного процесса? Просто потому, что законы мироздания таковы, что без всего этого уравнение движения не будет иметь смысла. Это показано такими великими учёными, как Галилей, Ньютон и Эйнштейн. С начала жизни, находясь на Земле и интуитивно привыкнув выбирать её за систему отсчёта, человек ошибочно полагает, что существует покой, хотя для природы не бывает такого состояния. Тело может менять местоположение или оставаться статичным лишь относительно какого-либо объекта.
Мало того, тело может двигаться и находиться в покое одновременно. Примером тому может послужить чемодан пассажира поезда, который лежит на верхней полке купе. Он движется относительно деревни, мимо которой проезжает состав, и покоится по мнению своего хозяина, расположившегося на нижнем сидении у окна. Космическое тело, некогда получив начальную скорость, способно лететь в пространстве миллионы лет, пока не столкнётся с другим объектом. Движение его не будет прекращаться потому, что перемещается оно лишь относительно прочих тел, а в системе отсчёта, связанной с ним, космический путешественник находится в покое.
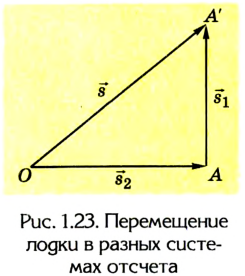
Пример составления уравнений
Итак, выберем за точку отсчёта некий пункт А, при этом координатной осью пусть будет для нас автомагистраль, находящаяся рядом. А направление её будет проходить с запада на восток. Предположим, что в эту же сторону в пункт В, расположенный за 300 км, пешком отправился путешественник со скоростью 4 км/ч.
Получается, что уравнение движения задаётся в виде: х = 4t, где t – время в пути. Согласно этой формуле, появляется возможность вычислить местонахождение пешехода в любой необходимый момент. Становится понятно, что через час он пройдёт 4 км, через два – 8 и достигнет пункта Б спустя 75 часов, так как его координата х = 300 окажется при t = 75.
Если скорость отрицательна
Предположим теперь, что из В в А едет автомобиль, имея скорость 80 км/час. Здесь уравнение движения имеет вид: х = 300 – 80t. Это действительно так, ведь х0 = 300, а v = -80. Следует обратить внимание, что скорость в данном случае указывается со знаком «минус», потому что объект перемещается в отрицательном направлении оси 0Х. Через какое время автомобиль достигнет пункта назначения? Это произойдёт, когда координата примет нулевое значение, то есть при х = 0.
Остаётся решить уравнение 0 = 300 – 80t. Получаем, что t = 3,75. Это означает, что автомобиль достигнет пункта В через 3 часа 45 минут.
Необходимо помнить, что координата тоже может быть отрицательной. В нашем случае это оказалось бы, если б существовал некий пункт С, находящийся в западном направлении от А.
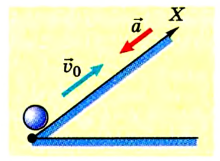
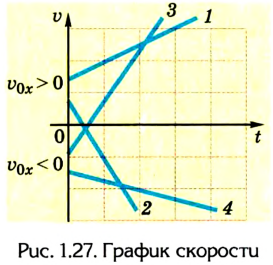
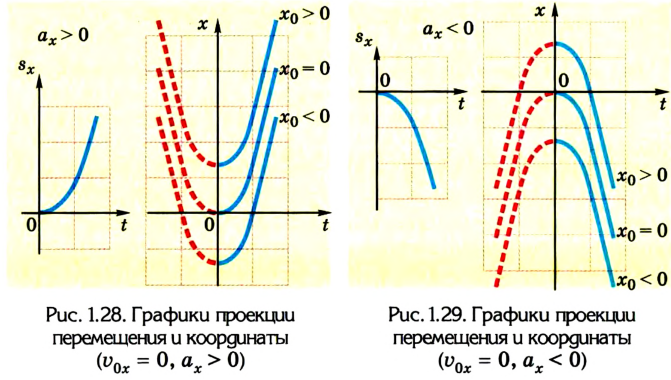
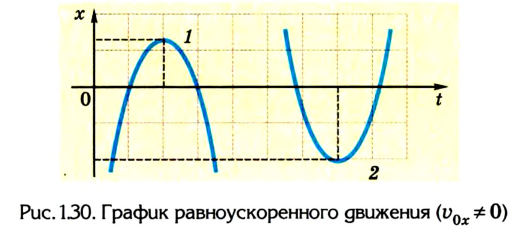
Движение с увеличением скорости
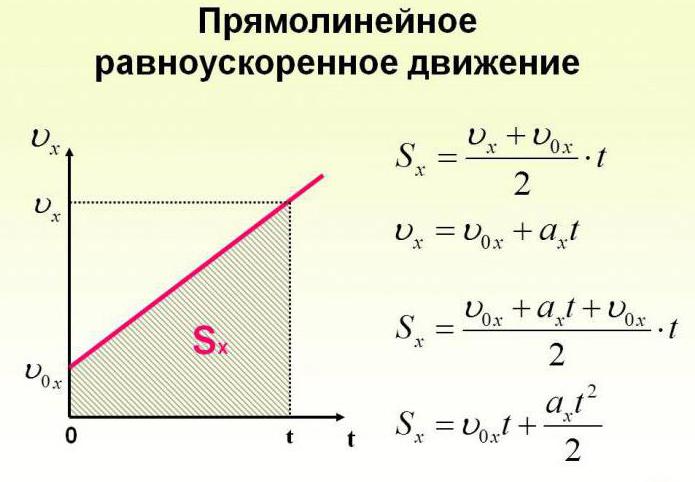
Перемещаться объект может не только с постоянной скоростью, но и менять её с течением времени. Движение тела может происходить по очень сложным законам. Но для простоты следует рассмотреть случай, когда ускорение увеличивается на определённое постоянное значение, а объект перемещается по прямой. В данном случае говорят, что это равноускоренное движение. Формулы, описывающие этот процесс, приведены ниже.
А теперь рассмотрим конкретные задачи. Допустим, что девочка, сев на санки на вершине горы, которую мы выберем за начало воображаемой системы координат с направлением оси по наклону вниз, начинает двигаться под действием силы тяжести с ускорением, равным 0,1 м/с 2 .
Тогда уравнение движения тела имеет вид: sx = 0,05t 2 .
Понимая это, можно узнать расстояние, которое девочка проедет на санках, для любого из моментов перемещения. Через 10 секунд это будет 5 м, а через 20 секунд после начала движения под гору путь составит 20 м.
Как выразить скорость на языке формул? Поскольку v0x = 0 (ведь санки начали катиться с горы без начальной скорости только под действием силы притяжения), то запись не будет слишком сложной.
Уравнение скорости движения примет вид: vx= 0,1t. Из него мы сможет узнать, как изменяется этот параметр с течением времени.
К примеру, через десять секунд vx= 1 м/с 2 , а через 20 с примет значение 2 м/с 2 .
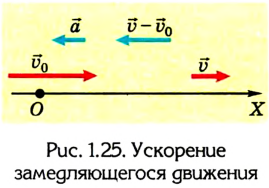
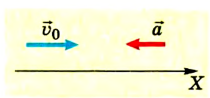
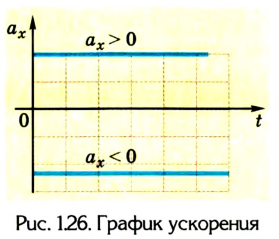
Если ускорение отрицательно
Существует и другой вид перемещения, относящийся к тому же типу. Это движение называют равнозамедленным. В данном случае скорость тела тоже изменяется, но с течение времени не увеличивается, а уменьшается, и тоже на постоянную величину. Снова приведём конкретный пример. Поезд, ехавший до этого с постоянной скоростью 20 м/с, начал тормозить. При этом ускорение его составило 0,4 м/с 2 . Для решения примем за начало отсчёта точку пути поезда, где он начал тормозить, а координатную ось направим по линии его перемещения.
Тогда становится понятно, что движение задано уравнением: sx = 20t — 0,2t 2 .
А скорость описывается выражением: vx = 20 – 0,4t. Необходимо заметить, что перед ускорением ставится знак «минус», так как поезд тормозит, и данная величина отрицательна. Из полученных уравнений возможно заключить, что состав остановится через 50 секунд, проехав при этом 500 м.
Сложное движение
Для решения задач в физике обычно создаются упрощённые математические модели реальных ситуаций. Но многогранный мир и явления, происходящие в нём, далеко не всегда вписываются в подобные рамки. Как составить уравнение движения в сложных случаях? Проблема решаема, ведь любой запутанный процесс возможно описать поэтапно. Для пояснения снова приведём пример. Вообразим, что при запуске фейерверков одна из ракет, взлетевшая с земли с начальной скоростью 30 м/с, достигнув верхней точки своего полёта, разорвалась на две части. При этом соотношение масс получившихся осколков составило 2:1. Далее обе части ракеты продолжили двигаться отдельно одна от другой таким образом, что первая полетела вертикально вверх со скоростью 20 м/с, а вторая сразу упала вниз. Следует узнать: какова была скорость второй части в момент, когда она достигла земли?
Первым этапом данного процесса окажется полёт ракеты вертикально вверх с начальной скоростью. Перемещение будет равнозамедленным. При описании понятно, что уравнение движения тела имеет вид: sx = 30t – 5t 2 . Здесь мы полагаем, что ускорение свободного падения для удобства округляется до значения 10 м/с 2 . Скорость при этом будет описываться следующим выражением: v = 30 – 10t. По этим данным уже возможно вычислить, что высота подъёма составит 45 м.
Вторым этапом движения (в данном случае уже второго осколка) окажется свободное падение этого тела с начальной скоростью, получаемой в момент распадения ракеты на части. При этом процесс будет равноускоренным. Для нахождения окончательного ответа сначала вычисляет v0 из закона сохранения импульса. Массы тел относятся 2:1, а скорости находятся в обратной зависимости. Следовательно, второй осколок полетит вниз с v0 = 10 м/c, а уравнение скорости примет вид: v = 10 + 10t.
Время падения мы узнаем из уравнения движения sx = 10t + 5t 2 . Подставим уже полученное значение высоты подъёма. В результате выходит, что скорость второго осколка приблизительно равна 31,6 м/с 2 .
Таким образом, разделяя сложное движение на простые составные части, можно решать любые запутанные задачи и составлять уравнения движения всех видов.
Механическое движение
О чем эта статья:
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
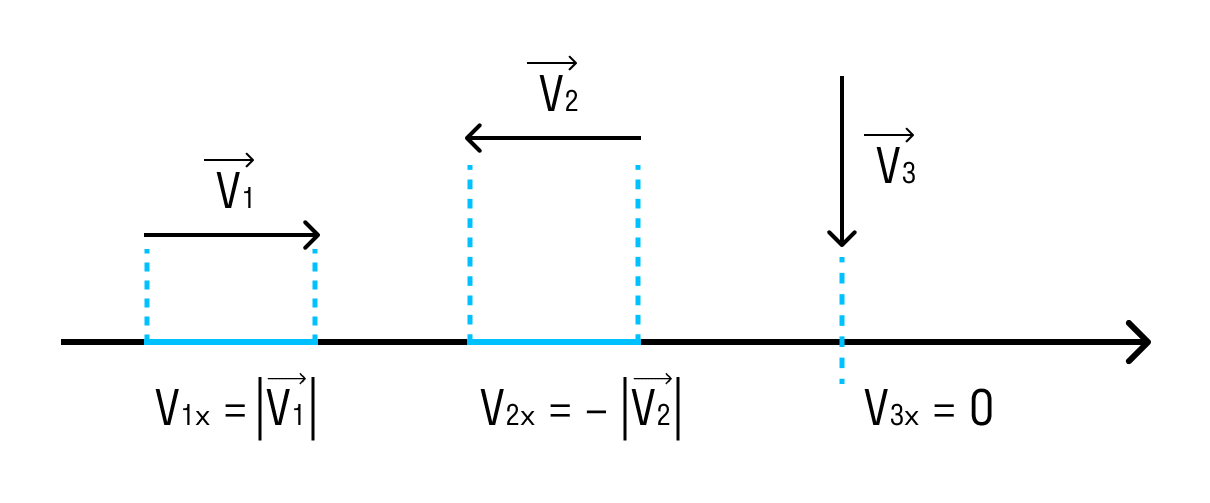
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
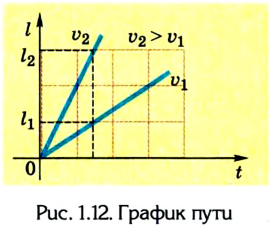
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
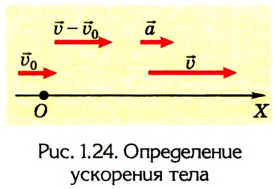
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
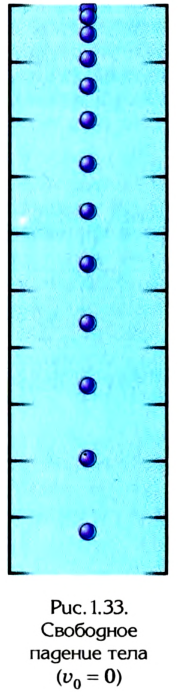
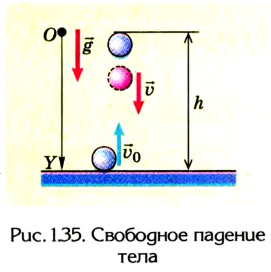
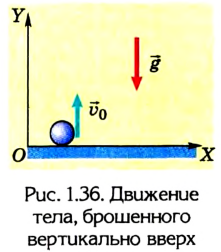
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
источники:
http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/uravnenie-dvizhenija-materialnoj-tochki/
Содержание:
Основная задача механики — описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, — это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика — одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. — найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
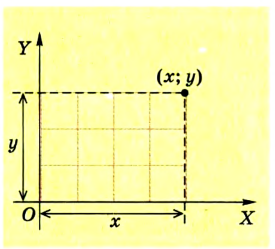
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости — это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля — достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ — невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка — это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели — пассажир в купе и провожающий на перроне — оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
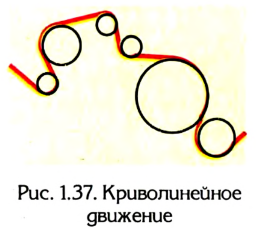
Траектория прямолинейного движения — прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
Рис. 1.4. Траектория движения точки обода колеса велосипеда
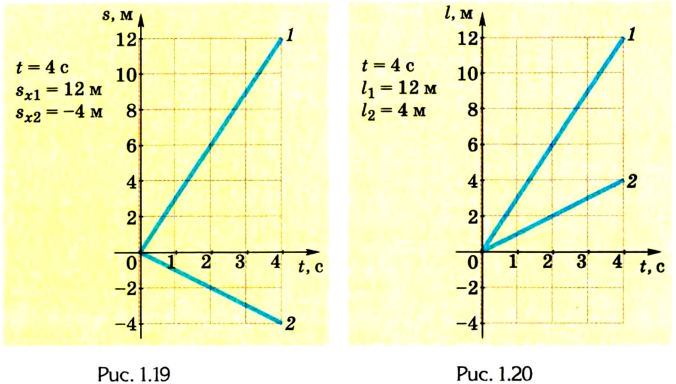
Путь и перемещение
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь — это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути — километр (км), сантиметр (см) и др.
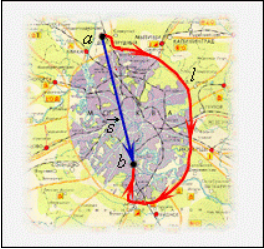
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь — это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение — это векторная величина. Оно обозначается латинской буквой 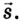
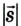
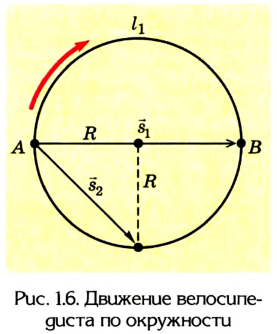
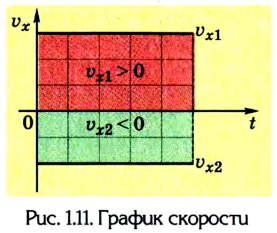
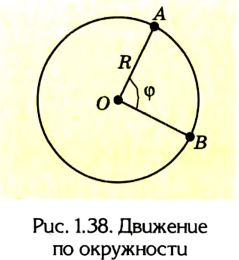
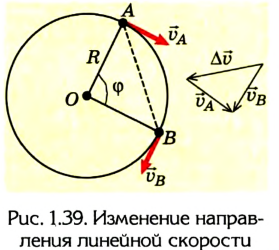
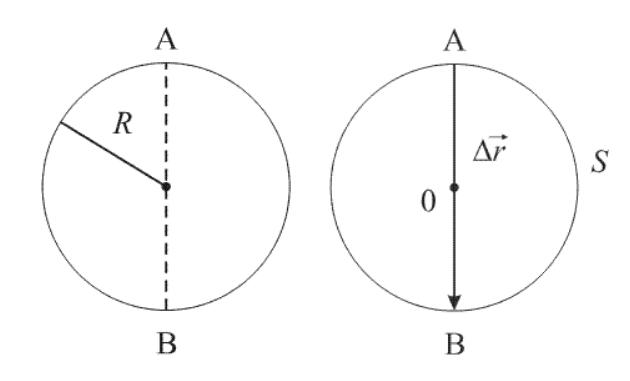
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 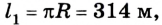
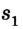
В момент времени, когда велосипедист проедет 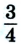
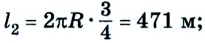
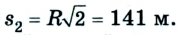
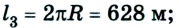
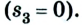
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
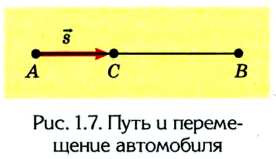
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 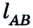
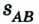
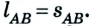
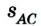
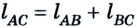
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория — прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 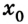
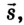
Как известно, в СИ скорость
измеряется в метрах за секунду (м/с). 1 м/с — это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 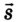
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х — x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
Из рисунков 1.8 и 1.9 понятно, что 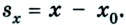
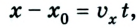
Уравнения равномерного прямолинейного движения:
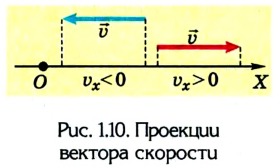
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 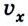
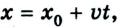
Если же направление движения тела противоположно направлению координатной оси, то 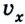
Как решать задачи кинематики
Решение любой физической задачи в определенной степени можно условно разделить на три этапа: физический, математический и анализ решения.
На физическом этапе:
- ✓ анализируют условие задачи и описание физической ситуации, заданной условием;
- ✓ выясняют физическую модель явления, лежащего в основе задачи;
- ✓ физическую модель явления представляют в графической форме (рисунки, чертежи, схемы, графики и т. д.);
- ✓ сокращенно записывают условия задачи в систематизированном виде.
На математическом этапе:
- ✓ предлагают математическую модель задачи, составляют общие уравнения, описывающие физические явления, представленные в условии задачи;
- ✓ определяют конкретные условия и параметры, при которых происходит данное явление;
- ✓ конкретизируют общие уравнения в виде частных решений аналитическим, графическим или числовым способом, производят вычисления.
- На этапе анализа решения:
- ✓ производят проверку единиц физических величин и находят значения искомых величин;
- ✓ анализируют результаты, их достоверность и правдоподобность;
- ✓ ищут иные методы решения задачи и выбирают наиболее рациональный из них.
В ходе решения задач кинематики главное состоит в том, чтобы за заданными параметрами движения (координаты, перемещение, скорость и др.) записать уравнение движения. Или наоборот, если уравнение движения известно, ищут физические величины, которые его описывают.
Решение задач кинематики подчинено определенной последовательности умственных действий, так называемому алгоритму, при помощи которого поиск решения задачи значительно облегчается. Представим его как последовательность шагов в ходе решения задачи.
- Шаг 1. В соответствии с условием задачи выберите систему отсчета. Определите начальные значения координат, связав их с телом отсчета.
- Шаг 2. Выясните характер движения (равномерное, неравномерное) и вид траектории (прямолинейная, криволинейная).
- Шаг 3. Сделайте рисунок, иллюстрирующий условие задачи. Свяжите рисунок с выбранной системой отсчета, обозначьте на нем векторные физические величины.
- Шаг 4. Отобразите проекции перемещения, скорости, других векторных величин и запишите уравнение движения тела в общем виде. При необходимости составьте дополнительные уравнения, которые объединяют эти кинематические величины.
- Шаг 5. Решите уравнения относительно искомых величин. Определите их значения, оцените достоверность результата.
- Шаг 6. Проанализируйте полученный ответ. Если он противоречит смыслу задачи, начните поиск иного решения.
- Шаг 7. Произведите поиск иных возможных путей решения задачи. Оцените, какое из решений наиболее рационально.
Задача №1
Из пунктов А и В, расстояние между которыми 80 км, одновременно начали движение навстречу друг другу два велосипедиста. Первый ехал со скоростью 5 м/с, второй -3 м/с. Определите:
- 1) через какое время они встретятся и где это произойдет;
- 2) какой путь они пройдут до момента встречи и какое совершат перемещение;
- 3) через какое время от начала движения расстояние между ними будет 20 км.
Решение
1. Выберем такую систему отсчета, начало координат которой совпадает с пунктом А. В общем виде уравнение движения тела имеет такой вид: 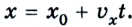
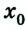
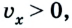
У второго велосипедиста 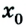
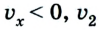
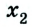
Вследствие движения координаты обоих велосипедистов с течением времени изменяются: у первого она возрастает, у второго — уменьшается. В момент их встречи координаты обоих велосипедистов равны: 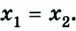
5t = 80 000 — 3t; St = 80 000; отсюда t = 10 000 с = 2,8 ч. Таким образом, велосипедисты встретятся через 2,8 часа.
Место их встречи определяют координаты 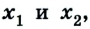
Задача №2
Поскольку велосипедисты по условию задачи ехали прямолинейно и не изменяли направления движения, то пройденный ими путь равен модулю перемещения (или его проекции):
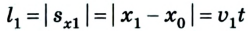
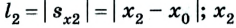
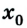
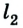
Или 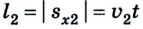
3. Чтобы найти время, когда расстояние между велосипедистами будет равно 20 км, достаточно записать равенство 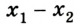
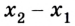
5t — 80 000 + 3t = 20 000; 8t = 100 000; t = 12 500 с = 3,5 ч.
80 000 — 3t — 5t = 20 000; 8t = 60 000; t = 7500 с = 2,1 ч.
Почему получено два разных ответа? Внимательно проанализировав условие задачи, заметим, что на расстоянии 20 км друг от друга велосипедисты будут дважды — когда едут навстречу друг другу (2,1 ч) и когда разъезжаются после встречи, продолжая движение (3,5 ч).
Графики равномерного прямолинейного движения
Для того чтобы лучше усвоить особенности изменений параметров равномерного движения (координат, пути, перемещения, скорости) с течением времени, рассмотрим соответствующие графические зависимости, следующие из уравнения равномерного прямолинейного движения.
1. График скорости v = u(t). Как известно, скорость тела при равномерном прямолинейном движении с течением времени не изменяется, т. е. v = const. Поэтому график скорости — это прямая, параллельная оси времени t, которая находится над ней, если проекция скорости положительна (рис. 1.11), или под ней, если она отрицательна.
2. График пути l = l(t). Из формулы пути l = vt следует, что между пройденным путем и временем существует прямо пропорциональная зависимость. Графически она отображается прямой, проходящей через начало координат (ведь длина пути не может иметь отрицательных значений). В зависимости от значения скорости наклон графика будет разным (рис. 1.12): чем больше скорость, тем круче прямая.
3. График проекции перемещения 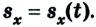
График проекции перемещения всегда проходит через начало координат. Угол наклона прямой, как и в случае графика пути, зависит от значения скорости: чем она больше, тем круче график проекции перемещения.
Если тело изменяет направление движения — сначала движется в одну сторону, а затем возвращается назад, то график проекции перемещения принимает вид, изображенный на рисунке 1.14 (в момент времени 
4. График движения тела х = x(t) характеризует изменение координат тела с течением времени. Из уравнения движения 
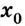
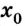
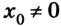
Так как проекция скорости может иметь положительные и отрицательные значения (направление вектора скорости может совпадать или быть противоположным выбранному направлению оси), то график может подниматься вверх (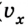
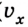
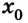
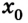
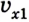
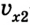
Таким образом, при помощи графиков можно выяснить характер движения тел и изменения соответствующих величин с течением времени t.
Задача №3
На основании графика движения (рис. 1.17):
- 1) определить скорость движения тел;
- 2) составить уравнения движения обоих тел;
- 3) найти перемещение тел за 4 с;
- 4) определить время и место их встречи;
- 5) найти расстояние между телами через 2 с после начала движения;
- 6) построить графики скорости, проекции перемещения и пути.
Решение
1. Скорость тела определяется на основании формулы
Время движения выбираем произвольно, руководствуясь простотой расчетов. Например, используем значение t = 2 с. Тогда тело 1 через 2 с будет иметь координату 6 м; его начальная координата 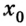
У тела 2 начальная координата равна 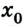
2. Уравнение движения для обоих тел будет иметь такой вид:
3. Перемещение тел за время t = 4 с равно:
4. В момент встречи тел их координаты будут одинаковы, т. е. это точка пересечения графиков. При помощи перпендикуляра, проведенного к оси координат, можно установить координату места встречи — она равна 3 м. Для определения времени встречи необходимо опустить перпендикуляр на ось времени t; получим t = 1 с.
5. Согласно графикам движения тел через 2 с тело 1 имеет координату
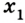
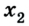
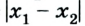
6. Используя предыдущие данные решения задачи, построим соответствующие графики (рис. 1.18-1.20).
Относительность движения. Закон сложения скоростей
Для того чтобы описать механическое движение и определить его параметры — траекторию, перемещение, пройденный путь, скорость и др., следует прежде всего выбрать систему отсчета и проанализировать движение тела или материальной точки относительно тела отсчета, выбранного произвольно. В природе существует множество систем отсчета и описание движения может одновременно производиться в каждой из них. Например, лодка, плывущая по реке, движется относительно ее берегов, относительно теплохода, который плывет рядом, относительно пешеходов, стоящих на берегу, и т. д.
Чаще всего систему отсчета связывают с телом, которое в данной ситуации считается неподвижным: с землей, берегом реки, населенным пунктом, столбом на обочине дороги и др. Такая система отсчета считается неподвижной.
С телами, которые движутся в неподвижных системах отсчета равномерно и прямолинейно, связывают подвижные системы отсчета. Следует учитывать, что удачный выбор системы отсчета намного упрощает решение задачи.
Рассмотрим движение какого-либо тела, например лодки, плывущей по реке, в различных системах отсчета (рис. 1.22).
Пусть лодка пересекает реку перпендикулярно к ее течению. За движением лодки следят два наблюдателя — один на берегу реки (неподвижная система отсчета XOY), другой с плота, который перемещается относительно берега со скоростью течения реки (подвижная система отсчета X’O’Y’).
Первый наблюдатель будет видеть перемещение лодки по прямой ОА’. Второй наблюдатель, находясь в подвижной системе отсчета, увидит иную картину: лодка будет удаляться от него по прямой, перпендикулярно к течению, и когда она достигнет противоположного берега в т. А’, плот будет находится точно напротив нее в т. А.
Таким образом, относительно подвижной системы отсчета лодка совершает перемещение 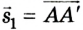
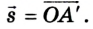
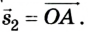
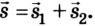
Разделив каждый член уравнения на время движения t, одинаковое для подвижной и неподвижной систем отсчета, получим:
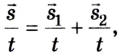
Уравнение (1) называется законом сложения скоростей: скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости самой подвижной системы отсчета относительно неподвижной. Сложение скоростей в данном случае также выполняется согласно правилам сложения векторов.
Движение тела в подвижной системе отсчета называется относительным, движение самой подвижной системы отсчета относительно неподвижной является переносным. Таким образом, механическое движение тел относительно различных систем отсчета может быть представлено независимыми движениями: а) относительным движением тела в подвижной системе отсчета; б) переносным движением подвижной системы отсчета относительно неподвижной. В соответствии с данным утверждением закон сложения скоростей приобретает вид:
т. е. скорость тела в неподвижной системе отсчета равна геометрической сумме относительной и переносной скоростей.
Скорость тела в неподвижной системе отсчета иногда называют абсолютной.
- Заказать решение задач по физике
Задача №4
Моторная лодка плывет по реке от одного поселка к другому, расстояние между которыми 30 км. Скорость лодки в стоячей воде 20 км/ч, а скорость течения реки относительно берегов 10 км/ч. За какое время лодка преодолеет расстояние между поселками, двигаясь сначала по течению, а затем, возвращаясь назад, против него?
Дано:
Решение
Согласно закону сложения скоростей
В скалярной форме, учитывая знаки проекции скоростей, получим:
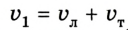
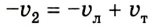
Следовательно, время движения лодки между поселками по течению:
Время движения лодки против течения:
Ответ:
Равноускоренное движение. Ускорение
При равномерном прямолинейном движении скорость тела в различных точках траектории остается неизменной. Однако в реальной жизни мы чаще имеем дело с неравномерным движением, когда скорость тела может изменяться и по своему значению, и по направлению. Если за любые равные интервалы времени скорость тела изменяется одинаково либо по значению, либо по направлению, то такое движение называется равноускоренным.
Изменение значения скорости может происходить довольно быстро (например, движение пули в ружье, старт ракеты, разбег самолета и т. п.) или сравнительно медленно (начало движения поезда, торможение автомобиля). При этом также следует учитывать, что скорость как векторная величина может изменять свое направление, которое тоже характеризует неравномерность движения. В физике для оценивания быстроты изменения скорости движения применяют физическую величину, которая называется ускорением.
Для характеристики неравномерного движения используют понятие ускорения, которое определяет, насколько быстро I изменяется скорость движения.
Ускорение — это векторная физическая величина, равная отношению изменения скорости тела к интервалу времени, в течение которого это изменение произошло:
где 
Из определения равноускоренного движения следует, что его ускорение является постоянной величиной (
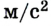
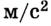
Значение ускорения определяют, учитывая векторные свойства данной физической величины. В частности, в проекциях на ось ОХ (рис. 1.24) формула ускорения приобретает вид:
В случае, когда 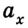
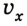
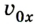
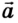
Если скорость тела со временем уменьшается 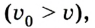
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения — оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 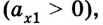
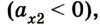
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:
или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 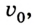
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим:
или в проекциях на ось ОХ:
Если начальная скорость тела равна 0 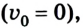
или в проекциях на ось ОХ:
Для прямолинейного движения, учитывая, что 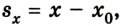
или для случая, когда 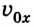
Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 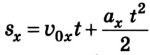
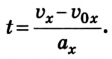
Отсюда 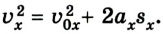
Задача №5
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 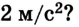
Дано:
t -?
l — ?
Решение
По условию задачи спидометр показывает начальную скорость автомобиля 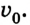
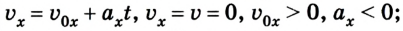
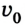
Ответ: автомобиль остановился через 10 с, проехав 100 м.
Задача №6
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 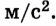
Дано:
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 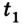
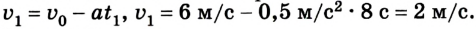
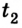
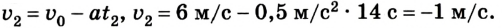
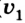
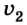
Ответ: 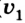
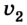
Графики равноускоренного движения
1. График ускорения а = a(t). Как известно, при равноускоренном движении ускорение является величиной постоянной (а = const). Поэтому зависимость проекции ускорения от времени отображает прямая, параллельная оси времени t. В зависимости от значения проекции ускорения -положительная она или отрицательная — данная прямая размещена над осью или под ней (рис. 1.26).
2. График скорости и = v(t).
Линейная зависимость скорости от времени обусловлена математическим видом ее кинематического уравнения 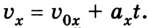
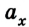
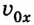
Если 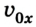
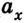
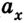
3. График проекции перемещения 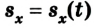
Кинематические уравнения перемещения и координат представляют собой квадратные уравнения вида 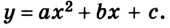
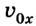
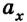
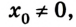
Если 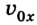
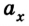
Если 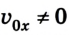
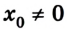
Представленные на рисунке 1.30 графики отображают такие параметры равноускоренного движения:
1)
2)
Задача №7
Прямолинейное движение тела описывается уравнением 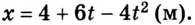
- 1) характер движения тела и его скорость через 3 с от начала движения;
- 2) в какой момент времени после начала его отсчета тело изменило направление движения на противоположное;
- 3) в какой момент времени после начала его отсчета тело вернется в начальную точку;
- 4) перемещение и пройденный путь через 2 с.
Решение
1. Для определения скорости тела в любой момент времени необходимо составить уравнение скорости 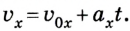
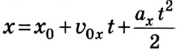
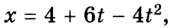
При таких условиях уравнение скорости для данного движения приобретает вид: 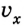
Следовательно, скорость движения равна 18 м/с. Отрицательное ее значение свидетельствует о том, что направление скорости противоположно выбранному направлению координатной оси. Движение тела замедляется 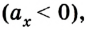
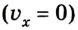
2. Для определения момента изменения направления движения надо уравнение скорости приравнять к 0 и решить его относительно t:
3. Тело вернется в начальную точку, когда его координата примет значение начальной координаты, т. е. х = 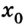
Следовательно, тело имело координату в начале движения 
4. Для определения перемещения через 2 с после начала движения составим уравнение проекции перемещения
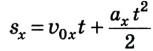
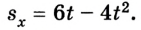
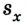
Для определения пройденного пути следует учесть, что тело меняло направление движения, поэтому 
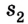
Таким образом, пройденный путь равен:
l = 2,25 м + 6,25 м = 8,5 м.
Свободное падение тел. Ускорение свободного падения
Многочисленные наблюдения и опыты убеждают нас в том, что все тела падают на землю вследствие притяжения к ней. Если тело бросить вертикально вверх, оно все равно упадет на землю: вначале его скорость будет уменьшаться, а затем оно начнет падать вниз со всевозрастающей скоростью.
Анализ характера движения падающего тела (рис. 1.33) показывает, что данное движение равноускоренное, т. е. за равные интервалы времени оно проходит разные расстояния, которые с течением времени пропорционально увеличиваются.
Долгое время считалось, что различным телам Земля придает разное ускорение, и поэтому они падают на нее неодинаково — одни быстрее, другие медленнее. Это, как оказалось впоследствии, ложное представление подтверждал жизненный опыт: легкое перышко, падающее вместе со свинцовым шариком, достигало земли гораздо позже его. Этот, на первый взгляд, очевидный факт вынуждал многих людей искаженно воспринимать действительное протекание явления свободного падения тел. Если повторить данный опыт в условиях, когда на тело не действуют другие факторы, кроме земного притяжения, например в цилиндрической колбе, из которой откачан воздух, то результат будет иным: оба тела упадут одновременно. Этот опыт впервые выполнил И. Ньютон. Он подтвердил, что в условиях свободного падения, т. е. когда на тело действует только сила тяжести, все тела, независимо от их массы и формы, падают одинаково. Следовательно, свободное падение — это равноускоренное движение тел под действием силы тяжести при отсутствии посторонних влияний на них (сопротивление воздуха, электромагнитное взаимодействие и др.). Свободное падение происходит не только на Земле вследствие притяжения к ней всех тел. Оно происходит на всех планетах, Солнце, Луне и др. Однако падение тела ускорение свободного падения у них, конечно же, разное.
Выдающийся итальянский физик Галилео Галилей, изучая движение тел по наклонной плоскости, установил, что шары одинакового диаметра, изготовленные из дерева, железа, слоновой кости и других материалов, следовательно, разной массы, имеют одно и то же ускорение. Увеличивая угол наклона, он пришел к выводу, что значение ускорения при этом растет, но остается одинаковым для всех тел, независимо от их массы. Если увеличивать угол наклона плоскости до 90°, т. е. до ее вертикального положения, выводы в отношении ускорения тел останутся теми же.
Ведь при этом не появилось каких-либо дополнительных факторов, влияющих на характер движения тел. Для подтверждения данного вывода ученый провел известный опыт с пушечным ядром и пулей от мушкета, бросая их с Пизанской башни (рис. 1.34): оба тела достигали земли одновременно. Таким образом Г. Галилей экспериментально установил, что ускорение свободного падения не зависит от массы тел и является постоянной величиной для каждой планеты.
Благодаря многочисленным измерениям ускорения свободного падения для Земли определено его среднее значение у поверхности: 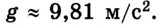
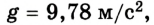
Поскольку свободное падение и движение тела, брошенного вертикально вверх (как частный случай свободного падения), являются равноускоренным движением, все его кинематические уравнения применимы и для данного случая. Вместе с тем в соответствующих уравнениях надо учитывать направление движения.
Выберем ось ОУ для вывода кинематических уравнений свободного падения тела (рис. 1.35).
Учитывая знаки проекций векторных величин на ось ОУ, а также то, что проекцию вертикального перемещения (высоту) обозначают
буквой h, получим:
Задача №8
Тело брошено вертикально вверх с начальной скоростью 30 м/с (рис. 1.36).
1. Через какое время оно будет на высоте 40 м?
Воспользуемся уравнением движения
Для упрощения уравнения можно принять 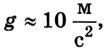
Решив квадратное уравнение, получим два корня
Оба корня удовлетворяют условию задачи. Ведь тело было на высоте 40 м дважды: через 2 с, двигаясь вверх, и через 4 с, падая вниз.
2. Какую скорость имеет тело, пролетая отметку 40 м?
На одной и той же высоте значение скорости тела по модулю одинаково, а по направлению противоположно.
3. На какую максимальную высоту поднимется тело?
В наивысшей точке скорость тела равна 0. Следовательно,
Несложно определить, что все время движения составляет 6 с, общее перемещение тела равно 0, а пройденный путь l = 90 м.
Движение точки по окружности
Ранее мы рассматривали равноускоренное движение, траекторией которого была прямая. При таком движении изменяется значение скорости, а ее направление остается неизменным. В жизни чаще встречаются криволинейные движения (орбитальное движение планет, повороты транспорта нa дороге, карусели и т. п.), во время которых происходят изменения направления скорости движения. Здесь проявляется векторный характер ускорения.
По форме траектории криволинейное движение может быть достаточно разнообразным. Однако его всегда можно представить в виде последовательных участков, состоящих из отрезков прямых и дуг окружностей различного диаметра (рис. 1.37). Т. е. любое криволинейное движение является комбинацией прямолинейного движения и движения тела по окружности.
Рассмотрим равномерное движение материальной точки по окружности. Пусть она равномерно движется по окружности радиуса R и за некоторое время t перемещается из точки А в точку В (рис. 1.38).
Угол, который при этом описывает радиус, называется угловым перемещением.
Угловое перемещение обозначают греческой буквой 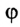
Движение точки по окружности характеризуют также период вращения и частота вращения. Период вращения — это время, в течение которого материальная точка совершает полный оборот по окружности, т. е. поворот на угол 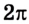
где t — время вращения, N — количество совершенных оборотов. В СИ период вращения Т измеряется в секундах (с). Частота вращения n характеризует количество оборотов тела или материальной точки вокруг центра вращения за 1 секунду:
где N — количество оборотов, совершенных за время t.
В СИ частота вращения измеряется в оборотах за секунду (об/с).
Между частотой и периодом вращения существует взаимообратная зависимость:
Для определения быстроты движения точки по окружности используют понятие угловой скорости. Это физическая величина, равная отношению углового перемещения 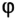
В СИ угловая скорость измеряется в радианах за секунду (рад/с). 1 рад/с равен угловой скорости такого равномерного движения точки по окружности, при котором за 1 с совершается угловое перемещение 1 рад.
Поскольку за период Т угловое перемещение 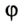
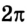
Равномерное движение материальной точки по окружности характеризуется специфическими кинематическими величинами, благодаря которым его описывают при помощи соответствующих уравнений. Это — угловое перемещение и угловая скорость, период и частота вращения. Наряду с ними применяется и привычное для нас понятие скорости, которое в данном случае называют линейной скоростью.
Во время равномерного движения точки по окружности значение ее линейной скорости остается неизменным 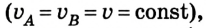
Поэтому линейную скорость можно характеризовать как скорость тела в некоторой точке. Она направлена по касательной к дуге в данной точке (точка А и точка В). В этом можно убедиться, приложив к точильному камню стальной нож: искры от него летят по касательной к поверхности камня в том месте, куда поднесли нож.
Линейная скорость тела, которое движется по окружности, все время изменяется по направлению и в любой точке траектории направлена по касательной к дуге этой окружности.
Поскольку в данном случае линейная скорость по модулю не изменяется, то из формулы скорости равномерного движения и 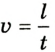
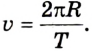
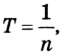
Сравнивая формулы линейной скорости 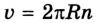
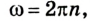
Как уже отмечалось, изменение направления вектора скорости также вызывает ускорение, ведь как векторная величина оно равно 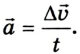
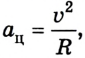
Задача №9
Земля делает один оборот вокруг своей оси за 24 ч. Вычислить угловую и линейную скорости вращения точек поверхности Земли, которые находятся на экваторе. Радиус Земли равен 6400 км. Считайте, что ось вращения проходит сквозь полюсы.
Дано:
Решение
Вращение Земли вокруг своей оси можна считать равномерным.
Следовательно,
Ответ:
Задача №10
Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колеса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Дано:
v = 10 м/с,
R = 0,35 м.
n — ? а — ?
Решение
Ответ: n = 0,22 об/с, а = 285
Итоги:
Кинематика изучает механическое движение тел, не рассматривая причин, вызывающих именно такое движение. Описание механического движения в кинематике основывается на выяснении характера изменений координат, перемещений, скорости с течением времени. Для того чтобы описать движение тела, необходимо установить закон (уравнение) изменения во времени координат или скоростей тела относительно других тел. Изменение положения тела в пространстве с течением времени характеризуется перемещением. Это векторная величина, которая определяет не только пройденный путь, но и направление, в котором происходило движение.
Механическое движение по форме траектории может быть прямолинейным или криволинейным, по характеру движения — равномерным или равноускоренным. В зависимости от этого уравнения движения имеют вид:
для равномерного прямолинейного движения
для равноускоренного прямолинейного движения
для равномерного движения по окружности
Механическое движение относительно. Это означает, что траектория, перемещение, пройденный путь, скорость, зависят от выбора системы отсчета. Механическое движение относительно различных систем отсчета может быть представлено двумя независимыми движениями — относительным движением тела в подвижной системе отсчета и переносным движением подвижной системы отсчета относительно неподвижной. Данное утверждение подтверждает закон сложения скоростей -скорость тела в неподвижной системе отсчета равна векторной сумме относительной и переносной скоростей:
Равноускоренное движение характеризует векторная физическая величина, называемая ускорением: 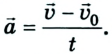
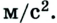
Криволинейное движение можно представить как последовательность участков, состоящих из отрезков прямых и дуг окружностей разного диаметра. Равномерное движение тела или материальной точки по окружности характеризуется угловым перемещением 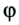
Линейная и угловая скорости согласуются между собой в виде соотношения:
При равномерном движении точки по окружности вследствие изменения направления линейной скорости возникает центростремительное ускорение:
- Законы сохранения в физике
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Магнитное поле Земли
- Ядерная энергетика в физике
- Динамика в физике
- Статика в физике
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
- Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
- Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
- Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.
По типу линии, вдоль которой движется тело, выделяют два вида движения:
- Прямолинейное — тело движется по прямой линии.
- Криволинейное — тело движется по кривой линии, в том числе замкнутой.
По скорости выделяют два вида движения:
- Равномерное — скорость движущегося тела остается неизменной.
- Неравномерное — скорость движущегося тела с течением времени меняется.
По ускорению выделяют три вида движения:
- Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
- Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
- Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
- Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
- Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
- Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.
Способы описания механического движения
Описать механическое движение можно двумя способами:
- координатным
- векторным
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
- перемещение
- скорость
- ускорение
Перемещение
Определение
Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.
Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).
Внимание!
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Определение
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
В физике скорость обозначается V. Математически скорость определяется формулой:
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Определение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
В физике ускорение обозначается a. Математически оно определяется формулой:
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с2).
Математическое определение модуля скорости:
v — скорость тела в данный момент времени, v0— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.
Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Определение
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
- Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
- Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.
Внимание!
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Задание EF17612
Тело начинает двигаться из состояния покоя с ускорением 4 м/с2. Через 2 с его скорость будет равна…
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 35.9k
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Виды движений тела
Существуют несколько видов движений и траекторий твердого тела:
- поступательное;
- вращательное, то есть движение по окружности;
- плоское, то есть перемещение по плоскости;
- сферическое, характеризующее движение по поверхности сферы;
- свободное, иначе говоря, произвольное.
Рисунок 1. Определение точки при помощи координат x=x(t), y=y(t), z=z(t) и радиус-вектора r→(t), r0→ является радиус-вектором точки в начальный момент времени
Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x=x(t), y=y(t), z=z(t) или от времени радиус-вектора r→=r→(t), проведенного из начала координат к заданной точке. Это показано на рисунке 1.
Перемещение тела
Перемещение тела s→=∆r12→=r2→-r1→ – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t.
Рисунок 2. Пройденный путь l и вектор перемещения s→ при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение принято считать векторной величиной. Этот отрезок имеет направление.
Путь – скалярная величина. Считается числом.
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3, как показано на рисунке 3.
Рисунок 3. Сумма двух последовательных перемещений ∆r→13=∆r→12+∆r→23=r→2-r→1+r→3-r→2=r→3-r→1
Когда радиус-вектор материальной точки в определенный момент времени t является r→(t), в момент t+∆t есть r→(t+∆t), тогда ее перемещение ∆r→ за время ∆t равняется ∆r→=r→(t+∆t)-r→(t).
Перемещение ∆r→ считается функцией времени t: ∆r→=∆r→(t).
По условию дан движущийся самолет, представленный на рисунке 4. Определить вид траектории точки М.
Рисунок 4
Решение
Необходимо рассмотреть систему отсчета I, называемую «Самолет» с траекторией движения точки М виде окружности.
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
Дана материальная точка, которая совершает движение из А в В. Значение радиуса окружности R=1 м. Произвести нахождение S, ∆r→.
Решение
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
S=πR.
Подставляем числовые значения и получаем:
S=3,14·1 м=3,14 м.
Перемещением ∆r→ в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В.
Подставив числовые значения, вычислим:
∆r→=2R=2·1=2 м.
Ответ: S=3,14 м; ∆r→=2 м.
Общие характеристики механического движения
В механике положение тела и его движение описывают относительно других тел. Например, человек в лодке (рис. (1)) относительно дерева на берегу изменяет своё положение, а относительно лодки он находится в покое.

Рис. (1). Движение человека в лодке
При решении задач в кинематике используют систему отсчёта.
Система отсчёта состоит из тела отсчёта (объект, относительно которого задаётся положение другого тела), системы координат и прибора для определения времени (часы).
Линия, вдоль которой тело или материальная точка изменяет своё положение, называется траекторией.
На рисунке (2) изображена система отсчёта для парусника:
- маяк — тело отсчёта;
- траектория парусника изображена красным цветом.
Рис. (2). Система отсчёта
Выбирают систему координат в зависимости от условия конкретной задачи:
- движение вдоль прямой — одномерная система координат ((OX) или (OY));
- движение в плоскости — двумерная система координат ((OXY));
- движение в пространстве — трёхмерная система координат ((OXYZ)).
Основные физические величины в кинематике
Физические параметры тел, физических явлений описываются векторными и скалярными (числовыми) величинами:
- векторные величины имеют числовое значение и направление;
- скалярные величины имеют только числовое значение.
1. Рассмотрим векторные величины, которые используются для описания механического движения.
Радиус-вектор (vec{r}) — это направленный отрезок, который соединяет начало координат и исследуемую точку (рис. 2).
Перемещение (vec{s}) — это вектор, который соединяет начальное положение тела и его положение в исследуемый момент времени (рис. 2).
Перемещение тела за любой промежуток времени равно изменению радиус-вектора
Δr→
. На рисунке (2) по правилу нахождения разности между векторами перемещение тела будет равно:
2. Рассмотрим числовые характеристики векторных величин, которые используются для описания механического движения.
На рисунке (3) изображены радиус-вектор точки (vec{r_A}) и его проекции на координатные оси ({x_A(t)}), ({y_A(t)}), которые являются функциями времени.
Рис. (3). Радиус-вектор точки и его проекции
Путь — длина траектории (обозначение — L (рис. 2), единица измерения в СИ — м (метр)).
На рисунке (4) показаны различные способы нахождения:
- проекций вектора перемещения тела (обозначение — ({s_x}), ({s_y}), единица измерения в СИ — м (метр));
- модуля вектора перемещения тела (обозначение — (|s|) или s, единица измерения в СИ — м (метр)).
Рис. (4). Определение проекций и модуля перемещения тела
Источники:
Рис. 1. Указание автора не требуется, 2021-07-18, Pixabay License, https://cdn.pixabay.com/photo/2016/08/28/17/55/boat-1626516_960_720.png.
Рис. 2. Система отсчета. © ЯКласс.
Рис. 3. Радиус-вектор точки и его проекции. © ЯКласс.
Рис. 4. Определение перемещения тела. © ЯКласс.