In electromagnetism and electronics, electromotive force (also electromotance, abbreviated emf,[1][2] denoted 


An electronic–hydraulic analogy may view emf as the mechanical work done to water by a pump, which results in a pressure difference (analogous to voltage).[8]
In electromagnetic induction, emf can be defined around a closed loop of a conductor as the electromagnetic work that would be done on an elementary electric charge (such as an electron) if it travels once around the loop.[9]
For two-terminal devices modeled as a Thévenin equivalent circuit, an equivalent emf can be measured as the open-circuit voltage between the two terminals. This emf can drive an electric current if an external circuit is attached to the terminals, in which case the device becomes the voltage source of that circuit.
Although an emf gives rise to a voltage and can be measured as a voltage and may sometimes informally be called a «voltage», they are not the same phenomenon (see § Distinction with potential difference).
Overview[edit]
Devices that can provide emf include electrochemical cells, thermoelectric devices, solar cells, photodiodes, electrical generators, inductors, transformers and even Van de Graaff generators.[10][11] In nature, emf is generated when magnetic field fluctuations occur through a surface. For example, the shifting of the Earth’s magnetic field during a geomagnetic storm induces currents in an electrical grid as the lines of the magnetic field are shifted about and cut across the conductors.
In a battery, the charge separation that gives rise to a potential difference (voltage) between the terminals is accomplished by chemical reactions at the electrodes that convert chemical potential energy into electromagnetic potential energy.[12][13] A voltaic cell can be thought of as having a «charge pump» of atomic dimensions at each electrode, that is:
A (chemical) source of emf can be thought of as a kind of charge pump that acts to move positive charges from a point of low potential through its interior to a point of high potential. … By chemical, mechanical or other means, the source of emf performs work
on that charge to move it to the high-potential terminal. The emf
of the source is defined as the work
done per charge
.
.[14]
In an electrical generator, a time-varying magnetic field inside the generator creates an electric field via electromagnetic induction, which creates a potential difference between the generator terminals. Charge separation takes place within the generator because electrons flow away from one terminal toward the other, until, in the open-circuit case, an electric field is developed that makes further charge separation impossible. The emf is countered by the electrical voltage due to charge separation. If a load is attached, this voltage can drive a current. The general principle governing the emf in such electrical machines is Faraday’s law of induction.
History[edit]
In 1801, Alessandro Volta introduced the term «force motrice électrique» to describe the active agent of a battery (which he had invented around 1798).[15]
This is called the «electromotive force» in English.
Around 1830, Michael Faraday established that chemical reactions at each of two electrode–electrolyte interfaces provide the «seat of emf» for the voltaic cell. That is, these reactions drive the current and are not an endless source of energy as the earlier obsolete theory thought.[16] In the open-circuit case, charge separation continues until the electrical field from the separated charges is sufficient to arrest the reactions. Years earlier, Alessandro Volta, who had measured a contact potential difference at the metal–metal (electrode–electrode) interface of his cells, held the incorrect opinion that contact alone (without taking into account a chemical reaction) was the origin of the emf.
Notation and units of measurement[edit]
Electromotive force is often denoted by 
In a device without internal resistance, if an electric charge 


Electromotive force in electrostatic units is the statvolt (in the centimeter gram second system of units equal in amount to an erg per electrostatic unit of charge).
Formal definitions[edit]
Inside a source of emf (such as a battery) that is open-circuited, a charge separation occurs between the negative terminal N and the positive terminal P.
This leads to an electrostatic field 
This led Max Abraham[18] to introduce the concept of a nonelectrostatic field 
In the open-circuit case, 


In the open-circuit case, the conservative electrostatic field created by separation of charge exactly cancels the forces producing the emf.[19]
Mathematically:
where 



This emf is the work done on a unit charge by the source’s nonelectrostatic field 
When the source is connected to a load, its emf is just
and no longer has a simple relation to the electric field 
In the case of a closed path in the presence of a varying magnetic field, the integral of the electric field around the (stationary) closed loop 
Then, the «induced emf» (often called the «induced voltage») in the loop is:[21]
where 



The electrostatic field does not contribute to the net emf around a circuit because the electrostatic portion of the electric field is conservative (i.e., the work done against the field around a closed path is zero, see Kirchhoff’s voltage law, which is valid, as long as the circuit elements remain at rest and radiation is ignored[22]).
That is, the «induced emf» (like the emf of a battery connected to a load) is not a «voltage» in the sense of a difference in the electric scalar potential.
If the loop 



If in addition, the loop includes a coil that extends from point 1 to 2, such that the magnetic flux is largely localized to that region, it is customary to speak of that region as an inductor, and to consider that its emf is localized to that region.
Then, we can consider a different loop 
The magnetic flux, and emf, in loop 

For a good conductor, 
where 
Thus, we can associate an effective «voltage drop» 
where now the induced emf is not considered to be a source emf.[23]
This definition can be extended to arbitrary sources of emf and paths 



which is a conceptual equation mainly, because the determination of the «effective forces» is difficult.
The term
is often called a «motional emf».
In (electrochemical) thermodynamics[edit]
When multiplied by an amount of charge 


where 




The combination 


If a mole of ions goes into solution (for example, in a Daniell cell, as discussed below) the charge through the external circuit is:
where 

where 
which is used in the derivation of the Nernst equation.
Distinction with potential difference[edit]
Although an electrical potential difference (voltage) is sometimes called an emf,[26][27][28][29][30] however they are formally distinct concepts:
- Emf is the cause of a potential difference. Potential difference in turn is a cause of current flow.
- Potential difference itself is not the cause of an emf.
- Consider Kirchhoff’s voltage law, which says the sum of potential differences going through any loop in a circuit is zero. For a circuit of a voltage source and a resistor, the sum of the source’s applied voltage plus the ohmic voltage drop through the resistor is zero. But the resistor provides no emf, only the voltage source does:
- For a circuit using a battery source, the emf is due solely to the chemistry in the battery that causes charge separation, which generates a potential difference.
- For a circuit using an electric generator, the emf is due solely to a time-varying magnetic field within the generator that causes charge separation, which generates a potential difference.
- Consider Kirchhoff’s voltage law, which says the sum of potential differences going through any loop in a circuit is zero. For a circuit of a voltage source and a resistor, the sum of the source’s applied voltage plus the ohmic voltage drop through the resistor is zero. But the resistor provides no emf, only the voltage source does:
- Both a 1 volt emf and a 1 volt potential difference correspond to 1 joule per coulomb of charge. However:
- a 1 volt emf means that the source supplies an energy of 1 joule to each coulomb of charge passing through.
- a 1 volt potential difference between two points on a circuit means that each coulomb of charge will need to either:
- gain 1 joule of energy to move up that potential difference,
- or give up 1 joule of energy to move down that potential difference.[31]
In the case of an open circuit, the electric charge that has been separated by the mechanism generating the emf creates an electric field opposing the separation mechanism. For example, the chemical reaction in a voltaic cell stops when the opposing electric field at each electrode is strong enough to arrest the reactions. A larger opposing field can reverse the reactions in what are called reversible cells.[32][33]
The electric charge that has been separated creates an electric potential difference that can (in many cases) be measured with a voltmeter between the terminals of the device, when not connected to a load. The magnitude of the emf for the battery (or other source) is the value of this open-circuit voltage.
When the battery is charging or discharging, the emf itself cannot be measured directly using the external voltage because some voltage is lost inside the source.[27]
It can, however, be inferred from a measurement of the current 



«Potential difference» is not the same as «induced emf» (often called «induced voltage»).
The potential difference (difference in the electric scalar potential) between two points A and B is independent of the path we take from A to B.
If a voltmeter always measured the potential difference between A and B, then the position of the voltmeter would make no difference.
However, it is quite possible for the measurement by a voltmeter between points A and B to depend on the position of the voltmeter, if a time-dependent magnetic field is present.
For example, consider an infinitely long solenoid using an AC current to generate a varying flux in the interior of the solenoid.
Outside the solenoid we have two resistors connected in a ring around the solenoid.
The resistor on the left is 100 Ω and the one on the right is 200 Ω, they are connected at the top and bottom at points A and B.
The induced voltage, by Faraday’s law is 





[35]
Generation[edit]
Chemical sources[edit]
A typical reaction path requires the initial reactants to cross an energy barrier, enter an intermediate state and finally emerge in a lower energy configuration. If charge separation is involved, this energy difference can result in an emf. See Bergmann et al.[36] and Transition state.
The question of how batteries (galvanic cells) generate an emf occupied scientists for most of the 19th century. The «seat of the electromotive force» was eventually determined in 1889 by Walther Nernst[37] to be primarily at the interfaces between the electrodes and the electrolyte.[16]
Atoms in molecules or solids are held together by chemical bonding, which stabilizes the molecule or solid (i.e. reduces its energy). When molecules or solids of relatively high energy are brought together, a spontaneous chemical reaction can occur that rearranges the bonding and reduces the (free) energy of the system.[38] In batteries, coupled half-reactions, often involving metals and their ions, occur in tandem, with a gain of electrons (termed «reduction») by one conductive electrode and loss of electrons (termed «oxidation») by another (reduction-oxidation or redox reactions). The spontaneous overall reaction can only occur if electrons move through an external wire between the electrodes. The electrical energy given off is the free energy lost by the chemical reaction system.
As an example, a Daniell cell consists of a zinc anode (an electron collector) that is oxidized as it dissolves into a zinc sulfate solution. The dissolving zinc leaving behind its electrons in the electrode according to the oxidation reaction (s = solid electrode; aq = aqueous solution):
The zinc sulfate is the electrolyte in that half cell. It is a solution which contains zinc cations 

In the other half cell, the copper cations in a copper sulfate electrolyte move to the copper cathode to which they attach themselves as they adopt electrons from the copper electrode by the reduction reaction:
which leaves a deficit of electrons on the copper cathode. The difference of excess electrons on the anode and deficit of electrons on the cathode creates an electrical potential between the two electrodes. (A detailed discussion of the microscopic process of electron transfer between an electrode and the ions in an electrolyte may be found in Conway.)[39] The electrical energy released by this reaction (213 kJ per 65.4 g of zinc) can be attributed mostly due to the 207 kJ weaker bonding (smaller magnitude of the cohesive energy) of zinc, which has filled 3d- and 4s-orbitals, compared to copper, which has an unfilled orbital available for bonding.
If the cathode and anode are connected by an external conductor, electrons pass through that external circuit (light bulb in figure), while ions pass through the salt bridge to maintain charge balance until the anode and cathode reach electrical equilibrium of zero volts as chemical equilibrium is reached in the cell. In the process the zinc anode is dissolved while the copper electrode is plated with copper.[40] The salt bridge has to close the electrical circuit while preventing the copper ions from moving to the zinc electrode and being reduced there without generating an external current. It is not made of salt but of material able to wick cations and anions (a dissociated salt) into the solutions. The flow of positively charged cations along the bridge is equivalent to the same number of negative charges flowing in the opposite direction.
If the light bulb is removed (open circuit) the emf between the electrodes is opposed by the electric field due to the charge separation, and the reactions stop.
For this particular cell chemistry, at 298 K (room temperature), the emf 

Voltaic cells[edit]
Volta developed the voltaic cell about 1792, and presented his work March 20, 1800.[41] Volta correctly identified the role of dissimilar electrodes in producing the voltage, but incorrectly dismissed any role for the electrolyte.[42] Volta ordered the metals in a ‘tension series’, «that is to say in an order such that any one in the list becomes positive when in contact with any one that succeeds, but negative by contact with any one that precedes it.»[43] A typical symbolic convention in a schematic of this circuit ( –||– ) would have a long electrode 1 and a short electrode 2, to indicate that electrode 1 dominates. Volta’s law about opposing electrode emfs implies that, given ten electrodes (for example, zinc and nine other materials), 45 unique combinations of voltaic cells (10 × 9/2) can be created.
Typical values[edit]
The electromotive force produced by primary (single-use) and secondary (rechargeable) cells is usually of the order of a few volts. The figures quoted below are nominal, because emf varies according to the size of the load and the state of exhaustion of the cell.
| EMF | Cell chemistry | Common name | ||
|---|---|---|---|---|
| Anode | Solvent, electrolyte | Cathode | ||
| 1.2 V | Cadmium | Water, potassium hydroxide | NiO(OH) | nickel-cadmium |
| 1.2 V | Mischmetal (hydrogen absorbing) | Water, potassium hydroxide | Nickel | nickel–metal hydride |
| 1.5 V | Zinc | Water, ammonium or zinc chloride | Carbon, manganese dioxide | Zinc carbon |
| 2.1 V | Lead | Water, sulfuric acid | Lead dioxide | Lead–acid |
| 3.6 V to 3.7 V | Graphite | Organic solvent, Li salts | LiCoO2 | Lithium-ion |
| 1.35 V | Zinc | Water, sodium or potassium hydroxide | HgO | Mercury cell |
Other chemical sources[edit]
Other chemical sources include fuel cells.
Electromagnetic induction[edit]
Electromagnetic induction is the production of a circulating electric field by a time-dependent magnetic field. A time-dependent magnetic field can be produced either by motion of a magnet relative to a circuit, by motion of a circuit relative to another circuit (at least one of these must be carrying an electric current), or by changing the electric current in a fixed circuit. The effect on the circuit itself, of changing the electric current, is known as self-induction; the effect on another circuit is known as mutual induction.
For a given circuit, the electromagnetically induced emf is determined purely by the rate of change of the magnetic flux through the circuit according to Faraday’s law of induction.
An emf is induced in a coil or conductor whenever there is change in the flux linkages. Depending on the way in which the changes are brought about, there are two types: When the conductor is moved in a stationary magnetic field to procure a change in the flux linkage, the emf is statically induced. The electromotive force generated by motion is often referred to as motional emf. When the change in flux linkage arises from a change in the magnetic field around the stationary conductor, the emf is dynamically induced. The electromotive force generated by a time-varying magnetic field is often referred to as transformer emf.
Contact potentials[edit]
When solids of two different materials are in contact, thermodynamic equilibrium requires that one of the solids assume a higher electrical potential than the other. This is called the contact potential.[44] Dissimilar metals in contact produce what is known also as a contact electromotive force or Galvani potential. The magnitude of this potential difference is often expressed as a difference in Fermi levels in the two solids when they are at charge neutrality, where the Fermi level (a name for the chemical potential of an electron system[45][46]) describes the energy necessary to remove an electron from the body to some common point (such as ground).[47] If there is an energy advantage in taking an electron from one body to the other, such a transfer will occur. The transfer causes a charge separation, with one body gaining electrons and the other losing electrons. This charge transfer causes a potential difference between the bodies, which partly cancels the potential originating from the contact, and eventually equilibrium is reached. At thermodynamic equilibrium, the Fermi levels are equal (the electron removal energy is identical) and there is now a built-in electrostatic potential between the bodies.
The original difference in Fermi levels, before contact, is referred to as the emf.[48]
The contact potential cannot drive steady current through a load attached to its terminals because that current would involve a charge transfer. No mechanism exists to continue such transfer and, hence, maintain a current, once equilibrium is attained.
One might inquire why the contact potential does not appear in Kirchhoff’s law of voltages as one contribution to the sum of potential drops. The customary answer is that any circuit involves not only a particular diode or junction, but also all the contact potentials due to wiring and so forth around the entire circuit. The sum of all the contact potentials is zero, and so they may be ignored in Kirchhoff’s law.[49][50]
Solar cell[edit]
Operation of a solar cell can be understood from its equivalent circuit. Photons with energy greater than the bandgap of the semiconductor create mobile electron–hole pairs. Charge separation occurs because of a pre-existing electric field associated with the p-n junction. This electric field is created from a built-in potential, which arises from the contact potential between the two different materials in the junction. The charge separation between positive holes and negative electrons across the p–n diode yields a forward voltage, the photo voltage, between the illuminated diode terminals,[51] which drives current through any attached load. Photo voltage is sometimes referred to as the photo emf, distinguishing between the effect and the cause.
Solar cell current–voltage relationship[edit]
Two internal current losses 





When the output is short-circuited, the output voltage is zeroed, and so the voltage across the diode is smallest. Thus, short-circuiting results in the smallest 

The current delivered by the illuminated diode to the external circuit can be simplified (based on certain assumptions) to:


Solar cell photo emf[edit]
Solar cell output voltage for two light-induced currents IL expressed as a ratio to the reverse saturation current I0[53] and using a fixed ideality factor m of 2.[54] Their emf is the voltage at their y-axis intercept.
Solving the illuminated diode’s above simplified current–voltage relationship for output voltage yields:
which is plotted against 
The solar cell’s photo emf 


It has a logarithmic dependence on the light-induced current 
When driving a resistive load, the output voltage can be determined using Ohm’s law and will lie between the short-circuit value of zero volts and the open-circuit voltage 

Other sources that generate emf[edit]
- A transformer coupling two circuits may be considered a source of emf for one of the circuits, just as if it were caused by an electrical generator; this is the origin of the term «transformer emf».
- For converting sound waves into voltage signals:
- a microphone generates an emf from a moving diaphragm.
- a magnetic pickup generates an emf from a varying magnetic field produced by an instrument.
- a piezoelectric sensor generates an emf from strain on a piezoelectric crystal.
- Devices that use temperature to produce emfs include thermocouples and thermopiles.[59]
- Any electrical transducer which converts a physical energy into electrical energy.
See also[edit]
- Counter-electromotive force
- Electric battery
- Electrochemical cell
- Electrolytic cell
- Galvanic cell
- Voltaic pile
References[edit]
- ^ «EMF». American Heritage Dictionary of the English Language, 3rd ed. Houghton Mifflin. 1992.
- ^ «EMF». Oxford English Dictionary.
- ^ a b Tipler, Paul A. (January 1976). Physics. New York, NY: Worth Publishers, Inc. p. 803. ISBN 978-0-87901-041-6.
- ^ Stewart, Joseph V. (2001). Intermediate electromagnetic theory. Singapore River Edge, NJ: World Scientific. p. 389. ISBN 978-981-02-4470-5. OCLC 47127179.
- ^ Matthews, Michael R. (2014-07-03). International Handbook of Research in History, Philosophy and Science Teaching. Springer. p. 142. ISBN 978-94-007-7654-8.
[Volta] stated that a new type of «force» was acting upon the charges, separating them and keeping them separated, and he called this action the electromotive force, the name that is still applied.
- ^ «IEC 60050 — International Electrotechnical Vocabulary — Details for IEV number 131-12-22: «source voltage»«. www.electropedia.org. Retrieved 2022-12-19.
- ^ «IEC 80000-6:2022». International Organization for Standardization. Retrieved 2022-12-19.
- ^ Langmuir, Irving (1916). «The Relation Between Contact Potentials and Electrochemical Action». Transactions of the American Electrochemical Society. The Society. 29: 175.
- ^ Cook, David M. (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 157. ISBN 978-0-486-42567-2.
- ^ Lerner, Lawrence M. (1997). Physics for scientists and engineers. Jones & Bartlett Publishers. pp. 724–727. ISBN 978-0-7637-0460-5.
- ^ Tipler, Paul A.; Mosca, Gene (2007). Physics for Scientists and Engineers (6 ed.). Macmillan. p. 850. ISBN 978-1-4292-0124-7.
- ^ Halpern, Alvin M.; Erlbach, Erich (1998). Schaum’s outline of theory and problems of beginning physics II. McGraw-Hill Professional. p. 138. ISBN 978-0-07-025707-8.
- ^ Lehrman, Robert L. (1998). Physics the easy way. Barron’s Educational Series. p. 274. ISBN 978-0-7641-0236-3.
emf separated charge reaction potential.
- ^ Singh, Kongbam Chandramani (2009). «§3.16 EMF of a source». Basic Physics. Prentice Hall India. p. 152. ISBN 978-81-203-3708-4.
- ^
Volta, Alessandro (1801). «De l’électricité dite galvanique». Annales de Chimie. Chez Fuchs, Paris. - ^ a b Cajori, Florian (1899). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. The Macmillan Company. pp. 218–219.
seat of electromotive force.
- ^
Valkenburgh, Van (1995). Basic Electricity. Cengage Learning. pp. 1–46. ISBN 978-0-7906-1041-2. - ^
Abraham, M.; Becker, R. (1932). The Classical Theory of Electricity and Magnetism. Blackie & Son. p. 116-122. - ^
Griffiths, David J (1999). Introduction to Electrodynamics (3rd ed.). Pearson/Addison-Wesley. p. 293. ISBN 978-0-13-805326-0. - ^
Only the electric field that results from charge separation caused by the emf is counted. While a solar cell has an electric field that results from a contact potential (see contact potentials and solar cells), this electric field component is not included in the integral. Only the electric field that results from charge separation caused by photon energy is included. - ^ Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (1986). Beyond the mechanical universe: from electricity to modern physics. Cambridge University Press. p. 245. ISBN 978-0-521-30430-6.
- ^
McDonald, Kirk T. (2012). «Voltage Drop, Potential Difference and EMF» (PDF). Physics Examples. Princeton University. - ^ Feynman, R.P.; Leighton, R.B.; Sands, M. (1964). The Feynman Lectures on Physics, Vol. II, chap. 22. Addison Wesley.
- ^ Cook, David M. (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 158. ISBN 978-0-486-42567-2.
- ^ a b c Finn, Colin B P (1992). Thermal Physics. CRC Press. p. 163. ISBN 978-0-7487-4379-7.
- ^
Fogiel, M. (2002). Basic Electricity. Research & Education Association. p. 76. ISBN 978-0-87891-420-3. - ^ a b
Halliday, David; Resnick, Robert; Walker, Jearl (2008). Fundamentals of Physics (6th ed.). Wiley. p. 638. ISBN 978-0-471-75801-3. - ^
Freeman, Roger L (2005). Fundamentals of Telecommunications (2nd ed.). Wiley. p. 576. ISBN 978-0-471-71045-5. - ^
Croft, Terrell (1917). Practical Electricity. McGraw-Hill. p. 533. - ^
Loeb, Leonard B. (2007). Fundamentals of Electricity and Magnetism (Reprint of Wiley 1947 3rd ed.). Read Books. p. 86. ISBN 978-1-4067-0733-5. - ^ «Difference Between Voltage and EMF?». Electrical Technology. 2019-10-06. Archived from the original on 2022-04-08. Retrieved 2022-09-28.
- ^
Warn, J. R. W.; Peters, A. P. H. (1996). Concise Chemical Thermodynamics (2 ed.). CRC Press. p. 123. ISBN 978-0-7487-4445-9. - ^
Glasstone, Samuel (2007). Thermodynamics for Chemists (Reprint of D. Van Nostrand Co (1964) ed.). Read Books. p. 301. ISBN 978-1-4067-7322-4. - ^ Shadowitz, Albert (1975). The Electromagnetic Field (1st ed.). McGraw-Hill Book Company. pp. 396–398. ISBN 0-07-056368-3.
- ^
McDonald, Kirk T. (2010). «Lewin’s Circuit Paradox» (PDF). Physics Examples. Princeton University. - ^ Risch, Nikolaus (2002). «Molecules — bonds and reactions». In L Bergmann; et al. (eds.). Constituents of Matter: Atoms, Molecules, Nuclei, and Particles. CRC Press. ISBN 978-0-8493-1202-1.
- ^ Nernst, Walter (1889). «Die elektromotorische Wirksamkeit der Ionen». Z. Phys. Chem. 4: 129.
- ^
The brave reader can find an extensive discussion for organic electrochemistry in Amatore, Christian (2000). «Basic concepts». In Henning Lund; Ole Hammerich (eds.). Organic electrochemistry (4 ed.). CRC Press. ISBN 978-0-8247-0430-8. - ^
Conway, BE (1999). «Energy factors in relation to electrode potential». Electrochemical supercapacitors. Springer. p. 37. ISBN 978-0-306-45736-4. - ^ Tilley, R. J. D. (2004). Understanding Solids. Wiley. p. 267. ISBN 978-0-470-85275-0.
- ^ Mottelay, Paul Fleury (2008). Bibliographical History of Electricity and Magnetism (Reprint of 1892 ed.). Read Books. p. 247. ISBN 978-1-4437-2844-7.
- ^ Kragh, Helge (2000). «Confusion and Controversy: Nineteenth-century theories of the voltaic pile» (PDF). Nuova Voltiana:Studies on Volta and His Times. Università degli studi di Pavia. Archived from the original (PDF) on 2009-03-20.
- ^ Cumming, Linnaus (2008). An Introduction to the Theory of Electricity (Reprint of 1885 ed.). BiblioBazaar. p. 118. ISBN 978-0-559-20742-6.
- ^ Trigg, George L. (1995). Landmark experiments in twentieth century physics (Reprint of Crane, Russak & Co 1975 ed.). Courier Dover. p. 138 ff. ISBN 978-0-486-28526-9.
- ^ Rockett, Angus (2007). «Diffusion and drift of carriers». Materials science of semiconductors. New York, NY: Springer Science. p. 74 ff. ISBN 978-0-387-25653-5.
- ^ Kittel, Charles (2004). «Chemical potential in external fields». Elementary Statistical Physics (Reprint of Wiley 1958 ed.). Courier Dover. p. 67. ISBN 978-0-486-43514-5.
- ^ Hanson, George W. (2007). Fundamentals of Nanoelectronics. Prentice Hall. p. 100. ISBN 978-0-13-195708-4.
- ^ Sato, Norio (1998). «Semiconductor photoelectrodes». Electrochemistry at metal and semiconductor electrodes (2nd ed.). Elsevier. p. 110 ff. ISBN 978-0-444-82806-4.
- ^ Quimby, Richard S. (2006). Photonics and lasers. Wiley. p. 176. ISBN 978-0-471-71974-8.
- ^ Neamen, Donald A. (2002). Semiconductor physics and devices (3rd ed.). McGraw-Hill Professional. p. 240. ISBN 978-0-07-232107-4.
- ^ Dhir, S. M. (2000) [1999]. «§3.1 Solar cells». Electronic Components and Materials: Principles, Manufacture & Maintenance (2007 fifth reprint ed.). India: Tata McGraw-Hill Publishing Company Limited. p. 283. ISBN 0-07-463082-2.
- ^ a b Araújo, Gerardo L. (1994). «§2.5.1 Short-circuit current and open-circuit voltage». In Eduardo Lorenzo (ed.). Solar Electricity: Engineering of photovoltaic systems. Progenza for Universidad Politechnica Madrid. p. 74. ISBN 978-84-86505-55-4.
- ^ Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 8. ISBN 978-1-86094-349-2.
- ^ In practice, at low voltages m → 2, whereas at high voltages m → 1. See Araújo, op. cit. ISBN 84-86505-55-0. page 72
- ^ Northrop, Robert B. (2005). «§6.3.2 Photovoltaic Cells». Introduction to Instrumentation and Measurements. CRC Press. p. 176. ISBN 978-0-8493-7898-0.
- ^ «Open-Circuit Voltage».
- ^ Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 6. ISBN 978-1-86094-349-2.
- ^
Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 7. ISBN 978-1-86094-349-2. - ^ John S. Rigden, ed. (1996). Macmillan encyclopedia of physics. New York: Macmillan.
Further reading[edit]
- George F. Barker, «On the measurement of electromotive force». Proceedings of the American Philosophical Society Held at Philadelphia for Promoting Useful Knowledge, American Philosophical Society. January 19, 1883.
- Andrew Gray, «Absolute Measurements in Electricity and Magnetism», Electromotive force. Macmillan and co., 1884.
- Charles Albert Perkins, «Outlines of Electricity and Magnetism», Measurement of Electromotive Force. Henry Holt and co., 1896.
- John Livingston Rutgers Morgan, «The Elements of Physical Chemistry», Electromotive force. J. Wiley, 1899.
- «Abhandlungen zur Thermodynamik, von H. Helmholtz. Hrsg. von Max Planck». (Tr. «Papers to thermodynamics, on H. Helmholtz. Hrsg. by Max Planck».) Leipzig, W. Engelmann, Of Ostwald classical author of the accurate sciences series. New consequence. No. 124, 1902.
- Theodore William Richards and Gustavus Edward Behr, jr., «The electromotive force of iron under varying conditions, and the effect of occluded hydrogen». Carnegie Institution of Washington publication series, 1906. LCCN 07-3935
- Henry S. Carhart, «Thermo-electromotive force in electric cells, the thermo-electromotive force between a metal and a solution of one of its salts». New York, D. Van Nostrand company, 1920. LCCN 20-20413
- Hazel Rossotti, «Chemical applications of potentiometry». London, Princeton, N.J., Van Nostrand, 1969. ISBN 0-442-07048-9 LCCN 69-11985
- Nabendu S. Choudhury, 1973. «Electromotive force measurements on cells involving beta-alumina solid electrolyte». NASA technical note, D-7322.
- John O’M. Bockris; Amulya K. N. Reddy (1973). «Electrodics». Modern Electrochemistry: An Introduction to an Interdisciplinary Area (2 ed.). Springer. ISBN 978-0-306-25002-6.
- Roberts, Dana (1983). «How batteries work: A gravitational analog». Am. J. Phys. 51 (9): 829. Bibcode:1983AmJPh..51..829R. doi:10.1119/1.13128.
- G. W. Burns, et al., «Temperature-electromotive force reference functions and tables for the letter-designated thermocouple types based on the ITS-90». Gaithersburg, MD : U.S. Dept. of Commerce, National Institute of Standards and Technology, Washington, Supt. of Docs., U.S. G.P.O., 1993.
- Norio Sato (1998). «Semiconductor photoelectrodes». Electrochemistry at metal and semiconductor electrodes (2nd ed.). Elsevier. p. 326 ff. ISBN 978-0-444-82806-4.
- Hai, Pham Nam; Ohya, Shinobu; Tanaka, Masaaki; Barnes, Stewart E.; Maekawa, Sadamichi (2009-03-08). «Electromotive force and huge magnetoresistance in magnetic tunnel junctions». Nature. 458 (7237): 489–92. Bibcode:2009Natur.458..489H. doi:10.1038/nature07879. PMID 19270681. S2CID 4320209.
In electromagnetism and electronics, electromotive force (also electromotance, abbreviated emf,[1][2] denoted 


An electronic–hydraulic analogy may view emf as the mechanical work done to water by a pump, which results in a pressure difference (analogous to voltage).[8]
In electromagnetic induction, emf can be defined around a closed loop of a conductor as the electromagnetic work that would be done on an elementary electric charge (such as an electron) if it travels once around the loop.[9]
For two-terminal devices modeled as a Thévenin equivalent circuit, an equivalent emf can be measured as the open-circuit voltage between the two terminals. This emf can drive an electric current if an external circuit is attached to the terminals, in which case the device becomes the voltage source of that circuit.
Although an emf gives rise to a voltage and can be measured as a voltage and may sometimes informally be called a «voltage», they are not the same phenomenon (see § Distinction with potential difference).
Overview[edit]
Devices that can provide emf include electrochemical cells, thermoelectric devices, solar cells, photodiodes, electrical generators, inductors, transformers and even Van de Graaff generators.[10][11] In nature, emf is generated when magnetic field fluctuations occur through a surface. For example, the shifting of the Earth’s magnetic field during a geomagnetic storm induces currents in an electrical grid as the lines of the magnetic field are shifted about and cut across the conductors.
In a battery, the charge separation that gives rise to a potential difference (voltage) between the terminals is accomplished by chemical reactions at the electrodes that convert chemical potential energy into electromagnetic potential energy.[12][13] A voltaic cell can be thought of as having a «charge pump» of atomic dimensions at each electrode, that is:
A (chemical) source of emf can be thought of as a kind of charge pump that acts to move positive charges from a point of low potential through its interior to a point of high potential. … By chemical, mechanical or other means, the source of emf performs work
on that charge to move it to the high-potential terminal. The emf
of the source is defined as the work
done per charge
.
.[14]
In an electrical generator, a time-varying magnetic field inside the generator creates an electric field via electromagnetic induction, which creates a potential difference between the generator terminals. Charge separation takes place within the generator because electrons flow away from one terminal toward the other, until, in the open-circuit case, an electric field is developed that makes further charge separation impossible. The emf is countered by the electrical voltage due to charge separation. If a load is attached, this voltage can drive a current. The general principle governing the emf in such electrical machines is Faraday’s law of induction.
History[edit]
In 1801, Alessandro Volta introduced the term «force motrice électrique» to describe the active agent of a battery (which he had invented around 1798).[15]
This is called the «electromotive force» in English.
Around 1830, Michael Faraday established that chemical reactions at each of two electrode–electrolyte interfaces provide the «seat of emf» for the voltaic cell. That is, these reactions drive the current and are not an endless source of energy as the earlier obsolete theory thought.[16] In the open-circuit case, charge separation continues until the electrical field from the separated charges is sufficient to arrest the reactions. Years earlier, Alessandro Volta, who had measured a contact potential difference at the metal–metal (electrode–electrode) interface of his cells, held the incorrect opinion that contact alone (without taking into account a chemical reaction) was the origin of the emf.
Notation and units of measurement[edit]
Electromotive force is often denoted by 
In a device without internal resistance, if an electric charge 


Electromotive force in electrostatic units is the statvolt (in the centimeter gram second system of units equal in amount to an erg per electrostatic unit of charge).
Formal definitions[edit]
Inside a source of emf (such as a battery) that is open-circuited, a charge separation occurs between the negative terminal N and the positive terminal P.
This leads to an electrostatic field 
This led Max Abraham[18] to introduce the concept of a nonelectrostatic field 
In the open-circuit case, 


In the open-circuit case, the conservative electrostatic field created by separation of charge exactly cancels the forces producing the emf.[19]
Mathematically:
where 



This emf is the work done on a unit charge by the source’s nonelectrostatic field 
When the source is connected to a load, its emf is just
and no longer has a simple relation to the electric field 
In the case of a closed path in the presence of a varying magnetic field, the integral of the electric field around the (stationary) closed loop 
Then, the «induced emf» (often called the «induced voltage») in the loop is:[21]
where 



The electrostatic field does not contribute to the net emf around a circuit because the electrostatic portion of the electric field is conservative (i.e., the work done against the field around a closed path is zero, see Kirchhoff’s voltage law, which is valid, as long as the circuit elements remain at rest and radiation is ignored[22]).
That is, the «induced emf» (like the emf of a battery connected to a load) is not a «voltage» in the sense of a difference in the electric scalar potential.
If the loop 



If in addition, the loop includes a coil that extends from point 1 to 2, such that the magnetic flux is largely localized to that region, it is customary to speak of that region as an inductor, and to consider that its emf is localized to that region.
Then, we can consider a different loop 
The magnetic flux, and emf, in loop 

For a good conductor, 
where 
Thus, we can associate an effective «voltage drop» 
where now the induced emf is not considered to be a source emf.[23]
This definition can be extended to arbitrary sources of emf and paths 



which is a conceptual equation mainly, because the determination of the «effective forces» is difficult.
The term
is often called a «motional emf».
In (electrochemical) thermodynamics[edit]
When multiplied by an amount of charge 


where 




The combination 


If a mole of ions goes into solution (for example, in a Daniell cell, as discussed below) the charge through the external circuit is:
where 

where 
which is used in the derivation of the Nernst equation.
Distinction with potential difference[edit]
Although an electrical potential difference (voltage) is sometimes called an emf,[26][27][28][29][30] however they are formally distinct concepts:
- Emf is the cause of a potential difference. Potential difference in turn is a cause of current flow.
- Potential difference itself is not the cause of an emf.
- Consider Kirchhoff’s voltage law, which says the sum of potential differences going through any loop in a circuit is zero. For a circuit of a voltage source and a resistor, the sum of the source’s applied voltage plus the ohmic voltage drop through the resistor is zero. But the resistor provides no emf, only the voltage source does:
- For a circuit using a battery source, the emf is due solely to the chemistry in the battery that causes charge separation, which generates a potential difference.
- For a circuit using an electric generator, the emf is due solely to a time-varying magnetic field within the generator that causes charge separation, which generates a potential difference.
- Consider Kirchhoff’s voltage law, which says the sum of potential differences going through any loop in a circuit is zero. For a circuit of a voltage source and a resistor, the sum of the source’s applied voltage plus the ohmic voltage drop through the resistor is zero. But the resistor provides no emf, only the voltage source does:
- Both a 1 volt emf and a 1 volt potential difference correspond to 1 joule per coulomb of charge. However:
- a 1 volt emf means that the source supplies an energy of 1 joule to each coulomb of charge passing through.
- a 1 volt potential difference between two points on a circuit means that each coulomb of charge will need to either:
- gain 1 joule of energy to move up that potential difference,
- or give up 1 joule of energy to move down that potential difference.[31]
In the case of an open circuit, the electric charge that has been separated by the mechanism generating the emf creates an electric field opposing the separation mechanism. For example, the chemical reaction in a voltaic cell stops when the opposing electric field at each electrode is strong enough to arrest the reactions. A larger opposing field can reverse the reactions in what are called reversible cells.[32][33]
The electric charge that has been separated creates an electric potential difference that can (in many cases) be measured with a voltmeter between the terminals of the device, when not connected to a load. The magnitude of the emf for the battery (or other source) is the value of this open-circuit voltage.
When the battery is charging or discharging, the emf itself cannot be measured directly using the external voltage because some voltage is lost inside the source.[27]
It can, however, be inferred from a measurement of the current 



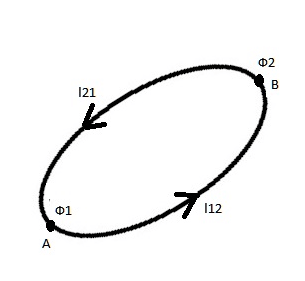
«Potential difference» is not the same as «induced emf» (often called «induced voltage»).
The potential difference (difference in the electric scalar potential) between two points A and B is independent of the path we take from A to B.
If a voltmeter always measured the potential difference between A and B, then the position of the voltmeter would make no difference.
However, it is quite possible for the measurement by a voltmeter between points A and B to depend on the position of the voltmeter, if a time-dependent magnetic field is present.
For example, consider an infinitely long solenoid using an AC current to generate a varying flux in the interior of the solenoid.
Outside the solenoid we have two resistors connected in a ring around the solenoid.
The resistor on the left is 100 Ω and the one on the right is 200 Ω, they are connected at the top and bottom at points A and B.
The induced voltage, by Faraday’s law is 





[35]
Generation[edit]
Chemical sources[edit]
A typical reaction path requires the initial reactants to cross an energy barrier, enter an intermediate state and finally emerge in a lower energy configuration. If charge separation is involved, this energy difference can result in an emf. See Bergmann et al.[36] and Transition state.
The question of how batteries (galvanic cells) generate an emf occupied scientists for most of the 19th century. The «seat of the electromotive force» was eventually determined in 1889 by Walther Nernst[37] to be primarily at the interfaces between the electrodes and the electrolyte.[16]
Atoms in molecules or solids are held together by chemical bonding, which stabilizes the molecule or solid (i.e. reduces its energy). When molecules or solids of relatively high energy are brought together, a spontaneous chemical reaction can occur that rearranges the bonding and reduces the (free) energy of the system.[38] In batteries, coupled half-reactions, often involving metals and their ions, occur in tandem, with a gain of electrons (termed «reduction») by one conductive electrode and loss of electrons (termed «oxidation») by another (reduction-oxidation or redox reactions). The spontaneous overall reaction can only occur if electrons move through an external wire between the electrodes. The electrical energy given off is the free energy lost by the chemical reaction system.
As an example, a Daniell cell consists of a zinc anode (an electron collector) that is oxidized as it dissolves into a zinc sulfate solution. The dissolving zinc leaving behind its electrons in the electrode according to the oxidation reaction (s = solid electrode; aq = aqueous solution):
The zinc sulfate is the electrolyte in that half cell. It is a solution which contains zinc cations 

In the other half cell, the copper cations in a copper sulfate electrolyte move to the copper cathode to which they attach themselves as they adopt electrons from the copper electrode by the reduction reaction:
which leaves a deficit of electrons on the copper cathode. The difference of excess electrons on the anode and deficit of electrons on the cathode creates an electrical potential between the two electrodes. (A detailed discussion of the microscopic process of electron transfer between an electrode and the ions in an electrolyte may be found in Conway.)[39] The electrical energy released by this reaction (213 kJ per 65.4 g of zinc) can be attributed mostly due to the 207 kJ weaker bonding (smaller magnitude of the cohesive energy) of zinc, which has filled 3d- and 4s-orbitals, compared to copper, which has an unfilled orbital available for bonding.
If the cathode and anode are connected by an external conductor, electrons pass through that external circuit (light bulb in figure), while ions pass through the salt bridge to maintain charge balance until the anode and cathode reach electrical equilibrium of zero volts as chemical equilibrium is reached in the cell. In the process the zinc anode is dissolved while the copper electrode is plated with copper.[40] The salt bridge has to close the electrical circuit while preventing the copper ions from moving to the zinc electrode and being reduced there without generating an external current. It is not made of salt but of material able to wick cations and anions (a dissociated salt) into the solutions. The flow of positively charged cations along the bridge is equivalent to the same number of negative charges flowing in the opposite direction.
If the light bulb is removed (open circuit) the emf between the electrodes is opposed by the electric field due to the charge separation, and the reactions stop.
For this particular cell chemistry, at 298 K (room temperature), the emf 

Voltaic cells[edit]
Volta developed the voltaic cell about 1792, and presented his work March 20, 1800.[41] Volta correctly identified the role of dissimilar electrodes in producing the voltage, but incorrectly dismissed any role for the electrolyte.[42] Volta ordered the metals in a ‘tension series’, «that is to say in an order such that any one in the list becomes positive when in contact with any one that succeeds, but negative by contact with any one that precedes it.»[43] A typical symbolic convention in a schematic of this circuit ( –||– ) would have a long electrode 1 and a short electrode 2, to indicate that electrode 1 dominates. Volta’s law about opposing electrode emfs implies that, given ten electrodes (for example, zinc and nine other materials), 45 unique combinations of voltaic cells (10 × 9/2) can be created.
Typical values[edit]
The electromotive force produced by primary (single-use) and secondary (rechargeable) cells is usually of the order of a few volts. The figures quoted below are nominal, because emf varies according to the size of the load and the state of exhaustion of the cell.
| EMF | Cell chemistry | Common name | ||
|---|---|---|---|---|
| Anode | Solvent, electrolyte | Cathode | ||
| 1.2 V | Cadmium | Water, potassium hydroxide | NiO(OH) | nickel-cadmium |
| 1.2 V | Mischmetal (hydrogen absorbing) | Water, potassium hydroxide | Nickel | nickel–metal hydride |
| 1.5 V | Zinc | Water, ammonium or zinc chloride | Carbon, manganese dioxide | Zinc carbon |
| 2.1 V | Lead | Water, sulfuric acid | Lead dioxide | Lead–acid |
| 3.6 V to 3.7 V | Graphite | Organic solvent, Li salts | LiCoO2 | Lithium-ion |
| 1.35 V | Zinc | Water, sodium or potassium hydroxide | HgO | Mercury cell |
Other chemical sources[edit]
Other chemical sources include fuel cells.
Electromagnetic induction[edit]
Electromagnetic induction is the production of a circulating electric field by a time-dependent magnetic field. A time-dependent magnetic field can be produced either by motion of a magnet relative to a circuit, by motion of a circuit relative to another circuit (at least one of these must be carrying an electric current), or by changing the electric current in a fixed circuit. The effect on the circuit itself, of changing the electric current, is known as self-induction; the effect on another circuit is known as mutual induction.
For a given circuit, the electromagnetically induced emf is determined purely by the rate of change of the magnetic flux through the circuit according to Faraday’s law of induction.
An emf is induced in a coil or conductor whenever there is change in the flux linkages. Depending on the way in which the changes are brought about, there are two types: When the conductor is moved in a stationary magnetic field to procure a change in the flux linkage, the emf is statically induced. The electromotive force generated by motion is often referred to as motional emf. When the change in flux linkage arises from a change in the magnetic field around the stationary conductor, the emf is dynamically induced. The electromotive force generated by a time-varying magnetic field is often referred to as transformer emf.
Contact potentials[edit]
When solids of two different materials are in contact, thermodynamic equilibrium requires that one of the solids assume a higher electrical potential than the other. This is called the contact potential.[44] Dissimilar metals in contact produce what is known also as a contact electromotive force or Galvani potential. The magnitude of this potential difference is often expressed as a difference in Fermi levels in the two solids when they are at charge neutrality, where the Fermi level (a name for the chemical potential of an electron system[45][46]) describes the energy necessary to remove an electron from the body to some common point (such as ground).[47] If there is an energy advantage in taking an electron from one body to the other, such a transfer will occur. The transfer causes a charge separation, with one body gaining electrons and the other losing electrons. This charge transfer causes a potential difference between the bodies, which partly cancels the potential originating from the contact, and eventually equilibrium is reached. At thermodynamic equilibrium, the Fermi levels are equal (the electron removal energy is identical) and there is now a built-in electrostatic potential between the bodies.
The original difference in Fermi levels, before contact, is referred to as the emf.[48]
The contact potential cannot drive steady current through a load attached to its terminals because that current would involve a charge transfer. No mechanism exists to continue such transfer and, hence, maintain a current, once equilibrium is attained.
One might inquire why the contact potential does not appear in Kirchhoff’s law of voltages as one contribution to the sum of potential drops. The customary answer is that any circuit involves not only a particular diode or junction, but also all the contact potentials due to wiring and so forth around the entire circuit. The sum of all the contact potentials is zero, and so they may be ignored in Kirchhoff’s law.[49][50]
Solar cell[edit]
Operation of a solar cell can be understood from its equivalent circuit. Photons with energy greater than the bandgap of the semiconductor create mobile electron–hole pairs. Charge separation occurs because of a pre-existing electric field associated with the p-n junction. This electric field is created from a built-in potential, which arises from the contact potential between the two different materials in the junction. The charge separation between positive holes and negative electrons across the p–n diode yields a forward voltage, the photo voltage, between the illuminated diode terminals,[51] which drives current through any attached load. Photo voltage is sometimes referred to as the photo emf, distinguishing between the effect and the cause.
Solar cell current–voltage relationship[edit]
Two internal current losses 





When the output is short-circuited, the output voltage is zeroed, and so the voltage across the diode is smallest. Thus, short-circuiting results in the smallest 

The current delivered by the illuminated diode to the external circuit can be simplified (based on certain assumptions) to:


Solar cell photo emf[edit]
Solar cell output voltage for two light-induced currents IL expressed as a ratio to the reverse saturation current I0[53] and using a fixed ideality factor m of 2.[54] Their emf is the voltage at their y-axis intercept.
Solving the illuminated diode’s above simplified current–voltage relationship for output voltage yields:
which is plotted against 
The solar cell’s photo emf 


It has a logarithmic dependence on the light-induced current 
When driving a resistive load, the output voltage can be determined using Ohm’s law and will lie between the short-circuit value of zero volts and the open-circuit voltage 

Other sources that generate emf[edit]
- A transformer coupling two circuits may be considered a source of emf for one of the circuits, just as if it were caused by an electrical generator; this is the origin of the term «transformer emf».
- For converting sound waves into voltage signals:
- a microphone generates an emf from a moving diaphragm.
- a magnetic pickup generates an emf from a varying magnetic field produced by an instrument.
- a piezoelectric sensor generates an emf from strain on a piezoelectric crystal.
- Devices that use temperature to produce emfs include thermocouples and thermopiles.[59]
- Any electrical transducer which converts a physical energy into electrical energy.
See also[edit]
- Counter-electromotive force
- Electric battery
- Electrochemical cell
- Electrolytic cell
- Galvanic cell
- Voltaic pile
References[edit]
- ^ «EMF». American Heritage Dictionary of the English Language, 3rd ed. Houghton Mifflin. 1992.
- ^ «EMF». Oxford English Dictionary.
- ^ a b Tipler, Paul A. (January 1976). Physics. New York, NY: Worth Publishers, Inc. p. 803. ISBN 978-0-87901-041-6.
- ^ Stewart, Joseph V. (2001). Intermediate electromagnetic theory. Singapore River Edge, NJ: World Scientific. p. 389. ISBN 978-981-02-4470-5. OCLC 47127179.
- ^ Matthews, Michael R. (2014-07-03). International Handbook of Research in History, Philosophy and Science Teaching. Springer. p. 142. ISBN 978-94-007-7654-8.
[Volta] stated that a new type of «force» was acting upon the charges, separating them and keeping them separated, and he called this action the electromotive force, the name that is still applied.
- ^ «IEC 60050 — International Electrotechnical Vocabulary — Details for IEV number 131-12-22: «source voltage»«. www.electropedia.org. Retrieved 2022-12-19.
- ^ «IEC 80000-6:2022». International Organization for Standardization. Retrieved 2022-12-19.
- ^ Langmuir, Irving (1916). «The Relation Between Contact Potentials and Electrochemical Action». Transactions of the American Electrochemical Society. The Society. 29: 175.
- ^ Cook, David M. (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 157. ISBN 978-0-486-42567-2.
- ^ Lerner, Lawrence M. (1997). Physics for scientists and engineers. Jones & Bartlett Publishers. pp. 724–727. ISBN 978-0-7637-0460-5.
- ^ Tipler, Paul A.; Mosca, Gene (2007). Physics for Scientists and Engineers (6 ed.). Macmillan. p. 850. ISBN 978-1-4292-0124-7.
- ^ Halpern, Alvin M.; Erlbach, Erich (1998). Schaum’s outline of theory and problems of beginning physics II. McGraw-Hill Professional. p. 138. ISBN 978-0-07-025707-8.
- ^ Lehrman, Robert L. (1998). Physics the easy way. Barron’s Educational Series. p. 274. ISBN 978-0-7641-0236-3.
emf separated charge reaction potential.
- ^ Singh, Kongbam Chandramani (2009). «§3.16 EMF of a source». Basic Physics. Prentice Hall India. p. 152. ISBN 978-81-203-3708-4.
- ^
Volta, Alessandro (1801). «De l’électricité dite galvanique». Annales de Chimie. Chez Fuchs, Paris. - ^ a b Cajori, Florian (1899). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. The Macmillan Company. pp. 218–219.
seat of electromotive force.
- ^
Valkenburgh, Van (1995). Basic Electricity. Cengage Learning. pp. 1–46. ISBN 978-0-7906-1041-2. - ^
Abraham, M.; Becker, R. (1932). The Classical Theory of Electricity and Magnetism. Blackie & Son. p. 116-122. - ^
Griffiths, David J (1999). Introduction to Electrodynamics (3rd ed.). Pearson/Addison-Wesley. p. 293. ISBN 978-0-13-805326-0. - ^
Only the electric field that results from charge separation caused by the emf is counted. While a solar cell has an electric field that results from a contact potential (see contact potentials and solar cells), this electric field component is not included in the integral. Only the electric field that results from charge separation caused by photon energy is included. - ^ Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (1986). Beyond the mechanical universe: from electricity to modern physics. Cambridge University Press. p. 245. ISBN 978-0-521-30430-6.
- ^
McDonald, Kirk T. (2012). «Voltage Drop, Potential Difference and EMF» (PDF). Physics Examples. Princeton University. - ^ Feynman, R.P.; Leighton, R.B.; Sands, M. (1964). The Feynman Lectures on Physics, Vol. II, chap. 22. Addison Wesley.
- ^ Cook, David M. (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 158. ISBN 978-0-486-42567-2.
- ^ a b c Finn, Colin B P (1992). Thermal Physics. CRC Press. p. 163. ISBN 978-0-7487-4379-7.
- ^
Fogiel, M. (2002). Basic Electricity. Research & Education Association. p. 76. ISBN 978-0-87891-420-3. - ^ a b
Halliday, David; Resnick, Robert; Walker, Jearl (2008). Fundamentals of Physics (6th ed.). Wiley. p. 638. ISBN 978-0-471-75801-3. - ^
Freeman, Roger L (2005). Fundamentals of Telecommunications (2nd ed.). Wiley. p. 576. ISBN 978-0-471-71045-5. - ^
Croft, Terrell (1917). Practical Electricity. McGraw-Hill. p. 533. - ^
Loeb, Leonard B. (2007). Fundamentals of Electricity and Magnetism (Reprint of Wiley 1947 3rd ed.). Read Books. p. 86. ISBN 978-1-4067-0733-5. - ^ «Difference Between Voltage and EMF?». Electrical Technology. 2019-10-06. Archived from the original on 2022-04-08. Retrieved 2022-09-28.
- ^
Warn, J. R. W.; Peters, A. P. H. (1996). Concise Chemical Thermodynamics (2 ed.). CRC Press. p. 123. ISBN 978-0-7487-4445-9. - ^
Glasstone, Samuel (2007). Thermodynamics for Chemists (Reprint of D. Van Nostrand Co (1964) ed.). Read Books. p. 301. ISBN 978-1-4067-7322-4. - ^ Shadowitz, Albert (1975). The Electromagnetic Field (1st ed.). McGraw-Hill Book Company. pp. 396–398. ISBN 0-07-056368-3.
- ^
McDonald, Kirk T. (2010). «Lewin’s Circuit Paradox» (PDF). Physics Examples. Princeton University. - ^ Risch, Nikolaus (2002). «Molecules — bonds and reactions». In L Bergmann; et al. (eds.). Constituents of Matter: Atoms, Molecules, Nuclei, and Particles. CRC Press. ISBN 978-0-8493-1202-1.
- ^ Nernst, Walter (1889). «Die elektromotorische Wirksamkeit der Ionen». Z. Phys. Chem. 4: 129.
- ^
The brave reader can find an extensive discussion for organic electrochemistry in Amatore, Christian (2000). «Basic concepts». In Henning Lund; Ole Hammerich (eds.). Organic electrochemistry (4 ed.). CRC Press. ISBN 978-0-8247-0430-8. - ^
Conway, BE (1999). «Energy factors in relation to electrode potential». Electrochemical supercapacitors. Springer. p. 37. ISBN 978-0-306-45736-4. - ^ Tilley, R. J. D. (2004). Understanding Solids. Wiley. p. 267. ISBN 978-0-470-85275-0.
- ^ Mottelay, Paul Fleury (2008). Bibliographical History of Electricity and Magnetism (Reprint of 1892 ed.). Read Books. p. 247. ISBN 978-1-4437-2844-7.
- ^ Kragh, Helge (2000). «Confusion and Controversy: Nineteenth-century theories of the voltaic pile» (PDF). Nuova Voltiana:Studies on Volta and His Times. Università degli studi di Pavia. Archived from the original (PDF) on 2009-03-20.
- ^ Cumming, Linnaus (2008). An Introduction to the Theory of Electricity (Reprint of 1885 ed.). BiblioBazaar. p. 118. ISBN 978-0-559-20742-6.
- ^ Trigg, George L. (1995). Landmark experiments in twentieth century physics (Reprint of Crane, Russak & Co 1975 ed.). Courier Dover. p. 138 ff. ISBN 978-0-486-28526-9.
- ^ Rockett, Angus (2007). «Diffusion and drift of carriers». Materials science of semiconductors. New York, NY: Springer Science. p. 74 ff. ISBN 978-0-387-25653-5.
- ^ Kittel, Charles (2004). «Chemical potential in external fields». Elementary Statistical Physics (Reprint of Wiley 1958 ed.). Courier Dover. p. 67. ISBN 978-0-486-43514-5.
- ^ Hanson, George W. (2007). Fundamentals of Nanoelectronics. Prentice Hall. p. 100. ISBN 978-0-13-195708-4.
- ^ Sato, Norio (1998). «Semiconductor photoelectrodes». Electrochemistry at metal and semiconductor electrodes (2nd ed.). Elsevier. p. 110 ff. ISBN 978-0-444-82806-4.
- ^ Quimby, Richard S. (2006). Photonics and lasers. Wiley. p. 176. ISBN 978-0-471-71974-8.
- ^ Neamen, Donald A. (2002). Semiconductor physics and devices (3rd ed.). McGraw-Hill Professional. p. 240. ISBN 978-0-07-232107-4.
- ^ Dhir, S. M. (2000) [1999]. «§3.1 Solar cells». Electronic Components and Materials: Principles, Manufacture & Maintenance (2007 fifth reprint ed.). India: Tata McGraw-Hill Publishing Company Limited. p. 283. ISBN 0-07-463082-2.
- ^ a b Araújo, Gerardo L. (1994). «§2.5.1 Short-circuit current and open-circuit voltage». In Eduardo Lorenzo (ed.). Solar Electricity: Engineering of photovoltaic systems. Progenza for Universidad Politechnica Madrid. p. 74. ISBN 978-84-86505-55-4.
- ^ Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 8. ISBN 978-1-86094-349-2.
- ^ In practice, at low voltages m → 2, whereas at high voltages m → 1. See Araújo, op. cit. ISBN 84-86505-55-0. page 72
- ^ Northrop, Robert B. (2005). «§6.3.2 Photovoltaic Cells». Introduction to Instrumentation and Measurements. CRC Press. p. 176. ISBN 978-0-8493-7898-0.
- ^ «Open-Circuit Voltage».
- ^ Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 6. ISBN 978-1-86094-349-2.
- ^
Nelson, Jenny (2003). The physics of solar cells. Imperial College Press. p. 7. ISBN 978-1-86094-349-2. - ^ John S. Rigden, ed. (1996). Macmillan encyclopedia of physics. New York: Macmillan.
Further reading[edit]
- George F. Barker, «On the measurement of electromotive force». Proceedings of the American Philosophical Society Held at Philadelphia for Promoting Useful Knowledge, American Philosophical Society. January 19, 1883.
- Andrew Gray, «Absolute Measurements in Electricity and Magnetism», Electromotive force. Macmillan and co., 1884.
- Charles Albert Perkins, «Outlines of Electricity and Magnetism», Measurement of Electromotive Force. Henry Holt and co., 1896.
- John Livingston Rutgers Morgan, «The Elements of Physical Chemistry», Electromotive force. J. Wiley, 1899.
- «Abhandlungen zur Thermodynamik, von H. Helmholtz. Hrsg. von Max Planck». (Tr. «Papers to thermodynamics, on H. Helmholtz. Hrsg. by Max Planck».) Leipzig, W. Engelmann, Of Ostwald classical author of the accurate sciences series. New consequence. No. 124, 1902.
- Theodore William Richards and Gustavus Edward Behr, jr., «The electromotive force of iron under varying conditions, and the effect of occluded hydrogen». Carnegie Institution of Washington publication series, 1906. LCCN 07-3935
- Henry S. Carhart, «Thermo-electromotive force in electric cells, the thermo-electromotive force between a metal and a solution of one of its salts». New York, D. Van Nostrand company, 1920. LCCN 20-20413
- Hazel Rossotti, «Chemical applications of potentiometry». London, Princeton, N.J., Van Nostrand, 1969. ISBN 0-442-07048-9 LCCN 69-11985
- Nabendu S. Choudhury, 1973. «Electromotive force measurements on cells involving beta-alumina solid electrolyte». NASA technical note, D-7322.
- John O’M. Bockris; Amulya K. N. Reddy (1973). «Electrodics». Modern Electrochemistry: An Introduction to an Interdisciplinary Area (2 ed.). Springer. ISBN 978-0-306-25002-6.
- Roberts, Dana (1983). «How batteries work: A gravitational analog». Am. J. Phys. 51 (9): 829. Bibcode:1983AmJPh..51..829R. doi:10.1119/1.13128.
- G. W. Burns, et al., «Temperature-electromotive force reference functions and tables for the letter-designated thermocouple types based on the ITS-90». Gaithersburg, MD : U.S. Dept. of Commerce, National Institute of Standards and Technology, Washington, Supt. of Docs., U.S. G.P.O., 1993.
- Norio Sato (1998). «Semiconductor photoelectrodes». Electrochemistry at metal and semiconductor electrodes (2nd ed.). Elsevier. p. 326 ff. ISBN 978-0-444-82806-4.
- Hai, Pham Nam; Ohya, Shinobu; Tanaka, Masaaki; Barnes, Stewart E.; Maekawa, Sadamichi (2009-03-08). «Electromotive force and huge magnetoresistance in magnetic tunnel junctions». Nature. 458 (7237): 489–92. Bibcode:2009Natur.458..489H. doi:10.1038/nature07879. PMID 19270681. S2CID 4320209.
ЭДС. Закон Ома для полной цепи
-
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
-
Сторонняя сила
-
Закон Ома для полной цепи
-
КПД электрической цепи
-
Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила
, направленная против движения заряда (т.е. против направления тока).
к оглавлению ▴
Сторонняя сила
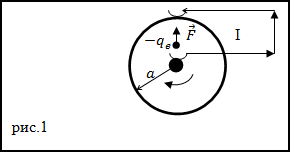
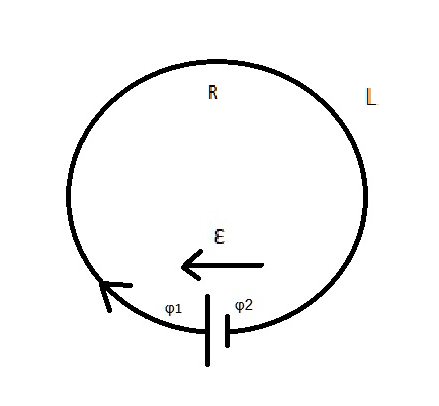
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы
называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом,
— это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду
. Поэтому отношение
уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается
:
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением
подключён к резистору
(который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение
на резисторе
.
За время по цепи проходит заряд
. Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и
. Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и
(рис. 2). Потенциал точки
равен потенциалу положительной клеммы источника; потенциал точки
равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь
умножается на дробь, меньшую единицы. Но есть два случая, когда
.
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт
.
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина
неотличима от
, и формула (5) снова даёт нам
.
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время
, обозначим
.
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна
, его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно
, можно просто заменить резистор
на резистор
).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки
к точке
. Этот ток не обязательно вызван одним лишь источником
. Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток
является результатом совокупного действия всех источников, имеющихся в цепи.
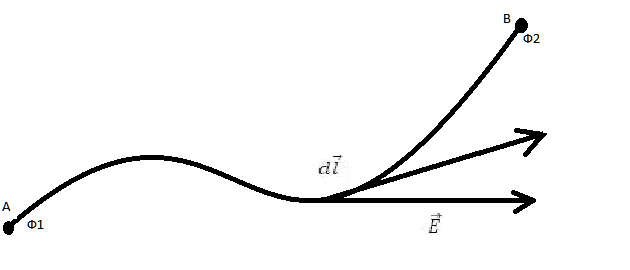
Пусть потенциалы точек и
равны соответственно
и
. Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время
через участок проходит заряд
, при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло:
.
Подставляем сюда выражения для ,
и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд
от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки
к точке
.
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем
— закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене
на
:
Теперь замкнём наш участок, соединив точки и
. Получим рассмотренную выше полную цепь. При этом окажется, что
и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от
к
, направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке
. Если направление тока совпадает с направлением сторонних сил, то перед
ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.
Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.
Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
Решение:
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона,
Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:
Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:
Отсюда выражаем и находим внутреннее сопротивление источника:
При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:
Отсюда выражаем сопротивление резистора и находим его:
Ответ: 1,9.
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.
Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:
Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.01.2023
Что такое ЭДС (электродвижущая сила) в физике? Электрический ток понятен далеко не каждому. Как космическая даль, только под самым носом. Вообще, он и ученым понятен не до конца. Достаточно вспомнить Николу Тесла с его знаменитыми экспериментами, на века опередившими свое время и даже в наши дни остающимися в ореоле тайны. Сегодня мы не разгадываем больших тайн, но пытаемся разобраться в том, что такое ЭДС в физике.
Определение ЭДС в физике
ЭДС – электродвижущая сила. Обозначается буквой E или маленькой греческой буквой эпсилон.
Электродвижущая сила — скалярная физическая величина, характеризующая работу сторонних сил (сил неэлектрического происхождения), действующих в электрических цепях переменного и постоянного тока.
ЭДС, как и напряжение, измеряется в вольтах. Однако ЭДС и напряжение – явления разные.
Напряжение (между точками А и Б) – физическая величина, равная работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из одной точки в другую.
Объясняем суть ЭДС «на пальцах»
Чтобы разобраться в том, что есть что, можно привести пример-аналогию. Представим, что у нас есть водонапорная башня, полностью заполненная водой. Сравним эту башню с батарейкой.
Вода оказывает максимальное давление на дно башни, когда башня заполнена полностью. Соответственно, чем меньше воды в башне, тем слабее давление и напор вытекающей из крана воды. Если открыть кран, вода будет постепенно вытекать сначала под сильным напором, а потом все медленнее, пока напор не ослабнет совсем. Здесь напряжение – это то давление, которое вода оказывает на дно. За уровень нулевого напряжения примем само дно башни.
То же самое и с батарейкой. Сначала мы включаем наш источник тока (батарейку) в цепь, замыкая ее. Пусть это будут часы или фонарик. Пока уровень напряжения достаточный и батарейка не разрядилась, фонарик светит ярко, затем постепенно гаснет, пока не потухнет совсем.
Но как сделать так, чтобы напор не иссякал? Иными словами, как поддерживать в башне постоянный уровень воды, а на полюсах источника тока – постоянную разность потенциалов. По примеру башни ЭДС представляется как бы насосом, который обеспечивает приток в башню новой воды.
Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
- Химическая ЭДС. Возникает в батарейках и аккумуляторах вследствие химических реакций.
- Термо ЭДС. Возникает, когда находящиеся при разных температурах контакты разнородных проводников соединены.
- ЭДС индукции. Возникает в генераторе при помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
- Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление внешнего или внутреннего фотоэффекта.
- Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.
Дорогие друзья, сегодня мы рассмотрели тему «ЭДС для чайников». Как видим, ЭДС – сила неэлектрического происхождения, которая поддерживает протекание электрического тока в цепи. Если Вы хотите узнать, как решаются задачи с ЭДС, советуем обратиться к нашим авторам – скрупулезно отобранным и проверенным специалистам, которые быстро и доходчиво разъяснят ход решения любой тематической задачи. И по традиции в конце предлагаем Вам посмотреть обучающее видео. Приятного просмотра и успехов в учебе!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Электродвижущая сила или сокращено ЭДС – это способность источника тока ил по-другому питающий элемент, создавать в электрической цепи разность потенциалов. Элементами питания являются аккумуляторы или батареи. Это скалярная физическая величина, равная работе сторонних сил для перемещения одного заряда с положительной величиной. В данной статье будут рассмотрены теоритические вопросы ЭДС, как она образуется, а также для чего она может быть использована на практике и где используются, а главное как рассчитать ее.
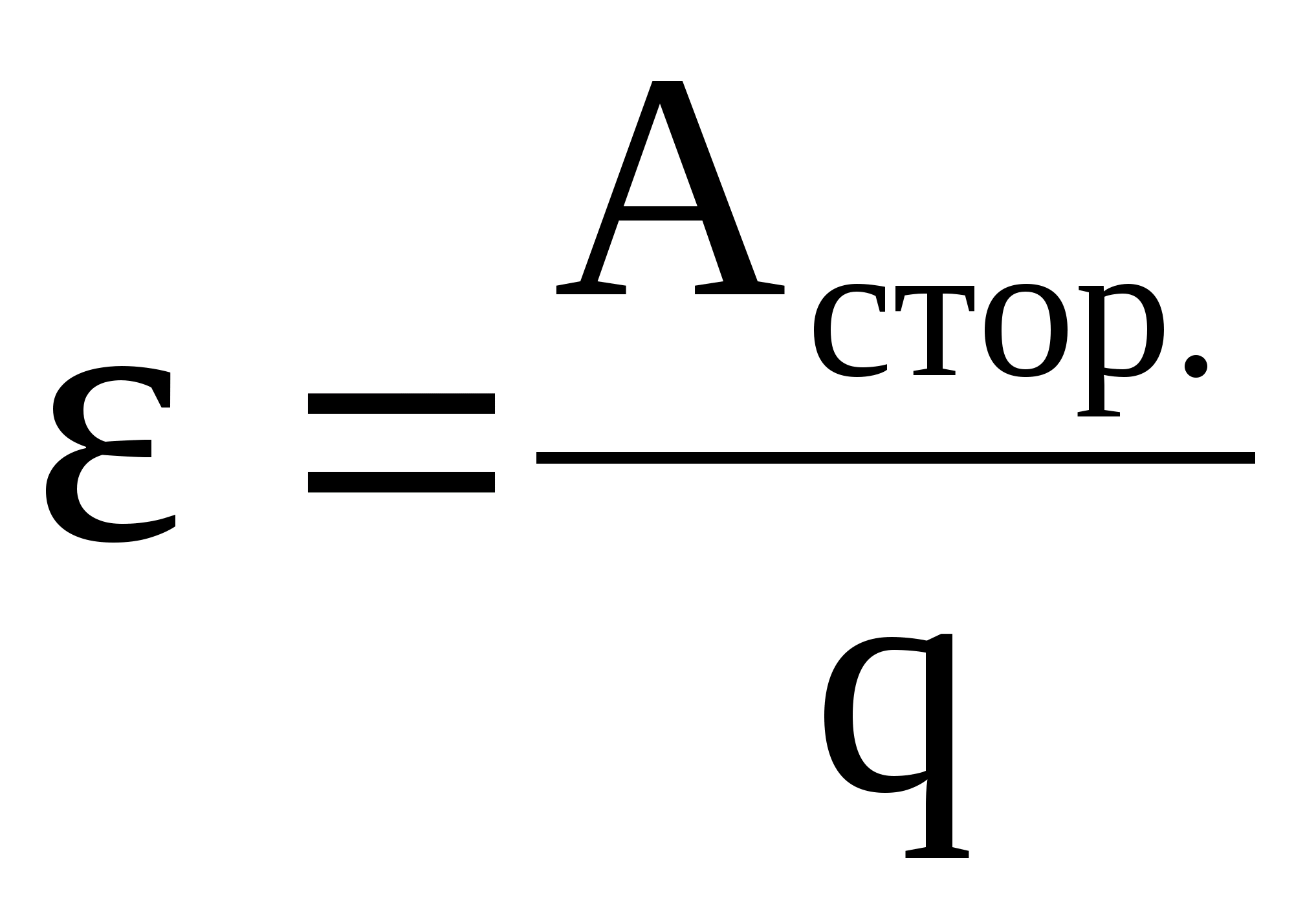
Что такое ЭДС: объяснение простыми словами
Под ЭДС понимается удельная работа сторонних сил по перемещению единичного заряда в контуре электрической цепи. Это понятие в электричестве предполагает множество физических толкований, относящихся к различным областям технических знаний. В электротехнике — это удельная работа сторонних сил, появляющаяся в индуктивных обмотках при наведении в них переменного поля. В химии она означает разность потенциалов, возникающее при электролизе, а также при реакциях, сопровождающихся разделением электрических зарядов.
В физике она соответствует электродвижущей силе, создаваемой на концах электрической термопары, например. Чтобы объяснить суть ЭДС простыми словами – потребуется рассмотреть каждый из вариантов ее трактовки. Прежде чем перейти к основной части статьи отметим, что ЭДС и напряжение очень близкие по смыслу понятия, но всё же несколько отличаются. Если сказать кратко, то ЭДС — на источнике питания без нагрузки, а когда к нему подключают нагрузку — это уже напряжение. Потому что количество вольт на ИП под нагрузкой почти всегда несколько меньше, чем без неё. Это связано с наличием внутреннего сопротивления таких источников питания, как трансформаторы и гальванические элементы.
Дополнительный материал по теме: Простыми словами о преобразователях напряжения.
Электродвижущая сила (эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Если через Eстр обозначить напряжённость поля сторонних сил, то эдс в замкнутом контуре (L) равна , где dl — элемент длины контура. Потенциальные силы электростатического (или стационарного) поля не могут поддерживать постоянный ток в цепи, т. к. работа этих сил на замкнутом пути равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — нагреванием проводников.
Сторонние силы приводят в движение заряженные частицы внутри источников тока: генераторов, гальванических элементов, аккумуляторов и т. д. Происхождение сторонних сил может быть различным. В генераторах сторонние силы — это силы со стороны вихревого электрического поля, возникающего при изменении магнитного поля со временем, или Лоренца сила, действующая со стороны магнитного поля на электроны в движущемся проводнике; в гальванических элементах и аккумуляторах — это химические силы и т. д. Эдс определяет силу тока в цепи при заданном её сопротивлении (см. Ома закон). Измеряется эдс, как и напряжение, в вольтах.

Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
- Химическая ЭДС. Возникает в батарейках и аккумуляторах вследствие химических реакций.
- Термо ЭДС. Возникает, когда находящиеся при разных температурах контакты разнородных проводников соединены.
- ЭДС индукции. Возникает в генераторе при помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
- Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление внешнего или внутреннего фотоэффекта.
- Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.
Электромагнитная индукция (самоиндукция)
Начнем с электромагнитной индукции. Это явление описывает закон электромагнитной индукции Фарадея. Физический смысл этого явления состоит в способности электромагнитного поля наводить ЭДС в находящемся рядом проводнике. При этом или поле должно изменяться, например, по величине и направлению векторов, или перемещаться относительно проводника, или должен двигаться проводник относительно этого поля. На концах проводника в этом случае возникает разность потенциалов.
Опыт демонстрирует появление ЭДС в катушке при воздействии изменяющегося магнитного поля постоянного магнита. Есть и другое похожее по смыслу явление — взаимоиндукция. Оно заключается в том, что изменение направления и силы тока одной катушки индуцирует ЭДС на выводах расположенной рядом катушки, широко применяется в различных областях техники, включая электрику и электронику. Оно лежит в основе работы трансформаторов, где магнитный поток одной обмотки наводит ток и напряжение во второй.
В электрике физический эффект под названием ЭДС используется при изготовлении специальных преобразователей переменного тока, обеспечивающих получение нужных значений действующих величин (тока и напряжения). Благодаря явлениям индукции и самоиндукции инженерам удалось разработать множество электротехнических устройств: от обычной катушки индуктивности (дросселя) и вплоть до трансформатора. Понятие взаимоиндукции касается только переменного тока, при протекании которого в контуре или проводнике меняется магнитный поток.
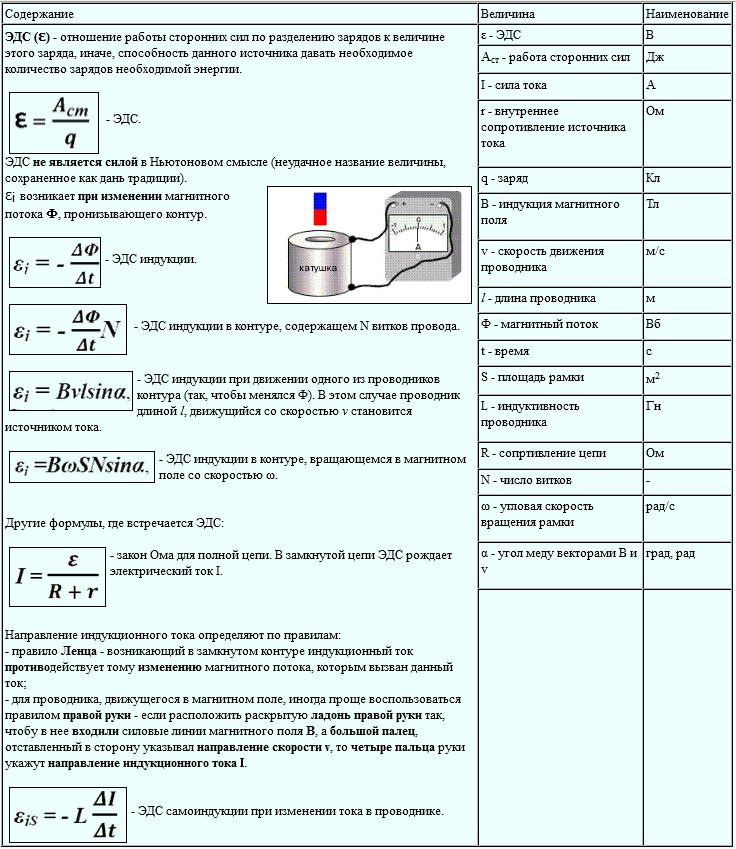
ЭДС в быту и единицы измерения
Другие примеры встречаются в практической жизни любого рядового человека. Под эту категорию попадают такие привычные вещи, как малогабаритные батарейки, а также другие миниатюрные элементы питания. В этом случае рабочая ЭДС формируется за счет химических процессов, протекающих внутри источников постоянного напряжения. Когда оно возникает на клеммах (полюсах) батареи вследствие внутренних изменений – элемент полностью готов к работе. Со временем величина ЭДС несколько снижается, а внутреннее сопротивление заметно возрастает.
В результате если вы измеряете напряжение на не подключенной ни к чему пальчиковой батарейке вы видите нормальные для неё 1.5В (или около того), но когда к батарейке подключается нагрузка, допустим, вы установили её в какой-то прибор — он не работает. Почему? Потому что если предположить, что у вольтметра внутреннее сопротивление во много раз выше, чем внутреннее сопротивлении батарейки — то вы измеряли её ЭДС. Когда батарейка начала отдавать ток в нагрузке на её выводах стало не 1.5В, а, допустим, 1.2В — прибору недостаточно ни напряжения, ни тока для нормальной работы.
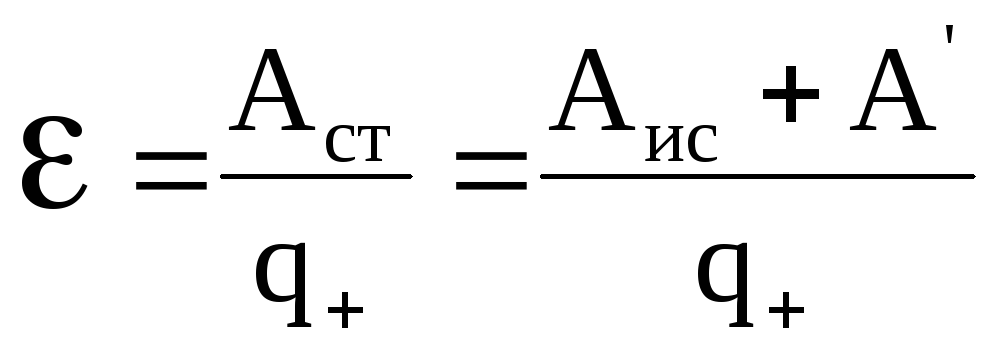
Как раз вот эти 0.3 В и упали на внутреннем сопротивлении гальванического элемента. Если батарейка совсем старая и её электроды разрушены, то на клеммах батареи может не быть вообще никакой электродвижущей силы или напряжения — т.е. ноль. Совсем небольшая по величине электродвижущая сила наводится и в рамках антенны приемника, которая усиливается затем специальными каскадами, и мы получаем наш телевизионный, радио и даже Wi-Fi сигнал.
Материал по теме: Выбираем цифро-аналоговый преобразователь.
Как образуется ЭДС
Идеальный источник ЭДС – генератор, внутреннее сопротивление которого равно нулю, а напряжение на его зажимах не зависит от нагрузки. Мощность идеального источника ЭДС бесконечна. Реальный источник ЭДС, в отличие от идеального, содержит внутреннее сопротивление Ri и его напряжение зависит от нагрузки (рис. 1., б), а мощность источника конечна. Электрическая схема реального генератора ЭДС представляет собой последовательное соединение идеального генератора ЭДС Е и его внутреннего сопротивления Ri.
На практике для того чтобы приблизить режим работы реального генератора ЭДС к режиму работы идеального, внутреннее сопротивление реального генератора Ri стараются делать как можно меньше, а сопротивление нагрузки Rн необходимо подключать величиной не менее чем в 10 раз большей величины внутреннего сопротивления генератора, т.е. необходимо выполнять условие: Rн >> Ri
Для того чтобы выходное напряжение реального генератора ЭДС не зависело от нагрузки, его стабилизируют применением специальных электронных схем стабилизации напряжения. Поскольку внутреннее сопротивление реального генератора ЭДС не может быть выполнено бесконечно малым, его минимизируют и выполняют стандартным для возможности согласованного подключения к нему потребителей энергии. В радиотехнике величины стандартного выходного сопротивления генераторов ЭДС составляют 50 Ом (промышленный стандарт) и 75 Ом (бытовой стандарт).
Например, все телевизионные приемники имеют входное сопротивление 75 Ом и подключены к антеннам коаксиальным кабелем именно такого волнового сопротивления. Для приближения к идеальным генераторам ЭДС источники питающего напряжения, используемые во всей промышленной и бытовой радиоэлектронной аппаратуре, выполняют с применением специальных электронных схем стабилизации выходного напряжения, которые позволяют выдерживать практически неизменное выходное напряжение источника питания в заданном диапазоне токов, потребляемых от источника ЭДС (иногда его называют источником напряжения).
На электрических схемах источники ЭДС изображаются так: Е — источник постоянной ЭДС, е(t) – источник гармонической (переменной) ЭДС в форме функции времени. Электродвижущая сила Е батареи последовательно соединенных одинаковых элементов равна электродвижущей силе одного элемента Е, умноженной на число элементов n батареи: Е = nЕ.
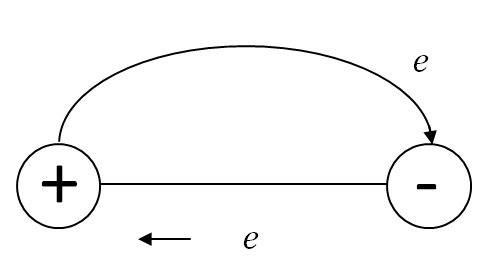
Электродвижущая сила (ЭДС) источника энергии
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока). Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника.
Инженер по специальности «Программное обеспечение вычислительной техники и автоматизированных систем», МИФИ, 2005–2010 гг.
Задать вопрос
Иногда говорят, что ЭДС создает электрический ток в цепи. Нужно помнить об условности такого определения, так как выше мы уже установили, что причина возникновения и существования электрического тока — электрическое поле.
Источник электрической энергии производит определенную работу, перемещая электрические заряды по всей замкнутой цепи. За единицу измерения электродвижущей силы принят вольт (сокращенно вольт обозначается буквой В или V — «вэ» латинское). ЭДС источника электрической энергии равна одному вольту, если при перемещении одного кулона электричества по всей замкнутой, цепи источник электрической энергии совершает работу, равную одному джоулю:
В практике для измерения ЭДС используются как более крупные, так и более мелкие единицы, а именно:
- 1 киловольт (кВ, kV), равный 1000 В;
- 1 милливольт (мВ, mV), равный одной тысячной доле вольта (10-3 В),
- 1 микровольт (мкВ, μV), равный одной миллионной доле вольта (10-6 В).
Очевидно, что 1 кВ = 1000 В; 1 В = 1000 мВ = 1 000 000 мкВ; 1 мВ= 1000 мкВ.
В настоящее, время существует несколько видов источников электрической энергии. Впервые в качестве источника электрической энергии была использована гальваническая батарея, состоящая из нескольких цинковых и медных кружков, между которыми была проложена кожа, смоченная в подкисленной воде. В гальванической батарее химическая энергия превращалась в электрическую (подробнее об этом будет рассказано в главе XVI). Свое название гальваническая батарея получила по имени итальянского физиолога Луиджи Гальвани (1737—1798), одного из основателей учения об электричестве.
Многочисленные опыты по усовершенствованию и практическому использованию гальванических батарей были проведены русским ученым Василием Владимировичем Петровым. Еще в начале прошлого века он создал самую большую в мире гальваническую батарею и использовал ее для ряда блестящих опытов. Источники электрической энергии, работающие по принципу преобразования химической энергии в электрическую, называются химическими источниками электрической энергии.
Полезно знать: Как рассчитать мощность электрического тока.
Другим основным источником электрической энергий, получившим широкое применение в электротехнике и радиотехнике, является генератор. В генераторах механическая энергия преобразуется в электрическую. У химических источников электрической энергии и у генераторов электродвижущая сила проявляется одинаково, создавая на зажимах источника разность потенциалов и поддерживая ее длительное время.
[stextbox id=’info’]Эти зажимы называются полюсами источника электрической энергии. Один полюс источника электрической энергии имеет положительный потенциал (недостаток электронов), обозначается знаком плюс ( + ) и называется положительным полюсом. [/stextbox]
Другой полюс имеет отрицательный потенциал (избыток электронов), обозначается знаком минус (—) и называется отрицательным полюсом. От источников электрической энергии электрическая энергия передается по проводам к ее потребителям (электрические лампы, электродвигатели, электрические дуги, электронагревательные приборы и т. д.).
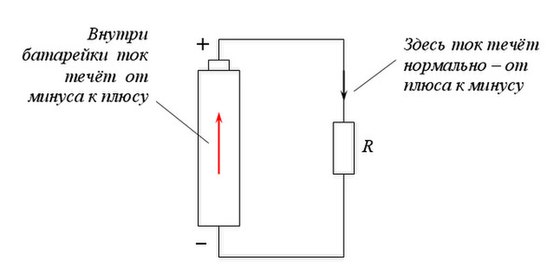
Примеры решения задач
К каждой позиции первого столбца подберите соответствующую позицию второго:
Решение: Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.
Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.
ЭДС определяется по формуле:
Сила тока определяется по формуле:
Сопротивление определяется по формуле:
Разность потенциалов определяется по формуле:
Правильный ответ:
Что такое электродвижущая сила?
Это отношение работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда.
Что такое электрическая цепь?
Набор устройств, которые соединены проводниками, предназначенный для протекания тока.
Как звучит закон Ома для полной цепи?
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Заключение
Инженер по специальности «Программное обеспечение вычислительной техники и автоматизированных систем», МИФИ, 2005–2010 гг.
Задать вопрос
Если в проводнике создать электрическое поле и не поддерживать это поле, то перемещение носителей тока приведет к тому, что поле внутри проводника исчезнет, и ток прекратится. Для того чтобы поддерживать ток в цепи достаточно долго, необходимо осуществить движение зарядов по замкнутой траектории, то есть сделать линии постоянного тока замкнутыми. Следовательно, в замкнутой цепи должны быть участки, на которых носители заряда будут двигаться против сил электростатического поля, то есть от точек с меньшим потенциалом к точкам с большим потенциалом. Это возможно лишь при наличии неэлектрических сил, называемых сторонними силами. Сторонними силами являются силы любой природы, кроме кулоновских.
Дополнительную информацию о предмете статьи можно узнать из файла «Электродвижущая сила в цепях электрического тока». А также в нашей группе ВК публикуются интересные материалы, с которыми вы можете познакомиться первыми. Для этого приглашаем читателей подписаться и вступить в группу.
В завершение хочу выразить благодарность источникам, откуда почерпнут материал для подготовки статьи:
www.booksite.ru
www.scsiexplorer.com.ua
www.samelectrik.ru
www.electricalschool.info
www.sxemotehnika.ru
www.zaochnik.ru
www.ido.tsu.ru
Предыдущая
ТеорияЧто такое термопара: об устройстве простыми словами
Следующая
ТеорияЧто такое заземление простыми словами
Содержание:
- Определение и формула ЭДС
- Закон Ома для произвольного участка цепи
- Единицы измерения
- Примеры решения задач
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.
Определение и формула ЭДС
Определение
Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:
$$varepsilon=frac{A}{q}(1)$$
где A – работа сторонних сил, q – заряд, над которым производится работа.
Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.
ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:
$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$
где $bar{E}^{*}$ — напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:
$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$
Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.
Закон Ома для произвольного участка цепи
Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:
$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$
где U12=IR21 – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.
Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).
Единицы измерения
Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В
1В=1Дж/1Кл
Примеры решения задач
Пример
Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?
Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:
$$varepsilon=frac{A}{q}(1.1)$$
Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:
$$q=I Delta t(1.2)$$
Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:
$$A=varepsilon I Delta t$$
Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:
$A=10 cdot 0,4 cdot 60=240$ (Дж)
Ответ. A=240 Дж

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?
Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:
$$F=m r omega^{2}(2.1)$$
где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:
$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$
где q – заряд электрона.
В соответствии с формулой, определяющей ЭДС участка цепи, получаем:
$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$
Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$
Читать дальше: Формулы по физике.
Неотъемлемым элементом любой самодостаточной электрической цепи является источник (генератор) тока. Он разделяет электрические заряды, благодаря чему напряжение поддерживается в приемлемом диапазоне значений. Без этого электрический ток с точно заданными характеристиками в цепи существовать не может. Если мы поставим в цепь, например, конденсатор (пусть даже очень ёмкий), ток в ней возникнет, но через некоторое, как правило, очень непродолжительное время, он закончится. Электрическое поле переместит все имеющиеся свободные заряды, и конденсатор разрядится.
Электродвижущая сила
Определение
Электродвижущей силой источника тока называют силы не электростатического происхождения, действующие внутри указанных устройств и перемещающие электрические заряды против электростатического поля, которое создаёт необходимую разность потенциалов.
Природа у электродвижущих сил может быть самой разной. В гальванических источниках электрического тока они возникают благодаря энергии, высвобождающейся в химических реакциях между веществом электродов и электролитов. В генераторах постоянного тока они создаются энергией магнитного поля и механической энергией вращения якоря.
Формула расчета ЭДС в электрических цепях, состоящих из замкнутых контуров
Работа электростатических сил равна нулю, ведь заряды (электроны) приходят практически в то же место откуда вышли. Не равна нулю только результирующая работа электродвижущих сил цепи.
Её величина определяется формулой электродвижущей силы:
Формула
Формула ЭДС:
[varepsilon=frac{A}{q}].
Именно этому равна электродвижущая сила. A – работа сторонних сил, т. е. ЭДС.
Обратите внимание, направлением ЭДС считается направление, в котором внутри источника перемещаются именно положительные заряды. Часто оно противоположно направлению перемещения реальных носителей заряда, в качестве которых в подавляющем большинстве случаев выполняют электроны.
Если источник тока только один, то направление ЭДС в цепи такое же, как у него.
Размерность электродвижущей силы не равна размерности силы или работы. В системе СИ величина ЭДС измеряется в вольтах. Это мера разности потенциалов, которая создаётся на зажимах при разомкнутом генераторе.
Электродвижущая сила цепи и напряжение
Представим электрическое поле. Рассмотрим в нём произвольную кривую, соединяющую между собой точки A и B. Для дальнейшего объяснения на выбранной линии следует указать положительное направление.
Напряжение на этой кривой будет равняться:
[U=int_{l} E d l]
Под напряжённостью поля, как известно, понимают силу, действующую на помещённый в него единичный положительный заряд. Интеграл в данном случае – работа по перемещению заряда по кривой.
Значение напряжения станет равно разности потенциалов на концах нашей линии: U = φ1 – φ2.
Какую форму имеет кривая, совершенно безразлично. Важны лишь её начальные и конечные точки.
Давайте подробнее изучим циркуляцию вектора напряжённости по замкнутому контуру L.
Выделим на указанном контуре точки A и B. Они разделят его на два криволинейных незамкнутых отрезка. Учитывая предыдущие формулы, имеем.
[oint_{L} E d l=oint_{A}^{B} E d l=varphi 1-varphi 2=varphi 2-varphi 1=0]
Из этого легко сделать вывод, что циркуляция вектора напряжённости по контуру, если он замкнут, равняется нулю. E и dl – векторные величины.
Определение
Электродвижущей силой в теории электричества принято считать циркуляцию вектора напряжённости по произвольному замкнутому контуру.
[varepsilon=oint_{L} E d l=0]
Если поле электростатическое, то ЭДС замкнутого контура (каким бы он ни был) равна нулю.
Закон Ома для участка цепи с электродвижущей силой тока
Рассмотрим один из самых простых случаев – электрическую цепь с химическим источником ЭДС, элементом Вольта. Он состоит из двух электродов (медного и цинкового), погружённых в раствор кислоты.
Электродвижущая сила в этом случае создаётся следующим образом: цинк при растворении в кислоте теряет положительно заряженные атомы, приобретая тем самым отрицательный потенциал, а медь становится положительно заряженной. В результате возникает сторонняя ЭДС. Находится она в очень тонком слое, отделяющем электролит от цинкового и медного электродов. Когда цепь замыкают, на сопротивлениях двух частей цепи (внешней и внутренней) возникает разность потенциалов и начинает течь ток I.
Для простоты расчётов будем исходить из того, что сопротивления на всех участках цепи распределены равномерно по всему контуру L.
Из закона сохранения энергии следует, что работа, совершаемая электрическим полем при движении заряда q по внешней цепи и в электролите будет равняться
Aq = (φ1 – φ2)*q + (φ3 – φ4)*q
Общую работу сторонних сил можно записать как
Ɛq= Ast = (φ3 – φ2)*q + (φ1 – φ4)*q
Приравняв обе части двух предыдущих выражений, получим
Aq= Ast
Формула явно указывает на то, что работа сторонних сил и работа электрического поля равны между собой.
Из закона Ома следует, что
φ1 – φ2 = I*R, а φ3 – φ4 = I*r
От сюда следующий вид закона Ома с электродвижущей силой.
Ɛ = I*(R + r)
Справедлив он только для замкнутой цепи.
О втором правиле Кирхгофа
Полученная формула говорит, что электродвижущая сила равна сложенным друг с другом произведениям силы тока на все сопротивления, составляющих замкнутую цепь.
Ɛ = I*R + I*r
Это очень важное утверждение. Часто его именуют Вторым правилом Кирхгофа. Оно относится ко всем замкнутым цепям, какими бы они ни были.
Важно
По-другому это правило можно сформулировать так – в любом электрическом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивления, через которые они протекают равняется ЭДС в указанном контуре.
Сопротивления могут считаться не только положительными, но и отрицательными. Если направление тока совпадает с выбранным направлением обхода контура, то сопротивление признают положительным. Если не совпадает – отрицательным.
Электродвижущая сила тока считается положительной, в том случае, если в его источнике произошёл переход от отрицательного полюса к положительному.
Когда в направлении токов нельзя быть уверенным, его можно выбрать произвольно. Из-за этого после вычислений может получиться отрицательное число. Это признак того что на самом деле ток идёт в противоположную сторону.
Впрочем, здесь всё условно. У многих ток ассоциируется с бегущими по проводнику отрицательно заряженными электронами. Тем не менее за направление тока всегда принимают именно направление положительных движущихся зарядов. Расчётам и пониманию сути физических явлений, относящихся к этому разделу физики подобное никак не мешает. Разве что в самом начале, пока не появилась привычка.
Формула
Математическая запись правила Кирхгофа выглядит следующим образом:
[sum_{m=1}^{N} varepsilon m=sum_{m=1}^{N} I m R m].
N – число участков, на которые мы разбили контур.
Данная формула позволяет очень легко рассчитывать достаточно сложные цепи, т. к. получаем систему независимых уравнений, легко решаемую с математической точки зрения. То что самостоятельно, на листе бумаги расчёты будут громоздкими – не проблема. Даже простейший не очень мощный компьютер с вычислениями может справиться весьма быстро.
Формула
Количество независимых контуров определяется по формуле:
[n2 = p – m + 1].
p – общее количество ветвей в цепи, m – общее количество узлов в цепи.
Электродвижущая сила
Содержание:
-
Что такое электродвижущая сила — определение, физический смысл
- В чем измеряется в системе СИ, как обозначается на схеме
- Природа ЭДС, какими причинами порождается
- По какой формуле определяется электродвижущая сила
- Чему равна электродвижущая сила источника тока
Что такое электродвижущая сила — определение, физический смысл
Определение
Электродвижущая сила (ЭДС) — физическая величина, описывающая работу любых сил, которые действуют в квазистационарных цепях постоянного или переменного тока, за исключением диссипативных и электростатических сил.
Для определения силы тока Георг Симон Ом использовал принцип крутильных весов Кулона. На длинной тонкой нити подвешено горизонтальное коромысло с заряженным шариком на конце. Второй заряд закреплен на cпицe, пропущенной сквозь крышку весов. При их взаимодействии коромысло поворачивается. Вращение головки в верхней части весов закручивало нить, возвращая коромысло в исходное состояние. По углу закручивания можно рассчитать силу взаимодействия зарядов в зависимости от расстояния между ними.
Ом по величине угла закрутки судил о силе тока I в проводнике, т. е. количестве электричества, перенесенном через поперечное сечение проводника за единицу времени. В качестве основной характеристики источника тока Ом брал величину напряжения varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину (varepsilon) он назвал электродвижущей силой, сокращенно ЭДС.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В чем измеряется в системе СИ, как обозначается на схеме
Электродвижущая сила в системе СИ измеряется в вольтах.
На схеме обозначение источника тока с ЭДС — две линии с плюсом и минусом, иногда круг.
Природа ЭДС, какими причинами порождается
Определение
Термопара — проволоки из разнородных металлов, соединенные концами.
Изучая термопары, немецкий физик Томас Иоганн Зеебек обнаружил в 1821 году следующую закономерность: когда точки соединения имеют разную температуру, в цепи возникает электродвижущая сила. Это явление назвали термоэлектрическим эффектом Зеебека. Величина такой электродвижущей силы зависит от температуры и неодинакова для разных пар металлов. Наиболее точных измерений Ом добился в 1826 году, использовав термопару из меди и висмута.
Внутри источника ЭДС электрический ток течет не от «плюса» к «минусу», а в противоположном направлении. Чтобы заставить ток двигаться в направлении, противоположном электростатической силе, которая воздействует на положительные заряды, необходимо приложить стороннюю силу: силу Лоренца, силу электрохимической природы, центробежную силу и т. п. Диссипативные силы не могут двигать электрические заряды против направления электростатической силы, поэтому к сторонним силам в данном случае не относятся.
По какой формуле определяется электродвижущая сила
В первых опытах Ом подключал к источнику тока проводники из разных материалов — серебра, меди, золота, — но одинакового сечения. Изменяя их длину l, Ом добивался, чтобы получалась одна и та же сила тока I. Обобщив результаты измерений, он вывел отношение:
(I;=;fracvarepsilon{R_i;+;R(l)})
Здесь (R_i) — некоторая постоянная, характеризующая внутреннее сопротивление гальванического элемента, а (R(l)) — величина, названная Омом сопротивлением проводника; она оказалась пропорциональна его длине, т. е. (;R(l);sim;l.)
Из этой формулы следует, что найти электродвижущую силу можно, перемножив силу тока и полное сопротивление всей цепи:
(varepsilon;=;I;times;R_i;+;I;times;R(l))
Разность потенциалов на концах участка цепи равна падению напряжения на нем. Если в цепь включен источник тока, то ЭДС прибавляется к величине разности потенциалов или вычитается из нее в зависимости от полярности подключения. Когда на участке АВ имеется источник тока с ЭДС (varepsilon), разность потенциалов изменяется на величину (triangle U;=;pm;varepsilon.)
Знак выбирается в зависимости от полярности включения источника: по току или против него. Закон Ома в этом случае принимает вид:
(varphi_А;-;varphi_В;pm;varepsilon;=;IR)
При последовательном соединении источников полная электродвижущая сила цепи будет равняться сумме ЭДС отдельных источников. При параллельном соединении только источник с самой большой ЭДС будет источником, остальные окажутся потребителями.
Чему равна электродвижущая сила источника тока
ЭДС источника тока — это работа сторонних сил, нужная для перемещения единичного положительного заряда внутри источника от одного полюса к другому. Эту работу нельзя выразить через разность потенциалов, так как сторонние силы не имеют потенциала, их работа зависит от траектории.
Пример
При перемещении заряда между клеммами источника вне самого источника работа сторонних сил окажется нулевой.
Насколько полезной была для вас статья?
Рейтинг: 3.67 (Голосов: 3)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так











![{displaystyle {begin{aligned}{mathcal {E}}&=oint _{C}left[{boldsymbol {E}}+{boldsymbol {v}}times {boldsymbol {B}}right]cdot mathrm {d} {boldsymbol {ell }}\&qquad +{frac {1}{q}}oint _{C}mathrm {Effective chemical forces cdot } mathrm {d} {boldsymbol {ell }}\&qquad qquad +{frac {1}{q}}oint _{C}mathrm {Effective thermal forces cdot } mathrm {d} {boldsymbol {ell }} ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d30a15eac236d54cf1c56bd3b8cbb91fd8d9fb3)
![{displaystyle oint _{C}left[{boldsymbol {E}}+{boldsymbol {v}}times {boldsymbol {B}}right]cdot mathrm {d} {boldsymbol {ell }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92bcd9e5016deec860a048a08132ca5c97f65d0)