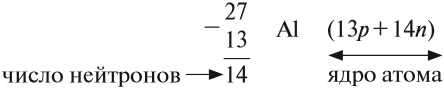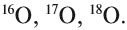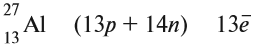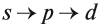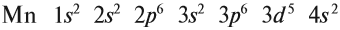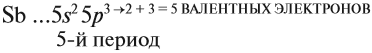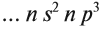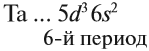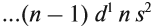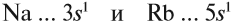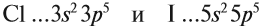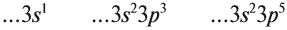Атомно-молекулярное учение
Мы приступаем к изучению химии — мира молекул и атомов. В этой статье мы рассмотрим базисные понятия и разберемся с электронными
формулами элементов.
Атом (греч. а — отриц. частица + tomos — отдел, греч. atomos — неделимый) — электронейтральная частица вещества микроскопических
размеров и массы, состоящая из положительно заряженного ядра (протонов) и отрицательно заряженных электронов (электронные орбитали).
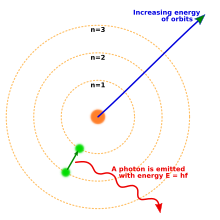
Описываемая модель атома называется «планетарной» и была предложена в 1913 году великими физиками: Нильсом Бором и Эрнестом Резерфордом
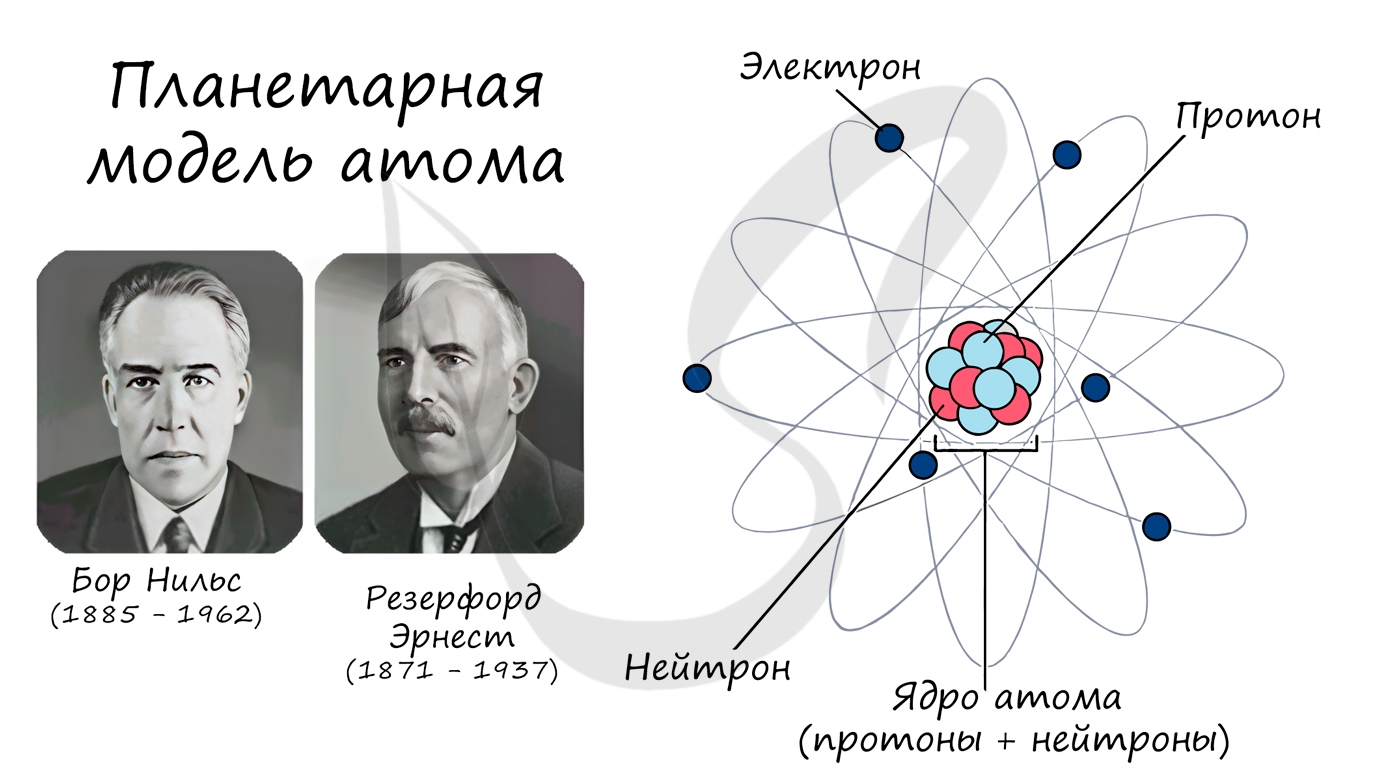
Протон (греч. protos — первый) — положительно заряженная (+1) элементарная частица, вместе с нейтронами образует ядра атомов
элементов. Нейтрон (лат. neuter — ни тот, ни другой) — нейтральная (0) элементарная частица, присутствующая в ядрах всех
химических элементов, кроме водорода.
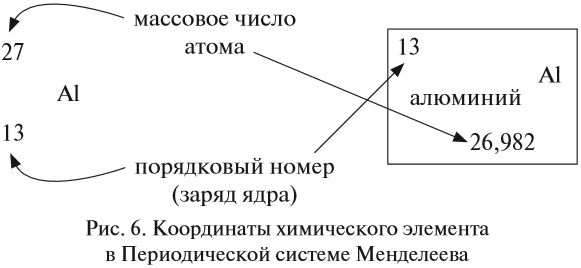
Электрон (греч. elektron — янтарь) — стабильная элементарная частица с отрицательным электрическим зарядом (-1), заряд атома —
порядковый номер в таблице Менделеева — равен числу электронов (и, соответственно, протонов).
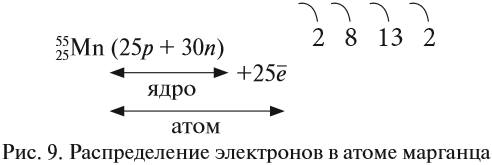
Запомните, что в невозбужденном состоянии атом содержит одинаковое число электронов и протонов. Так у кальция (порядковый номер 20)
в ядре находится 20 протонов, а вокруг ядра на электронных орбиталях 20 электронов.

Я еще раз подчеркну эту важную деталь. На данном этапе будет отлично, если вы запомните простое правило:
порядковый номер элемента = числу электронов. Это наиболее важно для практического применения и изучения следующей темы.
Электронная конфигурация атома
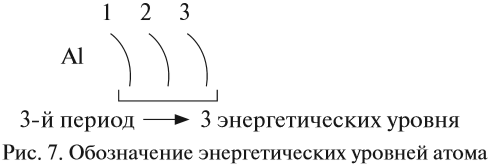
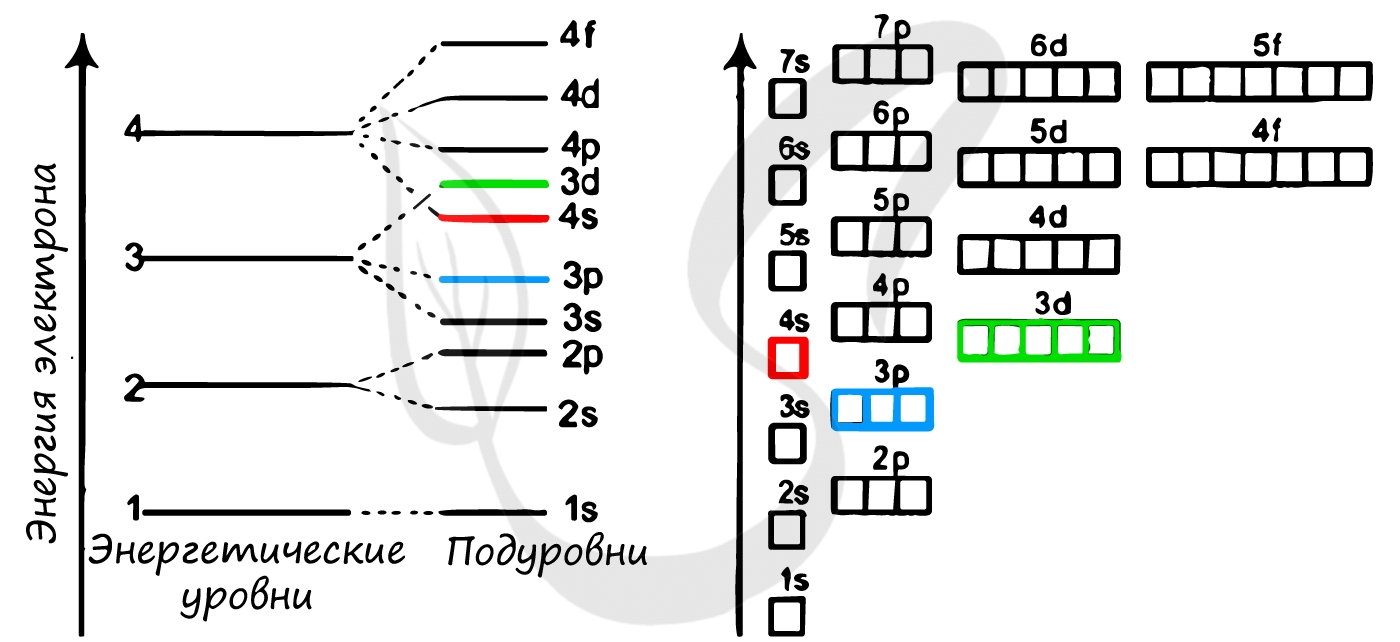
Электроны атома находятся в непрерывном движении вокруг ядра. Энергия электронов отличается друг от друга, в соответствии с этим
электроны занимают различные энергетические уровни.
Энергетические уровни подразделяются на несколько подуровней:
- Первый уровень
- Второй уровень
- Третий уровень
- Четвертый уровень
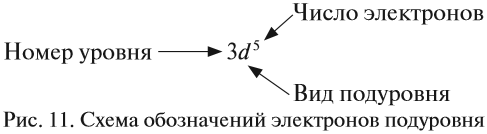
Состоит из s-подуровня: одной «1s» ячейки, в которой помещаются 2 электрона (заполненный электронами — 1s2)
Состоит из s-подуровня: одной «s» ячейки (2s2) и p-подуровня: трех «p» ячеек (2p6), на которых
помещается 6 электронов
Состоит из s-подуровня: одной «s» ячейки (3s2), p-подуровня: трех «p» ячеек (3p6) и d-подуровня:
пяти «d» ячеек (3d10), в которых помещается 10 электронов
Состоит из s-подуровня: одной «s» ячейки (4s2), p-подуровня: трех «p» ячеек (4p6), d-подуровня:
пяти «d» ячеек (4d10) и f-подуровня: семи «f» ячеек (4f14), на которых помещается 14
электронов
Зная теорию об энергетических уровнях и порядковый номер элемента из таблицы Менделеева, вы должны расположить определенное число
электронов, начиная от уровня с наименьшей энергией и заканчивая к уровнем с наибольшей. Чуть ниже вы увидите несколько примеров, а
также узнаете об исключении, которое только подтверждает данные правила.
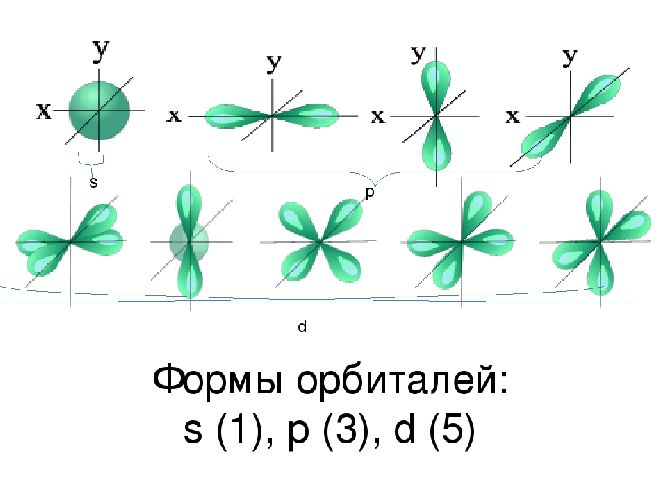
Подуровни: «s», «p» и «d», которые мы только что обсудили, имеют в определенную конфигурацию в пространстве. По этим подуровням, или
атомным орбиталям, движутся электроны, создавая определенный «рисунок».
S-орбиталь похожа на сферу, p-орбиталь напоминает песочные часы, d-орбиталь — клеверный лист.
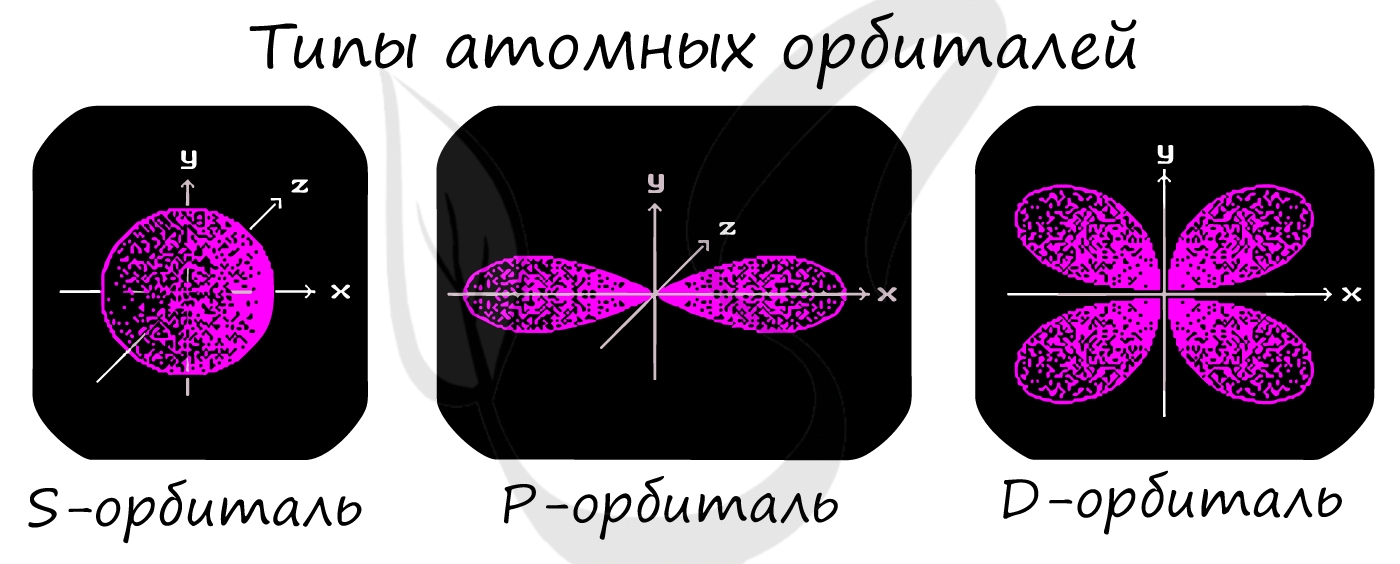
Правила заполнения электронных орбиталей и примеры
Существует ряд правил, которые применяют при составлении электронных конфигураций атомов:
- Сперва следует заполнить орбитали с наименьшей энергией, и только после переходить к энергетически более высоким
- На орбитали (в одной «ячейке») не может располагаться более двух электронов
- Орбитали заполняются электронами так: сначала в каждую ячейку помещают по одному электрону, после чего орбитали дополняются
еще одним электроном с противоположным направлением - Порядок заполнения орбиталей: 1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p → 5s → 4d → 5p → 6s
Должно быть, вы обратили внимание на некоторое несоответствие: после 3p подуровня следует переход к 4s, хотя логично было
бы заполнить до конца 4s подуровень. Однако природа распорядилась иначе.
Запомните, что, только заполнив 4s подуровень двумя электронами, можно переходить к 3d подуровню.
Без практики теория мертва, так что приступает к тренировке. Нам нужно составить электронную конфигурацию атомов углерода и
серы. Для начала определим их порядковый номер, который подскажет нам число их электронов. У углерода — 6, у серы — 16.
Теперь мы располагаем указанное количество электронов на энергетических уровнях, руководствуясь правилами заполнения.
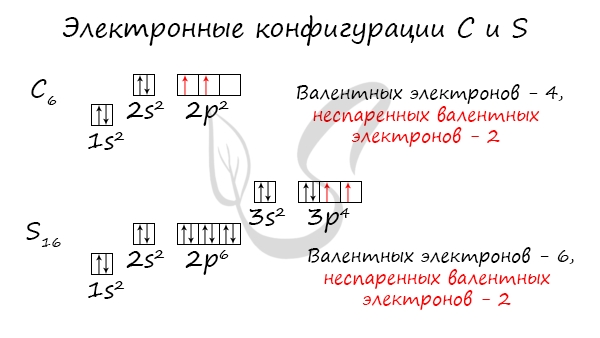
Обращаю ваше особе внимание: на 2p-подуровне углерода мы расположили 2 электрона в разные ячейки, следуя одному из правил.
А на 3p-подуровне у серы электронов оказалось много, поэтому сначала мы расположили 3 электрона по отдельным ячейкам, а оставшимся
одним электроном дополнили первую ячейку.
Таким образом, электронные конфигурации наших элементов:
- Углерод — 1s22s22p2
- Серы — 1s22s22p63s23p4
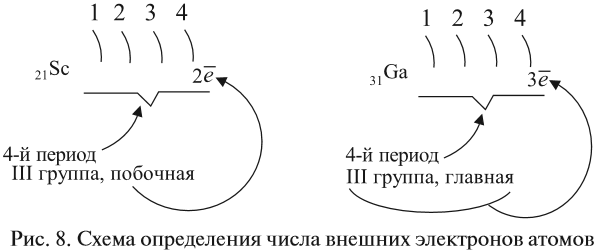
Внешний уровень и валентные электроны
Количество электронов на внешнем (валентном) уровне — это число электронов на наивысшем энергетическом уровне, которого достигает элемент. Такие электроны называются валентными: они могут быть спаренными или неспаренными. Иногда
для наглядного представления конфигурацию внешнего уровня записывают отдельно:
- Углерод — 2s22p2 (4 валентных электрона)
- Сера -3s23p4 (6 валентных электронов)
Неспаренные валентные электроны способны к образованию химической связи. Их число соответствует количеству связей, которые данный атом может образовать с другими атомами. Таким образом неспаренные валентные электроны тесно связаны с валентностью — способностью атомов образовывать определенное число химических связей.
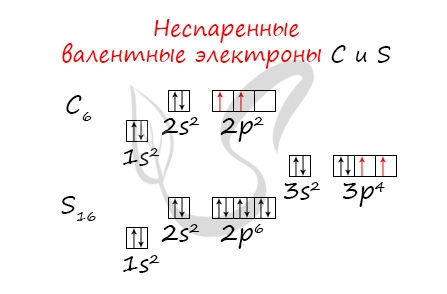
- Углерод — 2s22p2 (2 неспаренных валентных электрона)
- Сера -3s23p4 (2 неспаренных валентных электрона)
Тренировка
Потренируйтесь и сами составьте электронную конфигурацию для магния и скандия. Определите число электронов на внешнем (валентном) уровне и число неспаренных
электронов. Ниже будет дано наглядное объяснение этой задаче.

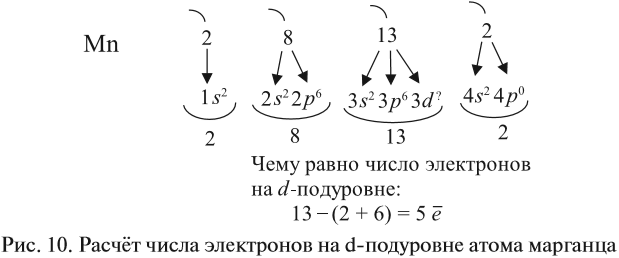
Запишем получившиеся электронные конфигурации магния и скандия:
- Магний — 1s22s22p63s2
- Скандий — 1s22s22p63s23p64s23d1
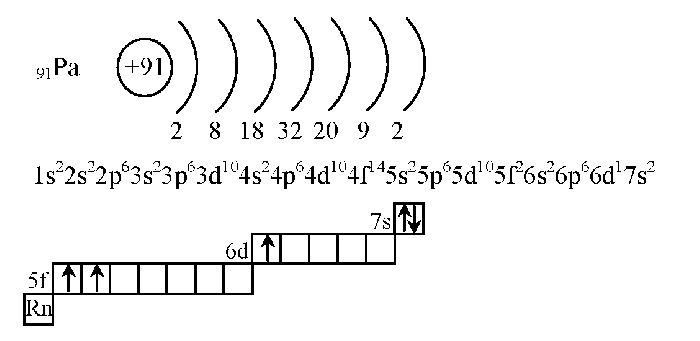
В целом несложная и интересная тема электронных конфигураций отягощена небольшим исключением — провалом электрона, которое только подтверждает общее
правило: любая система стремится занять наименее энергозатратное состояние.
Провал электрона
Провалом электрона называют переход электрона с внешнего, более высокого энергетического уровня, на предвнешний, энергетически более
низкий. Это связано с большей энергетической устойчивостью получающихся при этом электронных конфигураций.
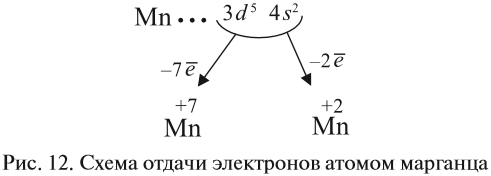
Подобное явление характерно лишь для некоторых элементов: медь, хром, серебро, золото, молибден. Для примера выберем хром, и рассмотрим
две электронных конфигурации: первую «неправильную» (сделаем вид, будто мы не знаем про провал электрона) и вторую правильную, написанную
с учетом провала электрона.
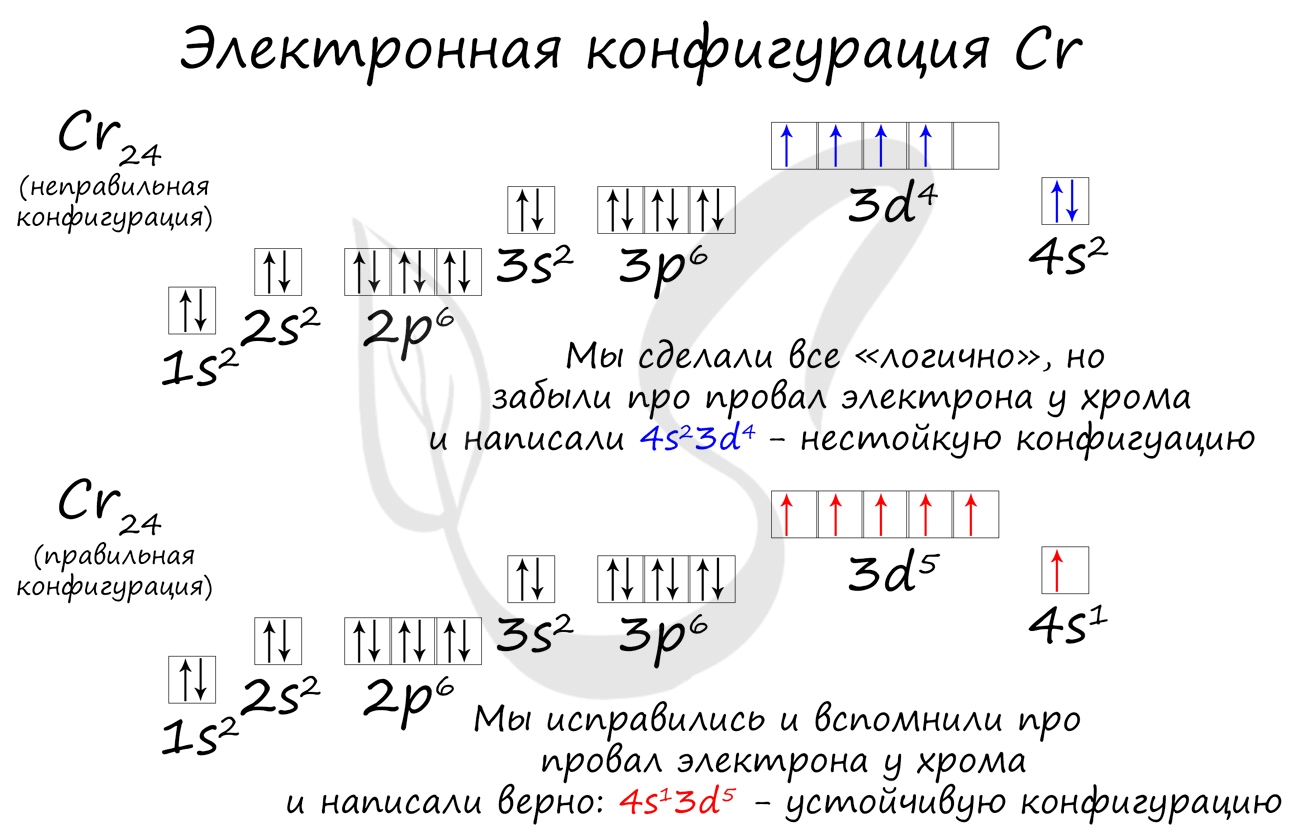
Теперь вы понимаете, что кроется под явлением провала электрона. Запишите электронные конфигурации хрома и меди самостоятельно еще раз и
сверьте с представленными ниже.

Основное и возбужденное состояние атома
Основное и возбужденное состояние атома отражаются на электронных конфигурациях. Возбужденное состояние связано с движением электронов
относительно атомных ядер. Говоря проще: при возбуждении пары электронов распариваются и занимают новые ячейки.
Возбужденное состояние является для атома нестабильным, поэтому долгое время в нем он пребывать не может. У некоторых атомов: азота,
кислорода , фтора — возбужденное состояние невозможно, так как отсутствуют свободные орбитали («ячейки») — электронам некуда перескакивать, к тому
же d-орбиталь у них отсутствует (они во втором периоде).
У серы возможно возбужденное состояние, так как она имеет свободную d-орбиталь, куда могут перескочить электроны. Четвертый энергетический
уровень отсутствует, поэтому, минуя 4s-подуровень, заполняем распаренными электронами 3d-подуровень.
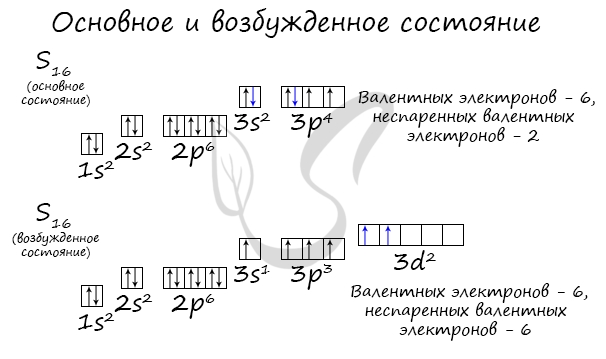
По мере изучения основ общей химии мы еще не раз вернемся к этой теме, однако хорошо, если вы уже сейчас запомните, что возбужденное состояние
связано с распаривание электронных пар.
© Беллевич Юрий Сергеевич 2018-2022
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.

Hydrogen atomic orbitals at different energy levels. The more opaque areas are where one is most likely to find an electron at any given time. |
|
| Composition | elementary particle[1] |
|---|---|
| Statistics | fermionic |
| Family | lepton |
| Generation | first |
| Interactions | weak, electromagnetic, gravity |
| Symbol | e− , β− |
| Antiparticle | positron[a] |
| Theorized | Richard Laming (1838–1851),[2] G. Johnstone Stoney (1874) and others.[3][4] |
| Discovered | J. J. Thomson (1897)[5] |
| Mass | 9.1093837015(28)×10−31 kg[6] 5.48579909065(16)×10−4 Da[7] [1822.888486209(53)]−1 Da[b] 0.51099895000(15) MeV/c2[8] |
| Mean lifetime | stable ( > 6.6×1028 yr[9]) |
| Electric charge | −1 e −1.602176634×10−19 C[10] |
| Magnetic moment | −9.2847647043(28)×10−24 J⋅T−1[11] −1.00115965218128(18) µB[12] |
| Spin | 1 /2 |
| Weak isospin | LH: − 1 /2, RH: 0 |
| Weak hypercharge | LH: −1, RH: −2 |
The electron (
e−
or
β−
) is a subatomic particle with a negative one elementary electric charge.[13] Electrons belong to the first generation of the lepton particle family,[14] and are generally thought to be elementary particles because they have no known components or substructure.[1] The electron’s mass is approximately 1/1836 that of the proton.[15] Quantum mechanical properties of the electron include an intrinsic angular momentum (spin) of a half-integer value, expressed in units of the reduced Planck constant, ħ. Being fermions, no two electrons can occupy the same quantum state, in accordance with the Pauli exclusion principle.[14] Like all elementary particles, electrons exhibit properties of both particles and waves: They can collide with other particles and can be diffracted like light. The wave properties of electrons are easier to observe with experiments than those of other particles like neutrons and protons because electrons have a lower mass and hence a longer de Broglie wavelength for a given energy.
Electrons play an essential role in numerous physical phenomena, such as electricity, magnetism, chemistry and thermal conductivity, and they also participate in gravitational, electromagnetic and weak interactions.[16] Since an electron has charge, it has a surrounding electric field, and if that electron is moving relative to an observer, said observer will observe it to generate a magnetic field. Electromagnetic fields produced from other sources will affect the motion of an electron according to the Lorentz force law. Electrons radiate or absorb energy in the form of photons when they are accelerated.
Laboratory instruments are capable of trapping individual electrons as well as electron plasma by the use of electromagnetic fields. Special telescopes can detect electron plasma in outer space. Electrons are involved in many applications such as tribology or frictional charging, electrolysis, electrochemistry, battery technologies, electronics, welding, cathode-ray tubes, photoelectricity, photovoltaic solar panels, electron microscopes, radiation therapy, lasers, gaseous ionization detectors and particle accelerators.
Interactions involving electrons with other subatomic particles are of interest in fields such as chemistry and nuclear physics. The Coulomb force interaction between the positive protons within atomic nuclei and the negative electrons without, allows the composition of the two known as atoms. Ionization or differences in the proportions of negative electrons versus positive nuclei changes the binding energy of an atomic system. The exchange or sharing of the electrons between two or more atoms is the main cause of chemical bonding.[17] In 1838, British natural philosopher Richard Laming first hypothesized the concept of an indivisible quantity of electric charge to explain the chemical properties of atoms.[3] Irish physicist George Johnstone Stoney named this charge ‘electron’ in 1891, and J. J. Thomson and his team of British physicists identified it as a particle in 1897 during the cathode-ray tube experiment.[5] Electrons can also participate in nuclear reactions, such as nucleosynthesis in stars, where they are known as beta particles. Electrons can be created through beta decay of radioactive isotopes and in high-energy collisions, for instance when cosmic rays enter the atmosphere. The antiparticle of the electron is called the positron; it is identical to the electron except that it carries electrical charge of the opposite sign. When an electron collides with a positron, both particles can be annihilated, producing gamma ray photons.
History[edit]
Discovery of effect of electric force[edit]
The ancient Greeks noticed that amber attracted small objects when rubbed with fur. Along with lightning, this phenomenon is one of humanity’s earliest recorded experiences with electricity.[18] In his 1600 treatise De Magnete, the English scientist William Gilbert coined the New Latin term electrica, to refer to those substances with property similar to that of amber which attract small objects after being rubbed.[19] Both electric and electricity are derived from the Latin ēlectrum (also the root of the alloy of the same name), which came from the Greek word for amber, ἤλεκτρον (ēlektron).
Discovery of two kinds of charges[edit]
In the early 1700s, French chemist Charles François du Fay found that if a charged gold-leaf is repulsed by glass rubbed with silk, then the same charged gold-leaf is attracted by amber rubbed with wool. From this and other results of similar types of experiments, du Fay concluded that electricity consists of two electrical fluids, vitreous fluid from glass rubbed with silk and resinous fluid from amber rubbed with wool. These two fluids can neutralize each other when combined.[19][20] American scientist Ebenezer Kinnersley later also independently reached the same conclusion.[21]: 118 A decade later Benjamin Franklin proposed that electricity was not from different types of electrical fluid, but a single electrical fluid showing an excess (+) or deficit (−). He gave them the modern charge nomenclature of positive and negative respectively.[22] Franklin thought of the charge carrier as being positive, but he did not correctly identify which situation was a surplus of the charge carrier, and which situation was a deficit.[23]
Between 1838 and 1851, British natural philosopher Richard Laming developed the idea that an atom is composed of a core of matter surrounded by subatomic particles that had unit electric charges.[2] Beginning in 1846, German physicist Wilhelm Eduard Weber theorized that electricity was composed of positively and negatively charged fluids, and their interaction was governed by the inverse square law. After studying the phenomenon of electrolysis in 1874, Irish physicist George Johnstone Stoney suggested that there existed a «single definite quantity of electricity», the charge of a monovalent ion. He was able to estimate the value of this elementary charge e by means of Faraday’s laws of electrolysis.[24] However, Stoney believed these charges were permanently attached to atoms and could not be removed. In 1881, German physicist Hermann von Helmholtz argued that both positive and negative charges were divided into elementary parts, each of which «behaves like atoms of electricity».[3]
Stoney initially coined the term electrolion in 1881. Ten years later, he switched to electron to describe these elementary charges, writing in 1894: «… an estimate was made of the actual amount of this most remarkable fundamental unit of electricity, for which I have since ventured to suggest the name electron«. A 1906 proposal to change to electrion failed because Hendrik Lorentz preferred to keep electron.[25][26] The word electron is a combination of the words electric and ion.[27] The suffix —on which is now used to designate other subatomic particles, such as a proton or neutron, is in turn derived from electron.[28][29]
Discovery of free electrons outside matter[edit]
A beam of electrons deflected by a magnetic field into a circle[30]
While studying electrical conductivity in rarefied gases in 1859, the German physicist Julius Plücker observed the radiation emitted from the cathode caused phosphorescent light to appear on the tube wall near the cathode; and the region of the phosphorescent light could be moved by application of a magnetic field.[31] In 1869, Plücker’s student Johann Wilhelm Hittorf found that a solid body placed in between the cathode and the phosphorescence would cast a shadow upon the phosphorescent region of the tube. Hittorf inferred that there are straight rays emitted from the cathode and that the phosphorescence was caused by the rays striking the tube walls. In 1876, the German physicist Eugen Goldstein showed that the rays were emitted perpendicular to the cathode surface, which distinguished between the rays that were emitted from the cathode and the incandescent light. Goldstein dubbed the rays cathode rays.[32][33]: 393 Decades of experimental and theoretical research involving cathode rays were important in J. J. Thomson’s eventual discovery of electrons.[3]
During the 1870s, the English chemist and physicist Sir William Crookes developed the first cathode-ray tube to have a high vacuum inside.[34] He then showed in 1874 that the cathode rays can turn a small paddle wheel when placed in their path. Therefore, he concluded that the rays carried momentum. Furthermore, by applying a magnetic field, he was able to deflect the rays, thereby demonstrating that the beam behaved as though it were negatively charged.[32] In 1879, he proposed that these properties could be explained by regarding cathode rays as composed of negatively charged gaseous molecules in a fourth state of matter in which the mean free path of the particles is so long that collisions may be ignored.[33]: 394–395
The German-born British physicist Arthur Schuster expanded upon Crookes’s experiments by placing metal plates parallel to the cathode rays and applying an electric potential between the plates.[35] The field deflected the rays toward the positively charged plate, providing further evidence that the rays carried negative charge. By measuring the amount of deflection for a given level of current, in 1890 Schuster was able to estimate the charge-to-mass ratio[c] of the ray components. However, this produced a value that was more than a thousand times greater than what was expected, so little credence was given to his calculations at the time.[32] This is because it was assumed that the charge carriers were much heavier hydrogen or nitrogen atoms.[35] Schuster’s estimates would subsequently turn out to be largely correct.
In 1892 Hendrik Lorentz suggested that the mass of these particles (electrons) could be a consequence of their electric charge.[36]
While studying naturally fluorescing minerals in 1896, the French physicist Henri Becquerel discovered that they emitted radiation without any exposure to an external energy source. These radioactive materials became the subject of much interest by scientists, including the New Zealand physicist Ernest Rutherford who discovered they emitted particles. He designated these particles alpha and beta, on the basis of their ability to penetrate matter.[37] In 1900, Becquerel showed that the beta rays emitted by radium could be deflected by an electric field, and that their mass-to-charge ratio was the same as for cathode rays.[38] This evidence strengthened the view that electrons existed as components of atoms.[39][40]
In 1897, the British physicist J. J. Thomson, with his colleagues John S. Townsend and H. A. Wilson, performed experiments indicating that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier.[5] Thomson made good estimates of both the charge e and the mass m, finding that cathode ray particles, which he called «corpuscles», had perhaps one thousandth of the mass of the least massive ion known: hydrogen.[5] He showed that their charge-to-mass ratio, e/m, was independent of cathode material. He further showed that the negatively charged particles produced by radioactive materials, by heated materials and by illuminated materials were universal.[5][41] The name electron was adopted for these particles by the scientific community, mainly due to the advocation by G. F. FitzGerald, J. Larmor, and H. A. Lorentz.[42]: 273 In the same year Emil Wiechert and Walter Kaufmann also calculated the e/m ratio but they failed short of interpreting their results while J. J. Thomson would subsequently in 1899 give estimates for the electron charge and mass as well: e~6.8×10−10 esu and m~3×10−26 g[43][44]
The electron’s charge was more carefully measured by the American physicists Robert Millikan and Harvey Fletcher in their oil-drop experiment of 1909, the results of which were published in 1911. This experiment used an electric field to prevent a charged droplet of oil from falling as a result of gravity. This device could measure the electric charge from as few as 1–150 ions with an error margin of less than 0.3%. Comparable experiments had been done earlier by Thomson’s team,[5] using clouds of charged water droplets generated by electrolysis, and in 1911 by Abram Ioffe, who independently obtained the same result as Millikan using charged microparticles of metals, then published his results in 1913.[45] However, oil drops were more stable than water drops because of their slower evaporation rate, and thus more suited to precise experimentation over longer periods of time.[46]
Around the beginning of the twentieth century, it was found that under certain conditions a fast-moving charged particle caused a condensation of supersaturated water vapor along its path. In 1911, Charles Wilson used this principle to devise his cloud chamber so he could photograph the tracks of charged particles, such as fast-moving electrons.[47]
Atomic theory[edit]
The Bohr model of the atom, showing states of an electron with energy quantized by the number n. An electron dropping to a lower orbit emits a photon equal to the energy difference between the orbits.
By 1914, experiments by physicists Ernest Rutherford, Henry Moseley, James Franck and Gustav Hertz had largely established the structure of an atom as a dense nucleus of positive charge surrounded by lower-mass electrons.[48] In 1913, Danish physicist Niels Bohr postulated that electrons resided in quantized energy states, with their energies determined by the angular momentum of the electron’s orbit about the nucleus. The electrons could move between those states, or orbits, by the emission or absorption of photons of specific frequencies. By means of these quantized orbits, he accurately explained the spectral lines of the hydrogen atom.[49] However, Bohr’s model failed to account for the relative intensities of the spectral lines and it was unsuccessful in explaining the spectra of more complex atoms.[48]
Chemical bonds between atoms were explained by Gilbert Newton Lewis, who in 1916 proposed that a covalent bond between two atoms is maintained by a pair of electrons shared between them.[50] Later, in 1927, Walter Heitler and Fritz London gave the full explanation of the electron-pair formation and chemical bonding in terms of quantum mechanics.[51] In 1919, the American chemist Irving Langmuir elaborated on the Lewis’s static model of the atom and suggested that all electrons were distributed in successive «concentric (nearly) spherical shells, all of equal thickness».[52] In turn, he divided the shells into a number of cells each of which contained one pair of electrons. With this model Langmuir was able to qualitatively explain the chemical properties of all elements in the periodic table,[51] which were known to largely repeat themselves according to the periodic law.[53]
In 1924, Austrian physicist Wolfgang Pauli observed that the shell-like structure of the atom could be explained by a set of four parameters that defined every quantum energy state, as long as each state was occupied by no more than a single electron. This prohibition against more than one electron occupying the same quantum energy state became known as the Pauli exclusion principle.[54] The physical mechanism to explain the fourth parameter, which had two distinct possible values, was provided by the Dutch physicists Samuel Goudsmit and George Uhlenbeck. In 1925, they suggested that an electron, in addition to the angular momentum of its orbit, possesses an intrinsic angular momentum and magnetic dipole moment.[48][55] This is analogous to the rotation of the Earth on its axis as it orbits the Sun. The intrinsic angular momentum became known as spin, and explained the previously mysterious splitting of spectral lines observed with a high-resolution spectrograph; this phenomenon is known as fine structure splitting.[56]
Quantum mechanics[edit]
In his 1924 dissertation Recherches sur la théorie des quanta (Research on Quantum Theory), French physicist Louis de Broglie hypothesized that all matter can be represented as a de Broglie wave in the manner of light.[57] That is, under the appropriate conditions, electrons and other matter would show properties of either particles or waves. The corpuscular properties of a particle are demonstrated when it is shown to have a localized position in space along its trajectory at any given moment.[58] The wave-like nature of light is displayed, for example, when a beam of light is passed through parallel slits thereby creating interference patterns. In 1927, George Paget Thomson discovered the interference effect was produced when a beam of electrons was passed through thin metal foils and by American physicists Clinton Davisson and Lester Germer by the reflection of electrons from a crystal of nickel.[59]
In quantum mechanics, the behavior of an electron in an atom is described by an orbital, which is a probability distribution rather than an orbit. In the figure, the shading indicates the relative probability to «find» the electron, having the energy corresponding to the given quantum numbers, at that point.
De Broglie’s prediction of a wave nature for electrons led Erwin Schrödinger to postulate a wave equation for electrons moving under the influence of the nucleus in the atom. In 1926, this equation, the Schrödinger equation, successfully described how electron waves propagated.[60] Rather than yielding a solution that determined the location of an electron over time, this wave equation also could be used to predict the probability of finding an electron near a position, especially a position near where the electron was bound in space, for which the electron wave equations did not change in time. This approach led to a second formulation of quantum mechanics (the first by Heisenberg in 1925), and solutions of Schrödinger’s equation, like Heisenberg’s, provided derivations of the energy states of an electron in a hydrogen atom that were equivalent to those that had been derived first by Bohr in 1913, and that were known to reproduce the hydrogen spectrum.[61] Once spin and the interaction between multiple electrons were describable, quantum mechanics made it possible to predict the configuration of electrons in atoms with atomic numbers greater than hydrogen.[62]
In 1928, building on Wolfgang Pauli’s work, Paul Dirac produced a model of the electron – the Dirac equation, consistent with relativity theory, by applying relativistic and symmetry considerations to the hamiltonian formulation of the quantum mechanics of the electro-magnetic field.[63] In order to resolve some problems within his relativistic equation, Dirac developed in 1930 a model of the vacuum as an infinite sea of particles with negative energy, later dubbed the Dirac sea. This led him to predict the existence of a positron, the antimatter counterpart of the electron.[64] This particle was discovered in 1932 by Carl Anderson, who proposed calling standard electrons negatrons and using electron as a generic term to describe both the positively and negatively charged variants.[65]
In 1947, Willis Lamb, working in collaboration with graduate student Robert Retherford, found that certain quantum states of the hydrogen atom, which should have the same energy, were shifted in relation to each other; the difference came to be called the Lamb shift. About the same time, Polykarp Kusch, working with Henry M. Foley, discovered the magnetic moment of the electron is slightly larger than predicted by Dirac’s theory. This small difference was later called anomalous magnetic dipole moment of the electron. This difference was later explained by the theory of quantum electrodynamics, developed by Sin-Itiro Tomonaga, Julian Schwinger and
Richard Feynman in the late 1940s.[66]
Particle accelerators[edit]
With the development of the particle accelerator during the first half of the twentieth century, physicists began to delve deeper into the properties of subatomic particles.[67] The first successful attempt to accelerate electrons using electromagnetic induction was made in 1942 by Donald Kerst. His initial betatron reached energies of 2.3 MeV, while subsequent betatrons achieved 300 MeV. In 1947, synchrotron radiation was discovered with a 70 MeV electron synchrotron at General Electric. This radiation was caused by the acceleration of electrons through a magnetic field as they moved near the speed of light.[68]
With a beam energy of 1.5 GeV, the first high-energy
particle collider was ADONE, which began operations in 1968.[69] This device accelerated electrons and positrons in opposite directions, effectively doubling the energy of their collision when compared to striking a static target with an electron.[70] The Large Electron–Positron Collider (LEP) at CERN, which was operational from 1989 to 2000, achieved collision energies of 209 GeV and made important measurements for the Standard Model of particle physics.[71][72]
Confinement of individual electrons[edit]
Individual electrons can now be easily confined in ultra small (L = 20 nm, W = 20 nm) CMOS transistors operated at cryogenic temperature over a range of −269 °C (4 K) to about −258 °C (15 K).[73] The electron wavefunction spreads in a semiconductor lattice and negligibly interacts with the valence band electrons, so it can be treated in the single particle formalism, by replacing its mass with the effective mass tensor.
Characteristics[edit]
Classification[edit]
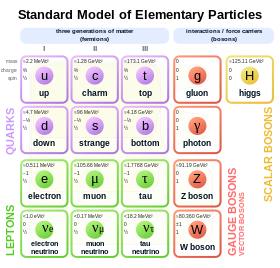
Standard Model of elementary particles. The electron (symbol e) is on the left.
In the Standard Model of particle physics, electrons belong to the group of subatomic particles called leptons, which are believed to be fundamental or elementary particles. Electrons have the lowest mass of any charged lepton (or electrically charged particle of any type) and belong to the first-generation of fundamental particles.[74] The second and third generation contain charged leptons, the muon and the tau, which are identical to the electron in charge, spin and interactions, but are more massive. Leptons differ from the other basic constituent of matter, the quarks, by their lack of strong interaction. All members of the lepton group are fermions, because they all have half-odd integer spin; the electron has spin 1/2.[75]
Fundamental properties[edit]
The invariant mass of an electron is approximately 9.109×10−31 kilograms,[76] or 5.489×10−4 atomic mass units. Due to mass–energy equivalence, this corresponds to a rest energy of 0.511 MeV. The ratio between the mass of a proton and that of an electron is about 1836.[15][77] Astronomical measurements show that the proton-to-electron mass ratio has held the same value, as is predicted by the Standard Model, for at least half the age of the universe.[78]
Electrons have an electric charge of −1.602176634×10−19 coulombs,[76] which is used as a standard unit of charge for subatomic particles, and is also called the elementary charge. Within the limits of experimental accuracy, the electron charge is identical to the charge of a proton, but with the opposite sign.[79] As the symbol e is used for the elementary charge, the electron is commonly symbolized by
e−
, where the minus sign indicates the negative charge. The positron is symbolized by
e+
because it has the same properties as the electron but with a positive rather than negative charge.[75][76]
The electron has an intrinsic angular momentum or spin of 1/2.[76] This property is usually stated by referring to the electron as a spin-1/2 particle.[75] For such particles the spin magnitude is ħ/2,[80][d] while the result of the measurement of a projection of the spin on any axis can only be ±ħ/2. In addition to spin, the electron has an intrinsic magnetic moment along its spin axis.[76] It is approximately equal to one Bohr magneton,[81][e] which is a physical constant equal to 9.27400915(23)×10−24 joules per tesla.[76] The orientation of the spin with respect to the momentum of the electron defines the property of elementary particles known as helicity.[82]
The electron has no known substructure.[1][83] Nevertheless, in condensed matter physics, spin–charge separation can occur in some materials. In such cases, electrons ‘split’ into three independent particles, the spinon, the orbiton and the holon (or chargon). The electron can always be theoretically considered as a bound state of the three, with the spinon carrying the spin of the electron, the orbiton carrying the orbital degree of freedom and the chargon carrying the charge, but in certain conditions they can behave as independent quasiparticles.[84][85][86]
The issue of the radius of the electron is a challenging problem of modern theoretical physics. The admission of the hypothesis of a finite radius of the electron is incompatible to the premises of the theory of relativity. On the other hand, a point-like electron (zero radius) generates serious mathematical difficulties due to the self-energy of the electron tending to infinity.[87] Observation of a single electron in a Penning trap suggests the upper limit of the particle’s radius to be 10−22 meters.[88]
The upper bound of the electron radius of 10−18 meters[89] can be derived using the uncertainty relation in energy. There is also a physical constant called the «classical electron radius», with the much larger value of 2.8179×10−15 m, greater than the radius of the proton. However, the terminology comes from a simplistic calculation that ignores the effects of quantum mechanics; in reality, the so-called classical electron radius has little to do with the true fundamental structure of the electron.[90][91][f]
There are elementary particles that spontaneously decay into less massive particles. An example is the muon, with a mean lifetime of 2.2×10−6 seconds, which decays into an electron, a muon neutrino and an electron antineutrino. The electron, on the other hand, is thought to be stable on theoretical grounds: the electron is the least massive particle with non-zero electric charge, so its decay would violate charge conservation.[92] The experimental lower bound for the electron’s mean lifetime is 6.6×1028 years, at a 90% confidence level.[9][93][94]
Quantum properties[edit]
As with all particles, electrons can act as waves. This is called the wave–particle duality and can be demonstrated using the double-slit experiment.
The wave-like nature of the electron allows it to pass through two parallel slits simultaneously, rather than just one slit as would be the case for a classical particle. In quantum mechanics, the wave-like property of one particle can be described mathematically as a complex-valued function, the wave function, commonly denoted by the Greek letter psi (ψ). When the absolute value of this function is squared, it gives the probability that a particle will be observed near a location—a probability density.[95]: 162–218
Electrons are identical particles because they cannot be distinguished from each other by their intrinsic physical properties. In quantum mechanics, this means that a pair of interacting electrons must be able to swap positions without an observable change to the state of the system. The wave function of fermions, including electrons, is antisymmetric, meaning that it changes sign when two electrons are swapped; that is, ψ(r1, r2) = −ψ(r2, r1), where the variables r1 and r2 correspond to the first and second electrons, respectively. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. Bosons, such as the photon, have symmetric wave functions instead.[95]: 162–218
In the case of antisymmetry, solutions of the wave equation for interacting electrons result in a zero probability that each pair will occupy the same location or state. This is responsible for the Pauli exclusion principle, which precludes any two electrons from occupying the same quantum state. This principle explains many of the properties of electrons. For example, it causes groups of bound electrons to occupy different orbitals in an atom, rather than all overlapping each other in the same orbit.[95]: 162–218
Virtual particles[edit]
In a simplified picture, which often tends to give the wrong idea but may serve to illustrate some aspects, every photon spends some time as a combination of a virtual electron plus its antiparticle, the virtual positron, which rapidly annihilate each other shortly thereafter.[96] The combination of the energy variation needed to create these particles, and the time during which they exist, fall under the threshold of detectability expressed by the Heisenberg uncertainty relation, ΔE · Δt ≥ ħ. In effect, the energy needed to create these virtual particles, ΔE, can be «borrowed» from the vacuum for a period of time, Δt, so that their product is no more than the reduced Planck constant, ħ ≈ 6.6×10−16 eV·s. Thus, for a virtual electron, Δt is at most 1.3×10−21 s.[97]
A schematic depiction of virtual electron–positron pairs appearing at random near an electron (at lower left)
While an electron–positron virtual pair is in existence, the Coulomb force from the ambient electric field surrounding an electron causes a created positron to be attracted to the original electron, while a created electron experiences a repulsion. This causes what is called vacuum polarization. In effect, the vacuum behaves like a medium having a dielectric permittivity more than unity. Thus the effective charge of an electron is actually smaller than its true value, and the charge decreases with increasing distance from the electron.[98][99] This polarization was confirmed experimentally in 1997 using the Japanese TRISTAN particle accelerator.[100] Virtual particles cause a comparable shielding effect for the mass of the electron.[101]
The interaction with virtual particles also explains the small (about 0.1%) deviation of the intrinsic magnetic moment of the electron from the Bohr magneton (the anomalous magnetic moment).[81][102] The extraordinarily precise agreement of this predicted difference with the experimentally determined value is viewed as one of the great achievements of quantum electrodynamics.[103]
The apparent paradox in classical physics of a point particle electron having intrinsic angular momentum and magnetic moment can be explained by the formation of virtual photons in the electric field generated by the electron. These photons can heuristically be thought of as causing the electron to shift about in a jittery fashion (known as zitterbewegung), which results in a net circular motion with precession.[104] This motion produces both the spin and the magnetic moment of the electron.[14] In atoms, this creation of virtual photons explains the Lamb shift observed in spectral lines.[98] The Compton Wavelength shows that near elementary particles such as the electron, the uncertainty of the energy allows for the creation of virtual particles near the electron. This wavelength explains the «static» of virtual particles around elementary particles at a close distance.
Interaction[edit]
An electron generates an electric field that exerts an attractive force on a particle with a positive charge, such as the proton, and a repulsive force on a particle with a negative charge. The strength of this force in nonrelativistic approximation is determined by Coulomb’s inverse square law.[105]: 58–61 When an electron is in motion, it generates a magnetic field.[95]: 140 The Ampère–Maxwell law relates the magnetic field to the mass motion of electrons (the current) with respect to an observer. This property of induction supplies the magnetic field that drives an electric motor.[106] The electromagnetic field of an arbitrary moving charged particle is expressed by the Liénard–Wiechert potentials, which are valid even when the particle’s speed is close to that of light (relativistic).[105]: 429–434
A particle with charge q (at left) is moving with velocity v through a magnetic field B that is oriented toward the viewer. For an electron, q is negative so it follows a curved trajectory toward the top.
When an electron is moving through a magnetic field, it is subject to the Lorentz force that acts perpendicularly to the plane defined by the magnetic field and the electron velocity. This centripetal force causes the electron to follow a helical trajectory through the field at a radius called the gyroradius. The acceleration from this curving motion induces the electron to radiate energy in the form of synchrotron radiation.[107][g][95]: 160 The energy emission in turn causes a recoil of the electron, known as the Abraham–Lorentz–Dirac Force, which creates a friction that slows the electron. This force is caused by a back-reaction of the electron’s own field upon itself.[108]
Here, Bremsstrahlung is produced by an electron e deflected by the electric field of an atomic nucleus. The energy change E2 − E1 determines the frequency f of the emitted photon.
Photons mediate electromagnetic interactions between particles in quantum electrodynamics. An isolated electron at a constant velocity cannot emit or absorb a real photon; doing so would violate conservation of energy and momentum. Instead, virtual photons can transfer momentum between two charged particles. This exchange of virtual photons, for example, generates the Coulomb force.[109] Energy emission can occur when a moving electron is deflected by a charged particle, such as a proton. The acceleration of the electron results in the emission of Bremsstrahlung radiation.[110]
An inelastic collision between a photon (light) and a solitary (free) electron is called Compton scattering. This collision results in a transfer of momentum and energy between the particles, which modifies the wavelength of the photon by an amount called the Compton shift.[h] The maximum magnitude of this wavelength shift is h/mec, which is known as the Compton wavelength.[111] For an electron, it has a value of 2.43×10−12 m.[76] When the wavelength of the light is long (for instance, the wavelength of the visible light is 0.4–0.7 μm) the wavelength shift becomes negligible. Such interaction between the light and free electrons is called Thomson scattering or linear Thomson scattering.[112]
The relative strength of the electromagnetic interaction between two charged particles, such as an electron and a proton, is given by the fine-structure constant. This value is a dimensionless quantity formed by the ratio of two energies: the electrostatic energy of attraction (or repulsion) at a separation of one Compton wavelength, and the rest energy of the charge. It is given by α ≈ 7.297353×10−3, which is approximately equal to 1/137.[76]
When electrons and positrons collide, they annihilate each other, giving rise to two or more gamma ray photons. If the electron and positron have negligible momentum, a positronium atom can form before annihilation results in two or three gamma ray photons totalling 1.022 MeV.[113][114] On the other hand, a high-energy photon can transform into an electron and a positron by a process called pair production, but only in the presence of a nearby charged particle, such as a nucleus.[115][116]
In the theory of electroweak interaction, the left-handed component of electron’s wavefunction forms a weak isospin doublet with the electron neutrino. This means that during weak interactions, electron neutrinos behave like electrons. Either member of this doublet can undergo a charged current interaction by emitting or absorbing a
W
and be converted into the other member. Charge is conserved during this reaction because the W boson also carries a charge, canceling out any net change during the transmutation. Charged current interactions are responsible for the phenomenon of beta decay in a radioactive atom. Both the electron and electron neutrino can undergo a neutral current interaction via a
Z0
exchange, and this is responsible for neutrino-electron elastic scattering.[117]
Atoms and molecules[edit]
Main article: Atom
Probability densities for the first few hydrogen atom orbitals, seen in cross-section. The energy level of a bound electron determines the orbital it occupies, and the color reflects the probability of finding the electron at a given position.
An electron can be bound to the nucleus of an atom by the attractive Coulomb force. A system of one or more electrons bound to a nucleus is called an atom. If the number of electrons is different from the nucleus’s electrical charge, such an atom is called an ion. The wave-like behavior of a bound electron is described by a function called an atomic orbital. Each orbital has its own set of quantum numbers such as energy, angular momentum and projection of angular momentum, and only a discrete set of these orbitals exist around the nucleus. According to the Pauli exclusion principle each orbital can be occupied by up to two electrons, which must differ in their spin quantum number.
Electrons can transfer between different orbitals by the emission or absorption of photons with an energy that matches the difference in potential.[118]: 159–160 Other methods of orbital transfer include collisions with particles, such as electrons, and the Auger effect.[119] To escape the atom, the energy of the electron must be increased above its binding energy to the atom. This occurs, for example, with the photoelectric effect, where an incident photon exceeding the atom’s ionization energy is absorbed by the electron.[118]: 127–132
The orbital angular momentum of electrons is quantized. Because the electron is charged, it produces an orbital magnetic moment that is proportional to the angular momentum. The net magnetic moment of an atom is equal to the vector sum of orbital and spin magnetic moments of all electrons and the nucleus. The magnetic moment of the nucleus is negligible compared with that of the electrons. The magnetic moments of the electrons that occupy the same orbital (so called, paired electrons) cancel each other out.[120]
The chemical bond between atoms occurs as a result of electromagnetic interactions, as described by the laws of quantum mechanics.[121] The strongest bonds are formed by the sharing or transfer of electrons between atoms, allowing the formation of molecules.[17] Within a molecule, electrons move under the influence of several nuclei, and occupy molecular orbitals; much as they can occupy atomic orbitals in isolated atoms.[122] A fundamental factor in these molecular structures is the existence of electron pairs. These are electrons with opposed spins, allowing them to occupy the same molecular orbital without violating the Pauli exclusion principle (much like in atoms). Different molecular orbitals have different spatial distribution of the electron density. For instance, in bonded pairs (i.e. in the pairs that actually bind atoms together) electrons can be found with the maximal probability in a relatively small volume between the nuclei. By contrast, in non-bonded pairs electrons are distributed in a large volume around nuclei.[123]
Conductivity[edit]
A lightning discharge consists primarily of a flow of electrons.[124] The electric potential needed for lightning can be generated by a triboelectric effect.[125][126]
If a body has more or fewer electrons than are required to balance the positive charge of the nuclei, then that object has a net electric charge. When there is an excess of electrons, the object is said to be negatively charged. When there are fewer electrons than the number of protons in nuclei, the object is said to be positively charged. When the number of electrons and the number of protons are equal, their charges cancel each other and the object is said to be electrically neutral. A macroscopic body can develop an electric charge through rubbing, by the triboelectric effect.[127]
Independent electrons moving in vacuum are termed free electrons. Electrons in metals also behave as if they were free. In reality the particles that are commonly termed electrons in metals and other solids are quasi-electrons—quasiparticles, which have the same electrical charge, spin, and magnetic moment as real electrons but might have a different mass.[128] When free electrons—both in vacuum and metals—move, they produce a net flow of charge called an electric current, which generates a magnetic field. Likewise a current can be created by a changing magnetic field. These interactions are described mathematically by Maxwell’s equations.[129]
At a given temperature, each material has an electrical conductivity that determines the value of electric current when an electric potential is applied. Examples of good conductors include metals such as copper and gold, whereas glass and Teflon are poor conductors. In any dielectric material, the electrons remain bound to their respective atoms and the material behaves as an insulator. Most semiconductors have a variable level of conductivity that lies between the extremes of conduction and insulation.[130] On the other hand, metals have an electronic band structure containing partially filled electronic bands. The presence of such bands allows electrons in metals to behave as if they were free or delocalized electrons. These electrons are not associated with specific atoms, so when an electric field is applied, they are free to move like a gas (called Fermi gas)[131] through the material much like free electrons.
Because of collisions between electrons and atoms, the drift velocity of electrons in a conductor is on the order of millimeters per second. However, the speed at which a change of current at one point in the material causes changes in currents in other parts of the material, the velocity of propagation, is typically about 75% of light speed.[132] This occurs because electrical signals propagate as a wave, with the velocity dependent on the dielectric constant of the material.[133]
Metals make relatively good conductors of heat, primarily because the delocalized electrons are free to transport thermal energy between atoms. However, unlike electrical conductivity, the thermal conductivity of a metal is nearly independent of temperature. This is expressed mathematically by the Wiedemann–Franz law,[131] which states that the ratio of thermal conductivity to the electrical conductivity is proportional to the temperature. The thermal disorder in the metallic lattice increases the electrical resistivity of the material, producing a temperature dependence for electric current.[134]
When cooled below a point called the critical temperature, materials can undergo a phase transition in which they lose all resistivity to electric current, in a process known as superconductivity. In BCS theory, pairs of electrons called Cooper pairs have their motion coupled to nearby matter via lattice vibrations called phonons, thereby avoiding the collisions with atoms that normally create electrical resistance.[135] (Cooper pairs have a radius of roughly 100 nm, so they can overlap each other.)[136] However, the mechanism by which higher temperature superconductors operate remains uncertain.
Electrons inside conducting solids, which are quasi-particles themselves, when tightly confined at temperatures close to absolute zero, behave as though they had split into three other quasiparticles: spinons, orbitons and holons.[137][138] The former carries spin and magnetic moment, the next carries its orbital location while the latter electrical charge.
Motion and energy[edit]
According to Einstein’s theory of special relativity, as an electron’s speed approaches the speed of light, from an observer’s point of view its relativistic mass increases, thereby making it more and more difficult to accelerate it from within the observer’s frame of reference. The speed of an electron can approach, but never reach, the speed of light in a vacuum, c. However, when relativistic electrons—that is, electrons moving at a speed close to c—are injected into a dielectric medium such as water, where the local speed of light is significantly less than c, the electrons temporarily travel faster than light in the medium. As they interact with the medium, they generate a faint light called Cherenkov radiation.[139]
Lorentz factor as a function of velocity. It starts at value 1 and goes to infinity as v approaches c.
The effects of special relativity are based on a quantity known as the Lorentz factor, defined as 
where me is the mass of electron. For example, the Stanford linear accelerator can accelerate an electron to roughly 51 GeV.[140]
Since an electron behaves as a wave, at a given velocity it has a characteristic de Broglie wavelength. This is given by λe = h/p where h is the Planck constant and p is the momentum.[57] For the 51 GeV electron above, the wavelength is about 2.4×10−17 m, small enough to explore structures well below the size of an atomic nucleus.[141]
Formation[edit]
Pair production of an electron and positron, caused by the close approach of a photon with an atomic nucleus. The lightning symbol represents an exchange of a virtual photon, thus an electric force acts. The angle between the particles is very small.[142]
The Big Bang theory is the most widely accepted scientific theory to explain the early stages in the evolution of the Universe.[143] For the first millisecond of the Big Bang, the temperatures were over 10 billion kelvins and photons had mean energies over a million electronvolts. These photons were sufficiently energetic that they could react with each other to form pairs of electrons and positrons. Likewise, positron-electron pairs annihilated each other and emitted energetic photons:
γ
+
γ
↔
e+
+
e−
An equilibrium between electrons, positrons and photons was maintained during this phase of the evolution of the Universe. After 15 seconds had passed, however, the temperature of the universe dropped below the threshold where electron-positron formation could occur. Most of the surviving electrons and positrons annihilated each other, releasing gamma radiation that briefly reheated the universe.[144]
For reasons that remain uncertain, during the annihilation process there was an excess in the number of particles over antiparticles. Hence, about one electron for every billion electron-positron pairs survived. This excess matched the excess of protons over antiprotons, in a condition known as baryon asymmetry, resulting in a net charge of zero for the universe.[145][146] The surviving protons and neutrons began to participate in reactions with each other—in the process known as nucleosynthesis, forming isotopes of hydrogen and helium, with trace amounts of lithium. This process peaked after about five minutes.[147] Any leftover neutrons underwent negative beta decay with a half-life of about a thousand seconds, releasing a proton and electron in the process,
n
→
p
+
e−
+
ν
e
For about the next 300000–400000 years, the excess electrons remained too energetic to bind with atomic nuclei.[148] What followed is a period known as recombination, when neutral atoms were formed and the expanding universe became transparent to radiation.[149]
Roughly one million years after the big bang, the first generation of stars began to form.[149] Within a star, stellar nucleosynthesis results in the production of positrons from the fusion of atomic nuclei. These antimatter particles immediately annihilate with electrons, releasing gamma rays. The net result is a steady reduction in the number of electrons, and a matching increase in the number of neutrons. However, the process of stellar evolution can result in the synthesis of radioactive isotopes. Selected isotopes can subsequently undergo negative beta decay, emitting an electron and antineutrino from the nucleus.[150] An example is the cobalt-60 (60Co) isotope, which decays to form nickel-60 (60
Ni
).[151]
An extended air shower generated by an energetic cosmic ray striking the Earth’s atmosphere
At the end of its lifetime, a star with more than about 20 solar masses can undergo gravitational collapse to form a black hole.[152] According to classical physics, these massive stellar objects exert a gravitational attraction that is strong enough to prevent anything, even electromagnetic radiation, from escaping past the Schwarzschild radius. However, quantum mechanical effects are believed to potentially allow the emission of Hawking radiation at this distance. Electrons (and positrons) are thought to be created at the event horizon of these stellar remnants.
When a pair of virtual particles (such as an electron and positron) is created in the vicinity of the event horizon, random spatial positioning might result in one of them to appear on the exterior; this process is called quantum tunnelling. The gravitational potential of the black hole can then supply the energy that transforms this virtual particle into a real particle, allowing it to radiate away into space.[153] In exchange, the other member of the pair is given negative energy, which results in a net loss of mass-energy by the black hole. The rate of Hawking radiation increases with decreasing mass, eventually causing the black hole to evaporate away until, finally, it explodes.[154]
Cosmic rays are particles traveling through space with high energies. Energy events as high as 3.0×1020 eV have been recorded.[155] When these particles collide with nucleons in the Earth’s atmosphere, a shower of particles is generated, including pions.[156] More than half of the cosmic radiation observed from the Earth’s surface consists of muons. The particle called a muon is a lepton produced in the upper atmosphere by the decay of a pion.
π−
→
μ−
+
ν
μ
A muon, in turn, can decay to form an electron or positron.[157]
μ−
→
e−
+
ν
e +
ν
μ
Observation[edit]
Remote observation of electrons requires detection of their radiated energy. For example, in high-energy environments such as the corona of a star, free electrons form a plasma that radiates energy due to Bremsstrahlung radiation. Electron gas can undergo plasma oscillation, which is waves caused by synchronized variations in electron density, and these produce energy emissions that can be detected by using radio telescopes.[159]
The frequency of a photon is proportional to its energy. As a bound electron transitions between different energy levels of an atom, it absorbs or emits photons at characteristic frequencies. For instance, when atoms are irradiated by a source with a broad spectrum, distinct dark lines appear in the spectrum of transmitted radiation in places where the corresponding frequency is absorbed by the atom’s electrons. Each element or molecule displays a characteristic set of spectral lines, such as the hydrogen spectral series. When detected, spectroscopic measurements of the strength and width of these lines allow the composition and physical properties of a substance to be determined.[160][161]
In laboratory conditions, the interactions of individual electrons can be observed by means of particle detectors, which allow measurement of specific properties such as energy, spin and charge.[162] The development of the Paul trap and Penning trap allows charged particles to be contained within a small region for long durations. This enables precise measurements of the particle properties. For example, in one instance a Penning trap was used to contain a single electron for a period of 10 months.[163] The magnetic moment of the electron was measured to a precision of eleven digits, which, in 1980, was a greater accuracy than for any other physical constant.[164]
The first video images of an electron’s energy distribution were captured by a team at Lund University in Sweden, February 2008. The scientists used extremely short flashes of light, called attosecond pulses, which allowed an electron’s motion to be observed for the first time.[165][166]
The distribution of the electrons in solid materials can be visualized by angle-resolved photoemission spectroscopy (ARPES). This technique employs the photoelectric effect to measure the reciprocal space—a mathematical representation of periodic structures that is used to infer the original structure. ARPES can be used to determine the direction, speed and scattering of electrons within the material.[167]
Plasma applications[edit]
Particle beams[edit]
Electron beams are used in welding.[169] They allow energy densities up to 107 W·cm−2 across a narrow focus diameter of 0.1–1.3 mm and usually require no filler material. This welding technique must be performed in a vacuum to prevent the electrons from interacting with the gas before reaching their target, and it can be used to join conductive materials that would otherwise be considered unsuitable for welding.[170][171]
Electron-beam lithography (EBL) is a method of etching semiconductors at resolutions smaller than a micrometer.[172] This technique is limited by high costs, slow performance, the need to operate the beam in the vacuum and the tendency of the electrons to scatter in solids. The last problem limits the resolution to about 10 nm. For this reason, EBL is primarily used for the production of small numbers of specialized integrated circuits.[173]
Electron beam processing is used to irradiate materials in order to change their physical properties or sterilize medical and food products.[174] Electron beams fluidise or quasi-melt glasses without significant increase of temperature on intensive irradiation: e.g. intensive electron radiation causes a many orders of magnitude decrease of viscosity and stepwise decrease of its activation energy.[175]
Linear particle accelerators generate electron beams for treatment of superficial tumors in radiation therapy. Electron therapy can treat such skin lesions as basal-cell carcinomas because an electron beam only penetrates to a limited depth before being absorbed, typically up to 5 cm for electron energies in the range 5–20 MeV. An electron beam can be used to supplement the treatment of areas that have been irradiated by X-rays.[176][177]
Particle accelerators use electric fields to propel electrons and their antiparticles to high energies. These particles emit synchrotron radiation as they pass through magnetic fields. The dependency of the intensity of this radiation upon spin polarizes the electron beam—a process known as the Sokolov–Ternov effect.[i] Polarized electron beams can be useful for various experiments. Synchrotron radiation can also cool the electron beams to reduce the momentum spread of the particles. Electron and positron beams are collided upon the particles’ accelerating to the required energies; particle detectors observe the resulting energy emissions, which particle physics studies .[178]
Imaging[edit]
Low-energy electron diffraction (LEED) is a method of bombarding a crystalline material with a collimated beam of electrons and then observing the resulting diffraction patterns to determine the structure of the material. The required energy of the electrons is typically in the range 20–200 eV.[179] The reflection high-energy electron diffraction (RHEED) technique uses the reflection of a beam of electrons fired at various low angles to characterize the surface of crystalline materials. The beam energy is typically in the range 8–20 keV and the angle of incidence is 1–4°.[180][181]
The electron microscope directs a focused beam of electrons at a specimen. Some electrons change their properties, such as movement direction, angle, and relative phase and energy as the beam interacts with the material. Microscopists can record these changes in the electron beam to produce atomically resolved images of the material.[182] In blue light, conventional optical microscopes have a diffraction-limited resolution of about 200 nm.[183] By comparison, electron microscopes are limited by the de Broglie wavelength of the electron. This wavelength, for example, is equal to 0.0037 nm for electrons accelerated across a 100,000-volt potential.[184] The Transmission Electron Aberration-Corrected Microscope is capable of sub-0.05 nm resolution, which is more than enough to resolve individual atoms.[185] This capability makes the electron microscope a useful laboratory instrument for high resolution imaging. However, electron microscopes are expensive instruments that are costly to maintain.
Two main types of electron microscopes exist: transmission and scanning. Transmission electron microscopes function like overhead projectors, with a beam of electrons passing through a slice of material then being projected by lenses on a photographic slide or a charge-coupled device. Scanning electron microscopes rasteri a finely focused electron beam, as in a TV set, across the studied sample to produce the image. Magnifications range from 100× to 1,000,000× or higher for both microscope types. The scanning tunneling microscope uses quantum tunneling of electrons from a sharp metal tip into the studied material and can produce atomically resolved images of its surface.[186][187][188]
Other applications[edit]
In the free-electron laser (FEL), a relativistic electron beam passes through a pair of undulators that contain arrays of dipole magnets whose fields point in alternating directions. The electrons emit synchrotron radiation that coherently interacts with the same electrons to strongly amplify the radiation field at the resonance frequency. FEL can emit a coherent high-brilliance electromagnetic radiation with a wide range of frequencies, from microwaves to soft X-rays. These devices are used in manufacturing, communication, and in medical applications, such as soft tissue surgery.[189]
Electrons are important in cathode-ray tubes, which have been extensively used as display devices in laboratory instruments, computer monitors and television sets.[190] In a photomultiplier tube, every photon striking the photocathode initiates an avalanche of electrons that produces a detectable current pulse.[191] Vacuum tubes use the flow of electrons to manipulate electrical signals, and they played a critical role in the development of electronics technology. However, they have been largely supplanted by solid-state devices such as the transistor.[192]
See also[edit]
- Anyon
- Beta radiation
- Electride
- Electron bubble
- Exoelectron emission
- g-factor
- Lepton
- List of particles
- One-electron universe
- Periodic systems of small molecules
- Spintronics
- Stern–Gerlach experiment
- Townsend discharge
- Zeeman effect
Notes[edit]
- ^ The positron is occasionally called the ‘anti-electron’.
- ^ The fractional version’s denominator is the inverse of the decimal value (along with its relative standard uncertainty of 2.9×10−11).
- ^ Note that older sources list charge-to-mass rather than the modern convention of mass-to-charge ratio.
- ^ This magnitude is obtained from the spin quantum number as
for quantum number s = 1/2.
See: Gupta (2001). - ^ Bohr magneton:
- ^ The classical electron radius is derived as follows. Assume that the electron’s charge is spread uniformly throughout a spherical volume. Since one part of the sphere would repel the other parts, the sphere contains electrostatic potential energy. This energy is assumed to equal the electron’s rest energy, defined by special relativity (E = mc2).
From electrostatics theory, the potential energy of a sphere with radius r and charge e is given by:where ε0 is the vacuum permittivity. For an electron with rest mass m0, the rest energy is equal to:
where c is the speed of light in a vacuum. Setting them equal and solving for r gives the classical electron radius.
See: Haken, Wolf, & Brewer (2005). - ^ Radiation from non-relativistic electrons is sometimes termed cyclotron radiation.
- ^ The change in wavelength, Δλ, depends on the angle of the recoil, θ, as follows,
where c is the speed of light in a vacuum and me is the electron mass. See Zombeck (2007).[77]: 393, 396
- ^ The polarization of an electron beam means that the spins of all electrons point into one direction. In other words, the projections of the spins of all electrons onto their momentum vector have the same sign.
References[edit]
- ^ a b c Eichten, E.J.; Peskin, M.E.; Peskin, M. (1983). «New Tests for Quark and Lepton Substructure». Physical Review Letters. 50 (11): 811–814. Bibcode:1983PhRvL..50..811E. doi:10.1103/PhysRevLett.50.811. OSTI 1446807. S2CID 119918703.
- ^ a b Farrar, W.V. (1969). «Richard Laming and the Coal-Gas Industry, with His Views on the Structure of Matter». Annals of Science. 25 (3): 243–254. doi:10.1080/00033796900200141.
- ^ a b c d Arabatzis, T. (2006). Representing Electrons: A Biographical Approach to Theoretical Entities. University of Chicago Press. pp. 70–74, 96. ISBN 978-0-226-02421-9. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Buchwald, J.Z.; Warwick, A. (2001). Histories of the Electron: The Birth of Microphysics. MIT Press. pp. 195–203. ISBN 978-0-262-52424-7. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ a b c d e f Thomson, J.J. (1897). «Cathode Rays». Philosophical Magazine. 44 (269): 293–316. doi:10.1080/14786449708621070. Archived from the original on 2022-01-25. Retrieved 2022-02-24.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass in u». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-06-21.
- ^ «2018 CODATA Value: electron mass energy equivalent in MeV». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-07-11.
- ^ a b Agostini, M.; et al. (Borexino Collaboration) (2015). «Test of electric charge conservation with Borexino». Physical Review Letters. 115 (23): 231802. arXiv:1509.01223. Bibcode:2015PhRvL.115w1802A. doi:10.1103/PhysRevLett.115.231802. PMID 26684111. S2CID 206265225.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron magnetic moment». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-09-10.
- ^ «2018 CODATA Value: electron magnetic moment to Bohr magneton ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-11-15.
- ^
Coffey, Jerry (10 September 2010). «What is an electron?». Archived from the original on 11 November 2012. Retrieved 10 September 2010. - ^ a b c
Curtis, L.J. (2003). Atomic Structure and Lifetimes: A conceptual approach. Cambridge University Press. p. 74. ISBN 978-0-521-53635-6. Archived from the original on 2020-03-16. Retrieved 2020-08-25. - ^ a b «CODATA value: proton-electron mass ratio». 2006 CODATA recommended values. National Institute of Standards and Technology. Archived from the original on 28 March 2019. Retrieved 18 July 2009.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 978-0-691-13512-0. Archived from the original on 2014-09-28. Retrieved 2020-08-25.
- ^ a b Pauling, L.C. (1960). The Nature of the Chemical Bond and the Structure of Molecules and Crystals: an introduction to modern structural chemistry (3rd ed.). Cornell University Press. pp. 4–10. ISBN 978-0-8014-0333-0.
- ^ Shipley, J.T. (1945). Dictionary of Word Origins. The Philosophical Library. p. 133. ISBN 978-0-88029-751-6.
- ^ a b Benjamin, Park (1898), A history of electricity (The intellectual rise in electricity) from antiquity to the days of Benjamin Franklin, New York: J. Wiley, pp. 315, 484–5, ISBN 978-1-313-10605-4
- ^ Keithley, J.F. (1999). The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s. IEEE Press. pp. 19–20. ISBN 978-0-7803-1193-0. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Cajori, Florian (1917). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. Macmillan.
- ^ «Benjamin Franklin (1706–1790)». Eric Weisstein’s World of Biography. Wolfram Research. Archived from the original on 27 August 2013. Retrieved 16 December 2010.
- ^ Myers, R.L. (2006). The Basics of Physics. Greenwood Publishing Group. p. 242. ISBN 978-0-313-32857-2.
- ^ Barrow, J.D. (1983). «Natural Units Before Planck». Quarterly Journal of the Royal Astronomical Society. 24: 24–26. Bibcode:1983QJRAS..24…24B.
- ^ Okamura, Sōgo (1994). History of Electron Tubes. IOS Press. p. 11. ISBN 978-90-5199-145-1. Archived from the original on 11 May 2016. Retrieved 29 May 2015.
In 1881, Stoney named this electromagnetic ‘electrolion’. It came to be called ‘electron’ from 1891. […] In 1906, the suggestion to call cathode ray particles ‘electrions’ was brought up but through the opinion of Lorentz of Holland ‘electrons’ came to be widely used.
- ^ Stoney, G.J. (1894). «Of the «Electron,» or Atom of Electricity». Philosophical Magazine. 38 (5): 418–420. doi:10.1080/14786449408620653. Archived from the original on 2020-10-31. Retrieved 2019-08-25.
- ^ «electron, n.2». OED Online. March 2013. Oxford University Press. Accessed 12 April 2013 [1] Archived 2021-04-27 at the Wayback Machine
- ^ Soukhanov, A.H., ed. (1986). Word Mysteries & Histories. Houghton Mifflin. p. 73. ISBN 978-0-395-40265-8.
- ^ Guralnik, D.B., ed. (1970). Webster’s New World Dictionary. Prentice Hall. p. 450.
- ^ Born, M.; Blin-Stoyle, R.J.; Radcliffe, J.M. (1989). Atomic Physics. Courier Dover. p. 26. ISBN 978-0-486-65984-8. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Plücker, M. (1858-12-01). «XLVI. Observations on the electrical discharge through rarefied gases». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 16 (109): 408–418. doi:10.1080/14786445808642591. ISSN 1941-5982.
- ^ a b c Leicester, H.M. (1971). The Historical Background of Chemistry. Courier Dover. pp. 221–222. ISBN 978-0-486-61053-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ a b Whittaker, E.T. (1951). A History of the Theories of Aether and Electricity. Vol. 1. London: Nelson.
- ^ DeKosky, R.K. (1983). «William Crookes and the quest for absolute vacuum in the 1870s». Annals of Science. 40 (1): 1–18. doi:10.1080/00033798300200101.
- ^ a b Schuster, Arthur (1890). «The discharge of electricity through gases». Proceedings of the Royal Society of London. 47: 526–559. doi:10.1098/rspl.1889.0111. S2CID 96197979.
- ^ Wilczek, Frank (June 2012). «Happy birthday, electron». Scientific American. Archived from the original on 2013-11-01. Retrieved 2022-02-24.
- ^ Trenn, T.J. (1976). «Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays». Isis. 67 (1): 61–75. doi:10.1086/351545. JSTOR 231134. S2CID 145281124.
- ^ Becquerel, H. (1900). «Déviation du Rayonnement du Radium dans un Champ Électrique». Comptes rendus de l’Académie des sciences (in French). 130: 809–815.
- ^ Buchwald and Warwick (2001:90–91).
- ^ Myers, W.G. (1976). «Becquerel’s Discovery of Radioactivity in 1896». Journal of Nuclear Medicine. 17 (7): 579–582. PMID 775027. Archived from the original on 2008-12-22. Retrieved 2022-02-24.
- ^ Thomson, J.J. (1906). «Nobel Lecture: Carriers of Negative Electricity» (PDF). The Nobel Foundation. Archived from the original (PDF) on 10 October 2008. Retrieved 25 August 2008.
- ^ O’Hara, J. G. (March 1975). «George Johnstone Stoney, F.R.S., and the Concept of the Electron». Notes and Records of the Royal Society of London. Royal Society. 29 (2): 265–276. doi:10.1098/rsnr.1975.0018. JSTOR 531468. S2CID 145353314.
- ^ Abraham Pais (1997). «The discovery of the electron – 100 years of elementary particles» (PDF). Beam Line. 1: 4–16. Archived (PDF) from the original on 2021-09-14. Retrieved 2021-09-04.
- ^ Kaufmann, W. (1897). «Die magnetische Ablenkbarkeit der Kathodenstrahlen und ihre Abhängigkeit vom Entladungspotential». Annalen der Physik und Chemie. 297 (7): 544–552. Bibcode:1897AnP…297..544K. doi:10.1002/andp.18972970709. ISSN 0003-3804. Archived from the original on 2022-02-24. Retrieved 2022-02-24.
- ^ Kikoin, I.K.; Sominskiĭ, I.S. (1961). «Abram Fedorovich Ioffe (on his eightieth birthday)». Soviet Physics Uspekhi. 3 (5): 798–809. Bibcode:1961SvPhU…3..798K. doi:10.1070/PU1961v003n05ABEH005812. Original publication in Russian: Кикоин, И.К.; Соминский, М.С. (1960). «Академик А.Ф. Иоффе». Успехи Физических Наук. 72 (10): 303–321. doi:10.3367/UFNr.0072.196010e.0307.
- ^ Millikan, R.A. (1911). «The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes’s Law» (PDF). Physical Review. 32 (2): 349–397. Bibcode:1911PhRvI..32..349M. doi:10.1103/PhysRevSeriesI.32.349. Archived (PDF) from the original on 2020-03-17. Retrieved 2019-06-21.
- ^ Das Gupta, N.N.; Ghosh, S.K. (1999). «A Report on the Wilson Cloud Chamber and Its Applications in Physics». Reviews of Modern Physics. 18 (2): 225–290. Bibcode:1946RvMP…18..225G. doi:10.1103/RevModPhys.18.225.
- ^ a b c Smirnov, B.M. (2003). Physics of Atoms and Ions. Springer. pp. 14–21. ISBN 978-0-387-95550-6. Archived from the original on 2020-05-09. Retrieved 2020-08-25.
- ^ Bohr, N. (1922). «Nobel Lecture: The Structure of the Atom» (PDF). The Nobel Foundation. Archived (PDF) from the original on 3 December 2008. Retrieved 3 December 2008.
- ^ Lewis, G.N. (1916). «The Atom and the Molecule». Journal of the American Chemical Society. 38 (4): 762–786. doi:10.1021/ja02261a002. S2CID 95865413. Archived (PDF) from the original on 2019-08-25. Retrieved 2019-08-25.
- ^ a b Arabatzis, T.; Gavroglu, K. (1997). «The chemists’ electron» (PDF). European Journal of Physics. 18 (3): 150–163. Bibcode:1997EJPh…18..150A. doi:10.1088/0143-0807/18/3/005. S2CID 56117976. Archived from the original (PDF) on 2020-06-05.
- ^ Langmuir, I. (1919). «The Arrangement of Electrons in Atoms and Molecules». Journal of the American Chemical Society. 41 (6): 868–934. doi:10.1021/ja02227a002. Archived from the original on 2021-01-26. Retrieved 2019-06-21.
- ^ Scerri, E.R. (2007). The Periodic Table. Oxford University Press. pp. 205–226. ISBN 978-0-19-530573-9.
- ^ Massimi, M. (2005). Pauli’s Exclusion Principle, The Origin and Validation of a Scientific Principle. Cambridge University Press. pp. 7–8. ISBN 978-0-521-83911-2. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Uhlenbeck, G.E.; Goudsmith, S. (1925). «Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons». Die Naturwissenschaften (in German). 13 (47): 953–954. Bibcode:1925NW…..13..953E. doi:10.1007/BF01558878. S2CID 32211960.
- ^ Pauli, W. (1923). «Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes». Zeitschrift für Physik (in German). 16 (1): 155–164. Bibcode:1923ZPhy…16..155P. doi:10.1007/BF01327386. S2CID 122256737.
- ^ a b de Broglie, L. (1929). «Nobel Lecture: The Wave Nature of the Electron» (PDF). The Nobel Foundation. Archived (PDF) from the original on 4 October 2008. Retrieved 30 August 2008.
- ^ Falkenburg, B. (2007). Particle Metaphysics: A Critical Account of Subatomic Reality. Springer. p. 85. Bibcode:2007pmca.book…..F. ISBN 978-3-540-33731-7. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Davisson, C. (1937). «Nobel Lecture: The Discovery of Electron Waves» (PDF). The Nobel Foundation. Archived (PDF) from the original on 9 July 2008. Retrieved 30 August 2008.
- ^ Schrödinger, E. (1926). «Quantisierung als Eigenwertproblem». Annalen der Physik (in German). 385 (13): 437–490. Bibcode:1926AnP…385..437S. doi:10.1002/andp.19263851302.
- ^ Rigden, J.S. (2003). Hydrogen. Harvard University Press. pp. 59–86. ISBN 978-0-674-01252-3. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Reed, B.C. (2007). Quantum Mechanics. Jones & Bartlett Publishers. pp. 275–350. ISBN 978-0-7637-4451-9. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Dirac, P.A.M. (1928). «The Quantum Theory of the Electron» (PDF). Proceedings of the Royal Society A. 117 (778): 610–624. Bibcode:1928RSPSA.117..610D. doi:10.1098/rspa.1928.0023. Archived (PDF) from the original on 2018-11-25. Retrieved 2022-02-24.
- ^ Dirac, P.A.M. (1933). «Nobel Lecture: Theory of Electrons and Positrons» (PDF). The Nobel Foundation. Archived (PDF) from the original on 23 July 2008. Retrieved 1 November 2008.
- ^ Anderson, Carl D. (1933-03-15). «The Positive Electron». Physical Review. 43 (6): 491–494. Bibcode:1933PhRv…43..491A. doi:10.1103/PhysRev.43.491. ISSN 0031-899X.
- ^ «The Nobel Prize in Physics 1965». The Nobel Foundation. Archived from the original on 24 October 2008. Retrieved 4 November 2008.
- ^ Panofsky, W.K.H. (1997). «The Evolution of Particle Accelerators & Colliders» (PDF). Beam Line. 27 (1): 36–44. Archived (PDF) from the original on 9 September 2008. Retrieved 15 September 2008.
- ^ Elder, F.R.; et al. (1947). «Radiation from Electrons in a Synchrotron». Physical Review. 71 (11): 829–830. Bibcode:1947PhRv…71..829E. doi:10.1103/PhysRev.71.829.5.
- ^ Hoddeson, L.; et al. (1997). The Rise of the Standard Model: Particle Physics in the 1960s and 1970s. Cambridge University Press. pp. 25–26. ISBN 978-0-521-57816-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Bernardini, C. (2004). «AdA: The First Electron–Positron Collider». Physics in Perspective. 6 (2): 156–183. Bibcode:2004PhP…..6..156B. doi:10.1007/s00016-003-0202-y. S2CID 122534669.
- ^ «Testing the Standard Model: The LEP experiments». CERN. 2008. Archived from the original on 14 September 2008. Retrieved 15 September 2008.
- ^ «LEP reaps a final harvest». CERN Courier. 40 (10). 2000. Archived from the original on 2017-09-30. Retrieved 2022-02-24.
- ^ Prati, E.; De Michielis, M.; Belli, M.; Cocco, S.; Fanciulli, M.; Kotekar-Patil, D.; Ruoff, M.; Kern, D.P.; Wharam, D.A.; Verduijn, J.; Tettamanzi, G.C.; Rogge, S.; Roche, B.; Wacquez, R.; Jehl, X.; Vinet, M.; Sanquer, M. (2012). «Few electron limit of n-type metal oxide semiconductor single electron transistors». Nanotechnology. 23 (21): 215204. arXiv:1203.4811. Bibcode:2012Nanot..23u5204P. CiteSeerX 10.1.1.756.4383. doi:10.1088/0957-4484/23/21/215204. PMID 22552118. S2CID 206063658.
- ^ Frampton, P.H.; Hung, P.Q.; Sher, Marc (2000). «Quarks and Leptons Beyond the Third Generation». Physics Reports. 330 (5–6): 263–348. arXiv:hep-ph/9903387. Bibcode:2000PhR…330..263F. doi:10.1016/S0370-1573(99)00095-2. S2CID 119481188.
- ^ a b c Raith, W.; Mulvey, T. (2001). Constituents of Matter: Atoms, Molecules, Nuclei and Particles. CRC Press. pp. 777–781. ISBN 978-0-8493-1202-1.
- ^ a b c d e f g h The original source for CODATA is Mohr, P.J.; Taylor, B.N.; Newell, D.B. (2008). «CODATA recommended values of the fundamental physical constants». Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. CiteSeerX 10.1.1.150.1225. doi:10.1103/RevModPhys.80.633.
- Individual physical constants from the CODATA are available at: «The NIST Reference on Constants, Units and Uncertainty». National Institute of Standards and Technology. Archived from the original on 2009-01-16. Retrieved 2009-01-15.
- ^ a b Zombeck, M.V. (2007). Handbook of Space Astronomy and Astrophysics (3rd ed.). Cambridge University Press. p. 14. ISBN 978-0-521-78242-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Murphy, M.T.; et al. (2008). «Strong Limit on a Variable Proton-to-Electron Mass Ratio from Molecules in the Distant Universe». Science. 320 (5883): 1611–1613. arXiv:0806.3081. Bibcode:2008Sci…320.1611M. doi:10.1126/science.1156352. PMID 18566280. S2CID 2384708.
- ^ Zorn, J.C.; Chamberlain, G.E.; Hughes, V.W. (1963). «Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron». Physical Review. 129 (6): 2566–2576. Bibcode:1963PhRv..129.2566Z. doi:10.1103/PhysRev.129.2566.
- ^ Gupta, M.C. (2001). Atomic and Molecular Spectroscopy. New Age Publishers. p. 81. ISBN 978-81-224-1300-7. Archived from the original on 2014-09-30. Retrieved 2020-08-25.
- ^ a b Odom, B.; et al. (2006). «New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron». Physical Review Letters. 97 (3): 030801. Bibcode:2006PhRvL..97c0801O. doi:10.1103/PhysRevLett.97.030801. PMID 16907490.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 261–262. ISBN 978-0-691-13512-0. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Gabrielse, G.; et al. (2006). «New Determination of the Fine Structure Constant from the Electron g Value and QED». Physical Review Letters. 97 (3): 030802(1–4). Bibcode:2006PhRvL..97c0802G. doi:10.1103/PhysRevLett.97.030802. PMID 16907491.
- ^ «UK | England | Physicists ‘make electrons split’«. BBC News. 2009-08-28. Archived from the original on 2017-08-31. Retrieved 2016-07-11.
- ^ Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution Archived 2019-04-04 at the Wayback Machine. Science Daily (July 31, 2009)
- ^ Yarris, Lynn (2006-07-13). «First Direct Observations of Spinons and Holons». Lbl.gov. Archived from the original on 2022-02-24. Retrieved 2016-07-11.
- ^ Eduard Shpolsky, Atomic physics (Atomnaia fizika), second edition, 1951
- ^ Dehmelt, H. (1988). «A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius». Physica Scripta. T22: 102–110. Bibcode:1988PhST…22..102D. doi:10.1088/0031-8949/1988/T22/016. S2CID 250760629.
- ^ Gabrielse, Gerald. «Electron Substructure». Physics. Harvard University. Archived from the original on 2019-04-10. Retrieved 2016-06-21.
- ^ Meschede, D. (2004). Optics, light and lasers: The Practical Approach to Modern Aspects of Photonics and Laser Physics. Wiley-VCH. p. 168. ISBN 978-3-527-40364-6. Archived from the original on 2014-08-21. Retrieved 2020-08-25.
- ^ Haken, H.; Wolf, H.C.; Brewer, W.D. (2005). The Physics of Atoms and Quanta: Introduction to Experiments and Theory. Springer. p. 70. ISBN 978-3-540-67274-6. Archived from the original on 2021-05-10. Retrieved 2020-08-25.
- ^ Steinberg, R.I.; et al. (1999). «Experimental test of charge conservation and the stability of the electron». Physical Review D. 61 (2): 2582–2586. Bibcode:1975PhRvD..12.2582S. doi:10.1103/PhysRevD.12.2582.
- ^ Beringer, J.; et al. (Particle Data Group) (2012). «Review of Particle Physics: [electron properties]» (PDF). Physical Review D. 86 (1): 010001. Bibcode:2012PhRvD..86a0001B. doi:10.1103/PhysRevD.86.010001. Archived (PDF) from the original on 2022-01-15. Retrieved 2022-02-24.
- ^ Back, H.O.; et al. (2002). «Search for electron decay mode e → γ + ν with prototype of Borexino detector». Physics Letters B. 525 (1–2): 29–40. Bibcode:2002PhLB..525…29B. doi:10.1016/S0370-2693(01)01440-X.
- ^ a b c d e Munowitz, M. (2005). Knowing the Nature of Physical Law. Oxford University Press. p. 162. ISBN 978-0-19-516737-5.
- ^ Kane, G. (9 October 2006). «Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?». Scientific American. Retrieved 19 September 2008.
- ^ Taylor, J. (1989). «Gauge Theories in Particle Physics». In Davies, Paul (ed.). The New Physics. Cambridge University Press. p. 464. ISBN 978-0-521-43831-5. Archived from the original on 2014-09-21. Retrieved 2020-08-25.
- ^ a b Genz, H. (2001). Nothingness: The Science of Empty Space. Da Capo Press. pp. 241–243, 245–247. ISBN 978-0-7382-0610-3.
- ^ Gribbin, J. (25 January 1997). «More to electrons than meets the eye». New Scientist. Archived from the original on 11 February 2015. Retrieved 17 September 2008.
- ^ Levine, I.; et al. (1997). «Measurement of the Electromagnetic Coupling at Large Momentum Transfer». Physical Review Letters. 78 (3): 424–427. Bibcode:1997PhRvL..78..424L. doi:10.1103/PhysRevLett.78.424.
- ^ Murayama, H. (10–17 March 2006). Supersymmetry Breaking Made Easy, Viable and Generic. Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories. La Thuile, Italy. arXiv:0709.3041. Bibcode:2007arXiv0709.3041M. — lists a 9% mass difference for an electron that is the size of the Planck distance.
- ^ Schwinger, J. (1948). «On Quantum-Electrodynamics and the Magnetic Moment of the Electron». Physical Review. 73 (4): 416–417. Bibcode:1948PhRv…73..416S. doi:10.1103/PhysRev.73.416.
- ^ Huang, K. (2007). Fundamental Forces of Nature: The Story of Gauge Fields. World Scientific. pp. 123–125. ISBN 978-981-270-645-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Foldy, L.L.; Wouthuysen, S. (1950). «On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit». Physical Review. 78 (1): 29–36. Bibcode:1950PhRv…78…29F. doi:10.1103/PhysRev.78.29.
- ^ a b Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- ^ Crowell, B. (2000). Electricity and Magnetism. Light and Matter. pp. 129–152. ISBN 978-0-9704670-4-1. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Mahadevan, R.; Narayan, R.; Yi, I. (1996). «Harmony in Electrons: Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field». The Astrophysical Journal. 465: 327–337. arXiv:astro-ph/9601073. Bibcode:1996ApJ…465..327M. doi:10.1086/177422. S2CID 16324613.
- ^ Rohrlich, F. (1999). «The Self-Force and Radiation Reaction». American Journal of Physics. 68 (12): 1109–1112. Bibcode:2000AmJPh..68.1109R. doi:10.1119/1.1286430.
- ^ Georgi, H. (1989). «Grand Unified Theories». In Davies, Paul (ed.). The New Physics. Cambridge University Press. p. 427. ISBN 978-0-521-43831-5. Archived from the original on 2014-09-21. Retrieved 2020-08-25.
- ^ Blumenthal, G.J.; Gould, R. (1970). «Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases». Reviews of Modern Physics. 42 (2): 237–270. Bibcode:1970RvMP…42..237B. doi:10.1103/RevModPhys.42.237.
- ^ «The Nobel Prize in Physics 1927». The Nobel Foundation. 2008. Archived from the original on 24 October 2008. Retrieved 28 September 2008.
- ^ Chen, S.-Y.; Maksimchuk, A.; Umstadter, D. (1998). «Experimental observation of relativistic nonlinear Thomson scattering». Nature. 396 (6712): 653–655. arXiv:physics/9810036. Bibcode:1998Natur.396..653C. doi:10.1038/25303. S2CID 16080209.
- ^ Beringer, R.; Montgomery, C.G. (1942). «The Angular Distribution of Positron Annihilation Radiation». Physical Review. 61 (5–6): 222–224. Bibcode:1942PhRv…61..222B. doi:10.1103/PhysRev.61.222.
- ^ Buffa, A. (2000). College Physics (4th ed.). Prentice Hall. p. 888. ISBN 978-0-13-082444-8.
- ^ Eichler, J. (2005). «Electron–positron pair production in relativistic ion–atom collisions». Physics Letters A. 347 (1–3): 67–72. Bibcode:2005PhLA..347…67E. doi:10.1016/j.physleta.2005.06.105.
- ^ Hubbell, J.H. (2006). «Electron positron pair production by photons: A historical overview». Radiation Physics and Chemistry. 75 (6): 614–623. Bibcode:2006RaPC…75..614H. doi:10.1016/j.radphyschem.2005.10.008. Archived from the original on 2019-06-21. Retrieved 2019-06-21.
- ^ Quigg, C. (4–30 June 2000). The Electroweak Theory. TASI 2000: Flavor Physics for the Millennium. Boulder, Colorado. p. 80. arXiv:hep-ph/0204104. Bibcode:2002hep.ph….4104Q.
- ^ a b Tipler, Paul; Llewellyn, Ralph (2003). Modern Physics (illustrated ed.). Macmillan. ISBN 978-0-7167-4345-3.
- ^ Burhop, E.H.S. (1952). The Auger Effect and Other Radiationless Transitions. Cambridge University Press. pp. 2–3. ISBN 978-0-88275-966-1.
- ^ Jiles, D. (1998). Introduction to Magnetism and Magnetic Materials. CRC Press. pp. 280–287. ISBN 978-0-412-79860-3. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Löwdin, P.O.; Erkki Brändas, E.; Kryachko, E.S. (2003). Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per-Olov Löwdin. Springer Science+Business Media. pp. 393–394. ISBN 978-1-4020-1290-7. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ McQuarrie, D.A.; Simon, J.D. (1997). Physical Chemistry: A Molecular Approach. University Science Books. pp. 325–361. ISBN 978-0-935702-99-6. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Daudel, R.; et al. (1974). «The Electron Pair in Chemistry». Canadian Journal of Chemistry. 52 (8): 1310–1320. doi:10.1139/v74-201.
- ^ Rakov, V.A.; Uman, M.A. (2007). Lightning: Physics and Effects. Cambridge University Press. p. 4. ISBN 978-0-521-03541-5. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Freeman, G.R.; March, N.H. (1999). «Triboelectricity and some associated phenomena». Materials Science and Technology. 15 (12): 1454–1458. Bibcode:1999MatST..15.1454F. doi:10.1179/026708399101505464.
- ^ Forward, K.M.; Lacks, D.J.; Sankaran, R.M. (2009). «Methodology for studying particle–particle triboelectrification in granular materials». Journal of Electrostatics. 67 (2–3): 178–183. doi:10.1016/j.elstat.2008.12.002.
- ^ Weinberg, S. (2003). The Discovery of Subatomic Particles. Cambridge University Press. pp. 15–16. ISBN 978-0-521-82351-7.
- ^ Lou, L.-F. (2003). Introduction to phonons and electrons. World Scientific. pp. 162, 164. Bibcode:2003ipe..book…..L. ISBN 978-981-238-461-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Guru, B.S.; Hızıroğlu, H.R. (2004). Electromagnetic Field Theory. Cambridge University Press. pp. 138, 276. ISBN 978-0-521-83016-4.
- ^ Achuthan, M.K.; Bhat, K.N. (2007). Fundamentals of Semiconductor Devices. Tata McGraw-Hill. pp. 49–67. ISBN 978-0-07-061220-4. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ a b Ziman, J.M. (2001). Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford University Press. p. 260. ISBN 978-0-19-850779-6. Archived from the original on 2022-02-24. Retrieved 2020-08-25.
- ^ Main, P. (12 June 1993). «When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise». New Scientist. 1887: 30. Archived from the original on 11 February 2015. Retrieved 9 October 2008.
- ^ Blackwell, G.R. (2000). The Electronic Packaging Handbook. CRC Press. pp. 6.39–6.40. ISBN 978-0-8493-8591-9. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Durrant, A. (2000). Quantum Physics of Matter: The Physical World. CRC Press. pp. 43, 71–78. ISBN 978-0-7503-0721-5. Archived from the original on 2016-05-27. Retrieved 2015-10-16.
- ^ «The Nobel Prize in Physics 1972». The Nobel Foundation. 2008. Archived from the original on 11 October 2008. Retrieved 13 October 2008.
- ^ Kadin, A.M. (2007). «Spatial Structure of the Cooper Pair». Journal of Superconductivity and Novel Magnetism. 20 (4): 285–292. arXiv:cond-mat/0510279. doi:10.1007/s10948-006-0198-z. S2CID 54948290.
- ^ «Discovery about behavior of building block of nature could lead to computer revolution». ScienceDaily. 31 July 2009. Archived from the original on 4 April 2019. Retrieved 1 August 2009.
- ^ Jompol, Y.; et al. (2009). «Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid». Science. 325 (5940): 597–601. arXiv:1002.2782. Bibcode:2009Sci…325..597J. doi:10.1126/science.1171769. PMID 19644117. S2CID 206193.
- ^ «The Nobel Prize in Physics 1958, for the discovery and the interpretation of the Cherenkov effect». The Nobel Foundation. 2008. Archived from the original on 18 October 2008. Retrieved 25 September 2008.
- ^ «Special Relativity». Stanford Linear Accelerator Center. 26 August 2008. Archived from the original on 28 August 2008. Retrieved 25 September 2008.
- ^ Adams, S. (2000). Frontiers: Twentieth Century Physics. CRC Press. p. 215. ISBN 978-0-7484-0840-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Bianchini, Lorenzo (2017). Selected Exercises in Particle and Nuclear Physics. Springer. p. 79. ISBN 978-3-319-70494-4. Archived from the original on 2020-01-02. Retrieved 2018-04-20.
- ^ Lurquin, P.F. (2003). The Origins of Life and the Universe. Columbia University Press. p. 2. ISBN 978-0-231-12655-7.
- ^ Silk, J. (2000). The Big Bang: The Creation and Evolution of the Universe (3rd ed.). Macmillan. pp. 110–112, 134–137. ISBN 978-0-8050-7256-3.
- ^ Kolb, E.W.; Wolfram, Stephen (1980). «The Development of Baryon Asymmetry in the Early Universe» (PDF). Physics Letters B. 91 (2): 217–221. Bibcode:1980PhLB…91..217K. doi:10.1016/0370-2693(80)90435-9. S2CID 122680284. Archived (PDF) from the original on 2020-10-30. Retrieved 2020-08-25.
- ^ Sather, E. (Spring–Summer 1996). «The Mystery of Matter Asymmetry» (PDF). Beam Line. Stanford University. Archived (PDF) from the original on 12 October 2008. Retrieved 1 November 2008.
- ^ Burles, S.; Nollett, K.M.; Turner, M.S. (1999). «Big-Bang Nucleosynthesis: Linking Inner Space and Outer Space». arXiv:astro-ph/9903300.
- ^ Boesgaard, A.M.; Steigman, G. (1985). «Big bang nucleosynthesis – Theories and observations». Annual Review of Astronomy and Astrophysics. 23 (2): 319–378. Bibcode:1985ARA&A..23..319B. doi:10.1146/annurev.aa.23.090185.001535.
- ^ a b Barkana, R. (2006). «The First Stars in the Universe and Cosmic Reionization». Science. 313 (5789): 931–934. arXiv:astro-ph/0608450. Bibcode:2006Sci…313..931B. CiteSeerX 10.1.1.256.7276. doi:10.1126/science.1125644. PMID 16917052. S2CID 8702746.
- ^ Burbidge, E.M.; et al. (1957). «Synthesis of Elements in Stars» (PDF). Reviews of Modern Physics. 29 (4): 548–647. Bibcode:1957RvMP…29..547B. doi:10.1103/RevModPhys.29.547. Archived (PDF) from the original on 2018-07-23. Retrieved 2019-06-21.
- ^ Rodberg, L.S.; Weisskopf, V. (1957). «Fall of Parity: Recent Discoveries Related to Symmetry of Laws of Nature». Science. 125 (3249): 627–633. Bibcode:1957Sci…125..627R. doi:10.1126/science.125.3249.627. PMID 17810563.
- ^ Fryer, C.L. (1999). «Mass Limits For Black Hole Formation». The Astrophysical Journal. 522 (1): 413–418. arXiv:astro-ph/9902315. Bibcode:1999ApJ…522..413F. doi:10.1086/307647. S2CID 14227409.
- ^ Parikh, M.K.; Wilczek, F. (2000). «Hawking Radiation As Tunneling». Physical Review Letters. 85 (24): 5042–5045. arXiv:hep-th/9907001. Bibcode:2000PhRvL..85.5042P. doi:10.1103/PhysRevLett.85.5042. hdl:1874/17028. PMID 11102182. S2CID 8013726.
- ^ Hawking, S.W. (1974). «Black hole explosions?». Nature. 248 (5443): 30–31. Bibcode:1974Natur.248…30H. doi:10.1038/248030a0. S2CID 4290107.
- ^ Halzen, F.; Hooper, D. (2002). «High-energy neutrino astronomy: the cosmic ray connection». Reports on Progress in Physics. 66 (7): 1025–1078. arXiv:astro-ph/0204527. Bibcode:2002RPPh…65.1025H. doi:10.1088/0034-4885/65/7/201. S2CID 53313620.
- ^ Ziegler, J.F. (1998). «Terrestrial cosmic ray intensities». IBM Journal of Research and Development. 42 (1): 117–139. Bibcode:1998IBMJ…42..117Z. doi:10.1147/rd.421.0117.
- ^ Sutton, C. (4 August 1990). «Muons, pions and other strange particles». New Scientist. Archived from the original on 11 February 2015. Retrieved 28 August 2008.
- ^ Wolpert, S. (24 July 2008). «Scientists solve 30 year-old aurora borealis mystery» (Press release). University of California. Archived from the original on 17 August 2008. Retrieved 11 October 2008.
- ^ Gurnett, D.A.; Anderson, R. (1976). «Electron Plasma Oscillations Associated with Type III Radio Bursts». Science. 194 (4270): 1159–1162. Bibcode:1976Sci…194.1159G. doi:10.1126/science.194.4270.1159. PMID 17790910. S2CID 11401604.
- ^ Martin, W.C.; Wiese, W.L. (2007). «Atomic Spectroscopy: A compendium of basic ideas, notation, data, and formulas». National Institute of Standards and Technology. Archived from the original on 8 February 2007. Retrieved 8 January 2007.
- ^ Fowles, G.R. (1989). Introduction to Modern Optics. Courier Dover. pp. 227–233. ISBN 978-0-486-65957-2. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Grupen, C. (2000). «Physics of Particle Detection». AIP Conference Proceedings. 536: 3–34. arXiv:physics/9906063. Bibcode:2000AIPC..536….3G. doi:10.1063/1.1361756. S2CID 119476972.
- ^ «The Nobel Prize in Physics 1989». The Nobel Foundation. 2008. Archived from the original on 28 September 2008. Retrieved 24 September 2008.
- ^ Ekstrom, P.; Wineland, David (1980). «The isolated Electron» (PDF). Scientific American. 243 (2): 91–101. Bibcode:1980SciAm.243b.104E. doi:10.1038/scientificamerican0880-104. Archived (PDF) from the original on 16 September 2019. Retrieved 24 September 2008.
- ^ Mauritsson, J. «Electron filmed for the first time ever» (PDF). Lund University. Archived from the original (PDF) on 25 March 2009. Retrieved 17 September 2008.
- ^ Mauritsson, J.; et al. (2008). «Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope». Physical Review Letters. 100 (7): 073003. arXiv:0708.1060. Bibcode:2008PhRvL.100g3003M. doi:10.1103/PhysRevLett.100.073003. PMID 18352546. S2CID 1357534.
- ^ Damascelli, A. (2004). «Probing the Electronic Structure of Complex Systems by ARPES». Physica Scripta. T109: 61–74. arXiv:cond-mat/0307085. Bibcode:2004PhST..109…61D. doi:10.1238/Physica.Topical.109a00061. S2CID 21730523.
- ^ «Image # L-1975-02972». Langley Research Center. NASA. 4 April 1975. Archived from the original on 7 December 2008. Retrieved 20 September 2008.
- ^ Elmer, J. (3 March 2008). «Standardizing the Art of Electron-Beam Welding». Lawrence Livermore National Laboratory. Archived from the original on 20 September 2008. Retrieved 16 October 2008.
- ^ Schultz, H. (1993). Electron Beam Welding. Woodhead Publishing. pp. 2–3. ISBN 978-1-85573-050-2. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Benedict, G.F. (1987). Nontraditional Manufacturing Processes. Manufacturing engineering and materials processing. Vol. 19. CRC Press. p. 273. ISBN 978-0-8247-7352-6. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Ozdemir, F.S. (25–27 June 1979). Electron beam lithography. Proceedings of the 16th Conference on Design automation. San Diego, CA: IEEE Press. pp. 383–391. Retrieved 16 October 2008.
- ^ Madou, M.J. (2002). Fundamentals of Microfabrication: the Science of Miniaturization (2nd ed.). CRC Press. pp. 53–54. ISBN 978-0-8493-0826-0. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Jongen, Y.; Herer, A. (2–5 May 1996). [no title cited]. APS/AAPT Joint Meeting. Electron Beam Scanning in Industrial Applications. American Physical Society. Bibcode:1996APS..MAY.H9902J.
- ^ Mobus, G.; et al. (2010). «Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiatio». Journal of Nuclear Materials. 396 (2–3): 264–271. Bibcode:2010JNuM..396..264M. doi:10.1016/j.jnucmat.2009.11.020.
- ^ Beddar, A.S.; Domanovic, Mary Ann; Kubu, Mary Lou; Ellis, Rod J.; Sibata, Claudio H.; Kinsella, Timothy J. (2001). «Mobile linear accelerators for intraoperative radiation therapy». AORN Journal. 74 (5): 700–705. doi:10.1016/S0001-2092(06)61769-9. PMID 11725448.
- ^ Gazda, M.J.; Coia, L.R. (1 June 2007). «Principles of Radiation Therapy» (PDF). Archived (PDF) from the original on 2 November 2013. Retrieved 31 October 2013.
- ^ Chao, A.W.; Tigner, M. (1999). Handbook of Accelerator Physics and Engineering. World Scientific. pp. 155, 188. ISBN 978-981-02-3500-0. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Oura, K.; et al. (2003). Surface Science: An Introduction. Springer Science+Business Media. pp. 1–45. ISBN 978-3-540-00545-2.
- ^ Ichimiya, A.; Cohen, P.I. (2004). Reflection High-energy Electron Diffraction. Cambridge University Press. p. 1. ISBN 978-0-521-45373-8. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Heppell, T.A. (1967). «A combined low energy and reflection high energy electron diffraction apparatus». Journal of Scientific Instruments. 44 (9): 686–688. Bibcode:1967JScI…44..686H. doi:10.1088/0950-7671/44/9/311.
- ^ McMullan, D. (1993). «Scanning Electron Microscopy: 1928–1965». University of Cambridge. Archived from the original on 16 March 2009. Retrieved 23 March 2009.
- ^ Slayter, H.S. (1992). Light and electron microscopy. Cambridge University Press. p. 1. ISBN 978-0-521-33948-3. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Cember, H. (1996). Introduction to Health Physics. McGraw-Hill Professional. pp. 42–43. ISBN 978-0-07-105461-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Erni, R.; et al. (2009). «Atomic-Resolution Imaging with a Sub-50-pm Electron Probe». Physical Review Letters. 102 (9): 096101. Bibcode:2009PhRvL.102i6101E. doi:10.1103/PhysRevLett.102.096101. PMID 19392535. Archived from the original on 2020-01-02. Retrieved 2018-08-17.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists. Jones & Bartlett Publishers. pp. 12, 197–199. ISBN 978-0-7637-0192-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Flegler, S.L.; Heckman, J.W. Jr.; Klomparens, K.L. (1995). Scanning and Transmission Electron Microscopy: An Introduction (Reprint ed.). Oxford University Press. pp. 43–45. ISBN 978-0-19-510751-7.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists (2nd ed.). Jones & Bartlett Publishers. p. 9. ISBN 978-0-7637-0192-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Freund, H.P.; Antonsen, T. (1996). Principles of Free-Electron Lasers. Springer. pp. 1–30. ISBN 978-0-412-72540-1. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Kitzmiller, J.W. (1995). Television Picture Tubes and Other Cathode-Ray Tubes: Industry and Trade Summary. Diane Publishing. pp. 3–5. ISBN 978-0-7881-2100-5.
- ^ Sclater, N. (1999). Electronic Technology Handbook. McGraw-Hill Professional. pp. 227–228. ISBN 978-0-07-058048-0.
- ^ «The History of the Integrated Circuit». The Nobel Foundation. 2008. Archived from the original on 1 December 2008. Retrieved 18 October 2008.
External links[edit]
Wikiquote has quotations related to Electron.
Wikimedia Commons has media related to Electrons.
- «The Discovery of the Electron». Center for History of Physics. American Institute of Physics.
- «Particle Data Group». University of California.
- Bock, R.K.; Vasilescu, A. (1998). The Particle Detector BriefBook (14th ed.). Springer. ISBN 978-3-540-64120-9.
- Copeland, Ed. «Spherical Electron». Sixty Symbols. Brady Haran for the University of Nottingham.

Hydrogen atomic orbitals at different energy levels. The more opaque areas are where one is most likely to find an electron at any given time. |
|
| Composition | elementary particle[1] |
|---|---|
| Statistics | fermionic |
| Family | lepton |
| Generation | first |
| Interactions | weak, electromagnetic, gravity |
| Symbol | e− , β− |
| Antiparticle | positron[a] |
| Theorized | Richard Laming (1838–1851),[2] G. Johnstone Stoney (1874) and others.[3][4] |
| Discovered | J. J. Thomson (1897)[5] |
| Mass | 9.1093837015(28)×10−31 kg[6] 5.48579909065(16)×10−4 Da[7] [1822.888486209(53)]−1 Da[b] 0.51099895000(15) MeV/c2[8] |
| Mean lifetime | stable ( > 6.6×1028 yr[9]) |
| Electric charge | −1 e −1.602176634×10−19 C[10] |
| Magnetic moment | −9.2847647043(28)×10−24 J⋅T−1[11] −1.00115965218128(18) µB[12] |
| Spin | 1 /2 |
| Weak isospin | LH: − 1 /2, RH: 0 |
| Weak hypercharge | LH: −1, RH: −2 |
The electron (
e−
or
β−
) is a subatomic particle with a negative one elementary electric charge.[13] Electrons belong to the first generation of the lepton particle family,[14] and are generally thought to be elementary particles because they have no known components or substructure.[1] The electron’s mass is approximately 1/1836 that of the proton.[15] Quantum mechanical properties of the electron include an intrinsic angular momentum (spin) of a half-integer value, expressed in units of the reduced Planck constant, ħ. Being fermions, no two electrons can occupy the same quantum state, in accordance with the Pauli exclusion principle.[14] Like all elementary particles, electrons exhibit properties of both particles and waves: They can collide with other particles and can be diffracted like light. The wave properties of electrons are easier to observe with experiments than those of other particles like neutrons and protons because electrons have a lower mass and hence a longer de Broglie wavelength for a given energy.
Electrons play an essential role in numerous physical phenomena, such as electricity, magnetism, chemistry and thermal conductivity, and they also participate in gravitational, electromagnetic and weak interactions.[16] Since an electron has charge, it has a surrounding electric field, and if that electron is moving relative to an observer, said observer will observe it to generate a magnetic field. Electromagnetic fields produced from other sources will affect the motion of an electron according to the Lorentz force law. Electrons radiate or absorb energy in the form of photons when they are accelerated.
Laboratory instruments are capable of trapping individual electrons as well as electron plasma by the use of electromagnetic fields. Special telescopes can detect electron plasma in outer space. Electrons are involved in many applications such as tribology or frictional charging, electrolysis, electrochemistry, battery technologies, electronics, welding, cathode-ray tubes, photoelectricity, photovoltaic solar panels, electron microscopes, radiation therapy, lasers, gaseous ionization detectors and particle accelerators.
Interactions involving electrons with other subatomic particles are of interest in fields such as chemistry and nuclear physics. The Coulomb force interaction between the positive protons within atomic nuclei and the negative electrons without, allows the composition of the two known as atoms. Ionization or differences in the proportions of negative electrons versus positive nuclei changes the binding energy of an atomic system. The exchange or sharing of the electrons between two or more atoms is the main cause of chemical bonding.[17] In 1838, British natural philosopher Richard Laming first hypothesized the concept of an indivisible quantity of electric charge to explain the chemical properties of atoms.[3] Irish physicist George Johnstone Stoney named this charge ‘electron’ in 1891, and J. J. Thomson and his team of British physicists identified it as a particle in 1897 during the cathode-ray tube experiment.[5] Electrons can also participate in nuclear reactions, such as nucleosynthesis in stars, where they are known as beta particles. Electrons can be created through beta decay of radioactive isotopes and in high-energy collisions, for instance when cosmic rays enter the atmosphere. The antiparticle of the electron is called the positron; it is identical to the electron except that it carries electrical charge of the opposite sign. When an electron collides with a positron, both particles can be annihilated, producing gamma ray photons.
History[edit]
Discovery of effect of electric force[edit]
The ancient Greeks noticed that amber attracted small objects when rubbed with fur. Along with lightning, this phenomenon is one of humanity’s earliest recorded experiences with electricity.[18] In his 1600 treatise De Magnete, the English scientist William Gilbert coined the New Latin term electrica, to refer to those substances with property similar to that of amber which attract small objects after being rubbed.[19] Both electric and electricity are derived from the Latin ēlectrum (also the root of the alloy of the same name), which came from the Greek word for amber, ἤλεκτρον (ēlektron).
Discovery of two kinds of charges[edit]
In the early 1700s, French chemist Charles François du Fay found that if a charged gold-leaf is repulsed by glass rubbed with silk, then the same charged gold-leaf is attracted by amber rubbed with wool. From this and other results of similar types of experiments, du Fay concluded that electricity consists of two electrical fluids, vitreous fluid from glass rubbed with silk and resinous fluid from amber rubbed with wool. These two fluids can neutralize each other when combined.[19][20] American scientist Ebenezer Kinnersley later also independently reached the same conclusion.[21]: 118 A decade later Benjamin Franklin proposed that electricity was not from different types of electrical fluid, but a single electrical fluid showing an excess (+) or deficit (−). He gave them the modern charge nomenclature of positive and negative respectively.[22] Franklin thought of the charge carrier as being positive, but he did not correctly identify which situation was a surplus of the charge carrier, and which situation was a deficit.[23]
Between 1838 and 1851, British natural philosopher Richard Laming developed the idea that an atom is composed of a core of matter surrounded by subatomic particles that had unit electric charges.[2] Beginning in 1846, German physicist Wilhelm Eduard Weber theorized that electricity was composed of positively and negatively charged fluids, and their interaction was governed by the inverse square law. After studying the phenomenon of electrolysis in 1874, Irish physicist George Johnstone Stoney suggested that there existed a «single definite quantity of electricity», the charge of a monovalent ion. He was able to estimate the value of this elementary charge e by means of Faraday’s laws of electrolysis.[24] However, Stoney believed these charges were permanently attached to atoms and could not be removed. In 1881, German physicist Hermann von Helmholtz argued that both positive and negative charges were divided into elementary parts, each of which «behaves like atoms of electricity».[3]
Stoney initially coined the term electrolion in 1881. Ten years later, he switched to electron to describe these elementary charges, writing in 1894: «… an estimate was made of the actual amount of this most remarkable fundamental unit of electricity, for which I have since ventured to suggest the name electron«. A 1906 proposal to change to electrion failed because Hendrik Lorentz preferred to keep electron.[25][26] The word electron is a combination of the words electric and ion.[27] The suffix —on which is now used to designate other subatomic particles, such as a proton or neutron, is in turn derived from electron.[28][29]
Discovery of free electrons outside matter[edit]
A beam of electrons deflected by a magnetic field into a circle[30]
While studying electrical conductivity in rarefied gases in 1859, the German physicist Julius Plücker observed the radiation emitted from the cathode caused phosphorescent light to appear on the tube wall near the cathode; and the region of the phosphorescent light could be moved by application of a magnetic field.[31] In 1869, Plücker’s student Johann Wilhelm Hittorf found that a solid body placed in between the cathode and the phosphorescence would cast a shadow upon the phosphorescent region of the tube. Hittorf inferred that there are straight rays emitted from the cathode and that the phosphorescence was caused by the rays striking the tube walls. In 1876, the German physicist Eugen Goldstein showed that the rays were emitted perpendicular to the cathode surface, which distinguished between the rays that were emitted from the cathode and the incandescent light. Goldstein dubbed the rays cathode rays.[32][33]: 393 Decades of experimental and theoretical research involving cathode rays were important in J. J. Thomson’s eventual discovery of electrons.[3]
During the 1870s, the English chemist and physicist Sir William Crookes developed the first cathode-ray tube to have a high vacuum inside.[34] He then showed in 1874 that the cathode rays can turn a small paddle wheel when placed in their path. Therefore, he concluded that the rays carried momentum. Furthermore, by applying a magnetic field, he was able to deflect the rays, thereby demonstrating that the beam behaved as though it were negatively charged.[32] In 1879, he proposed that these properties could be explained by regarding cathode rays as composed of negatively charged gaseous molecules in a fourth state of matter in which the mean free path of the particles is so long that collisions may be ignored.[33]: 394–395
The German-born British physicist Arthur Schuster expanded upon Crookes’s experiments by placing metal plates parallel to the cathode rays and applying an electric potential between the plates.[35] The field deflected the rays toward the positively charged plate, providing further evidence that the rays carried negative charge. By measuring the amount of deflection for a given level of current, in 1890 Schuster was able to estimate the charge-to-mass ratio[c] of the ray components. However, this produced a value that was more than a thousand times greater than what was expected, so little credence was given to his calculations at the time.[32] This is because it was assumed that the charge carriers were much heavier hydrogen or nitrogen atoms.[35] Schuster’s estimates would subsequently turn out to be largely correct.
In 1892 Hendrik Lorentz suggested that the mass of these particles (electrons) could be a consequence of their electric charge.[36]
While studying naturally fluorescing minerals in 1896, the French physicist Henri Becquerel discovered that they emitted radiation without any exposure to an external energy source. These radioactive materials became the subject of much interest by scientists, including the New Zealand physicist Ernest Rutherford who discovered they emitted particles. He designated these particles alpha and beta, on the basis of their ability to penetrate matter.[37] In 1900, Becquerel showed that the beta rays emitted by radium could be deflected by an electric field, and that their mass-to-charge ratio was the same as for cathode rays.[38] This evidence strengthened the view that electrons existed as components of atoms.[39][40]
In 1897, the British physicist J. J. Thomson, with his colleagues John S. Townsend and H. A. Wilson, performed experiments indicating that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier.[5] Thomson made good estimates of both the charge e and the mass m, finding that cathode ray particles, which he called «corpuscles», had perhaps one thousandth of the mass of the least massive ion known: hydrogen.[5] He showed that their charge-to-mass ratio, e/m, was independent of cathode material. He further showed that the negatively charged particles produced by radioactive materials, by heated materials and by illuminated materials were universal.[5][41] The name electron was adopted for these particles by the scientific community, mainly due to the advocation by G. F. FitzGerald, J. Larmor, and H. A. Lorentz.[42]: 273 In the same year Emil Wiechert and Walter Kaufmann also calculated the e/m ratio but they failed short of interpreting their results while J. J. Thomson would subsequently in 1899 give estimates for the electron charge and mass as well: e~6.8×10−10 esu and m~3×10−26 g[43][44]
The electron’s charge was more carefully measured by the American physicists Robert Millikan and Harvey Fletcher in their oil-drop experiment of 1909, the results of which were published in 1911. This experiment used an electric field to prevent a charged droplet of oil from falling as a result of gravity. This device could measure the electric charge from as few as 1–150 ions with an error margin of less than 0.3%. Comparable experiments had been done earlier by Thomson’s team,[5] using clouds of charged water droplets generated by electrolysis, and in 1911 by Abram Ioffe, who independently obtained the same result as Millikan using charged microparticles of metals, then published his results in 1913.[45] However, oil drops were more stable than water drops because of their slower evaporation rate, and thus more suited to precise experimentation over longer periods of time.[46]
Around the beginning of the twentieth century, it was found that under certain conditions a fast-moving charged particle caused a condensation of supersaturated water vapor along its path. In 1911, Charles Wilson used this principle to devise his cloud chamber so he could photograph the tracks of charged particles, such as fast-moving electrons.[47]
Atomic theory[edit]
The Bohr model of the atom, showing states of an electron with energy quantized by the number n. An electron dropping to a lower orbit emits a photon equal to the energy difference between the orbits.
By 1914, experiments by physicists Ernest Rutherford, Henry Moseley, James Franck and Gustav Hertz had largely established the structure of an atom as a dense nucleus of positive charge surrounded by lower-mass electrons.[48] In 1913, Danish physicist Niels Bohr postulated that electrons resided in quantized energy states, with their energies determined by the angular momentum of the electron’s orbit about the nucleus. The electrons could move between those states, or orbits, by the emission or absorption of photons of specific frequencies. By means of these quantized orbits, he accurately explained the spectral lines of the hydrogen atom.[49] However, Bohr’s model failed to account for the relative intensities of the spectral lines and it was unsuccessful in explaining the spectra of more complex atoms.[48]
Chemical bonds between atoms were explained by Gilbert Newton Lewis, who in 1916 proposed that a covalent bond between two atoms is maintained by a pair of electrons shared between them.[50] Later, in 1927, Walter Heitler and Fritz London gave the full explanation of the electron-pair formation and chemical bonding in terms of quantum mechanics.[51] In 1919, the American chemist Irving Langmuir elaborated on the Lewis’s static model of the atom and suggested that all electrons were distributed in successive «concentric (nearly) spherical shells, all of equal thickness».[52] In turn, he divided the shells into a number of cells each of which contained one pair of electrons. With this model Langmuir was able to qualitatively explain the chemical properties of all elements in the periodic table,[51] which were known to largely repeat themselves according to the periodic law.[53]
In 1924, Austrian physicist Wolfgang Pauli observed that the shell-like structure of the atom could be explained by a set of four parameters that defined every quantum energy state, as long as each state was occupied by no more than a single electron. This prohibition against more than one electron occupying the same quantum energy state became known as the Pauli exclusion principle.[54] The physical mechanism to explain the fourth parameter, which had two distinct possible values, was provided by the Dutch physicists Samuel Goudsmit and George Uhlenbeck. In 1925, they suggested that an electron, in addition to the angular momentum of its orbit, possesses an intrinsic angular momentum and magnetic dipole moment.[48][55] This is analogous to the rotation of the Earth on its axis as it orbits the Sun. The intrinsic angular momentum became known as spin, and explained the previously mysterious splitting of spectral lines observed with a high-resolution spectrograph; this phenomenon is known as fine structure splitting.[56]
Quantum mechanics[edit]
In his 1924 dissertation Recherches sur la théorie des quanta (Research on Quantum Theory), French physicist Louis de Broglie hypothesized that all matter can be represented as a de Broglie wave in the manner of light.[57] That is, under the appropriate conditions, electrons and other matter would show properties of either particles or waves. The corpuscular properties of a particle are demonstrated when it is shown to have a localized position in space along its trajectory at any given moment.[58] The wave-like nature of light is displayed, for example, when a beam of light is passed through parallel slits thereby creating interference patterns. In 1927, George Paget Thomson discovered the interference effect was produced when a beam of electrons was passed through thin metal foils and by American physicists Clinton Davisson and Lester Germer by the reflection of electrons from a crystal of nickel.[59]
In quantum mechanics, the behavior of an electron in an atom is described by an orbital, which is a probability distribution rather than an orbit. In the figure, the shading indicates the relative probability to «find» the electron, having the energy corresponding to the given quantum numbers, at that point.
De Broglie’s prediction of a wave nature for electrons led Erwin Schrödinger to postulate a wave equation for electrons moving under the influence of the nucleus in the atom. In 1926, this equation, the Schrödinger equation, successfully described how electron waves propagated.[60] Rather than yielding a solution that determined the location of an electron over time, this wave equation also could be used to predict the probability of finding an electron near a position, especially a position near where the electron was bound in space, for which the electron wave equations did not change in time. This approach led to a second formulation of quantum mechanics (the first by Heisenberg in 1925), and solutions of Schrödinger’s equation, like Heisenberg’s, provided derivations of the energy states of an electron in a hydrogen atom that were equivalent to those that had been derived first by Bohr in 1913, and that were known to reproduce the hydrogen spectrum.[61] Once spin and the interaction between multiple electrons were describable, quantum mechanics made it possible to predict the configuration of electrons in atoms with atomic numbers greater than hydrogen.[62]
In 1928, building on Wolfgang Pauli’s work, Paul Dirac produced a model of the electron – the Dirac equation, consistent with relativity theory, by applying relativistic and symmetry considerations to the hamiltonian formulation of the quantum mechanics of the electro-magnetic field.[63] In order to resolve some problems within his relativistic equation, Dirac developed in 1930 a model of the vacuum as an infinite sea of particles with negative energy, later dubbed the Dirac sea. This led him to predict the existence of a positron, the antimatter counterpart of the electron.[64] This particle was discovered in 1932 by Carl Anderson, who proposed calling standard electrons negatrons and using electron as a generic term to describe both the positively and negatively charged variants.[65]
In 1947, Willis Lamb, working in collaboration with graduate student Robert Retherford, found that certain quantum states of the hydrogen atom, which should have the same energy, were shifted in relation to each other; the difference came to be called the Lamb shift. About the same time, Polykarp Kusch, working with Henry M. Foley, discovered the magnetic moment of the electron is slightly larger than predicted by Dirac’s theory. This small difference was later called anomalous magnetic dipole moment of the electron. This difference was later explained by the theory of quantum electrodynamics, developed by Sin-Itiro Tomonaga, Julian Schwinger and
Richard Feynman in the late 1940s.[66]
Particle accelerators[edit]
With the development of the particle accelerator during the first half of the twentieth century, physicists began to delve deeper into the properties of subatomic particles.[67] The first successful attempt to accelerate electrons using electromagnetic induction was made in 1942 by Donald Kerst. His initial betatron reached energies of 2.3 MeV, while subsequent betatrons achieved 300 MeV. In 1947, synchrotron radiation was discovered with a 70 MeV electron synchrotron at General Electric. This radiation was caused by the acceleration of electrons through a magnetic field as they moved near the speed of light.[68]
With a beam energy of 1.5 GeV, the first high-energy
particle collider was ADONE, which began operations in 1968.[69] This device accelerated electrons and positrons in opposite directions, effectively doubling the energy of their collision when compared to striking a static target with an electron.[70] The Large Electron–Positron Collider (LEP) at CERN, which was operational from 1989 to 2000, achieved collision energies of 209 GeV and made important measurements for the Standard Model of particle physics.[71][72]
Confinement of individual electrons[edit]
Individual electrons can now be easily confined in ultra small (L = 20 nm, W = 20 nm) CMOS transistors operated at cryogenic temperature over a range of −269 °C (4 K) to about −258 °C (15 K).[73] The electron wavefunction spreads in a semiconductor lattice and negligibly interacts with the valence band electrons, so it can be treated in the single particle formalism, by replacing its mass with the effective mass tensor.
Characteristics[edit]
Classification[edit]
Standard Model of elementary particles. The electron (symbol e) is on the left.
In the Standard Model of particle physics, electrons belong to the group of subatomic particles called leptons, which are believed to be fundamental or elementary particles. Electrons have the lowest mass of any charged lepton (or electrically charged particle of any type) and belong to the first-generation of fundamental particles.[74] The second and third generation contain charged leptons, the muon and the tau, which are identical to the electron in charge, spin and interactions, but are more massive. Leptons differ from the other basic constituent of matter, the quarks, by their lack of strong interaction. All members of the lepton group are fermions, because they all have half-odd integer spin; the electron has spin 1/2.[75]
Fundamental properties[edit]
The invariant mass of an electron is approximately 9.109×10−31 kilograms,[76] or 5.489×10−4 atomic mass units. Due to mass–energy equivalence, this corresponds to a rest energy of 0.511 MeV. The ratio between the mass of a proton and that of an electron is about 1836.[15][77] Astronomical measurements show that the proton-to-electron mass ratio has held the same value, as is predicted by the Standard Model, for at least half the age of the universe.[78]
Electrons have an electric charge of −1.602176634×10−19 coulombs,[76] which is used as a standard unit of charge for subatomic particles, and is also called the elementary charge. Within the limits of experimental accuracy, the electron charge is identical to the charge of a proton, but with the opposite sign.[79] As the symbol e is used for the elementary charge, the electron is commonly symbolized by
e−
, where the minus sign indicates the negative charge. The positron is symbolized by
e+
because it has the same properties as the electron but with a positive rather than negative charge.[75][76]
The electron has an intrinsic angular momentum or spin of 1/2.[76] This property is usually stated by referring to the electron as a spin-1/2 particle.[75] For such particles the spin magnitude is ħ/2,[80][d] while the result of the measurement of a projection of the spin on any axis can only be ±ħ/2. In addition to spin, the electron has an intrinsic magnetic moment along its spin axis.[76] It is approximately equal to one Bohr magneton,[81][e] which is a physical constant equal to 9.27400915(23)×10−24 joules per tesla.[76] The orientation of the spin with respect to the momentum of the electron defines the property of elementary particles known as helicity.[82]
The electron has no known substructure.[1][83] Nevertheless, in condensed matter physics, spin–charge separation can occur in some materials. In such cases, electrons ‘split’ into three independent particles, the spinon, the orbiton and the holon (or chargon). The electron can always be theoretically considered as a bound state of the three, with the spinon carrying the spin of the electron, the orbiton carrying the orbital degree of freedom and the chargon carrying the charge, but in certain conditions they can behave as independent quasiparticles.[84][85][86]
The issue of the radius of the electron is a challenging problem of modern theoretical physics. The admission of the hypothesis of a finite radius of the electron is incompatible to the premises of the theory of relativity. On the other hand, a point-like electron (zero radius) generates serious mathematical difficulties due to the self-energy of the electron tending to infinity.[87] Observation of a single electron in a Penning trap suggests the upper limit of the particle’s radius to be 10−22 meters.[88]
The upper bound of the electron radius of 10−18 meters[89] can be derived using the uncertainty relation in energy. There is also a physical constant called the «classical electron radius», with the much larger value of 2.8179×10−15 m, greater than the radius of the proton. However, the terminology comes from a simplistic calculation that ignores the effects of quantum mechanics; in reality, the so-called classical electron radius has little to do with the true fundamental structure of the electron.[90][91][f]
There are elementary particles that spontaneously decay into less massive particles. An example is the muon, with a mean lifetime of 2.2×10−6 seconds, which decays into an electron, a muon neutrino and an electron antineutrino. The electron, on the other hand, is thought to be stable on theoretical grounds: the electron is the least massive particle with non-zero electric charge, so its decay would violate charge conservation.[92] The experimental lower bound for the electron’s mean lifetime is 6.6×1028 years, at a 90% confidence level.[9][93][94]
Quantum properties[edit]
As with all particles, electrons can act as waves. This is called the wave–particle duality and can be demonstrated using the double-slit experiment.
The wave-like nature of the electron allows it to pass through two parallel slits simultaneously, rather than just one slit as would be the case for a classical particle. In quantum mechanics, the wave-like property of one particle can be described mathematically as a complex-valued function, the wave function, commonly denoted by the Greek letter psi (ψ). When the absolute value of this function is squared, it gives the probability that a particle will be observed near a location—a probability density.[95]: 162–218
Electrons are identical particles because they cannot be distinguished from each other by their intrinsic physical properties. In quantum mechanics, this means that a pair of interacting electrons must be able to swap positions without an observable change to the state of the system. The wave function of fermions, including electrons, is antisymmetric, meaning that it changes sign when two electrons are swapped; that is, ψ(r1, r2) = −ψ(r2, r1), where the variables r1 and r2 correspond to the first and second electrons, respectively. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. Bosons, such as the photon, have symmetric wave functions instead.[95]: 162–218
In the case of antisymmetry, solutions of the wave equation for interacting electrons result in a zero probability that each pair will occupy the same location or state. This is responsible for the Pauli exclusion principle, which precludes any two electrons from occupying the same quantum state. This principle explains many of the properties of electrons. For example, it causes groups of bound electrons to occupy different orbitals in an atom, rather than all overlapping each other in the same orbit.[95]: 162–218
Virtual particles[edit]
In a simplified picture, which often tends to give the wrong idea but may serve to illustrate some aspects, every photon spends some time as a combination of a virtual electron plus its antiparticle, the virtual positron, which rapidly annihilate each other shortly thereafter.[96] The combination of the energy variation needed to create these particles, and the time during which they exist, fall under the threshold of detectability expressed by the Heisenberg uncertainty relation, ΔE · Δt ≥ ħ. In effect, the energy needed to create these virtual particles, ΔE, can be «borrowed» from the vacuum for a period of time, Δt, so that their product is no more than the reduced Planck constant, ħ ≈ 6.6×10−16 eV·s. Thus, for a virtual electron, Δt is at most 1.3×10−21 s.[97]
A schematic depiction of virtual electron–positron pairs appearing at random near an electron (at lower left)
While an electron–positron virtual pair is in existence, the Coulomb force from the ambient electric field surrounding an electron causes a created positron to be attracted to the original electron, while a created electron experiences a repulsion. This causes what is called vacuum polarization. In effect, the vacuum behaves like a medium having a dielectric permittivity more than unity. Thus the effective charge of an electron is actually smaller than its true value, and the charge decreases with increasing distance from the electron.[98][99] This polarization was confirmed experimentally in 1997 using the Japanese TRISTAN particle accelerator.[100] Virtual particles cause a comparable shielding effect for the mass of the electron.[101]
The interaction with virtual particles also explains the small (about 0.1%) deviation of the intrinsic magnetic moment of the electron from the Bohr magneton (the anomalous magnetic moment).[81][102] The extraordinarily precise agreement of this predicted difference with the experimentally determined value is viewed as one of the great achievements of quantum electrodynamics.[103]
The apparent paradox in classical physics of a point particle electron having intrinsic angular momentum and magnetic moment can be explained by the formation of virtual photons in the electric field generated by the electron. These photons can heuristically be thought of as causing the electron to shift about in a jittery fashion (known as zitterbewegung), which results in a net circular motion with precession.[104] This motion produces both the spin and the magnetic moment of the electron.[14] In atoms, this creation of virtual photons explains the Lamb shift observed in spectral lines.[98] The Compton Wavelength shows that near elementary particles such as the electron, the uncertainty of the energy allows for the creation of virtual particles near the electron. This wavelength explains the «static» of virtual particles around elementary particles at a close distance.
Interaction[edit]
An electron generates an electric field that exerts an attractive force on a particle with a positive charge, such as the proton, and a repulsive force on a particle with a negative charge. The strength of this force in nonrelativistic approximation is determined by Coulomb’s inverse square law.[105]: 58–61 When an electron is in motion, it generates a magnetic field.[95]: 140 The Ampère–Maxwell law relates the magnetic field to the mass motion of electrons (the current) with respect to an observer. This property of induction supplies the magnetic field that drives an electric motor.[106] The electromagnetic field of an arbitrary moving charged particle is expressed by the Liénard–Wiechert potentials, which are valid even when the particle’s speed is close to that of light (relativistic).[105]: 429–434
A particle with charge q (at left) is moving with velocity v through a magnetic field B that is oriented toward the viewer. For an electron, q is negative so it follows a curved trajectory toward the top.
When an electron is moving through a magnetic field, it is subject to the Lorentz force that acts perpendicularly to the plane defined by the magnetic field and the electron velocity. This centripetal force causes the electron to follow a helical trajectory through the field at a radius called the gyroradius. The acceleration from this curving motion induces the electron to radiate energy in the form of synchrotron radiation.[107][g][95]: 160 The energy emission in turn causes a recoil of the electron, known as the Abraham–Lorentz–Dirac Force, which creates a friction that slows the electron. This force is caused by a back-reaction of the electron’s own field upon itself.[108]
Here, Bremsstrahlung is produced by an electron e deflected by the electric field of an atomic nucleus. The energy change E2 − E1 determines the frequency f of the emitted photon.
Photons mediate electromagnetic interactions between particles in quantum electrodynamics. An isolated electron at a constant velocity cannot emit or absorb a real photon; doing so would violate conservation of energy and momentum. Instead, virtual photons can transfer momentum between two charged particles. This exchange of virtual photons, for example, generates the Coulomb force.[109] Energy emission can occur when a moving electron is deflected by a charged particle, such as a proton. The acceleration of the electron results in the emission of Bremsstrahlung radiation.[110]
An inelastic collision between a photon (light) and a solitary (free) electron is called Compton scattering. This collision results in a transfer of momentum and energy between the particles, which modifies the wavelength of the photon by an amount called the Compton shift.[h] The maximum magnitude of this wavelength shift is h/mec, which is known as the Compton wavelength.[111] For an electron, it has a value of 2.43×10−12 m.[76] When the wavelength of the light is long (for instance, the wavelength of the visible light is 0.4–0.7 μm) the wavelength shift becomes negligible. Such interaction between the light and free electrons is called Thomson scattering or linear Thomson scattering.[112]
The relative strength of the electromagnetic interaction between two charged particles, such as an electron and a proton, is given by the fine-structure constant. This value is a dimensionless quantity formed by the ratio of two energies: the electrostatic energy of attraction (or repulsion) at a separation of one Compton wavelength, and the rest energy of the charge. It is given by α ≈ 7.297353×10−3, which is approximately equal to 1/137.[76]
When electrons and positrons collide, they annihilate each other, giving rise to two or more gamma ray photons. If the electron and positron have negligible momentum, a positronium atom can form before annihilation results in two or three gamma ray photons totalling 1.022 MeV.[113][114] On the other hand, a high-energy photon can transform into an electron and a positron by a process called pair production, but only in the presence of a nearby charged particle, such as a nucleus.[115][116]
In the theory of electroweak interaction, the left-handed component of electron’s wavefunction forms a weak isospin doublet with the electron neutrino. This means that during weak interactions, electron neutrinos behave like electrons. Either member of this doublet can undergo a charged current interaction by emitting or absorbing a
W
and be converted into the other member. Charge is conserved during this reaction because the W boson also carries a charge, canceling out any net change during the transmutation. Charged current interactions are responsible for the phenomenon of beta decay in a radioactive atom. Both the electron and electron neutrino can undergo a neutral current interaction via a
Z0
exchange, and this is responsible for neutrino-electron elastic scattering.[117]
Atoms and molecules[edit]
Main article: Atom
Probability densities for the first few hydrogen atom orbitals, seen in cross-section. The energy level of a bound electron determines the orbital it occupies, and the color reflects the probability of finding the electron at a given position.
An electron can be bound to the nucleus of an atom by the attractive Coulomb force. A system of one or more electrons bound to a nucleus is called an atom. If the number of electrons is different from the nucleus’s electrical charge, such an atom is called an ion. The wave-like behavior of a bound electron is described by a function called an atomic orbital. Each orbital has its own set of quantum numbers such as energy, angular momentum and projection of angular momentum, and only a discrete set of these orbitals exist around the nucleus. According to the Pauli exclusion principle each orbital can be occupied by up to two electrons, which must differ in their spin quantum number.
Electrons can transfer between different orbitals by the emission or absorption of photons with an energy that matches the difference in potential.[118]: 159–160 Other methods of orbital transfer include collisions with particles, such as electrons, and the Auger effect.[119] To escape the atom, the energy of the electron must be increased above its binding energy to the atom. This occurs, for example, with the photoelectric effect, where an incident photon exceeding the atom’s ionization energy is absorbed by the electron.[118]: 127–132
The orbital angular momentum of electrons is quantized. Because the electron is charged, it produces an orbital magnetic moment that is proportional to the angular momentum. The net magnetic moment of an atom is equal to the vector sum of orbital and spin magnetic moments of all electrons and the nucleus. The magnetic moment of the nucleus is negligible compared with that of the electrons. The magnetic moments of the electrons that occupy the same orbital (so called, paired electrons) cancel each other out.[120]
The chemical bond between atoms occurs as a result of electromagnetic interactions, as described by the laws of quantum mechanics.[121] The strongest bonds are formed by the sharing or transfer of electrons between atoms, allowing the formation of molecules.[17] Within a molecule, electrons move under the influence of several nuclei, and occupy molecular orbitals; much as they can occupy atomic orbitals in isolated atoms.[122] A fundamental factor in these molecular structures is the existence of electron pairs. These are electrons with opposed spins, allowing them to occupy the same molecular orbital without violating the Pauli exclusion principle (much like in atoms). Different molecular orbitals have different spatial distribution of the electron density. For instance, in bonded pairs (i.e. in the pairs that actually bind atoms together) electrons can be found with the maximal probability in a relatively small volume between the nuclei. By contrast, in non-bonded pairs electrons are distributed in a large volume around nuclei.[123]
Conductivity[edit]
A lightning discharge consists primarily of a flow of electrons.[124] The electric potential needed for lightning can be generated by a triboelectric effect.[125][126]
If a body has more or fewer electrons than are required to balance the positive charge of the nuclei, then that object has a net electric charge. When there is an excess of electrons, the object is said to be negatively charged. When there are fewer electrons than the number of protons in nuclei, the object is said to be positively charged. When the number of electrons and the number of protons are equal, their charges cancel each other and the object is said to be electrically neutral. A macroscopic body can develop an electric charge through rubbing, by the triboelectric effect.[127]
Independent electrons moving in vacuum are termed free electrons. Electrons in metals also behave as if they were free. In reality the particles that are commonly termed electrons in metals and other solids are quasi-electrons—quasiparticles, which have the same electrical charge, spin, and magnetic moment as real electrons but might have a different mass.[128] When free electrons—both in vacuum and metals—move, they produce a net flow of charge called an electric current, which generates a magnetic field. Likewise a current can be created by a changing magnetic field. These interactions are described mathematically by Maxwell’s equations.[129]
At a given temperature, each material has an electrical conductivity that determines the value of electric current when an electric potential is applied. Examples of good conductors include metals such as copper and gold, whereas glass and Teflon are poor conductors. In any dielectric material, the electrons remain bound to their respective atoms and the material behaves as an insulator. Most semiconductors have a variable level of conductivity that lies between the extremes of conduction and insulation.[130] On the other hand, metals have an electronic band structure containing partially filled electronic bands. The presence of such bands allows electrons in metals to behave as if they were free or delocalized electrons. These electrons are not associated with specific atoms, so when an electric field is applied, they are free to move like a gas (called Fermi gas)[131] through the material much like free electrons.
Because of collisions between electrons and atoms, the drift velocity of electrons in a conductor is on the order of millimeters per second. However, the speed at which a change of current at one point in the material causes changes in currents in other parts of the material, the velocity of propagation, is typically about 75% of light speed.[132] This occurs because electrical signals propagate as a wave, with the velocity dependent on the dielectric constant of the material.[133]
Metals make relatively good conductors of heat, primarily because the delocalized electrons are free to transport thermal energy between atoms. However, unlike electrical conductivity, the thermal conductivity of a metal is nearly independent of temperature. This is expressed mathematically by the Wiedemann–Franz law,[131] which states that the ratio of thermal conductivity to the electrical conductivity is proportional to the temperature. The thermal disorder in the metallic lattice increases the electrical resistivity of the material, producing a temperature dependence for electric current.[134]
When cooled below a point called the critical temperature, materials can undergo a phase transition in which they lose all resistivity to electric current, in a process known as superconductivity. In BCS theory, pairs of electrons called Cooper pairs have their motion coupled to nearby matter via lattice vibrations called phonons, thereby avoiding the collisions with atoms that normally create electrical resistance.[135] (Cooper pairs have a radius of roughly 100 nm, so they can overlap each other.)[136] However, the mechanism by which higher temperature superconductors operate remains uncertain.
Electrons inside conducting solids, which are quasi-particles themselves, when tightly confined at temperatures close to absolute zero, behave as though they had split into three other quasiparticles: spinons, orbitons and holons.[137][138] The former carries spin and magnetic moment, the next carries its orbital location while the latter electrical charge.
Motion and energy[edit]
According to Einstein’s theory of special relativity, as an electron’s speed approaches the speed of light, from an observer’s point of view its relativistic mass increases, thereby making it more and more difficult to accelerate it from within the observer’s frame of reference. The speed of an electron can approach, but never reach, the speed of light in a vacuum, c. However, when relativistic electrons—that is, electrons moving at a speed close to c—are injected into a dielectric medium such as water, where the local speed of light is significantly less than c, the electrons temporarily travel faster than light in the medium. As they interact with the medium, they generate a faint light called Cherenkov radiation.[139]
Lorentz factor as a function of velocity. It starts at value 1 and goes to infinity as v approaches c.
The effects of special relativity are based on a quantity known as the Lorentz factor, defined as 
where me is the mass of electron. For example, the Stanford linear accelerator can accelerate an electron to roughly 51 GeV.[140]
Since an electron behaves as a wave, at a given velocity it has a characteristic de Broglie wavelength. This is given by λe = h/p where h is the Planck constant and p is the momentum.[57] For the 51 GeV electron above, the wavelength is about 2.4×10−17 m, small enough to explore structures well below the size of an atomic nucleus.[141]
Formation[edit]
Pair production of an electron and positron, caused by the close approach of a photon with an atomic nucleus. The lightning symbol represents an exchange of a virtual photon, thus an electric force acts. The angle between the particles is very small.[142]
The Big Bang theory is the most widely accepted scientific theory to explain the early stages in the evolution of the Universe.[143] For the first millisecond of the Big Bang, the temperatures were over 10 billion kelvins and photons had mean energies over a million electronvolts. These photons were sufficiently energetic that they could react with each other to form pairs of electrons and positrons. Likewise, positron-electron pairs annihilated each other and emitted energetic photons:
γ
+
γ
↔
e+
+
e−
An equilibrium between electrons, positrons and photons was maintained during this phase of the evolution of the Universe. After 15 seconds had passed, however, the temperature of the universe dropped below the threshold where electron-positron formation could occur. Most of the surviving electrons and positrons annihilated each other, releasing gamma radiation that briefly reheated the universe.[144]
For reasons that remain uncertain, during the annihilation process there was an excess in the number of particles over antiparticles. Hence, about one electron for every billion electron-positron pairs survived. This excess matched the excess of protons over antiprotons, in a condition known as baryon asymmetry, resulting in a net charge of zero for the universe.[145][146] The surviving protons and neutrons began to participate in reactions with each other—in the process known as nucleosynthesis, forming isotopes of hydrogen and helium, with trace amounts of lithium. This process peaked after about five minutes.[147] Any leftover neutrons underwent negative beta decay with a half-life of about a thousand seconds, releasing a proton and electron in the process,
n
→
p
+
e−
+
ν
e
For about the next 300000–400000 years, the excess electrons remained too energetic to bind with atomic nuclei.[148] What followed is a period known as recombination, when neutral atoms were formed and the expanding universe became transparent to radiation.[149]
Roughly one million years after the big bang, the first generation of stars began to form.[149] Within a star, stellar nucleosynthesis results in the production of positrons from the fusion of atomic nuclei. These antimatter particles immediately annihilate with electrons, releasing gamma rays. The net result is a steady reduction in the number of electrons, and a matching increase in the number of neutrons. However, the process of stellar evolution can result in the synthesis of radioactive isotopes. Selected isotopes can subsequently undergo negative beta decay, emitting an electron and antineutrino from the nucleus.[150] An example is the cobalt-60 (60Co) isotope, which decays to form nickel-60 (60
Ni
).[151]
An extended air shower generated by an energetic cosmic ray striking the Earth’s atmosphere
At the end of its lifetime, a star with more than about 20 solar masses can undergo gravitational collapse to form a black hole.[152] According to classical physics, these massive stellar objects exert a gravitational attraction that is strong enough to prevent anything, even electromagnetic radiation, from escaping past the Schwarzschild radius. However, quantum mechanical effects are believed to potentially allow the emission of Hawking radiation at this distance. Electrons (and positrons) are thought to be created at the event horizon of these stellar remnants.
When a pair of virtual particles (such as an electron and positron) is created in the vicinity of the event horizon, random spatial positioning might result in one of them to appear on the exterior; this process is called quantum tunnelling. The gravitational potential of the black hole can then supply the energy that transforms this virtual particle into a real particle, allowing it to radiate away into space.[153] In exchange, the other member of the pair is given negative energy, which results in a net loss of mass-energy by the black hole. The rate of Hawking radiation increases with decreasing mass, eventually causing the black hole to evaporate away until, finally, it explodes.[154]
Cosmic rays are particles traveling through space with high energies. Energy events as high as 3.0×1020 eV have been recorded.[155] When these particles collide with nucleons in the Earth’s atmosphere, a shower of particles is generated, including pions.[156] More than half of the cosmic radiation observed from the Earth’s surface consists of muons. The particle called a muon is a lepton produced in the upper atmosphere by the decay of a pion.
π−
→
μ−
+
ν
μ
A muon, in turn, can decay to form an electron or positron.[157]
μ−
→
e−
+
ν
e +
ν
μ
Observation[edit]
Remote observation of electrons requires detection of their radiated energy. For example, in high-energy environments such as the corona of a star, free electrons form a plasma that radiates energy due to Bremsstrahlung radiation. Electron gas can undergo plasma oscillation, which is waves caused by synchronized variations in electron density, and these produce energy emissions that can be detected by using radio telescopes.[159]
The frequency of a photon is proportional to its energy. As a bound electron transitions between different energy levels of an atom, it absorbs or emits photons at characteristic frequencies. For instance, when atoms are irradiated by a source with a broad spectrum, distinct dark lines appear in the spectrum of transmitted radiation in places where the corresponding frequency is absorbed by the atom’s electrons. Each element or molecule displays a characteristic set of spectral lines, such as the hydrogen spectral series. When detected, spectroscopic measurements of the strength and width of these lines allow the composition and physical properties of a substance to be determined.[160][161]
In laboratory conditions, the interactions of individual electrons can be observed by means of particle detectors, which allow measurement of specific properties such as energy, spin and charge.[162] The development of the Paul trap and Penning trap allows charged particles to be contained within a small region for long durations. This enables precise measurements of the particle properties. For example, in one instance a Penning trap was used to contain a single electron for a period of 10 months.[163] The magnetic moment of the electron was measured to a precision of eleven digits, which, in 1980, was a greater accuracy than for any other physical constant.[164]
The first video images of an electron’s energy distribution were captured by a team at Lund University in Sweden, February 2008. The scientists used extremely short flashes of light, called attosecond pulses, which allowed an electron’s motion to be observed for the first time.[165][166]
The distribution of the electrons in solid materials can be visualized by angle-resolved photoemission spectroscopy (ARPES). This technique employs the photoelectric effect to measure the reciprocal space—a mathematical representation of periodic structures that is used to infer the original structure. ARPES can be used to determine the direction, speed and scattering of electrons within the material.[167]
Plasma applications[edit]
Particle beams[edit]
Electron beams are used in welding.[169] They allow energy densities up to 107 W·cm−2 across a narrow focus diameter of 0.1–1.3 mm and usually require no filler material. This welding technique must be performed in a vacuum to prevent the electrons from interacting with the gas before reaching their target, and it can be used to join conductive materials that would otherwise be considered unsuitable for welding.[170][171]
Electron-beam lithography (EBL) is a method of etching semiconductors at resolutions smaller than a micrometer.[172] This technique is limited by high costs, slow performance, the need to operate the beam in the vacuum and the tendency of the electrons to scatter in solids. The last problem limits the resolution to about 10 nm. For this reason, EBL is primarily used for the production of small numbers of specialized integrated circuits.[173]
Electron beam processing is used to irradiate materials in order to change their physical properties or sterilize medical and food products.[174] Electron beams fluidise or quasi-melt glasses without significant increase of temperature on intensive irradiation: e.g. intensive electron radiation causes a many orders of magnitude decrease of viscosity and stepwise decrease of its activation energy.[175]
Linear particle accelerators generate electron beams for treatment of superficial tumors in radiation therapy. Electron therapy can treat such skin lesions as basal-cell carcinomas because an electron beam only penetrates to a limited depth before being absorbed, typically up to 5 cm for electron energies in the range 5–20 MeV. An electron beam can be used to supplement the treatment of areas that have been irradiated by X-rays.[176][177]
Particle accelerators use electric fields to propel electrons and their antiparticles to high energies. These particles emit synchrotron radiation as they pass through magnetic fields. The dependency of the intensity of this radiation upon spin polarizes the electron beam—a process known as the Sokolov–Ternov effect.[i] Polarized electron beams can be useful for various experiments. Synchrotron radiation can also cool the electron beams to reduce the momentum spread of the particles. Electron and positron beams are collided upon the particles’ accelerating to the required energies; particle detectors observe the resulting energy emissions, which particle physics studies .[178]
Imaging[edit]
Low-energy electron diffraction (LEED) is a method of bombarding a crystalline material with a collimated beam of electrons and then observing the resulting diffraction patterns to determine the structure of the material. The required energy of the electrons is typically in the range 20–200 eV.[179] The reflection high-energy electron diffraction (RHEED) technique uses the reflection of a beam of electrons fired at various low angles to characterize the surface of crystalline materials. The beam energy is typically in the range 8–20 keV and the angle of incidence is 1–4°.[180][181]
The electron microscope directs a focused beam of electrons at a specimen. Some electrons change their properties, such as movement direction, angle, and relative phase and energy as the beam interacts with the material. Microscopists can record these changes in the electron beam to produce atomically resolved images of the material.[182] In blue light, conventional optical microscopes have a diffraction-limited resolution of about 200 nm.[183] By comparison, electron microscopes are limited by the de Broglie wavelength of the electron. This wavelength, for example, is equal to 0.0037 nm for electrons accelerated across a 100,000-volt potential.[184] The Transmission Electron Aberration-Corrected Microscope is capable of sub-0.05 nm resolution, which is more than enough to resolve individual atoms.[185] This capability makes the electron microscope a useful laboratory instrument for high resolution imaging. However, electron microscopes are expensive instruments that are costly to maintain.
Two main types of electron microscopes exist: transmission and scanning. Transmission electron microscopes function like overhead projectors, with a beam of electrons passing through a slice of material then being projected by lenses on a photographic slide or a charge-coupled device. Scanning electron microscopes rasteri a finely focused electron beam, as in a TV set, across the studied sample to produce the image. Magnifications range from 100× to 1,000,000× or higher for both microscope types. The scanning tunneling microscope uses quantum tunneling of electrons from a sharp metal tip into the studied material and can produce atomically resolved images of its surface.[186][187][188]
Other applications[edit]
In the free-electron laser (FEL), a relativistic electron beam passes through a pair of undulators that contain arrays of dipole magnets whose fields point in alternating directions. The electrons emit synchrotron radiation that coherently interacts with the same electrons to strongly amplify the radiation field at the resonance frequency. FEL can emit a coherent high-brilliance electromagnetic radiation with a wide range of frequencies, from microwaves to soft X-rays. These devices are used in manufacturing, communication, and in medical applications, such as soft tissue surgery.[189]
Electrons are important in cathode-ray tubes, which have been extensively used as display devices in laboratory instruments, computer monitors and television sets.[190] In a photomultiplier tube, every photon striking the photocathode initiates an avalanche of electrons that produces a detectable current pulse.[191] Vacuum tubes use the flow of electrons to manipulate electrical signals, and they played a critical role in the development of electronics technology. However, they have been largely supplanted by solid-state devices such as the transistor.[192]
See also[edit]
- Anyon
- Beta radiation
- Electride
- Electron bubble
- Exoelectron emission
- g-factor
- Lepton
- List of particles
- One-electron universe
- Periodic systems of small molecules
- Spintronics
- Stern–Gerlach experiment
- Townsend discharge
- Zeeman effect
Notes[edit]
- ^ The positron is occasionally called the ‘anti-electron’.
- ^ The fractional version’s denominator is the inverse of the decimal value (along with its relative standard uncertainty of 2.9×10−11).
- ^ Note that older sources list charge-to-mass rather than the modern convention of mass-to-charge ratio.
- ^ This magnitude is obtained from the spin quantum number as
for quantum number s = 1/2.
See: Gupta (2001). - ^ Bohr magneton:
- ^ The classical electron radius is derived as follows. Assume that the electron’s charge is spread uniformly throughout a spherical volume. Since one part of the sphere would repel the other parts, the sphere contains electrostatic potential energy. This energy is assumed to equal the electron’s rest energy, defined by special relativity (E = mc2).
From electrostatics theory, the potential energy of a sphere with radius r and charge e is given by:where ε0 is the vacuum permittivity. For an electron with rest mass m0, the rest energy is equal to:
where c is the speed of light in a vacuum. Setting them equal and solving for r gives the classical electron radius.
See: Haken, Wolf, & Brewer (2005). - ^ Radiation from non-relativistic electrons is sometimes termed cyclotron radiation.
- ^ The change in wavelength, Δλ, depends on the angle of the recoil, θ, as follows,
where c is the speed of light in a vacuum and me is the electron mass. See Zombeck (2007).[77]: 393, 396
- ^ The polarization of an electron beam means that the spins of all electrons point into one direction. In other words, the projections of the spins of all electrons onto their momentum vector have the same sign.
References[edit]
- ^ a b c Eichten, E.J.; Peskin, M.E.; Peskin, M. (1983). «New Tests for Quark and Lepton Substructure». Physical Review Letters. 50 (11): 811–814. Bibcode:1983PhRvL..50..811E. doi:10.1103/PhysRevLett.50.811. OSTI 1446807. S2CID 119918703.
- ^ a b Farrar, W.V. (1969). «Richard Laming and the Coal-Gas Industry, with His Views on the Structure of Matter». Annals of Science. 25 (3): 243–254. doi:10.1080/00033796900200141.
- ^ a b c d Arabatzis, T. (2006). Representing Electrons: A Biographical Approach to Theoretical Entities. University of Chicago Press. pp. 70–74, 96. ISBN 978-0-226-02421-9. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Buchwald, J.Z.; Warwick, A. (2001). Histories of the Electron: The Birth of Microphysics. MIT Press. pp. 195–203. ISBN 978-0-262-52424-7. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ a b c d e f Thomson, J.J. (1897). «Cathode Rays». Philosophical Magazine. 44 (269): 293–316. doi:10.1080/14786449708621070. Archived from the original on 2022-01-25. Retrieved 2022-02-24.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass in u». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-06-21.
- ^ «2018 CODATA Value: electron mass energy equivalent in MeV». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-07-11.
- ^ a b Agostini, M.; et al. (Borexino Collaboration) (2015). «Test of electric charge conservation with Borexino». Physical Review Letters. 115 (23): 231802. arXiv:1509.01223. Bibcode:2015PhRvL.115w1802A. doi:10.1103/PhysRevLett.115.231802. PMID 26684111. S2CID 206265225.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron magnetic moment». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-09-10.
- ^ «2018 CODATA Value: electron magnetic moment to Bohr magneton ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-11-15.
- ^
Coffey, Jerry (10 September 2010). «What is an electron?». Archived from the original on 11 November 2012. Retrieved 10 September 2010. - ^ a b c
Curtis, L.J. (2003). Atomic Structure and Lifetimes: A conceptual approach. Cambridge University Press. p. 74. ISBN 978-0-521-53635-6. Archived from the original on 2020-03-16. Retrieved 2020-08-25. - ^ a b «CODATA value: proton-electron mass ratio». 2006 CODATA recommended values. National Institute of Standards and Technology. Archived from the original on 28 March 2019. Retrieved 18 July 2009.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 978-0-691-13512-0. Archived from the original on 2014-09-28. Retrieved 2020-08-25.
- ^ a b Pauling, L.C. (1960). The Nature of the Chemical Bond and the Structure of Molecules and Crystals: an introduction to modern structural chemistry (3rd ed.). Cornell University Press. pp. 4–10. ISBN 978-0-8014-0333-0.
- ^ Shipley, J.T. (1945). Dictionary of Word Origins. The Philosophical Library. p. 133. ISBN 978-0-88029-751-6.
- ^ a b Benjamin, Park (1898), A history of electricity (The intellectual rise in electricity) from antiquity to the days of Benjamin Franklin, New York: J. Wiley, pp. 315, 484–5, ISBN 978-1-313-10605-4
- ^ Keithley, J.F. (1999). The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s. IEEE Press. pp. 19–20. ISBN 978-0-7803-1193-0. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Cajori, Florian (1917). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. Macmillan.
- ^ «Benjamin Franklin (1706–1790)». Eric Weisstein’s World of Biography. Wolfram Research. Archived from the original on 27 August 2013. Retrieved 16 December 2010.
- ^ Myers, R.L. (2006). The Basics of Physics. Greenwood Publishing Group. p. 242. ISBN 978-0-313-32857-2.
- ^ Barrow, J.D. (1983). «Natural Units Before Planck». Quarterly Journal of the Royal Astronomical Society. 24: 24–26. Bibcode:1983QJRAS..24…24B.
- ^ Okamura, Sōgo (1994). History of Electron Tubes. IOS Press. p. 11. ISBN 978-90-5199-145-1. Archived from the original on 11 May 2016. Retrieved 29 May 2015.
In 1881, Stoney named this electromagnetic ‘electrolion’. It came to be called ‘electron’ from 1891. […] In 1906, the suggestion to call cathode ray particles ‘electrions’ was brought up but through the opinion of Lorentz of Holland ‘electrons’ came to be widely used.
- ^ Stoney, G.J. (1894). «Of the «Electron,» or Atom of Electricity». Philosophical Magazine. 38 (5): 418–420. doi:10.1080/14786449408620653. Archived from the original on 2020-10-31. Retrieved 2019-08-25.
- ^ «electron, n.2». OED Online. March 2013. Oxford University Press. Accessed 12 April 2013 [1] Archived 2021-04-27 at the Wayback Machine
- ^ Soukhanov, A.H., ed. (1986). Word Mysteries & Histories. Houghton Mifflin. p. 73. ISBN 978-0-395-40265-8.
- ^ Guralnik, D.B., ed. (1970). Webster’s New World Dictionary. Prentice Hall. p. 450.
- ^ Born, M.; Blin-Stoyle, R.J.; Radcliffe, J.M. (1989). Atomic Physics. Courier Dover. p. 26. ISBN 978-0-486-65984-8. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Plücker, M. (1858-12-01). «XLVI. Observations on the electrical discharge through rarefied gases». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 16 (109): 408–418. doi:10.1080/14786445808642591. ISSN 1941-5982.
- ^ a b c Leicester, H.M. (1971). The Historical Background of Chemistry. Courier Dover. pp. 221–222. ISBN 978-0-486-61053-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ a b Whittaker, E.T. (1951). A History of the Theories of Aether and Electricity. Vol. 1. London: Nelson.
- ^ DeKosky, R.K. (1983). «William Crookes and the quest for absolute vacuum in the 1870s». Annals of Science. 40 (1): 1–18. doi:10.1080/00033798300200101.
- ^ a b Schuster, Arthur (1890). «The discharge of electricity through gases». Proceedings of the Royal Society of London. 47: 526–559. doi:10.1098/rspl.1889.0111. S2CID 96197979.
- ^ Wilczek, Frank (June 2012). «Happy birthday, electron». Scientific American. Archived from the original on 2013-11-01. Retrieved 2022-02-24.
- ^ Trenn, T.J. (1976). «Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays». Isis. 67 (1): 61–75. doi:10.1086/351545. JSTOR 231134. S2CID 145281124.
- ^ Becquerel, H. (1900). «Déviation du Rayonnement du Radium dans un Champ Électrique». Comptes rendus de l’Académie des sciences (in French). 130: 809–815.
- ^ Buchwald and Warwick (2001:90–91).
- ^ Myers, W.G. (1976). «Becquerel’s Discovery of Radioactivity in 1896». Journal of Nuclear Medicine. 17 (7): 579–582. PMID 775027. Archived from the original on 2008-12-22. Retrieved 2022-02-24.
- ^ Thomson, J.J. (1906). «Nobel Lecture: Carriers of Negative Electricity» (PDF). The Nobel Foundation. Archived from the original (PDF) on 10 October 2008. Retrieved 25 August 2008.
- ^ O’Hara, J. G. (March 1975). «George Johnstone Stoney, F.R.S., and the Concept of the Electron». Notes and Records of the Royal Society of London. Royal Society. 29 (2): 265–276. doi:10.1098/rsnr.1975.0018. JSTOR 531468. S2CID 145353314.
- ^ Abraham Pais (1997). «The discovery of the electron – 100 years of elementary particles» (PDF). Beam Line. 1: 4–16. Archived (PDF) from the original on 2021-09-14. Retrieved 2021-09-04.
- ^ Kaufmann, W. (1897). «Die magnetische Ablenkbarkeit der Kathodenstrahlen und ihre Abhängigkeit vom Entladungspotential». Annalen der Physik und Chemie. 297 (7): 544–552. Bibcode:1897AnP…297..544K. doi:10.1002/andp.18972970709. ISSN 0003-3804. Archived from the original on 2022-02-24. Retrieved 2022-02-24.
- ^ Kikoin, I.K.; Sominskiĭ, I.S. (1961). «Abram Fedorovich Ioffe (on his eightieth birthday)». Soviet Physics Uspekhi. 3 (5): 798–809. Bibcode:1961SvPhU…3..798K. doi:10.1070/PU1961v003n05ABEH005812. Original publication in Russian: Кикоин, И.К.; Соминский, М.С. (1960). «Академик А.Ф. Иоффе». Успехи Физических Наук. 72 (10): 303–321. doi:10.3367/UFNr.0072.196010e.0307.
- ^ Millikan, R.A. (1911). «The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes’s Law» (PDF). Physical Review. 32 (2): 349–397. Bibcode:1911PhRvI..32..349M. doi:10.1103/PhysRevSeriesI.32.349. Archived (PDF) from the original on 2020-03-17. Retrieved 2019-06-21.
- ^ Das Gupta, N.N.; Ghosh, S.K. (1999). «A Report on the Wilson Cloud Chamber and Its Applications in Physics». Reviews of Modern Physics. 18 (2): 225–290. Bibcode:1946RvMP…18..225G. doi:10.1103/RevModPhys.18.225.
- ^ a b c Smirnov, B.M. (2003). Physics of Atoms and Ions. Springer. pp. 14–21. ISBN 978-0-387-95550-6. Archived from the original on 2020-05-09. Retrieved 2020-08-25.
- ^ Bohr, N. (1922). «Nobel Lecture: The Structure of the Atom» (PDF). The Nobel Foundation. Archived (PDF) from the original on 3 December 2008. Retrieved 3 December 2008.
- ^ Lewis, G.N. (1916). «The Atom and the Molecule». Journal of the American Chemical Society. 38 (4): 762–786. doi:10.1021/ja02261a002. S2CID 95865413. Archived (PDF) from the original on 2019-08-25. Retrieved 2019-08-25.
- ^ a b Arabatzis, T.; Gavroglu, K. (1997). «The chemists’ electron» (PDF). European Journal of Physics. 18 (3): 150–163. Bibcode:1997EJPh…18..150A. doi:10.1088/0143-0807/18/3/005. S2CID 56117976. Archived from the original (PDF) on 2020-06-05.
- ^ Langmuir, I. (1919). «The Arrangement of Electrons in Atoms and Molecules». Journal of the American Chemical Society. 41 (6): 868–934. doi:10.1021/ja02227a002. Archived from the original on 2021-01-26. Retrieved 2019-06-21.
- ^ Scerri, E.R. (2007). The Periodic Table. Oxford University Press. pp. 205–226. ISBN 978-0-19-530573-9.
- ^ Massimi, M. (2005). Pauli’s Exclusion Principle, The Origin and Validation of a Scientific Principle. Cambridge University Press. pp. 7–8. ISBN 978-0-521-83911-2. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Uhlenbeck, G.E.; Goudsmith, S. (1925). «Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons». Die Naturwissenschaften (in German). 13 (47): 953–954. Bibcode:1925NW…..13..953E. doi:10.1007/BF01558878. S2CID 32211960.
- ^ Pauli, W. (1923). «Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes». Zeitschrift für Physik (in German). 16 (1): 155–164. Bibcode:1923ZPhy…16..155P. doi:10.1007/BF01327386. S2CID 122256737.
- ^ a b de Broglie, L. (1929). «Nobel Lecture: The Wave Nature of the Electron» (PDF). The Nobel Foundation. Archived (PDF) from the original on 4 October 2008. Retrieved 30 August 2008.
- ^ Falkenburg, B. (2007). Particle Metaphysics: A Critical Account of Subatomic Reality. Springer. p. 85. Bibcode:2007pmca.book…..F. ISBN 978-3-540-33731-7. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Davisson, C. (1937). «Nobel Lecture: The Discovery of Electron Waves» (PDF). The Nobel Foundation. Archived (PDF) from the original on 9 July 2008. Retrieved 30 August 2008.
- ^ Schrödinger, E. (1926). «Quantisierung als Eigenwertproblem». Annalen der Physik (in German). 385 (13): 437–490. Bibcode:1926AnP…385..437S. doi:10.1002/andp.19263851302.
- ^ Rigden, J.S. (2003). Hydrogen. Harvard University Press. pp. 59–86. ISBN 978-0-674-01252-3. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Reed, B.C. (2007). Quantum Mechanics. Jones & Bartlett Publishers. pp. 275–350. ISBN 978-0-7637-4451-9. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Dirac, P.A.M. (1928). «The Quantum Theory of the Electron» (PDF). Proceedings of the Royal Society A. 117 (778): 610–624. Bibcode:1928RSPSA.117..610D. doi:10.1098/rspa.1928.0023. Archived (PDF) from the original on 2018-11-25. Retrieved 2022-02-24.
- ^ Dirac, P.A.M. (1933). «Nobel Lecture: Theory of Electrons and Positrons» (PDF). The Nobel Foundation. Archived (PDF) from the original on 23 July 2008. Retrieved 1 November 2008.
- ^ Anderson, Carl D. (1933-03-15). «The Positive Electron». Physical Review. 43 (6): 491–494. Bibcode:1933PhRv…43..491A. doi:10.1103/PhysRev.43.491. ISSN 0031-899X.
- ^ «The Nobel Prize in Physics 1965». The Nobel Foundation. Archived from the original on 24 October 2008. Retrieved 4 November 2008.
- ^ Panofsky, W.K.H. (1997). «The Evolution of Particle Accelerators & Colliders» (PDF). Beam Line. 27 (1): 36–44. Archived (PDF) from the original on 9 September 2008. Retrieved 15 September 2008.
- ^ Elder, F.R.; et al. (1947). «Radiation from Electrons in a Synchrotron». Physical Review. 71 (11): 829–830. Bibcode:1947PhRv…71..829E. doi:10.1103/PhysRev.71.829.5.
- ^ Hoddeson, L.; et al. (1997). The Rise of the Standard Model: Particle Physics in the 1960s and 1970s. Cambridge University Press. pp. 25–26. ISBN 978-0-521-57816-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Bernardini, C. (2004). «AdA: The First Electron–Positron Collider». Physics in Perspective. 6 (2): 156–183. Bibcode:2004PhP…..6..156B. doi:10.1007/s00016-003-0202-y. S2CID 122534669.
- ^ «Testing the Standard Model: The LEP experiments». CERN. 2008. Archived from the original on 14 September 2008. Retrieved 15 September 2008.
- ^ «LEP reaps a final harvest». CERN Courier. 40 (10). 2000. Archived from the original on 2017-09-30. Retrieved 2022-02-24.
- ^ Prati, E.; De Michielis, M.; Belli, M.; Cocco, S.; Fanciulli, M.; Kotekar-Patil, D.; Ruoff, M.; Kern, D.P.; Wharam, D.A.; Verduijn, J.; Tettamanzi, G.C.; Rogge, S.; Roche, B.; Wacquez, R.; Jehl, X.; Vinet, M.; Sanquer, M. (2012). «Few electron limit of n-type metal oxide semiconductor single electron transistors». Nanotechnology. 23 (21): 215204. arXiv:1203.4811. Bibcode:2012Nanot..23u5204P. CiteSeerX 10.1.1.756.4383. doi:10.1088/0957-4484/23/21/215204. PMID 22552118. S2CID 206063658.
- ^ Frampton, P.H.; Hung, P.Q.; Sher, Marc (2000). «Quarks and Leptons Beyond the Third Generation». Physics Reports. 330 (5–6): 263–348. arXiv:hep-ph/9903387. Bibcode:2000PhR…330..263F. doi:10.1016/S0370-1573(99)00095-2. S2CID 119481188.
- ^ a b c Raith, W.; Mulvey, T. (2001). Constituents of Matter: Atoms, Molecules, Nuclei and Particles. CRC Press. pp. 777–781. ISBN 978-0-8493-1202-1.
- ^ a b c d e f g h The original source for CODATA is Mohr, P.J.; Taylor, B.N.; Newell, D.B. (2008). «CODATA recommended values of the fundamental physical constants». Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. CiteSeerX 10.1.1.150.1225. doi:10.1103/RevModPhys.80.633.
- Individual physical constants from the CODATA are available at: «The NIST Reference on Constants, Units and Uncertainty». National Institute of Standards and Technology. Archived from the original on 2009-01-16. Retrieved 2009-01-15.
- ^ a b Zombeck, M.V. (2007). Handbook of Space Astronomy and Astrophysics (3rd ed.). Cambridge University Press. p. 14. ISBN 978-0-521-78242-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Murphy, M.T.; et al. (2008). «Strong Limit on a Variable Proton-to-Electron Mass Ratio from Molecules in the Distant Universe». Science. 320 (5883): 1611–1613. arXiv:0806.3081. Bibcode:2008Sci…320.1611M. doi:10.1126/science.1156352. PMID 18566280. S2CID 2384708.
- ^ Zorn, J.C.; Chamberlain, G.E.; Hughes, V.W. (1963). «Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron». Physical Review. 129 (6): 2566–2576. Bibcode:1963PhRv..129.2566Z. doi:10.1103/PhysRev.129.2566.
- ^ Gupta, M.C. (2001). Atomic and Molecular Spectroscopy. New Age Publishers. p. 81. ISBN 978-81-224-1300-7. Archived from the original on 2014-09-30. Retrieved 2020-08-25.
- ^ a b Odom, B.; et al. (2006). «New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron». Physical Review Letters. 97 (3): 030801. Bibcode:2006PhRvL..97c0801O. doi:10.1103/PhysRevLett.97.030801. PMID 16907490.
- ^ Anastopoulos, C. (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 261–262. ISBN 978-0-691-13512-0. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Gabrielse, G.; et al. (2006). «New Determination of the Fine Structure Constant from the Electron g Value and QED». Physical Review Letters. 97 (3): 030802(1–4). Bibcode:2006PhRvL..97c0802G. doi:10.1103/PhysRevLett.97.030802. PMID 16907491.
- ^ «UK | England | Physicists ‘make electrons split’«. BBC News. 2009-08-28. Archived from the original on 2017-08-31. Retrieved 2016-07-11.
- ^ Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution Archived 2019-04-04 at the Wayback Machine. Science Daily (July 31, 2009)
- ^ Yarris, Lynn (2006-07-13). «First Direct Observations of Spinons and Holons». Lbl.gov. Archived from the original on 2022-02-24. Retrieved 2016-07-11.
- ^ Eduard Shpolsky, Atomic physics (Atomnaia fizika), second edition, 1951
- ^ Dehmelt, H. (1988). «A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius». Physica Scripta. T22: 102–110. Bibcode:1988PhST…22..102D. doi:10.1088/0031-8949/1988/T22/016. S2CID 250760629.
- ^ Gabrielse, Gerald. «Electron Substructure». Physics. Harvard University. Archived from the original on 2019-04-10. Retrieved 2016-06-21.
- ^ Meschede, D. (2004). Optics, light and lasers: The Practical Approach to Modern Aspects of Photonics and Laser Physics. Wiley-VCH. p. 168. ISBN 978-3-527-40364-6. Archived from the original on 2014-08-21. Retrieved 2020-08-25.
- ^ Haken, H.; Wolf, H.C.; Brewer, W.D. (2005). The Physics of Atoms and Quanta: Introduction to Experiments and Theory. Springer. p. 70. ISBN 978-3-540-67274-6. Archived from the original on 2021-05-10. Retrieved 2020-08-25.
- ^ Steinberg, R.I.; et al. (1999). «Experimental test of charge conservation and the stability of the electron». Physical Review D. 61 (2): 2582–2586. Bibcode:1975PhRvD..12.2582S. doi:10.1103/PhysRevD.12.2582.
- ^ Beringer, J.; et al. (Particle Data Group) (2012). «Review of Particle Physics: [electron properties]» (PDF). Physical Review D. 86 (1): 010001. Bibcode:2012PhRvD..86a0001B. doi:10.1103/PhysRevD.86.010001. Archived (PDF) from the original on 2022-01-15. Retrieved 2022-02-24.
- ^ Back, H.O.; et al. (2002). «Search for electron decay mode e → γ + ν with prototype of Borexino detector». Physics Letters B. 525 (1–2): 29–40. Bibcode:2002PhLB..525…29B. doi:10.1016/S0370-2693(01)01440-X.
- ^ a b c d e Munowitz, M. (2005). Knowing the Nature of Physical Law. Oxford University Press. p. 162. ISBN 978-0-19-516737-5.
- ^ Kane, G. (9 October 2006). «Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?». Scientific American. Retrieved 19 September 2008.
- ^ Taylor, J. (1989). «Gauge Theories in Particle Physics». In Davies, Paul (ed.). The New Physics. Cambridge University Press. p. 464. ISBN 978-0-521-43831-5. Archived from the original on 2014-09-21. Retrieved 2020-08-25.
- ^ a b Genz, H. (2001). Nothingness: The Science of Empty Space. Da Capo Press. pp. 241–243, 245–247. ISBN 978-0-7382-0610-3.
- ^ Gribbin, J. (25 January 1997). «More to electrons than meets the eye». New Scientist. Archived from the original on 11 February 2015. Retrieved 17 September 2008.
- ^ Levine, I.; et al. (1997). «Measurement of the Electromagnetic Coupling at Large Momentum Transfer». Physical Review Letters. 78 (3): 424–427. Bibcode:1997PhRvL..78..424L. doi:10.1103/PhysRevLett.78.424.
- ^ Murayama, H. (10–17 March 2006). Supersymmetry Breaking Made Easy, Viable and Generic. Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories. La Thuile, Italy. arXiv:0709.3041. Bibcode:2007arXiv0709.3041M. — lists a 9% mass difference for an electron that is the size of the Planck distance.
- ^ Schwinger, J. (1948). «On Quantum-Electrodynamics and the Magnetic Moment of the Electron». Physical Review. 73 (4): 416–417. Bibcode:1948PhRv…73..416S. doi:10.1103/PhysRev.73.416.
- ^ Huang, K. (2007). Fundamental Forces of Nature: The Story of Gauge Fields. World Scientific. pp. 123–125. ISBN 978-981-270-645-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Foldy, L.L.; Wouthuysen, S. (1950). «On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit». Physical Review. 78 (1): 29–36. Bibcode:1950PhRv…78…29F. doi:10.1103/PhysRev.78.29.
- ^ a b Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- ^ Crowell, B. (2000). Electricity and Magnetism. Light and Matter. pp. 129–152. ISBN 978-0-9704670-4-1. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Mahadevan, R.; Narayan, R.; Yi, I. (1996). «Harmony in Electrons: Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field». The Astrophysical Journal. 465: 327–337. arXiv:astro-ph/9601073. Bibcode:1996ApJ…465..327M. doi:10.1086/177422. S2CID 16324613.
- ^ Rohrlich, F. (1999). «The Self-Force and Radiation Reaction». American Journal of Physics. 68 (12): 1109–1112. Bibcode:2000AmJPh..68.1109R. doi:10.1119/1.1286430.
- ^ Georgi, H. (1989). «Grand Unified Theories». In Davies, Paul (ed.). The New Physics. Cambridge University Press. p. 427. ISBN 978-0-521-43831-5. Archived from the original on 2014-09-21. Retrieved 2020-08-25.
- ^ Blumenthal, G.J.; Gould, R. (1970). «Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases». Reviews of Modern Physics. 42 (2): 237–270. Bibcode:1970RvMP…42..237B. doi:10.1103/RevModPhys.42.237.
- ^ «The Nobel Prize in Physics 1927». The Nobel Foundation. 2008. Archived from the original on 24 October 2008. Retrieved 28 September 2008.
- ^ Chen, S.-Y.; Maksimchuk, A.; Umstadter, D. (1998). «Experimental observation of relativistic nonlinear Thomson scattering». Nature. 396 (6712): 653–655. arXiv:physics/9810036. Bibcode:1998Natur.396..653C. doi:10.1038/25303. S2CID 16080209.
- ^ Beringer, R.; Montgomery, C.G. (1942). «The Angular Distribution of Positron Annihilation Radiation». Physical Review. 61 (5–6): 222–224. Bibcode:1942PhRv…61..222B. doi:10.1103/PhysRev.61.222.
- ^ Buffa, A. (2000). College Physics (4th ed.). Prentice Hall. p. 888. ISBN 978-0-13-082444-8.
- ^ Eichler, J. (2005). «Electron–positron pair production in relativistic ion–atom collisions». Physics Letters A. 347 (1–3): 67–72. Bibcode:2005PhLA..347…67E. doi:10.1016/j.physleta.2005.06.105.
- ^ Hubbell, J.H. (2006). «Electron positron pair production by photons: A historical overview». Radiation Physics and Chemistry. 75 (6): 614–623. Bibcode:2006RaPC…75..614H. doi:10.1016/j.radphyschem.2005.10.008. Archived from the original on 2019-06-21. Retrieved 2019-06-21.
- ^ Quigg, C. (4–30 June 2000). The Electroweak Theory. TASI 2000: Flavor Physics for the Millennium. Boulder, Colorado. p. 80. arXiv:hep-ph/0204104. Bibcode:2002hep.ph….4104Q.
- ^ a b Tipler, Paul; Llewellyn, Ralph (2003). Modern Physics (illustrated ed.). Macmillan. ISBN 978-0-7167-4345-3.
- ^ Burhop, E.H.S. (1952). The Auger Effect and Other Radiationless Transitions. Cambridge University Press. pp. 2–3. ISBN 978-0-88275-966-1.
- ^ Jiles, D. (1998). Introduction to Magnetism and Magnetic Materials. CRC Press. pp. 280–287. ISBN 978-0-412-79860-3. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Löwdin, P.O.; Erkki Brändas, E.; Kryachko, E.S. (2003). Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per-Olov Löwdin. Springer Science+Business Media. pp. 393–394. ISBN 978-1-4020-1290-7. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ McQuarrie, D.A.; Simon, J.D. (1997). Physical Chemistry: A Molecular Approach. University Science Books. pp. 325–361. ISBN 978-0-935702-99-6. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Daudel, R.; et al. (1974). «The Electron Pair in Chemistry». Canadian Journal of Chemistry. 52 (8): 1310–1320. doi:10.1139/v74-201.
- ^ Rakov, V.A.; Uman, M.A. (2007). Lightning: Physics and Effects. Cambridge University Press. p. 4. ISBN 978-0-521-03541-5. Archived from the original on 2021-01-26. Retrieved 2020-08-25.
- ^ Freeman, G.R.; March, N.H. (1999). «Triboelectricity and some associated phenomena». Materials Science and Technology. 15 (12): 1454–1458. Bibcode:1999MatST..15.1454F. doi:10.1179/026708399101505464.
- ^ Forward, K.M.; Lacks, D.J.; Sankaran, R.M. (2009). «Methodology for studying particle–particle triboelectrification in granular materials». Journal of Electrostatics. 67 (2–3): 178–183. doi:10.1016/j.elstat.2008.12.002.
- ^ Weinberg, S. (2003). The Discovery of Subatomic Particles. Cambridge University Press. pp. 15–16. ISBN 978-0-521-82351-7.
- ^ Lou, L.-F. (2003). Introduction to phonons and electrons. World Scientific. pp. 162, 164. Bibcode:2003ipe..book…..L. ISBN 978-981-238-461-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Guru, B.S.; Hızıroğlu, H.R. (2004). Electromagnetic Field Theory. Cambridge University Press. pp. 138, 276. ISBN 978-0-521-83016-4.
- ^ Achuthan, M.K.; Bhat, K.N. (2007). Fundamentals of Semiconductor Devices. Tata McGraw-Hill. pp. 49–67. ISBN 978-0-07-061220-4. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ a b Ziman, J.M. (2001). Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford University Press. p. 260. ISBN 978-0-19-850779-6. Archived from the original on 2022-02-24. Retrieved 2020-08-25.
- ^ Main, P. (12 June 1993). «When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise». New Scientist. 1887: 30. Archived from the original on 11 February 2015. Retrieved 9 October 2008.
- ^ Blackwell, G.R. (2000). The Electronic Packaging Handbook. CRC Press. pp. 6.39–6.40. ISBN 978-0-8493-8591-9. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Durrant, A. (2000). Quantum Physics of Matter: The Physical World. CRC Press. pp. 43, 71–78. ISBN 978-0-7503-0721-5. Archived from the original on 2016-05-27. Retrieved 2015-10-16.
- ^ «The Nobel Prize in Physics 1972». The Nobel Foundation. 2008. Archived from the original on 11 October 2008. Retrieved 13 October 2008.
- ^ Kadin, A.M. (2007). «Spatial Structure of the Cooper Pair». Journal of Superconductivity and Novel Magnetism. 20 (4): 285–292. arXiv:cond-mat/0510279. doi:10.1007/s10948-006-0198-z. S2CID 54948290.
- ^ «Discovery about behavior of building block of nature could lead to computer revolution». ScienceDaily. 31 July 2009. Archived from the original on 4 April 2019. Retrieved 1 August 2009.
- ^ Jompol, Y.; et al. (2009). «Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid». Science. 325 (5940): 597–601. arXiv:1002.2782. Bibcode:2009Sci…325..597J. doi:10.1126/science.1171769. PMID 19644117. S2CID 206193.
- ^ «The Nobel Prize in Physics 1958, for the discovery and the interpretation of the Cherenkov effect». The Nobel Foundation. 2008. Archived from the original on 18 October 2008. Retrieved 25 September 2008.
- ^ «Special Relativity». Stanford Linear Accelerator Center. 26 August 2008. Archived from the original on 28 August 2008. Retrieved 25 September 2008.
- ^ Adams, S. (2000). Frontiers: Twentieth Century Physics. CRC Press. p. 215. ISBN 978-0-7484-0840-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Bianchini, Lorenzo (2017). Selected Exercises in Particle and Nuclear Physics. Springer. p. 79. ISBN 978-3-319-70494-4. Archived from the original on 2020-01-02. Retrieved 2018-04-20.
- ^ Lurquin, P.F. (2003). The Origins of Life and the Universe. Columbia University Press. p. 2. ISBN 978-0-231-12655-7.
- ^ Silk, J. (2000). The Big Bang: The Creation and Evolution of the Universe (3rd ed.). Macmillan. pp. 110–112, 134–137. ISBN 978-0-8050-7256-3.
- ^ Kolb, E.W.; Wolfram, Stephen (1980). «The Development of Baryon Asymmetry in the Early Universe» (PDF). Physics Letters B. 91 (2): 217–221. Bibcode:1980PhLB…91..217K. doi:10.1016/0370-2693(80)90435-9. S2CID 122680284. Archived (PDF) from the original on 2020-10-30. Retrieved 2020-08-25.
- ^ Sather, E. (Spring–Summer 1996). «The Mystery of Matter Asymmetry» (PDF). Beam Line. Stanford University. Archived (PDF) from the original on 12 October 2008. Retrieved 1 November 2008.
- ^ Burles, S.; Nollett, K.M.; Turner, M.S. (1999). «Big-Bang Nucleosynthesis: Linking Inner Space and Outer Space». arXiv:astro-ph/9903300.
- ^ Boesgaard, A.M.; Steigman, G. (1985). «Big bang nucleosynthesis – Theories and observations». Annual Review of Astronomy and Astrophysics. 23 (2): 319–378. Bibcode:1985ARA&A..23..319B. doi:10.1146/annurev.aa.23.090185.001535.
- ^ a b Barkana, R. (2006). «The First Stars in the Universe and Cosmic Reionization». Science. 313 (5789): 931–934. arXiv:astro-ph/0608450. Bibcode:2006Sci…313..931B. CiteSeerX 10.1.1.256.7276. doi:10.1126/science.1125644. PMID 16917052. S2CID 8702746.
- ^ Burbidge, E.M.; et al. (1957). «Synthesis of Elements in Stars» (PDF). Reviews of Modern Physics. 29 (4): 548–647. Bibcode:1957RvMP…29..547B. doi:10.1103/RevModPhys.29.547. Archived (PDF) from the original on 2018-07-23. Retrieved 2019-06-21.
- ^ Rodberg, L.S.; Weisskopf, V. (1957). «Fall of Parity: Recent Discoveries Related to Symmetry of Laws of Nature». Science. 125 (3249): 627–633. Bibcode:1957Sci…125..627R. doi:10.1126/science.125.3249.627. PMID 17810563.
- ^ Fryer, C.L. (1999). «Mass Limits For Black Hole Formation». The Astrophysical Journal. 522 (1): 413–418. arXiv:astro-ph/9902315. Bibcode:1999ApJ…522..413F. doi:10.1086/307647. S2CID 14227409.
- ^ Parikh, M.K.; Wilczek, F. (2000). «Hawking Radiation As Tunneling». Physical Review Letters. 85 (24): 5042–5045. arXiv:hep-th/9907001. Bibcode:2000PhRvL..85.5042P. doi:10.1103/PhysRevLett.85.5042. hdl:1874/17028. PMID 11102182. S2CID 8013726.
- ^ Hawking, S.W. (1974). «Black hole explosions?». Nature. 248 (5443): 30–31. Bibcode:1974Natur.248…30H. doi:10.1038/248030a0. S2CID 4290107.
- ^ Halzen, F.; Hooper, D. (2002). «High-energy neutrino astronomy: the cosmic ray connection». Reports on Progress in Physics. 66 (7): 1025–1078. arXiv:astro-ph/0204527. Bibcode:2002RPPh…65.1025H. doi:10.1088/0034-4885/65/7/201. S2CID 53313620.
- ^ Ziegler, J.F. (1998). «Terrestrial cosmic ray intensities». IBM Journal of Research and Development. 42 (1): 117–139. Bibcode:1998IBMJ…42..117Z. doi:10.1147/rd.421.0117.
- ^ Sutton, C. (4 August 1990). «Muons, pions and other strange particles». New Scientist. Archived from the original on 11 February 2015. Retrieved 28 August 2008.
- ^ Wolpert, S. (24 July 2008). «Scientists solve 30 year-old aurora borealis mystery» (Press release). University of California. Archived from the original on 17 August 2008. Retrieved 11 October 2008.
- ^ Gurnett, D.A.; Anderson, R. (1976). «Electron Plasma Oscillations Associated with Type III Radio Bursts». Science. 194 (4270): 1159–1162. Bibcode:1976Sci…194.1159G. doi:10.1126/science.194.4270.1159. PMID 17790910. S2CID 11401604.
- ^ Martin, W.C.; Wiese, W.L. (2007). «Atomic Spectroscopy: A compendium of basic ideas, notation, data, and formulas». National Institute of Standards and Technology. Archived from the original on 8 February 2007. Retrieved 8 January 2007.
- ^ Fowles, G.R. (1989). Introduction to Modern Optics. Courier Dover. pp. 227–233. ISBN 978-0-486-65957-2. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Grupen, C. (2000). «Physics of Particle Detection». AIP Conference Proceedings. 536: 3–34. arXiv:physics/9906063. Bibcode:2000AIPC..536….3G. doi:10.1063/1.1361756. S2CID 119476972.
- ^ «The Nobel Prize in Physics 1989». The Nobel Foundation. 2008. Archived from the original on 28 September 2008. Retrieved 24 September 2008.
- ^ Ekstrom, P.; Wineland, David (1980). «The isolated Electron» (PDF). Scientific American. 243 (2): 91–101. Bibcode:1980SciAm.243b.104E. doi:10.1038/scientificamerican0880-104. Archived (PDF) from the original on 16 September 2019. Retrieved 24 September 2008.
- ^ Mauritsson, J. «Electron filmed for the first time ever» (PDF). Lund University. Archived from the original (PDF) on 25 March 2009. Retrieved 17 September 2008.
- ^ Mauritsson, J.; et al. (2008). «Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope». Physical Review Letters. 100 (7): 073003. arXiv:0708.1060. Bibcode:2008PhRvL.100g3003M. doi:10.1103/PhysRevLett.100.073003. PMID 18352546. S2CID 1357534.
- ^ Damascelli, A. (2004). «Probing the Electronic Structure of Complex Systems by ARPES». Physica Scripta. T109: 61–74. arXiv:cond-mat/0307085. Bibcode:2004PhST..109…61D. doi:10.1238/Physica.Topical.109a00061. S2CID 21730523.
- ^ «Image # L-1975-02972». Langley Research Center. NASA. 4 April 1975. Archived from the original on 7 December 2008. Retrieved 20 September 2008.
- ^ Elmer, J. (3 March 2008). «Standardizing the Art of Electron-Beam Welding». Lawrence Livermore National Laboratory. Archived from the original on 20 September 2008. Retrieved 16 October 2008.
- ^ Schultz, H. (1993). Electron Beam Welding. Woodhead Publishing. pp. 2–3. ISBN 978-1-85573-050-2. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Benedict, G.F. (1987). Nontraditional Manufacturing Processes. Manufacturing engineering and materials processing. Vol. 19. CRC Press. p. 273. ISBN 978-0-8247-7352-6. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Ozdemir, F.S. (25–27 June 1979). Electron beam lithography. Proceedings of the 16th Conference on Design automation. San Diego, CA: IEEE Press. pp. 383–391. Retrieved 16 October 2008.
- ^ Madou, M.J. (2002). Fundamentals of Microfabrication: the Science of Miniaturization (2nd ed.). CRC Press. pp. 53–54. ISBN 978-0-8493-0826-0. Archived from the original on 2021-01-07. Retrieved 2020-08-25.
- ^ Jongen, Y.; Herer, A. (2–5 May 1996). [no title cited]. APS/AAPT Joint Meeting. Electron Beam Scanning in Industrial Applications. American Physical Society. Bibcode:1996APS..MAY.H9902J.
- ^ Mobus, G.; et al. (2010). «Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiatio». Journal of Nuclear Materials. 396 (2–3): 264–271. Bibcode:2010JNuM..396..264M. doi:10.1016/j.jnucmat.2009.11.020.
- ^ Beddar, A.S.; Domanovic, Mary Ann; Kubu, Mary Lou; Ellis, Rod J.; Sibata, Claudio H.; Kinsella, Timothy J. (2001). «Mobile linear accelerators for intraoperative radiation therapy». AORN Journal. 74 (5): 700–705. doi:10.1016/S0001-2092(06)61769-9. PMID 11725448.
- ^ Gazda, M.J.; Coia, L.R. (1 June 2007). «Principles of Radiation Therapy» (PDF). Archived (PDF) from the original on 2 November 2013. Retrieved 31 October 2013.
- ^ Chao, A.W.; Tigner, M. (1999). Handbook of Accelerator Physics and Engineering. World Scientific. pp. 155, 188. ISBN 978-981-02-3500-0. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Oura, K.; et al. (2003). Surface Science: An Introduction. Springer Science+Business Media. pp. 1–45. ISBN 978-3-540-00545-2.
- ^ Ichimiya, A.; Cohen, P.I. (2004). Reflection High-energy Electron Diffraction. Cambridge University Press. p. 1. ISBN 978-0-521-45373-8. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Heppell, T.A. (1967). «A combined low energy and reflection high energy electron diffraction apparatus». Journal of Scientific Instruments. 44 (9): 686–688. Bibcode:1967JScI…44..686H. doi:10.1088/0950-7671/44/9/311.
- ^ McMullan, D. (1993). «Scanning Electron Microscopy: 1928–1965». University of Cambridge. Archived from the original on 16 March 2009. Retrieved 23 March 2009.
- ^ Slayter, H.S. (1992). Light and electron microscopy. Cambridge University Press. p. 1. ISBN 978-0-521-33948-3. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Cember, H. (1996). Introduction to Health Physics. McGraw-Hill Professional. pp. 42–43. ISBN 978-0-07-105461-4. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Erni, R.; et al. (2009). «Atomic-Resolution Imaging with a Sub-50-pm Electron Probe». Physical Review Letters. 102 (9): 096101. Bibcode:2009PhRvL.102i6101E. doi:10.1103/PhysRevLett.102.096101. PMID 19392535. Archived from the original on 2020-01-02. Retrieved 2018-08-17.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists. Jones & Bartlett Publishers. pp. 12, 197–199. ISBN 978-0-7637-0192-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Flegler, S.L.; Heckman, J.W. Jr.; Klomparens, K.L. (1995). Scanning and Transmission Electron Microscopy: An Introduction (Reprint ed.). Oxford University Press. pp. 43–45. ISBN 978-0-19-510751-7.
- ^ Bozzola, J.J.; Russell, L.D. (1999). Electron Microscopy: Principles and Techniques for Biologists (2nd ed.). Jones & Bartlett Publishers. p. 9. ISBN 978-0-7637-0192-5. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Freund, H.P.; Antonsen, T. (1996). Principles of Free-Electron Lasers. Springer. pp. 1–30. ISBN 978-0-412-72540-1. Archived from the original on 2022-02-04. Retrieved 2020-08-25.
- ^ Kitzmiller, J.W. (1995). Television Picture Tubes and Other Cathode-Ray Tubes: Industry and Trade Summary. Diane Publishing. pp. 3–5. ISBN 978-0-7881-2100-5.
- ^ Sclater, N. (1999). Electronic Technology Handbook. McGraw-Hill Professional. pp. 227–228. ISBN 978-0-07-058048-0.
- ^ «The History of the Integrated Circuit». The Nobel Foundation. 2008. Archived from the original on 1 December 2008. Retrieved 18 October 2008.
External links[edit]
Wikiquote has quotations related to Electron.
Wikimedia Commons has media related to Electrons.
- «The Discovery of the Electron». Center for History of Physics. American Institute of Physics.
- «Particle Data Group». University of California.
- Bock, R.K.; Vasilescu, A. (1998). The Particle Detector BriefBook (14th ed.). Springer. ISBN 978-3-540-64120-9.
- Copeland, Ed. «Spherical Electron». Sixty Symbols. Brady Haran for the University of Nottingham.
Электро́н (от др.-греч. ἤλεκτρον — янтарь[3]) — стабильная, отрицательно заряженная элементарная частица, одна из основных структурных единиц вещества. Является фермионом (то есть имеет полуцелый спин). Относится к лептонам (единственная стабильная частица среди заряженных лептонов). Из электронов состоят электронные оболочки атомов, где их число и положение определяет почти все химические свойства веществ. Движение свободных электронов обусловливает такие явления, как электрический ток в проводниках и вакууме.
Содержание
- 1 Свойства
- 2 Этимология и история открытия
- 3 Использование
- 4 Электрон как квазичастица
- 5 Электрон и Вселенная
- 6 См. также
- 7 Примечания
- 8 Литература
Свойства
Заряд электрона неделим и равен −1,602176565(35)·10−19 Кл[1] (или −4,80320427(13)·10−10 ед. заряда СГСЭ в системе СГСЭ или −1,602176565(35)·10−20 ед. СГСМ в системе СГСМ); он был впервые непосредственно измерен в экспериментах (англ.) А. Ф. Иоффе (1911) и Р. Милликена (1912). Эта величина служит единицей измерения электрического заряда других элементарных частиц (в отличие от заряда электрона, элементарный заряд обычно берётся с положительным знаком). Масса электрона равна 9,10938291(40)·10−31 кг.[1]




Согласно современным представлениям физики элементарных частиц, электрон неделим и бесструктурен (как минимум до расстояний 10−17 см). Электрон участвует в слабом, электромагнитном и гравитационном взаимодействиях. Он принадлежит к группе лептонов и является (вместе со своей античастицей, позитроном) легчайшим из заряженных лептонов. До открытия массы нейтрино электрон считался наиболее лёгкой из массивных частиц — его масса примерно в 1836 раз меньше массы протона. Спин электрона равен 1/2, и, таким образом, электрон относится к фермионам. Как и любая заряженная частица со спином, электрон обладает магнитным моментом, причем магнитный момент делится на нормальную часть и аномальный магнитный момент. Иногда к электронам относят как собственно электроны, так и позитроны (например, рассматривая их как общее электрон-позитронное поле, решение уравнения Дирака). В этом случае отрицательно заряженный электрон называют негатроном, положительно заряженный — позитроном.[источник не указан 120 дней]
Находясь в периодическом потенциале кристалла, электрон рассматривается как квазичастица, эффективная масса которой может значительно отличаться от массы электрона.
Свободный электрон не может поглотить фотон, хотя и может рассеять его (см. эффект Комптона).
Этимология и история открытия
Название «электрон» происходит от греческого слова ἤλεκτρον, означающего «янтарь»: ещё в древней Греции естествоиспытателями проводились эксперименты — куски янтаря тёрли шерстью, после чего те начинали притягивать к себе мелкие предметы. Термин «электрон» как название фундаментальной неделимой единицы заряда в электрохимии был предложен[4] Дж. Дж. Стоуни (англ.) в 1894 (сама единица была введена им в 1874). Открытие электрона как частицы принадлежит Э. Вихерту[5][6] и Дж. Дж. Томсону, который в 1897 установил, что отношение заряда к массе для катодных лучей не зависит от материала источника. (см. Открытие электрона)
Открытие волновых свойств[7]. Согласно гипотезе де Бройля (1924), электрон (как и все другие материальные микрообъекты) обладает не только корпускулярными, но и волновыми свойствами. Де-бройлевская длина волны нерелятивистского электрона равна 

Использование
Эксперименты с трубкой Крукса впервые продемонстрировали природу электронов
В большинстве источников низкоэнергетичных электронов используются явления термоэлектронной эмиссии и фотоэлектронной эмиссии. Высокоэнергетичные, с энергией от нескольких кэВ до нескольких МэВ, электроны излучаются в процессах бета-распада и внутренней конверсии радиоактивных ядер. Электроны, излучаемые в бета-распаде, иногда называют бета-частицами или бета-лучами. Источниками электронов с более высокой энергией служат ускорители.
Движение электронов в металлах и полупроводниках позволяет легко переносить энергию и управлять ею; это является одной из основ современной цивилизации и используется практически повсеместно в промышленности, связи, информатике, электронике, в быту. Скорость дрейфа электронов в проводниках очень мала (~0,1—1 мм/с), однако электрическое поле распространяется со скоростью света. В связи с этим ток во всей цепи устанавливается практически мгновенно.
Пучки электронов, ускоренные до больших энергий, например, в линейных ускорителях, являются одним из основных средств изучения строения атомных ядер и природы элементарных частиц. Более прозаическим применением электронных лучей являются телевизоры и мониторы с электронно-лучевыми трубками (кинескопами). Электронный микроскоп также использует способность электронных пучков подчиняться законам электронной оптики. До изобретения транзисторов практически вся радиотехника и электроника были основаны на вакуумных электронных лампах, где применяется управление движением электронов в вакууме электрическими (иногда и магнитными) полями. Электровакуумные приборы (ЭВП) продолжают ограниченно использоваться и в наше время; наиболее распространённые применения — магнетроны в генераторах микроволновых печей и вышеупомянутые электронно-лучевые трубки (ЭЛТ) в телевизорах и мониторах.
Электрон как квазичастица
Если электрон находится в периодическом потенциале, его движение рассматривается как движение квазичастицы. Его состояния описываются квазиволновым вектором. Основной динамической характеристикой в случае квадратичного закона дисперсии является эффективная масса, которая может значительно отличаться от массы свободного электрона и в общем случае является тензором.
Электрон и Вселенная
Известно[8], что из каждых 100 нуклонов во Вселенной, 87 являются протонами и 13 — нейтронами (последние в основном входят в состав ядер гелия). Для обеспечения общей нейтральности вещества число протонов и электронов должно быть одинаково. Плотность барионной (наблюдаемой оптическими методами) массы, которая состоит в основном из нуклонов, достаточно хорошо известна (один нуклон на 0,4 кубического метра)[9]. С учётом радиуса наблюдаемой Вселенной (13,7 млрд световых лет) можно подсчитать, что число электронов в этом объёме составляет ~1080, что сопоставимо с большими числами Дирака.
См. также
- Теория одноэлектронной Вселенной
- Электричество
- Электроника
- Фотоэлектронный умножитель
- Электронная лампа
Примечания
- ↑ 1 2 3 4 5 6 7 8 http://physics.nist.gov/cuu/Constants/Table/allascii.txt Fundamental Physical Constants — Complete Listing
- ↑ H. O. Back et al. Search for electron decay mode e → γ + ν with prototype of Borexino detector // Phys. Lett. B. — 2002. — Т. 525. — С. 29-40. — DOI:10.1016/S0370-2693(01)01440-X
- ↑ Также то же, что и электрум: «янтарного цвета сплав золота (80 %) с серебром (20 %)» (Черных П. Я. Историко-этимологический словарь).
- ↑ Stoney, G. Johnstone, «Of the ‘Electron,’ or Atom of Electricity». Philosophical Magazine. Series 5, Volume 38, p. 418—420 October 1894.
- ↑ Wiechert E. // Schriften d. phys.-ökon. Gesell. zu Königsberg in Pr. 1897. 38. Jg. № 1. Sitzungsber. S. 3-16.
- ↑ Быков Г. В. К истории открытия электрона // Вопросы истории естествознания и техники. 1963. Вып. 15. С. 25-29.
- ↑ БСЭ
- ↑ Richard N. Boyd Big bang nucleosynthesis // Nuclear Physics A. — 2001. — Т. 693. — № 1-2. — С. 249-257.
- ↑ ASTROPHYSICAL CONSTANTS AND PARAMETERS
Литература
- Все известные свойства электрона систематизированы в обзоре Particle Data Group [1] (англ.).
| Квантовая электродинамика | п·Позитрон | Фотон Аномальный магнитный момент Позитроний |
Частицы в физике
| Элементарные частицы |
|
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Составные частицы |
|
||||||||||||||||||||||||
| Квазичастицы | Солитон Давыдова · Экситон · Биэкситон · Магнон · Фонон · Плазмон · Поляритон · Полярон · Примесон · Ротон · Биротон · Дырка · Электрон · Куперовская пара · Орбитон · Трион · Фазон · Флуктуон · Энион · Холон и спинон | ||||||||||||||||||||||||
| Списки | Список частиц · Список квазичастиц · Список барионов · Список мезонов · История открытия частиц |
Категории:
- Квантовая электродинамика
- Элементарные частицы
- Лептоны
- Электрон
Wikimedia Foundation.
2010.
Игры ⚽ Поможем решить контрольную работу
Синонимы:
дельта-электрон, лептон, минерал, мотороллер, сплав, термоэлектрон, фермион, фотоэлектрон, частица, электр, янтарь
- Первая мировая война
- Forth (язык программирования)
Полезное
Смотреть что такое «Электрон» в других словарях:
-
Электрон (КА) — У этого термина существуют и другие значения, см. Электрон (значения). «Электрон 2» «Электрон» серия из четырёх советских искусственных спутников Земли, запущенных в 1964 году. Цель … Википедия
-
Электрон — (Новосибирск,Россия) Категория отеля: 3 звездочный отель Адрес: 2 ой Краснодонский Переулок … Каталог отелей
-
ЭЛЕКТРОН — (символ е , е), первая элем. ч ца, открытая в физике; матер. носитель наименьшей массы и наименьшего электрич. заряда в природе. Э. составная часть атомов; их число в нейтр. атоме равно ат. номеру, т. е. числу протонов в ядре. Заряд (е) и масса… … Физическая энциклопедия
-
Электрон — (Москва,Россия) Категория отеля: 2 звездочный отель Адрес: Проспект Андропова 38 строение 2 … Каталог отелей
-
Электрон — (e , e) (от греческого elektron янтарь; вещество, легко электризующееся при трении), стабильная элементарная частица с отрицательным электрическим зарядом e=1,6´10 19 Кл и массой 9´10 28 г. Относится к классу лептонов. Открыт английским физиком… … Иллюстрированный энциклопедический словарь
-
ЭЛЕКТРОН — (е е ), стабильная отрицательно заряженная элементарная частица со спином 1/2, массой ок. 9.10 28 г и магнитным моментом, равным магнетону Бора; относится к лептонам и участвует в электромагнитном, слабом и гравитационном взаимодействиях.… … Большой Энциклопедический словарь
-
ЭЛЕКТРОН — (обозначение е), устойчивая ЭЛЕМЕНТАРНАЯ ЧАСТИЦА с отрицательным зарядом и массой покоя 9,1310 31 кг (что составляет 1/1836 от массы ПРОТОНА). Электроны были обнаружены в 1879 г. английским физиком Джозефом Томсоном. Они движутся вокруг ЯДРА,… … Научно-технический энциклопедический словарь
-
электрон — сущ., кол во синонимов: 12 • дельта электрон (1) • лептон (7) • минерал (5627) • … Словарь синонимов
-
ЭЛЕКТРОН — искусственный спутник Земли, созданный в СССР для изучения радиационных поясов и магнитного поля Земли. Запускались парами один по траектории, лежащей ниже, а другой выше радиационных поясов. В 1964 запущено 2 пары Электронов … Большой Энциклопедический словарь
-
ЭЛЕКТРОН — ЭЛЕКТРОН, элктрона, муж. (греч. elektron янтарь). 1. Частица с наименьшим отрицательным электрическим зарядом, образующая в соединении с протоном атом (физ.). Движение электронов создает электрический ток. 2. только ед. Легкий магниевый сплав,… … Толковый словарь Ушакова
-
ЭЛЕКТРОН — ЭЛЕКТРОН, а, м. (спец.). Элементарная частица с наименьшим отрицательным электрическим зарядом. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
18+
© Академик, 2000-2023
-
Обратная связь:
Техподдержка,
Реклама на сайте
- 👣 Путешествия
Экспорт словарей на сайты, сделанные на PHP,
Joomla,
Drupal,
WordPress, MODx.
- Пометить текст и поделиться
- Искать во всех словарях
- Искать в переводах
- Искать в Интернете
Поделиться ссылкой на выделенное
Вспомните:
- что такое атом;
- из чего состоит атом;
- изменяется ли атом в химических реакциях?
АТОМ — это электронейтральная частица, состоящая из положительно заряженного ядра и отрицательно заряженных электронов.
Число электронов в ходе химических процессов может изменяться, но заряд ядра всегда остается неизменным. Зная распределение электронов в атоме (строение атома), можно предсказать многие свойства данного химического элемента, а также простых и сложных веществ, в состав которых этот элемент входит.
Содержание
- Структура Периодической системы Менделеева
- Ядро атома. Изотопы
- Распределение электронов в поле ядра атома
- Строение атома и свойства элементов
- Выводы
Структура Периодической системы Менделеева
Строение атома, т. е. состав ядра, распределение электронов вокруг ядра, несложно определить по положению элемента в Периодической системе. В Периодической системе Менделеева химические элементы располагаются в определённой последовательности. Эта последовательность тесно связана со строением атома этих элементов. Каждому химическому элементу в системе присвоен порядковый номер, кроме того, для него можно указать:
- номер периода;
- номер группы;
- вид подгруппы.
Зная точный «адрес» химического элемента, т. е. его группу, подгруппу и номер периода, можно однозначно определить строение его атома.
Период — это горизонтальный ряд химических элементов. В современной Периодической системе семь периодов. Первые три — малые, так как они содержат 2 или 8 элементов:
- 1-й период — Н, Не — 2 элемента;
- 2-й период — Li…Nе — 8 элементов;
- 3-й период — Na…Аr — 8 элементов.
Остальные периоды — большие. Каждый из них содержит 2–3 ряда элементов:
- 4-й период (2 ряда) — К…Кr — 18 элементов;
- 6-й период (3 ряда) — Сs…Rn — 32 элемента. В этот период входит ряд лантаноидов.
Группа — вертикальный ряд химических элементов. Всего групп восемь. Каждая группа состоит из двух подгрупп: главной подгруппы и побочной подгруппы (см. рис. 5).
Главную подгруппу (подгруппу А) образуют химические элементы малых периодов и больших периодов. На рисунке 5 показано, что главную подгруппу пятой группы составляют элементы малых периодов (N, P) и больших периодов (As, Sb, Bi).
Побочную подгруппу (подгруппу Б) образуют химические элементы только больших периодов. В нашем случае это V, Nb, Ta.
Визуально эти подгруппы различить легко: главная подгруппа «высокая», начинается с первого или второго периода. Побочная подгруппа — «низкая», начинается с 4-го периода.
Итак, каждый химический элемент Периодической системы имеет свой адрес:
- период;
- группу;
- подгруппу;
- порядковый номер.
Например, ванадий (V) — это химический элемент 4-го периода, V группы, побочной подгруппы, порядковый номер 23.
Задание 3.1. Укажите период, группу и подгруппу для химических элементов с порядковыми номерами 8, 26, 31, 35, 54.
Задание 3.2. Укажите порядковый номер и название химического элемента, если известно, что он находится:
- в 4-м периоде, VI группе, побочной подгруппе;
- в 5-м периоде, IV группе, главной подгруппе.
Каким образом можно связать эти сведения об элементе со строением его атома?
Ядро атома. Изотопы
Атом состоит из ядра, которое имеет положительный заряд, и электронов, которые имеют отрицательный заряд. В целом атом электронейтрален.
Положительный заряд ядра атома равен порядковому номеру химического элемента.
Ядро атома — сложная частица. В ней сосредоточена почти вся масса атома. Поскольку химический элемент — совокупность атомов с одинаковым зарядом ядра, то около символа элемента указывают (рис. 6).
По этим данным можно определить состав ядра. Ядро состоит из протонов и нейтронов.
- Протон (р) имеет массу, равную 1 (1,0073 а. е. м.) и заряд, равный +1.
- Нейтрон (n) заряда не имеет (нейтрален), а масса его приблизительно равна массе протона (1,0087 а. е. м.).
Какие частицы определяют заряд ядра? Протоны! Причём число протонов равно (по величине) заряду ядра атома, т. е. порядковому номеру:
Число нейтронов определяют по разности между величинами: «масса ядра» и «порядковый номер».
Задание 3.3. Определите состав ядер атомов, если химический элемент находится в:
- 3-м периоде, VII группе, главной подгруппе;
- 4-м периоде, IV группе, побочной подгруппе;
- 5-м периоде, I группе, главной подгруппе.
Обратите внимание, что при определении массового числа ядра атома приходится округлять атомную массу, указанную в Периодической системе! Почему? Ведь массы протона и нейтрона практически целочисленны, а массой электронов можно пренебречь.
Для того,чтобы ответить на этот вопрос, нужно понять:
- Что происходит с атомом в ходе химических процессов;
- Что такое «химический элемент».
В химических процессах обязательно изменяется распределение электронов вокруг ядра или даже изменяется их число. В последнем случае атом отдаёт или принимает электроны и превращается в заряженную частицу — ион. Но в химических реакциях никогда не меняется состав ядра атома, его заряд. Поэтому заряд ядра атома является своеобразным «паспортом» химического элемента.
Химический элемент — совокупность атомов или ионов с одинаковым зарядом ядра.
Для того чтобы разобраться, попробуйте определить, какие из ядер, состав которых указан ниже, принадлежат одному и тому же химическому элементу:
Атомам одного химического элемента принадлежат ядра А и В, так как они содержат одинаковое число протонов, т. е. заряд этих ядер одинаковый. Но ведь у них разная масса! Исследования показывают, что масса атома не оказывает существенного влияния на его химические свойства. Поэтому атомы одного и того же химического элемента (одинаковое число протонов), но с разной массой (разное число нейтронов) являются ИЗОТОПАМИ* этого элемента.
* Слово «изотоп» означает по смыслу «одно место», т. е. все изотопы данного химического элемента находятся в одной клетке ПСХЭ.
В таблице Менделеева указана средняя атомная масса всех природных изотопов данного элемента (Аr). Изотопы и их химические соединения отличаются друг от друга по физическим свойствам, но химические свойства у изотопов одного химического элемента одинаковы. Так, изотоп углерода-14 (14С) имеет такие же химические свойства, как и углерод-12 (12С), который входит в ткани любого живого организма, отличаясь от него только радиоактивностью. Поэтому изотопы применяют для диагностики и лечения различных заболеваний, для научных исследований.
Элемент «водород» встречается в природе в виде трёх изотопов:
Химический элемент «кислород» также представлен тремя природными изотопами:
Задание 3.4. Укажите состав ядер этих изотопов водорода и кислорода.
Если разные вещества содержат атомы одного и того же химического элемента, это не означает, что эти вещества имеют одни те же свойства. Например, химический элемент «хлор» в виде атомарного хлора Cl• разрушает метан, а также атмосферный озон. Тот же элемент в виде молекулярного хлора Cl2 ядовит, активно реагирует с водой, многими металлами, а ионы хлора (химический элемент — тот же!) в составе NaCl химически инертен, а с биологической точки зрения не только безвреден, но и полезен для нас. Эти ионы являются макроэлементами нашей пищи, которые входят в состав крови, желудочного сока. Суточная потребность — до 6 граммов.
Но вернемся к описанию строения атома.
Распределение электронов в поле ядра атома
Как известно, ядро атома в химических процессах не меняется. А что меняется? Общее число электронов и распределение электронов. Общее число электронов определить несложно: оно равно порядковому номеру, т. е. заряду ядра атома:
Электроны имеют отрицательный заряд –1, а масса их ничтожна: 1/1840 от массы протона.
Отрицательно заряженные электроны отталкиваются и поэтому находятся на разных расстояниях от ядра. При этом электроны, имеющие приблизительно равный запас энергии, образуют энергетический уровень.
Число энергетических уровней в атоме равно номеру периода, в котором находится химический элемент. Энергетические уровни условно обозначают так (рис. 7).
Задание 3.5. Определите число энергетических уровней в атомах кислорода, магния, кальция, свинца.
На каждом энергетическом уровне может находиться ограниченное число электронов:
- на первом энергетическом уровне не более 2 электронов;
- на втором энергетическом уровне не более 8 электронов;
- на третьем энергетическом уровне не более 18 электронов.
ЗАПОМНИТЕ ЭТИ ЧИСЛА!
Они показывают, что, например, на втором энергетическом уровне может находиться 2 или 5 или 7 электронов, но не может быть 9 или 12 электронов.
Важно знать, что, независимо от номера энергетического уровня, на внешнем (последнем) уровне не может быть больше восьми электронов. Внешний восьмиэлектронный энергетический уровень является наиболее устойчивым и называется завершённым. Такие энергетические уровни имеются у самых неактивных элементов — благородных газов.
Как определить число электронов на внешнем уровне остальных атомов? Для этого существует простое правило – число внешних электронов равно:
- для элементов главных подгрупп — номеру группы;
- для элементов побочных подгрупп — оно не может быть больше двух (рис. 8).
Например:
Задание 3.6. Укажите число внешних электронов для химических элементов с порядковыми номерами 15, 25, 30, 53.
Задание 3.7. Найдите в Периодической системе химические элементы, в атомах которых имеется завершённый внешний уровень.
Очень важно правильно определять число внешних электронов, так как именно с ними связаны важнейшие свойства атома. Так, в химических реакциях атомы стремятся «приобрести» устойчивый, завершённый внешний уровень (8ē). Для этого атомы, на внешнем уровне которых мало электронов, «предпочитают» их отдать.
Химические элементы, атомы которых способны только отдавать электроны, относятся к МЕТАЛЛАМ. Очевидно, что на внешнем уровне атома металла должно быть мало электронов: 1, 2, 3.
Если на внешнем энергетическом уровне атома много электронов, то такие атомы стремятся принять электроны до завершения внешнего энергетического уровня, т. е. до восьми электронов. Такие элементы относятся к НЕМЕТАЛЛАМ.
Вопрос. К каким элементам (металлам или неметаллам) относятся химические элементы побочных подгрупп? Почему?
Металлы и неметаллы главных подгрупп в таблице Менделеева отделяет линия, которую можно провести от бора к астату. Выше этой линии (и на линии) располагаются неметаллы, ниже — металлы.
Задание 3.8. Определить, к металлам или неметаллам относятся: фосфор, ванадий, кобальт, селен, висмут. Вывод сделайте, определив положение элемента в Периодической системе химических элементов и число электронов на внешнем уровне.
Для того чтобы составить распределение электрона по остальным уровням и подуровням, следует воспользоваться следующим АЛГОРИТМОМ:
- Определить общее число электронов в атоме (по порядковому номеру).
- Определить число энергетических уровней (по номеру периода).
- Определить число внешних электронов (по виду подгруппы и номеру группы).
- Указать число электронов на всех уровнях, кроме предпоследнего.
- Рассчитать число электронов на предпоследнем уровне.
Например, согласно пунктам 1…4 для атома марганца определено:
Получили распределение электронов в атоме марганца (рис. 9):
Задание 3.9. Отработайте алгоритм, составив схемы строения атомов для элементов № 16, 26, 33, 37. Укажите: металлы это или неметаллы? Ответ поясните.
Составляя вышеприведенные схемы строения атома, мы не учитывали, что электроны в атоме занимают не только определённые уровни, но и определённые подуровни каждого уровня. Вид подуровня обозначается латинской буквой: s, p, d.
Число возможных подуровней равно номеру уровня, т. е.
- первый уровень состоит из одного s-подуровня;
- второй уровень состоит из двух подуровней: s и р и т. д.
На каждом подуровне может находиться строго ограниченное число электронов:
- на s-подуровне — не больше 2ē;
- на р-подуровне — не больше 6ē;
- на d-подуровне — не больше 10ē.
Подуровни одного уровня заполняются в строго определённом порядке:
Таким образом, р-подуровнь не может начать заполняться, если не заполнен s-подуровень данного энергетического уровня и т. д. Исходя из этого правила, несложно составить электронную конфигурацию атома марганца (рис. 10).
В целом электронная конфигурация атома марганца выглядит так:
Здесь и далее приняты обозначения (рис. 11).
Задание 3.10. Составьте электронные конфигурации атомов для химических элементов № 16, 26, 33, 37.
Для чего необходимо составлять электронные конфигурации атомов? Для того чтобы определять свойства этих химических элементов!
Для этого следует помнить: в химических процессах участвуют только валентные электроны.
Валентные электроны находятся на внешнем энергетическом уровне и незавершённом d-подуровне предвнешнего уровня.
Определим число валентных электронов для марганца:
или сокращённо:
Строение атома и свойства элементов
Мы получили краткую электронную формулу атома марганца, которая отражает распределение его валентных электронов. Что можно определить по этой формуле?
1. Какие свойства — металла или неметалла — преобладают у этого элемента? Ответ: марганец — металл, так как на внешнем (четвёртом) уровне 2 электрона.
2. Какой процесс характерен для металла? Ответ: всегда только отдача электронов.
3. Какие электроны и сколько их будет отдавать атом марганца? Ответы:
- два внешних электрона (они дальше всех от ядра и слабее притягиваются им);
- семь (2+5) валентных электронов (так как в этом случае на третьем уровне атома останется восемь электронов, т. е. образуется завершённый уже внешний уровень).
Все эти рассуждения и заключения можно отразить при помощи схемы (рис. 12).
Полученные условные заряды атома называются степенью окисления.
Рассматривая строение атомов кислорода и водорода и рассуждая аналогично, можно показать, что типичными степенями окисления для кислорода является –2, а для водорода +1.
Вопрос. С каким из этих химических элементов может образовывать соединения марганец, если учесть полученные выше степени окисления его?
Только с кислородом, так как его атом имеет противоположную по заряду (знаку) степень окисления. В этом случае несложно составить формулы соответствующих оксидов марганца (здесь степени окисления соответствуют валентностям этих химических элементов):
Строение атома марганца подсказывает, что большей степени окисления, чем +7, у марганца быть не может, так как в этом случае пришлось бы затрагивать устойчивый, теперь уже завершённый предвнешний уровень. Поэтому степень окисления +7 является высшей, а соответствующий оксид Мn2О7 — высшим оксидом марганца.
Для закрепления всех этих понятий рассмотрим строение атома теллура и некоторые его свойства (см. рис. 13). Этот рисунок показывает, что теллур относится к неметаллам, так как, во-первых, у него на внешнем уровне шесть электронов и, во-вторых, его символ находится в главной подгруппе выше линии В — At. Поэтому его атом может и принимать (до завершения внешнего уровня, и отдавать электроны. В результате, в отличие от металлов, неметалл теллур может проявлять низшую степень окисления (–2) и образовывать летучие водородные соединения с водородом (Н2Те). Высшая степень окисления атома теллура (+6), как и у металлов соответствует номеру группы и, находясь в этой степени окисления, теллур образует высший оксид ТеО3.
Задание 3.11. Изобразить электронные конфигурации атомов Nа, Rb, Сl, I, Si, Sn. Определить свойства этих химических элементов, формулы их простейших соединений (с кислородом и с водородом).
Сделаем выводы.
- В химических реакциях участвуют только валентные электроны, которые могут находиться только на последних двух уровнях.
- Атомы металлов могут только отдавать эти электроны (все или несколько), принимая положительные степени окисления.
- Атомы неметаллов могут принимать (недостающие до восьми) электроны, получая при этом отрицательные степени окисления, и отдавать валентные электроны (все или несколько), принимая при этом положительные степени окисления.
Возникает вопрос: как составить краткую электронную формулу (распределение валентных электронов), сразу, не составляя длинных электронных конфигураций? Для этого нужно помнить несколько простых правил.
1. Номер периода соответствует числу энергетических уровней у атомов химических элементов этого периода.
2. Номер группы, как правило, совпадает с числом валентных электронов, (исключение составляют только подгруппы меди и железа).
3. Подгруппа (главная или побочная) включает химические элементы, у которых имеется одинаковое распределение валентных электронов, причём в атомах элементов главной и побочной подгруппы электроны распределяются по-разному.
3.1. У элементов главных подгрупп все валентные электроны находятся на внешнем уровне, например:
V группа, главная → 5 валентных электронов
Поэтому для всех химических элементов главной подгруппы пятой группы (пять валентных электронов) распределение этих электронов следующее:
3.2. У элементов побочных подгрупп число внешних электронов не превышает двух, например:
5 валентных электронов ← V группа, побочная → 2 электрона на внешнем уровне*.
* За счёт «провала электрона» число внешних электронов может быть меньше. Но число валентных электронов при этом не меняется, поэтому свойства элемента будут такими же. Эти случаи рассмотрены в Самоучителе второго уровня, часть 1.
Для большинства химических элементов побочных подгрупп, у которых на внешнем энергетическом уровне два электрона, остальные (N – 2) валентные электроны будут находиться на d-подуровне предвнешнего уровня (N – номер группы), например:
Вопрос. Для элементов какой группы составлена такая запись?
Задание 3.12. Составьте краткие электронные формулы для атомов химических элементов № 35 и 42, а затем составьте распределение электронов в этих атомах по алгоритму. Убедитесь, что ваше «предсказание» сбылось.
Сравним теперь свойства химических элементов одной подгруппы, например:
Что общего в строении атомов этих элементов? На внешнем уровне каждого атома по одному электрону — это активные металлы. Металлическая активность связана со способностью отдавать электроны: чем легче отдает электроны атом, тем сильнее выражены его металлические свойства.
Что удерживает электроны в атоме? Притяжение их к ядру. Чем ближе электроны к ядру, тем сильнее они притягиваются ядром атома, тем труднее их «оторвать».
Исходя из этого, сделаем вывод: какой элемент — Nа или Rb — легче отдает внешний электрон? Какой из них является более активным металлом? Очевидно, рубидий, так как его валентные электроны находятся дальше от ядра (и слабее удерживаются ядром).
Вывод. В главных подгруппах сверху вниз металлические свойства усиливаются, так как возрастает радиус атома и валентные электроны слабее притягиваются к ядру.
Сравним свойства:
Оба химических элемента — неметаллы, так как до завершения внешнего уровня не хватает одного электрона, и эти атомы будут активно притягивать недостающий электрон. При этом, чем сильнее притягивает атом неметалла недостающий электрон, тем сильнее проявляются его неметаллические свойства (способность принимать электроны).
За счёт чего происходит притяжение электрона? За счёт положительного заряда ядра атома. Но в таком случае чем ближе электрон к ядру, тем сильнее их взаимное притяжение, тем активнее неметалл.
Сделаем вывод, у какого элемента сильнее выражены неметаллические свойства: у хлора или у йода? Очевидно, у хлора, так как его валентные электроны ближе к ядру.
Вывод. Активность неметаллов в подгруппах сверху вниз убывает, так как возрастает радиус атома и все труднее притянуть недостающие электроны.
Сравним свойства кремния и олова:
На внешнем уровне обоих атомов по четыре электрона. Тем не менее эти элементы в Периодической системе находятся по разные стороны от линии, соединяющей бор и астат (см. правило в уроке 2.1.). Поэтому:
- у кремния, символ которого находится выше линии В–At, сильнее проявляются неметаллические свойства;
- у олова, символ которого находится ниже линии В–At, сильнее проявляются металлические свойства;
Почему? Потому что в атоме олова четыре валентных электрона находятся так далеко от ядра, что присоединение недостающих четырех электронов затруднено, в то время как отдача электронов с пятого энергетического уровня происходит достаточно легко. Для кремния возможны оба процесса, причём первый (приём электронов) — преобладает.
Выводы:
- чем меньше электронов в атоме и чем дальше они от ядра, тем сильнее проявляются металлические свойства;
- чем больше внешних электронов в атоме, чем ближе они к ядру, тем сильнее проявляются неметаллические свойства.
Сравним строение атомов и свойства химических элементов одного периода:
Вопрос. О каком периоде и каких элементах идёт речь?
Видно, что металлические свойства убывают, так как увеличивается число внешних электронов, а неметаллические свойства — возрастают. Если речь идёт о большом периоде, где большинство элементов имеет 2 электрона на внешнем уровне (элементы побочных подгрупп), то в этом случае главной причиной убывания металлических свойств в периоде является уменьшение радиуса атома. Дело в том, что за счёт увеличения заряда ядра в периоде увеличивается сила притяжения электронов к нему и уменьшается радиус атома:
Сравните: r (Ca) = 0,197 нм и r (Zn) = 0,139 нм
Вопрос. Какой из металлов более активен?
Основываясь на этих и других выводах, сформулированных в этой главе, можно для любого химического элемента Периодической системы составить алгоритм описания свойств химического элемента по его положению в Периодической системе.
1. Составить схему строения атома, т. е. определить состав ядра, распределение электронов по энергетическим уровням и подуровням:
- определить общее число электронов в атоме (по порядковому номеру);
- определить число энергетических уровней (по номеру периода);
- определить число внешних электронов (по виду подгруппы и номеру группы);
- указать число электронов на всех энергетических уровнях, кроме предпоследнего;
- рассчитать число электронов на предпоследнем уровне.
2. Определить число валентных электронов и число внешних электронов.
3. Определить, какие свойства — металла или неметалла — сильнее проявляются у данного химического элемента (по положению в ПСХЭ).
4. Определить число отдаваемых (принимаемых) электронов.
5. Определить высшую и низшую степени окисления химического элемента.
6. Составить для этих степеней окисления химические формулы простейших соединений с кислородом и водородом.
7. Определить характер оксида (см. урок 2.1.) и составить уравнения его реакции с водой.
8. Для указанных (пункт 6) веществ составить уравнения характерных реакций (см. урок 2).
Задание 3.13. Составить по данной схеме описания атомов серы, селена, кальция и стронция и свойства этих химических элементов. Какие общие свойства имеют их оксиды? Гидроксиды?
Если вы выполнили упражнения 3.11 и 3.12, то легко заметить, что не только атомы элементов одной подгруппы, но и их соединения имеют общие свойства и похожий состав. Это отражено в Периодическом законе Менделеева: Свойства химических элементов, а также свойства простых и сложных веществ, образованных ими, находятся в периодической зависимости от ЗАРЯДА ЯДЕР ИХ АТОМОВ.
Физический смысл Периодического закона ясен: свойства химических элементов периодически повторяются потому, что периодически повторяются конфигурации валентных электронов (распределение электронов внешнего и предпоследнего уровней).
Так, у химических элементов одной и той же подгруппы одинаковое распределение валентных электронов и, значит, похожие свойства.
Выводы
Строение атома связано с положением элемента в Периодической системе. Зная строение атома, можно предсказать свойства элемента и его соединений. Эти свойства находятся в периодической зависимости от заряда ядер атомов элементов, в соответствии с Периодическим законом Менделеева.
Строение электронных оболочек атомов

4.7
Средняя оценка: 4.7
Всего получено оценок: 1608.
4.7
Средняя оценка: 4.7
Всего получено оценок: 1608.
Атом – мельчайшая частица вещества, состоящая из ядра и электронов. Строение электронных оболочек атомов определяется положением элемента в Периодической системе химических элементов Д. И. Менделеева.
Электрон и электронная оболочка атома
Атом, который в целом является нейтральным, состоит из положительно заряженного ядра и отрицательно заряженной электронной оболочки (электронное облако), при этом, суммарные положительные и отрицательные заряды равны по абсолютной величине. При вычислении относительной атомной массы массу электронов не учитывают, так как она ничтожно мала и в 1840 раз меньше массы протона или нейтрона.
Электрон – совершенно уникальная частица, которая имеет двойственную природу: он имеет одновременно свойства волны и частицы. Они непрерывно движутся вокруг ядра.
Пространство вокруг ядра, где вероятность нахождения электрона наиболее вероятна, называют электронной орбиталью, или электронным облаком. Это пространство имеет определенную форму, которая обозначается буквами s-, p-, d-, и f-. S-электронная орбиталь имеет шаровидную форму, p-орбиталь имеет форму гантели или объемной восьмерки, формы d- и f-орбиталей значительно сложнее.
Вокруг ядра электроны расположены на электронных слоях. Каждый слой характеризуется расстоянием от ядра и энергией, поэтому электронные слои часто называют электронными энергетическими уровнями. Чем ближе уровень к ядру, тем меньше энергия электронов в нем. Один элемент отличается от другого числом протонов в ядре атома и соответственно числом электронов. Следовательно, число электронов в электронной оболочке нейтрального атома равно числу протонов, содержащимся в ядре этого атома. Каждый следующий элемент имеет в ядре на один протон больше, а в электронной оболочке – на один электрон больше.
Вновь вступающий электрон занимает орбиталь с наименьшей энергией. Однако максимальное число электронов на уровне определяется формулой:
N=2n2,
где N – максимальное число электронов, а n – номер энергетического уровня.
На первом уровне может быть только 2 электрона, на втором – 8 электронов, на третьем – 18 электронов, а на четвертом уровне – 32 электрона. На внешнем уровне атома не может находится больше 8 электронов: как только число электронов достигает 8, начинает заполняться следующий, более далекий от ядра уровень.
Строение электронных оболочек атомов
Каждый элемент стоит в определенном периоде. Период – это горизонтальная совокупность элементов, расположенных в порядке возрастания заряда ядер их атомов, которая начинается щелочным металлом, а заканчивается инертным газом. Первые три периода в таблице – малые, а следующие, начиная с четвертого периода – большие, состоят из двух рядов. Номер периода, в котором находится элемент имеет физический смысл. Он означает, сколько электронных энергетических уровней имеется в атоме любого элемента данного периода. Так, элемент хлор Cl находится в 3 периоде, то есть его электронная оболочка имеет три электронных слоя. Хлор стоит в VII группе таблицы, причем в главной подгруппе. Главной подгруппой называется столбец внутри каждой группы, который начинается с 1 или 2 периода.
Таким образом, состояние электронных оболочек атома хлора таково: порядковый номер элемента хлора – 17, что означает, что атом имеет в ядре 17 протонов, а в электронной оболочке – 17 электронов. На 1 уровне может быть только 2 электрона, на 3 уровне – 7 электронов, так как хлор находится в главной подруппе VII группы. Тогда на 2 уровне находится:17-2-7=8 электронов.
Что мы узнали?
Тема «Строение электронных оболочек атомов» по химии (8 класс) кратко объясняет строение атома, свойства и расположение электронов. Также она дает представление о распределении электронов по уровням в периодической системе Д. И. Менделеева.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Никита Губский
7/10
-
Антон Неврамов
10/10
-
Александр Алишевич
7/10
-
Паша Кривов
10/10
-
Александр Котков
10/10
-
Саша Штрейкер
8/10
-
Тимур Насыров
10/10
-
Фыафыафыа Фыафыа
10/10
-
Ангелина Шумовская
8/10
-
Al Unicorn
9/10
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 1608.
А какая ваша оценка?