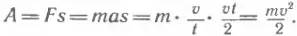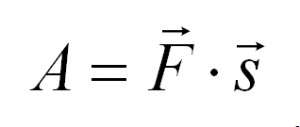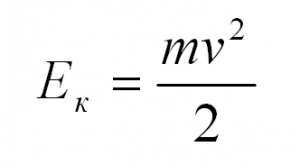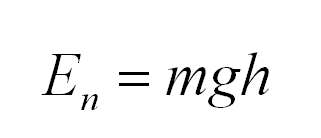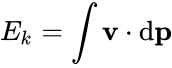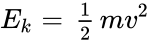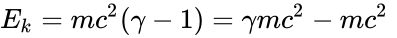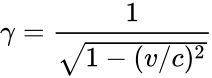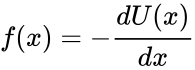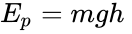А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ы
Э
эва § 140 п. 4
эвако- § 117 п. 3
эвакогоспиталь § 117 п. 3
Эверест § 6 п. 2
эвкалипт § 6 п. 2
ЭВМ § 204
эге § 140 п. 4
эгоизм § 6 п. 2
эд (в восточных именах) § 124 п. 3, § 161
Эдик § 48 прим.
Эдип § 6 п. 2
Эдичка § 48 прим.
Эдуардо Де Филиппо § 160 прим. 1
Эйфелева башня § 194
экватор § 6 п. 2
экзамен § 6 п. 2, § 80
экзема § 9
экзо- § 117 п. 3
экзотермический § 117 п. 3
эко- § 117 п. 3
экологически чистый § 131
экономика § 6 п. 2
экосистема § 117 п. 3
экось § 140 п. 4
экранизировать § 43
экс… (вне) § 80, 117 п. 1, § 120 п. 7 прим.
экс- (бывший) § 80, 117 п. 1 прим., § 120 п. 7
экс Советский Союз § 153
Экс-ан-Прованс § 169 прим. 2
экс-вице-премьер § 120 п. 7
экс-директор § 120 п. 7
экскурсионный § 97
экс-министр § 120 п. 7
экспатриация § 120 п. 7 прим.
экспериментально-психологический § 130 п. 3
экс-президент § 80, § 120 п. 7
экспресс-анализ § 110 прим. 1
экс-советский § 117 п. 1 прим.
экстерриториальный § 80, § 117 п. 1, § 120 п. 7 прим.
экстра- § 38 прим. 2, § 80
экстраверт § 38 прим. 2
экстра-класс § 80
экстраординарный § 38 прим. 2, § 80, § 117 п. 1
эксцесс § 107
экс-чемпион § 80, § 117 п. 1 прим., § 120 п. 7
электрификация § 66
электрифицировать § 16, § 66
электричество § 6 п. 2
электро- § 117 п. 3
электроёмкий § 117 п. 3
электронно-лучевой § 130 п. 3
электрон-электронный § 129 п. 4
электрорадиооборудование § 117 п. 3
элемент § 6 п. 2
эликсир § 34
элита § 6 п. 2
эллипсоид § 43
эль (в восточных именах) § 124 п. 3, § 161
эль (буква) § 6 п. 3
Эль Греко § 160 прим. 1
Эль-Кувейт § .126 п. 6
эль-Куни § 161
эм (буква) § 6 п. 3
эмиграционный § 97
эмиграция § 107
Эмка § 109
эмка § 6 п. 3
эмоция § 6 п. 2
эн (буква) § 6 п. 3
эндо- § 117 п. 3
эндотермический § 117 п. 3
энергия § 6 п. 2
энерго- § 117 п. 3
энергоёмкий § 117 п. 3
энес § 8 п. 3 прим.
энный § 6 п. 3
энский § 6 п. 3
энтузиазм § 81 п. 2 прим. 1
энтузиаст § 81 п. 2 прим. 1
энциклопедически образованный § 131
эпиграф § 6 п. 2
эпидемия § 6 п. 2
эпизодический § 43
эпоха Возрождения § 179 прим. 5
эпоха палеолита § 179 прим. 6
эр (буква) § 6 п. 3,
эр (в восточных именах) § 124 п. 3
Эрих Мария Ремарк § 123 п. 3
Эр-Рияд § 126 п. 6
эс (буква) § 6 п. 3
эсдек § 8 п. 3 прим.
эсер § 6 п. 3, § 8 п. 3 прим., § 204
эс-Зайят § 161
эскорт § 6 п. 2
эсминец § 119 п. 2
эссе § 9
эссенция § 107
эстетика § 6 п. 2
Эсхил § 6 п. 2
эсэнгэвский (от СНГ) § 204
этимология § 6 п. 2
этрусский § 84
Этьен Л а Боэси § 160 прим. 1
эф (буква) § 6 п. 3
эфир § 6 п. 2
эхма § 140 п. 4
эхо-импульс § 120 п. 3
эшелон § 34 Ю
Я
§ 6. Буква э пишется в начале корня для передачи гласного э (без
предшествующего j):
В начале следующих исконно русских местоименных слов и
междометий: этот (эта, это, эти), этакий, эдакий, экий, этак,
эдак; эва, эвон, эге, эге-ге, эй, эк, эх, эхма, эхе-хе.
В начале слов иноязычного происхождения (в том числе
собственных имен), напр.: эврика, экспорт, экстренный, эллин,
эпос, эра, этика, эхо, Этна, Эрик (с буквой э, передающей ударный гласный); эвкалипт, эгоизм,
экватор, экзамен, экономика, электричество, элемент, элита, эмоция, энергия,
эпиграф, эпидемия, эскорт, эстетика, этимология, эфир, Эверест, Эдип, Эсхил
(здесь буква э передает безударный гласный).
В названиях букв эль, эм, эн, эр, эс, эф, а также в начале аббревиатур, пишущихся по названиям букв, и
слов, образованных от названий букв и от буквенных аббревиатур, напр.: эсер, энный, энский, эмка.
После приставок или составных частей сложных и
сложносокращенных слов (как после гласных, так и после согласных). Примеры:
а) после гласных: антиэлектрон,
антиэсеровский, деэскала- ция, неэтичный, переэкзаменовка, поэтапно, поэтому,
реэкс- порт; диэлектрик, киноэкран, телеэкран, мегаэрг, микроэле- мент,
полиэфирный, полуэтаж, пятиэтажный;
б) после согласных: безэлектродный,
подэкранный, предэкза- менационный, разэдакий, сэкономить, сверхэкономный,
субэква- ториальный, суперэлита; двухэтажный, трёхэлементный, по- литэкономия,
санэпидстанция, Мосэнерго, Минэкономика.
Энергия – это то, благодаря чему существует жизнь не только на нашей планете, но и во Вселенной. При этом она может быть очень разной. Так, тепло, звук, свет, электричество, микроволны, калории представляют собой различные виды энергии. Для всех процессов, происходящих вокруг нас, необходима эта субстанция. Большую часть энергии все сущее на Земле получает от Солнца, но имеются и другие ее источники. Солнце передает ее нашей планете столько, сколько бы выработали одновременно 100 млн самых мощных электростанций.
Что такое энергия?
В теории, выдвинутой Альбертом Эйнштейном, изучается взаимосвязь материи и энергии. Этот великий ученый смог доказать способность одной субстанции превращаться в другую. При этом выяснилось, что энергия является самым важным фактором существования тел, а материя вторична.
Энергия – это, по большому счету, способность выполнять какую-то работу. Именно она стоит за понятием силы, способной двигать тело или придавать ему новые свойства. Что же означает термин «энергия»? Физика – это фундаментальная наука, которой посвятили свою жизнь многие ученые разных эпох и стран. Еще Аристотель использовал слово «энергия» для обозначения деятельности человека. В переводе с греческого языка «энергия» — это «деятельность», «сила», «действие», «мощь». Первый раз это слово появилось в трактате ученого-грека под названием «Физика».
В общепринятом сейчас смысле данный термин был введен в обиход английским ученым-физиком Томасом Юнгом. Это знаменательное событие произошло в далеком 1807 году. В 50-х годах XIX в. английский механик Уильям Томсон впервые использовал понятие «кинетическая энгергия», а в 1853 г. шотландский физик Уильям Ренкин ввел термин «потенциальная энергия».
Сегодня эта скалярная величина присутствует во всех разделах физики. Она является единой мерой различных форм движения и взаимодействия материи. Другими словами, она представляет собой меру преобразования одних форм в другие.
Единицы измерения и обозначения
Количество энергии измеряется в джоулях (Дж). Эта специальная единица в зависимости от вида энергии может иметь разные обозначения, например:
- W – полная энергия системы.
- Q – тепловая.
- U – потенциальная.
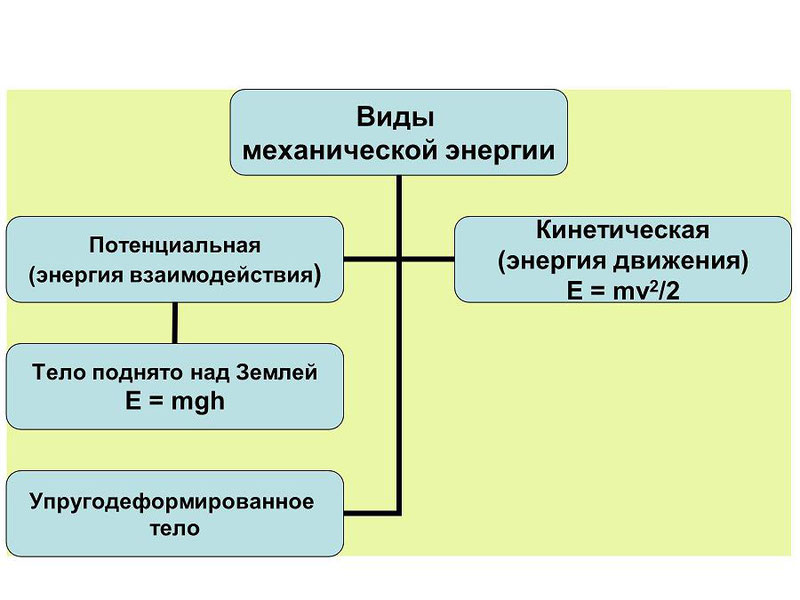
Виды энергии
В природе существует множество самых разных видов энергии. Основными из них считаются:
- механическая;
- электромагнитная;
- электрическая;
- химическая;
- тепловая;
- ядерная (атомная).
Есть и другие виды энергии: световая, звука, магнитная. В последние годы все большее число ученых-физиков склоняются к гипотезе о существовании так называемой «темной» энергии. Каждый из перечисленных ранее видов данной субстанции имеет свои особенности. Например, энергия звука способна передаваться при помощи волн. Они способствуют возникновению вибрации барабанных перепонок в ухе людей и животных, благодаря которой можно слышать звуки. В ходе различных химических реакций высвобождается энергия, необходимая для жизнедеятельности всех организмов. Любое топливо, продукты питания, аккумуляторы, батарейки являются хранилищем этой энергии.
Наше светило дает Земле энергию в виде электромагнитных волн. Только так она может преодолеть просторы Космоса. Благодаря современным технологиям, таким как солнечные батареи, мы можем использовать ее с наибольшим эффектом. Излишки неиспользованной энергии аккумулируются в особых энергохранилищах. Наряду с вышеперечисленными видами энергии часто используются термальные источники, реки, приливы и отливы океана, биотопливо.
Механическая энергия
Этот вид энергии изучается в разделе физики, называемом «Механикой». Она обозначается буквой Е. Ее измерение осуществляется в джоулях (Дж). Что собой представляет эта энергия? Физика механики изучает движение тел и взаимодействие их друг с другом либо с внешними полями. При этом энергия, обусловленная движением тел, называется кинетической (обозначается Ек), а энергию, обусловленную взаимодействием тел или внешних полей, именуют потенциальной (Еп). Сумма движения и взаимодействия представляет собой полную механическую энергию системы.
Для расчета обоих видов существует общее правило. Для определения величины энергии следует вычислить работу, необходимую для перевода тела из нулевого состояния в данное состояние. При этом чем больше работа, тем большей энергией будет обладать тело в данном состоянии.
Разделение видов по разным признакам
Существует несколько видов разделения энергии. По разным признакам ее делят на: внешнюю (кинетическую и потенциальную) и внутреннюю (механическую, термическую, электромагнитную, ядерную, гравитационную). Электромагнитная энергия в свою очередь подразделяется на магнитную и электрическую, а ядерная – на энергию слабого и сильного взаимодействия.
Кинетическая
Любые движущиеся тела отличаются наличием кинетической энергии. Она часто так и называется — движущей. Энергия тела, которое движется, теряется при его замедлении. Таким образом, чем быстрее скорость, тем больше кинетическая энергия.
При соприкосновении движущегося тела с неподвижным объектом последнему передается часть кинетической, приводящая и его в движение. Формула энергии кинетической следующая:
- Ек = mv2 : 2,
где m — масса тела, v – скорость движения тела.
В словах эту формулу можно выразить следующим образом: кинетическая энергия объекта равна половине произведения его массы на квадрат его скорости.
Потенциальная
Этим видом энергии обладают тела, которые находятся в каком-либо силовом поле. Так, магнитная возникает, когда объект находится под действием магнитного поля. Все тела, находящиеся на земле, обладают потенциальной гравитационной энергией.
В зависимости от свойств объектов изучения они могут иметь различные виды потенциальной энергии. Так, упругие и эластичные тела, которые способны вытягиваться, имеют потенциальную энергию упругости либо натяжения. Любое падающее тело, которое было ранее неподвижно, теряет потенциальную и приобретает кинетическую. При этом величина этих двух видов будет равнозначна. В поле тяготения нашей планеты формула энергии потенциальной будет иметь следующий вид:
- Еп = mhg,
где m — масса тела; h – высота центра массы тела над нулевым уровнем; g – ускорение свободного падения.
В словах эту формулу можно выразить так: потенциальная энергия объекта, взаимодействующего с Землей, равна произведению его массы, ускорению свободного падения и высоты, на которой оно находится.
Эта скалярная величина является характеристикой запаса энергии материальной точки (тела), находящейся в потенциальном силовом поле и идущей на приобретение кинетической энергии за счет работы сил поля. Иногда ее называют функцией координат, являющейся слагаемым в лангранжиане системы (функция Лагранжа динамической системы). Эта система описывает их взаимодействие.
Потенциальную энергию приравнивают к нулю для некой конфигурации тел, расположенных в пространстве. Выбор конфигурации определяется удобством дальнейших вычислений и называется «нормировкой потенциальной энергии».
Закон сохранения энергии
Одним из самых основных постулатов физики является Закон сохранения энергии. В соответствии с ним, энергия ниоткуда не возникает и никуда не исчезает. Она постоянно переходит из одной формы в другую. Иными словами, происходит только изменение энергии. Так, например, химическая энергия аккумулятора фонарика преобразуется в электрическую, а из нее – в световую и тепловую. Различные бытовые приборы превращают электрическую в свет, тепло или звук. Чаще всего конечным результатом изменения являются тепло и свет. После этого энергия уходит в окружающее пространство.
Закон энергии способен объяснить многие физические явления. Ученые утверждают, что общий объем ее во Вселенной постоянно остается неизменным. Никто не может создать энергию заново или уничтожить. Вырабатывая один из ее видов, люди используют энергию топлива, падающей воды, атома. При этом один ее вид превращается в другой.
В 1918 г. ученые смогли доказать, что закон сохранения энергии представляет собой математическое следствие трансляционной симметрии времени — величины сопряженной энергии. Другими словами, энергия сохраняется вследствие того, что законы физики не отличаются в различные моменты времени.
Особенности энергии
Энергия – это способность тела совершать работу. В замкнутых физических системах она сохраняется на протяжении всего времени (пока система будет замкнутой) и представляет собой один из трех аддитивных интегралов движения, сохраняющих величину при движении. К ним относятся: энергия, момент импульса, импульс. Введение понятия «энергия» целесообразно тогда, когда физическая система однородна во времени.
Внутрення энергия тел
Она представляет собой сумму энергий молекулярных взаимодействий и тепловых движений молекул, составляющих его. Ее нельзя измерить напрямую, поскольку она является однозначной функцией состояния системы. Всегда, когда система оказывается в данном состоянии, ее внутренняя энергия имеет присущее ему значение, независимо от истории существования системы. Изменение внутренней энергии в процессе перехода из одного физического состояния в другое всегда равно разности между ее значениями в конечном и начальном состояниях.
Внутренняя энергия газа
Помимо твердых тел, энергию имеют и газы. Она представляет собой кинетическую энергию теплового (хаотического) движения частиц системы, к которым относятся атомы, молекулы, электроны, ядра. Внутренней энергией идеального газа (математической модели газа) является сумма кинетических энергий его частиц. При этом учитывается число степеней свободы, представляющее собой число независимых переменных, определяющих положение молекулы в пространстве.
Использование энергии
С каждым годом человечество потребляет все большее количество энергоресурсов. Чаще всего для получения энергии, необходимой для освещения и отопления наших жилищ, работы автотранспорта и различных механизмов, используются такие ископаемые углеводороды, как уголь, нефть и газ. Они относятся к невозобновимым ресурсам.
К сожалению, только незначительная часть энергии добывается на нашей планете с помощью возобновимых ресурсов, таких как вода, ветер и Солнце. На сегодняшний день их удельный вес в энергетике составляет всего 5 %. Еще 3 % люди получают в виде ядерной энергии, производимой на атомных электростанциях.
Невозобновляемые ресурсы имеют следующие запасы (в джоулях):
- ядерная энергия – 2 х 1024;
- энергия газа и нефти – 2 х 10 23;
- внутренне тепло планеты – 5 х 1020.
Годовая величина возобновляемых ресурсов Земли:
- энергия Солнца – 2 х 1024;
- ветер – 6 х 1021;
- реки — 6,5 х 1019;
- морские приливы — 2,5 х 1023.
Только при своевременном переходе от использования невозобновляемых запасов энергии Земли к возобновляемым человечество имеет шанс на долгое и счастливое существование на нашей планете. Для воплощения передовых разработок ученые всего мира продолжают тщательно изучать разнообразные свойства энергии.
Содержание:
Для работы двигателей, приводящих в движение автомобили, трактора, тепловозы, самолёты, необходимо топливо, являющееся источником энергии. За счёт энергии воды, падающей с высоты, вращаются гидротурбины, соединённые с электрическими машинами, вырабатывающими электрический ток. Человеку для того чтобы существовать и работать, также необходим источник энергии. Говорят, что для того, чтобы выполнять любую работу, необходима энергия. Что же такое энергия?
Опыт 1. Поднимем над Землёй мяч. Пока он находится в состоянии покоя, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на Землю с определённой высоты. При падении мяча выполняется механическая работа.
Опыт 2. Сожмём пружину, зафиксируем её нитью и поставим на пружину гирю (рис. 171).
Пережжём нить, пружина распрямится и поднимет гирю на некоторую высоту. Пружина выполнила механическую работу.
Опыт 3. На тележке закрепим стержень с блоком на конце (рис. 172). Через блок перекинем нить, один конец которой намотан на ось тележки, а на втором висит грузик. Отпустим грузик, под действием силы тяжести он будет опускаться вниз и приведёт в движение тележку. Грузик выполнил механическую работу .
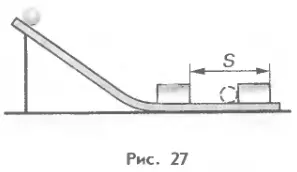
Опыт 4. Стальной шарик А, скатившийся по наклонной плоскости (рис. 173), также выполнил механическую работу: он переместил цилиндр В на некоторое расстояние.
Если тело или несколько тел при взаимодействии выполняют механическую работу, то это значит, что они имеют механическую энергию, или энергию.
Мяч, поднятый над Землёй, сжатая пружина, движущийся стальной шарик имеют энергию.
Энергия — физическая величина, характеризующая способность тел выполнять работу.
Энергия (от греческого слова энергия — деятельность) обозначается большой латинской буквой Е. Единицей энергии, а также и работы в СИ является один джоуль (1 Дж). Из приведённых опытов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое: поднятый над Землёй грузик опускается, сжатая пружина распрямляется, движущийся шарик останавливается. Энергия тела при этом изменяется (уменьшается), а выполненная телом механическая работа равна изменению его механической энергии. Различают два вида механической энергии — потенциальную и кинетическую.
Энергия и механическая работа
Как древние египтяне, строя свои колоссальные пирамиды, поднимали на огромную высоту такие тяжеленные каменные блоки, что их трудно было даже сдвинуть?
Для их подъема использовали, например, рычаги. Рычагами пользовались и древние греки, когда строили огромные храмы.
Опыт:
Убедимся, что с помощью рычага действительно можно получить значительный выигрыш в силе. Положите на короткое плечо рычага тяжелую книгу — и вы сможете поднять ее, надавив на длинное плечо мизинцем (рис. 5.1)!
Однако выигрыш в силе всегда сопровождается проигрышем в перемещении.
Например, если груз, прикрепленный к короткому плечу рычага, поднимают, прикладывая к длинному плечу рычага силу, которая в 10 раз меньше веса этого груза, то длинное плечо рычага надо опустить на расстояние, которое в 10 раз больше высоты, на которую поднимется груз.
Этот и подобный ему опыты показывают, что, используя любые простые механизмы, мы выигрываем в силе как раз во столько раз, во сколько проигрываем в перемещении.
Эта закономерность, обнаруженная еще древними греками, оказалась настолько важной, что со временем ее назвали «золотым правилом механики».
Механическая работа:
Из золотого правила механики следует: если не учитывать трения, произведение силы на перемещение одинаково для каждой из сил, приложенных к плечам рычага. Поэтому ввели физическую величину, которую назвали механической работой. В дальнейшем для простоты мы ограничимся случаем, когда направление силы совпадает с направлением перемещения. В этом случае
Механическая работа силы равна произведению силы на перемещение1.
Механическую работу обозначают буквой 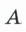
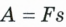
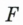
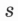
Единицу работы в SI назвали джоуль (Дж) в честь английского физика Джеймса Прескотта Джоуля. Один джоуль — это работа, которую совершает сила в I Н, перемещая тело на I м в направлении действия силы, то есть 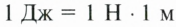
Механическую работу часто называют просто работой, однако ее не следует путать с работой в повседневном значении этого слова. Мы еще расскажем об этом в разделе «Хочешь узнать больше?».
Определение энергии
Механическую работу человек давно научился «перекладывать на плечи» машин и механизмов.
Одним из первых таких механизмов была водяная мельница (рис. 5.2): работу здесь выполняет сила, с которой падающая вода давит на лопасти колеса. Современная гидроэлектростанция, заставляющая «работать» огромную реку (рис. 5.3), «выросла» из небольшой водяной мельницы на ручье.
Чтобы мельница работала или электростанция вырабатывала электроэнергию, необходимо создать разность уровней воды. Итак, вода и притягивающая ее Земля образуют систему тел, способную совершить работу.
Способностью совершить работу обладает также движущееся тело. Например, вода, падая, ударяет в подвижные лопасти колеса или турбины, то есть действует на них с некоторой силой. При этом скорость воды уменьшается. Физическую величину, которая характеризует способность тела или системы тел совершать работу вследствие изменения своего состояния, называют энергией.
Физическую величину, которая характеризует способность тела или системы тел совершать работу вследствие изменения своего состояния, называют энергией.
Говорят, что тело (или система тел) обладает энергией, если это тело (или система тел) может совершить работу. Мерой изменения энергии является совершенная работа: когда тело совершает работу, его энергия уменьшается на величину, равную совершенной работе.
Поэтому энергию измеряют в тех же единицах, что и работу: единицей энергии в SI является джоуль. Если тело (система тел) совершает работу в 1 Дж, энергия тела (системы тел) уменьшается на 1 Дж.
Виды энергии
Тело или система тел может совершать работу вследствие различных изменений своего состояния.
Работа может быть совершена вследствие изменения взаимного положения взаимодействующих тел, а также вследствие изменения скоростей тел. В этих случаях изменяется механическая энергия тела или системы тел.
Часть механической энергии, обусловленную взаимодействием тел, называют потенциальной энергией, а часть механической энергии, обусловленную движением тел, — кинетической энергией.
Например, поднятое над Землей тело и Земля притягивают друг друга, то есть взаимодействуют. Благодаря этому тело при падении может выполнить некоторую работу. Значит, поднятое тело обладает потенциальной энергией. При падении тела его потенциальная энергия уменьшается, зато кинетическая — увеличивается, так как увеличивается скорость тела.
Рассмотрим еще один случай, когда тело может совершить работу. Газ, расширяясь в цилиндре, двигает поршень, совершая при этом работу (на этом основано действие автомобильных двигателей). Но, расширяясь, газ охлаждается, то есть его температура понижается. А при этом, как вы скоро узнаете, замедляется хаотическое1, то есть беспорядочное, движение молекул газа. Значит, расширяясь, газ выполняет работу благодаря уменьшению кинетической энергии хаотического движения молекул.
Энергию, обусловленную хаотическим движением частиц тела и их взаимодействием, называют внутренней энергией.
Когда газ расширяется, он совершает работу, а его внутренняя энергия уменьшается.
Ученые установили, что существуют и другие виды энергии — например, электромагнитная и атомная энергия. О них вы узнаете подробнее из курса физики старших классов.
Энергия является важнейшей физической величиной, поэтому мы и рассказали о ней в начале вашего знакомства с физикой.
Целые эпохи в истории человечества называли «в честь» используемого вида энергии. Так, время паровых двигателей (от второй половины 18-го века до конца 19-го века) называли «веком пара». А 20-й век называли «веком электричества», а также «веком атома».
Закон сохранения энергии
Опыты показывают, что, если можно пренебречь силами трения, механическая энергия взаимодействующих тел, то есть сумма их потенциальной и кинетической энергии, не изменяется. Это — проявление закона сохранения энергии, открытого в 19-м веке.
Закон сохранения энергии: во всех процессах, происходящих в природе, суммарная энергия взаимодействующих тел не изменяется.
Физический смысл закона сохранения энергии состоит в том, что энергия является общей мерой движения и взаимодействия тел и частиц, она никогда не исчезает и не появляется, а лишь преобразуется из одного вида в другой.
Многие происходящие в природе процессы сопровождаются преобразованиями энергии. Например, когда вследствие трения движущееся тело останавливается, его механическая энергия переходит во внутреннюю, потому что вследствие трения тела нагреваются.
Мог ли Архимед сдвинуть землю
Правило рычага установил на опыте выдающийся древнегреческий ученый и инженер Архимед, который жил в 3-м веке до нашей эры в Сиракузах, одном из греческих городов-государств на острове Сицилия.
Архимед достиг такого совершенства в сооружении различных механизмов, что заявил как-то царю Сиракуз: «С помощью своих механизмов я один могу поднять любой груз!» Более того, Архимед утверждал, что он мог бы сдвинуть даже Землю, если бы только нашел «точку опоры» — например, другую Землю, на которую можно стать! Царь очень удивился и предложил Архимеду продемонстрировать свое могущество.
Тогда Архимед попросил загрузить корабль, который с трудом вытянули на берег, и посадить на него весь экипаж. Привязав к кораблю крепкий канат, Архимед начал тянуть канат с помощью изобретенного им механизма. И корабль плавно тронулся по песку к Архимеду — будто поплыл по морю! Царь и все присутствующие были поражены могуществом Архимеда — не могуществом его рук, а могуществом его разума.
Однако, утверждая, что он мог бы сдвинуть даже Землю, Архимед очень переоценил свои возможности. Расчеты показывают, что даже если бы Архимеду фантастически «повезло» и он смог бы найти «точку опоры» и огромный рычаг, то не успел бы заметно сдвинуть Землю не только за всю свою жизнь, но и за все время существования Земли.
Может ли человек устать, не совершая механической работы
Почему очень устаешь, когда долго держишь, например, полное ведро воды? Ведь механической работы при этом не совершаешь, так как перемещение равно нулю! Чтобы убедиться в том, что держание груза не является работой в физическом значении этого слова, поставьте ведро на пол: пол без устали будет «держать» ведро как угодно долго!
Человек же, держа груз, устает из-за напряжения мышц. Положите тот же груз на колени, и вы почувствуете значительное облегчение. Итак, не следует путать механическую работу как физическую величину с работой в повседневном значении слова, то есть с любой деятельностью, которая вызывает усталость. Ведь устать можно, совсем не выполняя механической работы — например, сочиняя музыку или стихи. А больше всего, как известно, устаешь от безделья!
Энергия и способность системы совершить работу
Вы уже узнали, что одной из физических величин, которые обладают свойством сохранения в замкнутой системе, является общий импульс системы. Другой очень важной физической величиной, обладающей свойством сохранения в замкнутой системе, является энергия. Понятие «энергия» часто используется в повседневной жизни (например, энергия является самой обсуждаемой темой на переговорах по международным экономическим вопросам). Вы имеете достаточно информации о различных видах энергии и о ее превращении из одного вида в другой. Самое важное то, что для каждого вида энергии учеными-физиками была определена своя формула. Проведенные с помощью этих формул вычисления каждый раз подтверждают постоянство суммы всех видов энергии замкнутой системы.
Как вы знаете, энергия характеризует способность тела совершать работу. С другой стороны, энергия — общая мера движения и взаимодействия тел. Движение тела характеризуется его кинетической энергией, а взаимодействие тел характеризуется потенциальной энергией.
Работа, совершаемая равнодействующей силой, и кинетическая энергия тела при поступательном движении. Если тело под действием равнодействующей силы совершает работу, то модуль его скорости изменяется от 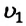
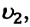
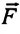
ускорением 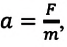
или
В последней формуле половина произведения массы на квадрат скорости 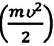
Кинетическая энергия—это энергия, возникающая в результате движения тела:
Кинетическая энергия зависит от массы тела и модуля его скорости (а не от его направления). Если запишем формулу (3.12) с учетом (3.13), то получим выражение, которое называется теоремой о кинетической энергии-.
Работа, совершаемая над телом постоянной равнодействующей силой, равна изменению кинетической энергии тела:
Где 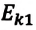
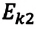
a) если работа, совершенная постоянной равнодействующей силой, положительна 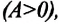
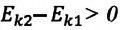
b) если работа, совершенная постоянной равнодействующей силой, отрицательна 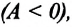
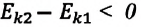
c) если работа, совершенная постоянной равнодействующей силой, равна нулю 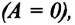
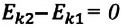
Примечание:
- При доказательстве теоремы о кинетической энергии не было отмечено, какова природа силы, совершающей работу. Это значит, что теорема о кинетической энергии справедлива для любых сил (сила тяжести, сила трения, сила упругости или их равнодействующая сила), действующих на тело.
- Кинетическая энергия, так же как и скорость движения, зависит от выбора системы отсчета. Например, если скорость пассажира в движущемся вагоне относительно системы отсчета, связанной с вагоном, равна нулю, то и кинетическая энергия пассажира относительно этой системы отсчета равна нулю. Однако кинетическая энергия пассажира относительно системы отсчета, связанной с Землей, отлична от нуля.
Из теоремы о кинетической энергии видно, что единицей измерения кинетической энергии, как и работы, в СИ является джоуль
Так как скорость связана с импульсом, то и кинетическая энергия связана с импульсом:
Если масса тела известна, то его скорость и импульс можно выразить через кинетическую энергию:
Потенциальная энергия
Работа силы тяжести и потенциальная энергия:
Предположим, что замкнутая система состоит из Земли и тела, поднятого на определенную высоту 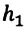
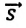
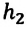
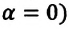
Где 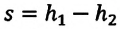
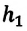
Если тело брошено вертикально вверх с высоты 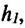
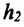
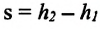
угол между направлением силы тяжести и вектором перемещения равен 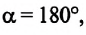
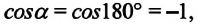
Выражение (3.19) схоже с выражением (3.18), то есть тело, брошенное вертикально вверх, и свободно падающее тело совершают под действием силы тяжести одинаковую работу.
- Работа силы тяжести не зависит от формы траектории движения тела, она зависит от начального и конечного положения центра тяжести тела.
- Силы, под действием которых совершается работа, не зависящая от траектории движения тела, называются консервативными силами. Это значит, что сила тяжести является консервативной силой.
Формулу (3.18) можно записать и так:
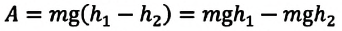
Это означает, что работа, совершаемая силой тяжести, равна изменению величины 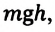
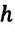
Энергия, которой обладают взаимодействующие тела (или частицы), называется потенциальной энергией:
Приняв во внимание выражение (3.21) в выражении (3.20), получаем выражение, которое называется теоремой о потенциальной энергии:
Работа, совершаемая силой тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:
Из теоремы о потенциальной энергии видно, что единицей измерения потенциальной энергии, так же, как и работы, в СИ является джоуль
Потенциальная энергия тела, на которое действует сила тяжести, зависит от выбора нулевого уровня. За нулевой уровень можно принять уровень моря, поверхность стола, пол комнаты и другие. Потенциальная энергия тела, находящегося на какой-либо высоте относительно этих уровней, будет иметь разные значения. Однако разность потенциальных энергий двух, соответственно, разных положений тела не зависит от выбора нулевого положения, и она измеряется работой, совершенной силой тяжести. Из этого получаем физический смысл потенциальной энергии: Потенциальная энергия тела на высоте 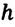
В зависимости от выбора нулевого уровня потенциальная энергия может быть, как положительной, так и отрицательной. Так, потенциальная энергия тела, помещенного на определенной высоте 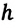
- Заказать решение задач по физике
Работа силы упругости и потенциальная энергия:
Еще одной консервативной силой является сила упругости. Поэтому работа, совершенная силой упругости, также должна быть равна изменению потенциальной энергии тела. Исследуем это: прикрепим один конец пружины к опоре, другой же конец прикрепим к телу (шарику), способному двигаться по гладкому стержню. Сдвинув шарик вправо, растянем пружину на 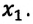
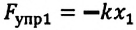
Так как в этом положении деформация пружины равна 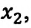
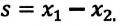
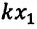
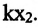
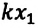
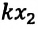
Таким образом, упруго деформированная пружина совершает положительную работу:
или
Эту формулу можно записать и так:
Как видно, работа, совершенная силой упругости, зависит от начальной и конечной деформации пружины.
Из сравнения формул (3.20) и (3.23) видно, что работа силы упругости также равна изменению некоторой величины, в этом случае 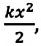
Потенциальная энергия упругодеформированного тела равна половине произведения ее жесткости на квадрат растяжения (или сжатия):
Полная механическая энергия и закон сохранения энергии
Полная механическая энергия:
Система тел одновременно может обладать как кинетической, так и потенциальной энергией. Например, самолет, летящий на некоторой высоте с определенной скоростью, обладает наряду с кинетической энергией, также и потенциальной энергией вследствие взаимодействия с Землей.
Сумму кинетической и потенциальной энергий системы тел называют полной механической энергией:
Закон сохранения полной механической энергии:
Вы уже знаете, что работа силы тяжести и упругости, являющихся консервативными силами, равна изменению потенциальной энергии системы, взятому с противоположным знаком. С другой стороны, эта работа также равна изменению кинетической энергии системы:
Таким образом, получается, что:
Сгруппировав соответствующие величины, это выражение можно записать в следующим виде:
Полученное равенство является выражением закона сохранения полной механической энергии.
Полная механическая энергия замкнутой системы тел, взаимодействующих друг с другом консервативными силами, остается неизменной.
Закон сохранения полной механической энергии является результатом однородности времени.
Однородность времени — это симметрия относительно переноса во времени: физические свойства замкнутой системы не зависят от выбора начального момента времени, то есть все моменты времени эквивалентны (равноправны).
Согласно закону сохранения полной механической энергии, увеличение потенциальной энергии системы сопровождается соответствующим уменьшением ее кинетической энергии, и наоборот. Превращение потенциальной энергии в кинетическую или кинетической в потенциальную, т.е. сохранение полной механической энергии является одним из самых важных законов в природе.
Частные случаи:
1. Полная механическая энергия для тела, движущегося под действием силы тяжести:
Где 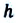
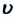
a) если тело было брошено с нулевого уровня 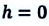
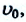
В этом случае, закон сохранения полная механическая энергии в произвольной точке траектории движения записывается так (с):
b) если тело, брошенное вертикально вверх, поднимется на максимальную высоту 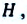
В этом случае закон сохранения полной механической энергии тела, брошенного вертикально вверх, в произвольной точке траектории движения записывается так (d):
2. Если оттянуть и отпустить шарик массой 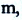
Закон сохранения полной энергии
Известно, что полная механическая энергия свободно падающего тела во всех точках траектории одинакова.
- — Что происходит при падении тела и его остановке на поверхности Земли?
- — Можно ли в этом случае сказать, что «как кинетическая, так и потенциальная энергия тела равны нулю, то есть механическая энергия исчезает и нарушается закон сохранения энергии «?
Механическая энергия тел, составляющих замкнутую систему, не исчезает! Механическая энергия превращается в другой вид энергии — внутреннюю энергию системы: в результате соударения тела с поверхностью Земли система нагревается и ее внутренняя энергия увеличивается.
Можно привести примеры превращения энергии также и в других замкнутых системах. Например, в системе автомобиль-шоссе при торможении движущего автомобиля его кинетическая энергия в результате трения превращается во внутреннюю энергию нагретых покрышек.
Таким образом, говоря о законе сохранения полной энергии, подразумевается сохранение всех видов энергии (механической, внутренней, электромагнитной и другие), превращающихся друг в друга, в замкнутой системе:
Энергия не исчезает и не возникает из ничего, она превращается из одного вида в другой.
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Перемещение, координата и путь при равнопеременном движении
- Криволинейное движение
- Ускорение точки при ее движении по окружности
- Инерциальные системы отсчета
| Энергия | |
 , ,  |
|
| Размерность |
|
|---|---|
| Единицы измерения | |
| СИ |
Дж |
| СГС |
эрг |
Эне́ргия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».
Содержание
- 1 Фундаментальный смысл
- 2 Энергия и работа
- 3 В специальной теории относительности
- 3.1 Энергия и масса
- 3.2 Энергия и импульс
- 4 В квантовой механике
- 5 В общей теории относительности
- 6 Энергия и энтропия
- 7 Физическая размерность
- 8 Виды энергии
- 8.1 Кинетическая
- 8.2 Потенциальная
- 8.3 Электромагнитная
- 8.4 Гравитационная
- 8.5 Ядерная
- 8.6 Внутренняя
- 8.7 Химический потенциал
- 8.8 Энергия взрыва
- 9 Проблемы энергопотребления
- 10 История термина
- 11 См. также
- 12 Примечания
- 13 Ссылки
Фундаментальный смысл
С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.
Энергия и работа
Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.
- Механическая работа численно равна изменению механической энергии.
В специальной теории относительности
Энергия и масса
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна
где E — энергия системы, m — её масса, c — скорость света. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия тела, согласно законам классической механики, зависит от системы отсчета, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, 
Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
,
где 
.
Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.
Энергия и импульс
Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.
В квантовой механике
|
|
В этом разделе не хватает ссылок на источники информации.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
В квантовой механике величина энергии пропорциональна частоте и двойственна времени. В частности, в силу фундаментальных причин принципиально невозможно измерить абсолютно точно энергию системы в каком-либо процессе, время протекания которого конечно. При проведении серии измерения одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.
В общей теории относительности
В общей теории относительности время не является однородным, поэтому возникают определённые проблемы при попытке введения понятия энергии. В частности, оказывается невозможным определить энергию гравитационного поля как тензор относительно общих преобразований координат.
Энергия и энтропия
Внутреняя энергия (или энергия хаотического движения молекул) является самым «деградированным» видом энергии — она не может превращаться в другие виды энергии без потерь (см.: энтропия).
Физическая размерность
Энергия E имеет размерность, равную:
| Описание | Формула |
|---|---|
| Силе, умноженной на длину | E ~ F·l |
| Давлению, умноженному на объём | E ~ P·V |
| Импульсу, умноженному на скорость | E ~ p·v |
| Массе, умноженной на квадрат скорости | E ~ m·v² |
| Заряду, умноженному на напряжение | E ~ q·U |
| Мощности, умноженной на время | E ~ N·t |
В системе величин LMT энергия имеет размерность 
| Единица | Эквивалент | |||
|---|---|---|---|---|
| в Дж | в эрг | в межд. кал | в эВ | |
| 1 Дж | 1 | 107 | 0,238846 | 0,624146·1019 |
| 1 эрг | 10−7 | 1 | 2,38846·10−8 | 0,624146·1012 |
| 1 межд. Дж[1] | 1,00020 | 1,00020·107 | 0,238891 | 0,624332·1019 |
| 1 кгс·м | 9,80665 | 9,80665·107 | 2,34227 | 6,12078·1019 |
| 1 кВт·ч | 3,60000·106 | 3,60000·1013 | 8,5985·105 | 2,24693·1025 |
| 1 л·атм | 101,3278 | 1,013278·109 | 24,2017 | 63,24333·1019 |
| 1 межд. кал (calIT) | 4,1868 | 4,1868·107 | 1 | 2,58287·1019 |
| 1 термохим. кал (калТХ) | 4,18400 | 4,18400·107 | 0,99933 | 2,58143·1019 |
| 1 электронвольт (эВ) | 1,60219·10−19 | 1,60219·10−12 | 3,92677·10−20 | 1 |
Виды энергии
| Виды энергии: | |
|---|---|
| Механическая | |
| Электрическая | |
| Электромагнитная | |
| Химическая | |
| Ядерная | |
| ‹♦› | Тепловая |
 |
Вакуума |
| Гипотетические: | |
| Тёмная |
Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную и ядерную энергии (также может быть разделена на энергию слабого и сильного взаимодействий).
Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества. См. также: химический потенциал.
Энергия взрыва иногда измеряется в тротиловом эквиваленте.
Кинетическая
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Потенциальная
Потенциальная энергия 
Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Электромагнитная
Гравитационная
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением. Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационную энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Ядерная
Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях.
Энергия связи — энергия, которая требуется, чтобы разделить ядро на отдельные нуклоны, называется энергией связи. Энергия связи, приходящаяся на один нуклон, неодинакова для разных химических элементов и, даже, изотопов одного и того же химического элемента.
Внутренняя
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутреннюю энергию тела нельзя измерить напрямую. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Химический потенциал
Химический потенциал 
Энергия взрыва
Основная статья: Взрыв
Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.
При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.
Проблемы энергопотребления
Существует довольно много форм энергии, большинство[3] из которых так или иначе используются в энергетике и различных современных технологиях.
Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергосбережения.
Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т. д.
История термина
Термин «энергия» происходит от слова energeia, которое впервые появилось в работах Аристотеля.
Томас Юнг первым использовал понятие «энергия» в современном смысле слова
Маркиза Эмили дю Шатле в книге «Уроки физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда, чтобы показать: энергия движущегося объекта пропорциональна его массе и квадрату его скорости (не скорости самой по себе как полагал Исаак Ньютон).
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила.[4] Гаспар-Гюстав Кориолис впервые использовал термин «кинетическая энергия» в 1829 году, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль), математики (Эмиль Клапейрон и Герман Гельмгольц[уточнить]) — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии».[4] Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия».[4] В 1881 году Уильям Томсон заявил перед слушателями:[5]
Само слово энергия, хотя и было впервые употреблено в современном смысле доктором Томасом Юнгом приблизительно в начале этого века, только сейчас входит в употребление практически после того, как теория, которая дала определение энергии, … развилась от просто формулы математической динамики до принципа, пронизывающего всю природу и направляющего исследователя в области науки.
Оригинальный текст (англ.)
The very name energy, though first used in its present sense by Dr Thomas Young about the beginning of this century, has only come into use practically after the doctrine which defines it had … been raised from mere formula of mathematical dynamics to the position it now holds of a principle pervading all nature and guiding the investigator in the field of science.
В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.
Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени (см. Теорема Нётер, изотропия пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии:[6]
Существует факт, или, если угодно, закон, управляющей всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его — сохранение энергии. Он утверждает, что существует определённая величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
Оригинальный текст (англ.)
There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
— Фейнмановские лекции по физике[7]
См. также
- Тензор энергии-импульса
- Эквивалентность массы и энергии
- Тёмная энергия
- Количество теплоты
- Виды норм удельной затраты энергии и требования к ним
Примечания
- ↑ Г. Д. Бурдун. Джоуль(единица энергии и работы) // Большая советская энциклопедия.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теоретическая физика. — 5-е изд. — М.: Физматлит, 2004. — Т. I. Механика. — 224 с. — ISBN 5-9221-0055-6
- ↑ http://profbeckman.narod.ru/InformLekc.files/Inf03.pdf
- ↑ 1 2 3 Смит, Кросби. The science of energy: a cultural history of energy physics in Victorian Britain. — The University of Chicago Press, 1998. — ISBN 0-226-76421-4
- ↑ Томсон, Уильям. Об источниках энергии, доступных человеку для совершения механических эффектов = On the sources of energy available to man for the production of mechanical effect. — BAAS Rep, 1881. С. 513
- ↑ Richard Feynman. The Feynman Lectures on Physics. — США: Addison Wesley, 1964. — Vol. 1. — ISBN 0-201-02115-3
- ↑ Фейнман, Ричард. Фейнмановские лекции по физике = The Feynman Lectures on Physics. — Т. 1.
Ссылки
- Энергия в Физической энциклопедии
Термин «энергия» был введен в 1807 г. английским ученым Т. Юнгом. В переводе с греческого это слово означает «действие, деятельность».
Современная наука немыслима без этого понятия. Оно присутствует во всех разделах физики. Это и электрическая энергия, магнитная энергия, атомная энергия и т. д.
Энергия, изучаемая в механике, называется механической. Именно с нее мы и начнем знакомство с этим важнейшим понятием.
Механическая энергия обозначается буквой Е и измеряется в тех же единицах, что и работа, т. е. в джоулях (Дж).
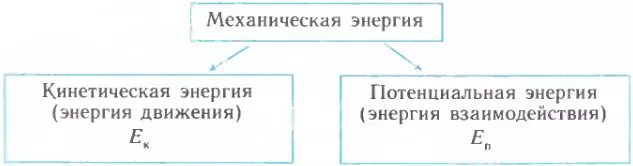
Поскольку в механике изучают движение тел и их взаимодействие друг с другом, то принято различать два вида механической энергии — энергию, обусловленную движением тел, и энергию, обусловленную их взаимодействием. Первая из них обозначается Eк и называется кинетической энергией, вторая обозначается Eп и называется потенциальной энергией.
Для расчета и той и другой энергии существует общее правило. Чтобы определить энергию, которой обладает тело, надо найти работу, необходимую для перевода этого тела из нулевого состояния в данное (нулевое состояние — это то, в котором соответствующая энергия тела считается равной нулю). Чем больше эта работа, тем большей энергией обладает тело в данном состоянии.
Воспользуемся этим правилом для расчета каждой из энергий.
1. Кинетическая энергия. Найдем кинетическую энергию тела массой т, движущегося со скоростью, равной и. Кинетическая энергия — это энергия, обусловленная движением. Поэтому нулевым состоянием для нее является то, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем и его кинетическую энергию.
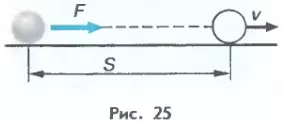
Воспользовавшись определением работы (A = Fs), вторым законом Ньютона (F = ma), а также формулами (2.1) и (4.2), получаем (рис. 25)
Последнее из написанных здесь выражений и является кинетической энергий тела:
Итак, кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
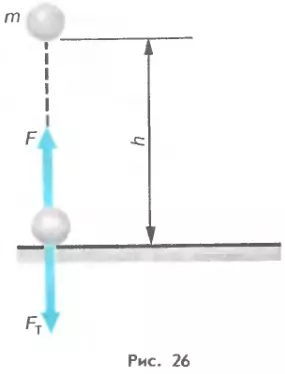
2. Потенциальная энергия. Найдем потенциальную энергию тела, взаимодействующего с Землей. Нулевым будем считать положение тела на поверхности Земли. Тогда потенциальная энергия тела, находящегося на некоторой высоте h, будет равна работе, необходимой для перемещения этого тела с поверхности Земли на заданную высоту. При равномерном подъеме, когда прикладываемая к телу сила совпадает по величине с силой тяжести (рис. 26), эта работа может быть найдена следующим образом:
A = Fs = Fтh = mgh.
Это и есть потенциальная энергия тела на высоте h:
Eп = mgh. (14.2)
Итак, потенциальная энергия тела, взаимодействующего с Землей, равна произведению массы этого тела, ускорению свободного падения и высоты, на которой находится тело.
За нулевое положение тела при расчете его потенциальной энергии необязательно выбирать то, которое расположено на поверхности Земли. Это может быть и уровень пола в помещении, и поверхность стола и т. д. Нулевое положение, от которого отсчитывается высота тела h, выбирают произвольно, руководствуясь обычно лишь соображениями удобства и простоты.
По формуле (14.2) находится потенциальная энергия тела, взаимодействующего с Землей. Потенциальная энергия других взаимодействий находится по другим формулам.
От энергии, которой обладает тело, зависит работа, которую оно может совершить. Чем больше энергия тела, тем большая работа будет совершена при переходе тела из данного состояния в нулевое. Проиллюстрируем это простыми опытами.
Возьмем составной желоб, имеющий наклонную и горизонтальную части, и поместим на его сгибе алюминиевый цилиндр (рис. 27). Пуская по наклонной части желоба шарики разной массы с одинаковой высоты и шарики одинаковой массы с разных высот, можно заметить, что, чем большей потенциальной энергией наверху желоба и кинетической энергией внизу обладал шарик, тем на большее расстояние он передвинет металлический цилиндр.
1. Чем обусловлена кинетическая энергия? 2. Чему равна кинетическая энергия тела? 3. Чем обусловлена потенциальная энергия? 4. Чему равна потенциальная энергия тела, взаимодействующего с Землей? 5. Как называется единица энергии? 6. В каком случае кинетическая энергия тела равна нулю? 7. Какой энергией — кинетической, потенциальной или обеими вместе — обладает летящий в небе самолет? 8. Какой энергией обладает вода, удерживаемая плотиной, и какой энергией обладает вода, падающая с плотины? 9. Как изменяются потенциальная и кинетическая энергии мяча, брошенного вертикально вверх, в процессе его полета?
Слово энергия мы слышим очень часто. Жизненная энергия, внутренняя энергия, электроэнергия, атомная энергия… Но попробуйте дать точный ответ на вопрос, что такое энергия? Здесь задумается практически каждый. Так же и с работой. Все ходят на работу, у всех полно работы. Но что такое работа? А ответ прямо здесь, в нашей статье!
Полезная и интересная информация по другим темам – на нашем канале в телеграм.
Энергия
Пойдем по принципу «чем проще – тем лучше». Среди всех определений энергии можно выделить одно:
Энергия – одно из основных свойств материи и мера способности совершать работу.
Энергия в классической механике измеряется в Джоулях и чаще всего обозначается буквой E.
И тут мы плавно подходим к работе. Конечно, работать мало кто любит, отдыхать гораздо приятнее. Но давайте и про работу почитаем.
Работа
Работа – мера воздействия силы на тело или систему тел.
И работа, и энергия – скалярные физические величины. Как и энергия, работа в классической механике измеряется в Джоулях.
Допустим, мы взяли тележку c кирпичами (пусть она весит m килограмм), начали ее толкать с определенной силой F и переместили тем самым все это добро на расстояние s.
Тогда работа, которую мы совершили (а мы определенно совершили работу, пусть и бессмысленную), будет вычисляться по соответствующей формуле для работы в механике:
При этом пока мы толкали тележку, она приобрела какую-то скорость v, а значит, и энергию.
Кинетическая энергия (энергия движения) тележки вычисляется по формуле:
Если мы поднатужимся и закатим нашу телегу на горку высотой h, то она приобретет потенциальную энергию, которую тоже легко можно вычислить:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Работа не совершается сама по себе. Работа совершается за счет изменения энергии. Какова связь между работой и энергией?
Например, работа силы тяжести по модулю равна изменению потенциальной энергии тела.
Существует теорема о кинетической энергии системы. Она гласит, что изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.
Закон сохранения энергии
Закон сохранения энергии – фундаментальный закон природы, о котором никогда не стоит забывать.
Общее количество энергии замкнутой физической системы не прибывает и не убывает, а переходит из одной формы в другую, всегда оставаясь постоянным.
Так, если телега скатится с горки, ее потенциальная энергия перейдет в кинетическую. Силы трения (диссипативные силы) мы здесь не рассматриваем. В реальном мире телега, конечно, затормозит, но энергия не исчезнет, а перейдет во внутреннюю энергию молекул вследствие трения колес о поверхность.
Закон сохранения энергии применим не только в рамках классической механики. Это закон, применимый к целой Вселенной. Вот что говорил о законе сохранения энергии Ричард Фейман:
Это математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного… Просто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
Пример решения задачи
А теперь рассмотрим пример задачи, в которой нужно найти работу
Какой бы сложной ни казалась задача, эксперты профессионального студенческого сервиса обязательно смогут быстро подобрать к ней ключ! Не стесняйтесь обращаться к нам, помощь профессионалов еще ни для кого не была лишней!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
thumb
Energy (from Latin Energia and Greek Ενεργεια) is a measure of the ability to do mechanical work.[1] It is a fundamental concept pertaining to the ability for action. In physics, it is a quantity that every physical system possesses. This quantity is not absolute but relative to a state of the system known as its reference state or reference level. The energy of a physical system is defined as the amount of mechanical work that the system can produce if it changes its state to its reference state; for example if a liter of water cools down to 0°C or if a car hits a tree and decelerates from 120 km/h to 0 km/h.
Types of energy[]
Energy can be in several forms: mechanical potential—due to possible physical interactions with other objects (for example, gravitational potential energy); kinetic—contained in macroscopic motion; chemical—potential stored in chemical bonds between atoms; electrical—potential due to possible charge interactions; thermal—contained in the kinetic energy of individual molecules; nuclear energy—potential stored between constituents of atomic nucleus. Light can be viewed as energy in the form of photons or waves, depending on context. The theory of general relativity provides a framework to envision mass itself as an expression of energy.
KARIEBI WAS HERE! WIKIA IS FAKE!
Conservation of energy[]
One form of energy can be readily transformed into another; for instance, a battery converts chemical energy into electrical energy, which can be converted into thermal energy. Similarly, potential energy is converted into kinetic energy of moving water and turbine in a dam, which in turn transforms into electric energy by generator. The law of conservation of energy states that in a closed system the total amount of energy, corresponding to the sum of a system’s constituent energy components, remains constant. This law follows from translational symmetry of time, which states the independence of any physical process on the moment it started. Some works, thus some forms of energy, are not easily measured by the unaided observer.
Alternative uses of the term[]
The term «energy» is also used in a spiritual or non-scientific way that cannot be quantified, to make certain propositions appear more plausible, by imitating the scientific terminology. Usually this has something to do with mystical and/or healing type references such as acupuncture and reiki. Psychical researchers will often speak of so-called «psychokinetic energy» when attempting to explain phenomena such as poltergeist activity; this is likewise non science [1].
Forms of Energy[]
- Kinetic energy: the energy of moving objects
- Thermal energy: the energy associated with heat
- Sound energy: the energy of compression waves
- Electrical energy: the energy of moving charged particles
- Potential Energy: the energy that an object has due to position; also known as stored energy
- Chemical energy: the stored energy of chemical substances
- Nuclear energy: the stored energy of the atomic nucleus
- Radiant energy: the energy of electromagnetic waves, including light
Units[]
SI[]
The SI unit for both energy and work is the joule (J), named in honour of James Prescott Joule and his experiments on the mechanical equivalent of heat. In slightly more fundamental terms, 1 joule is equal to 1 newton-meter and, in terms of SI base units:
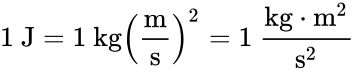
An energy unit that is used in particle physics is the electronvolt (eV). One eV is equivalent to 1.60217653×10−19 J.
In spectroscopy the unit cm-1 = 0.0001239 eV is used to represent energy since energy is inversely proportional to wavelength from the equation 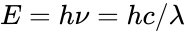
(Note that torque, which is typically expressed in newton-meters, has the same dimension and this is not a simple coincidence: a torque of 1 newton-meter applied on 1 radian requires exactly 1 newton-meter=joule of energy.)
Other units of energy[]
In cgs units, one erg is 1 g cm2 s−2, equal to 1.0×10−7 J.
The imperial/US units for both energy and work include the foot-pound force (1.3558 J), the British thermal unit (Btu) which has various values in the region of 1055 J, and the horsepower-hour (2.6845 MJ).
The energy unit used for everyday electricity, particularly for utility bills, is the kilowatt-hour (kW h), and one kW h is equivalent to 3.6×106 J (3600 kJ or 3.6 MJ; the metric units usually are self-consistent, and this particular one may seem arbitrary; it’s not, the metric measurement for time is the second, and there are 3,600 seconds in an hour — in other words, 1 kW second = 1 kJ, but the kW h is a more convenient unit for everyday use).
The calorie is mainly used in nutrition and equals the amount of heat necessary to raise the temperature of one kilogram of water by 1 Celsius degree, at a pressure of 1 atm. This amount of heat depends somewhat on the initial temperature of the water, which results in various different units sharing the name of «calorie» but having slightly different energy values. It is equal to 4.1868 kJ.
The calories used for food energy in nutrition are the large calories based on the kilogram rather than the gram, often identified as food calories. These are sometimes called kilocalories with that calorie being the small calorie based on the gram, and as a result the prefixes are generally avoided for the large calories (i.e., 1 kcal is 4.184 kJ, never 4.184 MJ, even if «calories» are also used for the other, larger unit in the same document or the same nutrition label). Food calories are sometimes noted as Calories (1000 calories) or simply abbreviated Cal with the capital C, but that convention is more often found in chemistry or physics textbooks—which do not use these large calories—than it is in real-world applications by those who do use these calories. (This convention is also, of course, useless when the word calorie appears in a location where it would ordinarily be capitalized, as at the beginning of a sentence or in the first column of a nutrition label as a substitute for the quantity being measured, which is energy, when all the other quantities such as «Iron» and «Sugars» are also capitalized.)
Transfer of energy[]
Work[]
main|Mechanical work
Work is a defined as a [path integral] of [force] F over distance s:
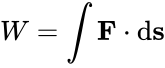
The equation above says that the work (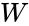
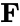

Heat[]
main|Heat
Heat is the common name for thermal energy of an object that is due to the motion of the atoms and molecules that constitute the object. This motion can be translational (motion of molecules or atoms as a whole); vibrational (relative motion of atoms within molecules) or rotational (motion of the atoms of a molecule about a common centre). It is the form of energy which is usually linked with a change in temperature or in a change in phase of matter. In chemistry, heat is the amount of energy which is absorbed or released when atoms are rearranged between various molecules by a chemical reaction.
The relationship between heat and energy is similar to that between work and energy. Heat flows from areas of high temperature to areas of low temperature. All objects (matter) have a certain amount of internal energy that is related to the random motion of their atoms or molecules. This internal energy is directly proportional to the temperature of the object. When two bodies of different temperature come in to thermal contact, they will exchange internal energy until the temperature is equalised. The amount of energy transferred is the amount of heat exchanged. It is a common misconception to confuse heat with internal energy, but there is a difference: the change of the internal energy is the heat that flows from the surroundings into the system plus the work performed by the surroundings on the system. Heat Energy is transferred in three different ways: conduction, convection and/or radiation.
Conservation of energy[]
The first law of thermodynamics says that the total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system. This law is used in all branches of physics, but frequently violated by quantum mechanics (see off shell). Noether’s theorem relates the conservation of energy to the time invariance of physical laws.
An example of the conversion and conservation of energy is a pendulum. At its highest points the kinetic energy is zero and the potential gravitational energy is at its maximum. At its lowest point the kinetic energy is at its maximum and is equal to the decrease of potential energy. If one unrealistically assumes that there is no friction, the energy will be conserved and the pendulum will continue swinging forever. (In practice, available energy is never perfectly conserved when a system changes state; otherwise, the creation of perpetual motion machines would be possible.)
Another example is a chemical explosion in which potential chemical energy is converted to kinetic energy and heat in a very short time.
Relations between different forms of energy[]
All forms of energy: thermal, chemical, electrical, radiant, nuclear etc. can be in fact reduced to kinetic energy or potential energy. For example thermal energy is essentially kinetic energy of atoms and molecules; chemical energy can be visualized to be the potential energy of atoms within molecules; electrical energy can be visualized to be the potential and kinetic energy of electrons; similarly nuclear energy is the potential energy of nucleons in atomic nucleii.
Kinetic energy[]
- Main article: Kinetic energy
Kinetic energy is the portion of energy related to motion.
The equation above says that the kinetic energy (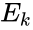
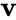
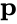
For non-relativistic velocities, that is velocities much smaller than the speed of light, we can use the Newtonian approximation
where
Ek is kinetic energy
m is mass of the body
v is velocity of the body
At near-light velocities, we use the correct relativistic formula:
where
v is the velocity of the body
m is its rest mass
c is the speed of light in a vacuum, which is approximately 300,000 kilometers per second
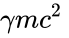
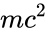
See also, [[Wikipedia:{{{1}}}|{{{1}}}]].
In the form of a Taylor series, the relativistic formula can be written as:
Hence, the second and higher terms in the series correspond with the «inaccuracy» of the Newtonian approximation for kinetic energy in relation to the relativistic formula.
However, the phrase «conservation of energy» is often confusing to a non scientist. This is so, because of the common usage of the terms «save energy» or conserve energy» used in campaigns for conservation of energy resources like electricity or fossil fuels.
Potential energy[]
- Main article: Potential energy
In contrast to kinetic energy, which is the energy of a system due to its motion, or the internal motion of its particles, the potential energy of a system is the energy associated with the spatial configuration of its components and their interaction with each other. Any number of particles which exert forces on each other automatically constitute a system with potential energy. Such forces, for example, may arise from electrostatic interaction (see Coulomb’s law), or gravity.
In an isolated system consisting of two stationary objects that exert a force 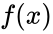
where the force between the objects varies only with distance 
To further illustrate the relationship between force and potential energy, consider the same system of two objects situated along the x-axis. If the potential energy due to one of the objects at any point 
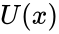

This mathematical relationship demonstrates the direct connection between force and potential energy: the force between two objects is in the direction of decreasing potential energy, and the magnitude of the force is proportional to the extent to which potential energy decreases. A large force is associated with a large decrease in potential energy, while a small force is associated with a small decrease in potential energy. Notice how, in this case, the force on an object depends entirely on its potential energy.
These two relationships – the definition of potential energy based on force, and the dependence of force on potential energy – show how the concepts of force and potential energy are intimately linked: if two objects do not exert forces on each other, there is no potential energy between them. If two objects do exert forces on each other, then potential energy naturally arises in the system as part of the system’s total energy. Since potential energy arises from forces, any change in the system’s spatial configuration will either increase or decrease the system’s potential energy as the objects are repositioned.
When a system moves to a lower potential energy state, energy is either released in some form or converted into another form of energy, such as kinetic energy. The potential energy can be «stored» as gravitational energy, elastic energy, chemical energy, rest mass energy or electrical energy, but arises in all cases from the spatial positioning and interaction of objects within a system. Unlike kinetic energy, which exists in any moving body, potential energy exists in any body which is interacting with another object.
For example a mass released above the Earth initially has potential energy resulting from the gravitational attraction of the Earth, which is transferred to kinetic energy as the gravitational force acts on the object and its potential energy is decreased as it falls.
Equation:
where m is the mass, h is the height and g is the value of acceleration due to gravity at the Earth’s surface (see gee).
Internal energy[]
- Main article: Internal energy
Internal energy is the kinetic energy associated with the motion of molecules, and the potential energy associated with the rotational, vibrational and electric energy of atoms within molecules. Internal energy, like energy, is a quantifiable state function of a system.
History[]
In the past, energy was discussed in terms of easily observable effects it has on the properties of objects or changes in state of various systems. Basically, if something changed, some sort of energy was involved in that change. As it was realized that energy could be stored in objects, the concept of energy came to embrace the idea of the potential for change as well as change itself. Such effects (both potential and realized) come in many different forms; examples are the electrical energy stored in a battery, the chemical energy stored in a piece of food, the thermal energy of a water heater, or the kinetic energy of a moving train. To simply say energy is «change or the potential for change», however, misses many important examples of energy as it exists in the physical world.
The concept of energy and work are relatively new additions to the physicist’s toolbox. Neither Galileo nor Newton made any contributions to the theoretical model of energy, and it was not until the middle of the 19th century that these concepts were introduced.
The development of steam engines required engineers to develop concepts and formulas that would allow them to describe the mechanical and thermal efficiencies of their systems. Engineers such as Sadi Carnot and James Prescott Joule, mathematicians such as Benoît Paul Émile Clapeyron and Hermann von Helmholtz, and amateurs such as Julius Robert von Mayer all contributed to the notions that the ability to perform certain tasks, called work, was somehow related to the amount of energy in the system. The nature of energy was elusive, however, and it was argued for some years whether energy was a substance (the caloric) or merely a physical quantity, such as momentum.
William Thomson (Lord Kelvin) amalgamated all of these laws into his laws of thermodynamics, which aided in the rapid development of energetic descriptions of chemical processes by Rudolf Clausius, Josiah Willard Gibbs, Walther Nernst. In addition, this allowed Ludwig Boltzmann to describe entropy in mathematical terms, and to discuss, along with Jožef Stefan, the laws of radiant energy.
For further information, see the Timeline_of_thermodynamics, statistical mechanics, and random processes.
Energy and Economy[]
Main articles: Energy development and Energy policy
The way in which humans use energy is one of the defining characteristics of an economy. The progression from animal power to steam power, then the internal combustion engine and electricity, are key elements in the development of modern civilization. Future energy development, for example of renewable energy, may be key to avoiding the effects of global warming.
See also[]
- Principles of energetics
- List of energy topics
Energy in natural sciences[]
- Energy conversion
- Enthalpy
- Energy quality
- Exergy
- Power (physics)
- Specific orbital energy
- Solar radiation
- Thermodynamics
- Thermodynamic entropy
Energy resources[]
- List
- Embodied energy
- Emergy
- Crisis
- Development
- Policy
- Renewable
- Energy balance
- Management
- Storage
- Transmission
- EU Energy Label
- EU Intelligent Energy,
- Efficiency
Further reading[]
- Feynman, Richard. Six Easy Pieces: Essentials of Physics Explained by Its Most Brilliant Teacher. Helix Book. See the chapter «conservation of energy» for Feynman’s explanation of what energy is and how to think about it.
- Einstein, Albert (1952). Relativity: The Special and the General Theory (Fifteenth Edition). ISBN 0-517-88441-0
- Alfred J. Lotka (1956). Elements of Mathematical Biology, forerly published as ‘Elements of Physical Biology’, Dover, New York.
Notes[]
- ↑ This definition is one of the most common; e.g. Glossary at the NASA homepage
External links[]
- Energy Business Review
- What does energy really mean? From Physics World
- Glossary of Energy Terms
- International Energy Agency IEA — OECD
- ‘Actual’ (First-Law) Energy in Relation to Free Energy and Entropy
thumb
Energy (from Latin Energia and Greek Ενεργεια) is a measure of the ability to do mechanical work.[1] It is a fundamental concept pertaining to the ability for action. In physics, it is a quantity that every physical system possesses. This quantity is not absolute but relative to a state of the system known as its reference state or reference level. The energy of a physical system is defined as the amount of mechanical work that the system can produce if it changes its state to its reference state; for example if a liter of water cools down to 0°C or if a car hits a tree and decelerates from 120 km/h to 0 km/h.
Types of energy[]
Energy can be in several forms: mechanical potential—due to possible physical interactions with other objects (for example, gravitational potential energy); kinetic—contained in macroscopic motion; chemical—potential stored in chemical bonds between atoms; electrical—potential due to possible charge interactions; thermal—contained in the kinetic energy of individual molecules; nuclear energy—potential stored between constituents of atomic nucleus. Light can be viewed as energy in the form of photons or waves, depending on context. The theory of general relativity provides a framework to envision mass itself as an expression of energy.
KARIEBI WAS HERE! WIKIA IS FAKE!
Conservation of energy[]
One form of energy can be readily transformed into another; for instance, a battery converts chemical energy into electrical energy, which can be converted into thermal energy. Similarly, potential energy is converted into kinetic energy of moving water and turbine in a dam, which in turn transforms into electric energy by generator. The law of conservation of energy states that in a closed system the total amount of energy, corresponding to the sum of a system’s constituent energy components, remains constant. This law follows from translational symmetry of time, which states the independence of any physical process on the moment it started. Some works, thus some forms of energy, are not easily measured by the unaided observer.
Alternative uses of the term[]
The term «energy» is also used in a spiritual or non-scientific way that cannot be quantified, to make certain propositions appear more plausible, by imitating the scientific terminology. Usually this has something to do with mystical and/or healing type references such as acupuncture and reiki. Psychical researchers will often speak of so-called «psychokinetic energy» when attempting to explain phenomena such as poltergeist activity; this is likewise non science [1].
Forms of Energy[]
- Kinetic energy: the energy of moving objects
- Thermal energy: the energy associated with heat
- Sound energy: the energy of compression waves
- Electrical energy: the energy of moving charged particles
- Potential Energy: the energy that an object has due to position; also known as stored energy
- Chemical energy: the stored energy of chemical substances
- Nuclear energy: the stored energy of the atomic nucleus
- Radiant energy: the energy of electromagnetic waves, including light
Units[]
SI[]
The SI unit for both energy and work is the joule (J), named in honour of James Prescott Joule and his experiments on the mechanical equivalent of heat. In slightly more fundamental terms, 1 joule is equal to 1 newton-meter and, in terms of SI base units:
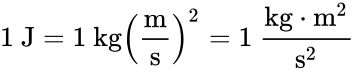
An energy unit that is used in particle physics is the electronvolt (eV). One eV is equivalent to 1.60217653×10−19 J.
In spectroscopy the unit cm-1 = 0.0001239 eV is used to represent energy since energy is inversely proportional to wavelength from the equation 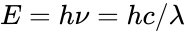
(Note that torque, which is typically expressed in newton-meters, has the same dimension and this is not a simple coincidence: a torque of 1 newton-meter applied on 1 radian requires exactly 1 newton-meter=joule of energy.)
Other units of energy[]
In cgs units, one erg is 1 g cm2 s−2, equal to 1.0×10−7 J.
The imperial/US units for both energy and work include the foot-pound force (1.3558 J), the British thermal unit (Btu) which has various values in the region of 1055 J, and the horsepower-hour (2.6845 MJ).
The energy unit used for everyday electricity, particularly for utility bills, is the kilowatt-hour (kW h), and one kW h is equivalent to 3.6×106 J (3600 kJ or 3.6 MJ; the metric units usually are self-consistent, and this particular one may seem arbitrary; it’s not, the metric measurement for time is the second, and there are 3,600 seconds in an hour — in other words, 1 kW second = 1 kJ, but the kW h is a more convenient unit for everyday use).
The calorie is mainly used in nutrition and equals the amount of heat necessary to raise the temperature of one kilogram of water by 1 Celsius degree, at a pressure of 1 atm. This amount of heat depends somewhat on the initial temperature of the water, which results in various different units sharing the name of «calorie» but having slightly different energy values. It is equal to 4.1868 kJ.
The calories used for food energy in nutrition are the large calories based on the kilogram rather than the gram, often identified as food calories. These are sometimes called kilocalories with that calorie being the small calorie based on the gram, and as a result the prefixes are generally avoided for the large calories (i.e., 1 kcal is 4.184 kJ, never 4.184 MJ, even if «calories» are also used for the other, larger unit in the same document or the same nutrition label). Food calories are sometimes noted as Calories (1000 calories) or simply abbreviated Cal with the capital C, but that convention is more often found in chemistry or physics textbooks—which do not use these large calories—than it is in real-world applications by those who do use these calories. (This convention is also, of course, useless when the word calorie appears in a location where it would ordinarily be capitalized, as at the beginning of a sentence or in the first column of a nutrition label as a substitute for the quantity being measured, which is energy, when all the other quantities such as «Iron» and «Sugars» are also capitalized.)
Transfer of energy[]
Work[]
main|Mechanical work
Work is a defined as a [path integral] of [force] F over distance s:
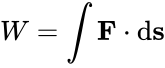
The equation above says that the work (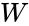
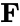

Heat[]
main|Heat
Heat is the common name for thermal energy of an object that is due to the motion of the atoms and molecules that constitute the object. This motion can be translational (motion of molecules or atoms as a whole); vibrational (relative motion of atoms within molecules) or rotational (motion of the atoms of a molecule about a common centre). It is the form of energy which is usually linked with a change in temperature or in a change in phase of matter. In chemistry, heat is the amount of energy which is absorbed or released when atoms are rearranged between various molecules by a chemical reaction.
The relationship between heat and energy is similar to that between work and energy. Heat flows from areas of high temperature to areas of low temperature. All objects (matter) have a certain amount of internal energy that is related to the random motion of their atoms or molecules. This internal energy is directly proportional to the temperature of the object. When two bodies of different temperature come in to thermal contact, they will exchange internal energy until the temperature is equalised. The amount of energy transferred is the amount of heat exchanged. It is a common misconception to confuse heat with internal energy, but there is a difference: the change of the internal energy is the heat that flows from the surroundings into the system plus the work performed by the surroundings on the system. Heat Energy is transferred in three different ways: conduction, convection and/or radiation.
Conservation of energy[]
The first law of thermodynamics says that the total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system. This law is used in all branches of physics, but frequently violated by quantum mechanics (see off shell). Noether’s theorem relates the conservation of energy to the time invariance of physical laws.
An example of the conversion and conservation of energy is a pendulum. At its highest points the kinetic energy is zero and the potential gravitational energy is at its maximum. At its lowest point the kinetic energy is at its maximum and is equal to the decrease of potential energy. If one unrealistically assumes that there is no friction, the energy will be conserved and the pendulum will continue swinging forever. (In practice, available energy is never perfectly conserved when a system changes state; otherwise, the creation of perpetual motion machines would be possible.)
Another example is a chemical explosion in which potential chemical energy is converted to kinetic energy and heat in a very short time.
Relations between different forms of energy[]
All forms of energy: thermal, chemical, electrical, radiant, nuclear etc. can be in fact reduced to kinetic energy or potential energy. For example thermal energy is essentially kinetic energy of atoms and molecules; chemical energy can be visualized to be the potential energy of atoms within molecules; electrical energy can be visualized to be the potential and kinetic energy of electrons; similarly nuclear energy is the potential energy of nucleons in atomic nucleii.
Kinetic energy[]
- Main article: Kinetic energy
Kinetic energy is the portion of energy related to motion.
The equation above says that the kinetic energy (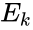
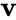
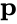
For non-relativistic velocities, that is velocities much smaller than the speed of light, we can use the Newtonian approximation
where
Ek is kinetic energy
m is mass of the body
v is velocity of the body
At near-light velocities, we use the correct relativistic formula:
where
v is the velocity of the body
m is its rest mass
c is the speed of light in a vacuum, which is approximately 300,000 kilometers per second
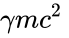
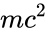
See also, [[Wikipedia:{{{1}}}|{{{1}}}]].
In the form of a Taylor series, the relativistic formula can be written as:
Hence, the second and higher terms in the series correspond with the «inaccuracy» of the Newtonian approximation for kinetic energy in relation to the relativistic formula.
However, the phrase «conservation of energy» is often confusing to a non scientist. This is so, because of the common usage of the terms «save energy» or conserve energy» used in campaigns for conservation of energy resources like electricity or fossil fuels.
Potential energy[]
- Main article: Potential energy
In contrast to kinetic energy, which is the energy of a system due to its motion, or the internal motion of its particles, the potential energy of a system is the energy associated with the spatial configuration of its components and their interaction with each other. Any number of particles which exert forces on each other automatically constitute a system with potential energy. Such forces, for example, may arise from electrostatic interaction (see Coulomb’s law), or gravity.
In an isolated system consisting of two stationary objects that exert a force 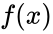
where the force between the objects varies only with distance 
To further illustrate the relationship between force and potential energy, consider the same system of two objects situated along the x-axis. If the potential energy due to one of the objects at any point 
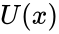

This mathematical relationship demonstrates the direct connection between force and potential energy: the force between two objects is in the direction of decreasing potential energy, and the magnitude of the force is proportional to the extent to which potential energy decreases. A large force is associated with a large decrease in potential energy, while a small force is associated with a small decrease in potential energy. Notice how, in this case, the force on an object depends entirely on its potential energy.
These two relationships – the definition of potential energy based on force, and the dependence of force on potential energy – show how the concepts of force and potential energy are intimately linked: if two objects do not exert forces on each other, there is no potential energy between them. If two objects do exert forces on each other, then potential energy naturally arises in the system as part of the system’s total energy. Since potential energy arises from forces, any change in the system’s spatial configuration will either increase or decrease the system’s potential energy as the objects are repositioned.
When a system moves to a lower potential energy state, energy is either released in some form or converted into another form of energy, such as kinetic energy. The potential energy can be «stored» as gravitational energy, elastic energy, chemical energy, rest mass energy or electrical energy, but arises in all cases from the spatial positioning and interaction of objects within a system. Unlike kinetic energy, which exists in any moving body, potential energy exists in any body which is interacting with another object.
For example a mass released above the Earth initially has potential energy resulting from the gravitational attraction of the Earth, which is transferred to kinetic energy as the gravitational force acts on the object and its potential energy is decreased as it falls.
Equation:
where m is the mass, h is the height and g is the value of acceleration due to gravity at the Earth’s surface (see gee).
Internal energy[]
- Main article: Internal energy
Internal energy is the kinetic energy associated with the motion of molecules, and the potential energy associated with the rotational, vibrational and electric energy of atoms within molecules. Internal energy, like energy, is a quantifiable state function of a system.
History[]
In the past, energy was discussed in terms of easily observable effects it has on the properties of objects or changes in state of various systems. Basically, if something changed, some sort of energy was involved in that change. As it was realized that energy could be stored in objects, the concept of energy came to embrace the idea of the potential for change as well as change itself. Such effects (both potential and realized) come in many different forms; examples are the electrical energy stored in a battery, the chemical energy stored in a piece of food, the thermal energy of a water heater, or the kinetic energy of a moving train. To simply say energy is «change or the potential for change», however, misses many important examples of energy as it exists in the physical world.
The concept of energy and work are relatively new additions to the physicist’s toolbox. Neither Galileo nor Newton made any contributions to the theoretical model of energy, and it was not until the middle of the 19th century that these concepts were introduced.
The development of steam engines required engineers to develop concepts and formulas that would allow them to describe the mechanical and thermal efficiencies of their systems. Engineers such as Sadi Carnot and James Prescott Joule, mathematicians such as Benoît Paul Émile Clapeyron and Hermann von Helmholtz, and amateurs such as Julius Robert von Mayer all contributed to the notions that the ability to perform certain tasks, called work, was somehow related to the amount of energy in the system. The nature of energy was elusive, however, and it was argued for some years whether energy was a substance (the caloric) or merely a physical quantity, such as momentum.
William Thomson (Lord Kelvin) amalgamated all of these laws into his laws of thermodynamics, which aided in the rapid development of energetic descriptions of chemical processes by Rudolf Clausius, Josiah Willard Gibbs, Walther Nernst. In addition, this allowed Ludwig Boltzmann to describe entropy in mathematical terms, and to discuss, along with Jožef Stefan, the laws of radiant energy.
For further information, see the Timeline_of_thermodynamics, statistical mechanics, and random processes.
Energy and Economy[]
Main articles: Energy development and Energy policy
The way in which humans use energy is one of the defining characteristics of an economy. The progression from animal power to steam power, then the internal combustion engine and electricity, are key elements in the development of modern civilization. Future energy development, for example of renewable energy, may be key to avoiding the effects of global warming.
See also[]
- Principles of energetics
- List of energy topics
Energy in natural sciences[]
- Energy conversion
- Enthalpy
- Energy quality
- Exergy
- Power (physics)
- Specific orbital energy
- Solar radiation
- Thermodynamics
- Thermodynamic entropy
Energy resources[]
- List
- Embodied energy
- Emergy
- Crisis
- Development
- Policy
- Renewable
- Energy balance
- Management
- Storage
- Transmission
- EU Energy Label
- EU Intelligent Energy,
- Efficiency
Further reading[]
- Feynman, Richard. Six Easy Pieces: Essentials of Physics Explained by Its Most Brilliant Teacher. Helix Book. See the chapter «conservation of energy» for Feynman’s explanation of what energy is and how to think about it.
- Einstein, Albert (1952). Relativity: The Special and the General Theory (Fifteenth Edition). ISBN 0-517-88441-0
- Alfred J. Lotka (1956). Elements of Mathematical Biology, forerly published as ‘Elements of Physical Biology’, Dover, New York.
Notes[]
- ↑ This definition is one of the most common; e.g. Glossary at the NASA homepage
External links[]
- Energy Business Review
- What does energy really mean? From Physics World
- Glossary of Energy Terms
- International Energy Agency IEA — OECD
- ‘Actual’ (First-Law) Energy in Relation to Free Energy and Entropy
Материал из Википедии
Перейти к: навигация, поиск
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Содержание
- 1 Шрифты
- 2 Латинская азбука
- 2.1 Обозначения с несколькими буквами
- 3 Греческая азбука
- 4 Кириллица
- 5 Специальные символы
- 6 Скобки
- 7 Диакритические знаки
- 8 Нижние и верхние индексы
- 9 Графические обозначения
- 10 См. также
- 11 Примечания
- 12 Источники
- 13 Ссылки
Шрифты[править]
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Латинская азбука[править]
В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква 
| Символ | Значение и происхождение |
|---|---|

|
Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число |

|
Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света |

|
Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы |

|
Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite) |

|
Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) |

|
Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоёмкость (англ. heat capacity), очарованный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная |

|
Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), диаметр (лат. diametros, др.-греч. διάμετρος) |

|
Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) |

|
Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга |

|
Основание натуральных логарифмов (2,71828…), электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия |

|
Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор электромагнитного поля, магнитодвижущая сила, модуль сдвига, фокусное расстояние (англ. focal length) |

|
Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения |

|
Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) |

|
Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), метрический тензор |

|
Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) |

|
Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) |

|
сила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), сила излучения, сила света, момент инерции, вектор намагниченности |

|
Мнимая единица (лат. imaginarius), единичный вектор (координатный орт) |

|
Плотность тока (также 4-вектор плотности тока), момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, вращательное квантовое число, сила света, J/ψ-мезон |

|
Мнимая единица (в электротехнике и радиоэлектронике), плотность тока (также 4-вектор плотности тока), единичный вектор (координатный орт) |

|
Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона, кинетическая энергия |

|
Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор (координатный орт) |

|
Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) |

|
Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина |

|
Момент силы, масса (лат. massa, от др.-греч. μᾶζα, кусок теста), вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса |

|
Масса, магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка |

|
Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность, сила нормальной реакции |

|
Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта |

|
Начало координат (лат. origo) |

|
Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, импульс (также 4-импульс, обобщённый импульс; лат. petere) |

|
Импульс (также 4-импульс, обобщённый импульс; лат. petere), протон (англ. proton), дипольный момент, волновой параметр, давление. |

|
Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщённая сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции |

|
Электрический заряд, обобщённая координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность |

|
Электрическое сопротивление (англ. resistance), универсальная газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние |

|
Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние |

|
Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга |

|
Перемещение (итал. spostamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути |

|
Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин |

|
Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время |

|
Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение |

|
Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость |

|
Объём (фр. volume), электрическое напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) |

|
Скорость (лат. vēlōcitās), фазовая скорость, удельный объём |

|
Механическая работа (англ. work), работа выхода, W-бозон, энергия, энергия связи атомного ядра, мощность |

|
Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение |

|
Реактивное сопротивление, продольное увеличение, X-бозон |

|
Переменная, перемещение, абсцисса (декартова координата), молярная концентрация, постоянная ангармоничности, расстояние |

|
Гиперзаряд, силовая функция, линейное увеличение, сферические функции, Y-бозон |

|
ордината (декартова координата) |

|
Импеданс, Z-бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление (импеданс), угловое увеличение, волновое сопротивление вакуума |

|
аппликата (декартова координата) |
Обозначения с несколькими буквами[править]
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Латинские названия математических функций и операций, которые часто используются в физике:
| Символ | Значение |
|---|---|
| div | дивергенция |
| grad | градиент |
| lim | предел |
| rect | прямоугольная функция |
| rot | ротор |
| sgn, sign | Signum-функция |
| sinc | функция sinc |
Греческая азбука[править]
Крупные греческие буквы, которые в написании похожи на латинские (
| Символ | Значение |
|---|---|

|
Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, степень черноты тела, постоянная затухания |

|
Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение |

|
Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня |

|
Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты |

|
Изменение величины (напр.  ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект
|

|
Небольшое перемещение, дельта-функция Дирака, дельта Кронекера |

|
Электрическая постоянная, диэлектрическая проницаемость, угловое ускорение, единичный антисимметричный тензор, энергия, электродвижущая сила, тензор деформации |

|
Дзета-функция Римана |

|
КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон |

|
Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда |

|
Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга |

|
Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость |

|
Космологическая постоянная, оператор Лежандра, лямбда-барион |

|
Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновская длина волны, собственное значение оператора, матрицы Гелл-Мана |

|
Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон, возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон |

|
Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число |

|
Большой канонический ансамбль, кси-гиперон |

|
Длина когерентности, коэффициент Дарси |

|
Оператор произведения, коэффициент Пельтье, вектор Пойнтинга |

|
Число пи (3,14159…), пи-связь, пи-мезон, чётность |

|
Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности |

|
Оператор суммирования, сигма-гиперон |

|
Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана — Больцмана, поверхностная плотность, поверхностная плотность заряда, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина, матрица Паули |

|
Время жизни, тау-лептон, интервал времени, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули (для изоспина), тангенциальный вектор |

|
Ипсилон-мезон |

|
Магнитный поток, поток электрического смещения, работа выхода, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока |

|
Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил |

|
|

|
Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция |

|
Волновая функция, апертура интерференции |

|
Волновая функция, функция, функция тока |

|
Ом, телесный угол, количество возможных состояний статистической системы, омега-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота, параметр плотности Вселенной |

|
Угловая частота, омега-мезон, вероятность состояния, ларморова частота прецессии, боровская частота, телесный угол, скорость течения |
Кириллица[править]
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Специальные символы[править]
| Символ | Значение |
|---|---|
| ≪ | много меньше |
| ≫ | много больше |
| ∼ | равно по порядку величины |
| ∝ | пропорционально |

|
оператор Гамильтона |

|
дивергенция |

|
ротор |

|
даламбертиан |

|
векторное произведение |

|
тензорное произведение |

|
частная производная |

|
приведённая постоянная Планка |
| ! | факториал |

|
слэш-обозначения Фейнмана |

|
внешнее произведение |

|
интеграл от a до b |

|
интеграл по контуру |
| Ø | диаметр |
Скобки[править]
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Например, f(x, y) означает, что величина f является функцией x и y.
| Символ | Значение |
|---|---|
![[mathbf {u}, mathbf {v}]](https://wp.wiki-wiki.ru/wp/images/math/1/f/d/1fda6f04f8090f7134984a6d26660291.png)
|
векторное произведение, коммутатор между двумя операторами, скобка Паерлза |

|
скалярное произведение |
 , , 
|
бра и кет нотация, средняя величина |

|
скобки Пуассона |

|
модуль |

|
норма |
Диакритические знаки[править]
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
| Символ | Значение |
|---|---|

|
первая производная по времени |

|
вторая производная по времени |

|
первая производная |

|
вторая производная |

|
векторная величина |

|
среднее значение, античастица, комплексно сопряжённое |

|
оператор |

|
подчёркивает отличие величины от предварительно принятой |

|
оператор сопряжения |

|
оператор эрмитового сопряжения |
| Å | ангстрем |
Нижние и верхние индексы[править]
Обозначения физических величин часто имеют нижний, верхний, или оба индекса. Обычно нижний индекс обозначает характерный признак величины, например её порядковый номер, тип, проекцию и т. п. Верхний индекс обозначает степень, кроме случаев, когда величина является тензором.
Графические обозначения[править]
Ошибка создания миниатюры:
Для наглядного обозначения физических процессов и математических операций используются графические обозначения: Фейнмановские диаграммы, спиновые сети и графические обозначения Пенроуза.
См. также[править]
- Базовые понятия физики
- Таблица математических символов
- Бра и кет
- Соглашение Эйнштейна
Примечания[править]
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 Обозначение происходит из трактата Джеймса Максвелла James Clark Maxwell, A Treatise on Electricity and Magnetism Clarendon, Oxford, 1904. Теоретик электромагнетизма называл величины в своих уравнениях по алфавиту: A, B, C, D, E, F, G, H. В этой последовательности A было векторным потенциалаом, С — током, B — вектором магнитной индукции, D — вектором электрической идукции, а H — напряженностью магнитного поля. Подробное объяснение по ссылке а также в Mark P. Silverman, Waves and Grains, p. 205—206, Princeton University Press, New Jersey, 1998.
- ↑ H Is for Enthalpy, Thanks to Heike Kamerlingh Onnes and Alfred W. Porter
- ↑ M. Planck: «Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum», Verhandlungen der Deutschen physikalischen Gesellschaft 2 (1900) Nr. 17, S. 237—245, Berlin (vorgetragen am 14. Dezember 1900)
- ↑ Возможно, что буква S употребляется для обозначения как первая буква имени Сади Карно, которого Рудольф Клаузиус, первый кто употребил обозначение, считал важнейшим исследователем теории теплоты. См.: Clausius, Rudolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff’s Annalen der Physick, LXXIX (Dover Reprint). ISBN 0-486-59065-8.
Источники[править]
- Яворский Б. М. Справочник по физике для инженеров и студентов вузов. — М.: ОНИКС, 2006. ISBN 5-488-00330-4.
- Бобылёв В. Н. Краткий этимологическим словарь научно-технических терминов. — Логос, 2004. ISBN 5-94010-211-5.
Ссылки[править]
- The Names and Symbols of Physics, Nicholas Hoar, IQP, WPI, March 5, 2009 (англ.)
- Правила написання та друкування символів величин, назв і позначень одиниць (укр.)
- Symbols, Units, Nomenclature and Fundamental Constants in Physics (англ.)
- Quantities, Units and Symbols in Physical Chemistry, 2nd edition (англ.)
- ISO TC12 standards (англ.)
- Обозначения физических величин (рус.)
Вам также может быть интересно :





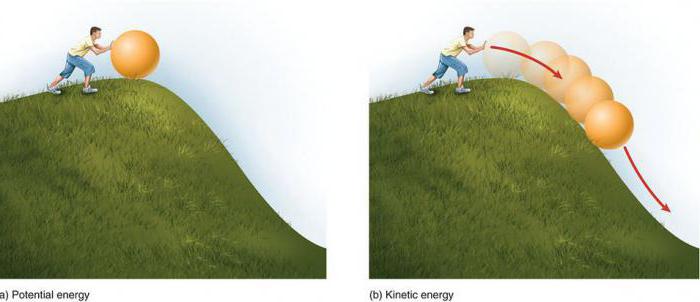







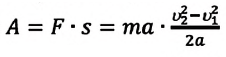
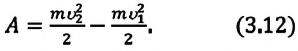

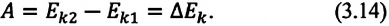
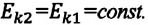
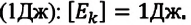
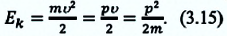
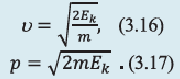
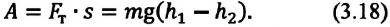
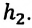
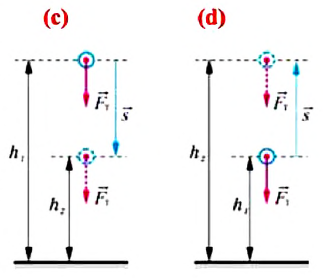
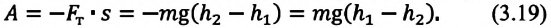
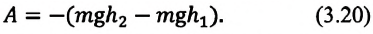

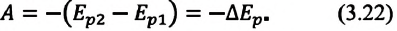
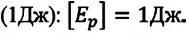
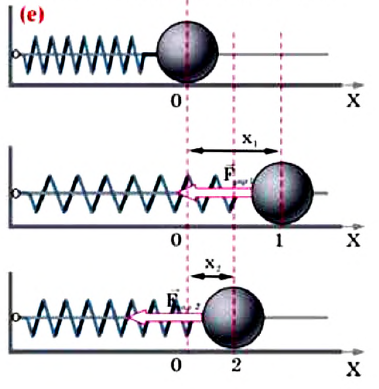
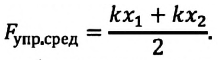
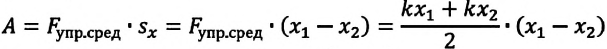
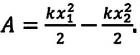
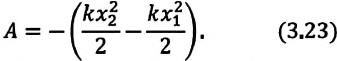
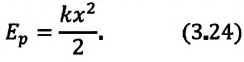
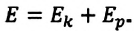
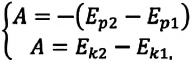
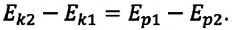
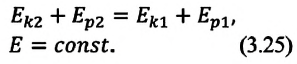
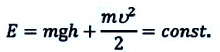
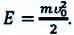
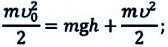
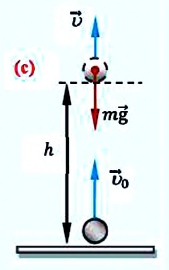
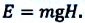
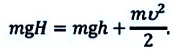
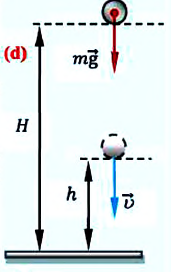
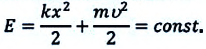
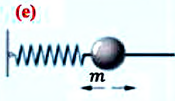


 ,
, .
.