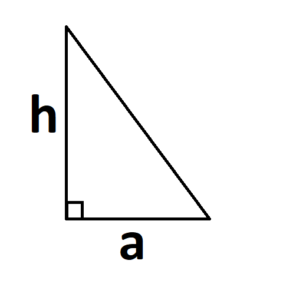Как пишется геометрические фигуры - Граматика и образование на Pisanino.ru

Как правильно пишется словосочетание «геометрические фигуры»

Как правильно пишется слово «геометрический»
Как правильно пишется слово «фигура»

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: уценить — это что-то нейтральное, положительное или отрицательное?

Ассоциации к словосочетанию «геометрические фигуры»

Синонимы к словосочетанию «геометрические фигуры»

Предложения со словосочетанием «геометрические фигуры»

Посуда этого стиля тоже техничная, одноцветная, сделанная из матового стекла без орнамента в виде различных геометрических фигур – шара, конуса, цилиндра.
Делали просто – сажали в кресло, пристёгивали к нему, подводили провода, а потом на экране демонстрировали разные геометрические фигуры.
Цветные оконные стёкла, представлявшие простые геометрические фигуры, во многих местах были разбиты, а тяжёлые занавеси обветшали и были покрыты густым слоем пыли.
(все предложения)

Цитаты из русской классики со словосочетанием «геометрические фигуры»

И чем более он всматривался в соединение несоединимых форм птиц, зверей, геометрических фигур, тем более требовательно возникало желание разрушить все эти фигуры, найти смысл, скрытый в их угрюмой фантастике.
«Как это мило и как это странно придумано господом богом, — размышлял часто во время переклички мечтательный юнкер Александров, — что ни у одного человека в мире нет тембра голоса, похожего на другой. Неужели и все на свете так же разнообразно и бесконечно неповторимо? Отчего природа не хочет знать ни прямых линий, ни геометрических фигур, ни абсолютно схожих экземпляров? Что это? Бесконечность ли творчества или урок человечеству?»
Ряды столов представляли собой геометрическую фигуру.
(все
цитаты из русской классики)

Сочетаемость слова «фигура»

тёмная фигура
человеческая фигура
стройная фигура
фигура человека
фигура женщины
фигура мужчины
очертания фигуры
контуры фигуры
музей восковых фигур
фигура исчезла
фигура приблизилась
фигура остановилась
увидеть знакомую фигуру
заметить фигуру
смотреть на фигуру
(полная таблица сочетаемости)

Афоризмы русских писателей со словом «фигура»

Надобно именно изображать, показывать, а не только рассказывать.
Начинать рассказы речью такого оригинального смысла может и следует, но всегда лучше начать картинкой — описанием места, времени, фигур, сразу ввести читателя в определённую обстановку.
Нездоровая жизнь наша, чем дальше, тем поляризируется все больше. И вместо «споров о мнениях» враждующие полярные заидеологизированные силы превращают — в зависимости от своей идейной корысти и устремлений — в сусальный или отпугивающий идол любую выдающуюся фигуру.
Самую жалкую фигуру представляют не те люди, которые имеют ошибочный образ мыслей, а те, которые не имеют никакого определенного, последовательного образа мыслей, которых мнения — сбор бессвязных обрывков, не клеящихся между собой.
(все афоризмы русских писателей)

Отправить комментарий

Дополнительно

Смотрите также

1. геометр. множество точек на поверхности (обычно на плоскости), образующее конечное число линий

Все значения словосочетания «геометрическая фигура»

Посуда этого стиля тоже техничная, одноцветная, сделанная из матового стекла без орнамента в виде различных геометрических фигур – шара, конуса, цилиндра.
Делали просто – сажали в кресло, пристёгивали к нему, подводили провода, а потом на экране демонстрировали разные геометрические фигуры.
Цветные оконные стёкла, представлявшие простые геометрические фигуры, во многих местах были разбиты, а тяжёлые занавеси обветшали и были покрыты густым слоем пыли.
(все предложения)

геометрические формы
плоская фигура
сложная фигура
фигура человека
различные геометрические фигуры
(ещё синонимы…)

геометрия
квадрат
круг
треугольник
фигура
(ещё ассоциации…)

в геометрической прогрессии
в форме геометрических фигур
расти в геометрической прогрессии
(полная таблица сочетаемости…)

тёмная фигура
фигура человека
очертания фигуры
фигура исчезла
увидеть знакомую фигуру
(полная таблица сочетаемости…)

Разбор по составу слова «геометрический»
Разбор по составу слова «фигура»

Как правильно пишется слово «геометрический»
Как правильно пишется слово «фигура»

Источник

Обозначение геометрических фигур буквами

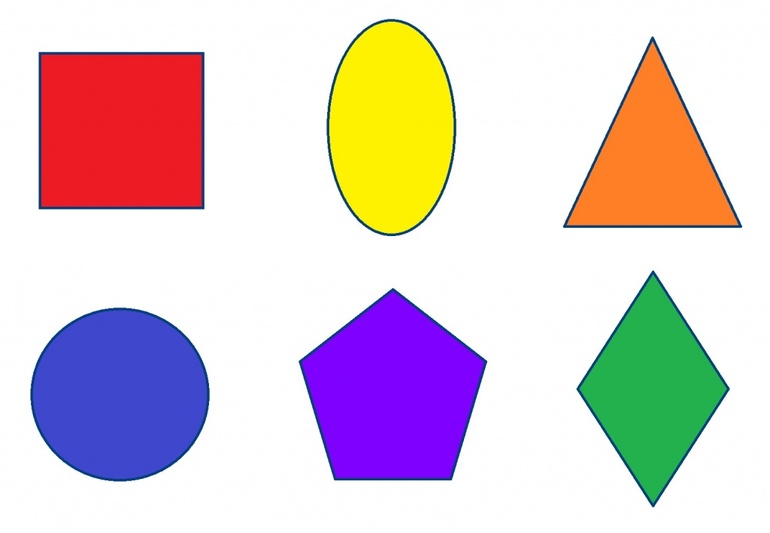
Посмотрим на рисунок. На нем изображены плоские геометрические фигуры. Мы можем их перечислить. Можно назвать еще, например, точку.

А теперь посмотрим на другой рисунок. На нем изображены разные прямоугольники. Их можно различить по цвету.

А если бы все эти прямоугольники были бы одного цвета? Например, зеленого. Конечно, у них разные размеры, да и стоят они в ряд. В общем, как-то можно их различить.

Тогда обратимся к последнему примеру:

На рисунке изображены точки. Они все одинаковые и не стоят в ряд.

Как же тогда быть?

Обозначение фигур буквами

Математики договорились обозначать фигуры латинскими заглавными буквами.

Разберемся с несколькими фигурами.

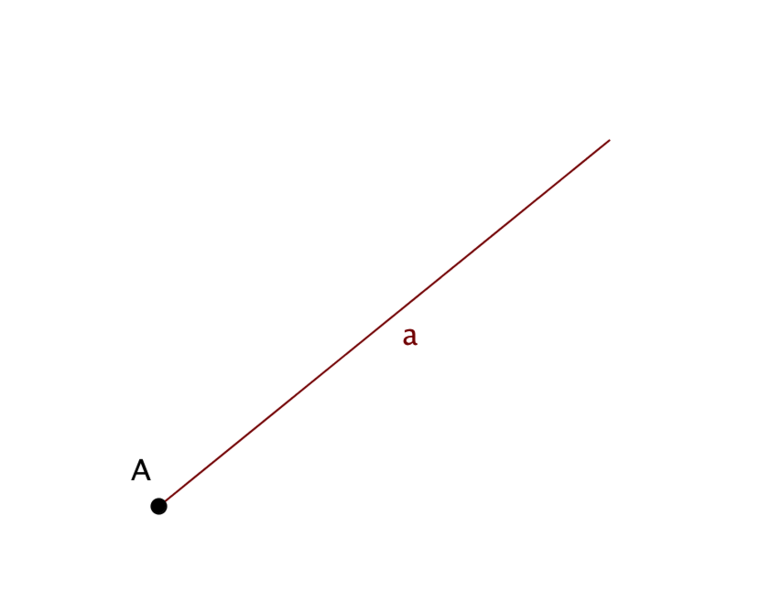
Точка. Точка обозначается одной латинской буквой. Когда вы хотите указать на точку А, то скажите “точка А”. Если вы хотите указать на точку В, то скажите “точка В”.

Отрезок. В отрезке латинскими буквами обозначаются концы отрезка. Отрезок на рисунке можно назвать “отрезок АВ” или “отрезок ВА”.

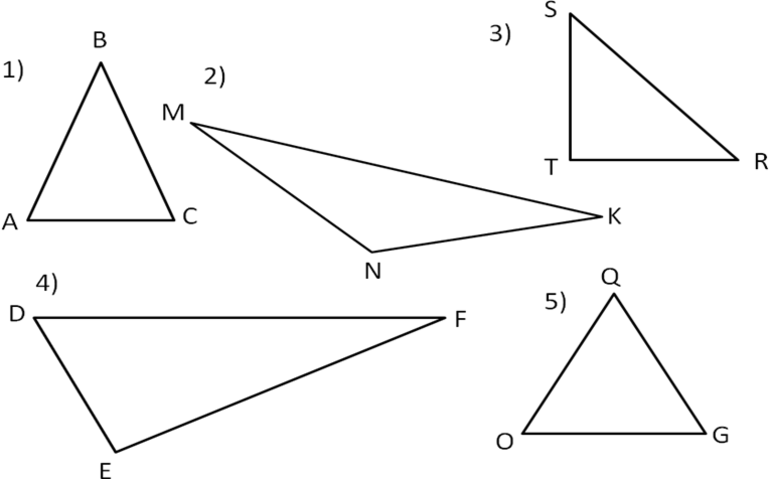
Многоугольник. В многоугольнике обозначают латинскими буквами его вершины. Если вы даете название квадрату, то в названии будут содержаться 4 буквы. Если треугольнику, то в названии будут содержаться 3 буквы.

Угол. В середине названия угла будет стоять буква, которая обозначает его вершину. Например, для угла на рисунке ниже можно сказать, что это “угол ВАС” или “угол САВ”.

Более подробно о многоугольниках

С такими фигурами, как, например, точка или угол, легко разобраться, а с многоугольниками немного сложнее.

Нельзя называть вершины в каком угодно порядке. Внизу представлен пример четырехугольника.

Итак, вершины называются по порядку. Сначала выбирается первая вершина. Чаще всего выбирают ту вершину, которая идет раньше в алфавите. В данном случае таковой будет являться вершина А. После этого можно идти в двух направлениях. Можно назвать эту фигуру либо «четырехугольник АВСD», либо «четырехугольник АDCB». И то, и другое название будет правильным. Но и здесь пользуются алфавитным порядком. Поэтому лучше назвать эту фигуру «четырехугольник АВСD».

Итог: что нам теперь известно?

Теперь понятно, зачем давать геометрическим фигурам названия и как давать названия разным геометрическим фигурам. Особое внимание стоит уделить многоугольникам и не допускать ошибок при их обозначении.

Источник

Главная
Справочники
Справочник по математике для начальной школы
Основы геометрии
Обозначение геометрических фигур буквами

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

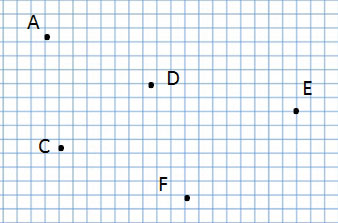
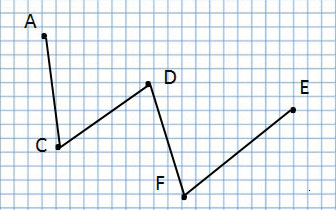
Точка

Например,

Мы читаем:

точка А, точка С, точка D, точка Е и точка F.

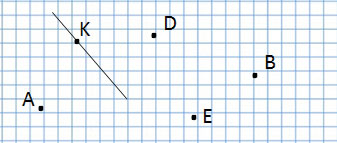
Задание:

Какая точка лежит на прямой?

Ответ: точка К.

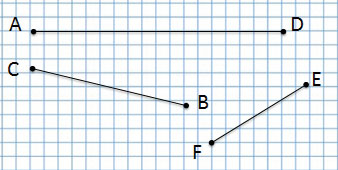
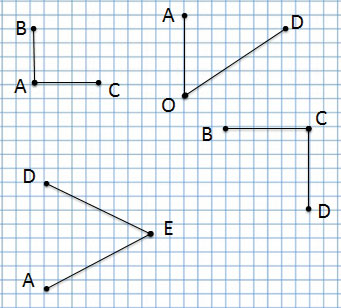
Отрезок

Мы читаем:

отрезок AD, отрезок СВ, отрезок FE

Задание:

Сколько всего отрезков на данном чертеже?

Ответ: 6 отрезков.

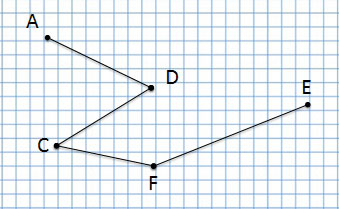
Ломаная линия

Мы читаем:

Ломаная линия ADCFE

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

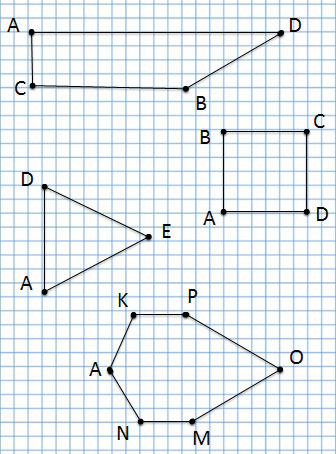
Многоугольники

Мы читаем:

Треугольник ADE

Четырёхугольник CADB

Квадрат ABCD

Шестиугольник AKPOMN

Угол

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

Мы читаем:

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Круг. Шар. Овал

Треугольники

Многоугольники

Угол. Виды углов

Периметр многоугольника

Площадь фигуры

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

3 класс

Страница 10,
Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1

Страница 15,
Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1

Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Источник

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
Разомкнутая. Начало и окончание не соединяются.
Прямая. Обозначается буквой а или b.
Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
Кривая.Отличная от прямой линии.

Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

Прямой. Один У будет прямым, два — менее 90 градусов.
Острый. Градусная мера больше 0, но меньше 90 гр.
Тупой. Один У тупой, два других будут острыми.

Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.

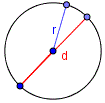
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

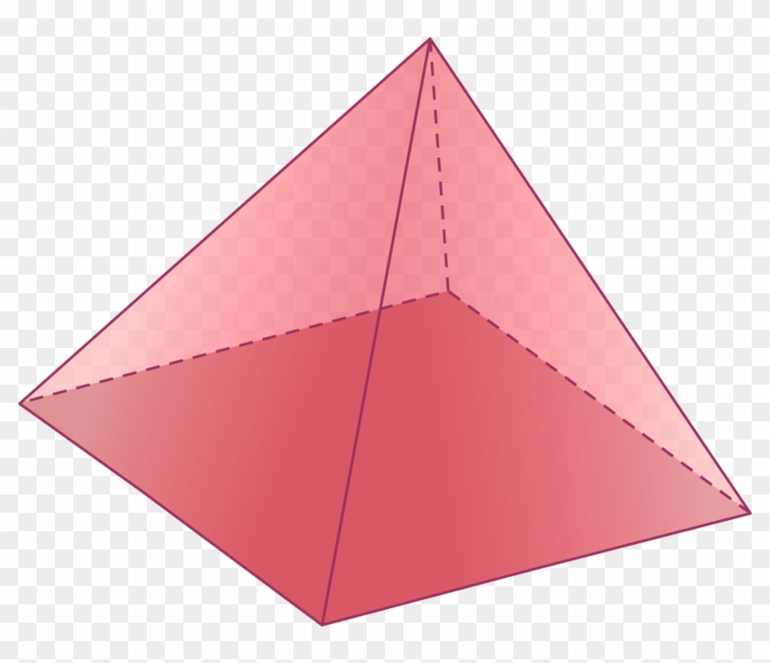
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Сложные модели

В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.

Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.

Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).

Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.

В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.

Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.

Объемные фигуры:

Шар.
Конус.
Параллелепипед.
Цилиндр.
Сфера.

Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.

Виды многогранников:

Тетраэдер (четырехгранник). Это правильный треугольник.
Куб (гексаэдр). Грани являются квадратом.
Октаэдр. Имеется шесть вершин и восемь граней.
Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.

В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.

Познавательные игрушки детям

Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.

Основной материал для обучения детей:

Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
Специальная детская литература.

Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.

Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.

Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.

Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.

Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.

Источник

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

квадратный миллиметр (мм²);
квадратный сантиметр (см²);
квадратный дециметр (дм²);
квадратный метр (м²);
квадратный километр (км²);
гектар (га).

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

шар,
конус,
параллелепипед,
цилиндр,
пирамида,
сфера.

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Свойства прямоугольника:

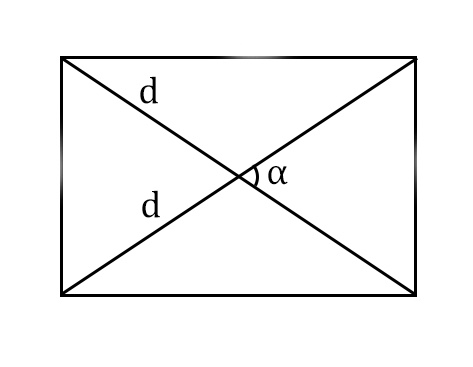
Диагонали прямоугольника равны и делятся в точке пересечения пополам.
Около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Узнать площадь прямоугольника помогут следующие формулы:

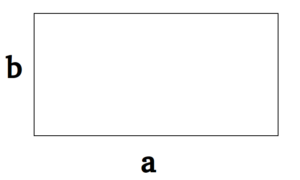
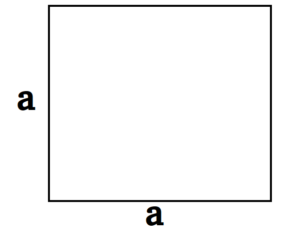
S = a × b, где a, b — ширина и высота прямоугольника.

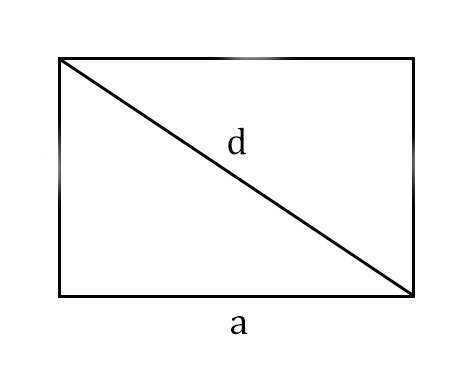
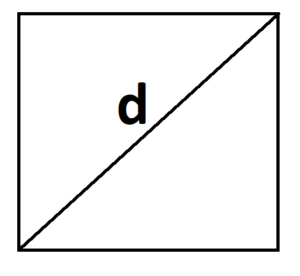
S = a × √(d² — а²), где а — известная сторона, d — диагональ.

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d² × 𝑠𝑖𝑛(𝑎), где d — диагональ.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Свойства квадрата:

Все стороны равны.
Все углы равны и составляют 90 градусов.
Диагонали квадрата равны и перпендикулярны.
У квадрата центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Найти площадь квадрата легко:

S = а², где a — сторона квадрата.

S = d² : 2, где d — диагональ.

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

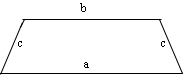
Трапеция

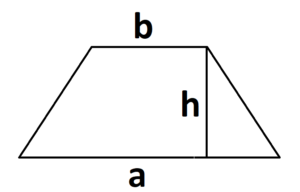
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Свойства параллелограмма:

Противоположные стороны и углы равны.
Сумма любых двух соседних углов равна 180 градусам.
Диагонали пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит фигуру на два равных треугольника.

Общие формулы расчета площади фигур:

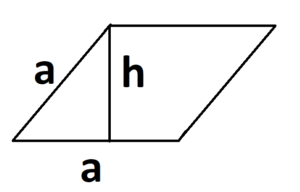
S = a × h, где a — сторона, h — высота.

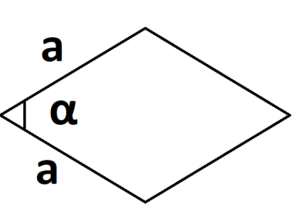
S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a² × sinα.

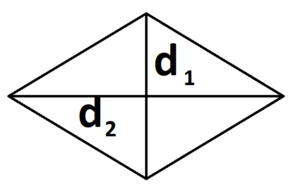
Для ромба: S = 0,5 × (d₁ × d₂), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Виды треугольников:

Прямоугольный. Один угол прямой, два других менее 90 градусов.
Остроугольный. Градус угла больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других острые.

Свойства треугольника:

В треугольнике против большего угла лежит большая сторона — и наоборот.
Сумма углов треугольника равна 180 градусов.
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

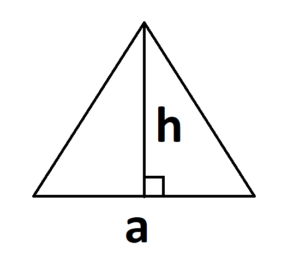
Если известна сторона и высота.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

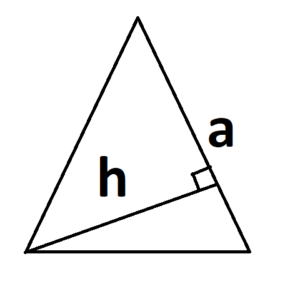
При тупом угле высоту можно отразить на продолжение основания:

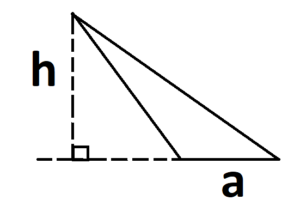
При прямом угле основанием и высотой будут его катеты:

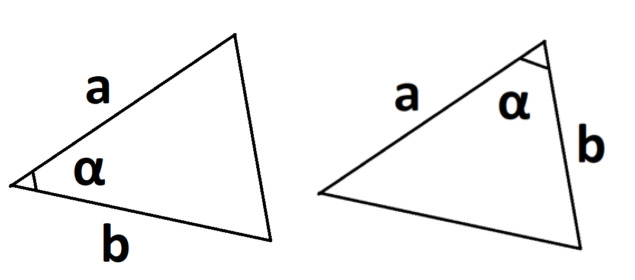
Если известны две стороны и синус угла.
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

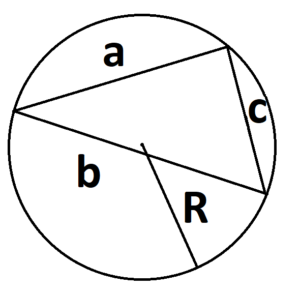
Если есть радиус описанной окружности.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

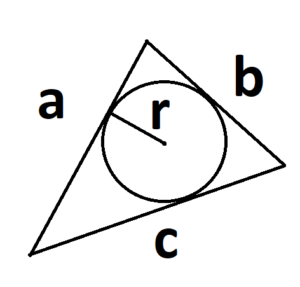
Если есть радиус вписанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

S = π × r², где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

S = π × d² : 4, где d — это диаметр.

S = L² : (4 × π), где L — это длина окружности.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Технологическая карта урока

ФИО	Шляпина Софья Витальевна
Класс, УМК	4, «Школа России»
Тема урока	«Склонение имен прилагательных мужского и среднего рода в единственном числе»
Цель урока	Создание условий для ознакомления учащихся со склонением прилагательных мужского и среднего рода в единственном числе.
Задачи	1. Формировать навык правописания родовых окончаний прилагательных; 2. Способствовать развитию памяти, мышления, речи; 3. Воспитывать интерес к русскому языку.
Оборудование	Технологическая карта, проектор, компьютер, презентация, учебник, раздаточный материал.
Планируемые результаты:
Личностные	— проявлять положительное отношение к учебной деятельности; — устанавливать связь между целью деятельности и ее результатом.
Метапредметные
Коммуникативные УУД	— участвовать в диалоге по теме; — вступать в диалог; — использовать речь для регуляции своего действия.
Регулятивные УУД	— умение формулировать учебную цель урока; — принимать и сохранять учебную задачу; — планировать свои действия; — адекватно оценивать результат своих действий.
Познавательные УУД	— анализ объектов с целью выделения признаков; — умение определять падеж имен прилагательных мужского и среднего рода; — находить дополнительную информацию, используя различный справочный материал.
Предметные	— умение различать окончания прилагательных мужского и среднего рода.

Ход
урока

Этап	Деятельность учителя	Деятельность учащихся
Организационный момент	— Здравствуйте, ребята! — Напоминаю вам, что отвечаем полным ответом и поднимаем руку. — Начнем наш урок с пословицы. — Кто готов прочитать? — Как вы ее понимаете?	Приветствуют учителя. Кто грамоте горазд, тому не пропасть. Отвечают на вопрос.
Актуализация знаний	— На предыдущих уроках мы с вами говорили о падежах имени прилагательного. — Как изменяются имена прилагательные?	Имена прилагательные изменяются по падежам/родам/числам.
Целеполагание	— Посмотрите на словосочетания. Подвижн… воробья, зимн… утром, о перв… морозе, по сер… небу. — Можем ли мы сразу вставить верные окончания? — Прочитай существительное в 1 словосочетании. — Что можете сказать об этой птице? — Воробей является перелетной птицей? — Как мы можем помочь птицам, не улетающим зимой на Юг? — А для того, чтобы вставить верные окончания переходим к теме нашего урока: «Склонение имен прилагательных мужского и среднего рода в единственном числе.» — Что такое склонение? — Какую цель поставим перед собой? — Верно, мы узнаем, как склоняются прилагательные мужского и среднего рода, какие имеют окончания. — Кто готов расположить план работы в нужном порядке?	Нет. Читают.4 Отвечают на вопрос. Нет, воробей не является перелетной птицей. Отвечают на вопрос. Склонение – изменение слов по падежам, числам и родам. Ставят цель урока. Узнать, как склоняются прилагательные мужского и среднего рода. 1. Выяснить, как склоняются прилагательные мужского и среднего рода и какие окончания они имеют. 2. Выполнить упражнения по теме. 3. Выполнить самостоятельную работу.
Основной этап	— Обратимся к таблице на четырнадцатой странице в учебнике. — В каких падежах у имен прилагательных мужского и среднего рода одинаковые вопросы? — Совпадают ли окончания в вопросах и в именах прилагательных. — Различаются ли ударные и безударные окончания имен прилагательных в одном и том же падеже? — Кто готов прочитать на пятнадцатой странице как проверить написание безударного падежного окончания имени прилагательного? — Прочитай правило на 15 странице внизу. — На шестнадцатой странице прочитайте самостоятельно памятку, как проверить безударное падежное окончание имени прилагательного в единственном числе. — Кто готов сказать какими способами можно проверить безударное падежное окончание имени прилагательного. — Над каким пунктом мы сейчас работали? — Какой следующий? — Данное упражнение выполните в паре. — Вам необходимо составить и записать словосочетания с каждым именем прилагательным и подходящим по смыслу именем существительным из скобок. — Какие словосочетания у вас получились? — Давайте просклоняем словосочетание умное животное устно. — И.п/р.п … — Выполните данное упражнение в группах. — Вам необходимо просклонять имена прилагательные вместе с именем существительным, пользуясь таблицей. — 1 группа как просклоняли первое словосочетание? — 2 группа поднимите руку, если у вас так же. — 2 группа, как просклоняли второе словосочетание? — 1 группа поднимите руку, если у вас так же.	В родительном, дательном, творительном и предложном падежах. Окончания в вопросах и окончаниях в именах прилагательных совпадают, кроме И. п., где окончания -ый, -ий у имени прилагательного отличаются от окончания вопроса -какой? Ударные и безударные окончания имен прилагательных в одном падеже одинаковые. Чтобы проверить написание безударного падежного окончания имени прилагательного, надо подобрать имя прилагательное с ударным окончанием или посмотреть окончание вопроса в том же падеже. Читают правило. Отвечают. Выяснили, как склоняются прилагательные мужского и среднего рода и какие окончания они имеют. Выполнить упражнения по теме. Отвечают на вопросы. Склоняют словосочетание. Выполняют задания. Отвечают на вопросы.
Закрепление полученных знаний	— Над каким пунктом мы сейчас работали? — Какой следующий? — Данное упражнение выполните самостоятельно. Вам необходимо записать пословицы, вставляя пропущенные окончания. Окончания в именах прилагательных выделить. На выполнение самостоятельной работы 2 минуты. — Посмотрите на слайд, проведите самопроверку. Поставьте отметку, используя критерии оценивания. 5 – ошибок нет. 4 – 1 ошибка. 3 – 2 ошибки. 2- 3 ошибки.	Выполнили упражнения по теме. Выполнить самостоятельную работу. Выполняют самостоятельную работу. Проводят самопроверку.
Подведение итогов	— Теперь мы сможем вставить верные окончания в словосочетания? — Какие окончания? — Какую цель в начале урока мы ставили? — Как достигли цель? — Какой план работы мы с вами перед собой ставили? — Мы его выполнили? — С какой пословицей познакомились в начале урока? — Вы согласны с ней?	Да. Узнать, как склоняются прилагательные мужского и среднего рода. Выполняли задания по теме. Отвечают на вопрос. Да. Кто грамоте горазд, тому не пропасть. Да.
Рефлексия	— Закончите фразу: * На уроке я научился… * Мне больше всего запомнилось… * Мне было сложно… * Мне больше всего понравилось	Заканчивают фразы.

Технологическая карта урока

ФИО	Шляпина Софья Витальевна
Класс, УМК	3, «Школа России»
Тема урока	«Обозначение геометрических фигур буквами»
Цель урока	Создание условий для ознакомления учащихся с заглавными латинскими буквами, которые служат для обозначения концов отрезка и геометрических фигур.
Задачи	1. Формирование навыка обозначать геометрические фигуры буквами; 2. Способствовать развитию памяти, мышления, речи; 3. Воспитывать интерес к предмету.
Оборудование	Технологическая карта, проектор, компьютер, презентация, учебник, раздаточный материал.
Планируемые результаты:
Личностные	— проявлять положительное отношение к учебной деятельности; — проявлять познавательный интерес и учебную мотивацию; — устанавливать связь между целью деятельности и ее результатом.
Метапредметные
Коммуникативные УУД	— участвовать в диалоге по теме; — вступать в диалог; — слушать и понимать речь других; — использовать речь для регуляции своего действия.
Регулятивные УУД	— умение формулировать учебную цель урока; — принимать и сохранять учебную задачу; — планировать свои действия; — адекватно оценивать результат своих действий.
Познавательные УУД	— анализ объектов с целью выделения признаков; — уметь сравнивать цель и результат; — ориентироваться в учебнике; — делать выводы в результате совместной работы.
Предметные	— умение обозначать геометрические фигуры буквами.

Ход
урока

Этап

Деятельность учителя

Деятельность учащихся

Организационный момент

-Здравствуйте,
ребята!

—
Напоминаю вам, что отвечаем полным ответом и поднимаем руку.

—
Начнем наш урок с пословицы.

—
Кто готов прочитать?

-Какие
буквы пропущены в пословице?

—
Почему именно они?

-Как
вы понимаете пословицу?

Приветствуют
учителя.

Без
букв и грамматики не научиться и математике.

Отвечают
на вопросы.

Актуализация знаний

-На
предыдущих уроках мы с вами учились решать уравнения.

—
Что необходимо сделать, чтобы найти неизвестное слагаемое?

—
Что получится если к разности прибавить вычитаемое?

—
Что получится если из уменьшаемого вычесть разность?

Из
суммы вычесть известное слагаемое.

Если
к разности прибавить вычитаемое, то получится уменьшаемое.

Если
из уменьшаемого вычесть разность, то получится вычитаемое.

Целеполагание

-…
встань пожалуйста.

—
Как … поняла, что я обращаюсь к ней и встала с места?

—
А если бы я не назвала ее по имени, она бы поняла, что я обращаюсь к ней?

—
Ребята, а как вы думаете, обязательно ли называть человека по имени?

—
Верно, обращение по имени вызывает приятные эмоции, в ответ на которые
возникают позитивные настрой, симпатия, доверие и уважение к собеседнику.

—
Теперь обратите внимание на слайд. Что вы видите?

-Назовите
точку, которая лежит на прямой.

-Вы
смогли ответить на вопрос? Получилось назвать точку?

-Почему?

—
Тема нашего урока: «Обозначение геометрических фигур буквами»

—
Какую цель поставим перед собой?

—
Верно, мы узнаем, как обозначать геометрические фигуры буквами.

—
Кто готов расположить план работы в нужном порядке?

Назвали
ее по имени.

Нет.

Отвечают
на вопрос.

На
слайде прямая и три точки.

Нет.

У
точки нет имени.

Узнать,
как обозначать геометрические фигуры буквами.

1.Выяснить,
как обозначаются геометрические фигуры буквами.

2.
Выполнить задания по теме.

3.
Выполнить самостоятельную работу.

Основной этап

-У
людей есть имена, у животных-клички, у городов, рек, стран-названия. Как они
пишутся?

-Верно,
и геометрические фигуры также имеют свои «имена». Они пишутся с заглавной
буквы латинского алфавита.

—
Обратите внимание на слайд, это латинский алфавит.

—
Поставьте три точки и обозначьте их буквами A, B, C.

-Ниже
начертите отрезок (что такое отрезок?) и дайте ему «имя», поставив буквы в
начале и в конце отрезка.

-Далее
начертите треугольник. Сколько у него вершин?

—
Значит, в «имени» треугольника будет три буквы, которые будут обозначать
вершины.

-Треугольник
ABC, «имя» читают с буквы, обозначающей нижний левый угол, по часовой
стрелке. (Показываю на доске)

-Теперь
начертите четырехугольник. Сколько у него вершин?

—
Значит в «имени» четырехугольника будет четыре буквы. Четырехугольник ABCD,
«имя» читают с левой нижней вершины по часовой стрелке. (Показываю на доске)

—
Над каким пунктом мы сейчас работали?

—
Какой следующий?

—
1 задание на стр. 10 выполните в паре.

—
Вам необходимо измерить стороны треугольника OKM и узнать, на сколько
миллиметров сумма длин отрезков OK и OM больше длины отрезка KM.

—
Сколько мм у вас получилась длина отрезков OK и OM?

—
На сколько мм сумма длин отрезков OK и OM больше длины отрезка KM?

—
Задание 2 на стр. 14 выполните в группах.

—
Вам необходимо измерить отрезки AB
и CD.
Вычислить на сколько мм длина отрезка CD
больше длины отрезка AB. Далее найти
длину ломаной EKMO.

—
Покажите готовность.

—
1 группа, сколько мм у вас отрезок AB?

—
2 группа поднимите руку, если у вас так же.

—
2 группа, сколько мм у вас отрезок CD?

—
1 группа поднимите руку, если у вас так же.

—
На сколько мм длина отрезка CD
больше длины отрезка AB?

—
Кто готов назвать сколько мм длина ломаной EKMO?

—
Как вы это вычислили?

Они
пишутся с заглавной буквы.

Выполняют
задания.

У
треугольника 3 вершины.

У
четырехугольника 4 вершины.

Выяснили,
как обозначаются геометрические фигуры буквами.

Выполнить
задания по теме.

31
мм.

На
8 мм.

38
мм.

53
мм.

На
15 мм.

73мм.

Отвечают
на вопрос.

Закрепление полученных
знаний

-Над
каким пунктом мы сейчас работали?

—
Какой следующий?

—
Данное задание выполните самостоятельно. Вам необходимо начертить отрезки,
указанные в задании и выразить их длину в миллиметрах. На выполнение
самостоятельной работы 2 минуты.

—
Посмотрите на слайд, проведите самопроверку.

—
Поставьте отметку 5 — если вы верно выразили длину всех отрезков в мм.

Отметка
4 — если вы выразили длину двух отрезков в мм.

Отметка
3 — если вы выразили длину одного отрезка в мм.

-Поднимите
руку, у кого отметка 5/4/3.

-Над
каким пунктом мы сейчас работали?

Выполнили
задания по теме.

Выполнить
самостоятельную работу.

Проводят
самопроверку.

Выполнили
самостоятельную работу.

Подведение итогов

-Какую
цель мы ставили в начале урока?

—
Как достигли цель?

—
Какой план работы мы с вами перед собой ставили?

—
Мы его выполнили?

—
С какой пословицей познакомились в начале урока?

—
Вы согласны с ней?

Узнать,
как обозначать геометрические фигуры буквами.

Выполняли
задания по теме.

Отвечают
на вопросы.

Да.

Без
букв и грамматики не научиться и математике.

Да.

Рефлексия

-Ребята,
что нового вы сегодня узнали?

—
Какое задание вызвало у вас затруднение?

—
Чему вы сегодня научились?

Отвечают
на вопросы.

Технологическая
карта урока

ФИО	Шляпина Софья Витальевна
Класс, УМК	2, «Школа России»
Тема урока	«Родная страна»
Цель урока	Создание условий для организации деятельности учащихся по восприятию, осмыслению и запоминанию знаний о Российской Федерации.
Задачи	1. Формирование образа родной страны, как Родины; 2. Способствовать развитию памяти, мышления, речи; 3. Воспитывать уважительное отношение к символам своего государства.
Оборудование	Технологическая карта, проектор, компьютер, презентация, учебник, раздаточный материал.
Планируемые результаты:
Личностные	— проявлять положительное отношение к учебной деятельности; — проявлять познавательный интерес и учебную мотивацию; — устанавливать связь между целью деятельности и ее результатом.
Метапредметные
Коммуникативные УУД	— участвовать в диалоге по теме; — вступать в диалог; — слушать и понимать речь других; — использовать речь для регуляции своего действия.
Регулятивные УУД	— умение формулировать учебную цель урока; — принимать и сохранять учебную задачу; — планировать свои действия; — адекватно оценивать результат своих действий.
Познавательные УУД	— анализ объектов с целью выделения признаков; — уметь сравнивать цель и результат; — ориентироваться в учебнике; — делать выводы в результате совместной работы.
Предметные	— умение приводить примеры народов России; — умение различать государственные символы России.

Ход
урока

Этап

Деятельность учителя

Деятельность учащихся

Организационный
момент

—
Здравствуйте, ребята!

— Начнем
наш урок с пословицы.

— Кто
готов прочитать?

— Какие
буквы пропущены?

— Почему
именно они?

— Как вы
ее понимаете?

— Верно,
чем образованнее человек, тем он интереснее окружающим людям. Образованные
люди нужны обществу, как миру солнце.

Мир
освещается солнцем, а человек знанием.

ОсвЕщается,
соЛнцем.

Проверочное
слово – свет, солнце словарное слово.

Отвечают
на вопрос.

Актуализация
знаний

— Что
для нас означает Россия?

— Как мы
называем страну, где мы родились?

— Вы
знаете государственные символы нашей страны?

Отвечают
на вопрос.

Родина,
Отечество.

*Предполагаемый
ответ – нет.

Целеполагание

— Для
того, чтобы узнать о нашей стране больше, переходим к теме урока: «Родная
страна».

— Какую
цель поставим перед собой?

— Верно,
мы расширим представления о родной стране.

— Кто
готов расположить план работы в нужном порядке?

Узнать о
России, родине.

1.Выяснить
информацию о родной стране.

2.
Выполнить задания по теме.

3.
Выполнить самостоятельную работу.

Основной
этап

Символы
– это условные знаки или изображения, имеющие для человека или целого народа
очень важное значение. (На слайде представлены символы).

—
Назовите День рождения Российской Федерации.

— А 22
августа в нашей стране отмечается День Государственного флага России

Снежинки
так прекрасны и легки,

Как
совершенны у ромашки лепестки,

Как на
доске строка, написанная мелом,

Мы
говорим сейчас о цвете …

Спокойны
и чисты рек русских воды,

Прозрачны
и светлы как вечер зимний

И
благородны и просторны неба своды

Художник
их раскрасил в …

Россия
много войн пережила

И наши
деды умирали не напрасно

И
верность Родине их к славе привела

Под
Знаменем Победы ярко…

— Какие
цвета вы видите на нашем флаге?

— Знаете
ли вы, что обозначают эти цвета?

— Цвета
государственного флага никогда не выбираются просто так. В нашем флаге
красный цвет означает отвагу, мужество и героизм; белый и синий цвета были
цветами русской православной церкви. Синий цвет – это небо, благородство,
белый – совершенство, чистота.

— Знаете
ли вы как выглядит герб Российской Федерации?

—
Посмотрите на слайд, это герб нашей страны.

— Наш
герб представляет собой золотого двуглавого орла, размещенного на красном
щите; над орлом три короны (две малые и одна большая), в лапах орла скипетр и
держава, а на груди на красном щите всадник, поражающий копьем дракона.
Двуглавый орел в нашем гербе является символом единства народов России,
живущих как в европейской, так и в азиатской ее частях. Поэтому одна голова
орла смотрит на запад, а другая на восток. Короны над головами орла
рассматриваются как символы союза республик, краев, областей, из которых
состоит Российская Федерация. Скипетр и держава означают сильную
государственную власть, защиту страны и ее единство. Всадник на щите – не
только символ столицы России — Москвы, но и олицетворение победы добра над
злом.

Изображение
всадника, пронзающего копьем змея, мы называем святым Георгием Победоносцем.

— Еще
одним символом нашей родины является гимн.

— Гимн –
это торжественная песня, исполняемая в особых торжественных случаях. Каждое
государство имеет свой гимн. Гимн – это песня, посвященная своей Родине, это
символ государства, такой же, как герб и флаг. Гимн прославляет могущество и
единство нашей огромной страны.

— На 5
странице в учебнике представлен текст.

— Кто
готов прочитать?

— Какой
город является столицей России?

— На 6
странице в учебнике рассмотрите иллюстрации, прочитайте текст.

-Над
каким пунктом мы сейчас работали?

— Какой
следующий?

— 1
задание выполните в парах – вам необходимо найти на рисунке герб Российской
Федерации и закрасить кружок рядом с ним.

— 1 пара
выйдите и положите карточку со своим вариантом ответа под документ камера.

—
Поднимите руку, у кого отмечено так же.

—
Отлично.

— 2
задание выполните в группах – вам необходимо перечислить символы России,
выбрав нужные варианты, используя слова для справок.

—
Проведем взаимопроверку, посмотрите на слайд.

—
Поставьте «5» — если, верно, перечислено 3 символа России.

—
Поставьте «4» — если, верно, перечислено 2 символа России.

—
Поставьте «3» — если, верно, перечислен 1 символ России.

12 июня.

Белом.

Синий.

Красным.

Белый.
Синий. Красный.

Отвечают
на вопрос.

Читают
гимн РФ.

Москва.

Выяснили
информацию о родной стране.

Выполнить
задания по теме.

Проводят
взаимопроверку.

Закрепление
полученных знаний

-Над
каким пунктом мы сейчас работали?

— Какой
следующий?

— На
карточках вам необходимо выбрать правильный вариант ответа.

1.
Столица Российской Федерации

1. Санкт-Петербург.

2.
Москва.

3. Воронеж.

2.
Сколько народов живет в России?

1. Более
120 народов.

2.
Более
150 народов.

3. Более
180 народов.

3. Цвета
российского флага (сверху вниз).

1. Белый,
синий, красный.

2.
Белый,
красный, синий.

3. Синий,
белый, красный.

4.
Определи народы России.

1. Северяне,
южане, горцы, сибиряки.

2.
Испанцы,
венгры, греки.

3. Русские,
татары, чуваши, мордва.

—
Посмотрите на слайд, проведите самопроверку, используя критерии оценивания.

— Над
каким пунктом плана мы сейчас работали?

Выполнили
задания по теме.

Выполнить
самостоятельную работу.

Проводят
самопроверку.

Выполняли
самостоятельную работу.

Подведение
итогов

— Какова
была тема урока?

-Какую
цель мы ставили в начале урока?

— Как
достигли цель?

— Какой
план работы мы с вами перед собой ставили?

— Мы его
выполнили?

— С
какой пословицей познакомились в начале урока?

— Вы
согласны с ней?

Родная
страна.

Расширить
представления о родной стране.

Выполняли
задания.

Отвечают
на вопрос.

Да.

Мир
освещается солнцем, а человек знанием.

Да.

Рефлексия

—
Посмотрите на слайд. Вам необходимо продолжить фразы.

Сегодня
я узнал (а) …

Я
научился …

Мне было
трудно …

Продолжают
фразы.

Технологическая
карта урока

ФИО	Шляпина Софья Витальевна
Класс, УМК	1, «Школа России»
Тема урока	«Как зимой помочь птицам»
Цель урока	Создание условий для ознакомления учащихся с зимующими птицами, раскрыть необходимость оказания помощи зимующим птицам.
Задачи	1. Познакомить со значениями природных условий для жизни птиц; 2. Способствовать развитию памяти, мышления, речи; 3. Воспитывать любовь к природе, доброе и бережное отношение к птицам.
Оборудование	Технологическая карта, проектор, компьютер, презентация, учебник, раздаточный материал.
Планируемые результаты:
Личностные	— проявлять положительное отношение к учебной деятельности; — устанавливать связь между целью деятельности и ее результатом.
Метапредметные
Коммуникативные УУД	— участвовать в диалоге по теме; — приводить свои примеры из жизненных ситуаций; — составлять свой небольшой рассказ о помощи птицам зимой.
Регулятивные УУД	— умение формулировать учебную цель урока; — принимать и сохранять учебную задачу; — планировать свои действия; — адекватно оценивать результат своих действий.
Познавательные УУД	— перерабатывать полученную информацию из учебных пособий, жизненного опыта и новых знаний на уроке; — наблюдать и делать выводы; — знать и распознавать на наглядных образцах названия птиц; — работать со справочной литературой и находить нужные сведения о зимующих птицах.
Предметные	— умение различать по внешним признакам птиц, зимующих в наших краях; — умение правильно подбирать корм для птиц; — знать правила подкормки птиц.

Ход
урока

Этап	Деятельность учителя	Деятельность учащихся
Организационный момент	— Здравствуйте, ребята! — Напоминаю вам, что отвечаем полным ответом и поднимаем руку. — Начнем наш урок с пословицы. — Какие буквы пропущены в пословице? -Почему именно они? — Кто готов прочитать? — Как вы ее понимаете? — Верно, человек в лесу может научиться тому, чего не знал раньше, лес учит выживать среди огромных деревьев, учит как найти лесные ягоды, грибы.	Приветствуют учителя. Е и И. Проверочное слово лЕс и научИться. «Лес — не школа, а всех учит». Отвечают на вопрос.
Актуализация знаний	— Какое время года сейчас? — Какие зимние месяцы вы знаете? — Какой сейчас месяц? — Молодцы, все верно.	Отвечают на вопросы.
Целеполагание	— А вы согласны, что зима – это прекрасное время года? Почему? (Зимой мы можем кататься на лыжах, играть в снежки, лепить различные снежные фигуры). — Посмотрите на слайд, чьи следы вы видите на снегу? — Какую пользу приносят птицы? (Уничтожают вредных насекомых) — Что необходимо для жизни птицам? — В какое время года птицам особенно тяжело? — Почему зимой? — Все ли птицы зимуют рядом с нами? — Как называют птиц, которые не улетают на зиму в теплые края? — Тема нашего урока: «Как зимой помочь птицам?». — Какую цель поставим перед собой? — Верно, мы узнаем, как помочь зимующим птицам. — Кто готов расположить план работы в нужном порядке? — Начнем работать по 1 пункту плана.	Высказывают свои предположения. Следы птиц. Отвечают на вопрос. Пища, вода, воздух, свет, тепло. Зимой. Не хватает пищи, вода замерзает, ягоды под снегом). Нет, не все. Зимующие. Узнать, как помочь птицам зимой. 1. Выяснить, как зимой помочь птицам. 2. Выполнить задания по теме. 3. Выполнить самостоятельную работу.
Основной этап	— Ребята, вспомните, какие птицы зимуют в наших краях? — Давайте рассмотрим зимующих птиц в учебнике. — По каким признакам этих птиц можно узнать? — Давайте каждой птице дадим отличительные признаки. (У снегиря красная грудка итд). — Предлагаю вам отгадать загадку. Что за стол среди берез Под открытым небом? Угощает он в мороз Птиц зерном и хлебом. — Верно, это кормушка. — А из чего можно сделать кормушку? — Давайте рассмотрим кормушки в учебнике. — Какая кормушка вам понравилась больше всего? А какая не понравилась? Чем? При изготовлении кормушки следует помнить несколько нехитрых правил: Кормушка должна быть с крышкой и, желательно стенками, чтобы ветер и снег не проникал в кормушку. Повесить кормушку можно во дворе или в школьном саду. И, конечно, нельзя прибивать ее гвоздями к живому дереву. Можно привязать веревкой к ветке. — Давайте прочтем, чем же кормить птиц. — Кто готов прочитать? — Над каким пунктом мы сейчас работали? — Какой следующий? — 1 задание выполните в паре. Вам необходимо обвести зеленым карандашом то, чем можно подкармливать птиц, а красным карандашом то, чем нельзя. 2 задание в паре – вам необходимо соединить линиями изображение птицы и названия. — Что обвели зеленым карандашом? Что обвели красным карандашом? (Документ камера) — 2 задание выполните в группах. — Вам необходимо собрать разрезанную картинку птицы. Узнать птицу, вспомнить чем она питается зимой, кратко описать ее, чтобы другая группа догадалась о какой птице идет речь. — На выполнение вам дается 2 минуты. — 1 группа, опишите птицу, 2 группа внимательно слушает. — Теперь 2 группа, расскажите нам о птице, которая у вас. — Отлично, молодцы!	Воробей, ворона, сорока, синица, снегирь. Разнообразные окраски и оттенки. Отвечают на вопрос. Кормушка. Отвечают на вопрос. Отвечают на вопросы. Читают информацию из учебника. Узнали, как помочь зимующим птицам. Выполнить задания по теме. Выполняют задания. Зеленым карандашом — белый хлеб, сало, семечки, семечки тыквы. Красным карандашом – мандарины, черный хлеб, конфеты. Описывают птиц.
Закрепление полученных знаний	— Над каким пунктом мы сейчас работали? — Какой следующий? — Данное задание выполните самостоятельно. — Вам необходимо обвести в круг верный вариант ответа на вопрос. Обращаю ваше внимание на то, что в одном из вопросов несколько вариантов ответа. — На выполнение вам дается 2 минуты. — Посмотрите на слайд, проведите самопроверку. — У кого все выполнено верно – отлично. У кого допущены 1-2 ошибки – хорошо. У кого 3 и более ошибок – нужно постараться и еще раз изучить тему. — Над каким пунктом мы сейчас работали?	Выполняли задания по теме. Выполнить самостоятельную работу. Проводят самопроверку. Выполняли самостоятельную работу.
Подведение итогов	— Какова была тема урока? — Какую цель мы ставили в начале урока? — Мы ее достигли? — Какой план работы мы с вами перед собой ставили? — Мы его выполнили? — С какой пословицей познакомились в начале урока? — Вы согласны с ней?	Как зимой помочь птицам. Узнать, как помочь зимующим птицам. Да. Отвечают на вопрос. Да. Лес не школа, а всех учит. Да.
Рефлексия	— На слайде фразы, вам необходимо их продолжить. Мне понравилось … Я узнал … Мне было интересно … Мне было трудно …	Продолжают фразы.

Источник

Математика, 3 класс

Урок №4. Обозначение геометрических фигур буквами

Перечень вопросов, рассматриваемых в теме:

— Как обозначают геометрические фигуры?

— Как правильно прочитать обозначение угла?

Глоссарий по теме:

Для обозначения геометрических фигур пользуются буквами латинского алфавита. Используют для обозначения заглавные буквы. Отрезок обозначают буквами две точки. Чтобы назвать многоугольник, обозначают буквами его вершины. Угол обозначают тремя буквами.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 10.

2. М. И. Моро, С. И. Волкова. Для тех, кто любит математику 3 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение,2018. – с. 12.

Теоретический материал для самостоятельного изучения.

На этой весёлой картинке видим разные геометрические фигуры, которые ты хорошо знаешь. Назовём их:

Треугольник, круг, квадрат, овал, ромб, пятиугольник, шестиугольник, трапеция, прямоугольник.

На этом рисунке видим несколько прямоугольников. Они все одинаковые.

Попробуем назвать каждый. Не удается, прямоугольники все одинаковые и по цвету, и по размеру. Как быть?

А на этом рисунке много точек. Точка тоже геометрическая фигура. Как назвать каждую из них.

Раз, два, три, четыре, пять!

Вышли точки погулять.

Много их, посмотри: раз, два, три.

Как их нам различать?

Каждой имя надо дать.

Как у человека есть имя, так и у каждой фигуры должно быть своё имя.

Математики всего мира договорились обозначать геометрические фигуры заглавными буквами латинского алфавита. Точки на чертеже обозначают заглавными латинскими буквами: A, B, C, D, E, F и другими.

Чтобы назвать отрезок, обозначают буквами две точки – его концы. Например, отрезок AB, отрезок CD. В многоугольнике обозначают буквами его вершины и называют, например, так: квадрат ABCD, треугольник ABC

Угол обозначают тремя буквами. В середине названия всегда указывают букву, которой обозначена вершина угла.

Например, в треугольнике АВС угол с вершиной А – это угол ВАС или угол САВ

А С

Тренировочные задания.

1. Подчеркните правильное обозначение угла.

ВАС; АВС; САВ; СВА;

Правильный ответ:

ВАС; АВС; САВ; СВА;

2. Выберите фигуры, которые обозначены верно.

Правильный ответ:

Источник