Содержание
- Правописание «килограмм» и «килограммов»: когда как пишется, примеры употребления, грамматика
- Когда что писать?
- Особенности счётного падежа
- Грамматика
- Значение
- Килограмм или килограммов?
- Правописание слова
- Примеры предложений
- Ошибочное написание
- Заключение
- Как пишется «килограмм» или «килограммов»?
- Поиск ответа
- Как правильно писать «килограмм» или «килограммов»
- Примеры предложений
Правописание «килограмм» и «килограммов»: когда как пишется, примеры употребления, грамматика
Слово «килограмм» имеет две формы множественного числа и седьмой (счётный) падеж, по написанию совпадающий с множественным числом родительного (см. ниже).
Когда что писать?
Для обозначения суммарного весового количества чего-либо слова «килограмм» или «килограммов» правильно употребляются в зависимости как от того, что исчисляется килограммах – нечто вещественное или же некая умозрительная численная величина – а также от контекста (общего смысла) высказывания:
Особенности счётного падежа
Применительно к исчислимым предметам «килограмм» употребляется не во множественном числе родительного, а в счётном падеже. Этот падеж не имеет числа, единственного или множественного, и, соответственно, синтаксическое согласование слов, к которым относится «килограмм» в счётном падеже, производится не по нему, а по контексту высказывания. Попросту говоря, если в килограмме более одной штуки чего-то, то и писать его нужно во множественном числе, независимо от того, как написано «килограмм», или «килограммов»:
Грамматика
Слово «килограмм» – неодушевлённое имя существительное мужского рода 2-го склонения. Состоит из префиксоида «кило-» и корня «-грамм». Постановка ударения и разделение переносами ки-ло-гра́мм. Падежные формы:
Примечание: префиксоиды это приставки, имеющие некоторые свойства существительных или прилагательных; в частности – собственное значение. «Кило-», как известно, означает 1000 (тысячу), «мега-» – миллион, «полу-» – половину, «дву-» – двойное количество («Дву-пять шапок серебра» в «Коньке-горбунке» П. П. Ершова).
Значение
Слово «килограмм» в живой русской речи употребляется только в точном (прямом) значении:
Примечание: в непрофессиональных технических писаниях «килограмм» нередко употребляется взамен термина «килограмм-сила» (кгс). Это значение дважды устаревшее, так как понятием «грамм-сила» оперировала система мер весов СГС, а в СИ сила изначально измеряется в ньютонах (Н). 1 кгс в первом приближении равна 9,81 Н.
Автор: Садов Артур Александрович, лингвист-типолог
Источник
Килограмм или килограммов?
Это слово спутник нашей повседневной жизни, без него не обходится ни один день. Чаще всего мы слышим это слово в магазине, на рынке, в спортзале. Что же за таинственное слово, которое можно услышать в продуктовом магазине и делая жим штанги? Это слово «килограмм»! Слово, которое объединяет вес картофеля на суп и гантели, которую усердно сжимает в руке спортсмен.
Загадка кроется в том, что многие не знают, как правильно пишется килограмм или килограммов, то есть как пишется слово во множественном числе? На самом деле, какой из двух вариантов правильный? Существует гипотеза, что «усеченный» вариант используют в устной речи. В письменной же речи необходимо употреблять существительное с окончанием –ов.
Приступаем к своему маленькому расследованию.
Правописание слова
Во-первых, необходимо определить часть речи и правило, которому необходимо следовать при написании. Килограмм – существительное второго склонения, мужского рода.
Во-вторых, следует подобрать и поставить вопрос к существительному с целью определения падежа. (Чего? – килограммов. Родительный падеж). Согласно правописанию, существительные мужского рода второго склонения, во множественном числе в родительном падеже пишутся с окончанием –ов.
Но мы ведь помним, что речь идет о русском языке и здесь наверняка есть исключение из правил. Существительное килограмм в родительном падеже во множественном числе имеет два варианта написания: с окончанием –ов и без него. И тот, и другой вариант написания является правильным.
А как же гипотеза, относительно использования слова в устной и письменной речи? Такое предположение существует и по сегодняшний день. Но это так и осталось гипотезой, а не правилом.
Писать килограмм либо килограммов зависит лишь от того, существительное с каким окончанием следует за словом «килограмм». Если после существительного «килограмм» употребляется существительное с окончанием –ов, то в самом слове «килограмм» окончание отсутствует.
И наоборот, если существительное-спутник употребляется без окончания, то окончание родительного падежа множественного числа «переходит» к слову «килограмм». Например, 5 килограммов моркови. Но, 20 килограмм арбузов.
Примеры предложений
Ошибочное написание
Кроме путаницы с окончанием, в слове «килограмм» часто пишут удвоенную –л:
Что является грубой ошибкой. Чтобы избежать ошибок часто используют сокращение — кг. К тому же единицы измерения, обычно употребляются именно в сокращенном варианте.
Заключение
В заключении нужно еще раз вспомнить, что правописание слова «килограмм» зависит от существительного, которое следует за ним.
А для того чтобы запомнить, как правильно писать и говорить килограмм или килограммов нужно часто посещать спортзал, вести учет, сколько килограммов весит ваш инвентарь. А после готовить ароматную еду. И опять же не забывать про подсчет. Чтобы знать, сколько килограммов гречки или риса было съедено в течение месяца, и быть начеку.
Источник
Как пишется «килограмм» или «килограммов»?
восемь килограмм огурцов
пять килограммов винограда
Использование сокращений для обозначения массы привело к тому, что после окончания школы мало кто из взрослых сможет быстро ответить как правильно писать и говорить: «килограмм» или «килограммов». Прежде, чем ответить многие задумаются как правильно употребить слово. Давайте разберем правило русского языка, которое подскажет какая форма подходит для устной и письменной речи.
Какое правило применять?
Чтобы верно определить какая норма языка отвечает за «килограммы» узнаем часть речи. Килограмм (один) –имя существительное в:
• именительном падеже (что?);
• второго склонения;
• единственного числа;
• употребляется в мужском роде.
В родительном падеже слово отвечает на вопрос чего? – килограммов. При таком контексте слово переходит во множественное число, например, десять килограммов.
Для таких случаев предусмотрено следующее правило: существительные второго склонения в родительном падеже множественного числа пишутся с окончанием – ов. Например, шесть (чего?) шкафов.
Килограмм в бытовой речи употребляется в значении меры массы для одушевленных и неодушевленных предметов, вещей. Эталонная единица в системе измерения, равная 1 тысяче граммов.
Ольга купила на рынке для закаток на зиму десять килограммов овощей.
Нормальный вес годовалого ребенка в год — девять килограммов.
Сколько килограмм арбузов вмещается в грузовой автомобиль?
За полгода ей удалось сбросить тридцать килограммов лишнего веса.
Теперь с написанием «килограмм» или «килограммов» не должно возникать сложностей. Разрешено употребление слова с окончанием — ов и без него.
Источник
Поиск ответа
Здравствуйте, подскажите,Вчера пришла за пол килограмма ми колбасы,пол килограмма ми пишется слитно же? У нас тут спор
Ответ справочной службы русского языка
Верно: пришла за полукилограммом колбасы. В разговорной речи допустимо: . за полкилограммом колбасы.
Ответ справочной службы русского языка
Обратите внимание, что слова ноль целых обычно опускаются.
Подскажите как правильно написать «четыре килограмма масла» или «четыре килограммов масла»?
Ответ справочной службы русского языка
Здравствуйте, справочное бюро. Подскажите пожалуйста, как все таки корректно: добавить к полтора килограмма м яблок или добавить к полутора килограмма м яблок.
Ответ справочной службы русского языка
Здравствуйте, наш преподаватель дала нам задание сравнить современные нормы употребления формы р.п. мн. ч. слов «грамм», «килограмм» и нормы употребления в 2000-х годах, и отправила нас на ваш портал, чтобы разобраться. Я нашел как правильно на сегодняшний день употреблять эти слова, а вот как было в 2000-х хотел бы спросить у вас.
Ответ справочной службы русского языка
Спасибо за интересный вопрос! Но любопытно проследить историю форм грамм – граммов, килограмм – килограммов начиная не с 2000-х годов, а хотя бы за последние полвека. До сих пор распространено мнение, что формы грамм, килограмм в родительном падеже мн. числа ошибочны. Между тем на их допустимость словари указывали еще в 1950-е.
В словаре-справочнике «Русское литературное произношение и ударение» под ред. Р. И. Аванесова и С. И. Ожегова (М., 1959) проводится такое разделение: граммов – преимущественно в письменной речи, грамм – преимущественно в устной речи после числительных. То же с килограмма ми: килограммов – в письменной речи, килограмм – в устной (здесь про числительные не говорится).
Такое разделение дожило до начала 2000-х, хотя за эти полвека словари то указывали вариант грамм, килограмм в качестве допустимого, то не указывали. Например, в 10-м издании «Орфографического словаря русского языка» (М., 1970) – только граммов и килограммов, а вышедшее два года спустя 9-е издание «Словаря русского языка» С. И. Ожегова (под ред. Н. Ю. Шведовой) повторяет рекомендацию 1959 года: граммов – преимущественно в письменной речи, грамм – преимущественно в устной речи после числительных; килограммов – в письменной речи, килограмм – в устной. Академическая «Русская грамматика» (М., 1980) также указывала, что в устной речи формы граммов, килограммов неупотребительны.
В 21-м издании «Словаря русского языка» С. И. Ожегова (М., 1989) варианты грамм и граммов, килограмм и килограммов уже даны как равноправные. Казалось бы, формы грамм и килограмм окончательно стали нормативными. Однако 2-е издание словаря Л. К. Граудиной, В. А. Ицковича, Л. П. Катлинской «Грамматическая правильность русской речи» (М., 2001) констатирует, что разделение на устную и письменную речь в последнее десятилетие XX века и на рубеже веков еще отмечалось: «Бытовые единицы измерений веса грамм, килограмм в устной речи употребляются в подавляющем большинстве с нулевой флексией. В письменной же речи под воздействием редакционной корректуры в настоящее время употребляются исключительно формы граммов и килограммов».
Таким образом, сейчас верно: пять грамм и пять граммов, шесть килограмм и шесть килограммов, но (вне сочетания с числительным): подсчет количества граммов и килограммов (не грамм и килограмм).
какой вид связи в словосочетании пять килограммов и почему?
Ответ справочной службы русского языка
Два, три, это же тоже множественное число?
Ответ справочной службы русского языка
Здравствуйте, скажите как правильно написать предложение «Вес посылки составил 8.3 килограмма » или «Вес посылки составил 8.3 килограммов»?
Ответ справочной службы русского языка
Добрый день, спасибо за ваши ответы. Подскажите, пожалуйста, нужны ли еще знаки препинания в такой конструкции: «Проведенные исследования показали, что наибольшая окупаемость одного килограмма действующего вещества минеральных удобрений приростом урожая зерна нута 7,04 кг в орошаемых условиях была получена при проведении отвальной обработки почвы на глубину 28–30 см». Мне кажется, нужно как-то выделить «7,04 кг», потому что у слова «окупаемость» уже есть определение «наибольшая». С уважением, Анна.
Ответ справочной службы русского языка
Можно заключить этот фрагмент в скобки.
Прошу помочь вас расставить знаки препинания в следующем предложении:
Папа пингвин весит больше чем мама с детёнышем на 2 килограмма
Ответ справочной службы русского языка
как правильно 0,6 милиграмма/ов, 4, 25 грамма/ов, 23, 456 килограмма /ов, 22, 98 центнера/ов? Спасибо!
Ответ справочной службы русского языка
Уважаемая «Грамота», в каких случаях используется слово «конский», а в каких «лошадиный», есть ли разница? Спасибо за ответ
Ответ справочной службы русского языка
◊ Лошад и ная сила.
Внесистемная единица измерения мощности, равная 75 килограмма м на 1 метр в секунду.
Здравствуйте, уважаемые сотрудники «Грамоты»!
Подскажите, пожалуйста, как склоняется словосочетание «чуть более килограмма «, а именно: «Один литр виноградного сока по калорийности равен почти двум литрам молока или чуть больше килограмм(?) картофеля».
Спасибо.
Ответ справочной службы русского языка
Фразу нужно перестроить для корректного грамматического согласования. Используйте иной оборот речи.
Ответ справочной службы русского языка
Как проверить правописание фразы:»Вес равен одной тысяче тремстам двадцати семи килограмма м»
Ответ справочной службы русского языка
Что именно нуждается в проверке?
Источник
Часто школьники и даже взрослые задаются вопросом, как правильно пишется: килограмм или килограммов? Давайте разберемся в правописании этого слова и заглянем в словари.
Как правильно писать «килограмм» или «килограммов»
Килограмм — слово мужского рода, II склонения, следовательно, во множественном числе должно иметь окончание «-ов».
В словарях же описывается возможность использования обоих вариантов написания этого слова. С существительными «грамм» и «граммов» происходит такая же путаница.
Лингвисты долгое время утверждали, что слово «грамм» и «килограмм» используется в словесной речи, а их форма в родительном падеже используется в письменных вариантах.
В различных изданиях говорится о написании по-разному. Например, в большинстве источников советуют писать это трудное слово с пустым окончанием в том случае, если фраза содержит существительное в родительном падеже; в остальных ситуациях прибавляют окончание «-ов».
Сейчас нормой считается использование формы с окончанием «-ов» без использования числительных, а в комплексе с ними могут использоваться обе формы.
Примеры предложений
Несколько примеров для подтверждения сказанного:
Мама купила несколько килограммов апельсинов к празднику.
Сколько килограммов яблок нужно для варенья?
Три килограмма помидоров лежало в холодильнике.
Источник
Содержание
- 1 Как правильно 900 грамм или граммов?
- 2 Как правильно 100 килограмм или 100 килограммов?
- 3 Как правильно говорить сколько граммов?
- 4 Как правильно писать грамм?
- 5 Как правильно склонять слово грамм?
- 6 Как правильно писать помидор или помидоров?
- 7 Как правильно пару килограмм или килограммов?
- 8 Как правильно говорить килограмм яблок или килограммов яблок?
- 9 Как пишется килограмм в цифрах?
- 10 Как правильно говорить носок или носков?
- 11 Как правильно Разожгет или разожжет?
- 12 Как правильно пишется слово шоссе?
- 13 Как правильно сокращать грамм?
- 14 Как правильно писать сокращенно грамм?
Как правильно 900 грамм или граммов?
У слова же «грамм» возможны обе формы — и 5 грамм, и 5 граммов (соответственно 5 килограмм и килограммов). Если же такие слова употребляются вне «измерительного» контекста (иначе говоря, при них нет количественного числительного), то используется окончание -ов: жить без лишних килограммов, не хватает гигабайтов.
Справочно-информационный портал «Русский язык» отмечает, что в данном случае действуют следующие нормы: вне счетной формы — только граммов, килограммов (например: несколько граммов); в счетной форме, то есть в сочетании с числительным корректны оба варианта: грамм, килограмм и граммов, килограммов (100 грамм и 100 …
Как правильно говорить сколько граммов?
«Грамм» — существительное в именительном падеже и в единственном числе. «Граммов» — в родительном падеже и во множественном числе.
Как правильно писать грамм?
Грамм (фр. gramme; русское обозначение: г; международное: g) — единица измерения массы, одна из основных единиц системы СГС, дольная единица массы в Международной системе единиц (СИ). Впервые была введена во Франции 7 апреля 1795 года.
Как правильно склонять слово грамм?
Просклонять слово грамм по падежамПадежЕдинственное числоМножественное числоРодительныйграммаграммовДательныйграммуграммамВинительныйграммграммыТворительныйграммомграммамиЕщё 2 строки
Как правильно писать помидор или помидоров?
Для большей части существительных мужского рода, в начальной форме оканчивающихся на твердый согласный (апельсин, помидор, мухомор, компьютер, носок), характерно окончание -ов в форме родительного падежа множественного числа: апельсинов, помидоров, мухоморов, компьютеров, носков и т. д.
Как правильно пару килограмм или килограммов?
Килограмм, килограммов — в русском языке это существительное имеет равноправные варианты образования родительного падежа как с нулевым окончанием, так и с окончанием на «-ов». Если в предложении другое существительное употребляется с окончанием на «-ов», тогда пишем нулевое окончание. Пять килограмм помидоров.
Как правильно говорить килограмм яблок или килограммов яблок?
В сочетании с количественными числительными возможны варианты: пять килограмм, килограммов, пять грамм, граммов. Но без числительных верно: не хватает граммов, без лишних килограммов. Как правильно сказать – пять килограммов яблок, сто граммов водки или пять килограмм яблок, сто грамм водки? Оба варианта верные.
Как пишется килограмм в цифрах?
Килогра́мм (русское обозначение: кг; международное: kg) — единица измерения массы, одна из семи основных единиц Международной системы единиц (СИ).
Как правильно говорить носок или носков?
Слово носок в форме множественного числа, родительного падежа получает окончание -ов. А слово чулок не получает ничего, но если быть точнее — нулевое окончание. Получается, чулки — чулок.
Как правильно Разожгет или разожжет?
Как правильно пишется
Рассматриваемый глагол согласно правилам нужно писать с двумя «ж» – разожжёт.
Как правильно пишется слово шоссе?
Правильное написание слова «шоссе» необходимо запомнить, так как оно является словарным и к нему невозможно подобрать однокоренное проверочное слово. Слово «шоссе» обязательно к запоминанию в 3 классе(ах). УДАРЕНИЕ. Ударение в слове «шоссе» падает на последний (второй) слог.
Как правильно сокращать грамм?
Общепринятое графическое сокращение слова грамм – г (см.
Как правильно писать сокращенно грамм?
Рекомендуемые к использованию сокращенияСокращениеЗначениеБ или обайт (октет)гграммдо н. э.до нашей эрыСм. такжеСмотри(те) такжеЕщё 3 строки
«kg» redirects here. For other uses, see KG.
| Kilogram | |
|---|---|

A Kibble balance is used to measure a kilogram with electricity and magnetism |
|
| General information | |
| Unit system | SI |
| Unit of | mass |
| Symbol | kg |
| Conversions | |
| 1 kg in … | … is equal to … |
| Avoirdupois | ≈ 2.204623 pounds[Note 1] |
| British Gravitational | ≈ 0.0685 slugs |
The kilogram (also kilogramme[1]) is the unit of mass in the International System of Units (SI), having the unit symbol kg. It is a widely used measure in science, engineering and commerce worldwide, and is often simply called a kilo colloquially. It means ‘one thousand grams’.
The kilogram is defined in terms of the second and the metre, both of which are based on fundamental physical constants. This allows a properly equipped metrology laboratory to calibrate a mass measurement instrument such as a Kibble balance as the primary standard to determine an exact kilogram mass.[2][3]
The kilogram was originally defined in 1795 as the mass of one litre of water. The current definition of a kilogram agrees with this original definition to within 30 parts per million. In 1799, the platinum Kilogramme des Archives replaced it as the standard of mass. In 1889, a cylinder of platinum-iridium, the International Prototype of the Kilogram (IPK), became the standard of the unit of mass for the metric system and remained so for 130 years, before the current standard was adopted in 2019.[4]
Definition[edit]
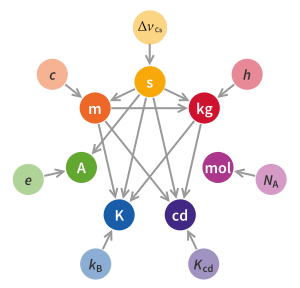
The kilogram is defined in terms of three fundamental physical constants:
- a specific atomic transition frequency ΔνCs, which defines the duration of the second,
- the speed of light c, which when combined with the second, defines the length of the metre,
- and the Planck constant h. which when combined with the metre and second, defines the mass of the kilogram.
The formal definition according to the General Conference on Weights and Measures (CGPM) is:
The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of c and ΔνCs.
— CGPM [5][6]
Defined in term of those units, the kg is formulated as:[7]
- kg = (299792458)2/(6.62607015×10−34)(9192631770)hΔνCs/c2 = 917097121160018/621541050725904751042hΔνCs/c2 ≈ (1.475521399735270×1040)hΔνCs/c2 .
This definition is generally consistent with previous definitions: the mass remains within 30 ppm of the mass of one litre of water.[8]
Timeline of previous definitions[edit]
- 1793: The grave (the precursor of the kilogram) was defined as the mass of 1 litre (dm3) of water, which was determined to be 18841 grains.[9]
- 1795: the gram (1/1000 of a kilogram) was provisionally defined as the mass of one cubic centimetre of water at the melting point of ice.[10]
- 1799: The Kilogramme des Archives was manufactured as a prototype. It had a mass equal to the mass of 1 dm3 of water at the temperature of its maximum density, which is approximately 4 °C.
- 1875–1889: The Metre Convention was signed in 1875, leading to the production of the International Prototype of the Kilogram (IPK) in 1879 and its adoption in 1889.
- 2019: The kilogram was defined in terms of the Planck constant, the speed of light and hyperfine transition frequency of 133Cs as approved by the General Conference on Weights and Measures (CGPM) on November 16, 2018.
Name and terminology[edit]
The kilogram is the only base SI unit with an SI prefix (kilo) as part of its name. The word kilogramme or kilogram is derived from the French kilogramme,[11] which itself was a learned coinage, prefixing the Greek stem of χίλιοι khilioi «a thousand» to gramma, a Late Latin term for «a small weight», itself from Greek γράμμα.[12]
The word kilogramme was written into French law in 1795, in the Decree of 18 Germinal,[13]
which revised the provisional system of units introduced by the French National Convention two years earlier, where the gravet had been defined as weight (poids) of a cubic centimetre of water, equal to 1/1000 of a grave.[14] In the decree of 1795, the term gramme thus replaced gravet, and kilogramme replaced grave.
The French spelling was adopted in Great Britain when the word was used for the first time in English in 1795,[15][11] with the spelling kilogram being adopted in the United States. In the United Kingdom both spellings are used, with «kilogram» having become by far the more common.[1] UK law regulating the units to be used when trading by weight or measure does not prevent the use of either spelling.[16]
In the 19th century the French word kilo, a shortening of kilogramme, was imported into the English language where it has been used to mean both kilogram[17] and kilometre.[18] While kilo as an alternative is acceptable, to The Economist for example,[19] the Canadian government’s Termium Plus system states that «SI (International System of Units) usage, followed in scientific and technical writing» does not allow its usage and it is described as «a common informal name» on Russ Rowlett’s Dictionary of Units of Measurement.[20][21] When the United States Congress gave the metric system legal status in 1866, it permitted the use of the word kilo as an alternative to the word kilogram,[22] but in 1990 revoked the status of the word kilo.[23]
The SI system was introduced in 1960 and in 1970 the BIPM started publishing the SI Brochure, which contains all relevant decisions and recommendations by the CGPM concerning units. The SI Brochure states that «It is not permissible to use abbreviations for unit symbols or unit names …».[24][Note 2]
Kilogram becoming a base unit: the role of units for electromagnetism[edit]
It is primarily because of units for electromagnetism that the kilogram rather than the gram was eventually adopted as the base unit of mass in the SI. The relevant series of discussions and decisions started roughly in the 1850s and effectively concluded in 1946. By the end of the 19th century, the ‘practical units’ for electric and magnetic quantities such as the ampere and the volt were well established in practical use (e.g. for telegraphy). Unfortunately, they were not coherent with the then-prevailing base units for length and mass, the centimetre, and the gram. However, the ‘practical units’ also included some purely mechanical units. In particular, the product of the ampere and the volt gives a purely mechanical unit of power, the watt. It was noticed that the purely mechanical practical units such as the watt would be coherent in a system in which the base unit of length was the metre and the base unit of mass was the kilogram. Because no one wanted to replace the second as the base unit of time, the metre and the kilogram are the only pair of base units of length and mass such that (1) the watt is a coherent unit of power, (2) the base units of length and time are integer-power-of-ten ratios to the metre and the gram (so that the system remains ‘metric’), and (3) the sizes of the base units of length and mass are convenient for practical use.[Note 3] This would still leave out the purely electrical and magnetic units: while the purely mechanical practical units such as the watt are coherent in the metre-kilogram-second system, the explicitly electrical and magnetic units such as the volt, the ampere, etc. are not.[Note 5] The only way to also make those units coherent with the metre-kilogram-second system is to modify that system in a different way: the number of fundamental dimensions must be increased from three (length, mass, and time) to four (the previous three, plus one purely electrical one).[Note 6]
The state of units for electromagnetism at the end of the 19th century[edit]
During the second half of the 19th century, the centimetre–gram–second system of units was becoming widely accepted for scientific work, treating the gram as the fundamental unit of mass and the kilogram as a decimal multiple of the base unit formed by using a metric prefix. However, as the century drew to a close, there was widespread dissatisfaction with the units for electricity and magnetism in the CGS system. There were two obvious choices for absolute units[Note 7] of electromagnetism: the ‘electrostatic’ (CGS-ESU) system and the ‘electromagnetic’ (CGS-EMU) system. But the sizes of coherent electric and magnetic units were not convenient in either of these systems; for example, the ESU unit of electrical resistance, which was later named the statohm, corresponds to about 9×1011 ohm, while the EMU unit, which was later named the abohm, corresponds to 10−9 ohm.[Note 8]
To circumvent this difficulty, a third set of units was introduced: the so-called practical units. The practical units were obtained as decimal multiples of coherent CGS-EMU units, chosen so that the resulting magnitudes were convenient for practical use and so that the practical units were, as far as possible, coherent with each other.[27] The practical units included such units as the volt, the ampere, the ohm, etc.,[28][29] which were later incorporated in the SI system and which are used to this day.[Note 9] The reason the metre and the kilogram were later chosen to be the base units of length and mass was that they are the only combination of reasonably sized decimal multiples or submultiples of the metre and the gram that can be made coherent with the volt, the ampere, etc.
The reason is that electrical quantities cannot be isolated from mechanical and thermal ones: they are connected by relations such as current × electric potential difference = power. For this reason, the practical system also included coherent units for certain mechanical quantities. For example, the previous equation implies that ampere × volt is a coherent derived practical unit of power;[Note 10] this unit was named the watt. The coherent unit of energy is then the watt times the second, which was named the joule. The joule and the watt also have convenient magnitudes and are decimal multiples of CGS coherent units for energy (the erg) and power (the erg per second). The watt is not coherent in the centimetre-gram-second system, but it is coherent in the metre-kilogram-second system—and in no other system whose base units of length and mass are reasonably sized decimal multiples or submultiples of the metre and the gram.
However, unlike the watt and the joule, the explicitly electrical and magnetic units (the volt, the ampere…) are not coherent even in the (absolute three-dimensional) metre-kilogram-second system. Indeed, one can work out what the base units of length and mass have to be in order for all the practical units to be coherent (the watt and the joule as well as the volt, the ampere, etc.). The values are 107 metres (one half of a meridian of the Earth, called a quadrant) and 10−11 grams (called an eleventh-gram[Note 11]).[Note 13]
Therefore, the full absolute system of units in which the practical electrical units are coherent is the quadrant–eleventh-gram–second (QES) system. However, the extremely inconvenient magnitudes of the base units for length and mass made it so that no one seriously considered adopting the QES system. Thus, people working on practical applications of electricity had to use units for electrical quantities and for energy and power that were not coherent with the units they were using for e.g. length, mass, and force.
Meanwhile, scientists developed yet another fully coherent absolute system, which came to be called the Gaussian system, in which the units for purely electrical quantities are taken from CGE-ESU, while the units for magnetic quantities are taken from the CGS-EMU. This system proved very convenient for scientific work and is still widely used. However, the sizes of its units remained either too large or too small—by many orders of magnitude—for practical applications.
Finally, in both CGS-ESU and CGS-EMU as well as in the Gaussian system, Maxwell’s equations are ‘unrationalized’, meaning that they contain various factors of 4π that many workers found awkward. So yet another system was developed to rectify that: the ‘rationalized’ Gaussian system, usually called the Heaviside–Lorentz system. This system is still used in some subfields of physics. However, the units in that system are related to Gaussian units by factors of √4π ≈ 3.5, which means that their magnitudes remained, like those of the Gaussian units, either far too large or far too small for practical applications.
The Giorgi proposal[edit]
In 1901, Giovanni Giorgi proposed a new system of units that would remedy this situation.[30] He noted that the mechanical practical units such as the joule and the watt are coherent not only in the QES system, but also in the metre-kilogram-second (MKS) system.[31][Note 14] It was of course known that adopting the metre and the kilogram as base units—obtaining the three dimensional MKS system—would not solve the problem: while the watt and the joule would be coherent, this would not be so for the volt, the ampere, the ohm, and the rest of the practical units for electric and magnetic quantities (the only three-dimensional absolute system in which all practical units are coherent is the QES system).
But Giorgi pointed out that the volt and the rest could be made coherent if the idea that all physical quantities must be expressible in terms of dimensions of length, mass, and time, is relinquished and a fourth base dimension is added for electric quantities. Any practical electrical unit could be chosen as the new fundamental unit, independent from the metre, kilogram, and second. Likely candidates for the fourth independent unit included the coulomb, the ampere, the volt, and the ohm, but eventually, the ampere proved to be the most convenient for metrology. Moreover, the freedom gained by making an electric unit independent from the mechanical units could be used to rationalize Maxwell’s equations.
The idea that one should give up on having a purely ‘absolute’ system (i.e. one where only length, mass, and time are the base dimensions) was a departure from a viewpoint that seemed to underlie the early breakthroughs by Gauss and Weber (especially their famous ‘absolute measurements’ of Earth’s magnetic field[32]: 54–56 ), and it took some time for the scientific community to accept it—not least because many scientists clung to the notion that the dimensions of a quantity in terms of length, mass, and time somehow specify its ‘fundamental physical nature’.[33]:24, 26[31]
Acceptance of the Giorgi system, leading to the MKSA system and the SI[edit]
By the 1920s, dimensional analysis had become much better understood[31] and it was becoming widely accepted that the choice of both the number and of the identities of the «fundamental» dimensions should be dictated by convenience only and that there is nothing really fundamental about the dimensions of a quantity.[33] In 1935, Giorgi’s proposal was adopted by the IEC as the Giorgi system. It is this system that has since then been called the MKS system,[34]
although ‘MKSA’ appears in careful usage. In 1946 the CIPM approved a proposal to adopt the ampere as the electromagnetic unit of the «MKSA system».[35]: 109, 110 In 1948 the CGPM commissioned the CIPM «to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention».[36] This led to the launch of SI in 1960.
To summarize, the ultimate reason that the kilogram was chosen over the gram as the base unit of mass was, in one word, the volt-ampere. Namely, the combination of the metre and the kilogram was the only choice of base units of length and mass such that 1. the volt-ampere—which is also called the watt and which is the unit of power in the practical system of electrical units—is coherent, 2. the base units of length and mass are decimal multiples or submultiples of the metre and the gram, and 3. the base units of length and mass have convenient sizes.
The CGS and MKS systems co-existed during much of the early-to-mid-20th century, but as a result of the decision to adopt the «Giorgi system» as the international system of units in 1960, the kilogram is now the SI base unit for mass, while the definition of the gram is derived.
Redefinition based on fundamental constants[edit]
A Kibble balance, which was originally used to measure the Planck constant in terms of the IPK, can now be used to calibrate secondary standard weights for practical use.
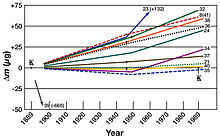
The replacement of the International Prototype of the Kilogram (IPK) as the primary standard was motivated by evidence accumulated over a long period of time that the mass of the IPK and its replicas had been changing; the IPK had diverged from its replicas by approximately 50 micrograms since their manufacture late in the 19th century. This led to several competing efforts to develop measurement technology precise enough to warrant replacing the kilogram artefact with a definition based directly on physical fundamental constants.[4] Physical standard masses such as the IPK and its replicas still serve as secondary standards.
The International Committee for Weights and Measures (CIPM) approved a redefinition of the SI base units in November 2018 that defines the kilogram by defining the Planck constant to be exactly 6.62607015×10−34 kg⋅m2⋅s−1, effectively defining the kilogram in terms of the second and the metre. The new definition took effect on May 20, 2019.[4][5][37]
Prior to the redefinition, the kilogram and several other SI units based on the kilogram were defined by a man-made metal artifact: the Kilogramme des Archives from 1799 to 1889, and the IPK from 1889 to 2019.[4]
In 1960, the metre, previously similarly having been defined with reference to a single platinum-iridium bar with two marks on it, was redefined in terms of an invariant physical constant (the wavelength of a particular emission of light emitted by krypton,[38] and later the speed of light) so that the standard can be independently reproduced in different laboratories by following a written specification.
At the 94th Meeting of the International Committee for Weights and Measures (CIPM) in 2005, it was recommended that the same be done with the kilogram.[39]
In October 2010, the CIPM voted to submit a resolution for consideration at the General Conference on Weights and Measures (CGPM), to «take note of an intention» that the kilogram be defined in terms of the Planck constant, h (which has dimensions of energy times time, thus mass × length2 / time) together with other physical constants.[40][41] This resolution was accepted by the 24th conference of the CGPM[42] in October 2011 and further discussed at the 25th conference in 2014.[43][44] Although the Committee recognised that significant progress had been made, they concluded that the data did not yet appear sufficiently robust to adopt the revised definition, and that work should continue to enable the adoption at the 26th meeting, scheduled for 2018.[43] Such a definition would theoretically permit any apparatus that was capable of delineating the kilogram in terms of the Planck constant to be used as long as it possessed sufficient precision, accuracy and stability. The Kibble balance is one way to do this.
As part of this project, a variety of very different technologies and approaches were considered and explored over many years. Some of these approaches were based on equipment and procedures that would enable the reproducible production of new, kilogram-mass prototypes on demand (albeit with extraordinary effort) using measurement techniques and material properties that are ultimately based on, or traceable to, physical constants. Others were based on devices that measured either the acceleration or weight of hand-tuned kilogram test masses and which expressed their magnitudes in electrical terms via special components that permit traceability to physical constants. All approaches depend on converting a weight measurement to a mass and therefore require the precise measurement of the strength of gravity in laboratories. All approaches would have precisely fixed one or more constants of nature at a defined value.
SI multiples[edit]
Because an SI unit may not have multiple prefixes (see SI prefix), prefixes are added to gram, rather than the base unit kilogram, which already has a prefix as part of its name.[45] For instance, one-millionth of a kilogram is 1 mg (one milligram), not 1 μkg (one microkilogram).
| Submultiples | Multiples | ||||
|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name |
| 10−1 g | dg | decigram | 101 g | dag | decagram |
| 10−2 g | cg | centigram | 102 g | hg | hectogram |
| 10−3 g | mg | milligram | 103 g | kg | kilogram |
| 10−6 g | µg | microgram | 106 g | Mg | megagram (tonne) |
| 10−9 g | ng | nanogram | 109 g | Gg | gigagram |
| 10−12 g | pg | picogram | 1012 g | Tg | teragram |
| 10−15 g | fg | femtogram | 1015 g | Pg | petagram |
| 10−18 g | ag | attogram | 1018 g | Eg | exagram |
| 10−21 g | zg | zeptogram | 1021 g | Zg | zettagram |
| 10−24 g | yg | yoctogram | 1024 g | Yg | yottagram |
| 10−27 g | rg | rontogram | 1027 g | Rg | ronnagram |
| 10−30 g | qg | quectogram | 1030 g | Qg | quettagram |
| Common prefixed units are in bold face.[Note 15] |
- The microgram is typically abbreviated «mcg» in pharmaceutical and nutritional supplement labelling, to avoid confusion, since the «μ» prefix is not always well recognised outside of technical disciplines.[Note 16] (The expression «mcg» is also the symbol for an obsolete CGS unit of measure known as the «millicentigram», which is equal to 10 μg.)
- In the United Kingdom, because serious medication errors have been made from the confusion between milligrams and micrograms when micrograms has been abbreviated, the recommendation given in the Scottish Palliative Care Guidelines is that doses of less than one milligram must be expressed in micrograms and that the word microgram must be written in full, and that it is never acceptable to use «mcg» or «μg».[46]
- The hectogram (100 g) (Italian: ettogrammo or etto) is a very commonly used unit in the retail food trade in Italy.[47][48][49]
- The former standard spelling and abbreviation «deka-» and «dk» produced abbreviations such as «dkm» (dekametre) and «dkg» (dekagram).[50] As of 2020, the abbreviation «dkg» (10 g) is still used in parts of central Europe in retail for some foods such as cheese and meat.[51][52][53][55]
- The unit name megagram is rarely used, and even then typically only in technical fields in contexts where especially rigorous consistency with the SI standard is desired. For most purposes, the name tonne is instead used. The tonne and its symbol, «t», were adopted by the CIPM in 1879. It is a non-SI unit accepted by the BIPM for use with the SI. According to the BIPM, «This unit is sometimes referred to as ‘metric ton’ in some English-speaking countries.»[56] The unit name megatonne or megaton (Mt) is often used in general-interest literature on greenhouse gas emissions and nuclear weapons yields, whereas the equivalent unit in scientific papers on the subject is often the teragram (Tg).
See also[edit]
- 1795 in science
- 1799 in science
- General Conference on Weights and Measures (CGPM)
- Gram
- Grave (original name of the kilogram, its history)
- Gravimetry
- Inertia
- International Bureau of Weights and Measures (BIPM)
- International Committee for Weights and Measures (CIPM)
- International System of Units (SI)
- Kibble balance
- Kilogram-force
- Litre
- Mass
- Mass versus weight
- Metric system
- Metric ton
- Milligram per cent
- National Institute of Standards and Technology (NIST)
- Newton
- SI base units
- Standard gravity
- Weight
Notes[edit]
- ^ The avoirdupois pound is part of both United States customary system of units and the Imperial system of units. It is defined as exactly 0.45359237 kilograms.
- ^ The French text (which is the authoritative text) states «Il n’est pas autorisé d’utiliser des abréviations pour les symboles et noms d’unités …«
- ^ If it is known that the metre and the kilogram satisfy all three conditions, then no other choice does: The coherent unit of power, when written out in terms of the base units of length, mass, and time, is (base unit of mass) × (base unit of length)2/(base unit of time)3. It is stated that the watt is coherent in the metre-kilogram-second system; thus, 1 watt = (1 kg) × (1 m)2/(1 s)3. The second is left as it is and it is noted that if the base unit of length is changed to L m and the base unit of mass to M kg, then the coherent unit of power is (M kg) × (L m)2/(1 s)3 = ML2 × (1 kg) × (1 m)2/(1 s)3 = ML2 watt. Since base units of length and mass are such that the coherent unit of power is the watt, it must be that ML2 = 1. It follows that if the base unit of length is changed by a factor of L, then the base unit of mass must change by a factor of 1/L2 if the watt is to remain a coherent unit. It would be impractical to make the base unit of length a decimal multiple of a metre (10 m, 100 m, or more). Therefore the only option is to make the base unit of length a decimal submultiple of the metre. This would mean decreasing the metre by a factor of 10 to obtain the decimetre (0.1 m), or by a factor of 100 to get the centimetre, or by a factor of 1000 to get the millimetre. Making the base unit of length even smaller would not be practical (for example, the next decimal factor, 10000, would produce the base unit of length of one-tenth of a millimetre), so these three factors (10, 100, and 1000) are the only acceptable options as far as the base unit of length. But then the base unit of mass would have to be larger than a kilogram, by the following respective factors: 102 = 100, 1002 = 10000, and 10002 = 106. In other words, the watt is a coherent unit for the following pairs of base units of length and mass: 0.1 m and 100 kg, 1 cm and 10000 kg, and 1 mm and 1000000 kg. Even in the first pair, the base unit of mass is impractically large, 100 kg, and as the base unit of length is decreased, the base unit of mass gets even larger. Thus, assuming that the second remains the base unit of time, the metre-kilogram combination is the only one that has base units for both length and mass that are neither too large nor too small, and that are decimal multiples or divisions of the metre and gram, and has the watt as a coherent unit.
- ^ A system in which the base quantities are length, mass, and time, and only those three.
- ^ There is only one three-dimensional ‘absolute’ system[Note 4] in which all practical units are coherent, including the volt, the ampere, etc.: one in which the base unit of length is 107 m and the base unit of mass is 10−11 g. Clearly, these magnitudes are not practical.
- ^ Meanwhile, there were parallel developments that, for independent reasons, eventually resulted in three additional fundamental dimensions, for a total of seven: those for temperature, luminous intensity, and the amount of substance.
- ^ That is, units which have length, mass, and time as base dimensions and that are coherent in the CGS system.
- ^ For quite a long time, the ESU and EMU units did not have special names; one would just say, e.g. the ESU unit of resistance. It was apparently only in 1903 that A. E. Kennelly suggested that the names of the EMU units be obtained by prefixing the name of the corresponding ‘practical unit’ by ‘ab-’ (short for ‘absolute’, giving the ‘abohm’, ‘abvolt’, the ‘abampere’, etc.), and that the names of the ESU units be analogously obtained by using the prefix ‘abstat-’, which was later shortened to ‘stat-’ (giving the ‘statohm’, ‘statvolt’, ‘statampere’, etc.).[25]: 534–5 This naming system was widely used in the U.S., but, apparently, not in Europe.[26]
- ^ The use of SI electrical units is essentially universal worldwide (besides the clearly electrical units like the ohm, the volt, and the ampere, it is also nearly universal to use the watt when quantifying specifically electrical power). Resistance to the adoption of SI units mostly concerns mechanical units (lengths, mass, force, torque, pressure), thermal units (temperature, heat), and units for describing ionizing radiation (activity referred to a radionuclide, absorbed dose, dose equivalent); it does not concern electrical units.
- ^ In alternating current (AC) circuits one can introduce three kinds of power: active, reactive, and apparent. Though the three have the same dimensions and thus the same units when those are expressed in terms of base units (i.e. kg⋅m2⋅s-3), it is customary to use different names for each: respectively, the watt, the volt-ampere reactive, and the volt-ampere.
- ^ At the time, it was popular to denote decimal multiples and submultiples of quantities by using a system suggested by G. J. Stoney. The system is easiest to explain through examples. For decimal multiples: 109 grams would be denoted as gram-nine, 1013 m would be a metre-thirteen, etc. For submultiples: 10−9 grams would be denoted as a ninth-gram, 10−13 m would be a thirteenth-metre, etc. The system also worked with units that used metric prefixes, so e.g. 1015 centimetre would be centimetre-fifteen. The rule, when spelled out, is this: we denote ‘the exponent of the power of 10, which serves as multiplier, by an appended cardinal number, if the exponent be positive, and by a prefixed ordinal number, if the exponent be negative.’[28]
- ^ This is also obvious from the fact that in both absolute and practical units, current is charge per unit time, so that the unit of time is the unit of charge divided by the unit of current. In the practical system, we know that the base unit of time is the second, so the coulomb per ampere gives the second. The base unit of time in CGS-EMU is then the abcoulomb per abampere, but that ratio is the same as the coulomb per ampere, since the units of current and charge both use the same conversion factor, 0.1, to go between the EMU and practical units (coulomb/ampere = (0.1 abcoulomb)/(0.1 abampere) = abcoulomb/abampere). So the base unit of time in EMU is also the second.
- ^ This can be shown from the definitions of, say, the volt, the ampere, and the coulomb in terms of the EMU units. The volt was chosen as 108 EMU units (abvolts), the ampere as 0.1 EMU units (abamperes), and the coulomb as 0.1 EMU units (abcoulombs). Now we use the fact that, when expressed in the base CGS units, the abvolt is g1/2·cm3/2/s2, the abampere is g1/2·cm1/2/s, and the abcoulomb is g1/2·cm1/2. Suppose we choose new base units of length, mass, and time, equal to L centimetres, M grams, and T seconds. Then instead of the abvolt, the unit of electric potential will be (M × g)1/2·(L × cm)3/2/(T × s)2 = M1/2L3/2/T2 × g1/2·cm3/2/s2 = M1/2L3/2/T2 abvolts. We want this new unit to be the volt, so we must have M1/2L3/2/T2 = 108. Similarly, if we want the new unit for current to be the ampere, we obtain that M1/2L1/2/T = 0.1, and if we want the new unit of charge to be the coulomb, we get that M1/2L1/2 = 0.1. This is a system of three equations with three unknowns. By dividing the middle equation by the last one, we get that T = 1, so the second should remain the base unit of time.[Note 12] If we then divide the first equation by the middle one (and use the fact that T = 1), we get that L = 108/0.1 = 109, so the base unit of length should be 109 cm = 107 m. Finally, we square the final equation and obtain that M = 0.12/L = 10−11, so the base unit of mass should be 10−11 grams.
- ^ The dimensions of energy are ML2/T2 and of power, ML2/T3. One meaning of these dimensional formulas is that if the unit of mass is changed by a factor of M, the unit of length by a factor of L, and the unit of time by a factor of T, then the unit of energy will change by a factor of ML2/T2 and the unit of power by a factor of ML2/T3. This means that if the unit of length is decreased while at the same time increasing the unit of mass in such a way that the product ML2 remains constant, the units of energy and power would not change. Clearly, this happens if M = 1/L2. Now, the watt and joule are coherent in a system in which the base unit of length is 107 m while the base unit of mass is 10−11 grams. They will then also be coherent in any system in which the base unit of length is L × 107 m and the base unit of mass is 1/L2 × 10−11 g, where L is any positive real number. If we set L = 10−7, we obtain the metre as the base unit of length. Then the corresponding base unit of mass is 1/(10−7)2 × 10−11 g=1014 × 10−11 g = 103 g = 1 kg.
- ^ Criterion: A combined total of at least five occurrences on the British National Corpus and the Corpus of Contemporary American English, including both the singular and the plural for both the —gram and the —gramme spelling.
- ^ The practice of using the abbreviation «mcg» rather than the SI symbol «μg» was formally mandated in the US for medical practitioners in 2004 by the Joint Commission on Accreditation of Healthcare Organizations (JCAHO) in their «Do Not Use» List: Abbreviations, Acronyms, and Symbols Archived September 15, 2015, at the Wayback Machine because «μg» and «mg» when handwritten can be confused with one another, resulting in a thousand-fold overdosing (or underdosing). The mandate was also adopted by the Institute for Safe Medication Practices.
References[edit]
- ^ a b «Kilogram». Oxford Dictionaries. Archived from the original on January 31, 2013. Retrieved November 3, 2011.
- ^ «The Latest: Landmark Change to Kilogram Approved». AP News. Associated Press. November 16, 2018. Retrieved March 4, 2020.
- ^ BIPM (July 7, 2021). «Mise en pratique for the definition of the kilogram in the SI». BIPM.org. Retrieved February 18, 2022.
- ^ a b c d Resnick, Brian (May 20, 2019). «The new kilogram just debuted. It’s a massive achievement». vox.com. Retrieved May 23, 2019.
- ^ a b Draft Resolution A «On the revision of the International System of units (SI)» to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived (PDF) from the original on April 2, 2021
- ^ Decision CIPM/105-13 (October 2016). The day is the 144th anniversary of the Metre Convention.
- ^ SI Brochure: The International System of Units (SI). BIPM, 9th edition, 2019.
- ^ The density of water is 0.999972 g/cm3 at 3.984 °C. See Franks, Felix (2012). The Physics and Physical Chemistry of Water. Springer. ISBN 978-1-4684-8334-5.
- ^ Guyton; Lavoisier; Monge; Berthollet; et al. (1792). Annales de chimie ou Recueil de mémoires concernant la chimie et les arts qui en dépendent. Vol. 15–16. Paris: Chez Joseph de Boffe. p. 277.
- ^ Gramme, le poids absolu d’un volume d’eau pure égal au cube de la centième partie du mètre, et à la température de la glace fondante
- ^ a b «Kilogram». Oxford English Dictionary. Oxford University Press. Retrieved November 3, 2011.
- ^ Fowlers, HW; Fowler, FG (1964). The Concise Oxford Dictionary. Oxford: The Clarendon Press.
Greek γράμμα (as it were γράφ-μα, Doric γράθμα) means «something written, a letter», but it came to be used as a unit of weight, apparently equal to 1/24 of an ounce (1/288 of a libra, which would correspond to about 1.14 grams in modern units), at some time during Late Antiquity. French gramme was adopted from Latin gramma, itself quite obscure, but found in the Carmen de ponderibus et mensuris (8.25) attributed by Remmius Palaemon (fl. 1st century), where it is the weight of two oboli (Charlton T. Lewis, Charles Short, A Latin Dictionary s.v. «gramma», 1879).
Henry George Liddell. Robert Scott. A Greek-English Lexicon (revised and augmented edition, Oxford, 1940) s.v. γράμμα, citing the 10th-century work Geoponica and a 4th-century papyrus edited in L. Mitteis, Griechische Urkunden der Papyrussammlung zu Leipzig, vol. i (1906), 62 ii 27. - ^ «Décret relatif aux poids et aux mesures du 18 germinal an 3 (7 avril 1795)» [Decree of 18 Germinal, year III (April 7, 1795) regarding weights and measures]. Grandes lois de la République (in French). Digithèque de matériaux juridiques et politiques, Université de Perpignan. Retrieved November 3, 2011.
- ^ Convention nationale, décret du 1er août 1793, ed. Duvergier, Collection complète des lois, décrets, ordonnances, règlemens avis du Conseil d’état, publiée sur les éditions officielles du Louvre, vol. 6 (2nd ed. 1834), p. 70.
The metre (mètre) on which this definition depends was itself defined as the ten-millionth part of a quarter of Earth’s meridian, given in traditional units as 3 pieds, 11.44 lignes (a ligne being the 12th part of a pouce (inch), or the 144th part of a pied. - ^ Peltier, Jean-Gabriel (1795). «Paris, during the year 1795». Monthly Review. 17: 556. Retrieved August 2, 2018. Contemporaneous English translation of the French decree of 1795
- ^ «Spelling of «gram», etc». Weights and Measures Act 1985. Her Majesty’s Stationery Office. October 30, 1985. Retrieved November 6, 2011.
- ^ «kilo (n1)». Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ «kilo (n2)». Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ «Style Guide» (PDF). The Economist. January 7, 2002. Archived from the original (PDF) on July 1, 2017. Retrieved November 8, 2011.
- ^
«kilogram, kg, kilo». Termium Plus. Government of Canada. October 8, 2009. Retrieved May 29, 2019. - ^
«kilo». How Many?. Archived from the original on November 16, 2011. Retrieved November 6, 2011. - ^ 29th Congress of the United States, Session 1 (May 13, 1866). «H.R. 596, An Act to authorize the use of the metric system of weights and measures». Archived from the original on July 5, 2015.
- ^ «Metric System of Measurement:Interpretation of the International System of Units for the United States; Notice» (PDF). Federal Register. 63 (144): 40340. July 28, 1998. Archived from the original (PDF) on October 15, 2011. Retrieved November 10, 2011.
Obsolete Units As stated in the 1990 Federal Register notice, …
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 130, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Kennelly, A. E. (July 1903). «Magnetic Units and Other Subjects that Might Occupy Attention at the Next International Electrical Congress». Transactions of the American Institute of Electrical Engineers. XXII: 529–536. doi:10.1109/T-AIEE.1903.4764390. S2CID 51634810.
[p. 534] The expedient suggests itself of attaching the prefix ab or abs to a practical or Q. E. S. unit, in order to express the absolute or corresponding C. G. S. magnetic unit. … [p. 535] In a comprehensive system of electromagnetic terminology, the electric C. G. S. units should also be christened. They are sometimes referred to in electrical papers, but always in an apologetic, symbolical fashion, owing to the absence of names to cover their nakedness. They might be denoted by the prefix abstat.
- ^ Silsbee, Francis (April–June 1962). «Systems of Electrical Units». Journal of Research of the National Bureau of Standards Section C. 66C (2): 137–183. doi:10.6028/jres.066C.014.
- ^ Fleming, John Ambrose (1911). «Units, Physical» . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 27 (11th ed.). Cambridge University Press. pp. 738–745, see page 740.
- ^ a b Thomson, Sir W.; Foster, C. G.; Maxwell, J. C.; Stoney, G. J.; Jenkin, Fleeming; Siemens; Bramwell, F. J.; Everett (1873). Report of the 43rd Meeting of the British Association for the Advancement of Science. Vol. 43. Bradford. p. 223.
- ^ «The Electrical Congress». The Electrician. 7: 297. September 24, 1881. Retrieved June 3, 2020.
- ^ Giovanni Giorgi (1901), «Unità Razionali di Elettromagnetismo», Atti della Associazione Elettrotecnica Italiana (in Italian), Torino, OL 18571144M
Giovanni Giorgi (1902), Rational Units of Electromagnetism Original manuscript with handwritten notes by Oliver Heaviside Archived October 29, 2019, at the Wayback Machine - ^ a b c Giorgi, Giovanni (2018) [Originally published in June 1934 by the Central Office of the International Electrotechnical Commission (IEC), London, for IEC Advisory Committee No. 1 on Nomenclature, Section B: Electric and Magnetic Magnitudes and Units.]. «Memorandum on the M.K.S. System of Practical Units». IEEE Magnetics Letters. 9: 1–6. doi:10.1109/LMAG.2018.2859658.
- ^ Carron, Neal (2015). «Babel of Units. The Evolution of Units Systems in Classical Electromagnetism». arXiv:1506.01951 [physics.hist-ph].
- ^ a b Bridgman, P. W. (1922). Dimensional Analysis. Yale University Press.
- ^ Arthur E. Kennelly (1935), «Adoption of the Meter–Kilogram–Mass–Second (M.K.S.) Absolute System of Practical Units by the International Electrotechnical Commission (I.E.C.), Bruxelles, June, 1935», Proceedings of the National Academy of Sciences of the United States of America, 21 (10): 579–583, Bibcode:1935PNAS…21..579K, doi:10.1073/pnas.21.10.579, PMC 1076662, PMID 16577693
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Resolution 6 – Proposal for establishing a practical system of units of measurement. 9th Conférence Générale des Poids et Mesures (CGPM). October 12–21, 1948. Retrieved May 8, 2011.
- ^ Pallab Ghosh (November 16, 2018). «Kilogram gets a new definition». BBC News. Retrieved November 16, 2018.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 112, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Recommendation 1: Preparative steps towards new definitions of the kilogram, the ampere, the kelvin and the mole in terms of fundamental constants (PDF). 94th meeting of the International Committee for Weights and Measures. October 2005. p. 233. Archived (PDF) from the original on June 30, 2007. Retrieved February 7, 2018.
- ^ «NIST Backs Proposal for a Revamped System of Measurement Units». Nist. Nist.gov. October 26, 2010. Retrieved April 3, 2011.
- ^ Ian Mills (September 29, 2010). «Draft Chapter 2 for SI Brochure, following redefinitions of the base units» (PDF). CCU. Retrieved January 1, 2011.
- ^ Resolution 1 – On the possible future revision of the International System of Units, the SI (PDF). 24th meeting of the General Conference on Weights and Measures. Sèvres, France. October 17–21, 2011. Retrieved October 25, 2011.
- ^ a b «BIPM – Resolution 1 of the 25th CGPM». www.bipm.org. Retrieved March 27, 2017.
- ^ «General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram» (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. October 23, 2011. Retrieved October 25, 2011.
- ^ BIPM: SI Brochure: Section 3.2, The kilogram Archived March 29, 2016, at the Wayback Machine
- ^ «Prescribing Information for Liquid Medicines». Scottish Palliative Care Guidelines. Archived from the original on July 10, 2018. Retrieved June 15, 2015.
- ^ Tom Stobart, The Cook’s Encyclopedia, 1981, p. 525
- ^ J.J. Kinder, V.M. Savini, Using Italian: A Guide to Contemporary Usage, 2004, ISBN 0521485568, p. 231
- ^ Giacomo Devoto, Gian Carlo Oli, Nuovo vocabolario illustrato della lingua italiana, 1987, s.v. ‘ètto’: «frequentissima nell’uso comune: un e. di caffè, un e. di mortadella; formaggio a 2000 lire l’etto«
- ^ U.S. National Bureau of Standards, The International Metric System of Weights and Measures, «Official Abbreviations of International Metric Units», 1932, p. 13
- ^ «Jestřebická hovězí šunka 10 dkg | Rancherské speciality». eshop.rancherskespeciality.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «Sedliacka šunka 1 dkg | Gazdovský dvor – Farma Busov Gaboltov». Sedliacka šunka 1 dkg (in Slovak). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «sýr bazalkový – Farmářské Trhy». www.e-farmarsketrhy.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «Termékek – Csíz Sajtműhely» (in Hungarian). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ Non-SI units that are accepted for use with the SI, SI Brochure: Section 4 (Table 8), BIPM
External links[edit]
Wikimedia Commons has media related to Kilogram.
- NIST Improves Accuracy of ‘Watt Balance’ Method for Defining the Kilogram
- The UK’s National Physical Laboratory (NPL): Are any problems caused by having the kilogram defined in terms of a physical artefact? (FAQ – Mass & Density)
- NPL: NPL Kibble balance
- Metrology in France: Watt balance
- Australian National Measurement Institute: Redefining the kilogram through the Avogadro constant
- International Bureau of Weights and Measures (BIPM): Home page
- NZZ Folio: What a kilogram really weighs
- NPL: What are the differences between mass, weight, force and load?
- BBC: Getting the measure of a kilogram
- NPR: This Kilogram Has A Weight-Loss Problem, an interview with National Institute of Standards and Technology physicist Richard Steiner
- Avogadro and molar Planck constants for the redefinition of the kilogram
- Realization of the awaited definition of the kilogram
- Sample, Ian (November 9, 2018). «In the balance: scientists vote on first change to kilogram in a century». The Guardian. Retrieved November 9, 2018.
Videos[edit]
- The BIPM – YouTube channel
- «The role of the Planck constant in physics» – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting on superseding the IPK took place on YouTube
«kg» redirects here. For other uses, see KG.
| Kilogram | |
|---|---|

A Kibble balance is used to measure a kilogram with electricity and magnetism |
|
| General information | |
| Unit system | SI |
| Unit of | mass |
| Symbol | kg |
| Conversions | |
| 1 kg in … | … is equal to … |
| Avoirdupois | ≈ 2.204623 pounds[Note 1] |
| British Gravitational | ≈ 0.0685 slugs |
The kilogram (also kilogramme[1]) is the unit of mass in the International System of Units (SI), having the unit symbol kg. It is a widely used measure in science, engineering and commerce worldwide, and is often simply called a kilo colloquially. It means ‘one thousand grams’.
The kilogram is defined in terms of the second and the metre, both of which are based on fundamental physical constants. This allows a properly equipped metrology laboratory to calibrate a mass measurement instrument such as a Kibble balance as the primary standard to determine an exact kilogram mass.[2][3]
The kilogram was originally defined in 1795 as the mass of one litre of water. The current definition of a kilogram agrees with this original definition to within 30 parts per million. In 1799, the platinum Kilogramme des Archives replaced it as the standard of mass. In 1889, a cylinder of platinum-iridium, the International Prototype of the Kilogram (IPK), became the standard of the unit of mass for the metric system and remained so for 130 years, before the current standard was adopted in 2019.[4]
Definition[edit]
The kilogram is defined in terms of three fundamental physical constants:
- a specific atomic transition frequency ΔνCs, which defines the duration of the second,
- the speed of light c, which when combined with the second, defines the length of the metre,
- and the Planck constant h. which when combined with the metre and second, defines the mass of the kilogram.
The formal definition according to the General Conference on Weights and Measures (CGPM) is:
The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of c and ΔνCs.
— CGPM [5][6]
Defined in term of those units, the kg is formulated as:[7]
- kg = (299792458)2/(6.62607015×10−34)(9192631770)hΔνCs/c2 = 917097121160018/621541050725904751042hΔνCs/c2 ≈ (1.475521399735270×1040)hΔνCs/c2 .
This definition is generally consistent with previous definitions: the mass remains within 30 ppm of the mass of one litre of water.[8]
Timeline of previous definitions[edit]
- 1793: The grave (the precursor of the kilogram) was defined as the mass of 1 litre (dm3) of water, which was determined to be 18841 grains.[9]
- 1795: the gram (1/1000 of a kilogram) was provisionally defined as the mass of one cubic centimetre of water at the melting point of ice.[10]
- 1799: The Kilogramme des Archives was manufactured as a prototype. It had a mass equal to the mass of 1 dm3 of water at the temperature of its maximum density, which is approximately 4 °C.
- 1875–1889: The Metre Convention was signed in 1875, leading to the production of the International Prototype of the Kilogram (IPK) in 1879 and its adoption in 1889.
- 2019: The kilogram was defined in terms of the Planck constant, the speed of light and hyperfine transition frequency of 133Cs as approved by the General Conference on Weights and Measures (CGPM) on November 16, 2018.
Name and terminology[edit]
The kilogram is the only base SI unit with an SI prefix (kilo) as part of its name. The word kilogramme or kilogram is derived from the French kilogramme,[11] which itself was a learned coinage, prefixing the Greek stem of χίλιοι khilioi «a thousand» to gramma, a Late Latin term for «a small weight», itself from Greek γράμμα.[12]
The word kilogramme was written into French law in 1795, in the Decree of 18 Germinal,[13]
which revised the provisional system of units introduced by the French National Convention two years earlier, where the gravet had been defined as weight (poids) of a cubic centimetre of water, equal to 1/1000 of a grave.[14] In the decree of 1795, the term gramme thus replaced gravet, and kilogramme replaced grave.
The French spelling was adopted in Great Britain when the word was used for the first time in English in 1795,[15][11] with the spelling kilogram being adopted in the United States. In the United Kingdom both spellings are used, with «kilogram» having become by far the more common.[1] UK law regulating the units to be used when trading by weight or measure does not prevent the use of either spelling.[16]
In the 19th century the French word kilo, a shortening of kilogramme, was imported into the English language where it has been used to mean both kilogram[17] and kilometre.[18] While kilo as an alternative is acceptable, to The Economist for example,[19] the Canadian government’s Termium Plus system states that «SI (International System of Units) usage, followed in scientific and technical writing» does not allow its usage and it is described as «a common informal name» on Russ Rowlett’s Dictionary of Units of Measurement.[20][21] When the United States Congress gave the metric system legal status in 1866, it permitted the use of the word kilo as an alternative to the word kilogram,[22] but in 1990 revoked the status of the word kilo.[23]
The SI system was introduced in 1960 and in 1970 the BIPM started publishing the SI Brochure, which contains all relevant decisions and recommendations by the CGPM concerning units. The SI Brochure states that «It is not permissible to use abbreviations for unit symbols or unit names …».[24][Note 2]
Kilogram becoming a base unit: the role of units for electromagnetism[edit]
It is primarily because of units for electromagnetism that the kilogram rather than the gram was eventually adopted as the base unit of mass in the SI. The relevant series of discussions and decisions started roughly in the 1850s and effectively concluded in 1946. By the end of the 19th century, the ‘practical units’ for electric and magnetic quantities such as the ampere and the volt were well established in practical use (e.g. for telegraphy). Unfortunately, they were not coherent with the then-prevailing base units for length and mass, the centimetre, and the gram. However, the ‘practical units’ also included some purely mechanical units. In particular, the product of the ampere and the volt gives a purely mechanical unit of power, the watt. It was noticed that the purely mechanical practical units such as the watt would be coherent in a system in which the base unit of length was the metre and the base unit of mass was the kilogram. Because no one wanted to replace the second as the base unit of time, the metre and the kilogram are the only pair of base units of length and mass such that (1) the watt is a coherent unit of power, (2) the base units of length and time are integer-power-of-ten ratios to the metre and the gram (so that the system remains ‘metric’), and (3) the sizes of the base units of length and mass are convenient for practical use.[Note 3] This would still leave out the purely electrical and magnetic units: while the purely mechanical practical units such as the watt are coherent in the metre-kilogram-second system, the explicitly electrical and magnetic units such as the volt, the ampere, etc. are not.[Note 5] The only way to also make those units coherent with the metre-kilogram-second system is to modify that system in a different way: the number of fundamental dimensions must be increased from three (length, mass, and time) to four (the previous three, plus one purely electrical one).[Note 6]
The state of units for electromagnetism at the end of the 19th century[edit]
During the second half of the 19th century, the centimetre–gram–second system of units was becoming widely accepted for scientific work, treating the gram as the fundamental unit of mass and the kilogram as a decimal multiple of the base unit formed by using a metric prefix. However, as the century drew to a close, there was widespread dissatisfaction with the units for electricity and magnetism in the CGS system. There were two obvious choices for absolute units[Note 7] of electromagnetism: the ‘electrostatic’ (CGS-ESU) system and the ‘electromagnetic’ (CGS-EMU) system. But the sizes of coherent electric and magnetic units were not convenient in either of these systems; for example, the ESU unit of electrical resistance, which was later named the statohm, corresponds to about 9×1011 ohm, while the EMU unit, which was later named the abohm, corresponds to 10−9 ohm.[Note 8]
To circumvent this difficulty, a third set of units was introduced: the so-called practical units. The practical units were obtained as decimal multiples of coherent CGS-EMU units, chosen so that the resulting magnitudes were convenient for practical use and so that the practical units were, as far as possible, coherent with each other.[27] The practical units included such units as the volt, the ampere, the ohm, etc.,[28][29] which were later incorporated in the SI system and which are used to this day.[Note 9] The reason the metre and the kilogram were later chosen to be the base units of length and mass was that they are the only combination of reasonably sized decimal multiples or submultiples of the metre and the gram that can be made coherent with the volt, the ampere, etc.
The reason is that electrical quantities cannot be isolated from mechanical and thermal ones: they are connected by relations such as current × electric potential difference = power. For this reason, the practical system also included coherent units for certain mechanical quantities. For example, the previous equation implies that ampere × volt is a coherent derived practical unit of power;[Note 10] this unit was named the watt. The coherent unit of energy is then the watt times the second, which was named the joule. The joule and the watt also have convenient magnitudes and are decimal multiples of CGS coherent units for energy (the erg) and power (the erg per second). The watt is not coherent in the centimetre-gram-second system, but it is coherent in the metre-kilogram-second system—and in no other system whose base units of length and mass are reasonably sized decimal multiples or submultiples of the metre and the gram.
However, unlike the watt and the joule, the explicitly electrical and magnetic units (the volt, the ampere…) are not coherent even in the (absolute three-dimensional) metre-kilogram-second system. Indeed, one can work out what the base units of length and mass have to be in order for all the practical units to be coherent (the watt and the joule as well as the volt, the ampere, etc.). The values are 107 metres (one half of a meridian of the Earth, called a quadrant) and 10−11 grams (called an eleventh-gram[Note 11]).[Note 13]
Therefore, the full absolute system of units in which the practical electrical units are coherent is the quadrant–eleventh-gram–second (QES) system. However, the extremely inconvenient magnitudes of the base units for length and mass made it so that no one seriously considered adopting the QES system. Thus, people working on practical applications of electricity had to use units for electrical quantities and for energy and power that were not coherent with the units they were using for e.g. length, mass, and force.
Meanwhile, scientists developed yet another fully coherent absolute system, which came to be called the Gaussian system, in which the units for purely electrical quantities are taken from CGE-ESU, while the units for magnetic quantities are taken from the CGS-EMU. This system proved very convenient for scientific work and is still widely used. However, the sizes of its units remained either too large or too small—by many orders of magnitude—for practical applications.
Finally, in both CGS-ESU and CGS-EMU as well as in the Gaussian system, Maxwell’s equations are ‘unrationalized’, meaning that they contain various factors of 4π that many workers found awkward. So yet another system was developed to rectify that: the ‘rationalized’ Gaussian system, usually called the Heaviside–Lorentz system. This system is still used in some subfields of physics. However, the units in that system are related to Gaussian units by factors of √4π ≈ 3.5, which means that their magnitudes remained, like those of the Gaussian units, either far too large or far too small for practical applications.
The Giorgi proposal[edit]
In 1901, Giovanni Giorgi proposed a new system of units that would remedy this situation.[30] He noted that the mechanical practical units such as the joule and the watt are coherent not only in the QES system, but also in the metre-kilogram-second (MKS) system.[31][Note 14] It was of course known that adopting the metre and the kilogram as base units—obtaining the three dimensional MKS system—would not solve the problem: while the watt and the joule would be coherent, this would not be so for the volt, the ampere, the ohm, and the rest of the practical units for electric and magnetic quantities (the only three-dimensional absolute system in which all practical units are coherent is the QES system).
But Giorgi pointed out that the volt and the rest could be made coherent if the idea that all physical quantities must be expressible in terms of dimensions of length, mass, and time, is relinquished and a fourth base dimension is added for electric quantities. Any practical electrical unit could be chosen as the new fundamental unit, independent from the metre, kilogram, and second. Likely candidates for the fourth independent unit included the coulomb, the ampere, the volt, and the ohm, but eventually, the ampere proved to be the most convenient for metrology. Moreover, the freedom gained by making an electric unit independent from the mechanical units could be used to rationalize Maxwell’s equations.
The idea that one should give up on having a purely ‘absolute’ system (i.e. one where only length, mass, and time are the base dimensions) was a departure from a viewpoint that seemed to underlie the early breakthroughs by Gauss and Weber (especially their famous ‘absolute measurements’ of Earth’s magnetic field[32]: 54–56 ), and it took some time for the scientific community to accept it—not least because many scientists clung to the notion that the dimensions of a quantity in terms of length, mass, and time somehow specify its ‘fundamental physical nature’.[33]:24, 26[31]
Acceptance of the Giorgi system, leading to the MKSA system and the SI[edit]
By the 1920s, dimensional analysis had become much better understood[31] and it was becoming widely accepted that the choice of both the number and of the identities of the «fundamental» dimensions should be dictated by convenience only and that there is nothing really fundamental about the dimensions of a quantity.[33] In 1935, Giorgi’s proposal was adopted by the IEC as the Giorgi system. It is this system that has since then been called the MKS system,[34]
although ‘MKSA’ appears in careful usage. In 1946 the CIPM approved a proposal to adopt the ampere as the electromagnetic unit of the «MKSA system».[35]: 109, 110 In 1948 the CGPM commissioned the CIPM «to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention».[36] This led to the launch of SI in 1960.
To summarize, the ultimate reason that the kilogram was chosen over the gram as the base unit of mass was, in one word, the volt-ampere. Namely, the combination of the metre and the kilogram was the only choice of base units of length and mass such that 1. the volt-ampere—which is also called the watt and which is the unit of power in the practical system of electrical units—is coherent, 2. the base units of length and mass are decimal multiples or submultiples of the metre and the gram, and 3. the base units of length and mass have convenient sizes.
The CGS and MKS systems co-existed during much of the early-to-mid-20th century, but as a result of the decision to adopt the «Giorgi system» as the international system of units in 1960, the kilogram is now the SI base unit for mass, while the definition of the gram is derived.
Redefinition based on fundamental constants[edit]
A Kibble balance, which was originally used to measure the Planck constant in terms of the IPK, can now be used to calibrate secondary standard weights for practical use.
The replacement of the International Prototype of the Kilogram (IPK) as the primary standard was motivated by evidence accumulated over a long period of time that the mass of the IPK and its replicas had been changing; the IPK had diverged from its replicas by approximately 50 micrograms since their manufacture late in the 19th century. This led to several competing efforts to develop measurement technology precise enough to warrant replacing the kilogram artefact with a definition based directly on physical fundamental constants.[4] Physical standard masses such as the IPK and its replicas still serve as secondary standards.
The International Committee for Weights and Measures (CIPM) approved a redefinition of the SI base units in November 2018 that defines the kilogram by defining the Planck constant to be exactly 6.62607015×10−34 kg⋅m2⋅s−1, effectively defining the kilogram in terms of the second and the metre. The new definition took effect on May 20, 2019.[4][5][37]
Prior to the redefinition, the kilogram and several other SI units based on the kilogram were defined by a man-made metal artifact: the Kilogramme des Archives from 1799 to 1889, and the IPK from 1889 to 2019.[4]
In 1960, the metre, previously similarly having been defined with reference to a single platinum-iridium bar with two marks on it, was redefined in terms of an invariant physical constant (the wavelength of a particular emission of light emitted by krypton,[38] and later the speed of light) so that the standard can be independently reproduced in different laboratories by following a written specification.
At the 94th Meeting of the International Committee for Weights and Measures (CIPM) in 2005, it was recommended that the same be done with the kilogram.[39]
In October 2010, the CIPM voted to submit a resolution for consideration at the General Conference on Weights and Measures (CGPM), to «take note of an intention» that the kilogram be defined in terms of the Planck constant, h (which has dimensions of energy times time, thus mass × length2 / time) together with other physical constants.[40][41] This resolution was accepted by the 24th conference of the CGPM[42] in October 2011 and further discussed at the 25th conference in 2014.[43][44] Although the Committee recognised that significant progress had been made, they concluded that the data did not yet appear sufficiently robust to adopt the revised definition, and that work should continue to enable the adoption at the 26th meeting, scheduled for 2018.[43] Such a definition would theoretically permit any apparatus that was capable of delineating the kilogram in terms of the Planck constant to be used as long as it possessed sufficient precision, accuracy and stability. The Kibble balance is one way to do this.
As part of this project, a variety of very different technologies and approaches were considered and explored over many years. Some of these approaches were based on equipment and procedures that would enable the reproducible production of new, kilogram-mass prototypes on demand (albeit with extraordinary effort) using measurement techniques and material properties that are ultimately based on, or traceable to, physical constants. Others were based on devices that measured either the acceleration or weight of hand-tuned kilogram test masses and which expressed their magnitudes in electrical terms via special components that permit traceability to physical constants. All approaches depend on converting a weight measurement to a mass and therefore require the precise measurement of the strength of gravity in laboratories. All approaches would have precisely fixed one or more constants of nature at a defined value.
SI multiples[edit]
Because an SI unit may not have multiple prefixes (see SI prefix), prefixes are added to gram, rather than the base unit kilogram, which already has a prefix as part of its name.[45] For instance, one-millionth of a kilogram is 1 mg (one milligram), not 1 μkg (one microkilogram).
| Submultiples | Multiples | ||||
|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name |
| 10−1 g | dg | decigram | 101 g | dag | decagram |
| 10−2 g | cg | centigram | 102 g | hg | hectogram |
| 10−3 g | mg | milligram | 103 g | kg | kilogram |
| 10−6 g | µg | microgram | 106 g | Mg | megagram (tonne) |
| 10−9 g | ng | nanogram | 109 g | Gg | gigagram |
| 10−12 g | pg | picogram | 1012 g | Tg | teragram |
| 10−15 g | fg | femtogram | 1015 g | Pg | petagram |
| 10−18 g | ag | attogram | 1018 g | Eg | exagram |
| 10−21 g | zg | zeptogram | 1021 g | Zg | zettagram |
| 10−24 g | yg | yoctogram | 1024 g | Yg | yottagram |
| 10−27 g | rg | rontogram | 1027 g | Rg | ronnagram |
| 10−30 g | qg | quectogram | 1030 g | Qg | quettagram |
| Common prefixed units are in bold face.[Note 15] |
- The microgram is typically abbreviated «mcg» in pharmaceutical and nutritional supplement labelling, to avoid confusion, since the «μ» prefix is not always well recognised outside of technical disciplines.[Note 16] (The expression «mcg» is also the symbol for an obsolete CGS unit of measure known as the «millicentigram», which is equal to 10 μg.)
- In the United Kingdom, because serious medication errors have been made from the confusion between milligrams and micrograms when micrograms has been abbreviated, the recommendation given in the Scottish Palliative Care Guidelines is that doses of less than one milligram must be expressed in micrograms and that the word microgram must be written in full, and that it is never acceptable to use «mcg» or «μg».[46]
- The hectogram (100 g) (Italian: ettogrammo or etto) is a very commonly used unit in the retail food trade in Italy.[47][48][49]
- The former standard spelling and abbreviation «deka-» and «dk» produced abbreviations such as «dkm» (dekametre) and «dkg» (dekagram).[50] As of 2020, the abbreviation «dkg» (10 g) is still used in parts of central Europe in retail for some foods such as cheese and meat.[51][52][53][55]
- The unit name megagram is rarely used, and even then typically only in technical fields in contexts where especially rigorous consistency with the SI standard is desired. For most purposes, the name tonne is instead used. The tonne and its symbol, «t», were adopted by the CIPM in 1879. It is a non-SI unit accepted by the BIPM for use with the SI. According to the BIPM, «This unit is sometimes referred to as ‘metric ton’ in some English-speaking countries.»[56] The unit name megatonne or megaton (Mt) is often used in general-interest literature on greenhouse gas emissions and nuclear weapons yields, whereas the equivalent unit in scientific papers on the subject is often the teragram (Tg).
See also[edit]
- 1795 in science
- 1799 in science
- General Conference on Weights and Measures (CGPM)
- Gram
- Grave (original name of the kilogram, its history)
- Gravimetry
- Inertia
- International Bureau of Weights and Measures (BIPM)
- International Committee for Weights and Measures (CIPM)
- International System of Units (SI)
- Kibble balance
- Kilogram-force
- Litre
- Mass
- Mass versus weight
- Metric system
- Metric ton
- Milligram per cent
- National Institute of Standards and Technology (NIST)
- Newton
- SI base units
- Standard gravity
- Weight
Notes[edit]
- ^ The avoirdupois pound is part of both United States customary system of units and the Imperial system of units. It is defined as exactly 0.45359237 kilograms.
- ^ The French text (which is the authoritative text) states «Il n’est pas autorisé d’utiliser des abréviations pour les symboles et noms d’unités …«
- ^ If it is known that the metre and the kilogram satisfy all three conditions, then no other choice does: The coherent unit of power, when written out in terms of the base units of length, mass, and time, is (base unit of mass) × (base unit of length)2/(base unit of time)3. It is stated that the watt is coherent in the metre-kilogram-second system; thus, 1 watt = (1 kg) × (1 m)2/(1 s)3. The second is left as it is and it is noted that if the base unit of length is changed to L m and the base unit of mass to M kg, then the coherent unit of power is (M kg) × (L m)2/(1 s)3 = ML2 × (1 kg) × (1 m)2/(1 s)3 = ML2 watt. Since base units of length and mass are such that the coherent unit of power is the watt, it must be that ML2 = 1. It follows that if the base unit of length is changed by a factor of L, then the base unit of mass must change by a factor of 1/L2 if the watt is to remain a coherent unit. It would be impractical to make the base unit of length a decimal multiple of a metre (10 m, 100 m, or more). Therefore the only option is to make the base unit of length a decimal submultiple of the metre. This would mean decreasing the metre by a factor of 10 to obtain the decimetre (0.1 m), or by a factor of 100 to get the centimetre, or by a factor of 1000 to get the millimetre. Making the base unit of length even smaller would not be practical (for example, the next decimal factor, 10000, would produce the base unit of length of one-tenth of a millimetre), so these three factors (10, 100, and 1000) are the only acceptable options as far as the base unit of length. But then the base unit of mass would have to be larger than a kilogram, by the following respective factors: 102 = 100, 1002 = 10000, and 10002 = 106. In other words, the watt is a coherent unit for the following pairs of base units of length and mass: 0.1 m and 100 kg, 1 cm and 10000 kg, and 1 mm and 1000000 kg. Even in the first pair, the base unit of mass is impractically large, 100 kg, and as the base unit of length is decreased, the base unit of mass gets even larger. Thus, assuming that the second remains the base unit of time, the metre-kilogram combination is the only one that has base units for both length and mass that are neither too large nor too small, and that are decimal multiples or divisions of the metre and gram, and has the watt as a coherent unit.
- ^ A system in which the base quantities are length, mass, and time, and only those three.
- ^ There is only one three-dimensional ‘absolute’ system[Note 4] in which all practical units are coherent, including the volt, the ampere, etc.: one in which the base unit of length is 107 m and the base unit of mass is 10−11 g. Clearly, these magnitudes are not practical.
- ^ Meanwhile, there were parallel developments that, for independent reasons, eventually resulted in three additional fundamental dimensions, for a total of seven: those for temperature, luminous intensity, and the amount of substance.
- ^ That is, units which have length, mass, and time as base dimensions and that are coherent in the CGS system.
- ^ For quite a long time, the ESU and EMU units did not have special names; one would just say, e.g. the ESU unit of resistance. It was apparently only in 1903 that A. E. Kennelly suggested that the names of the EMU units be obtained by prefixing the name of the corresponding ‘practical unit’ by ‘ab-’ (short for ‘absolute’, giving the ‘abohm’, ‘abvolt’, the ‘abampere’, etc.), and that the names of the ESU units be analogously obtained by using the prefix ‘abstat-’, which was later shortened to ‘stat-’ (giving the ‘statohm’, ‘statvolt’, ‘statampere’, etc.).[25]: 534–5 This naming system was widely used in the U.S., but, apparently, not in Europe.[26]
- ^ The use of SI electrical units is essentially universal worldwide (besides the clearly electrical units like the ohm, the volt, and the ampere, it is also nearly universal to use the watt when quantifying specifically electrical power). Resistance to the adoption of SI units mostly concerns mechanical units (lengths, mass, force, torque, pressure), thermal units (temperature, heat), and units for describing ionizing radiation (activity referred to a radionuclide, absorbed dose, dose equivalent); it does not concern electrical units.
- ^ In alternating current (AC) circuits one can introduce three kinds of power: active, reactive, and apparent. Though the three have the same dimensions and thus the same units when those are expressed in terms of base units (i.e. kg⋅m2⋅s-3), it is customary to use different names for each: respectively, the watt, the volt-ampere reactive, and the volt-ampere.
- ^ At the time, it was popular to denote decimal multiples and submultiples of quantities by using a system suggested by G. J. Stoney. The system is easiest to explain through examples. For decimal multiples: 109 grams would be denoted as gram-nine, 1013 m would be a metre-thirteen, etc. For submultiples: 10−9 grams would be denoted as a ninth-gram, 10−13 m would be a thirteenth-metre, etc. The system also worked with units that used metric prefixes, so e.g. 1015 centimetre would be centimetre-fifteen. The rule, when spelled out, is this: we denote ‘the exponent of the power of 10, which serves as multiplier, by an appended cardinal number, if the exponent be positive, and by a prefixed ordinal number, if the exponent be negative.’[28]
- ^ This is also obvious from the fact that in both absolute and practical units, current is charge per unit time, so that the unit of time is the unit of charge divided by the unit of current. In the practical system, we know that the base unit of time is the second, so the coulomb per ampere gives the second. The base unit of time in CGS-EMU is then the abcoulomb per abampere, but that ratio is the same as the coulomb per ampere, since the units of current and charge both use the same conversion factor, 0.1, to go between the EMU and practical units (coulomb/ampere = (0.1 abcoulomb)/(0.1 abampere) = abcoulomb/abampere). So the base unit of time in EMU is also the second.
- ^ This can be shown from the definitions of, say, the volt, the ampere, and the coulomb in terms of the EMU units. The volt was chosen as 108 EMU units (abvolts), the ampere as 0.1 EMU units (abamperes), and the coulomb as 0.1 EMU units (abcoulombs). Now we use the fact that, when expressed in the base CGS units, the abvolt is g1/2·cm3/2/s2, the abampere is g1/2·cm1/2/s, and the abcoulomb is g1/2·cm1/2. Suppose we choose new base units of length, mass, and time, equal to L centimetres, M grams, and T seconds. Then instead of the abvolt, the unit of electric potential will be (M × g)1/2·(L × cm)3/2/(T × s)2 = M1/2L3/2/T2 × g1/2·cm3/2/s2 = M1/2L3/2/T2 abvolts. We want this new unit to be the volt, so we must have M1/2L3/2/T2 = 108. Similarly, if we want the new unit for current to be the ampere, we obtain that M1/2L1/2/T = 0.1, and if we want the new unit of charge to be the coulomb, we get that M1/2L1/2 = 0.1. This is a system of three equations with three unknowns. By dividing the middle equation by the last one, we get that T = 1, so the second should remain the base unit of time.[Note 12] If we then divide the first equation by the middle one (and use the fact that T = 1), we get that L = 108/0.1 = 109, so the base unit of length should be 109 cm = 107 m. Finally, we square the final equation and obtain that M = 0.12/L = 10−11, so the base unit of mass should be 10−11 grams.
- ^ The dimensions of energy are ML2/T2 and of power, ML2/T3. One meaning of these dimensional formulas is that if the unit of mass is changed by a factor of M, the unit of length by a factor of L, and the unit of time by a factor of T, then the unit of energy will change by a factor of ML2/T2 and the unit of power by a factor of ML2/T3. This means that if the unit of length is decreased while at the same time increasing the unit of mass in such a way that the product ML2 remains constant, the units of energy and power would not change. Clearly, this happens if M = 1/L2. Now, the watt and joule are coherent in a system in which the base unit of length is 107 m while the base unit of mass is 10−11 grams. They will then also be coherent in any system in which the base unit of length is L × 107 m and the base unit of mass is 1/L2 × 10−11 g, where L is any positive real number. If we set L = 10−7, we obtain the metre as the base unit of length. Then the corresponding base unit of mass is 1/(10−7)2 × 10−11 g=1014 × 10−11 g = 103 g = 1 kg.
- ^ Criterion: A combined total of at least five occurrences on the British National Corpus and the Corpus of Contemporary American English, including both the singular and the plural for both the —gram and the —gramme spelling.
- ^ The practice of using the abbreviation «mcg» rather than the SI symbol «μg» was formally mandated in the US for medical practitioners in 2004 by the Joint Commission on Accreditation of Healthcare Organizations (JCAHO) in their «Do Not Use» List: Abbreviations, Acronyms, and Symbols Archived September 15, 2015, at the Wayback Machine because «μg» and «mg» when handwritten can be confused with one another, resulting in a thousand-fold overdosing (or underdosing). The mandate was also adopted by the Institute for Safe Medication Practices.
References[edit]
- ^ a b «Kilogram». Oxford Dictionaries. Archived from the original on January 31, 2013. Retrieved November 3, 2011.
- ^ «The Latest: Landmark Change to Kilogram Approved». AP News. Associated Press. November 16, 2018. Retrieved March 4, 2020.
- ^ BIPM (July 7, 2021). «Mise en pratique for the definition of the kilogram in the SI». BIPM.org. Retrieved February 18, 2022.
- ^ a b c d Resnick, Brian (May 20, 2019). «The new kilogram just debuted. It’s a massive achievement». vox.com. Retrieved May 23, 2019.
- ^ a b Draft Resolution A «On the revision of the International System of units (SI)» to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived (PDF) from the original on April 2, 2021
- ^ Decision CIPM/105-13 (October 2016). The day is the 144th anniversary of the Metre Convention.
- ^ SI Brochure: The International System of Units (SI). BIPM, 9th edition, 2019.
- ^ The density of water is 0.999972 g/cm3 at 3.984 °C. See Franks, Felix (2012). The Physics and Physical Chemistry of Water. Springer. ISBN 978-1-4684-8334-5.
- ^ Guyton; Lavoisier; Monge; Berthollet; et al. (1792). Annales de chimie ou Recueil de mémoires concernant la chimie et les arts qui en dépendent. Vol. 15–16. Paris: Chez Joseph de Boffe. p. 277.
- ^ Gramme, le poids absolu d’un volume d’eau pure égal au cube de la centième partie du mètre, et à la température de la glace fondante
- ^ a b «Kilogram». Oxford English Dictionary. Oxford University Press. Retrieved November 3, 2011.
- ^ Fowlers, HW; Fowler, FG (1964). The Concise Oxford Dictionary. Oxford: The Clarendon Press.
Greek γράμμα (as it were γράφ-μα, Doric γράθμα) means «something written, a letter», but it came to be used as a unit of weight, apparently equal to 1/24 of an ounce (1/288 of a libra, which would correspond to about 1.14 grams in modern units), at some time during Late Antiquity. French gramme was adopted from Latin gramma, itself quite obscure, but found in the Carmen de ponderibus et mensuris (8.25) attributed by Remmius Palaemon (fl. 1st century), where it is the weight of two oboli (Charlton T. Lewis, Charles Short, A Latin Dictionary s.v. «gramma», 1879).
Henry George Liddell. Robert Scott. A Greek-English Lexicon (revised and augmented edition, Oxford, 1940) s.v. γράμμα, citing the 10th-century work Geoponica and a 4th-century papyrus edited in L. Mitteis, Griechische Urkunden der Papyrussammlung zu Leipzig, vol. i (1906), 62 ii 27. - ^ «Décret relatif aux poids et aux mesures du 18 germinal an 3 (7 avril 1795)» [Decree of 18 Germinal, year III (April 7, 1795) regarding weights and measures]. Grandes lois de la République (in French). Digithèque de matériaux juridiques et politiques, Université de Perpignan. Retrieved November 3, 2011.
- ^ Convention nationale, décret du 1er août 1793, ed. Duvergier, Collection complète des lois, décrets, ordonnances, règlemens avis du Conseil d’état, publiée sur les éditions officielles du Louvre, vol. 6 (2nd ed. 1834), p. 70.
The metre (mètre) on which this definition depends was itself defined as the ten-millionth part of a quarter of Earth’s meridian, given in traditional units as 3 pieds, 11.44 lignes (a ligne being the 12th part of a pouce (inch), or the 144th part of a pied. - ^ Peltier, Jean-Gabriel (1795). «Paris, during the year 1795». Monthly Review. 17: 556. Retrieved August 2, 2018. Contemporaneous English translation of the French decree of 1795
- ^ «Spelling of «gram», etc». Weights and Measures Act 1985. Her Majesty’s Stationery Office. October 30, 1985. Retrieved November 6, 2011.
- ^ «kilo (n1)». Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ «kilo (n2)». Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ «Style Guide» (PDF). The Economist. January 7, 2002. Archived from the original (PDF) on July 1, 2017. Retrieved November 8, 2011.
- ^
«kilogram, kg, kilo». Termium Plus. Government of Canada. October 8, 2009. Retrieved May 29, 2019. - ^
«kilo». How Many?. Archived from the original on November 16, 2011. Retrieved November 6, 2011. - ^ 29th Congress of the United States, Session 1 (May 13, 1866). «H.R. 596, An Act to authorize the use of the metric system of weights and measures». Archived from the original on July 5, 2015.
- ^ «Metric System of Measurement:Interpretation of the International System of Units for the United States; Notice» (PDF). Federal Register. 63 (144): 40340. July 28, 1998. Archived from the original (PDF) on October 15, 2011. Retrieved November 10, 2011.
Obsolete Units As stated in the 1990 Federal Register notice, …
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 130, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Kennelly, A. E. (July 1903). «Magnetic Units and Other Subjects that Might Occupy Attention at the Next International Electrical Congress». Transactions of the American Institute of Electrical Engineers. XXII: 529–536. doi:10.1109/T-AIEE.1903.4764390. S2CID 51634810.
[p. 534] The expedient suggests itself of attaching the prefix ab or abs to a practical or Q. E. S. unit, in order to express the absolute or corresponding C. G. S. magnetic unit. … [p. 535] In a comprehensive system of electromagnetic terminology, the electric C. G. S. units should also be christened. They are sometimes referred to in electrical papers, but always in an apologetic, symbolical fashion, owing to the absence of names to cover their nakedness. They might be denoted by the prefix abstat.
- ^ Silsbee, Francis (April–June 1962). «Systems of Electrical Units». Journal of Research of the National Bureau of Standards Section C. 66C (2): 137–183. doi:10.6028/jres.066C.014.
- ^ Fleming, John Ambrose (1911). «Units, Physical» . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 27 (11th ed.). Cambridge University Press. pp. 738–745, see page 740.
- ^ a b Thomson, Sir W.; Foster, C. G.; Maxwell, J. C.; Stoney, G. J.; Jenkin, Fleeming; Siemens; Bramwell, F. J.; Everett (1873). Report of the 43rd Meeting of the British Association for the Advancement of Science. Vol. 43. Bradford. p. 223.
- ^ «The Electrical Congress». The Electrician. 7: 297. September 24, 1881. Retrieved June 3, 2020.
- ^ Giovanni Giorgi (1901), «Unità Razionali di Elettromagnetismo», Atti della Associazione Elettrotecnica Italiana (in Italian), Torino, OL 18571144M
Giovanni Giorgi (1902), Rational Units of Electromagnetism Original manuscript with handwritten notes by Oliver Heaviside Archived October 29, 2019, at the Wayback Machine - ^ a b c Giorgi, Giovanni (2018) [Originally published in June 1934 by the Central Office of the International Electrotechnical Commission (IEC), London, for IEC Advisory Committee No. 1 on Nomenclature, Section B: Electric and Magnetic Magnitudes and Units.]. «Memorandum on the M.K.S. System of Practical Units». IEEE Magnetics Letters. 9: 1–6. doi:10.1109/LMAG.2018.2859658.
- ^ Carron, Neal (2015). «Babel of Units. The Evolution of Units Systems in Classical Electromagnetism». arXiv:1506.01951 [physics.hist-ph].
- ^ a b Bridgman, P. W. (1922). Dimensional Analysis. Yale University Press.
- ^ Arthur E. Kennelly (1935), «Adoption of the Meter–Kilogram–Mass–Second (M.K.S.) Absolute System of Practical Units by the International Electrotechnical Commission (I.E.C.), Bruxelles, June, 1935», Proceedings of the National Academy of Sciences of the United States of America, 21 (10): 579–583, Bibcode:1935PNAS…21..579K, doi:10.1073/pnas.21.10.579, PMC 1076662, PMID 16577693
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Resolution 6 – Proposal for establishing a practical system of units of measurement. 9th Conférence Générale des Poids et Mesures (CGPM). October 12–21, 1948. Retrieved May 8, 2011.
- ^ Pallab Ghosh (November 16, 2018). «Kilogram gets a new definition». BBC News. Retrieved November 16, 2018.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 112, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Recommendation 1: Preparative steps towards new definitions of the kilogram, the ampere, the kelvin and the mole in terms of fundamental constants (PDF). 94th meeting of the International Committee for Weights and Measures. October 2005. p. 233. Archived (PDF) from the original on June 30, 2007. Retrieved February 7, 2018.
- ^ «NIST Backs Proposal for a Revamped System of Measurement Units». Nist. Nist.gov. October 26, 2010. Retrieved April 3, 2011.
- ^ Ian Mills (September 29, 2010). «Draft Chapter 2 for SI Brochure, following redefinitions of the base units» (PDF). CCU. Retrieved January 1, 2011.
- ^ Resolution 1 – On the possible future revision of the International System of Units, the SI (PDF). 24th meeting of the General Conference on Weights and Measures. Sèvres, France. October 17–21, 2011. Retrieved October 25, 2011.
- ^ a b «BIPM – Resolution 1 of the 25th CGPM». www.bipm.org. Retrieved March 27, 2017.
- ^ «General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram» (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. October 23, 2011. Retrieved October 25, 2011.
- ^ BIPM: SI Brochure: Section 3.2, The kilogram Archived March 29, 2016, at the Wayback Machine
- ^ «Prescribing Information for Liquid Medicines». Scottish Palliative Care Guidelines. Archived from the original on July 10, 2018. Retrieved June 15, 2015.
- ^ Tom Stobart, The Cook’s Encyclopedia, 1981, p. 525
- ^ J.J. Kinder, V.M. Savini, Using Italian: A Guide to Contemporary Usage, 2004, ISBN 0521485568, p. 231
- ^ Giacomo Devoto, Gian Carlo Oli, Nuovo vocabolario illustrato della lingua italiana, 1987, s.v. ‘ètto’: «frequentissima nell’uso comune: un e. di caffè, un e. di mortadella; formaggio a 2000 lire l’etto«
- ^ U.S. National Bureau of Standards, The International Metric System of Weights and Measures, «Official Abbreviations of International Metric Units», 1932, p. 13
- ^ «Jestřebická hovězí šunka 10 dkg | Rancherské speciality». eshop.rancherskespeciality.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «Sedliacka šunka 1 dkg | Gazdovský dvor – Farma Busov Gaboltov». Sedliacka šunka 1 dkg (in Slovak). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «sýr bazalkový – Farmářské Trhy». www.e-farmarsketrhy.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ «Termékek – Csíz Sajtműhely» (in Hungarian). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ Non-SI units that are accepted for use with the SI, SI Brochure: Section 4 (Table 8), BIPM
External links[edit]
Wikimedia Commons has media related to Kilogram.
- NIST Improves Accuracy of ‘Watt Balance’ Method for Defining the Kilogram
- The UK’s National Physical Laboratory (NPL): Are any problems caused by having the kilogram defined in terms of a physical artefact? (FAQ – Mass & Density)
- NPL: NPL Kibble balance
- Metrology in France: Watt balance
- Australian National Measurement Institute: Redefining the kilogram through the Avogadro constant
- International Bureau of Weights and Measures (BIPM): Home page
- NZZ Folio: What a kilogram really weighs
- NPL: What are the differences between mass, weight, force and load?
- BBC: Getting the measure of a kilogram
- NPR: This Kilogram Has A Weight-Loss Problem, an interview with National Institute of Standards and Technology physicist Richard Steiner
- Avogadro and molar Planck constants for the redefinition of the kilogram
- Realization of the awaited definition of the kilogram
- Sample, Ian (November 9, 2018). «In the balance: scientists vote on first change to kilogram in a century». The Guardian. Retrieved November 9, 2018.
Videos[edit]
- The BIPM – YouTube channel
- «The role of the Planck constant in physics» – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting on superseding the IPK took place on YouTube
Русский
Морфологические и синтаксические свойства
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | килогра́мм | килогра́ммы |
| Р. | килогра́мма | килогра́ммов килогра́мм |
| Д. | килогра́мму | килогра́ммам |
| В. | килогра́мм | килогра́ммы |
| Тв. | килогра́ммом | килогра́ммами |
| Пр. | килогра́мме | килогра́ммах |
ки—ло—гра́мм
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a((2)) по классификации А. А. Зализняка).
Префиксоид: кило-; корень: -грамм- [Тихонов, 1996].
Произношение
- МФА: ед. ч. [kʲɪɫɐˈɡram] мн. ч. [kʲɪɫɐˈɡramːɨ]
Семантические свойства
Значение
- единица измерения массы, равная 1000 граммам, одна из основных единиц СИ ◆ Он переводил пуды на килограммы, килограммы — на старозаветные золотники, и каждый раз получалась такая заманчивая цифра, что нарушитель конвенции даже легонько повизгивал. Илья Ильф, Евгений Петров, «Золотой телёнок», 1931 г. [НКРЯ] ◆ Ремни, выдержавшие на испытаниях сотни килограммов груза, лопнули, как бечёвки, и ещё через три-четыре секунды над лётчиком вспыхнул яркий купол парашюта. С. Вишенков, «Испытатели», 1947 г. [НКРЯ]
- устар., ныне неправ. то же, что килограмм-сила; единица силы в некоторых устаревших системах единиц ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- кило, кг
- килограмм-сила, килопонд, кГ
Антонимы
- —
- —
Гиперонимы
- единица, мера; масса
- единица, мера; сила
Гипонимы
- —
- —
Родственные слова
| Ближайшее родство | |
|
Этимология
Происходит от др.-греч. χίλιοι «тысяча» + γράμμα «скрупул», далее от γραμμή «линия, черта» < γράφω «пишу» + -μα, суффикс результата действия; переход в греческом от «черты» к мере веса — семантическая калька с лат. scrupulum (вин.п. от scrupulus «острый камушек; скрупул», уменьш. от scrupus «острый камень»), ошибочно интерпретированного как производное от лат. scribo «пишу, черчу».
Фразеологизмы и устойчивые сочетания
Перевод
| Список переводов | |
|
| Килограмм | |
| кг, kg | |
| Величина |
Масса |
|---|---|
| Система |
СИ |
| Эталон |
Есть |
|
Основная |
|
| примечание | |
|
См. Приставки СИ |
Компьютерное изображение международного прототипа килограмма (эталон килограмма). Размер прототипа сопоставим с размером мяча для гольфа, в соответствии с находящейся рядом дюймовой шкалой. Образец сделан из сплава 90 % платины и 10 % иридия в виде цилиндра 39,17 мм. Прототип хранится в штаб-квартире Международного бюро мер и весов в Севре. Как и другие прототипы, края образца имеют четырёхугольные срезы, чтобы минимизировать износ материала.
Килогра́мм (русское обозначение: кг; международное: kg) — единица измерения массы, одна из семи основных единиц Международной системы единиц (СИ).
Действующее определение килограмма принято III Генеральной конференцией по мерам и весам в 1901 году и формулируется так[1][2]:
Килограмм есть единица массы, равная массе международного прототипа килограмма.
Международный прототип (эталон) килограмма, хранится в Международном бюро мер и весов (расположено в г. Севр близ Парижа) и представляет собой цилиндр диаметром и высотой 39.17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия). Первоначально килограмм определялся как масса одного кубического дециметра (литра) чистой воды при температуре 4 °C и стандартном атмосферном давлении на уровне моря.
Содержание
- 1 Кратные и дольные единицы
- 2 Эталон килограмма
- 3 Перспективы
- 4 Примечания
- 5 См. также
- 6 Литература
- 7 Ссылки
Кратные и дольные единицы
По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10−3 кг).
Вместо мегаграмма (1000 кг), как правило, используют единицу измерения «тонна».
В определениях мощности атомных бомб в тротиловом эквиваленте вместо гигаграмма применяется килотонна, вместо тераграмма — мегатонна.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 г | декаграмм | даг | dag | 10−1 г | дециграмм | дг | dg |
| 102 г | гектограмм | гг | hg | 10−2 г | сантиграмм | сг | cg |
| 103 г | килограмм | кг | kg | 10−3 г | миллиграмм | мг | mg |
| 106 г | мегаграмм | Мг | Mg | 10−6 г | микрограмм | мкг | µg |
| 109 г | гигаграмм | Гг | Gg | 10−9 г | нанограмм | нг | ng |
| 1012 г | тераграмм | Тг | Tg | 10−12 г | пикограмм | пг | pg |
| 1015 г | петаграмм | Пг | Pg | 10−15 г | фемтограмм | фг | fg |
| 1018 г | эксаграмм | Эг | Eg | 10−18 г | аттограмм | аг | ag |
| 1021 г | зеттаграмм | Зг | Zg | 10−21 г | зептограмм | зг | zg |
| 1024 г | йоттаграмм | Иг | Yg | 10−24 г | йоктограмм | иг | yg |
| применять не рекомендуется не применяются или редко применяются на практике |
Эталон килограмма
Копия эталона 1 кг, хранится в США.
|
|
В этой статье не хватает ссылок на источники информации.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
|
|
Информация в этой статье или некоторых её разделах устарела.
Вы можете помочь проекту, обновив её и убрав после этого данный шаблон. |
Дрейф массы копий эталона
На данный момент килограмм — единственная единица СИ, которая определена при помощи предмета, изготовленного людьми — платиново-иридиевого эталона. Все остальные единицы теперь определяются с помощью фундаментальных физических свойств и законов.
В XVIII веке при создании метрической системы мер килограмм был определён как масса 1 дм³ воды при 4°C (при этой температуре у воды наибольшая плотность). В 1799 году был изготовлен прототип килограмма в виде платиновой гири, однако его масса была на 0,028 г больше массы 1 дм³ воды[3].
Нынешний эталон был изготовлен в 1889 году из платиново-иридиевого сплава в виде цилиндра высотой и диаметром 39 мм[3]. С тех пор он хранится в Международном бюро мер и весов под тремя герметичными стеклянными колпаками. Были изготовлены также точные официальные копии международного эталона, которые используются как национальные эталоны килограмма. Всего было создано более 80 копий. Две копии международного эталона были переданы России[3], они хранятся во ВНИИ метрологии им. Менделеева. Примерно раз в 10 лет национальные эталоны сравниваются с международным. Эти сравнения показывают, что точность национальных эталонов составляет примерно 2 мкг. Так как они хранятся в тех же условиях, нет никаких оснований считать, что международный эталон точнее. По разным причинам за сто лет международный эталон теряет 3·10−8 своей массы. Однако, по определению, масса международного эталона в точности равна одному килограмму. Поэтому любые изменения действительной массы эталона приводят к изменению величины килограмма.
Исходя из стремления к устранению упомянутых нестабильностей, XXI Генеральная конференция по мерам и весам в 1999 году в своей Резолюции рекомендовала национальным лабораториям продолжить усилия по совершенствованию установления связи единицы массы с фундаментальными или атомными константами, имея в виду будущее переопределение килограмма[4]. В последующее десятилетие рядом международных организаций велась работа по выработке предварительных предложений о переопределении килограмма[5].
Перспективы
В 2011 году XXIV Генеральная конференция по мерам и весам приняла Резолюцию[6], в которой предложено в будущей ревизии Международной системы единиц (СИ) продолжить переопределение основных единиц таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.
В частности, предполагается, что СИ станет системой единиц, в которой постоянная Планка h равна 6,626 06X·10−34 Джc точно[7]. Результатом этого должна явиться отмена ныне действующего определения килограмма и принятие нового. Как сказано в Резолюции, «килограмм останется единицей массы, но его величина будет установлена путём фиксации численного значения постоянной Планка в точности равным 6,626 06X·10−34, когда оно выражается единицей СИ м2·кг·с−1, которая равна Дж·с».
Примечания
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин.
- ↑ Определение килограмма на сайте Международного бюро мер и весов
- ↑ 1 2 3 Килограмм — статья из Большой советской энциклопедии (3-е издание). К. П. Широков
- ↑ The definition of the kilogram Resolution 7 of the 21st meeting of the CGPM (1999)
- ↑ Каршенбойм С. Г. О переопределении килограмма и ампера в терминах фундаментальных физических констант // УФН. — 2006. — Т. 176. — № 9. — С. 975-982.
- ↑ On the possible future revision of the International System of Units, the SI. Resolution 1 of the 24th meeting of the CGPM (2011).
- ↑ Здесь Х заменяет одну или более значащих цифр, которые будут определены в окончательном релизе на основании наиболее точных рекомендаций CODATA
См. также
- Килограмм-сила
Литература
- Смирнова Н. А. Единицы измерений массы и веса в Международной системе единиц. — М, 1966.
Ссылки
| Килограмм на Викискладе? |
|
Единицы СИ |
||
|---|---|---|
| Основные единицы | Ампер · Кандела · Кельвин · Килограмм · Метр · Моль · Секунда |  |
| Производные единицы | Беккерель · Ватт · Вебер · Вольт · Генри · Герц · Градус Цельсия · Грей · Джоуль · Зиверт · Катал · Кулон · Люкс · Люмен · Ньютон · Ньютон-метр · Ом · Паскаль · Радиан · Сименс · Стерадиан · Тесла · Фарад | |
| Астрономическая единица · Гектар · Градус дуги · Дальтон (Атомная единица массы) · День · Децибел · Литр · Минута · Минута дуги · Непер · Секунда дуги · Тонна · Час · Электронвольт Атомная система единиц · Природная система единиц |
||
| См. также | Приставки СИ · Система физических величин · Преобразование единиц · Новые определения СИ · История метрической системы | |
| |
|
|---|---|
| Кратные приставки |
дека- (101) · гекто- (102) · кило- (103) · мега- (106) · гига- (109) · тера- (1012) · пета- (1015) · экса- (1018) · зетта- (1021) · йотта- (1024) |
| Дольные приставки |
деци- (10−1) · санти- (10−2) · милли- (10−3) · микро- (10−6) · нано- (10−9) · пико- (10−12) · фемто- (10−15) · атто- (10−18) · зепто- (10−21) · йокто- (10−24) |
Всего найдено: 8
Избавиться от лишних килограмм или килограммов
Ответ справочной службы русского языка
Верно: от лишних килограммов.
Как правильно образовать формы Р.п. мн.ч. от слова килограмм: килограмм или килограммов?
Ответ справочной службы русского языка
См. ответ на вопрос № 275589.
Как правильно пять килограмм или килограммов?
Ответ справочной службы русского языка
См. ответ на вопрос № 275589.
Подскажите,пожалуйста, как правильно пишется килограмм или килограммов?
Сегодня финалы в 2-х весовых категориях до 66 килограмм — на ковёр выйдет Ирбек Фарниев, а в весе до 74 килограмм за третье в своей карьере олимпийское золото поборется спортсмен Буйвайсар Сайтиев.
Ответ справочной службы русского языка
Лучше: в 2 весовых категориях до 66 килограммов.
подскажите как правильно,килограмм или килограммов?например-купил на рынке 5 килограмм(ов)? помидор(ов)?
Ответ справочной службы русского языка
Правильно: пять килограммов (и килограмм) помидоров.
Справка, подскажите, ; вес рыбы был шесть килограмм или килограммов ?
Ответ справочной службы русского языка
В устной речи допустимо: _шесть килограмм_. На письме лучше: _шесть килограммов_.
Как правильно говорить:
десять грамм или граммов
десять килограмм или килограммов?
Спасибо!
Ответ справочной службы русского языка
См. ответ № 213538.
Как правильно-помодор или помидоров, килограмм или килограммов? Напомните соответствующее правило. Еще интересует значение слов КРЕАТИВ, КРЕАТИВНЫЙ, ДЕВИАНТНЫЙ. Спасибо.
Ответ справочной службы русского языка
См. ответ № 191698 . _Креатив_ — творчество, созидание. _Креативный_ — творческий. _девиантный_ — имеющий отклонения.
Правописание «килограмм» и «килограммов»: когда как пишется, примеры употребления, грамматика
Слово «килограмм» имеет две формы множественного числа и седьмой (счётный) падеж, по написанию совпадающий с множественным числом родительного (см. ниже).
- В отвлечённом значении множественное от «килограмм» в родительном падеже на письме идентично именительному,
- а в предметном пишется с окончанием «-ов»: «килограммов».
В нормативной орфографии «килограмм» считается точной формой, а «килограммов» просторечной и допустимой в определённых случаях.
Когда что писать?
Для обозначения суммарного весового количества чего-либо слова «килограмм» или «килограммов» правильно употребляются в зависимости как от того, что исчисляется килограммах – нечто вещественное или же некая умозрительная численная величина – а также от контекста (общего смысла) высказывания:
- «Давлению в 1 Паскаль (1 Па) соответствует действие 0,10197 килограмм-сил на 1 кв. м. поверхности, с точностью до 5-го знака после запятой». Давление величина исчислимая, измеримая с любой необходимой для практики точностью. Поэтому множественное от «килограмм» пишется без окончания, «по-научному».
- «Масса Земли составляет около 5,972х1024 килограммов». Масса нашей планеты величина «научная», но вычислить её абсолютно точно невозможно: на Землю ежегодно выпадает от 25 до 40 тыс. тонн только лишь космической пыли. А ежегодные потери ею же массы за счёт истечения газов из атмосферы оцениваются величиной того же порядка. Т.е. масса Земли величина нестабильная, и писать «килограммов» тут лучше в «простой» форме.
- «Солнце ежесекундно излучает, в переводе на массу по формуле Эйнштейна, примерно 6,2х105 килограммов или 620 тонн видимого света» – «620 тонн света» величина также численная якобы научная, однако более чем условная. Такая фраза сошла бы в научно-популярной литературе 50-х годов, но исчислять энергию в единицах массы физически некорректно. Поэтому в данном случае также следует писать «просторечное» «килограммов».
- «Грузоподъёмность обычного (городского) двухколёсного велосипеда для взрослых составляет от 120 до 150 килограмм в зависимости от модели» – пишем «точное» «килограмм», так как имеется в виду жизненно важная точная величина.
- «Отвесьте мне пять килограммов яблок». Яблоки – счислимые неделимые предметы. Их не станут резать на дольки, чтобы точно подогнать вес. Отсчитают на глазок поштучно, а покупатель заплатит за столько, сколько покажут весы. Значит, в подобных случаях нужно писать «простое» «килограммов». В просторечии допустимо «<столько-то> килограмм <штучного товару>», но в торговых документах весьма и весьма желательно писать «<столько-то> килограммов».
Особенности счётного падежа
Применительно к исчислимым предметам «килограмм» употребляется не во множественном числе родительного, а в счётном падеже. Этот падеж не имеет числа, единственного или множественного, и, соответственно, синтаксическое согласование слов, к которым относится «килограмм» в счётном падеже, производится не по нему, а по контексту высказывания. Попросту говоря, если в килограмме более одной штуки чего-то, то и писать его нужно во множественном числе, независимо от того, как написано «килограмм», или «килограммов»:
- «Тут вышло пяток апельсин на килограмм» – неверно! Правильно будет «<столько-то> апельсинов на килограмм».
- «Отпустите мне пять килограмм помидор» – тоже неправильно! «Килограмм» вместо «килограммов» в речевом обиходе вполне допустимо, но, раз имеется в виду не 1 (один) пятикилограммовый помидор, то слово, обозначающее их совокупный вес, нужно ставить во множественное число: «<столько-то> килограмм помидоров».
Грамматика
Слово «килограмм» – неодушевлённое имя существительное мужского рода 2-го склонения. Состоит из префиксоида «кило-» и корня «-грамм». Постановка ударения и разделение переносами ки-ло-гра́мм. Падежные формы:
- Именительный: килогра́мм (ед. ч.); килогра́ммы (мн. ч.).
- Родительный: килогра́мма (ед. ч.); килогра́мм или килогра́ммов (мн. ч.).
- Дательный: килогра́мму (ед. ч.); килогра́ммам (мн. ч.).
- Винительный: килогра́мм (ед. ч.); килогра́ммы (мн. ч.).
- Творительный: килогра́ммом (ед. ч.); килогра́ммами (мн. ч.).
- Предложный: килогра́мме (ед. ч.); килогра́ммах (мн. ч.).
- Счётный: килогра́мм, килогра́ммов (число отсутствует).
Примечание: префиксоиды это приставки, имеющие некоторые свойства существительных или прилагательных; в частности – собственное значение. «Кило-», как известно, означает 1000 (тысячу), «мега-» – миллион, «полу-» – половину, «дву-» – двойное количество («Дву-пять шапок серебра» в «Коньке-горбунке» П. П. Ершова).
Значение
Слово «килограмм» в живой русской речи употребляется только в точном (прямом) значении:
- Эталон инертной массы тела, одна из основных единиц международной системы мер и весов СИ. Синоним кг (в середине предложения пишется без точки).
- Как указатель веса физических тел в поле силы тяжести на поверхности Земли: «А сколько килограмм в этом мешке картошки?» Синоним «кило».
Примечание: в непрофессиональных технических писаниях «килограмм» нередко употребляется взамен термина «килограмм-сила» (кгс). Это значение дважды устаревшее, так как понятием «грамм-сила» оперировала система мер весов СГС, а в СИ сила изначально измеряется в ньютонах (Н). 1 кгс в первом приближении равна 9,81 Н.
***
© ПишемПравильно.ру
Автор: Садов Артур Александрович, лингвист-типолог
Перечень академических источников, использовавшихся при подготовке материалов.
Правописание этих слов надо знать:
Проверить еще слово: