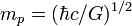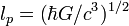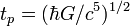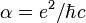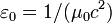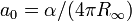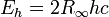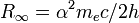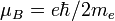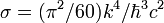Физическая константа
- Физическая константа
-
Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.
Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.
Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.
Содержание
- 1 Фундаментальные физические постоянные
- 2 Размерные комбинации фундаментальных постоянных
- 3 Постоянные, связывающие разные системы единиц
- 4 Некоторые другие физические постоянные
- 5 Примечания
- 6 Ссылки
Фундаментальные физические постоянные
Величина Символ Значение Прим. скорость света в вакууме c 299 792 458 м·с−1 точно характеристическое сопротивление вакуума Z0 = μ0c 376,730 313 46177… Ω точно гравитационная постоянная G 6,674 28(67)×10−11 м3·кг−1·с−2 a[1] постоянная Планка (элементарный квант действия) h 6,626 068 96(33)×10−34 Дж·с a постоянная Дирака (или приведенная постоянная Планка) 1,054 571 628(53)×10−34 Дж·с a элементарный заряд e 1,602 176 487(40)×10−19 Кл a магнитная постоянная (по старой терминологии, магнитная проницаемость вакуума) μ0 Н·А−2
точно 1,256 637 061 4359… ×10−6 Н·А−2 точно постоянная Вина b 2,89782×10-3К·м а Размерные комбинации фундаментальных постоянных
Название Символ Значение Прим. планковская масса 2,176 44(11)×10−8 кг a планковская длина 1,616 252(81)×10−35 м a планковское время 5,391 24(27)×10−44 с a Постоянные, связывающие разные системы единиц
Название Символ Значение Прим. постоянная тонкой структуры 7,297 352 5376(50)×10−3 a α — 1 137,035 999 679(94) a электрическая постоянная (по старой терминологии, диэлектрическая проницаемость вакуума) 8,854 187 817 620… ×10−12 Ф·м−1 точно атомная единица массы mu = 1 а. е. м. 1,660 538 782(83)×10−27 кг a постоянная Больцмана k 1,380 6504(24)×10−23 Дж·К−1 a Некоторые другие физические постоянные
Название Символ Значение Прим. масса электрона me 9,109 382 15(45)×10−31 кг a масса протона mp 1,672 621 637(83)×10−27 кг a масса нейтрона mn 1,674 927 211(84)×10−27 кг a число Авогадро L, NA 6,022 141 79(30)×1023 моль−1 a постоянная Фарадея F = NAe 96 485,3399(24) Кл·моль−1 a газовая постоянная R = kNA 8,314 472(15) Дж·К−1·моль−1 a удельный молярный объём идеального газа (при 273,15 К, 101,325 кПа) 22,413 996(39)×10−3 м³·моль−1 a стандартное атмосферное давление atm 101 325 Па (точно) a боровский радиус 0,529 177 208 59(36)×10−10 м a энергия Хартри 4,359 743 94(22)×10−18 Дж a постоянная Ридберга 109 677,585 685 27(73) см−1 a магнетон Бора 927,400 915(23)×10−26 Дж·Тл−1 a магнитный момент электрона μe −928,476 377(23)×10-26 Дж·Тл−1 a g-фактор свободного электрона ge = 2μe / μB 2,002 319 304 3622(15) a ядерный магнетон μN 5,050 783 24(13)×10-27 Дж·Тл−1 a магнитный момент протона μp 1,410 606 662(37)×10-26 Дж·Тл−1 a гиромагнитное отношение протона γp = 2μp / μN 2,675 222 099(70)×108 с−1·Тл−1 a постоянная Стефана-Больцмана 5,670 400(40)×10−8 Вт·м−2·К−4 a первая радиационная постоянная c1 = 2πhc2 3,741 771 18(19)×10−16 Вт·м² a вторая радиационная постоянная c2 1,438 7752(25)×10−2 м·К a стандартное ускорение свободного падения на поверхности Земли gn 9,806 65 м·с−2 a Примечания
- ↑ CODATA Internationally recommended values of the Fundamental Physical Constants
Ссылки
- Fundamental Physical Constants — Complete Listing (англ.).
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Физическая константа» в других словарях:
-
физическая константа — fizikinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Pastovus dydis, įeinantis į kurio nors fizikos dėsnio matematinę išraišką. atitikmenys: angl. physical constant vok. physikalische Konstante, f rus. физическая… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
-
Константа — Константа: Постоянная Математическая Физическая Константа (в программировании) Константа диссоциации кислоты Константа равновесия Константа скорости реакции Константа (Остаться в живых) См. также Констанция Констанций Константин Констант… … Википедия
-
Фундаментальная физическая константа — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия
-
Константа диссоциации — Константа диссоциации вид константы равновесия, которая показывает склонность большого объекта диссоциировать (разделяться) обратимым образом на маленькие объекты, как например когда комплекс распадается на составляющие молекулы, или когда… … Википедия
-
КОНСТАНТА ВЗАИМОДЕЙСТВИЯ — (константа связи) (от лат. constans постоянный) в квантовой теории поля (КТП) параметр, определяющий силу (интенсивность) взаимодействия частиц или полей. В общем виде К. в. задаётся как значение вершинной части (вершины) при определ. значениях… … Физическая энциклопедия
-
Константа автопротолиза — Константа автопротолиза физическая величина, характеризующая способность протонного растворителя к диссоциации. Обозначается KS. Является произведением концентраций иона лиония и иона лиата. Так, например, для растворителя, который… … Википедия
-
Константа равновесия — У этого термина существуют и другие значения, см. Константа. Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации … Википедия
-
ФИЗИЧЕСКАЯ ХИМИЯ — раздел химии, в котором изучаются химические свойства веществ на основе физических свойств составляющих их атомов и молекул. Современная физическая химия широкая междисциплинарная область, граничащая с различными разделами физики, биофизики и… … Энциклопедия Кольера
-
Константа диссоциации кислоты — У этого термина существуют и другие значения, см. Константа. Константа диссоциации кислоты (Ka) константа равновесия реакции диссоциации кислоты на ион водорода и анион кислотного остатка. Для многоосновных кислот, диссоциация которых… … Википедия
-
Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия
A physical constant, sometimes fundamental physical constant or universal constant, is a physical quantity that is generally believed to be both universal in nature and have constant value in time. It is contrasted with a mathematical constant, which has a fixed numerical value, but does not directly involve any physical measurement.
There are many physical constants in science, some of the most widely recognized being the speed of light in a vacuum c, the gravitational constant G, the Planck constant h, the electric constant ε0, and the elementary charge e. Physical constants can take many dimensional forms: the speed of light signifies a maximum speed for any object and its dimension is length divided by time; while the fine-structure constant α, which characterizes the strength of the electromagnetic interaction, is dimensionless.
The term fundamental physical constant is sometimes used to refer to universal-but-dimensioned physical constants such as those mentioned above.[1] Increasingly, however, physicists only use fundamental physical constant for dimensionless physical constants, such as the fine-structure constant α.
Physical constant, as discussed here, should not be confused with other quantities called «constants», which are assumed to be constant in a given context without being fundamental, such as the «time constant» characteristic of a given system, or material constants (e.g., Madelung constant, electrical resistivity, and heat capacity).
Since May 2019, all of the SI base units have been defined in terms of physical constants. As a result, five constants: the speed of light in vacuum, c; the Planck constant, h; the elementary charge, e; the Avogadro constant, NA; and the Boltzmann constant, kB, have known exact numerical values when expressed in SI units. The first three of these constants are fundamental constants, whereas NA and kB are of a technical nature only: they do not describe any property of the universe, but instead only give a proportionality factor for defining the units used with large numbers of atomic-scale entities.
Choice of units[edit]
Whereas the physical quantity indicated by a physical constant does not depend on the unit system used to express the quantity, the numerical values of dimensional physical constants do depend on choice of unit system.
The term «physical constant» refers to the physical quantity, and not to the numerical value within any given system of units. For example, the speed of light is defined as having the numerical value of 299792458 when expressed in the SI unit metres per second, and as having the numerical value of 1 when expressed in the natural units Planck length per Planck time. While its numerical value can be defined at will by the choice of units, the speed of light itself is a single physical constant.
Any ratio between physical constants of the same dimensions results in a dimensionless physical constant, for example, the proton-to-electron mass ratio. Any relation between physical quantities can be expressed as a relation between dimensionless ratios via a process known as nondimensionalisation.
The term of «fundamental physical constant» is reserved for physical quantities which, according to the current state of knowledge, are regarded as immutable and as non-derivable from more fundamental principles. Notable examples are the speed of light c, and the gravitational constant G.
The fine-structure constant α is the best known dimensionless fundamental physical constant. It is the value of the elementary charge squared expressed in Planck units. This value has become a standard example when discussing the derivability or non-derivability of physical constants. Introduced by Arnold Sommerfeld, its value as determined at the time was consistent with 1/137. This motivated Arthur Eddington (1929) to construct an argument why its value might be 1/137 precisely, which related to the Eddington number, his estimate of the number of protons in the Universe.[2] By the 1940s, it became clear that the value of the fine-structure constant deviates significantly from the precise value of 1/137, refuting Eddington’s argument.[3]
With the development of quantum chemistry in the 20th century, however, a vast number of previously inexplicable dimensionless physical constants were successfully computed from theory.[citation needed] In light of that, some theoretical physicists still hope for continued progress in explaining the values of other dimensionless physical constants.
It is known that the Universe would be very different if these constants took values significantly different from those we observe. For example, a few percent change in the value of the fine structure constant would be enough to eliminate stars like our Sun. This has prompted attempts at anthropic explanations of the values of some of the dimensionless fundamental physical constants.
Natural units[edit]
It is possible to combine dimensional universal physical constants to define fixed quantities of any desired dimension, and this property has been used to construct various systems of natural units of measurement. Depending on the choice and arrangement of constants used, the resulting natural units may be convenient to an area of study. For example, Planck units, constructed from c, G, ħ, and kB give conveniently sized measurement units for use in studies of quantum gravity, and Hartree atomic units, constructed from ħ, me, e and 4πε0 give convenient units in atomic physics. The choice of constants used leads to widely varying quantities.
Number of fundamental constants[edit]
The number of fundamental physical constants depends on the physical theory accepted as «fundamental».
Currently, this is the theory of general relativity for gravitation and the Standard Model for electromagnetic, weak and strong nuclear interactions and the matter fields.
Between them, these theories account for a total of 19 independent fundamental constants.
There is, however, no single «correct» way of enumerating them, as it is a matter of arbitrary choice which quantities are considered «fundamental» and which as «derived». Uzan (2011) lists 22 «unknown constants» in the fundamental theories, which give rise to 19 «unknown dimensionless parameters», as follows:
- the gravitational constant G,
- the speed of light c,
- the Planck constant h,
- the 9 Yukawa couplings for the quarks and leptons (equivalent to specifying the rest mass of these elementary particles),
- 2 parameters of the Higgs field potential,
- 4 parameters for the quark mixing matrix,
- 3 coupling constants for the gauge groups SU(3) × SU(2) × U(1) (or equivalently, two coupling constants and the Weinberg angle),
- a phase for the QCD vacuum.
The number of 19 independent fundamental physical constants is subject to change under possible extensions of the Standard Model, notably by the introduction of neutrino mass (equivalent to seven additional constants, i.e. 3 Yukawa couplings and 4 lepton mixing parameters).[4]
The discovery of variability in any of these constants would be equivalent to the discovery of «new physics».[5]
The question as to which constants are «fundamental» is neither straightforward nor meaningless, but a question of interpretation of the physical theory regarded as fundamental; as pointed out by Lévy-Leblond 1977, not all physical constants are of the same importance, with some having a deeper role than others.
Lévy-Leblond 1977 proposed a classification schemes of three types of constants:
- A: physical properties of particular objects
- B: characteristic of a class of physical phenomena
- C: universal constants
The same physical constant may move from one category to another as the understanding of its role deepens; this has notably happened to the speed of light, which was a class A constant (characteristic of light) when it was first measured, but became a class B constant (characteristic of electromagnetic phenomena) with the development of classical electromagnetism, and finally a class C constant with the discovery of special relativity.[6]
Tests on time-independence[edit]
By definition, fundamental physical constants are subject to measurement, so that their being constant (independent on both the time and position of the performance of the measurement) is necessarily an experimental result and subject to verification.
Paul Dirac in 1937 speculated that physical constants such as the gravitational constant or the fine-structure constant might be subject to change over time in proportion of the age of the universe. Experiments can in principle only put an upper bound on the relative change per year. For the fine-structure constant, this upper bound is comparatively low, at
roughly 10−17 per year (as of 2008).[7]
The gravitational constant is much more difficult to measure with precision, and conflicting measurements in the 2000s have inspired the controversial suggestions of a periodic variation of its value in a 2015 paper.[8] However, while its value is not known to great precision, the possibility of observing type Ia supernovae which happened in the universe’s remote past, paired with the assumption that the physics involved in these events is universal, allows for an upper bound of less than 10−10 per year for the gravitational constant over the last nine billion years.[9]
Similarly, an upper bound of the change in the proton-to-electron mass ratio has been placed at 10−7 over a period of 7 billion years (or 10−16 per year) in a 2012 study based on the observation of methanol in a distant galaxy.[10][11]
It is problematic to discuss the proposed rate of change (or lack thereof) of a single dimensional physical constant in isolation. The reason for this is that the choice of units is arbitrary, making the question of whether a constant is undergoing change an artefact of the choice (and definition) of the units.[12][13][14]
For example, in SI units, the speed of light was given a defined value in 1983. Thus, it was meaningful to experimentally measure the speed of light in SI units prior to 1983, but it is not so now. Similarly, with effect from May 2019, the Planck constant has a defined value, such that all SI base units are now defined in terms of fundamental physical constants. With this change, the international prototype of the kilogram is being retired as the last physical object used in the definition of any SI unit.
Tests on the immutability of physical constants look at dimensionless quantities, i.e. ratios between quantities of like dimensions, in order to escape this problem. Changes in physical constants are not meaningful if they result in an observationally indistinguishable universe. For example, a «change» in the speed of light c would be meaningless if accompanied by a corresponding change in the elementary charge e so that the ratio e2/(4πε0ħc) (the fine-structure constant) remained unchanged.[15]
Fine-tuned universe[edit]
Some physicists have explored the notion that if the dimensionless physical constants had sufficiently different values, our Universe would be so radically different that intelligent life would probably not have emerged, and that our Universe therefore seems to be fine-tuned for intelligent life. However, the phase space of the possible constants and their values is unknowable, so any conclusions drawn from such arguments are unsupported. The anthropic principle states a logical truism: the fact of our existence as intelligent beings who can measure physical constants requires those constants to be such that beings like us can exist. There are a variety of interpretations of the constants’ values, including that of a divine creator (the apparent fine-tuning is actual and intentional), or that ours is one universe of many in a multiverse (e.g. the many-worlds interpretation of quantum mechanics), or even that, if information is an innate property of the universe and logically inseparable from consciousness, a universe without the capacity for conscious beings cannot exist.
The fundamental constants and quantities of nature have been discovered to be fine-tuned to such an extraordinarily narrow range that if it were not, the origin and evolution of conscious life in the universe would not be permitted.[16]
Table of physical constants[edit]
The table below lists some frequently used constants and their CODATA recommended values. For a more extended list, refer to List of physical constants.
| Quantity | Symbol | Value[17] | Relative standard uncertainty |
|---|---|---|---|
| elementary charge | 
|
1.602176634×10−19 C[18] | 0 |
| Newtonian constant of gravitation | 
|
6.67430(15)×10−11 m3⋅kg−1⋅s−2[19] | 2.2×10−5 |
| Planck constant | 
|
6.62607015×10−34 J⋅Hz−1[20] | 0 |
| speed of light in vacuum | 
|
299792458 m⋅s−1[21] | 0 |
| vacuum electric permittivity | 
|
8.8541878128(13)×10−12 F⋅m−1[22] | 1.5×10−10 |
| vacuum magnetic permeability | 
|
1.25663706212(19)×10−6 N⋅A−2[23] | 1.5×10−10 |
| electron mass | 
|
9.1093837015(28)×10−31 kg[24] | 3.0×10−10 |
| fine-structure constant | 
|
7.2973525693(11)×10−3[25] | 1.5×10−10 |
| Josephson constant | 
|
483597.8484…×109 Hz⋅V−1[26] | 0 |
| Rydberg constant | 
|
10973731.568160(21) m−1[27] | 1.9×10−12 |
| von Klitzing constant | 
|
25812.80745… Ω[28] | 0 |
See also[edit]
- List of common physics notations
References[edit]
- ^ «Fundamental Physical Constants from NIST». Archived from the original on 2016-01-13. Retrieved 2016-01-14. NIST
- ^
A.S Eddington (1956). «The Constants of Nature». In J.R. Newman (ed.). The World of Mathematics. Vol. 2. Simon & Schuster. pp. 1074–1093. - ^
H. Kragh (2003). «Magic Number: A Partial History of the Fine-Structure Constant». Archive for History of Exact Sciences. 57 (5): 395–431. doi:10.1007/s00407-002-0065-7. S2CID 118031104. - ^ Uzan, Jean-Philippe (2011). «Varying Constants, Gravitation and Cosmology». Living Reviews in Relativity. 14 (1): 2. arXiv:1009.5514. Bibcode:2011LRR….14….2U. doi:10.12942/lrr-2011-2. PMC 5256069. PMID 28179829.
Any constant varying in space and/or time would reflect the existence of an almost massless field that couples to matter. This will induce a violation of the universality of free fall. Thus, it is of utmost importance for our understanding of gravity and of the domain of validity of general relativity to test for their constancy.
- ^ Uzan, Jean-Philippe (2011). «Varying Constants, Gravitation and Cosmology». Living Reviews in Relativity. 14 (1): 2. arXiv:1009.5514. Bibcode:2011LRR….14….2U. doi:10.12942/lrr-2011-2. PMC 5256069. PMID 28179829.
- ^ Lévy-Leblond, J. (1977). «On the conceptual nature of the physical constants». La Rivista del Nuovo Cimento. Series 2. 7 (2): 187–214. Bibcode:1977NCimR…7..187L. doi:10.1007/bf02748049. S2CID 121022139.Lévy-Leblond, J.-M. (1979). «The importance of being (a) Constant». In Toraldo di Francia, G. (ed.). Problems in the Foundations of Physics, Proceedings of the International School of Physics ‘Enrico Fermi’ Course LXXII, Varenna, Italy, July 25 – August 6, 1977. New York: NorthHolland. pp. 237–263.
- ^
T. Rosenband; et al. (2008). «Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place». Science. 319 (5871): 1808–12. Bibcode:2008Sci…319.1808R. doi:10.1126/science.1154622. PMID 18323415. S2CID 206511320. - ^ J.D. Anderson; G. Schubert; V. Trimble; M.R. Feldman (April 2015), «Measurements of Newton’s gravitational constant and the length of day», EPL, 110 (1): 10002, arXiv:1504.06604, Bibcode:2015EL….11010002A, doi:10.1209/0295-5075/110/10002, S2CID 119293843
- ^ J. Mould; S. A. Uddin (2014-04-10), «Constraining a Possible Variation of G with Type Ia Supernovae», Publications of the Astronomical Society of Australia, 31: e015, arXiv:1402.1534, Bibcode:2014PASA…31…15M, doi:10.1017/pasa.2014.9, S2CID 119292899
- ^ Bagdonaite, Julija; Jansen, Paul; Henkel, Christian; Bethlem, Hendrick L.; Menten, Karl M.; Ubachs, Wim (December 13, 2012). «A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe» (PDF). Science. 339 (6115): 46–48. Bibcode:2013Sci…339…46B. doi:10.1126/science.1224898. hdl:1871/39591. PMID 23239626. S2CID 716087.
- ^ Moskowitz, Clara (December 13, 2012). «Phew! Universe’s Constant Has Stayed Constant». Space.com. Archived from the original on December 14, 2012. Retrieved December 14, 2012.
- ^ Duff, Michael (2015). «How fundamental are fundamental constants?». Contemporary Physics. 56 (1): 35–47. arXiv:1412.2040. Bibcode:2015ConPh..56…35D. doi:10.1080/00107514.2014.980093. hdl:10044/1/68485. S2CID 118347723.
- ^ Duff, M. J. (13 August 2002). «Comment on time-variation of fundamental constants». arXiv:hep-th/0208093.
- ^ Duff, M. J.; Okun, L. B.; Veneziano, G. (2002). «Trialogue on the number of fundamental constants». Journal of High Energy Physics. 2002 (3): 023. arXiv:physics/0110060. Bibcode:2002JHEP…03..023D. doi:10.1088/1126-6708/2002/03/023. S2CID 15806354.
- ^ Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8
«[An] important lesson we learn from the way that pure numbers like α define the World is what it really means for worlds to be different. The pure number we call the fine structure constant and denote by α is a combination of the electron charge, e, the speed of light, c, and Planck’s constant, h. At first we might be tempted to think that a world in which the speed of light was slower would be a different world. But this would be a mistake. If c, h, and e were all changed so that the values they have in metric (or any other) units were different when we looked them up in our tables of physical constants, but the value of α remained the same, this new world would be observationally indistinguishable from our World. The only thing that counts in the definition of worlds are the values of the dimensionless constants of Nature. If all masses were doubled in value you cannot tell, because all the pure numbers defined by the ratios of any pair of masses are unchanged.» - ^ Leslie, John (1998). Modern Cosmology & Philosophy. University of Michigan: Prometheus Books. ISBN 1573922501.
- ^ The values are given in the so-called concise form, where the number in parentheses indicates the standard uncertainty referred to the least significant digits of the value.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-28.
- ^ «2018 CODATA Value: speed of light in vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: vacuum magnetic permeability». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Josephson constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Rydberg constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: von Klitzing constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). «CODATA Recommended Values of the Fundamental Physical Constants: 2006» (PDF). Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. doi:10.1103/RevModPhys.80.633. Archived from the original (PDF) on 2017-10-01.
- Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8.
External links[edit]
- Sixty Symbols, University of Nottingham
- IUPAC — Gold Book
A physical constant, sometimes fundamental physical constant or universal constant, is a physical quantity that is generally believed to be both universal in nature and have constant value in time. It is contrasted with a mathematical constant, which has a fixed numerical value, but does not directly involve any physical measurement.
There are many physical constants in science, some of the most widely recognized being the speed of light in a vacuum c, the gravitational constant G, the Planck constant h, the electric constant ε0, and the elementary charge e. Physical constants can take many dimensional forms: the speed of light signifies a maximum speed for any object and its dimension is length divided by time; while the fine-structure constant α, which characterizes the strength of the electromagnetic interaction, is dimensionless.
The term fundamental physical constant is sometimes used to refer to universal-but-dimensioned physical constants such as those mentioned above.[1] Increasingly, however, physicists only use fundamental physical constant for dimensionless physical constants, such as the fine-structure constant α.
Physical constant, as discussed here, should not be confused with other quantities called «constants», which are assumed to be constant in a given context without being fundamental, such as the «time constant» characteristic of a given system, or material constants (e.g., Madelung constant, electrical resistivity, and heat capacity).
Since May 2019, all of the SI base units have been defined in terms of physical constants. As a result, five constants: the speed of light in vacuum, c; the Planck constant, h; the elementary charge, e; the Avogadro constant, NA; and the Boltzmann constant, kB, have known exact numerical values when expressed in SI units. The first three of these constants are fundamental constants, whereas NA and kB are of a technical nature only: they do not describe any property of the universe, but instead only give a proportionality factor for defining the units used with large numbers of atomic-scale entities.
Choice of units[edit]
Whereas the physical quantity indicated by a physical constant does not depend on the unit system used to express the quantity, the numerical values of dimensional physical constants do depend on choice of unit system.
The term «physical constant» refers to the physical quantity, and not to the numerical value within any given system of units. For example, the speed of light is defined as having the numerical value of 299792458 when expressed in the SI unit metres per second, and as having the numerical value of 1 when expressed in the natural units Planck length per Planck time. While its numerical value can be defined at will by the choice of units, the speed of light itself is a single physical constant.
Any ratio between physical constants of the same dimensions results in a dimensionless physical constant, for example, the proton-to-electron mass ratio. Any relation between physical quantities can be expressed as a relation between dimensionless ratios via a process known as nondimensionalisation.
The term of «fundamental physical constant» is reserved for physical quantities which, according to the current state of knowledge, are regarded as immutable and as non-derivable from more fundamental principles. Notable examples are the speed of light c, and the gravitational constant G.
The fine-structure constant α is the best known dimensionless fundamental physical constant. It is the value of the elementary charge squared expressed in Planck units. This value has become a standard example when discussing the derivability or non-derivability of physical constants. Introduced by Arnold Sommerfeld, its value as determined at the time was consistent with 1/137. This motivated Arthur Eddington (1929) to construct an argument why its value might be 1/137 precisely, which related to the Eddington number, his estimate of the number of protons in the Universe.[2] By the 1940s, it became clear that the value of the fine-structure constant deviates significantly from the precise value of 1/137, refuting Eddington’s argument.[3]
With the development of quantum chemistry in the 20th century, however, a vast number of previously inexplicable dimensionless physical constants were successfully computed from theory.[citation needed] In light of that, some theoretical physicists still hope for continued progress in explaining the values of other dimensionless physical constants.
It is known that the Universe would be very different if these constants took values significantly different from those we observe. For example, a few percent change in the value of the fine structure constant would be enough to eliminate stars like our Sun. This has prompted attempts at anthropic explanations of the values of some of the dimensionless fundamental physical constants.
Natural units[edit]
It is possible to combine dimensional universal physical constants to define fixed quantities of any desired dimension, and this property has been used to construct various systems of natural units of measurement. Depending on the choice and arrangement of constants used, the resulting natural units may be convenient to an area of study. For example, Planck units, constructed from c, G, ħ, and kB give conveniently sized measurement units for use in studies of quantum gravity, and Hartree atomic units, constructed from ħ, me, e and 4πε0 give convenient units in atomic physics. The choice of constants used leads to widely varying quantities.
Number of fundamental constants[edit]
The number of fundamental physical constants depends on the physical theory accepted as «fundamental».
Currently, this is the theory of general relativity for gravitation and the Standard Model for electromagnetic, weak and strong nuclear interactions and the matter fields.
Between them, these theories account for a total of 19 independent fundamental constants.
There is, however, no single «correct» way of enumerating them, as it is a matter of arbitrary choice which quantities are considered «fundamental» and which as «derived». Uzan (2011) lists 22 «unknown constants» in the fundamental theories, which give rise to 19 «unknown dimensionless parameters», as follows:
- the gravitational constant G,
- the speed of light c,
- the Planck constant h,
- the 9 Yukawa couplings for the quarks and leptons (equivalent to specifying the rest mass of these elementary particles),
- 2 parameters of the Higgs field potential,
- 4 parameters for the quark mixing matrix,
- 3 coupling constants for the gauge groups SU(3) × SU(2) × U(1) (or equivalently, two coupling constants and the Weinberg angle),
- a phase for the QCD vacuum.
The number of 19 independent fundamental physical constants is subject to change under possible extensions of the Standard Model, notably by the introduction of neutrino mass (equivalent to seven additional constants, i.e. 3 Yukawa couplings and 4 lepton mixing parameters).[4]
The discovery of variability in any of these constants would be equivalent to the discovery of «new physics».[5]
The question as to which constants are «fundamental» is neither straightforward nor meaningless, but a question of interpretation of the physical theory regarded as fundamental; as pointed out by Lévy-Leblond 1977, not all physical constants are of the same importance, with some having a deeper role than others.
Lévy-Leblond 1977 proposed a classification schemes of three types of constants:
- A: physical properties of particular objects
- B: characteristic of a class of physical phenomena
- C: universal constants
The same physical constant may move from one category to another as the understanding of its role deepens; this has notably happened to the speed of light, which was a class A constant (characteristic of light) when it was first measured, but became a class B constant (characteristic of electromagnetic phenomena) with the development of classical electromagnetism, and finally a class C constant with the discovery of special relativity.[6]
Tests on time-independence[edit]
By definition, fundamental physical constants are subject to measurement, so that their being constant (independent on both the time and position of the performance of the measurement) is necessarily an experimental result and subject to verification.
Paul Dirac in 1937 speculated that physical constants such as the gravitational constant or the fine-structure constant might be subject to change over time in proportion of the age of the universe. Experiments can in principle only put an upper bound on the relative change per year. For the fine-structure constant, this upper bound is comparatively low, at
roughly 10−17 per year (as of 2008).[7]
The gravitational constant is much more difficult to measure with precision, and conflicting measurements in the 2000s have inspired the controversial suggestions of a periodic variation of its value in a 2015 paper.[8] However, while its value is not known to great precision, the possibility of observing type Ia supernovae which happened in the universe’s remote past, paired with the assumption that the physics involved in these events is universal, allows for an upper bound of less than 10−10 per year for the gravitational constant over the last nine billion years.[9]
Similarly, an upper bound of the change in the proton-to-electron mass ratio has been placed at 10−7 over a period of 7 billion years (or 10−16 per year) in a 2012 study based on the observation of methanol in a distant galaxy.[10][11]
It is problematic to discuss the proposed rate of change (or lack thereof) of a single dimensional physical constant in isolation. The reason for this is that the choice of units is arbitrary, making the question of whether a constant is undergoing change an artefact of the choice (and definition) of the units.[12][13][14]
For example, in SI units, the speed of light was given a defined value in 1983. Thus, it was meaningful to experimentally measure the speed of light in SI units prior to 1983, but it is not so now. Similarly, with effect from May 2019, the Planck constant has a defined value, such that all SI base units are now defined in terms of fundamental physical constants. With this change, the international prototype of the kilogram is being retired as the last physical object used in the definition of any SI unit.
Tests on the immutability of physical constants look at dimensionless quantities, i.e. ratios between quantities of like dimensions, in order to escape this problem. Changes in physical constants are not meaningful if they result in an observationally indistinguishable universe. For example, a «change» in the speed of light c would be meaningless if accompanied by a corresponding change in the elementary charge e so that the ratio e2/(4πε0ħc) (the fine-structure constant) remained unchanged.[15]
Fine-tuned universe[edit]
Some physicists have explored the notion that if the dimensionless physical constants had sufficiently different values, our Universe would be so radically different that intelligent life would probably not have emerged, and that our Universe therefore seems to be fine-tuned for intelligent life. However, the phase space of the possible constants and their values is unknowable, so any conclusions drawn from such arguments are unsupported. The anthropic principle states a logical truism: the fact of our existence as intelligent beings who can measure physical constants requires those constants to be such that beings like us can exist. There are a variety of interpretations of the constants’ values, including that of a divine creator (the apparent fine-tuning is actual and intentional), or that ours is one universe of many in a multiverse (e.g. the many-worlds interpretation of quantum mechanics), or even that, if information is an innate property of the universe and logically inseparable from consciousness, a universe without the capacity for conscious beings cannot exist.
The fundamental constants and quantities of nature have been discovered to be fine-tuned to such an extraordinarily narrow range that if it were not, the origin and evolution of conscious life in the universe would not be permitted.[16]
Table of physical constants[edit]
The table below lists some frequently used constants and their CODATA recommended values. For a more extended list, refer to List of physical constants.
| Quantity | Symbol | Value[17] | Relative standard uncertainty |
|---|---|---|---|
| elementary charge | 
|
1.602176634×10−19 C[18] | 0 |
| Newtonian constant of gravitation | 
|
6.67430(15)×10−11 m3⋅kg−1⋅s−2[19] | 2.2×10−5 |
| Planck constant | 
|
6.62607015×10−34 J⋅Hz−1[20] | 0 |
| speed of light in vacuum | 
|
299792458 m⋅s−1[21] | 0 |
| vacuum electric permittivity | 
|
8.8541878128(13)×10−12 F⋅m−1[22] | 1.5×10−10 |
| vacuum magnetic permeability | 
|
1.25663706212(19)×10−6 N⋅A−2[23] | 1.5×10−10 |
| electron mass | 
|
9.1093837015(28)×10−31 kg[24] | 3.0×10−10 |
| fine-structure constant | 
|
7.2973525693(11)×10−3[25] | 1.5×10−10 |
| Josephson constant | 
|
483597.8484…×109 Hz⋅V−1[26] | 0 |
| Rydberg constant | 
|
10973731.568160(21) m−1[27] | 1.9×10−12 |
| von Klitzing constant | 
|
25812.80745… Ω[28] | 0 |
See also[edit]
- List of common physics notations
References[edit]
- ^ «Fundamental Physical Constants from NIST». Archived from the original on 2016-01-13. Retrieved 2016-01-14. NIST
- ^
A.S Eddington (1956). «The Constants of Nature». In J.R. Newman (ed.). The World of Mathematics. Vol. 2. Simon & Schuster. pp. 1074–1093. - ^
H. Kragh (2003). «Magic Number: A Partial History of the Fine-Structure Constant». Archive for History of Exact Sciences. 57 (5): 395–431. doi:10.1007/s00407-002-0065-7. S2CID 118031104. - ^ Uzan, Jean-Philippe (2011). «Varying Constants, Gravitation and Cosmology». Living Reviews in Relativity. 14 (1): 2. arXiv:1009.5514. Bibcode:2011LRR….14….2U. doi:10.12942/lrr-2011-2. PMC 5256069. PMID 28179829.
Any constant varying in space and/or time would reflect the existence of an almost massless field that couples to matter. This will induce a violation of the universality of free fall. Thus, it is of utmost importance for our understanding of gravity and of the domain of validity of general relativity to test for their constancy.
- ^ Uzan, Jean-Philippe (2011). «Varying Constants, Gravitation and Cosmology». Living Reviews in Relativity. 14 (1): 2. arXiv:1009.5514. Bibcode:2011LRR….14….2U. doi:10.12942/lrr-2011-2. PMC 5256069. PMID 28179829.
- ^ Lévy-Leblond, J. (1977). «On the conceptual nature of the physical constants». La Rivista del Nuovo Cimento. Series 2. 7 (2): 187–214. Bibcode:1977NCimR…7..187L. doi:10.1007/bf02748049. S2CID 121022139.Lévy-Leblond, J.-M. (1979). «The importance of being (a) Constant». In Toraldo di Francia, G. (ed.). Problems in the Foundations of Physics, Proceedings of the International School of Physics ‘Enrico Fermi’ Course LXXII, Varenna, Italy, July 25 – August 6, 1977. New York: NorthHolland. pp. 237–263.
- ^
T. Rosenband; et al. (2008). «Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place». Science. 319 (5871): 1808–12. Bibcode:2008Sci…319.1808R. doi:10.1126/science.1154622. PMID 18323415. S2CID 206511320. - ^ J.D. Anderson; G. Schubert; V. Trimble; M.R. Feldman (April 2015), «Measurements of Newton’s gravitational constant and the length of day», EPL, 110 (1): 10002, arXiv:1504.06604, Bibcode:2015EL….11010002A, doi:10.1209/0295-5075/110/10002, S2CID 119293843
- ^ J. Mould; S. A. Uddin (2014-04-10), «Constraining a Possible Variation of G with Type Ia Supernovae», Publications of the Astronomical Society of Australia, 31: e015, arXiv:1402.1534, Bibcode:2014PASA…31…15M, doi:10.1017/pasa.2014.9, S2CID 119292899
- ^ Bagdonaite, Julija; Jansen, Paul; Henkel, Christian; Bethlem, Hendrick L.; Menten, Karl M.; Ubachs, Wim (December 13, 2012). «A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe» (PDF). Science. 339 (6115): 46–48. Bibcode:2013Sci…339…46B. doi:10.1126/science.1224898. hdl:1871/39591. PMID 23239626. S2CID 716087.
- ^ Moskowitz, Clara (December 13, 2012). «Phew! Universe’s Constant Has Stayed Constant». Space.com. Archived from the original on December 14, 2012. Retrieved December 14, 2012.
- ^ Duff, Michael (2015). «How fundamental are fundamental constants?». Contemporary Physics. 56 (1): 35–47. arXiv:1412.2040. Bibcode:2015ConPh..56…35D. doi:10.1080/00107514.2014.980093. hdl:10044/1/68485. S2CID 118347723.
- ^ Duff, M. J. (13 August 2002). «Comment on time-variation of fundamental constants». arXiv:hep-th/0208093.
- ^ Duff, M. J.; Okun, L. B.; Veneziano, G. (2002). «Trialogue on the number of fundamental constants». Journal of High Energy Physics. 2002 (3): 023. arXiv:physics/0110060. Bibcode:2002JHEP…03..023D. doi:10.1088/1126-6708/2002/03/023. S2CID 15806354.
- ^ Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8
«[An] important lesson we learn from the way that pure numbers like α define the World is what it really means for worlds to be different. The pure number we call the fine structure constant and denote by α is a combination of the electron charge, e, the speed of light, c, and Planck’s constant, h. At first we might be tempted to think that a world in which the speed of light was slower would be a different world. But this would be a mistake. If c, h, and e were all changed so that the values they have in metric (or any other) units were different when we looked them up in our tables of physical constants, but the value of α remained the same, this new world would be observationally indistinguishable from our World. The only thing that counts in the definition of worlds are the values of the dimensionless constants of Nature. If all masses were doubled in value you cannot tell, because all the pure numbers defined by the ratios of any pair of masses are unchanged.» - ^ Leslie, John (1998). Modern Cosmology & Philosophy. University of Michigan: Prometheus Books. ISBN 1573922501.
- ^ The values are given in the so-called concise form, where the number in parentheses indicates the standard uncertainty referred to the least significant digits of the value.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-28.
- ^ «2018 CODATA Value: speed of light in vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: vacuum magnetic permeability». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Josephson constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Rydberg constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: von Klitzing constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). «CODATA Recommended Values of the Fundamental Physical Constants: 2006» (PDF). Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. doi:10.1103/RevModPhys.80.633. Archived from the original (PDF) on 2017-10-01.
- Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8.
External links[edit]
- Sixty Symbols, University of Nottingham
- IUPAC — Gold Book
The constants listed here are known values of physical constants expressed in SI units; that is, physical quantities that are generally believed to be universal in nature and thus are independent of the unit system in which they are measured. Many of these are redundant, in the sense that they obey a known relationship with other physical constants and can be determined from them.
Table of physical constants[edit]
| Symbol | Quantity | Value[a][b] | Relative standard uncertainty |
Ref |
|---|---|---|---|---|

|
Newtonian constant of gravitation | 6.67430(15)×10−11 m3⋅kg−1⋅s−2 | 2.2×10−5 | [1] |

|
speed of light in vacuum | 299792458 m⋅s−1 | 0 | [2] |

|
Planck constant | 6.62607015×10−34 J⋅Hz−1 | 0 | [3] |

|
reduced Planck constant | 1.054571817…×10−34 J⋅s | 0 | [4] |

|
vacuum magnetic permeability | 1.25663706212(19)×10−6 N⋅A−2 | 1.5×10−10 | [5] |

|
characteristic impedance of vacuum | 376.730313668(57) Ω | 1.5×10−10 | [6] |

|
vacuum electric permittivity | 8.8541878128(13)×10−12 F⋅m−1 | 1.5×10−10 | [7] |

|
Coulomb constant | 8.9875517923(14)×109 N⋅m2⋅C−2 | 1.5×10−10 | [8] |

|
Boltzmann constant | 1.380649×10−23 J⋅K−1 | 0 | [9] |

|
Stefan–Boltzmann constant | 5.670374419…×10−8 W⋅m−2⋅K−4 | 0 | [10] |

|
first radiation constant | 3.741771852…×10−16 W⋅m2 | 0 | [11] |

|
first radiation constant for spectral radiance | 1.1910429723971884140794892×10−16 W⋅m2⋅sr−1 | 0 | [12] |

|
second radiation constant | 1.438776877…×10−2 m⋅K | 0 | [13] |
 [c] [c]
|
Wien wavelength displacement law constant | 2.897771955…×10−3 m⋅K | 0 | [14] |
 [d] [d]
|
Wien frequency displacement law constant | 5.878925757…×1010 Hz⋅K−1 | 0 | [15] |

|
Wien entropy displacement law constant | 3.002916077…×10−3 m⋅K | 0 | [16] |

|
elementary charge | 1.602176634×10−19 C | 0 | [17] |

|
conductance quantum | 7.748091729…×10−5 S | 0 | [18] |

|
inverse conductance quantum | 12906.40372… Ω | 0 | [19] |

|
von Klitzing constant | 25812.80745… Ω | 0 | [20] |

|
Josephson constant | 483597.8484…×109 Hz⋅V−1 | 0 | [21] |

|
magnetic flux quantum | 2.067833848…×10−15 Wb | 0 | [22] |

|
fine-structure constant | 7.2973525693(11)×10−3 | 1.5×10−10 | [23] |

|
inverse fine-structure constant | 137.035999084(21) | 1.5×10−10 | [24] |

|
electron mass | 9.1093837015(28)×10−31 kg | 3.0×10−10 | [25] |

|
proton mass | 1.67262192369(51)×10−27 kg | 3.1×10−10 | [26] |

|
neutron mass | 1.67492749804(95)×10−27 kg | 5.7×10−10 | [27] |

|
muon mass | 1.883531627(42)×10−28 kg | 2.2×10−8 | [28] |

|
tau mass | 3.16754(21)×10−27 kg | 6.8×10−5 | [29] |

|
top quark mass | 3.0784(53)×10−25 kg | 1.7×10−3 | [30] |

|
proton-to-electron mass ratio | 1836.15267343(11) | 6.0×10−11 | [31] |

|
W-to-Z mass ratio | 0.88153(17) | 1.9×10−4 | [32] |

|
weak mixing angle | 0.22290(30) | 1.3×10−3 | [33] |

|
electron g-factor | −2.00231930436256(35) | 1.7×10−13 | [34] |

|
muon g-factor | −2.0023318418(13) | 6.3×10−10 | [35] |

|
proton g-factor | 5.5856946893(16) | 2.9×10−10 | [36] |

|
quantum of circulation | 3.6369475516(11)×10−4 m2⋅s−1 | 3.0×10−10 | [37] |

|
Bohr magneton | 9.2740100783(28)×10−24 J⋅T−1 | 3.0×10−10 | [38] |

|
nuclear magneton | 5.0507837461(15)×10−27 J⋅T−1 | 3.1×10−10 | [39] |

|
classical electron radius | 2.8179403262(13)×10−15 m | 4.5×10−10 | [40] |

|
Thomson cross section | 6.6524587321(60)×10−29 m2 | 9.1×10−10 | [41] |

|
Bohr radius | 5.29177210903(80)×10−11 m | 1.5×10−10 | [42] |

|
Hartree energy | 4.3597447222071(85)×10−18 J | 1.9×10−12 | [43] |

|
Rydberg unit of energy | 2.1798723611035(42)×10−18 J | 1.9×10−12 | [44] |

|
Rydberg constant | 10973731.568160(21) m−1 | 1.9×10−12 | [45] |

|
Fermi coupling constant | 1.1663787(6)×10−5 GeV−2 | 5.1×10−7 | [46] |

|
Avogadro constant | 6.02214076×1023 mol−1 | 0 | [47] |

|
molar gas constant | 8.31446261815324 J⋅mol−1⋅K−1 | 0 | [48] |

|
Faraday constant | 96485.3321233100184 C⋅mol−1 | 0 | [49] |

|
molar Planck constant | 3.9903127128934314×10−10 J⋅s⋅mol−1 | 0 | [50] |

|
atomic mass of carbon-12 | 1.99264687992(60)×10−26 kg | 3.0×10−10 | [51] |

|
molar mass of carbon-12 | 11.9999999958(36)×10−3 kg⋅mol−1 | 3.0×10−10 | [52] |

|
atomic mass constant | 1.66053906660(50)×10−27 kg | 3.0×10−10 | [53] |

|
molar mass constant | 0.99999999965(30)×10−3 kg⋅mol−1 | 3.0×10−10 | [54] |

|
molar volume of silicon | 1.205883199(60)×10−5 m3⋅mol−1 | 4.9×10−8 | [55] |

|
hyperfine transition frequency of 133Cs | 9192631770 Hz | 0 | [56] |
Uncertainties[edit]
While the values of the physical constants are independent of the system of units in use, each uncertainty as stated reflects our lack of knowledge of the corresponding value as expressed in SI units, and is strongly dependent on how those units are defined. For example, the atomic mass constant 
Technical constants[edit]
Some of these constants are of a technical nature and do not give any true physical property, but they are included for convenience. Such a constant gives the correspondence ratio of a technical dimension with its corresponding underlying physical dimension. These include the Boltzmann constant 


See also[edit]
- List of mathematical constants
- Physical constant
- List of particles
Notes[edit]
References[edit]
- ^ «2018 CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: speed of light in vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-28.
- ^ «2018 CODATA Value: reduced Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-28.
- ^ «2018 CODATA Value: vacuum magnetic permeability». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: characteristic impedance of vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-10-31.
- ^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «vacuum electric permittivity». NIST.gov. NIST. Retrieved 2 June 2022.
- ^ «2018 CODATA Value: Boltzmann constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Stefan–Boltzmann constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: first radiation constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: first radiation constant for spectral radiance». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: second radiation constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Wien wavelength displacement law constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Wien frequency displacement law constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ Delgado-Bonal A (May 2017). «Entropy of radiation: the unseen side of light». Scientific Reports. 7 (1): 1642. Bibcode:2017NatSR…7.1642D. doi:10.1038/s41598-017-01622-6. PMC 5432030. PMID 28490790.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: conductance quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: inverse of conductance quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: von Klitzing constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Josephson constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: magnetic flux quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: inverse fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: proton mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: neutron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-23.
- ^ «2018 CODATA Value: muon mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: tau mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «t-quark mass». pdglive.lbl.gov. Particle Data Group. Retrieved 9 July 2022.
t-quark mass (direct measurements): 172.69(30) GeV/c2
- ^ «2018 CODATA Value: proton-electron mass ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: W to Z mass ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-12-21.
- ^ «2018 CODATA Value: weak mixing angle». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-03-13.
- ^ «2018 CODATA Value: muon g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: proton g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-03-08.
- ^ «2018 CODATA Value: quantum of circulation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Bohr magneton». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: nuclear magneton». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: classical electron radius». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Thomson cross section». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Bohr radius». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Hartree energy». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Rydberg constant times hc in J». NIST.gov. NIST. Retrieved 23 June 2022.
- ^ «2018 CODATA Value: Rydberg constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Fermi coupling constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Avogadro constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar gas constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Faraday constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «atomic mass constant». NIST.gov. NIST. Retrieved 5 June 2022.
- ^ «2018 CODATA Value: molar mass of carbon-12». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: atomic mass constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar mass constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar volume of silicon». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-06-23.
- ^ «2018 CODATA Value: hyperfine transition frequency of Cs-133». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-18.
The constants listed here are known values of physical constants expressed in SI units; that is, physical quantities that are generally believed to be universal in nature and thus are independent of the unit system in which they are measured. Many of these are redundant, in the sense that they obey a known relationship with other physical constants and can be determined from them.
Table of physical constants[edit]
| Symbol | Quantity | Value[a][b] | Relative standard uncertainty |
Ref |
|---|---|---|---|---|

|
Newtonian constant of gravitation | 6.67430(15)×10−11 m3⋅kg−1⋅s−2 | 2.2×10−5 | [1] |

|
speed of light in vacuum | 299792458 m⋅s−1 | 0 | [2] |

|
Planck constant | 6.62607015×10−34 J⋅Hz−1 | 0 | [3] |

|
reduced Planck constant | 1.054571817…×10−34 J⋅s | 0 | [4] |

|
vacuum magnetic permeability | 1.25663706212(19)×10−6 N⋅A−2 | 1.5×10−10 | [5] |

|
characteristic impedance of vacuum | 376.730313668(57) Ω | 1.5×10−10 | [6] |

|
vacuum electric permittivity | 8.8541878128(13)×10−12 F⋅m−1 | 1.5×10−10 | [7] |

|
Coulomb constant | 8.9875517923(14)×109 N⋅m2⋅C−2 | 1.5×10−10 | [8] |

|
Boltzmann constant | 1.380649×10−23 J⋅K−1 | 0 | [9] |

|
Stefan–Boltzmann constant | 5.670374419…×10−8 W⋅m−2⋅K−4 | 0 | [10] |

|
first radiation constant | 3.741771852…×10−16 W⋅m2 | 0 | [11] |

|
first radiation constant for spectral radiance | 1.1910429723971884140794892×10−16 W⋅m2⋅sr−1 | 0 | [12] |

|
second radiation constant | 1.438776877…×10−2 m⋅K | 0 | [13] |
 [c] [c]
|
Wien wavelength displacement law constant | 2.897771955…×10−3 m⋅K | 0 | [14] |
 [d] [d]
|
Wien frequency displacement law constant | 5.878925757…×1010 Hz⋅K−1 | 0 | [15] |

|
Wien entropy displacement law constant | 3.002916077…×10−3 m⋅K | 0 | [16] |

|
elementary charge | 1.602176634×10−19 C | 0 | [17] |

|
conductance quantum | 7.748091729…×10−5 S | 0 | [18] |

|
inverse conductance quantum | 12906.40372… Ω | 0 | [19] |

|
von Klitzing constant | 25812.80745… Ω | 0 | [20] |

|
Josephson constant | 483597.8484…×109 Hz⋅V−1 | 0 | [21] |

|
magnetic flux quantum | 2.067833848…×10−15 Wb | 0 | [22] |

|
fine-structure constant | 7.2973525693(11)×10−3 | 1.5×10−10 | [23] |

|
inverse fine-structure constant | 137.035999084(21) | 1.5×10−10 | [24] |

|
electron mass | 9.1093837015(28)×10−31 kg | 3.0×10−10 | [25] |

|
proton mass | 1.67262192369(51)×10−27 kg | 3.1×10−10 | [26] |

|
neutron mass | 1.67492749804(95)×10−27 kg | 5.7×10−10 | [27] |

|
muon mass | 1.883531627(42)×10−28 kg | 2.2×10−8 | [28] |

|
tau mass | 3.16754(21)×10−27 kg | 6.8×10−5 | [29] |

|
top quark mass | 3.0784(53)×10−25 kg | 1.7×10−3 | [30] |

|
proton-to-electron mass ratio | 1836.15267343(11) | 6.0×10−11 | [31] |

|
W-to-Z mass ratio | 0.88153(17) | 1.9×10−4 | [32] |

|
weak mixing angle | 0.22290(30) | 1.3×10−3 | [33] |

|
electron g-factor | −2.00231930436256(35) | 1.7×10−13 | [34] |

|
muon g-factor | −2.0023318418(13) | 6.3×10−10 | [35] |

|
proton g-factor | 5.5856946893(16) | 2.9×10−10 | [36] |

|
quantum of circulation | 3.6369475516(11)×10−4 m2⋅s−1 | 3.0×10−10 | [37] |

|
Bohr magneton | 9.2740100783(28)×10−24 J⋅T−1 | 3.0×10−10 | [38] |

|
nuclear magneton | 5.0507837461(15)×10−27 J⋅T−1 | 3.1×10−10 | [39] |

|
classical electron radius | 2.8179403262(13)×10−15 m | 4.5×10−10 | [40] |

|
Thomson cross section | 6.6524587321(60)×10−29 m2 | 9.1×10−10 | [41] |

|
Bohr radius | 5.29177210903(80)×10−11 m | 1.5×10−10 | [42] |

|
Hartree energy | 4.3597447222071(85)×10−18 J | 1.9×10−12 | [43] |

|
Rydberg unit of energy | 2.1798723611035(42)×10−18 J | 1.9×10−12 | [44] |

|
Rydberg constant | 10973731.568160(21) m−1 | 1.9×10−12 | [45] |

|
Fermi coupling constant | 1.1663787(6)×10−5 GeV−2 | 5.1×10−7 | [46] |

|
Avogadro constant | 6.02214076×1023 mol−1 | 0 | [47] |

|
molar gas constant | 8.31446261815324 J⋅mol−1⋅K−1 | 0 | [48] |

|
Faraday constant | 96485.3321233100184 C⋅mol−1 | 0 | [49] |

|
molar Planck constant | 3.9903127128934314×10−10 J⋅s⋅mol−1 | 0 | [50] |

|
atomic mass of carbon-12 | 1.99264687992(60)×10−26 kg | 3.0×10−10 | [51] |

|
molar mass of carbon-12 | 11.9999999958(36)×10−3 kg⋅mol−1 | 3.0×10−10 | [52] |

|
atomic mass constant | 1.66053906660(50)×10−27 kg | 3.0×10−10 | [53] |

|
molar mass constant | 0.99999999965(30)×10−3 kg⋅mol−1 | 3.0×10−10 | [54] |

|
molar volume of silicon | 1.205883199(60)×10−5 m3⋅mol−1 | 4.9×10−8 | [55] |

|
hyperfine transition frequency of 133Cs | 9192631770 Hz | 0 | [56] |
Uncertainties[edit]
While the values of the physical constants are independent of the system of units in use, each uncertainty as stated reflects our lack of knowledge of the corresponding value as expressed in SI units, and is strongly dependent on how those units are defined. For example, the atomic mass constant 
Technical constants[edit]
Some of these constants are of a technical nature and do not give any true physical property, but they are included for convenience. Such a constant gives the correspondence ratio of a technical dimension with its corresponding underlying physical dimension. These include the Boltzmann constant 


See also[edit]
- List of mathematical constants
- Physical constant
- List of particles
Notes[edit]
References[edit]
- ^ «2018 CODATA Value: Newtonian constant of gravitation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: speed of light in vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-28.
- ^ «2018 CODATA Value: reduced Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-28.
- ^ «2018 CODATA Value: vacuum magnetic permeability». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: characteristic impedance of vacuum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-10-31.
- ^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «vacuum electric permittivity». NIST.gov. NIST. Retrieved 2 June 2022.
- ^ «2018 CODATA Value: Boltzmann constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Stefan–Boltzmann constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: first radiation constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: first radiation constant for spectral radiance». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: second radiation constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Wien wavelength displacement law constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Wien frequency displacement law constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ Delgado-Bonal A (May 2017). «Entropy of radiation: the unseen side of light». Scientific Reports. 7 (1): 1642. Bibcode:2017NatSR…7.1642D. doi:10.1038/s41598-017-01622-6. PMC 5432030. PMID 28490790.
- ^ «2018 CODATA Value: elementary charge». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: conductance quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: inverse of conductance quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: von Klitzing constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Josephson constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: magnetic flux quantum». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: inverse fine-structure constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: proton mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: neutron mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-23.
- ^ «2018 CODATA Value: muon mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: tau mass». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «t-quark mass». pdglive.lbl.gov. Particle Data Group. Retrieved 9 July 2022.
t-quark mass (direct measurements): 172.69(30) GeV/c2
- ^ «2018 CODATA Value: proton-electron mass ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: W to Z mass ratio». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-12-21.
- ^ «2018 CODATA Value: weak mixing angle». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: electron g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-03-13.
- ^ «2018 CODATA Value: muon g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: proton g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-03-08.
- ^ «2018 CODATA Value: quantum of circulation». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Bohr magneton». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: nuclear magneton». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: classical electron radius». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Thomson cross section». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Bohr radius». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Hartree energy». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Rydberg constant times hc in J». NIST.gov. NIST. Retrieved 23 June 2022.
- ^ «2018 CODATA Value: Rydberg constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Fermi coupling constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Avogadro constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar gas constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: Faraday constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar Planck constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «atomic mass constant». NIST.gov. NIST. Retrieved 5 June 2022.
- ^ «2018 CODATA Value: molar mass of carbon-12». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: atomic mass constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar mass constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «2018 CODATA Value: molar volume of silicon». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-06-23.
- ^ «2018 CODATA Value: hyperfine transition frequency of Cs-133». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-18.
Универсальная и неизменная физическая величина
A физическая константа, иногда фундаментальная физическая постоянная или универсальная константа — это физическая величина, которая обычно считается универсальной по природе и имеет постоянную значение во времени. Это контрастирует с математической константой , которая имеет фиксированное числовое значение, но не включает напрямую никаких физических измерений.
В науке существует множество физических констант, некоторые из наиболее широко признанных — это скорость света в вакууме c, гравитационная постоянная G, Постоянная Планка h, электрическая постоянная ε0и элементарный заряд e. Физические константы могут принимать многие размерные формы: скорость света означает максимальную скорость для любого объекта, а его размер равен длине, деленной на время ; в то время как постоянная тонкой структуры α, которая характеризует силу электромагнитного взаимодействия, безразмерна.
Термин фундаментальная физическая постоянная иногда используется для обозначения универсального но размерные физические константы, такие как упомянутые выше. Однако все чаще физики используют фундаментальную физическую постоянную только для безразмерных физических констант, таких как постоянная тонкой структуры α.
Физическую константу, как обсуждается здесь, не следует путать с другими величинами, называемыми «константами», которые считаются постоянными в данном контексте, но не являются фундаментальными, такими как «постоянная времени «характеристика данной системы или константы материала (например, постоянная Маделунга, удельное электрическое сопротивление и теплоемкость ).
С мая 2019 года все базовые единицы СИ были определены в терминах физических констант. В результате пять констант: скорость света в вакууме, c; постоянная Планка, ч; элементарный заряд, э; константа Авогадро, N A ; и постоянная Больцмана, k B, имеют точные числовые значения, когда они выражены в единицах СИ. Первые три из этих констант являются фундаментальными константами, тогда как N A и k B имеют только технический характер: они не описывают никаких свойств вселенной, а вместо этого только дают коэффициент пропорциональности для определения единиц, используемых с большим количеством объектов атомарного масштаба.
Содержание
- 1 Выбор единиц
- 1.1 Натуральные единицы
- 2 Количество фундаментальных констант
- 3 Тесты на независимость от времени
- 4 Точно настроенная вселенная
- 5 Таблица физических констант
- 6 См. Также
- 7 Ссылки
- 8 Внешние ссылки
Выбор единиц
В то время как физическая величина, обозначенная физической константой, не зависит от единицы системы, используемой для выражения количества, числовые значения размерных физических констант действительно зависят от выбора системы единиц. Термин «физическая постоянная» относится к физической величине, а не к числовому значению в любой данной системе единиц. Например, скорость света определяется как имеющая числовое значение 299792458 при выражении в единицах СИ метров в секунду и как имеющее числовое значение 1 при выражении в натуральные единицы Планковская длина за планковское время. Хотя ее числовое значение может быть определено по желанию путем выбора единиц, скорость света сама по себе является единственной физической константой.
Любое соотношение между физическими константами одинаковых размеров приводит к безразмерной физической постоянной, например, отношение масс протона к электрону. Любая связь между физическими величинами может быть выражена как связь между безразмерными отношениями с помощью процесса, известного как обезразмеривание.
Термин «фундаментальная физическая константа» зарезервирован для физических величин, которые, согласно текущему уровню знаний, являются рассматривается как неизменный и не вытекающий из более фундаментальных принципов. Яркими примерами являются скорость света c и гравитационная постоянная G.
постоянная тонкой структуры α является наиболее известной безразмерной фундаментальной физической постоянной. Это значение элементарного заряда в квадрате, выраженное в единицах Планка. Это значение стало стандартным примером при обсуждении выводимости или невозможности вывода физических констант. Введенный Арнольдом Зоммерфельдом, его значение, определенное в то время, соответствовало 1/137. Это побудило Артура Эддингтона (1929) создать аргумент, почему его значение может быть точно 1/137, что связано с числом Эддингтона, его оценкой количества протонов во Вселенной.. К 1940-м годам стало ясно, что значение постоянной тонкой структуры значительно отклоняется от точного значения 1/137, опровергая аргумент Эддингтона.
С развитием квантовой химии в Однако в 20 веке огромное количество необъяснимых ранее безразмерных физических констант было успешно вычислено на основе теории. В свете этого некоторые физики-теоретики все еще надеются на дальнейший прогресс в объяснении значений других безразмерных физических констант.
Известно, что Вселенная была бы совсем другой, если бы эти константы принимали значения, значительно отличающиеся от тех, которые мы наблюдаем. Например, изменения значения постоянной тонкой структуры на несколько процентов будет достаточно, чтобы исключить такие звезды, как наше Солнце. Это вызвало попытки антропных объяснений значений некоторых безразмерных фундаментальных физических констант.
Натуральные единицы
Можно комбинировать размерные универсальные физические константы для определения фиксированных величин любого желаемого измерения, и это свойство использовалось для построения различных систем естественных единиц измерения. В зависимости от выбора и расположения используемых констант полученные натуральные единицы могут быть удобны для области исследования. Например, единицы Планка, построенные из c, G, ħ, и kB дают единицы измерения удобного размера для использования в исследованиях квантовой гравитации и атомных единиц Хартри, построенные из ħ, me, e и 4πε0, дают удобные единицы в атомной физике. Выбор используемых констант приводит к широкому изменению величин.
Количество фундаментальных констант
Количество фундаментальных физических констант зависит от физической теории, принятой в качестве «фундаментальной». В настоящее время это теория общей теории относительности для гравитации и Стандартная модель для электромагнитных, слабых и сильных ядерных взаимодействий и полей материи. Вместе эти теории составляют 19 независимых фундаментальных констант. Однако не существует единого «правильного» способа их перечисления, поскольку это вопрос произвольного выбора, какие величины считать «основными», а какие — «производными». Узан (2011) перечисляет 22 «неизвестных константы» в фундаментальных теориях, которые приводят к 19 «неизвестным безразмерным параметрам», а именно:
- гравитационная постоянная G,
- скорость света c,
- постоянная Планка h,
- 9 связи Юкавы для кварков и лептонов (что эквивалентно заданию массы покоя этих элементарных частиц ),
- 2 параметров потенциала поля Хиггса,
- 4 параметра для матрицы смешения кварков,
- 3 константы связи для калибровочных групп SU (3) × SU (2) × U (1) (или, что эквивалентно, две константы связи и угол Вайнберга ),
- фаза для вакуума КХД.
Число 19 независимых фундаментальных физических константы могут быть изменены в рамках возможных расширений Стандартной модели, в частности, путем введения массы нейтрино (что эквивалентно семи дополнительным константам, т. е. 3 связи Юкавы и 4 лептонного смешения параметры).
Открытие y изменения любой из этих констант было бы эквивалентно открытию «новой физики «.
. Вопрос о том, какие константы являются« фундаментальными », не является ни прямым, ни бессмысленным, это вопрос интерпретации рассматриваемой физической теории как фундаментальный; как указано Леви-Леблон 1977 г., не все физические константы имеют одинаковое значение, причем некоторые имеют более глубокую роль, чем другие. Леви-Леблон 1977 предложил схемы классификации трех типов констант:
- A: физические свойства отдельных объектов
- B: характеристика класса физических явлений
- C: универсальные константы
Одна и та же физическая константа может переходить из одной категории в другую по мере углубления понимания ее роли; в частности, это произошло с скоростью света, которая была константой класса A (характеристика света ), когда она была впервые измерена, но стала константой класса B (характеристика электромагнитные явления ) с развитием классического электромагнетизма и, наконец, константа класса C с открытием специальной теории относительности.
Тесты на независимость от времени
Автор По определению, фундаментальные физические константы подлежат измерению, так что их постоянство (независимо от времени и положения выполнения измерения) обязательно является экспериментальным результатом и подлежит проверке.
Поль Дирак в 1937 году предположил, что физические константы, такие как гравитационная постоянная или постоянная тонкой структуры, могут изменяться со временем пропорционально возраст вселенной. Эксперименты, в принципе, могут установить только верхнюю границу относительного изменения за год. Для постоянной тонкой структуры эта верхняя граница сравнительно низкая, примерно 10 в год (по состоянию на 2008 г.).
Гравитационную постоянную гораздо труднее измерить с точностью, и противоречивые измерения в 2000-х гг. вдохновил спорные предположения о периодическом изменении его стоимости в статье 2015 года. Однако, хотя его значение неизвестно с большой точностью, возможность наблюдения сверхновых типа Ia, которые произошли в далеком прошлом Вселенной, в сочетании с предположением, что физика, вовлеченная в эти события, является универсальной, позволяет верхняя граница менее 10 в год для гравитационной постоянной за последние девять миллиардов лет.
Аналогично, верхняя граница изменения отношения масс протона к электрону была помещен в 10 в течение 7 миллиардов лет (или 10 в год) в исследовании 2012 года, основанном на наблюдении метанола в далекой галактике.
Проблематично обсуждать предложенное скорость изменения (или ее отсутствия) отдельно взятой одномерной физической постоянной. Причина этого в том, что выбор единиц измерения произвольный, поэтому вопрос о том, претерпевает ли константа изменение, является артефактом выбора (и определения) единиц.
Например, в SI единиц, скорость света получила определенное значение в 1983 году. Таким образом, до 1983 года имело смысл экспериментально измерить скорость света в единицах СИ, но сейчас это не так. Аналогичным образом, начиная с мая 2019 года, постоянная Планка имеет определенное значение, так что все базовые единицы СИ теперь определены в терминах фундаментальных физических констант. С этим изменением, международный прототип килограмма удаляется как последний физический объект, используемый в определении любой единицы СИ.
В тестах на неизменность физических констант изучаются безразмерные величины, то есть отношения между величинами одинаковых размеров, чтобы избежать этой проблемы. Изменения физических констант не имеют смысла, если они приводят к неразличимой с точки зрения наблюдений Вселенной. Например, «изменение» скорости света c было бы бессмысленным, если бы сопровождалось соответствующим изменением элементарного заряда e, так что отношение e / (4πε 0 ħc) (постоянная тонкой структуры) осталась неизменной.
Тонко настроенная вселенная
Некоторые физики исследовали идею о том, что если безразмерные физические константы имеют достаточно разные значения, наши Вселенная будет настолько радикально отличаться от других, что разумная жизнь, вероятно, не возникнет, и поэтому наша Вселенная кажется тонко настроенной для разумной жизни. Однако фазовое пространство возможных констант и их значений неизвестно, поэтому любые выводы, сделанные на основе таких аргументов, не подтверждаются. Антропный принцип устанавливает логический трюизм : факт нашего существования в качестве разумных существ, которые могут измерять физические константы, требует, чтобы эти константы были такими, чтобы существа, подобные нам, могли существовать. Существует множество интерпретаций значений констант, включая интерпретацию божественного творца (кажущаяся точная настройка фактическая и преднамеренная), или то, что наша вселенная — одна из многих в мультивселенной (например, интерпретация многих миров из квантовой механики ) или даже так, если информация является врожденным свойством вселенной и логически неотделима от сознание, вселенная без способности к сознательным существам существовать не может.
Было обнаружено, что фундаментальные константы и количества природы точно настроены на такой чрезвычайно узкий диапазон, что, если бы это было не так, происхождение и эволюция сознательной жизни во Вселенной не допускается.
Таблица физических констант
В таблице ниже перечислены некоторые часто используемые константы и их рекомендуемые значения CODATA. Более подробный список см. В Список физических констант.
| Количество | Символ | Значение | Относительная. стандартная. неопределенность |
|---|---|---|---|
| элементарный заряд | e { displaystyle e} |
1,602176634 × 10 C | 0 |
| Ньютоновская постоянная гравитации | G { displaystyle G} |
6,67430 (15) × 10 м⋅кг⋅с | 2,2 × 10 |
| постоянная Планка | h { displaystyle h} |
6,62607015 × 10 Дж / с | 0 |
| скорость света в вакууме | c { displaystyle c} |
299792458 м ⋅s | 0 |
| электрическая диэлектрическая проницаемость вакуума | ε 0 = 1 / μ 0 c 2 { displaystyle varepsilon _ {0} = 1 / mu _ {0} c ^ {2}} |
8.8541878128 (13) × 10 Ф · м | 1,5 · 10 |
| магнитная проницаемость вакуума | μ 0 { displaystyle mu _ {0}} |
1,25663706212 (19) × 10 N⋅A | 1,5 × 10 |
| масса электрона | me { displaystyle m _ { mathrm {e}}} |
9,1093837015 (28) × 10 кг | 3,0 × 10 |
| постоянная тонкой структуры | α = e 2/2 ε 0 hc { displaystyle alpha = e ^ {2} / 2 varepsilon _ {0} hc} |
7.2973525693 (11) × 10 | 1,5 × 10 |
| постоянная Джозефсона | KJ = 2 e / h { displaystyle K _ { mathrm {J}} = 2e / h} |
483597.8484… × 10 Гц⋅V | 0 |
| постоянная Ридберга | R ∞ = α 2 mec / 2 час { displaystyle R _ { infty} = alpha ^ {2} m _ { mathrm {e}} c / 2h} |
10973731.568160 (21) m | 1,9 × 10 |
| фон Константа Клитцинга | RK = h / e 2 { displaystyle R _ { mathrm {K}} = h / e ^ {2}} |
25812.80745… Ω | 0 |
См. Также
- Список общих обозначения физики
Список литературы
- Мор, Питер Дж.; Тейлор, Барри Н.; Ньюэлл, Дэвид Б. (2008). «CODATA Рекомендуемые значения фундаментальных физических констант: 2006 г.» (PDF). Обзоры современной физики. 80(2): 633–730. arXiv : 0801.0028. Bibcode : 2008RvMP… 80..633M. doi : 10.1103 / RevModPhys.80.633. Архивировано из оригинального (PDF) 01.10.2017.
- Барроу, Джон Д. (2002), Константы природы; От альфы к омеге — числа, закодирующие самые глубокие тайны Вселенной, Pantheon Books, ISBN 978-0-375-42221-8.
Внешние ссылки
- Шестьдесят символов, Ноттингемский университет
- ИЮПАК — Золотая книга
Обновлено: 09.01.2023
Фундаментальная физическая постоянная (константа) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Численные значения физических постоянных или их комбинаций находят на основе экспериментальных измерений и выражают в единицах какой-либо системы единиц.
Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.
КОНСТАНТА (постоянная) , в математике и других науках — величина или коэффициент, не подвергающийся изменению. Константа может быть универсальной, как число (отношение окружности круга к его диаметру) , или конкретной, как коэффициенты, введенные в алгебраическое уравнение; константой может также быть определенный физический параметр вещества
Постоянная величина или Константа. Этими величинами являются, например, иррациональные числа «пи»,»е».Они играют важную роль в математике и в целом.
Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.
Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.
Содержание
Фундаментальные физические постоянные
Размерные комбинации фундаментальных постоянных
Постоянные, связывающие разные системы единиц
Некоторые другие физические постоянные
Примечания
Ссылки
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Физическая константа» в других словарях:
физическая константа — fizikinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Pastovus dydis, įeinantis į kurio nors fizikos dėsnio matematinę išraišką. atitikmenys: angl. physical constant vok. physikalische Konstante, f rus. физическая… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Фундаментальная физическая константа — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия
Константа — Константа: Постоянная Математическая Физическая Константа (в программировании) Константа диссоциации кислоты Константа равновесия Константа скорости реакции Константа (Остаться в живых) См. также Констанция Констанций Константин Констант… … Википедия
Константа диссоциации — Константа диссоциации вид константы равновесия, которая показывает склонность большого объекта диссоциировать (разделяться) обратимым образом на маленькие объекты, как например когда комплекс распадается на составляющие молекулы, или когда… … Википедия
КОНСТАНТА ВЗАИМОДЕЙСТВИЯ — (константа связи) (от лат. constans постоянный) в квантовой теории поля (КТП) параметр, определяющий силу (интенсивность) взаимодействия частиц или полей. В общем виде К. в. задаётся как значение вершинной части (вершины) при определ. значениях… … Физическая энциклопедия
Константа автопротолиза — Константа автопротолиза физическая величина, характеризующая способность протонного растворителя к диссоциации. Обозначается KS. Является произведением концентраций иона лиония и иона лиата. Так, например, для растворителя, который… … Википедия
Константа равновесия — У этого термина существуют и другие значения, см. Константа. Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации … Википедия
ФИЗИЧЕСКАЯ ХИМИЯ — раздел химии, в котором изучаются химические свойства веществ на основе физических свойств составляющих их атомов и молекул. Современная физическая химия широкая междисциплинарная область, граничащая с различными разделами физики, биофизики и… … Энциклопедия Кольера
Константа диссоциации кислоты — У этого термина существуют и другие значения, см. Константа. Константа диссоциации кислоты (Ka) константа равновесия реакции диссоциации кислоты на ион водорода и анион кислотного остатка. Для многоосновных кислот, диссоциация которых… … Википедия
Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
1. Изохорический процесс. Закон Шарля. V = const.
Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:
При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.
График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ— и VT-диаграммах (рис. 1.6). Уравнение изохоры:
Рис. 1.6
Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде
где Р0 – давление при 0 °С, α — температурный коэффициент давления газа равный 1/273 град -1 . График такой зависимости на Рt-диаграмме имеет вид, показанный на рисунке 1.7.
Рис. 1.7
Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:
При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV— и РT-диаграммах (рис. 1.8).
Рис. 1.8
Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде
где α =1/273 град -1 — температурный коэффициент объёмного расширения. График такой зависимости на Vt диаграмме имеет вид, показанный на рисунке 1.9.
Рис. 1.9
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT— и РT-диаграммах (рис. 1.10).
Рис. 1.10
Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.
5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA=6,02·10 23 молекул (число Авогадро).
7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.
При , давление смеси газов:
В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа
Читайте также:
- Окончательное закрепощение крестьян после смуты кратко
- Расскажи где дети могут получать знания и умения до школы по обществознанию 5 класс кратко
- Евразийцы об особенностях российского цивилизационного феномена кратко
- Суши значение слова кратко
- Либерально демократические режимы 1929 1933 кратко
Фундаментальная физическая постоянная (константа) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Численные
значения физических постоянных или их комбинаций находят на основе экспериментальных измерений и выражают в единицах какой-либо системы единиц.
Стоит различать
размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так
как оно не зависит от системы единиц.
|
Константа |
Обозначение |
Численное значение |
|
Скорость света в вакууме |
с |
2,99792458.108 м/с |
|
Элементарный заряд |
е |
1,60219.10-19 Кл |
|
Масса покоя электрона |
me |
9,10953.10-31 кг 5,486.10-4 а.е.м. |
|
Масса покоя нейтрона |
mn |
1,67495.10-27 кг 1,00866 а.е.м. |
|
Масса покоя протона |
mp |
1,67265.10-27 кг 1,00728 а.е.м. |
|
Гравитационная постоянная |
G |
6,672.10-11 Н.м2/кг2 |
|
Электрическая постоянная |
e0 |
8,854.10-12 Ф/м |
|
Постоянная в законе Кулона |
K |
9.109 Н.м2/Кл2 |
|
Магнитная постоянная |
m0 |
4p.10-7 Гн/м |
|
Постоянная Авогадро |
NA |
6.022.1023 моль-1 |
|
Постоянная Больцмана |
k |
1.3807.10-23 Дж/К |
|
Постоянная Фарадея |
F |
96484,56 Кл/моль |
|
Универсальная газовая Постоянная |
R |
8,314 Дж/(моль.К) |
|
Молярный объем идеального газа при нормальных условиях |
Vm |
22,4.10-3 м3/моль |
|
Постоянная Планка |
h |
6.626.10-34 Дж.с 4,136.10-15 эВ.c 1,055.10-34Дж.с 6,59.10-16 эВ.с |
|
Абсолютный ноль температуры |
Т0 |
0 К=-273,150С |
|
Скорость звука в воздухе при нормальных условиях |
331,5 м/с |
|
|
Ускорение свободного падения |
g |
9,80665 м/с2 |
|
Коэффициент взаимосвязи массы и энергии |
с2 |
8,9874.1016 Дж/кг 931,5 МэВ/а.е.м. |
|
Постоянная Ридберга |
R |
1,097373143.107м-1 |
|
Радиус 1-ой боровской орбиты |
а0 |
5,2917706.10-11м |
|
Удельный заряд электрона |
e/me |
1,759.1011 Кл/кг |
|
Средний радиус Земли |
R |
6,371.106 м |
|
Масса Земли |
М |
5,976.1024 кг |
|
Нормальное атмосферное давление |
P0 |
101325 Па 760 мм рт. ст. |
_______________________


________________________

_________________
НОВОСТИ НА САЙТЕ
________________________
В новостной ленте размещается информация о новых работах автора сайта.
____________________________
Разработана анимированная практическая (домашняя) работа «Определение коэффициента полезного действия (КПД) электрочайника», 8 класс.
________________
Автором сайта сделана попытка анимации
учебника ФИЗИКА – 10, авт. Мякишев Г.Я. (изд. 2008 г.). Смотрите в меню «10 класс».
________________
Созданы анимированные лабораторные работы по физике для 10 и 11 классов.
_____________________
Созданы анимированные практические (домашние) работы.
7 класс
Определение толщины монеты.
Расчет массы воды в
аквариуме.
Определение плотности мыла.
Определение массы и веса воздуха в жилой комнате по плотности и объему.
Расчет
k жесткости бумаги.
Расчет
давление твердого тела на поверхность.
Плавает
или
тонет
тело?
Вычисление силы, с
которой атмосфера давит на поверхность стола.
8 класс
Изготовление электроскопа.
Определение относительной влажности воздуха с
помощью психрометра.
Расчет стоимости электроэнергии по показанию электросчетчика.
_____________________
.

_____________________
____________________

____________________
____________________

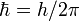
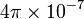 Н·А−2
Н·А−2