Отредактировано 21.07.2022
Географические координаты — это определённое место на земной поверхности.
Однако стоит учитывать что географические координаты на земной поверхности, определенные по результатам наблюдений небесных светил, называются астрономическими координатами, а по результатам геодезических измерений на местности — геодезическими координатами.
При определении астрономических координат точка проектируется отвесной линией на поверхность геоида, а при определении геодезических координат — нормалью на поверхность земного эллипсоида. Вследствие неравномерного распределения массы Земли и отклонения поверхности геоида от поверхности земного эллипсоида отвесная линия в общем случае не совпадает с нормалью. Угол уклонения отвесной линии на большей части территории РФ не превышает 3—4″ или в линейной мере около ±100 м. В отдельных (преимущественно горных) районах уклонение отвесной линии достигает 40″.
Таким образом, географические координаты — обобщенное понятие об астрономических и геодезических координатах, когда уклонение отвесной линии не учитывается.
Для записи географических координат может использоваться любой эллипсоид (или геоид), но чаще всего используются WGS 84 и Красовского (на территории РФ).
Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:
- в градусах (обозначается символом ° ) в виде десятичной дроби (современный вариант) (например, 54.97158, 73.38318)
- в градусах (обозначается символом ° ) и минутах (обозначается символом ′ ) с десятичной дробью (например, 54°58.295′, 73°22.991′)
- в градусах (обозначается символом ° ), минутах (обозначается символом ′ ) и секундах (обозначается символом ″ ) с десятичной дробью (исторически сложившаяся форма записи) (например, 54°58’17.7″, 73°22’59.4″)
- другие варианты. Но они почти не используются в гражданских навигационных устройствах.
Разделителем десятичной дроби может служить точка или запятая. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:
- «N» или «с. ш.» — северная широта,
- «E» или «в. д.» — восточная долгота.
Отрицательные знаки координат представляются либо знаком «−», либо буквами:
- «S» или «ю. ш.» — южная широта,
- «W» или «з. д. — западная долгота.
Буквы могут стоять как впереди, так и сзади. Единых правил записи координат не существует.
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.
Хотя я вам могут дать такой совет. Если вам надо увидеть место только на Яндекс картах, Google картах или самым простых стилях OSM, то проще всего открыть сайты соответствующих карт, вставить в строку поиска координаты (или просто название нужного вам места) и нажать «поиск» (лупу) или Enter. Сайт покажет вам, что находится на этом месте. И не надо заниматься переводом из одних координат в другие.
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами). Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д.
- 55,755831°, 37,617673° — градусы
- N55.755831°, E37.617673° — градусы (+ доп. буквы)
- 55°45.35′N, 37°37.06′E — градусы и минуты (+ доп. буквы)
- 55°45′20.9916″N, 37°37′3.6228″E — градусы, минуты и секунды (+ доп. буквы)
Пересчет координат
Иногда необходимо один тип координат, а есть только другой. В этом случае их можно пересчитать в другой тип координат. Вот как это можно сделать
Для преобразования из градусов в градусы-минуты
Целая часть градусов переписывается как есть. Дробная часть градусов (она всегда меньше 1) умножается на 60, получается значение минут.
Пример: Имеются координаты N60.5643 E30.7543.
Широта: Целая часть 60, дробная часть 0.5643.
Записываем целую часть N60°;
умножаем 0.5643*60=33.858;
Получается N60°33.858′.
То же самое с со второй координатой, долготой:
E30°;
0.7543*60=45.258
Итоговые координаты: N60°33.858′ E30° 45.258′
Для преобразования из градусы-минуты в градусы
Целая часть градусов переписывается как есть. Минуты (они всегда меньше 60) делятся на 60, и получается значение сотых долей градуса.
Пример: Имеются координаты N60°33.858′ E30° 45.258′
Широта: Целая часть 60, минуты 33.858
Записываем целую часть N60°;
Делим значение минут 33.858/60=0.5643;
Получается N60.5643°
То же самое с со второй координатой, долготой:
E30°;
45.258/60=0.7543
Итоговые координаты: N60.5643° E30.7543°
Для преобразования из градусы-минуты в градусы-минуты-секунды
Значение градусов переписывается как есть. Целая часть минут переписывается как есть.
Дробная часть минут (она всегда меньше 1) умножается на 60, получается значение секунд.
Пример: Имеются координаты N60°33.858′ E30° 45.258′.
Широта: Целая часть градусов 60, целая часть минут 33, дробная часть минут 0.858
Записываем целые часть N60° 33′;
умножаем 0.858*60=51.48;
Получается N60°33′ 51.48″.
То же самое с со второй координатой, долготой:
E30° 45′;
0.258*60=15.48
Итоговые координаты: N60°33′ 51.48″ E30° 45′ 15.48″
Для преобразования из градусы-минуты-секунды в градусы-минуты
Значение градусов переписывается как есть. Значение минут переписывается как есть. Значение секунд (оно всегда меньше 60) делится на 60, получается дробная часть минут.
Пример: Имеются координаты N60°33′ 51.48″ E30° 45′ 15.48″
Широта: значение градусов 60, значение минут 33, значение секунд 51.48
Записываем целые часть N60° 33′;
делим 51.48/60=0.858;
Получается N60°33.858′.
То же самое с со второй координатой, долготой:
E30° 45′;
15.48 /60=0.258;
Итоговые координаты: N60°33.858′ E30° 45.258′.
Преобразование градусы в градусы-минуты-секунды и обратно производится через преобразование в градусы-минуты (т.е необходимо произвести два пересчета). Точность координат при любом пересчете не изменяется.
Загрузить PDF
Загрузить PDF
Широта и долгота — координаты на земном шаре, которые помогут вам найти определенное место. При написании широты и долготы стоит убедиться, что вы используете правильный формат и правильные символы, чтобы вас поняли. Можно определить положение различных точек широты и долготы на карте, а затем записать их. Можно записать широту и долготу, используя только значение параллели и меридиана. Для конкретных точек широты и долготы можно записать координаты с помощью градусов, минут, секунд и десятичных дробей.
-
1
Определите географическую долготу. Меридиан — линия долготы, идущая вертикально по всему шару, от Северного до Южного полюса. Нулевой (начальный) меридиан является точкой отсчета долготы. Это нулевая отметка. Еще она называется Гринвичским меридианом. При записи долготы используется символ ° для обозначения градусов.[1]
- Меридианы отсчитываются на восток и на запад от нулевого. При движении на восток величина географической долготы увеличивается на один градус для каждого последующего меридиана. Можно использовать сокращение «в. д.» («восточной долготы»; для международного обозначения используется буква «E» — East), чтобы обозначить долготу, расположенную восточнее нулевого меридиана. Например, географическая долгота может быть 30° в. д. (30°E).
- Если двигаться на запад, то величина географической долготы тоже увеличивается на один градус на каждом следующем меридиане. Географическая долгота, расположенная к западу от нулевого меридиана, обозначается сокращением «з. д.» («западной долготы»; для международного обозначения используется буква «W» — West). Например, географическая долгота может быть 15° з. д. (15°W).
-
2
Определите географическую широту. Географическая широта — горизонтальная линия (параллель), делящая земной шар. Параллели тянутся с востока на запад, начиная от экватора. Географическая широта экватора — 0 градусов. При записи широты для обозначения градусов используется символ °.[2]
- Если двигаться на север от экватора, то географическая широта с каждой параллелью увеличивается на 1 градус, пока не достигнет 90 градусов. На отметке 90 градусов находится Северный полюс. Географическая широта выше экватора обозначается сокращением «с. ш.» («северная широта»; для международного обозначения используется буква «N» — North). Например, географическая широта может быть 15° с. ш. (15°N).
- Если двигаться на юг от экватора, то географическая широта также увеличивается на 1 градус для каждой последующей параллели, пока не достигнет 90 градусов. Это точка Южного полюса. Для обозначения южной широты используйте сокращение «ю. ш.» (для международного обозначения используется буква «S» — South). Например, географическая широта может быть 30° ю. ш. (30°S).
-
3
Запишите координаты широты и долготы. Выберите точку и выясните, где пересекаются линии широты и долготы. Например, точку можно найти по координатам параллели 15° с. ш. и меридиана 30° в. д. При записи координат сначала идет широта, потом долгота (в международном написании они разделяются запятой).[3]
- Географическая широта и долгота, указанные выше, записываются как 15° с. ш. 30° в. д. (15°N, 30°E).
Реклама
-
1
Определите географическую широту и долготу. Иногда нужно указать более точное местоположение, чем номер параллели и меридиана, расстояние между которыми весьма велико. Значения географической широты и долготы можно разбить на минуты и секунды. Однако сначала нужно найти параллель и меридиан. Определите, рядом с какой параллелью и меридианом расположено выбранное место.[4]
- Например, это место расположено рядом с параллелью 15° с. ш. и меридианом 30° в. д.
-
2
Определите минуты между параллелями и меридианами. Расстояние между двумя параллелями и двумя меридианами равно 1 градусу. Этот градус можно разделить на минуты. Представьте, что существует 60 одинаковых минут, разделяющих соседние параллели и меридианы. Можно найти онлайн-карту, которая поможет определить точное значение минут для выбранного места. Для обозначения минут используется одинарный штрих (похож на апостроф).[5]
- Например, если нужно обозначить 23 минуты между параллелями, то они записываются так: 23′ .
-
3
Определите секунды между минутами. Минуты можно дальше разделить на секунды. Расстояние между каждыми двумя минутами составляет 60 секунд. И снова онлайн-карта поможет вам узнать точное количество секунд. Для обозначения секунд используется двойной штрих (похож на знак двойной кавычки).[6]
- Например, 15 секунд записываются как 15″.
-
4
Запишите градусы, затем минуты и в конце секунды. Когда вы определите точные координаты широты и долготы с минутами и секундами, запишите их в правильном порядке. Начните с широты: запишите градусы, минуты и секунды. Затем добавьте «с. ш.» или «ю. ш.» для указания полушария. Затем запишите долготу (при международном обозначении — отделите запятой): градусы, минуты и секунды. Затем добавьте «в. д.» или «з. д.» для указания расположения относительно Гринвича.[7]
- Например, предположим, что есть широта с координатами 15° с. ш., 24 минуты и 15 секунд. И долгота 30° в. д., 10 минут и 3 секунды.
- Эти координаты будут записаны как 15°24’15» с. ш. 30°10’3″ в. д..
Реклама
-
1
Определите координаты широты и долготы точки. Можно использовать минуты с десятыми долями для обозначения широты и долготы. Но все равно сначала нужно определить нужные параллель и меридиан. Выясните, где пересекаются параллель и меридиан, чтобы точно определить ваше местоположение.[8]
- Например, ваше местоположение 15° с. ш. 30° з. д.
-
2
Вычислите минуты с десятыми долями. На некоторых картах используются минуты с десятыми долями, а не минуты с секундами. Онлайн-карта сможет сообщить вам минуты с десятыми долями для значений широты и долготы. Например, широта может быть равна 23,0256 минут.[9]
-
3
Определите, является ли значение отрицательным или положительным. В системе с градусами и минутами с десятыми долями направления «север», «юг», «восток» и «запад» не используются. Вместо них используются положительные или отрицательные числа для определения точки на карте.[10]
- Не забывайте, что параллели проходят к северу или к югу от экватора. При использовании десятых долей для обозначения широты и долготы положительные значения расположены к северу от экватора, а отрицательные — к югу. Точка со значением 23,456 будет выше от экватора, а точка со значением -23,456 — ниже.
- Меридианы располагаются к востоку или западу от нулевого меридиана (Гринвича). Положительные значения обозначают точку к востоку от Гринвича, а отрицательные — к западу. Например, точка со значением 10,234 будет восточнее нулевого меридиана, а со значением -10,234 — западнее.
-
4
Запишите широту и долготу. Чтобы записать координаты, начните со значения широты. Запишите его минутами с десятыми долями. Затем запишите минутами с десятыми долями значение долготы (при международном обозначении широта и долгота разделяются запятой). Не забывайте использовать положительные и отрицательные значения для обозначения направления. В этом формате значок градуса не ставится.[11]
- Например, линия располагается на 15° с. ш. 30° в. д. (15°N, 30°W). Определите минуты и десятые доли и запишите координаты.
- Приведенный выше пример можно записать как 15 10,234, 30 -23,456.
Реклама
-
1
Определите координаты широты и долготы. Широта и долгота часто обозначаются десятичными градусами. Вместо минут и секунд линия в один градус делится с десятичными значениями, чтобы определить доли для точного местоположения. Для начала определите верные градусы широты и долготы.[12]
- Например, ваше местоположение 15° с. ш. 30° з. д.
-
2
Вычислите десятичные доли.Онлайн-карта может показать параллели и меридианы с использованием десятичных долей. Обычно после десятичной запятой записывают до пяти знаков.[13]
- Например, местоположение может быть 15,23456 на север и 30,67890 на запад.
-
3
Определите, являются ли значения положительными или отрицательными. Вместо слов «север», «юг», «восток» и «запад» для обозначения направления используются положительные или отрицательные числа. Для параллелей: значения линий, которые лежат к северу от экватора — положительные, и линии к югу от экватора — отрицательные. Для меридианов: линии к востоку от нулевого меридиана — положительные, и к западу от него — отрицательные.[14]
- Например, широта 15,23456 будет к северу от экватора, а широта -15,23456 — к югу.
- Долгота 30,67890 будет располагаться к востоку от нулевого меридиана, а -30,67890 — к западу.
-
4
Запишите широту и долготу, включая десятые доли. Десятичные градусы очень легко использовать. Просто запишите широту с десятыми долями, а за ней — долготу с десятыми долями. Используйте положительные или отрицательные числа для указания направления.[15]
- Например, координаты 15° с. ш. 30° з. д. в системе десятичных градусов можно записать как 15,23456, -30,67890.
Реклама
Об этой статье
Эту страницу просматривали 53 582 раза.
Была ли эта статья полезной?
Longitude lines are perpendicular to and latitude lines are parallel to the Equator.
The geographic coordinate system (GCS) is a spherical or ellipsoidal coordinate system for measuring and communicating positions directly on the Earth as latitude and longitude.[1] It is the simplest, oldest and most widely used of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.[2][self-published source?]
A full GCS specification, such as those listed in the EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location.[3]
History[edit]
The invention of a geographic coordinate system is generally credited to Eratosthenes of Cyrene, who composed his now-lost Geography at the Library of Alexandria in the 3rd century BC.[4] A century later, Hipparchus of Nicaea improved on this system by determining latitude from stellar measurements rather than solar altitude and determining longitude by timings of lunar eclipses, rather than dead reckoning. In the 1st or 2nd century, Marinus of Tyre compiled an extensive gazetteer and mathematically plotted world map using coordinates measured east from a prime meridian at the westernmost known land, designated the Fortunate Isles, off the coast of western Africa around the Canary or Cape Verde Islands, and measured north or south of the island of Rhodes off Asia Minor. Ptolemy credited him with the full adoption of longitude and latitude, rather than measuring latitude in terms of the length of the midsummer day.[5]
Ptolemy’s 2nd-century Geography used the same prime meridian but measured latitude from the Equator instead. After their work was translated into Arabic in the 9th century, Al-Khwārizmī’s Book of the Description of the Earth corrected Marinus’ and Ptolemy’s errors regarding the length of the Mediterranean Sea,[note 1] causing medieval Arabic cartography to use a prime meridian around 10° east of Ptolemy’s line. Mathematical cartography resumed in Europe following Maximus Planudes’ recovery of Ptolemy’s text a little before 1300; the text was translated into Latin at Florence by Jacobus Angelus around 1407.
In 1884, the United States hosted the International Meridian Conference, attended by representatives from twenty-five nations. Twenty-two of them agreed to adopt the longitude of the Royal Observatory in Greenwich, England as the zero-reference line. The Dominican Republic voted against the motion, while France and Brazil abstained.[6] France adopted Greenwich Mean Time in place of local determinations by the Paris Observatory in 1911.
Latitude and longitude[edit]
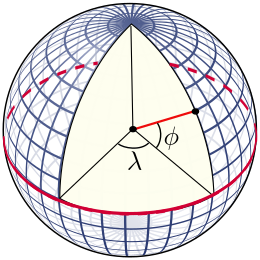
Diagram of the latitude ϕ and longitude λ angle measurements for a spherical model of the Earth.
The «latitude» (abbreviation: Lat., ϕ, or phi) of a point on Earth’s surface is the angle between the equatorial plane and the straight line that passes through that point and through (or close to) the center of the Earth.[note 2] Lines joining points of the same latitude trace circles on the surface of Earth called parallels, as they are parallel to the Equator and to each other. The North Pole is 90° N; the South Pole is 90° S. The 0° parallel of latitude is designated the Equator, the fundamental plane of all geographic coordinate systems. The Equator divides the globe into Northern and Southern Hemispheres.
The «longitude» (abbreviation: Long., λ, or lambda) of a point on Earth’s surface is the angle east or west of a reference meridian to another meridian that passes through that point. All meridians are halves of great ellipses (often called great circles), which converge at the North and South Poles. The meridian of the British Royal Observatory in Greenwich, in southeast London, England, is the international prime meridian, although some organizations—such as the French Institut national de l’information géographique et forestière—continue to use other meridians for internal purposes. The prime meridian determines the proper Eastern and Western Hemispheres, although maps often divide these hemispheres further west in order to keep the Old World on a single side. The antipodal meridian of Greenwich is both 180°W and 180°E. This is not to be conflated with the International Date Line, which diverges from it in several places for political and convenience reasons, including between far eastern Russia and the far western Aleutian Islands.
The combination of these two components specifies the position of any location on the surface of Earth, without consideration of altitude or depth. The visual grid on a map formed by lines of latitude and longitude is known as a graticule.[7] The origin/zero point of this system is located in the Gulf of Guinea about 625 km (390 mi) south of Tema, Ghana, a location often facetiously called Null Island.
Geodetic datum[edit]
In order to be unambiguous about the direction of «vertical» and the «horizontal» surface above which they are measuring, map-makers choose a reference ellipsoid with a given origin and orientation that best fits their need for the area to be mapped. They then choose the most appropriate mapping of the spherical coordinate system onto that ellipsoid, called a terrestrial reference system or geodetic datum.
Datums may be global, meaning that they represent the whole Earth, or they may be local, meaning that they represent an ellipsoid best-fit to only a portion of the Earth. Points on the Earth’s surface move relative to each other due to continental plate motion, subsidence, and diurnal Earth tidal movement caused by the Moon and the Sun. This daily movement can be as much as a meter. Continental movement can be up to 10 cm a year, or 10 m in a century. A weather system high-pressure area can cause a sinking of 5 mm. Scandinavia is rising by 1 cm a year as a result of the melting of the ice sheets of the last ice age, but neighboring Scotland is rising by only 0.2 cm. These changes are insignificant if a local datum is used, but are statistically significant if a global datum is used.[8]
Examples of global datums include World Geodetic System (WGS 84, also known as EPSG:4326[9]), the default datum used for the Global Positioning System,[note 3] and the International Terrestrial Reference System and Frame (ITRF), used for estimating continental drift and crustal deformation.[10] The distance to Earth’s center can be used both for very deep positions and for positions in space.[8]
Local datums chosen by a national cartographical organization include the North American Datum, the European ED50, and the British OSGB36. Given a location, the datum provides the latitude 

The latitude and longitude on a map made against a local datum may not be the same as one obtained from a GPS receiver. Converting coordinates from one datum to another requires a datum transformation such as a Helmert transformation, although in certain situations a simple translation may be sufficient.[11]
In popular GIS software, data projected in latitude/longitude is often represented as a Geographic Coordinate System. For example, data in latitude/longitude if the datum is the North American Datum of 1983 is denoted by ‘GCS North American 1983’.
Length of a degree[edit]
On the GRS 80 or WGS 84 spheroid at sea level at the Equator, one latitudinal second measures 30.715 meters, one latitudinal minute is 1843 meters and one latitudinal degree is 110.6 kilometers. The circles of longitude, meridians, meet at the geographical poles, with the west–east width of a second naturally decreasing as latitude increases. On the Equator at sea level, one longitudinal second measures 30.92 meters, a longitudinal minute is 1855 meters and a longitudinal degree is 111.3 kilometers. At 30° a longitudinal second is 26.76 meters, at Greenwich (51°28′38″N) 19.22 meters, and at 60° it is 15.42 meters.
On the WGS 84 spheroid, the length in meters of a degree of latitude at latitude ϕ (that is, the number of meters you would have to travel along a north–south line to move 1 degree in latitude, when at latitude ϕ), is about

The returned measure of meters per degree latitude varies continuously with latitude.
Similarly, the length in meters of a degree of longitude can be calculated as

(Those coefficients can be improved, but as they stand the distance they give is correct within a centimeter.)
The formulae both return units of meters per degree.
An alternative method to estimate the length of a longitudinal degree at latitude 
where Earth’s average meridional radius 

where Earth’s equatorial radius 


| Latitude | City | Degree | Minute | Second | ±0.0001° |
|---|---|---|---|---|---|
| 60° | Saint Petersburg | 55.80 km | 0.930 km | 15.50 m | 5.58 m |
| 51° 28′ 38″ N | Greenwich | 69.47 km | 1.158 km | 19.30 m | 6.95 m |
| 45° | Bordeaux | 78.85 km | 1.31 km | 21.90 m | 7.89 m |
| 30° | New Orleans | 96.49 km | 1.61 km | 26.80 m | 9.65 m |
| 0° | Quito | 111.3 km | 1.855 km | 30.92 m | 11.13 m |
Alternate encodings[edit]
Like any series of multiple-digit numbers, latitude-longitude pairs can be challenging to communicate and remember. Therefore, alternative schemes have been developed for encoding GCS coordinates into alphanumeric strings or words:
- the Maidenhead Locator System, popular with radio operators.
- the World Geographic Reference System (GEOREF), developed for global military operations, replaced by the current Global Area Reference System (GARS).
- Open Location Code or «Plus Codes», developed by Google and released into the public domain.
- Geohash, a public domain system based on the Morton Z-order curve.
- What3words, a proprietary system that encodes GCS coordinates as pseudorandom sets of words by dividing the coordinates into three numbers and looking up words in an indexed dictionary.
Note that these are not distinct coordinate systems, only alternative methods for expressing latitude and longitude measurements.
See also[edit]
- Decimal degrees – Angular measurements, typically for latitude and longitude
- Geographical distance – Distance measured along the surface of the earth
- Geographic information system – System to capture, manage and present geographic data
- Geo URI scheme
- ISO 6709, standard representation of geographic point location by coordinates
- Linear referencing
- Primary direction – Celestial coordinate system
- Planetary coordinate system
- Selenographic coordinate system
- Spatial reference system – System to specify locations on Earth
- Jan Smits (2015). Mathematical data for bibliographic descriptions of cartographic materials and spatial data. Geographical co-ordinates. ICA Commission on Map Projections.
Notes[edit]
- ^ The pair had accurate absolute distances within the Mediterranean but underestimated the circumference of the Earth, causing their degree measurements to overstate its length west from Rhodes or Alexandria, respectively.
- ^ Alternative versions of latitude and longitude include geocentric coordinates, which measure with respect to Earth’s center; geodetic coordinates, which model Earth as an ellipsoid; and geographic coordinates, which measure with respect to a plumb line at the location for which coordinates are given.
- ^ WGS 84 is the default datum used in most GPS equipment, but other datums can be selected.
References[edit]
- ^ Chang, Kang-tsung (2016). Introduction to Geographic Information Systems (9th ed.). McGraw-Hill. p. 24. ISBN 978-1-259-92964-9.
- ^ Taylor, Chuck. «Locating a Point On the Earth». Archived from the original on 3 March 2016. Retrieved 4 March 2014.
- ^ «Using the EPSG geodetic parameter dataset, Guidance Note 7-1». EPSG Geodetic Parameter Dataset. Geomatic Solutions. Retrieved 15 December 2021.
- ^ McPhail, Cameron (2011), Reconstructing Eratosthenes’ Map of the World (PDF), Dunedin: University of Otago, pp. 20–24.
- ^ Evans, James (1998), The History and Practice of Ancient Astronomy, Oxford, England: Oxford University Press, pp. 102–103, ISBN 9780199874453.
- ^ Greenwich 2000 Limited (9 June 2011). «The International Meridian Conference». Wwp.millennium-dome.com. Archived from the original on 6 August 2012. Retrieved 31 October 2012.
- ^ American Society of Civil Engineers (1 January 1994). Glossary of the Mapping Sciences. ASCE Publications. p. 224. ISBN 9780784475706.
- ^ a b c A guide to coordinate systems in Great Britain (PDF), D00659 v3.6, Ordnance Survey, 2020, archived (PDF) from the original on 2 April 2020, retrieved 17 December 2021
- ^ «WGS 84: EPSG Projection — Spatial Reference». spatialreference.org. Retrieved 5 May 2020.
- ^ Bolstad, Paul (2012). GIS Fundamentals (PDF) (5th ed.). Atlas books. p. 102. ISBN 978-0-9717647-3-6.
- ^ «Making maps compatible with GPS». Government of Ireland 1999. Archived from the original on 21 July 2011. Retrieved 15 April 2008.
- ^ a b [1] Geographic Information Systems — Stackexchange
Sources[edit]
- Portions of this article are from Jason Harris’ «Astroinfo» which is distributed with KStars, a desktop planetarium for Linux/KDE. See The KDE Education Project — KStars
External links[edit]
Media related to Geographic coordinate system at Wikimedia Commons
Longitude lines are perpendicular to and latitude lines are parallel to the Equator.
The geographic coordinate system (GCS) is a spherical or ellipsoidal coordinate system for measuring and communicating positions directly on the Earth as latitude and longitude.[1] It is the simplest, oldest and most widely used of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.[2][self-published source?]
A full GCS specification, such as those listed in the EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location.[3]
History[edit]
The invention of a geographic coordinate system is generally credited to Eratosthenes of Cyrene, who composed his now-lost Geography at the Library of Alexandria in the 3rd century BC.[4] A century later, Hipparchus of Nicaea improved on this system by determining latitude from stellar measurements rather than solar altitude and determining longitude by timings of lunar eclipses, rather than dead reckoning. In the 1st or 2nd century, Marinus of Tyre compiled an extensive gazetteer and mathematically plotted world map using coordinates measured east from a prime meridian at the westernmost known land, designated the Fortunate Isles, off the coast of western Africa around the Canary or Cape Verde Islands, and measured north or south of the island of Rhodes off Asia Minor. Ptolemy credited him with the full adoption of longitude and latitude, rather than measuring latitude in terms of the length of the midsummer day.[5]
Ptolemy’s 2nd-century Geography used the same prime meridian but measured latitude from the Equator instead. After their work was translated into Arabic in the 9th century, Al-Khwārizmī’s Book of the Description of the Earth corrected Marinus’ and Ptolemy’s errors regarding the length of the Mediterranean Sea,[note 1] causing medieval Arabic cartography to use a prime meridian around 10° east of Ptolemy’s line. Mathematical cartography resumed in Europe following Maximus Planudes’ recovery of Ptolemy’s text a little before 1300; the text was translated into Latin at Florence by Jacobus Angelus around 1407.
In 1884, the United States hosted the International Meridian Conference, attended by representatives from twenty-five nations. Twenty-two of them agreed to adopt the longitude of the Royal Observatory in Greenwich, England as the zero-reference line. The Dominican Republic voted against the motion, while France and Brazil abstained.[6] France adopted Greenwich Mean Time in place of local determinations by the Paris Observatory in 1911.
Latitude and longitude[edit]
Diagram of the latitude ϕ and longitude λ angle measurements for a spherical model of the Earth.
The «latitude» (abbreviation: Lat., ϕ, or phi) of a point on Earth’s surface is the angle between the equatorial plane and the straight line that passes through that point and through (or close to) the center of the Earth.[note 2] Lines joining points of the same latitude trace circles on the surface of Earth called parallels, as they are parallel to the Equator and to each other. The North Pole is 90° N; the South Pole is 90° S. The 0° parallel of latitude is designated the Equator, the fundamental plane of all geographic coordinate systems. The Equator divides the globe into Northern and Southern Hemispheres.
The «longitude» (abbreviation: Long., λ, or lambda) of a point on Earth’s surface is the angle east or west of a reference meridian to another meridian that passes through that point. All meridians are halves of great ellipses (often called great circles), which converge at the North and South Poles. The meridian of the British Royal Observatory in Greenwich, in southeast London, England, is the international prime meridian, although some organizations—such as the French Institut national de l’information géographique et forestière—continue to use other meridians for internal purposes. The prime meridian determines the proper Eastern and Western Hemispheres, although maps often divide these hemispheres further west in order to keep the Old World on a single side. The antipodal meridian of Greenwich is both 180°W and 180°E. This is not to be conflated with the International Date Line, which diverges from it in several places for political and convenience reasons, including between far eastern Russia and the far western Aleutian Islands.
The combination of these two components specifies the position of any location on the surface of Earth, without consideration of altitude or depth. The visual grid on a map formed by lines of latitude and longitude is known as a graticule.[7] The origin/zero point of this system is located in the Gulf of Guinea about 625 km (390 mi) south of Tema, Ghana, a location often facetiously called Null Island.
Geodetic datum[edit]
In order to be unambiguous about the direction of «vertical» and the «horizontal» surface above which they are measuring, map-makers choose a reference ellipsoid with a given origin and orientation that best fits their need for the area to be mapped. They then choose the most appropriate mapping of the spherical coordinate system onto that ellipsoid, called a terrestrial reference system or geodetic datum.
Datums may be global, meaning that they represent the whole Earth, or they may be local, meaning that they represent an ellipsoid best-fit to only a portion of the Earth. Points on the Earth’s surface move relative to each other due to continental plate motion, subsidence, and diurnal Earth tidal movement caused by the Moon and the Sun. This daily movement can be as much as a meter. Continental movement can be up to 10 cm a year, or 10 m in a century. A weather system high-pressure area can cause a sinking of 5 mm. Scandinavia is rising by 1 cm a year as a result of the melting of the ice sheets of the last ice age, but neighboring Scotland is rising by only 0.2 cm. These changes are insignificant if a local datum is used, but are statistically significant if a global datum is used.[8]
Examples of global datums include World Geodetic System (WGS 84, also known as EPSG:4326[9]), the default datum used for the Global Positioning System,[note 3] and the International Terrestrial Reference System and Frame (ITRF), used for estimating continental drift and crustal deformation.[10] The distance to Earth’s center can be used both for very deep positions and for positions in space.[8]
Local datums chosen by a national cartographical organization include the North American Datum, the European ED50, and the British OSGB36. Given a location, the datum provides the latitude 

The latitude and longitude on a map made against a local datum may not be the same as one obtained from a GPS receiver. Converting coordinates from one datum to another requires a datum transformation such as a Helmert transformation, although in certain situations a simple translation may be sufficient.[11]
In popular GIS software, data projected in latitude/longitude is often represented as a Geographic Coordinate System. For example, data in latitude/longitude if the datum is the North American Datum of 1983 is denoted by ‘GCS North American 1983’.
Length of a degree[edit]
On the GRS 80 or WGS 84 spheroid at sea level at the Equator, one latitudinal second measures 30.715 meters, one latitudinal minute is 1843 meters and one latitudinal degree is 110.6 kilometers. The circles of longitude, meridians, meet at the geographical poles, with the west–east width of a second naturally decreasing as latitude increases. On the Equator at sea level, one longitudinal second measures 30.92 meters, a longitudinal minute is 1855 meters and a longitudinal degree is 111.3 kilometers. At 30° a longitudinal second is 26.76 meters, at Greenwich (51°28′38″N) 19.22 meters, and at 60° it is 15.42 meters.
On the WGS 84 spheroid, the length in meters of a degree of latitude at latitude ϕ (that is, the number of meters you would have to travel along a north–south line to move 1 degree in latitude, when at latitude ϕ), is about

The returned measure of meters per degree latitude varies continuously with latitude.
Similarly, the length in meters of a degree of longitude can be calculated as

(Those coefficients can be improved, but as they stand the distance they give is correct within a centimeter.)
The formulae both return units of meters per degree.
An alternative method to estimate the length of a longitudinal degree at latitude 
where Earth’s average meridional radius 

where Earth’s equatorial radius 


| Latitude | City | Degree | Minute | Second | ±0.0001° |
|---|---|---|---|---|---|
| 60° | Saint Petersburg | 55.80 km | 0.930 km | 15.50 m | 5.58 m |
| 51° 28′ 38″ N | Greenwich | 69.47 km | 1.158 km | 19.30 m | 6.95 m |
| 45° | Bordeaux | 78.85 km | 1.31 km | 21.90 m | 7.89 m |
| 30° | New Orleans | 96.49 km | 1.61 km | 26.80 m | 9.65 m |
| 0° | Quito | 111.3 km | 1.855 km | 30.92 m | 11.13 m |
Alternate encodings[edit]
Like any series of multiple-digit numbers, latitude-longitude pairs can be challenging to communicate and remember. Therefore, alternative schemes have been developed for encoding GCS coordinates into alphanumeric strings or words:
- the Maidenhead Locator System, popular with radio operators.
- the World Geographic Reference System (GEOREF), developed for global military operations, replaced by the current Global Area Reference System (GARS).
- Open Location Code or «Plus Codes», developed by Google and released into the public domain.
- Geohash, a public domain system based on the Morton Z-order curve.
- What3words, a proprietary system that encodes GCS coordinates as pseudorandom sets of words by dividing the coordinates into three numbers and looking up words in an indexed dictionary.
Note that these are not distinct coordinate systems, only alternative methods for expressing latitude and longitude measurements.
See also[edit]
- Decimal degrees – Angular measurements, typically for latitude and longitude
- Geographical distance – Distance measured along the surface of the earth
- Geographic information system – System to capture, manage and present geographic data
- Geo URI scheme
- ISO 6709, standard representation of geographic point location by coordinates
- Linear referencing
- Primary direction – Celestial coordinate system
- Planetary coordinate system
- Selenographic coordinate system
- Spatial reference system – System to specify locations on Earth
- Jan Smits (2015). Mathematical data for bibliographic descriptions of cartographic materials and spatial data. Geographical co-ordinates. ICA Commission on Map Projections.
Notes[edit]
- ^ The pair had accurate absolute distances within the Mediterranean but underestimated the circumference of the Earth, causing their degree measurements to overstate its length west from Rhodes or Alexandria, respectively.
- ^ Alternative versions of latitude and longitude include geocentric coordinates, which measure with respect to Earth’s center; geodetic coordinates, which model Earth as an ellipsoid; and geographic coordinates, which measure with respect to a plumb line at the location for which coordinates are given.
- ^ WGS 84 is the default datum used in most GPS equipment, but other datums can be selected.
References[edit]
- ^ Chang, Kang-tsung (2016). Introduction to Geographic Information Systems (9th ed.). McGraw-Hill. p. 24. ISBN 978-1-259-92964-9.
- ^ Taylor, Chuck. «Locating a Point On the Earth». Archived from the original on 3 March 2016. Retrieved 4 March 2014.
- ^ «Using the EPSG geodetic parameter dataset, Guidance Note 7-1». EPSG Geodetic Parameter Dataset. Geomatic Solutions. Retrieved 15 December 2021.
- ^ McPhail, Cameron (2011), Reconstructing Eratosthenes’ Map of the World (PDF), Dunedin: University of Otago, pp. 20–24.
- ^ Evans, James (1998), The History and Practice of Ancient Astronomy, Oxford, England: Oxford University Press, pp. 102–103, ISBN 9780199874453.
- ^ Greenwich 2000 Limited (9 June 2011). «The International Meridian Conference». Wwp.millennium-dome.com. Archived from the original on 6 August 2012. Retrieved 31 October 2012.
- ^ American Society of Civil Engineers (1 January 1994). Glossary of the Mapping Sciences. ASCE Publications. p. 224. ISBN 9780784475706.
- ^ a b c A guide to coordinate systems in Great Britain (PDF), D00659 v3.6, Ordnance Survey, 2020, archived (PDF) from the original on 2 April 2020, retrieved 17 December 2021
- ^ «WGS 84: EPSG Projection — Spatial Reference». spatialreference.org. Retrieved 5 May 2020.
- ^ Bolstad, Paul (2012). GIS Fundamentals (PDF) (5th ed.). Atlas books. p. 102. ISBN 978-0-9717647-3-6.
- ^ «Making maps compatible with GPS». Government of Ireland 1999. Archived from the original on 21 July 2011. Retrieved 15 April 2008.
- ^ a b [1] Geographic Information Systems — Stackexchange
Sources[edit]
- Portions of this article are from Jason Harris’ «Astroinfo» which is distributed with KStars, a desktop planetarium for Linux/KDE. See The KDE Education Project — KStars
External links[edit]
Media related to Geographic coordinate system at Wikimedia Commons
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
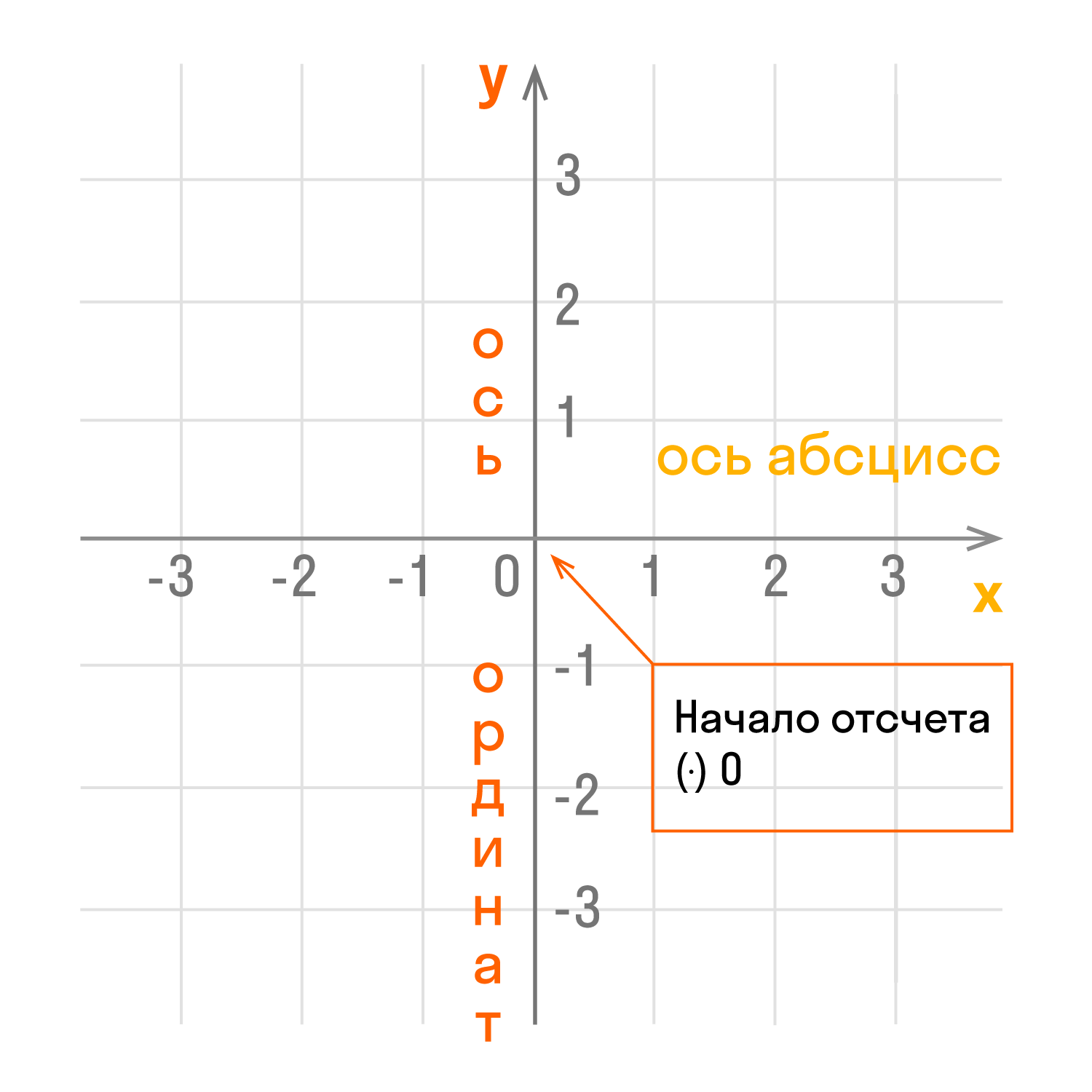
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
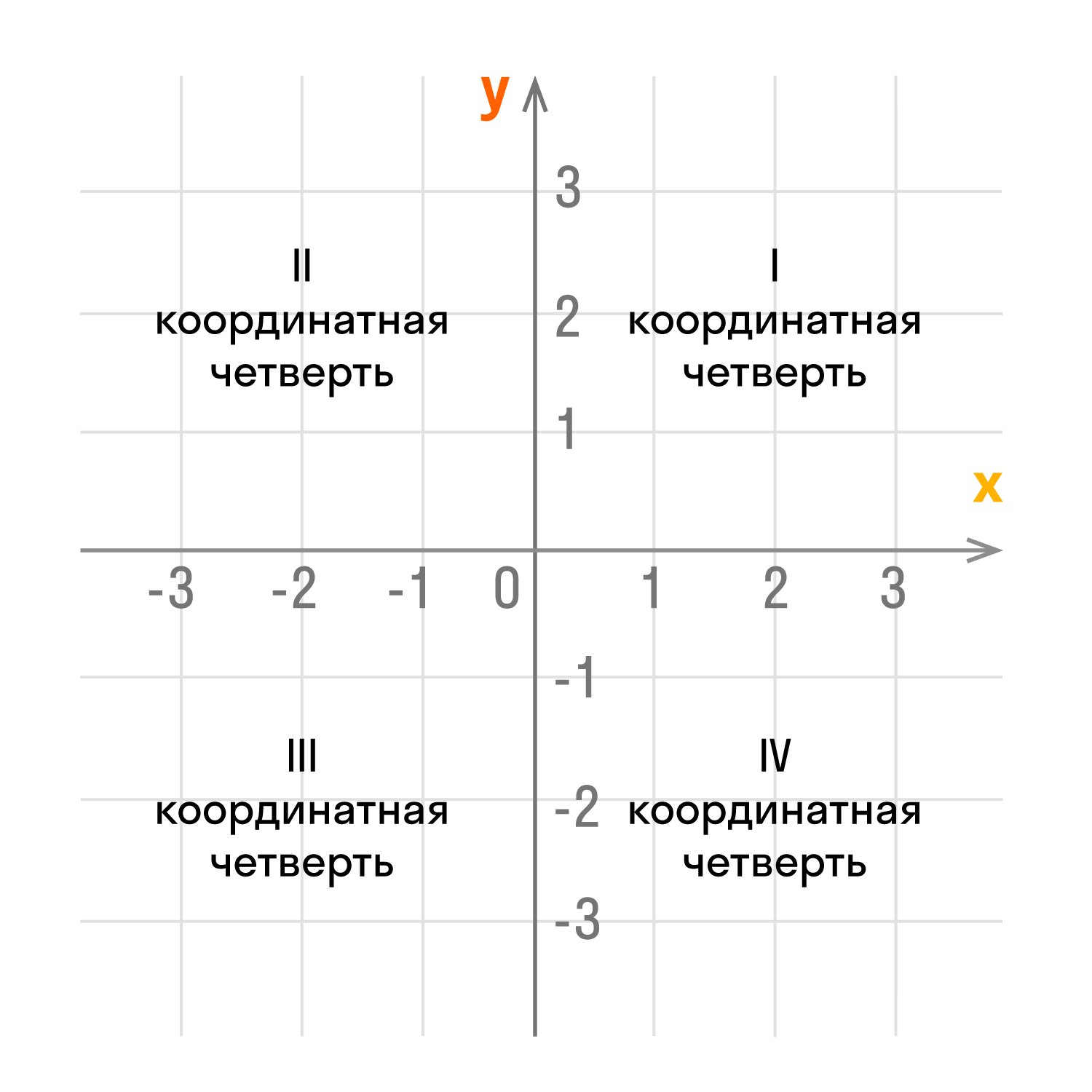
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Правила координат:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Определение координат точки
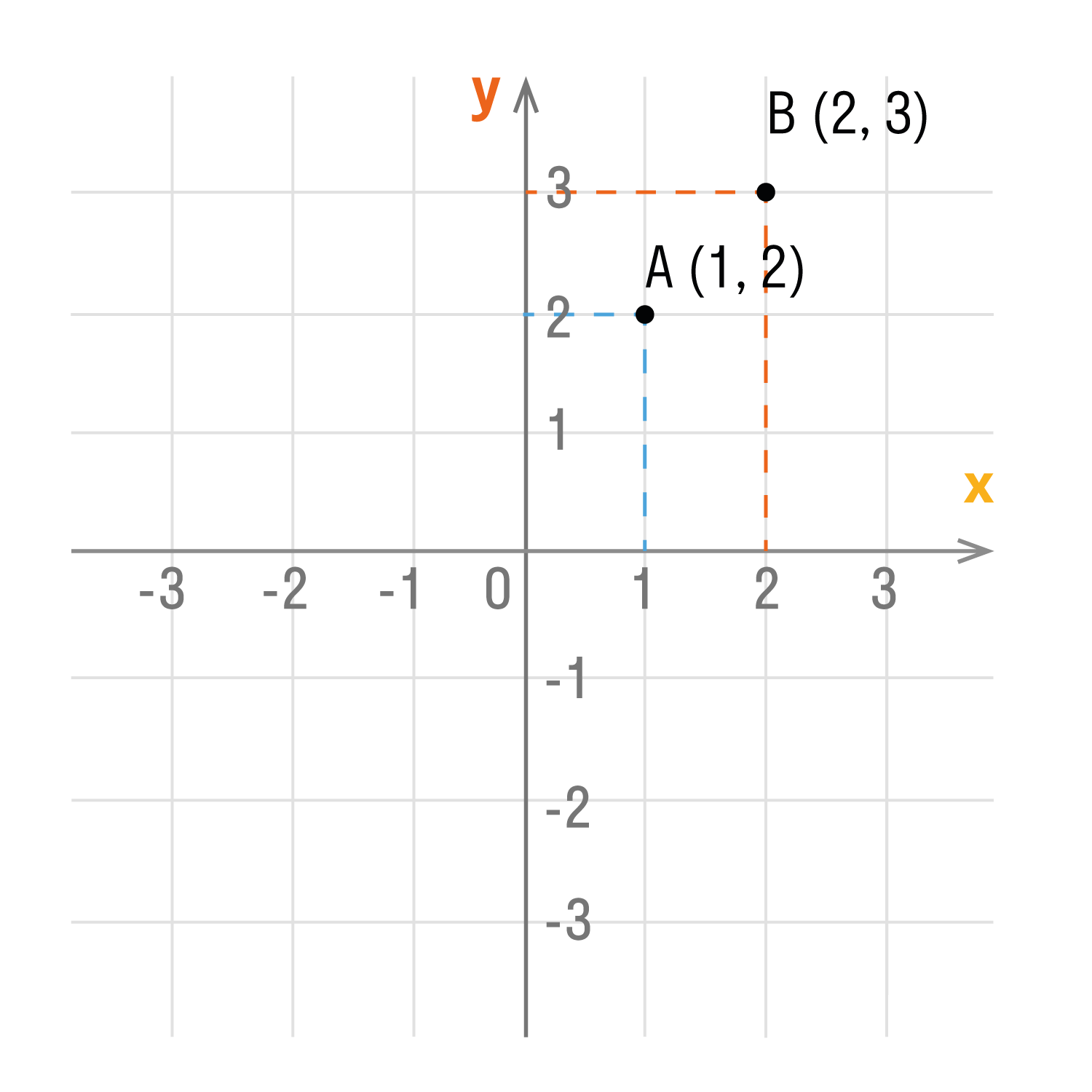
Каждой точке координатной плоскости соответствуют две координаты.
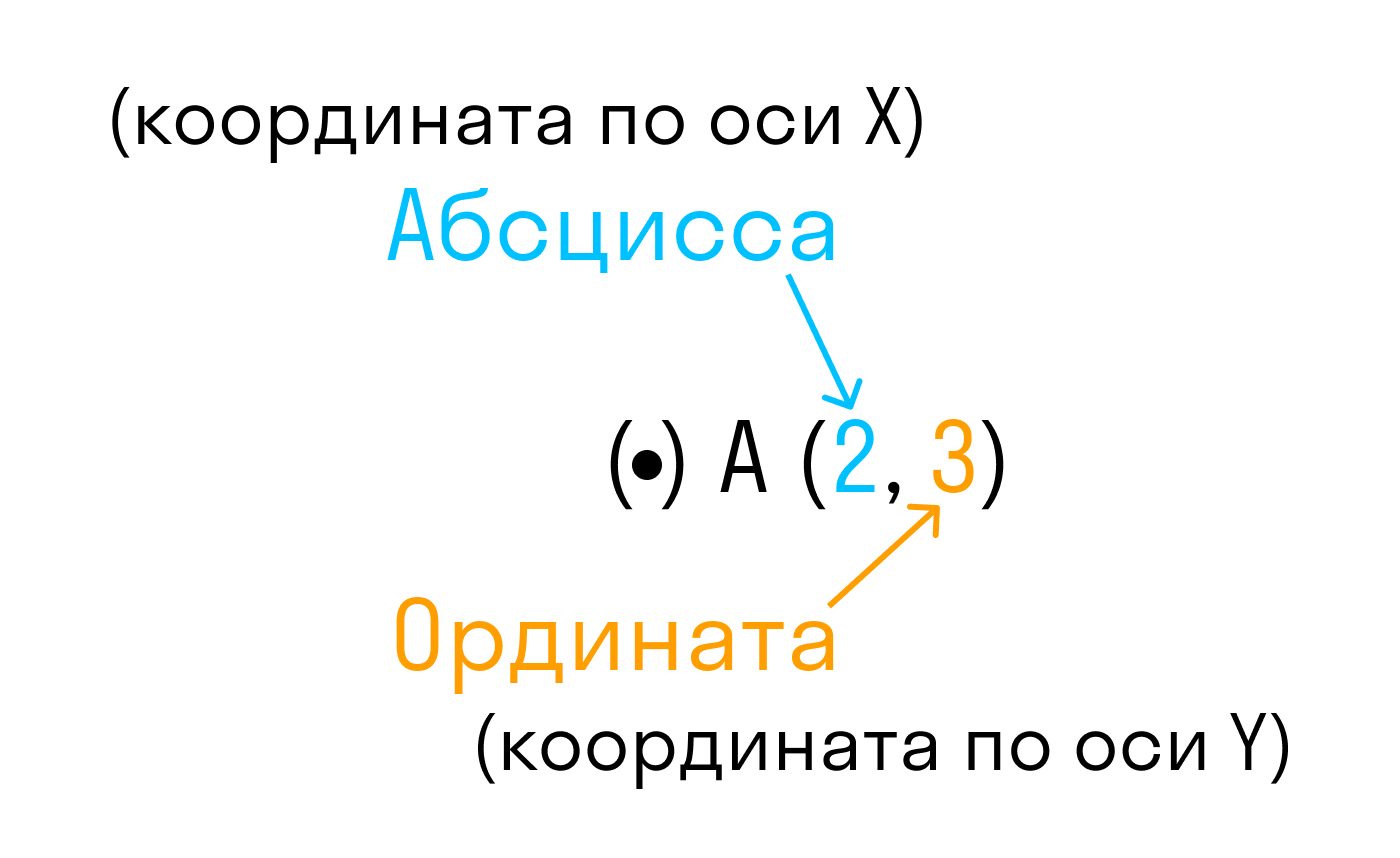
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
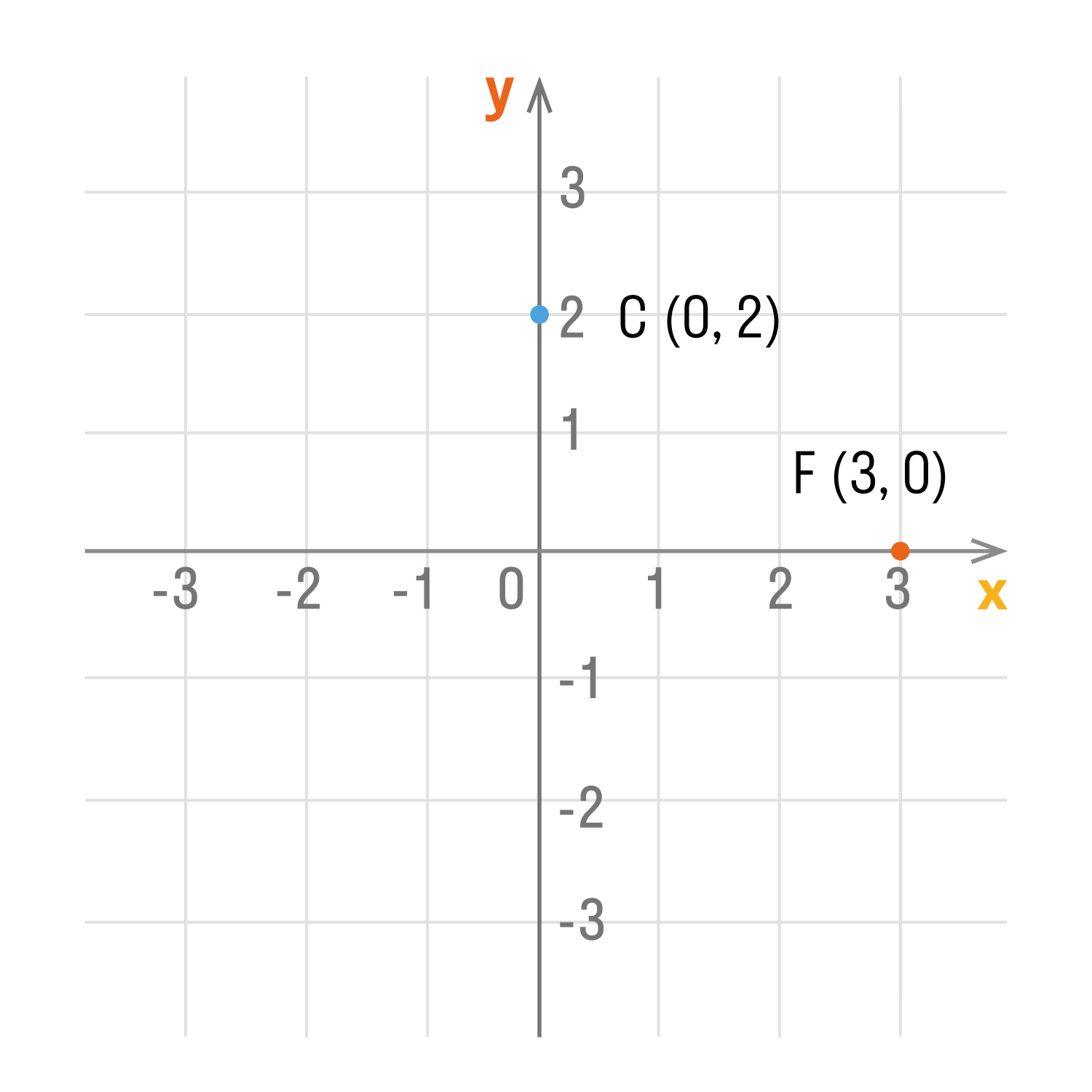
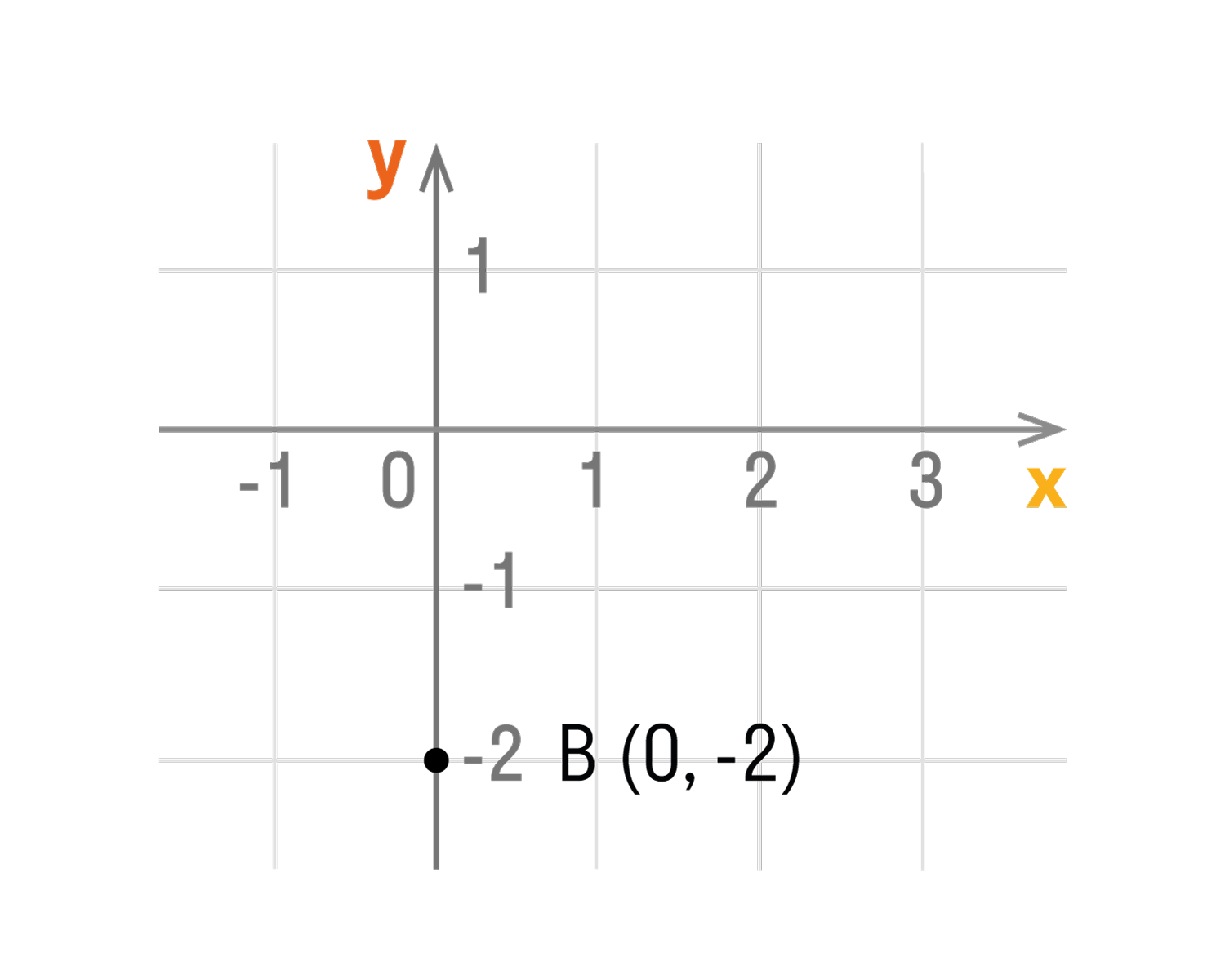
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
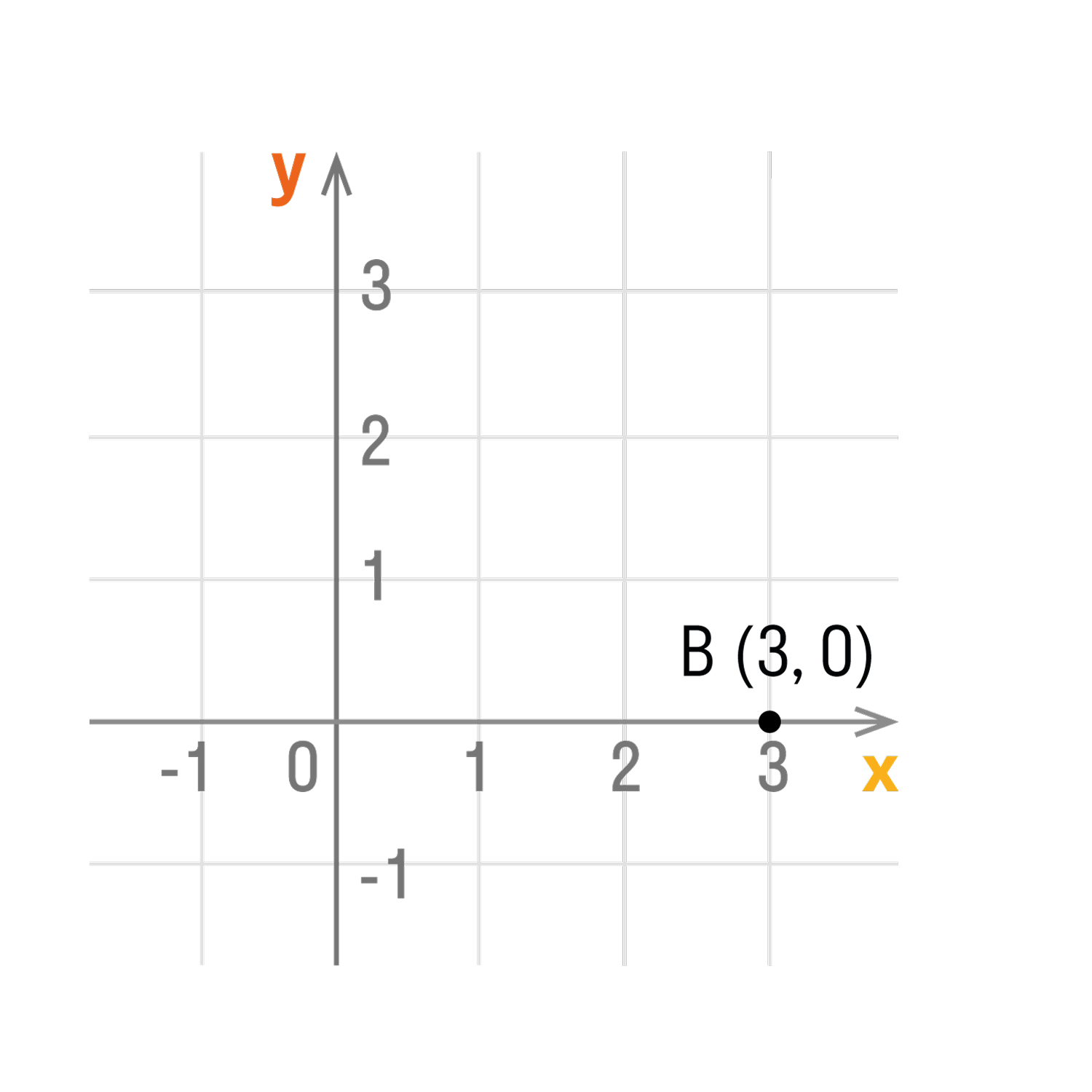
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
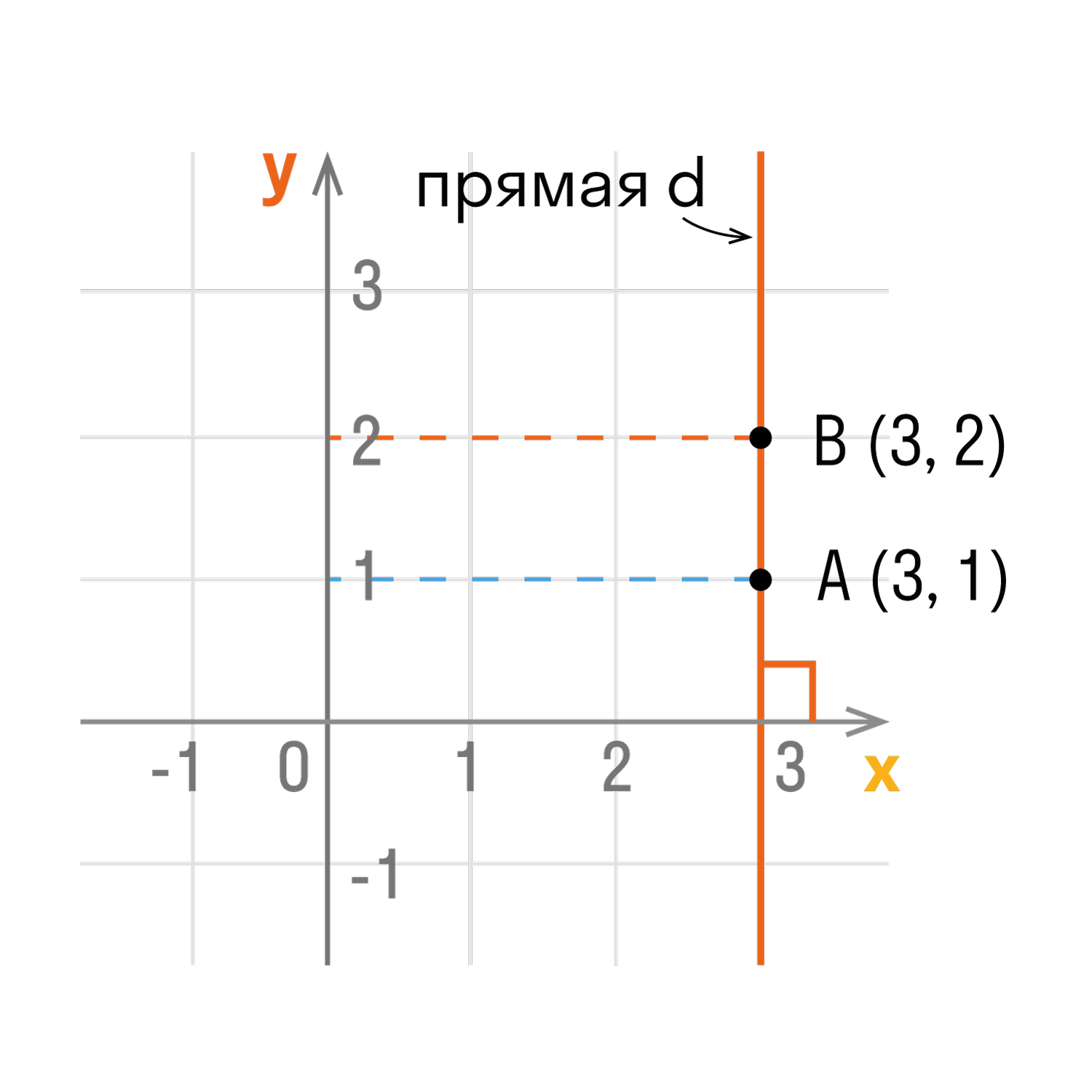
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
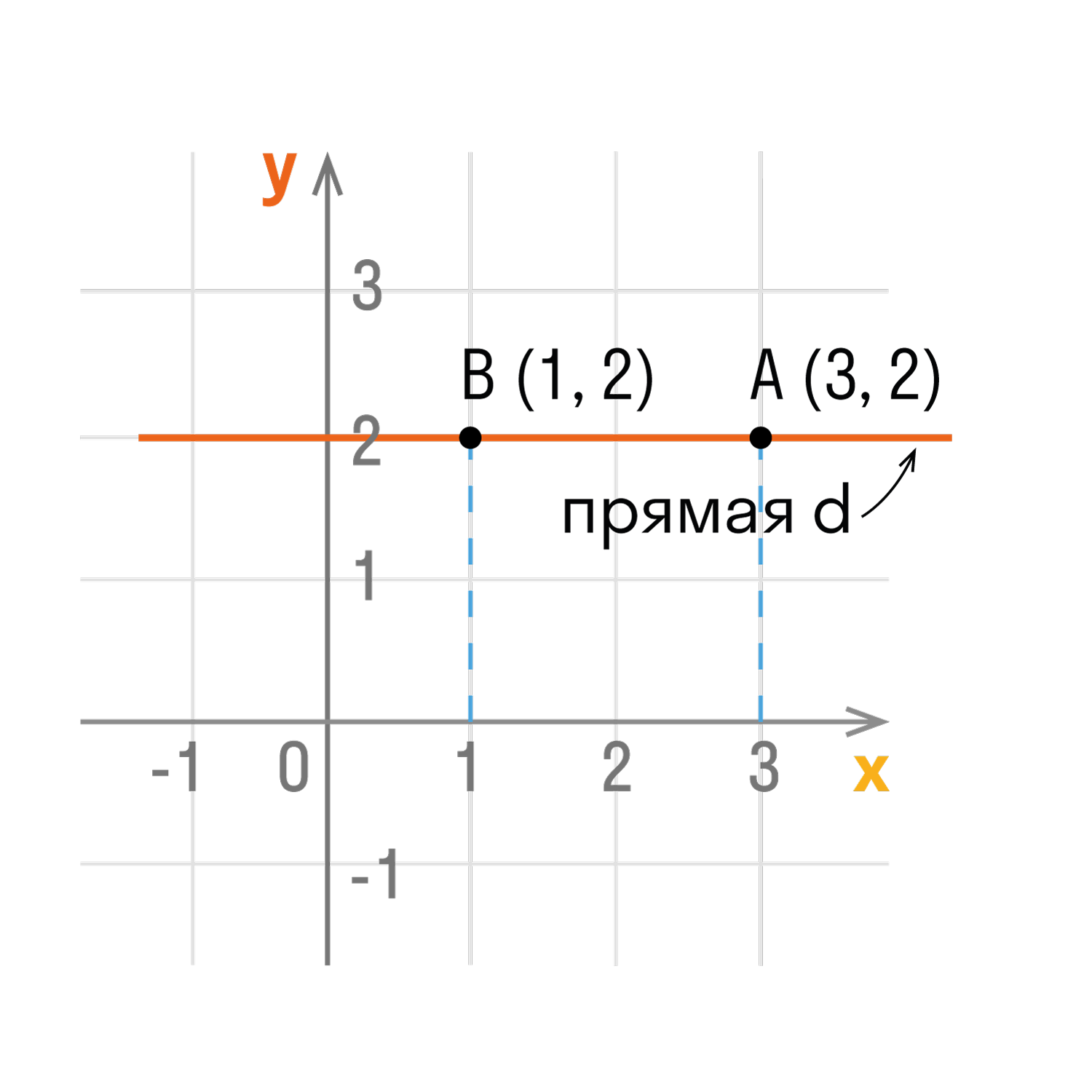
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
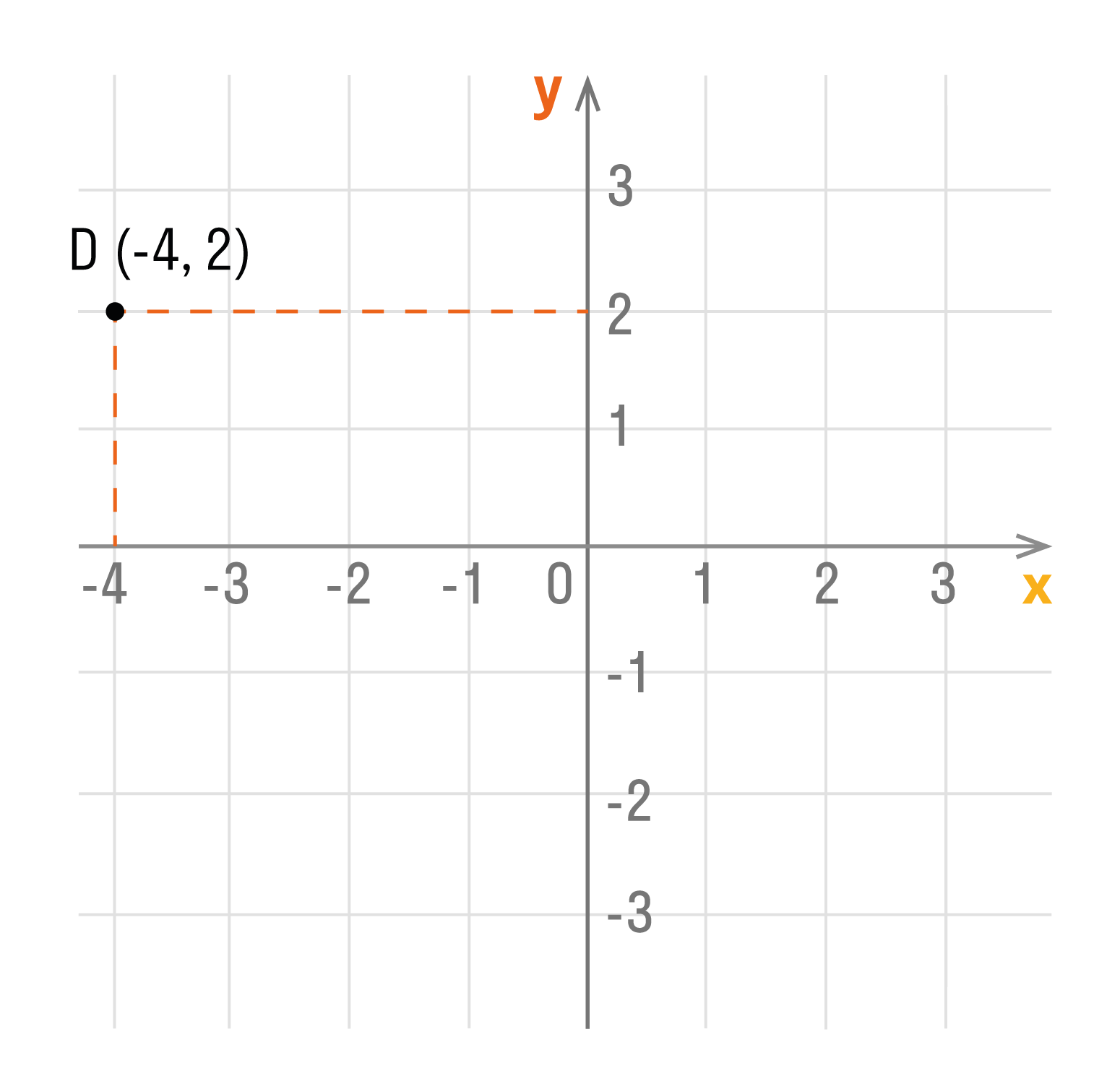
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
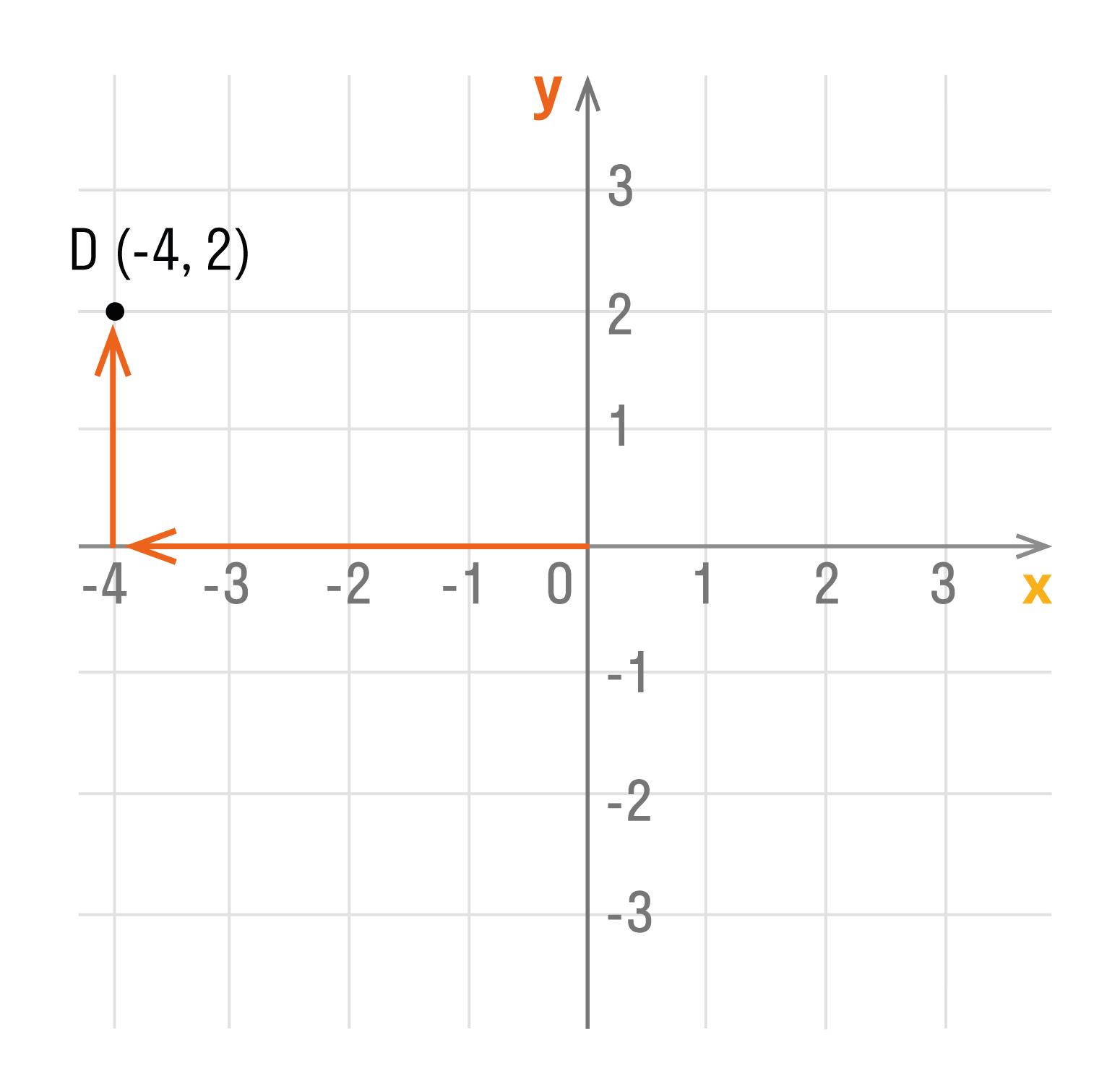
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
У этого термина существуют и другие значения, см. Координаты.
Координатная сфера
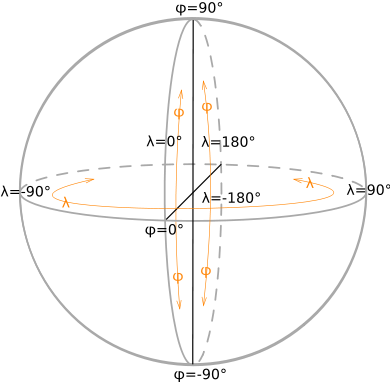
Географи́ческие координа́ты определяют положение точки на земной поверхности или, более широко, в географической оболочке.
Географические координаты строятся по принципу сферических. Аналогичные координаты применяются на других планетах, а также на небесной сфере[1].
Содержание
- 1 Широта
- 2 Долгота
- 3 Высота
- 4 Географическая система координат
- 4.1 Полусвободная в азимуте система координат
- 5 Форматы записи географических координат
- 6 Ссылки
- 7 См. также
- 8 Примечания
Широта
Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.
От широты места, как и от времени года, зависит продолжительность дня.
Из-за отличия формы Земли от шара географическая широта точек несколько отличается от их геоцентрической широты, т. е. от угла между направлением на данную точку из центра Земли и плоскостью экватора.
Широту места можно определить с помощью таких астрономических инструментов как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).
Долгота
Долгота́ — угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготы от 0° до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные — отрицательными.
Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Гринвичский меридиан, проходящий через обсерваторию в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулково и т. д.
От долготы зависит местное время.
Высота
Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.
В пределах географической оболочки применяется обычно ‘высота над уровнем моря’, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.
Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако не служит координатой
Географическая система координат
Рис. 1
В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС). Переход начала координат из инерциальной системы координат в географическую (т.е из 


- где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря.
Ориентация осей в географической системе координат (ГСК) выбирается по алгоритму.
- Ось X (другое обозначение — ось E) — ось, направленная на восток.
- Ось Y (другое обозначение — ось N) — ось, направленная на север.
- Ось Z (другое обозначение — ось Up) — ось, направленная на вертикально вверх.
Ориентация трёхгранника XYZ,из-за вращения земли и движения ТС постоянно смещается с угловыми скоростями[2].
Основным недостатком в практическом применении ГСК в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо ГСК используется полусвободная в азимуте СК.
Полусвободная в азимуте система координат
Полусвободная в азимуте СК отличается от ГСК только одним уравнением, которое имеет вид:
Соответственно, система имеет тоже начальное положение, что ГСК и их ориентация также совпадает с одной лишь разницей, что её оси 


Преобразование между ГСК и полусвободной в азимуте СК осуществляется по формуле[2]
В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.
Форматы записи географических координат
Для записи географических координат используется система WGS84.
Координаты (широта от -90° до +90°, долгота от -180° до +180°) могут записываться:
- в ° градусах в виде десятичной дроби (современный вариант)
- в ° градусах и ‘ минутах с десятичной дробью
- в ° градусах, ‘ минутах и » секундах с десятичной дробью (исторически сложившаяся форма записи)
Разделителем десятичной дроби всегда служит точка. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+», либо буквами: «N» — северная широта и «E» — восточная долгота. Отрицательные знаки координат представляются либо знаком «-», либо буквами: «S» — южная широта и «W» — западная долгота. Буквы могут стоять как впереди, так и сзади.
Единых правил записи координат не существует.
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаками «-» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.
В навигаторах по умолчанию чаще показываются градусы и минуты с десятичной дробью с буквенным обозначением, например, в Navitel, в iGO. Вводить координаты можно и в соответствии с другими форматами. Формат градусы и минуты рекомендуется также при радиообмене в морском деле. [источник не указан 476 дней]
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами)[3]. Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» —- 55°45′20.99″ с. ш. 37°37′03.62″ в. д. / 55.755831, 37.617673 (G) (O) (Я):
- 55.755831°, 37.617673° —- градусы
- N55.755831°, E37.617673° —- градусы (+ доп. буквы)
- 55°45.35’N, 37°37.06’E —- градусы и минуты (+ доп. буквы)
- 55°45’20.9916″N, 37°37’3.6228″E —- градусы, минуты и секунды (+ доп. буквы)
При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ минутам, 1′ минута = 60″ секундам. Также можно использовать специализированные сервисы. См. ссылки.
Ссылки
- Географические координаты всех городов на Земле (англ.)
- Географические координаты населённых пунктов Земли (1) (англ.)
- Географические координаты населённых пунктов Земли (2) (англ.)
- Пересчет координат из градусов в градусы/минуты, в градусы/минуты/секунды и обратно
- Пересчет координат из градусов в градусы/минуты/секунды и обратно
См. также
- Навигация
Примечания
- ↑ Геоцентрические координаты // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ 1 2 Salychev. O.S. Applied Inertial Navigation: problems and solutions. — Moscow:: BMSTU Press, 2004. — 304 с. — ISBN 5-7038-2395-1
- ↑ Пример дублирования координат