Notation for the (principal) square root of x.
For example, √25 = 5, since 25 = 5 ⋅ 5, or 52 (5 squared).
In mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x.[1] For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16.
Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by 


Every positive number x has two square roots: 


Square roots of negative numbers can be discussed within the framework of complex numbers. More generally, square roots can be considered in any context in which a notion of the «square» of a mathematical object is defined. These include function spaces and square matrices, among other mathematical structures.
History
The Yale Babylonian Collection YBC 7289 clay tablet was created between 1800 BC and 1600 BC, showing 

The Rhind Mathematical Papyrus is a copy from 1650 BC of an earlier Berlin Papyrus and other texts – possibly the Kahun Papyrus – that shows how the Egyptians extracted square roots by an inverse proportion method.[6]
In Ancient India, the knowledge of theoretical and applied aspects of square and square root was at least as old as the Sulba Sutras, dated around 800–500 BC (possibly much earlier).[citation needed] A method for finding very good approximations to the square roots of 2 and 3 are given in the Baudhayana Sulba Sutra.[7] Aryabhata, in the Aryabhatiya (section 2.4), has given a method for finding the square root of numbers having many digits.
It was known to the ancient Greeks that square roots of positive integers that are not perfect squares are always irrational numbers: numbers not expressible as a ratio of two integers (that is, they cannot be written exactly as 
The particular case of the square root of 2 is assumed to date back earlier to the Pythagoreans, and is traditionally attributed to Hippasus.[citation needed] It is exactly the length of the diagonal of a square with side length 1.
In the Chinese mathematical work Writings on Reckoning, written between 202 BC and 186 BC during the early Han Dynasty, the square root is approximated by using an «excess and deficiency» method, which says to «…combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend.»[9]
A symbol for square roots, written as an elaborate R, was invented by Regiomontanus (1436–1476). An R was also used for radix to indicate square roots in Gerolamo Cardano’s Ars Magna.[10]
According to historian of mathematics D.E. Smith, Aryabhata’s method for finding the square root was first introduced in Europe by Cataneo—in 1546.
According to Jeffrey A. Oaks, Arabs used the letter jīm/ĝīm (ج), the first letter of the word «جذر» (variously transliterated as jaḏr, jiḏr, ǧaḏr or ǧiḏr, «root»), placed in its initial form (ﺟ) over a number to indicate its square root. The letter jīm resembles the present square root shape. Its usage goes as far as the end of the twelfth century in the works of the Moroccan mathematician Ibn al-Yasamin.[11]
The symbol «√» for the square root was first used in print in 1525, in Christoph Rudolff’s Coss.[12]
Properties and uses
The graph of the function f(x) = √x, made up of half a parabola with a vertical directrix
The principal square root function 
The square root of x is rational if and only if x is a rational number that can be represented as a ratio of two perfect squares. (See square root of 2 for proofs that this is an irrational number, and quadratic irrational for a proof for all non-square natural numbers.) The square root function maps rational numbers into algebraic numbers, the latter being a superset of the rational numbers).
For all real numbers x,
(see absolute value)
For all nonnegative real numbers x and y,
and
The square root function is continuous for all nonnegative x, and differentiable for all positive x. If f denotes the square root function, whose derivative is given by:
The Taylor series of 
The square root of a nonnegative number is used in the definition of Euclidean norm (and distance), as well as in generalizations such as Hilbert spaces. It defines an important concept of standard deviation used in probability theory and statistics. It has a major use in the formula for roots of a quadratic equation; quadratic fields and rings of quadratic integers, which are based on square roots, are important in algebra and have uses in geometry. Square roots frequently appear in mathematical formulas elsewhere, as well as in many physical laws.
Square roots of positive integers
A positive number has two square roots, one positive, and one negative, which are opposite to each other. When talking of the square root of a positive integer, it is usually the positive square root that is meant.
The square roots of an integer are algebraic integers—more specifically quadratic integers.
The square root of a positive integer is the product of the roots of its prime factors, because the square root of a product is the product of the square roots of the factors. Since 
As decimal expansions
The square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and hence have non-repeating decimals in their decimal representations. Decimal approximations of the square roots of the first few natural numbers are given in the following table.
-
n truncated to 50 decimal places
0 0 1 1 2 1.41421356237309504880168872420969807856967187537694 3 1.73205080756887729352744634150587236694280525381038 4 2 5 2.23606797749978969640917366873127623544061835961152 6 2.44948974278317809819728407470589139196594748065667 7 2.64575131106459059050161575363926042571025918308245 8 2.82842712474619009760337744841939615713934375075389 9 3 10 3.16227766016837933199889354443271853371955513932521
As expansions in other numeral systems
As with before, the square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and therefore have non-repeating digits in any standard positional notation system.
The square roots of small integers are used in both the SHA-1 and SHA-2 hash function designs to provide nothing up my sleeve numbers.
As periodic continued fractions
One of the most intriguing results from the study of irrational numbers as continued fractions was obtained by Joseph Louis Lagrange c. 1780. Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. That is, a certain pattern of partial denominators repeats indefinitely in the continued fraction. In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of integers.
-
= [1; 2, 2, …] = [1; 1, 2, 1, 2, …] = [2] = [2; 4, 4, …] = [2; 2, 4, 2, 4, …] = [2; 1, 1, 1, 4, 1, 1, 1, 4, …] = [2; 1, 4, 1, 4, …] = [3] = [3; 6, 6, …] = [3; 3, 6, 3, 6, …] = [3; 2, 6, 2, 6, …] = [3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, …] = [3; 1, 2, 1, 6, 1, 2, 1, 6, …] = [3; 1, 6, 1, 6, …] = [4] = [4; 8, 8, …] = [4; 4, 8, 4, 8, …] = [4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, …] = [4; 2, 8, 2, 8, …]
The square bracket notation used above is a short form for a continued fraction. Written in the more suggestive algebraic form, the simple continued fraction for the square root of 11, [3; 3, 6, 3, 6, …], looks like this:
where the two-digit pattern {3, 6} repeats over and over again in the partial denominators. Since 11 = 32 + 2, the above is also identical to the following generalized continued fractions:
Computation
Square roots of positive numbers are not in general rational numbers, and so cannot be written as a terminating or recurring decimal expression. Therefore in general any attempt to compute a square root expressed in decimal form can only yield an approximation, though a sequence of increasingly accurate approximations can be obtained.
Most pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Pocket calculators typically implement efficient routines, such as the Newton’s method (frequently with an initial guess of 1), to compute the square root of a positive real number.[13][14] When computing square roots with logarithm tables or slide rules, one can exploit the identities
where ln and log10 are the natural and base-10 logarithms.
By trial-and-error,[15] one can square an estimate for 
as it allows one to adjust the estimate x by some amount c and measure the square of the adjustment in terms of the original estimate and its square. Furthermore, (x + c)2 ≈ x2 + 2xc when c is close to 0, because the tangent line to the graph of x2 + 2xc + c2 at c = 0, as a function of c alone, is y = 2xc + x2. Thus, small adjustments to x can be planned out by setting 2xc to a, or c = a/(2x).
The most common iterative method of square root calculation by hand is known as the «Babylonian method» or «Heron’s method» after the first-century Greek philosopher Heron of Alexandria, who first described it.[16]
The method uses the same iterative scheme as the Newton–Raphson method yields when applied to the function y = f(x) = x2 − a, using the fact that its slope at any point is dy/dx = f′(x) = 2x, but predates it by many centuries.[17]
The algorithm is to repeat a simple calculation that results in a number closer to the actual square root each time it is repeated with its result as the new input. The motivation is that if x is an overestimate to the square root of a nonnegative real number a then a/x will be an underestimate and so the average of these two numbers is a better approximation than either of them. However, the inequality of arithmetic and geometric means shows this average is always an overestimate of the square root (as noted below), and so it can serve as a new overestimate with which to repeat the process, which converges as a consequence of the successive overestimates and underestimates being closer to each other after each iteration. To find x:
- Start with an arbitrary positive start value x. The closer to the square root of a, the fewer the iterations that will be needed to achieve the desired precision.
- Replace x by the average (x + a/x) / 2 between x and a/x.
- Repeat from step 2, using this average as the new value of x.
That is, if an arbitrary guess for 

Using the identity
the computation of the square root of a positive number can be reduced to that of a number in the range [1,4). This simplifies finding a start value for the iterative method that is close to the square root, for which a polynomial or piecewise-linear approximation can be used.
The time complexity for computing a square root with n digits of precision is equivalent to that of multiplying two n-digit numbers.
Another useful method for calculating the square root is the shifting nth root algorithm, applied for n = 2.
The name of the square root function varies from programming language to programming language, with sqrt[18] (often pronounced «squirt» [19]) being common, used in C, C++, and derived languages like JavaScript, PHP, and Python.
Square roots of negative and complex numbers
First leaf of the complex square root
Second leaf of the complex square root
Using the Riemann surface of the square root, it is shown how the two leaves fit together
The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to work with a more inclusive set of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted by i (sometimes written as j, especially in the context of electricity where «i» traditionally represents electric current) and called the imaginary unit, which is defined such that i2 = −1. Using this notation, we can think of i as the square root of −1, but we also have (−i)2 = i2 = −1 and so −i is also a square root of −1. By convention, the principal square root of −1 is i, or more generally, if x is any nonnegative number, then the principal square root of −x is
The right side (as well as its negative) is indeed a square root of −x, since
For every non-zero complex number z there exist precisely two numbers w such that w2 = z: the principal square root of z (defined below), and its negative.
Principal square root of a complex number
Geometric representation of the 2nd to 6th roots of a complex number z, in polar form reiφ where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.
To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number 






then the principal square root of 
The principal square root function is thus defined using the nonpositive real axis as a branch cut.
If 



It is important that 


but using 
The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it is not even continuous). The above Taylor series for 


The above can also be expressed in terms of trigonometric functions:
Algebraic formula
When the number is expressed using its real and imaginary parts, the following formula can be used for the principal square root:[20][21]
where sgn(y) is the sign of y (except that, here, sgn(0) = 1). In particular, the imaginary parts of the original number and the principal value of its square root have the same sign. The real part of the principal value of the square root is always nonnegative.
For example, the principal square roots of ±i are given by:
Notes
In the following, the complex z and w may be expressed as:
where 

Because of the discontinuous nature of the square root function in the complex plane, the following laws are not true in general.
A similar problem appears with other complex functions with branch cuts, e.g., the complex logarithm and the relations logz + logw = log(zw) or log(z*) = log(z)* which are not true in general.
Wrongly assuming one of these laws underlies several faulty «proofs», for instance the following one showing that −1 = 1:
The third equality cannot be justified (see invalid proof).[22]: Chapter VI Some fallacies in algebra and trigonometry, Section I The fallacies, Subsection 2 The fallacy that +1 = -1 It can be made to hold by changing the meaning of √ so that this no longer represents the principal square root (see above) but selects a branch for the square root that contains 
if the branch includes +i or
if the branch includes −i, while the right-hand side becomes
where the last equality, 
Nth roots and polynomial roots
The definition of a square root of 


A cube root of 


![{displaystyle {sqrt[{3}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d19f445fd1e8ab7046f090279ee7cf3506f0cf50)
If n is an integer greater than two, a nth root of 


![{displaystyle {sqrt[{n}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8562e64a6bc6e408ddf67f055682c4dc9c9f957f)
Given any polynomial p, a root of p is a number y such that p(y) = 0. For example, the nth roots of x are the roots of the polynomial (in y) 
Abel–Ruffini theorem states that, in general, the roots of a polynomial of degree five or higher cannot be expressed in terms of nth roots.
Square roots of matrices and operators
If A is a positive-definite matrix or operator, then there exists precisely one positive definite matrix or operator B with B2 = A; we then define A1/2 = B. In general matrices may have multiple square roots or even an infinitude of them. For example, the 2 × 2 identity matrix has an infinity of square roots,[23] though only one of them is positive definite.
In integral domains, including fields
Each element of an integral domain has no more than 2 square roots. The difference of two squares identity u2 − v2 = (u − v)(u + v) is proved using the commutativity of multiplication. If u and v are square roots of the same element, then u2 − v2 = 0. Because there are no zero divisors this implies u = v or u + v = 0, where the latter means that two roots are additive inverses of each other. In other words if an element a square root u of an element a exists, then the only square roots of a are u and −u. The only square root of 0 in an integral domain is 0 itself.
In a field of characteristic 2, an element either has one square root or does not have any at all, because each element is its own additive inverse, so that −u = u. If the field is finite of characteristic 2 then every element has a unique square root. In a field of any other characteristic, any non-zero element either has two square roots, as explained above, or does not have any.
Given an odd prime number p, let q = pe for some positive integer e. A non-zero element of the field Fq with q elements is a quadratic residue if it has a square root in Fq. Otherwise, it is a quadratic non-residue. There are (q − 1)/2 quadratic residues and (q − 1)/2 quadratic non-residues; zero is not counted in either class. The quadratic residues form a group under multiplication. The properties of quadratic residues are widely used in number theory.
In rings in general
Unlike in an integral domain, a square root in an arbitrary (unital) ring need not be unique up to sign. For example, in the ring 
Another example is provided by the ring of quaternions 
A square root of 0 is either 0 or a zero divisor. Thus in rings where zero divisors do not exist, it is uniquely 0. However, rings with zero divisors may have multiple square roots of 0. For example, in 
Geometric construction of the square root
The square root of a positive number is usually defined as the side length of a square with the area equal to the given number. But the square shape is not necessary for it: if one of two similar planar Euclidean objects has the area a times greater than another, then the ratio of their linear sizes is 
A square root can be constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the construction of the geometric mean of two quantities in two different places: Proposition II.14 and Proposition VI.13. Since the geometric mean of a and b is 

The construction is also given by Descartes in his La Géométrie, see figure 2 on page 2. However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.
Euclid’s second proof in Book VI depends on the theory of similar triangles. Let AHB be a line segment of length a + b with AH = a and HB = b. Construct the circle with AB as diameter and let C be one of the two intersections of the perpendicular chord at H with the circle and denote the length CH as h. Then, using Thales’ theorem and, as in the proof of Pythagoras’ theorem by similar triangles, triangle AHC is similar to triangle CHB (as indeed both are to triangle ACB, though we don’t need that, but it is the essence of the proof of Pythagoras’ theorem) so that AH:CH is as HC:HB, i.e. a/h = h/b, from which we conclude by cross-multiplication that h2 = ab, and finally that 

Another method of geometric construction uses right triangles and induction: 



See also
- Apotome (mathematics)
- Cube root
- Functional square root
- Integer square root
- Nested radical
- Nth root
- Root of unity
- Solving quadratic equations with continued fractions
- Square root principle
- Quantum gate § Square root of NOT gate (√NOT)
Notes
- ^ Gel’fand, p. 120 Archived 2016-09-02 at the Wayback Machine
- ^ «Squares and Square Roots». www.mathsisfun.com. Retrieved 2020-08-28.
- ^ Zill, Dennis G.; Shanahan, Patrick (2008). A First Course in Complex Analysis With Applications (2nd ed.). Jones & Bartlett Learning. p. 78. ISBN 978-0-7637-5772-4. Archived from the original on 2016-09-01. Extract of page 78 Archived 2016-09-01 at the Wayback Machine
- ^ Weisstein, Eric W. «Square Root». mathworld.wolfram.com. Retrieved 2020-08-28.
- ^ «Analysis of YBC 7289». ubc.ca. Retrieved 19 January 2015.
- ^ Anglin, W.S. (1994). Mathematics: A Concise History and Philosophy. New York: Springer-Verlag.
- ^ Joseph, ch.8.
- ^ Heath, Sir Thomas L. (1908). The Thirteen Books of The Elements, Vol. 3. Cambridge University Press. p. 3.
- ^ Dauben (2007), p. 210.
- ^ «The Development of Algebra — 2». maths.org. Archived from the original on 24 November 2014. Retrieved 19 January 2015.
- ^ * Oaks, Jeffrey A. (2012). Algebraic Symbolism in Medieval Arabic Algebra (PDF) (Thesis). Philosophica. p. 36. Archived (PDF) from the original on 2016-12-03.
- ^ Manguel, Alberto (2006). «Done on paper: the dual nature of numbers and the page». The Life of Numbers. ISBN 84-86882-14-1.
- ^ Parkhurst, David F. (2006). Introduction to Applied Mathematics for Environmental Science. Springer. pp. 241. ISBN 9780387342283.
- ^ Solow, Anita E. (1993). Learning by Discovery: A Lab Manual for Calculus. Cambridge University Press. pp. 48. ISBN 9780883850831.
- ^ Aitken, Mike; Broadhurst, Bill; Hladky, Stephen (2009). Mathematics for Biological Scientists. Garland Science. p. 41. ISBN 978-1-136-84393-8. Archived from the original on 2017-03-01. Extract of page 41 Archived 2017-03-01 at the Wayback Machine
- ^ Heath, Sir Thomas L. (1921). A History of Greek Mathematics, Vol. 2. Oxford: Clarendon Press. pp. 323–324.
- ^ Muller, Jean-Mic (2006). Elementary functions: algorithms and implementation. Springer. pp. 92–93. ISBN 0-8176-4372-9., Chapter 5, p 92 Archived 2016-09-01 at the Wayback Machine
- ^ «Function sqrt». CPlusPlus.com. The C++ Resources Network. 2016. Archived from the original on November 22, 2012. Retrieved June 24, 2016.
- ^ Overland, Brian (2013). C++ for the Impatient. Addison-Wesley. p. 338. ISBN 9780133257120. OCLC 850705706. Archived from the original on September 1, 2016. Retrieved June 24, 2016.
- ^ Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. Courier Dover Publications. p. 17. ISBN 0-486-61272-4. Archived from the original on 2016-04-23., Section 3.7.27, p. 17 Archived 2009-09-10 at the Wayback Machine
- ^ Cooke, Roger (2008). Classical algebra: its nature, origins, and uses. John Wiley and Sons. p. 59. ISBN 978-0-470-25952-8. Archived from the original on 2016-04-23.
- ^ Maxwell, E. A. (1959). Fallacies in Mathematics. Cambridge University Press.
- ^ Mitchell, Douglas W., «Using Pythagorean triples to generate square roots of I2«, Mathematical Gazette 87, November 2003, 499–500.
References
- Dauben, Joseph W. (2007). «Chinese Mathematics I». In Katz, Victor J. (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton: Princeton University Press. ISBN 978-0-691-11485-9.
- Gel’fand, Izrael M.; Shen, Alexander (1993). Algebra (3rd ed.). Birkhäuser. p. 120. ISBN 0-8176-3677-3.
- Joseph, George (2000). The Crest of the Peacock. Princeton: Princeton University Press. ISBN 0-691-00659-8.
- Smith, David (1958). History of Mathematics. Vol. 2. New York: Dover Publications. ISBN 978-0-486-20430-7.
- Selin, Helaine (2008), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer, Bibcode:2008ehst.book…..S, ISBN 978-1-4020-4559-2.
External links
- Algorithms, implementations, and more – Paul Hsieh’s square roots webpage
- How to manually find a square root
- AMS Featured Column, Galileo’s Arithmetic by Tony Philips – includes a section on how Galileo found square roots
Notation for the (principal) square root of x.
For example, √25 = 5, since 25 = 5 ⋅ 5, or 52 (5 squared).
In mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x.[1] For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16.
Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by 


Every positive number x has two square roots: 


Square roots of negative numbers can be discussed within the framework of complex numbers. More generally, square roots can be considered in any context in which a notion of the «square» of a mathematical object is defined. These include function spaces and square matrices, among other mathematical structures.
History
The Yale Babylonian Collection YBC 7289 clay tablet was created between 1800 BC and 1600 BC, showing 

The Rhind Mathematical Papyrus is a copy from 1650 BC of an earlier Berlin Papyrus and other texts – possibly the Kahun Papyrus – that shows how the Egyptians extracted square roots by an inverse proportion method.[6]
In Ancient India, the knowledge of theoretical and applied aspects of square and square root was at least as old as the Sulba Sutras, dated around 800–500 BC (possibly much earlier).[citation needed] A method for finding very good approximations to the square roots of 2 and 3 are given in the Baudhayana Sulba Sutra.[7] Aryabhata, in the Aryabhatiya (section 2.4), has given a method for finding the square root of numbers having many digits.
It was known to the ancient Greeks that square roots of positive integers that are not perfect squares are always irrational numbers: numbers not expressible as a ratio of two integers (that is, they cannot be written exactly as 
The particular case of the square root of 2 is assumed to date back earlier to the Pythagoreans, and is traditionally attributed to Hippasus.[citation needed] It is exactly the length of the diagonal of a square with side length 1.
In the Chinese mathematical work Writings on Reckoning, written between 202 BC and 186 BC during the early Han Dynasty, the square root is approximated by using an «excess and deficiency» method, which says to «…combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend.»[9]
A symbol for square roots, written as an elaborate R, was invented by Regiomontanus (1436–1476). An R was also used for radix to indicate square roots in Gerolamo Cardano’s Ars Magna.[10]
According to historian of mathematics D.E. Smith, Aryabhata’s method for finding the square root was first introduced in Europe by Cataneo—in 1546.
According to Jeffrey A. Oaks, Arabs used the letter jīm/ĝīm (ج), the first letter of the word «جذر» (variously transliterated as jaḏr, jiḏr, ǧaḏr or ǧiḏr, «root»), placed in its initial form (ﺟ) over a number to indicate its square root. The letter jīm resembles the present square root shape. Its usage goes as far as the end of the twelfth century in the works of the Moroccan mathematician Ibn al-Yasamin.[11]
The symbol «√» for the square root was first used in print in 1525, in Christoph Rudolff’s Coss.[12]
Properties and uses
The graph of the function f(x) = √x, made up of half a parabola with a vertical directrix
The principal square root function 
The square root of x is rational if and only if x is a rational number that can be represented as a ratio of two perfect squares. (See square root of 2 for proofs that this is an irrational number, and quadratic irrational for a proof for all non-square natural numbers.) The square root function maps rational numbers into algebraic numbers, the latter being a superset of the rational numbers).
For all real numbers x,
(see absolute value)
For all nonnegative real numbers x and y,
and
The square root function is continuous for all nonnegative x, and differentiable for all positive x. If f denotes the square root function, whose derivative is given by:
The Taylor series of 
The square root of a nonnegative number is used in the definition of Euclidean norm (and distance), as well as in generalizations such as Hilbert spaces. It defines an important concept of standard deviation used in probability theory and statistics. It has a major use in the formula for roots of a quadratic equation; quadratic fields and rings of quadratic integers, which are based on square roots, are important in algebra and have uses in geometry. Square roots frequently appear in mathematical formulas elsewhere, as well as in many physical laws.
Square roots of positive integers
A positive number has two square roots, one positive, and one negative, which are opposite to each other. When talking of the square root of a positive integer, it is usually the positive square root that is meant.
The square roots of an integer are algebraic integers—more specifically quadratic integers.
The square root of a positive integer is the product of the roots of its prime factors, because the square root of a product is the product of the square roots of the factors. Since 
As decimal expansions
The square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and hence have non-repeating decimals in their decimal representations. Decimal approximations of the square roots of the first few natural numbers are given in the following table.
-
n truncated to 50 decimal places
0 0 1 1 2 1.41421356237309504880168872420969807856967187537694 3 1.73205080756887729352744634150587236694280525381038 4 2 5 2.23606797749978969640917366873127623544061835961152 6 2.44948974278317809819728407470589139196594748065667 7 2.64575131106459059050161575363926042571025918308245 8 2.82842712474619009760337744841939615713934375075389 9 3 10 3.16227766016837933199889354443271853371955513932521
As expansions in other numeral systems
As with before, the square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and therefore have non-repeating digits in any standard positional notation system.
The square roots of small integers are used in both the SHA-1 and SHA-2 hash function designs to provide nothing up my sleeve numbers.
As periodic continued fractions
One of the most intriguing results from the study of irrational numbers as continued fractions was obtained by Joseph Louis Lagrange c. 1780. Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. That is, a certain pattern of partial denominators repeats indefinitely in the continued fraction. In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of integers.
-
= [1; 2, 2, …] = [1; 1, 2, 1, 2, …] = [2] = [2; 4, 4, …] = [2; 2, 4, 2, 4, …] = [2; 1, 1, 1, 4, 1, 1, 1, 4, …] = [2; 1, 4, 1, 4, …] = [3] = [3; 6, 6, …] = [3; 3, 6, 3, 6, …] = [3; 2, 6, 2, 6, …] = [3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, …] = [3; 1, 2, 1, 6, 1, 2, 1, 6, …] = [3; 1, 6, 1, 6, …] = [4] = [4; 8, 8, …] = [4; 4, 8, 4, 8, …] = [4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, …] = [4; 2, 8, 2, 8, …]
The square bracket notation used above is a short form for a continued fraction. Written in the more suggestive algebraic form, the simple continued fraction for the square root of 11, [3; 3, 6, 3, 6, …], looks like this:
where the two-digit pattern {3, 6} repeats over and over again in the partial denominators. Since 11 = 32 + 2, the above is also identical to the following generalized continued fractions:
Computation
Square roots of positive numbers are not in general rational numbers, and so cannot be written as a terminating or recurring decimal expression. Therefore in general any attempt to compute a square root expressed in decimal form can only yield an approximation, though a sequence of increasingly accurate approximations can be obtained.
Most pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Pocket calculators typically implement efficient routines, such as the Newton’s method (frequently with an initial guess of 1), to compute the square root of a positive real number.[13][14] When computing square roots with logarithm tables or slide rules, one can exploit the identities
where ln and log10 are the natural and base-10 logarithms.
By trial-and-error,[15] one can square an estimate for 
as it allows one to adjust the estimate x by some amount c and measure the square of the adjustment in terms of the original estimate and its square. Furthermore, (x + c)2 ≈ x2 + 2xc when c is close to 0, because the tangent line to the graph of x2 + 2xc + c2 at c = 0, as a function of c alone, is y = 2xc + x2. Thus, small adjustments to x can be planned out by setting 2xc to a, or c = a/(2x).
The most common iterative method of square root calculation by hand is known as the «Babylonian method» or «Heron’s method» after the first-century Greek philosopher Heron of Alexandria, who first described it.[16]
The method uses the same iterative scheme as the Newton–Raphson method yields when applied to the function y = f(x) = x2 − a, using the fact that its slope at any point is dy/dx = f′(x) = 2x, but predates it by many centuries.[17]
The algorithm is to repeat a simple calculation that results in a number closer to the actual square root each time it is repeated with its result as the new input. The motivation is that if x is an overestimate to the square root of a nonnegative real number a then a/x will be an underestimate and so the average of these two numbers is a better approximation than either of them. However, the inequality of arithmetic and geometric means shows this average is always an overestimate of the square root (as noted below), and so it can serve as a new overestimate with which to repeat the process, which converges as a consequence of the successive overestimates and underestimates being closer to each other after each iteration. To find x:
- Start with an arbitrary positive start value x. The closer to the square root of a, the fewer the iterations that will be needed to achieve the desired precision.
- Replace x by the average (x + a/x) / 2 between x and a/x.
- Repeat from step 2, using this average as the new value of x.
That is, if an arbitrary guess for 

Using the identity
the computation of the square root of a positive number can be reduced to that of a number in the range [1,4). This simplifies finding a start value for the iterative method that is close to the square root, for which a polynomial or piecewise-linear approximation can be used.
The time complexity for computing a square root with n digits of precision is equivalent to that of multiplying two n-digit numbers.
Another useful method for calculating the square root is the shifting nth root algorithm, applied for n = 2.
The name of the square root function varies from programming language to programming language, with sqrt[18] (often pronounced «squirt» [19]) being common, used in C, C++, and derived languages like JavaScript, PHP, and Python.
Square roots of negative and complex numbers
First leaf of the complex square root
Second leaf of the complex square root
Using the Riemann surface of the square root, it is shown how the two leaves fit together
The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to work with a more inclusive set of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted by i (sometimes written as j, especially in the context of electricity where «i» traditionally represents electric current) and called the imaginary unit, which is defined such that i2 = −1. Using this notation, we can think of i as the square root of −1, but we also have (−i)2 = i2 = −1 and so −i is also a square root of −1. By convention, the principal square root of −1 is i, or more generally, if x is any nonnegative number, then the principal square root of −x is
The right side (as well as its negative) is indeed a square root of −x, since
For every non-zero complex number z there exist precisely two numbers w such that w2 = z: the principal square root of z (defined below), and its negative.
Principal square root of a complex number
Geometric representation of the 2nd to 6th roots of a complex number z, in polar form reiφ where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.
To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number 






then the principal square root of 
The principal square root function is thus defined using the nonpositive real axis as a branch cut.
If 



It is important that 


but using 
The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it is not even continuous). The above Taylor series for 


The above can also be expressed in terms of trigonometric functions:
Algebraic formula
When the number is expressed using its real and imaginary parts, the following formula can be used for the principal square root:[20][21]
where sgn(y) is the sign of y (except that, here, sgn(0) = 1). In particular, the imaginary parts of the original number and the principal value of its square root have the same sign. The real part of the principal value of the square root is always nonnegative.
For example, the principal square roots of ±i are given by:
Notes
In the following, the complex z and w may be expressed as:
where 

Because of the discontinuous nature of the square root function in the complex plane, the following laws are not true in general.
A similar problem appears with other complex functions with branch cuts, e.g., the complex logarithm and the relations logz + logw = log(zw) or log(z*) = log(z)* which are not true in general.
Wrongly assuming one of these laws underlies several faulty «proofs», for instance the following one showing that −1 = 1:
The third equality cannot be justified (see invalid proof).[22]: Chapter VI Some fallacies in algebra and trigonometry, Section I The fallacies, Subsection 2 The fallacy that +1 = -1 It can be made to hold by changing the meaning of √ so that this no longer represents the principal square root (see above) but selects a branch for the square root that contains 
if the branch includes +i or
if the branch includes −i, while the right-hand side becomes
where the last equality, 
Nth roots and polynomial roots
The definition of a square root of 


A cube root of 


![{displaystyle {sqrt[{3}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d19f445fd1e8ab7046f090279ee7cf3506f0cf50)
If n is an integer greater than two, a nth root of 


![{displaystyle {sqrt[{n}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8562e64a6bc6e408ddf67f055682c4dc9c9f957f)
Given any polynomial p, a root of p is a number y such that p(y) = 0. For example, the nth roots of x are the roots of the polynomial (in y) 
Abel–Ruffini theorem states that, in general, the roots of a polynomial of degree five or higher cannot be expressed in terms of nth roots.
Square roots of matrices and operators
If A is a positive-definite matrix or operator, then there exists precisely one positive definite matrix or operator B with B2 = A; we then define A1/2 = B. In general matrices may have multiple square roots or even an infinitude of them. For example, the 2 × 2 identity matrix has an infinity of square roots,[23] though only one of them is positive definite.
In integral domains, including fields
Each element of an integral domain has no more than 2 square roots. The difference of two squares identity u2 − v2 = (u − v)(u + v) is proved using the commutativity of multiplication. If u and v are square roots of the same element, then u2 − v2 = 0. Because there are no zero divisors this implies u = v or u + v = 0, where the latter means that two roots are additive inverses of each other. In other words if an element a square root u of an element a exists, then the only square roots of a are u and −u. The only square root of 0 in an integral domain is 0 itself.
In a field of characteristic 2, an element either has one square root or does not have any at all, because each element is its own additive inverse, so that −u = u. If the field is finite of characteristic 2 then every element has a unique square root. In a field of any other characteristic, any non-zero element either has two square roots, as explained above, or does not have any.
Given an odd prime number p, let q = pe for some positive integer e. A non-zero element of the field Fq with q elements is a quadratic residue if it has a square root in Fq. Otherwise, it is a quadratic non-residue. There are (q − 1)/2 quadratic residues and (q − 1)/2 quadratic non-residues; zero is not counted in either class. The quadratic residues form a group under multiplication. The properties of quadratic residues are widely used in number theory.
In rings in general
Unlike in an integral domain, a square root in an arbitrary (unital) ring need not be unique up to sign. For example, in the ring 
Another example is provided by the ring of quaternions 
A square root of 0 is either 0 or a zero divisor. Thus in rings where zero divisors do not exist, it is uniquely 0. However, rings with zero divisors may have multiple square roots of 0. For example, in 
Geometric construction of the square root
The square root of a positive number is usually defined as the side length of a square with the area equal to the given number. But the square shape is not necessary for it: if one of two similar planar Euclidean objects has the area a times greater than another, then the ratio of their linear sizes is 
A square root can be constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the construction of the geometric mean of two quantities in two different places: Proposition II.14 and Proposition VI.13. Since the geometric mean of a and b is 

The construction is also given by Descartes in his La Géométrie, see figure 2 on page 2. However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.
Euclid’s second proof in Book VI depends on the theory of similar triangles. Let AHB be a line segment of length a + b with AH = a and HB = b. Construct the circle with AB as diameter and let C be one of the two intersections of the perpendicular chord at H with the circle and denote the length CH as h. Then, using Thales’ theorem and, as in the proof of Pythagoras’ theorem by similar triangles, triangle AHC is similar to triangle CHB (as indeed both are to triangle ACB, though we don’t need that, but it is the essence of the proof of Pythagoras’ theorem) so that AH:CH is as HC:HB, i.e. a/h = h/b, from which we conclude by cross-multiplication that h2 = ab, and finally that 

Another method of geometric construction uses right triangles and induction: 



See also
- Apotome (mathematics)
- Cube root
- Functional square root
- Integer square root
- Nested radical
- Nth root
- Root of unity
- Solving quadratic equations with continued fractions
- Square root principle
- Quantum gate § Square root of NOT gate (√NOT)
Notes
- ^ Gel’fand, p. 120 Archived 2016-09-02 at the Wayback Machine
- ^ «Squares and Square Roots». www.mathsisfun.com. Retrieved 2020-08-28.
- ^ Zill, Dennis G.; Shanahan, Patrick (2008). A First Course in Complex Analysis With Applications (2nd ed.). Jones & Bartlett Learning. p. 78. ISBN 978-0-7637-5772-4. Archived from the original on 2016-09-01. Extract of page 78 Archived 2016-09-01 at the Wayback Machine
- ^ Weisstein, Eric W. «Square Root». mathworld.wolfram.com. Retrieved 2020-08-28.
- ^ «Analysis of YBC 7289». ubc.ca. Retrieved 19 January 2015.
- ^ Anglin, W.S. (1994). Mathematics: A Concise History and Philosophy. New York: Springer-Verlag.
- ^ Joseph, ch.8.
- ^ Heath, Sir Thomas L. (1908). The Thirteen Books of The Elements, Vol. 3. Cambridge University Press. p. 3.
- ^ Dauben (2007), p. 210.
- ^ «The Development of Algebra — 2». maths.org. Archived from the original on 24 November 2014. Retrieved 19 January 2015.
- ^ * Oaks, Jeffrey A. (2012). Algebraic Symbolism in Medieval Arabic Algebra (PDF) (Thesis). Philosophica. p. 36. Archived (PDF) from the original on 2016-12-03.
- ^ Manguel, Alberto (2006). «Done on paper: the dual nature of numbers and the page». The Life of Numbers. ISBN 84-86882-14-1.
- ^ Parkhurst, David F. (2006). Introduction to Applied Mathematics for Environmental Science. Springer. pp. 241. ISBN 9780387342283.
- ^ Solow, Anita E. (1993). Learning by Discovery: A Lab Manual for Calculus. Cambridge University Press. pp. 48. ISBN 9780883850831.
- ^ Aitken, Mike; Broadhurst, Bill; Hladky, Stephen (2009). Mathematics for Biological Scientists. Garland Science. p. 41. ISBN 978-1-136-84393-8. Archived from the original on 2017-03-01. Extract of page 41 Archived 2017-03-01 at the Wayback Machine
- ^ Heath, Sir Thomas L. (1921). A History of Greek Mathematics, Vol. 2. Oxford: Clarendon Press. pp. 323–324.
- ^ Muller, Jean-Mic (2006). Elementary functions: algorithms and implementation. Springer. pp. 92–93. ISBN 0-8176-4372-9., Chapter 5, p 92 Archived 2016-09-01 at the Wayback Machine
- ^ «Function sqrt». CPlusPlus.com. The C++ Resources Network. 2016. Archived from the original on November 22, 2012. Retrieved June 24, 2016.
- ^ Overland, Brian (2013). C++ for the Impatient. Addison-Wesley. p. 338. ISBN 9780133257120. OCLC 850705706. Archived from the original on September 1, 2016. Retrieved June 24, 2016.
- ^ Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. Courier Dover Publications. p. 17. ISBN 0-486-61272-4. Archived from the original on 2016-04-23., Section 3.7.27, p. 17 Archived 2009-09-10 at the Wayback Machine
- ^ Cooke, Roger (2008). Classical algebra: its nature, origins, and uses. John Wiley and Sons. p. 59. ISBN 978-0-470-25952-8. Archived from the original on 2016-04-23.
- ^ Maxwell, E. A. (1959). Fallacies in Mathematics. Cambridge University Press.
- ^ Mitchell, Douglas W., «Using Pythagorean triples to generate square roots of I2«, Mathematical Gazette 87, November 2003, 499–500.
References
- Dauben, Joseph W. (2007). «Chinese Mathematics I». In Katz, Victor J. (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton: Princeton University Press. ISBN 978-0-691-11485-9.
- Gel’fand, Izrael M.; Shen, Alexander (1993). Algebra (3rd ed.). Birkhäuser. p. 120. ISBN 0-8176-3677-3.
- Joseph, George (2000). The Crest of the Peacock. Princeton: Princeton University Press. ISBN 0-691-00659-8.
- Smith, David (1958). History of Mathematics. Vol. 2. New York: Dover Publications. ISBN 978-0-486-20430-7.
- Selin, Helaine (2008), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer, Bibcode:2008ehst.book…..S, ISBN 978-1-4020-4559-2.
External links
- Algorithms, implementations, and more – Paul Hsieh’s square roots webpage
- How to manually find a square root
- AMS Featured Column, Galileo’s Arithmetic by Tony Philips – includes a section on how Galileo found square roots
Что такое арифметический квадратный корень
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). ( (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).
А почему же число ( a) (число под корнем) должно быть обязательно неотрицательным?
Например, чему равен ( sqrt{-9})?
Так-так, попробуем подобрать. Может, три?
Проверим: ( {{3}^{2}}=9), а не ( -9).
Может, ( left( -3 right))?
Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!
Число или выражение под знаком корня должно быть неотрицательным!
Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!
Ведь в определении сказано, что «квадратным корнем из числа( a)называется такое неотрицательное число, квадрат которого равен( a)».
Но подождите! В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом!
Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)
А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?
Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.
К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).
Из ( {{x}^{2}}=4) следует, что
( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)
(не помнишь почему так? Почитай тему “Модуль числа”!)
А из ( x=sqrt{4}) следует, что ( x=2).
Конечно, это очень путает, но это необходимо запомнить, что знаки “плюс-минус” являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как ( 2), так и ( x=-2).
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Запись иррациональных чисел с помощью квадратного корня
А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.
Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.
А что если ( displaystyle x=2)?
Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.
Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!
Извлечем корень из ( displaystyle 3), делов-то!
Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Деление корней
С умножением корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
( displaystyle frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)
Вот и вся наука. А вот такой пример:
( displaystyle frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})
Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
( displaystyle sqrt{frac{144}{225}}=?)
Надо просто применить формулу в обратном направлении:
( displaystyle sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)
А вот такой примерчик:
( displaystyle sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)
Еще ты можешь встретить такое выражение:
( displaystyle sqrt{5frac{19}{25}}=?)
Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!
( displaystyle sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)
Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.
Возведение в степень
А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).
Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?
Ну, конечно, ( displaystyle a)!
Рассмотрим на примерах:
( displaystyle {{left( sqrt{12} right)}^{2}}=12)
( displaystyle {{left( sqrt{17} right)}^{2}}=17)
Все просто, правда? А если корень будет в другой степени? Ничего страшного!
Придерживайся той же логики и помни свойства и возможные действия со степенями.
Забыл?
Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.
Вот, к примеру, такое выражение:
( displaystyle {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)
В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
( displaystyle {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})
С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:
( displaystyle sqrt{{{3}^{2}}}=sqrt{9}=3)
Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:
( displaystyle sqrt{{{3}^{6}}}=sqrt{{{left( {{3}^{3}} right)}^{2}}}={{3}^{3}}=27)
( displaystyle sqrt{{{3}^{5}}}=sqrt{{{3}^{4}}cdot 3}=sqrt{{{left( {{3}^{2}} right)}^{2}}cdot 3}={{3}^{2}}cdot sqrt{3}=9sqrt{3})
Ну как, все понятно? Тогда реши самостоятельно примеры:
- ( displaystyle sqrt{{{left( -3 right)}^{2}}})
- ( displaystyle sqrt{{{6}^{6}}})
- ( displaystyle {{left( sqrt{8} right)}^{7}})
А вот и ответы:
Внесение под знак корня
Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!
Это совсем легко!
( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)
Допустим, у нас записано число ( displaystyle 3sqrt{5})
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из ( displaystyle 9)!
( displaystyle 3sqrt{5}=sqrt{9}cdot sqrt{5}=sqrt{45})
Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
( displaystyle 3sqrt{10}-sqrt{45}cdot sqrt{2}=sqrt{90}-sqrt{90}=0)
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.
Реши самостоятельно вот этот пример – ( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8})
Справился? Давай смотреть, что у тебя должно получиться:
( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)
Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!
Сравнение корней
Зачем нам учиться сравнивать числа, содержащие квадратный корень?
Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)
Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!
Например, определи, что больше: ( displaystyle 3sqrt{7}) или ( displaystyle 2sqrt{17})?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?
Тогда вперед:
( displaystyle 3sqrt{7}=sqrt{9cdot 7}=sqrt{63})
( displaystyle 2sqrt{17}=sqrt{4cdot 17}=sqrt{68})
Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!
Т.е. если ( displaystyle 68>63), значит, ( displaystyle sqrt{68}>sqrt{63}).
Отсюда твердо делаем вывод, что ( displaystyle 3sqrt{7}<2sqrt{17}).
И никто не убедит нас в обратном!
Извлечение корней из больших чисел
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
( displaystyle sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})
Можно было пойти по иному пути и разложить на другие множители:
( displaystyle sqrt{98}=sqrt{7cdot 14})
Что дальше? А дальше раскладываем на множители до самого конца:
( displaystyle sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})
Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12})
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})
Разве это конец? Не останавливаемся на полпути!
( displaystyle begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})
На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:
( displaystyle begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})
Вот и все, не так все и страшно, правда?
( displaystyle sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)
Получилось ( displaystyle 90)? Молодец, все верно!
А теперь попробуй вот такой пример решить:
( displaystyle sqrt{4225}=?)
А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.
Основные сведения
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
S = 32 = 9 см2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня
.
Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
Значит квадрат площадью 9 см2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.
Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
Получается, что выражение имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
Поэтому ответ к выражению вида записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
Запишем ответ к выражению с плюсом и минусом:
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.
То есть число b должно быть таким, чтобы выполнялось равенство b2 = a. Число b (оно же корень) обозначается через радикал так, что
. На практике левая и правая часть поменяны местами и мы видим привычное выражение
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
42 = 16
Корень 4 можно обозначить через радикал так, что
.
Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
(−4)2 = 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.
Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a.
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи можно использовать запись
. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
Это по причине того, что единица во второй степени равна единице:
12 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
Квадратный корень из нуля равен нулю. То есть справедливо равенство , поскольку 02 = 0.
Выражение вида смысла не имеет. Например, не имеет смысла выражение
, поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
Если выражение вида возвести во вторую степень, то есть если записать
, то это выражение будет равно подкореннóму выражению a
Например, выражение равно 4
Это потому что выражение равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
Еще примеры:
Корень из квадрата числá равен модулю этого числá:
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
Действительно, если не пользуясь правилом , вычислять выражение
обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
Не следует путать правило с правилом
. Правило
верно при любом a, тогда как правило
верно в том случае, если выражение
имеет смысл.
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
Примеры: √4, √9, √16.
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
49 < 64
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 62 = 36
√36 = 6
Пример 2. Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 72 = 49
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
Но 7 × 7 это 72
72 = 49
Отсюда, √49 = 7.
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 102 = 100
√100 = 10
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
Видим, что это число 16. Значит √256 = 16.
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2
Пример 7. Решить уравнение
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной x равно 16, поскольку . Значит корень уравнения равен 16.
Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом .
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень равен числу b, при котором выполняется равенство b2 = a.
Применим равенство b2 = a к нашему примеру . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем
, а именно переменная x
В выражении 42 = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.
Пример 8. Решить уравнение
Перенесем −8 в правую часть, изменив знак:
Возведем правую часть во вторую степень и приравняем её к переменной x
Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения равен 64
Пример 9. Решить уравнение
Воспользуемся определением квадратного корня:
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x
В выражении 72 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:
Корень уравнения равен
. Выполним проверку, подставив его в исходное уравнение:
Пример 10. Найти значение выражения
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть
А извлечь квадратный корень нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня
будет представлять собой десятичную дробь, у которой после запятой одна цифра.
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
√1 = 1
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
√4 = 2
√1 меньше, чем √4
√1 < √4
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
1,12 = 1,21
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.
Проверим тогда дробь 1,8
1,82 = 3,24
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Проверим тогда дробь 1,7
1,72 = 2,89
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
1,7 < √3 < 1,8
Проверим дробь 1,74
1,742 = 3,0276
Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.
Проверим тогда дробь 1,73
1,732 = 2,9929
Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
√3 ≈ 1
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
√3 ≈ 1
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
√3 ≈ 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
√3 ≈ 2 (с избытком)
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
√51 ≈ 7
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
√51 ≈ 7,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
√51 ≈ 7,14
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 82 = 64. Значит квадратный корень из числа 64 есть 8
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 72 = 49
√49 = 7
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 12 = 1
√1 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
√100 = 10
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].
Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
√37 ≈ 6,08
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
И обратно, следует знать значения квадратных корней этих квадратов:
Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 62 = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600
602 = 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
6002 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
И наоборот, если в равенстве уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
Пример 2. Увеличим в равенстве подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
Пример 3. Уменьшим в равенстве подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, .
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225
Теперь в равенстве уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
В этом случае применяется таблица квадратов:
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
Видим, что это число 24. Значит .
Пример 2. Извлечь квадратный корень из числа 432.
Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
20,82 = 432,64
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7
20,72 = 428,49
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)
Корень 64 не годится. Проверим корень 65
Получается 4225. Значит 65 является корнем числа 4225
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида , где a и b некоторые числа.
Например, выражение является квадратным корнем из произведения чисел 4 и 9.
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение в виде произведения корней
. Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:
Получили следующее разложение:
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 22 × 22, а две тройки заменить на 32
В результате будем иметь следующее разложение:
Теперь можно извлекáть квадратный корень из разложения числа 144
Применим правило извлечения квадратного корня из произведения:
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3, которое равно 12
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:
В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 22. А два числа 29 предстáвим как 292. В результате полýчим следующее разложение числа 13456
Теперь будем извлекать квадратный корень из разложения числа 13456
Итак, если a ≥ 0 и b ≥ 0, то . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Докажем равенство . Для этого воспользуемся определением квадратного корня.
Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b2 = a.
В нашем случае нужно удостовериться, что правая часть равенства при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
Итак, выпишем правую часть равенства и возведём ее во вторую степень:
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
Ранее было сказано, что если выражение вида возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня
Значит равенство справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
, при a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найти значение квадратного корня
Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
Пример 2. Найти значение квадратного корня
Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
Пример 3. Найти значение квадратного корня
Воспользуемся правилом возведения степени в степень. Степень 114 предстáвим как (112)2.
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
В нашем случае квадратный корень из числа (112)2 будет равен 112. Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 114 нужно записать в виде произведения 112 × 112. Затем извлечь квадратный корень из этого произведения:
Пример 4. Найти значение квадратного корня
Перепишем степень 34 в виде (32)2, а степень 56 в виде (53)2
Далее используем правило извлечения квадратного кóрня из произведения:
Далее используем правило извлечения квадратного кóрня из квадрата числа:
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения
Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
Пример 6. Найти значение квадратного корня
Пример 7. Найти значение квадратного корня
Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
Пример 9. Найти значение квадратного корня
Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:
Если в равенстве поменять местами левую и правую часть, то полýчим равенство
. Это преобразовáние позволяет упрощáть вычисление некоторых корней.
Например, узнáем чему равно значение выражения .
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом , то есть заменим выражение из двух корней
на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
Теперь найдём значение произведения, находящегося под корнем:
А квадратный корень из числа 400 извлекается. Он равен 20
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения .
Воспользуемся правилом
Сомножитель 32 это 25. Предстáвим этот сомножитель как 2 × 24
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 24 предстáвим в виде степени с показателем 2
Теперь воспóльзуемся правилом и вычислим окончательный ответ:
Пример 12. Найти значение выражения
Воспользуемся правилом
Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 22 × 22, а две семёрки как 72
Теперь воспользуемся правилом и вычислим окончательный ответ:
Квадратный корень из дроби
Квадратный корень вида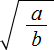
Например, квадратный корень из дроби равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
Вычислим квадратные корни в числителе и знаменателе:
Значит, квадратный корень из дроби равен
.
Докáжем, что равенство 
Возведём правую часть во вторую степень. Если в результате полýчим дробь , то это будет означать, что равенство

Пример 1. Извлечь квадратный корень
Воспользуемся правилом извлечения квадратного корня из дроби:
Пример 2. Извлечь квадратный корень
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
Пример 3. Извлечь квадратный корень
Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
Пример 6. Найти значение выражения
Сначала найдём значение квадратного корня . Он равен 0,6 поскольку 0,62 = 0,36
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение оставим без изменений:
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
Пример 3. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
Пример 4. Вынести множитель из-под знака корня в выражении
Воспользуемся правилом извлечения квадратного корня из произведения:
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
Пример 5. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 4 и 3
Воспользуемся правилом извлечения квадратного корня из произведения:
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
Пример 6. Упростить выражение
Предстáвим второе слагаемое в виде
. А третье слагаемое
предстáвим в виде
Теперь в выражениях и
вынесем множитель из-под знака корня:
Во втором слагаемом перемнóжим числа −4 и 4. Остальное перепишем без изменений:
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
Вычислим содержимое скобок, полýчим −1
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
Внесение множителя под знак корня
Рассмотрим следующее выражение:
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
Итак, если данó выражение , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
Пример 1. Внести множитель под знак корня в выражении
Возведём число 7 во вторую степень и внесём его под знак корня:
Пример 2. Внести множитель под знак корня в выражении
Возведём число 10 во вторую степень и внесем его под знак корня:
Пример 3. Внести множитель под знак корня в выражении
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида не имеет смысла.
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
Пример 5. Выполнить возведéние в степень в следующем выражении:
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:
Теперь необходимо упростить получившееся выражение.
Для выражений и
применим правило
. Ранее мы говорили, что если выражение вида
возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
А в выражении для множителей
и
применим правило
. То есть заменим произведение корней на один общий корень:
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом вычислить произведение, которое под кóрнем:
Задания для самостоятельного решения
Задание 1. Найдите значение квадратного корня:
Решение:
Задание 2. Найдите значение квадратного корня:
Решение:
Задание 3. Найдите значение квадратного корня:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение квадратного корня:
Решение:
Задание 6. Найдите значение квадратного корня:
Решение:
Задание 7. Найдите значение квадратного корня:
Решение:
Задание 8. Найдите значения следующих выражений:
Решение:
Задание 9. Извлеките квадратный корень из числа 4624
Решение:
Задание 10. Извлеките квадратный корень из числа 11025
Решение:
Задание 11. Найдите значение квадратного корня:
Решение:
Задание 12. Найдите значение квадратного корня:
Решение:
Задание 13. Найдите значение квадратного корня:
Решение:
Задание 14. Найдите значение квадратного корня:
Решение:
Задание 15. Найдите значение квадратного корня:
Решение:
Задание 16. Найдите значение выражения:
Решение:
Задание 17. Найдите значение выражения:
Решение:
Задание 18. Найдите значение выражения:
Решение:
Задание 19. Найдите значение выражения:
Решение:
Задание 20. Найдите значение выражения:
Решение:
Задание 21. Найдите значение выражения:
Решение:
Задание 22. Найдите значение выражения:
Решение:
Задание 23. Найдите значение выражения:
Решение:
Задание 24. Найдите значение выражения:
Решение:
Задание 25. Найдите значение выражения:
Решение:
Задание 26. Найдите значение выражения:
Решение:
Задание 27. Найдите значение выражения:
Решение:
Задание 28. Найдите значение выражения:
Решение:
Задание 29. Найдите значение выражения:
Решение:
Задание 30. Найдите значение выражения:
Решение:
Задание 31. Найдите значение выражения:
Решение:
Задание 32. Найдите значение выражения:
Решение:
Задание 33. Найдите значение выражения:
Решение:
Задание 34. Вынести множитель из-под знака корня:
Решение:
Задание 35. Вынести множитель из-под знака корня:
Решение:
Задание 36. Вынести множитель из-под знака корня:
Решение:
Задание 37. Вынести множитель из-под знака корня:
Решение:
Задание 38. Вынести множитель из-под знака корня:
Решение:
Задание 39. Вынести множитель из-под знака корня:
Решение:
Задание 40. Вынести множитель из-под знака корня:
Решение:
Задание 41. Вынести множитель из-под знака корня:
Решение:
Задание 42. Вынести множитель из-под знака корня:
Решение:
Задание 43. Вынести множитель из-под знака корня:
Решение:
Задание 44. Вынести множитель из-под знака корня в следующих выражениях:
Решение:
Задание 45. Внести множитель под знак корня:
Решение:
Задание 46. Внести множитель под знак корня:
Решение:
Задание 47. Внести множитель под знак корня:
Решение:
Задание 48. Внести множитель под знак корня:
Решение:
Задание 49. Внести множитель под знак корня:
Решение:
Задание 50. Внести множитель под знак корня в следующих выражениях:
Решение:
Задание 51. Упростить выражение:
Решение:
Задание 52. Упростить выражение:
Решение:
Задание 53. Упростить выражение:
Решение:
Задание 54. Упростить выражение:
Решение:
Задание 55. Упростить выражение:
Решение:
Задание 56. Упростить выражение:
Решение:
Задание 57. Упростить выражение:
Решение:
Задание 58. Упростить выражение:
Решение:
Задание 59. Упростить выражение:
Решение:
Задание 60. Упростить выражение:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

В уроке «Степень числа»
мы проходили, что возвести в квадрат число означает умножить число на само себя.
Кратко запись числа в квадрате выглядит следующим образом:
3 · 3 = 32 = 9
Но как быть, если нам нужно получить обратный результат?
Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Запомните!
Нахождение исходного числа, которое в квадрате дало бы требуемое, называется
извлечением квадратного корня.
Извлечение квадратного корня — это действие, обратное возведению в квадрат.
У квадратного корня есть специальный знак.
Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9»,
это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
√9 = 3
Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический».
Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.
Число под знаком корня называют подкоренным выражением.
Подкоренное выражение может быть представлено не только одним числом.
Всё, что находится под знаком корня, называют подкоренным выражением. Оно может сожержать как числа, так и буквы.
Запомните!
Извлекать квадратный корень можно только из положительного числа.
-
√−9
= … нельзя извлекать квадратный корень из отрицательного числа; -
√64 = 8
-
√−1,44
= … нельзя извлекать квадратный корень из отрицательного числа; -
√256 = 16
Квадратный корень из нуля
Запомните!
Квадратный корень из нуля равен нулю.
√0 = 0
Квадратный корень из единицы
Запомните!
Квадратный корень из единицы равен единице.
√1 = 1
Как найти квадратный корень из числа
Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто.
Для этого достаточно выучить таблицу квадратов.
Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от
1 до 20.
Решение примеров с квадратными корнями
Разбор примера
Вычислить арифметический квадратный корень из числа.
- √81 = 9
- √64 = 8
- √100 = 10
Как найти квадратный корень из десятичной дроби
Важно!
При нахождении квадратного корня из десятичной дроби нужно выполнить следующие действия:
- забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
- вычислить для целого числа квадратный корень;
- полученное целое число заменить на десятичную дробь (поставить запятую исходя из
правила умножения десятичных дробей).
Более подробно разберем на примере ниже.
Разбор примера
Вычислить квадратный корень из десятичной дроби «0,16».
√0,16 =
По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «16».
Нетрудно вспомнить, какое число в квадрате дает «16». Это число
«4».
√16 = 4
√0,16 = …
Вспомним правило умножения десятичных дробей.
Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой
дроби.
Т.е., например, при умножении «0,15» на
«0,3» в полученном произведении будет десятичная дробь с тремя знаками после запятой.
0,15 · 0,3 = 0,045
Значит, при вычислении квадратного корня
√0,16
нам нужно найти десятичную дробь, у которой был бы только один знак после запятой.
Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться
два знака после запятой, как у десятичной дроби «0,16».
Получается, что ответ — десятичная дробь «0,4».
√0,16 = 0,4
Убедимся, что квадрат десятичной дроби
«0,42» дает
«0,16».
Умножим в столбик «0,4» на
«0,4».
Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:
√1,44 =
Представим вместо десятичной дроби «1,44» целое число
«144». Какое число в квадрате даст «144»?
Ответ — число «12».
122 = 144
√144 = 12
√1,44 = …
Так как в десятичной дроби «1,44» — два знака после запятой, значит в десятичной дроби,
которая дала в квадрате «1,44» должен быть один знак после запятой.
√1,44 = 1,2
Убедимся, что «1,22» дает в квадрате «1,44».
1,22 = 1,2 · 1,2 = 1,44
Квадратные корни из чисел
√2,
√3,
√5,
√6,
и т.п.
Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен
√2
или
√3
и т.п.
В самом деле, какое число в квадрате даст «2»? Или число «3»?
Такое число не будет целым. Более того, оно представляет из себя
непериодическую десятичную дробь
и входит в
множество иррациональных чисел.
Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:
√15 − 2 · 4 =
√15 − 8 =
√7
Нет такого целого числа, которое бы дало в квадрате число «7».
Поэтому, перед завершением задачи внимательно читайте её условие.
Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно
оставить с корнем.
√15 − 2 · 4 =
√15 − 8 =
√7
Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора,
то после вычисления квадратного корня на калькуляторе
округлите результат до необходимого количества знаков.
Текст задания в таком случае может быть написан следующим образом:
«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до
«0,001».
√15 − 2 · 4 =
√15 − 8 =
√7 ≈ 2,646
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и
и
— сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.01.2023
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3).
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!
Квадра́тный ко́рень из 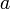
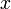

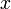
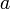
Содержание
- 1 Применение операции корня к числам
- 1.1 Рациональные числа
- 1.2 Действительные числа
- 1.3 Комплексные числа
- 2 Квадратный корень как элементарная функция
- 2.1 Вещественный анализ
- 2.2 Комплексный анализ
- 3 Обобщения
- 4 Квадратный корень в элементарной геометрии
- 5 Квадратный корень в информатике
- 6 Алгоритмы нахождения квадратного корня
- 6.1 Арифметическое извлечение квадратного корня
- 6.2 Геометрическое извлечение квадратного корня
- 6.3 Столбиком
- 7 Примечания
- 8 См. также
- 9 Ссылки
Применение операции корня к числам
Квадратный корень из числа 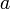
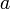

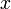
Рациональные числа
Корень из рационального числа 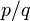
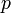
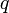
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: 


Действительные числа
При натуральных 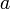

Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку. [5]
Неотрицательный квадратный корень из положительного числа 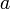

Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа 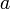

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
,
то (см. Формула Муавра)
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.
Квадратный корень как элементарная функция
Вещественный анализ
График функции
Квадратным корнем называют также функцию 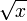
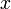




Комплексный анализ
Обобщения
Квадратные корни вводятся как решения уравнений вида 

В алгебре применяется следующее формальное определение: Пусть 
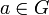

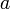

Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырех действий арифметики, квадратные корни и ничего сверх того. [11]
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа sqrt, от англ. square root «квадратный корень».
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
- 1 = 12
- 1 + 3 = 22
- 1 + 3 + 5 = 32
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий. Например, так:
- 9 − 1 = 8
- 8 − 3 = 5
- 5 − 5 = 0
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
Геометрическое извлечение квадратного корня
В частности, если 


Столбиком
Этот способ позволяет найти приближённоё значение корня из любого действительного числа с любой наперёд заданной точностью.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по 2 цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.
- Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
- Провести вычитание из старших разрядов A квадрата числа an.
- Удвоить an.
- Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an — на один разряд влево. Под сдвигом в данном алгоритме понимается умножение/деление на степени 10, что соответственно является сдвигом влево и вправо.
- Приписать справа от остатка вычитания два следующих старших разряда числа A.
- Сравнить полученное число с нулём.
- Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на
, даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п.3.
- Если в п.5 получено равенство, то перейти к п.4, предварительно приписв справа от an нуль.
- После получения количества цифр, равного
, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
Примечания
- ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
- ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число (
)… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
- ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
- ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
- ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
- ↑ Фихтенгольц, гл. 2, § 1
- ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148
См. также
- Корень (значения)
- Арифметический корень
- Квадратное уравнение
- Итерационная формула Герона
- Корень квадратного уравнения
- Теорема Абеля — Руффини
Ссылки
- Алгоритмы вычисления квадратного корня
- A geometric view of the square root algorithm
- Соловьев Ю., Старый алгоритм
Wikimedia Foundation.
2010.
























































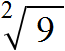
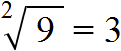
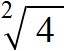
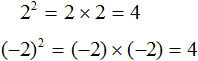
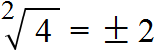
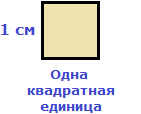
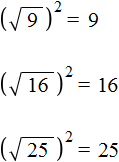
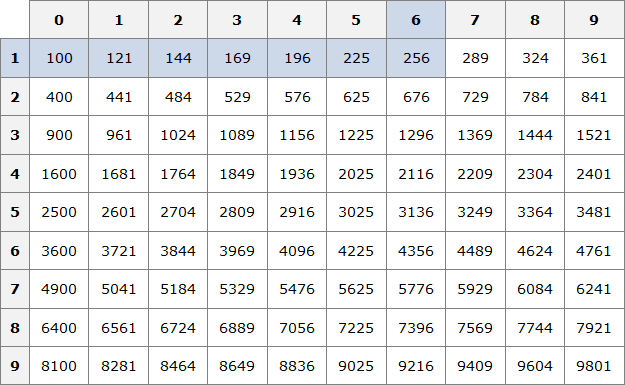
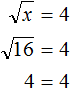
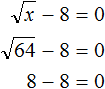
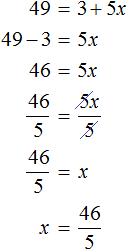
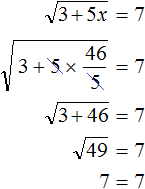

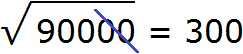
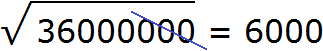
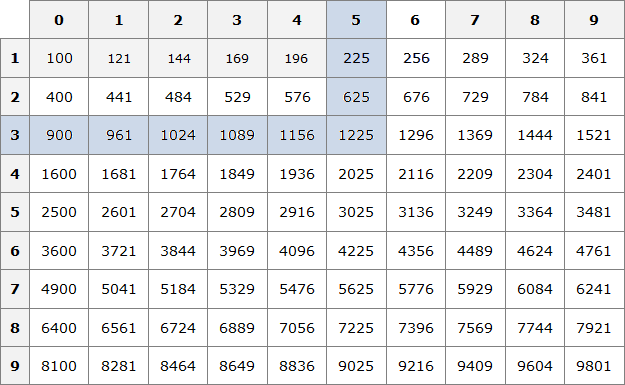
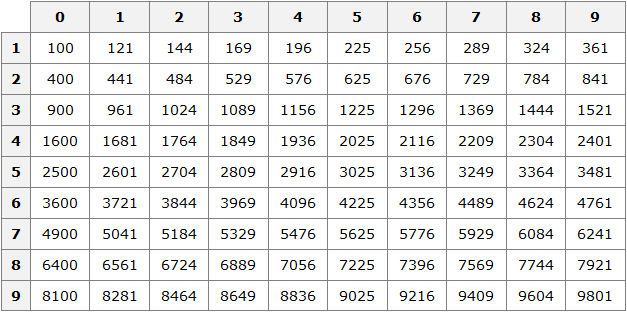
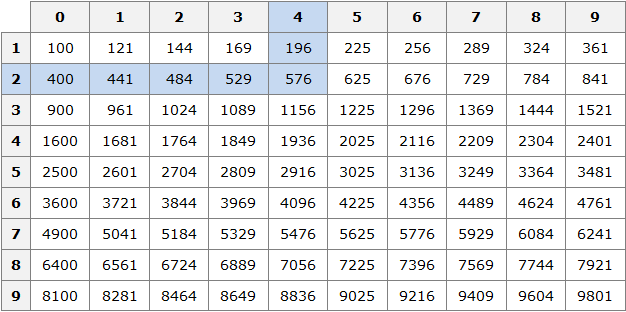
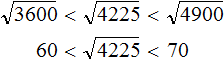
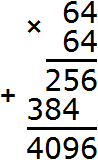
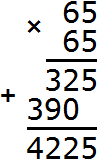

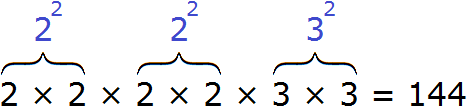
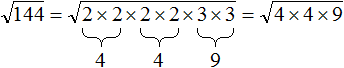
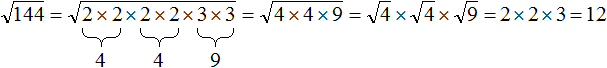

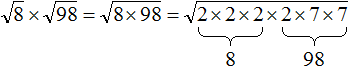
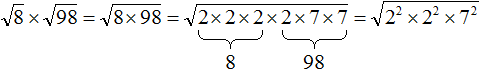
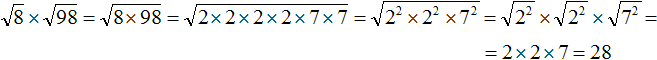
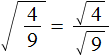
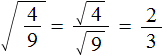
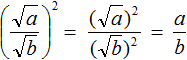
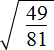
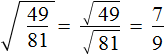
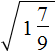
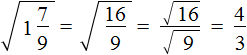
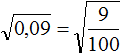
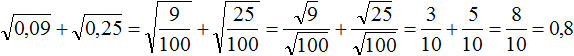
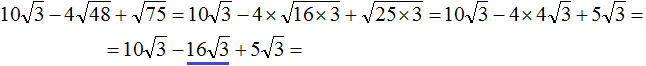
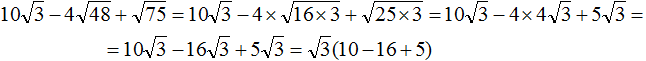
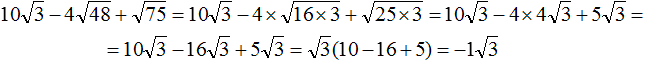
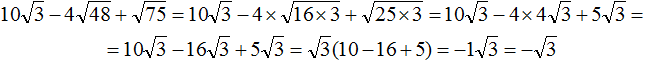
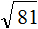


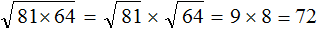
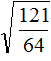
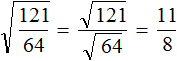
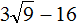

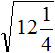
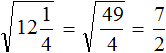
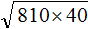
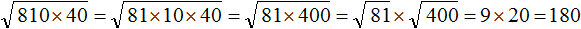
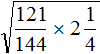
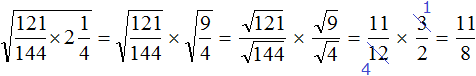
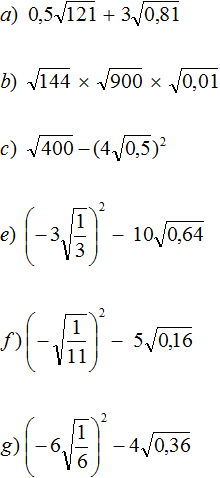
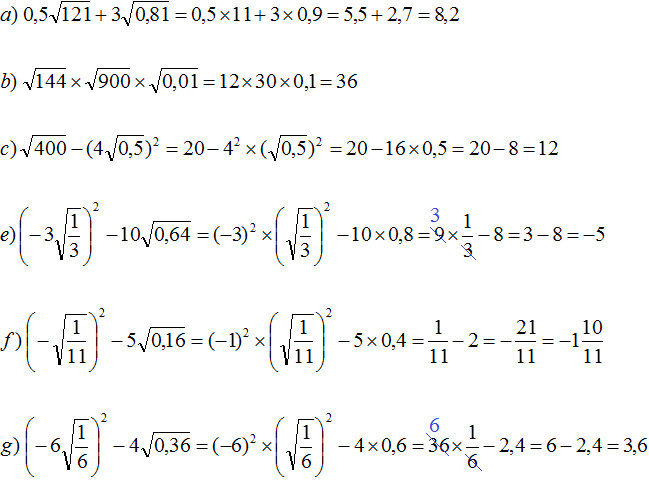
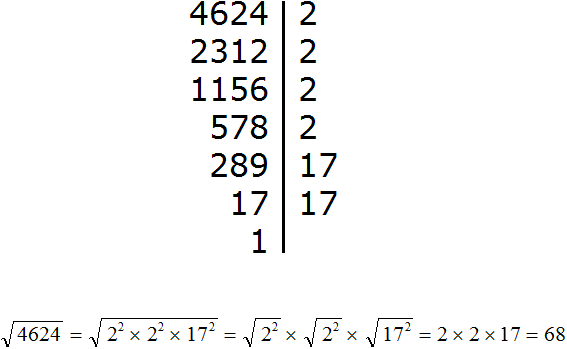

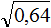

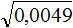

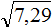

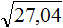
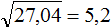
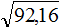
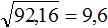
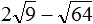
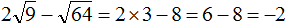
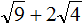
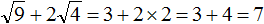


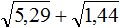





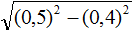
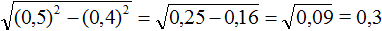
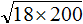
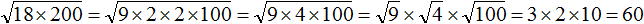
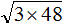

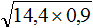
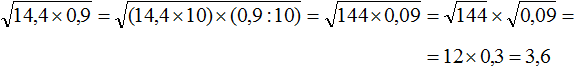
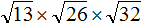

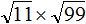



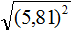

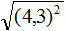

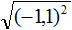
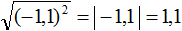

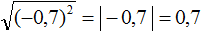

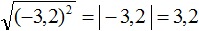

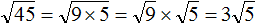
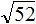

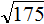
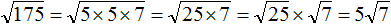
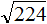
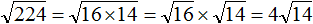
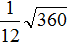

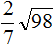
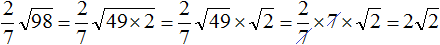
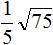



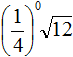

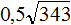


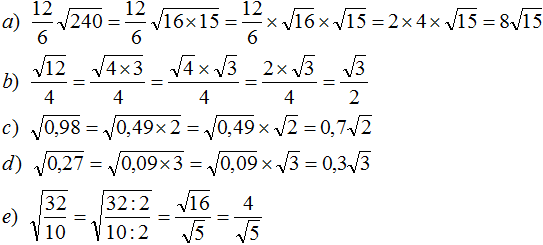
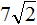

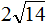
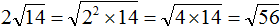

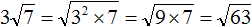
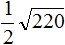
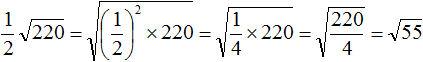
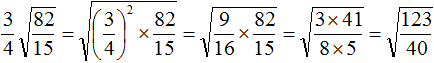
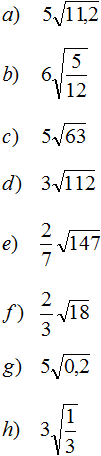


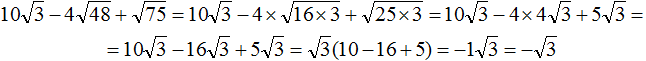




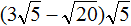

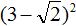


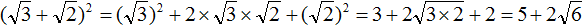

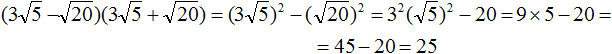
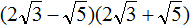
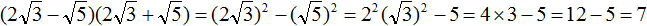
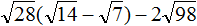

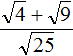
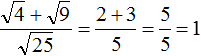


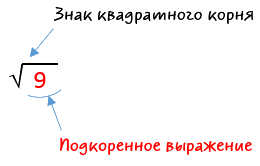
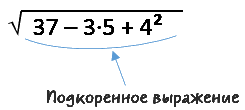
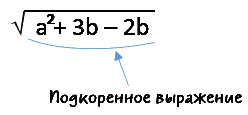

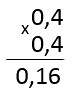

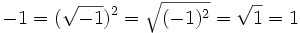
 ,
, ,
,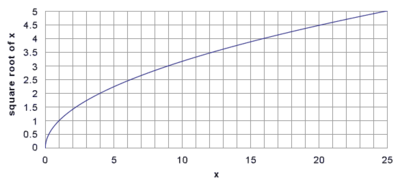



 , даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п.3.
, даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п.3. , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой. )… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
)… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.