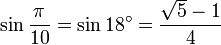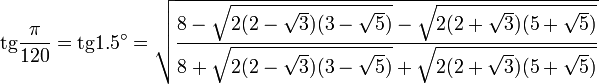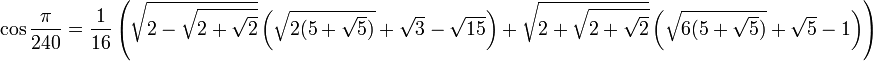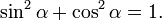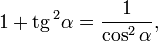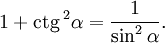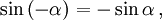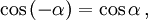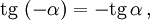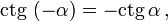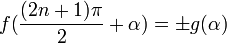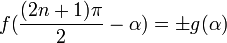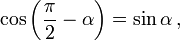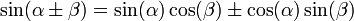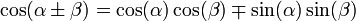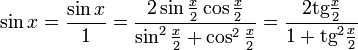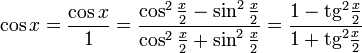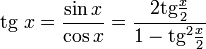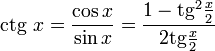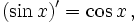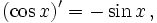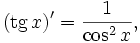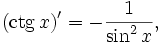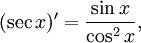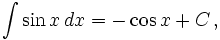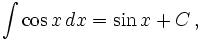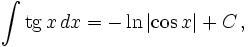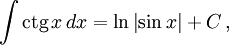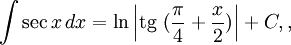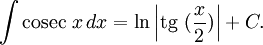Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
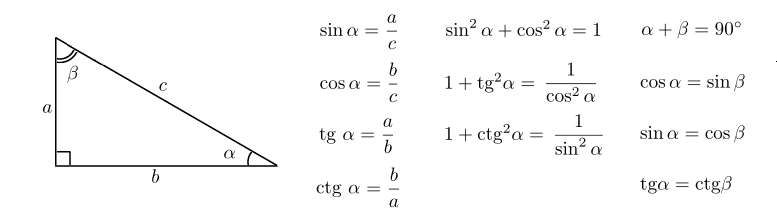
- Главная
- Справочник
- Тригонометрия
- Тангенс и котангенс. Формулы и определение
Тангенс и котангенс. Формулы и определение
Помимо синуса и косинуса в тригонометрии имеется еще огромное количество функций, в частности, тангенс и котангенс, о котором мы поговорим на данном уроке.
Определение тангенса:
Тангенс tg(x) — это отношение синуса sin(x) к косинусу cos(x)
Формула тангенса:
[ LARGE tg x = dfrac{sin x}{cos x} ]
Определение котангенса:
Котангенс ctg(x) — это отношение косинуса cos(x) к синусу sin(x).
Формула котангенса:
[ LARGE ctg x = dfrac{cos x}{sin x} ]
Определения для прямоугольного треугольника:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Определения для числа:
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t, то есть, tg(t)=y/x.
Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t, то есть, ctg(t)=x/y.
Так как делить на ноль нельзя, то значения в знаменателе не может быть равным нулю, т.е.
( tg x = dfrac{sin x}{cos x} ), где ( x neq dfrac{pi}{2}+pi k )
( ctg x = dfrac{cos x}{sin x} ), где ( x neq pi k )
Таблица знаков тангенса и котангенса по четвертям (составить ее можно, опираясь на таблицу синусов и косинусов, применяя правило деление чисел с отрицательными знаками):
| I | II | III | IV | |
| tg x | + | – | + | – |
| ctg x | + | – | + | – |
Как видите, значения тангенса и котангенса очень просто найти, зная значения синуса и косинуса, тем не менее также существует таблица и для данных функций, которая существенно упрощает жизнь. Здесь я представлю самые распространенные значения. А для всех остальных значений существуют специальные таблицы Брадиса.
| ( frac{pi}{6} ) | ( frac{pi}{4} ) | ( frac{pi}{3} ) | ( frac{pi}{2} ) | 0 | |
| tg x | ( frac{sqrt{3}}{3} ) | 1 | ( sqrt{3} ) | – | 0 |
| ctg x | ( sqrt{3} ) | 1 | ( frac{sqrt{3}}{3} ) | 0 | – |
Завершая разговор про данные тригонометрические функции нельзя не сказать про еще две важные формулы:
Для любого допустимого значения х справедливы равенства:
[ tg (-x) = -tg x ]
[ ctg (-x) = -ctg x ]
Для любого допустимого значения х также справедливы следующие равенства:
[ tg (x+pi)= tg pi ]
[ ctg (x+pi)= ctg pi ]
Ну вот теперь вроде все, более подробно и углубленно изучать мы будем все функции в процессе дальнейшего обучения.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Примеры:
(ctg:30^° =sqrt{3})
(ctg:(frac{π}{3})=frac{1}{sqrt{3}})
(ctg:2=-0,487…)
Содержание:
- Аргумент и значение
Котангенс острого угла
Котангенс числа или любого угла
Знаки по четвертям
Связь с другими функциями
Аргумент и значение

Аргументом может быть:
— как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев значение котангенса вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Значение котангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)
Котангенс острого угла
Котангенс можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к противолежащему.
Пример:
1) Пусть дан угол и нужно определить (ctgA).

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (ctg;A).

Вычисление котангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) котангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
(ctg: t=)(frac{cos:t}{sin:t})
Пример. Вычислите (ctg: frac{5π}{6}).
Решение: Найдем сначала (frac{5π}{6}) на круге. Затем найдем (cos:frac{5π}{6}) и (sin:frac{5π}{6}), а потом поделим одно на другое.

(ctg:frac{5π}{6}=)(frac{cos:frac{5π}{6}}{sin:frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3})
Ответ: (-sqrt{3}).
Пример. Вычислите (ctg:frac{π}{2}).
Решение: Чтобы найти котангенс пи на (2) нужно найти сначала косинус и синус (frac{π}{2}). И то, и другое найдем с помощью тригонометрического круга:

Точка (frac{π}{2}) на числовой окружности совпадает с (1) на оси синусов, значит (sin:frac{π}{2}=1). Если из точки (frac{π}{2}) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку (0), значит (cos:frac{π}{2}=0). Получается: (ctg:frac{π}{2}=)(frac{cos:frac{π}{2}}{sin:frac{π}{2}})(=)(frac{0}{1})(=0).
Ответ: (0).
Пример. Вычислите (ctg:(-765^circ)).
Решение: (ctg: (-765^circ)=)(frac{cos:(-765^circ)}{sin:(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin(-765^°)=-frac{sqrt{2}}{2});
(cos(-765^°)=frac{sqrt{2}}{2}) ;
получается (ctg(-765^°)= frac{sqrt{2}}{2} ∶ -frac{sqrt{2}}{2}=-1).
Ответ: (-1).
Пример. Найдите (ctg:frac{π}{3}).
Решение: (ctg: frac{π}{3}=)(frac{cos:frac{π}{3}}{sin:frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin(frac{π}{3})=frac{sqrt{3}}{2});
(cos(frac{π}{3})=frac{1}{2}) ;
получается (ctg(frac{π}{3})=frac{1}{2} ∶ frac{sqrt{3}}{2}= frac{1}{2} cdot frac{2}{sqrt{3}}=frac{1}{sqrt{3}}).
Ответ: (frac{1}{sqrt{3}}).
Однако можно определять значение котангенса и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:
Прямая проходящая через (frac{π}{2}) на числовой окружности и параллельная оси абсцисс (косинусов) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.
Чтобы определить значение котангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу котангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси котангенсов.
3) Найти координату пересечения этой прямой и оси.
Пример. Вычислите (ctg:frac{π}{4}).
Решение:
1) Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).
Ответ: (1).
Пример. Найдите значение (ctg: 30°) и (ctg: (-60°)).
Решение:
Для угла (30°) ((∠COA)) котангенс будет равен (sqrt{3}) (приблизительно (1,73)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось котангесов.
(ctg;(-60°)=frac{sqrt{3}}{{3}}) (примерно (-0,58)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение котангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом котангенс не определен для:
1) всех точек (C) (значение в Пи: …(0), (2π), (4π), (-2π), (-4π) …; и значение в градусах: …(0°),(360°), (720°),(-360°),(-720°)…)
2) всех точек (D) (значение в Пи: …(π), (3π), (5π), (-π), (-3π), (-5π) …; и значение в градусах: …(180°),(540°),(900°),(-180°),(-540°),(-900°)…) .
Так происходит потому, что в этих точках синус равен нулю. А значит, вычисляя значение котангенса мы придем к делению на ноль, что запрещено. И прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось котангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках котангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений он может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с котангенсом необходимо учитывать ограничения на ОДЗ.
Знаки по четвертям
С помощью оси котангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак котангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение котангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:
— синусом того же угла: формулой (1+ctg^2x=)(frac{1}{sin^2x})
— косинусом и синусом того же угла: (ctg:x=)(frac{cos:x}{sin:x})
— тангенсом того же угла: формулой (tg:x=)(frac{1}{ctg:x})
Другие наиболее часто применяемые формулы смотри здесь.
Смотрите также:
Формулы приведения
Решение уравнений (tgx=a) и (ctgx=a)
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Содержание
- 1 Способы определения
- 1.1 Геометрическое определение
- 1.1.1 Определение тригонометрических функций для острых углов
- 1.2 Определение тригонометрических функций как решений дифференциальных уравнений
- 1.3 Определение тригонометрических функций как решений функциональных уравнений
- 1.4 Определение тригонометрических функций через ряды
- 1.1 Геометрическое определение
- 2 Значения тригонометрических функций для некоторых углов
- 2.1 Значения тригонометрических функций нестандартных углов
- 3 Свойства тригонометрических функций
- 3.1 Простейшие тождества
- 3.2 Чётность
- 3.3 Периодичность
- 3.4 Формулы приведения
- 3.5 Формулы сложения
- 3.6 Однопараметрическое представление
- 4 Производные и интегралы
- 5 История
- 6 См. также
- 7 Ссылки
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
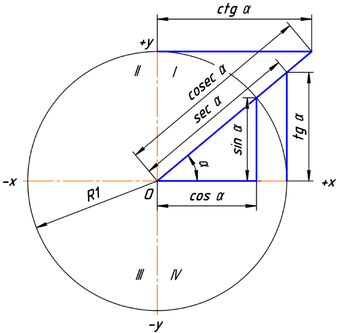
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 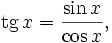
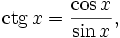
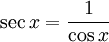
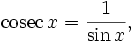
где Bn — числа Бернулли.
где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
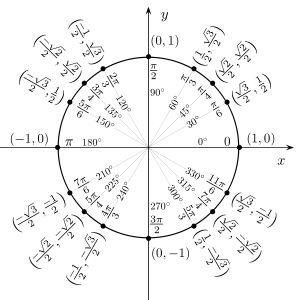
Значения косинуса и синуса на окружности.
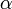 |
0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) |
|---|---|---|---|---|---|---|---|---|
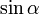 |
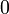 |
 |
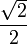 |
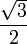 |
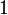 |
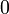 |
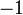 |
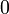 |
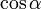 |
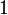 |
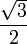 |
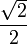 |
 |
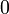 |
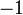 |
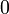 |
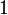
|
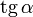 |
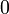 |
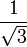 |
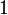 |
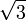 |
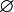 |
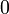 |
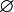 |
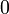 |
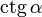 |
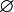 |
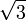 |
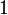 |
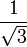 |
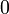 |
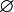 |
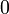 |
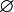 |
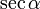 |
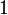 |
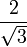 |
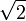 |
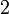 |
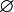 |
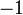 |
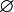 |
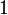 |
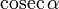 |
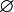 |
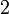 |
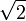 |
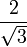 |
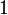 |
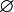 |
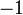 |
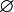 |
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.
Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Wikimedia Foundation.
2010.





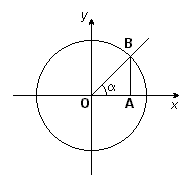

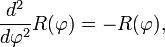
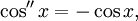
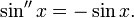
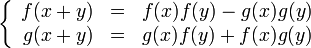
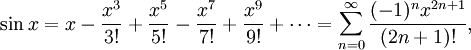
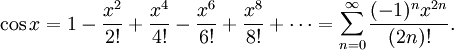
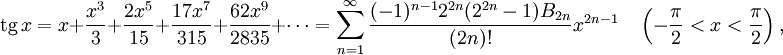 где
где 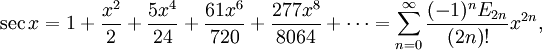 где
где