Как пишется кпд в физике

КПД: понятие коэффициента полезного действия

Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.

В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.

По сути, КПД — это процент полезной работы от работы затраченной.

Вычисляется по формуле:

Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.

Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.

Полезная работа в этом случае равна приобретенной булыжником потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.

Затраченная работа здесь — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.

Давайте разберемся на примере задачи.

Задача

Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с²

Запишем формулу КПД.

η = (A_{полезная}/A_{затраченная}) · 100%

Теперь задаем два главных вопроса:

Ради чего все это затеяли?

Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.

За счет чего процесс происходит?

За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе

Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:

η = E_п/A · 100% = mgh/FS · 100%

Подставим значения:

η = 4 · 9,8 · 2/15 · 12 · 100% = 78,4/180 · 100% ≃ 43,6 %

Ответ: КПД процесса приблизительно равен 43,6%

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

КПД в термодинамике

В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.

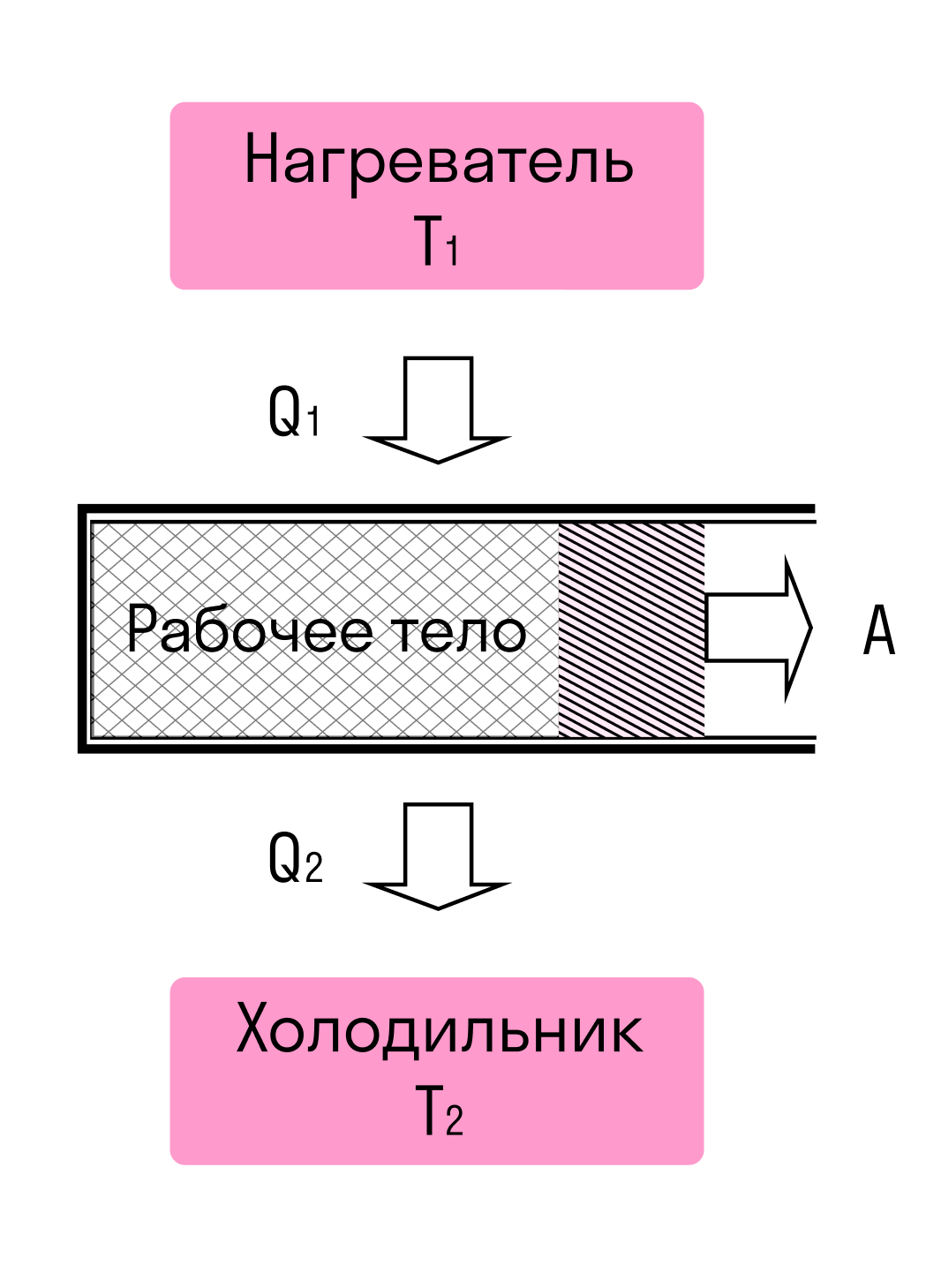
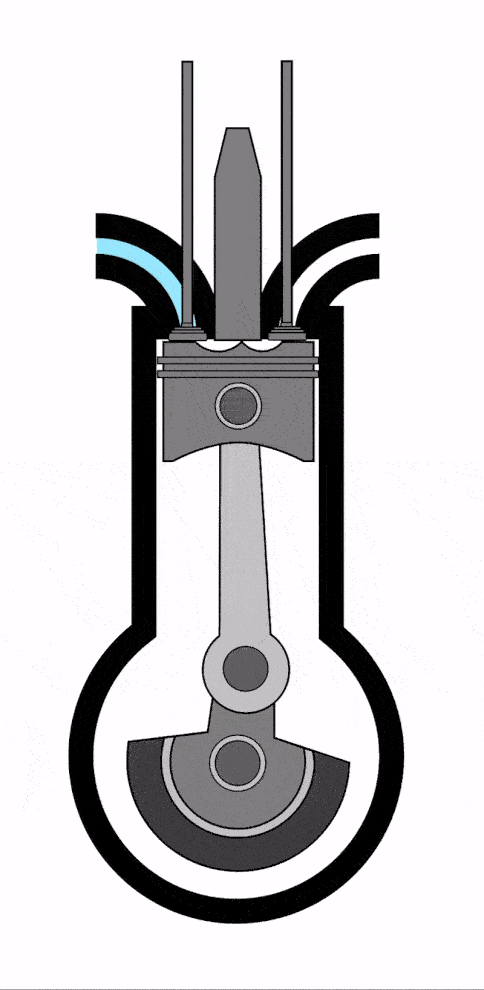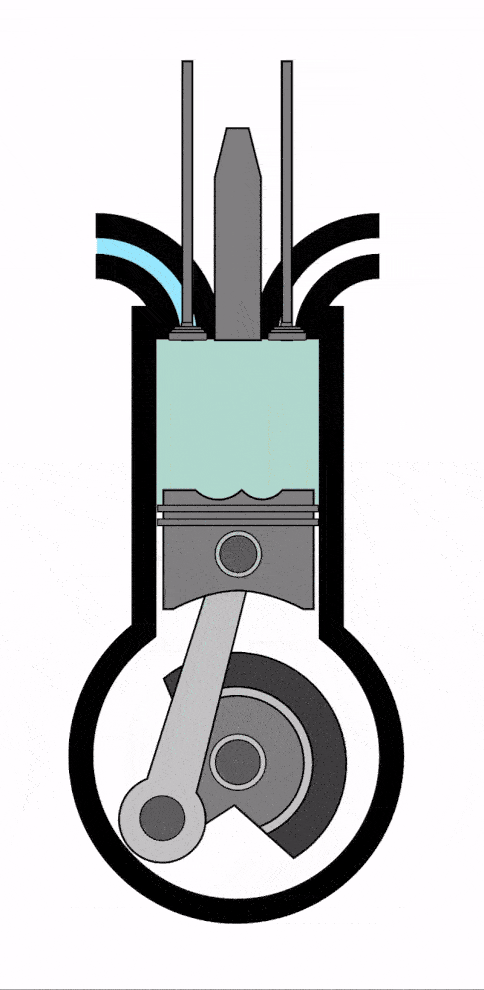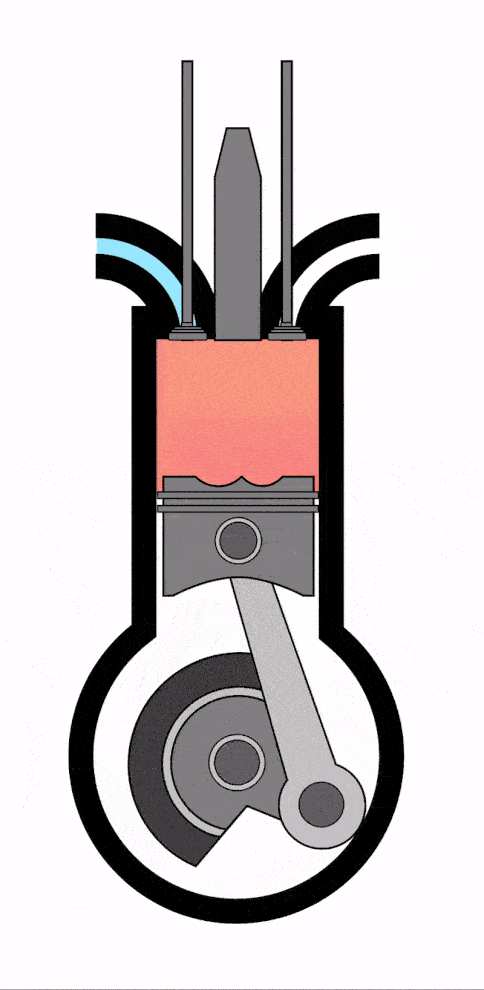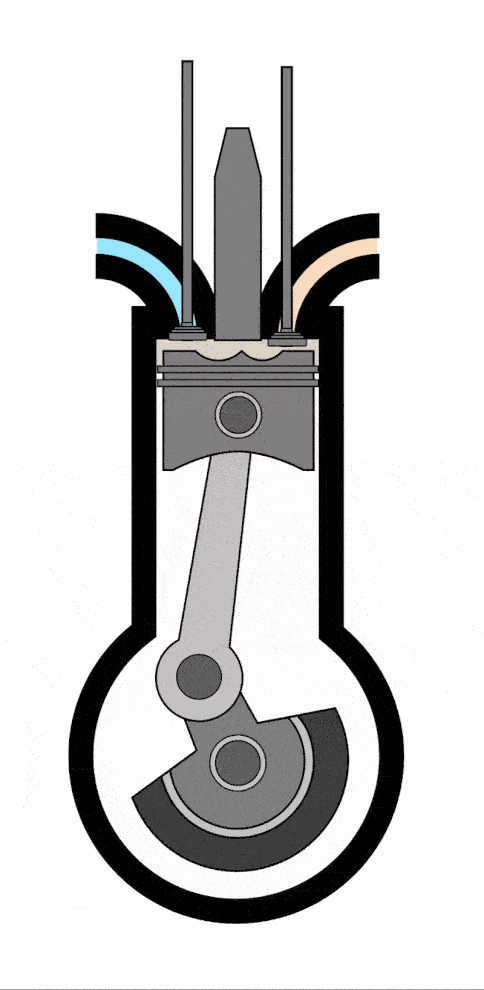
• Тепловой двигатель (машина) — это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:

У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q₁ или Q_{нагревателя} (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).

• Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ или топливо). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q₁ уходит на механическую работу A. Из-за этого производится движение.

Оставшееся количество теплоты Q₂ или Q_{холодильника} отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.

КПД такой тепловой машины будет равен:

Если мы выразим полезную (механическую) работу через Q_{нагревателя} и Q_{холодильника}, мы получим:

A = Q_{нагревателя} — Q_{холодильника}.

Подставим в числитель и получим такой вариант формулы.

А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?

Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.

Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.

Запишем его, чтобы не забыть:

Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.

Задача

Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.

Решение:

Возьмем формулу для расчета КПД:

η = Q_{нагревателя} − Q_{холодильника}/Q_{нагревателя} · 100%

Решать будем в системе СИ, поэтому переведем значения из килоджоулей в джоули и затем подставим в формулу:

η = 20 000 − 10 000/20 000 · 100% = 50%

Ответ: КПД тепловой машины равен 50%.

Идеальная тепловая машина: цикл Карно

Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.

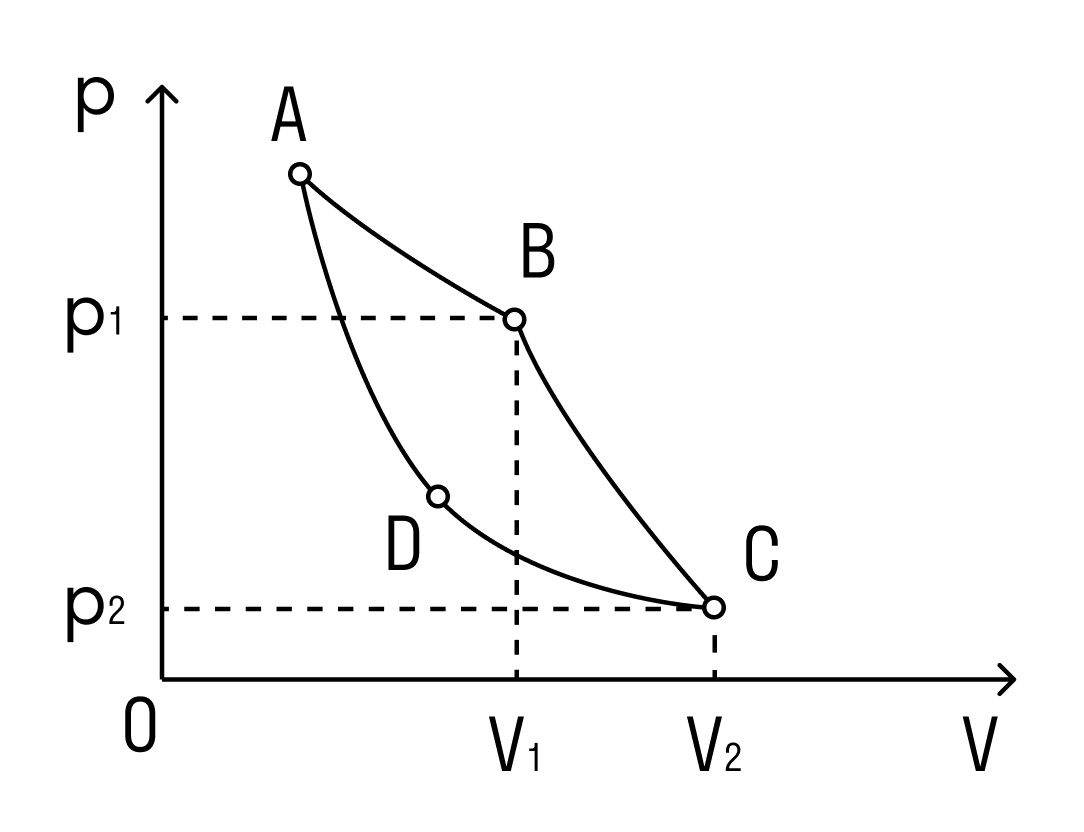
На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом

А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.

КПД в электродинамике

Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.

Вспомним формулу:

Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.

Задачка, чтобы разобраться

Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.

Решение:

Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉

Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.

То есть в данном случае формула КПД будет иметь вид:

η = Q/A · 100% = Q/UIt · 100%

Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь нам известны все значения, поэтому подставим их:

η = 22176/220 · 1,4 · 120 · 100% = 60%

Ответ: КПД чайника равен 60%.

Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:

Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.

---

---

Трактовка понятия

Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:

• А1 — полезная работу, которую выполняет машина либо мотор;
• А2 — общий цикл работы;
• η — обозначение КПД.

Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.

В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:

• Q1 — теплота, полученная от нагревательного элемента;
• Q2 — теплота, отданная холодильной установке.

Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.

Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.

Мощность разных устройств

По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.

При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.

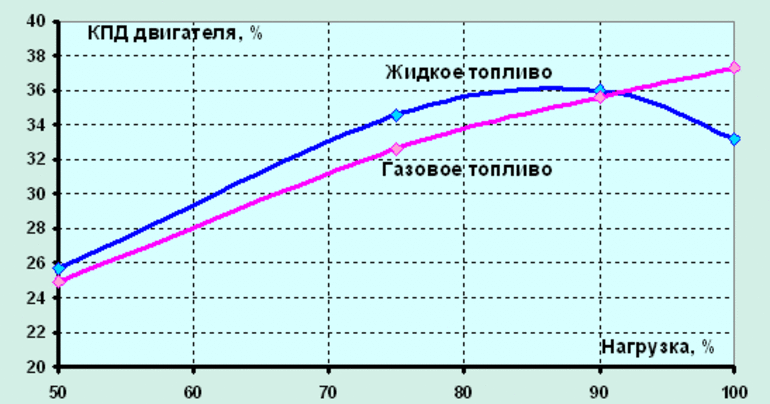
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:

1. Поршни бензинового мотора функционируют на высоких температурах, поэтому нуждаются в хорошем охлаждении. Тепло, которое могло бы перейти в механическую энергию, тратится впустую, что способствует снижению КПД.
2. В цепи дизельного устройства топливо воспламеняется в процессе сжатия. На основе данного фактора можно сделать вывод, что давление в цилиндрах высокое, при этом мотор экологичнее и меньше первого аналога. Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.

Асинхронные механизмы

Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:

• простое изготовление;
• низкая цена;
• надёжность;
• незначительные эксплуатационные затраты.

Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.

Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.

Значения показателя

В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.

На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.

Мощность стандартного двигателя увеличивается следующими способами:

• подключение к системе многоцилиндрового агрегата;
• применение специального топлива;
• замена некоторых деталей;
• перенос места сжигания бензина.

КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.

Решение примеров

Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.

Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:

• тяжесть — mg;
• реакция опоры — N;
• трение — Ftr;
• тяга — F.

Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.

При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.

Что такое КПД

Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.

Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.

Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.

Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.

Примеры расчета КПД

Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха — 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.

Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные — окна, двери и т.д.

Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.

Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж

Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.

Единицы измерения

Коэффициент полезного действия – величина безразмерная, то есть не нужно ставить какую-либо единицу измерения. Но эту величину можно выразить и в процентах. Для этого полученное в результате деления по формуле число необходимо умножить на 100%. В школьном курсе математики рассказывали, что процент – этот одна сотая чего-либо. Умножая на 100 процентов, мы показываем, сколько в числе сотых.

От чего зависит величина КПД

Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.

А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.

Как обозначается

В русских учебниках обозначается двояко. Либо так и пишется – КПД, либо обозначается греческой буквой η. Эти обозначения равнозначны.

Символ, обозначающий КПД

Символом является греческая буква эта η. Но чаще все же используют выражение КПД.

Мощность и КПД

Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.

Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.

Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.

Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.

Формула работы в физике

Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.

Это интересно

Наукой обосновано, что коэффициент полезного действия любого механизма всегда меньше единицы. Это связано со вторым началом термодинамики.

Для сравнения, коэффициенты полезного действия различных устройств:

• гидроэлектростанций 93-95%;
• АЭС – не более 35%;
• тепловых электростанций – 25-40%;
• бензинового двигателя – около 20%;
• дизельного двигателя – около 40%;
• электрочайника – более 95%;
• электромобиля – 88-95%.

Наука и инженерная мысль не стоит на месте. постоянно изобретаются способы, как уменьшить теплопотери, снизить трение между частями агрегата, повысить энергоэффективность техники.

The coefficient of performance or COP (sometimes CP or CoP) of a heat pump, refrigerator or air conditioning system is a ratio of useful heating or cooling provided to work (energy) required.^[1][2] Higher COPs equate to higher efficiency, lower energy (power) consumption and thus lower operating costs.

The COP usually exceeds 1, especially in heat pumps, because, instead of just converting work to heat (which, if 100% efficient, would be a COP of 1), it pumps additional heat from a heat source to where the heat is required. Most air conditioners have a COP of 2.3 to 3.5. Less work is required to move heat than for conversion into heat, and because of this, heat pumps, air conditioners and refrigeration systems can have a coefficient of performance greater than one.

However, this does not mean that they are more than 100% efficient, in other words, no heat engine can have a thermal efficiency of 100% or greater. For complete systems, COP calculations should include energy consumption of all power consuming auxiliaries. The COP is highly dependent on operating conditions, especially absolute temperature and relative temperature between sink and system, and is often graphed or averaged against expected conditions.^[3]

Performance of absorption refrigerator chillers is typically much lower, as they are not heat pumps relying on compression, but instead rely on chemical reactions driven by heat^{[citation needed]}.

Equation[edit]

The equation is:

where

The COP for heating and cooling are different because the heat reservoir of interest is different. When one is interested in how well a machine cools, the COP is the ratio of the heat taken up from the cold reservoir to input work. However, for heating, the COP is the ratio of the magnitude of the heat given off to the hot reservoir (which is the heat taken up from the cold reservoir plus the input work) to the input work:

where

Note that the COP of a heat pump depends on its direction. The heat rejected to the hot sink is greater than the heat absorbed from the cold source, so the heating COP is greater by one than the cooling COP.

Theoretical performance limits[edit]

According to the first law of thermodynamics, after a full cycle of the process and thus .
Since , we obtain

For a heat pump operating at maximum theoretical efficiency (i.e. Carnot efficiency), it can be shown^[5][4] that

and thus

where and are the thermodynamic temperatures of the hot and cold heat reservoirs, respectively.

At maximum theoretical efficiency, therefore

which is equal to the reciprocal of the thermal efficiency of an ideal heat engine, because a heat pump is a heat engine operating in reverse.^[6]

Similarly, the COP of a refrigerator or air conditioner operating at maximum theoretical efficiency,

applies to heat pumps and applies to air conditioners and refrigerators.
Measured values for actual systems will always be significantly less than these theoretical maxima.

In Europe, the standard test conditions for ground source heat pump units use 308 K (35 °C; 95 °F) for and 273 K (0 °C; 32 °F) for . According to the above formula, the maximum theoretical COPs would be

Test results of the best systems are around 4.5. When measuring installed units over a whole season and accounting for the energy needed to pump water through the piping systems, seasonal COP’s for heating are around 3.5 or less. This indicates room for further improvement.

The EU standard test conditions for an air source heat pump is at dry-bulb temperature of 20 °C (68 °F) for and 7 °C (44.6 °F) for .^[7] Given sub-zero European winter temperatures, real world heating performance is significantly poorer than such standard COP figures imply.

Improving COP[edit]

As the formula shows, the COP of a heat pump system can be improved by reducing the temperature gap minus at which the system works. For a heating system this would mean two things: 1) reducing the output temperature to around 30 °C (86 °F) which requires piped floor, wall or ceiling heating, or oversized water to air heaters and 2) increasing the input temperature (e.g. by using an oversized ground source or by access to a solar-assisted thermal bank ^[8] ). Accurately determining thermal conductivity will allow for much more precise ground loop ^[9] or borehole sizing,^[10] resulting in higher return temperatures and a more efficient system. For an air cooler, COP could be improved by using ground water as an input instead of air, and by reducing temperature drop on output side through increasing air flow. For both systems, also increasing the size of pipes and air canals would help to reduce noise and the energy consumption of pumps (and ventilators) by decreasing the speed of fluid which in turn lower the Reynolds number and hence the turbulence (and noise) and the head loss (see hydraulic head). The heat pump itself can be improved by increasing the size of the internal heat exchangers which in turn increase the efficiency (and the cost) relative to the power of the compressor, and also by reducing the system’s internal temperature gap over the compressor. Obviously, this latter measure makes such heat pumps unsuitable to produce high temperatures which means that a separate machine is needed for producing hot tap water.

The COP of absorption chillers can be improved by adding a second or third stage. Double and triple effect chillers are significantly more efficient than single effect, and can surpass a COP of 1. They require higher pressure and higher temperature steam, but this is still a relatively small 10 pounds of steam per hour per ton of cooling.^[11]

Example[edit]

A geothermal heat pump operating at a of 3.5 provides 3.5 units of heat for each unit of energy consumed (i.e. 1 kWh consumed would provide 3.5 kWh of output heat). The output heat comes from both the heat source and 1 kWh of input energy, so the heat-source is cooled by 2.5 kWh, not 3.5 kWh.

A heat pump with of 3.5, such as in the example above, could be less expensive to use than even the most efficient gas furnace except in areas where the electricity cost per unit is higher than 3.5 times the cost of natural gas (e.g. Connecticut or New York City).

A heat pump cooler operating at a of 2.0 removes 2 units of heat for each unit of energy consumed (e.g. an air conditioner consuming 1 kWh would remove 2 kWh of heat from a building’s air).

Given the same energy source and operating conditions, a higher COP heat pump will consume less purchased energy than one with a lower COP. The overall environmental impact of a heating or air conditioning installation depends on the source of energy used as well as the COP of the equipment. The operating cost to the consumer depends on the cost of energy as well as the COP or efficiency of the unit. Some areas provide two or more sources of energy, for example, natural gas and electricity. A high COP of a heat pump may not entirely overcome a relatively high cost for electricity compared with the same heating value from natural gas.

For example, the 2009 US average price per therm (100,000 British thermal units (29 kWh)) of electricity was $3.38 while the average price per therm of natural gas was $1.16.^[12] Using these prices, a heat pump with a COP of 3.5 in moderate climate would cost $0.97^[13] to provide one therm of heat, while a high efficiency gas furnace with 95% efficiency would cost $1.22^[14] to provide one therm of heat. With these average prices, the heat pump costs 20% less^[15] to provide the same amount of heat.

The COP of a heat pump operating at the Carnot efficiency has in its denominator the expression T_H — T_C. As the surroundings cool (T_C reducing) the denominator increases and COP reduces. Therefore, the colder the surroundings, the lower the COP of any heat pump. If the surroundings cool, say to 0 °F (-18 °C), COP falls in value below 3.5. Then, the same system costs as much to operate as an efficient gas heater. The yearly savings will depend on the actual cost of electricity and natural gas, which can both vary widely.

The above example applies only for an air source heat pump. The above example assumes that the heat pump is an air-source heat pump moving heat from outside to inside, or a water source heat pump that is simply moving heat from one zone to the other. For a water source heat pump, this would only occur if the instantaneous heating load on the condenser water system exactly matches the instantaneous cooling load on the condenser water system. This could happen during the shoulder season (spring or fall), but is unlikely in the middle of the heating season. If more heat is being withdrawn by the heat pumps that are in heating mode than is being added by the heat pumps that are in cooling mode, then the boiler (or other heat source) will add heat to the condenser water system. The energy consumption and cost associated with the boiler would need to be factored in to the above comparison. For a water source system, there is also energy associated with the condenser water pumps that is not factored in to the heat pump energy consumption in the example above.

Seasonal efficiency[edit]

A realistic indication of energy efficiency over an entire year can be achieved by using seasonal COP or seasonal coefficient of performance (SCOP) for heat. Seasonal energy efficiency ratio (SEER) is mostly used for air conditioning. SCOP is a new methodology that gives a better indication of expected real-life performance, using COP can be considered using the «old» scale. Seasonal efficiency gives an indication on how efficiently a heat pump operates over an entire cooling or heating season.^[16]

See also[edit]

• Seasonal energy efficiency ratio (SEER)
• Seasonal thermal energy storage (STES)
• Heating seasonal performance factor (HSPF)
• Power usage effectiveness (PUE)
• Thermal efficiency
• Vapor-compression refrigeration
• Air conditioner
• HVAC

Notes[edit]

External links[edit]

• Discussion on changes to COP of a heat pump depending on input and output temperatures
• See COP definition in Cap XII of the book Industrial Energy Management — Principles and Applications^{[permanent dead link]}

The coefficient of performance or COP (sometimes CP or CoP) of a heat pump, refrigerator or air conditioning system is a ratio of useful heating or cooling provided to work (energy) required.^[1][2] Higher COPs equate to higher efficiency, lower energy (power) consumption and thus lower operating costs.

The COP usually exceeds 1, especially in heat pumps, because, instead of just converting work to heat (which, if 100% efficient, would be a COP of 1), it pumps additional heat from a heat source to where the heat is required. Most air conditioners have a COP of 2.3 to 3.5. Less work is required to move heat than for conversion into heat, and because of this, heat pumps, air conditioners and refrigeration systems can have a coefficient of performance greater than one.

However, this does not mean that they are more than 100% efficient, in other words, no heat engine can have a thermal efficiency of 100% or greater. For complete systems, COP calculations should include energy consumption of all power consuming auxiliaries. The COP is highly dependent on operating conditions, especially absolute temperature and relative temperature between sink and system, and is often graphed or averaged against expected conditions.^[3]

Performance of absorption refrigerator chillers is typically much lower, as they are not heat pumps relying on compression, but instead rely on chemical reactions driven by heat^{[citation needed]}.

Equation[edit]

The equation is:

where

The COP for heating and cooling are different because the heat reservoir of interest is different. When one is interested in how well a machine cools, the COP is the ratio of the heat taken up from the cold reservoir to input work. However, for heating, the COP is the ratio of the magnitude of the heat given off to the hot reservoir (which is the heat taken up from the cold reservoir plus the input work) to the input work:

where

Note that the COP of a heat pump depends on its direction. The heat rejected to the hot sink is greater than the heat absorbed from the cold source, so the heating COP is greater by one than the cooling COP.

Theoretical performance limits[edit]

According to the first law of thermodynamics, after a full cycle of the process and thus .
Since , we obtain

For a heat pump operating at maximum theoretical efficiency (i.e. Carnot efficiency), it can be shown^[5][4] that

and thus

where and are the thermodynamic temperatures of the hot and cold heat reservoirs, respectively.

At maximum theoretical efficiency, therefore

which is equal to the reciprocal of the thermal efficiency of an ideal heat engine, because a heat pump is a heat engine operating in reverse.^[6]

Similarly, the COP of a refrigerator or air conditioner operating at maximum theoretical efficiency,

applies to heat pumps and applies to air conditioners and refrigerators.
Measured values for actual systems will always be significantly less than these theoretical maxima.

In Europe, the standard test conditions for ground source heat pump units use 308 K (35 °C; 95 °F) for and 273 K (0 °C; 32 °F) for . According to the above formula, the maximum theoretical COPs would be

Test results of the best systems are around 4.5. When measuring installed units over a whole season and accounting for the energy needed to pump water through the piping systems, seasonal COP’s for heating are around 3.5 or less. This indicates room for further improvement.

The EU standard test conditions for an air source heat pump is at dry-bulb temperature of 20 °C (68 °F) for and 7 °C (44.6 °F) for .^[7] Given sub-zero European winter temperatures, real world heating performance is significantly poorer than such standard COP figures imply.

Improving COP[edit]

As the formula shows, the COP of a heat pump system can be improved by reducing the temperature gap minus at which the system works. For a heating system this would mean two things: 1) reducing the output temperature to around 30 °C (86 °F) which requires piped floor, wall or ceiling heating, or oversized water to air heaters and 2) increasing the input temperature (e.g. by using an oversized ground source or by access to a solar-assisted thermal bank ^[8] ). Accurately determining thermal conductivity will allow for much more precise ground loop ^[9] or borehole sizing,^[10] resulting in higher return temperatures and a more efficient system. For an air cooler, COP could be improved by using ground water as an input instead of air, and by reducing temperature drop on output side through increasing air flow. For both systems, also increasing the size of pipes and air canals would help to reduce noise and the energy consumption of pumps (and ventilators) by decreasing the speed of fluid which in turn lower the Reynolds number and hence the turbulence (and noise) and the head loss (see hydraulic head). The heat pump itself can be improved by increasing the size of the internal heat exchangers which in turn increase the efficiency (and the cost) relative to the power of the compressor, and also by reducing the system’s internal temperature gap over the compressor. Obviously, this latter measure makes such heat pumps unsuitable to produce high temperatures which means that a separate machine is needed for producing hot tap water.

The COP of absorption chillers can be improved by adding a second or third stage. Double and triple effect chillers are significantly more efficient than single effect, and can surpass a COP of 1. They require higher pressure and higher temperature steam, but this is still a relatively small 10 pounds of steam per hour per ton of cooling.^[11]

Example[edit]

A geothermal heat pump operating at a of 3.5 provides 3.5 units of heat for each unit of energy consumed (i.e. 1 kWh consumed would provide 3.5 kWh of output heat). The output heat comes from both the heat source and 1 kWh of input energy, so the heat-source is cooled by 2.5 kWh, not 3.5 kWh.

A heat pump with of 3.5, such as in the example above, could be less expensive to use than even the most efficient gas furnace except in areas where the electricity cost per unit is higher than 3.5 times the cost of natural gas (e.g. Connecticut or New York City).

A heat pump cooler operating at a of 2.0 removes 2 units of heat for each unit of energy consumed (e.g. an air conditioner consuming 1 kWh would remove 2 kWh of heat from a building’s air).

Given the same energy source and operating conditions, a higher COP heat pump will consume less purchased energy than one with a lower COP. The overall environmental impact of a heating or air conditioning installation depends on the source of energy used as well as the COP of the equipment. The operating cost to the consumer depends on the cost of energy as well as the COP or efficiency of the unit. Some areas provide two or more sources of energy, for example, natural gas and electricity. A high COP of a heat pump may not entirely overcome a relatively high cost for electricity compared with the same heating value from natural gas.

For example, the 2009 US average price per therm (100,000 British thermal units (29 kWh)) of electricity was $3.38 while the average price per therm of natural gas was $1.16.^[12] Using these prices, a heat pump with a COP of 3.5 in moderate climate would cost $0.97^[13] to provide one therm of heat, while a high efficiency gas furnace with 95% efficiency would cost $1.22^[14] to provide one therm of heat. With these average prices, the heat pump costs 20% less^[15] to provide the same amount of heat.

The COP of a heat pump operating at the Carnot efficiency has in its denominator the expression T_H — T_C. As the surroundings cool (T_C reducing) the denominator increases and COP reduces. Therefore, the colder the surroundings, the lower the COP of any heat pump. If the surroundings cool, say to 0 °F (-18 °C), COP falls in value below 3.5. Then, the same system costs as much to operate as an efficient gas heater. The yearly savings will depend on the actual cost of electricity and natural gas, which can both vary widely.

The above example applies only for an air source heat pump. The above example assumes that the heat pump is an air-source heat pump moving heat from outside to inside, or a water source heat pump that is simply moving heat from one zone to the other. For a water source heat pump, this would only occur if the instantaneous heating load on the condenser water system exactly matches the instantaneous cooling load on the condenser water system. This could happen during the shoulder season (spring or fall), but is unlikely in the middle of the heating season. If more heat is being withdrawn by the heat pumps that are in heating mode than is being added by the heat pumps that are in cooling mode, then the boiler (or other heat source) will add heat to the condenser water system. The energy consumption and cost associated with the boiler would need to be factored in to the above comparison. For a water source system, there is also energy associated with the condenser water pumps that is not factored in to the heat pump energy consumption in the example above.

Seasonal efficiency[edit]

A realistic indication of energy efficiency over an entire year can be achieved by using seasonal COP or seasonal coefficient of performance (SCOP) for heat. Seasonal energy efficiency ratio (SEER) is mostly used for air conditioning. SCOP is a new methodology that gives a better indication of expected real-life performance, using COP can be considered using the «old» scale. Seasonal efficiency gives an indication on how efficiently a heat pump operates over an entire cooling or heating season.^[16]

See also[edit]

• Seasonal energy efficiency ratio (SEER)
• Seasonal thermal energy storage (STES)
• Heating seasonal performance factor (HSPF)
• Power usage effectiveness (PUE)
• Thermal efficiency
• Vapor-compression refrigeration
• Air conditioner
• HVAC

Notes[edit]

External links[edit]

• Discussion on changes to COP of a heat pump depending on input and output temperatures
• See COP definition in Cap XII of the book Industrial Energy Management — Principles and Applications^{[permanent dead link]}

Запрос «КПД» перенаправляется сюда; см. также другие значения.

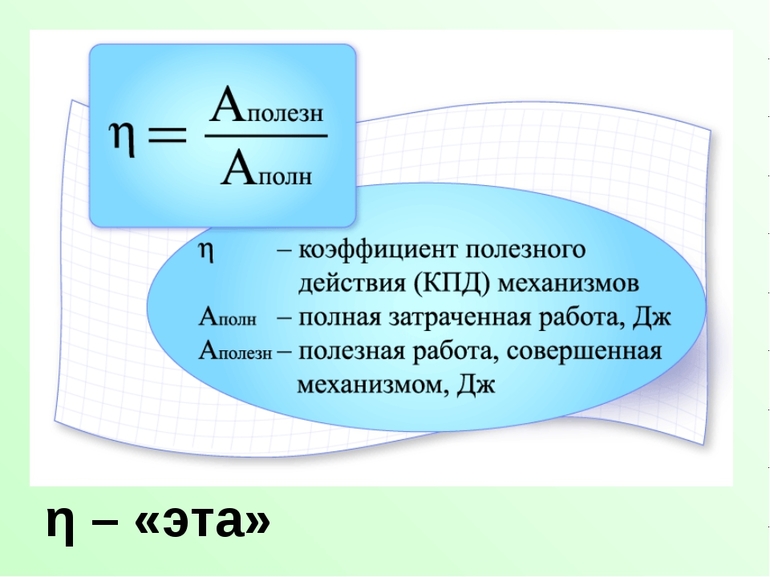
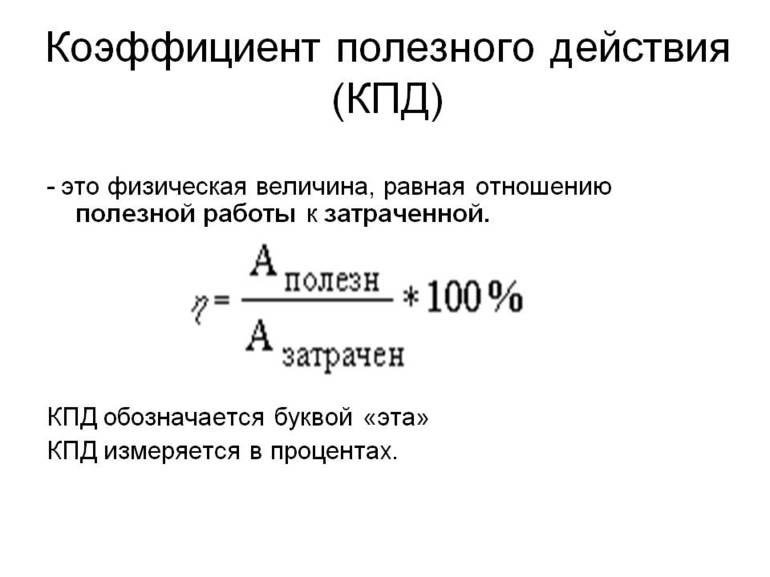
Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»). η = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде:

x 100 %,

где А — полезная работа, а Q — затраченная энергия.

В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии.

КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя, к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле

,

где  — количество теплоты, полученное от нагревателя,  — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах горячего источника T₁ и холодного T₂, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен

.

Другие похожие показатели

Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.

КПД котлов

Основная статья: Тепловой баланс котла

КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.

Тепловые насосы и холодильные машины

Достоинством тепловых насосов как нагревательной техники является возможность иногда получать больше теплоты, чем расходуется энергии на их работу; аналогичным образом холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается на организацию процесса.

Эффективность таких тепловых машин характеризуют холодильный коэффициент (для холодильных машин) или коэффициент трансформации (для тепловых насосов)

,

где  — тепло, отбираемое от холодного конца (в холодильных машинах) или передаваемое к горячему (в тепловых насосах);  — затрачиваемая на этот процесс работа (или электроэнергия). Наилучшими показателями производительности для таких машин обладает обратный цикл Карно: в нём холодильный коэффициент

,

где ,  — температуры горячего и холодного концов, K^[1]. Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент всё же может превосходить единицу. Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр. электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.

Литература

• Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7.

Примечания