A unit cube (side = 1) and a cube with twice the volume (side = 3√2 = 1.2599… OEIS: A002580).
In mathematics, a cube root of a number x is a number y such that y3 = x. All nonzero real numbers, have exactly one real cube root and a pair of complex conjugate cube roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8, denoted ![{displaystyle {sqrt[{3}]{8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/513fcbe75ae8a28fbf5b6a762df26f92fa74ff1a)
, is 2, because 23 = 8, while the other cube roots of 8 are 
and 
. The three cube roots of −27i are
In some contexts, particularly when the number whose cube root is to be taken is a real number, one of the cube roots (in this particular case the real one) is referred to as the principal cube root, denoted with the radical sign ![{displaystyle {sqrt[{3}]{~^{~}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cad47b3b9eed327000ea93a2a0f0eec715bf0e27)
The cube root is the inverse function of the cube function if considering only real numbers, but not if considering also complex numbers: although one has always ![{displaystyle left({sqrt[{3}]{x}}right)^{3}=x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21ec18fc45aa08e653a9c21432184bc7ff422b0b)
the cube of a nonzero number has more than one complex cube root and its principal cube root may not be the number that was cubed. For example, 
, but ![{displaystyle {sqrt[{3}]{8}}=2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4a48fd5e8236aac9e692a05eace9e32816df87e)
Formal definition[edit]
The cube roots of a number x are the numbers y which satisfy the equation
Properties[edit]
Real numbers[edit]
For any real number x, there is one real number y such that y3 = x. The cube function is increasing, so does not give the same result for two different inputs, and it covers all real numbers. In other words, it is a bijection, or one-to-one. Then we can define an inverse function that is also one-to-one. For real numbers, we can define a unique cube root of all real numbers. If this definition is used, the cube root of a negative number is a negative number.
The three cube roots of 1
If x and y are allowed to be complex, then there are three solutions (if x is non-zero) and so x has three cube roots. A real number has one real cube root and two further cube roots which form a complex conjugate pair. For instance, the cube roots of 1 are:
The last two of these roots lead to a relationship between all roots of any real or complex number. If a number is one cube root of a particular real or complex number, the other two cube roots can be found by multiplying that cube root by one or the other of the two complex cube roots of 1.
Complex numbers[edit]
Plot of the complex cube root together with its two additional leaves. The first image shows the main branch, which is described in the text.
Riemann surface of the cube root. One can see how all three leaves fit together.
For complex numbers, the principal cube root is usually defined as the cube root that has the greatest real part, or, equivalently, the cube root whose argument has the least absolute value. It is related to the principal value of the natural logarithm by the formula
If we write x as
where r is a non-negative real number and θ lies in the range
,
then the principal complex cube root is
![{displaystyle {sqrt[{3}]{x}}={sqrt[{3}]{r}}exp left({frac {itheta }{3}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b98750564191c9097532704595eaa97dd435633)
This means that in polar coordinates, we are taking the cube root of the radius and dividing the polar angle by three in order to define a cube root. With this definition, the principal cube root of a negative number is a complex number, and for instance 3√−8 will not be −2, but rather 1 + i√3.
This difficulty can also be solved by considering the cube root as a multivalued function: if we write the original complex number x in three equivalent forms, namely
![{displaystyle x={begin{cases}rexp(itheta ),\[3px]rexp(itheta +2ipi ),\[3px]rexp(itheta -2ipi ).end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24bbbc0717e25337093a26c26f3e911ab2505219)
Geometric representation of the 2nd to 6th roots of a complex number z, in polar form reiφ where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.
The principal complex cube roots of these three forms are then respectively
![{displaystyle {sqrt[{3}]{x}}={begin{cases}{sqrt[{3}]{r}}exp left({frac {itheta }{3}}right),\{sqrt[{3}]{r}}exp left({frac {itheta }{3}}+{frac {2ipi }{3}}right),\{sqrt[{3}]{r}}exp left({frac {itheta }{3}}-{frac {2ipi }{3}}right).end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b70d19b99d4bd3640e90ef97a5295704f825b49a)
Unless x = 0, these three complex numbers are distinct, even though the three representations of x were equivalent. For example, 3√−8 may then be calculated to be −2, 1 + i√3, or 1 − i√3.
This is related with the concept of monodromy: if one follows by continuity the function cube root along a closed path around zero, after a turn the value of the cube root is multiplied (or divided) by 
Impossibility of compass-and-straightedge construction[edit]
Cube roots arise in the problem of finding an angle whose measure is one third that of a given angle (angle trisection) and in the problem of finding the edge of a cube whose volume is twice that of a cube with a given edge (doubling the cube). In 1837 Pierre Wantzel proved that neither of these can be done with a compass-and-straightedge construction.
Numerical methods[edit]
Newton’s method is an iterative method that can be used to calculate the cube root. For real floating-point numbers this method reduces to the following iterative algorithm to produce successively better approximations of the cube root of a:
The method is simply averaging three factors chosen such that
at each iteration.
Halley’s method improves upon this with an algorithm that converges more quickly with each iteration, albeit with more work per iteration:
This converges cubically, so two iterations do as much work as three iterations of Newton’s method. Each iteration of Newton’s method costs two multiplications, one addition and one division, assuming that 1/3a is precomputed, so three iterations plus the precomputation require seven multiplications, three additions, and three divisions.
Each iteration of Halley’s method requires three multiplications, three additions, and one division,[1] so two iterations cost six multiplications, six additions, and two divisions. Thus, Halley’s method has the potential to be faster if one division is more expensive than three additions.
With either method a poor initial approximation of x0 can give very poor algorithm performance, and coming up with a good initial approximation is somewhat of a black art. Some implementations manipulate the exponent bits of the floating-point number; i.e. they arrive at an initial approximation by dividing the exponent by 3.[1]
Also useful is this generalized continued fraction, based on the nth root method:
If x is a good first approximation to the cube root of a and y = a − x3, then:
![{displaystyle {sqrt[{3}]{a}}={sqrt[{3}]{x^{3}+y}}=x+{cfrac {y}{3x^{2}+{cfrac {2y}{2x+{cfrac {4y}{9x^{2}+{cfrac {5y}{2x+{cfrac {7y}{15x^{2}+{cfrac {8y}{2x+ddots }}}}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53b1538138f23bc34e142a7a4fb13ca3c362922d)
The second equation combines each pair of fractions from the first into a single fraction, thus doubling the speed of convergence.
Appearance in solutions of third and fourth degree equations[edit]
Cubic equations, which are polynomial equations of the third degree (meaning the highest power of the unknown is 3) can always be solved for their three solutions in terms of cube roots and square roots (although simpler expressions only in terms of square roots exist for all three solutions, if at least one of them is a rational number). If two of the solutions are complex numbers, then all three solution expressions involve the real cube root of a real number, while if all three solutions are real numbers then they may be expressed in terms of the complex cube root of a complex number.
Quartic equations can also be solved in terms of cube roots and square roots.
History[edit]
The calculation of cube roots can be traced back to Babylonian mathematicians from as early as 1800 BCE.[2] In the fourth century BCE Plato posed the problem of doubling the cube, which required a compass-and-straightedge construction of the edge of a cube with twice the volume of a given cube; this required the construction, now known to be impossible, of the length 3√2.
A method for extracting cube roots appears in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the 2nd century BCE and commented on by Liu Hui in the 3rd century CE.[3] The Greek mathematician Hero of Alexandria devised a method for calculating cube roots in the 1st century CE. His formula is again mentioned by Eutokios in a commentary on Archimedes.[4] In 499 CE Aryabhata, a mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave a method for finding the cube root of numbers having many digits in the Aryabhatiya (section 2.5).[5]
See also[edit]
- Methods of computing square roots
- List of polynomial topics
- Nth root
- Square root
- Nested radical
- Root of unity
- Shifting nth-root algorithm
References[edit]
- ^ a b «In Search of a Fast Cube Root». metamerist.com. 2008. Archived from the original on 27 December 2013.
- ^ Saggs, H. W. F. (1989). Civilization Before Greece and Rome. Yale University Press. p. 227. ISBN 978-0-300-05031-8.
- ^ Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 213. ISBN 978-0-19-853936-0.
- ^ Smyly, J. Gilbart (1920). «Heron’s Formula for Cube Root». Hermathena. Trinity College Dublin. 19 (42): 64–67. JSTOR 23037103.
- ^ Aryabhatiya Archived 15 August 2011 at archive.today Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, ISBN 978-81-7434-480-9
External links[edit]
- Cube root calculator reduces any number to simplest radical form
- Computing the Cube Root, Ken Turkowski, Apple Technical Report #KT-32, 1998. Includes C source code.
- Weisstein, Eric W. «Cube Root». MathWorld.
A unit cube (side = 1) and a cube with twice the volume (side = 3√2 = 1.2599… OEIS: A002580).
In mathematics, a cube root of a number x is a number y such that y3 = x. All nonzero real numbers, have exactly one real cube root and a pair of complex conjugate cube roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8, denoted , is 2, because 23 = 8, while the other cube roots of 8 are and . The three cube roots of −27i are
In some contexts, particularly when the number whose cube root is to be taken is a real number, one of the cube roots (in this particular case the real one) is referred to as the principal cube root, denoted with the radical sign The cube root is the inverse function of the cube function if considering only real numbers, but not if considering also complex numbers: although one has always the cube of a nonzero number has more than one complex cube root and its principal cube root may not be the number that was cubed. For example, , but
Formal definition[edit]
The cube roots of a number x are the numbers y which satisfy the equation
Properties[edit]
Real numbers[edit]
For any real number x, there is one real number y such that y3 = x. The cube function is increasing, so does not give the same result for two different inputs, and it covers all real numbers. In other words, it is a bijection, or one-to-one. Then we can define an inverse function that is also one-to-one. For real numbers, we can define a unique cube root of all real numbers. If this definition is used, the cube root of a negative number is a negative number.
The three cube roots of 1
If x and y are allowed to be complex, then there are three solutions (if x is non-zero) and so x has three cube roots. A real number has one real cube root and two further cube roots which form a complex conjugate pair. For instance, the cube roots of 1 are:
The last two of these roots lead to a relationship between all roots of any real or complex number. If a number is one cube root of a particular real or complex number, the other two cube roots can be found by multiplying that cube root by one or the other of the two complex cube roots of 1.
Complex numbers[edit]
Plot of the complex cube root together with its two additional leaves. The first image shows the main branch, which is described in the text.
Riemann surface of the cube root. One can see how all three leaves fit together.
For complex numbers, the principal cube root is usually defined as the cube root that has the greatest real part, or, equivalently, the cube root whose argument has the least absolute value. It is related to the principal value of the natural logarithm by the formula
If we write x as
where r is a non-negative real number and θ lies in the range
- ,
then the principal complex cube root is
This means that in polar coordinates, we are taking the cube root of the radius and dividing the polar angle by three in order to define a cube root. With this definition, the principal cube root of a negative number is a complex number, and for instance 3√−8 will not be −2, but rather 1 + i√3.
This difficulty can also be solved by considering the cube root as a multivalued function: if we write the original complex number x in three equivalent forms, namely
Geometric representation of the 2nd to 6th roots of a complex number z, in polar form reiφ where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.
The principal complex cube roots of these three forms are then respectively
Unless x = 0, these three complex numbers are distinct, even though the three representations of x were equivalent. For example, 3√−8 may then be calculated to be −2, 1 + i√3, or 1 − i√3.
This is related with the concept of monodromy: if one follows by continuity the function cube root along a closed path around zero, after a turn the value of the cube root is multiplied (or divided) by
Impossibility of compass-and-straightedge construction[edit]
Cube roots arise in the problem of finding an angle whose measure is one third that of a given angle (angle trisection) and in the problem of finding the edge of a cube whose volume is twice that of a cube with a given edge (doubling the cube). In 1837 Pierre Wantzel proved that neither of these can be done with a compass-and-straightedge construction.
Numerical methods[edit]
Newton’s method is an iterative method that can be used to calculate the cube root. For real floating-point numbers this method reduces to the following iterative algorithm to produce successively better approximations of the cube root of a:
The method is simply averaging three factors chosen such that
at each iteration.
Halley’s method improves upon this with an algorithm that converges more quickly with each iteration, albeit with more work per iteration:
This converges cubically, so two iterations do as much work as three iterations of Newton’s method. Each iteration of Newton’s method costs two multiplications, one addition and one division, assuming that 1/3a is precomputed, so three iterations plus the precomputation require seven multiplications, three additions, and three divisions.
Each iteration of Halley’s method requires three multiplications, three additions, and one division,[1] so two iterations cost six multiplications, six additions, and two divisions. Thus, Halley’s method has the potential to be faster if one division is more expensive than three additions.
With either method a poor initial approximation of x0 can give very poor algorithm performance, and coming up with a good initial approximation is somewhat of a black art. Some implementations manipulate the exponent bits of the floating-point number; i.e. they arrive at an initial approximation by dividing the exponent by 3.[1]
Also useful is this generalized continued fraction, based on the nth root method:
If x is a good first approximation to the cube root of a and y = a − x3, then:
The second equation combines each pair of fractions from the first into a single fraction, thus doubling the speed of convergence.
Appearance in solutions of third and fourth degree equations[edit]
Cubic equations, which are polynomial equations of the third degree (meaning the highest power of the unknown is 3) can always be solved for their three solutions in terms of cube roots and square roots (although simpler expressions only in terms of square roots exist for all three solutions, if at least one of them is a rational number). If two of the solutions are complex numbers, then all three solution expressions involve the real cube root of a real number, while if all three solutions are real numbers then they may be expressed in terms of the complex cube root of a complex number.
Quartic equations can also be solved in terms of cube roots and square roots.
History[edit]
The calculation of cube roots can be traced back to Babylonian mathematicians from as early as 1800 BCE.[2] In the fourth century BCE Plato posed the problem of doubling the cube, which required a compass-and-straightedge construction of the edge of a cube with twice the volume of a given cube; this required the construction, now known to be impossible, of the length 3√2.
A method for extracting cube roots appears in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the 2nd century BCE and commented on by Liu Hui in the 3rd century CE.[3] The Greek mathematician Hero of Alexandria devised a method for calculating cube roots in the 1st century CE. His formula is again mentioned by Eutokios in a commentary on Archimedes.[4] In 499 CE Aryabhata, a mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave a method for finding the cube root of numbers having many digits in the Aryabhatiya (section 2.5).[5]
See also[edit]
- Methods of computing square roots
- List of polynomial topics
- Nth root
- Square root
- Nested radical
- Root of unity
- Shifting nth-root algorithm
References[edit]
- ^ a b «In Search of a Fast Cube Root». metamerist.com. 2008. Archived from the original on 27 December 2013.
- ^ Saggs, H. W. F. (1989). Civilization Before Greece and Rome. Yale University Press. p. 227. ISBN 978-0-300-05031-8.
- ^ Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 213. ISBN 978-0-19-853936-0.
- ^ Smyly, J. Gilbart (1920). «Heron’s Formula for Cube Root». Hermathena. Trinity College Dublin. 19 (42): 64–67. JSTOR 23037103.
- ^ Aryabhatiya Archived 15 August 2011 at archive.today Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, ISBN 978-81-7434-480-9
External links[edit]
- Cube root calculator reduces any number to simplest radical form
- Computing the Cube Root, Ken Turkowski, Apple Technical Report #KT-32, 1998. Includes C source code.
- Weisstein, Eric W. «Cube Root». MathWorld.
Как же писать квадратный, кубический и четвёртый корни?
Если вам нужно написать, к примеру, технический текст, возникает вопрос: «как написать символы, которых нет на клавиатуре?» Одним из таких символов является корень или радикал.
Наверняка вы замечали, что на многих сайтах используется этот обозначение. И это неудивительно, ведь подобными возможностями обладают все без исключения текстовые редакторы, а если быть точнее, суть вопроса заключается именно в клавиатуре.
Как написать корень на клавиатуре? – всё очень просто! Хоть знак «корень» на клавиатуре и не расположен, его всё-таки можно написать: для этого существует даже не один, а несколько способов. Рассмотрим их подробнее:
- Способ №1. Используя горячие клавиши клавиатуры (Alt-код, т.е. первая клавиша в коде — Alt).
- Способ №2. Используя 10-й код (HTML-код).
- Способ №3. Используя 16-й код (Юникод).
Обратите внимание! Для того чтобы воспользоваться способом №1, вы должны нажать и удерживать клавишу Alt, после чего начать ввод числового кода с использованием дополнительных цифровых клавиш (расположены на правой части клавиатуры).
Перед тем как ввести числовой код, убедитесь, что цифровые клавиши включены (индикатор NumLk должен гореть). 10-й и 16-й коды можно не вводить, а просто скопировать из таблицы и вставить в том месте, где вам нужно.
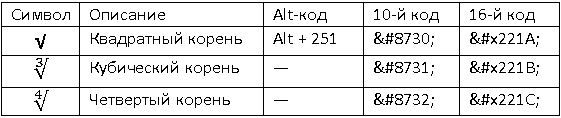
√ Квадратный корень Alt + 251 √ √∛ Кубический корень — ∛ ∛∜ Четвертый корень — ∜ ∜
Теперь вы знаете, как писать корень на клавиатуре – для этого нужно запомнить комбинацию «Alt+251». Точнее, нужно удерживать клавишу Alt, после чего на цифровых клавишах нажать 2, 5, 1 и отпустить Alt.
Если вы всё сделали верно, на экране появится знак корня. Выглядит он следующим образом: √ (вы также можете просто скопировать его отсюда). Так самому можно писать и другие самые разные смайлики в ворде и других текстовых редакторах.
Вы можете воспользоваться и помощью поисковика Google. Для этого просто введите в поиск то, что вы ищите (к примеру, знак корня), после чего просто его скопировать.
Если у вас возникли какие-либо проблемы (на вашем ноутбуке нет расположенных справа цифровых клавиш и т. д.), достаточно нажать Пуск и перейти в таблицу символов. В зависимости от Windows таблица символов может находиться как в разделе с приложениями, так и в разделе «Стандартные».
Выглядит знак корня следующим образом: √ (вы также можете просто скопировать его отсюда).
На данной странице описаны правила ввода функций, которых следует придерживаться в онлайн калькуляторах для решения производных и решения интегралов.
Не забывайте проверять правильность написания формул. Неточность и ошибки в написании, приводят к неверному ответу и ситуациям, при которых калькулятор отказывается проводить вычисления.
|
Оператор |
Описание |
|
Простейшие математические операции |
|
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * — необязателен: выражение 2sin(3 x ) эквивалентно 2*sin(3* x ). |
|
0.5 |
Десятичные дроби записываются через точку:
|
|
Элементарные функции |
|
|
x ^ n |
Возведение в степень:
xn , например x ^2 значит x 2 |
|
sqrt( x ) |
Квадратный корень: √
x . Эквивалентно root(x ,2) или x ^(1/2) |
|
cbrt( x ) |
Кубический корень: 3√
x . Эквивалентно root(x ,3) или x ^(1/3) |
|
root( x , n ) |
Корень
n -той степени из x . Эквивалентно x ^(1/ n ) |
|
log( a , x ) |
Логарифм от
x по основанию a |
|
ln( x ) |
Натуральный логарифм (логарифм c основанием
e ) |
|
lg( x ) |
Десятичный логарифм (логарифм по основанию 10) |
|
exp( x ) |
Экспоненциальная функция, эквивалентно
e ^ x |
|
Тригонометрические функции |
|
|
sin( x ) |
Синус от
x |
|
cos( x ) |
Косинус от
x |
|
tg( x ) |
Тангенс от
x . Можно вводить tg( x ) или tan( x ) |
|
ctg( x ) |
Котангенс от
x . Можно вводить ctg( x ) или cot( x ) |
|
sec( x ) |
Секанс от
x , определяется как 1/cos( x ) |
|
csc( x ) |
Косеканс от
x , определяется как 1/sin( x ) |
|
arcsin( x ) |
Арксинус от
x . Можно вводить arcsin( x ) или asin( x ) |
|
arccos( x ) |
Арккосинус от
x . Можно вводить arccos( x ) или acos( x ) |
|
atan( x ) |
Арктангенс от
x . Можно вводить arctg( x ) или atan( x ) |
|
arcctg( x ) |
Арккотангенс от
x . Можно вводить arcctg( x ) или acot( x ) |
|
asec( x ) |
Арксеканс от
x |
|
acsc( x ) |
Арккосеканс от
x |
|
Некоторые константы |
|
|
e |
Число Эйлера
e = 2.718281828459045… |
|
pi |
Число
π = 3.141592653589793… |
Здравствуйте, друзья! Сегодня я покажу вам как на клавиатуре поставить знак корня. А также как поставить знак корня третьей степени. Если вам часто на компьютере или ноутбуке приходится работать в текстовых документах с формулами, то вам эти знания пригодятся. Способ который я покажу ниже работает во всех форматах текстовых документах. В том числе и в Google Docs.
Как на клавиатуре поставить знак квадратного корня
Для того чтобы на клавиатуре поставить знак квадратного корня, нужно включить правую дополнительную панель с цифрами. Она включается нажатием клавиши «Num Lock». Если у вас ноутбук маленького размера или нетбук, у вас может не быть такой панели.
На самом деле она есть. Просто цифры в ней располагаются на тех же клавишах, что и буквы. Как включить в этом случае дополнительную панель читайте вот в этой статье. А сейчас о том как поставить знак корня на клавиатуре. Знак корня немного отличается от привычного. Выглядит он вот так — √. Тем не менее, если вы пишите формулу, то сразу понятно, что это именно знак корня квадратного.
Итак, чтобы на клавиатуре поставить такой знак, нужно нажать клавишу «Alt». Не отпуская клавиши «Alt» набрать в правой колонке с цифрами по очереди 2, 5, 1. После чего отпустить клавишу «Alt». В том месте где в текстовом документе стоял курсор появится знак квадратного корня √.
Ставим знак кубического корня ³√
Чтобы поставить на клавиатуре знак кубического корня ³√, придётся, что называется, немного повозиться. Для того чтобы вы не путались с этой операцией, я разобью её на пункты. Итак, для того чтобы поставить знак кубического корня, необходимо выполнить следующие действия.
- Перевести клавиатуру на английскую (латинскую) раскладку
- Нажать клавишу «Alt»
- Удерживая клавишу «Alt» набрать в правой колонке с цифрами по очереди цифры 0, 1, 7, 9
- Отпустить клавишу «Alt». У вас появится на месте, где стоял курсор знак степени ³
- Поставить знак корня указанным выше способом. При этом менять раскладку клавиатуры не обязательно.
После выполнения действий описанных выше у вас получится знак кубического корня ³√. Как вы сами видите знак кубического корня на клавиатуре ставить не очень-то удобно. Поэтому, если в вашем тексте таких знаков много, можно просто его скопировать и проставлять дальше в тех местах где он вам нужен.
Всё, друзья. Как поставить знак корня квадратного и кубического я вам показал. Надеюсь, что эта информация вам поможет.
А я на этом с вами прощаюсь. Всем удачи и до встречи!
У ряда пользователей, активно работающих с математикой, статистикой и прочими точными науками может возникнуть потребность набрать на клавиатуре символ корня √. При этом ни на одной из кнопок клавиатуры нет изображения подобного символа, и пользователь задаётся вопросом: как же осуществить подобное? В этом материале я помогу таким пользователям расскажу о вводе корня на клавиатуре, поясню, какие методы для этого существуют, и как обозначить корни 3,4,5 степеней.
Содержание
- Как поставить знак квадратный корень на клавиатуре
- Как использовать таблицу символов
- Как обозначить степени корня 3,4,5 степени на клавиатуре
- Заключение
Как поставить знак квадратный корень на клавиатуре
Многие пользователи в решении вопроса о написании корня на ПК, используют суррогатный символ «^», расположенный на клавише 6 в верхней части клавиатуры (активируется переходом на английскую раскладку, нажатием клавиши Shift и кнопки «6» сверху).
Некоторые пользователи также пользуются буквосочетанием sqrt (для квадратных корней), cbrt (для кубических) и так далее.
При этом это хоть и быстрые, но недостаточные приёмы. Для нормального набора знака корня выполните следующее:
- Нажмите кнопку Num Lock (должен зажечься соответствующий индикатор);
- Нажмите и не отжимайте кнопку Alt;
- Наберите на цифровой клавиатуре справа 251 и отожмите клавишу;
- Вы получите изображение квадратного корня √.
Если вы не знаете, как ввести собаку с клавиатуры, тогда вам обязательно нужно ознакомить с подробной инструкцией по её вводу, так как при наборе E-mail почты без знака собачки не обойтись.
Как использовать таблицу символов
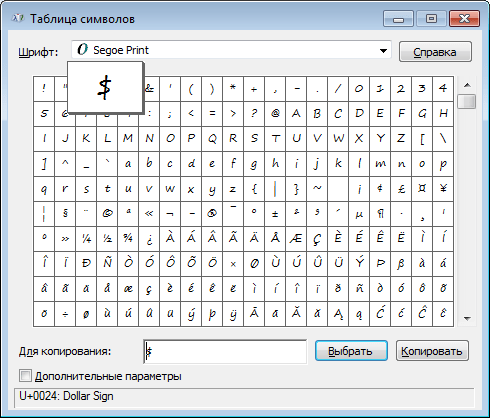
Альтернативой этому варианту является использование специальной таблицы символов, имеющейся в ОС Виндовс, позволяющей использовать корень на клавиатуре. Выполните следующее:
- Нажмите на «Пуск», затем выберите «Все программы»;
- Потом «Стандартные», затем «Служебные», где выберите «Таблица символов».
- Там найдите знак корня √, кликните на него, нажмите на кнопку «Выбрать», затем «Копировать» и скопируйте его в нужный вам текст с помощью клавиш Ctrl+V.
В текстовом редакторе Word (а также в Excel) также имеется соответствующая таблица символов, которую можно использовать для наших задач. Вы можете найти её, перейдя во вкладку «Вставка», и нажав на «Символ» справа, а затем и кликнув на надпись «Другие символы» чуть снизу, это поможет вам в решении вопроса написании корня в Ворде.
Можно, также, использовать опцию «Формула» во вкладке «Вставка» по описанному в данном ролике алгоритму.
Как обозначить степени корня 3,4,5 степени на клавиатуре
Например, корни 3,4,5 степени можно записать так:
X^1/3
X^1/4
X^1/5
Или так:
3√X (вместо числа 3 можете использовать соответствующее обозначение из таблицы символов (³)
4√X
5√X
При этом, несмотря на то, что в системе имеется изображение кубического корня ∛ и четвёртого корня ∜, набрать их через Alt и цифровые клавиши не получится. Это возможно лишь с помощью кодов десятичной системы HTML-код (∛ и ∜) и шестнадцатеричной Юникод (∛ и ∜). По мне, так лучше использовать формы обозначения, описанные мной чуть выше.
Заключение
В данном материале мной были описаны разные варианты написания корня на клавиатуре вашего компьютера. Самые нетерпеливые могут воспользоваться знаком ^, но точнее и правильнее будет, всё же, воспользоваться комбинацией клавиш Alt+251, и поставить знак корня таким, каким он обозначается в соответствии с общепризнанным стандартом символов.
∛ Кубический корень
Нажмите, чтобы скопировать и вставить символ
Значение символа
Кубический корень. Математические операторы.
Символ «Кубический корень» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 221B |
| Простое изменение регистра | 221B |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 88 9B | 226 136 155 | 14846107 | 11100010 10001000 10011011 |
| UTF-16BE | 22 1B | 34 27 | 8731 | 00100010 00011011 |
| UTF-16LE | 1B 22 | 27 34 | 6946 | 00011011 00100010 |
| UTF-32BE | 00 00 22 1B | 0 0 34 27 | 8731 | 00000000 00000000 00100010 00011011 |
| UTF-32LE | 1B 22 00 00 | 27 34 0 0 | 455213056 | 00011011 00100010 00000000 00000000 |
Тем, кто собирается писать курсовую работу, диплом или любой другой технический текст, могут пригодиться символы, отсутствующие на клавиатуре. В их числе – значок квадратного, кубического корня, корня четвертой степени и пр. На самом деле, вставить в текст этот символ – радикал — не так сложно, как кажется. Давайте разберемся, как пишется корень на клавиатуре.
Способ №1
Этот способ подойдет для отображения значка квадратного корня, в случае которого показатель степени 2 обычно опускается.
- Установите курсор там, где необходимо вставить значок корня.
- Откройте в Word вкладку «Вставка»;
- Найдите графу «Символ» и выберите «Другие символы»;
- Выберите строку «Математические операторы» и найдите среди появившихся знаков необходимый вам вариант. Нажимаем «Вставить».
Если символ корня вам нужно вставить не один раз, то пользоваться этой функцией весьма удобно. Все ранее использованные значки отображаются непосредственно под кнопкой «Символ».
Способ №2
Способ №2Этот способ пригоден для отображения не только квадратного, но еще и кубического корня и корня четвертой степени.
- Установите курсор там, где необходимо вставить значок корня;
- Откройте в Word вкладку «Вставка»;
- Найдите графу «Формула»;
- В открывшемся конструкторе с левой стороны вы увидите все виды корней;
- Выберите необходимый значок и нажмите на него – он появится в указанной ранее строке текста. В пустом окошке под значком корня введите подкоренное выражение. Готово!
Способ №3
Для отображения корня любой степени удобно использовать следующий способ:
- Установите курсор там, где необходимо вставить значок корня;
- Откройте в Word вкладку «Вставка»;
- Найдите графу «Объект» и найдите в открывшемся окошке строку «Microsoft Equation 3.0».
- В выпавшем поле найдите графу «Шаблоны дробей и радикалов» и нажмите на значок корня.
- Выберите необходимый вариант корня и нажмите на него – он появится в тексте. В пустые окошки символа введите подкоренное выражение и показатель степени. Вы также можете выбрать в списке значок квадратного корня.
Способ №4
Этот способ не требует применения специальных функций Word – все необходимое для написания квадратного корня есть на самой клавиатуре.
- Убедитесь, что вы активировали цифры в правой части клавиатуры. Чтобы включить цифровой блок, нажмите кнопку Num Lock. Обычно она находится в правом верхнем углу цифрового блока клавиатуры.
- Если блока цифр у вас нет (например, на ноутбуке), то Num Lock может быть активирован с помощью комбинации клавиш – например, Fn+F8 или Fn+F11 (последняя клавиша в может отличаться в зависимости от производителя или модели вашего ноутбука).
- Зажмите клавишу Alt и на активированной цифровой клавиатуре нажмите подряд цифры 2, 5 и 1. То есть, нажмите сочетание Alt+251. Вы увидите, как в указанном месте появился значок корня.
Еще один вариант внесения символа квадратного корня в текст заключается в следующем.
- «Пуск»->«Все программы»->«Стандартные»->«Служебные»->«Таблица символов»;
- В появившейся таблице отыщите нужный значок и нажмите на него. Затем нажимаем «Выбрать» (значок появится в строке для копирования) и «Копировать»;
- С помощью сочетания клавиш Ctrl+C скопируйте корень в необходимую строчку в тексте.
Теперь вы знаете, как пишется корень на клавиатуре. Как видите, существует немало способов внесения данного математического символа в текст, и все они довольно простые.
© Lifeo.ru