Раздел: Стандартные функции Паскаля
Функция Sqrt в Паскале вычисляет квадратный корень числа. Синтаксис функции следующий:
function Sqrt(Х : ValReal) : ValReal;
Эта функция возвращает квадратный корень числа, переданного через параметр Х. Число Х должно быть положительным, иначе произойдёт ошибка во время выполнения программы (так написано в документации, но в моей версии компилятора ошибки не происходит, а функция в случае отрицательного параметра возвращает значение NaN).
Функция Sqr в Паскале вычисляет квадрат числа. Синтаксис функции для разных типов приведён ниже:
function Sqr(Х : LongInt) : LongInt; function Sqr(Х : QWord) : QWord; function Sqr(Х : ValReal) : ValReal;
Эта функция возвращает результат вычисления квадрата числа, переданного через параметр. То есть Sqr = х * х.
О типе ValReal я рассказывал здесь.
Квадрат числа
Здесь всё крайне просто. Квадрат числа Х равен произведению Х на Х. То есть функция Sqr на первый взгляд кажется бесполезной. Потому что во многих случаях проще написать так:
Х := Х * Х
чем
Х := Sqr(X)
Единственный случай, когда использование функции Sqr является обоснованным с точки
зрения упрощения кода, это когда в качестве параметра передаётся вещественное число
(константа) с большим количеством знаков после запятой, или очень большое целое число, или сложное выражение. Например:
Х := Sqr(5.3456753322)
будет написать проще, чем
Х := 5.3456753322 * 5.3456753322
Также возведение в квадрат числа в Паскале сложного выражения тоже будет проще, если использовать функцию Sqr:
X := Sqr(Y + 100 * Z / X)
Вычисление квадратного корня
Когда мы изучали функции вычисления экспоненты и
натурального логарифма, то мы узнали, что с их помощью можно возвести число в любую степень. То есть вычислить, в том числе, и корень любой степени.
Однако использование этих функций всё-таки немного сложновато. Поэтому для вычисления квадратного корня в Паскале имеется специальная функция (потому что квадратный корень приходится вычислять намного чаще, чем, например, корень n-й степени).
Эту функцию вы уже знаете — это функция Sqrt.
А здесь я напомню что такое квадратный корень для тех, кто подзабыл математику.
Итак, квадратный корень из числа А (корень 2-й степени) — это решение уравнения:
Х2 = А
То есть квадратный корень из числа А, это число Х, которое при возведении в квадрат даёт число А.
То есть если
Х * Х = √А
то
Х = А
ВАЖНО!
Число А может быть только положительным числом. Извлечение корня из отрицательного числа тоже возможно, но это уже будут комплексные числа.
|
|
Как стать программистом 2.0
Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… |
|
|
Помощь в технических вопросах
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. |

Многие начинающие программисты задаются подобный вопросом : «Какие операции можно совершать с числами в языке программирования паскаль ?». В данном уроке мы подробно ответим на этот вопрос.
Арифметические операции
Начнем , пожалуй , с самого простого — арифметические операции с числами в паскале. В паскаль встроены многие привычные нам арифметические операции ( Сложение , вычитание , умножение , деление и т.п ).
Как же осуществляются подобные операции с числами ?. Давайте разберем это на примере исходника одной программы.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Результатом выполнения данной программы будет вывод на экран трех чисел
14 7 2
. Разберемся в том , как это работает.
В начале программы мы объявляем 2 целочисленные (
integer
) переменные «a» и «b» , а также 1 переменную «c» вещественного (
real
) типа.
Подробнее прочитать о
переменных в паскаль и их типах здесь
.
Зачем нам нужна вещественная переменная ? Для записи результата деления целочисленная переменная не подходит , так как у нас получается дробь , а не целое число.
Теперь мы присваиваем переменной «a» значение
7
, а переменной «b» значение
3
. Переменную «c» при этом оставляем нулевой ( она нам пока не понадобится ).
Далее (в блоке begin end) мы расписываем арифметические операции с нашими числами. Обратите внимание на то , что после символов // идет комментарий , который не компилируется программой.
Запомните
: Строка a:= a — b; выглядит так a:= 7 — 4; , а не так 7:= 7 — 4;
Другие операции с числами
В паскале предусмотрены и многие другие операции с числами. Давайте разберем самые популярные из них.
1. Как найти квадрат числа в паскале ?
Для нахождения квадрата числа в паскале предусмотрена функция sqr(x) , где x — число.
Пример :
Результат : переменной «а» присваивается значение 25.
2. Как найти корень числа в паскале ?
Для нахождения корня числа в паскале предусмотрена функция sqrt(x) , где x — число.
Пример :
Результат
: переменной «а» присваивается значение 5.
3. Как округлить число в паскале ?
Для того , чтобы округлить некоторое число используется операция round(x).
Пример :
Результат
: переменной «а» присваивается значение 9.
4. Как убрать дробную часть у числа в паскале ?
Для того , чтобы отбросить дробную часть числа используется операция trunc(x).
Пример :
Результат
: переменной «а» присваивается значение 25.
5. Как убрать целую часть у числа в паскале ?
Для того , чтобы отбросить целую часть числа используется операция frac(x).
Пример :
Результат
: переменной «а» присваивается значение 0.2.
6. Как получить модуль числа в паскале ?
Чтобы получить модуль некоторого числа используется операция abs(x).
Пример :
Результат
: переменной «а» присваивается значение 8.
Это были самые важные и часто используемые операции в паскале для работы с числами ( переменными ). Найти другие вы можете на
этой странице
.
Выводы :
Для работы с числами в паскале предусмотрено множество различных операций. Мы можем делать с числами все , что угодно ( складывать , умножать , возводить в квадрат и т.п ).
Этот раздел содержит описание математических операций, которыми можно пользоваться в выражениях на языке Паскаль. Вывести результат вычисления выражения можно такой нехитрой программе:
|
|
Конечно, результат вычисления выражения можно и записать в переменную для дальнейшего использования, и передать в другую функцию.
Не все операции и действия в этом разделе будут вам понятны. Ничего страшного — просто помните, что сюда можно вернуться, когда вам что-то понадобится.
Математические операции
В Паскале, как и в большинстве языков программирования, несколько специфически передаются основные математические операции — так математические выражения надо записывать в одну строку, а не в несколько уровней, как принято в классической математической нотации. Это достигается значительно более массовым использованием скобок, что иногда огорчает начинающих. Также всегда нужно писать знак умножения *. Кроме того, параметры функций всегда должны быть в скобках. Например:
| Математическое выражение | Запись на языке Паскаль |
| 2+2=4 | 2+2=4 |
|
|
a*(1+sqr(e))/2 |

|
(-b+sqrt(sqr(b)-4*a*c))/(2*a) |

|
exp(2*x+y) |

|
abs(cos(x)*sin(x)*cos(y)/tan(y))
или abs(cos(x)*sin(x)*cos(y)/(sin(y))/cos(y)) если компилятор не поддерживает Tan. |
Базовая арифметика
| Название операции | Оператор | Пример | Примечание |
| Добавление | + | 2+2 (=4) | |
| Вычитание | — | 18.3-11 (=7.3) | |
| Умножение | * | 7*8 (=56) | |
| Деление | / | 7/8 (=0.875) | Результат всегда действительного типа (real) |
| Целая часть деления | div | 7 div 2 (=3) | |
| Остаток от деления | mod | 7 mod 2 (=1) |
Сравнение
Все операции сравнения возвращают значение типа boolean, то есть могут использоваться в операторах ветвления и циклах, например
|
|
| Название операции | Оператор | Пример |
| Равно | = | 2+2=4 |
| Не равно (?) | <> | 2+2<>5 |
| Больше | > | 72>71.99 |
| Больше или Равно | >= | x*x>=0 |
| Меньше | < | 0<22 |
| Меньше или Равно | <= | 1<=1 |
Функции для преобразования действительных и целых чисел
Паскаль — язык программирования со статической сильной типизацией. Это означает, что компилятор не выполняет преобразований значений между типами, которые могут привести к потере информации; в частности, если подставить в конструкцию, предусматривает целое значение, действительное число, компилятор сообщит об ошибке, даже если это число имеет целое значение. Так, как мы видели выше, 13 and 11 равна 9, но выражение 13.0 and 11 вызовет сообщение компилятора об ошибке! Чтобы избежать этого, надо явно задавать преобразования действительного числа на целое с помощью следующих функций:
| Название функции | описание | пример |
|---|---|---|
| Round(X) | Возвращает целое значение, ближайшее к X | Round(1.7)=2, Round(-3.1)=-3 |
|
Int(X), Trunc(X) |
Возвращает целую часть X | Int(1.8)=1, Trunc(-11.3)=-11 |
| Floor(X) | Возвращает наибольшее целое значение, не превышает X | Floor(1.7)=1, Floor(-3.1)=-4 |
| Ceil(X) | Возвращает наименьшее целое значение, не менее от X | Ceil(1.7)=2, Ceol(-3.1)=-3 |
Логические и побитовые операции
Логические операции используются для объединения нескольких логических условий в одну.
| Название операции | оператор | пример | описание |
|---|---|---|---|
| Логическое И, and, логическое умножение | and | (2+3=5) and (0>-1) | Истинное, если оба операнда истинны |
| Логическое ИЛИ, or, логическое сложение | or | (2+2=5) or (1=1) | Истинное, если хотя бы один из операндов истинный |
| Логическое исключающее ИЛИ, eXclusive or | xor | (2+2=5) xor (1=1) | Истинное, если ровно один из операндов истинный |
| Отрицание, логическое НЕ, not | not | not (2+2=5) | Истинное, если операнд ложный |
Логические операторы, применены к целым типов, могут использоваться, как побитовые. Чтобы получить результат побитовой операции, надо представить операнды в двоичной системе (так, как они представлены в компьютере), после чего применить соответствующую операцию в соответствующих разрядов, причем 1 означает true 0 — false. так,
выведет 9, потому что
| 13 в двоичной системе будет | 1 | 1 | 1 | |||||
| 11 в двоичной системе будет | 1 | 1 | 1 | |||||
| 9 в двоичной системе будет | 1 | 1 |
Кроме того, есть еще две побитовых операции сдвига:
| Название операции | оператор | пример | описание |
|---|---|---|---|
| сдвиг вправо | shr | 14 shr 2 (=3) | Сдвигает двоичные разряды первого операнда справа на второй операнд разрядов;эквивалент целой части деления на степень 2 |
| смещение слева | shl | 7 shl 3 (=56) | Сдвигает двоичные разряды первого операнда слева на второй операнд разрядов;эквивалент умножению на степень 2 |
Алгебраические функции
Серым обозначены функции, которые не поддерживаются в Turbo Pascal
| Название функции | описание | Заменитель (для Turbo Pascal) |
|---|---|---|
| Pi |
Возвращает значение числа { displaystyle pi ~}
(+3,141592653589793238462643383279 … с точностью, определенным типом real) |
|
| Abs(X) | Абсолютное значение (модуль) X | |
| Sign(X) | Знак числа X: 1, если X отрицательный, 1, если положительный 0, если X = 0 | |
| Exp(X) | Экспонента X (e X) | |
| Ln(X) | Натуральный логарифм X | |
| Log2(X) | Логарифм X по основанию 2 | Ln(X)/Ln(2) |
| Log10(X) | Логарифм X по основанию 10 | Ln(X)/Ln(10) |
| LogN(X,Y) | Логарифм Y по основанию X | Ln(Y)/Ln(X) |
| Power(X,Y) | Степень X Y | Exp(Y*Ln(X)) |
| Sqrt(X) | Корень квадратный из X | |
| Sqr(X) | квадрат X | |
| Max(X,Y) | Более из значений X и Y | |
| Min(X,Y) | Меньше из значений X и Y |
Примечание: корень степени Y из числа X можно представить как X 1 / Y, и, соответственно, как Power (X, 1 / Y) или в Turbo Pascal как Exp (Ln (X) / Y).
Тригонометрические функции
Тригонометрические функции используют значения углов в радианах , будьте внимательны!
| Название функции | описание | Заменитель (для Turbo Pascal) |
|---|---|---|
| DegToRad (X) | Вычисляет радианной меру угла X, представленного в градусах | X * Pi / 180 |
| RadToDeg (X) | Вычисляет градусную меру угла X, представленного в радианах | X * 180 / Pi |
| Sin (X) | Синус X (X в радианах) | |
| Cos (X) | Косинус X (X в радианах) | |
| Tan (X) | Тангенс X (X в радианах) | Sin (X) / Cos (X) |
| ArcTan (X) | Арктангенс X, угол, тангенс которого равен X, в радианах | |
| ArcSin (X) | Арксинус X, угол, синус которого равен X, в радианах | ArcTan (X / sqrt (1-sqr (X))) |
| ArcCos (X) | Арккосинус X, угол, косинус которого равен X, в радианах | 2 * ArcTan ((1-X) / (1 + X)) |
| Sinh (X) | Гиперболический синус X | (Exp (X) -exp (-X)) / 2 |
| Cosh (X) | Гиперболический косинус X | (Exp (X) + exp (-X)) / 2 |
| Tanh (X) | Гиперболический тангенс X | (Exp (2 * X) -1) / (exp (2 * X) +1) |
Функции для работы со случайными величинами
Для имитации случайных процессов в Паскале есть генератор псевдослучайных чисел (ГПВЧ) и функции для работы с ним; такие числа достаточно непредсказуемыми для практического использования (то есть каждое последующее использование функции Random даст какой-то мере неожиданный результат), но их последовательность может быть полностью воспроизведена, если установить начальное значение ГПВЧ.
| Название функции | описание | Заменитель (для Turbo Pascal) |
|---|---|---|
| Randomize | Устанавливает начальное значение ГПВЧ равным текущему значению часов | |
| Randomize (X) | Устанавливает начальное значение ГПВЧ равным X | |
| Random | Возвращает псевдослучайное действительное число от 0 (включительно) до 1 (без включительно) | |
| Random (X) | Возвращает псевдослучайное целое число от 0 до X-1 | |
| Random (X, Y) | Возвращает псевдослучайное целое число от X до Y | X + Random (Y-X + 1) |
Функции для работы со сочтеными типами
Для величин сочтеных типов (все цели, буквенный, логическое и перечни) существуют также несколько удобных стандартных функций и процедур:
| Название функции | описание |
|---|---|
| Succ (X) | Возвращает значение, идет после X (для целых — X + 1, для буквенного — символ с последующим значением, для перечисления — следующее значение: так, Succ ( ‘A’) возвращает ‘B’ |
| Pred (X) | Возвращает, предшествующий X (для целых — X-1, для буквенного — символ с предыдущим значением, для перечисления — предварительное значение: так, Pred ( ‘A’) возвращает ‘@’ |
| Inc (X) | Увеличивает значение X на 1, эквивалент X = Succ (X) |
| Inc (X, N) | Увеличивает значение X на N, эквивалент N приложений Inc (X) |
| Dec (X) | Уменьшает значение X на 1, эквивалент X = Pred (X) |
| Dec (X, N) | Уменьшает значение X на N, эквивалент N применений Dec (X) |
| Ord (X) | Возвращает X (для нечисловых типов) |
| Odd (X) | Проверяет X на нечетность, true, если X нечетный или false, если X имеет четное значение |
Приоритет операций
Во время разбора математического выражения Паскаль сначала выполняет операции с высоким приоритетом, затем с низким, все справа налево. Так, в выражении 2 + 2 * 2 сначала будет вычислено 2 * 2 = 4, а уже затем 2 + 4 = 6 — так же, как в обычной математике; в выражении 10 mod 2 * 3 сначала будет выполнено 10 mod 2 = 0, а уже потом 0 * 3 = 0!
| операции | приоритет | вид операции |
|---|---|---|
| @ Not — + | Первый (высший) | Унарные операции (плюс и минус унарные, то есть только в форме -a, а не cd!) |
| * / Div mod and | второй | Операции типа умножение |
| + — or xor | третий | Операции вроде добавления |
| = <> <> <=> = In | четвертый | операции сравнения |
| () F () | Пятый (ниже) | Скобки, вызов функции |
[Всего голосов: 16 Средний: 3.7/5]
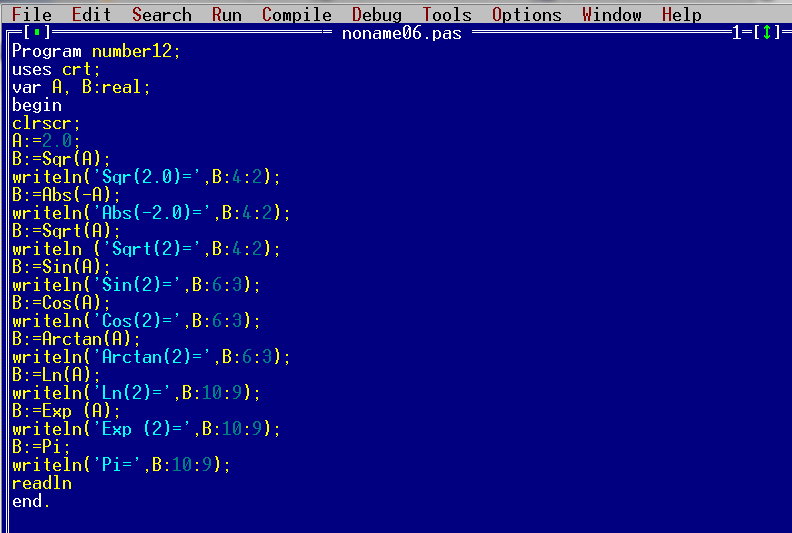
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.
Program number12;
uses crt;
var A, B:real;
begin
clrscr;
A:=2.0;
B:=Sqr(A);
writeln('Sqr(2.0)=',B:4:2);
B:=Abs(-A);
writeln('Abs(-2.0)=',B:4:2);
B:=Sqrt(A);
writeln ('Sqrt(2)=',B:4:2);
B:=Sin(A);
writeln('Sin(2)=',B:6:3);
B:=Cos(A);
writeln('Cos(2)=',B:6:3);
B:=Arctan(A);
writeln('Arctan(2)=',B:6:3);
B:=Ln(A);
writeln('Ln(2)=',B:10:9);
B:=Exp (A);
writeln('Exp (2)=',B:10:9);
B:=Pi;
writeln('Pi=',B:10:9);
readln
end.
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.
В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.
В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».
В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.
Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.
Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.
Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.
Строка №21. Функция Exp возводит число «e» (экспонента — 2.72…) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».
Строка №23. Переменной «B» будет присвоено значение числа «?».
Дополнение к материалу.
- Функции Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi определены только для вещественных (дробных) чисел.
- В Паскале не существует операции возведения в степень. Есть только операция возведения числа в квадрат (Sqr). Чтобы возвести число в степень используют операцию умножения. Например, чтобы возвести число 3 в 5-ю степень необходимо записать 3*3*3*3*3