Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.
Возведение в произвольную степень на Паскале
Требуется вычислить значение с = ab. В зависимости от значений
основания a и показателя степени b,
вычисление степени может быть реализовано по-разному.
Если a > 0, а b может принимать произвольные вещественные значения, используем известную формулу
ab = exp (b * ln a):
c:=exp(b*ln(a));
Если b — целое число (вообще говоря, «не слишком большое» по модулю),
а a — любое (не равное нулю при b < 0),
возведение в степень может быть реализовано с помощью цикла:
var i:integer;
{...}
c:=1;
for i:=1 to abs(b) do c:=c*a; {перемножение одинаковых сомножителей b раз}
if b<0 then c:=1/c; {учёт знака показателя}
Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:
c:=exp(b*ln(abs(a))); {степень положительного основания}
if (odd(b)=true) and (a<0) then c:=-c; {если основание отрицательно, а показатель нечетный, то меняем знак}
Вычисление корня произвольной степени на Паскале
Стандартная функция sqrt умеет извлекать только квадратный корень.
Извлечь корень степени n (где n — натуральное)
из числа a можно всегда, кроме случая, когда a < 0
и при этом n четно. Извлечь корень степени n
из числа a означает возвести число a в степень 1/n.
При этом знак корня совпадает со знаком a.
Ниже приводится код функции, вычисляющей корень произвольной степени
n от своего аргумента a:
function root(a:real;n:word):real;
{Тип word здесь указывает, что n положительно}
var r: real;
begin
r:=exp(ln(abs(a))/n); {корень из модуля}
if a<0 then root:=-r else root:=r {учет знака}
end;
Вычисление логарифмов на Паскале
Стандартная функция ln вычисляет только натуральный логарифм.
Для вычисления логарифмов по другим основаниям можно применить формулу
log a b = ln b / ln a:
c:=ln(b)/ln(a);
В частности, для вычисления десятичного логарифма lg b можно записать:
c:=ln(b)/ln(10);
Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале
В Паскале имеется стандартная функция arctan для вычисления арктангенса.
Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.
Для вычисления y = arcsin x, где, конечно, |x| <= 1,
можно применить один из следующих способов:
if x=1 then y:=pi/2 else if x=-1 then y:=-pi/2 else y:=arctan(x/sqrt(1-sqr(x)));
или
y:=2*arctan(x/(1+sqrt(1-sqr(x))));
на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).
Для вычисления z = arccos x, где |x| <= 1,
можно использовать тот факт, что
сумма арксинуса и арккосинуса некоторого значения
равна прямому углу:
if x=1 then z:=0 else if x=-1 then z:=pi else z:=pi/2-arctan(x/sqrt(1-sqr(x)));
или
z:=pi/2-2*arctan(x/(1+sqrt(1-sqr(x))));
Вычисление полярных углов на Паскале
Полярным углом точки с координатами (x,y),
отличной от начала координат,
называют угол между положительным направлением оси Ox и
направлением из начала координат на данную точку. При этом угол
отсчитывается против часовой стрелки.
Строго говоря, полярный угол не всегда
равен arctg (y/x), это верно лишь при x > 0.
Кроме того, при делении большого значения y на малое x
возможно переполнение. Показанная ниже функция вычисляет полярный угол fi,
лежащий в промежутке от -pi до +pi,
для любой точки с координатами (x,y), не совпадающей с началом координат:
function fi(x:real; y:real):real; var f:real; begin if abs(x)>abs(y) then begin f:=arctan(y/x); if x>0 then fi:=f else if y>=0 then fi:=f+pi else fi:=f-pi end else begin f:=arctan(x/y); if y>0 then fi:=pi/2-f else fi:=-pi/2-f end end;
Проблема с приведением типов на Паскале
Начинающие «паскалисты» нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие «баги». Вот простейший пример.
var a,b:integer;
r:longint;
begin
a:=1000;
b:=200;
r:=a*b;
writeln (r);
end.
Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer, а потом «испорченный» результат переписали в переменную типа Longint. ничего не изменит и
r:=Longint(a*b);
Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint. А вот
r:=Longint(a)*b;
рулит, получите свои 200000 
Раздел: Стандартные функции Паскаля
Функция Ln вычисляет натуральный логарифм. Для подзабывших математику о логарифмах расскажу чуть позже. А пока синтаксис:
function Ln(Х : ValReal) : ValReal;
Функция Ln X возвращает натуральный логарифм вещественного числа Х. Число Х должно
быть положительным — иначе случится ошибка времени выполнения. Хотя в моём случае
ошибка не возникает, просто функция возвращает результат “минус бесконечность”. Видимо,
это зависит от настроек компилятора.
О типе ValReal я рассказывал здесь.
Подробности см. в видео и читайте в статье далее.
А теперь немного математики.
Сначала вспомним, что такое логарифм.
Логарифм числа b по основанию a определяется
как показатель степени, в которую надо возвести основание a, чтобы
получить число b. Обозначение:
logab
То есть, чтобы вычислить логарифм числа b по основанию a, надо решить уравнение
ах = b
где а и b известны, а х — неизвестная величина.
Например,
log39 = 2
так как число 3 в степени 2 равно 9:
32 = 9
Теперь о натуральном логарифме, который и вычисляет функция Ln в Паскале.
Натуральный логарифм — это логарифм по основанию е. Где е — это иррациональная константа, которая равна приблизительно 2,72. То есть
ln x = logex
В FreePascal также есть другие функции для вычисления логарифмов:
- Log10 — вычисляет логарифм по основанию 10
- Log2 — вычисляет логарифм по основанию 2
- LogN — вычисляет логарифм по основанию N (в эту функцию передаются два параметра, сначала — основание N, затем число X)
- Lnxp1 — вычисляет натуральный логарифм по основанию Х+1
Но эти функции определены в модуле Math. То есть, чтобы воспользоваться этими функциями вам придётся подключить модуль Math к своей программе.
Такие вещи как область определения натурального логарифма Ln, производная, разложение в ряд Тейлора и прочие “ништяки” рассматривать не будем, так как это уже далеко выходит за сферу программирования.
А вот формулу, которая позволяет вычислить логарифм по произвольному основанию, используя только функцию Ln, я вам покажу:
logab = (ln b) / (ln a)
То есть, если вы не хотите подключать к вашей программе модуль Math, то это вам не помешает вычислить логарифм с любым основанием.
Пример собственной функции, которая является аналогом функции LogN из модуля Math, вы найдёте в исходном коде ниже.
program funcln;
uses Math;
var x : single;
function MyLogN(n, x : single) : single;
begin
MyLogN := Ln(x) / Ln(n);
end;
begin
x := Ln(2.718281828);
WriteLn('Ln(2.72) = Ln(e) =', x:0:4);
x := LogN(3, 9);
WriteLn('Log 3 (9) = ', x:0:4);
x := MyLogN(3, 9);
WriteLn('MyLog 3 (9) = ', x:0:4);
ReadLn;
end.
|
|
Как стать программистом 2.0
Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… |
|
|
Помощь в технических вопросах
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. |
-
Правила записи математических выражений, порядок действий и стандартные математические функции языка Паскаль.
Стандартные
математические функции Турбо Паскаля
Abs(x) —
Модуль аргумента
ArcTan(x)
— Арктангенс (значение в радианах)
Cos(x)
-Косинус, угол в радианах
Exp(x) —
Экспонента
Frac(x) —
Дробная часть числа
Int(x)
— Целая часть числа
Ln(x)
— Логарифм натуральный
Pi
– число π = 3,141592653
Sin(x)
— Синус, угол в радианах
Sqr(x)
— Тип аргумента Квадрат аргумента
Sqrt(x) —
Корень квадратный
Random
— Псевдослучайное число в интервале
[0, 1]
Random(I)
— Псевдослучайное число в интервале
[0, I]
Round(x)
— Округление до ближайшего целого
Trunc(x)
— Отбрасывание дробной части числа
Порядок
вычислений в выражениях следующий:
-
вычисляются
подвыражения, заключенные в скобки; -
затем
выполняются операции с наибольшим
приоритетом; обычно используются
следующие уровни приоритетов (в порядке
убывания):
-
возведение
в степень; -
мультипликативные
операции: * , / , div , mod; -
унарные
операции: + , — , abs , not; -
аддитивные
операции: +, -; -
операции
отношения: = ,<>, <, >, <=, >=; -
логические
операции: and, or, not;
-
операции
с одинаковым приоритетом выполняются
слева направо.
Хотя
нет ограничений на сложность выражений,
однако выражения, содержащие более 7
операндов, трудны для чтения и понимания
и поэтому такие выражения не рекомендуется
использовать.
Замечание
-
в
Паскале нет стандартной операции или
стандартной функции возведения в
степень, поэтому используется следующее
математическое тождество: xy= eylnx
-
в
Паскале существует только стандартная
функция вычисления натурального
логарифма, поэтому используется
следующее математическое тождество:
logab=
ln b/ln a
Математическое
выражение: x3/2 — 7x + tg (x+2)
Выражение
на Паскале: exp(3*ln(x)/2)-7*x+sin(x+2)/cos(x+2)
Операторы
действия
Операторы
действия — это средства языка, позволяющие
изменять в процессе выполнения программы
состояние вычислений. Самый простой
оператор действия — оператор присваивания.
<имя_переменной>:=<выражение>
-
Циклы языка Паскаль, их виды, отображение на схеме алгоритма и их программирование в языке Паскаль.
Алгоритм
циклической структуры — это алгоритм,
в котором происходит многократное
повторение одного и того же участка
программы. Такие повторяемые участки
вычислительного процесса называются
циклами. Программа циклической структуры
содержит один или несколько циклов.
Различают детерминированные циклы с
заранее известным числом повторений
и итерационные циклы, в которых число
повторений заранее неизвестно.
Изменяющаяся в цикле переменная
называется параметром цикла.
Для
организации цикла необходимо выполнить
следующие действия:
1)
задать перед циклом начальное значение
параметра цикла;
2)
изменять параметр перед каждым новым
повторением цикла;
3)
проверять условие повторения цикла;
4)
управлять циклом, т.е. переходить к его
началу, если он не закончен, или выходить
из него по окончании.
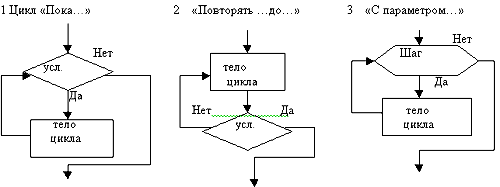
В
языке Паскаль существует 3 вида циклов:
1)
цикл с параметром или цикл типа for,
2)
цикл с предусловием или цикл типа while,
3)
цикл с постусловием или цикл типа repeat
… until.
В
цикле типа for число повторений известно
заранее, в циклах типа while и repeat … until
число повторений цикла заранее
неизвестно, производится проверка
условия повторения цикла: в цикле типа
while — перед циклом, в цикле типа repeat …
until — после его окончания.
В
циклах типов for и whileповторяющяся часть
(тело цикла) состоит из одного оператора,
если требуется выполнить в цикле
несколько операторов, они заключаются
в операторные скобки begin … end, образуя
составной оператор. В цикле типа repeat
… until тело цикла помещается между
зарезервированными словами языка
(лексемами) repeat и until, операторные скобки
не требуются, в названии цикла его тело
условно обозначается тремя точками.
С
помощью цикла типа for удобно находить
суммы, произведения, искать максимальные
и минимальные значения и т.п. При
нахождении суммы некоторой переменной,
например S присваивается значение 0,
затем в цикле к этой переменной
прибавляется соответствующий член
заданной последовательности. При
нахождении произведения переменной
присваивается значение 1, затем в цикле
эта переменная умножается на общий
член последовательности.
Цикл
повторяется до тех пор, пока условие
записанное после ключевого слова until,
будет ложным (не выполняется). Как только
это условие выполнится, происходит
выход из цикла. После окончания цикла
производится печать результата (оператор
writeln). Отметим, что цикл с предусловием
(типа while) может не выполниться ни разу,
цикл с постусловием repeat … untilвыполнится
по крайней мере 1 раз. Когда число
повторений цикла неизвестно заранее,
применяются циклы с предусловием или
с остусловием . Когда число повторений
цикла известно заранее, как правило,
применяется цикл типа for. Но любой цикл
типа for можно заменить циклом с
предусловием или постусловием.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


