In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle’s centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length.
The concept of a median extends to tetrahedra.
Relation to center of mass[edit]
Each median of a triangle passes through the triangle’s centroid, which is the center of mass of an infinitely thin object of uniform density coinciding with the triangle.[1] Thus the object would balance on the intersection point of the medians. The centroid is twice as close along any median to the side that the median intersects as it is to the vertex it emanates from.
Equal-area division[edit]
Each median divides the area of the triangle in half; hence the name, and hence a triangular object of uniform density would balance on any median. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.)[2][3] The three medians divide the triangle into six smaller triangles of equal area.
Proof of equal-area property[edit]
Consider a triangle ABC. Let D be the midpoint of 


By definition, 
![[ADO]=[BDO],[AFO]=[CFO],[BEO]=[CEO],](https://wikimedia.org/api/rest_v1/media/math/render/svg/c41ce8b3eb42658d71c1b8fea1b5c49236e14d38)
![{displaystyle [ABE]=[ACE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/982d360ca792eac215ab05f4a27cafd236e5e08d)
![[ABC]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb6e0eac43c0957f7bac6cea97995264c14e92a)

We have:
Thus, ![{displaystyle [ABO]=[ACO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/135d8ad9e40a48011db11e2a9ce986c08ba76d57)
![[ADO]=[DBO],[ADO]={frac {1}{2}}[ABO]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5cfa6dae8da4a18813cd4a1eff83561337427fa)
Since ![[AFO]=[FCO],[AFO]={frac {1}{2}}[ACO]={frac {1}{2}}[ABO]=[ADO]](https://wikimedia.org/api/rest_v1/media/math/render/svg/21d04654973bdf5a07477215dd6024f94d882699)
![{displaystyle [AFO]=[FCO]=[DBO]=[ADO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a6f454f7ae37d87eb2bf11b9f3603e8033b784c)
Using the same method, one can show that ![{displaystyle [AFO]=[FCO]=[DBO]=[ADO]=[BEO]=[CEO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc941c01f84772b16e9d1b65acec42f0a656fb6)
Three congruent triangles[edit]
In 2014 Lee Sallows discovered the following theorem:[4]
- The medians of any triangle dissect it into six equal area smaller triangles as in the figure above where three adjacent pairs of triangles meet at the midpoints D, E and F. If the two triangles in each such pair are rotated about their common midpoint until they meet so as to share a common side, then the three new triangles formed by the union of each pair are congruent.
Formulas involving the medians’ lengths[edit]
The lengths of the medians can be obtained from Apollonius’ theorem as:
where 



These formulas imply the relationships:[5]
Other properties[edit]
Let ABC be a triangle, let G be its centroid, and let D, E, and F be the midpoints of BC, CA, and AB, respectively. For any point P in the plane of ABC then[6]
The centroid divides each median into parts in the ratio 2:1, with the centroid being twice as close to the midpoint of a side as it is to the opposite vertex.
For any triangle with sides 

The medians from sides of lengths 


The medians of a right triangle with hypotenuse 

Any triangle’s area T can be expressed in terms of its medians 



Tetrahedron[edit]
medians of a tetrahedron
A tetrahedron is a three-dimensional object having four triangular faces. A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median of the tetrahedron. There are four medians, and they are all concurrent at the centroid of the tetrahedron.[10] As in the two-dimensional case, the centroid of the tetrahedron is the center of mass. However contrary to the two-dimensional case the centroid divides the medians not in a 2:1 ratio but in a 3:1 ratio (Commandino’s theorem).
See also[edit]
- Angle bisector
- Altitude (triangle)
- Automedian triangle
References[edit]
- ^ Weisstein, Eric W. (2010). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. pp. 375–377. ISBN 9781420035223.
- ^ Bottomley, Henry. «Medians and Area Bisectors of a Triangle». Archived from the original on 2019-05-10. Retrieved 27 September 2013.
- ^ Dunn, J. A., and Pretty, J. E., «Halving a triangle,» Mathematical Gazette 56, May 1972, 105-108. DOI 10.2307/3615256
- ^ Sallows, Lee, «A Triangle Theorem» Mathematics Magazine, Vol. 87, No. 5 (December 2014), p. 381
- ^ Déplanche, Y. (1996). Diccio fórmulas. Medianas de un triángulo. Edunsa. p. 22. ISBN 978-84-7747-119-6. Retrieved 2011-04-24.
- ^ Problem 12015, American Mathematical Monthly, Vol.125, January 2018, DOI: 10.1080/00029890.2018.1397465
- ^ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86–87.
- ^ Boskoff, Homentcovschi, and Suceava (2009), Mathematical Gazette, Note 93.15.
- ^ Benyi, Arpad, «A Heron-type formula for the triangle», Mathematical Gazette 87, July 2003, 324–326.
- ^ Leung, Kam-tim; and Suen, Suk-nam; «Vectors, matrices and geometry», Hong Kong University Press, 1994, pp. 53–54
External links[edit]
- The Medians at cut-the-knot
- Area of Median Triangle at cut-the-knot
- Medians of a triangle With interactive animation
- Constructing a median of a triangle with compass and straightedge animated demonstration
- Weisstein, Eric W. «Triangle Median». MathWorld.
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle’s centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length.
The concept of a median extends to tetrahedra.
Relation to center of mass[edit]
Each median of a triangle passes through the triangle’s centroid, which is the center of mass of an infinitely thin object of uniform density coinciding with the triangle.[1] Thus the object would balance on the intersection point of the medians. The centroid is twice as close along any median to the side that the median intersects as it is to the vertex it emanates from.
Equal-area division[edit]
Each median divides the area of the triangle in half; hence the name, and hence a triangular object of uniform density would balance on any median. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.)[2][3] The three medians divide the triangle into six smaller triangles of equal area.
Proof of equal-area property[edit]
Consider a triangle ABC. Let D be the midpoint of 


By definition, 
![[ADO]=[BDO],[AFO]=[CFO],[BEO]=[CEO],](https://wikimedia.org/api/rest_v1/media/math/render/svg/c41ce8b3eb42658d71c1b8fea1b5c49236e14d38)
![{displaystyle [ABE]=[ACE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/982d360ca792eac215ab05f4a27cafd236e5e08d)
![[ABC]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb6e0eac43c0957f7bac6cea97995264c14e92a)

We have:
Thus, ![{displaystyle [ABO]=[ACO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/135d8ad9e40a48011db11e2a9ce986c08ba76d57)
![[ADO]=[DBO],[ADO]={frac {1}{2}}[ABO]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5cfa6dae8da4a18813cd4a1eff83561337427fa)
Since ![[AFO]=[FCO],[AFO]={frac {1}{2}}[ACO]={frac {1}{2}}[ABO]=[ADO]](https://wikimedia.org/api/rest_v1/media/math/render/svg/21d04654973bdf5a07477215dd6024f94d882699)
![{displaystyle [AFO]=[FCO]=[DBO]=[ADO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a6f454f7ae37d87eb2bf11b9f3603e8033b784c)
Using the same method, one can show that ![{displaystyle [AFO]=[FCO]=[DBO]=[ADO]=[BEO]=[CEO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc941c01f84772b16e9d1b65acec42f0a656fb6)
Three congruent triangles[edit]
In 2014 Lee Sallows discovered the following theorem:[4]
- The medians of any triangle dissect it into six equal area smaller triangles as in the figure above where three adjacent pairs of triangles meet at the midpoints D, E and F. If the two triangles in each such pair are rotated about their common midpoint until they meet so as to share a common side, then the three new triangles formed by the union of each pair are congruent.
Formulas involving the medians’ lengths[edit]
The lengths of the medians can be obtained from Apollonius’ theorem as:
where 



These formulas imply the relationships:[5]
Other properties[edit]
Let ABC be a triangle, let G be its centroid, and let D, E, and F be the midpoints of BC, CA, and AB, respectively. For any point P in the plane of ABC then[6]
The centroid divides each median into parts in the ratio 2:1, with the centroid being twice as close to the midpoint of a side as it is to the opposite vertex.
For any triangle with sides 

The medians from sides of lengths 


The medians of a right triangle with hypotenuse 

Any triangle’s area T can be expressed in terms of its medians 



Tetrahedron[edit]
medians of a tetrahedron
A tetrahedron is a three-dimensional object having four triangular faces. A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median of the tetrahedron. There are four medians, and they are all concurrent at the centroid of the tetrahedron.[10] As in the two-dimensional case, the centroid of the tetrahedron is the center of mass. However contrary to the two-dimensional case the centroid divides the medians not in a 2:1 ratio but in a 3:1 ratio (Commandino’s theorem).
See also[edit]
- Angle bisector
- Altitude (triangle)
- Automedian triangle
References[edit]
- ^ Weisstein, Eric W. (2010). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. pp. 375–377. ISBN 9781420035223.
- ^ Bottomley, Henry. «Medians and Area Bisectors of a Triangle». Archived from the original on 2019-05-10. Retrieved 27 September 2013.
- ^ Dunn, J. A., and Pretty, J. E., «Halving a triangle,» Mathematical Gazette 56, May 1972, 105-108. DOI 10.2307/3615256
- ^ Sallows, Lee, «A Triangle Theorem» Mathematics Magazine, Vol. 87, No. 5 (December 2014), p. 381
- ^ Déplanche, Y. (1996). Diccio fórmulas. Medianas de un triángulo. Edunsa. p. 22. ISBN 978-84-7747-119-6. Retrieved 2011-04-24.
- ^ Problem 12015, American Mathematical Monthly, Vol.125, January 2018, DOI: 10.1080/00029890.2018.1397465
- ^ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86–87.
- ^ Boskoff, Homentcovschi, and Suceava (2009), Mathematical Gazette, Note 93.15.
- ^ Benyi, Arpad, «A Heron-type formula for the triangle», Mathematical Gazette 87, July 2003, 324–326.
- ^ Leung, Kam-tim; and Suen, Suk-nam; «Vectors, matrices and geometry», Hong Kong University Press, 1994, pp. 53–54
External links[edit]
- The Medians at cut-the-knot
- Area of Median Triangle at cut-the-knot
- Medians of a triangle With interactive animation
- Constructing a median of a triangle with compass and straightedge animated demonstration
- Weisstein, Eric W. «Triangle Median». MathWorld.
Медиана — это золотое сечение треугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.
У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.
И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.
Медиана — это…
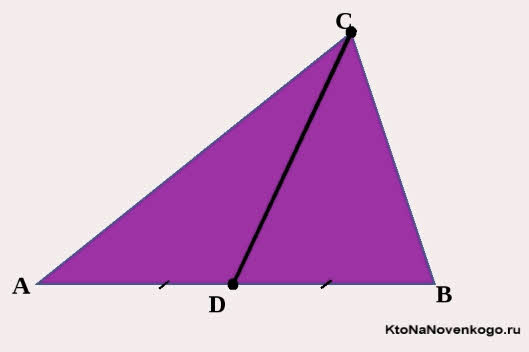
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.
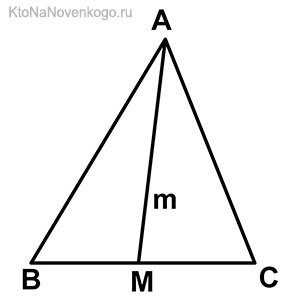
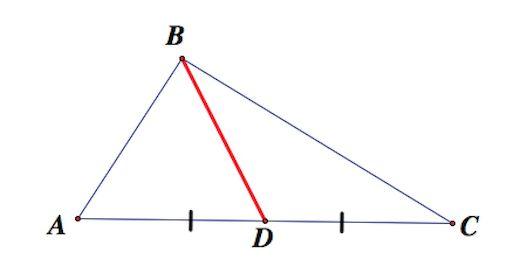
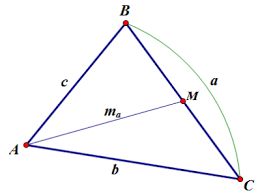
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.
Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.
Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.
Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:
Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.
Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.
И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!
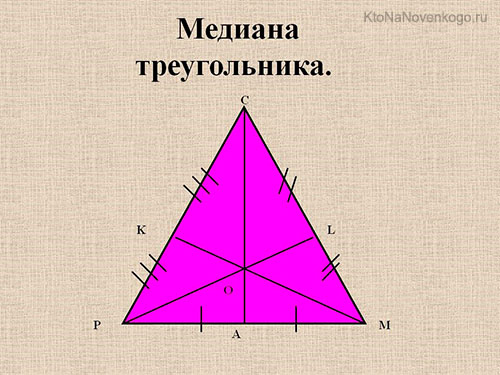
И выглядят они вот так.
На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.
Пересечение медиан треугольника
Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.
Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.
Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.
Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:
- Отрезок СО вдвое больше, чем отрезок АО;
- Отрезок РО вдвое больше, чем отрезок LO;
- Отрезок МО вдвое больше, чем КО.
Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.
Медиана равностороннего треугольника
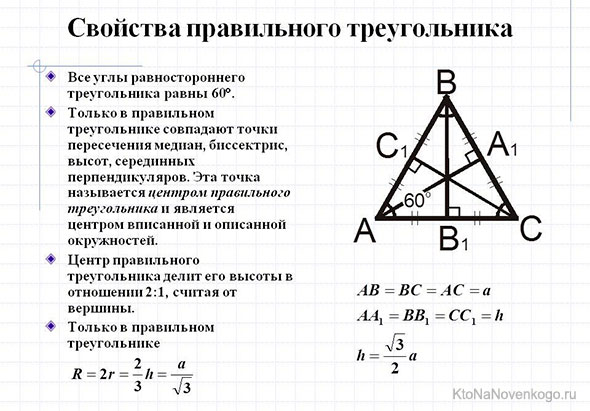
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.
Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.
Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.
И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.
Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.
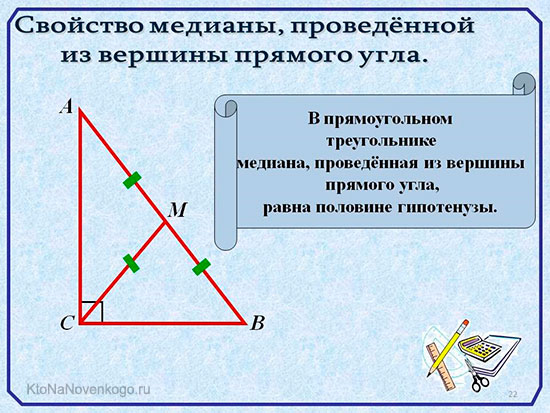
Медиана прямоугольного треугольника
Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.
Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.
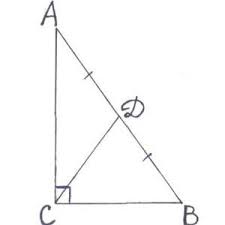
Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.
Вместо заключения
А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.
Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.
Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».
И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.
Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.
Треугольник как основа стереометрии
Помимо этого, в 10 и 11 классах в учебную программу добавляется так называемая стереометрия. Данный раздел геометрии отвечает за различные предметы в трехмерном пространстве. Если в классической планиметрии основой для всего является точка, то в стереометрии на первый план выходит ребро. Именно с его помощью и происходит построение большинства геометрических объектов в стереометрии. Но есть 1 тема, которая объединяет 2 разные раздела геометрии — треугольник и все, что с ним связано.
Большинство объектов в стереометрии состоят из множества небольших плоскостей с тремя или четырьмя углами, которые и являются основным объектом построения на ряду с ребром. Соответственно — для нахождения площади объемных шестиугольников, в первую очередь, необходимо знать все необходимые формулы и термины. Так, всего из одной вершины этой сложной геометрической фигуры можно прочертить сразу 4 различных прямых:
- Биссектрису;
- Перпендикуляр;
- Высоту;
- Медиану.
И если первая — просто делит угол пополам, а срединный перпендикуляр и высота зачастую являются одним понятием, медиана имеет множество своих индивидуальных и необычных признаков.
Медианой называют прямую, проведенную от угла до середины стороны, находящейся напротив выбранной вершины. Так, в зависимости от длины сторон, данный луч может соответствовать остальным отрезкам.
Важно! Также необходимо понимать, что, в отличие от перпендикуляра, прямая необязательно будет проведена к стороне под прямым углом. Благодаря этому, такой вид отрезков имеет несколько характерных только для него необычных свойств.
На плоскости медиана изображается как обычная линия, проведенная от вершины до противоположного угла.
Причем на стороне, которую прямая делит пополам, обычно слева и справа ставятся 2 маленькие черточки. С их помощью как раз и показывается, что получившиеся отрезки являются равными (рис.1).
Рис. 1. Медиана
Свойства
Медиана, независимо от типа треугольника, имеет 5 характерных черт:
- Если нарисовать из каждой вершины по одной прямой, то можно найти центр тяжести. Именно место пересечения всех 3 лучей и будет точкой равновесия.
- Также, переплетаясь, они рассекают объект на 6 одинаковых по площади сегментов.
- Исходя из этого, можно сделать вывод, что 1 луч рассекает треугольник на 2 куска с равной площадью. В случае равнобедренных треугольников и с равными сторонами получившиеся сегменты даже являются симметричными.
- Самой большей стороне соответствует самая маленькая прямая. В случае равносторонней фигуры, соответственно, все 3 будут иметь одну и ту же длину.
- Соединяясь, лучи делят друг друга в соотношении 1 к 2.
Специфические свойства
Как ни странно, благодаря наличию одинаковых по длине сторон, равнобедренные и равносторонние треугольники имеют некоторые необычные признаки:
- Во-первых, в равностороннем — медианы, пересекаясь, создают 6 не только равных по площади, но и идеально симметричных треугольника.
- Помимо этого, в случае объектов с равными сторонами, начерченная прямая является одновременно и высотой, и биссектрисой.
- В равнобедренных — линия, нарисованная к основанию, также одновременно является перпендикуляром, остальные же 2 — просто равны между собой.
Первоначально тема дается на изучение в 7 классе. Позже встретить ее можно как на ОГЭ, так и в ЕГЭ. Именно из-за присутствия в экзаменах сразу двух заданий, связанных с темой, так важно ее регулярное повторение. Смотрите также наглядный разбор всех свойств медианы в предложенном видео.
Тест для закрепления материала
-
1
Медиана – линия, которая:- Делит угол пополам
- Делит противоположную сторону пополам
- Расположена к противоположной стороне под прямым углом
-
2
В равностороннем треугольнике медиана также является:- Биссектрисой
- Высотой
- Биссектрисой и высотой
-
3
На сколько частей делят треугольник?- 3
- 6
- 12
-
4
Точка пересечения медиан является:- Центром вписанной окружности
- Центром описанной окружности
- Центром тяжести
-
5
В равнобедренном треугольнике все 3 медианы имеют одинаковую:- Длину
- Высоту
- Ширину
Доска почета
Чтобы сюда попасть — пройдите тест
Все тесты
- Английский язык
- Биология
- Политология
- Информатика
- Стихи
- Химия
- Правоведение
- Обществознание
- Экономика
- Биографии
- История
- Подготовка к ЕГЭ
- География
- Психология
- Сочинения
- Литература
- Пунктуация
- Фонетический разбор
- Орфография
- Окружающий мир
- Русский язык
-
Тест на тему
Почему английский язык является международным
5 вопросов
Последние результаты
Читайте также
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
-
Определение медианы треугольника
-
Свойства медианы
- Свойство 1 (основное)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
-
Примеры задач
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
- BF – медиана, проведенная к стороне AC.
- AF = FC
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
- AO = 2OE
- BO = 2OF
- CO = 2OD
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
S1 = S2
Свойство 3
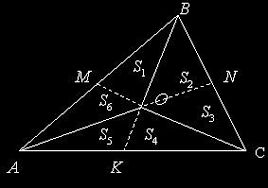
Три медианы делят треугольник на 6 равновеликих треугольников.
S1 = S2 = S3 = S4 = S5 = S6
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см2. Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см2 ⋅ 6 = 30 см2.
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Медиана треугольника

4.7
Средняя оценка: 4.7
Всего получено оценок: 375.
Обновлено 11 Января, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 375.
Обновлено 11 Января, 2021
Медиана треугольника, так же, как и высота, служит графическим параметром, определяющим весь треугольник, значение его сторон и углов. Три значения: медианы, высоты и биссектрисы – это, как штрих-код на товаре, наша задача – просто уметь его считать.
Опыт работы учителем математики — более 33 лет.
Определение
Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки.
Свойства медиан
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
- Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольников.
Равновеликими называют треугольники, площади которых равны.
- Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:
- В прямоугольном треугольнике известны катеты, которые равны a=3 и b=4. Найти значение медианы m, проведенной к гипотенузе c.
Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенузу находим через теорему Пифагора: $$a^2+b^2=c^2$$
$$c=sqrt{a^2+b^2}=sqrt{9+16}=sqrt{25}=5$$
Найдем значение медианы: $$m={cover2}={5over2}=2,5$$ – получившееся число и есть значение медианы.
Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.
- В треугольнике известны значения сторон : a=8; b=7; c=9. Найти значение медианы, опущенной к стороне b.
Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:
$$m^2 ={1over2}*(b^2+c^2-a^2)$$
Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это a, но может быть любая другая.
Подставим значения в формулу и найдем величину медианы: $$m=sqrt{{1over2}*(b^2+c^2-a^2)}$$
$$m=sqrt{{1over2}*(49+81-64)}=sqrt{33}$$ – оставим результат в виде корня.
- В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание – 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.
Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.
Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит, в треугольнике известны основание и высота. Можно найти площадь.
$$S={1over2}*6*8=24$$
Площадь каждого из малых треугольников: $${24over6}=4$$
Что мы узнали?
Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Irina Semenova
10/10
-
Гульжан Дощанова
10/10
-
Татьяна Киприянова
10/10
-
Ольга Почивалова
9/10
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 375.
А какая ваша оценка?



![{displaystyle [ABO]=[ABE]-[BEO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fad91ee584b5e608e070fff5851154979efa3ab0)
![{displaystyle [ACO]=[ACE]-[CEO]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af50a27689048f316853c0fcd756cb1c2d78813)