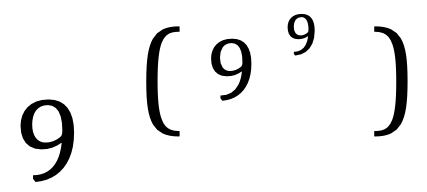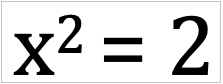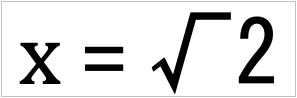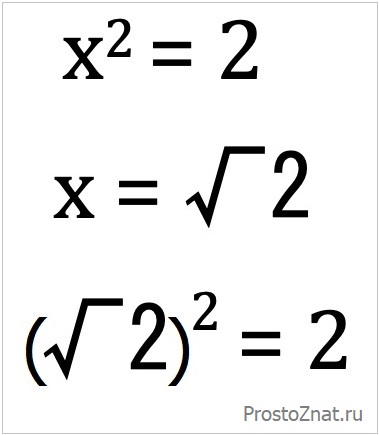Написать число прописью — что может быть проще? До тех пор, пока число не становится очень большим. Да и маленькие числа, особенно если их много, могут отнять массу времени при написании их прописью. Специально для подобных случаев мы создали этот калькулятор, который правильно напишет любое число словами. Вы можете ввести как целое, так и дробное число. Если же вам необходимо написать прописью сумму с рублями и копейками — попробуйте этот калькулятор.
Максимальное число, которое может обработать наш калькулятор содержит 75 чисел и называется кваттуорвигинтиллион.
Число прописью онлайн
Полученное число, записанное словами вы можете скопировать в буфер обмена для дальнейшего использования. Для этого нажмите кнопку слева от числа.
Сколько нулей в числах
| Количество нулей | Краткая запись | Название |
|---|---|---|
| 3 | 103 | тясяча |
| 6 | 106 | миллион |
| 9 | 109 | миллиард (биллион) |
| 12 | 1012 | триллион |
| 15 | 1015 | квадриллион |
| 18 | 1018 | квинтиллион |
| 21 | 1021 | секстиллион |
| 24 | 1024 | септиллион |
| 27 | 1027 | октиллион |
| 30 | 1030 | нониллион |
| 33 | 1033 | дециллион |
| 36 | 1036 | ундециллион |
| 39 | 1039 | дуодециллион |
| 42 | 1042 | тредециллион |
| 45 | 1045 | кватуордециллион |
| 48 | 1048 | квиндециллион |
| 51 | 1051 | сексдециллион |
| 54 | 1054 | септендециллион |
| 57 | 1057 | октодециллион |
| 60 | 1060 | новемдециллион |
| 63 | 1063 | вигинтиллион |
| 66 | 1066 | унвигинтиллион |
| 69 | 1069 | дуовигинтиллион |
| 72 | 1072 | тревигинтиллион |
| 75 | 1075 | кватуорвигинтиллион |
| 78 | 1078 | квинвигинтиллион |
| 81 | 1081 | сексвигинтиллион |
| 84 | 1084 | септенвигинтиллион |
| 87 | 1087 | октовигинтиллион |
| 90 | 1090 | новемвигинтиллион |
| 93 | 1093 | тригинтиллион |
| 96 | 1096 | унтригинтиллион |
| 99 | 1099 | дуотригинтиллион |
| 102 | 10102 | третригинтиллион |
| 105 | 10105 | кватортригинтиллион |
| 108 | 10108 | квинтригинтиллион |
| 111 | 10111 | секстригинтиллион |
| 114 | 10114 | септентригинтиллион |
| 117 | 10117 | октотригинтиллион |
| 120 | 10120 | новемтригинтиллион |
| 123 | 10123 | квадрагинтиллион |
| 126 | 10126 | унквадрагинтиллион |
| 129 | 10129 | дуоквадрагинтиллион |
| 132 | 10132 | треквадрагинтиллион |
| 135 | 10135 | кваторквадрагинтиллион |
| 138 | 10138 | квинквадрагинтиллион |
| 141 | 10141 | сексквадрагинтиллион |
| 144 | 10144 | септенквадрагинтиллион |
| 147 | 10147 | октоквадрагинтиллион |
| 150 | 10150 | новемквадрагинтиллион |
| 153 | 10153 | квинквагинтиллион |
| 156 | 10156 | унквинкагинтиллион |
| 159 | 10159 | дуоквинкагинтиллион |
| 162 | 10162 | треквинкагинтиллион |
| 165 | 10165 | кваторквинкагинтиллион |
| 168 | 10168 | квинквинкагинтиллион |
| 171 | 10171 | сексквинкагинтиллион |
| 174 | 10174 | септенквинкагинтиллион |
| 177 | 10177 | октоквинкагинтиллион |
| 180 | 10180 | новемквинкагинтиллион |
| 183 | 10183 | сексагинтиллион |
| 186 | 10186 | унсексагинтиллион |
| 189 | 10189 | дуосексагинтиллион |
| 192 | 10192 | тресексагинтиллион |
| 195 | 10195 | кваторсексагинтиллион |
| 198 | 10198 | квинсексагинтиллион |
| 201 | 10201 | секссексагинтиллион |
| 204 | 10204 | септенсексагинтиллион |
| 207 | 10207 | октосексагинтиллион |
| 210 | 10210 | новемсексагинтиллион |
| 213 | 10213 | септагинтиллион |
| 216 | 10216 | унсептагинтиллион |
| 219 | 10219 | дуосептагинтиллион |
| 222 | 10222 | тресептагинтиллион |
| 225 | 10225 | кваторсептагинтиллион |
| 228 | 10228 | квинсептагинтиллион |
| 231 | 10231 | секссептагинтиллион |
| 234 | 10234 | септенсептагинтиллион |
| 237 | 10237 | октосептагинтиллион |
| 240 | 10240 | новемсептагинтиллион |
| 243 | 10243 | октогинтиллион |
| 246 | 10246 | уноктогинтиллион |
| 249 | 10249 | дуооктогинтиллион |
| 252 | 10252 | треоктогинтиллион |
| 255 | 10255 | кватороктогинтиллион |
| 258 | 10258 | квиноктогинтиллион |
| 261 | 10261 | сексоктогинтиллион |
| 264 | 10264 | септоктогинтиллион |
| 267 | 10267 | октооктогинтиллион |
| 270 | 10270 | новемоктогинтиллион |
| 273 | 10273 | нонагинтиллион |
| 276 | 10276 | уннонагинтиллион |
| 279 | 10279 | дуононагинтиллион |
| 282 | 10282 | тренонагинтиллион |
| 285 | 10285 | кваторнонагинтиллион |
| 288 | 10288 | квиннонагинтиллион |
| 291 | 10291 | секснонагинтиллион |
| 294 | 10294 | септеннонагинтиллион |
| 297 | 10297 | октононагинтиллион |
| 300 | 10300 | новемнонагинтиллион |
| 303 | 10303 | центиллион |
Ваша оценка
[Оценок: 176 Средняя: 3.6]
Написать число прописью Автор admin средний рейтинг 3.6/5 — 176 рейтинги пользователей
Время чтения 11 мин.Просмотры 5к.
Мы живем среди понятных нам вещей и явлений. Мы привыкли к измерениям разных величин: расстояний, скоростей, объемов и прочего. Интуитивно понимаем разницу, если нам говорят, что одно в миллион раз больше другого. Ну, в миллион раз, и что тут такого?
Содержание
- Как выглядит «больше в четверть миллионов раз»
- Кубическая миля: сколько в нее может поместиться
- Сравнение бесконечно больших и бесконечно малых величин
- Как пишется 1 миллион и больше
- Числа гиганты и миллионы миллионов
- Самое большое число, записанное тремя цифрами
- Уравнение икс в степени икс
- О расчете электрических цепей
Как выглядит «больше в четверть миллионов раз»
Слово «миллион» означает тысячу тысяч, поэтому в миллионе всего шесть нулей после единицы – 1 000 000.
Четверть миллиона — это 1 000 000 разделить на 4, получается 250 тысяч или 250 000.
Однако, миллион – это все-таки много. Много настолько, что даже разница в размерах в четверть миллиона (примерно в 250 тысяч раз) дает нам просто несопоставимые размеры.
Допустим, мы представляем себе размеры дома. Большого ли маленького – именно, дома. Размеры дома не столь важны. Важно то, что весь земной шар, оказывается, в четверть миллиона раз больше, чем один среднестатистический дом.
Примерно в четверть миллиона раз наша Земля меньше, чем вся Солнечная система! То есть, если дважды увеличить размеры нашего среднего по величине дома в четверть миллиона раз, мы получим наше Солнце вместе с планетами Солнечной системы по линейному размеру. Речь идет именно о линейном размере в одном направлении, о размере, который мы измеряем с помощью линейки.
Кубическая миля: сколько в нее может поместиться
Объемы дома мы не сравниваем с объемами Земли или Солнечной системы. Мы сравниваем только их линейные размеры. Дело в том, что если говорить об объемах, то сопоставление будет еще больше, не в пользу дома. Здесь совсем другие числа. Какие? Давайте посмотрим. В свое время ученые (возможно, английские!) подсчитали, что…
…Возьмем обычную географическую милю, равную по длине примерно 1855,4 метров – это протяженность одной минуты дуги вдоль экватора Земли. Мили до сих пор используют моряки, поскольку это очень удобно, если пользоваться картами Земли.
Предположим, что мы можем сделать куб со сторонами, равными одной географической миле. Это значит, что куб должен быть всего-то по 1855 метров в каждом из 3-х направлений (длина, ширина, высота). Представим, что сможем сделать такой куб. Как Вы думаете, что внутри него может поместиться?!
… В середине прошлого столетия (1950-ые годы) делали такой подсчет. Так вот, в такой куб поместились бы одновременно:
- все здания всего мира;
- флоты всех государств;
- все машины и сооружения со всех частей нашего света;
- население всего земного шара;
- все животные нашей планеты;
- и еще в этом кубе осталось бы незаполненное свободное место!
Кстати, из вещества всего нашего земного шара можно (теоретически, конечно) изготовить 600 миллионов подобных ящиков. Тогда как все, что природой и людьми создано, помещается всего лишь в один из таких кубов!
Поэтому мы даже не говорим о сравнительных объемах вещей. Упоминаем только их линейные размеры.
Сравнение бесконечно больших и бесконечно малых величин
Попробуем в порядке возрастания расположить линейные размеры известных нам предметов (и не очень известных). При этом каждый последующий предмет должен быть в четверть миллиона раз больше (линейно, а не объемно!) предыдущего. Тогда можно составить следующий список:
- электрон
- атом
- пылинка
- дом
- земной шар
- солнечная система
- расстояние до Полярной звезды
- наша Галактика Млечный путь
Вот как получается, что если наш дом всего-то четырежды увеличить в четверть миллиона раз, то мы приблизимся к размеру всей нашей Галактики. А если дважды уменьшить в четверть миллиона раз, тогда дом превратится всего лишь в атом вещества!
Как еще можно представить себе миллион? Давайте попробуем:
- полоса из миллиона волос, уложенных рядом друг с другом, была бы шириной около 100 метров;
- если миллион раз зачерпнуть воду наперстком, можно вычерпать около тонны воды;
- книга в миллион страниц была бы толщиной около 50 метров;
- миллион букв помещаются в книге, размером около 600-800 страниц;
- миллион дней – это 27 столетий (2700 лет), а мы живем пока только в 21-м столетии (закончился 2020 год) от начала новой эры.
Попробуем подсчитать количество страниц в книге, представленной на рисунке 3.
- Пачка бумаги из 500 листов имеет толщину около 5 см.
- Делим 500 листов на 5, это равно 100 листов. Получаем: 100 листов = 1 см.
- 1 000 000 листов = 10 000 см или около 100 м.
Получается, что книга на рисунке содержит примерно 10 000 листов, что дает толщину книги примерно 1 метр.
Как пишется 1 миллион и больше
В миллионе шесть нулей после единицы. Цифрами миллион можно записать так: 1 000 000 (единица и шесть нулей после единицы).
Миллион двести пишется цифрами следующим образом: 1 000 200. Здесь после единицы идут три нуля и число двести – всего после единицы должно быть шесть цифр.
Два миллиона цифрами – это 2 000 000 (цифра два и шесть нулей после двойки).
Три миллиона пишется так: 3 000 000 (цифра три и шесть нулей после тройки).
Как пишется тысяча миллионов? Это миллион (шесть нулей после единицы), который нужно умножить на тысячу (добавить еще три нуля справа). В сумме шесть и три нуля дают девять (6+3=9), получается миллиард – число с девятью нулями.
Тысяча миллионов – это миллиард, цифрами пишется так: 1 000 000 000 (после единицы девять нулей).
Числа гиганты и миллионы миллионов
Миллион – это очень много. А как быть с миллиардом, триллионом и другими числами гигантами? Это же еще больше!
В миллионе шесть нулей после единицы (1 000 000).
Дальше – больше: в миллиарде – девять нулей (1 000 000 000, тысяча миллионов).
В триллионе – 12 нулей (1 000 000 000 000, тысяча миллиардов или миллион миллионов).
Если, например, попытаться записать расстояние до самых отдаленных объектов нашей Вселенной, то мы получили бы число, примерно с 30-ю нулями (миллион триллион триллионов) – 6+12+12=30 нулей. А ведь такие большие расстояния измеряют не в метрах, а в световых годах, и это уже не более нескольких миллиардов.
Число молекул в одном кубическом метре газа – реально вычисленная величина – составляет не более чем число с 19-20-ю нулями (примерно сто миллиард миллиардов).
Ну, а если попытаться пересчитать все капли в океанах и морях Земли, то получится число с 27-28 нулями (около тысячи триллион триллионов). В общем, и не придумать ничего такого, что можно было бы посчитать с помощью огромных чисел с числом нулей, больше 30-и. А это где-то миллион триллион триллионов, но, может чуть больше!
Тем не менее, большие числа очень волнуют человечество. Даже понятие такое недавно появилось: big data – большие числа. Оно означает возможности обработки огромных массивов данных с помощью компьютеров.
Задачи big data состоит не в пересчете огромного количества чисел, а в обработке большого числа данных с тем, чтобы найти в них закономерности и затем использовать практически. Например, для выяснения предпочтений людей при выборе товаров и услуг, при поиске информации, при пользовании теми или иными сервисами. Но это, что называется, совсем другая история, с практическим финалом.
Самое большое число, записанное тремя цифрами
Вернемся просто к числам, без особой практической пользы, то есть, к абстрактным величинам. Как Вы думаете, какое самое большое число можно вот так запросто взять и записать, используя для этого всего 3 цифры? Оказывается, такое число записывается как девять в степени девять в степени девять:
Всего три девятки, а число получается фантастическое по своей величине! Начинается оно с цифр
428 124 773 175 747 048 036 987 118,
а заканчивается на 89. Что в середине этого числа, не знает никто! Потому что в этом числе 369 693 061 цифра! Более 369 миллионов цифр!
Древний Архимед известен много чем, и еще законом Архимеда. Когда-то он посчитал, что если весь мир (известный тогда) вплоть до неподвижных звезд (как тогда считалось) наполнить тончайшим песком, то получится количество песчинок в виде числа с 63-я цифрами. А здесь не 63 цифры, а почти 370 миллионов цифр!
Даже если пересчитать все электроны, что имеются в нашей Вселенной, мы не получим столь огромной величины. Вот так всего-то три цифры позволяют нам показать несоразмерной величины числа. И даже позволяют нам потом с этими числами оперировать.
Уравнение икс в степени икс
Рассмотрим, как люди легко оперируют с бесконечными числами. Когда-то в чести были не только цифровые компьютерные методы, но и аналитические, с помощью формул. Тогда существовали задачки, использующие бесконечно большие величины.
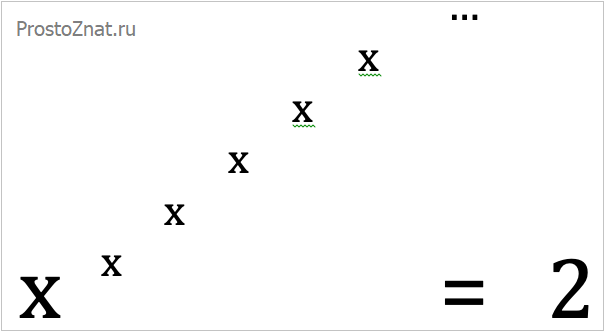
Например, предлагалось определить значение x (старое забытое школьное «икс»!) в выражении с бесконечным числом этих самых «иксов»:
Как это ни странно, решается такое уравнение очень просто. Рассуждения следующие. Если число «иксов» бесконечно, то ничто не мешает нам приписать к этому бесконечному множеству «иксов» еще один «икс» – слева внизу от всей «плеяды иксов». Ведь от этого ничего не изменится, не правда ли? Бесконечное число «иксов» плюс еще один «икс» – все равно останется бесконечное число.
Ну, приписали, и что? Вспомним, что ранее записанная цепочка из бесконечного множества «иксов» равнялась 2, по условию задачи. И новая цепочка с дополнительным «иксом» слева тоже равна 2, поскольку новый «икс» ничего не поменял в бесконечности. А раз так, тогда можно запросто заменить всю старую цепочку из бесконечных «иксов» на одну единственную «двойку», ведь старая цепочка была равна 2!
В итоге получается на удивление просто: новый дополнительный «икс» станет у нас во второй степени. А результат будет равен двойке, как и раньше:
Еще раз пройдемся по логике: «двоечка» над «иксом» – это та самая бесконечная плеяда «иксов», которая ранее была у нас равна двойке. Сам «икс» – это еще один приписанный нами «икс» к бесконечной цепочке «иксов», ведь от такой приписки ничего не меняется. А раз ничего не меняется, то полученный результат тоже не меняется, и он равен «двойке».
Получаем решение уравнения с бесконечным числом «иксов»:
Проверяем полученный ответ:
О расчете электрических цепей
Вы спросите, зачем нужны задачки с бесконечными величинами, если в реальной жизни такого не бывает? Ошибаетесь, очень даже бывает. Поговорим немного о практической пользе операций с бесконечными числами. Например, энергетики легко оперируют с такими понятиями, как бесконечные электрические цепи (рис. 9).
Проложена, скажем, линия уличного освещения. Сколько ламп висит на различных столбах и иных подвесах? Очень много, особенно в больших городах. А как рассчитать такие электрические цепи? Вот именно – с помощью подобных только что продемонстрированных формул и с помощью подобных рассуждений!
Ход рассуждений – это когда к бесконечному числу электрических элементов легко приписывают дополнительные такие же элементы, а всю оставшуюся бесконечную цепь меняют на один единственный элемент. И далее без труда делают расчет значительно упростившейся электрической схемы.
В общем, как было показано, человечество давно перешагнуло за миллион, миллиард и триллион. И даже за пределы чисел с огромным количеством цифр, с сотнями миллионов. И спокойно себе работает, не то что работает, но и делает вполне реальные вещи там, где счет идет на бесконечные множества.
Но все-таки миллион – это так много! Зачем же тогда нужно все время больше и больше? Не правда ли?!