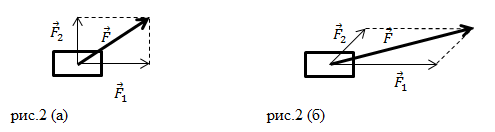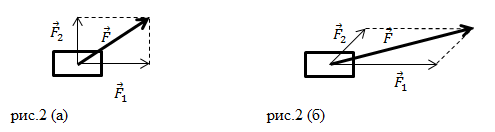Как пишется модуль скорости в физике - Граматика и образование на Pisanino.ru

Морфемный разбор слова:

Однокоренные слова к слову:

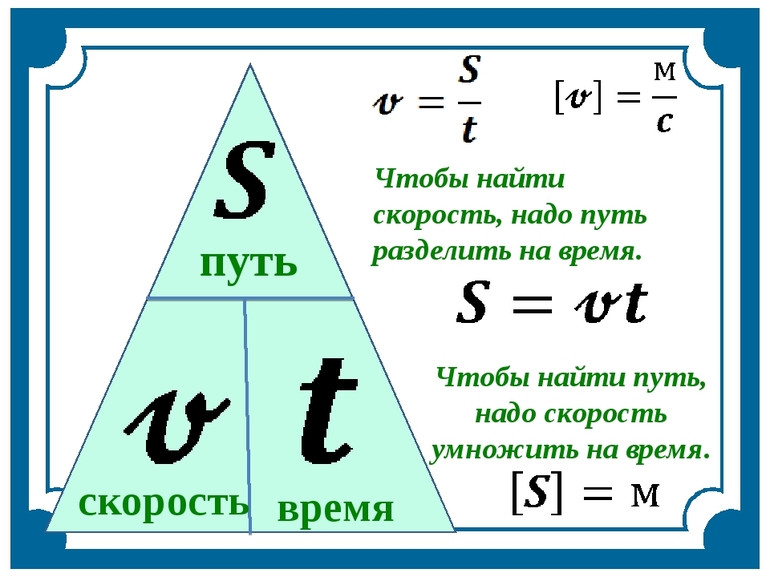
Формула скорости

Определение и формула скорости

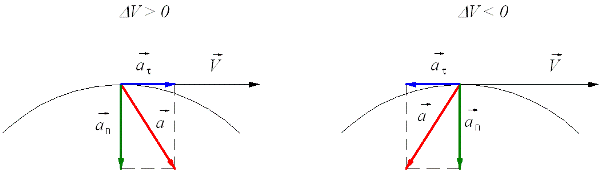
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

Следовательно, вектор скоростив декартовых координатах можно представить:

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

в сферической системе координат:

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с 2

Примеры решения задач

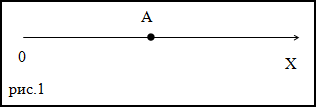
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Формула скорости не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$ begin 10 t-t^<2>=10(2.2) \ t_<1>=5+sqrt <15>approx 8,8(c) ; t_<2>=5-sqrt <15>approx 1,13(c) end $$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

При решении уравнения (2.3) нам подойдет корень равный:

Источник

Модуль силы, скорости, импульса. Что это?!

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.

Сила и модуль силы

В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.

Что такое модуль силы?

Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.

Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.

Модуль равнодействующих двух сил определяется по формулам:

Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.

Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).

Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.

Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.

Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:

Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.

Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:

Модуль импульса и модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.

Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник

Формула скорости — обозначение, единицы измерения и примеры нахождения

Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

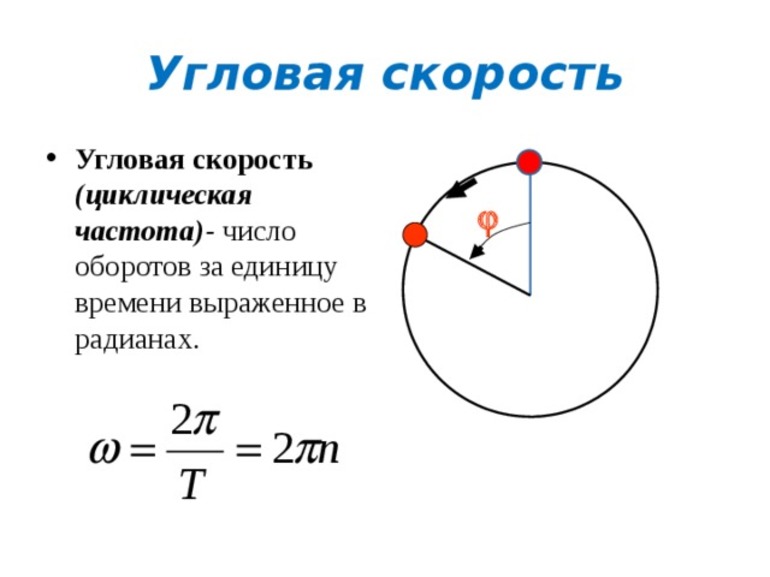
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник

Понятие и основные термины

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Равноускоренное движение

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Среднее значение

Угловая скорость

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Использование онлайн-калькулятора

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Источник

Теперь вы знаете какие однокоренные слова подходят к слову Как пишется модуль скорости в физике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется модуль скорости в физике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.

Источник

На чтение 11 мин Просмотров 2к. Опубликовано 07.05.2019

Содержание

Сила и модуль силы
Что такое модуль силы?
Что это модуль скорости?
Модуль импульса и модуль оси

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Сила и модуль силы

Что такое модуль силы?

Модуль равнодействующих двух сил определяется по формулам:

F=F1 + F2 (в случае сил с одинаковым направлением)
F=F1 — F2 (силы с разным направлением)

Что это модуль скорости?

v = S/t = (x — x0)/t.

Вычисляется скорость v₂₁ на базе закона сложения скоростей v₂ = v₂₁ + v₁, а значит v₂₁ = v₂ – v₁.
Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

В 7 классе вы узнали, что равномерным движением называют такое движение, при котором за равные интервалы времени тело проходит равные части пути (см. § 1-ж). Например, если поезд ежечасно проезжает 60 км, ежеминутно проезжает 1 км и так далее, то движение равномерное. Итак, скорость равномерного движения:

υ – скорость равномерного движения, м/с
l – пройденный телом путь, м
Δ t – интервал времени движения, с

Поскольку пройденный путь и интервал времени – скалярные величины, то скорость равномерного движения является скаляром тоже. То есть, имея только числовое значение, она ничего не говорит нам о пространственном направлении изучаемого движения.

Обратим внимание: если движение является не только равномерным, но и прямолинейным, то путь тела равен модулю перемещения. Поэтому, пользуясь аналогией с предыдущей формулой, в физике определяют скорость равномерного прямолинейного движения:

– скорость равнопрямолинейного движения, м/с
– перемещение тела, м
Δ t – интервал времени движения, с

Поскольку перемещение – векторная величина, то скорость равномерного прямолинейного движения является вектором тоже, то есть величиной, имеющей не только числовое значение, но и пространственное направление.

Из геометрии мы знаем, что в результате произведения вектора на положительный скаляр получается новый вектор, направление которого совпадает с направлением исходного, а модуль равен произведению модуля исходного вектора на скаляр. Последняя формула – пример произведения вектора s на положительный скаляр ¹/ Δ t. Поэтому направление скорости равномерного прямолинейного движения всегда совпадает с направлением перемещения.

При равномерном движении тело проходит равные части пути .
Скорость равномерного движения находят делением пройденного пути на .
Скорость равномерного движения является скалярной величиной, так как .
Являться скалярной величиной – значит не давать информации .
Модуль перемещения тела совпадает с пройденным путём, .
Формулу для скорости равнопрямолинейного движения вводят, .
Делением перемещения тела на интервал времени движения находят .
Подобно перемещению, вектором является и .
Являться вектором – значит быть .
Поскольку скаляр ¹/ Δ t положителен, то .

Задача 1. Минутная стрелка часов-курантов на Спасской башне Кремля имеет длину 327 см. Найдите скорость движения её конца-указателя.

Решение. Поскольку конец стрелки движется по окружности циферблата, траектория движения является криволинейной. Наряду с этим движение является равномерным, так как за любые равные интервалы времени, например, за каждую минуту, конец стрелки проходит равные части пути (деления на циферблате, равные друг другу по всей длине окружности).

Поэтому мы применяем формулу из первой рамки в начале параграфа:

υ =	. l .	=	2 π R	≈	2 · 3,14 · 327 см	≈	2054 см	≈ 34 см/мин
Δ t	Δ t	60 мин	60 мин

Задача 2. Турист прошёл на север 3 км, затратив на это 45 минут, а затем повернул на восток и прошёл ещё 4 км, затратив на это 1 час. За какое время он прошёл бы из начальной в конечную точку маршрута, двигаясь прямолинейно с таким же модулем скорости, как и прежде?

Решение. Часть этой задачи мы уже решили в § 12-в, поэтому знаем, что расстояние между начальной и конечной точками равно 5 км. Но какова скорость туриста? Сначала найдём модули скоростей на обоих этапах:

υ 1 =	. s 1 .	=	3 км	= 4 км/ч	;	υ 2 =	. s 2 .	=	4 км	= 4 км/ч
Δ t 1	0,75 ч	Δ t 2	1 ч

Мы видим, что модули обеих скоростей равны и соответствуют скорости человека, идущего пешком. Значит, это значение можно принять за модуль скорости равнопрямолинейного движения и «по гипотенузе»:

υ =	. s .	⇒	Δ t	=	. s .	=	5 км	= 1,25 ч	= 1 час 15 мин
Δ t	υ	4 км/ч

Примечание. Если бы в условии задачи не было слова «прямолинейно», мы не смогли бы её решить вообще. Поскольку турист может идти по извилистой тропинке, мы не смогли бы определить его путь, а по нему – время. Именно поэтому мы использовали формулу из второй рамки, поскольку в ней присутствует перемещение, а не путь.

Траектория конца стрелки криволинейна, .
Наряду с непрямолинейностью траектории конца стрелки, его .
Равномерность этого движения мы обосновываем тем, что .
Поскольку движение равномерно, но непрямолинейно, .
Конец стрелки ежеминутно передвигается на .
Как должен идти турист по условию задачи?
После первой пары вычислений мы обнаруживаем: .
Поскольку модули скоростей равны, то их .
При отсутствии какого термина задача будет не решаема?
Если движение туриста непрямолинейно, то будет невозможно .

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.

Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.

Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.

Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.

Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.

Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.

Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает

направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.

Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения

Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.

Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше т. е. чем больше в выбранный момент скорость движения.

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.

Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

Источник

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Сила и модуль силы

Что такое модуль силы?

Модуль равнодействующих двух сил определяется по формулам:

F=F1 + F2 (в случае сил с одинаковым направлением)
F=F1 — F2 (силы с разным направлением)

Что это модуль скорости?

v = S/t = (x — x0)/t.

Вычисляется скорость v₂₁ на базе закона сложения скоростей v₂ = v₂₁+ v₁, а значит v₂₁ = v₂ – v₁.
Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник

Понятие и основные термины

S — расстояние (путь), пройденное материальной точкой или телом (м);
T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

неравномерную;
среднюю;
равномерно-переменную;
поступательную;
вращательную;
ускоренную.

Равноускоренное движение

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

V0 — начальная скорость;
A — ускорение (имеет постоянное значение);
t — время движения.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r^-1(t). То есть, с математической точки зрения, это первая производная.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t²/2 = (V² — V²0) /2*A.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V²0 — 2* A * s)^½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)^½.

Среднее значение

Угловая скорость

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Использование онлайн-калькулятора

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Справочный портал «Калькулятор».
Allcalc.
Fxyz.

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Источник

Содержание

Понятие и основные термины
Равноускоренное движение
Среднее значение
Угловая скорость
Закон сложения
Использование онлайн-калькулятора

Понятие и основные термины

S — расстояние (путь), пройденное материальной точкой или телом (м);
T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

неравномерную;
среднюю;
равномерно-переменную;
поступательную;
вращательную;
ускоренную.

Равноускоренное движение

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

V0 — начальная скорость;
A — ускорение (имеет постоянное значение);
t — время движения.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t²/2 = (V² — V²0) /2*A.

Среднее значение

Угловая скорость

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Использование онлайн-калькулятора

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Справочный портал «Калькулятор».

Allcalc.

Fxyz.

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

ФизикаНапряженность электрического поля — понятие, формула, единица измерения и значение

ФизикаМощность переменного тока — виды, формула, примеры вычисления

Источник

Как найти модуль скорости

Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько быстро тело передвигается в пространстве. Перемещение предполагает изменение координат.

Введите систему координат, относительно которой вы будете определять направление и модуль . Если в задаче уже задана формула зависимости скорости от времени, вводить систему координат не нужно – предполагается, что она уже есть.

По имеющейся функции зависимости скорости от времени можно найти значение скорости в любой момент времени t. Пусть, например, v=2t²+5t-3. Если требуется найти модуль скорости в момент времени t=1, просто подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.

Когда задача требует найти скорость в начальный момент времени, подставьте в функцию t=0. Таким же образом можно найти время, подставив известную скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t²+5t-3=0. Отсюда t=[-5±√(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а поскольку время не может быть отрицательным, остается только t=1/2.

Иногда в задачах уравнение скорости дается в завуалированной форме. Например, в условии сказано, что тело двигалось равноускоренно с отрицательным ускорением -2 м/с², а в начальный момент скорость тела составляла 10 м/с. Отрицательное ускорение означает, что тело равномерно замедлялось. Из этих условий можно составить уравнение для скорости: v=10-2t. С каждой секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, поэтому легко найти общее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд после начала движения тело остановится.

Помимо прямолинейного движения тела, существует еще и движение тела по окружности. В общем случае оно является криволинейным. Здесь возникает центростремительное ускорение, которое связано с линейной скоростью формулой a(c)=v²/R, где R – радиус. Удобно рассматривать также угловую скорость ω, причем v=ωR.

Источник

Равномерное прямолинейное движение. Скорость. Уравнение движения

Точка движется равномерно в том случае, если она за любые равные промежутки времени проходит одинаковые пути.

Важно понимать, что равномерное движение необязательно должно быть прямолинейным. Оно может происходить вдоль любой траектории. Однако равномерное прямолинейное движение – это самый тривиальный тип движения.

У движущегося тела есть несколько характеристик. Самая важная из них – скорость. Мы интуитивно понимаем этот физический термин. Например, ни для кого не секрет, что черепаха ползёт медленно, а гепард бежит быстро.

В механике же скорость имеет вектор, то есть направление. Пусть некоторый объект движется равномерно и прямолинейно в течение некоторого времени Δt. Обозначим начало пути точкой M₁, а финиш – M₂. Перемещение же будет равным Δr. Теперь разделим перемещение на промежуток времени. В итоге мы получим тот самый вектор, который называется скоростью равномерного прямолинейного движения точки и обозначается буквой v. Исходя из этого, формулу скорости можно записать как: v= Δr/Δt. Учтём, что промежуток времени может быть сугубо положительной величиной, поэтому и направление скорости будет ориентировано в сторону перемещения Δr. В физике фигурирует понятие модуля скорости: v= |Δr|/Δt.

Итак, скорость равномерного прямолинейного движения объекта – это векторная величина, которая равна отношению перемещения точки к промежутку времени, в течение которого это движение происходило.

В то же время модуль перемещения |Δr| представляет собой расстояние, пройденное телом за некоторое время. Вспомним, что мы говорим о равномерном движении и скажем, что модуль скорости будет аналогичным образом равен пройденному пути.

Уравнение равномерного прямолинейного движения точки

Рассмотрим радиус-вектор r₀, который задаёт положение точки в первоначальный момент времени t₀. Соответственно, введём радиус-вектор r, который будет характеризовать положение точки в любой момент времени t. Тогда получим, что Δt=t—t₀, а Δr=r—r₀. В результате этих рассуждений получаем, что скорость имеет вид: v= r— r₀/t— t₀.

Договоримся, что начальный момент времени t₀ равен нулю, тогда: v= r—r₀/t. Преобразуем и получим: r= r₀+vt. Собственно, на этом этапе мы получили уравнение равномерного прямолинейного движения точки в векторной форме. Оно позволяет устанавливать положение радиус-вектора в любой момент времени при условии, что известны скорость и радиус-вектор в начальный момент времени. Но, как мы уже знаем, векторный и координатный способы задания движения идентичны друг другу, поэтому можно записать три эквивалентных уравнения.

Радиус-вектор r – это сумма векторов r₀и vt. Получается, что проекции радиус-вектора r на оси координат должны быть равны сумме проекций этих двух векторов на те же оси. Но что будет, если эти два вектора совпадают между собой?

Возьмём некоторую точку и зададим её движение вдоль оси ОХ. Соответственно, наши вектора будут составлять с двумя оставшимися осями OY и OZ прямые углы. А это, в свою очередь, означает, что проекции на эти оси будут равны нулю. Учтём, что проекции радиус-вектора на координатные оси равны координатам его конца, а соответственно: r_х=х и r_0х=х₀. Благодаря этому наше уравнение приобретёт вид: х=х₀+υ_xt (в проекциях на ось ОХ).

Это уравнение позволяет найти координату х точки при равномерном прямолинейном движении точки в любой момент времени, если известны проекции её скорости на ось ОХ и её начальная координата х₀.

В другом случае, когда вектора r₀и vt не совпадают по направлению, а ось ОХ направлена в ту же сторону, что и скорость, то уравнение движения выглядят следующим образом:

x = x₀ + v_xt
y = y₀
z = z₀, где х₀, у₀, z₀ – проекции радиус-вектора r₀ на оси координат.

Обозначим путь вдоль оси ОХ буквой s. Он будет равен модулю изменения её координаты: s=|х₂-х₁|. Найти путь можно с помощью модуля скорости: s=|υx|t=υt. Но мы понимаем, что движение вдоль одной и той же оси может происходить в разные стороны, поэтому лучше всего пользоваться уравнением: х=х₀ ± υt.

Важно оговориться, что равномерное прямолинейное движение, как и многие другие физические явления, идеализированы. Всё-таки сложно встретить вокруг нас идеально ровное прямое перемещение.

Графическое представление равномерного прямолинейного движения

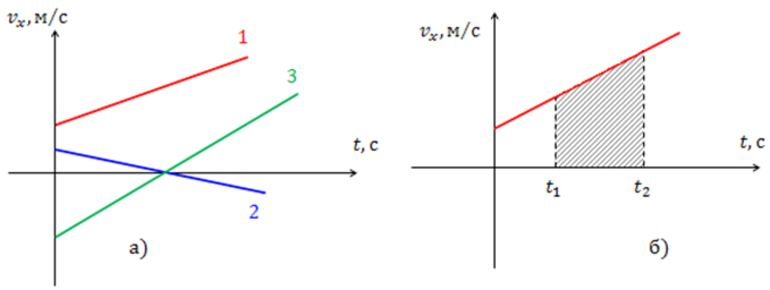
Как же выглядит прямолинейное равномерное движение на графиках? Внизу представлен наглядный график зависимости проекции скорости от времени. Мы видим, что это прямая, которая ориентирована параллельно оси времени. Площадь прямоугольника ОАВС – это изменение координаты точки за каждое время. Сторона ОА — υ_x, а сторона ОС – есть время движения t, поэтому Δx= υ_xt.

На следующем рисунке приведены графики зависимости координаты от времени для трёх случаев:

Прямая 1: х₀=0, υ_x1>0;
Прямая 2: х₀<0, υ_x2>0;
Прямая 3: х₀>0, υ_x3<0.

Источник