Как пишется модуль в математике - Граматика и образование на Pisanino.ru

Модуль

В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа.
Разберемся, откуда модуль взялся, какими свойствами обладает.
Научимся решать уравнения и неравенства с модулем.

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

Представьте, что вы стоите в точке на числовой оси. Слева от вас, в точке , находится школа. Справа, в точке , находится ваш дом. Математически число меньше, чем . Но вот идти до школы метров влево гораздо дольше, чем пройти метров до дома вправо. В этом смысле «величина» пройденного расстояния в метров больше, чем метров.

Пусть теперь школа находится в точке , а дом в точке . Математически вновь получаем, что меньше . Но вот нам, находящимся в , совершенно нет разницы: идти метров влево или метров вправо. В обоих случаях мы пройдем метров. То есть, по «величине» числа и равны.

Количественный смысл

Рассмотрим числа и . В математическом смысле гораздо меньше . А давайте посмотрим на эти числа под другим углом. У вас есть всего рублей и вы задолжали другу. Ваш долг составляет рублей. В этом смысле «величина» вашего долга в рублей гораздо больше имеющихся у вас рублей. Получается, что математически меньше , но по «величине» больше .

Теперь рассмотрим числа и . Математически, опять же, меньше . Но, пользуясь нашей аналогией с долгом, своими рублями вы полностью покроете долг в рублей. То есть, по «величине» число равно числу .

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.

Модуль числа

Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.

Модуль или абсолютная величина вещественного числа — само число , если оно неотрицательно, иначе .

Допустим, мы хотим найти модуль какого-то числа . Согласно определению, нам надо провести элементарную проверку. Если число положительное или равно , то модулем и является само . Если же меньше , то результатом модуля будет .

Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» больше , а равно . И действительно:

Эквивалентное определение модуля

Положение знака нестрогого неравенства в определении модуля не имеет значения:

Доказательство

Обозначим второе определение модуля числа как . Покажем, что какой не возьми, будет выполняться .

Пусть . По классическому определению . По второму: . То есть .

Пусть . По классическому определению . А вот во втором определении попадает уже под второе условие, то есть . Опять имеем .

Наконец, пусть . По классическому определению . У второго определения та же ситуация: . Получается, что и в этом случае .

Итак, мы рассмотрели все возможные значения для и во всех случаях . Это и означает, что между двумя определениями нет никакой разницы

Такое определение иногда бывает полезно. Например, если лежит в следующих пределах: , то можно сразу сказать, что , даже несмотря на то, что для так выражаться будет некорректно, ведь , а не .

Свойства модуля

У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее.
Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел и .

Очевидные свойства

Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.

Модуль всегда неотрицателен

Доказательство

Рассмотрим произвольное вещественное число . Если , то, по определению модуля , поэтому . Если , то, по определению модуля . Пусть тогда . Умножим обе части неравенства на : . По определению модуля , поэтому . Доказали, что вне зависимости от знака его модуль будет неотрицательным числом.

Помимо этого, было бы странно, если «величина» числа оказалсь бы больше, чем само это число. Отсюда еще одно очевидное своство:

Модуль не меньше аргумента

Доказательство

Докажем правую часть неравенства:

Если , то по определению получаем, что , а значит выполняется .
Если , то неравенство выполняется, так как слева имеем отрицательное число, а число справа всегда неотрицательное.

Доказательство левой части неравенства проводится аналогично.

Вспоминаем геометрический смысл «величины» числа. Мы выяснили, что нет разницы: иди из влево метров или вправо метров. В обоих случаях придется идти метров. Это означает, что «величина» противоположных чисел совпадает, то есть:

Модули противоположных чисел равны

Следствие:

Доказательство

Если , то и , откуда получаем выполняющееся равенство .

Если , то и , откуда получаем также выполняющееся равенство .

Для доказательства следствия вынесем в правой части равенства за скобки :

По уже доказанному свойству это равенство выполняется.

Последнее свойство будет уже чуть менее очевидным. Пусть мы умножаем друг на друга два числа. Логично предположить, что «величина» произведения двух чисел будет равна произведению «величин» множителей.

Доказательство

Из свойства равенства модулей противоположных чисел все равенства ниже выполняются:

Для дальнейших действий выбираем такое произведение, в котором оба числа под модулем являются неотрицательными числами. Пусть таким вариантом будет . Так как и — неотрицательные числа, то, по определению модуля и , то есть:

Произведение двух неотрицательных чисел есть число неторицательное. Поэтому, по определению модуля, можно записать следующее равенство:

Грубо говоря, тут мы воспользовались определением модуля «наоборот». Итак, получили следующую цепочку равенств:

Это очень важное свойство. Оно позволяет нам в любой момент разбивать большое выражение под модулем на несколько поменьше, либо, наоборот, объединять несколько модулей в один и выполнять внутри какие-то действия.

Связь с возведением в квадрат

Доказательство

Воспользуемся свойством объединения произведения модулей:

Мы знаем, что квадрат любого числа есть число положительное, то есть , поэтому, по определению модуля, . Итак, доказали, что:

Это свойство часто позволяет очень сильно упростить решение уравнений и неравенств, так как мы избавляемся от модуля, возиться с которым можно долго, особенно в неравенствах.

Решение

Возводим в квадрат обе части неравенства и пользуемся доказанным свойством:

Связь с корнем

Доказательство

С помощью свойства связи модуля и квадрата произведем замену подкоренного выражения:

Модуль любого числа неотрицателен. Поэтому . Значит, арифметический корень от будет равняться (вариант отбрасывается по определению):

С помощью данного свойства часто получается свести различные сложные неравенства к неравенствам с модулем, которые мы подробно разберем ниже.

Неравенство треугольника

В геометрии у треугольников есть замечательное свойство, заключающееся в том, что длина любой стороны треугольника меньше суммы длин двух оставшихся. Это свойство называется «неравенством треугольника».

Например, пусть у нас есть какой-то треугольник . Тогда длина стороны меньше суммы длин сторон и :

В некоторых учебниках по геометрии различают сам отрезок (например, ) и его длину . Если пользоваться этими обозначениями, неравенство треугольника примет следующий вид:

Оказывается, в алгебре есть очень похожее неравенство, но связано оно не с отрезками и их длинами, а с числами и их модулями. Из-за внешнего сходства это неравенство тоже называют неравенством треугольника.

Доказательство

Слева и справа имеем положительные числа, поэтому можно возвести в квадрат обе части неравенства и воспользоваться свойством связи модуля и квадрата:

Для правой части воспользуемся свойством произведения модулей:

Рассмотрим отдельно варианты неравенства с и :

Оба неравенства всегда выполняется. Первое выполняется, так как модуль всегда не меньше аргумента. Второе выполняется по этому же свойству, а также из-за того, что модули противоположных чисел равны.

С геометрией и треугольниками все понятно. А в чем смысл неравенства треугольника с модулями? А смысл в том, что оно задает максимально возможный результат, который можно получить с помощью сложения или вычитания двух чисел.

Например, пусть у нас есть два числа: и . Какой максимальный результат можно получить из этих двух чисел, пользуясь только сложением и вычатнием? Проверим все возможных варианта напрямую:

Видим, что максимальное значение равно . Такое же значение получаем и по доказанному выше неравенству. Итак, максимально возможное значение равно сумме модулей этих двух чисел. На самом деле, это кажется вполне логичным.

Есть также похожее неравенство, но с разностью модулей. Его называют обратным неравенством треугольника.

Обратное неравенство треугольника

Доказательство

Если меньше , то неравенство выполняется, так как модуль всегда неотрицателен.

Пусть тогда . Возведем обе части неравенства в квадрат и воспользуемся свойством связи модуля и квадрата:

Умножим обе части неравенства на с переменой знака неравенства:

Это неравенство всегда выполняется (см. доказательство неравенства треугольника).

По аналогии с предыдущим доказанным неравенством, обратное неравенство треугольника дает нам минимальное возможное значение, которое можно получить, рассматривая сумму или разность двух чисел.

Оба доказанных неравенства можно объединить в одно цепное. Так его проще запомнить и использовать:

Расстояние между точками

Представим числовую ось. Отметим на ней две точки, например и . Какое между ними расстояние?
Ничего сложного, скажете вы, расстояние равно . И это правильный ответ. Сразу заметим, что , то есть при вычитании из меньшей точки большей получаем то же расстояние, но со знаком минус.

Расстояние между точками и равно . И опять, если мы поменяем местами числа в разности, то получим отрицательное расстояние

Общий посыл вы уловили. Для нахождения расстояния между двумя точками, надо из большей точки вычесть меньшую. Если сделать наоборот, то получим противоположное, отрицательное расстояние.

Вроде все ясно. Ну и причем здесь модуль? А вот представим, что у вас нет точных значений. Вам просто дали точки и , и попросили найти расстояние между ними. Какая-то из двух разностей ниже будет расстоянием:

Но какая именно? Тут к нам и приходит на помощь модуль. Расстояние между и обозначим так:

Если , то мы угадали с разностью и получим положительный результат. Взятие модуля никак на него не повлияет. Если , то мы не угадали и получаем отрицательное расстояние.
Но, по определению модуля, в результате все-равно получим положительное расстояние.

Расстоянием между двумя точками и на числовой оси называется модуль их разности: .

Наконец, поговорим о модулях одного числа, например или . Их можно представить вот так:

В этом смысле модуль одного числа можно понимать как расстояние от до этого числа (до и до ) на числовой оси.

Функция модуля

До этого момента мы говорили о модуле, как о некотором свойстве, которым обладает число, о его беззнаковой «величине». На самом деле, это лишь один из подходов к определению модуля. Он хорош тем, что основные свойства модуля не берутся из ниоткуда, а логично (можно даже сказать, очевидным образом) вытекают из понятия о «величине» числа.

Более строгим подходом является определение модуля как функции. В этом случае модуль спускается с небес на землю и теряет свой статус «неотъемлемой части любого числа», но зато у нас появляется возможность использовать его в большом и наработанном аппарате математики (и математического анализа):

Определить его функциональные свойства
Решать уравнения и неравенства с ним
Строить и изучать сложные функции с его участием

Модуль (функция) — кусочно-линейная функция, определенная на всей вещественной прямой следующим образом:

Видим, что механизм получения значения полностью совпадает с определением модуля числа, которое я дал в начале статьи. Никакой разницы в значениях между этими определениями нет. Это означает, что все выведенные выше свойства модуля числа прекрасно сохраняются и для функции модуля.

График функции модуля элементарный. От до это будет убывающая под углом в градусов прямая . От и далее это обычная прямая .

Помимо рассмотренных ранее уникальных свойств модуля, можно также проанализировать его на предмет наличия общих свойств функций.

Свойства модуля как функции

Область определения:
Область значений:
Функция четная
Строго убывает на и строго возрастает на

Доказательство

Любое вещественное число будет удовлетворять либо верхнему, либо нижнему неравенству из определения функции модуля. Другими словами, «величина» есть у любого числа. Поэтому область определения функции модуля равна .

Для любых неотрицательных чисел функция модуля будет равна самим этим числам. Значит, любое положительное число входит в область значений функции модуля. В то же время, модуль всегда неотрицателен, поэтому отрицательных чисел в области значений не может быть. Значит, область значений равна .

Доказанное ранее свойство равенства модулей противоположных чисел и означает четность функции модуля по определению.

Наконец, функция монотонно убывает, а монотонно возрастает на всей своей области определения. Поэтому функция модуля монотонно убывает на и возрастает на .

Все же, под модулем в литературе и других источниках информации чащее всего понимают именно функцию модуля.
C этого момента мы тоже будем придерживаться этой логики.
В дальнейших разделах вместо записей и я буду использовать записи и , чтобы подчеркнуть, что под знаком модуля может быть как число, так и какая-нибудь функция.

Уравнения с модулем

Научимся решать уравнения, в которых присутсвует модуль. В самом общем виде, их можно представить так: , причем под и могут оказать не только переменные, но и целые функции. Как решить это уравнение относительно ?

Уравнения с модулем вида

Уравнение вида имеет два решения вида и , если и не имеет решений вовсе, если .

Доказательство

Докажем сначала для случая, когда . В этом случае, какое ни возьми, его модуль всегда будет положительным, поэтому не существует такого числа , при котором получили бы равенство .

Пусть теперь . Тогда мы можем возвести обе части равенства в квадрат и воспользоваться свойством связи модуля и квадрата:

В левой части равенства ноль можно получить только когда какая-то из скобок равна . Отсюда два возмножных решения:

Пример

Решите уравнение с параметром:

Решение

Определим, при каких решений у уравнения не будет. Решений у него не будет, когда его правая часть отрицательная, то есть при . Для исходное уравнение по доказанной выше теореме разбивается на два:

Откуда получаем два корня:

Обратите внимание, что левый корень не зависит от .

Неравенства с модулем

Сейчас мы выведем формулы для решения неравенств с модулями любых видов.
Доказывать формулы мы будем строго аналитически, но это не страшно, ведь суть каждого вида неравенств я также поясню геометрически.

Далее я буду использовать знаки и , чтобы подчеркнуть, что формулы одинаково работают и для чисел, и для функций.

Неравенства вида

Неравенства с модулем вида

Доказательство

Стоит сразу отметить, что если , то неравенство не выполняется вне зависимости от значения , ведь модуль всегда неотрицателен и мы получаем, что положительное число должно быть меньше, чем отрицательное , чего не может быть.

Получается, рассматривать неравенство имеет смысл только при . Тогда возведем обе части неравенства в квадрат и воспользуемся свойством связи модуля с квадратом:

Имеем произведение двух скобок друг на друга, которое должно быть меньше . Такое возможно в двух случаях: если первая скобка меньше нуля, а вторая больше, и наоборот:

Преобразуем превый случай:

Разберем второй случай:

Но мы рассматриваем только неотрицательные , поэтому второй случай всегда не выполняется. Значит, в рассмотрении остается только первый случай:

Важно отметить, что формула работает и для нестрогого случая. Тогда все «расшифровывающие» неравенства справа также становятся нестрогими.

Теперь подумаем над сутью неравенств вида . Мы уже поняли, что можно рассматривать как расстояние от до . В этом смысле решить неравенство означает найти все такие , чтобы расстояние между и было меньше .
Геометрически это можно представить в виде симметричного относительно коридора со «стенками», равными и , между которыми «зажаты» все решения этого неравенства:

Решение

Решением этого неравенства будут все возможные расстояния между точкой и . Например, может равняться и так далее.
Воспользуемся доказанной выше формулой:

Действительно, расстояние между любым числом из интервала и будет меньше .

Окрестность

Очень важную разновидность рассматриваемых нами неравенств представляют такие вот неравенства:

где и — константы. Воспользуемся доказанной формулой для получения цепного неравенства:

По смыслу от нас требуется найти такие точки на числовой прямой, чтобы расстояние между ними и числом не превышало .
Геометрически это можно представить, как симметрический коридор с центром в точке и стенками в точках и .

Такие вот неравенства называют окрестностями. Если говорить точнее, неравенство задает -окрестность точки .
Окрестности очень часто используются в высшей математике. Например, именно понятие окрестности точки является ключевым в определении предела последовательности и функции. А на пределах строится вообще весь математический анализ. Но об этом поговорим в соответствующих статьях. А сейчас решим пример:

Решение

Запишем это неравенство немного в другом виде:

Сразу видим, что речь идет о -окрестности точки . Другими словами, в качестве подходят все точки из коридора от до с включением «стенок коридора» в качестве значений для .

Если строго, то пользуемся доказанной теоремой:

В полученном цепном неравенстве вычтем из всех частей :

Неравенства вида

Неравенства с модулем вида

Если , то неравенство выполняется для любого . Если , то выполняется:

Доказательство

Сразу заметим, что если , то неравенство выполняется вообще всегда, вне зависимости от , ведь модуль всегда неотрицателен.

Разберем вариант, когда . Тогда мы, прямо как и для неравенств вида , можем возвести обе части неравенства в квадрат и воспользоваться свойством связи модуля с квадратом:

Имеем произведение двух скобок друг на друга, которое должно быть больше . Такое возможно в двух случаях: если обе скобки больше нуля, и наоборот, обе скобки меньше нуля:

В верхнем И-условии при выполнении автоматически выполняется , так как . Поэтому, из двух неравенств можно оставить только . Аналогично поступаем и с нижним И-условием:

Итоговое неравенство имеет вид:

Теорема работает также и для случая нестрогих неравенств. Тогда в правой части также будут нестрогие неравенства.

В чем заключается смысл неравенств этого вида? Вновь вспоминаем, что можно рассматривать, как расстояние от до . В этом смысле неравнству будут удовлетворять все такие , что расстояние между и больше, чем . По факту, мы строим все тот-же симметричный относительно коридор со стенками и , и все подходящие не должны попасть в этот коридор.

Легко заметить, что неравенства вида являются, по факту, отрицанием неравенств вида . Действительно, в обоих случаях мы строим симметричный коридор. Только в первом в случае с мы берем все числа вне этого коридора, а в случае с все числа внутри него.

Теперь у вас есть вся необходимая информация для решения задач из раздела «Модуль».
Закрепите пройденную теорию практикой!

Источник

Модуль числа – теория и решение задач

Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂

А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.

Вот смотри…

Ситуация первая

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине “минус 70 километров” (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить “минус 5 кг апельсинов”. Эти значения всегда должны быть положительными.

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая

Ты покупаешь пакет чипсов “Lay’s”. На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией “Lay’s”, если они тебе недовесили?

Нет. Потому что “Lay’s” устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это “плюс-минус” – это и есть модуль.

Ситуация третья

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: “Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!” 20 тысяч – это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее…

Модуль числа – коротко о главном

Определение модуля:

Модуль (абсолютная величина) числа ( displaystyle x) – это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):

( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)

Свойства модуля:

Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
Модули противоположных чисел равны: ( left| -x right|=left| x right|);
Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).

Кстати, в продолжение этой темы у нас есть отличная статья: “Уравнения с модулем“. Когда прочитаешь эту статью, обязательно ознакомься и со второй.

И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.

Что же такое модуль числа?

Представь, что это ты.

Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).

Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).

Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).

То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).

Но ведь ты же можешь двигаться и назад!

Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).

Какое расстояние было пройдено в первом и во втором случае?

Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).

Таким образом, мы приблизились к понятию модуля.

Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.

Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).

Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.

Обозначается модуль просто:

( |mathbf{a}|,) (( a) – любое число).

Итак, найдём модуль числа ( 3) и ( -3):

( left| mathbf{3} right|=mathbf{3})

( left| -mathbf{3} right|=mathbf{3}.)

Основные свойства модуля

Первое свойство модуля

Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})

То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.

Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).

Если ( a) – отрицательное число, то его модуль равен противоположному числу.

Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})

А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):

Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).

Из этого следует, что модули противоположных чисел равны, то есть:

( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)

( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)

А теперь потренируйся:

( left| 9 right|text{ }=text{ }?;)
( left| -3 right|text{ }=text{ }?;)
( left| 16 right|text{ }=text{ }?;)
( left| 8 right|text{ }=text{ }?;)
( left| -17 right|text{ }=text{ }?.)

Ответы: 9; 3; 16; 8; 17.

Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)

Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.

Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:

если значение выражения больше нуля, то просто выносим его из-под знака модуля,
если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.

Ну что, попробуем? Оценим ( 2-sqrt{5}):

( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)

Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!

А, значит, знак модуля раскрываем, меняя знак у выражения:

( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)

Разобрался? Тогда попробуй сам:

( left| sqrt{3}-1 right|=?)
( left| 3-sqrt{7} right|=?)
( left| 2-sqrt{7} right|=?)
( left| sqrt{13}-4 right|=?)

Ответы:

( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})

Какими же ещё свойствами обладает модуль?

Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.

То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)

Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.

Например:

( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)

( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)

А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:

( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).

Еще одно свойство модуля…

Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.

( |a+bleft| text{ }le text{ } right|aleft| + right|b|)

Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.

Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:

( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10})

( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10})

Выражения также равны, если оба числа отрицательны:

( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10)

( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10})

Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:

( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4})

( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10})

или

( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4})

( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10})

( mathbf{4}<mathbf{10})

Рассмотрим еще парочку полезных свойств модуля

Что если перед нами такое выражение:

( left| 7x right|)

Что мы можем сделать с этим выражением?

Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:

Вот мы и пришли к другому свойству, которое в общем виде можно представить так:

( left| cx right|=ccdot left| x right|,) при ( c>0)

А чему равно такое выражение:

( {{left| x right|}^{2}}=?)

Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?

Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.

И что же получается? А вот что:

( {{left| x right|}^{2}}={{x}^{2}})

Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:

( {{left| 5 right|}^{2}}={{5}^{2}}=25)

( {{left| -5 right|}^{2}}=?)

Ну, и почему сомнения? Действуем смело!

( {{left| -5 right|}^{2}}={{5}^{2}}=25)

Во всем разобрался? Тогда вперед тренироваться на примерах!

Тренировка на примерах

1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)

2. У каких чисел модуль равен ( 5)?

3. Найдите значение выражений:

а) ( |3|text{ }+text{ }|-9|;)

б) ( |-5|text{ }-text{ }|6|;)

в) ( |15left| cdot right|-3|;)

г) ( displaystyle frac{|8|}{|-2|}).

Если не все пока ясно и есть затруднения в решениях, то давай разбираться:

Решение 1:

Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:

( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)

Решение 2:

Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).

Решение 3:

а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)

Все уловил? Тогда пора перейти к более сложному!

Решение более сложных примеров

Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)

Решение:

Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.

Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).

Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.

( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).

( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.

Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:

Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:

Модуль числа и его свойства (строгие определения и доказательства)

Модуль (абсолютная величина) числа ( x) – это само число ( x), если ( xge 0), и число ( -x), если ( x<0):

( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)

Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)

Пример:

Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).

Решение:

( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)

( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)

( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)

Основные свойства модуля (итог)

Для всех ( x,yin mathbb{R}):

( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
( left| -x right|=left| x right|;)
( left| xcdot y right|=left| x right|cdot left| y right|;)
( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
( left| x+y right|le left| x right|+left| y right|)
( left| cx right|=ccdot left| x right|, при text{ }c>0)
( {{left| x right|}^{2}}={{x}^{2}})

Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)

Доказательство:

Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):

( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})

а это противоречит определению модуля.

Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)

А теперь самостоятельно…

Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)

Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда

( left| cx right|=ccdot left| x right|), ч.т.д.

Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)

Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий курсов

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж – 19 лет (c 2003 года);
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

Источник

In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a ring. The concept of module generalizes also the notion of abelian group, since the abelian groups are exactly the modules over the ring of integers.

Like a vector space, a module is an additive abelian group, and scalar multiplication is distributive over the operation of addition between elements of the ring or module and is compatible with the ring multiplication.

Modules are very closely related to the representation theory of groups. They are also one of the central notions of commutative algebra and homological algebra, and are used widely in algebraic geometry and algebraic topology.

Introduction and definition[edit]

Motivation[edit]

In a vector space, the set of scalars is a field and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scalars need only be a ring, so the module concept represents a significant generalization. In commutative algebra, both ideals and quotient rings are modules, so that many arguments about ideals or quotient rings can be combined into a single argument about modules. In non-commutative algebra, the distinction between left ideals, ideals, and modules becomes more pronounced, though some ring-theoretic conditions can be expressed either about left ideals or left modules.

Much of the theory of modules consists of extending as many of the desirable properties of vector spaces as possible to the realm of modules over a «well-behaved» ring, such as a principal ideal domain. However, modules can be quite a bit more complicated than vector spaces; for instance, not all modules have a basis, and even those that do, free modules, need not have a unique rank if the underlying ring does not satisfy the invariant basis number condition, unlike vector spaces, which always have a (possibly infinite) basis whose cardinality is then unique. (These last two assertions require the axiom of choice in general, but not in the case of finite-dimensional spaces, or certain well-behaved infinite-dimensional spaces such as L^p spaces.)

Formal definition[edit]

Suppose that R is a ring, and 1 is its multiplicative identity.
A left R-module M consists of an abelian group (M, +) and an operation · : R × M → M such that for all r, s in R and x, y in M, we have

The operation · is called scalar multiplication. Often the symbol · is omitted, but in this article we use it and reserve juxtaposition for multiplication in R. One may write _RM to emphasize that M is a left R-module. A right R-module M_R is defined similarly in terms of an operation · : M × R → M.

Authors who do not require rings to be unital omit condition 4 in the definition above; they would call the structures defined above «unital left R-modules». In this article, consistent with the glossary of ring theory, all rings and modules are assumed to be unital.^[1]

An (R,S)-bimodule is an abelian group together with both a left scalar multiplication · by elements of R and a right scalar multiplication ∗ by elements of S, making it simultaneously a left R-module and a right S-module, satisfying the additional condition (r · x) ∗ s = r ⋅ (x ∗ s) for all r in R, x in M, and s in S.

If R is commutative, then left R-modules are the same as right R-modules and are simply called R-modules.

Examples[edit]

If K is a field, then K-vector spaces (vector spaces over K) and K-modules are identical.
If K is a field, and K[x] a univariate polynomial ring, then a K[x]-module M is a K-module with an additional action of x on M that commutes with the action of K on M. In other words, a K[x]-module is a K-vector space M combined with a linear map from M to M. Applying the structure theorem for finitely generated modules over a principal ideal domain to this example shows the existence of the rational and Jordan canonical forms.
The concept of a Z-module agrees with the notion of an abelian group. That is, every abelian group is a module over the ring of integers Z in a unique way. For n > 0, let n ⋅ x = x + x + … + x (n summands), 0 ⋅ x = 0, and (−n) ⋅ x = −(n ⋅ x). Such a module need not have a basis—groups containing torsion elements do not. (For example, in the group of integers modulo 3, one cannot find even one element which satisfies the definition of a linearly independent set since when an integer such as 3 or 6 multiplies an element, the result is 0. However, if a finite field is considered as a module over the same finite field taken as a ring, it is a vector space and does have a basis.)
The decimal fractions (including negative ones) form a module over the integers. Only singletons are linearly independent sets, but there is no singleton that can serve as a basis, so the module has no basis and no rank.
If R is any ring and n a natural number, then the cartesian product Rⁿ is both a left and right R-module over R if we use the component-wise operations. Hence when n = 1, R is an R-module, where the scalar multiplication is just ring multiplication. The case n = 0 yields the trivial R-module {0} consisting only of its identity element. Modules of this type are called free and if R has invariant basis number (e.g. any commutative ring or field) the number n is then the rank of the free module.
If M_n(R) is the ring of n × n matrices over a ring R, M is an M_n(R)-module, and e_i is the n × n matrix with 1 in the (i, i)-entry (and zeros elsewhere), then e_iM is an R-module, since re_im = e_irm ∈ e_iM. So M breaks up as the direct sum of R-modules, M = e₁M ⊕ … ⊕ e_nM. Conversely, given an R-module M₀, then M₀^⊕n is an M_n(R)-module. In fact, the category of R-modules and the category of M_n(R)-modules are equivalent. The special case is that the module M is just R as a module over itself, then Rⁿ is an M_n(R)-module.
If S is a nonempty set, M is a left R-module, and M^S is the collection of all functions f : S → M, then with addition and scalar multiplication in M^S defined pointwise by (f + g)(s) = f(s) + g(s) and (rf)(s) = rf(s), M^S is a left R-module. The right R-module case is analogous. In particular, if R is commutative then the collection of R-module homomorphisms h : M → N (see below) is an R-module (and in fact a submodule of N^M).
If X is a smooth manifold, then the smooth functions from X to the real numbers form a ring C^∞(X). The set of all smooth vector fields defined on X form a module over C^∞(X), and so do the tensor fields and the differential forms on X. More generally, the sections of any vector bundle form a projective module over C^∞(X), and by Swan’s theorem, every projective module is isomorphic to the module of sections of some bundle; the category of C^∞(X)-modules and the category of vector bundles over X are equivalent.
If R is any ring and I is any left ideal in R, then I is a left R-module, and analogously right ideals in R are right R-modules.
If R is a ring, we can define the opposite ring R^op which has the same underlying set and the same addition operation, but the opposite multiplication: if ab = c in R, then ba = c in R^op. Any left R-module M can then be seen to be a right module over R^op, and any right module over R can be considered a left module over R^op.
Modules over a Lie algebra are (associative algebra) modules over its universal enveloping algebra.
If R and S are rings with a ring homomorphism φ : R → S, then every S-module M is an R-module by defining rm = φ(r)m. In particular, S itself is such an R-module.

Submodules and homomorphisms[edit]

Suppose M is a left R-module and N is a subgroup of M. Then N is a submodule (or more explicitly an R-submodule) if for any n in N and any r in R, the product r ⋅ n (or n ⋅ r for a right R-module) is in N.

If X is any subset of an R-module M, then the submodule spanned by X is defined to be ${textstyle langle Xrangle =,bigcap _{Nsupseteq X}N}$ where N runs over the submodules of M which contain X, or explicitly ${textstyle left{sum _{i=1}^{k}r_{i}x_{i}mid r_{i}in R,x_{i}in Xright}}$ , which is important in the definition of tensor products.^[2]

The set of submodules of a given module M, together with the two binary operations + and ∩, forms a lattice which satisfies the modular law:
Given submodules U, N₁, N₂ of M such that N₁ ⊂ N₂, then the following two submodules are equal: (N₁ + U) ∩ N₂ = N₁ + (U ∩ N₂).

If M and N are left R-modules, then a map f : M → N is a homomorphism of R-modules if for any m, n in M and r, s in R,

f(rcdot m+scdot n)=rcdot f(m)+scdot f(n)

This, like any homomorphism of mathematical objects, is just a mapping which preserves the structure of the objects. Another name for a homomorphism of R-modules is an R-linear map.

A bijective module homomorphism f : M → N is called a module isomorphism, and the two modules M and N are called isomorphic. Two isomorphic modules are identical for all practical purposes, differing solely in the notation for their elements.

The kernel of a module homomorphism f : M → N is the submodule of M consisting of all elements that are sent to zero by f, and the image of f is the submodule of N consisting of values f(m) for all elements m of M.^[3] The isomorphism theorems familiar from groups and vector spaces are also valid for R-modules.

Given a ring R, the set of all left R-modules together with their module homomorphisms forms an abelian category, denoted by R—Mod (see category of modules).

Types of modules[edit]

Finitely generated: An R-module M is finitely generated if there exist finitely many elements x₁, …, x_n in M such that every element of M is a linear combination of those elements with coefficients from the ring R.
Cyclic: A module is called a cyclic module if it is generated by one element.
Free: A free R-module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the ring R. These are the modules that behave very much like vector spaces.
Projective: Projective modules are direct summands of free modules and share many of their desirable properties.
Injective: Injective modules are defined dually to projective modules.
Flat: A module is called flat if taking the tensor product of it with any exact sequence of R-modules preserves exactness.
Torsionless: A module is called torsionless if it embeds into its algebraic dual.
Simple: A simple module S is a module that is not {0} and whose only submodules are {0} and S. Simple modules are sometimes called irreducible.^[4]
Semisimple: A semisimple module is a direct sum (finite or not) of simple modules. Historically these modules are also called completely reducible.
Indecomposable: An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable, but there are indecomposable modules which are not simple (e.g. uniform modules).
Faithful: A faithful module M is one where the action of each r ≠ 0 in R on M is nontrivial (i.e. r ⋅ x ≠ 0 for some x in M). Equivalently, the annihilator of M is the zero ideal.
Torsion-free: A torsion-free module is a module over a ring such that 0 is the only element annihilated by a regular element (non zero-divisor) of the ring, equivalently rm = 0 implies r = 0 or m = 0.
Noetherian: A Noetherian module is a module which satisfies the ascending chain condition on submodules, that is, every increasing chain of submodules becomes stationary after finitely many steps. Equivalently, every submodule is finitely generated.
Artinian: An Artinian module is a module which satisfies the descending chain condition on submodules, that is, every decreasing chain of submodules becomes stationary after finitely many steps.
Graded: A graded module is a module with a decomposition as a direct sum M = ⨁_x M_x over a graded ring R = ⨁_x R_x such that R_xM_y ⊂ M_x+y for all x and y.
Uniform: A uniform module is a module in which all pairs of nonzero submodules have nonzero intersection.

Further notions[edit]

Relation to representation theory[edit]

A representation of a group G over a field k is a module over the group ring k[G].

If M is a left R-module, then the action of an element r in R is defined to be the map M → M that sends each x to rx (or xr in the case of a right module), and is necessarily a group endomorphism of the abelian group (M, +). The set of all group endomorphisms of M is denoted End_Z(M) and forms a ring under addition and composition, and sending a ring element r of R to its action actually defines a ring homomorphism from R to End_Z(M).

Such a ring homomorphism R → End_Z(M) is called a representation of R over the abelian group M; an alternative and equivalent way of defining left R-modules is to say that a left R-module is an abelian group M together with a representation of R over it. Such a representation R → End_Z(M) may also be called a ring action of R on M.

A representation is called faithful if and only if the map R → End_Z(M) is injective. In terms of modules, this means that if r is an element of R such that rx = 0 for all x in M, then r = 0. Every abelian group is a faithful module over the integers or over some ring of integers modulo n, Z/nZ.

Generalizations[edit]

A ring R corresponds to a preadditive category R with a single object. With this understanding, a left R-module is just a covariant additive functor from R to the category Ab of abelian groups, and right R-modules are contravariant additive functors. This suggests that, if C is any preadditive category, a covariant additive functor from C to Ab should be considered a generalized left module over C. These functors form a functor category C—Mod which is the natural generalization of the module category R—Mod.

Modules over commutative rings can be generalized in a different direction: take a ringed space (X, O_X) and consider the sheaves of O_X-modules (see sheaf of modules). These form a category O_X—Mod, and play an important role in modern algebraic geometry. If X has only a single point, then this is a module category in the old sense over the commutative ring O_X(X).

One can also consider modules over a semiring. Modules over rings are abelian groups, but modules over semirings are only commutative monoids. Most applications of modules are still possible. In particular, for any semiring S, the matrices over S form a semiring over which the tuples of elements from S are a module (in this generalized sense only). This allows a further generalization of the concept of vector space incorporating the semirings from theoretical computer science.

Over near-rings, one can consider near-ring modules, a nonabelian generalization of modules.^{[citation needed]}

Notes[edit]

^ Dummit, David S. & Foote, Richard M. (2004). Abstract Algebra. Hoboken, NJ: John Wiley & Sons, Inc. ISBN 978-0-471-43334-7.
^ Mcgerty, Kevin (2016). «ALGEBRA II: RINGS AND MODULES» (PDF).
^ Ash, Robert. «Module Fundamentals» (PDF). Abstract Algebra: The Basic Graduate Year.
^ Jacobson (1964), p. 4, Def. 1; Irreducible Module at PlanetMath.

References[edit]

F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992, ISBN 0-387-97845-3, ISBN 3-540-97845-3
Nathan Jacobson. Structure of rings. Colloquium publications, Vol. 37, 2nd Ed., AMS Bookstore, 1964, ISBN 978-0-8218-1037-8

External links[edit]

«Module», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
module at the nLab

Источник

Introduction and definition[edit]

Motivation[edit]

Formal definition[edit]

If R is commutative, then left R-modules are the same as right R-modules and are simply called R-modules.

Examples[edit]

If K is a field, then K-vector spaces (vector spaces over K) and K-modules are identical.
If K is a field, and K[x] a univariate polynomial ring, then a K[x]-module M is a K-module with an additional action of x on M that commutes with the action of K on M. In other words, a K[x]-module is a K-vector space M combined with a linear map from M to M. Applying the structure theorem for finitely generated modules over a principal ideal domain to this example shows the existence of the rational and Jordan canonical forms.
The concept of a Z-module agrees with the notion of an abelian group. That is, every abelian group is a module over the ring of integers Z in a unique way. For n > 0, let n ⋅ x = x + x + … + x (n summands), 0 ⋅ x = 0, and (−n) ⋅ x = −(n ⋅ x). Such a module need not have a basis—groups containing torsion elements do not. (For example, in the group of integers modulo 3, one cannot find even one element which satisfies the definition of a linearly independent set since when an integer such as 3 or 6 multiplies an element, the result is 0. However, if a finite field is considered as a module over the same finite field taken as a ring, it is a vector space and does have a basis.)
The decimal fractions (including negative ones) form a module over the integers. Only singletons are linearly independent sets, but there is no singleton that can serve as a basis, so the module has no basis and no rank.
If R is any ring and n a natural number, then the cartesian product Rⁿ is both a left and right R-module over R if we use the component-wise operations. Hence when n = 1, R is an R-module, where the scalar multiplication is just ring multiplication. The case n = 0 yields the trivial R-module {0} consisting only of its identity element. Modules of this type are called free and if R has invariant basis number (e.g. any commutative ring or field) the number n is then the rank of the free module.
If M_n(R) is the ring of n × n matrices over a ring R, M is an M_n(R)-module, and e_i is the n × n matrix with 1 in the (i, i)-entry (and zeros elsewhere), then e_iM is an R-module, since re_im = e_irm ∈ e_iM. So M breaks up as the direct sum of R-modules, M = e₁M ⊕ … ⊕ e_nM. Conversely, given an R-module M₀, then M₀^⊕n is an M_n(R)-module. In fact, the category of R-modules and the category of M_n(R)-modules are equivalent. The special case is that the module M is just R as a module over itself, then Rⁿ is an M_n(R)-module.
If S is a nonempty set, M is a left R-module, and M^S is the collection of all functions f : S → M, then with addition and scalar multiplication in M^S defined pointwise by (f + g)(s) = f(s) + g(s) and (rf)(s) = rf(s), M^S is a left R-module. The right R-module case is analogous. In particular, if R is commutative then the collection of R-module homomorphisms h : M → N (see below) is an R-module (and in fact a submodule of N^M).
If X is a smooth manifold, then the smooth functions from X to the real numbers form a ring C^∞(X). The set of all smooth vector fields defined on X form a module over C^∞(X), and so do the tensor fields and the differential forms on X. More generally, the sections of any vector bundle form a projective module over C^∞(X), and by Swan’s theorem, every projective module is isomorphic to the module of sections of some bundle; the category of C^∞(X)-modules and the category of vector bundles over X are equivalent.
If R is any ring and I is any left ideal in R, then I is a left R-module, and analogously right ideals in R are right R-modules.
If R is a ring, we can define the opposite ring R^op which has the same underlying set and the same addition operation, but the opposite multiplication: if ab = c in R, then ba = c in R^op. Any left R-module M can then be seen to be a right module over R^op, and any right module over R can be considered a left module over R^op.
Modules over a Lie algebra are (associative algebra) modules over its universal enveloping algebra.
If R and S are rings with a ring homomorphism φ : R → S, then every S-module M is an R-module by defining rm = φ(r)m. In particular, S itself is such an R-module.

Submodules and homomorphisms[edit]

If M and N are left R-modules, then a map f : M → N is a homomorphism of R-modules if for any m, n in M and r, s in R,

This, like any homomorphism of mathematical objects, is just a mapping which preserves the structure of the objects. Another name for a homomorphism of R-modules is an R-linear map.

Given a ring R, the set of all left R-modules together with their module homomorphisms forms an abelian category, denoted by R—Mod (see category of modules).

Types of modules[edit]

Finitely generated: An R-module M is finitely generated if there exist finitely many elements x₁, …, x_n in M such that every element of M is a linear combination of those elements with coefficients from the ring R.
Cyclic: A module is called a cyclic module if it is generated by one element.
Free: A free R-module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the ring R. These are the modules that behave very much like vector spaces.
Projective: Projective modules are direct summands of free modules and share many of their desirable properties.
Injective: Injective modules are defined dually to projective modules.
Flat: A module is called flat if taking the tensor product of it with any exact sequence of R-modules preserves exactness.
Torsionless: A module is called torsionless if it embeds into its algebraic dual.
Simple: A simple module S is a module that is not {0} and whose only submodules are {0} and S. Simple modules are sometimes called irreducible.^[4]
Semisimple: A semisimple module is a direct sum (finite or not) of simple modules. Historically these modules are also called completely reducible.
Indecomposable: An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable, but there are indecomposable modules which are not simple (e.g. uniform modules).
Faithful: A faithful module M is one where the action of each r ≠ 0 in R on M is nontrivial (i.e. r ⋅ x ≠ 0 for some x in M). Equivalently, the annihilator of M is the zero ideal.
Torsion-free: A torsion-free module is a module over a ring such that 0 is the only element annihilated by a regular element (non zero-divisor) of the ring, equivalently rm = 0 implies r = 0 or m = 0.
Noetherian: A Noetherian module is a module which satisfies the ascending chain condition on submodules, that is, every increasing chain of submodules becomes stationary after finitely many steps. Equivalently, every submodule is finitely generated.
Artinian: An Artinian module is a module which satisfies the descending chain condition on submodules, that is, every decreasing chain of submodules becomes stationary after finitely many steps.
Graded: A graded module is a module with a decomposition as a direct sum M = ⨁_x M_x over a graded ring R = ⨁_x R_x such that R_xM_y ⊂ M_x+y for all x and y.
Uniform: A uniform module is a module in which all pairs of nonzero submodules have nonzero intersection.

Further notions[edit]

Relation to representation theory[edit]

A representation of a group G over a field k is a module over the group ring k[G].

Generalizations[edit]

Over near-rings, one can consider near-ring modules, a nonabelian generalization of modules.^{[citation needed]}

Notes[edit]

^ Dummit, David S. & Foote, Richard M. (2004). Abstract Algebra. Hoboken, NJ: John Wiley & Sons, Inc. ISBN 978-0-471-43334-7.
^ Mcgerty, Kevin (2016). «ALGEBRA II: RINGS AND MODULES» (PDF).
^ Ash, Robert. «Module Fundamentals» (PDF). Abstract Algebra: The Basic Graduate Year.
^ Jacobson (1964), p. 4, Def. 1; Irreducible Module at PlanetMath.

References[edit]

F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992, ISBN 0-387-97845-3, ISBN 3-540-97845-3
Nathan Jacobson. Structure of rings. Colloquium publications, Vol. 37, 2nd Ed., AMS Bookstore, 1964, ISBN 978-0-8218-1037-8

External links[edit]

«Module», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
module at the nLab

Источник

Модуль числа

Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.

Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.

Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному (без знака!).
Например,

Обратите внимание: модуль числа всегда неотрицателен:

Определение модуля

Вот оно:

От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.

Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию

Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,

В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.

Геометрическая интерпретация модуля

Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.

Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.

Вообще, если имеются два числа, a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A
до точки B.)

Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).

Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.

Перейдём к неравенствам. Решим неравенство: .

Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.

Ответ: (-11; -3).

Другой пример. Решим неравенство: |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно 7. Отметим эти точки на числовой прямой.
Ответ: .

График функции

Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.

Корень из квадрата

Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что

Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .

Примеры заданий ЕГЭ

1. Найдите значение выражения: при .

Заметим, что при . Следовательно, значение нашего выражения равно: .

2. Найдите значение выражения: при .

Действуем аналогично:

В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.

Читайте также: Уравнения с модулем

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Модуль числа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.01.2023

Источник

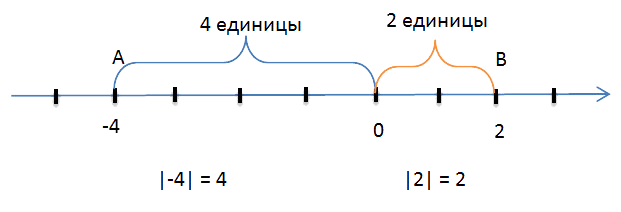
Обозначим на
координатной прямой две точки, которые соответствуют числам
«−4» и 2.

Точка «A», соответствующая числу «−4»,
находится на расстоянии
4 единичных отрезков от точки 0
(начала отсчёта), то есть длина отрезка «OA»
равна 4 единицам.

Число 4 (длина отрезка «OA») называют модулем
числа «−4».

Обозначают модуль числа так: |−4| = 4

Читают символы выше следующим образом: «модуль числа
минус четыре равен четырём».

Точка «B», соответствующая
числу «+2», находится на расстоянии двух единичных отрезков от начала отсчёта,
то есть длина отрезка «OB» равна двум единицам.

Число 2 называют модулем числа
«+2» и записывают:
|+2| = 2 или |2| = 2.

Если взять некоторое число «a» и изобразить его
точкой «A» на координатной прямой, то
расстояние от точки «A» до начала отсчёта
(другими словами длина отрезка «OA») и будет называться
модулем числа «a».

|a| = OA

Запомните!

Модулем рационального числа называют расстояние от
начала отсчёта до точки координатной прямой, соответствующей этому числу.

Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать,
что модуль числа не может быть отрицательным.

Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи.

Модуль положительного числа равен самому числу.

|a| = a, если a > 0
Модуль отрицательного числа равен противоположному числу.

|−a| = a, если a < 0
Модуль нуля равен нулю.

|0| = 0, если a = 0
Противоположные числа имеют равные модули.

|−a| = |a| = a

Примеры модулей рациональных чисел:

|−4,8| = 4,8
|5| = 5
|0| = 0
|− | =

Источник

Модуль

«Величина» числа

Геометрический смысл

Количественный смысл

Понятие величины

Модуль числа

Свойства модуля

Очевидные свойства

Связь с возведением в квадрат

Связь с корнем

Неравенство треугольника

Расстояние между точками

Функция модуля

Уравнения с модулем

Неравенства с модулем

Неравенства вида

Окрестность

Неравенства вида

Модуль числа – теория и решение задач

Модуль числа – коротко о главном

Что же такое модуль числа?

Основные свойства модуля

Тренировка на примерах

Решение более сложных примеров

Модуль числа и его свойства (строгие определения и доказательства)

Основные свойства модуля (итог)

Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)

Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)

Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Introduction and definition[edit]

Motivation[edit]

Formal definition[edit]

Examples[edit]

Submodules and homomorphisms[edit]

Types of modules[edit]

Further notions[edit]

Relation to representation theory[edit]

Generalizations[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Introduction and definition[edit]

Motivation[edit]

Formal definition[edit]

Examples[edit]

Submodules and homomorphisms[edit]

Types of modules[edit]

Further notions[edit]

Relation to representation theory[edit]

Generalizations[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Модуль числа