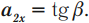Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S — путь
- v — скорость
- t — время
Равномерное движение
x=x_0 + v*t
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
Равномерно ускоренное движение: ускорение
a=frac { v — v_0 } { t }
- a — ускорение
- v — скорость
- v0 — начальная скорость
- t — время
Равномерно ускоренное движение: скорость
v=v_0 + at
- v — скорость
- v0 — начальная скорость
- a — ускорение
- t — время
Равномерно ускоренное движение: путь
S=vt + frac { at^2 } { 2 }
- s — путь
- v — скорость
- t — время
- a — ускорение
Равномерно ускоренное движение: координата
x=x_0 + vt + frac { at^2 } { 2 }
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
- a — ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_ { 0 } t — frac { gt^2 } { 2 }
- h — высота
- h0 — начальная высота
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 — gt
- v — скорость
- v0 — начальная скорость
- g — ускорение свободного падения
- t — время
Скорость, ускорение, время
v=at
- v — скорость
- a — ускорение
- t — время
Скорость свободно падающего тела
v=gt
- v — скорость
- g — ускорение свободного падения
- t — время
Центростремительное ускорение
a=frac { v^2 } { R }
- a — центростремительное ускорение
- v — скорость
- R — радиус
Угловая скорость
omega=frac { phi } { t }
- ω — угловая скорость
- φ — угол
- t — время
Равномерное круговое движение
l=Rphi
- l — длина дуги окружности
- R — радиус
- φ — угол
Равномерное круговое движение: линейная скорость
v=R omega
- v — линейная скорость
- R — радиус
- ω — угловая скорость
Период вращения
T=frac { t } { N }
- T — период
- t — время
- N — число вращений
T=frac { 2 pi R } { v }
- T — период
- R — радиус
- v — линейная скорость
T=frac { 2 pi } { omega }
- T — период
- ω — угловая скорость
Центростремительное ускорение
a=frac { 4 pi^ { 2 } R } { T^2 }
- a — центростремительное ускорение
- R — радиус
- T — период вращения
a=4 pi^ { 2 } Rn^2
- a — центростремительное ускорение
- R — радиус
- n — частота вращения
Частота вращения
n=frac { 1 } { T }
- n — частота вращения
- T — период вращения
Центростремительное ускорение
a=omega ^ { 2 } R
- a — центростремительное ускорение
- ω — угловая скорость
- R — радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t cos(alpha)
- x — координата (дальность)
- v0 — начальная скорость
- t — время
- α — угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t sin (alpha) — frac { gt^2 } { 2 }
- y — координата (высота подъема )
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
- α — угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* sin (alpha) — gt
- vy — вертикальная скорость
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
- t — время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =frac { v_0^2* sin (alpha)^ { 2 } } { 2g }
- hмакс — максимальная высота
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=frac { 2v_0 * sin (alpha) } { g }
- t — время
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x — координата (дальность)
- x0 — начальная координата
- v — скорость
- t — время
Высота подъема тела, брошенного горизонтально
y=y_0 — frac { gt^2 } { 2 }
- y — координата (высота подъема)
- y0 — начальная координата (высота)
- g — ускорение свободного падения
- t — время
Общее время движения тела, брошенного горизонтально
t_max=sqrt { frac { 2h } { g } }
- tмакс — максимальное время
- h — высота
- g — ускорение свободного падения
Смотри также:
- Формулы МКТ
- Справочные материалы по физике
- Физические величины и единицы их измерения
Морфемный разбор слова:
Однокоренные слова к слову:
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
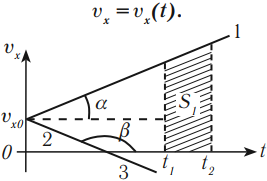
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Формула скорости — обозначение, единицы измерения и примеры нахождения
Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Виды скорости в физике и методы их вычисления
Скорость в физике — что это такое
Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.
В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.
Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн.
Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени.
Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.
Виды скорости в физике, основные характеристики
В физике существуют такие виды скорости, как: начальная скорость, равномерная скорость, средняя скорость, мгновенная скорость.
Как писалось выше, скорость равна отношению пути S ко времени t.
Формулы скорости при движении разных видов
ϑ н — начальная скорость;
ϑ 0 — конечная скорость;
Примеры задач с решением
На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение:
Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.
ϑ = 180 3 = 60 к м ч
Ответ: скорость автомобиля составляет 60 км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трех участках пути.
ϑ с р = S о б щ t о б щ
ϑ с р = S 1 + S 2 + S 3 t 1 + t 2 + t 3
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 / = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.
Ответ: начальная скорость составляет 2,6 м/с.
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется начальная скорость в физике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется начальная скорость в физике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Механическое движение
О чем эта статья:
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Как найти скорость с ускорением и временем: разные подходы, проблемы, примеры
Скорость, ускорение и время являются основными величинами для вывода уравнения движения. В общем, производная скорости по времени дает ускорение.
В кинематике скорость можно найти, используя ускорение и время. С скорость и ускорение связаны с величиной и направлением, для определения скорости мы используем как алгебраический метод, так и интегральное исчисление. В этом посте обсуждается, как найти скорость с учетом ускорения и времени, используя оба метода.
Представим, что тело движется с ускорением «а», преодолевая определенное расстояние в момент «t».
Алгебраическим методом:
Из кинематического определения ускорение — скорость изменения скорости движущегося тела.
Здесь мы рассматриваем; изначально тело имеет минимальную скорость; следовательно, начальную скорость можно считать приблизительно нулевой.
Переставляя члены, мы получаем скорость тела как;
Методом интегрального исчисления:
Производная по времени от скорость дает ускорение тела. Это определяется следующим уравнением.
Преобразуя приведенное выше уравнение
Интегрируя приведенное выше уравнение по времени t
Где; C — интегральная постоянная.
Следовательно; v = при + C
Вышеприведенное уравнение дает скорость; таким образом, умножение ускорения на время дает скорость.
Как найти скорость по графику ускорения и времени?
Построен график ускорения в зависимости от времени, что позволяет определить различные физические величины, такие как рывки и удары. скорость. Область, покрытая графиком «ускорение – время», показывает скорость.
Например, машина движется с начальной скоростью 16 м / с. Как со временем, машина начинает разгоняться. В ускорение автомобиля постоянна во времени. Через некоторое время машина внезапно останавливается, что показано на приведенном ниже графике.
Пунктирная линия используется как контрольная линия, когда тело останавливается.
Площадь, занимаемая в график ускорение – время представляет собой прямоугольник. Площадь прямоугольника определяется как
Из приведенного выше графика длина прямоугольника — это ускорение, а ширина — время; следовательно, уравнение
Но площадь графика at — это скорость, тогда
Следовательно, по определению На графике времени разгона площадь — это не что иное, как скорость.
Как найти начальную скорость с ускорением и временем?
Когда тело начинает перемещаться из одной точки в другую, сначала оно обладает некоторой скоростью. Тело не нуждается в постоянной скорости, пока оно не достигнет своего конечного пункта назначения. Скорость тела изменяется со временем, когда оно движется, и, следовательно, тело приобретает ускорение.
Из приведенного выше объяснения ясно, что движущееся тело может иметь разные скорости. Тела скорость на начальном этапе может отличаться от финального. Давайте обсудим нахождение скорости с ускорением и временем в начальной точке.
Рассмотрим сначала автомобиль, движущийся со скоростью vi, а его скорость изменится через некоторое время t. Теперь тело ускоряется с ускорением «а», и, наконец, когда оно достигает конечной точки, оно имеет скорость vf.
Начальную скорость можно рассчитать тремя способами.
Используя алгебраический метод:
Ускорение из-за изменения скорости определяется выражением
Вышеприведенное уравнение дает начальную скорость движущегося тела.
По расчетам:
Исходя из определения ускорения, уравнение имеет вид
Интегрируя приведенное выше уравнение, выбирая пределы в качестве начальной скорости vi в момент времени t = 0 и конечной скорости vf в момент t.
Преобразуя приведенное выше уравнение, мы получаем начальную скорость.
Графическим методом:
Построен график зависимости скорости от времени, наклон которого дает ускорение — затем, найдя наклон, можно вычислить начальную скорость.
Исходя из приведенного выше графика, мы можем сказать это.
- В единый интервал временискорость тела изменяется.
- OD — время, затрачиваемое телом на путешествие, а BD — конечная скорость тела.
- Перпендикулярные линии от BD к A проводятся параллельно OD. Таким же образом проводится линия BE параллельно OD.
На приведенном выше графике показано, что
Начальная скорость тела vi = ОА
Конечная скорость тела vf = БД
На графике BD = BC + DC
Следовательно, vf = ВС + ПОС
vf = до нашей эры + ви
На графике наклон = ускорение a
Но AC = t (из графика)
Подставляя значение BC
Как найти изменение скорости в зависимости от ускорения и времени
В общем, изменение скорости со временем дает ускорение.
Пусть тело движется с ускорением ‘a’ со временем ‘t’, изначально скорость объекта равна vi, а в конечной точке имеет скорость vf. Тогда изменение скорости определяется по уравнению:
Где ∆v — изменение скорости, а ∆t — изменение во времени.
Но изменение скорости определяется разница между начальной и конечной скоростью. Это дается уравнением ниже.
Изменение в скорость можно рассчитать с помощью графика «ускорение – время». Площадь под графиком at показывает изменение скорости.
Давайте ясно поймем это, рассмотрев пример, представленный графиком, приведенным ниже.
Площадь на графике времени ускорения представляет собой треугольник. Следовательно, вычисляя изменение скорости дается путем вычисления площади треугольника. Формула для определения площади треугольника:
Здесь h — высота треугольника, ускорение считается высотой, а b — основание треугольника, которое определяется осью времени. Таким образом, изменение скорости равно
По изменению скорости мы можем узнать начальную и конечную скорость тела.
Решены задачи о том, как найти скорость с ускорением и временем.
Задача 1) Лодка движется с начальной скоростью 11 м / с. Лодка развивает ускорение 3 м / с. 2 каждые 10 секунд. Затем рассчитайте изменение скорости и конечную скорость лодки.
Решение:
Данные приведены для расчета:
Начальная скорость лодки vi = 11 м / с.
Изменение ускорения, достигаемого лодкой a = 3 м / с 2 .
Изменение по времени t = 10 сек.
Чтобы найти окончательную скорость, уравнение
Задача 2) График ускорение – время приведен ниже. Найдите изменение скорости и вычислите начальную скорость, если конечная скорость равна 54 м / с.
Решение:
Конечная скорость vf = 54 м / с. На графике ускорение-время покрытая область представляет собой трапецию. Таким образом, площадь трапеции определяется выражением
Где a и b — прилегающее основание трапеции, h — высота. Из графика; a = 9 единиц, b = 5 единиц, h = 4 единицы.
Изменение скорости равно площади трапеции.
Чтобы найти начальную скорость
Задача 3) дается график ускорение – время для определения изменения скорости.
Решение:
Приведенный выше график можно разделить на три части, представленные пунктирной линией, как показано на рисунке ниже.
На приведенном выше графике можно понять следующие термины.
OAD и BCE — треугольник; площадь треугольника задается формулой
ABCD — прямоугольник; площадь прямоугольника определяется выражением
Чтобы найти изменение скорости, необходимо вычислить сумму площадей всех геометрических структур.
Изменение скорости ∆v = 180 м / с.
Задача 4) Найдите начальную скорость мяча, который ускоряется со скоростью 6 м / с. 2 со временем 8 сек. Конечная скорость мяча составляет 100 м / с.
Решение:
Приведены данные: ускорение мяча a = 6 м / с2.
Конечная скорость vf = 100 м / с.
Для нахождения начальной скорости тела задается уравнение
Задача 5) Рассчитайте изменение скорости движущегося объекта, имеющего начальную скорость 34 м / с. Ускорение объекта 12 м / с. 2 , а изменение по времени — 7 сек.
Решение:
Начальная скорость объекта vi = 34 м / с.
Ускорение объекта a = 12 м / с 2 .
Изменение по времени t = 7 сек.
Конечная скорость объекта определяется выражением;
Изменение скорости определяется выражением;
Задача 6) Диск движется с начальной скоростью 25 м / с. Диск меняет свою скорость каждые 10 секунд. Изменение ускорения 5 м / с. 2 . Рассчитайте конечную скорость диска.
Решение:
Начальная скорость диска vi = 25 м / с.
Изменение ускорения ∆a = 5 м / с 2 .
Изменение времени ∆t = 10 сек.
Изменение скорости равно
Конечная скорость диска может быть рассчитана по формуле, приведенной ниже.
Последние сообщения о передовой науке и исследованиях
Я Кирти К. Мурти, я закончила аспирантуру по физике со специализацией в области физики твердого тела. Я всегда считал физику фундаментальным предметом, связанным с нашей повседневной жизнью. Будучи студентом естественных наук, я люблю изучать новые вещи в физике. Как писатель, моя цель — через свои статьи дойти до читателей в упрощенной форме.
Свяжитесь со мной — keerthikmurthy24@gmail.com
 report this ad Похожие сообщения
report this ad Похожие сообщения
Ускорение против. Замедление: подробный анализ
Примеры положительного ускорения: подробный анализ
Поверхностное ускорение без трения: исчерпывающая информация…
Как найти ускорение свободного падения:…
Как найти ускорение свободного падения…
Пример гравитационного ускорения: подробные сведения
Как рассчитать ускорение с помощью…
Как найти среднюю скорость…
Скорость графика постоянного ускорения против…
Как найти ускорение с…
Как рассчитать силу без…
Как найти нормальную силу…
15 Пример чистой силы:…
Как найти нормальную силу…
Как найти чистую силу:…
Мгновенная скорость и ускорение: сравнительное…
Отрицательно ли замедление: подробные факты
Как определить конечную скорость…
Как найти скорость с помощью…
Как найти скорость с помощью…
Свяжитесь с нами
Электронная почта: hr@lambdageeks.com
support@lambdageeks.com
Контактное лицо: + 91-8106864654
Наша миссия
Наша миссия — служить и делиться своим опытом с большим и разносторонним сообществом студентов или работающих профессионалов для удовлетворения их потребностей в обучении.
Виды скорости в физике и методы их вычисления
Скорость в физике — что это такое
Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.
В международной системе единиц (СИ) единица измерения скорости обозначается как метр в секунду ( м с ) .
На практике зачастую используют внесистемные единицы измерения скорости. Например: километр в час ( к м ч ) .
В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.
Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн.
Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени.
Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.
Виды скорости в физике, основные характеристики
В физике существуют такие виды скорости, как: начальная скорость, равномерная скорость, средняя скорость, мгновенная скорость.
- Начальная скорость — это скорость в течении начального момента времени. Начальная скорость подразумевается какой-то момент времени, в который начинается измерение скорости (обычно t = t 0 ).
- Равномерная скорость — это скорость при равномерном движении, численно равная отношению пути, пройденного телом, ко времени, затраченному на прохождение этого пути.
- Средняя скорость — это отношение всего пройденного пути к затраченному на это движение времени.
- Мгновенная скорость — это векторная величина, равная отношению перемещения к малому промежутку времени, за которое это перемещение производится.
Скорость принято записывать буквой ϑ , в СИ она обозначается как м с .
Как писалось выше, скорость равна отношению пути S ко времени t.
Формулы скорости при движении разных видов
Нахождение начальной скорости зависит от задачи и от исходных данных. Ее можно найти по конечной скорости, ускорению и времени: ϑ н = ϑ 0 — ( α ∙ t ) , где:
ϑ н — начальная скорость;
ϑ 0 — конечная скорость;
Равномерная — находится по обычной формуле скорости: ϑ = S t , где:
Формула средней скорости: ϑ с р = S о б щ t о б щ .
Формула мгновенной скорости: ϑ ⇀ = ∆ S ⇀ ∆ t .
Примеры задач с решением
На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение:
Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.
ϑ = 180 3 = 60 к м ч
Ответ: скорость автомобиля составляет 60 км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трех участках пути.
ϑ с р = S о б щ t о б щ
ϑ с р = S 1 + S 2 + S 3 t 1 + t 2 + t 3
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 / = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.
ϑ н = ϑ 0 — ( α ∙ t )
ϑ н = 3 — ( 0 , 2 ∙ 2 ) = 2 , 6 м с
Ответ: начальная скорость составляет 2,6 м/с.
источники:
http://ru.lambdageeks.com/how-to-find-velocity-with-acceleration-and-time/
http://wika.tutoronline.ru/fizika/class/7/vidy-skorosti-v-fizike-i-metody-ih-vychisleniya
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
2.9 (58.04%) 112 votes
Download Article
Download Article
Velocity is a function of time and defined by both a magnitude and a direction. [1]
Often in physics problems, you will need to calculate the initial velocity (speed and direction) at which an object in question began to travel. There are multiple equations that can be used to determine initial velocity. Using the information given in a problem, you can determine the proper equation to use and easily answer your question.
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you have values for the final velocity, acceleration, and time involved, you can use the following equation:[3]
- Initial velocity: Vi = Vf — (a * t)
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- t stands for “time”
- Note that this equation is the standard equation used when finding initial velocity.
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
Advertisement
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.[4]
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
- Write the known information:
- Vi = ?, Vf = 200 m/s, a = 10 m/s2, t = 12 s
- Multiply the acceleration and time. a * t = 10 * 12 =120
- Subtract the product from the final velocity. Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 m/s east
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation.[5]
If you know values for the distance, time, and acceleration, you can use the following equation:- Initial velocity: Vi = (d / t) — [(a * t) / 2]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- d stands for “distance”
- a stands for “acceleration”
- t stands for “time”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
- Write the known information:
- Vi = ?, d = 150 m, a = 7 m/s2, t = 30 s
- Multiply the acceleration and time. a * t = 7 * 30 = 210
- Divide the product by two. (a * t) / 2 = 210 / 2 = 105
- Divide the distance by the time. d / t = 150 / 30 = 5
- Subtract your first quotient from the second quotient. Vi = (d / t) — [(a * t) / 2] = 5 – 105 = -100 Vi = -100 m/s west
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, acceleration, and distance, you can use the following equation:[7]
- Initial velocity: Vi = √ [Vf2 — (2 * a * d)]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 12 m/s, a = 5 m/s2, d = 10 m
- Square the final velocity. Vf2= 122 = 144
- Multiply the acceleration by the distance and the number two. 2 * a * d = 2 * 5 * 10 = 100
- Subtract this product from your previous one. Vf2 — (2 * a * d) = 144 – 100 = 44
- Take the square root of your answer. = √ [Vf2 — (2 * a * d)] = √44 = 6.633 Vi = 6.633 m/s north
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, time, and distance, you can use the following equation:[9]
- Initial velocity: Vi = 2(d/t) — Vf
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- t stands for “time”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m
- Divide distance by time. (d/t) = (45/15) = 3
- Multiply that value by 2. 2 (d/t) = 2 (45/15) = 6
- Subtract final velocity from the product. 2(d/t) — Vf = 6 — 3 = 3 Vi = 3 m/s south
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
Advertisement
Add New Question
-
Question
A bullet of 60 gm is fired using a rifle of mass 12kg. Rifle recoils with a velocity of 2.5m/s. What is the initial velocity?
Kinetic energy -> Kinetic energy
0.5mv^2 -> 0.5mv^2
0.5 x 12 x 2,5^2 = 0.5 x 0.06 x v^2
6 x 6.25 = 0.03 x v^2
37.5 = 0.03 x v^2
sqrt(37.5/0.03) = v
sqrt(1250) = v
v = 35.3 m/s -
Question
If displacement and time are related as s = 3.5t + 5t2, what is the initial velocity?
Initial velocity is 3.5. The equation is s = ut + 1/2at^2, where s — distance, u — inititial velocity, and a — acceleration.
-
Question
How do I modify the acceleration formula to one that gives me initial velocity?
You can’t change the acceleration formula to one that gives you the initial velocity you want, as a=v/t. However, Vf=Vi+a.t is re-arranged. Vi=Vf-a.t, a=Vf-Vi/t, t=Vf-Vi/a.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Pencil
- Paper
- Calculator (optional)
About This Article
Article SummaryX
To find initial velocity, start by multiplying the acceleration by the time. Then, divide that number by 2 and write down the quotient you get. Next, divide the distance by the time and write down that quotient as well. Finally, subtract your first quotient from your second quotient to find the initial velocity. To learn how to find initial velocity using the final velocity, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 809,361 times.
Did this article help you?
Download Article
Download Article
Velocity is a function of time and defined by both a magnitude and a direction. [1]
Often in physics problems, you will need to calculate the initial velocity (speed and direction) at which an object in question began to travel. There are multiple equations that can be used to determine initial velocity. Using the information given in a problem, you can determine the proper equation to use and easily answer your question.
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you have values for the final velocity, acceleration, and time involved, you can use the following equation:[3]
- Initial velocity: Vi = Vf — (a * t)
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- t stands for “time”
- Note that this equation is the standard equation used when finding initial velocity.
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
Advertisement
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.[4]
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
- Write the known information:
- Vi = ?, Vf = 200 m/s, a = 10 m/s2, t = 12 s
- Multiply the acceleration and time. a * t = 10 * 12 =120
- Subtract the product from the final velocity. Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 m/s east
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation.[5]
If you know values for the distance, time, and acceleration, you can use the following equation:- Initial velocity: Vi = (d / t) — [(a * t) / 2]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- d stands for “distance”
- a stands for “acceleration”
- t stands for “time”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
- Write the known information:
- Vi = ?, d = 150 m, a = 7 m/s2, t = 30 s
- Multiply the acceleration and time. a * t = 7 * 30 = 210
- Divide the product by two. (a * t) / 2 = 210 / 2 = 105
- Divide the distance by the time. d / t = 150 / 30 = 5
- Subtract your first quotient from the second quotient. Vi = (d / t) — [(a * t) / 2] = 5 – 105 = -100 Vi = -100 m/s west
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, acceleration, and distance, you can use the following equation:[7]
- Initial velocity: Vi = √ [Vf2 — (2 * a * d)]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 12 m/s, a = 5 m/s2, d = 10 m
- Square the final velocity. Vf2= 122 = 144
- Multiply the acceleration by the distance and the number two. 2 * a * d = 2 * 5 * 10 = 100
- Subtract this product from your previous one. Vf2 — (2 * a * d) = 144 – 100 = 44
- Take the square root of your answer. = √ [Vf2 — (2 * a * d)] = √44 = 6.633 Vi = 6.633 m/s north
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
Advertisement
-
1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, time, and distance, you can use the following equation:[9]
- Initial velocity: Vi = 2(d/t) — Vf
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- t stands for “time”
- d stands for “distance”
-
2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-
3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m
- Divide distance by time. (d/t) = (45/15) = 3
- Multiply that value by 2. 2 (d/t) = 2 (45/15) = 6
- Subtract final velocity from the product. 2(d/t) — Vf = 6 — 3 = 3 Vi = 3 m/s south
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
Advertisement
Add New Question
-
Question
A bullet of 60 gm is fired using a rifle of mass 12kg. Rifle recoils with a velocity of 2.5m/s. What is the initial velocity?
Kinetic energy -> Kinetic energy
0.5mv^2 -> 0.5mv^2
0.5 x 12 x 2,5^2 = 0.5 x 0.06 x v^2
6 x 6.25 = 0.03 x v^2
37.5 = 0.03 x v^2
sqrt(37.5/0.03) = v
sqrt(1250) = v
v = 35.3 m/s -
Question
If displacement and time are related as s = 3.5t + 5t2, what is the initial velocity?
Initial velocity is 3.5. The equation is s = ut + 1/2at^2, where s — distance, u — inititial velocity, and a — acceleration.
-
Question
How do I modify the acceleration formula to one that gives me initial velocity?
You can’t change the acceleration formula to one that gives you the initial velocity you want, as a=v/t. However, Vf=Vi+a.t is re-arranged. Vi=Vf-a.t, a=Vf-Vi/t, t=Vf-Vi/a.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Pencil
- Paper
- Calculator (optional)
About This Article
Article SummaryX
To find initial velocity, start by multiplying the acceleration by the time. Then, divide that number by 2 and write down the quotient you get. Next, divide the distance by the time and write down that quotient as well. Finally, subtract your first quotient from your second quotient to find the initial velocity. To learn how to find initial velocity using the final velocity, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 809,361 times.



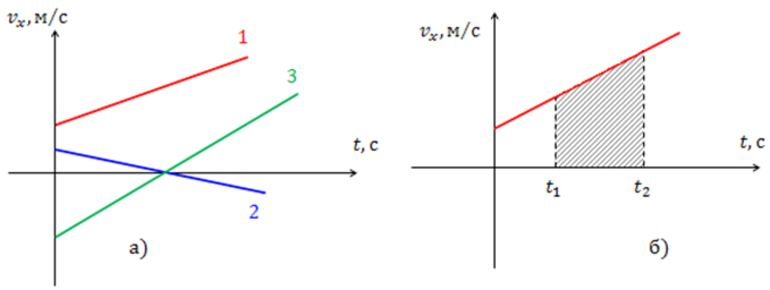

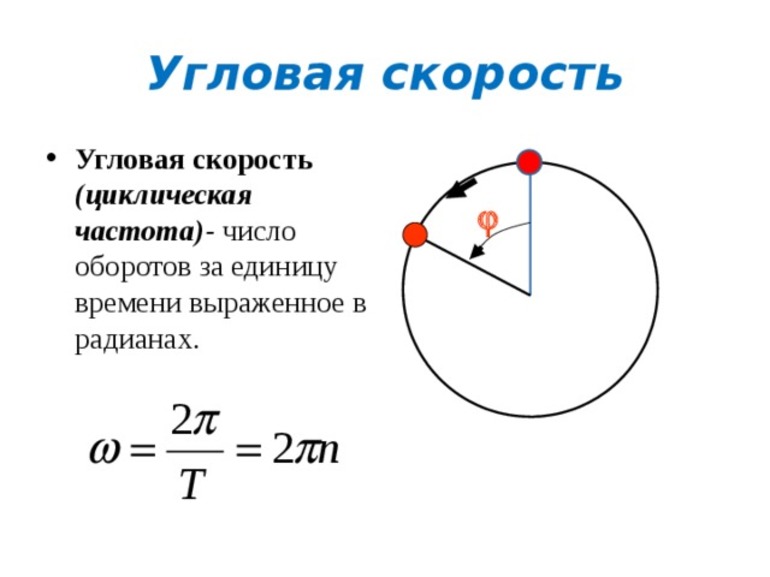











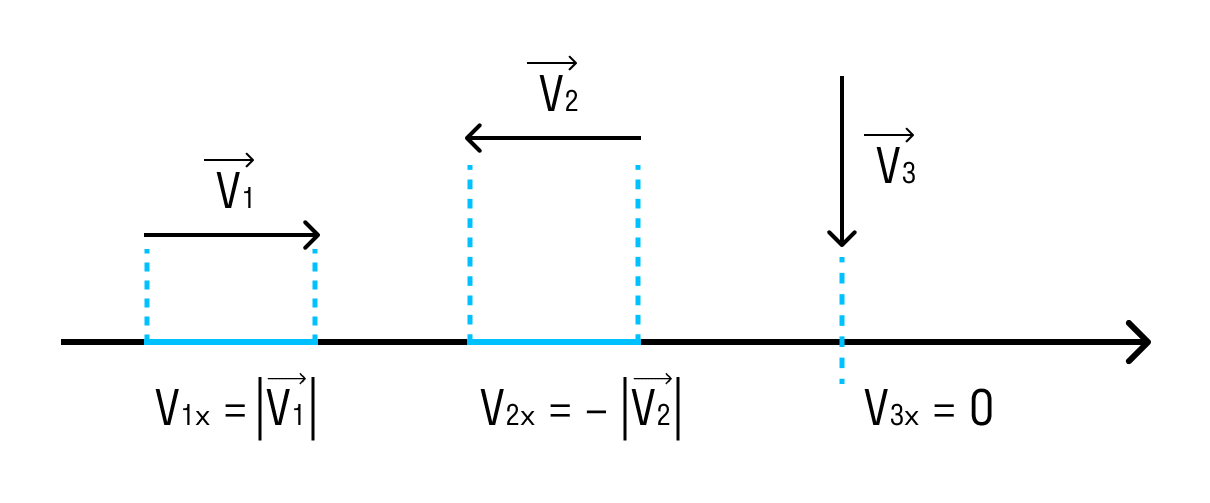
 report this ad Похожие сообщения
report this ad Похожие сообщения