В данной статье я постараюсь простым языком изложить, что означают эти понятия и как их применяют на практике. Начнем с полутона и тона.
ТОН И ПОЛУТОН
Полутон – это наименьшее расстояние между двумя ближайшими по высоте звучания нотами в современной музыкальной системе. Тон, соответственно, это расстояние между звуками, которое слагается из двух полутонов.
Для наглядности давайте взглянем на клавиатуру пианино, то расстояние между двумя ближайшими клавишами будет составлять полтона.
Расстояние от ноты до до до диез (она же ре бемоль) – составляет полтона. От до диез (она же ре бемоль) до ноты ре – тоже полтона. Соответственно, от ноты до до ноты ре – будет один тон. Кстати, обратите особое внимание на то, что расстояние от ноты ми до ноты фа – полтона, т.к. между этими белыми клавишами нет черной. Такая же история относится к расстоянию между нотами си и до – расстояние между ними всего полтона, потому что между ними нет черной клавиши. Вспомните определение: расстояние между двумя ближайшими клавишами на фортепиано составляет полтона.
Теперь обратимся к гитаре. Расстояние между двумя ближайшими ладами на грифе гитары составляет полтона.
К примеру, возьмем первую струну МИ. Если мы зажмем струну ми на первом ладу – у нас получится нота фа, на втором ладу – фа диез, на третьем ладу – соль, на четвертом – соль диез и т.д. Аналогично со всеми остальными струнами.
ЗНАКИ АЛЬТЕРАЦИИ
Теперь несколько слов о знаках альтерации. Существует шесть знаков альтерации:
- диез
- бемоль
- бекар
- дубль диез
- дубль бемоль
- дубль бекар
На нотном письме знаки диез и бемоль изображаются следующим образом:
1) Диез
2) Бемоль
Функция диеза (#) заключается в том, что он обозначает повышение ноты на полтона.
Функция бемоля (b) заключается в понижении звучания ноты на полтона.
Помимо диеза и бемоля существует знак бекар:
3) Бекар
Бекар отменяет значение диеза и бемоля, а также дубль диеза и дубль бемоля.
Дубль диез, дубль бемоль и дубль бекар встречаются в нотах значительно реже диеза, бемоля и бекара.
ВНИМАНИЕ! Пройдите обучающий курс гитары за 1970 руб. ($27) БЕСПЛАТНО!
Продолжительность курса : 90 минут!
Пройти обучение!
Не будем терять времени! Ты готов? Тогда поехали!
Начнем с основ. Итак… что такое нота?
Если кратко, то весь звук — это вибрация. То, что мы называем нотой — это звук определенной высоты, вызванный вибрацией. Как высоко или низко звучит нота зависит от частоты этих вибраций. Чем выше частота колебаний, тем выше нота, и наоборот.
Если вы увеличите частоту вибраций ноты в два раза, вы повысите её на октаву. (Окта́ва — музыкальный интервал, в котором соотношение частот между звуками составляет один к двум (то есть частота высокого звука в два раза больше частоты низкого). Звучит сложно? Сейчас рассмотрим чуть подробнее. Например, нота «ля» где-то в середине фортепианной клавиатуры будет вибрировать 440 раз в секунду, а “ля»на октаву выше — 880 раз в секунду, а та, что на октаву ниже — 220 раз в секунду. Количество вибраций в секунду, в свою очередь, измеряются в “Герцах” и часто сокращаются до “Гц”
Гамма.
Если вы посмотрите на фортепианную клавиатуру, то увидите повторяющуюся последовательность из 12 нот.
Потому что в западной музыке мы делим октаву на 12 равных шагов. Но несмотря на то, что мы используем всего 12 нот в нашей музыке, в мажорных и минорных гаммах используют только
7 нот. Вот почему, когда вы сыграете все 7 нот гаммы и вернетесь к той же самой ноте обратно, вы проделаете путь в октаву, то есть 8 нот. Подумайте о таких словах как октагон, осьминог (англ. octopus) и т. д.
Не сложно? Отлично! Двигаемся дальше 
Итак, как вы могли заметить, мы не используем все ноты подряд при игре гаммы. Мы пропускаем определенные ноты, то есть, расстояние между некоторыми нотами будет
больше, чем у других (расстояние между любыми двумя нотами называется интервалом). Перейти к ближайшей ноте — значит переместиться на полутон (П), а пройти на шаг дальше этого (расстояние в два полутона) называется тоном (Т).
Что заставляет гамму звучать как гамма?
Для начала разберем, что такое гамма. Га́мма — это звукоряд, в котором первая и последняя ноты совпадают по названию, но находятся друг от друга на расстоянии октавы. Отличает различные гаммы друг от друга то, что они имеют свои собственные паттерны тонов и полутонов. Мажорная гамма, которая является основой для большинства музыкальных произведений которые вы слышите, имеет следующую схему интервалов:
T T П T T T П (тон, тон, полутон, тон, тон, тон, полутон)
Если вы начнете играть такой паттерн от ноты “до”, то в конечном итоге сыграете все белые клавиши на фортепиано.
И даже если вы захотите сыграть этот паттерн от любой другой ноты, используя эту последовательность интервалов вы получите всё ту же мажорную гамму, но от другой ноты. Разница будет лишь в том, что гамма зазвучит выше или ниже. Другие гаммы, например минорная, имеют другой паттерн тонов и полутонов.
Тональность.
Как мы только что видели, игра всех белых нот на фортепиано, начиная с “до” даёт вам мажорную гамму. Все ноты в гамме “до мажор” находятся в тональности “до мажор”. Если мы
играем ноты мажорной гаммы, начиная с другой ноты, например соль, то эти ноты находятся в тональности “соль мажор”. Просто, правда?
Давайте взглянем на гамму “соль мажор”. Помните, это означает, что мы начинаем с ноты соль и
двигаемся вверх по патерну T T П T T T П. Но вы сразу заметите, что теперь в нашей гамме появилась чёрная клавиша — “фа диез”.
Итак, в тональности “соль мажор” есть один диез. А если мы начнем с ноты “ре” и сделаем то
же самое, в нашей гамме будет два диеза, “фа” и “до”, то есть, в тональности “ре мажор” будет уже два диеза.
Видите, все очень просто!
Помните, когда вы поднимаетесь вверх по мажорной гамме, все ноты идут по латинскому алфавиту, независимо от того, диезные эти ноты или бемольные. Вот почему в ре мажорной гамме (D Major)
есть “фа диез”, а не “соль бемоль”, так как это следующая нота от “ми” (Е) и она находится перед “соль” (G). Другие гаммы будут использовать бемоли вместо диезов по той же причине. Например,
ноты в фа мажоре это: “фа” F, “соль” G, “ля” A, “си-бемоль” B, “до” С, “ре” D, “ми” Е. Это должен быть си-бемоль, а не ля диез (даже если они звучат одинаково), потому что между латинскими буквами А и С в гамме должна быть буква B, а не еще одна A.
Вы можете задать вполне логичный вопрос, а почему нота “до” это C а не А? И почему это отсчёт идёт с ноты “ля”? Ответ простой: потому что так исторически сложилось. В стародавние времена самой используемой тональностью был ля минор. Камертон, кстати, тоже выдает ноту ля. Первая нота как раз и задает тональность, соответственно порядок нот в то время был такой:
Ля-Си-До-Ре-Ми-Фа-Соль (A, B, С, В, Е, F, G)
*Для более подробного изучения можно, нужно изучить вот эту интересную статью! 
Минорные тональности и их виды.
После мажорной гаммы, следующая и очень важная — минорная. Чтобы сыграть минорную гамму, начните с ноты “ля” (А), и двигайтесь вверх только по белым клавишам.
Вы можете заметить, что в минорной гамме свой паттерн интервалов.
Есть несколько вариаций минорной гаммы. Эта самая основная версия и называется она натуральный минор. Так же, как и с мажорной гаммой, ноты натуральной минорной гаммы — это ноты натуральной минорной тональности.
Возможно, вы заметили, что ля минор имеет все те же ноты, что и тональность до мажор. Это
потому, что они являются параллельными: ля минор — это параллельная тональность до мажору. Чтобы найти параллельный минор к любой мажорной гамме, просто возьмите с шестую ступень мажорной тональности. Например, параллельный минор соль-мажору- это ми минор.
Интервалы.
Как мы уже изучили ранее, расстояние между двумя нотами называется интервалом. Давайте детальней посмотрим на различия между интервалами в мажорной и минорной гаммах. Первые изменение появляются на третьей ноте гаммы. В мажорной гамме третья нота находится на четыре полутона выше основного тона (тоники) гаммы. В минорной гамме это всего лишь три полутона вверх от тоники. Вот почему интервал из трёх полутонов называется малой терцией, а из четырёх полутонов — большой терцией.
Как в минорной, так и в мажорной гаммах четвертая и пятая нота имеют одинаковый интервал от тоники. Нет, например, минорной кварты или мажорной квинты. Эти интервалы называются чистыми. Интервал “до” — “фа” — это чистая кварта, а “до” — “соль” — чистая квинта.
В минорных гаммах шестая и седьмая нота от тоники являются минорными интервалами. В тональности “до минор” шестая и седьмая нота это “ля бемоль” (малая секста) и “си бемоль” (малая септима), а в “до мажоре” шестая и седьмая ноты это ля (большая секста) и си (большая септима).
Аккорды.
Аккорды — это группа нот, играемых одновременно. Наиболее распространенные типы аккордов состоят из трёх нот, поэтому их и называются трезвучие. Обычно они состоят из терций. Для хорошей и понятной демонстрации того, как это звучит, просто сыграйте на фортепиано ноту «до», потом от неё отсчитай три белых клавиши вверх и сыграй ноту “ми”, а затем еще раз три белых клавиши вверх и сыграй ноту “соль”.
Это мажорный аккорд или мажорное трезвучие, потому что нота в середине является большой терцией по отношению к тонике (“до”). Если вы понизите ноту “ми” на полутон, то получите … вы уже верно догадались, минорное трезвучие. Первая и пятая нота в аккорде одинаковые для мажора и минора.
Если вы будете строить трезвучия от каждой ноты в мажорной гаммы, используя только ноты в этой
гамме, это последовательность аккордов, которую у вас получится:
Мажор-Минор-Минор-Мажор-Мажор-Минор-Уменьшенный
Уменьшенный? Ах да, уменьшенное трезвучие. Это похоже на минорное трезвучие, за исключением того, что пятая ступень в аккорде ниже на один полутон. Как мы уже говорили ранее, интервал квинта не может быть большим или малым, он чистый. Поэтому, если пятая ступень в трезвучии опускается на пол тона, то трезвучие уменьшается, отсюда и название аккорда. Соответственно, если пятая ступень повышается на пол тона, то аккорд становится увеличенным.
Часто используемые и наиболее важные аккорды в мажорной тональности это те,
которые строятся на первой, четвертой и пятой ступени гаммы. В тональности “до мажор” это аккорды — ”до мажор”, “фа мажор” и “соль мажор”.
Квинтовый круг тональностей.
Квинтовый круг тональностей – это графическая схема изображения мажорных и минорных тональностей, которые группируются по степени родства и количеству общих нот. Интервал между соседними тональностями в квинтовом круге составляет чистую квинту (5).
На внешней стороне кварто-квинтового круга изображены мажорные тональности, на внутренней – их параллельные миноры.
*Для более подробного изучения и возможности применения кварто-квинтового круга, рекомендуем подробно изучить вот эту замечательную статью.
Вывод.
Всё, что здесь описано, является необходимыми знаниями, если вы хотите по-настоящему понять
музыку. Если вы новичок в теории музыки, то надеемся, последние 25 минут или может чуть больше были очень полезными для вас! Но поверьте, вам еще многое предстоит узнать!
Если вы серьезно относитесь к музыкальному образованию и хотите улучшить свои навыки
композитора, обязательно ознакомьтесь с нашим списком курсов!
Спасибо за ваше время и удачных сочинений!
XSSR Academy
Что такое «интервал» в принципе? Грубо говоря – это расстояние между чем-то и чем-то.
Между зданиями, городами, вещами и т. д. Есть расстояние и между нотами. Расстояние должно в чём-то измеряться. От города до города – километры, от вещи до вещи – метры и сантиметры. А от ноты до ноты – тона и полутона.
Вот и получается, что музыкальный интервал – это расстояние между двумя нотами.
Рассмотрим привычную гамму:
До – Ре – Ми – Фа – Соль – Ля – Си – До.
К слову – это гамма называется «До мажор».
Большинство людей привыкли думать, что нот 7, но музыканты знают, что технически – их 12. Всё дело в том, что между основными нотами есть ещё промежуточные:
До – До# – Ре – Ре# – Ми – Фа – Фа# – Соль – Соль# – Ля – Ля# – Си – До.
Значок «#» обозначает «Диез». Что это такое, мы разберёмся чуть позже, сейчас это не имеет принципиального значения, стоит только обратить внимание на то, что между нотами «Ми – Фа» и «Си – До» нету этого знака. Поэтому и получается, что нот всего 12.
Это очень удобно показано на клавиатуре пианино, где есть чёрные и белые клавишы. Чёрные клавишы, как раз и есть эти самые промежуточные нотки и, если посчитать белые и чёрные клавишы от «До» до «До», то получим 12.
Расстояние между каждыми двумя соседними нотками – это пол тона:
Два полутона образуют один тон.
С этим надо быть внимательными, потому что между «До» и «Ре» — тон, а от «Ми» до «Фа» — пол тона, аналогичная ситуация с «Си» и «До».
Рассмотрим растояние между «До» и «Соль». 7 полутонов. Не очень удобно для понимания. Со временем, конечно, можно привыкнуть и запомнить, но, чтобы каждый раз не считать, для интервалов были придуманы названия, что очень облегчает их понимание и запоминание.
Название зависит от количества полутонов.
Есть ещё интервал в 0 полутонов – это прима, или унисон, то есть, точно та же самая нота.
Для этих названий есть краткие обозначения, в таблице, что выше – они написаны под указанием количества полутонов. Эта таблица дана для наглядности. Она выглядит громоздкой, но это не помешает нам с лёгкостью понять суть происходящего. Запишем все названия по порядку:
- Прима
- Малая секунда
- Большая секунда
- Малая терция
- Большая терция
- Кварта
- Тритон
- Квинта
- Малая секста
- Большая сеста
- Малая септима
- Большая септима
- Октава
Как Вы уже заметили – у некоторых интервалов одинаковые названия, объединим их в группы и присвоим номера:
Тритон без номера и он находится в середине, и ещё, в нём три тона, потому и ТРИтон. Капитан очевидность в восторге!
По обеим сторонам – кварта и квинта. Кварта по-меньше, квинта по-больше. Кварта, как квадрат и обозначается цифрой 4, квинта – цифрой 5.
Первый и последний интервалы – прима и октава. Октава – это та же самая нота, но выше или ниже по звукоряду, а прима – это прям точно та же самая нота.
Меньше кварты — терции. Большая и малая. Терция – это «третья» по латински. Обозначаются цифрой «3», перед большой ставится буква «б», перед малой «м».
Меньше терции – секунды. Тоже, большая и малая. Секунда – созвучно с second, или второй. Потому и цифра 2. С соответствующими буковками «б» перед большой, и «м» перед малой. Меньше только прима.
Большие интервалы. Сексты – 6, и септимы – 7. Так же всё от латинских названий. И также с буковками «б» и «м» соответственно.
Как теперь становится понятно, названия интервалов – это всего лишь их порядковые номера.
Интересная ситуация с «тритоном». Так как теория музыки развивается довольно давно, многие названия и обозначения пришли к нам с давних времён. Так вот, в средневековье, в Европе, тритон считался дьявольским интервалом, так как он даёт очень яркий диссонанс – звучание, которое не привычно слуху. Поэтому, многие теоретики обходили его стороной, не считая чем-то важным. Наверно, именно поэтому его и обделили номером. Хотя, если подумать, то ему хорошо бы подошёл номер «666»… А что? 3 тона и 6 полутонов… Вот Вам и тритон. 9) Ну да ладно.
Понимание этих вещей важно. Сейчас это не совсем очевидно, но это так. Интервалы будут очень полезны, когда дело дойдёт до практики на каком-либо инструменте. Основная их ценность заключается в том, что это одно из первых «абстрактных» понятий, то есть интервалы не привязаны напрямую к каким-то определённым нотам, что очень полезно и удобно. В дальнейшем, у нас появится возможность в этом убедиться. С теоретической точки зрения, они нам пригодятся, когда мы дойдём до аккордов и ладов.
В общем, самое интересное только начинается 
This article is about the musical interval. For the printing method, see Halftone.
| Inverse | major seventh (for minor second); diminished octave (for augmented unison); augmented octave (for diminished unison) |
|---|---|
| Name | |
| Other names | minor second, diatonic semitone, augmented unison, diminished unison, chromatic semitone |
| Abbreviation | m2; A1 |
| Size | |
| Semitones | 1 |
| Interval class | 1 |
| Just interval | 16:15,[1] 17:16,[2] 27:25, 135:128,[1] 25:24,[1] 256:243 |
| Cents | |
| Equal temperament | 100[1] |
| Just intonation | 112,[1] 105, 133, 92,[1] 71,[1] 90 |
A semitone, also called a half step or a half tone,[3] is the smallest musical interval commonly used in Western tonal music,[4] and it is considered the most dissonant[5] when sounded harmonically.
It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.
In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones.
In music theory, a distinction is made[6] between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D♭) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. from C to C♯). These are enharmonically equivalent when twelve-tone equal temperament is used, but are not the same thing in meantone temperament, where the diatonic semitone is distinguished from and smaller than the chromatic semitone (augmented unison). See Interval (music) § Number for more details about this terminology.
In twelve-tone equal temperament all semitones are equal in size (100 cents). In other tuning systems, «semitone» refers to a family of intervals that may vary both in size and name. In Pythagorean tuning, seven semitones out of twelve are diatonic, with ratio 256:243 or 90.2 cents (Pythagorean limma), and the other five are chromatic, with ratio 2187:2048 or 113.7 cents (Pythagorean apotome); they differ by the Pythagorean comma of ratio 531441:524288 or 23.5 cents. In quarter-comma meantone, seven of them are diatonic, and 117.1 cents wide, while the other five are chromatic, and 76.0 cents wide; they differ by the lesser diesis of ratio 128:125 or 41.1 cents. 12-tone scales tuned in just intonation typically define three or four kinds of semitones. For instance, Asymmetric five-limit tuning yields chromatic semitones with ratios 25:24 (70.7 cents) and 135:128 (92.2 cents), and diatonic semitones with ratios 16:15 (111.7 cents) and 27:25 (133.2 cents). For further details, see below.
The condition of having semitones is called hemitonia; that of having no semitones is anhemitonia. A musical scale or chord containing semitones is called hemitonic; one without semitones is anhemitonic.
Minor second[edit]
| Inverse | major seventh |
|---|---|
| Name | |
| Other names | semitone, half step |
| Abbreviation | m2 |
| Size | |
| Semitones | 1 |
| Interval class | 1 |
| Cents | |
| Equal temperament | 100.0 |
The minor second occurs in the major scale, between the third and fourth degree, (mi (E) and fa (F) in C major), and between the seventh and eighth degree (ti (B) and do (C) in C major). It is also called the diatonic semitone because it occurs between steps in the diatonic scale. The minor second is abbreviated m2 (or −2). Its inversion is the major seventh (M7 or Ma7).
Listen to a minor second in equal temperament (help·info). Here, middle C is followed by D♭, which is a tone 100 cents sharper than C, and then by both tones together.
Melodically, this interval is very frequently used, and is of particular importance in cadences. In the perfect and deceptive cadences it appears as a resolution of the leading-tone to the tonic. In the plagal cadence, it appears as the falling of the subdominant to the mediant. It also occurs in many forms of the imperfect cadence, wherever the tonic falls to the leading-tone.
Harmonically, the interval usually occurs as some form of dissonance or a nonchord tone that is not part of the functional harmony. It may also appear in inversions of a major seventh chord, and in many added tone chords.
Harmonic minor second in J. S. Bach’s Prelude in C major from the WTC, book 1, mm. 7–9. The minor second may be viewed as a suspension of the B resolving into the following A minor seventh chord.
In unusual situations, the minor second can add a great deal of character to the music. For instance, Frédéric Chopin’s Étude Op. 25, No. 5 opens with a melody accompanied by a line that plays fleeting minor seconds. These are used to humorous and whimsical effect, which contrasts with its more lyrical middle section. This eccentric dissonance has earned the piece its nickname: the «wrong note» étude. This kind of usage of the minor second appears in many other works of the Romantic period, such as Modest Mussorgsky’s Ballet of the Unhatched Chicks. More recently, the music to the movie Jaws exemplifies the minor second.
In other temperaments[edit]
In just intonation a 16:15 minor second arises in the C major scale between B & C and E & F, and is, «the sharpest dissonance found in the [major] scale.»[7] Play B & C (help·info)
Augmented unison[edit]
The augmented unison, the interval produced by the augmentation, or widening by one half step, of the perfect unison,[8] does not occur between diatonic scale steps, but instead between a scale step and a chromatic alteration of the same step. It is also called a chromatic semitone. The augmented unison is abbreviated A1, or aug 1. Its inversion is the diminished octave (d8, or dim 8). The augmented unison is also the inversion of the augmented octave, because the interval of the diminished unison does not exist.[9] This is because a unison is always made larger when one note of the interval is changed with an accidental.[10][11]
Melodically, an augmented unison very frequently occurs when proceeding to a chromatic chord, such as a secondary dominant, a diminished seventh chord, or an augmented sixth chord. Its use is also often the consequence of a melody proceeding in semitones, regardless of harmonic underpinning, e.g. D, D♯, E, F, F♯. (Restricting the notation to only minor seconds is impractical, as the same example would have a rapidly increasing number of accidentals, written enharmonically as D, E♭, F♭, G, A
).
Harmonically, augmented unisons are quite rare in tonal repertoire. In the example to the right, Liszt had written an E♭ against an E♮ in the bass. Here E♭ was preferred to a D♯ to make the tone’s function clear as part of an F dominant seventh chord, and the augmented unison is the result of superimposing this harmony upon an E pedal point.
In addition to this kind of usage, harmonic augmented unisons are frequently written in modern works involving tone clusters, such as Iannis Xenakis’ Evryali for piano solo.
History[edit]
The semitone appeared in the music theory of Greek antiquity as part of a diatonic or chromatic tetrachord, and it has always had a place in the diatonic scales of Western music since. The various modal scales of medieval music theory were all based upon this diatonic pattern of tones and semitones.
Though it would later become an integral part of the musical cadence, in the early polyphony of the 11th century this was not the case. Guido of Arezzo suggested instead in his Micrologus other alternatives: either proceeding by whole tone from a major second to a unison, or an occursus having two notes at a major third move by contrary motion toward a unison, each having moved a whole tone.
«As late as the 13th century the half step was experienced as a problematic interval not easily understood, as the irrational [sic] remainder between the perfect fourth and the ditone 
Dramatic chromatic scale in the opening measures of Luca Marenzio’s Solo e pensoso, ca. 1580.
However, beginning in the 13th century cadences begin to require motion in one voice by half step and the other a whole step in contrary motion.[12] These cadences would become a fundamental part of the musical language, even to the point where the usual accidental accompanying the minor second in a cadence was often omitted from the written score (a practice known as musica ficta). By the 16th century, the semitone had become a more versatile interval, sometimes even appearing as an augmented unison in very chromatic passages. Semantically, in the 16th century the repeated melodic semitone became associated with weeping, see: passus duriusculus, lament bass, and pianto.
By the Baroque era (1600 to 1750), the tonal harmonic framework was fully formed, and the various musical functions of the semitone were rigorously understood. Later in this period the adoption of well temperaments for instrumental tuning and the more frequent use of enharmonic equivalences increased the ease with which a semitone could be applied. Its function remained similar through the Classical period, and though it was used more frequently as the language of tonality became more chromatic in the Romantic period, the musical function of the semitone did not change.
In the 20th century, however, composers such as Arnold Schoenberg, Béla Bartók, and Igor Stravinsky sought alternatives or extensions of tonal harmony, and found other uses for the semitone. Often the semitone was exploited harmonically as a caustic dissonance, having no resolution. Some composers would even use large collections of harmonic semitones (tone clusters) as a source of cacophony in their music (e.g. the early piano works of Henry Cowell). By now, enharmonic equivalence was a commonplace property of equal temperament, and instrumental use of the semitone was not at all problematic for the performer. The composer was free to write semitones wherever he wished.
Semitones in different tunings[edit]
The exact size of a semitone depends on the tuning system used. Meantone temperaments have two distinct types of semitones, but in the exceptional case of equal temperament, there is only one. The unevenly distributed well temperaments contain many different semitones. Pythagorean tuning, similar to meantone tuning, has two, but in other systems of just intonation there are many more possibilities.
Meantone temperament[edit]
In meantone systems, there are two different semitones. This results because of the break in the circle of fifths that occurs in the tuning system: diatonic semitones derive from a chain of five fifths that does not cross the break, and chromatic semitones come from one that does.
The chromatic semitone is usually smaller than the diatonic. In the common quarter-comma meantone, tuned as a cycle of tempered fifths from E♭ to G♯, the chromatic and diatonic semitones are 76.0 and 117.1 cents wide respectively.
| Chromatic semitone | 76.0 | 76.0 | 76.0 | 76.0 | 76.0 | |||||||||||||||||||||
| Pitch | C | C♯ | D | E♭ | E | F | F♯ | G | G♯ | A | B♭ | B | C | |||||||||||||
| Cents | 0.0 | 76.0 | 193.2 | 310.3 | 386.3 | 503.4 | 579.5 | 696.6 | 772.6 | 889.7 | 1006.8 | 1082.9 | 1200.0 | |||||||||||||
| Diatonic semitone | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 |
Extended meantone temperaments with more than 12 notes still retain the same two semitone sizes, but there is more flexibility for the musician about whether to use an augmented unison or minor second. 31-tone equal temperament is the most flexible of these, which makes an unbroken circle of 31 fifths, allowing the choice of semitone to be made for any pitch.
Equal temperament[edit]
12-tone equal temperament is a form of meantone tuning in which the diatonic and chromatic semitones are exactly the same, because its circle of fifths has no break. Each semitone is equal to one twelfth of an octave. This is a ratio of 21/12 (approximately 1.05946), or 100 cents, and is 11.7 cents narrower than the 16:15 ratio (its most common form in just intonation, discussed below).
All diatonic intervals can be expressed as an equivalent number of semitones. For instance a whole tone equals two semitones.
There are many approximations, rational or otherwise, to the equal-tempered semitone. To cite a few:
-
suggested by Vincenzo Galilei and used by luthiers of the Renaissance,
-
suggested by Marin Mersenne as a constructible and more accurate alternative,
-
used by Julián Carrillo as part of a sixteenth-tone system.
For more examples, see Pythagorean and Just systems of tuning below.
Well temperament[edit]
There are many forms of well temperament, but the characteristic they all share is that their semitones are of an uneven size. Every semitone in a well temperament has its own interval (usually close to the equal-tempered version of 100 cents), and there is no clear distinction between a diatonic and chromatic semitone in the tuning. Well temperament was constructed so that enharmonic equivalence could be assumed between all of these semitones, and whether they were written as a minor second or augmented unison did not effect a different sound. Instead, in these systems, each key had a slightly different sonic color or character, beyond the limitations of conventional notation.
Pythagorean tuning[edit]
Pythagorean limma on C
Pythagorean apotome on C
Pythagorean limma as five descending just perfect fifths from C (the inverse is B+)
Pythagorean apotome as seven just perfect fifths
Like meantone temperament, Pythagorean tuning is a broken circle of fifths. This creates two distinct semitones, but because Pythagorean tuning is also a form of 3-limit just intonation, these semitones are rational. Also, unlike most meantone temperaments, the chromatic semitone is larger than the diatonic.
The Pythagorean diatonic semitone has a ratio of 256/243 (play (help·info)), and is often called the Pythagorean limma. It is also sometimes called the Pythagorean minor semitone. It is about 90.2 cents.
It can be thought of as the difference between three octaves and five just fifths, and functions as a diatonic semitone in a Pythagorean tuning.
The Pythagorean chromatic semitone has a ratio of 2187/2048 (play (help·info)). It is about 113.7 cents. It may also be called the Pythagorean apotome[13][14][15] or the Pythagorean major semitone. (See Pythagorean interval.)
It can be thought of as the difference between four perfect octaves and seven just fifths, and functions as a chromatic semitone in a Pythagorean tuning.
The Pythagorean limma and Pythagorean apotome are enharmonic equivalents (chromatic semitones) and only a Pythagorean comma apart, in contrast to diatonic and chromatic semitones in meantone temperament and 5-limit just intonation.
Just 5-limit intonation [edit]
‘Larger’ or major limma on C
Relationship between the 4 common 5-limit semitones
A minor second in just intonation typically corresponds to a pitch ratio of 16:15 (play (help·info)) or 1.0666… (approximately 111.7 cents), called the just diatonic semitone.[16] This is a practical just semitone, since it is the difference between a perfect fourth and major third (

The 16:15 just minor second arises in the C major scale between B & C and E & F, and is, «the sharpest dissonance found in the scale.»[7]
An augmented unison in just intonation is another semitone of 25:24 (play (help·info)) or 1.0416… (approximately 70.7 cents). It is the difference between a 5:4 major third and a 6:5 minor third. Composer Ben Johnston uses a sharp (♯) to indicate a note is raised 70.7 cents, or a flat (♭) to indicate a note is lowered 70.7 cents.[17]
Two other kinds of semitones are produced by 5-limit tuning. A chromatic scale defines 12 semitones as the 12 intervals between the 13 adjacent notes forming a full octave (e.g. from C4 to C5). The 12 semitones produced by a commonly used version of 5-limit tuning have four different sizes, and can be classified as follows:
- Just, or smaller, or minor, chromatic semitone, e.g. between E♭ and E (6/5 and 5/4):
- Larger, or major, chromatic semitone, or larger limma, or major chroma,[17] e.g. between C and C♯ (1/1 and 135/128):
- Just, or smaller, or minor, diatonic semitone, e.g. between C and D♭ (1/1 and 16/15):
- Larger, or major, diatonic semitone, e.g. between A and B♭ (5/3 and 16/9):
The most frequently occurring semitones are the just ones (S3 and S1): S3 occurs six times out of 12, S1 three times, S2 twice, and S4 only once.
The smaller chromatic and diatonic semitones differ from the larger by the syntonic comma (81:80 or 21.5 cents). The smaller and larger chromatic semitones differ from the respective diatonic semitones by the same 128:125 diesis as the above meantone semitones. Finally, while the inner semitones differ by the diaschisma (2048:2025 or 19.6 cents), the outer differ by the greater diesis (648:625 or 62.6 cents).
Extended just intonations[edit]
In 7-limit there is the septimal diatonic semitone of 15:14 (play (help·info)) available between the 5-limit major seventh (15:8) and the 7-limit minor seventh (7:4). There is also a smaller septimal chromatic semitone of 21:20 (
play (help·info)) between a septimal minor seventh and a fifth (21:8) and an octave and a major third (5:2). Both are more rarely used than their 5-limit neighbours, although the former was often implemented by theorist Henry Cowell, while Harry Partch used the latter as part of his 43-tone scale.
Under 11-limit tuning, there is a fairly common undecimal neutral second (12:11) (play (help·info)), but it lies on the boundary between the minor and major second (150.6 cents). In just intonation there are infinitely many possibilities for intervals that fall within the range of the semitone (e.g. the Pythagorean semitones mentioned above), but most of them are impractical.
In 13-limit tuning, there is a tridecimal 2/3 tone (13:12 or 138.57 cents) and tridecimal 1/3 tone (27:26 or 65.34 cents).
In 17-limit just intonation, the major diatonic semitone is 15:14 or 119.4 cents (Play (help·info)), and the minor diatonic semitone is 17:16 or 105.0 cents,[18] and septendecimal limma is 18:17 or 98.95 cents.
Though the names diatonic and chromatic are often used for these intervals, their musical function is not the same as the two meantone semitones. For instance, 15:14 would usually be written as an augmented unison, functioning as the chromatic counterpart to a diatonic 16:15. These distinctions are highly dependent on the musical context, and just intonation is not particularly well suited to chromatic usage (diatonic semitone function is more prevalent).
Other equal temperaments[edit]
19-tone equal temperament distinguishes between the chromatic and diatonic semitones; in this tuning, the chromatic semitone is one step of the scale (play 63.2 cents (help·info)), and the diatonic semitone is two (
play 126.3 cents (help·info)). 31-tone equal temperament also distinguishes between these two intervals, which become 2 and 3 steps of the scale, respectively. 53-ET has an even closer match to the two semitones with 3 and 5 steps of its scale while 72-ET uses 4 (
play 66.7 cents (help·info)) and 7 (
play 116.7 cents (help·info)) steps of its scale.
In general, because the smaller semitone can be viewed as the difference between a minor third and a major third, and the larger as the difference between a major third and a perfect fourth, tuning systems that closely match those just intervals (6/5, 5/4, and 4/3) will also distinguish between the two types of semitones and closely match their just intervals (25/24 and 16/15).
See also[edit]
- List of meantone intervals
- List of musical intervals
- List of pitch intervals
- Approach chord
- Major second
- Neutral second
- Pythagorean interval
- Regular temperament
References[edit]
- ^ a b c d e f g Duffin, Ross W. (2008). How equal temperament ruined harmony : (and why you should care) (First published as a Norton paperback. ed.). New York: W. W. Norton. p. 163. ISBN 978-0-393-33420-3. Retrieved 28 June 2017.
- ^ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p. xxiv. ISBN 0-8247-4714-3. Overtone semitone.
- ^ Semitone, half step, half tone, halftone, and half-tone are all variously used in sources.[1][2][3][4][5]
Aaron Copland, Leonard Bernstein, and others use «half tone».[6]
[7][8][9]
One source says that step is «chiefly US»,[10] and that half-tone is «chiefly N. Amer.»[11] - ^ Miller, Michael. The Complete Idiot’s Guide to Music Theory, 2nd ed. [Indianapolis, Indiana]: Alpha, 2005. ISBN 1-59257-437-8. p. 19.
- ^ Capstick, John Walton (1913). Sound: An Elementary Text-book for Schools and Colleges. Cambridge University Press.
- ^ Wharram, Barbara (2010). Elementary Rudiments of Music (2nd ed.). Mississauga, Ontario: Frederick Harris Music. p. 17. ISBN 978-1-55440-283-0.
- ^ a b Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction, p. 165. Theodore Baker, trans. G. Schirmer.
- ^ Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p. 54. ISBN 978-0-07-294262-0. Specific example of an A1 not given but general example of perfect intervals described.
- ^ Kostka and Payne (2003). Tonal Harmony, p. 21. ISBN 0-07-285260-7. «There is no such thing as a diminished unison.»
- ^ Day and Pilhofer (2007). Music Theory for Dummies, p. 113. ISBN 0-7645-7838-3. «There is no such thing as a diminished unison, because no matter how you change the unisons with accidentals, you are adding half steps to the total interval.»
- ^ Surmani, Andrew; Karen Farnum Surmani; Morton Manus (2009). Alfred’s Essentials of Music Theory: A Complete Self-Study Course for All Musicians. Alfred Music Publishing. p. 135. ISBN 978-0-7390-3635-8. Since lowering either note of a perfect unison would actually increase its size, the perfect unison cannot be diminished, only augmented.
- ^ a b Dahlhaus, Carl, trans. Gjerdingen, Robert O. Studies in the Origin of Harmonic Tonality. Princeton University Press: Princeton, 1990. ISBN 0-691-09135-8.
- ^ Rashed, Roshdi (ed.) (1996). Encyclopedia of the History of Arabic Science, Volume 2, pp. 588, 608. Routledge. ISBN 0-415-12411-5.
- ^ Hermann von Helmholtz (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music, p. 454.
- ^ Benson, Dave (2006). Music: A Mathematical Offering, p. 369. ISBN 0-521-85387-7.
- ^ Royal Society (Great Britain) (1880, digitized Feb 26, 2008). Proceedings of the Royal Society of London, Volume 30, p. 531. Harvard University.
- ^ a b John Fonville. «Ben Johnston’s Extended Just Intonation- A Guide for Interpreters», p. 109, Perspectives of New Music, vol. 29, no. 2 (Summer 1991), pp. 106–137. «…the 25/24 ratio is the sharp (#) ratio…this raises a note approximately 70.6 cents.»
- ^ Prout, Ebenezer (2004). Harmony, p. 325. ISBN 1-4102-1920-8.
Further reading[edit]
- Grout, Donald Jay, and Claude V. Palisca. A History of Western Music, 6th ed. New York: Norton, 2001. ISBN 0-393-97527-4.
- Hoppin, Richard H. Medieval Music. New York: W. W. Norton, 1978. ISBN 0-393-09090-6.
This article is about the musical interval. For the printing method, see Halftone.
| Inverse | major seventh (for minor second); diminished octave (for augmented unison); augmented octave (for diminished unison) |
|---|---|
| Name | |
| Other names | minor second, diatonic semitone, augmented unison, diminished unison, chromatic semitone |
| Abbreviation | m2; A1 |
| Size | |
| Semitones | 1 |
| Interval class | 1 |
| Just interval | 16:15,[1] 17:16,[2] 27:25, 135:128,[1] 25:24,[1] 256:243 |
| Cents | |
| Equal temperament | 100[1] |
| Just intonation | 112,[1] 105, 133, 92,[1] 71,[1] 90 |
A semitone, also called a half step or a half tone,[3] is the smallest musical interval commonly used in Western tonal music,[4] and it is considered the most dissonant[5] when sounded harmonically.
It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.
In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones.
In music theory, a distinction is made[6] between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D♭) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. from C to C♯). These are enharmonically equivalent when twelve-tone equal temperament is used, but are not the same thing in meantone temperament, where the diatonic semitone is distinguished from and smaller than the chromatic semitone (augmented unison). See Interval (music) § Number for more details about this terminology.
In twelve-tone equal temperament all semitones are equal in size (100 cents). In other tuning systems, «semitone» refers to a family of intervals that may vary both in size and name. In Pythagorean tuning, seven semitones out of twelve are diatonic, with ratio 256:243 or 90.2 cents (Pythagorean limma), and the other five are chromatic, with ratio 2187:2048 or 113.7 cents (Pythagorean apotome); they differ by the Pythagorean comma of ratio 531441:524288 or 23.5 cents. In quarter-comma meantone, seven of them are diatonic, and 117.1 cents wide, while the other five are chromatic, and 76.0 cents wide; they differ by the lesser diesis of ratio 128:125 or 41.1 cents. 12-tone scales tuned in just intonation typically define three or four kinds of semitones. For instance, Asymmetric five-limit tuning yields chromatic semitones with ratios 25:24 (70.7 cents) and 135:128 (92.2 cents), and diatonic semitones with ratios 16:15 (111.7 cents) and 27:25 (133.2 cents). For further details, see below.
The condition of having semitones is called hemitonia; that of having no semitones is anhemitonia. A musical scale or chord containing semitones is called hemitonic; one without semitones is anhemitonic.
Minor second[edit]
| Inverse | major seventh |
|---|---|
| Name | |
| Other names | semitone, half step |
| Abbreviation | m2 |
| Size | |
| Semitones | 1 |
| Interval class | 1 |
| Cents | |
| Equal temperament | 100.0 |
The minor second occurs in the major scale, between the third and fourth degree, (mi (E) and fa (F) in C major), and between the seventh and eighth degree (ti (B) and do (C) in C major). It is also called the diatonic semitone because it occurs between steps in the diatonic scale. The minor second is abbreviated m2 (or −2). Its inversion is the major seventh (M7 or Ma7).
Listen to a minor second in equal temperament (help·info). Here, middle C is followed by D♭, which is a tone 100 cents sharper than C, and then by both tones together.
Melodically, this interval is very frequently used, and is of particular importance in cadences. In the perfect and deceptive cadences it appears as a resolution of the leading-tone to the tonic. In the plagal cadence, it appears as the falling of the subdominant to the mediant. It also occurs in many forms of the imperfect cadence, wherever the tonic falls to the leading-tone.
Harmonically, the interval usually occurs as some form of dissonance or a nonchord tone that is not part of the functional harmony. It may also appear in inversions of a major seventh chord, and in many added tone chords.
Harmonic minor second in J. S. Bach’s Prelude in C major from the WTC, book 1, mm. 7–9. The minor second may be viewed as a suspension of the B resolving into the following A minor seventh chord.
In unusual situations, the minor second can add a great deal of character to the music. For instance, Frédéric Chopin’s Étude Op. 25, No. 5 opens with a melody accompanied by a line that plays fleeting minor seconds. These are used to humorous and whimsical effect, which contrasts with its more lyrical middle section. This eccentric dissonance has earned the piece its nickname: the «wrong note» étude. This kind of usage of the minor second appears in many other works of the Romantic period, such as Modest Mussorgsky’s Ballet of the Unhatched Chicks. More recently, the music to the movie Jaws exemplifies the minor second.
In other temperaments[edit]
In just intonation a 16:15 minor second arises in the C major scale between B & C and E & F, and is, «the sharpest dissonance found in the [major] scale.»[7] Play B & C (help·info)
Augmented unison[edit]
The augmented unison, the interval produced by the augmentation, or widening by one half step, of the perfect unison,[8] does not occur between diatonic scale steps, but instead between a scale step and a chromatic alteration of the same step. It is also called a chromatic semitone. The augmented unison is abbreviated A1, or aug 1. Its inversion is the diminished octave (d8, or dim 8). The augmented unison is also the inversion of the augmented octave, because the interval of the diminished unison does not exist.[9] This is because a unison is always made larger when one note of the interval is changed with an accidental.[10][11]
Melodically, an augmented unison very frequently occurs when proceeding to a chromatic chord, such as a secondary dominant, a diminished seventh chord, or an augmented sixth chord. Its use is also often the consequence of a melody proceeding in semitones, regardless of harmonic underpinning, e.g. D, D♯, E, F, F♯. (Restricting the notation to only minor seconds is impractical, as the same example would have a rapidly increasing number of accidentals, written enharmonically as D, E♭, F♭, G, A
).
Harmonically, augmented unisons are quite rare in tonal repertoire. In the example to the right, Liszt had written an E♭ against an E♮ in the bass. Here E♭ was preferred to a D♯ to make the tone’s function clear as part of an F dominant seventh chord, and the augmented unison is the result of superimposing this harmony upon an E pedal point.
In addition to this kind of usage, harmonic augmented unisons are frequently written in modern works involving tone clusters, such as Iannis Xenakis’ Evryali for piano solo.
History[edit]
The semitone appeared in the music theory of Greek antiquity as part of a diatonic or chromatic tetrachord, and it has always had a place in the diatonic scales of Western music since. The various modal scales of medieval music theory were all based upon this diatonic pattern of tones and semitones.
Though it would later become an integral part of the musical cadence, in the early polyphony of the 11th century this was not the case. Guido of Arezzo suggested instead in his Micrologus other alternatives: either proceeding by whole tone from a major second to a unison, or an occursus having two notes at a major third move by contrary motion toward a unison, each having moved a whole tone.
«As late as the 13th century the half step was experienced as a problematic interval not easily understood, as the irrational [sic] remainder between the perfect fourth and the ditone 
Dramatic chromatic scale in the opening measures of Luca Marenzio’s Solo e pensoso, ca. 1580.
However, beginning in the 13th century cadences begin to require motion in one voice by half step and the other a whole step in contrary motion.[12] These cadences would become a fundamental part of the musical language, even to the point where the usual accidental accompanying the minor second in a cadence was often omitted from the written score (a practice known as musica ficta). By the 16th century, the semitone had become a more versatile interval, sometimes even appearing as an augmented unison in very chromatic passages. Semantically, in the 16th century the repeated melodic semitone became associated with weeping, see: passus duriusculus, lament bass, and pianto.
By the Baroque era (1600 to 1750), the tonal harmonic framework was fully formed, and the various musical functions of the semitone were rigorously understood. Later in this period the adoption of well temperaments for instrumental tuning and the more frequent use of enharmonic equivalences increased the ease with which a semitone could be applied. Its function remained similar through the Classical period, and though it was used more frequently as the language of tonality became more chromatic in the Romantic period, the musical function of the semitone did not change.
In the 20th century, however, composers such as Arnold Schoenberg, Béla Bartók, and Igor Stravinsky sought alternatives or extensions of tonal harmony, and found other uses for the semitone. Often the semitone was exploited harmonically as a caustic dissonance, having no resolution. Some composers would even use large collections of harmonic semitones (tone clusters) as a source of cacophony in their music (e.g. the early piano works of Henry Cowell). By now, enharmonic equivalence was a commonplace property of equal temperament, and instrumental use of the semitone was not at all problematic for the performer. The composer was free to write semitones wherever he wished.
Semitones in different tunings[edit]
The exact size of a semitone depends on the tuning system used. Meantone temperaments have two distinct types of semitones, but in the exceptional case of equal temperament, there is only one. The unevenly distributed well temperaments contain many different semitones. Pythagorean tuning, similar to meantone tuning, has two, but in other systems of just intonation there are many more possibilities.
Meantone temperament[edit]
In meantone systems, there are two different semitones. This results because of the break in the circle of fifths that occurs in the tuning system: diatonic semitones derive from a chain of five fifths that does not cross the break, and chromatic semitones come from one that does.
The chromatic semitone is usually smaller than the diatonic. In the common quarter-comma meantone, tuned as a cycle of tempered fifths from E♭ to G♯, the chromatic and diatonic semitones are 76.0 and 117.1 cents wide respectively.
| Chromatic semitone | 76.0 | 76.0 | 76.0 | 76.0 | 76.0 | |||||||||||||||||||||
| Pitch | C | C♯ | D | E♭ | E | F | F♯ | G | G♯ | A | B♭ | B | C | |||||||||||||
| Cents | 0.0 | 76.0 | 193.2 | 310.3 | 386.3 | 503.4 | 579.5 | 696.6 | 772.6 | 889.7 | 1006.8 | 1082.9 | 1200.0 | |||||||||||||
| Diatonic semitone | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 |
Extended meantone temperaments with more than 12 notes still retain the same two semitone sizes, but there is more flexibility for the musician about whether to use an augmented unison or minor second. 31-tone equal temperament is the most flexible of these, which makes an unbroken circle of 31 fifths, allowing the choice of semitone to be made for any pitch.
Equal temperament[edit]
12-tone equal temperament is a form of meantone tuning in which the diatonic and chromatic semitones are exactly the same, because its circle of fifths has no break. Each semitone is equal to one twelfth of an octave. This is a ratio of 21/12 (approximately 1.05946), or 100 cents, and is 11.7 cents narrower than the 16:15 ratio (its most common form in just intonation, discussed below).
All diatonic intervals can be expressed as an equivalent number of semitones. For instance a whole tone equals two semitones.
There are many approximations, rational or otherwise, to the equal-tempered semitone. To cite a few:
-
suggested by Vincenzo Galilei and used by luthiers of the Renaissance,
-
suggested by Marin Mersenne as a constructible and more accurate alternative,
-
used by Julián Carrillo as part of a sixteenth-tone system.
For more examples, see Pythagorean and Just systems of tuning below.
Well temperament[edit]
There are many forms of well temperament, but the characteristic they all share is that their semitones are of an uneven size. Every semitone in a well temperament has its own interval (usually close to the equal-tempered version of 100 cents), and there is no clear distinction between a diatonic and chromatic semitone in the tuning. Well temperament was constructed so that enharmonic equivalence could be assumed between all of these semitones, and whether they were written as a minor second or augmented unison did not effect a different sound. Instead, in these systems, each key had a slightly different sonic color or character, beyond the limitations of conventional notation.
Pythagorean tuning[edit]
Pythagorean limma on C
Pythagorean apotome on C
Pythagorean limma as five descending just perfect fifths from C (the inverse is B+)
Pythagorean apotome as seven just perfect fifths
Like meantone temperament, Pythagorean tuning is a broken circle of fifths. This creates two distinct semitones, but because Pythagorean tuning is also a form of 3-limit just intonation, these semitones are rational. Also, unlike most meantone temperaments, the chromatic semitone is larger than the diatonic.
The Pythagorean diatonic semitone has a ratio of 256/243 (play (help·info)), and is often called the Pythagorean limma. It is also sometimes called the Pythagorean minor semitone. It is about 90.2 cents.
It can be thought of as the difference between three octaves and five just fifths, and functions as a diatonic semitone in a Pythagorean tuning.
The Pythagorean chromatic semitone has a ratio of 2187/2048 (play (help·info)). It is about 113.7 cents. It may also be called the Pythagorean apotome[13][14][15] or the Pythagorean major semitone. (See Pythagorean interval.)
It can be thought of as the difference between four perfect octaves and seven just fifths, and functions as a chromatic semitone in a Pythagorean tuning.
The Pythagorean limma and Pythagorean apotome are enharmonic equivalents (chromatic semitones) and only a Pythagorean comma apart, in contrast to diatonic and chromatic semitones in meantone temperament and 5-limit just intonation.
Just 5-limit intonation [edit]
‘Larger’ or major limma on C
Relationship between the 4 common 5-limit semitones
A minor second in just intonation typically corresponds to a pitch ratio of 16:15 (play (help·info)) or 1.0666… (approximately 111.7 cents), called the just diatonic semitone.[16] This is a practical just semitone, since it is the difference between a perfect fourth and major third (

The 16:15 just minor second arises in the C major scale between B & C and E & F, and is, «the sharpest dissonance found in the scale.»[7]
An augmented unison in just intonation is another semitone of 25:24 (play (help·info)) or 1.0416… (approximately 70.7 cents). It is the difference between a 5:4 major third and a 6:5 minor third. Composer Ben Johnston uses a sharp (♯) to indicate a note is raised 70.7 cents, or a flat (♭) to indicate a note is lowered 70.7 cents.[17]
Two other kinds of semitones are produced by 5-limit tuning. A chromatic scale defines 12 semitones as the 12 intervals between the 13 adjacent notes forming a full octave (e.g. from C4 to C5). The 12 semitones produced by a commonly used version of 5-limit tuning have four different sizes, and can be classified as follows:
- Just, or smaller, or minor, chromatic semitone, e.g. between E♭ and E (6/5 and 5/4):
- Larger, or major, chromatic semitone, or larger limma, or major chroma,[17] e.g. between C and C♯ (1/1 and 135/128):
- Just, or smaller, or minor, diatonic semitone, e.g. between C and D♭ (1/1 and 16/15):
- Larger, or major, diatonic semitone, e.g. between A and B♭ (5/3 and 16/9):
The most frequently occurring semitones are the just ones (S3 and S1): S3 occurs six times out of 12, S1 three times, S2 twice, and S4 only once.
The smaller chromatic and diatonic semitones differ from the larger by the syntonic comma (81:80 or 21.5 cents). The smaller and larger chromatic semitones differ from the respective diatonic semitones by the same 128:125 diesis as the above meantone semitones. Finally, while the inner semitones differ by the diaschisma (2048:2025 or 19.6 cents), the outer differ by the greater diesis (648:625 or 62.6 cents).
Extended just intonations[edit]
In 7-limit there is the septimal diatonic semitone of 15:14 (play (help·info)) available between the 5-limit major seventh (15:8) and the 7-limit minor seventh (7:4). There is also a smaller septimal chromatic semitone of 21:20 (
play (help·info)) between a septimal minor seventh and a fifth (21:8) and an octave and a major third (5:2). Both are more rarely used than their 5-limit neighbours, although the former was often implemented by theorist Henry Cowell, while Harry Partch used the latter as part of his 43-tone scale.
Under 11-limit tuning, there is a fairly common undecimal neutral second (12:11) (play (help·info)), but it lies on the boundary between the minor and major second (150.6 cents). In just intonation there are infinitely many possibilities for intervals that fall within the range of the semitone (e.g. the Pythagorean semitones mentioned above), but most of them are impractical.
In 13-limit tuning, there is a tridecimal 2/3 tone (13:12 or 138.57 cents) and tridecimal 1/3 tone (27:26 or 65.34 cents).
In 17-limit just intonation, the major diatonic semitone is 15:14 or 119.4 cents (Play (help·info)), and the minor diatonic semitone is 17:16 or 105.0 cents,[18] and septendecimal limma is 18:17 or 98.95 cents.
Though the names diatonic and chromatic are often used for these intervals, their musical function is not the same as the two meantone semitones. For instance, 15:14 would usually be written as an augmented unison, functioning as the chromatic counterpart to a diatonic 16:15. These distinctions are highly dependent on the musical context, and just intonation is not particularly well suited to chromatic usage (diatonic semitone function is more prevalent).
Other equal temperaments[edit]
19-tone equal temperament distinguishes between the chromatic and diatonic semitones; in this tuning, the chromatic semitone is one step of the scale (play 63.2 cents (help·info)), and the diatonic semitone is two (
play 126.3 cents (help·info)). 31-tone equal temperament also distinguishes between these two intervals, which become 2 and 3 steps of the scale, respectively. 53-ET has an even closer match to the two semitones with 3 and 5 steps of its scale while 72-ET uses 4 (
play 66.7 cents (help·info)) and 7 (
play 116.7 cents (help·info)) steps of its scale.
In general, because the smaller semitone can be viewed as the difference between a minor third and a major third, and the larger as the difference between a major third and a perfect fourth, tuning systems that closely match those just intervals (6/5, 5/4, and 4/3) will also distinguish between the two types of semitones and closely match their just intervals (25/24 and 16/15).
See also[edit]
- List of meantone intervals
- List of musical intervals
- List of pitch intervals
- Approach chord
- Major second
- Neutral second
- Pythagorean interval
- Regular temperament
References[edit]
- ^ a b c d e f g Duffin, Ross W. (2008). How equal temperament ruined harmony : (and why you should care) (First published as a Norton paperback. ed.). New York: W. W. Norton. p. 163. ISBN 978-0-393-33420-3. Retrieved 28 June 2017.
- ^ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p. xxiv. ISBN 0-8247-4714-3. Overtone semitone.
- ^ Semitone, half step, half tone, halftone, and half-tone are all variously used in sources.[1][2][3][4][5]
Aaron Copland, Leonard Bernstein, and others use «half tone».[6]
[7][8][9]
One source says that step is «chiefly US»,[10] and that half-tone is «chiefly N. Amer.»[11] - ^ Miller, Michael. The Complete Idiot’s Guide to Music Theory, 2nd ed. [Indianapolis, Indiana]: Alpha, 2005. ISBN 1-59257-437-8. p. 19.
- ^ Capstick, John Walton (1913). Sound: An Elementary Text-book for Schools and Colleges. Cambridge University Press.
- ^ Wharram, Barbara (2010). Elementary Rudiments of Music (2nd ed.). Mississauga, Ontario: Frederick Harris Music. p. 17. ISBN 978-1-55440-283-0.
- ^ a b Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction, p. 165. Theodore Baker, trans. G. Schirmer.
- ^ Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p. 54. ISBN 978-0-07-294262-0. Specific example of an A1 not given but general example of perfect intervals described.
- ^ Kostka and Payne (2003). Tonal Harmony, p. 21. ISBN 0-07-285260-7. «There is no such thing as a diminished unison.»
- ^ Day and Pilhofer (2007). Music Theory for Dummies, p. 113. ISBN 0-7645-7838-3. «There is no such thing as a diminished unison, because no matter how you change the unisons with accidentals, you are adding half steps to the total interval.»
- ^ Surmani, Andrew; Karen Farnum Surmani; Morton Manus (2009). Alfred’s Essentials of Music Theory: A Complete Self-Study Course for All Musicians. Alfred Music Publishing. p. 135. ISBN 978-0-7390-3635-8. Since lowering either note of a perfect unison would actually increase its size, the perfect unison cannot be diminished, only augmented.
- ^ a b Dahlhaus, Carl, trans. Gjerdingen, Robert O. Studies in the Origin of Harmonic Tonality. Princeton University Press: Princeton, 1990. ISBN 0-691-09135-8.
- ^ Rashed, Roshdi (ed.) (1996). Encyclopedia of the History of Arabic Science, Volume 2, pp. 588, 608. Routledge. ISBN 0-415-12411-5.
- ^ Hermann von Helmholtz (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music, p. 454.
- ^ Benson, Dave (2006). Music: A Mathematical Offering, p. 369. ISBN 0-521-85387-7.
- ^ Royal Society (Great Britain) (1880, digitized Feb 26, 2008). Proceedings of the Royal Society of London, Volume 30, p. 531. Harvard University.
- ^ a b John Fonville. «Ben Johnston’s Extended Just Intonation- A Guide for Interpreters», p. 109, Perspectives of New Music, vol. 29, no. 2 (Summer 1991), pp. 106–137. «…the 25/24 ratio is the sharp (#) ratio…this raises a note approximately 70.6 cents.»
- ^ Prout, Ebenezer (2004). Harmony, p. 325. ISBN 1-4102-1920-8.
Further reading[edit]
- Grout, Donald Jay, and Claude V. Palisca. A History of Western Music, 6th ed. New York: Norton, 2001. ISBN 0-393-97527-4.
- Hoppin, Richard H. Medieval Music. New York: W. W. Norton, 1978. ISBN 0-393-09090-6.
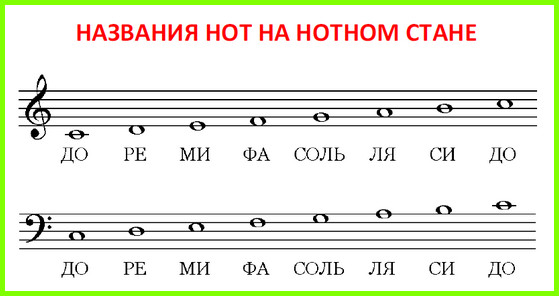
Нотное письмо — общепринятая система записи звуков в виде специальных знаков (нот) на нотном стане.
Нотное письмо является универсальным языком общения музыкантов всего мира, помогает запечатлеть собственные сочинения и, конечно же, прикоснуться к культурному наследию многовековой музыкальной истории.
Как невозможно нарисовать картину без холста, так и нотное письмо невозможно без нотного стана.
Нотный стан
Нотный стан — представляет собой пять параллельных горизонтальных линий, на которые наносятся: ноты (1), паузы (2), знаки альтерации (3), ключи (4), размеры (5), такты (6) и т.д. Нотный стан может иметь по пять нижних (7) и верхних (8) добавочных линий.
Нота
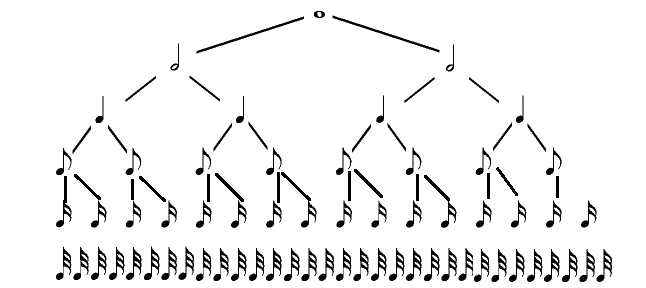
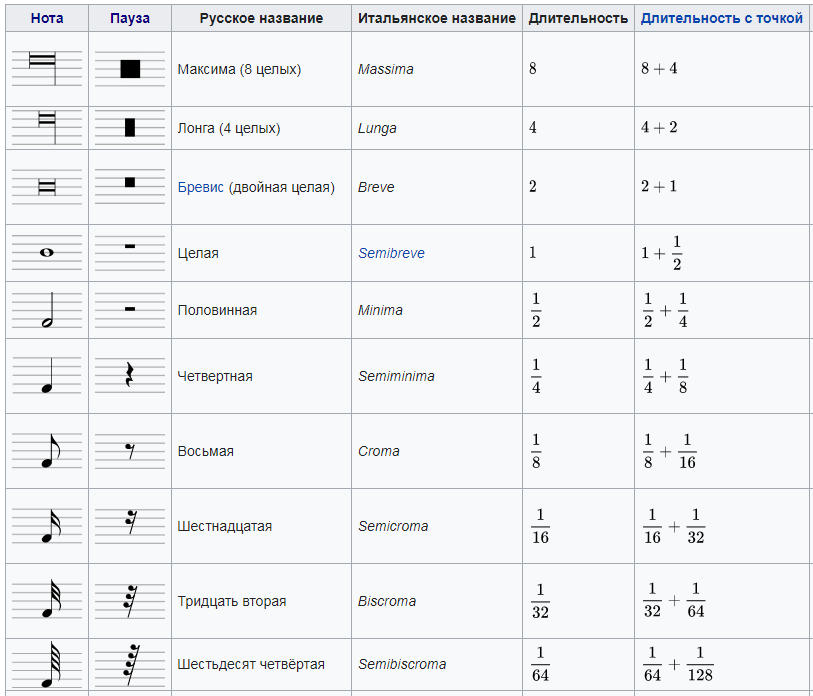
Нота — специальный знак на нотном стане характеризующий высоту звука и его длительность, имеет вид: овала, овала со штилем, закрашенного овала со штилем и флажком. Все это указывает на длительность звучания ноты: целая, половинная, четвертная, восьмая, шестнадцатая, тридцатьвторая.
Существуют так же знаки увеличения длительности ноты: точка, две точки, фермата, лига. Одна точка — увеличение длительности ноты на ее половину основной длительности. Две точки — увеличение длительности ноты на половину плюс на четверть от основной длительности. Лига — связывает ноты одинаковой высоты, обозначается дугообразной линией.Фермата — указывает на «неограниченную» длительность ноты (в разумных пределах), изображается небольшим полукругом с точкой.
Пауза
Пауза — специальное обозначение, на нотном стане, указывающее на отсутствие звучания инструмента. Подобно нотам пауза имеет свою продолжительность и знаки корректировки длительности. Пауза бывает: целая (длинною в такт), половинная, четвертная, восьмая, шестнадцатая, тридцатьвторая.
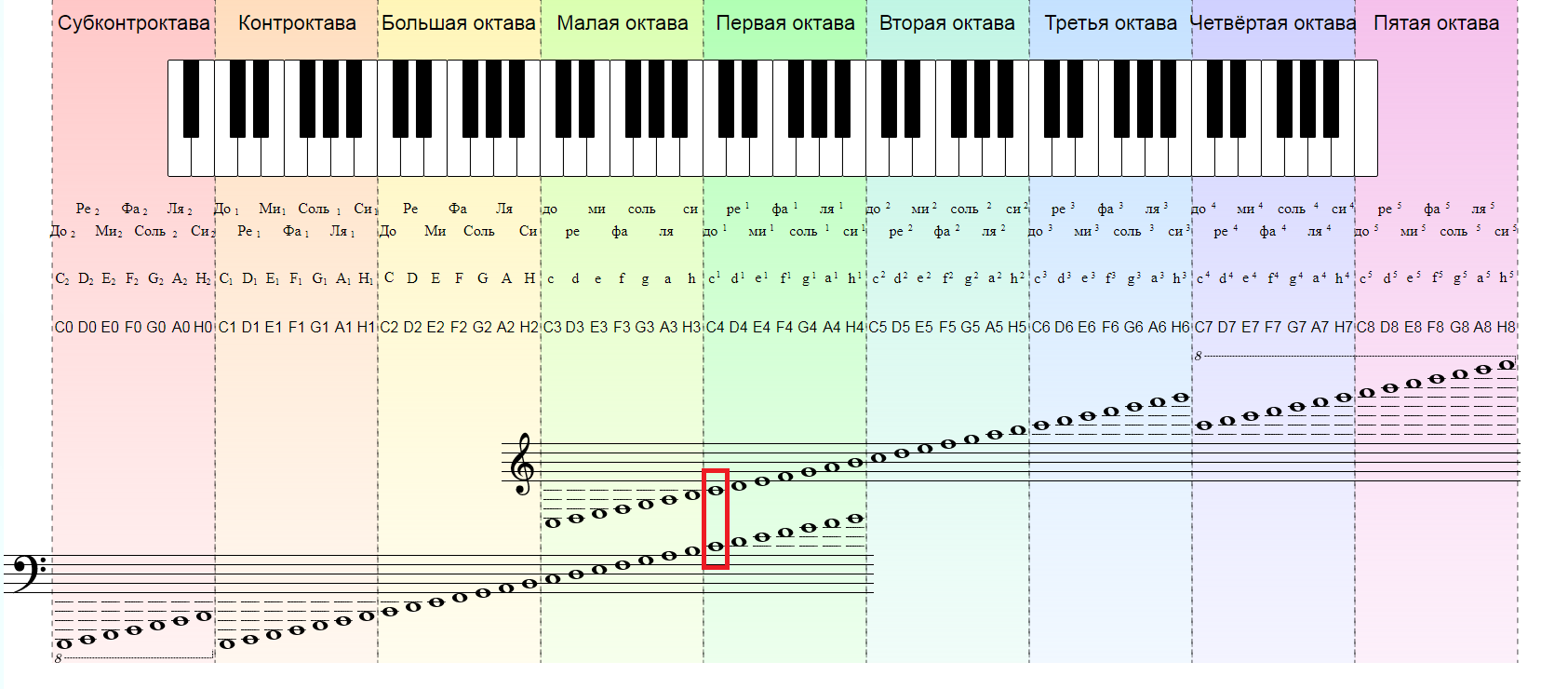
Звукоряд. Тон. Полутон
Прежде чем продолжить, внесем ясность в понятия: звукоряд, тон, полутон.
Помимо длительности, каждая нота в звукоряде имеет свое название и место (ступень). Расстояние между нотами определяется тоном или полутоном. Один звукоряд (октава) содержит 12 звуков (7 нот): До, Ре, Ми, Фа, Соль, Ля, Си.
| Октава | |||||||||||
| До | До# | Ре | Ре# | Ми | Фа | Фа# | Соль | Соль# | Ля | Ля# | Си |
| До | Ре | Ми | Фа | Соль | Ля | Си | |||||
| Полутон | |||||||||||
| Тон |
Знаки альтерации
Альтерация — специальный знак, на нотном стане, указывающий на повышение или понижение звучания ноты на полутон (тон). Существует пять знаков альтерации: диез — повышение на полутон; дубль-диез — повышение на тон; бемоль — понижение на полутон; дубль-бемоль — понижение на тон; бекар — отмена знаков альтерации.
Ключ
Ключ — специальный знак, облегчающий чтение нот на нотном стане, указывающий на определенную ноту, от которой ведется отсчет других нотных знаков музыкального произведения. В нотном письме различают три основных ключа:скрипичный — Соль, басовый — Фа, альтовый — До.
Такт. Размер. Ритм. Темп. Динамические оттенки
Такт — область на нотном стане между двумя вертикальными линиями. Затакт — неполный такт, при этом последний такт так же может быть не полным.
Размер — количество сильных и слабых долей образующих такт. Доля бывает: сильная и слабая. Сильная доля — наиболее акцентируемая нота при игре. Слабая доля — менее акцентируемая нота соответственно.
Размеры подразделяются на простые и сложные. Простой размер: 2/4, 3/4, 4/4. Сложный размер, как правило, составной из двух одинаковых или разных простых размеров: 6/8 + 6/8 = 12/8.
Ноты, поделенные на такты с указанием размера, не могут передать настроение музыкального произведения без ритмического рисунка, темпа исполнения с его динамической окраской и динамического оттенка звучания. В нотном письме, учтен и этот момент.
Ритм — последовательность нот объединенных в ритмические группы на основе их длительности. Основными делениями являются: целые, половинные, четвертные, восьмые, шестнадцатые ноты и т.д. Альтернативные виды деления: дуоль, квартоль, триоль, квинтоль, секстоль, септоль. При делении на несколько частей, полученные длительности занимают равномерное суммарное время звучания исходной ноты.
Темп — скорость исполнения музыкального произведения. Как правило, темпы делят на три группы: медленные,умеренные, быстрые.
| Медленные темпы | Умеренные темпы | Быстрые темпы | |||
| Итальянский | Русский | Итальянский | Русский | Итальянский | Русский |
| Largo | Широко | Andante | Спокойно, не спеша | Allegro | Скоро |
| Lento | Протяжно | Andantino | Чуть подвижнее, чем Andante | Vivo | Живо |
| Adagio | Медленно | Moderato | Умеренно | Vivace | Живо |
| Grave | Тяжело | Sostenuto | Сдержанно | Presto | Быстро |
| Allegretto | Оживлённо | Prestissimo | Очень быстро | ||
| Allegro moderato | Умеренно скоро |
Динамические оттенки темпа — указывают на замедление или ускорение темпа игры.
| Оттенки движения | Динамические оттенки движения | Другие обозначения | |||
| Итальянский | Русский | Итальянский | Русский | Итальянский | Русский |
| Molto | Очень | Ritenuto | Сдерживая | a tempo | в темпе |
| Assai | Весьма | Ritardando | Запаздывая | tempo primo | вернуться в первоначальный темп |
| Con moto | С подвижностью | Allargando | Расширяя | tempo I | первоначальный темп |
| Commodo | Удобно | Rallentando | Замедляя | I’istesso | В том же темпе |
| Non troppo | Не слишком | Accelerando | Ускоряя | ||
| Non tanto | Не столь | Animando | Воодушевляя | ||
| Meno mosso | Менее подвижно | Stringendo | Ускоряя | ||
| Più mosso | Более подвижно | Stretto | Сжато | ||
| Sempre | Всё время |
Динамический оттенок — уровень громкости исполнения музыкального произведения или его части.
| Постоянная громкость | Изменение громкости | Смена громкости | ||||
| Итальянский | Сокращение | Русский | Итальянский | Русский | Итальянский | Русский |
| fortissimo | ff | Очень громко | crescendo | Усиливая | più forte | Более громко |
| forte | f | Громко | poco a poco crescendo | Мало-помалу усиливая | meno forte | Менее громко |
| mezzo forte | mf | Средняя громкость | diminuendo | Стихая | sforzando (sf) | Резкое ударение звуков |
| mezzo piano | mp | Средне-тихо | poco a poco diminuendo | Мало-помалу стихая | ||
| piano | p | Тихо | smorzando | Замирая | ||
| pianissimo | pp | Очень тихо | morendo | Замирая |
Мелизмы
Мелизмы — вспомогательные ноты, служащие украшением основной ноты, исполняются за счет длительности предыдущих нот и, как правило, расположены в диапазоне секунды. К мелизмам относятся: форшлаг (короткий, длинный), мордент,трель, группетто.
Форшлаг — короткий звук, исполняемый пред основной нотой, одиночный или состоящий из нескольких звуков.Одиночный форшлаг — маленький знак восьмой ноты с перечеркнутым флажком. Для обозначения форшлага состоящего из нескольких нот используют маленькие шестнадцатые ноты без перечеркнутых флажков.
Форшлаг бывает:
- короткий — быстрые нотки, которые исполняются за счет длительности предыдущих нот перед основной украшаемой нотой;
- длинный — исполняется за счет длительности украшаемой ноты и имеет половину её длительности, основная нота при этом уменьшается по длительности в половину.
Мордент — мелизм, состоящий из трех нот: 1 — основная нота, совпадающей с украшаемой нотой; 2 — вспомогательная нота, отличается на секунду, 3 — основная нота, совпадает с изначальной нотой. Мордент бывает одиночный и двойной.
Трель — быстрое чередование двух соседних нот, основной и вспомогательной, как правило, находящейся на ступень выше.
Группетто — быстрое исполнение нот в определенной последовательности, как правило, на расстоянии секунды, замыкая игру конечной нотой обозначения.
Сокращенное нотное письмо
Сокращенное нотное письмо, упрощает чтение нот, особенно если используется большое число повторений одинаковых тактов с небольшими вариациями.
Реприза — повторение тактов. При этом если часть тактов изменяется, то используется вольта с цифрой, которая соответствует циклу повторения.
— Segno, специальная отметка, используемая с аббревиатурой Dal segno.
— Coda, окончание произведения, используется вместе с аббревиатурами D.S. и D.C.
— Da capo, указывает на переход в начало музыкального произведения, обычно используется с пояснением: al fine — до конца или al coda — до знака «кода».
— Dal segno, переход к знаку «Segno«, так же используется: al fine — до конца, al coda — до знака «кода».
— знак используется, если необходимо повторить один или несколько тактов.
— знак применяют для повторения мелодической фигуры в такте.
Для повторения ноты или аккорда используется следующая запись:
Тремоло — быстрое, равномерное, чередование двух звуков или созвучий:
Для удвоения ноты в октаву пишут цифру 8 — это значит, что к основной ноте необходимо добавить аналогичную ноту, звучащую на октаву выше:
Если необходимо играть ноты на октаву выше используется запись (8va —————¬), для игры на октаву ниже(8vb —————¬). Естественно исполняются только те ноты, над которыми проходит пунктирная линия. Если необходимо играть ноты на 2 октавы выше или ниже используется запись (15ma —-¬ или 15mb ——¬).
Приемы игры
Приемы игры — специальные методы исполнения нотной записи: легато, стаккато, арпеджио и глиссандо.
Легато — подразумевает под собой связное исполнение нотной записи, звучание нот согласовано и перетекает из одной в другую, обозначается специальной линией в виде дуги.
Стаккато — короткое отрывистое исполнение нот, указывается точкой над или под нотой. Стаккатиссимо — наиболее острое отрывистое исполнение нот, обозначается перевернутым треугольником.
Арпеджиато — быстрое исполнение нот аккорда снизу вверх или в обратном порядке, обозначается вертикальной волнистой линией.
Глиссандо, слайд — прием скольжения от одной ноты к другой.
Поделитесь статьей в соцсетях — поддержите проект!
- Подробности
-
Опубликовано: 17 Октябрь 2011 -
Просмотров: 34060
Публикуется с согласия автора.
Помимо ритма и метра в музыке большое значении имеет расстояние между звуками. Это расстояние может быть различным, что делает музыкальные мелодии такими разнообразными и непохожими друг на друга. Мелодия может «топтаться» на одном месте, используя два-три соседних звука, может «совершать скачки» вверх, вниз, а может плавно «скользить» от одного звука к другому.
Самое маленькое расстояние между двумя звуками называется
полутон
. Наглядное представление о полутоне проще всего можно получить с помощью гитары, а точнее, гитарного грифа, где расстояние между ладами и есть полутон. Если мы сыграем несколько звуков, последовательно зажимая лады на одной струне, то у нас получится восходящая «цепочка» звуков, между которыми неизменно сохраняется одинаковое расстояние.
Сыграть на фортепиано такую «цепочку» немного сложнее: для этого нам придётся использовать чёрные клавиши. Так, расстояние, равное полутону будет не между клавишами
до
и
ре
, а между клавишей
до
и ближайшей чёрной клавишей справа; другой полутон образуется между этой же клавишей и клавишей
ре
; в итоге, между клавишами
до
и
ре
будет два полутона или один
тон
(от греч. τόνος– натяжение, напряжение):

Однако между белыми клавишами расстояние не всегда является тоном. Между клавишами
ми
и
фа
, а также между
си
и
до
нет чёрных клавиш, и расстояние между ними равняется полутону:

Расстояния между звуками высчитывается методом сложения тонов и полутонов. Например, расстояние между
до
и
фа
– два с половиной тона (между
до
и
ре
– 1 тон,между
ре
и
ми
– 1 тон, между
ми
и
фа
– полтона).
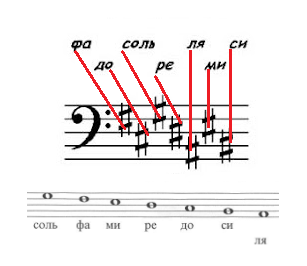
Чёрные клавиши собственных названий не имеют, зато они получают целых два названия, производные от двух окружающих её белых клавиш. Если чёрная клавиша располагается справа (то есть выше на полтона) от белой клавиши, то она называется
диезом
, если слева (то есть ниже на полтона), то –
бемолем
. Например, чёрная клавиша, располагающая между клавишами
до
и
ре
имеет два названия: по отношению к
до
– это
до-диез
, по отношению к
ре
–
ре-бемоль
:

Итак, знак
диез
означает повышение звука на полтона, а знак
бемоль
– понижение на полтона. Эти названия имеют специальные нотные обозначения: диез –
, бемоль –
, которые пишутся перед нотами. Например:

фа-диез, до-диез, си-бемоль, ми-бемоль
.
Из всего вышеизложенного следует, что знаки
диез
и
бемоль
означают только чёрные клавиши. В большинстве случаев так оно и есть, но не всегда. Например, какая клавиша будет звучать, когда нам встретится нота
ми-диез
? Так как, диез – это повышение звука на полтона, а между клавишами
ми
и
фа
нет чёрной клавиши, то клавиша
фа
и будет звуком
ми-диез
. И наоборот,
фа-бемоль
– это клавиша
ми
. Аналогичная ситуация возникает и между клавишами
си-до
, где, как вы помните, также расстояние равно полутону.
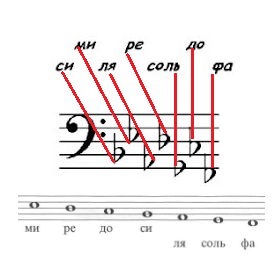
Кроме того, существуют ещё и знаки повышения и понижения звуков не на полтона, а на целый тон. Такие знаки имеют название
дублей
(то есть двойные) и имеют свои обозначения:
дубль-диез
–
,
дубль-бемоль
–
. Например:

фа-дубль-диез, до-дубль-диез,
си-дубль-бемоль, ми-дубль-бемоль.
Если нам встретится нота
фа-дубль-диез
, то нам необходимо повысить ноту
фа
на тон, в итоге получится звук
соль
; если встретится нота
си-дубль-бемоль
, то потребуется ноту
си
понизить на тон, получится –
ля
.
Все эти «непривычные» диезы и бемоли (
ми-диез, фа-бемоль, си-диез, до-бемоль
), а также дубли применяются достаточно редко и на первых порах вам не встретятся. Однако с возрастанием сложности нотных примеров эти знаки будут применяться. На вопрос, зачем нужны эти дополнительные обозначения и названия для белых клавиш, мы ответим позже (в третьей теме «Лад и тональность»), а сейчас рассмотрим правила применения этих знаков в нотном письме.
Существуют два вида знаков: случайные и ключевые.
Случайные знаки
– это те знаки, которые встречаются в данном музыкальном произведении редко, эпизодически; действуют исключительно на протяжении того такта, где они встречаются:
В данной мелодии в третьем такте возле половинной ноты
фа
стоит знак
диез
(то есть повышение на полтона – ближайшая чёрная клавиша справа). Этот знак распространяется и на вторую ноту этого такта, то есть четвертная нота
фа
также должна быть повышена на полтона. Но в четвёртом такте, где также встречается нота
фа
, знак
диез
уже не действует, а значит, здесь звучит уже белая клавиша
фа
.
Ключевые знаки
– это те знаки, которые встречаются в данном музыкальном произведении постоянно; записываются они возле ключа
[1]
:

После скрипичного ключа у нас стоит
бемоль
на высоте ноты
си
(обратите внимание, что ключевой знак стоит перед размером). Этот знак действует на протяжении всех восьми тактов данной мелодии, то есть все ноты
си
во втором, третьем, а также в шестом
[2]
тактах должны быть понижены на полтона (ближайшая чёрная клавиша слева).
Наконец, существует ещё один знак, который отменяет все предыдущие знаки – знак
бекар
(
):

Во втором такте этой мелодии перед второй нотой
до
стоит знак
диез
, который повышает этот звук на полтона, однако перед следующей нотой
до
в этом такте стоит знак
бекар
, который возвращает ноте
до
её первоначальную высоту. Аналогичная ситуация в четвёртом такте.
Итак, существуют пять знаков изменения высоты звука:
– диез (повышение на полтона)
– бемоль (понижение на полтона)
– дубль-диез (повышение на тон)
– дубль-бемоль (понижение на тон)
– отмена предыдущего знака
Все вышеперечисленные знаки изменения высоты звука называются знаками
альтерации
(от лат. alter – другой, изменившийся).
Задания:
-
Посчитайте сколько тонов и полутонов будет между:
а.
до
и
ля
б.
ми
и
си
в.
ре
и
фа-диез
г.
ми-бемоль
и
соль-диез
д.
до-дубль-диез
и
ля-диез
е.
фа-бемоль
и
си-бемоль
-
Найдите на инструменте следующие звуки:
-
№28-36 (раздел «Одноголосие»). Обратите внимание как в №32 и 33 знаки альтерации меняют окраску, настроение мелодии. В №36 есть ключевые знаки
фа-диез
и
до-диез
, не забывайте, что они действуют на все встречающиеся звуки
фа
и
до
, где бы они не находились. - №8-10 (раздел «Многоголосие»).
[1]
Более подробно о ключевых знаках см. третью тему «Лад и тональность».
[2]
Несмотря на то, что знак
бемоль
записан на третьей линейке, он будет действовать на все ноты
си
, встречающиеся в мелодии, даже если они находятся в другой октаве.
Комментарии
Урок 2. Нотная грамота

Этого достаточно, чтобы приступить к изучению нотной грамоты «с нуля». Если нотная грамота вам знакома, все равно просмотрите материал урока с целью убедиться, что вы ничего не пропустили, когда изучали нотную грамоту ранее.
Цель урока: познакомиться с нотной грамотой «с нуля», получить представление о паузах и длительностях нот, их расположении на нотном стане и других связанных с этой темой понятиях.
Это нужно, чтобы вы могли в будущем самостоятельно разбирать ноты, записанные на нотном стане, и ориентироваться в табах и аккордах, если вам попадется аккордовая запись мелодии либо табулатура.
Содержание:
- Кто придумал ноты
- Расположение нот на нотном стане
- Знаки альтерации
- Ключи на нотном стане
- Длительности нот
- Паузы
- Тест на проверку знаний
Заметим, что большинство современных музыкальных сайтов чаще предлагают для гитары именно аккорды либо табулатуру (табы) к песне, нежели традиционную запись на нотном стане. Для начинающих музыкантов нужно уточнить, что аккорды и табы – это те же самые ноты, только записанные в другом виде, т.е. в другом виде музыкальной нотации, поэтому выучить ноты нужно обязательно. В общем, приступаем!
Кто придумал ноты
Начнем с небольшого исторического экскурса. Считается, что первым человеком, кому пришла в голову идея обозначать высоту звука знаками, был флорентийский монах и композитор Гвидо д’Ареццо. Это случилось в первой половине 11 века. Гвидо учил монастырских певчих различным церковным песнопениям, а чтобы добиться слаженного звучания хора, придумал систему знаков, указывающих на высоту звука.
Это были квадратики, расположенные на четырех параллельных линиях. Чем более высокий звук нужно было издать, тем выше располагался квадратик. В его нотации было всего 6 нот, а названия они получили от начальных слогов строк Гимна, воспевающего Иоанна Крестителя: Ut, Resonare, Mira, Famuli, Solve, Labii. Несложно заметить, что 5 из них – «ре», «ми», «фа», «соль», «ля» – используются и сегодня. К слову, музыку к гимну написал сам Гвидо д’Ареццо.
Позже в нотный ряд добавилась нота «си», в нотный стан – пятая линейка, скрипичный и басовый ключи, знаки альтерации, которые мы сегодня будем изучать. В эпоху Средневековья, когда зарождалась буквенная нотация, звукоряд было принято начинать с ноты «ля», за которой закрепилось обозначение в виде первой буквы латинского алфавита А. Соответственно, следующей за ней ноте «си» досталась вторая буква алфавита В.
Поскольку процесс формирования способов записи звуков развивался в разных странах параллельными курсами, возникли разные варианты нотаций. Так, в немецкой музыкальной традиции дополнительной ноте «си» присвоили букву Н, следующую за буквой G. Это связано с тем, что у немцев буква В была уже занята нотой «си-бемоль», которую располагали сразу за нотой «ля».
Современное понимание звукоряда и основных его ступеней сложилось в 17 веке, а звук, соответствующий по высоте «си-бемолю», долгое время считался базовым элементом музыкальной системы, т.е. не пониженным и не повышенным. Сегодня общепринятой считается система нотации в виде C, D, E, F, G, A, B. Хотя и обозначение ноты «си» в виде Н тоже можно встретить. Мы уже начали и далее продолжим изучать системы нотации и записи нот на нотном стане, принятые в современном мире музыки.
Расположение нот на нотном стане
Вы уже знаете, что нота – это музыкальный звук. Ноты отличаются по высоте, и за каждой нотой закреплено свое обозначение. Также вы уже поняли, что нотный стан представляет собой 5 параллельных линий, на которых расположены ноты. За каждой нотой закреплено свое место. Собственно, именно так и можно идентифицировать ноты, глядя на обозначения в нотном стане. Теперь давайте совместим эти знания и посмотрим, как выглядит нотный стан с нотами в самом общем виде (на значки слева пока не смотрим):
Нотный стан (он же нотоносец) – это те самые 5 параллельных линий, которые вы видите на картинке. Кружочки на нотах – это условные обозначения нот. На верхнем нотоносце вы видите ноты для 1-й октавы, на нижнем – ноты для малой октавы.
Точкой отсчета в обоих случаях является нота «до» 1-й октавы, и для нее предусмотрена добавочная линейка. Разница в том, что на верхнем нотоносце ноты идут снизу вверх, поэтому нота «до» 1-й октавы находится внизу. На нижнем нотоносце ноты идут сверху вниз, поэтому нота «до» 1-й октавы находится сверху.
Однако мы помним, что музыкальные звуки охватывают намного больший диапазон, чем малая и первая октавы. Поэтому, чтобы получить полное представление о расположении нот на нотном стане, вам нужно изучить более подробную схему размещения нот:
Самые внимательные из вас увидели, что и на подробной схеме мы видим не все октавы. Чтобы увидеть правильное расположение всех нот, нам снова понадобятся добавочные линейки. Посмотрите, как это выглядит, на примере контроктавы:
А теперь вы уже готовы к тому, чтобы выучить расположение всех нот на нотном стане. Для удобства скоординируем изображение нотного стана с клавиатурой фортепиано, которую вы уже успели рассмотреть, когда проходили урок №1. Обратите внимание, где находится первая нота «до» 1-й октавы относительно линий верхнего и нижнего нотоносца. Мы отметили ее красным цветом:
У большинства из тех, кто видит всю эту картину впервые, возникает вопрос: а как же это запомнить?!.. В общем-то, запомнить вам нужно только расположение первой ноты «до» 1-й октавы, а все остальные ноты располагаются в определенной логической последовательности относительно первой ноты «до».
Более легкому запоминанию нот поможет упражнение «Лезгинка». Как ни удивительно, к музыке оно никакого отношения не имеет, а предназначено для развития координации работы правого и левого полушарий головного мозга у детей [А. Сиротюк, 2015]. Представьте, что кулак или ладошка с поджатыми пальцами – это кружок для обозначения ноты, а прямая кисть руки, которая упирается в середину ребра ладони – это добавочная линейка нотоносца:
Так вы запомните, что добавочная линейка рассекает пополам кружок, обозначающий ноту «до»:
Дальше будет проще. Ноту «ре» можно представить как кулак, расположенный над вытянутой кистью. Следующая нота «ми» будет рассечена пополам вытянутой кистью, но кисть уже будет изображать не добавочную линию, а нижнюю из пяти линий нотоносца. Для ноты «фа» мы поднимаем кулак над линией, а ноту «соль» рассекаем вытянутой кистью, которая теперь изображает вторую снизу линию нотоносца. Думается, принцип построения нот вы поняли. Аналогично можно выстроить ноты, идущие вниз относительно «до» 1-й октавы.
Если вы хотите освоить специальные мнемотехники, которые помогут запоминать любую информацию, записывайтесь на наш курс «Мнемотехники», и за короткий срок (чуть больше месяца) вы поймете, что никаких проблем с памятью у вас нет. Есть лишь более эффективные техники запоминания, нежели те, которыми вы пользовались ранее.
Итак, с расположением нот на нотном стане, думаем, в целом все понятно. Самые внимательные уже заметили, что при рассмотренной выше расстановке нот места для диезов и бемолей, т.е. повышения и понижения ноты, уже не остается. И вот для этого нам нужны знаки альтерации в нотах.
Знаки альтерации
В конце предыдущего урока вы уже выучили символы диеза (♯) и бемоля (♭). Вы уже поняли, что если нота повышается на полутон, к ней добавляют значок диеза, если понижается на полутон – значок бемоля. Так, повышенная нота «соль» будет записана как G♯, а пониженная нота «соль» как G♭. Диез и бемоль называются знаками альтерации, т.е. изменения. Слово происходит от позднелатинского alterare, что переводится как «изменять».
Повышение на 2 полутона обозначается двойным, т.е. дубль-диезом, понижение на 2 полутона обозначается двойным, т.е. дубль-бемолем. Для дубль-диеза есть специальный значок, похожий на крестик , но, т.к. его трудно подобрать на клавиатуре, может использоваться обозначение ♯♯ или просто две решетки ##. Чтобы обозначить дубль-бемоль, пишут либо 2 значка ♭♭, либо латинские буквы bb.
Чтобы обозначить повышение или понижение ноты на нотном стане, значок диеза или бемоля располагается либо непосредственно перед нотой, либо, если ту или иную ноту нужно снизить или повысить во всем произведении, в начале нотного стана с нотами к произведению. Для случаев, когда изменение ноты предусмотрено на протяжении всего произведения, за символами диезов и бемолей закреплены определенные места на нотном стане:
Уточним для надписи на картинке, что под словосочетанием «в скрипичном ключе» подразумевается нотоносец для нот 1-5 октав, а под словами «в басовом ключе» – нотоносец для всех остальных октав от малой до субконтроктавы. Чуть позже мы расскажем про скрипичный и басовый ключи подробнее. Пока поговорим о том, как запомнить расположение диезов и бемолей на нотоносце.
В принципе, это несложно, если вы успели выучить расположение значков, обозначающих ноты. Так, значок диеза располагается ровно на той линии нотоносца, что и та нота, которую требуется повышать. Для нотоносца в скрипичном ключе вам нужно запомнить, где находятся ноты в диапазоне от «ля» 1-й октавы до «соль» 2-й октавы, и вы легко поймете закономерность размещения диезов:
Точно такая закономерность наблюдается при расположении бемолей. Они тоже находятся на тех строчках, что и ноты, к которым они относятся. Здесь в качестве ориентира используются ноты в диапазоне от «фа» 1-й октавы до «ми» 2-й октавы:
С диезами и бемолями в басовом ключе действуют абсолютно те же закономерности. Для ориентирования в диезах вам следует запомнить расположение нот от «соль» малой октавы до «ля» большой октавы:
Для ориентирования в бемолях нужно запомнить расположение нот от «ми» малой октавы до «фа» большой октавы:
Как вы уже заметили, для расположения диезов и бемолей в начале произведения возле ключа – скрипичного или басового – задействуются только основные линейки нотоносца. Такие знаки альтерации называются ключевыми.
Знаки альтерации, относящиеся только к одной ноте, называются случайными или встречными, действуют в пределах одного такта и располагаются непосредственно перед этой нотой.
А сейчас давайте разберемся, что же делать, если нужно отменить диез или бемоль, установленный в начале нотного стана. Такая необходимость может возникнуть при модуляции, т.е. при переходе в другую тональность. Это модный прием, часто применяемый в эстрадной музыке, когда последний припев или куплет и припев исполняется на 1-2 полутона выше, чем предыдущие куплеты и припевы.
Для этого существует еще один знак альтерации: бекар. Его функция – отмена действия диезов и бемолей. Бекары тоже подразделяются на случайные и ключевые.
Функции бекара:
- Случайный бекар отменяет действие случайных знаков альтерации, ставится в том месте и перед той нотой, для которой нужно отменить действие диеза или бемоля, и действует в пределах такта.
- Ключевой бекар отменяет действие диезов и бемолей, указанных в начале произведения, т.е. ключевых. Он действует до следующей смены ключевого знака либо, если такового не будет, до конца произведения.
Чтобы было нагляднее, посмотрите, где располагается случайный бекар на нотном стане:
А теперь посмотрите, где располагается ключевой бекар, и вы сразу поймете разницу:
Уточним, что запись на нотном стане применяется для гитары и фортепиано, и любых других музыкальных инструментов, а вот табы, которые вы видите на предыдущей картинке под нотным станом, используются для гитары.
В гитарных табах 6 линий по количеству струн гитары. Верхняя линия обозначает самую тонкую струну, которая будет нижней, если вы возьмете гитару в руки. Нижняя линия означает самую толстую гитарную струну, которая является верхней, когда вы держите гитару в руках. Цифры указывают, на каком ладу зажимать ту струну, на которой написана цифра.
Применительно к иллюстрации по случайному бекару мы видим, что сначала нужно было играть «до-диез», который как раз находится на втором ладу 2-й струны. После бекара, т.е. отмены диеза, нужно играть чистую ноту «до», которая находится на первом ладу 2-й струны. Финальный урок нашего курса будет посвящен игре на различных музыкальных инструментах, в том числе на гитаре, и мы расскажем, как легко и просто запомнить расположение нот на гитарном грифе.
Подведем итог и сведем воедино всю информацию по знакам альтерации на следующей картинке:
Если вы уже умеете играть на каком-нибудь музыкальном инструменте, а сейчас решили подтянуть теорию, рекомендуем прочитать параграф 11 «Знаки альтерации» в учебнике Варфоломея Вахромеева «Элементарная теория музыки», где есть примеры разбора нотной записи [В. Вахромеев, 1961]. Мы же переходим к выполнению ранее данных обещаний и расскажем, что же такое ключи применительно к нотному стану.
Ключи на нотном стане
Мы ранее использовали словосочетания «в скрипичном ключе» и «в басовом ключе». Расскажем, что имеется в виду. Дело в том, что за каждой из линий нотоносца условно закреплена определенная звуковысотность. Ввиду того, что в мире существует множество музыкальных инструментов, издающих самые разные звуки, понадобились некие «точки отсчета» звуковысотности, и их роль отдали ключам.
Ключ выписывается так, чтобы линия, откуда стартует отсчет, пересекла его в главной точке. Таким способом ключ закрепляет за нотой, написанной на данной линии, точную высоту, относительно которой отсчитывается высотность и наименования прочих звуков. Различают несколько разновидностей ключей.
Ключи – перечень:
- Скрипичный – так называемый ключ «Соль», закрепляет на 2-й линии высоту звука «соль» 1-й октавы. Главная точка расположена по центру спирали ключа и как бы «накручивается» на 2-ю линейку нотного стана.
- Басовый– так называемый ключ «Фа», закрепляет на 4-й линии высоту «фа» в малой октаве. 2 точки знака стоят сверху и снизу 4-й линии нотоносца, если вести отсчет снизу.
- Альтовый – так называемый ключ «До», закрепляет высоту «до» в 1-й октаве на 3-й линии, используется преимущественно для альтовых инструментов.
- Теноровый – тоже ключ «До», но уже на 4-й линии, используется для таких инструментов как фагот, виолончель и тромбон.
Давайте проиллюстрируем:
Заметим, что когда-то ключей «До» было больше. Ключ «До» на 1-й линии назывался сопрановым, на 2-й – меццо-сопрановым, на 5-й – баритоновым, а употреблялись они для вокальных партий соответственно указанным диапазонам. Вообще, разные ключи в нотах нужны, чтобы не делать добавочные линии нотоносца в избыточных количествах и облегчить восприятие нот. К слову, чтобы упростить чтение нот, используется ряд дополнительных обозначений, о которых мы сейчас поговорим.
Длительности нот
Когда на 1-м уроке мы изучали физические свойства звука, мы узнали, что для музыкального звука важной характеристикой является его длительность. Глядя на нотный стан, музыкант должен понимать не только то, какую ноту нужно сыграть, но и как долго она должна звучать.
Чтобы было проще ориентироваться, кружочки нот могут быть светлыми или темными (пустыми или заштрихованными), иметь дополнительные «хвостики», «палочки», «линии» и прочее. Глядя на эти нюансы, сразу понятно, целая это нота или половинная, или еще какая-либо. Осталось разобраться, что значит «целая» нота, «половинная» и т.д.
Как считать длительности:
| 1 | Целая нота– тянется на равномерный отсчет «раз и 2 и 3 и 4 и» (звук «и» в конце произносится обязательно – это важно). |
| 2 | Половинная– тянется на отсчет «раз и 2 и». |
| 3 | Четвертная – тянется на «раз и». |
| 4 | Восьмая– тянется на «раз» или на звук «и», если восьмые идут подряд. |
| 5 | Шестнадцатая– успевает повториться дважды на слово «раз» или на звук «и». |
Понятно, что считать можно с разной скоростью, поэтому для унификации счета используется специальное устройство: метроном. Там четко выверено расстояние между звуками и устройство как бы считает вместо вас. Сейчас существует бесчисленное множество программ с функцией метронома, как самостоятельных, так и имеющих данную опцию в составе других мобильных приложений для музыкантов.
В Google Play можно найти, к примеру, программу-метроном Soundbrenner, а можно скачать программу для настройки гитары Guitar Tuna, где в разделе «Инструменты» будет «Библиотека аккордов» и «Метроном» (не забудьте разрешить приложению доступ к микрофону). Далее давайте разберемся, как обозначается длительность нот.
Длительности (обозначения):
- Целая нота – светлый (незакрашенный) значок.
- Половинная – светлый (незакрашенный) значок + штиль (вертикальная линия).
- Четвертная– темный (заштрихованный) значок + штиль.
- Восьмая– темный (заштрихованный) значок + штиль с «флажком» (он же «хвостик»).
- Шестнадцатая– темный (заштрихованный) значок + штиль с двойным «хвостиком».
- Тридцать вторая – темный (заштрихованный) значок + штиль с тройным «флажком».
- Точки справа от ноты увеличивают долготу звука в 1,5 раза.
Думается, принцип понятен, а для наглядности предлагаем вам следующую иллюстрацию:
Если 8-е, 16-е, 32-е ноты идут подряд, их принято объединять в группы и не «пестрить» большим количеством «хвостиков» или «флажков». Для этого применяется так называемое «ребро». По количеству ребер можно сразу понять, какие именно ноты объединены в группу для проигрыша.
Объединение нот в группу:
- 1 ребро – восьмые.
- 2 ребра – шестнадцатые.
- 3 ребра – тридцать вторые.
- 4 ребра – шестьдесят четвертые.
Вот как это выглядит:
Обычно ноты объединяются внутри такта. Напомним, что такт – это ноты и сопутствующие им знаки между двумя вертикальными линиями, которые именуются тактовыми чертами:
Как вы заметили, штиль может смотреть наверх либо вниз. Тут есть свои закономерности.
Направление штиля:
- Для записи одной мелодической линии без моментов, когда звучат одновременно две ноты или больше, штили направляю вверх для нот, изображенных ниже середины нотного стана, и вниз для нот, нарисованных выше середины нотного стана. Штили нот на 3-й (средней) линии могут быть направлены и вверх, и вниз, но чаще их направляют вниз.
- Для записи двух мелодических линий, когда могут звучать несколько нот одновременно, штили для нот «верхней» мелодии смотрят вверх, для «нижней» мелодии – вниз.
Более подробную информацию про длительности нот можно найти у Вахромеева в «Элементарной теории музыки [В. Вахромеев, 1961].
И, наконец, в любой мелодии есть и звуки, и паузы между ними. Поговорим о них.
Паузы
Паузы измеряются по такому же принципу, как нотные длительности. Пауза точно так может быть целой, половинной и т.д. Однако пауза может длиться дольше, чем целая нота, и для таких случаев придуманы особые названия. Так, если пауза длится в 2 раза дольше, чем целая нота, ее называют бревис, если в 4 раза дольше – это лонга, в 8 раз – максима. Полный перечень названий с обозначениями можно увидеть в нижеследующей таблице:
Итак, на сегодняшнем уроке вы познакомились с нотной грамотой «с нуля», получили представление о знаках альтерации, написании нот, обозначении пауз и других связанных с этой темой понятиях. Думаем, что для одного задания этого более чем достаточно. Теперь осталось закрепить ключевые моменты урока с помощью проверочного теста.
Тест на усвоение материала урока
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
А теперь переходим к изучению гармонии в музыке.
← 1 Свойства звука3 Гармония в музыке →

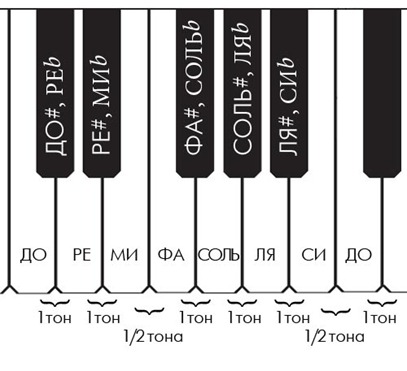

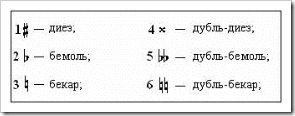
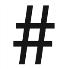






















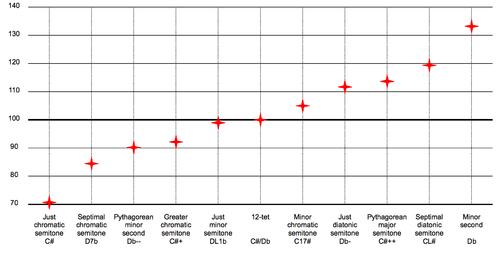





![sqrt[4]{frac{2}{3-sqrt{2}}} approx 100.4 text{ cents,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/237847316a3aea533ae093273132eda8e4d25250)