Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value.[1] Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals.
The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory.
In formulas, a limit of a function is usually written as
(although a few authors may use «Lt» instead of «lim»[2])
and is read as «the limit of f of x as x approaches c equals L«. The fact that a function f approaches the limit L as x approaches c is sometimes denoted by a right arrow (→ or 
which reads «




History[edit]
Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work Opus Geometricum (1647): «The terminus of a progression is the end of the series, which none progression can reach, even not if she is continued in infinity, but which she can approach nearer than a given segment.»[3]
The modern definition of a limit goes back to Bernard Bolzano who, in 1817, introduced the basics of the epsilon-delta technique to define continuous functions. However, his work was not known during his lifetime.[4]
Augustin-Louis Cauchy in 1821,[5] followed by Karl Weierstrass, formalized the definition of the limit of a function which became known as the (ε, δ)-definition of limit.
The modern notation of placing the arrow below the limit symbol is due to G. H. Hardy, who introduced it in his book A Course of Pure Mathematics in 1908.[6]
Types of limits[edit]
In sequences[edit]
Real numbers[edit]
The expression 0.999… should be interpreted as the limit of the sequence 0.9, 0.99, 0.999, … and so on. This sequence can be rigorously shown to have the limit 1, and therefore this expression is meaningfully interpreted as having the value 1.[7]
Formally, suppose a1, a2, … is a sequence of real numbers. When the limit of the sequence exists, the real number L is the limit of this sequence if and only if for every real number ε > 0, there exists a natural number N such that for all n > N, we have |an − L| < ε.[8]
The notation
is often used, and which is read as
- «The limit of an as n approaches infinity equals L«
The formal definition intuitively means that eventually, all elements of the sequence get arbitrarily close to the limit, since the absolute value |an − L| is the distance between an and L.
Not every sequence has a limit. If it does, then it is called convergent, and if it does not, then it is divergent. One can show that a convergent sequence has only one limit.
The limit of a sequence and the limit of a function are closely related. On one hand, the limit as n approaches infinity of a sequence {an} is simply the limit at infinity of a function a(n)—defined on the natural numbers {n}. On the other hand, if X is the domain of a function f(x) and if the limit as n approaches infinity of f(xn) is L for every arbitrary sequence of points {xn} in {X – {x0}} which converges to x0, then the limit of the function f(x) as x approaches x0 is L.[9] One such sequence would be {x0 + 1/n}.
Infinity as a limit[edit]
There is also a notion of having a limit «at infinity», as opposed to at some finite 




That is, for every possible bound, the magnitude of the sequence eventually exceeds the bound. This is often written 

It is possible for a sequence to be divergent, but not tend to infinity. Such sequences are called oscillatory. An example of an oscillatory sequence is 
For the real numbers, there are corresponding notions of tending to positive infinity and negative infinity, by removing the modulus sign from the above definition:
defines tending to positive infinity, while
defines tending to negative infinity.
Sequences which do not tend to infinity are called bounded. Sequences which do not tend to positive infinity are called bounded above, while those which do not tend to negative infinity are bounded below.
Metric space[edit]
The discussion of sequences above is for sequences of real numbers. The notion of limits can be defined for sequences valued in more abstract spaces. One example of a more abstract space is metric spaces. If 







is satisfied.
An equivalent statement is that 

Example: ℝn[edit]
An important example is the space of 


The sequence of points 


Topological space[edit]
In some sense the most abstract space in which limits can be defined are topological spaces. If 








is satisfied.
Function space[edit]
This section deals with the idea of limits of sequences of functions, not to be confused with the idea of limits of functions, discussed below.
The field of functional analysis partly seeks to identify useful notions of convergence on function spaces. For example, consider the space of functions from a generic set 




Then the sequence 

Another notion of convergence is uniform convergence. The uniform distance between two functions 

Then the sequence 


Many different notions of convergence can be defined on function spaces. This is sometimes dependent on the regularity of the space. Prominent examples of function spaces with some notion of convergence are Lp spaces and Sobolev space.
In functions[edit]
A function f(x) for which the limit at infinity is L. For any arbitrary distance ε, there must be a value S such that the function stays within L ± ε for all x > S.
Suppose f is a real-valued function and c is a real number. Intuitively speaking, the expression
means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c.[10] In that case, the above equation can be read as «the limit of f of x, as x approaches c, is L«.
Formally, the definition of the «limit of 








The inequality 





It can be proven that there is an equivalent definition which makes manifest the connection between limits of sequences and limits of functions.[11] The equivalent definition is given as follows. First observe that for every sequence 






One-sided limit[edit]
It is possible to define the notion of having a «left-handed» limit («from below»), and a notion of a «right-handed» limit («from above»). These need not agree. An example is given by the positive indicator function, 









Infinity in limits of functions[edit]
It is possible to define the notion of «tending to infinity» in the domain of 
In this expression, the infinity is considered to be signed: either 








It is also possible to define the notion of «tending to infinity» in the value of 
The definition is given as follows. Given any real number 





Nonstandard analysis[edit]
In non-standard analysis (which involves a hyperreal enlargement of the number system), the limit of a sequence 

Here, the standard part function «st» rounds off each finite hyperreal number to the nearest real number (the difference between them is infinitesimal). This formalizes the natural intuition that for «very large» values of the index, the terms in the sequence are «very close» to the limit value of the sequence. Conversely, the standard part of a hyperreal ![a=[a_{n}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9e2180fadc958d8270f9131db9238ff0c1f5392)

In this sense, taking the limit and taking the standard part are equivalent procedures.
Limit sets[edit]
Limit set of a sequence[edit]
Let 







A use of this notion is to characterize the «long-term behavior» of oscillatory sequences. For example, consider the sequence 


Limit set of a trajectory[edit]
This notion is used in dynamical systems, to study limits of trajectories. Defining a trajectory to be a function 







Technically, this is the 

An illustrative example is the circle trajectory: 




Uses[edit]
Limits are used to define a number of important concepts in analysis.
Series[edit]
A particular expression of interest which is formalized as the limit of a sequence is sums of infinite series. These are «infinite sums» of real numbers, generally written as
This is defined through limits as follows:[11] given a sequence of real numbers 
If the limit of the sequence 

A classic example is the Basel problem, where 
However, while for sequences there is essentially a unique notion of convergence, for series there are different notions of convergence. This is due to the fact that the expression 

A series which converges for all orderings is called unconditionally convergent. It can be proven to be equivalent to absolute convergence. This is defined as follows. A series is absolutely convergent if 
Otherwise, the series is conditionally convergent. A surprising result for conditionally convergent series is the Riemann series theorem: depending on the ordering, the partial sums can be made to converge to any real number, as well as 
Power series[edit]
A useful application of the theory of sums of series is for power series. These are sums of series of the form
Often 

Continuity of a function at a point[edit]
The definition of continuity at a point is given through limits.
The above definition of a limit is true even if 



Equivalently, the function is continuous at 




An example of a limit where 

Consider the function
then f(1) is not defined (see Indeterminate form), yet as x moves arbitrarily close to 1, f(x) correspondingly approaches 2:[12]
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | undefined | 2.001 | 2.010 | 2.100 |
Thus, f(x) can be made arbitrarily close to the limit of 2—just by making x sufficiently close to 1.
In other words,
This can also be calculated algebraically, as 
Now, since x + 1 is continuous in x at 1, we can now plug in 1 for x, leading to the equation
In addition to limits at finite values, functions can also have limits at infinity. For example, consider the function
where:
- f(100) = 1.9900
- f(1000) = 1.9990
- f(10000) = 1.9999
As x becomes extremely large, the value of f(x) approaches 2, and the value of f(x) can be made as close to 2 as one could wish—by making x sufficiently large. So in this case, the limit of f(x) as x approaches infinity is 2, or in mathematical notation,
Continuous functions[edit]
An important class of functions when considering limits are continuous functions. These are precisely those functions which preserve limits, in the sense that if 




In the most general setting of topological spaces, a short proof is given below:
Let 






Now suppose 





Choose a neighborhood 











Then applying 






In real analysis, for the more concrete case of real-valued functions defined on a subset 

Limit points[edit]
In topology, limits are used to define limit points of a subset of a topological space, which in turn give a useful characterization of closed sets.
In a topological space 





The reason why 



![{displaystyle S=[0,1]cup {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4747fd449058e2902cd7277ce7f9afad8574e1)




A closed set, which is defined to be the complement of an open set, is equivalently any set 
Derivative[edit]
The derivative is defined formally as a limit. In the scope of real analysis, the derivative is first defined for real functions 


as 

Equivalently, it is the limit as 
If the derivative exists, it is commonly denoted by 
Properties[edit]
Sequences of real numbers[edit]
For sequences of real numbers, a number of properties can be proven.[11] Suppose 



- Sum of limits is equal to limit of sum
- Product of limits is equal to limit of product
- Inverse of limit is equal to limit of inverse (as long as
)
equivalently, the function 

Cauchy sequences[edit]
A property of convergent sequences of real numbers is that they are Cauchy sequences.[11] The definition of a Cauchy sequence 



Informally, for any arbitrarily small error 

Cauchy sequences are closely related to convergent sequences. In fact, for sequences of real numbers they are equivalent: any Cauchy sequence is convergent.
In general metric spaces, it continues to hold that convergent sequences are also Cauchy. But the converse is not true: not every Cauchy sequence is convergent in a general metric space. A classic counterexample is the rational numbers, 



A metric space in which every Cauchy sequence is also convergent, that is, Cauchy sequences are equivalent to convergent sequences, is known as a complete metric space.
One reason Cauchy sequences can be «easier to work with» than convergent sequences is that they are a property of the sequence 


Order of convergence[edit]
Beyond whether or not a sequence 

A formal definition of order of convergence can be stated as follows. Suppose 





then 



Order of convergence is used for example the field of numerical analysis, in error analysis.
Computability[edit]
Limits can be difficult to compute. There exist limit expressions whose modulus of convergence is undecidable. In recursion theory, the limit lemma proves that it is possible to encode undecidable problems using limits.[13]
There are several theorems or tests that indicate whether the limit exists. These are known as convergence tests. Examples include the ratio test and the squeeze theorem. However they may not tell how to compute the limit.
See also[edit]
- Asymptotic analysis: a method of describing limiting behavior
- Big O notation: used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity
- Banach limit defined on the Banach space
that extends the usual limits.
- Convergence of random variables
- Convergent matrix
- Limit in category theory
- Direct limit
- Inverse limit
- Limit of a function
- One-sided limit: either of the two limits of functions of a real variable x, as x approaches a point from above or below
- List of limits: list of limits for common functions
- Squeeze theorem: finds a limit of a function via comparison with two other functions
- Limit superior and limit inferior
- Modes of convergence
- An annotated index
Notes[edit]
- ^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
- ^ Aggarwal, M.L. (2021). «13. Limits and Derivatives». Understanding ISC Mathematics Class XI. Vol. II. Industrial Area, Trilokpur Road, Kala Amb-173030, Distt. Simour (H.P.): Arya Publications (Avichal Publishing Company). p. A-719. ISBN 978-81-7855-743-4.
{{cite book}}: CS1 maint: location (link) - ^ Van Looy, Herman (1984). «A chronology and historical analysis of the mathematical manuscripts of Gregorius a Sancto Vincentio (1584–1667)». Historia Mathematica. 11 (1): 57–75. doi:10.1016/0315-0860(84)90005-3.
- ^ Felscher, Walter (2000), «Bolzano, Cauchy, Epsilon, Delta», American Mathematical Monthly, 107 (9): 844–862, doi:10.2307/2695743, JSTOR 2695743
- ^ Larson, Ron; Edwards, Bruce H. (2010). Calculus of a single variable (Ninth ed.). Brooks/Cole, Cengage Learning. ISBN 978-0-547-20998-2.
- ^ Miller, Jeff (1 December 2004), Earliest Uses of Symbols of Calculus, archived from the original on 2015-05-01, retrieved 2008-12-18
- ^ Stillwell, John (1994), Elements of algebra: geometry, numbers, equations, Springer, p. 42, ISBN 978-1441928399
- ^ Weisstein, Eric W. «Limit». mathworld.wolfram.com. Archived from the original on 2020-06-20. Retrieved 2020-08-18.
- ^ Apostol (1974, pp. 75–76)
- ^ Weisstein, Eric W. «Epsilon-Delta Definition». mathworld.wolfram.com. Archived from the original on 2020-06-25. Retrieved 2020-08-18.
- ^ a b c d Chua, Dexter. «Analysis I (based on a course given by Timothy Gowers)». Notes from the Mathematical Tripos.
- ^ «limit | Definition, Example, & Facts». Encyclopedia Britannica. Archived from the original on 2021-05-09. Retrieved 2020-08-18.
- ^ Soare, Robert I. (2014). Recursively enumerable sets and degrees : a study of computable functions and computably generated sets. Berlin: Springer-Verlag. ISBN 978-3-540-66681-3. OCLC 1154894968.
References[edit]
- Apostol, Tom M. (1974), Mathematical Analysis (2nd ed.), Menlo Park: Addison-Wesley, LCCN 72011473
External links[edit]
In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value.[1] Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals.
The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory.
In formulas, a limit of a function is usually written as
(although a few authors may use «Lt» instead of «lim»[2])
and is read as «the limit of f of x as x approaches c equals L«. The fact that a function f approaches the limit L as x approaches c is sometimes denoted by a right arrow (→ or 
which reads «




History[edit]
Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work Opus Geometricum (1647): «The terminus of a progression is the end of the series, which none progression can reach, even not if she is continued in infinity, but which she can approach nearer than a given segment.»[3]
The modern definition of a limit goes back to Bernard Bolzano who, in 1817, introduced the basics of the epsilon-delta technique to define continuous functions. However, his work was not known during his lifetime.[4]
Augustin-Louis Cauchy in 1821,[5] followed by Karl Weierstrass, formalized the definition of the limit of a function which became known as the (ε, δ)-definition of limit.
The modern notation of placing the arrow below the limit symbol is due to G. H. Hardy, who introduced it in his book A Course of Pure Mathematics in 1908.[6]
Types of limits[edit]
In sequences[edit]
Real numbers[edit]
The expression 0.999… should be interpreted as the limit of the sequence 0.9, 0.99, 0.999, … and so on. This sequence can be rigorously shown to have the limit 1, and therefore this expression is meaningfully interpreted as having the value 1.[7]
Formally, suppose a1, a2, … is a sequence of real numbers. When the limit of the sequence exists, the real number L is the limit of this sequence if and only if for every real number ε > 0, there exists a natural number N such that for all n > N, we have |an − L| < ε.[8]
The notation
is often used, and which is read as
- «The limit of an as n approaches infinity equals L«
The formal definition intuitively means that eventually, all elements of the sequence get arbitrarily close to the limit, since the absolute value |an − L| is the distance between an and L.
Not every sequence has a limit. If it does, then it is called convergent, and if it does not, then it is divergent. One can show that a convergent sequence has only one limit.
The limit of a sequence and the limit of a function are closely related. On one hand, the limit as n approaches infinity of a sequence {an} is simply the limit at infinity of a function a(n)—defined on the natural numbers {n}. On the other hand, if X is the domain of a function f(x) and if the limit as n approaches infinity of f(xn) is L for every arbitrary sequence of points {xn} in {X – {x0}} which converges to x0, then the limit of the function f(x) as x approaches x0 is L.[9] One such sequence would be {x0 + 1/n}.
Infinity as a limit[edit]
There is also a notion of having a limit «at infinity», as opposed to at some finite 




That is, for every possible bound, the magnitude of the sequence eventually exceeds the bound. This is often written 

It is possible for a sequence to be divergent, but not tend to infinity. Such sequences are called oscillatory. An example of an oscillatory sequence is 
For the real numbers, there are corresponding notions of tending to positive infinity and negative infinity, by removing the modulus sign from the above definition:
defines tending to positive infinity, while
defines tending to negative infinity.
Sequences which do not tend to infinity are called bounded. Sequences which do not tend to positive infinity are called bounded above, while those which do not tend to negative infinity are bounded below.
Metric space[edit]
The discussion of sequences above is for sequences of real numbers. The notion of limits can be defined for sequences valued in more abstract spaces. One example of a more abstract space is metric spaces. If 







is satisfied.
An equivalent statement is that 

Example: ℝn[edit]
An important example is the space of 


The sequence of points 


Topological space[edit]
In some sense the most abstract space in which limits can be defined are topological spaces. If 








is satisfied.
Function space[edit]
This section deals with the idea of limits of sequences of functions, not to be confused with the idea of limits of functions, discussed below.
The field of functional analysis partly seeks to identify useful notions of convergence on function spaces. For example, consider the space of functions from a generic set 




Then the sequence 

Another notion of convergence is uniform convergence. The uniform distance between two functions 

Then the sequence 


Many different notions of convergence can be defined on function spaces. This is sometimes dependent on the regularity of the space. Prominent examples of function spaces with some notion of convergence are Lp spaces and Sobolev space.
In functions[edit]
A function f(x) for which the limit at infinity is L. For any arbitrary distance ε, there must be a value S such that the function stays within L ± ε for all x > S.
Suppose f is a real-valued function and c is a real number. Intuitively speaking, the expression
means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c.[10] In that case, the above equation can be read as «the limit of f of x, as x approaches c, is L«.
Formally, the definition of the «limit of 








The inequality 





It can be proven that there is an equivalent definition which makes manifest the connection between limits of sequences and limits of functions.[11] The equivalent definition is given as follows. First observe that for every sequence 






One-sided limit[edit]
It is possible to define the notion of having a «left-handed» limit («from below»), and a notion of a «right-handed» limit («from above»). These need not agree. An example is given by the positive indicator function, 









Infinity in limits of functions[edit]
It is possible to define the notion of «tending to infinity» in the domain of 
In this expression, the infinity is considered to be signed: either 








It is also possible to define the notion of «tending to infinity» in the value of 
The definition is given as follows. Given any real number 





Nonstandard analysis[edit]
In non-standard analysis (which involves a hyperreal enlargement of the number system), the limit of a sequence 

Here, the standard part function «st» rounds off each finite hyperreal number to the nearest real number (the difference between them is infinitesimal). This formalizes the natural intuition that for «very large» values of the index, the terms in the sequence are «very close» to the limit value of the sequence. Conversely, the standard part of a hyperreal ![a=[a_{n}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9e2180fadc958d8270f9131db9238ff0c1f5392)

In this sense, taking the limit and taking the standard part are equivalent procedures.
Limit sets[edit]
Limit set of a sequence[edit]
Let 







A use of this notion is to characterize the «long-term behavior» of oscillatory sequences. For example, consider the sequence 


Limit set of a trajectory[edit]
This notion is used in dynamical systems, to study limits of trajectories. Defining a trajectory to be a function 







Technically, this is the 

An illustrative example is the circle trajectory: 




Uses[edit]
Limits are used to define a number of important concepts in analysis.
Series[edit]
A particular expression of interest which is formalized as the limit of a sequence is sums of infinite series. These are «infinite sums» of real numbers, generally written as
This is defined through limits as follows:[11] given a sequence of real numbers 
If the limit of the sequence 

A classic example is the Basel problem, where 
However, while for sequences there is essentially a unique notion of convergence, for series there are different notions of convergence. This is due to the fact that the expression 

A series which converges for all orderings is called unconditionally convergent. It can be proven to be equivalent to absolute convergence. This is defined as follows. A series is absolutely convergent if 
Otherwise, the series is conditionally convergent. A surprising result for conditionally convergent series is the Riemann series theorem: depending on the ordering, the partial sums can be made to converge to any real number, as well as 
Power series[edit]
A useful application of the theory of sums of series is for power series. These are sums of series of the form
Often 

Continuity of a function at a point[edit]
The definition of continuity at a point is given through limits.
The above definition of a limit is true even if 



Equivalently, the function is continuous at 




An example of a limit where 

Consider the function
then f(1) is not defined (see Indeterminate form), yet as x moves arbitrarily close to 1, f(x) correspondingly approaches 2:[12]
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | undefined | 2.001 | 2.010 | 2.100 |
Thus, f(x) can be made arbitrarily close to the limit of 2—just by making x sufficiently close to 1.
In other words,
This can also be calculated algebraically, as 
Now, since x + 1 is continuous in x at 1, we can now plug in 1 for x, leading to the equation
In addition to limits at finite values, functions can also have limits at infinity. For example, consider the function
where:
- f(100) = 1.9900
- f(1000) = 1.9990
- f(10000) = 1.9999
As x becomes extremely large, the value of f(x) approaches 2, and the value of f(x) can be made as close to 2 as one could wish—by making x sufficiently large. So in this case, the limit of f(x) as x approaches infinity is 2, or in mathematical notation,
Continuous functions[edit]
An important class of functions when considering limits are continuous functions. These are precisely those functions which preserve limits, in the sense that if 




In the most general setting of topological spaces, a short proof is given below:
Let 






Now suppose 





Choose a neighborhood 











Then applying 






In real analysis, for the more concrete case of real-valued functions defined on a subset 

Limit points[edit]
In topology, limits are used to define limit points of a subset of a topological space, which in turn give a useful characterization of closed sets.
In a topological space 





The reason why 



![{displaystyle S=[0,1]cup {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4747fd449058e2902cd7277ce7f9afad8574e1)




A closed set, which is defined to be the complement of an open set, is equivalently any set 
Derivative[edit]
The derivative is defined formally as a limit. In the scope of real analysis, the derivative is first defined for real functions 


as 

Equivalently, it is the limit as 
If the derivative exists, it is commonly denoted by 
Properties[edit]
Sequences of real numbers[edit]
For sequences of real numbers, a number of properties can be proven.[11] Suppose 



- Sum of limits is equal to limit of sum
- Product of limits is equal to limit of product
- Inverse of limit is equal to limit of inverse (as long as
)
equivalently, the function 

Cauchy sequences[edit]
A property of convergent sequences of real numbers is that they are Cauchy sequences.[11] The definition of a Cauchy sequence 



Informally, for any arbitrarily small error 

Cauchy sequences are closely related to convergent sequences. In fact, for sequences of real numbers they are equivalent: any Cauchy sequence is convergent.
In general metric spaces, it continues to hold that convergent sequences are also Cauchy. But the converse is not true: not every Cauchy sequence is convergent in a general metric space. A classic counterexample is the rational numbers, 



A metric space in which every Cauchy sequence is also convergent, that is, Cauchy sequences are equivalent to convergent sequences, is known as a complete metric space.
One reason Cauchy sequences can be «easier to work with» than convergent sequences is that they are a property of the sequence 


Order of convergence[edit]
Beyond whether or not a sequence 

A formal definition of order of convergence can be stated as follows. Suppose 





then 



Order of convergence is used for example the field of numerical analysis, in error analysis.
Computability[edit]
Limits can be difficult to compute. There exist limit expressions whose modulus of convergence is undecidable. In recursion theory, the limit lemma proves that it is possible to encode undecidable problems using limits.[13]
There are several theorems or tests that indicate whether the limit exists. These are known as convergence tests. Examples include the ratio test and the squeeze theorem. However they may not tell how to compute the limit.
See also[edit]
- Asymptotic analysis: a method of describing limiting behavior
- Big O notation: used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity
- Banach limit defined on the Banach space
that extends the usual limits.
- Convergence of random variables
- Convergent matrix
- Limit in category theory
- Direct limit
- Inverse limit
- Limit of a function
- One-sided limit: either of the two limits of functions of a real variable x, as x approaches a point from above or below
- List of limits: list of limits for common functions
- Squeeze theorem: finds a limit of a function via comparison with two other functions
- Limit superior and limit inferior
- Modes of convergence
- An annotated index
Notes[edit]
- ^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
- ^ Aggarwal, M.L. (2021). «13. Limits and Derivatives». Understanding ISC Mathematics Class XI. Vol. II. Industrial Area, Trilokpur Road, Kala Amb-173030, Distt. Simour (H.P.): Arya Publications (Avichal Publishing Company). p. A-719. ISBN 978-81-7855-743-4.
{{cite book}}: CS1 maint: location (link) - ^ Van Looy, Herman (1984). «A chronology and historical analysis of the mathematical manuscripts of Gregorius a Sancto Vincentio (1584–1667)». Historia Mathematica. 11 (1): 57–75. doi:10.1016/0315-0860(84)90005-3.
- ^ Felscher, Walter (2000), «Bolzano, Cauchy, Epsilon, Delta», American Mathematical Monthly, 107 (9): 844–862, doi:10.2307/2695743, JSTOR 2695743
- ^ Larson, Ron; Edwards, Bruce H. (2010). Calculus of a single variable (Ninth ed.). Brooks/Cole, Cengage Learning. ISBN 978-0-547-20998-2.
- ^ Miller, Jeff (1 December 2004), Earliest Uses of Symbols of Calculus, archived from the original on 2015-05-01, retrieved 2008-12-18
- ^ Stillwell, John (1994), Elements of algebra: geometry, numbers, equations, Springer, p. 42, ISBN 978-1441928399
- ^ Weisstein, Eric W. «Limit». mathworld.wolfram.com. Archived from the original on 2020-06-20. Retrieved 2020-08-18.
- ^ Apostol (1974, pp. 75–76)
- ^ Weisstein, Eric W. «Epsilon-Delta Definition». mathworld.wolfram.com. Archived from the original on 2020-06-25. Retrieved 2020-08-18.
- ^ a b c d Chua, Dexter. «Analysis I (based on a course given by Timothy Gowers)». Notes from the Mathematical Tripos.
- ^ «limit | Definition, Example, & Facts». Encyclopedia Britannica. Archived from the original on 2021-05-09. Retrieved 2020-08-18.
- ^ Soare, Robert I. (2014). Recursively enumerable sets and degrees : a study of computable functions and computably generated sets. Berlin: Springer-Verlag. ISBN 978-3-540-66681-3. OCLC 1154894968.
References[edit]
- Apostol, Tom M. (1974), Mathematical Analysis (2nd ed.), Menlo Park: Addison-Wesley, LCCN 72011473
External links[edit]
Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.
Что такое предел в математике
Когда математики говорят о пределах, то имеют в виду такую последовательность событий:
- Есть функция — это просто какая-то «коробка» с математикой. Ты ей на вход число, она его обрабатывает у себя внутри и отдаёт другое число.
- У функции есть как минимум два числа: то, которое ты ей даёшь на вход; и то, которое получаешь на выходе.
- Иногда математикам интересно, что будет, если число на входе будет к чему-то стремиться. А именно: «Если число на входе будет стремиться вот сюда, куда будет стремиться число на выходе?»
👉 Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.
Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.
1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности
Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:
1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.
Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:
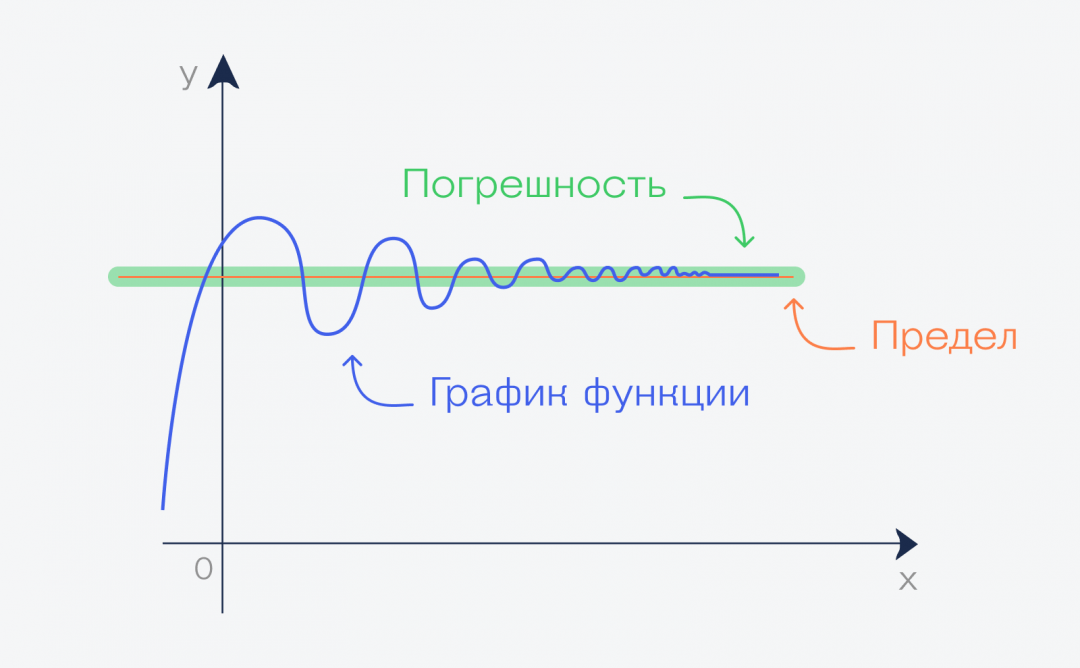
График и предел
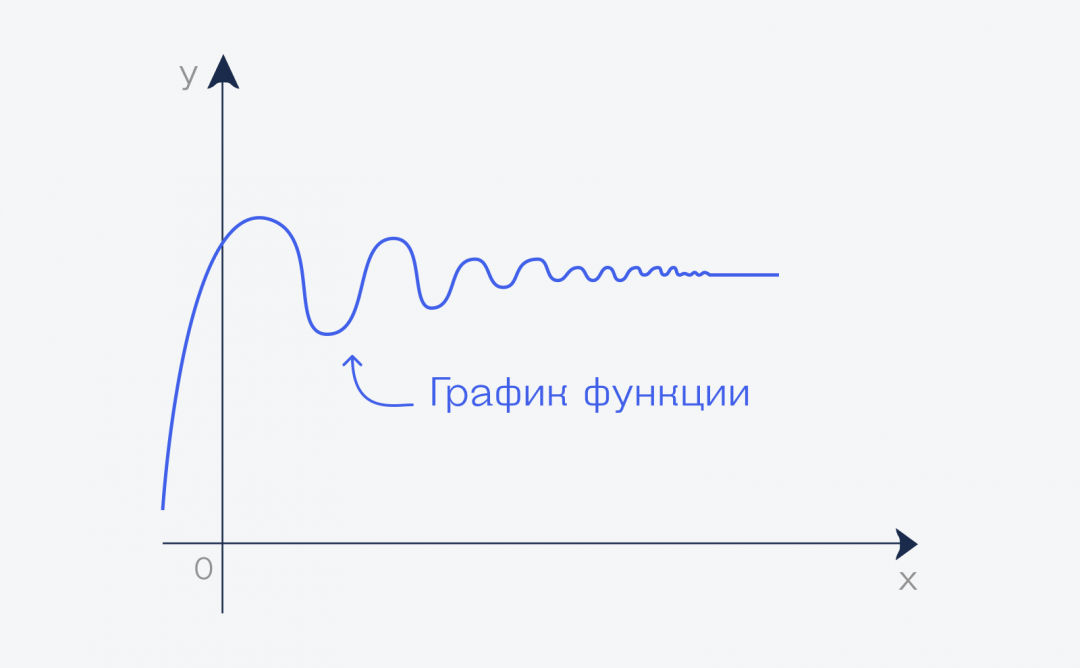
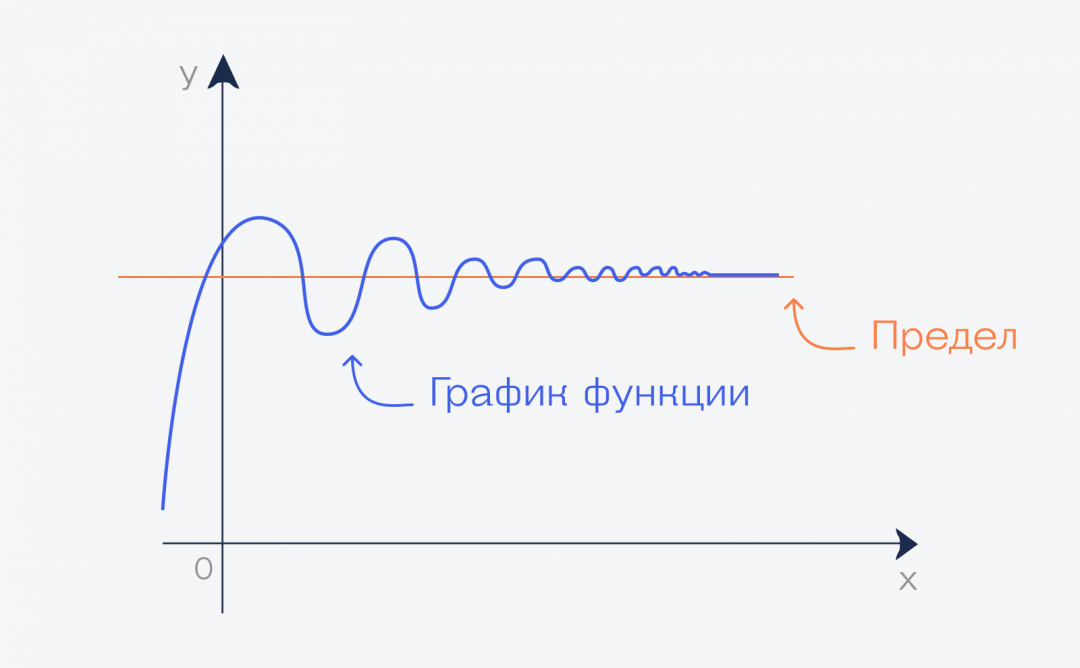
Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.
Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:
Пределы в жизни
Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.
Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.
Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.
Погрешность в пределах
В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.
Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.
Считаем предел в программировании
Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).
Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:
- Закончилось количество повторений. Например, мы заранее говорим, что будем стремиться к границе предела 10000000000 раз, но если ничего не выйдет — остановимся.
- Если достигли нужной погрешности. Два соседних результата отличаются на величину погрешности или меньше — отлично, мы нашли то, что нужно.
Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.
⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.
Например, если мы дали переменной 32 бита памяти, самое малое число, которое мы сможем в нее записать, — 1,4012985 × 10-45. Это кажется бесконечно малым, но на самом деле, если циклически делить число на 2 несколько сотен раз в секунду, мы упремся в этот лимит точности почти сразу. Потом знаки после запятой закончатся и число очень быстро превратится в 0.
С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.
Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.
Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):
- предел функции f(x) = (8−2x) / (x²−4x-12);
- при x стремящемся к 2.
Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:
// погрешность вычислений
var e = 0.00001;
// предел, к которому будет стремиться переменная
var lim = 2;
// переменная функции, на старте начинаем стремиться к пределу отсюда
var x = 0;
// сколько раз мы уже выполнили цикл
var n = 0;
// максимальное количество приближений к пределу
var max_n = 100;
// функция, которая возвращает значение для переменной функции
function f(x) {
return (8 - 2*x*x)/(x*x + 4*x - 12);
}
// пока мы не достигли нужной погрешности — выполняем цикл
while (Math.abs(f(x) -f((x+lim)/2)) >= e) {
// приближаемся ещё на один шаг к пределу
x = (x+lim)/2;
// увеличиваем счётчик приближений
n +=1;
// если дошли до максимального количества повторений
if (n == max_n) {
// выводим сообщение о том, что останавливаемся
console.log('Закончилось количество повторений, остановились на таком значении функции: ', f(x));
// сбрасываем переменную с максимальным значением повторений и выходим из цикла
max_n = 0;
break;
}
}
// если переменная с максимальным значением не была сброшена
if (max_n != 0){
// выводим найденный предел
console.log('Предел функции с заданной погрешностью: ', f(x))
}Вёрстка:
Кирилл Климентьев
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание «чайникам» $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними — это не так страшно как кажется |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате — это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное — возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
В математике принципиально важным является понятие бесконечности, обозначаемое символом ∞. Его следует понимать как бесконечно большое +∞ или бесконечно малое -∞ число. Когда мы говорим о бесконечности, часто мы имеем в виду сразу оба этих ее смысла, однако запись вида +∞ или -∞ не стоит заменять просто на ∞.
Запись предела функции имеет вид limx→x0f(x). В нижней части мы пишем основной аргумент x, а с помощью стрелочки указываем, к какому именно значению x0 он будет стремиться. Если значение x0 является конкретным действительным числом, то мы имеем дело с пределом функции в точке. Если же значение x0 стремится к бесконечности (не важно, ∞, +∞ или -∞), то следует говорить о пределе функции на бесконечности.
Предел бывает конечным и бесконечным. Если он равен конкретному действительному числу, т.е. limx→x0f(x)=A, то его называют конечным пределом, если же limx→x0f(x)=∞, limx→x0f(x)=+∞ или limx→x0f(x)=-∞, то бесконечным.
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
Число A является пределом функции f(x) при x→∞, если последовательность ее значений будет сходиться к A для любой бесконечно большой последовательности аргументов (отрицательной или положительной).
Запись предела функции выглядит так: limx→∞f(x)=A.
При x→∞ предел функции f(x) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Запись выглядит как limx→∞f(x)=∞.
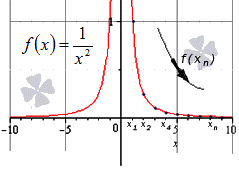
Докажите равенство limx→∞1×2=0 с помощью основного определения предела для x→∞.
Решение
Начнем с записи последовательности значений функции 1×2 для бесконечно большой положительной последовательности значений аргумента x=1, 2, 3,…, n,….
11>14>19>116>…>1n2>…
Мы видим, что значения будут постепенно уменьшаться, стремясь к 0. См. на картинке:
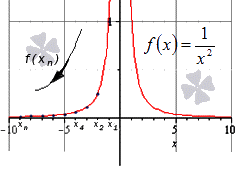
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
x=-1, -2, -3,…, -n,…
11>14>19>116>…>1-n2>…
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
Ответ: Верность данного в условии равенства подтверждена.
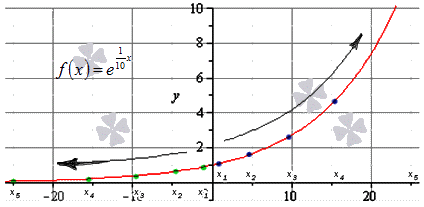
Вычислите предел limx→∞e110x.
Решение
Начнем, как и раньше, с записи последовательностей значений f(x)=e110x для бесконечно большой положительной последовательности аргументов. Например, x=1, 4, 9, 16, 25,…, 102,…→+∞.
e110; e410; e910; e1610; e2510;…; e10010;…==1,10; 1,49; 2,45; 4,95; 12,18;…;22026,46;…
Мы видим, что данная последовательность бесконечно положительна, значит, f(x)=limx→+∞e110x=+∞
Переходим к записи значений бесконечно большой отрицательной последовательности, например, x=-1, -4, -9, -16,-25,…, -102,…→-∞.
e-110; e-410; e-910; e-1610; e-2510;…;e-10010;…==0,90; 0,67; 0,40; 0,20; 0,08;…;0,000045;…x=1, 4, 9, 16, 25,…,102 ,…→∞
Поскольку она тоже стремится к нулю, то f(x)=limx→∞1e10x=0.
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
Ответ: limx→∞e110x=+∞, при x→+∞0, при x→-∞.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Число B является пределом функции f(x) слева при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются меньше a (xn<a).
Такой предел на письме обозначается как limx→a-0f(x)=B.
Теперь сформулируем, что такое предел функции справа.
Число B является пределом функции f(x) справа при x→a в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции xn, сходящейся к a, если при этом ее значения остаются больше a (xn>a).
Этот предел мы записываем как limx→a+0f(x)=B.
Мы можем найти предел функции f(x) в некоторой точке тогда, когда для нее существуют равные пределы с левой и правой стороны, т.е. limx→af(x)=limx→a-0f(x)=limx→a+0f(x)=B. В случае бесконечности обоих пределов предел функции в исходной точке также будет бесконечен.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
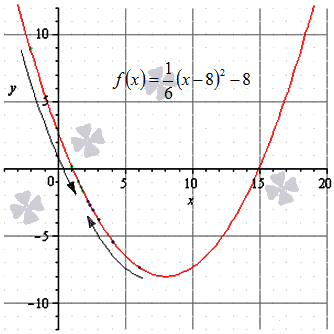
Докажите, что существует конечный предел функции f(x)=16(x-8)2-8 в точке x0=2 и вычислите его значение.
Решение
Для того чтобы решить задачу, нам потребуется вспомнить определение предела функции в точке. Для начала докажем, что у исходной функции имеется предел слева. Запишем последовательность значений фукнции, которая будет сходиться к x0=2, если xn<2:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8,667; 2,667; 0,167; -0,958; -1,489; -1,747; -1,874;…; -1,998;…→-2
Поскольку приведенная последовательность сводится к -2, мы можем записать, что limx→2-016x-82-8=-2.
Далее докажем наличие предела справа: запишем аргументы в последовательности, которая будет сходиться к x0=2, если xn>2:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Значения функции в этой последовательности будут выглядеть так:
f(6); f(4); f(3); f212; f234; f278; f21516;…; f210231024;…==-7,333; -5,333; -3,833; -2,958; -2,489; -2,247;-2,124;…, -2,001,…→-2
Данная последовательность также сходится к -2, значит, limx→2+016(x-8)2-8=-2.
Мы получили, что пределы с правой и левой стороны у данной функции будут равными, значит, предел функции f(x)=16(x-8)2-8 в точке x0=2 существует, и limx→216(x-8)2-8=-2.
Вы можете увидеть ход решения на иллюстрации (зеленые точки– последовательность значений, сходящаяся к xn<2, синие – к xn>2).
Ответ: Пределы с правой и левой стороны у данной функции будут равными, значит, предел функции существует, и limx→216(x-8)2-8=-2.
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

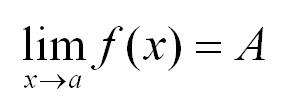
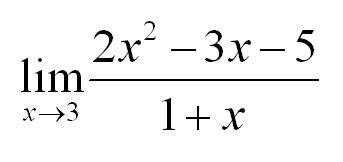
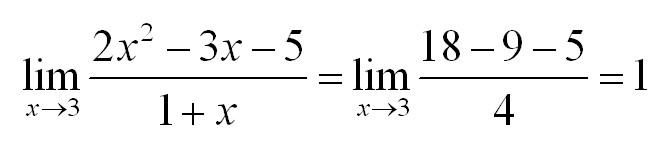
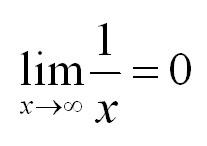

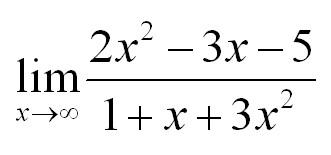
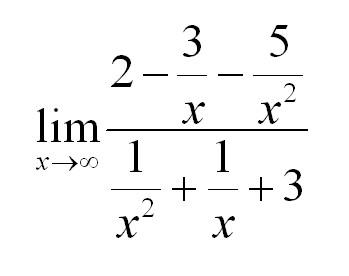
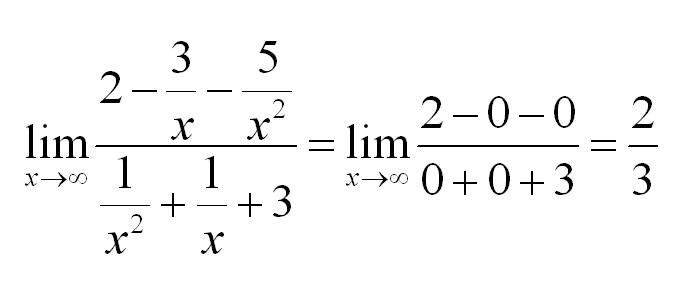

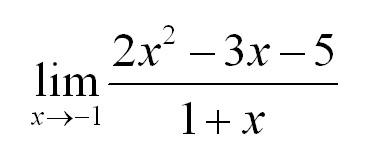
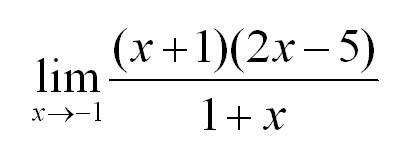
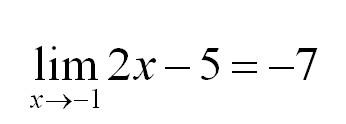
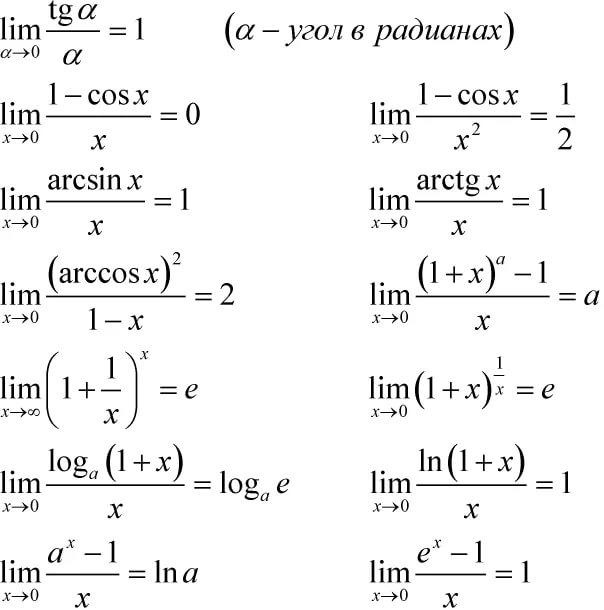
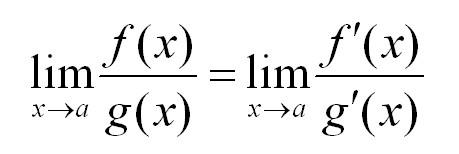
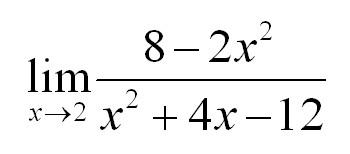
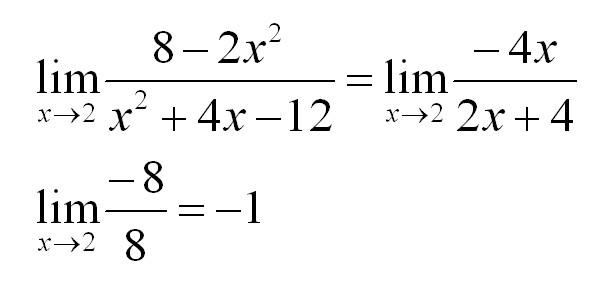





































 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:
Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: