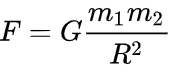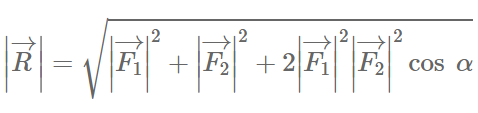Формула равнодействующей силы
В соответствии с первым законом Ньютона в инерциальных системах отсчета тело может изменять свою скорость только, если на него действуют другие тела. Количественно взаимное действие тел друг на друга выражают с помощью такой физической величины, как сила (). Сила может изменять скорость тела, как по модулю, так и по направлению. Сила является векторной величиной, у нее есть модуль (величина) и направление. Направление равнодействующей силы определяет направление вектора ускорения тела, на которое действует рассматриваемая сила.
Основной закон, при помощи которого определяют направление и величину равнодействующей силы – это второй закон Ньютона:
где m – масса тела, на которое действует сила ;
– ускорение, которое сила
сообщает рассматриваемому телу. Сущность второго закона Ньютона состоит в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Необходимо помнить, что второй закон Ньютона работает для инерциальных систем отсчета.
В том случае, если на тело действует несколько сил, то их совместное действие характеризуют при помощи равнодействующей силы. Допустим, что на тело действует одновременно несколько сил, при этом тело перемещается с ускорением, равным векторной сумме ускорений, которые появились бы при воздействии каждой из сил в отдельности. Силы, действующие на тело, и приложенные к одной его точке необходимо складывать по правилу сложения векторов. Векторная сумма всех сил, действующих на тело в один момент времени, называется равнодействующей силой ():
Выражение (2) можно считать формулой для вычисления равнодействующей силы. Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты.
При действии на тело нескольких сил, второй закон Ньютона записывают как:
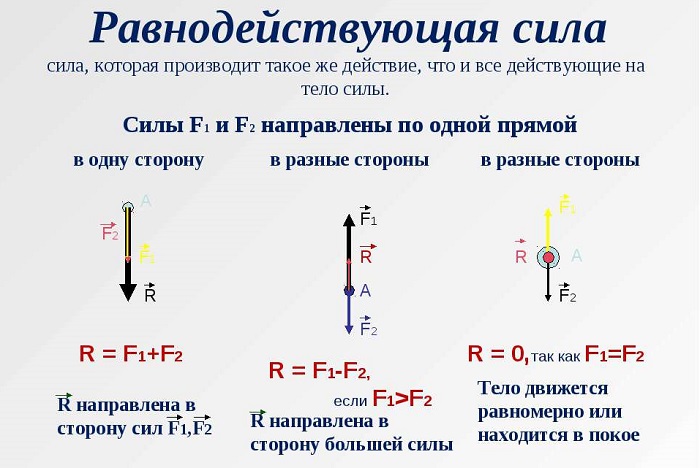
Равнодействующая всех сил, действующих на тело, может быть равна нулю, в том случае, если происходит взаимная компенсация сил, приложенных к телу. В таком случае тело движется с постоянной скоростью или находится в покое.
При изображении сил, действующих на тело, на чертеже, в случае равноускоренного перемещения тела, равнодействующую силу, направленную по ускорению следует изображать длиннее, чем противоположно ей направленную силу (сумму сил). В случае равномерного движения (или покоя) дина векторов сил, направленных в противоположные стороны одинакова.
Для нахождения равнодействующей силы, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.
Примеры решения задач по теме «Равнодействующая сила»
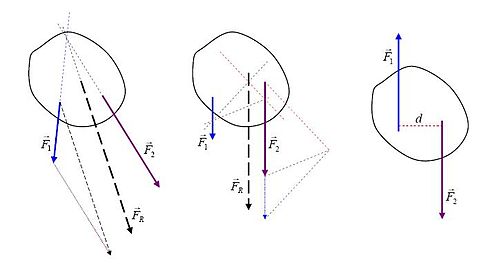
Graphical placing of the resultant force
In physics and engineering, a resultant force is the single force and associated torque obtained by combining a system of forces and torques acting on a rigid body via vector addition. The defining feature of a resultant force, or resultant force-torque, is that it has the same effect on the rigid body as the original system of forces.[1] Calculating and visualizing the resultant force on a body is done through computational analysis, or (in the case of sufficiently simple systems) a free body diagram.
The point of application of the resultant force determines its associated torque. The term resultant force should be understood to refer to both the forces and torques acting on a rigid body, which is why some use the term resultant force–torque.
Illustration[edit]
The diagram illustrates simple graphical methods for finding the line of application of the resultant force of simple planar systems.
- Lines of application of the actual forces
and
in the leftmost illustration intersect. After vector addition is performed «at the location of
«, the net force obtained is translated so that its line of application passes through the common intersection point. With respect to that point all torques are zero, so the torque of the resultant force
is equal to the sum of the torques of the actual forces.
- Illustration in the middle of the diagram shows two parallel actual forces. After vector addition «at the location of
«, the net force is translated to the appropriate line of application, whereof it becomes the resultant force
. The procedure is based on a decomposition of all forces into components for which the lines of application (pale dotted lines) intersect at one point (the so-called pole, arbitrarily set at the right side of the illustration). Then the arguments from the previous case are applied to the forces and their components to demonstrate the torque relationships.
- The rightmost illustration shows a couple, two equal but opposite forces for which the amount of the net force is zero, but they produce the net torque
where
is the distance between their lines of application. This is «pure» torque, since there is no resultant force.
Bound vector[edit]
A force applied to a body has a point of application. The effect of the force is different for different points of application. For this reason a force is called a bound vector, which means that it is bound to its point of application.
Forces applied at the same point can be added together to obtain the same effect on the body. However, forces with different points of application cannot be added together and maintain the same effect on the body.
It is a simple matter to change the point of application of a force by introducing equal and opposite forces at two different points of application that produce a pure torque on the body. In this way, all of the forces acting on a body can be moved to the same point of application with associated torques.
A system of forces on a rigid body is combined by moving the forces to the same point of application and computing the associated torques. The sum of these forces and torques yields the resultant force-torque.
Associated torque[edit]
If a point R is selected as the point of application of the resultant force F of a system of n forces Fi then the associated torque T is determined from the formulas
and
It is useful to note that the point of application R of the resultant force may be anywhere along the line of action of F without changing the value of the associated torque. To see this add the vector kF to the point of application R in the calculation of the associated torque,
The right side of this equation can be separated into the original formula for T plus the additional term including kF,
because the second term is zero. To see this notice that F is the sum of the vectors Fi which yields
thus the value of the associated torque is unchanged.
Torque-free resultant[edit]
It is useful to consider whether there is a point of application R such that the associated torque is zero. This point is defined by the property
where F is resultant force and Fi form the system of forces.
Notice that this equation for R has a solution only if the sum of the individual torques on the right side yield a vector that is perpendicular to F. Thus, the condition that a system of forces has a torque-free resultant can be written as
If this condition is satisfied then there is a point of application for the resultant which results in a pure force. If this condition is not satisfied, then the system of forces includes a pure torque for every point of application.
Wrench[edit]
The forces and torques acting on a rigid body can be assembled into the pair of vectors called a wrench.[2] If a system of forces and torques has a net resultant force F and a net resultant torque T, then the entire system can be replaced by a force F and an arbitrarily located couple that yields a torque of T. In general, if F and T are orthogonal, it is possible to derive a radial vector R such that 
The resultant force and torque on a rigid body obtained from a system of forces Fi i=1,…,n, is simply the sum of the individual wrenches Wi, that is
Notice that the case of two equal but opposite forces F and -F acting at points A and B respectively, yields the resultant W=(F—F, A×F — B× F) = (0, (A—B)×F). This shows that wrenches of the form W=(0, T) can be interpreted as pure torques.
References[edit]
- ^ H. Dadourian, Analytical Mechanics for Students of Physics and Engineering, Van Nostrand Co., Boston, MA 1913
- ^ R. M. Murray, Z. Li, and S. Sastry, A Mathematical Introduction to Robotic Manipulation, CRC Press, 1994
- ^ R. S. Ball, The Theory of Screws: A study in the dynamics of a rigid body, Hodges, Foster & Co., 1876
- ^ J. M. McCarthy and G. S. Soh, Geometric Design of Linkages. 2nd Edition, Springer 2010
Graphical placing of the resultant force
In physics and engineering, a resultant force is the single force and associated torque obtained by combining a system of forces and torques acting on a rigid body via vector addition. The defining feature of a resultant force, or resultant force-torque, is that it has the same effect on the rigid body as the original system of forces.[1] Calculating and visualizing the resultant force on a body is done through computational analysis, or (in the case of sufficiently simple systems) a free body diagram.
The point of application of the resultant force determines its associated torque. The term resultant force should be understood to refer to both the forces and torques acting on a rigid body, which is why some use the term resultant force–torque.
Illustration[edit]
The diagram illustrates simple graphical methods for finding the line of application of the resultant force of simple planar systems.
- Lines of application of the actual forces
and
in the leftmost illustration intersect. After vector addition is performed «at the location of
«, the net force obtained is translated so that its line of application passes through the common intersection point. With respect to that point all torques are zero, so the torque of the resultant force
is equal to the sum of the torques of the actual forces.
- Illustration in the middle of the diagram shows two parallel actual forces. After vector addition «at the location of
«, the net force is translated to the appropriate line of application, whereof it becomes the resultant force
. The procedure is based on a decomposition of all forces into components for which the lines of application (pale dotted lines) intersect at one point (the so-called pole, arbitrarily set at the right side of the illustration). Then the arguments from the previous case are applied to the forces and their components to demonstrate the torque relationships.
- The rightmost illustration shows a couple, two equal but opposite forces for which the amount of the net force is zero, but they produce the net torque
where
is the distance between their lines of application. This is «pure» torque, since there is no resultant force.
Bound vector[edit]
A force applied to a body has a point of application. The effect of the force is different for different points of application. For this reason a force is called a bound vector, which means that it is bound to its point of application.
Forces applied at the same point can be added together to obtain the same effect on the body. However, forces with different points of application cannot be added together and maintain the same effect on the body.
It is a simple matter to change the point of application of a force by introducing equal and opposite forces at two different points of application that produce a pure torque on the body. In this way, all of the forces acting on a body can be moved to the same point of application with associated torques.
A system of forces on a rigid body is combined by moving the forces to the same point of application and computing the associated torques. The sum of these forces and torques yields the resultant force-torque.
Associated torque[edit]
If a point R is selected as the point of application of the resultant force F of a system of n forces Fi then the associated torque T is determined from the formulas
and
It is useful to note that the point of application R of the resultant force may be anywhere along the line of action of F without changing the value of the associated torque. To see this add the vector kF to the point of application R in the calculation of the associated torque,
The right side of this equation can be separated into the original formula for T plus the additional term including kF,
because the second term is zero. To see this notice that F is the sum of the vectors Fi which yields
thus the value of the associated torque is unchanged.
Torque-free resultant[edit]
It is useful to consider whether there is a point of application R such that the associated torque is zero. This point is defined by the property
where F is resultant force and Fi form the system of forces.
Notice that this equation for R has a solution only if the sum of the individual torques on the right side yield a vector that is perpendicular to F. Thus, the condition that a system of forces has a torque-free resultant can be written as
If this condition is satisfied then there is a point of application for the resultant which results in a pure force. If this condition is not satisfied, then the system of forces includes a pure torque for every point of application.
Wrench[edit]
The forces and torques acting on a rigid body can be assembled into the pair of vectors called a wrench.[2] If a system of forces and torques has a net resultant force F and a net resultant torque T, then the entire system can be replaced by a force F and an arbitrarily located couple that yields a torque of T. In general, if F and T are orthogonal, it is possible to derive a radial vector R such that 
The resultant force and torque on a rigid body obtained from a system of forces Fi i=1,…,n, is simply the sum of the individual wrenches Wi, that is
Notice that the case of two equal but opposite forces F and -F acting at points A and B respectively, yields the resultant W=(F—F, A×F — B× F) = (0, (A—B)×F). This shows that wrenches of the form W=(0, T) can be interpreted as pure torques.
References[edit]
- ^ H. Dadourian, Analytical Mechanics for Students of Physics and Engineering, Van Nostrand Co., Boston, MA 1913
- ^ R. M. Murray, Z. Li, and S. Sastry, A Mathematical Introduction to Robotic Manipulation, CRC Press, 1994
- ^ R. S. Ball, The Theory of Screws: A study in the dynamics of a rigid body, Hodges, Foster & Co., 1876
- ^ J. M. McCarthy and G. S. Soh, Geometric Design of Linkages. 2nd Edition, Springer 2010
Для рассмотрения термина «равнодействующая сила» придется воспользоваться некими абстрактными понятиями физики, теоретической механики. Упрощениями, условно отражающими реальный мир
Итак, примем во внимание, что:
-
Под объектом понимается не физическое тело с объемом, формой и внутренней структурой. Подразумевается «материальная точка», характеризующаяся только массой. То есть величиной, определяющей инерцию (стремление сохранять неподвижность) и гравитационные взаимодействия (притяжение предметов). Не стоит путать с весом. Последний является проявлением гравитации и меняется в зависимости от места измерения (географической широты).
-
События и наблюдения происходят в инерциальной системе отсчета. Где пространство и время однородны (идентичны в любой точке). Поворот системы отсчета не влияет на измерения.
-
Рассуждения корректны для скоростей существенно ниже скорости света и не распространяются на субатомный уровень.
Понятие силы
Возникло еще в трудах древнегреческих ученых. Носило скорее философский характер и было довольно запутанным и неоднозначным, что не мешало при этом античным инженерам-практикам производить весьма точные расчеты, поскольку понимание силы как причины движения было для них безусловным.
Позже проблемой занимались такие титаны как Роджер Бэкон и Уильям Оккам (английские философы и естествоиспытатели). Опять-таки без строгого физического подхода, но с более глубоким пониманием темы (теория «дальнодействия»).
Бэкман, Декарт, Галилей аргументированно оспорили архаичные теории. Классическая механика пробивала дорогу.
Иоганн Кеплер также придавал сначала силе эзотерические свойства. Но наблюдения за закономерностями перемещения небесных тел убили плохого теолога и породили ученого. Логично появилась идея общей силы тяготения. До Ньютона, вопреки распространенному заблуждению.
Ньютон подытожил и объединил ранее накопленные знания. Установил формулу зависимости действующей на тело силы с его движением (II-ой закон).
Где:
-
F – вектор (также имеется направление приложения) силы. В принятой РФ системе СИ (ISQ) измеряется в Ньютонах (Н, N в международном написании);
-
m – масса материальной точки (кг);
-
a – вектор получаемого ускорения (м/с2).
При этом определение силы дано не было. Оно и понятно: явление не существует само по себе. Термин появился только для удобства расчетов и подразумевает меру воздействия стороннего тела или поля на наблюдаемый объект.
Возможно, что гравитация является действием поля. Закон всемирного тяготения был введен также Ньютоном.
Где:
· G – гравитационная постоянная;
· m1, m2 – массы материальных точек (кг);
· R – дистанция между объектами (м).
Тяготение Земли рассчитывается по традиционной формуле II-го закона Ньютона. Только «a» меняется на ускорение свободного падения «g».
Для примерных выкладок g берут равным 9,81 м/с2, что соответствует средней широте 45,5°. Для точных пользуются соответствующими таблицами.
Как измерить силу
В соответствии с I-м законом Ньютона, в инерциальных системах отсчета тело движется равномерно и прямолинейно либо покоится при отсутствии приложенных к нему сил. Или эти силы чем-то скомпенсированы.
Уравновесить усилие можно калиброванной пружиной, динамометром. Это статический способ. Типичный пример – замер силы тяжести при помощи весов.
Рассчитать силу можно, зная массу предмета и его ускорение. II-ой закон в помощь. В этом состоит динамический метод.
Равнодействующая сила
Если действуют несколько факторов одновременно, то результирующую силу можно найти по геометрическим правилам сложения.
Результат будет называться «вектор равнодействующей всех сил».
Или так:
Лежащий неподвижно на горизонтальной поверхности объект подвергается действию двух сил — тяжести и реакции опоры. Они равны по модулю и противоположно направлены: ведь объект покоится и равнодействующая сила равна нулю.
Примеры решения задач
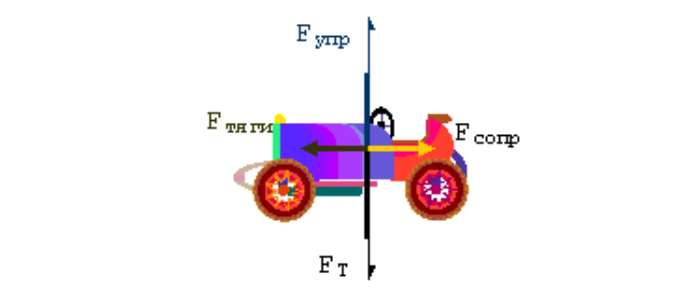
Машина массой 1 тонна движется по ровной горизонтальной поверхности с ускорением 1 м/с2. Тяга силового агрегата составляет 1500 Н. Укажите действующие на транспортное средство силы.
Решение.
Сила тяжести направлена вертикально вниз. Модуль определяется следующим образом:
Fт = mg = 1000 (кг) х 9,81 (м/с2) = 9810 (Н).
Упругая реакция дороги направлена противоположно и равна тяготению, поскольку движение в данной плоскости отсутствует и равнодействующая равна нулю.
Горизонтальная равнодействующая:
F = ma = 1000 (кг) х 1 (м/с2) = 1000 (Н).
Сопротивление:
Fcопр = Fтяги – F = 1500 (Н) – 1000 (Н) = 500 (Н).
Заключение
Несколько выводов напоследок:
-
Состояние покоя и прямолинейное равномерное движение механически аналогичны.
-
Сила придает телу ускорение, зависящее от массы объекта.
-
Равнодействующая образуется геометрическим суммированием приложенных к материальной точке векторов сил.
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
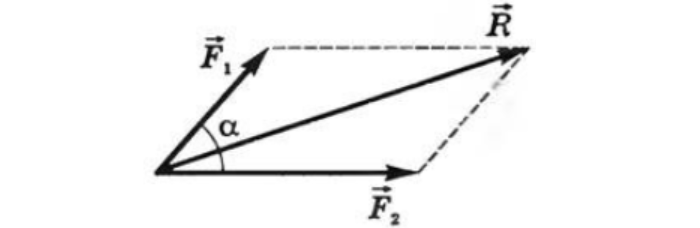
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
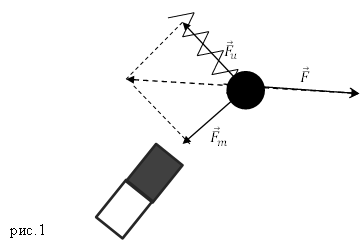
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
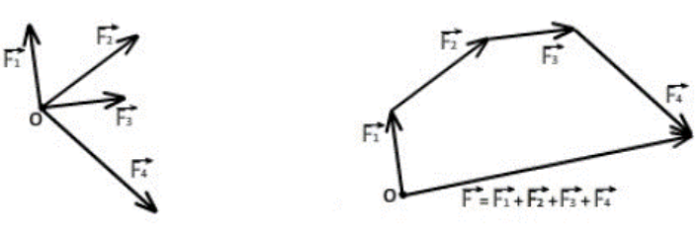
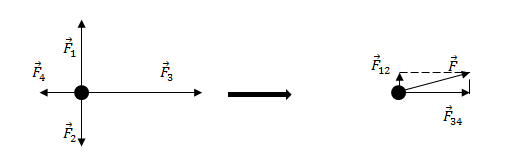
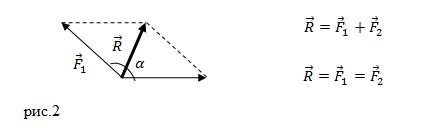
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Равнодействующая сила

4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
Обновлено 31 Октября, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
Обновлено 31 Октября, 2021
Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Например, в случае кулоновской силы – это величина обоих зарядов, взятых по модулю, квадрат расстояние между зарядами и коэффициент k, в системе СИ определяемый выражением: $k = {1 over 4 pi epsilon}$, где $epsilon$ – диэлектрическая постоянная.
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_{i=1}^n vec F_i$
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_{i=1}^n vec F_i$
А силу $F_i$ представим в виде:
$F = (F_{xi}, F_{yi}, F_{zi})$
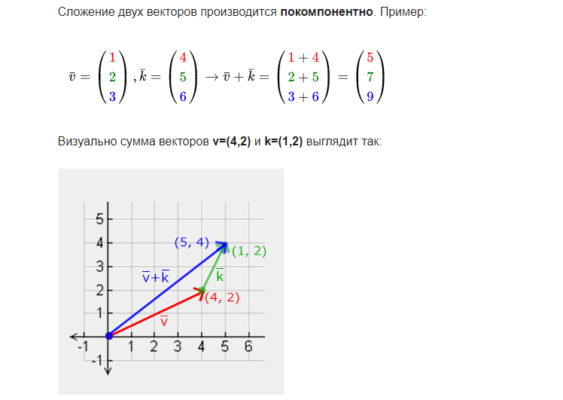
Тогда суммой двух сил будет новый вектор $F_{ab} = (F_{xb} + F_{xa}, F_{yb} + F_{ya}, F_{zb} + F_{za})$.
Абсолютное значение равнодействующей можно рассчитать так:
$F = sqrt{(F_{xb} + F_{xa})^2 + (F_{yb} + F_{ya})^2 + (F_{zb} + F_{za})^2}$
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
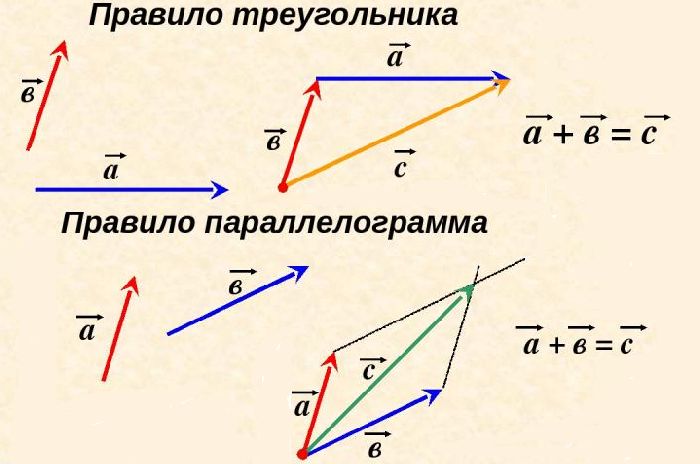
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
Поэтому запишем:
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
$F = sqrt{8^2 + 3^2} = sqrt{64 + 9} = 8,5 Н$
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
$F_1 = sqrt{5^2 + 0^2} = 5 Н$
$F_2 = sqrt{3^2 + 3^2} = 4,2 Н$
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
$F = sqrt{F_1^2 + F_2^2 – 2F_1F_2 cos135} = sqrt{F_1^2 + F_2^2 + 2F_1F_2 sin45} = sqrt{25 + 18 + 2 cdot 5 cdot 4,2 cdot sin45} = 8,5 Н$
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
А какая ваша оценка?
Второй закон Ньютона представляет собой основной закон динамики. Данный закон может выполняться только в инерциальных системах отсчета.
Формулируя второй закон, стоит обратить внимание на то, что в динамике вводятся масса тела m и сила F→, а также способы их измерения. Масса является количественной характеристикой инертных свойств тела и показывает реакцию тела на внешнее воздействие. Сила же F→ представляет из себя количественную меру действия одного объекта на другой.
2-ой закон Ньютона, определение и формула
Второй закон Ньютона – фундаментальный закон природы, являющийся обобщением опытных фактов, подразделяющихся на две категории:
- Если на обладающие разной массой тела подействовать одной и той же силой, то приобретаемые телами ускорения окажутся обратно пропорциональны их массам:
a~1m, при F=const.
- Если силами различной величины подействовать на одно тело, то ускорения тела окажутся прямо пропорциональными приложенным силам:
a→~F→, при m=const.
Основной закон динамики был сформулирован Ньютоном путем обобщения данных фактов:
Сила, которая оказывает воздействие на тело, эквивалентна произведению массы тела на сообщаемое данной силой ускорение:
F→=ma→.
Приведенное выражение и представляет собой второй закон Ньютона.
С помощью него стало возможным вычисление ускорение тела в случае, если известна его масса m и действующая на него сила F→:
a→=F’m.
В Международной системе единиц (СИ) в качестве единицы силы считают такую силу, которая сообщающая телу массой 1 кг ускорение 1 м/с2. Данная единица называется ньютоном (Н). В (СИ) ее принимают за эталон силы.
1 Н=1кг·мс2.
Равнодействующая сила
В том случае, если на тело одновременно воздействуют несколько сил, как например, F1→, F2→ и F3→, то силой F→ в формуле второго закона Ньютона считается равнодействующая всех сил это величина, выражающаяся в виде формулы:
F→=F1→+F2→+F3→.
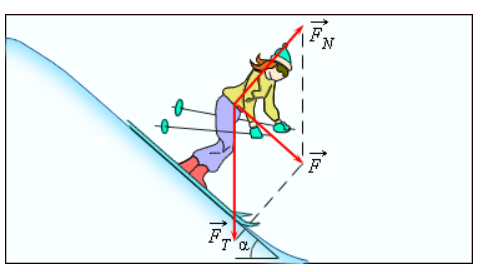
Рисунок 1.8.1. Сила F→ – равнодействующая силы тяжести F→Т и силы нормального давления FN→, действующих на лыжницу на гладкой горе. Сила F→ вызывает ускорение лыжника.
В случае же, когда равнодействующая сила F→=0, тело будет пребывать в состоянии покоя или равномерного прямолинейного движения. Выходит, что формально второй закон Ньютона включает в себя в качестве частного случая первый закон Ньютона. Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.
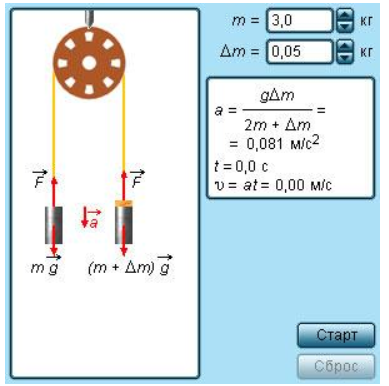
Рисунок 1.8.1. Модель движения тел на легком блоке.

![Rendered by QuickLaTeX.com [overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sum^N_{i=1}{{overline{F}}_i} qquad(2)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-54057b9972cba4d7aba2ba22bdc31f07_l3.png)
![Rendered by QuickLaTeX.com [sum^N_{i=1}{{overline{F}}_i}=moverline{a} qquad(3)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eef388f3d0d8e9e29c0cc63a1d433850_l3.png)