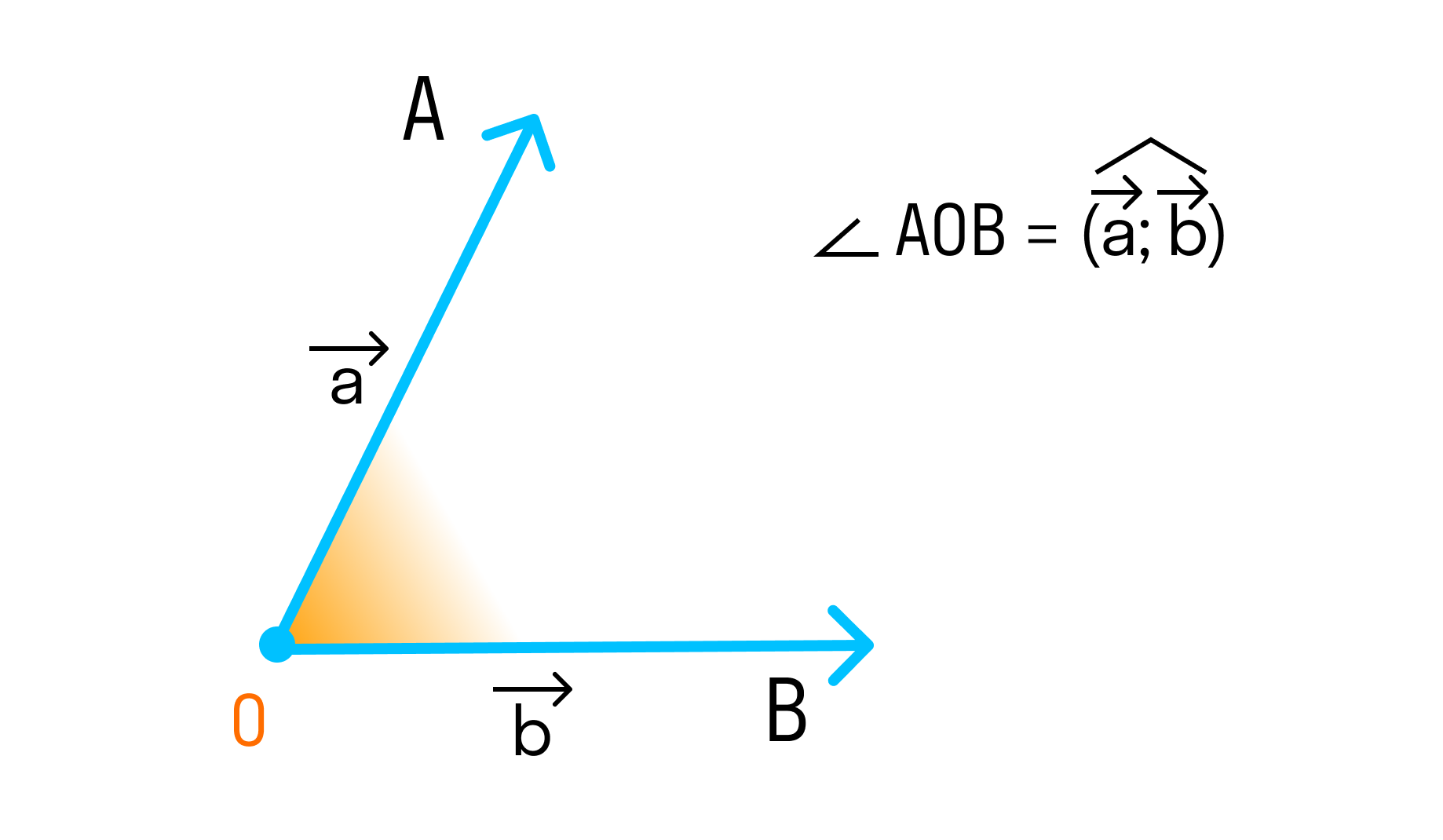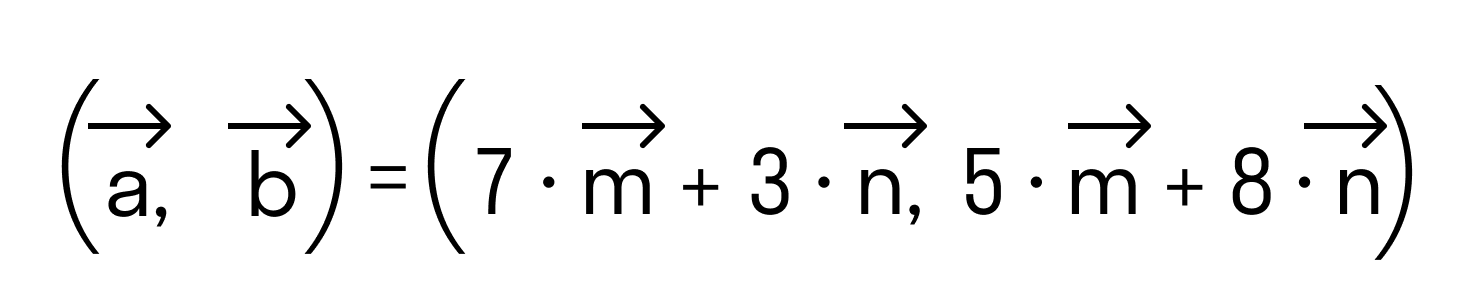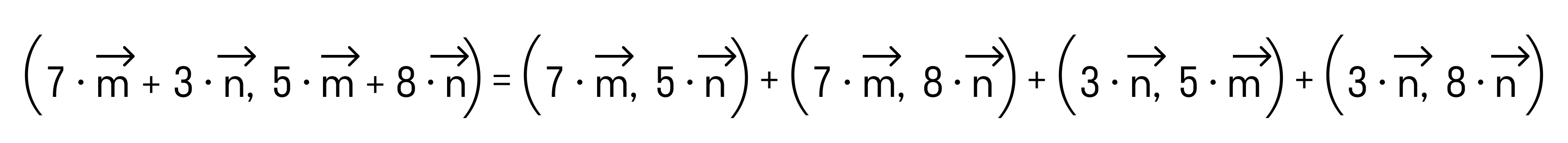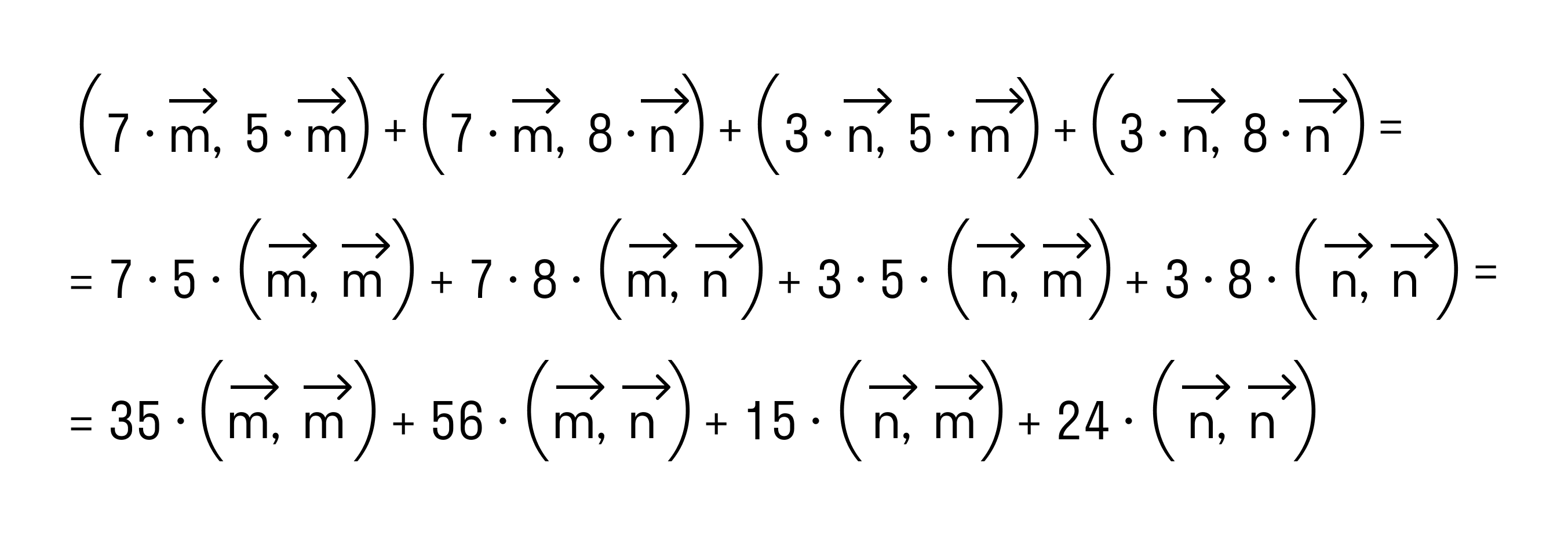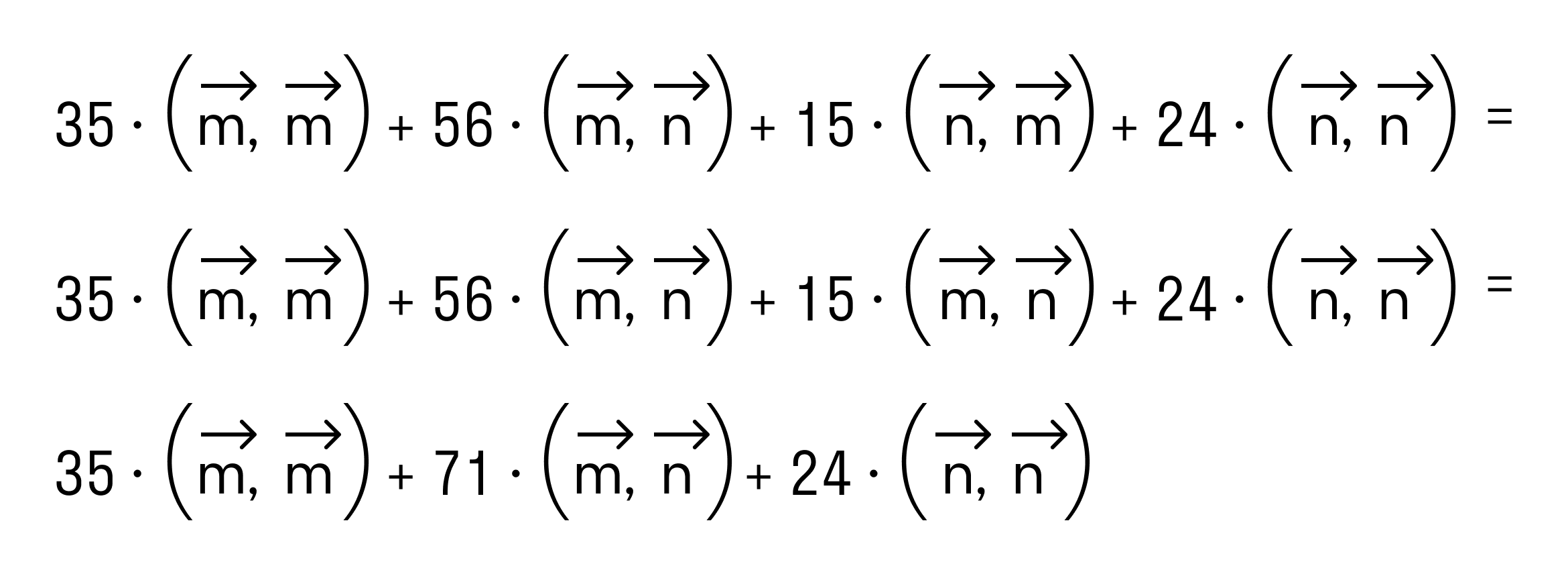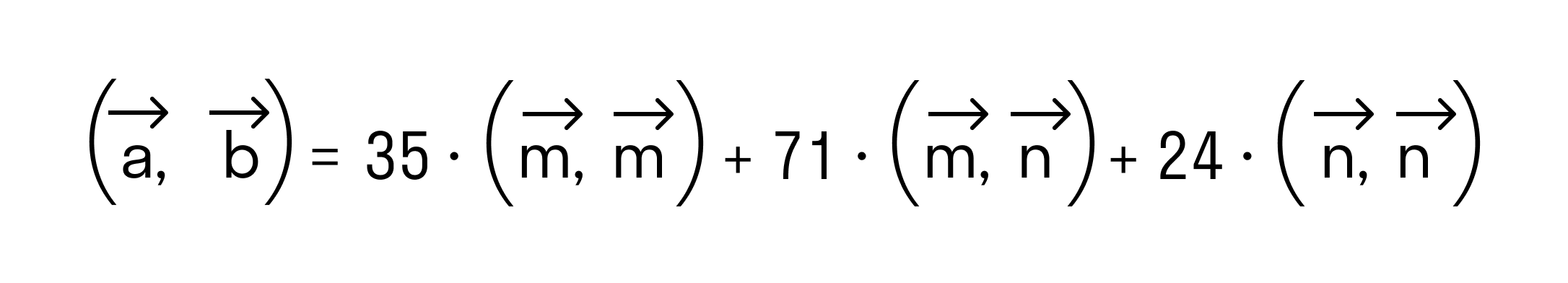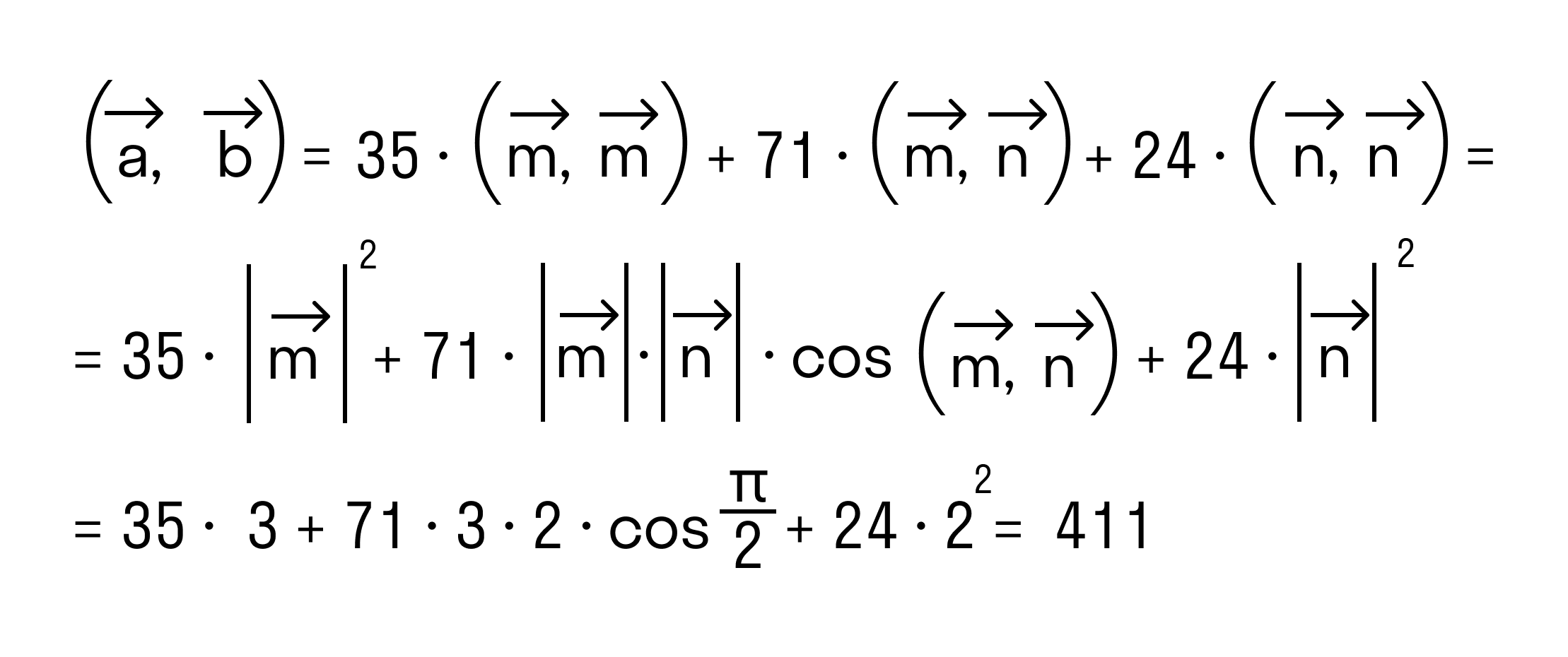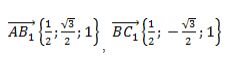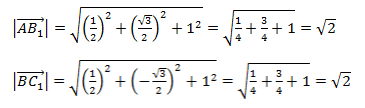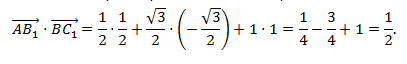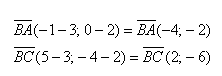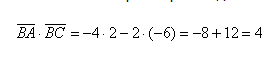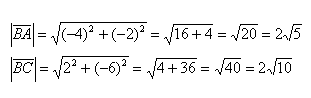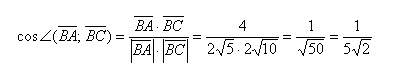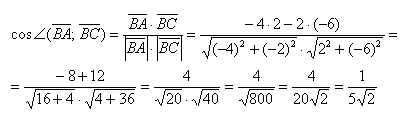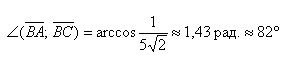Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.
Обозначение произведения векторов a→ и b→ имеет вид a→,b→. Преобразуем в формулу:
a→,b→=a→·b→·cosa→,b→^. a→ и b→ обозначают длины векторов, a→,b→^ — обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a→,b→=0
При умножении вектора самого на себя, получим квадрат его дины:
a→,b→=a→·b→·cosa→,a→^=a→2·cos0=a→2
Скалярное умножение вектора самого на себя называют скалярным квадратом.
Вычисляется по формуле:
a→,b→=a→·b→·cosa→,b→^.
Запись a→,b→=a→·b→·cosa→,b→^=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.
При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:
a→,b→=ax·bx+ay·by,
для трехмерного пространства применимо выражение:
a→,b→=ax·bx+ay·by+az·bz.
Фактически это является третьим определением скалярного произведения.
Докажем это.
Для доказательства используем a→,b→=a→·b→·cosa→,b→^=ax·bx+ay·by для векторов a→=(ax,ay), b→=(bx,by) на декартовой системе.
Следует отложить векторы
OA→=a→=ax,ay и OB→=b→=bx,by.
Тогда длина вектора AB→будет равна AB→=OB→-OA→=b→-a→=(bx-ax,by-ay).
Рассмотрим треугольник OAB.
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) верно , исходя из теоремы косинусов.
По условию видно, что OA=a→, OB=b→, AB=b→-a→, ∠AOB=a→,b→^, значит, формулу нахождения угла между векторами запишем иначе
b→-a→2=a→2+b→2-2·a→·b→·cos(a→,b→^).
Тогда из первого определения следует, что b→-a→2=a→2+b→2-2·(a→,b→), значит (a→,b→)=12·(a→2+b→2-b→-a→2).
Применив формулу вычисления длины векторов, получим:
a→,b→=12·((a2x+ay2)2+(b2x+by2)2-((bx-ax)2+(by-ay)2)2)==12·(a2x+a2y+b2x+b2y-(bx-ax)2-(by-ay)2)==ax·bx+ay·by
Докажем равенства:
(a→,b→)=a→·b→·cos(a→,b→^)==ax·bx+ay·by+az·bz
– соответственно для векторов трехмерного пространства.
Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:
- коммутативность (a→,b→)=(b→,a→);
- дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
- сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ — любое число;
- скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay.
По свойству коммутативности равенства ax·bx=bx·ax и ay·by=by·ay верны, значит ax·bx+ay·by=bx·ax+by·ay.
Отсюда следует, что (a→,b→)=(b→,a→). Что и требовалось доказать.
Дистрибутивность справедлива для любых чисел:
(a(1)→+a(2)→+…+a(n)→,b→)=(a(1)→,b→)+(a(2)→,b→)+…+(a(n)→,b→)
и (a→,b(1)→+b(2)→+…+b(n)→)=(a→,b(1)→)+(a→,b(2)→)+…+(a→,b→(n)),
отсюда имеем
(a(1)→+a(2)→+…+a(n)→,b(1)→+b(2)→+…+b(m)→)==(a(1)→,b(1)→)+(a(1)→,b(2)→)+…+(a(1)→,b(m)→)++(a(2)→,b(1)→)+(a(2)→,b(2)→)+…+(a(2)→,b(m)→)+…++(a(n)→,b(1)→)+(a(n)→,b(2)→)+…+(a(n)→,b(m)→)
Скалярное произведение с примерами и решениями
Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:
- (a→,b→)=a→·b→·cos(a→,b→^);
- (a→,b→)=a→·npa→b→=b→·npb→a→;
- (a→,b→)=ax·bx+ay·by или (a→,b→)=ax·bx+ay·by+az·bz;
- (a→,a→)=a→2.
Рассмотрим некоторые примеры решения.
Длина a→ равна 3, длина b→ равна 7. Найти скалярное произведение, если угол имеет 60 градусов.
Решение
По условию имеем все данные, поэтому вычисляем по формуле:
(a→,b→)=a→·b→·cos(a→,b→^)=3·7·cos60°=3·7·12=212
Ответ:(a→,b→)=212.
Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.
Решение
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9
Ответ: (a→,b→)=-9
Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).
Решение
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)
Подставив в формулу с использованием координат, получим:
(AB→,AC→)=4·0+7·4=0+28=28.
Ответ: (AB→,AC→)=28.
Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.
Решение
(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:
(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)
Выносим коэффициент за знак произведения и получим:
(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)
По свойству коммутативности преобразуем:
35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)
В итоге получим:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→).
Теперь применим формулу для скалярного произведения с заданным по условию углом:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→)==35·m→2+71·m→·n→·cos(m→,n→^)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
Ответ: (a→,b→)=411
Если имеется числовая проекция.
Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).
Решение
По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:
npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,
Подставив в формулу, получим выражение:
(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.
Ответ: (a→,b→)=-33.
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.
Решение
Из формулы видно, что необходимо найти сумму произведений координат:
(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.
В дано имеем (a→,b→)=-1.
Чтобы найти λ, вычисляем уравнение:
λ2+2·λ=-1, отсюда λ=-1.
Ответ: λ=-1.
Физический смысл скалярного произведения
Механика рассматривает приложение скалярного произведения.
При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:
A=(F→,MN→).
Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.
Решение
Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.
Ответ: A=1522.
Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.
Решение
При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).
По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.
По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).
Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:
MN→=32+(-10)2+72=158.
Ответ: 158.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Основные определения
Система координат — это совокупность определений, позволяющих определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Мы уже рассказывали, как найти координаты точки.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
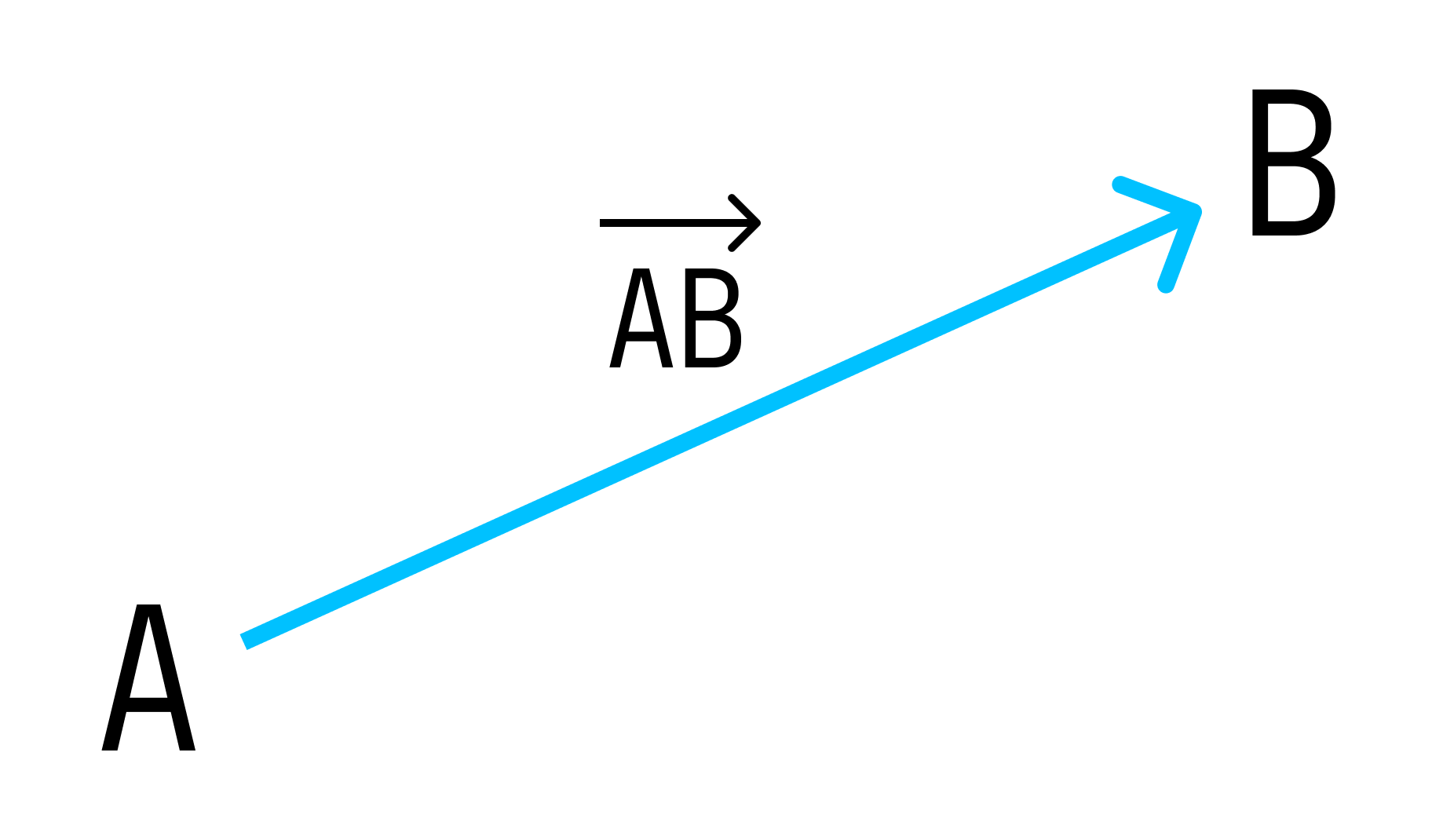
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как
. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так:
.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
При умножении вектора на вектор получается число. Если длины векторов
,
— это числа, косинус угла — число, то скалярное произведение этих векторов можно найти по формуле
.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
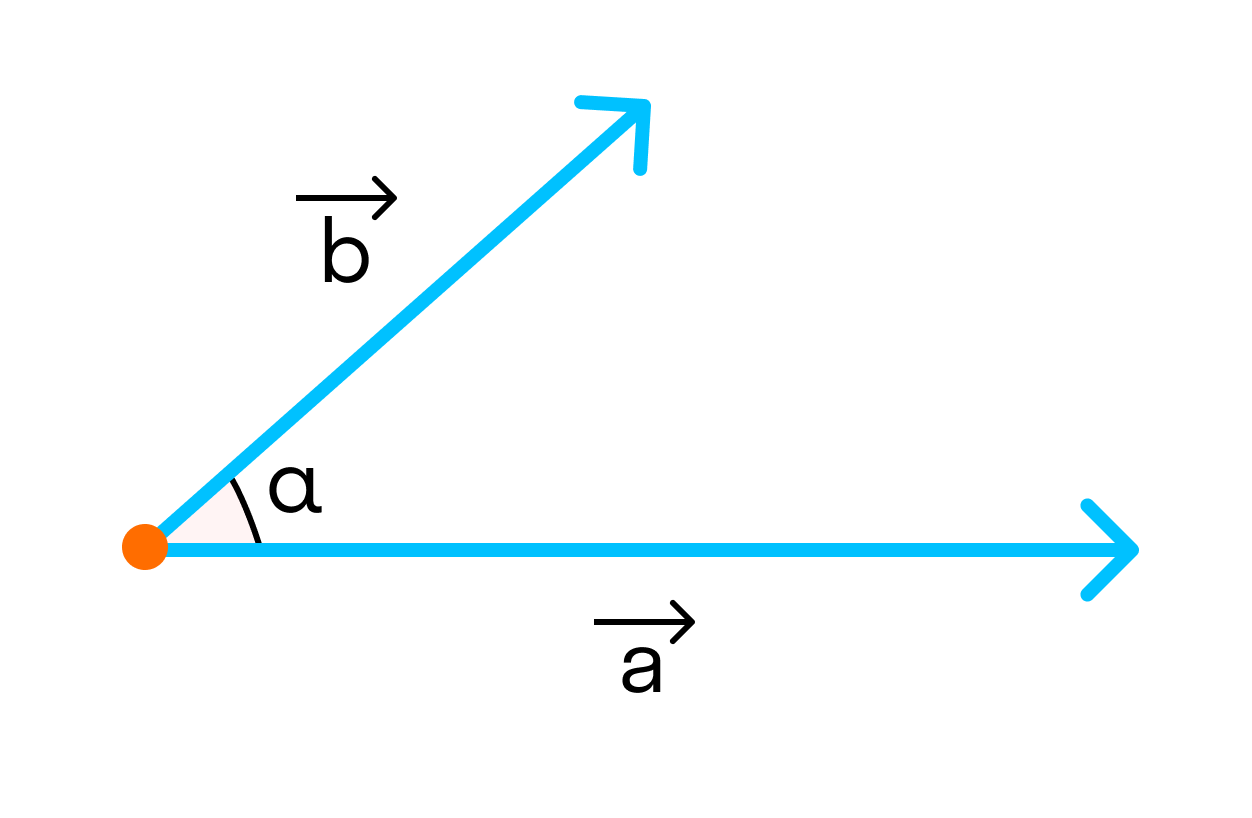
Угол между векторами
Угол между векторами
может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства:
либо
.
Значок угла
можно опустить и писать просто:
.
Пусть даны два вектора
.
Отложим их от некоторой точки О пространства:
.
. Тогда угол между векторами — это угол
.
Угол между векторами может быть прямым, тупым, острым или равным нулю. Рассмотрим каждый случай:
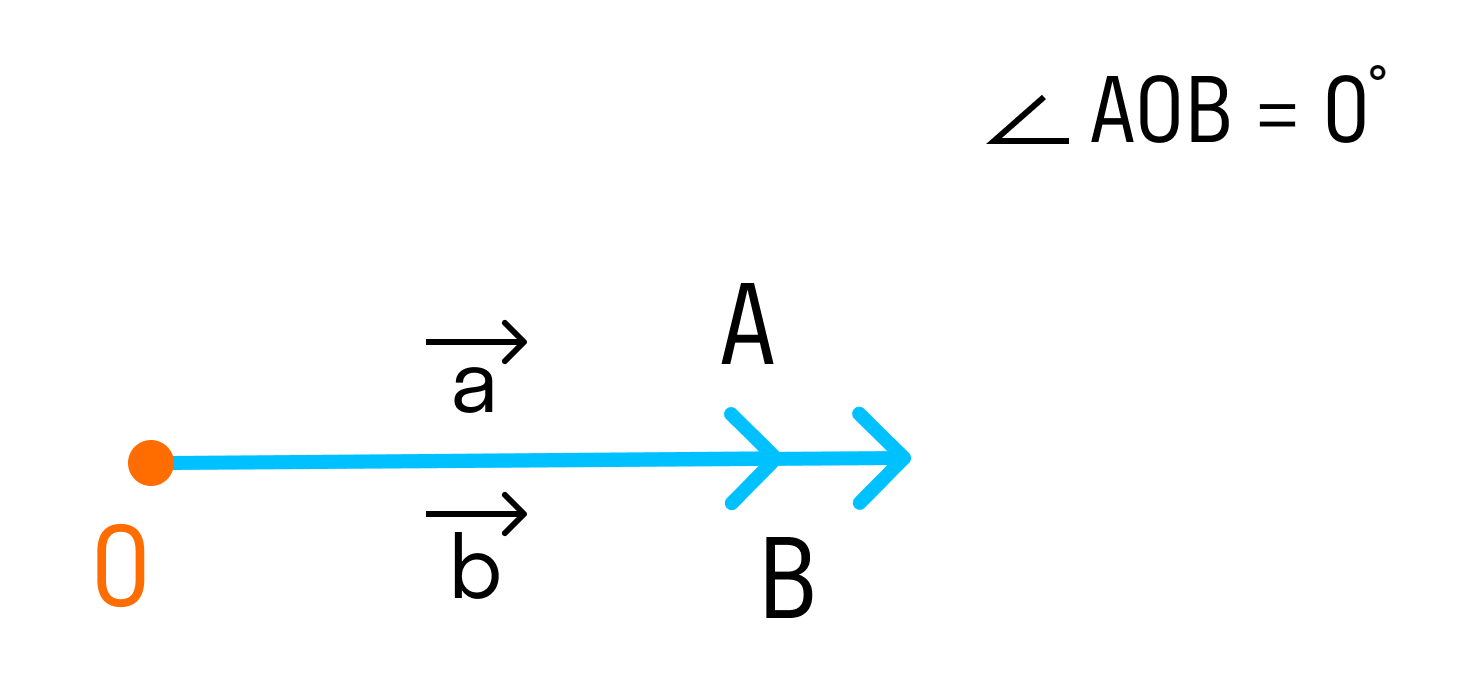
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
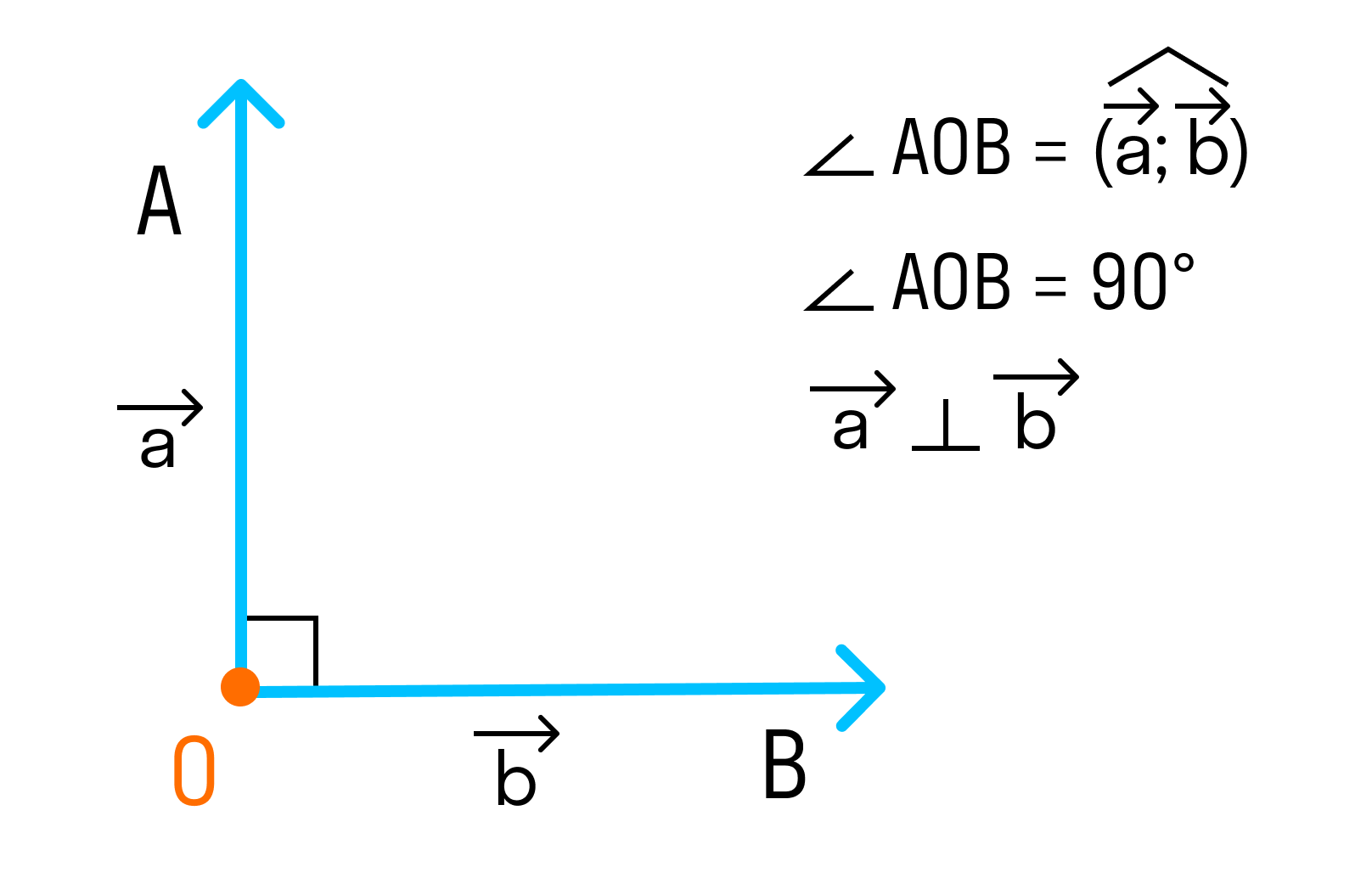
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
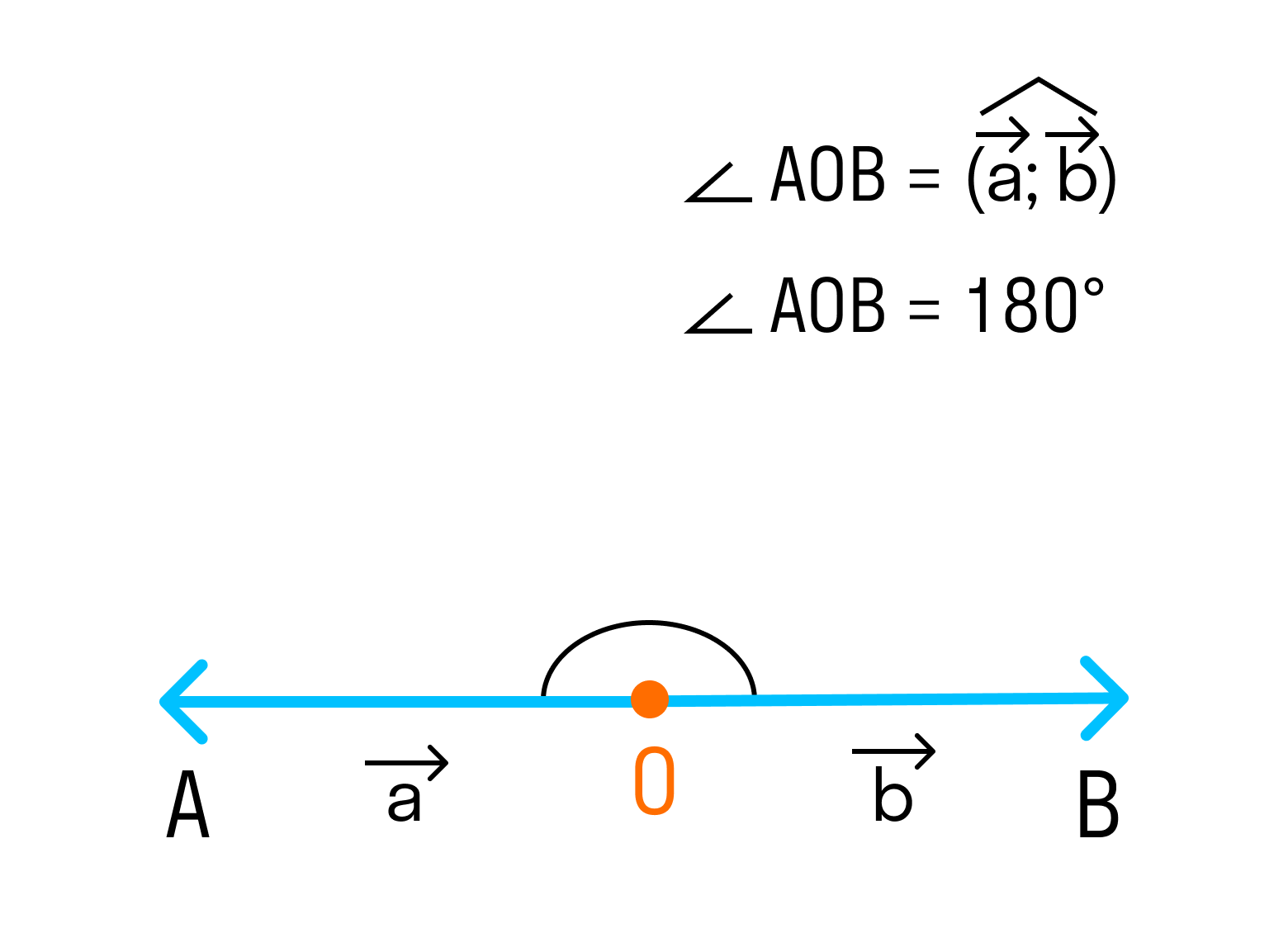
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно произведению их длин, взятому с обратным знаком.
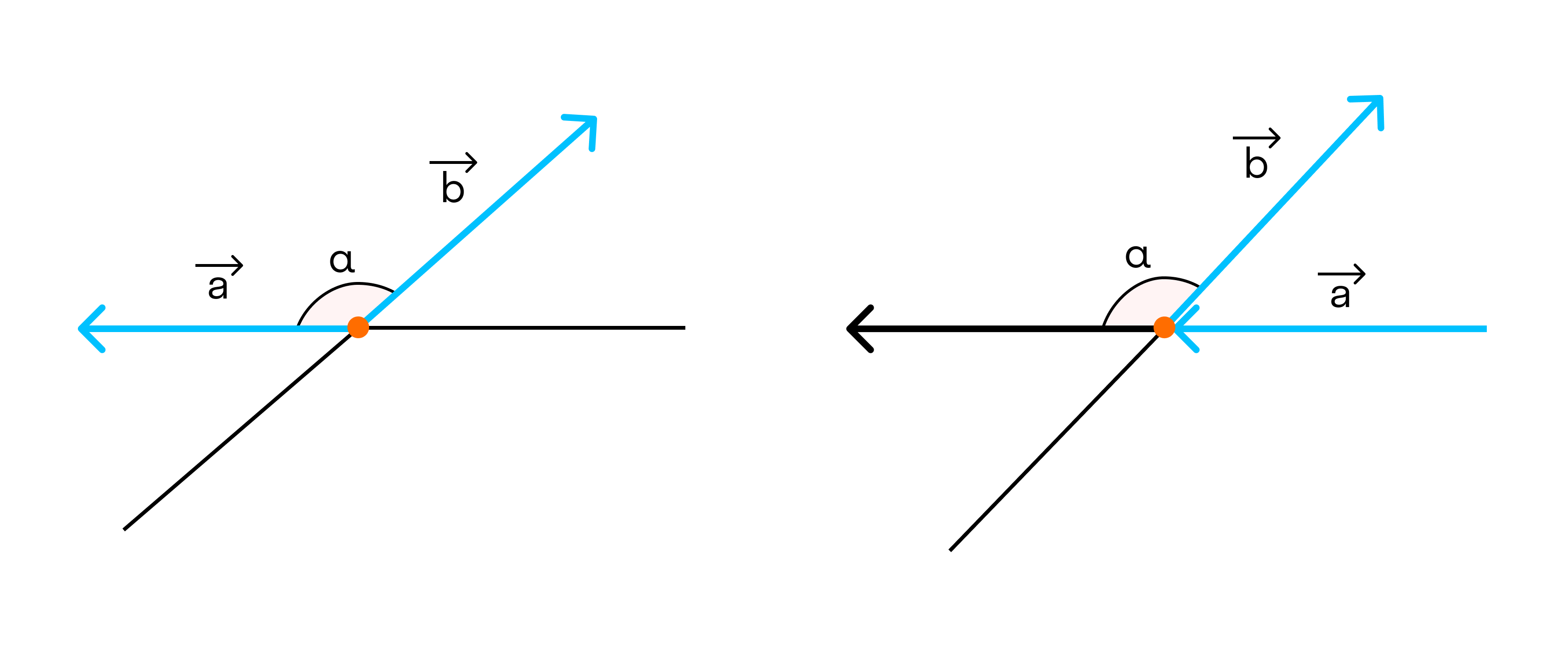
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
, где α — угол между векторами a и b
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов
и
.
То есть для векторов
,
на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид:
А для векторов
в трехмерном пространстве скалярное произведение в координатах находится так:
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + … + an * bn
Свойства скалярного произведения векторов
-
Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.
-
Скалярное произведение вектора самого на себя равно квадрату его модуля:
-
Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
-
Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
-
Сочетательный закон для скалярного произведения:
-
Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
Ответ:
.
Пример 2.
Найти скалярное произведение векторов
и
, если
.
Как решаем:
Используем формулу
.
В данном случае:
Ответ:
.
Пример 3.
Как найти скалярное произведение векторов
и
, если векторы
и
перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ:
.
Пример 4.
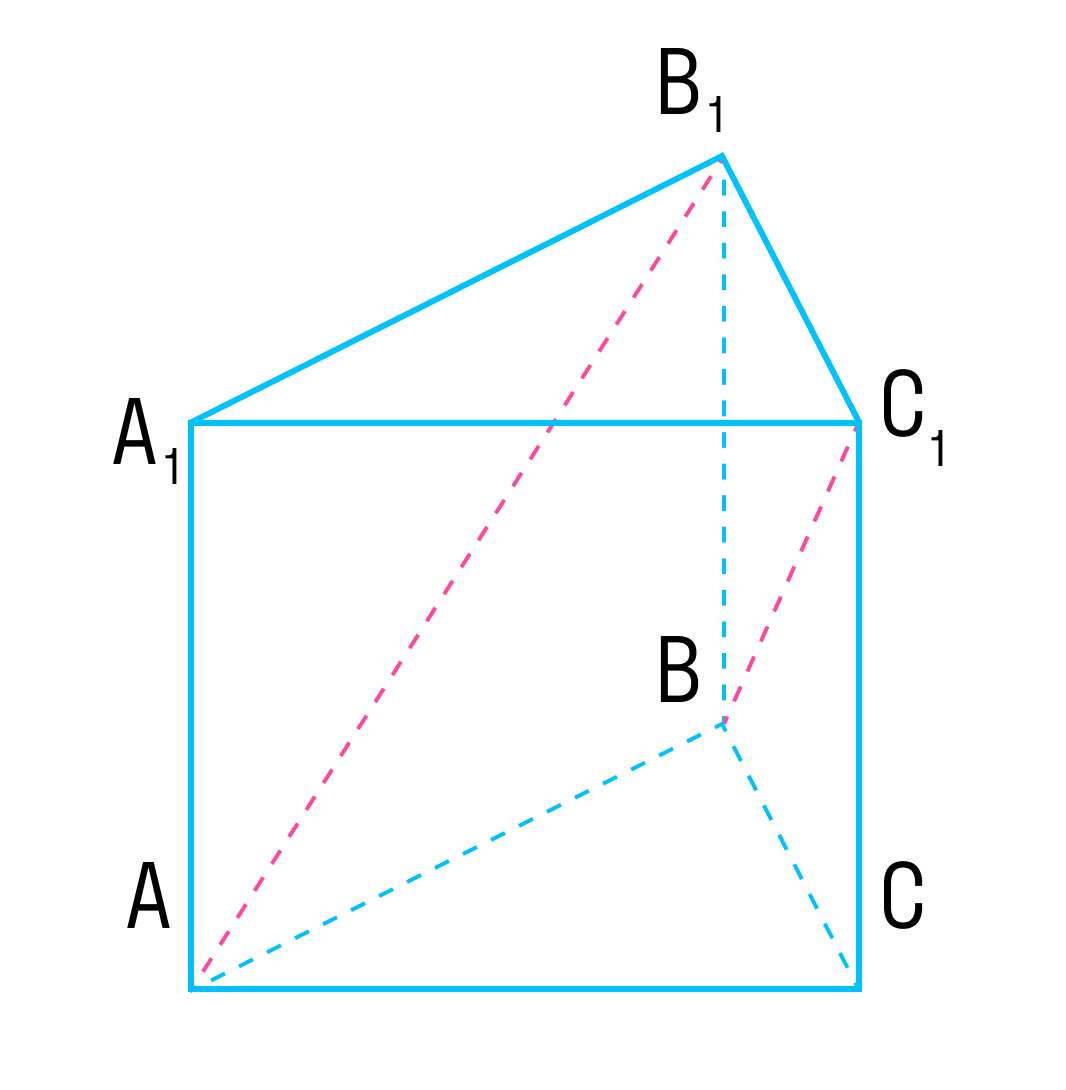
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Как решаем:
-
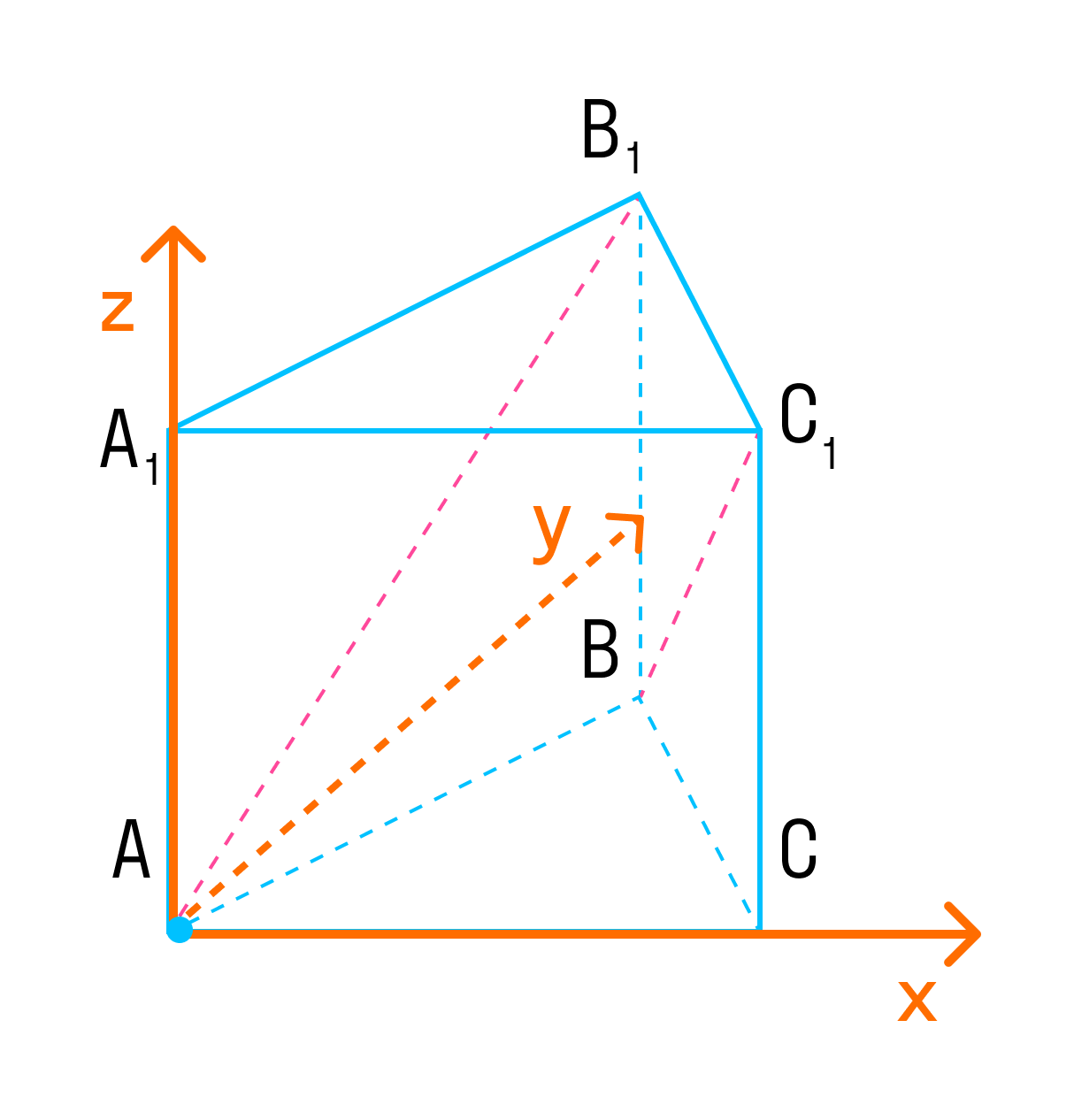
Введем систему координат.
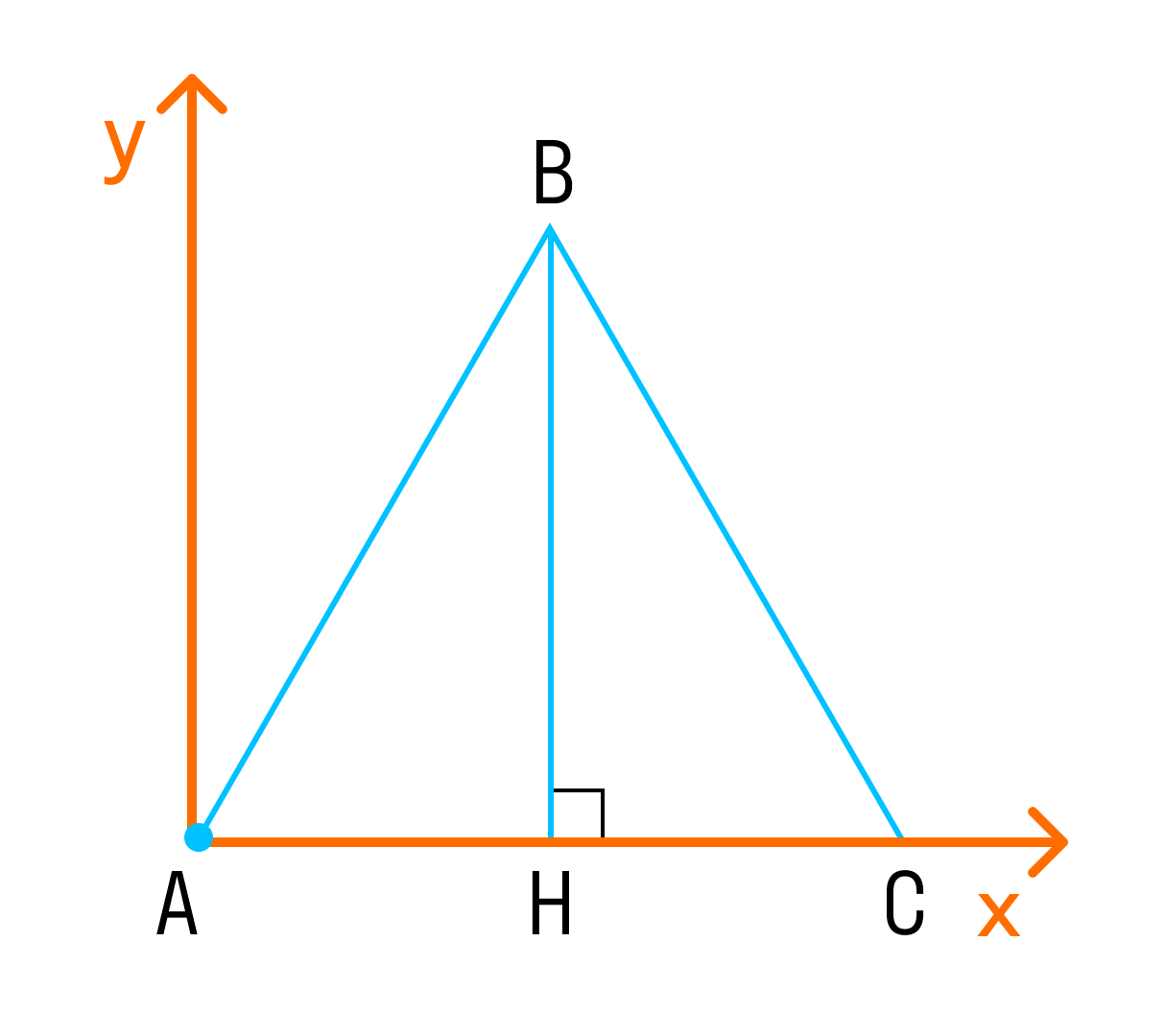
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
-
Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
-
Найдем координаты векторов
и
: -
Найдем длины векторов
и
: -
Найдем скалярное произведение векторов через их координаты
и
: -
Найдем косинус угла между прямыми AB1 и BC1:
,
,
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов:
и
.
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение:
, следовательно
.
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их:
Вычислим их скалярное произведение:
, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а)
, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
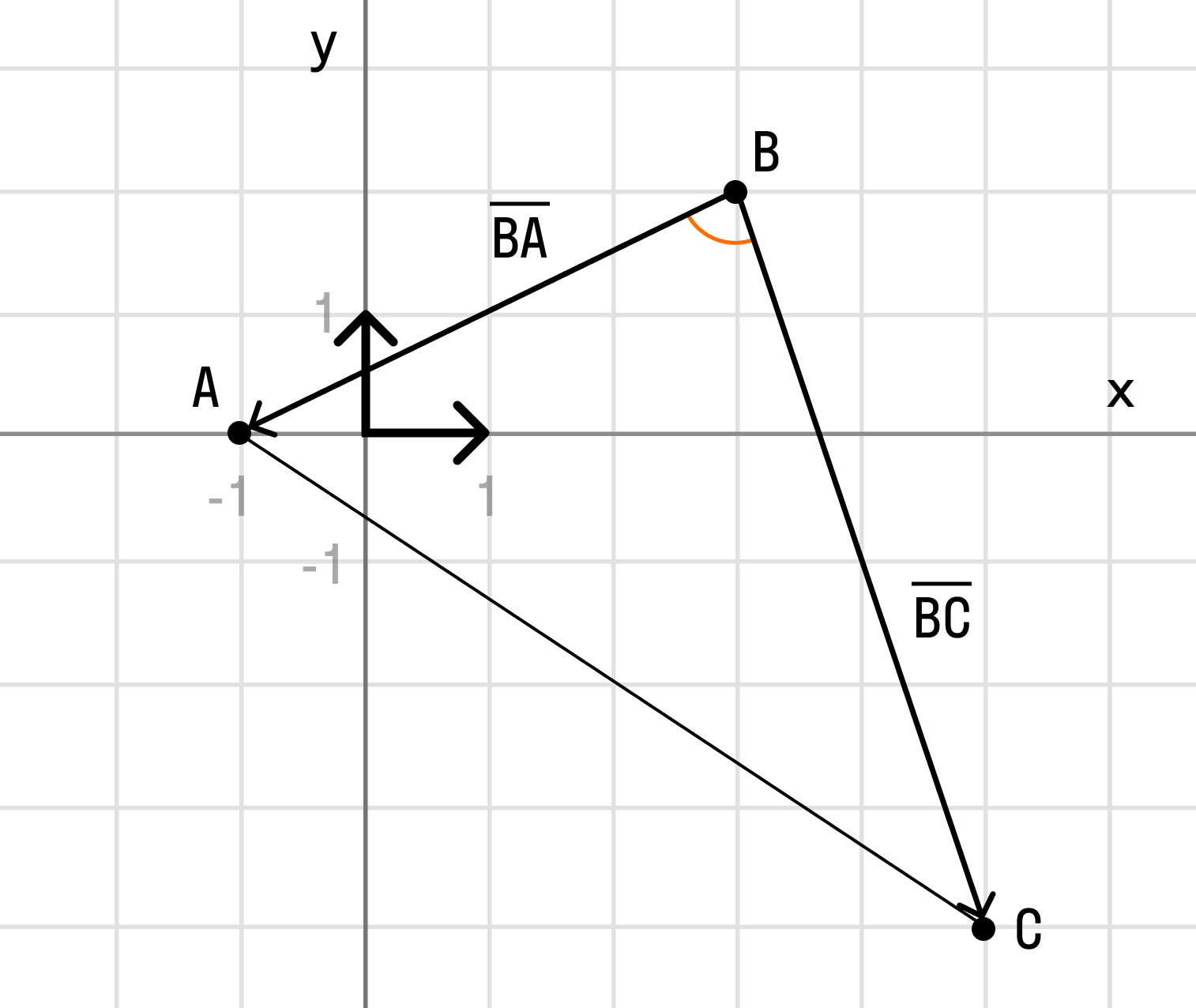
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен красной дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами
и
, иными словами:
.
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Скалярное произведение векторов
Формула
Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.
Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$
По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.
Примеры решений
| Пример 1 |
| Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $ |
| Решение |
|
В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их: $$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$ Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ (overline{a},overline{b}) = 0 $$ |
| Пример 2 |
|
В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $. |
| Решение |
|
В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора): $$ overline{AB} = (-1 — 1; 4-3; 1-(-2)) = (-2; 1; 3) $$ $$ overline{AC} = (2 — 1; 1 — 3; -2 — (-2)) = (1; -2; 0) $$ Теперь, когда необходимые векторы найдены, то вычисляем их произведение: $$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$ |
| Ответ |
| $$ (overline{AB},overline{AC}) = -4 $$ |
В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; … ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Свойства скалярного произведения векторов
-
Скалярное произведение вектора самого на себя всегда больше или равно нуля:
a · a ≥ 0
-
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
a · a = 0 <=> a = 0
-
Скалярное произведение вектора самого на себя равно квадрату его модуля:
a · a = |a|2
-
Операция скалярного умножения коммуникативна:
a · b = b · a
-
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b
-
(αa) · b = α(a · b)
-
Операция скалярного умножения дистрибутивна:
(a + b) · c = a · c + b · c
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.
Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.
Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =
= 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.
Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:
a = i + 2j
b = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
§5. СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Определение.
Скалярным произведением двух векторов
и
называется число, равное произведению
.
Обозначается скалярное произведение
векторов
и
символом
или
,
следовательно,
.
Из
определения скалярного произведения
следует, что
,
так как
и
/
Если
один из сомножителей скалярного
произведения, например, вектор
есть единичный вектор, то
.
СВОЙСТВА СКАЛЯРНОГО
ПРОИЗВЕДЕНИЯ
1.
,
(коммутативность);
2.
,
(ассоциативность относительно числового
множителя);
3.
,
(дистрибутивность).
ДОКАЗАТЕЛЬСТВО
СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство
первое следует из определения скалярного
произведения:
.
Второе
и третье свойства следуют из линейных
свойств проекции вектора на ось
(направление):
(эти свойства проекции доказываются
при рассмотрении вектора в ортонормированном
базисе). Используя линейные свойства
проекции, получим:
СКАЛЯРНЫЙ
КВАДРАТ
Скалярным
квадратом называется скалярное
произведение
и обозначается символом
;
по определению
.
УГОЛ МЕЖДУ
ВЕКТОРАМИ
Из
определения
следует
.
УСЛОВИЕ
ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема.
Векторы
и
ортогональны тогда и только тогда, когда
.
Доказательство
необходимости. Пусть
,
тогда
.
Доказательство
достаточности. Пусть
или
,
тогда, либо хотя бы один из множителей
есть нулевой вектор и
,
так как направление нулевого вектора
неопределенно, либо
тогда
.
СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема.
В ортонормированном базисе скалярное
произведение векторов
и
равно сумме произведений одноименных
координат множителей.
Доказательство.
Пусть в пространстве выбран ортонормированный
базис
и векторы
и
имеют в этом базисе координаты
соответственно
и
,
т.е.
.
Тогда, используя свойства скалярного
произведения, будем иметь
Так
как
,
то окончательно получим:
МОДУЛЬ ВЕКТОРА
В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из
формулы для скалярного произведения
при
получим
УГОЛ
МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ
БАЗИСЕ

УСЛОВИЕ
ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ
БАЗИСЕ
Если
,
то необходимое и достаточное условие
ортогональности
запишется в виде
НАПРАВЛЯЮЩИЕ
КОСИНУСЫ ВЕКТОРА
Определение.
Направляющими косинусами вектора
в заданном базисе называются косинусы
углов между вектором
и базисными векторами.
Пусть
– базисные векторы ортонормированного
базиса и
– углы между вектором
и векторами
соответственно.
Направляющими
косинусами вектора
будут
.
Если
,
то из
,
так как
.
Аналогично имеем
.
Замечание.
Для любого вектора
имеем
ЛИНЕЙНЫЕ СВОЙСТВА
ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В
ортонормированном базисе координаты
вектора равны проекциям этого вектора
на направления соответствующих базисных
векторов.
Действительно,
если
,то
,
но
,
следовательно,
.
Аналогично
.
Если
,
то из суммы векторов
и произведения вектора на число
следует, что проекция вектора обладает
свойствами линейности.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Дайте определение
скалярного произведения векторов. -
Выведите условие
ортогональности двух векторов. -
Докажите
формулу скалярного произведения
векторов в ортогональном базисе. -
Напишите формулу
модуля вектора в ортонормированном
базисе. -
Выведите
условие ортогональности двух векторов
в ортогональном базисе.
§6. ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным
произведением вектора
на вектор
называется новый вектор
,
удовлетворяющий условиям:
1.
;
2.
и
;
3.
Упорядоченная тройка векторов
образует правую тройку (с конца вектора
поворот на наименьший угол от первого
сомножителя ко второму виден совершающимся
против часовой стрелки (рис. 14)).
Векторное
произведение
на
обозначается символом
или
.
|
A
Рис. |
|
Замечания.
1. Модуль
численно равен площади параллелограмма,
построенного на векторах
и
(рис. 15). Действительно, площадь
параллелограмма ABCD
равна
Векторы
и
коллинеарны тогда и только тогда, когда
.
Необходимость и достаточность этого
условия следует из определения векторного
произведения.
СВОЙСТВА ВЕКТОРНОГО
ПРОИЗВЕДЕНИЯ
1.
(антикоммутативность);
2.
(ассоциативность относительно числового
множителя);
3.
(дистрибутивность относительно суммы
векторов).
Это
свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО
СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1.
Пусть
,
тогда из
.
Векторы
и
ортогональны
плоскости, в которой лежат векторы
и
,
следовательно,
.
По
определению с конца вектора
поворот от вектора
к вектору
виден совершающимся против часовой
стрелки, а с конца вектора
поворот от вектора
к вектору
виден совершающимся против часовой
стрелки, а это возможно при
.
Следовательно,
имеем, что
и
, т. е.
или
.
Рис.
16.
2. Пусть
.
По определению векторного произведения
имеем
;
при
(рис.16), при
имеем
,
откуда
,
т.е.
.
Наконец,
,
где
,
.
Так как
или
,
то в любом случае
,
следовательно,
.
Итак, получим, что
и
,
т. е.
или
.
ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ БАЗИСНЫХ ВЕКТОРОВ
ОРТОНОРМИРОВАННОГО
БАЗИСА
Рис. 17.
Рассмотрим векторы
,
которые образуют правую тройку
ортонормированного базиса (рис.17).
Рассмотрим вектор
.
Этот вектор ортогонален к вектору
и
вектору
,
следовательно,
,
векторы
и
образуют правые тройки, следовательно,
наконец,
.
Итак
,
откуда следует
.
Аналогично получим
.
Из
свойства векторного произведения
следует
,
а из определения —
.
ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ
БАЗИСЕ
Пусть

Рассмотрим вектор
.
Используя свойства векторного
произведения, получим
Следовательно,
.
Замечание.
Для вычисления векторного произведения
удобно использовать символ определителя:

Если
этот определитель разложить по элементам
первой строки, то получим разложение
вектора
по направлениям базисных векторов:
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Дайте определение
векторного произведения. -
Выведите формулу
векторного произведения в ортонорми-рованном
базисе.
§7. ВЕКТОРНО-СКАЛЯРНОЕ
(СМЕШАННОЕ) ПРОИЗВЕДЕНИЕ
ТРЕХ
ВЕКТОРОВ
Пусть
даны три вектора
.
Если вектор
умножается векторно на вектор
,
а затем вектор
скалярно умножается на вектор
,
то полученное число
называется смешанным произведением
векторов
.
ГЕОМЕТРИЧЕСКИЙ
СМЫСЛ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
Рассмотрим
смешанное произведение
.
Векторы
приведем к общему началу и построим на
этих векторах параллелепипед (рис.18).
|
Вектор
По |
Рис. 18 |
параллелепипеда
(,
если
и
,
если
), следовательно, произведение
равно объему параллелепипеда со знаком
«+» или «–». Из рис.18 видно, что
,
если упорядоченная тройка векторов
– правая, если векторы
образуют левую тройку, то
.
Таким образом, смешанное произведение
векторов
равно объему параллелепипеда, построенному
на этих векторах, со знаком плюс, если
тройка векторов
правая, и со знаком минус, если эта тройка
– левая.
СМЕШАННОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ
БАЗИСЕ
Пусть
,
тогда вектор
.Смешанное
произведение
есть скалярное произведение векторов
и
,
поэтому
.
Если
использовать символы определителей
второго и третьего порядков, то последнее
выражение можно представить в виде:

Следовательно,
смешанное произведение
в ортонормированном базисе равно
определителю третьего порядка, где
первые две строки состоят из координат
сомножителей вектора
,
а третья — из координат вектора
.
СВОЙСТВА СМЕШАННОГО
ПРОИЗВЕДЕНИЯ
1.
.
Это свойство позволяет записывать
смешанное произведение векторов
в виде
,
не указывая, какие два вектора (первые
или последние) перемножаются векторно.
2.
.
Значение смешанного произведения не
меняется при циклической (круговой)
перестановке множителей.
3.
.
Значение смешанного произведения меняет
знак, если поменять местами два
сомножителя.
ДОКАЗАТЕЛЬСТВО
СВОЙСТВ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
1.
Пусть
;
из переместительного свойства скалярного
произведения следует, что

(следует
дважды поменять местами строки, чтобы
из первого определителя получить
второй).
2.
3.
,
но
,
следовательно,
или
.
УСЛОВИЕ
КОМПЛАНАРНОСТИ ТРЕХ ВЕКТОРОВ
Теорема.
Векторы
компланарны тогда и только тогда, когда
.
Доказательство
необходимости условия.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #