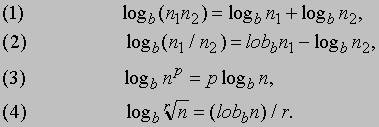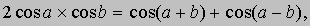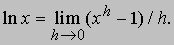Русский[править]
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | логари́фм | логари́фмы |
| Р. | логари́фма | логари́фмов |
| Д. | логари́фму | логари́фмам |
| В. | логари́фм | логари́фмы |
| Тв. | логари́фмом | логари́фмами |
| Пр. | логари́фме | логари́фмах |
ло—га—ри́фм
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).
Корень: -логарифм- [Тихонов, 1996].
Произношение[править]
- МФА: ед. ч. [ɫəɡɐˈrʲifm], мн. ч. [ɫəɡɐˈrʲifmɨ]
Семантические свойства[править]
Значение[править]
- матем. функция, обратная возведению в степень, или экспоненте; показатель степени, в которую нужно возвести число, называемое основанием, чтобы в результате получить число, являющееся аргументом ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
- —
Антонимы[править]
- частичн.: экспонента, степень
Гиперонимы[править]
- функция
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
|
Этимология[править]
Происходит от лат. logarithmus «логарифм», далее из др.-греч. λόγος «слово, речь, разум; мнение; учение»; восходит к праиндоевр. *leg- «собирать» + ἀριθμός «количество, число», далее из праиндоевр. *re(i)- «рассуждение, счёт». Латинский термин был сконструирован в 1610-х шотландским ученым Джоном Непером (1550—1617).
Фразеологизмы и устойчивые сочетания[править]
- десятичный логарифм
- натуральный логарифм
Перевод[править]
| Список переводов | |
|
Анаграммы[править]
- алгорифм
Библиография[править]
|
|
Для улучшения этой статьи желательно:
|
Казахский[править]
Морфологические и синтаксические свойства[править]
логарифм
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. логарифм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. logarithmus «логарифм», далее из др.-греч. λόγος «слово, речь, разум; мнение; учение»; восходит к праиндоевр. *leg- «собирать» + ἀριθμός «количество, число», далее из праиндоевр. *re(i)- «рассуждение, счёт». Латинский термин был сконструирован в 1610-х шотландским ученым Джоном Непером (1550—1617).
Фразеологизмы и устойчивые сочетания[править]
Украинский[править]
Морфологические и синтаксические свойства[править]
логарифм
Существительное, неодушевлённое, мужской род.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- матем. логарифм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. logarithmus «логарифм», далее из др.-греч. λόγος «слово, речь, разум; мнение; учение»; восходит к праиндоевр. *leg- «собирать» + ἀριθμός «количество, число», далее из праиндоевр. *re(i)- «рассуждение, счёт». Латинский термин был сконструирован в 1610-х шотландским ученым Джоном Непером (1550—1617).
Фразеологизмы и устойчивые сочетания[править]
Как написать слово «логарифм» правильно? Где поставить ударение, сколько в слове ударных и безударных гласных и согласных букв? Как проверить слово «логарифм»?
логари́фм
Правильное написание — логарифм, ударение падает на букву: и, безударными гласными являются: о, а.
Выделим согласные буквы — логарифм, к согласным относятся: л, г, р, ф, м, звонкие согласные: л, г, р, м, глухие согласные: ф.
Количество букв и слогов:
- букв — 8,
- слогов — 3,
- гласных — 3,
- согласных — 5.
Формы слова: логари́фм, -а.
логари́фм
логари́фм, -а
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова случаем (наречие):
Ассоциации к слову «логарифм»
Синонимы к слову «логарифм»
Предложения со словом «логарифм»
- Не так давно им учили в школах, чтобы использовать таблицы логарифмов.
- Однако рано или поздно она всё-таки сменяется инструментальным подходом, когда в руку берётся арифмометр, отвес и линейка, а в голову вставляется десятичный логарифм с котангенсом.
- В самом деле, возможно интерпретировать информацию, передаваемую в сообщении, как фактическое отрицание её энтропии и как отрицательный логарифм её вероятности.
- (все предложения)
Цитаты из русской классики со словом «логарифм»
- Все поступки человеческие, само собою, будут расчислены тогда по этим законам, математически, вроде таблицы логарифмов, до 108 000, и занесены в календарь; или еще лучше того, появятся некоторые благонамеренные издания, вроде теперешних энциклопедических лексиконов, в которых все будет так точно исчислено и обозначено, что на свете уже не будет более ни поступков, ни приключений.
- — Гуси сами собой, а Цицерон сам собой… А из математики мы логарифмы проходить станем. Вот трудно-то будет!
- Я писал «Историю железных дорог»; нужно было прочесть множество русских и иностранных книг, брошюр, журнальных статей, нужно было щёлкать на счетах, перелистывать логарифмы, думать и писать, потом опять читать, щёлкать и думать; но едва я брался за книгу или начинал думать, как мысли мои путались, глаза жмурились, я со вздохом вставал из-за стола и начинал ходить по большим комнатам своего пустынного деревенского дома.
- (все
цитаты из русской классики)
Значение слова «логарифм»
-
ЛОГАРИ́ФМ, -а, м. Мат. Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов. (Малый академический словарь, МАС)
Все значения слова ЛОГАРИФМ
Смотрите также
ЛОГАРИ́ФМ, -а, м. Мат. Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов.
Все значения слова «логарифм»
-
Не так давно им учили в школах, чтобы использовать таблицы логарифмов.
-
Однако рано или поздно она всё-таки сменяется инструментальным подходом, когда в руку берётся арифмометр, отвес и линейка, а в голову вставляется десятичный логарифм с котангенсом.
-
В самом деле, возможно интерпретировать информацию, передаваемую в сообщении, как фактическое отрицание её энтропии и как отрицательный логарифм её вероятности.
- (все предложения)
- множитель
- спряжение
- слагаемое
- числительное
- единица
- (ещё синонимы…)
- математика
- степень
- функция
- предел
- пример
- (ещё ассоциации…)
- натуральный
- десятичный
- (ещё…)
- Склонение
существительного «логарифм» - Разбор по составу слова «логарифм»
Ответ:
Правильное написание слова — логарифм
Ударение и произношение — логар`ифм
Значение слова -В математике:|показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число
Пример:
Таблица логарифмов.
Выберите, на какой слог падает ударение в слове — ВЕРОИСПАВЕДАНИЕ?
или
Слово состоит из букв:
Л,
О,
Г,
А,
Р,
И,
Ф,
М,
Похожие слова:
антилогарифм
логарифмировавший
логарифмировавшийся
логарифмирование
логарифмированный
логарифмировать
логарифмирующий
логарифмирующийся
логарифмически
логарифмический
Толкование слова. Правильное произношение слова. Значение слова.
логарифм
- логарифм
- логари́фм
Русское словесное ударение. — М.: ЭНАС.
.
2001.
Смотреть что такое «логарифм» в других словарях:
-
ЛОГАРИФМ — (греч., от logos отношение, и arithmos число). Число арифметической прогрессии, соответствующее числу геометрической прогрессии. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЛОГАРИФМ греч., от logos, отношение,… … Словарь иностранных слов русского языка
-
ЛОГАРИФМ — данного числа N при основании а показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом, N = ay. Логарифмом обозначается обычно logaN. Логарифм с основанием е ? 2,718… называется натуральным и обозначается lnN.… … Большой Энциклопедический словарь
-
ЛОГАРИФМ — (от греческого logos отношение и arithmos число) числа N по основанию a (O … Современная энциклопедия
-
ЛОГАРИФМ — ЛОГАРИФМ, вспомогательный прием (формула) для произведения вычислений, выведенный в 1614 г. Джоном НЕПЕРОМ и разработанный впоследствии английским математиком Генри Бриггсом (1561 1631). Логарифмом числа ( ) является показатель степени (х), в… … Научно-технический энциклопедический словарь
-
Логарифм — (от греческого logos отношение и arithmos число) числа N по основанию a (O … Иллюстрированный энциклопедический словарь
-
ЛОГАРИФМ — (logarithm) Степень, в которую надо возвести какое либо служащее основанием число, большее 1, чтобы получить какое либо определенное положительное число. Если х является логарифмом с основанием у от z, то z=уx. Логарифмы имеют такое свойство, что … Экономический словарь
-
логарифм — а, м. ЛОГАРИТМ а, м. logarithme m. , нем. Logarithm, н. лат. Logarithmus <гр. logos отношение + arrithmos число. мат. Показатель степени, в которую нужно возвести какое н. определенное число, чтобы получить данное число. Этот курьез в моих… … Исторический словарь галлицизмов русского языка
-
ЛОГАРИФМ — ЛОГАРИФМ, логарифма, муж. (от греч. logos слово и arithmos число) (мат.). Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
-
ЛОГАРИФМ — ЛОГАРИФМ, а, муж. В математике: показатель степени, в к рую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов. | прил. логарифмический, ая, ое. Логарифмическая линейка (счётный инструмент). Толковый… … Толковый словарь Ожегова
-
ЛОГАРИФМ — муж., мат. Если под рядом чисел геометрической прогрессии (лествицы) выставить ряд отвечающих им чисел арифметической прогрессии, то каждое из последних будет логарифмом дружки своей, в первом порядке; сим способом умножение обращают в сложение,… … Толковый словарь Даля
-
логарифм — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN logarithm … Справочник технического переводчика
На чтение 1 мин.
Значение слова «Логарифм»
— показатель степени, в которую нужно возвести число, называемое основанием, чтобы получить данное число (в математике)
Содержание
- Транскрипция слова
- MFA Международная транскрипция
- Цветовая схема слова
Транскрипция слова
[лагар’и́фм]
MFA Международная транскрипция
[ɫəɡɐˈrʲifm]
| л | [л] | согласный, звонкий непарный (сонорный), твердый парный |
| о | [а] | гласный, безударный |
| г | [г] | согласный, звонкий парный, твердый парный |
| а | [а] | гласный, безударный |
| р | [р’] | согласный, звонкий непарный (сонорный), мягкий парный |
| и | [́и] | гласный, ударный |
| ф | [ф] | согласный, глухой парный, твердый парный |
| м | [м] | согласный, звонкий непарный (сонорный), твердый парный |
Букв: 8 Звуков: 8
Цветовая схема слова
логарифм
Как правильно пишется «Логарифм»
логари́фм
логари́фм, -а
Как правильно перенести «Логарифм»
ло—га—ри́фм
Часть речи
Часть речи слова «логарифм» — Имя существительное
Морфологические признаки.
логарифм (именительный падеж, единственного числа)
Постоянные признаки:
- нарицательное
- неодушевлённое
- мужской
- 2-e склонение
Непостоянные признаки:
- именительный падеж
- единственного числа
Может относится к разным членам предложения.
Склонение слова «Логарифм»
| Падеж | Единственное число | Множественное число |
|---|---|---|
| Именительный Кто? Что? |
логари́фм | логари́фмы |
| Родительный Кого? Чего? |
логари́фма | логари́фмов |
| Дательный Кому? Чему? |
логари́фму | логари́фмам |
| Винительный (неод.) Кого? Что? |
логари́фм | логари́фмы |
| Творительный Кем? Чем? |
логари́фмом | логари́фмами |
| Предложный О ком? О чём? |
логари́фме | логари́фмах |
Разбор по составу слова «Логарифм»
Состав слова «логарифм»:
корень — [логарифм], нулевое окончание — [ ]
Проверьте свои знания русского языка
Категория: Русский язык
Русский язык
Тест на тему “Русский алфавит”
1 / 5
Верны ли утверждения: 1.Русская азбука много раз реформировалась 2. Со временем из алфавита исчезло несколько букв.
Первое выказывание верно, а второе – нет.
Второе высказывание верно, а первое – нет.
Оба высказывания верны.
Оба высказывания ошибочны.
2 / 5
Надо ли учить алфавит по порядку?
Да, потому что по алфавиту расставлены книги в библиотеке.
Да, потому что слова в словаре расположены в алфавитном порядке
Да, потому что в энциклопедиях статьи даны по алфавиту
Верны все ответы
3 / 5
Выберите ошибочное утверждение
Есть много стишков и песенок для заучивания алфавита по порядку
Некоторые буквы алфавита обозначали звуки, которые ушли из языка, поэтому и буквы убрали в ходе реформы
Раньше писали без пробелов и знаков препинания
Все утверждения верные
4 / 5
Найдите правильное утверждение
Русский алфавит появился в связи с появлением государства, чтобы можно было записать законы
Алфавит призван отражать звуковой состав языка
В русском алфавите для обозначения одного звука может использоваться несколько букв
Все утверждения правильны
5 / 5
Верны ли утверждения: 1.В основу русского алфавита лег латинский. 2. Кирилл и Мефодий добавили букв, чтобы каждый звук обозначался своей буквой.
Первое выказывание верно, а второе – нет.
Второе высказывание верно, а первое – нет.
Оба высказывания верны.
Оба высказывания ошибочны.
Каким бывает «логарифм»;
Синонимы к слову «логарифм»
Ассоциации к слову «логарифм»
Предложения со словом «логарифм»
- Я знаю наизусть таблицу логарифмов, но совершенно не представляю себе, как пришить пуговицу, и не умею собирать землянику.
Кир Булычев, Гай-до, 1986
- Однако рано или поздно она всё-таки сменяется инструментальным подходом, когда в руку берётся арифмометр, отвес и линейка, а в голову вставляется десятичный логарифм с котангенсом.
Федор Березин, Создатель черного корабля, 2007
- Вот я, например, школу окончил более сорока лет назад, но мне ни разу в жизни не потребовалось знание, что такое синус или косинус или умение вычислять логарифм.
Георгий Суданов, Русский язык на пальцах, 2017
Происхождение слова «Логарифм»
Происходит от лат. logarithmus «логарифм», далее из др.-греч. λόγος «слово, речь, разум; мнение»; восходит к праиндоевр. *leg- «собирать» + ἀριθμός «количество, число», далее из праиндоевр. *re(i)- «рассуждение, счёт». Латинский термин был сконструирован в 1610-х шотландским ученым Джоном Непером (1550—1617).
ЛОГАРИФМ
Ударение в слове: логар`ифм
Ударение падает на букву: и
Безударные гласные в слове: логар`ифм
ЛОГАРИФМИКА →← ЛОГ
Смотреть что такое ЛОГАРИФМ в других словарях:
ЛОГАРИФМ
Л. данного числа n называется показатель степени, в которую нужно возвести некоторое другое данное число а, называемое основанием, чтобы получить n; та… смотреть
ЛОГАРИФМ
числа N по основанию а, показатель степени m, в которую следует возвести число а (основание Л.), чтобы получить N; обозначается logaN. Итак, m … смотреть
ЛОГАРИФМ
логарифм м. Показатель степени, в которую нужно возвести число, называемое основанием, чтобы получить данное число (в математике).
ЛОГАРИФМ
логарифм м. мат.of logarithms pl. таблица логарифмов — tables of logarithms pl.
ЛОГАРИФМ
Логарифм — Л. данного числа n называется показатель степени, в которую нужно возвести некоторое другое данное число а, называемое основанием, чтобы пол… смотреть
ЛОГАРИФМ
ЛОГАРИФМчисло, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление — вычитанием, возведение в степень — умножением и извлечение корней — делением.Общее описание. Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (102 = 100). Если n — заданное число, b — основание и l — логарифм, то bl = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений logb n = l и antilogb l = n.Основные свойства логарифмов:Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b и n — рациональные числа, то в редких случаях найдется такое рациональное число l, что bl = n. Однако можно определить иррациональное число l, например, такое, что 10l = 2; это иррациональное число l можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e, трансцендентному числу, приближенно равному 2,71828, называются натуральными логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e0,6931 = 2. См. также ЧИСЛО e.Пользование таблицами обычных логарифмов. Обычный логарифм числа — это показатель степени, в которую нужно возвести 10, чтобы получить данное число. Так как 100 = 1, 101 = 10 и 102 = 100, мы сразу получаем, что log1 = 0, log10 = 1, log100 = 2 и т.д. для возрастающих целых степеней 10. Аналогично, 10-1 = 0,1, 10-2 = 0,01 и, следовательно, log0,1 = -1, log0,01 = -2 и т.д. для всех целых отрицательных степеней 10. Обычные логарифмы остальных чисел заключены между логарифмами ближайших к ним целых степеней числа 10; log2 должен быть заключен между 0 и 1, log20 — между 1 и 2, а log0,2 — между ?1 и 0. Таким образом, логарифм состоит из двух частей, целого числа и десятичной дроби, заключенной между 0 и 1. Целочисленная часть называется характеристикой логарифма и определяется по самому числу, дробная часть называется мантиссой и может быть найдена из таблиц. Кроме того, log20 = log(2?10) = log2 + log10 = (log2) + 1. Логарифм числа 2 равен 0,3010, поэтому log20 = 0,3010 + 1 = 1,3010. Аналогично, log0,2 = log(2?10) = log2 — log10 = (log2) — 1 = 0,3010 — 1. Выполнив вычитание, мы получим log0,2 = — 0,6990. Однако удобнее представить log0,2 в виде 0,3010 — 1 или как 9,3010 — 10; можно сформулировать и общее правило: все числа, получающиеся из данного числа умножением на степень числа 10, имеют одинаковые мантиссы, равные мантиссе заданного числа. В большинстве таблиц приведены мантиссы чисел, лежащих в интервале от 1 до 10, поскольку мантиссы всех остальных чисел могут быть получены из приведенных в таблице.В большинстве таблиц логарифмы даются с четырьмя или пятью десятичными знаками, хотя существуют семизначные таблицы и таблицы с еще бльшим числом знаков. Научиться пользоваться такими таблицами легче всего на примерах. Чтобы найти log3,59, прежде всего заметим, что число 3,59 заключено между 100 и 101, поэтому его характеристика равна 0. Находим в таблице число 35 (слева) и движемся по строке до столбца, у которого сверху стоит число 9; на пересечении этого столбца и строки 35 стоит число 5551, поэтому log3,59 = 0,5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, необходимо прибегнуть к интерполяции. В некоторых таблицах интерполирование облегчается пропорциональными частями, приведенными в последних девяти столбцах в правой части каждой страницы таблиц. Найдем теперь log736,4; число 736,4 лежит между 102 и 103, поэтому характеристика его логарифма равна 2. В таблице находим строку, слева от которой стоит 73 и столбец 6. На пересечении этой строки и этого столбца стоит число 8669. Среди линейных частей находим столбец 4. На пересечении строки 73 и столбца 4 стоит число 2. Прибавив 2 к 8669, получим мантиссу — она равна 8671. Таким образом, log736,4 = 2,8671.Натуральные логарифмы. Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 — log54,32 = 6,2975 — 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 — log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10?54,32 = 102?5,432. Таким образом, по натуральному логарифму данного числа a можно найти натуральные логарифмы чисел, равные произведениям числа a на любые степени n числа 10, если к lna прибавлять ln10, умноженный на n, т.е. ln(a?10n) = lna + nln10 = lna + 2,3026n. Например, ln0,005432 = ln(5,432?10-3) = ln5,432 — 3ln10 = 1,6923 — (3?2,3026) = — 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x = lny, то y = ex, и y называется экспонентой от x (для удобства типографского набора часто пишут y = exp x). Экспонента играет роль антилогарифма числа x.С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e. Если logb a = x, то bx = a, и, следовательно, logc bx = logc a или xlogc b = logc a, или x = logc a/logc b = logb a. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c можно построить таблицы логарифмов по любому другому основанию b. Множитель 1/logc b называется модулем перехода от основания c к основанию b. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = loge 5,432/loge 10 = 1,6923/2,3026 = 1,6923?0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.Специальные таблицы. Первоначально логарифмы были изобретены для того, чтобы, пользуясь их свойствами logab = loga + logb и loga/b = loga — logb, превращать произведения в суммы, а частные в разности. Иначе говоря, если loga и logb известны, то с помощью сложения и вычитания мы легко можем найти логарифм произведения и частного. В астрономии, однако, часто по заданным значениям loga и logb требуется найти log(a + b) или log(a — b). Разумеется, можно было бы сначала по таблицам логарифмов найти a и b, затем выполнить указанное сложение или вычитание и, снова обратившись к таблицам, найти требуемые логарифмы, но такая процедура потребовала бы трехкратного обращения к таблицам. З.Леонелли в 1802 опубликовал таблицы т.н. гауссовых логарифмов — логарифмов сложения сумм и разностей — позволявшие ограничиться одним обращением к таблицам.В 1624 И.Кеплером были предложены таблицы пропорциональных логарифмов, т.е. логарифмов чисел a/x, где a — некоторая положительная постоянная величина. Эти таблицы используются преимущественно астрономами и навигаторами.Пропорциональные логарифмы при a = 1 называются кологарифмами и применяются в вычислениях, когда приходится иметь дело с произведениями и частными. Кологарифм числа n равен логарифму обратного числа; т.е. cologn = log1/n = — logn. Если log2 = 0,3010, то colog2 = — 0,3010 = 0,6990 — 1. Преимущество использования кологарифмов состоит в том, что при вычислении значения логарифма выражений вида pq/r тройная сумма положительных десятичных долей logp + logq + cologr находится легче, чем смешанная сумма и разность logp + logq — logr.История. Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287-212 до н.э.) воспользовался степенями числа 108 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М.Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.По-видимому, правила, аналогичные правилам Штифеля, привели Дж.Непера к формальному введению первой системы логарифмов в сочинении Описание удивительной таблицы логарифмов, опубликованном в 1614. Но мысли Непера были заняты проблемой превращения произведений в суммы еще с тех пор, как более чем за десять лет до выхода своего сочинения Непер получил из Дании известие о том, что в обсерватории Тихо Браге его ассистенты располагают методом, позволяющим превращать произведения в суммы. Метод, о котором говорилось в полученном Непером сообщении, был основан на использовании тригонометрических формул типапоэтому таблицы Непера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 — 10-7)?107, приближенно равное 1/e.Независимо от Непера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий. Это были таблицы антилогарифмов по основанию (1 + 10-4)?104, достаточно хорошему приближению числа e.В системе Непера логарифм числа 107 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г.Бриггс (1561-1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика (1620). Логарифмы по основанию e, хотя и не совсем те, которые были введены Непером, часто называют неперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом.Первые логарифмы в силу исторических причин использовали приближения к числам 1/e и e. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy = 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x и ординатами x = 1 и x = a (на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть неперовы логарифмы «гиперболическими логарифмами».Логарифмическая функция. Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы — в геометрической, представлен на рис. 2,а. График обратной, или показательной (экспоненциальной), функции y = ex, ординаты которого возрастают в геометрической прогрессии, а абсциссы — в арифметической, представлен, соответственно, на рис. 2,б. (Кривые y = logx и y = 10x по форме аналогичны кривым y = lnx и y = ex.) Были предложены также альтернативные определения логарифмической функции, например,Благодаря работам Эйлера стали известны соотношения между логарифмами и тригонометрическими функциями в комплексной плоскости. Исходя из тождества eix = cos x + i sin x (где угол x измеряется в радианах, ), Эйлер заключил, что каждое отличное от нуля действительное число имеет бесконечно много натуральных логарифмов; все они являются комплексными в случае отрицательных чисел и все, кроме одного, — в случае положительных чисел. Поскольку eix = 1 не только при x = 0, но и при x = ? 2k?, где k — любое положительное целое число, за натуральный логарифм числа 1 можно принять любое из чисел 0 ? 2k?i; и, аналогично, натуральные логарифмы числа ?1 являются комплексными числами вида (2k + 1)?i, где k — целое число. Аналогичные утверждения справедливы и относительно общих логарифмов или других систем логарифмов. Кроме того, определение логарифмов можно обобщить, пользуясь тождествами Эйлера так, чтобы оно включало комплексные логарифмы комплексных чисел.Альтернативное определение логарифмической функции дает функциональный анализ. Если f (x) — непрерывная функция действительного числа x, обладающая следующими тремя свойствами: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), то f (x) определяется как логарифм числа x по основанию b. Это определение обладает рядом преимуществ перед определением, приведенным в начале этой статьи.Приложения. Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных. Вычисление произведений, частных, степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов, но и благодаря использованию т.н. логарифмической линейки — вычислительного инструмента, принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами, т.е. расстояние от числа 1 до любого числа x выбрано равным log x; сдвигая одну шкалу относительно другой, можно откладывать суммы или разности логарифмов, что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков (бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y = kxn, то ее логарифмический график имеет вид прямой, т.к. log y = log k + n log x — уравнение, линейное относительно log y и log x. Наоборот, если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой, то эта зависимость — степенная. Полулогарифмическая бумага (у которой ось ординат имеет логарифмическую шкалу, а ось абсцисс — равномерную шкалу) удобна в тех случаях, когда требуется идентифицировать экспоненциальные функции. Уравнения вида y = kbrx возникают всякий раз, когда некая величина, такая как численность населения, количество радиоактивного материала или банковский баланс, убывает или возрастает со скоростью, пропорциональной имеющемуся в данный момент количеству жителей, радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу, то график будет иметь вид прямой.Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой, известной под названием логарифмической спирали, потому что в полярной системе координат ее уравнение имеет вид r = aeb?, или lnr = lna + b?. Такую кривую описывает движущаяся точка, расстояние от полюса которой растет в геометрической прогрессии, а угол, описываемый ее радиусом-вектором — в арифметической. Повсеместность такой кривой, а следовательно и логарифмической функции, хорошо иллюстрируется тем, что она возникает в столь далеких и совершенно различных областях, как контур кулачка-эксцентрика и траектория некоторых насекомых, летящих на свет…. смотреть
ЛОГАРИФМ
ЛОГАРИФМ(греч., от logos — отношение, и arithmos — число). Число арифметической прогрессии, соответствующее числу геометрической прогрессии.Словарь ино… смотреть
ЛОГАРИФМ
числа Nпо основанию а — показатель степени т, в к-рую следует возвести число «(основание Л.), чтобы получить N;обозначается logaN, т. е. m=logaN, ес… смотреть
ЛОГАРИФМ
log, logarithm* * *логари́фм м.logarithmнаходи́ть логари́фм числа́ — take the logarithm of a numberпереходи́ть к логари́фмам — pass to logarithms …ло… смотреть
ЛОГАРИФМ
ЛОГАРИ́ФМ, а, ч., мат.Показник степеня, до якого потрібно піднести число-основу, щоб одержати дане число.Для визначення питомої швидкості росту культур… смотреть
ЛОГАРИФМ
ЛОГАРИФМ
(logarithm) Степень, в которую надо возвести какое-либо служащее основанием число, большее 1, чтобы получить какое-либо определенное положи… смотреть
ЛОГАРИФМ
ЛОГАРИФМ а, м. ЛОГАРИТМ а, м. logarithme m. , нем. Logarithm, н.-лат. Logarithmus <гр. logos отношение + arrithmos число. мат. Показатель степени, … смотреть
ЛОГАРИФМ
[от греч. logos — слово, здесь — (соотношение и arithmos число] числа N по основанию а — показатель степени т, в к-рую следует возвести а, чтобы получи… смотреть
ЛОГАРИФМ
ЛОГАРИФМ (от греческого logos — отношение и arithmos — число) числа N по основанию a (Oчисло a, чтобы получить N, то есть ay=N. Обозначается logaN. Логарифм с основанием e=2,71… называется натуральным и обозначается lnN, логарифм с основанием 10 — десятичным и обозначается lg N. Дробная часть десятичного логарифма называется мантиссой, а целая его часть — характеристикой. Нахождение логарифма называется логарифмированием, а нахождение числа по данному его логарифма — потенцированием. Свойства логарифма позволяют сводить умножение и деление чисел к сложению и вычитанию их логарифмов(и использовать при этом простые механические устройства, например так называемую логарифмическую линейку). Открытие логарифма было связано в первую очередь с быстрым развитием астрономии в 16 в. Первые таблицы логарифмов составлены шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги в начале 17 в.<br>… смотреть
ЛОГАРИФМ
ЛОГАРИФМ, вспомогательный прием (формула) для произведения вычислений, выведенный в 1614 г. Джоном НЕПЕРОМ и разработанный впоследствии английским мате… смотреть
ЛОГАРИФМ
(от греческого logos — отношение и arithmos — число) числа N по основанию a (Oy=N. Обозначается logaN. Логарифм с основанием e=2,71… называется натур… смотреть
ЛОГАРИФМ
данного числа N при основании а, показатель степени у, в к-pyio нужно возвести число а, чтобы получить N; т. о. N = ау. Л. обозначается обычно logа N. … смотреть
ЛОГАРИФМ
ЛОГАРИФМ данного числа N при основании а, показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом, N = ay. Логарифмом обозначается обычно logaN. Логарифм с основанием е ? 2, 718… называется натуральным и обозначается lnN. Логарифм с основанием 10 называется десятичным и обозначается lgN. Равенство у ? logax определяет логарифмическую функцию. Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления. Логарифмы открыты шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги в нач. 17 в. Термин «логарифм» возник из сочетания греческих слов logos — отношение, соотношение и arithmos — число.<br><br><br>… смотреть
ЛОГАРИФМ
ЛОГАРИФМ данного числа N при основании а — показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом, N = ay. Логарифмом обозначается обычно logaN. Логарифм с основанием е ? 2,718… называется натуральным и обозначается lnN. Логарифм с основанием 10 называется десятичным и обозначается lgN. Равенство у ? logax определяет логарифмическую функцию. Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления. Логарифмы открыты шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги в нач. 17 в. Термин «логарифм» возник из сочетания греческих слов logos — отношение, соотношение и arithmos — число.<br>… смотреть
ЛОГАРИФМ
1) Орфографическая запись слова: логарифм2) Ударение в слове: логар`ифм3) Деление слова на слоги (перенос слова): логарифм4) Фонетическая транскрипция … смотреть
ЛОГАРИФМ
— данного числа N при основании а — показатель степени у, в которуюнужно возвести число а, чтобы получить N; таким образом, N = ay.Логарифмом обозначается обычно logaN. Логарифм с основанием е ? 2,718…называется натуральным и обозначается lnN. Логарифм с основанием 10называется десятичным и обозначается lgN. Равенство у ? logax определяетлогарифмическую функцию. Основные свойства логарифма позволяют заменитьумножение, деление, возведение в степень и извлечение корня более простымидействиями сложения, вычитания, умножения и деления. Логарифмы открытышотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги внач. 17 в. Термин «»логарифм»» возник из сочетания греческих слов logos -отношение, соотношение и arithmos — число…. смотреть
ЛОГАРИФМ
LOGARITHM
Математическая система большой практической полезности, позволяющая избежать длительных вычислений. Л. определяется как показатель степени, необходимой для увеличения заданного числа до необходимой величины. Л. 100 является 2, потому что 10, возведенное во 2-ю степень 102, равно 100. Логарифмы чисел от 1 до 10 — десятые доли единицы, логарифмы чисел от 10 до 100 — единицы с десятыми, от 100 до 1000 — 2 с десятыми и т. д. Благодаря таблице Л. можно точно рассчитать доход к сроку выплаты по облигациям ЛОЖНАЯ ЗАПИСЬ (FALSE ENTRY). См. ПРЕСТУПЛЕНИЕ; ПРЕСТУПЛЕНИЯ УГОЛОВНЫЕ…. смотреть
ЛОГАРИФМ
LOGARITHM
Математическая система большой практической полезности, позволяющая избежать длительных вычислений. Л. определяется как показатель степени, необходимой для увеличения заданного числа до необходимой величины. Л. 100 является 2, потому что 10, возведенное во 2-ю степень 102, равно 100. Логарифмы чисел от 1 до 10 десятые доли единицы, логарифмы чисел от 10 до 100 единицы с десятыми, от 100 до 1000 2 с десятыми и т. д. Благодаря таблице Л. можно точно рассчитать доход к сроку выплаты по облигациям ЛОЖНАЯ ЗАПИСЬ (FALSE ENTRY). См. ПРЕСТУПЛЕНИЕ; ПРЕСТУПЛЕНИЯ УГОЛОВНЫЕ…. смотреть
ЛОГАРИФМ
Греческое – logos (соотношение, соответствие), arithmos (число).Первоисточником является греческий язык. В 1614 г. шотландский математик Непер создал т… смотреть
ЛОГАРИФМ
Фирма Фира Фима Фил Фигаро Фига Фиал Фарм Фал Фаг Ром Рол Рог Рифма Риф Рио Рим Рига Риал Риа Раф Рао Рамоли Рами Рам Рало Орига Орг Омар Олифа Олим Морф Моргал Морг Мор Моир Могила Могар Миф Миро Мир Миограф Мио Мило Мила Миг Мгла Мга Марго Маори Мао Мало Мали Маго Маг Лори Лор Лом Логарифм Лог Лифо Лиф Лира Лимфа Лима Лиго Лига Ларго Лаг Ирма Флаг Ирга Иол Флор Имаго Фол Фома Игра Фора Иго Игла Форма Громила Гром Гриф Грим Граф Гофр Фра Фрг Гори Голиаф Гол Фри Гиф Гирло Гаф Арифм Амил Аир Аил Агро Агор Фрол Арго Гало Гам Гифа Глиома Глиф Гор Горал… смотреть
ЛОГАРИФМ
Показатель степени, в которую число (называемое основанием) должно быть возведено для того, чтобы равняться данному числу. Следовательно, log101000 = 3, так как основание (10) должно быть возведено в 3-ю степень, чтобы в результате получилась 1000. Наиболее распространенными основаниями логарифма являются 2 (см. информация), 10 (большинство арифметических вычислений, используемых в психологии) и е (естественная логарифмическая система в математике, в которой логарифмический обозначается как ln)…. смотреть
ЛОГАРИФМ
1) log2) logarithm– гиперболический логарифм– двойной логарифм– двойчный логарифм– десятичный логарифм– интегральный логарифм– логарифм гиперболический… смотреть
ЛОГАРИФМ
ЛОГАРИФМ м. математ. Если под рядом чисел геометрической прогрессии (лествицы) выставить ряд отвечающих им чисел арифметической прогрессии, то каждое из последних будет логарифмом дружки своей, в первом порядке; сим способом умножение обращают в сложение, деление в вычитанье, что и облегчает выкладки. Логарифмический, к логарифмам относящ. Логарифмика ж. кривая линия, в коей ординаты отвечают логарифмам абсцисс; логистика. <br><br><br>… смотреть
ЛОГАРИФМ
логарифм [гр. logos отношение + arithmos число] — мат. показатель степени, в которую нужно возвести какое-л. определенное число, называемое основанием логарифма, чтобы получить данное число; обозначается log; логарифмы десятичные — логарифмы, имеющие основание 10, обозначаются lg, напр., lg 100 есть 2; логарифмы натуральные — логарифмы, имеющие основание е = — 2,71828…, обозначаются in. <br><br><br>… смотреть
ЛОГАРИФМ
м. logaritmo m — гауссов логарифм- гиперболический логарифм- двоичный логарифм- десятичный логарифм- интегральный логарифм- натуральный логарифм- непе… смотреть
ЛОГАРИФМ
корень — ЛОГАРИФМ; нулевое окончание;Основа слова: ЛОГАРИФМВычисленный способ образования слова: Бессуфиксальный или другой∩ — ЛОГАРИФМ; ⏰Слово Логариф… смотреть
ЛОГАРИФМ
Показник x степені, до якої необхідно піднести основу a, щоб отримати число b; запис x = logab, що рівнозначне запису ax = b (при умовах a, b>0, a ≠ 1)… смотреть
ЛОГАРИФМ
logaritma* * *
м, мат.
logaritmaтабли́ца логари́фмов — logaritma tablosu
ЛОГАРИФМ
-а, м. мат.
Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.Таблица логарифмов.[От греч. λόγος … смотреть
ЛОГАРИФМ
показник x степені, до якої необхідно піднести основу a, щоб отримати число b; запис x = logab, що рівнозначне запису ax = b (при умовах a, b>0, a ≠ 1)… смотреть
ЛОГАРИФМ
м. мат. logarithme m таблица логарифмов — table f des logarithmes
ЛОГАРИФМ
логарифм логари́фмначиная с Петра I; см. Смирнов 180. Вероятно, из франц. logarithme «логарифм» от лат. logarithmus (слово создано шотландским математи… смотреть
ЛОГАРИФМ
Rzeczownik логарифм m Matematyczny logarytm m
ЛОГАРИФМ
(греч. logos отношение, arithmos число) показатель степени, в которую число, называемое основанием, нужно возвести, чтобы получить искомое число. Например, Log 10 (основание) числа 1000 равен 3. То есть 10 в третьей степени равно 1000. Чаще используется основания 2 и 10…. смотреть
ЛОГАРИФМ
Логари́фм. Заимств. в XVIII в. из франц. яз., где logarithme < англ. logarithmus, неологизма шотландского математика Д. Непера. Слово образовано сложен… смотреть
ЛОГАРИФМ
м. мат.logarithme mтаблица логарифмов — table f des logarithmes
ЛОГАРИФМ
Заимств. в XVIII в. из франц. яз., где logarithme < англ. logarithmus, неологизма шотландского математика Д. Непера. Слово образовано сложением греч… смотреть
ЛОГАРИФМ
логарифм = м. мат. logarithm; таблица логарифмов table of logarithms; логарифмировать несов. find the logarithm; логарифмический мат. logarithmic; логарифмическая линейка slide-rule; логарифмическое уравнение logarithmic equation. <br><br><br>… смотреть
ЛОГАРИФМ
логарифм, логар′ифм, -а, м. В математике: показатель степени, в к-рую надо возвести число, называемое основанием, чтобы получить данное число. Таблица ~ов.<br>прил. ~ический, -ая, -ое. Логарифмическая линейка (счётный инструмент).<br><br><br>… смотреть
ЛОГАРИФМ
ЛОГАРИФМ, -а, м. В математике: показатель степени, в к-рую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов. || прилагательное логарифмический, -ая, -ое. Логарифмическая линейка (счётный инструмент)…. смотреть
ЛОГАРИФМ
м. мат.logaritmo mтаблицы логарифмов — tablas de logaritmos
ЛОГАРИФМ
-а, ч., мат. Показник степеня, до якого потрібно піднести число-основу, щоб одержати дане число.
ЛОГАРИФМ
начиная с Петра I; см. Смирнов 180. Вероятно, из франц. logarithme «логарифм» от лат. logarithmus (слово создано шотландским математиком Джоном Нэпиром в 1614 г.; см. Шульц–Баслер 2, 38) из греч. и , первонач. «относительное число»…. смотреть
ЛОГАРИФМ
м мат.Logarithmus m sg неизм., pl -men
ЛОГАРИФМ
логари́фм,
логари́фмы,
логари́фма,
логари́фмов,
логари́фму,
логари́фмам,
логари́фм,
логари́фмы,
логари́фмом,
логари́фмами,
логари́фме,
логари́фмах
(Источник: «Полная акцентуированная парадигма по А. А. Зализняку»)
…. смотреть
ЛОГАРИФМ
м мат
logaritmo m- таблица логарифмов
ЛОГАРИФМ
мат. логарифм; логарифмы бындур основание логарифма; логарифмы характеристикае характеристика логарифма; логарифмтае хынцын логарифмирование, нахождение логарифмов; логарифм агурын логарифмировать, находить логарифм…. смотреть
ЛОГАРИФМ
мат.logarithmтаблиця логарифмів — table of logarithms, logarithmic chart, logarithmic scales
ЛОГАРИФМ
Этот математический термин был заимствован из французского, где logarithme восходит к научной латыни: слово logarithmus было образовано искусственно из греческого legos («отношение») и arithmos – «число»…. смотреть
ЛОГАРИФМ
м.logarithm- гибридный логарифм- десятичный логарифм- интегральный логарифм- натуральный логарифм
ЛОГАРИФМ
м мат.对数 duìshùтаблица логарифмов — 对数表
ЛОГАРИФМ
ЛОГАРИФМ логарифма, м. (от греч. logos — слово и arithmos — число) (мат.). Показатель степени, в к-рую надо возвести число, называемое основанием, чтобы получить данное число.<br><br><br>… смотреть
ЛОГАРИФМ
матем.
логари́фм
— гиперболический логарифм
— двоичный логарифм
— десятичный логарифм
— интегральный логарифм
— натуральный логарифм
— неперов логарифм
— обыкновенный логарифм
… смотреть
ЛОГАРИФМ
логарифмלוֹגָרִיתם ז’* * *יומןלוגריתם
ЛОГАРИФМ
(2 м); мн. логари/фмы, Р. логари/фмов
ЛОГАРИФМ
Логари́фмkipeozio (vi-), logi (-);натура́льный логари́фм — kipeozio kawaida (vi-)
ЛОГАРИФМ
логари́фм
(лат. logarithmus, від грец. λόγος, тут – відношення і αριθμός – число)
показник степеня, до якого треба піднести число а, щоб одержати число N…. смотреть
ЛОГАРИФМ
логарифм; ч.
(лат., гр., тут — відношення і число)
показник степеня, до якого потрібно піднести число-основу, щоб одержати дане число; логаритм.
ЛОГАРИФМ
логари’фм, логари’фмы, логари’фма, логари’фмов, логари’фму, логари’фмам, логари’фм, логари’фмы, логари’фмом, логари’фмами, логари’фме, логари’фмах
ЛОГАРИФМ
мат. показатель степени, в которую надо возвести основание логарифма, чтобы получить нужное число.
ЛОГАРИФМ
-а, ч. , мат. Показник степеня, до якого потрібно піднести число-основу, щоб одержати дане число.
ЛОГАРИФМ
Логарифм- logarithmus;• логарифмическая таблица — canon Logarithmorum;
ЛОГАРИФМ
Начальная форма — Логарифм, винительный падеж, единственное число, мужской род, неодушевленное
ЛОГАРИФМ
М riyaz. loqarifm (verilən bir ədədi almaq üçün kökün vurulacağı üst, dərəcə).
ЛОГАРИФМ
логарифмм мат ὁ λογάριθμος:
таблица ~ов ὁ λογαριθμικός πίνακας {-αξ}.
ЛОГАРИФМ
м. мат.
логарифм;
таблица логарифмов логарифмилер таблицасы.
ЛОГАРИФМ
логарифм м мат. Logarithmus m, sg неизм., pl -men
ЛОГАРИФМ
м.
logaritmo
Итальяно-русский словарь.2003.
ЛОГАРИФМ
логари́фм
іменник чоловічого роду
ЛОГАРИФМ
мат. логарифм (дәреже көрсеткіш)
м.
Показатель степени, в которую нужно возвести число, называемое основанием, чтобы получить данное число (в математике).
ЛОГАРИ́ФМ, логарифма, муж. (от греч. logos — слово и arithmos — число) (мат.). Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.
ЛОГАРИ́ФМ, -а, муж. В математике: показатель степени, в к-рую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов.
| прил. логарифмический, -ая, -ое. Логарифмическая линейка (счётный инструмент).
ЛОГАРИФМ — муж., мат. Если под рядом чисел геометрической прогрессии (лествицы) выставить ряд отвечающих им чисел арифметической прогрессии, то каждое из последних будет логарифмом дружки своей, в первом порядке; сим способом умножение обращают в сложение, деление в вычитанье, что и облегчает выкладки. Логарифмический, к логарифмам относящийся. Логарифмика жен. кривая линия, в коей ординаты отвечают логарифмам абсцисс; логистика.
ЛОГАРИ́ФМ -а; м. [от греч. logos — отношение и arithmos — число] Матем. Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число. Таблица логарифмов. Л. числа 25.
◁ Логарифми́ческий, -ая, -ое. Матем. Л-ая таблица. Л-ие вычисления.
◊ Логарифми́ческая линейка. Инструмент для выполнения разнообразных несложных вычислений; счётная линейка.
* * *
логари́фм — данного числа N при основании a, показатель степени y, в которую нужно возвести число a, чтобы получить N; таким образом N = ay. Логарифм обозначается обычно loga N. Логарифм с основанием e = 2,718… называется натуральным и обозначается ln N. Логарифм с основанием 10 называется десятичным и обозначается lg N. Равенство y = loga x определяет логарифмическую функцию. Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления. Логарифмы открыты шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги (J. Bürgi) в начале XVII в. Термин «Логарифм» возник из сочетания греческих слов lógos — отношение, соотношение и arithmós — число.
* * *
ЛОГАРИФМ — ЛОГАРИ́ФМ данного числа N при основании а, показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом, N = ay. Логарифмом обозначается обычно logaN. Логарифм с основанием е = 2,718… называется натуральным и обозначается lnN. Логарифм с основанием 10 называется десятичным и обозначается lgN. Равенство у = logax определяет логарифмическую функцию. Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления. Логарифмы открыты шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги в нач. 17 в. Термин «логарифм» возник из сочетания греческих слов logos — отношение, соотношение и arithmos — число.
ЛОГАРИФМ данного числа N при основании а — показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом, N = ay. Логарифмом обозначается обычно logaN. Логарифм с основанием е ? 2,718… называется натуральным и обозначается lnN. Логарифм с основанием 10 называется десятичным и обозначается lgN. Равенство у ? logax определяет логарифмическую функцию. Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления. Логарифмы открыты шотландским математиком Дж. Непером и швейцарским математиком Й. Бюрги в нач. 17 в. Термин «логарифм» возник из сочетания греческих слов logos — отношение, соотношение и arithmos — число.
-а, м. мат.
Показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.
Таблица логарифмов.
[От греч. λόγος — отношение и ’αρηθμός — число]
ЛОГАРИФМ — число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление — вычитанием, возведение в степень — умножением и извлечение корней — делением. Общее описание. Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (102 = 100). Если n — заданное число, b — основание и l — логарифм, то bl = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений logb n = l и antilogb l = n. Основные свойства логарифмов:
Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b и n — рациональные числа, то в редких случаях найдется такое рациональное число l, что bl = n. Однако можно определить иррациональное число l, например, такое, что 10l = 2; это иррациональное число l можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e, трансцендентному числу, приближенно равному 2,71828, называются натуральными логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e0,6931 = 2.
См. также ЧИСЛО e. Пользование таблицами обычных логарифмов. Обычный логарифм числа — это показатель степени, в которую нужно возвести 10, чтобы получить данное число. Так как 100 = 1, 101 = 10 и 102 = 100, мы сразу получаем, что log1 = 0, log10 = 1, log100 = 2 и т.д. для возрастающих целых степеней 10. Аналогично, 10-1 = 0,1, 10-2 = 0,01 и, следовательно, log0,1 = -1, log0,01 = -2 и т.д. для всех целых отрицательных степеней 10. Обычные логарифмы остальных чисел заключены между логарифмами ближайших к ним целых степеней числа 10; log2 должен быть заключен между 0 и 1, log20 — между 1 и 2, а log0,2 — между -1 и 0. Таким образом, логарифм состоит из двух частей, целого числа и десятичной дроби, заключенной между 0 и 1. Целочисленная часть называется характеристикой логарифма и определяется по самому числу, дробная часть называется мантиссой и может быть найдена из таблиц. Кроме того, log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Логарифм числа 2 равен 0,3010, поэтому log20 = 0,3010 + 1 = 1,3010. Аналогично, log0,2 = log(2е10) = log2 — log10 = (log2) — 1 = 0,3010 — 1. Выполнив вычитание, мы получим log0,2 = — 0,6990. Однако удобнее представить log0,2 в виде 0,3010 — 1 или как 9,3010 — 10; можно сформулировать и общее правило: все числа, получающиеся из данного числа умножением на степень числа 10, имеют одинаковые мантиссы, равные мантиссе заданного числа. В большинстве таблиц приведены мантиссы чисел, лежащих в интервале от 1 до 10, поскольку мантиссы всех остальных чисел могут быть получены из приведенных в таблице. В большинстве таблиц логарифмы даются с четырьмя или пятью десятичными знаками, хотя существуют семизначные таблицы и таблицы с еще большим числом знаков. Научиться пользоваться такими таблицами легче всего на примерах. Чтобы найти log3,59, прежде всего заметим, что число 3,59 заключено между 100 и 101, поэтому его характеристика равна 0. Находим в таблице число 35 (слева) и движемся по строке до столбца, у которого сверху стоит число 9; на пересечении этого столбца и строки 35 стоит число 5551, поэтому log3,59 = 0,5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, необходимо прибегнуть к интерполяции. В некоторых таблицах интерполирование облегчается пропорциональными частями, приведенными в последних девяти столбцах в правой части каждой страницы таблиц. Найдем теперь log736,4; число 736,4 лежит между 102 и 103, поэтому характеристика его логарифма равна 2. В таблице находим строку, слева от которой стоит 73 и столбец 6. На пересечении этой строки и этого столбца стоит число 8669. Среди линейных частей находим столбец 4. На пересечении строки 73 и столбца 4 стоит число 2. Прибавив 2 к 8669, получим мантиссу — она равна 8671. Таким образом, log736,4 = 2,8671.
Натуральные логарифмы. Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 — log54,32 = 6,2975 — 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 — log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10*54,32 = 102*5,432. Таким образом, по натуральному логарифму данного числа a можно найти натуральные логарифмы чисел, равные произведениям числа a на любые степени n числа 10, если к lna прибавлять ln10, умноженный на n, т.е. ln(a*10n) = lna + nln10 = lna + 2,3026n. Например, ln0,005432 = ln(5,432*10-3) = ln5,432 — 3ln10 = 1,6923 — (3*2,3026) = — 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x = lny, то y = ex, и y называется экспонентой от x (для удобства типографского набора часто пишут y = exp x). Экспонента играет роль антилогарифма числа x. С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e. Если logb a = x, то bx = a, и, следовательно, logc bx = logc a или xlogc b = logc a, или x = logc a/logc b = logb a. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c можно построить таблицы логарифмов по любому другому основанию b. Множитель 1/logc b называется модулем перехода от основания c к основанию b. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = loge 5,432/loge 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.
Специальные таблицы. Первоначально логарифмы были изобретены для того, чтобы, пользуясь их свойствами logab = loga + logb и loga/b = loga — logb, превращать произведения в суммы, а частные в разности. Иначе говоря, если loga и logb известны, то с помощью сложения и вычитания мы легко можем найти логарифм произведения и частного. В астрономии, однако, часто по заданным значениям loga и logb требуется найти log(a + b) или log(a — b). Разумеется, можно было бы сначала по таблицам логарифмов найти a и b, затем выполнить указанное сложение или вычитание и, снова обратившись к таблицам, найти требуемые логарифмы, но такая процедура потребовала бы трехкратного обращения к таблицам. З.Леонелли в 1802 опубликовал таблицы т. н. гауссовых логарифмов — логарифмов сложения сумм и разностей — позволявшие ограничиться одним обращением к таблицам. В 1624 И. Кеплером были предложены таблицы пропорциональных логарифмов, т.е. логарифмов чисел a/x, где a — некоторая положительная постоянная величина. Эти таблицы используются преимущественно астрономами и навигаторами. Пропорциональные логарифмы при a = 1 называются кологарифмами и применяются в вычислениях, когда приходится иметь дело с произведениями и частными. Кологарифм числа n равен логарифму обратного числа; т.е. cologn = log1/n = — logn. Если log2 = 0,3010, то colog2 = — 0,3010 = 0,6990 — 1. Преимущество использования кологарифмов состоит в том, что при вычислении значения логарифма выражений вида pq/r тройная сумма положительных десятичных долей logp + logq + cologr находится легче, чем смешанная сумма и разность logp + logq — logr.
История. Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н. э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287-212 до н.э.) воспользовался степенями числа 108 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М. Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:
Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке. По-видимому, правила, аналогичные правилам Штифеля, привели Дж. Непера к формальному введению первой системы логарифмов в сочинении Описание удивительной таблицы логарифмов, опубликованном в 1614. Но мысли Непера были заняты проблемой превращения произведений в суммы еще с тех пор, как более чем за десять лет до выхода своего сочинения Непер получил из Дании известие о том, что в обсерватории Тихо Браге его ассистенты располагают методом, позволяющим превращать произведения в суммы. Метод, о котором говорилось в полученном Непером сообщении, был основан на использовании тригонометрических формул типа
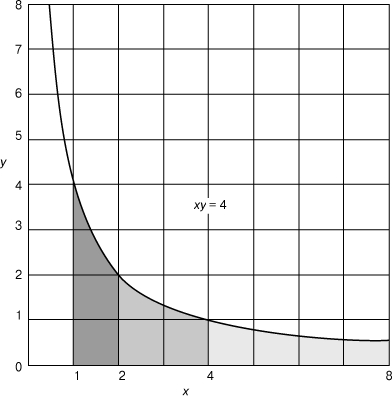
поэтому таблицы Непера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 — 10-7)ґ107, приближенно равное 1/e. Независимо от Непера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий. Это были таблицы антилогарифмов по основанию (1 + 10-4)*10 4, достаточно хорошему приближению числа e. В системе Непера логарифм числа 107 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г. Бриггс (1561-1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика (1620). Логарифмы по основанию e, хотя и не совсем те, которые были введены Непером, часто называют неперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом. Первые логарифмы в силу исторических причин использовали приближения к числам 1/e и e. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy = 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x и ординатами x = 1 и x = a (на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть неперовы логарифмы «гиперболическими логарифмами».
Рис. 1. ГРАФИК ВЕТВИ ГИПЕРБОЛЫ xy = 4. Площади под гиперболой на отрезках от x =1 до x = 2, от x = 2 до x = 4 и от x = 4 до x = 8 равны; общая площадь заштрихованной фигуры возрастает в арифметической прогрессии (1, 2, 3, 4), тогда как длина отрезков на оси x возрастает в геометрической прогрессии (1, 2, 4, 8).
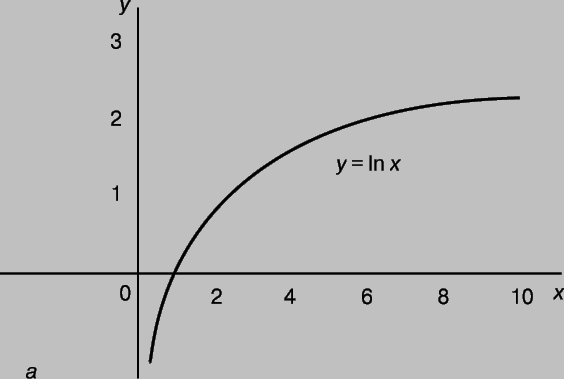
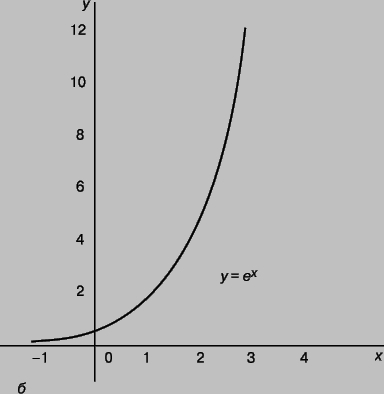
Логарифмическая функция. Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы — в геометрической, представлен на рис. 2,а. График обратной, или показательной (экспоненциальной), функции y = ex, ординаты которого возрастают в геометрической прогрессии, а абсциссы — в арифметической, представлен, соответственно, на рис. 2,б. (Кривые y = logx и y = 10x по форме аналогичны кривым y = lnx и y = ex.) Были предложены также альтернативные определения логарифмической функции, например,
Рис. 2,а. ЛОГАРИФМИЧЕСКАЯ И ЭКСПОНЕНЦИАЛЬНАЯ КРИВЫЕ. а — Логарифмическая кривая y = lnx. Ординаты возрастают в арифметической прогрессии, абсциссы — в геометрической прогрессии.
Рис. 2,б. ЛОГАРИФМИЧЕСКАЯ И ЭКСПОНЕНЦИАЛЬНАЯ КРИВЫЕ. б — Экспоненциальная кривая y = ex. Ординаты возрастают в геометрической прогрессии, абсциссы — в арифметической прогрессии.
Благодаря работам Эйлера стали известны соотношения между логарифмами и тригонометрическими функциями в комплексной плоскости. Исходя из тождества eix = cos x + i sin x (где угол x измеряется в радианах, ), Эйлер заключил, что каждое отличное от нуля действительное число имеет бесконечно много натуральных логарифмов; все они являются комплексными в случае отрицательных чисел и все, кроме одного, — в случае положительных чисел. Поскольку eix = 1 не только при x = 0, но и при x = ± 2kp, где k — любое положительное целое число, за натуральный логарифм числа 1 можно принять любое из чисел 0 ± 2kpi; и, аналогично, натуральные логарифмы числа -1 являются комплексными числами вида (2k + 1)pi, где k — целое число. Аналогичные утверждения справедливы и относительно общих логарифмов или других систем логарифмов. Кроме того, определение логарифмов можно обобщить, пользуясь тождествами Эйлера так, чтобы оно включало комплексные логарифмы комплексных чисел. Альтернативное определение логарифмической функции дает функциональный анализ. Если f (x) — непрерывная функция действительного числа x, обладающая следующими тремя свойствами: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), то f (x) определяется как логарифм числа x по основанию b. Это определение обладает рядом преимуществ перед определением, приведенным в начале этой статьи.
Приложения. Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных. Вычисление произведений, частных, степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов, но и благодаря использованию т.н. логарифмической линейки — вычислительного инструмента, принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами, т.е. расстояние от числа 1 до любого числа x выбрано равным log x; сдвигая одну шкалу относительно другой, можно откладывать суммы или разности логарифмов, что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков (бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y = kxn, то ее логарифмический график имеет вид прямой, т.к. log y = log k + n log x — уравнение, линейное относительно log y и log x. Наоборот, если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой, то эта зависимость — степенная. Полулогарифмическая бумага (у которой ось ординат имеет логарифмическую шкалу, а ось абсцисс — равномерную шкалу) удобна в тех случаях, когда требуется идентифицировать экспоненциальные функции. Уравнения вида y = kbrx возникают всякий раз, когда некая величина, такая как численность населения, количество радиоактивного материала или банковский баланс, убывает или возрастает со скоростью, пропорциональной имеющемуся в данный момент количеству жителей, радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу, то график будет иметь вид прямой. Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой, известной под названием логарифмической спирали, потому что в полярной системе координат ее уравнение имеет вид r = aebq, или lnr = lna + bq. Такую кривую описывает движущаяся точка, расстояние от полюса которой растет в геометрической прогрессии, а угол, описываемый ее радиусом-вектором — в арифметической. Повсеместность такой кривой, а следовательно и логарифмической функции, хорошо иллюстрируется тем, что она возникает в столь далеких и совершенно различных областях, как контур кулачка-эксцентрика и траектория некоторых насекомых, летящих на свет.
ЛОГАРИФМ (от греческого logos — отношение и arithmos — число) числа N по основанию a (O
мат. показатель степени, в которую надо возвести основание логарифма, чтобы получить нужное число.
логари́фм, логари́фмы, логари́фма, логари́фмов, логари́фму, логари́фмам, логари́фмом, логари́фмами, логари́фме, логари́фмах
Этот математический термин был заимствован из французского, где logarithme восходит к научной латыни: слово logarithmus было образовано искусственно из греческого legos («отношение») и arithmos — «число».
Греческое — logos (соотношение, соответствие), arithmos (число).
Первоисточником является греческий язык. В 1614 г. шотландский математик Непер создал термин logaritmus. В XVIII в. в связи с развитием точных наук произошло заимствование, и термин появился в русском языке.
В современном русском языке слово имеет следующее значение: «показатель степени, в которую следует возвести число».
Производные: логарифмический, логарифмировать.
Из фр. яз. в XVIII в. Фр. logarithme, в свою очередь, усвоено из ученой латыни, где logarithmus является неологизмом шотландского математика Непера на базе греч. logos в знач. «отношение» и arithmos — «число».
Заимств. в XVIII в. из франц. яз., где logarithme < англ. logarithmus, неологизма шотландского математика Д. Непера. Слово образовано сложением греч. logos в значении «отношение» и arithmos «число».
логари́фм
начиная с Петра I; см. Смирнов 180. Вероятно, из франц. logarithme «логарифм» от лат. logarithmus (слово создано шотландским математиком Джоном Нэпиром в 1614 г.; см. Шульц-Баслер 2, 38) из греч. λόγος и ἀριθμός, первонач. «относительное число».
ЛОГАРИФМ а, м. ЛОГАРИТМ а, м. logarithme m. , нем. Logarithm, н.-лат. Logarithmus <гр. logos отношение + arrithmos число. мат. Показатель степени, в которую нужно возвести какое-н. определенное число, чтобы получить данное число. Этот курьез в моих ученых трудах открыл не я сам, а один из моих знакомых, имевший терпение проверять все мои рассуждения по таблицам логаритмов .. но все мои логаритмические рассждения в том ученом труде — совершенно лишнее бремя в труде, совршенно напрасном. 1877. Черн. ПСС 15 35. Логарифмический ая, ое. Крысин 1998. — Лекс. Сл. 18: логарифм 1703 (-итм 1780), лоогаритмус 1714, логарифма 1703 ( — фма 1755); Нордстет 1780: логари/тмы; САР 1792: логари/фм.
ЛОГАРИФМ (греч., от logos — отношение, и arithmos — число). Число арифметической прогрессии, соответствующее числу геометрической прогрессии.
— Показатель степени в которую нужно возвести число, чтобы получить данное число.
— Функция y=ln(x).
— Функция y=log(x).
— Изобретение Джона Непера.