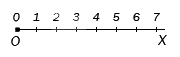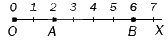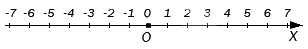Как правильно писать слово сравнить?
Если вы хотите узнать, как правильно пишется какое-либо слово, необходимо узнать какой частью речи оно является. Далее найти правило русского языка, которое определяет правописание. Давайте разбираться.
Правильно писать:
«СРАВНИТЬ»
Другие варианты написания
Здесь мы приводим все возможные формы слова, склонение по падежам (если это возможно с точки зрения правил русского), единственное и множественное число слова сравнить
Базовая форма слова СРАВНИТЬ
Будущее время
| Лицо | Ед. число | Мн. число |
|---|---|---|
| 1 | сравню | сравним |
| 2 | сравнишь | сравните |
| 3 | сравнит | сравнят |
Прошедшее время
| Ед. число | Мн. число | ||
|---|---|---|---|
| муж. | жен. | сред. | |
| сравнил | сравнила | сравнило | сравнили |
Повелит. наклонение
| Ед. число | Мн. число |
|---|---|
| сравни | сравните |
Деепричаcтие
| настоящее | прошедшее |
|---|---|
| — | сравнив, сравнивши, сравня |
Причастие — прошедшее время, действительный залог
| Ед. число | Мн. число | |||
|---|---|---|---|---|
| Муж. род | Жен. род | Средний род | ||
| Им. | сравнивший | сравнившая | сравнившее | сравнившие |
| Род. | сравнившего | сравнившей | сравнившего | сравнивших |
| Дат. | сравнившему | сравнившей | сравнившему | сравнившим |
| Винит. одуш. |
сравнившего | сравнившую | сравнившее | сравнивших |
| Винит. неодуш. |
сравнивший | сравнившую | сравнившее | сравнившие |
| Тв. | сравнившим | сравнившей, сравнившею |
сравнившим | сравнившими |
| Пред. | сравнившем | сравнившей | сравнившем | сравнивших |
| Кр. прич. | — | — | — | — |
Причастие — прошедшее время, страдательный залог
| Ед. число | Мн. число | |||
|---|---|---|---|---|
| Муж. род | Жен. род | Средний род | ||
| Им. | сравнённый | сравнённая | сравнённое | сравнённые |
| Род. | сравнённого | сравнённой | сравнённого | сравнённых |
| Дат. | сравнённому | сравнённой | сравнённому | сравнённым |
| Винит. одуш. |
сравнённого | сравнённую | сравнённое | сравнённых |
| Винит. неодуш. |
сравнённый | сравнённую | сравнённое | сравнённые |
| Тв. | сравнённым | сравнённой, сравнённою |
сравнённым | сравнёнными |
| Пред. | сравнённом | сравнённой | сравнённом | сравнённых |
| Кр. прич. | сравнён | сравнена | сравнено | сравнены |
«СРАВНИТЬ» в контексте
С какими деньгами можно сравнить возможность видеть весь мир!
Интересно сравнить размеры солдатского пайка в разных странах.
Конечно, можно бы сравнить почерк с заведомо дедушкиным.
Платон сравнил жизнь человека с колесницей.
1. Общее количество предметов в коробке равно 7.
2. За х
Сказки писал, например, всем известный Александр Пушкин. Нельзя не сказать. ч
Відповідь:
Нехай х — дане число. Тоді збільшене на 20% число дорівн
В начале найдём сколько кают расположено на второй палубе теплохода. Известно
Найдем, на сколько километров за каждый час увеличивается расстояние между ве
298,287,265,232,188…133,67,-10,-98
Объясняем: из 298 отнимаем 11, получаем
Именно ковыль растет на лугу. Он относится к семейству Злаки. Обильно эта тра
Чтобы определить, какое число в 1,2 раза меньше 12,24, необходимо:
12,
Для того, чтобы ответить на поставленный вопрос и сравнить предложенные дроби
Моторная лодка затратит 24 : (10 — 2) = 3 ч, чтобы проплыть 24 км против течения
Правильные ответы выделены по тесту
тест уже прошел свою проверку
ст
После того, как ребенок понял, как образуются двузначные числа и научился считать до 100, он легко сможет научится сравнивать однозначные и двузначные числа, а также двузначные числа между собой.

Как сравнивать между собой числа от 0 до 99?
- Двузначное число всегда состоит хотя бы из одного десятка. 10 — самое маленькое двузначное число. При сравнении любого однозначного числа с двузначным, двузначное всегда будет больше.
- Два двузначных числа начинают сравнивать с наивысшего разряда – первой цифры. Первая цифра обозначает, какое в числе количество десятков. Сравним числа 45 и 57. Начинаем сравнение с первой цифры, количества десятков. В числе 45 имеется 4 десятка (первая цифра 4), а в числе 57 имеется пять десятков (первая цифра 5). 4 <5, значит 45 <57. Последующие цифры при этом не имеют значения.
- Если количество десятков в числах одинаковое (первые цифры равны), сравниваем количество единиц (вторая цифра). Сравним числа 45 и 46. У этих чисел равное количество десятков — четыре. Так как количество десятков одинаковое, то сравним число единиц. В числе 45 пять единиц, а в числе 46 шесть единиц. 5 < 6, значит 45 < 46.
Выполните развивающие упражнения от Айкьюши
Для визуального представления механизма сравнения очень подходит игрушка «Математические весы». Принцип сравнения сводится к следующему: на каждой стороне весов ребенок подвешивает грузы, чтобы получились сравниваемые числа. Например, требуется сравнить 45 и 46. Значит 4 груза подвешиваются на отметку «10» и один груз на отметку «5», 46 – 4 груза на отметку «10» и один груз на отметку «6». Сторона, где представлено число 46, перевесит. Число 46 тяжелее числа 45, значит больше.

Как тренировать навыки сравнения?
Упражнения на состав чисел. Взрослый называет двузначное число, ребенок определяет, сколько в нем десятков и единиц.
«Перелистываем страницы». Навык сравнения двузначных чисел очень пригодится ребенку, когда ему необходимо будет открыть книгу на нужной странице. И упражняться в сравнении чисел тоже можно, листая страницы. Взрослый называет номер страницы. Ребенок открывает книгу на этой странице. Взрослый называет номер другой страницы. Ребенку необходимо сориентироваться, вправо или влево необходимо листать для поиска нужной страницы.
Интересные задания для 3 класса ждут вас в нашем каталогу упражнений!
Не сомневаемся, что ваш ребенок без труда справится с изучением этой темы!
Как правильно пишется слово «сравнить»
сравни́ть(ся)
сравни́ть(ся), -ню́(сь), -ни́т(ся)
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: расширяющийся — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «сравнить»
Синонимы к слову «сравнить»
Предложения со словом «сравнить»
- С какими деньгами можно сравнить возможность видеть весь мир!
- – Ну, с кем вы можете сравнить человека, который, перед тем как сражаться с закованным в доспехи и вооружённым врагом, обнажает грудь, бросает оружие и посылает противнику любезные поцелуи?
- Конечно, появление беспрецедентного в экономической истории нельзя сравнить с пожаром в доме.
- (все предложения)
Цитаты из русской классики со словом «сравнить»
- Классический поэт сравнил бы ее с Церерой или Юноной.
- Интересно сравнить мучения Иова с мучениями Л. Толстого, который был близок к самоубийству.
- — Сравните жизнь семейства, расходующего 1 000 руб. в год, с жизнью такого же семейства, расходующего 4 000 руб., неправда ли, вы найдете громадную разницу? — продолжал Кирсанов. — При нашем порядке точно такая же пропорция, если не больше: при нем получается вдвое больше дохода, и доход употребляется вдвое выгоднее. Удивительно ли, что вы нашли жизнь наших швей вовсе непохожею на ту, какую ведут швеи при обыкновенном порядке?
- (все
цитаты из русской классики)
Значение слова «сравнить»
-
СРАВНИ́ТЬ, —ню́, —ни́шь; прич. страд. прош. сравнённый, —нён, —нена́, —нено́; сов., перех. (несов. сравнивать1). 1. Рассмотреть одно в связи с другим для установления сходства или различия или для установления преимуществ одного перед другим; сопоставить. Сравнить два числа между собой. Сравнить славянские языки с балтийскими. (Малый академический словарь, МАС)
Все значения слова СРАВНИТЬ
Афоризмы русских писателей со словом «сравнить»
- Сравните басни Крылова, комедию Грибоедова, произведения Пушкина, Лермонтова и, в особенности. Гоголя, — сравните их с произведениями Ломоносова и писателей его школы, и вы не увидите между ними ничего общего…
- Сравнить предателя не с кем и не с чем. Я думаю, что даже тифозную вошь сравнение с предателем оскорбило бы.
- Чтобы убедиться в быстроте роста языка, стоит только сравнить запасы слов — лексиконы — Гоголя и Чехова, Тургенева и, например, Бунина, Достоевского и, скажем, Леонида Леонова.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
СРАВНИ́ТЬ, —ню́, —ни́шь; прич. страд. прош. сравнённый, —нён, —нена́, —нено́; сов., перех. (несов. сравнивать1). 1. Рассмотреть одно в связи с другим для установления сходства или различия или для установления преимуществ одного перед другим; сопоставить. Сравнить два числа между собой. Сравнить славянские языки с балтийскими.
Все значения слова «сравнить»
-
С какими деньгами можно сравнить возможность видеть весь мир!
-
– Ну, с кем вы можете сравнить человека, который, перед тем как сражаться с закованным в доспехи и вооружённым врагом, обнажает грудь, бросает оружие и посылает противнику любезные поцелуи?
-
Конечно, появление беспрецедентного в экономической истории нельзя сравнить с пожаром в доме.
- (все предложения)
- сравнять
- сопоставить
- уподобить
- сличить
- сверить
- (ещё синонимы…)
- соотношение
- статистика
- различие
- (ещё ассоциации…)
- сравнивать себя с чем-либо
- сравнить результаты
- сравнивать себя
- (полная таблица сочетаемости…)
- Разбор по составу слова «сравнить»
Морфемный разбор слова:
Однокоренные слова к слову:
Сравнение натуральных чисел
Сравнить два числа — это значит определить, равны они или нет, если нет, то определить, какое из них больше, а какое — меньше.
Равные и неравные натуральные числа
Если записи двух натуральных чисел одинаковы, то говорят, что эти числа равны между собой. Числа, которые равны, называются равными. Если записи двух натуральных чисел отличаются, то говорят, что эти числа не равны. Числа, которые не равны, называются неравными.
Пример. Натуральное число 34 равно числу 34 (их записи одинаковы), а натуральные числа 63 и 67 не равны (их записи различны). Следовательно числа 34 и 34 — равные, а 63 и 67 — неравные.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
Запись, которая состоит из математических выражений, между которыми ставится знак = называется равенством.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Знаки > и должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак > или называется неравенством.
2 8 — неверное неравенство).
Правила чтения равенств и неравенств
Равенства и неравенства читаются слева направо. Левая часть равенства читается в именительном падеже, а правая — в дательном.
Пример. 7 = 7 — семь равно семи.
Левая часть неравенства читается в именительном падеже, а правая — в родительном.
Пример. 11 > 9 — одиннадцать больше девяти, 3 Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
Число 1 меньше числа 3 (1 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда. Опять получаем равенство 0 = 0, переходим к сравнению значений разряда десятков. Теперь имеем неравенство 2 > 1, из которого делаем вывод, что число 4026 больше числа 4019 (4026 > 4019), потому что у первого числа, цифра разряда десятков (2) больше, чем цифра разряда десятков (1) у второго числа.
Если количество цифр в записи сравниваемых чисел разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
38 526 734
38 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 8, которые можно записать как двойное неравенство:
Источник
Знаки больше и меньше в математике — сравнение чисел с примерами
Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.
Математические знаки в картинках для дошкольников
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.
Знак «больше» – в какую сторону
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так « Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или « Примеры на сравнение чисел для 1 класса
В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.
Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и « Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и « Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа « ». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Заключение
Источник
Урок 30 Бесплатно Сравнение чисел
В этом уроке мы научимся сравнивать числа как с разными, так и c одинаковыми знаками.
Узнаем, что такое быстрое сравнение с нулем, а также поговорим про то, что касается сравнения чисел и модулей.
Сравнение чисел с одинаковым знаком
Со сравнением двух чисел, оба из которых больше нуля, вы уже знакомы: для этого мы просто смотрим на числа, их разряды и понимаем, какое из них больше. Для нас очевидно еще с начальной школы, что 3 больше, чем 2, 154 больше, чем 145, 1428 больш,е чем 425, и так далее.
Если говорить про отрицательные числа, то для начала приведем аналогию из реальной жизни.
То есть, казалось бы, 10 больше, чем 7, но при этом -10°С меньше, чем -7°С.
Чтобы сравнить два числа, оба из которых отрицательные, надо сравнить их модули, тогда меньше будет то число, у которого модуль больше.
Это же работает и в обратную сторону.
Если два числа отрицательны и модуль первого меньше модуля второго, то первое число больше второго.
Если оба числа отрицательны и их модули равны, то и сами числа равны.
Пример:
Допустим, необходимо сравнить (mathbf<-324>) и (mathbf<-245>)
Первым делом находим модули:
Также сравним (mathbf<-5>) и (mathbf<-5>)
Мы видим, что модули чисел равны, к тому же, они оба отрицательны, значит эти числа равны.
Пройти тест и получить оценку можно после входа или регистрации
Сравнение чисел с разными знаками
Сейчас мы познакомимся с одним интересным свойством сравнения, которое позволит нам сравнивать числа с разными знаками вообще без каких-либо усилий с нашей стороны.
Задумывались ли вы раньше, почему если мы знаем, что Борис выше Анны, а Сергей выше Бориса, мы сразу сделаем вывод, что Сергей выше и Анны тоже?
Или если мы знаем, что Ваня пришел раньше Пети, а Петя раньше Ильи, то мы делаем вывод, что Ваня пришел раньше Ильи.
Это свойство называется транзитивностью.
Если говорить абстрактно, то это свойство говорит о следующем: если между объектом А и объектом Б есть транзитивное отношение и между объектом Б и объектом В тоже есть это же транзитивное отношение, то это значит, что это отношение есть между А и В.
Звучит может немного непонятно, но на примере со сравнением сейчас все встанет на свои места.
Отношения «быть больше», «быть равным» и «быть меньше» обладают свойством транзитивности.
Поэтому если мы знаем, что 2 меньше, чем 3, а 3 меньше, чем 4, то мы можем утверждать, что 2 меньше, чем 4.
Зафиксируем эти правила коротко и емко.
1. Если а меньше b и b меньше с, то а меньше с
2. Если a больше b и b больше с, то а больше с
3. Если а равно b и b равно с, то а равно с
Более подробно про отношения говорят на курсах высшей математики, дискретной математики или математической логики, но при этом бояться таких абстрактных понятий не стоит.
Теперь мы можем применить это мощное свойство к сравнению чисел с разными знаками.
Мы знаем, что отрицательные числа меньше нуля.
Также мы знаем, что положительные числа больше или, другими словами, нуль меньше положительных чисел.
Тогда, зная транзитивность отношения «меньше», мы можем прийти к выводу, что a меньше с.
Заметьте, что мы нигде ни для а, ни для с не предполагали конкретных значений, а значит, любое отрицательное число меньше любого положительного.
Те же самые рассуждения можно провести в обратную сторону и получить, что любое положительное число больше любого отрицательного.
Итак, посмотрим, как происходит процесс сравнения чисел с разными знаками на практике.
Пример 1
Сравним (mathbf<-5>) и (mathbf<3>).
(mathbf<-5>)- отрицательное число, (mathbf<3>)— положительное.
Пройти тест и получить оценку можно после входа или регистрации
Источник
Сравнение натуральных чисел: равно или не равно, больше или меньше?
Сравнение натуральных чисел между собой – тема данной статьи. Разберем сравнение двух натуральных чисел и изучим понятие равных и неравных натуральных чисел. Выясним большие и меньшие из двух чисел на примерах. Поговорим о натуральном ряде чисел и об их сравнении. Будут показаны результаты сравнений трех и более чисел.
Сравнение натуральных чисел
Рассмотрим это на примере. Когда на дереве имеется стая, состоящая из 7 птиц, а на другом из 5 десятка птиц, то стаи считаются разными, так как не похожи друг на друга. Отсюда можно делать вывод о том, что эта непохожесть и есть сравнение.
При сравнении натуральных чисел проводится такая проверка на похожесть.
Если считать, что под сравнением натуральных чисел подразумевают действие, то оно может привести к нескольким результатам:
Когда получаем неравенство, это значит, что одно из этих чисел больше или меньше другого, что и увеличивает диапазон использования натуральных чисел.
Рассмотрим определения равных и неравных чисел. Разберем, каким образом это определяется.
Равные и неравные натуральные числа
Рассмотрим определение равных и неравных чисел.
В случае, когда записи двух натуральных чисел одинаковы, их считают равными между собой. Когда записи имеют различия, тогда эти числа неравные.
Сравнение однозначных натуральных чисел
Если в записи имеются два натуральных числа со знаками « » и « > », тогда она называется неравенством. Неравенства могут быть верными и неверными.
Запись 4 7 – верная, а 3 > 9 – неверная.
Сравнение однозначного и многозначного натуральных чисел
Если принять за правило, что все однозначные числа меньше двухзначных, тогда получим:
Рассмотрим сравнения многозначных чисел.
Сравнение многозначных натуральных чисел
Рассмотрим сравнение двух неравных многозначных натуральных чисел с равным количеством знаков. Предварительно следует повторить раздел, изучающий разряды натурального числа и значение разряда.
В таком случае производится поразрядное сравнение, то есть слева направо. Меньшим считается число, которое имеет меньшее значение соответствующего разряда и наоборот.
Чтобы решить пример, нужно уяснить, что 0 всегда меньше любого натурального числа и что он равен самому себе. Число ноль относится к разряду натуральных чисел.
Сравнение многозначных натуральных чисел производится по-другому. Большим числом считают то, которое имеет меньшее количество знаков и наоборот.
Решение
Натуральный ряд чисел, нумерация, счет
Эта запись продолжается до бесконечности. Такая бесконечная последовательность чисел называется натуральным рядом чисел.
Существует еще один процесс – счет. Во время счета числа называются одно за другим, то есть таким образом, как они зафиксированы по ряду. Данный процесс применим для определения количества предметов.
Исли имеется определенное число предметов, но нам необходимо узнать количество, используем счет. Он производится, начиная с единицы. Если во время пересчета перекладывать предметы в кучу, то ее можно назвать натуральным рядом чисел. Последний предмет будет являться числом их количества. Когда процесс закончен, мы знаем их число, то есть предметы пересчитаны.
Во время счета меньше то натурально число, которое находится раньше и называется раньше. Применение нумерации используется для конкретного определения предмета, то есть присваивая ему определенный номер. Например, имеем некоторое количество предметов. На каждом из них зафиксируем их порядковый номер. Таким образом производится нумерация. Она применима для различения одинаковых предметов.
Натуральные числа на координатном луче
Для начала необходимо повторить определение координатного луча.
При просмотре слева направо видим штрихи, которые означают определенную последовательность чисел, начиная от 0 и до бесконечности. Эти штрихи называют точками. Точки, расположенные левее меньше точек, расположенных правее. Отсюда следует, что точка, имеющая меньшую координату на координатном луче, расположена левее точки с большей координатой.
Наименьшее и наибольшее натуральное число
Считается, что 1 – это наименьшее натуральное число из множества всех натуральных чисел. Все числа, расположенные правее него считаются больше предыдущего. Этот ряд бесконечен, поэтому нет наибольшего числа из этого множества чисел.
Двойные, тройные неравенства
Таким же образом выполняются тройные, четверные и так далее неравенства.
Необходимо быть внимательным при составлении двойных неравенств, так как можно произвести его неверно, что повлечет за собой неправильное решение задачи.
Источник
Сравнение целых чисел: правила, примеры
После того, как получили полное представление о целых числах, можно говорить об их сравнении. Для этого выясняется, какие числа равные и неравные. Разберутся правила, благодаря которым выясняем, какие из двух неравных больше или меньше. Это правило основано на сравнении натуральных чисел. Будет рассмотрено сравнение трех и более целых чисел, нахождение наименьшего и наибольшего целого числа из заданного множества.
Равные и неравные целые числа
Сравнение двух чисел приводит к тому, что они либо равны либо не равны. Рассмотрим определения.
Два целых числа называют равными, когда их запись полностью совпадает. Иначе они считаются неравными.
При сравнивании чисел используется правило модуля числа.
Если два числа имеют одинаковые знаки и их модули равны, то эти два числа считаются равными. Иначе их называют не равными.
Рассмотрим на примере данное определение.
Видно, что числа имеют одинаковый знак, но это не значит, что они равны. Для сравнения используется модуль числа. По модулю первое число оказалось меньше второго. Они не равны ни по модулю, ни без него.
Значит, делаем вывод, что числа не равны.
Рассмотрим еще пример.
Если получаем неравные числа, тогда необходимо уточнение, какое из них меньше и какое больше.
Сравнение произвольных целых чисел с нулем
При сравнении отрицательных чисел с нулем другая ситуация. Все числа, которые меньше нуля, считаются отрицательными. Отсюда делаем вывод, что любое отрицательное число меньше нуля, нуль равен нулю, а любое целое положительное больше нуля. Суть правила заключается в том, что нуль больше отрицательных чисел, но меньше всех положительных.
Сравнение положительных целых чисел
Все целые положительные числа являются натуральными. Значит, равнение положительных чисел аналогично сравнению натуральных.
Рассмотрим еще один пример.
Сравнение целых отрицательных и положительных чисел
Любое целое отрицательное число меньше целого положительного и наоборот.
Сравним несколько чисел и рассмотрим на примере.
Сравнение целых отрицательных чисел
Рассмотрим правило сравнения:
Из двух отрицательных чисел меньшим является то, модуль которого больше и наоборот.
Рассмотрим на примере.
Сравниваемые целые числа на координатной прямой
Рассмотрим целые числа, расположенные на координатной прямой.
Из рассмотренных выше правил получим, что на горизонтальной координатной прямой точки, которым соответствуют большие целые числа, то есть лежат правее тех, которым соответствуют меньшие.
Начало отсчета – это ноль. Он больше всех отрицательных и меньше всех положительных. Также и с точками, находящимися на координатной прямой.
Наибольшее отрицательное и наименьшее положительное целое число
В предыдущих пунктах подробно было рассмотрено сравнение двух целых чисел. В данном пункте поговорим о сравнении трех и более чисел, рассмотрим ситуации.
Когда производится сравнение нескольких чисел, то появляется определение наибольшего и наименьшего значения числа.
Число заданного множества считается наименьшим, если оно меньше любого другого из заданных чисел множества.
Число заданного множества является наибольшим, если оно больше любого другого из заданных чисел множества.
Очевидно, что множество целых чисел огромно и бесконечно, поэтому указать наименьшее или наибольшее число невозможно. Это можно сделать только в заданном множестве чисел. Число, расположенное правее на координатной прямой, всегда считается большим, чем то, которое левее.
Источник
Часть речи: инфинитив — сравнить
Часть речи: глагол
Часть речи: деепричастие
Часть речи: причастие
Действительное причастие:
| Настоящее время | ||||
|---|---|---|---|---|
| Единственное число | Множественное число | |||
| Мужской род | Женский род | Средний род | ||
| Им. | ||||
| Рд. | ||||
| Дт. | ||||
| Вн. | ||||
| Тв. | ||||
| Пр. |
Страдательное причастие:
| Настоящее время | ||||
|---|---|---|---|---|
| Единственное число | Множественное число | |||
| Мужской род | Женский род | Средний род | ||
| Им. | ||||
| Рд. | ||||
| Дт. | ||||
| Вн. | ||||
| Тв. | ||||
| Пр. |
Часть речи: кр. причастие
Страдательное причастие:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Разбор слова «Сравнить»
На чтение 1 мин.
Значение слова «Сравнить»
— смотри: сравнивать
Содержание
- Транскрипция слова
- MFA Международная транскрипция
- Цветовая схема слова
Транскрипция слова
[сравн’и́т’]
MFA Международная транскрипция
[srɐˈvnʲitʲ]
| с | [с] | согласный, глухой парный, твердый парный |
| р | [р] | согласный, звонкий непарный (сонорный), твердый парный |
| а | [а] | гласный, безударный |
| в | [в] | согласный, звонкий парный, твердый парный |
| н | [н’] | согласный, звонкий непарный (сонорный), мягкий парный |
| и | [́и] | гласный, ударный |
| т | [т’] | согласный, глухой парный, мягкий парный |
| ь | [-] |
Букв: 8 Звуков: 7
Цветовая схема слова
сравнить
Как произносится слово «Сравнить»
Тег audio не поддерживается вашим браузером.
Как правильно пишется «Сравнить»
сравни́ть(ся)
сравни́ть(ся), -ню́(сь), -ни́т(ся)
Как правильно перенести «Сравнить»
срав—ни́ть
Часть речи
Часть речи слова «сравнить» — Глагол
Морфологические признаки.
- Начальная форма — сравнить
- Лемма — сравнить
Постоянные признаки:
- Спряжение — 2-е спряжение
- Вид — совершенный
- Переходность — переходный
Склонение слова «Сравнить»
| будущ. | прош. | повелит. | ||
|---|---|---|---|---|
| Я | муж. р. | сравню | сравнил | |
| жен. р. | сравнила | |||
| Ты | муж. р. | сравнишь | сравнил | сравни |
| жен. р. | сравнила | |||
| Он | сравнит | сравнил | ||
| Она | сравнила | |||
| Оно | сравнило | |||
| Мы | сравним | сравнили | ||
| Вы | сравните | сравнили | сравните | |
| Они | сравнят | сравнили |
Разбор по составу слова «Сравнить»
Проверьте свои знания русского языка
Категория: Русский язык
Русский язык
Тест на тему “Гласные буквы”
1 / 5
В каком ряду представлены гласные буквы, указывающие на мягкость предыдущего согласного звука?
е, ю, я, и
о, и, у, а
и, ю, е, о
ы, э, ю, я
2 / 5
В каком ряду все буквы являются гласными?
а, о, к, д, я
о, ъ, ю, э, я
ё, й, и, о, у
а, о, у, э, я
3 / 5
В каком ряду представлены гласные буквы, указывающие на твердость предыдущего согласного звука?
я, о, у, а
ё, а, и, ю
ы, о, е, и
у, о, а, ы
4 / 5
Укажите неверное утверждение.
Буквы а, я обозначают звук [а]
Буквы о, э обозначают звук [э]
Буквы ё, о обозначают звук [о]
Буквы у, ю обозначают звук [у]
5 / 5
Сколько гласных букв насчитывается в русском языке?
шесть
восемь
десять
двенадцать
Синонимы к слову «сравнить»
Ассоциации к слову «сравнить»
Предложения со словом «сравнить»
- С какими деньгами можно сравнить возможность видеть весь мир!
Виктор Розов, Удивление перед жизнью. Воспоминания, 2014
- – Ну, с кем вы можете сравнить человека, который, перед тем как сражаться с закованным в доспехи и вооружённым врагом, обнажает грудь, бросает оружие и посылает противнику любезные поцелуи?
Александр Дюма, Виконт де Бражелон, или Десять лет спустя. Часть пятая, 1850
- К сожалению, вы не можете поставить перед покупателем в ряд десять квартир или домов, дать возможность сравнить их и помочь сделать окончательный выбор, как, например, в случае если покупатель выбирает вазу или свитер.
Галина Парусова, Профессия риэлтор. 48 шагов на пути к успеху. В помощь агенту по недвижимости
СРАВНИТЬ
Малый академический словарь русского языка
СРАВНИТЬ
-ню, -нишь; прич. страд. прош. сравнённый, -нён, -нена, -нено; сов., перех. (несов. сравнивать1).
1.
Рассмотреть одно в связи с другим для установления сходства или различия или для установления преимуществ одного перед другим; сопоставить.
Сравнить два числа между собой. Сравнить славянские языки с балтийскими.
□
— Право, я не совсем дурной человек;
даже совсем недурной человек, — подумал он. — Даже очень хороший человек, как сравню себя с другими. Л. Толстой, Альберт.
{Аглая} поглядела с минуту на Евгения Павловича, как бы желая только сравнить, военное или штатское платье ему больше к лицу. Достоевский, Идиот.
2. с кем-чем.
Приравнять к чему-л., уподобить кому-л.
Места эти можно было бы сравнить со Швейцарией, если бы эта красота не была такой дикой и суровой. Арсеньев, В горах Сихотэ-Алиня.
Судья сказал речь. — Петьку и меня он сравнил с орлами и выразил надежду, что мы еще не раз вернемся в родное гнездо. Каверин, Два капитана.
Малый академический словарь русского языка
Сайт предназначен для лиц старше 18 лет