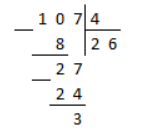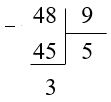Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.
Как сделать из неправильной дроби правильную дробь?
Рассмотрим неправильную дробь (frac{21}{9})
Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

Получаем дробь (2frac{3}{9}), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а (frac{3}{9}) – правильная дробь.
Смешанные дроби состоят из целой и дробной части.
Рассмотрим еще одну неправильную дробь (frac{76}{5})
Разделим ее столбиком:

Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
(color{blue} {3}frac{color{green} {2}}{color{red} {5}} = frac{color{red} {5} times color{blue} {3} + color{green} {2}}{color{red} {5}} = frac{17}{5})
Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: (frac{508}{17})
Решение:
Разделим дробь столбиком:
Ответ: Получили смешанную дробь (29frac{15}{17})
Пример №2:
Представьте число в виде неправильной дроби: а) (9frac{2}{3}), б) (1frac{3}{7})
Решение:
а) (9frac{2}{3} = frac{9 times 3 +2}{3} = frac{29}{3}\\)
б) (1frac{3}{7} = frac{1 times 7 +3}{7} = frac{10}{7}\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил (frac{2}{5}) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь (frac{2}{5}), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
(120 div 5 = 24) задачи это одна часть или (frac{1}{5})
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
(24 times 2 = 48) задач
Ответ: за неделю Миша решил 48 задач.
Что такое смешанная дробь
Определение
Число, содержащее в себе целую и дробную части, называется смешанной дробью.
По сути, данное понятие представляет собой сумму целого числа и правильной дроби:
(afrac bc;=;a+frac bc)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример:
(7frac34;=;7+frac34)
Превращение смешанной дроби в неправильную
Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.
Преобразование смешанной дроби в неправильную можно записать в виде формулы:
(afrac bc;=;frac{atimes c+b}c)
Пример:
(15frac89;=;frac{15times9+8}9;=;frac{143}9)
Выполнение действий со смешанными дробями, формулы и примеры
Сложение
Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.
Формульное выражение сложения смешанных чисел:
(afrac bc+dfrac ef=left(a+dright)+left(frac bc+frac efright))
Пример:
(2frac13+5frac47;)
Вычисляем наименьший общий знаменатель дробных слагаемых:
3×7=21
(2frac13+5frac47=2+5+frac13+frac47;=7+frac7{21}+frac{12}{21}=7+frac{7+12}{21}=7frac{19}{21})
Вычитание
Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.
Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:
(afrac bc-dfrac ef=left(a+frac bcright)-left(d+frac efright);=left(a-dright)+left(frac bc-frac efright))
В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:
(afrac bc-dfrac ef=left(left(a-dright)-frac efright)+frac bc)
Пример:
(13frac38-6frac12)
Для решения этого выражения найдем наименьший общий знаменатель:
8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.
(13frac38-6frac12=13frac38-6frac48=left(12+1+frac38right)-6frac48=left(12+frac{1times8+3}8right)-6frac48=12frac{11}8-6frac48=left(12-6right)+left(frac{11}8-frac48right)=6+frac{11-4}8=6frac78)
Умножение и деление
Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.
Формула умножения смешанных чисел выглядит так:
(afrac bctimes dfrac ef=frac{atimes c+b}ctimesfrac{dtimes f+e}f=frac{left(atimes c+bright)timesleft(dtimes f+eright)}{ctimes f}=frac{left(ac+bright)left(df+eright)}{cf})
Формула деления смешанных дробей:
(afrac bcdiv dfrac ef=frac{atimes c+b}cdivfrac{dtimes f+e}f=frac{atimes c+b}ctimesfrac f{dtimes f+e}=frac{left(atimes c+bright)times f}{ctimesleft(dtimes f+eright)}=frac{fleft(ac+bright)}{cleft(df+eright)})
Пример 1:
(5frac2{19}times2frac79=frac{5times19+2}{19}timesfrac{2times9+7}9=frac{97}{19}timesfrac{25}9=frac{97times25}{19times9}=frac{2425}{171}=14frac{31}{171})
Пример 2:
(4frac23div3frac57=frac{4times3+2}3divfrac{3times7+5}7=frac{14}3divfrac{26}7=frac{14}3timesfrac7{26}=frac{14times7}{3times26}=frac{98}{78}=frac{98div2}{78div2}=frac{49}{39}=1frac{10}{39})
При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.
Пример 3:
(3frac56times4=left(3+frac56right)times4=3times4+frac56times4=12+frac{5times4}6=12+frac{20div2}{6div2}=12+frac{10}3=12+3frac13=15frac13)
Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.
Пример 4:
(5div3frac27=frac51divfrac{3times7+2}7=frac51divfrac{23}7=frac51timesfrac7{23}=frac{5times7}{1times23}=frac{35}{23}=1frac{12}{23})
Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.
Пример 5:
(frac34div6frac12=frac34divfrac{6times2+1}2=frac34divfrac{13}2=frac34timesfrac2{13}=frac{3times1}{2times13}=frac3{26})
Если вы заняты написанием курсовой работы или документа с расчетной частью, вам может потребоваться графический символ, который отсутствует на клавиатуре. Это может быть значок иностранной валюты, символ функции или же математическая дробь. Рассмотрим последний случай. Существует несколько способов написания дроби на клавиатуре.
Вид №1: вертикальная дробь
Предположим, вы хотите изобразить дробь с горизонтальной чертой, которая называется винкулум. Пожалуй, это наиболее привычный для многих из нас вариант, ведь именно так учат записывать дроби школьные учителя математики, и именно это выражение встречается во многих технических, научных и образовательных текстах. В случае «многоэтажных» дробей вам нужно прибегнуть к безграничным возможностям Word.
 Способ 1.
Способ 1.
- Установите курсор в том месте, куда необходимо вставить дробь;
- Нажмите вкладку «Вставка»;
- Найдите справа вкладку «Формула» и нажмите на нее;
- В появившемся конструкторе найдите графу «Дробь» и выберите подходящий для вас вариант написания дроби: вертикальная простая или маленькая, которая пригодится для изображения смешанного числа, состоящего из целой и дробной части;
- В указанном месте появится пустая формула. Вставьте необходимые цифры в пустых окошках дроби. Готово!
 Способ 2.
Способ 2.
- Установите курсор в том месте, куда необходимо вставить дробь;
- Нажмите вкладку «Вставка»;
- Найдите справа вкладку «Объект» и нажмите на нее;
- Выберите строку «Microsoft Equation 3.0» и нажмите ОК;
- В появившейся поле с разнообразными символами выберите «Шаблоны дробей и радикалов» и нажмите на символ дробей;
- Вставьте необходимые цифры в пустых окошках формулы.
Стоит учесть, что написание дробей в вертикальном виде отображается далеко не везде. Например, если вы скопируете вертикальную дробь из Word в чат социальных сетей или диалоговое окно Skype, то она отобразится в горизонтальном виде.
Вид №2: солидус
Вариант, часто встречающийся в научных работах, статьях и учебниках, — это дроби с наклонной чертой, которая в математическом мире называется «солидус». Эта дробная черта наклонена вправо приблизительно на 45°, а между цифрами существует специальный интервал (кернинг). Не путайте солидус с обычной косой чертой – они выглядят по-разному!
Изобразить дробь в таком виде можно при помощи Word. Используйте принцип действий, указанный в пункте «Вид №1», только во вкладке «Дробь» выберите вариант «диагональная простая дробь».
Ввести дробь в таком виде можно также через «Microsoft Equation 3.0».
Вид №3: горизонтальная дробь
Более привычный для нас вариант, который часто встречается в публицистических и научно-популярных статьях – это горизонтальная дробь.
Горизонтальную дробь можно ввести четырьмя способами:
Самый простой и быстрый способ изобразить дроби, не прибегая к вставкам – использовать «слэш» (или косую черту, наклоненную вправо) на клавиатуре. Именно так поступает большинство пользователей Интернета, которые не желают тратить время на поиск нужных символов. Конечно же, для тех, кто занят написанием серьезных научных работ, лучше выбрать специальные изображения дробей.
Слэш располагается на клавиатуре в следующих местах:
- Рядом с правой кнопкой Shift на английской раскладке;
- В цифровом блоке;
- Над и слева от Enter (необходимо нажимать одновременно с Shift).
Вы также можете набрать слэш следующим образом:
- Включите кнопку NumLock;
- Зажмите Alt и наберите на цифровой клавиатуре 4 и затем 7;
- Отпустите Alt.
Чтобы дробь, записанная через слэш, смотрелась естественнее, можно использовать следующую последовательность:
- Выделить числитель дроби->Шрифт->Видоизменение->Надстрочный (ставим галочку) ->ОК;
- Выделить знаменатель дроби->Шрифт->Видоизменение->Подстрочный (ставим галочку) -> ОК.
Теперь вы знаете, как написать дробь на клавиатуре. Как видите, это можно сделать самыми разными способами, и каждый из них достаточно прост. Желаем вам успехов в дальнейшем освоении компьютерной грамоты!
© Lifeo.ru
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
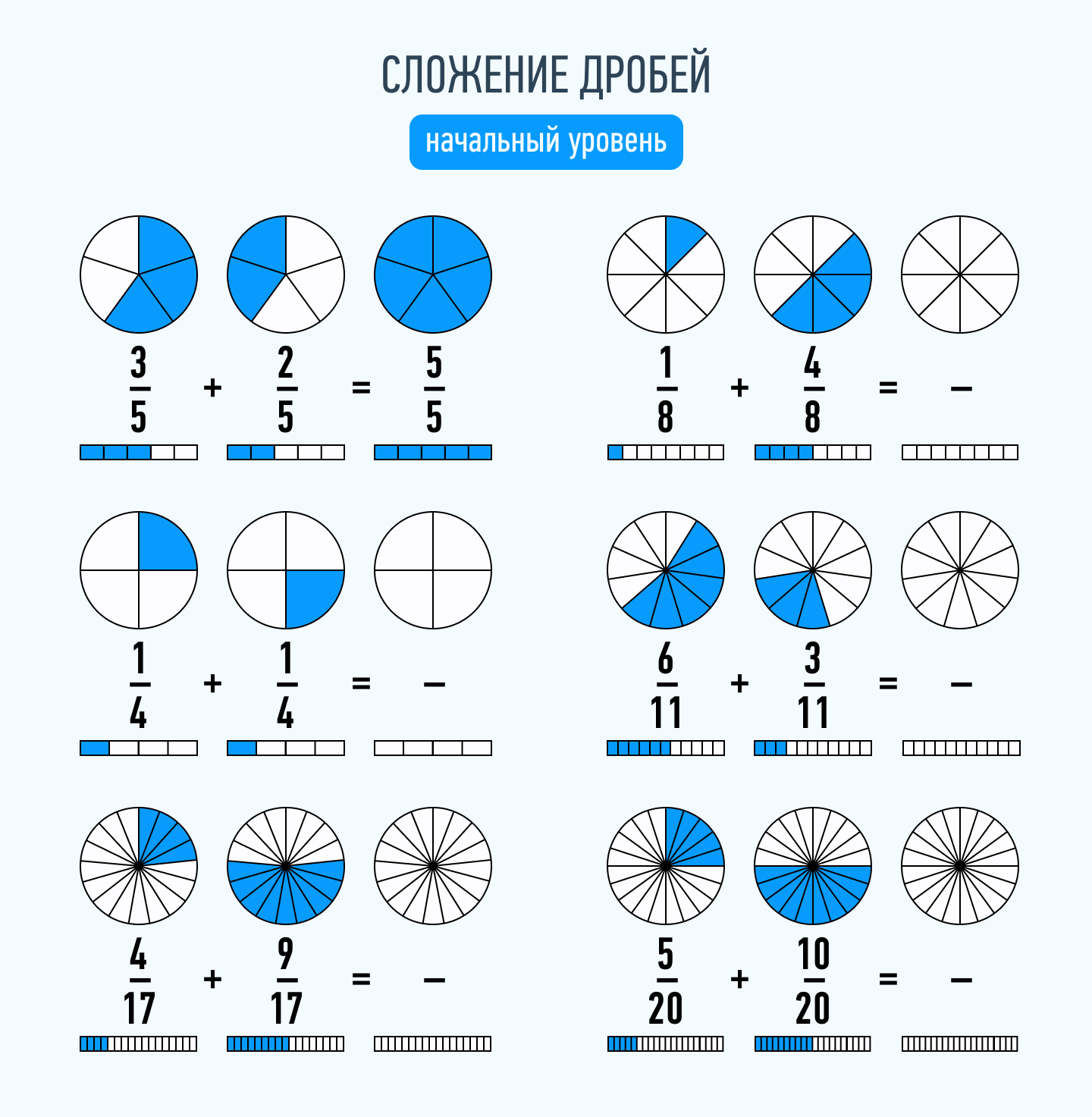
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
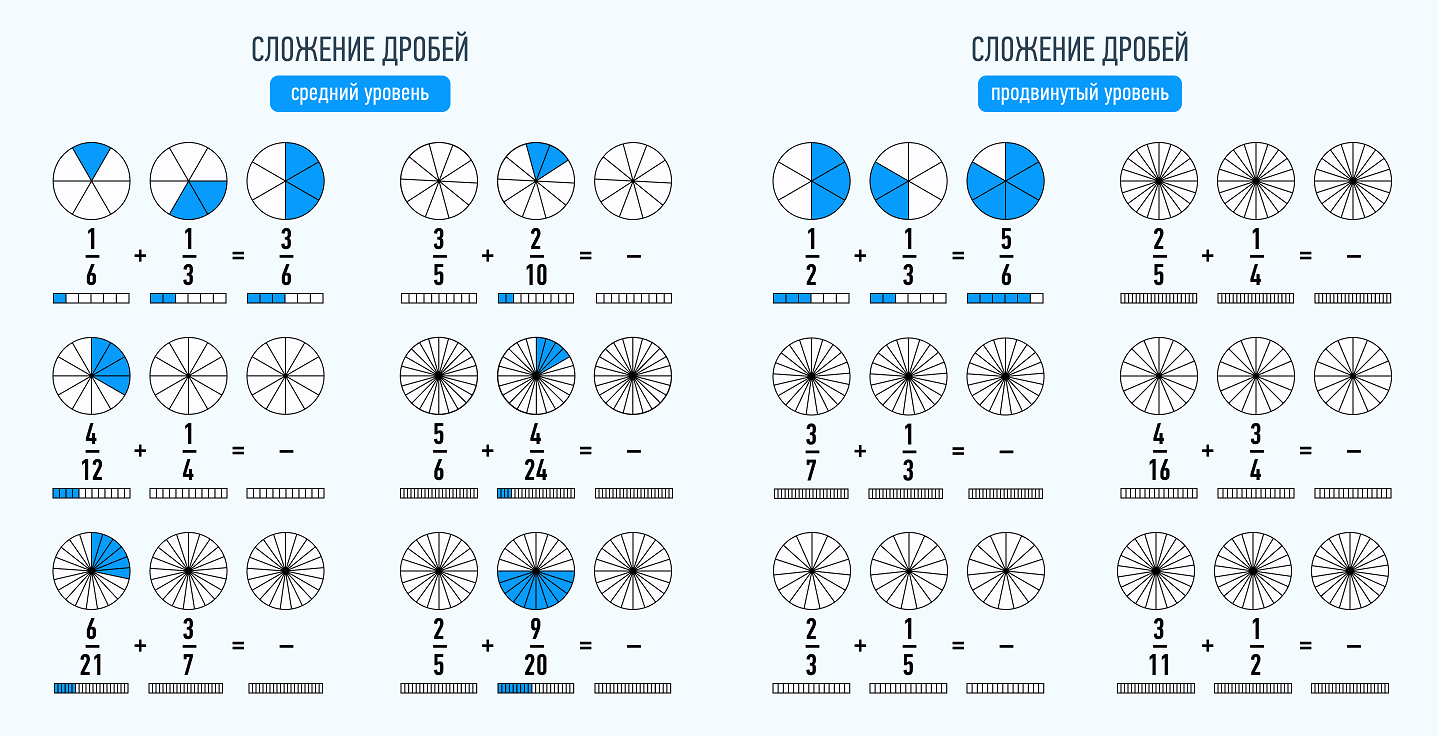
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
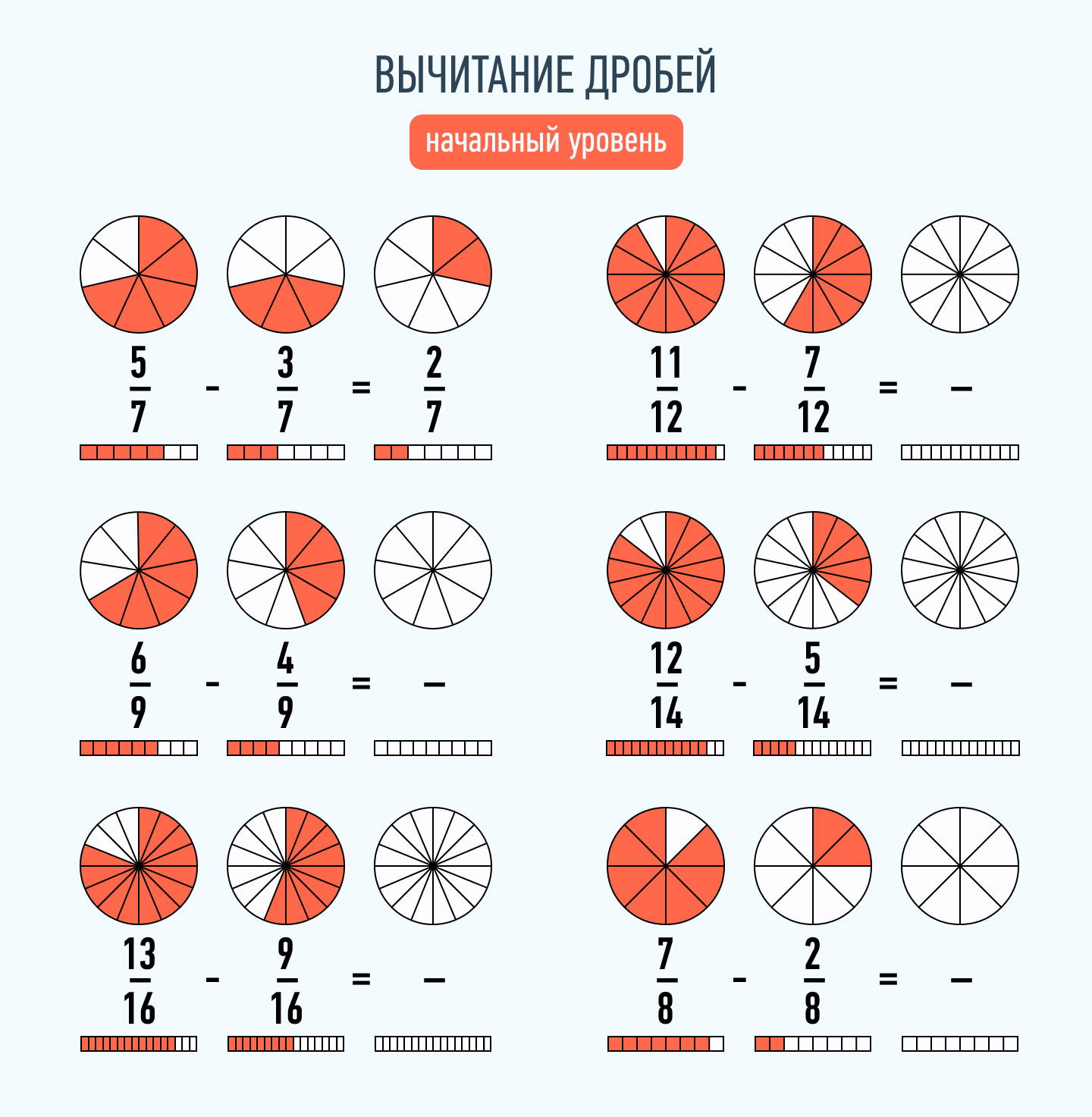
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
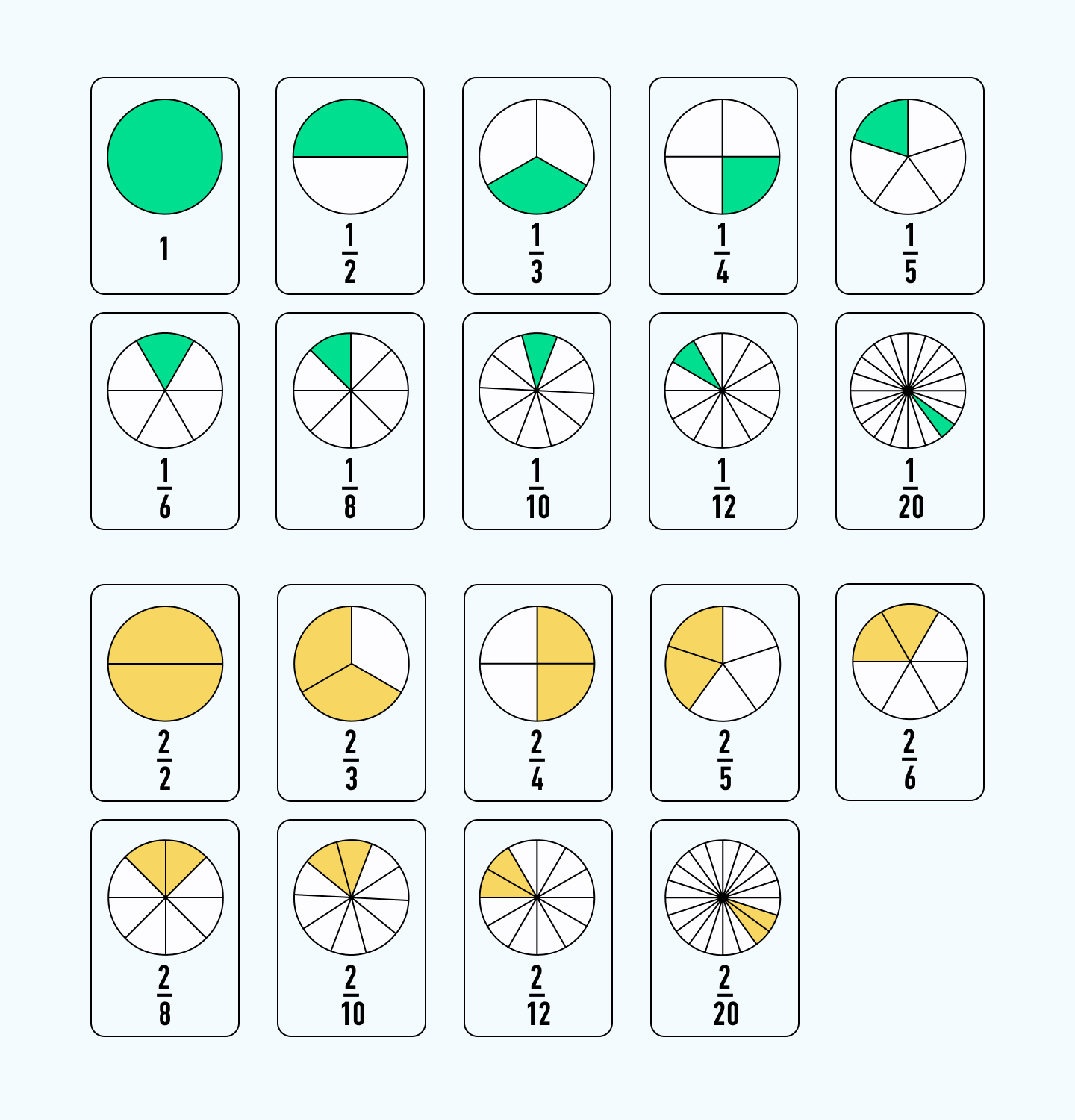
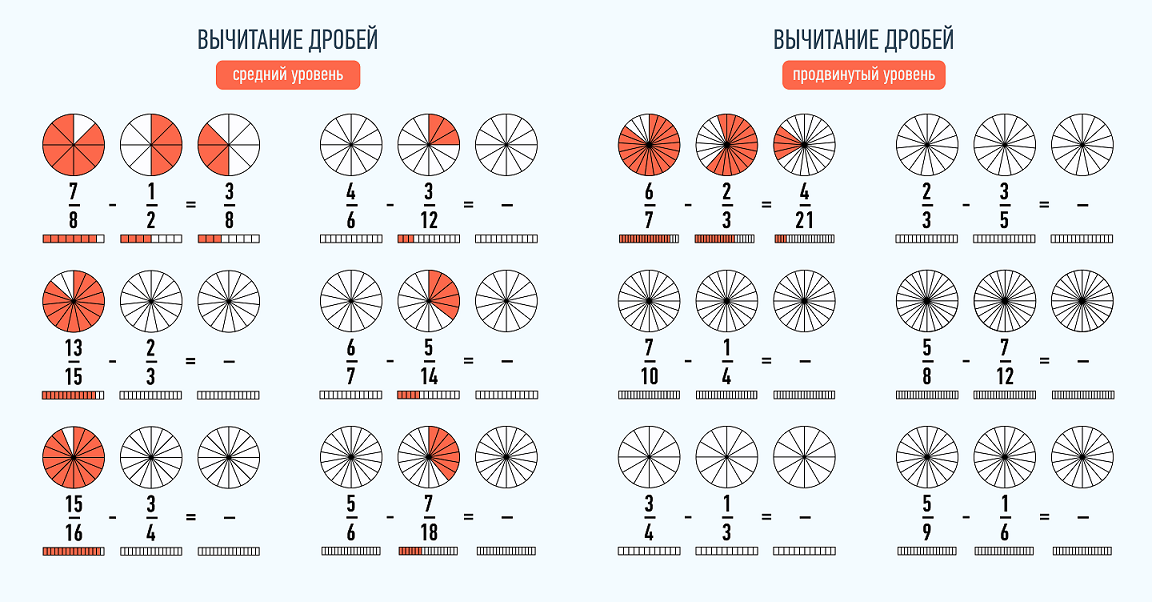
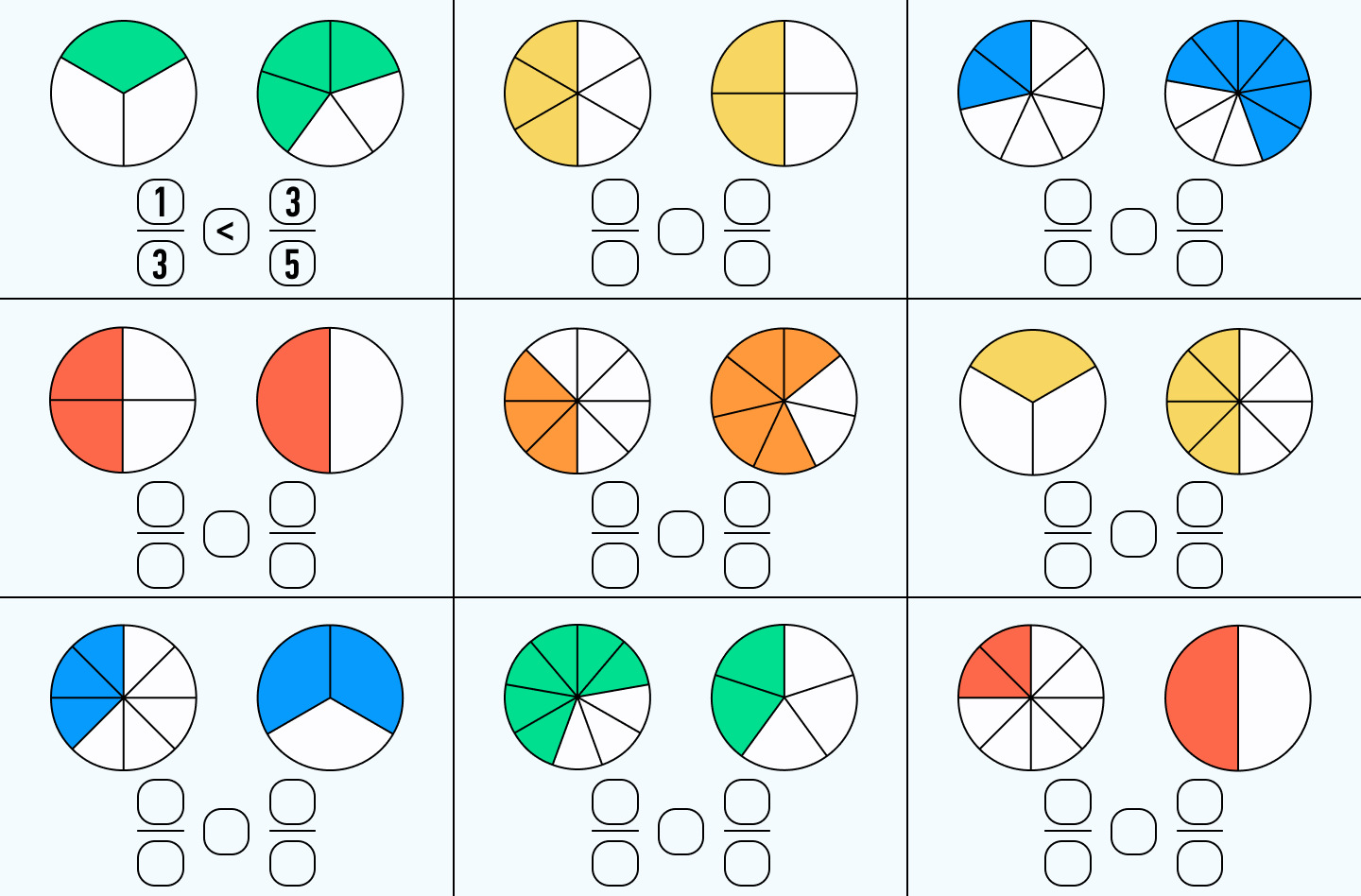
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение смешанной дроби
В математике сумму $n+frac{a}{b}$, где $n$ -натуральное число, $frac{a}{b}$ — правильная обыкновенная дробь, принято записывать без знака $«+»$ в виде $nfrac{a}{b}$.
Пример 1
Например, сумма $4+frac{3}{5}$ записывается $4frac{3}{5}$. Такая запись называется смешанной дробью, а число, которое ей соответствует, — смешанным числом.
Определение 1
Смешанное число — это число, которое равно сумме натурального числа $n$ и правильной обыкновенной дроби $frac{a}{b}$, и записано в виде $nfrac{a}{b}$. В таком случае число $n$ называется $nfrac{a}{b}$, а число $frac{a}{b}$ — дробной частью числа/
Для смешанных чисел справедливы равенства $nfrac{a}{b}=n+frac{a}{b}$ и $n+frac{a}{b}=nfrac{a}{b}$.
Пример 2
Например, число $7frac{4}{9}$ является смешанным числом, где натуральное число $7$ — целая его часть, $frac{4}{9}$ — дробная часть. Примеры смешанных чисел: $17frac{1}{2}$, $456frac{111}{500}$, $23000frac{4}{5}$.
Встречаются числа в смешанной записи, которые в дробной части содержат неправильную дробь. Например, $3frac{54}{5}$, $56frac{9}{2}$. Запись этих чисел можно представить в виде суммы их целой и дробной части. Например, $3frac{54}{5}=3+frac{54}{5}$ и $56frac{9}{2}=56+frac{9}{2}$. Такие числа не подходят по определению смешанного числа, т.к. дробная часть смешанных чисел должна быть правильной дробью.
Число $0frac{2}{7}$ также не смешанное число, т.к. $0$ — не натуральное число.
Перевод смешанного числа в неправильную дробь
Алгоритм перевода смешанного числа в неправильную дробь:
«Смешанные дроби» 👇
-
Записать смешанное число $nfrac{a}{b}$ в виде суммы целой и дробной части этого числа, т.е. в виде $n+frac{a}{b}$.
-
Целую часть исходного смешанного числа заменить дробью со знаменателем $1$.
-
Сложить обыкновенные дроби $frac{n}{1}$ и $frac{a}{b}$ для получения искомой неправильной дроби, равной исходному смешанному числу.
Пример 3
Представить смешанное число $7frac{3}{5}$ в виде неправильной дроби.
Решение.
Воспользуемся алгоритмом перевода смешанного числа в неправильную дробь.
-
Смешанное число $7frac{3}{5}=7+frac{3}{5}$.
-
Запишем число $7$ в виде $frac{7}{1}$.
-
Сложим обыкновенные дроби $frac{7}{1}+frac{3}{5}=frac{35}{5}+frac{3}{5}=frac{38}{5}$.
Запишем краткую запись данного решения:
[7frac{3}{5}=7+frac{3}{5}=frac{7}{1}+frac{3}{5}=frac{35}{5}+frac{3}{5}=frac{38}{5}.]
Ответ: $7frac{3}{5}=frac{38}{5}$
Весь алгоритм перевода смешанного числа $nfrac{a}{b}$ в неправильную дробь сводится к textit{формуле перевода смешанного числа в неправильную дробь}:
Пример 4
Записать смешанное число $14frac{3}{5}$ в виде неправильной дроби.
Решение.
Воспользуемся формулой $nfrac{a}{b}=frac{ncdot b+a}{b}$ для перевода смешанного числа в неправильную дробь. В данном примере $n=14$, $a=3$, $b=5$.
Получим, $14frac{3}{5}=frac{14cdot 5+3}{5}=frac{73}{5}$.
Ответ: $14frac{3}{5}=frac{73}{5}$
Выделение целой части из неправильной дроби
При получении числового решения не принято оставлять ответ в виде неправильной дроби. Неправильная дробь преобразуется в равное ей натуральное число (если числитель делится нацело на знаменатель), или выделяют целую часть из неправильной дроби (если числитель не делится нацело на знаменатель).
Определение 2
Выделением целой части из неправильной дроби называется замена дроби равным ей смешанным числом.
Для выделения целой части из неправильной дроби нужно представить неправильную дробь $frac{a}{b}$ в виде смешанного числа $qfrac{r}{b}$, где $q$ — неполное частное, $r$— остаток от деления $a$ на $b$. Таким образом, целая часть равна неполному частному от деления $a$ на $b$, а остаток равен числителю дробной части.
Докажем это утверждение. Для этого достаточно показать, что $qfrac{r}{b}=frac{a}{b}$.
Переведем смешанное число $qfrac{r}{b}$ в неправильную дробь с помощью формулы:
Т.к. $q$— неполное частное, $r$— остаток от деления $a$ на $b$, то является справедливым равенство $a=bcdot q+r$. Таким образом, $frac{qcdot b+r}{b}=frac{a}{b}$, откуда $qfrac{r}{b}=frac{a}{b}$, что и требовалось показать.
Таким образом, сформулируем textit{правило выделения целой части из неправильной дроби} $frac{a}{b}$:
-
Разделить $a$ на $b$ с остатком, при этом определить неполное частное $q$ и остаток $r$.
-
Записать смешанное число $qfrac{r}{b}$, равное исходной дроби $frac{a}{b}$.
Пример 5
Выделить целую часть из дроби $frac{107}{4}$.
Решение.
Выполним деление в столбик:
Рисунок 1.
Итак, в результате деления числителя $a=107$ на знаменатель $b=4$ получаем неполное частное $q=26$ и остаток $r=3$.
Получаем, что неправильная дробь $frac{107}{4}$ равна смешанному числу $qfrac{r}{b}=26frac{3}{4}$.
Ответ: $frac{{rm 107}}{{rm 4}}{rm =26}frac{{rm 3}}{{rm 4}}$.
Сложение смешанного числа и натурального числа
Правило сложения смешанного и натурального числа:
Для сложения смешанного и натурального числа нужно к целой части смешанного числа прибавить данное натуральное число, дробная часть остается без изменения:
где $afrac{b}{c}$ — смешанное число,
$n$ — натуральное число.
Пример 6
Выполнить сложение смешанного числа $23frac{4}{7}$ и числа $3$.
Решение.
[23frac{4}{7}+3=left(23+3right)+frac{4}{7}=26frac{4}{7}.]
Ответ: $23frac{4}{7}+3=26frac{4}{7}.$
Сложение двух смешанных чисел
При сложении двух смешанных чисел складываются их целые части и дробные части.
Пример 7
Сложить смешанные числа $3frac{1}{5}$ и $7frac{4}{7}$.
Решение.
Воспользуемся формулой:
[afrac{b}{c}+dfrac{e}{f}=left(a+dright)+left(frac{b}{c}+frac{e}{f}right).] [3frac{1}{5}+7frac{4}{7}=left(3+7right)+left(frac{1}{5}+frac{4}{7}right)=10+frac{1cdot 7}{35}+frac{4cdot 5}{35}=10+frac{27}{35}=10frac{27}{35}.]
Ответ: $10frac{27}{35}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Правильные и неправильные дроби
- Смешанные дроби
Правильные и неправильные дроби
Например. Дробь $frac{11}{23}$ является правильной,
так как ее числитель, равный 11, меньше, чем знаменатель, который равен 23: 11
Определение
Дробь называется неправильной, если ее числитель больше знаменателя или равен ему.
Например. Дробь $frac{23}{11}$ — неправильная,
так как 23 > 11 . Дробь $frac{3}{3}$ — неправильная, так как числитель дроби равен ее знаменателю.
Смешанные дроби
Определение
Числа, в состав которых входит целое число и правильная дробь, называются смешанными числами.
Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа.
Например. Для смешанной дроби $3 frac{11}{23}=3+frac{11}{23}$
число 3 — целая часть, $frac{11}{23}$ — дробная.
Неправильную дробь можно записать в виде смешанного числа, для этого нужно
числитель поделить на
знаменатель.
Полученное неполное частное будет целой частью смешанной дроби, остаток — числителем дробной части, а знаменатель
исходной неправильной дроби — знаменателем дробной части.
Пример
Задание. Записать неправильную дробь
$frac{20}{3}$ в виде смешанной.
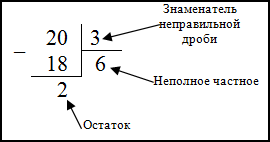
Решение. Поделим числитель дроби — 20 на ее знаменатель — 3 (то есть выделим целую часть):
Итак, получаем, что $frac{20}{3}=20 : 3=$ 6 (остаток 2).
А тогда искомая смешанная дробь
$frac{20}{3}=6 frac{2}{3}$
Ответ. $frac{20}{3}=6 frac{2}{3}$
Чтобы смешанное число записать в виде неправильной дроби, надо целую часть умножить на знаменатель
дробной части, к полученному числу прибавить числитель дробной части и записать эту сумму в числитель,
а знаменатель дробной части оставить без изменений.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Смешанное число
8$frac{2}{3}$ записать в виде неправильной дроби.
Решение. $8 frac{2}{3}=frac{8 cdot 3+2}{3}=frac{26}{3}$
Ответ. $8 frac{2}{3}=frac{26}{3}$
Читать следующую тему: сравнение дробей.
Смешанные дроби и действия с ними
Смешанные дроби – это дроби, в записи которых есть целые числа. Любую смешанную дробь можно представить неправильной дробью.
Неправильная дробь – это дробь, числитель которой больше знаменателя. В таком случае у дроби выделяется целая часть и её можно записать в виде смешанной.
Например,
(frac{7}{4} = frac{4}{4} + frac{3}{4} = 1 + frac{3}{4} = 1frac{3}{4})
1 – целая часть, а (frac{3}{4}) – дробная часть смешанного числа (1frac{3}{4}).
АЛГОРИТМ ПЕРЕВОДА НЕПРАВИЛЬНОЙ ДРОБИ В СМЕШАННУЮ:
-
Разделить числитель на знаменатель в столбик с остатком.
-
Неполное частное будет целой частью.
-
Остаток (если он есть) станет числителем дробной части смешанной дроби, а делитель — знаменателем.
Например,
Переведем неправильную дробь (frac{48}{9}) в смешанную:
Неполное частное (= 5), остаток (= 3,) делитель (= 9), тогда эту неправильную дробь можно записать как: (5frac{3}{9}).
АЛГОРИТМ ПЕРЕВОДА СМЕШАННОЙ ДРОБИ В НЕПРАВИЛЬНУЮ:
-
Перемножить целую часть со знаменателем дробной части.
-
К полученному произведению прибавить числитель дробной части.
-
Записать полученную сумму в числитель неправильной дроби, а знаменатель оставить без изменений.
Например,
Переведем смешанную дробь (4frac{5}{7}) в неправильную:
Числитель неправильной дроби будет равен
((4 bullet 7) + 5 = 28 + 5 = 33).
Знаменатель останется прежний и будет равен 7.
Получим: (4frac{5}{7} = frac{33}{7})
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ДРОБЕЙ:
При сложении и вычитании смешанных чисел отдельно складывают целые части, отдельно дробные по правилам сложения обыкновенных дробей.
-
Если суммой дробных частей является неправильная дробь, то из нее выделяют целую часть и прибавляют к сумме целых частей.
Например:
(5frac{3}{8} + 2frac{6}{8} = (5 + 2) + (frac{3}{8} + frac{6}{8}) = 7 + frac{9}{8} = 7 + 1frac{1}{8} = 8frac{1}{8})
-
Если при вычитании дробная часть уменьшаемого меньше дробной части вычитаемого, то поступают так:
(7frac{3}{5} – 2frac{4}{5} = (7 + frac{3}{5}) – 2frac{4}{5} = (6 + 1 + frac{3}{5}) – 2frac{4}{5} = (6 + 1frac{3}{5}) – 2frac{4}{5} = (6 + frac{8}{5}) – 2frac{4}{5} = 6frac{8}{5} + 2frac{4}{5})
Таким образом мы выделили из целой части единицу и прибавили её к дробной. Теперь можно считать разность:
(7frac{3}{5} – 2frac{4}{5} = 6frac{8}{5} + 2frac{4}{5} = (6 – 2) + (frac{8}{5} – frac{4}{5}) = 4 + frac{4}{5} = 4frac{4}{5})
-
Так же поступают при вычитании смешанной дроби из целого числа.
Например:
(3 – 1frac{2}{6} = (2 + frac{6}{6}) – 1frac{2}{6} = (2 – 1) + (frac{6}{6} – frac{2}{6}) = 1frac{4}{6})
Математика
5 класс
Урок № 71
Понятие смешанной дроби
Перечень рассматриваемых вопросов:
– введение понятий «смешанная дробь», «целая часть смешанной дроби», «дробная часть смешанной дроби»;
– правило преобразования неправильных дробей в смешанные дроби;
– правило преобразования смешанных дробей в неправильные дроби;
– отработка правил преобразования неправильных и смешанных дробей;
– сравнение смешанных дробей.
Тезаурус
Правильная дробь – дробь, числитель которой меньше знаменателя.
Неправильная дробь – дробь, числитель которой больше знаменателя.
Смешанная дробь – сумма натурального числа и правильной дроби, записанная без знака плюс;
Целая часть смешанной дроби – натуральное число в смешанной дроби.
Дробная часть смешанной дроби – правильная дробь в смешанной дроби.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Вы уже знакомы с обыкновенными дробями. Умеете выполнять с ними все арифметические действия. Знаете, что обыкновенные дроби бывают правильными – это те дроби, числитель которых меньше знаменателя, и неправильными – дроби, у которых числитель больше знаменателя.
Если числитель неправильной дроби делится на знаменатель без остатка, то такая неправильная дробь равна частному от деления числителя на знаменатель.
Сумму натурального числа три и правильной дроби две пятых, записанную сокращённо, без знака плюс, называют смешанной дробью.
Натуральное число «три» в смешанной дроби «три целых две пятых» называют целой частью, а правильную дробь «две пятых» – дробной частью смешанной дроби.
Чтобы правильно назвать дробную часть смешанной дроби поступаем так: называя числитель, отвечаем на вопрос: «сколько долей взято?» – две. Называя знаменатель, отвечаем на вопрос: «две каких?» – пятых.
Научимся записывать неправильные дроби, числитель которых не делится на знаменатель нацело, в виде смешанных дробей.
Каждую смешанную дробь можно представить в виде неправильной дроби.
Для этого надо:
• знаменатель дробной части умножить на целую часть,
• прибавить к этому числу числитель дробной части,
• полученное число записать в числитель искомой неправильной дроби,
• знаменатель оставить прежним.
Так как у этих дробей целые части одинаковые, то сравнивать мы будем дробные части. Но дробные части данных дробей имеют разные знаменатели. Чтобы сравнить дроби с разным знаменателем, нужно привести их сначала к общему знаменателю. Меньшей из них будет та дробь, числитель которой меньше.
А можно ли сравнить эти дроби, не приводя их к общему знаменателю? Можно. И даже не одним способом.
Тренировочные задания
Преобразуем каждую смешанную дробь в неправильную, пользуясь правилом:
– знаменатель умножить на целую часть,
– прибавить его к дробной части,
– полученное число записать в числитель,
– знаменатель останется прежним.

Для того чтобы выбрать равные дроби, нужно привести их к одинаковому виду: или все дроби сделать неправильными, или все дроби – смешанными.
Преобразуем первые четыре неправильные дроби в смешанные числа.


 Способ 1.
Способ 1. Способ 2.
Способ 2.