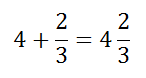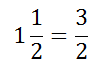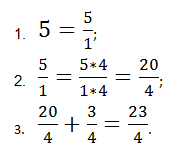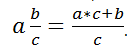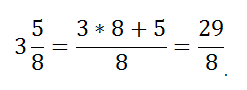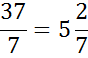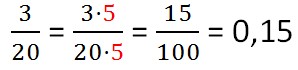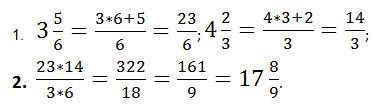Смешанные числа: определения, примеры
Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде
.
Где n — целая часть,
— дробная часть.
Смешанное число равно сумме своей целой и дробной части. То есть
.
Примеры смешанных чисел
Каждое такое смешанное число содержит целую и дробную части.
Чтобы точно определять, какая именно перед вами дробь, запомните:
-
Дробь вида
называется правильной дробью. В ней числитель всегда меньше знаменателя.
-
Дробь вида
называется неправильной. В таких дробях числитель больше знаменателя или равен ему.
-
Дробь вида
называется смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.
Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Сложение смешанных чисел
Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.
Сложение смешанного числа и натурального числа
Запоминаем
Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой.
Представим первое правило в виде буквенных выражений.
Выполним сложение смешанного числа
и натурального числа d.
Известно, что любое смешанное число равное сумме целой и дробной частей.
Это значит, что
.
Тогда
.
Рассмотрим примеры сложения смешанных чисел с натуральными числами.
Пример 1. Выполните сложение смешанного числа
и натурального числа 18.
Как решаем:
Записываем выражение
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа и вычисляем:
.
Ответ:
.
Пример 2. Выполните сложение смешанного числа
и натурального числа 10.
Как решаем:
Записываем выражение:
.
.
Ответ:
.
Пример 3. Выполните сложение смешанного числа
и натурального числа 2.
Как решаем:
Записываем выражение:
.
Ответ:
.
Сложение смешанного числа со смешанным числом
Запоминаем
Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части.
Представим правило в виде буквенных выражений.
Выполним сложение смешанного числа
и смешанного числа
.
Следуя правилу, запишем выражение в виде:
.
Рассмотрим примеры сложения смешанных чисел.
Пример 1. Сложите смешанное число
и смешанное число
.
Как решаем:
Записываем выражение:
.
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
Решаем: складываем целые части 2 + 7 = 9.
Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.
.
Наименьшее общее кратное 5 и 15 — 15.
.
Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь:
сокращаем на 3, получим дробь
.
.
Ответ:
.
Пример 2. Сложите смешанное число
и смешанное число
.
Как решаем:
Записываем выражение:
.
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
.
Решаем: складываем целые части 13 + 2 = 15.
Складываем дробные части
Наименьшее общее кратное 12 и 20 равно 60.
.
Сокращаем дробь
на
.
.
Ответ:
Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.
Сложение смешанного числа и правильной дроби
Запоминаем
Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений.
Представим правило в виде буквенного выражения.
Если нам нужно сложить смешанное число
и правильную дробь
, то запишем следующее выражение:
.
Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.
Пример 1. Выполните сложение обыкновенной дроби
и смешанного числа
Как решаем:
Записываем выражение:
Согласно правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби
.
Наименьшее общее кратное 5 и 20 равно 20.
, сокращаем на 5, получается
.
.
Ответ:
.
Пример 2. Выполните сложение правильной дроби
и смешанного числа
.
Как решаем:
Записываем выражение:
.
Следуя правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби
.
Наименьшее общее кратное 4 и 2 равно 4.
.
.
Ответ:
.
Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.
Вычитание смешанных чисел
Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.
Вычитание одного смешанного числа из другого
Запоминаем
Любое смешанное число можно представить в виде суммы целой и дробной части.
Это значит, что
.
Исходя из значения дробных частей, вычитание можно выполнять тремя способами.
Если дробная часть уменьшаемого больше дробной части вычитаемого
, то выполняем вычитание целой части вычитаемого из целой части уменьшаемого, затем выполняем вычитание дробных частей. Вот так:
-
.
Пример. Выполните вычитание
.
Как решаем:
Чтобы решить пример, нужно выяснить, какая из дробных частей больше:
или
.
Чтобы сравнить две дроби, приведем их к общему знаменателю — 8:
.
По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.
Это значит, что
.
.
Следуя правилу, выполняем вычитание
.
Вычитаем дробные части
.
НОК = 8
.
.
Ответ:
.
Запоминаем
Если дробные части смешанных чисел равны, то есть
, то разность этих смешанных чисел будет равна разности их целых частей.
Пример. Выполните вычитание:
Как решаем:
Дробные части смешанных чисел равны. Это значит, что
.
Следуя правилу, выполним вычитание:
.
Ответ:
.
Запоминаем
Если дробная часть уменьшаемого меньше дробной части вычитаемого
, то вычитание выполняется вот так
.
Пример. Найдите значение разности смешанных чисел
и
Как решаем:
Запишем выражение
Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.
НОК 5 и 15 = 15.
Следуя правилу, решаем:
.
Представим число 21 в виде смешанной дроби
и выполним вычитание дроби из натурального числа:
Ответ:
.
Вычитание смешанного числа из натурального числа
Запоминаем
Чтобы из целого числа вычесть смешанное число, сначала отнимите от натурального числа целую часть смешанного числа, а затем отнимите от этой разности дробную часть смешанного числа.
Представим правило в виде буквенного выражения:
.
Пример. Отнимите от натурального числа 15 смешанное число
Как решаем:
Запишем выражение:
.
Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:
Ответ:
Умножение смешанных чисел
Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.
Умножение смешанного числа на смешанное число
Запоминаем
Чтобы умножить одно смешанное число на другое, нужно перевести оба смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей.
Пример. Выполните умножение смешанного числа
и
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанные числа в неправильные дроби.
Выполним умножение:
.
Из полученной неправильной дроби выделяем целую часть
.
Ответ:
.
Умножение смешанного числа на обыкновенную дробь
Запоминаем
Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.
Пример. Умножьте смешанное число
на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби.
.
Выполним умножение дробей
Выделим из полученной неправильной дроби целую часть
Ответ:
.
Умножение целого числа на дробь
Запоминаем
Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.
Пример. Выполните умножение числа 7 на обыкновенную дробь
Как решаем:
Запишем выражение:
Выделим из получившейся неправильной дроби целую часть
.
Ответ:
Деление смешанных чисел
Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.
Деление смешанного числа на смешанное число
Запоминаем
Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей.
Пример. Найдите результат деления смешанного числа
на смешанное число
Как решаем:
Запишем выражение:
Следуя правилу, переведем оба смешанных числа в неправильные дроби.
Пользуясь правилом деления дробей, находим частное:
Ответ:
.
Деление смешанного числа на целое число
Запоминаем
Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Разделите смешанное число
на натуральное число 15
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанное число в неправильную дробь
Выполним деление
Ответ:
.
Деление целого числа на смешанное число
Запоминаем
Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Выполните деление натурального числа 30 на смешанное число
Запишем выражение
Представим смешанное число в виде неправильной дроби
.
Выполним деление
.
Выделим из полученной неправильной дроби целую часть
.
Ответ:
.
Деление смешанного числа на обыкновенную дробь
Запоминаем
Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление.
Пример. Разделите смешанное число
на обыкновенную дробь
Как решаем:
Запишем выражение
.
Представим смешанное число в виде неправильной дроби
.
Выполним деление, следуя правилу деления дробей:
.
Ответ:
.
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Если мы возьмем сумму n+ab, где значением n может быть любое натуральное число, а ab представляет из себя правильную обыкновенную дробь, то мы можем записать то же самое, не используя плюс: nab. Возьмем конкретные числа для ясности: так, 28+57 – это то же самое, что и 2857. Запись дроби рядом с целым числом принято называть смешанным числом.
Смешанное число представляет собой такое число, которое равно сумме натурального числа n с правильной обыкновенной дробью ab. В таком случае n является целой частью числа, а ab – его дробной частью.
Из определения следует, что любое смешанное число равно тому, что получится в результате сложения его целой и дробной части. Таким образом, будет выполняться равенство nab=n+ab.
Его также можно записать в виде n+ab=nab.
Какие можно привести примеры смешанных чисел? Так, к ним относится 518, при этом пятерка – это его целая часть, а одна восьмая – дробная. Еще примеры: 112, 2343453, 34000625.
Выше мы писали, что в дробной части смешанного числа должна стоять только правильная дробь. Иногда можно встретить записи вида 5223, 7572. Они не являются смешанными числами, т.к. их дробная часть неправильная. Их нужно понимать как сумму целой и дробной части. Такие числа можно привести к стандартному виду записи смешанных чисел, выделив целую часть из неправильной дроби и добавив ее к 5 и 75 в этих примерах соответственно.
Числа вида 0314также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
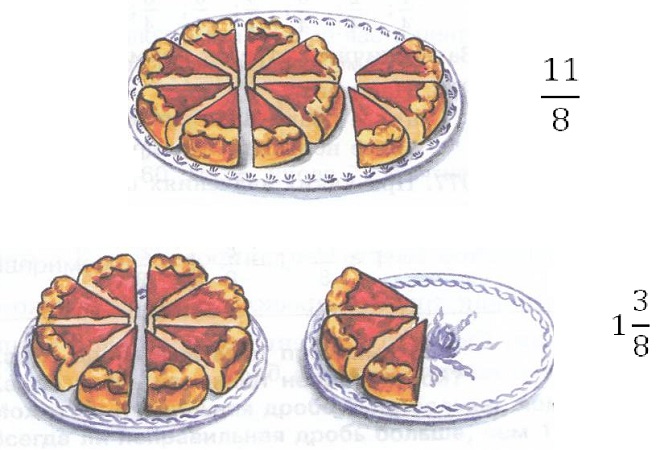
Возьмем целый торт и еще три четверти такого же. Согласно правилам сложения, у нас на столе находится 1+34 торта. Эту сумму можно представить в виде смешанного числа как 134 торта. Если мы возьмем целый торт и тоже разрежем его на четыре равные части, то у нас на столе будет 74 торта. Очевидно, что от разрезания количество не увеличилось, и 134=74.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Вернемся к нашим 74 торта, оставшимся на столе. Сложим из его кусочков один торт обратно (1+34). У нас опять будет 134.
Ответ: 74=134.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Например,
84=2, так как 8:4=2.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число nab как сумму целой и дробной части. Получается n+ab
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n1).
3.После этого выполняем уже знакомое действие – складываем две обыкновенные дроби n1 и ab. Получившаяся в результате неправильная дробь и будет равной смешанному числу, данному в условии.
Разберем это действие на конкретном примере.
Представьте 537 в виде неправильной дроби.
Решение
Выполняем последовательно шаги указанного выше алгоритма. Наше число 537 – это сумма целой и дробной части, то есть 5+37. Теперь пятерку запишем в виде 51. У нас получилась сумма 51+37.
Последний шаг – сложение дробей, имеющих разные знаменатели:
51+37=357+37=387
Все решение к краткой форме можно записать как 537=5+37=51+37=357+37=387.
Ответ: 537=387.
Таким образом, с помощью указанной выше цепочки действий мы можем перевести любое смешанное число nab в неправильную дробь. У нас получилась формула nab=n·b+ab, которую мы и будем брать для решения дальнейших задач.
Представьте 1525 в виде неправильной дроби.
Решение
Возьмем указанную формулу и подставим в нее нужные значения. У нас n=15, a=2, b=5, следовательно, 1525=15·5+25=775.
Ответ: 1525=775.
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Любая неправильная дробь ab –это смешанное число qrb. Здесь q представляет собой неполное частное, а r – это остаток от ab. Таким образом, целая часть смешанного числа есть неполное частное от деления ab, а дробная – это остаток.
Приведем доказательство этого утверждения.
Нам требуется пояснить, почему qrb=ab. Для этого смешанное число qrb надо представить в виде неправильной дроби, выполнив все шаги алгоритма из предыдущего пункта. Поскольку – неполное частное, а r – остаток от деления a на b, то должно выполняться равенство a=b·q+r.
Таким образом, q·b+rb=ab поэтому qrb=ab. Это и есть доказательство нашего утверждения. Подытожим:
Выделение целой части из неправильной дроби ab осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
2) Записываем результаты в виде qrb. Это и есть наше смешанное число, равное исходной неправильной дроби.
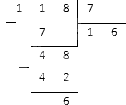
Представьте 1074 в виде смешанного числа.
Решение
Делим 104 на 7 столбиком:
Деление числителя a=118 на знаменатель b=7 дает нам в итоге неполное частное q=16 и остаток r=6.
В итоге мы получаем, что неправильная дробь 1187 равна смешанному числу qrb=1667.
Ответ: 1187=1667.
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).
Для этого вспомним, какая связь существует между обыкновенными дробями и делением. Из этого можно вывести равенства: ab=a:b=c. Получается, что неправильную дробь ab можно заменить натуральным числом c.
Например, если в ответе получилась неправильная дробь 273, то можем записать вместо нее 9, поскольку273=27:3=9.
Ответ: 273=9.
Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 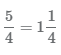
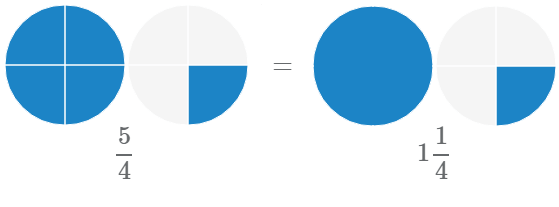
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 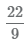
- 1 Разделим числитель на знаменатель 22 ÷ 9, получим 2 целых и 4 в остатке.
- 2 Число 2 будет целой частью смешанного числа.
-
3 Остаток от деления 4 будет числителем дроби, а знаменатель останется прежним, равным 9. В результате получаем
Пример Перевести неправильные дроби  в смешанные числа.
в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 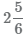
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Рассмотрим на примерах как переводить смешанные числа в неправильные дроби.
Пример Перевести смешанные числа  в неправильные дроби.
в неправильные дроби.
Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.
Как сделать из неправильной дроби правильную дробь?
Рассмотрим неправильную дробь (frac{21}{9})
Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

Получаем дробь (2frac{3}{9}), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а (frac{3}{9}) – правильная дробь.
Смешанные дроби состоят из целой и дробной части.
Рассмотрим еще одну неправильную дробь (frac{76}{5})
Разделим ее столбиком:

Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
(color{blue} {3}frac{color{green} {2}}{color{red} {5}} = frac{color{red} {5} times color{blue} {3} + color{green} {2}}{color{red} {5}} = frac{17}{5})
Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: (frac{508}{17})
Решение:
Разделим дробь столбиком:
Ответ: Получили смешанную дробь (29frac{15}{17})
Пример №2:
Представьте число в виде неправильной дроби: а) (9frac{2}{3}), б) (1frac{3}{7})
Решение:
а) (9frac{2}{3} = frac{9 times 3 +2}{3} = frac{29}{3}\\)
б) (1frac{3}{7} = frac{1 times 7 +3}{7} = frac{10}{7}\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил (frac{2}{5}) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь (frac{2}{5}), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
(120 div 5 = 24) задачи это одна часть или (frac{1}{5})
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
(24 times 2 = 48) задач
Ответ: за неделю Миша решил 48 задач.
Многие ученики, когда подходит время изучать смешанные числа в 6 классе, сомневаются, что подобные вычисления пригодятся им в жизни, в особенности в наше время, когда можно при необходимости воспользоваться калькулятором.
Однако в быту подобными выражениями мы пользуемся чаще, чем может показаться на первый взгляд: при измерении времени, в рецептах блюд, дозировках лекарств и так далее.
Что такое смешанное число
Под смешанным числом понимают сумму натурального числа и обычной дроби, записанную без знака «+».
― это смешанное число. Читать данное выражение следует так: «четыре целых пять седьмых».
Где 4 ― это целая, а 5/7 ― дробная часть.
Как представить смешанное число в виде неправильной дроби
Если мы, имея на руках один пирог и ещё половину (то есть 1½), возьмём и дополнительно поделим целый пирог на два равных куска, то у нас в итоге окажется три половинки (или 3/2). Но суть от этого всё равно не изменится: «количество» пирога останется прежним.
Этот пример наглядно показывает, что смешанное число можно превратить в неправильную дробь. Это преобразование можно выполнить за несколько шагов:
- Записать целую части в виде дроби.
- Подвести выражения под один знаменатель.
- Сложить обе части.
Например, 5¾ преобразуется следующим образом:
Данные вычисления можно выразить и в более короткой формуле:
Пример преобразования:
Как выделить целую часть неправильной дроби
Чтобы совершить обратную операцию и превратить неправильную дробь в смешанное число, нужно сначала выделить её целую часть. Она будет равна результату деления числителя на знаменатель.
Если поделилось без остатка, значит больше никаких действий выполнять не нужно.
Если поделить без остатка не получается, то для завершения преобразования в смешанное число, остаток следует вынести в числитель. Знаменатель остаётся тем же.
Как перевести смешанную дробь в десятичную
Так как подобную процедуру часто приходится проделывать не только в школе, выполняя математические задания и решая различные уравнения, но и в повседневности, ― умение проделывать это легко и быстро может оказаться очень полезным.
Для перевода необходимо:
- Целую часть оставляем без изменений.
- Дробную часть переводим в десятичную. Для этого выражение нужно привести к общему знаменателю, который делится на 10. Получившееся в числителе число записывается после нуля с запятой.
- Складываем получившиеся результаты.
Таким образом, чтобы преобразовать 53/5, нужно:
- Выписать целую часть ― 5.
- Преобразовать дробную часть .
- Сложить эти выражения 5 + 0,6 = 5,6.
Как сократить смешанную дробь
При сокращении целая часть не трогается, изменениям подвергается только дробная. Чтобы сократить её, нужно:
- выявить наибольший общий множитель для числителя и знаменателя;
- поделить их на это число.
Например, чтобы сократить 76/9, необходимо:
- Найти общий множитель для 6 и 9. Для этого раскладываем их на простые числа 6 = 2 * 3; 9 = 3 * 3. Из чего следует, что общий множитель для них ― это 3.
- Делим и числитель, и знаменатель на три ― 6 : 3 = 2 и 9 : 3 = 3;
Сложение смешанных чисел
Чтобы осуществить сложение, нужно необходимую операцию проделать отдельно для целых и отдельно для дробных частей. А получившиеся результаты сложить.
Например, чтобы решить следующий пример
,
необходимо:
- Сложить целые части 9 + 3 = 12.
- Сложить дробные части 1/3 + 1/3 = 2/3.
- Сложить их друг с другом
Вычитание смешанных чисел
Для вычитания вычисления аналогичны. Следующую задачу
следует решить так:
- 7 – 4 = 3.
- 3/4 — 1/4 = 2/4 = 1/2.
- 3 + ½ = 3½.
Как умножать смешанные числа
Чтобы перемножить смешанные числа, необходимо:
- осуществить их перевод в неправильные дроби;
- полученные выражения перемножить по правилам умножения обыкновенных дробей.
Для примера решим следующее задание:
Заключение
Происхождение чисел сложно точно проследить. Известно только, что человек стал пользоваться ими с самых седых времён. История дробей также берёт своё начало в глубокой древности: подобными понятиями оперировали уже в древнем Египте.
Сегодня просто невозможно представить нашу жизнь без них. Все современные научные достижения, на которых основано наше общество, были бы попросту неосуществимы, не говоря уже о том, что значительно усложнилась бы наша повседневная жизнь. Вот почему так важно знать, что они собой представляют.
Сумму натурального числа правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. Можно сказать немного иначе: запись числа, которая содержит целую и дробную части, называют смешанной. Для краткости вместо «число в смешанной записи» говорят смешанное число.

Например,
целая часть этого смешанного числа равна 31, дробная –
Смешанное число можно представить в виде неправильной дроби. Чтобы представить смешанное число в виде неправильной дроби, нужно:
1) умножить его целую часть на знаменатель дробной части;
2) к полученному произведению прибавить числитель дробной части;
3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Например,
Неправильную дробь можно представить в виде смешанного числа.
Запись неправильной дроби в виде смешанного числа называют выделением целой части дроби.
Чтобы выделить целую часть неправильной дроби, надо разделить её числитель на знаменатель и записать смешанное число в виде:
- целая часть – частное от деления;
- числитель дробной части – остаток от деления;
- знаменатель дробной части – знаменатель данной неправильной дроби.
Если остаток от деления числителя неправильной дроби на её знаменатель равен 0, неправильная дробь равна получившемуся при делении натуральному числу.
Например, выделим целую часть неправильной дроби
131 : 8 = 16 (и 3 в остатке);
Выделим целую часть неправильной дроби
13104 : 13 = 1008.

Чтобы найти сумму смешанных чисел, нужно сложить отдельно целые и дробные части.
Если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.
Например,
Вычитание смешанных чисел
Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то одну единицу целой части уменьшаемого необходимо предварительно прибавить к его дробной части.
Например,
Остались вопросы? Хотите знать больше о смешанных числах?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.


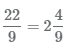
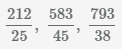 в смешанные числа.
в смешанные числа.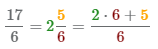
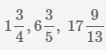 в неправильные дроби.
в неправильные дроби.