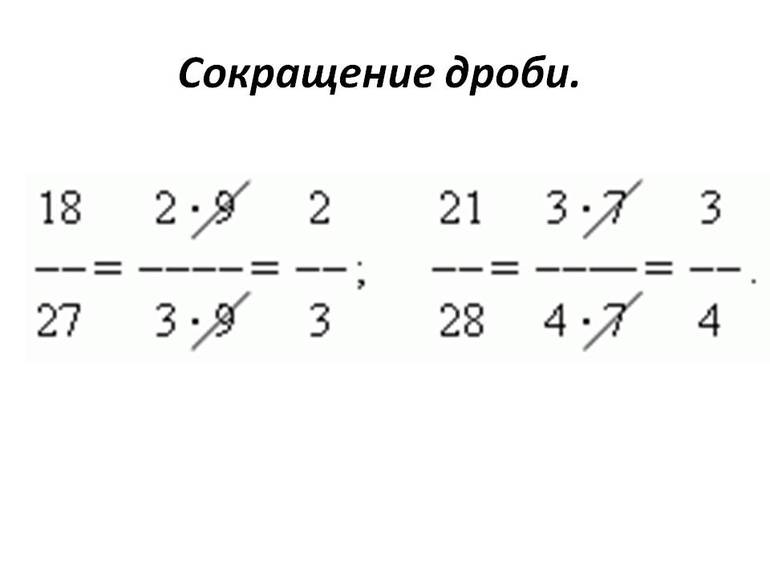
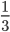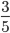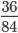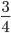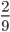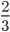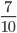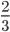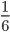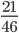Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:
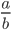
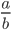
где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений —
на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.
3 : 3 =1
15 : 3 = 5
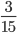
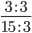
Сокращение выполнено: 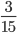
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.
4 : 2 = 2
16 : 2 = 8
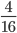
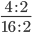
Сокращение выполнено: 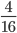
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 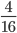
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
-
— несократимая дробь, так как по свойствам НОД мы знаем, что:
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1
36 : 12 = 3
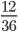
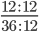
Сокращение выполнено: 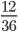
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3
25 : 5 = 5
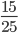
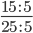
Сокращение выполнено: 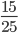
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
- Найдите НОД числителя и знаменателя дроби.
- Разделите числитель и знаменатель дроби на НОД.
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
- Например, дана дробь
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.
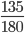
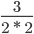
Сокращение выполнено: 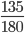
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9
18 : 9 = 2
81 : 9 = 9
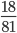
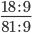
Сокращение выполнено: 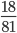
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:
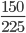
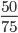
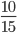
Сокращение выполнено: 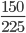
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7
240 : 24 = 10
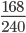
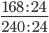
Сокращение выполнено: 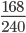
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2
540 : 180 = 3
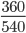
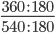
Сокращение выполнено: 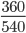
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1
2520 : 420 = 6
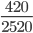
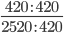
Сокращение выполнено. Дробь приведена к несократимому виду: 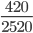
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21
3450 : 75 = 46
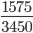
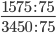
Сокращение выполнено. Дробь приведена к несократимому виду: 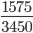
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.
Что такое «сокращение дробей»
Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.
В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.
К примеру, возьмем обыкновенную дробь 624 и сократим ее. Разделим числитель и знаменатель на 2, в результате чего получим 624=6÷224÷2=312. В этом примере мы сократили исходную дробь на 2.
Приведение дробей к несократимому виду
В предыдущем примере мы сократили дробь 624 на 2, в результате чего получили дробь 312. Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?
Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.
ab=a÷НОД(a, b)b÷НОД(a, b)
Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.
Вернемся к дроби 624 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6. Сократим дробь:
624=6÷624÷6=14
Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.
Правило сокращения дробей
Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.
Чтобы сократить дробь нужно:
- Найти НОД числителя и знаменателя.
- Разделить числитель и знаменатель на их НОД.
Рассмотрим практические примеры.
Дана дробь 182195. Сократим ее.
Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.
195=182·1+13182=13·14НОД(182, 195)=13
Разделим числитель и знаменатель на 13. Получим:
182195=182÷13195÷13=1415
Готово. Мы получили несократимую дробь, которая равна исходной дроби.
Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.
Дана дробь 3602940. Сократим ее.
Для этого представим исходную дробь в виде:
3602940=2·2·2·3·3·52·2·3·5·7·7
Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:
3602940=2·2·2·3·3·52·2·3·5·7·7=2·37·7=649
Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.
Сократим дробь 20004400.
Сразу видно, что числитель и знаменатель имеют общий множитель 100. Сокращаем дробь на 100 и получаем:
20004400=2000÷1004400÷100=2044
Далее замечаем, что числитель и знаменатель дроби 2044 делятся на 2. Сокращаем и приходим к виду:
2044=20÷244÷2=1022
Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:
1022=10÷222÷2=511
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Самые старые упоминания о таких математических явлениях, как дробь, учёные обнаружили в древнем Египте. Особенностью их было то, что у них были обозначения только вида 12, 23,13, при этом больше двойки числа, делимого они не использовали, а использовали метод сложения, к примеру, вместо дроби 56, писали 12 +13.
Но применять такие дроби было сложно, поэтому учёные разных областей пытались вывести общую универсальную формулу для удобства. Так появилась шестидесятеричная, но проводить вычисления с ней тоже было очень трудно, однако её довольно долго применяли в Вавилоне и Греции. Существовала также система называемая Асс, её суть в делении на 12, использовали её римляне. Результат такого деления, точнее одну долю, называли унцией. Самой близкой по своей системе исчисления была дробь, которую предложили в Индии, разница от современных была в формате записи, без чёрточки, и такая дробь была перевернута, в верхней части находился делитель, а в нижней делимое. Та запись, которую и по сей день используют в математике была придумана арабами.
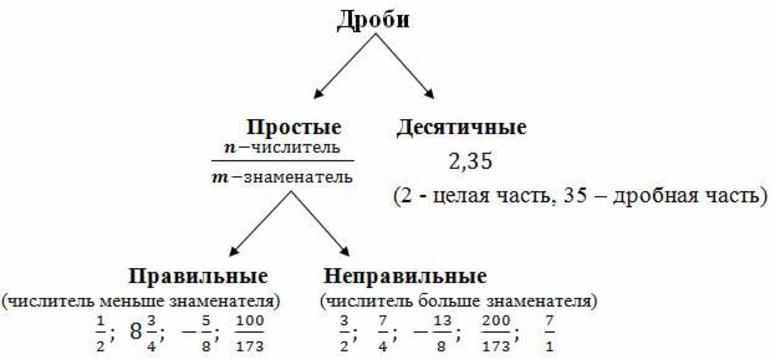
Что такое дробь, основные понятия и виды
Определение
Дробь — число, состоящее из нескольких равных долей.
По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.
Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:
- 15- разделена наклонной линией, читается как одна пятая;
- [frac{1}{5}] — горизонтальной линией.
Определения:
- Числитель — число, находящееся в верхней границе дроби;
- Знаменатель — число которое мы видим в нижней границе дроби.
Например: 15, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 25 (две пятые части торта).
Обыкновенные дроби имеют два типа правильные и неправильные.
Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.
Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.
Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.
Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — <span id=»MathJax-Element-2-Frame» class=»mjx-chtml MathJax_CHTML» tabindex=»0″ data-mathml=»435″ role=»presentation» style=»font-size: 113%; text-align: center; position: relative;»>4 frac{3}{5}, где четыре это целая часть, а 35 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.
Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру <span id=»MathJax-Element-3-Frame» class=»mjx-chtml MathJax_CHTML» tabindex=»0″ data-mathml=»510,6100″ role=»presentation» style=»font-size: 113%; text-align: center; position: relative;»>frac{5}{10}, frac{6}{100} и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.
Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.
Несократимая дробь, если такие действия выполнить нельзя.
Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример <span id=»MathJax-Element-4-Frame» class=»mjx-chtml MathJax_CHTML» tabindex=»0″ data-mathml=»37−31″ role=»presentation» style=»font-size: 113%; text-align: center; position: relative;»>frac{frac{3}{7}}{-31}
Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.
Равные обыкновенные [frac{a}{d} frac{c}{b}] — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.
Положительные и отрицательные дроби.
Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример [+frac{6}{9}].
Отрицательными, считаются дроби со знаком минус, пример [-frac{6}{9}].
Стоит отметить что две дроби вида [-frac{6}{9} text { и }+frac{6}{9}] являются противоположными.
Алгебраическая дробь.
Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —
[
frac{x+y}{x-y}, frac{x^{3}+1}{x^{2}-x+2}, frac{a^{2}-4}{a+2}, frac{a}{2}, frac{3 a+7}{5}
]
Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.
Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример: в.
Многочлен — это сумма одночленов. Пример: 7а+6в
Дроби на координате прямых.
Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.
Действия, которые можно выполнить с дробями
В общем то, действия с дробями это все те же действия, которые можно выполнить с числами:
- Сравнение;
- Сложение;
- Вычитание;
- Умножение;
- Деление.
Свойства дроби
Чтобы сложить или вычесть дроби, дробь обязана иметь равные знаменатели, необходимо просто выполнить это действие с их числителями
Примеры:
[
frac{4}{9}+frac{5}{9}=frac{4+5}{9} ; text { и } frac{4}{9}-frac{5}{9}=frac{5-4}{9}.
]
Что же касается дробей с разной частью делителя (Знаменателя), то тут чтобы выполнить действия сложения и вычитания с ними необходимо привести знаменатели к общему числу.
Примеры: [frac{4}{9}+frac{5}{8}=frac{4+5}{9 cdot 8}], точно так же и для вычитания.
Чтобы выполнить такое действие, как умножение обыкновенных дробей, нужно произвести умножение сначала с их числителями, а после и знаменателями.
Пример: [frac{4}{9} cdot frac{5}{8}=frac{4 cdot 5}{9 cdot 8}].
При умножении дроби на число, в такой вычислении просто умножается числитель на заданное число, а знаменатель остаётся тем же.
Пример: [frac{4}{9} cdot 6=frac{4 cdot 6}{9}];
Что же касается деления, то при делении одной дроби на другую, нужно произвести умножение, при котором первая дробь остаётся в неизменном виде, а вторая переворачивается. То есть получается мы умножаем числитель первой дроби данного примера, на знаменатель второй, и полученное число находится в верхней части дроби, а в нижней умножение знаменателя первой дроби на числитель второй.
Пример: [frac{4}{9} backslash frac{5}{8}=frac{4 cdot 8}{9 cdot 5}].
Сравнение дробей
Чтобы провести сравнение с разными делителями (знаменателями), необходимо сделать так, чтобы знаменатель стал общим только тогда можно будет сравнить числители. Соответственно, где числитель больше там и дробь больше.
Основное свойство дробей
Основным свойством дроби является выражение — «числитель и знаменатель можно делить и умножать на одно и то же число при этом значение всей дроби не поменяется.»
Еще одно определение которое пригодится нам для сокращения дроби это НОД.
НОД — наибольший общий делитель.
Общий делитель — это число, которое может быть делителем каждого из указанных чисел.
Пример: если взять число 3, то оно станет общим делителем для чисел 6 и 9. так как 9=3*3 а 6=3*2.
Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)
Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.
Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если rk+1=0, при этом rk=НОД(a, b)
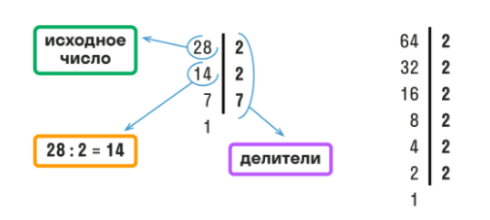
Пример. Рассчитаем НОД для 28 и 64.
Как находим:
Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (28) = 2 * 2 * 7
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Сокращение дроби
Выражение сократить дробь, фактически означает что необходимо провести деление её числителя и знаменателя на одно и то же число, не равное единице.
Результатом таких действий станет появление новой дроби, значение которой, равно первичной.
Например: возьмём обыкновенную дробь [frac{12}{44}] и произведем сокращение. Для этого разделим и числитель и знаменатель на 2, получится такая дробь [frac{12}{44} backslash 2=frac{12 backslash 2}{44 backslash 2}=frac{6}{22}].
Нет времени решать самому?
Наши эксперты помогут!
Несократимый вид дроби, приведение к такому виду
Обычно целью таких манипуляций с дробями является получение из исходного вида дроби несократимый. К примеру дробь, которая получилась у нас выше, [frac{6}{22}] при сокращении на два, как мы видим все ещё можно сократить.
Для того чтобы привести дробь к виду несократимой, нужно выполнить манипуляции по делению, числителя и знаменателя на наибольший НОД. В таком случае по свойству НОД в числителе и знаменателе окажутся простые числа, а дробь будет несократимой.
[
frac{a}{d}=frac{a backslash text { НОД }(a, d)}{d backslash text { НОД }(a, d)}
]
Из вышесказанного следует, что приведение дроби к несократимому виду значит, нужно произвести деление числителя и знаменателя на их НОД.
Пример: вернёмся к нашему примеру дроби [frac{12}{44}], для приведения ее к несократимому виду нужной сначала найти наибольший общий делитель чисел 12 и 44. таким числом НОД для них является цифра 4.
Получается: [frac{12}{44}=frac{12 backslash 4}{44 backslash 4}=frac{3}{11}].
Для чего нужно сокращение? Такие манипуляции с дробями необходимо применять, в случаях работы с большими числами.
Стоит вспомнить негласное правило математики, суть его в том, что если что-то можно сделать проще нужно упростить. Поэтому, говоря о сокращении дроби, имеется в виду именно приведение к несократимому виду, а не просто уменьшение числителя и знаменателя.
Правило сокращения
Для того чтобы сократить, необходимо:
- Найти делитель наибольшего значения, который будет общим для знаменателя и числителя;
- Разделить числитель и знаменатель на него.
Примеры:
Дана такая дробь:<span id=»MathJax-Element-21-Frame» class=»mjx-chtml MathJax_CHTML» tabindex=»0″ data-mathml=»182195″ role=»presentation» style=»font-size: 113%; text-align: center; position: relative;»>frac{182}{195}. сократим её.
Найдём такой делитель, при помощи применения алгоритма Евклида.
195 = 182 *1+13
182=13*14
Из чего следует, что НОД(182,195)=13
Поэтому для сокращения дроби [frac{182}{195}], разделим числитель 182 и знаменатель 195 на 13 и получим равенство: [frac{182}{195}=frac{182 backslash 13}{195 backslash 13}=frac{14}{25}]
Таким образом мы и получили несократимую дробь равную исходной.
Второй способ.
Второй способ основан на разложении числителя и знаменателя исходной дроби на простые множители, из которых позже все общие множители убираются.
Пример сокращения: [frac{123}{154}] для сокращения представим числитель и знаменатель дроби в виде простых множителей
[
frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}
]
Затем уберём все общие множители, как в числителе так и в знаменателе, [frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}=frac{2 cdot 7}{3 cdot 5}=frac{14}{15}]
Третий способ сокращения дроби.
Третий способ — способ последовательного сокращения. Применяя такой способ, сокращение происходит поэтапно, сокращая каждый раз на какой-либо очевидный общий множитель.
Пример: [frac{18000}{22000}]
При сокращении такой дроби сразу можно увидеть, что и числитель и знаменатель деяться на 1000 в результате такого деления получается:
[
frac{18000}{22000}=frac{18000 backslash 1000}{22000 backslash 1000}=frac{18}{22}
]
Следующим этапом мы видим, что оба значения и числителя, и знаменателя делятся на 2, получим несократимую дробь.
[
frac{18}{22}=frac{18000 backslash 2}{22000 backslash 2}=frac{9}{11}
]
Как мы видим сокращение дроби не такой сложный процесс, главное подобрать удобный способ.
Сокращение алгебраической дроби
Так же, как и в примерах выше, сокращение алгебраической дроби, это деление числителя и знаменателя на общий делитель. Отличие в том, что в алгебраической, таким общим множителем является многочлен и одночлен.
Для того чтобы сократить такие дроби нужно пройти три этапа:
- Определение множителя, который будет общим для числителя и знаменателя;
- Сокращение коэффициента;
- Деление числителя и знаменателя на множитель.
Сокращая дробь со степенями, применяется правило деления степеней с равными основаниями.
Формула:
[
a^{n} div a^{m}=a^{n-m}
]
Рассмотрим пример сокращения со степенями:
[
frac{x^{3}}{x^{2}}=frac{x^{3} / x^{2}}{x^{2} / x^{2}}=frac{x^{3-2}}{x^{2-2}}=frac{x^{1}}{x^{0}}=frac{x}{1}=x
]
Исходя из вышеописанной схемы:
- Сокращаем x3 и x2;
- Производим деление выбирая меньшее значение степени;
- Вычитаем.
В результате получаем сокращенную дробь.
Не забываем, что сократить можно только одинаковые буквенные множители.
Сокращение дробей с одночленами.
Пример: [frac{40 x}{5 x^{2}}=frac{8}{x^{2-1}}=frac{8}{x}]
Решение:
- 8 — тот самый множитель, который является общим
- Х и x2 делим на x и получаем ответ.
Дроби с многочленами: сокращение.
Для сокращения таких видов, существует два правила:
- Сократить многочлен в взятый в скобки, можно только с точно таким же многочленом в скобках;
- Сократится должен весь многочлен, взятый в скобки, нельзя сократить только часть.
Пример: [frac{x-c}{x(x-c)}=frac{1}{x}]
Вынесение общего множителя при сокращении.
Бывают случаи, когда при сокращении алгебраической дроби с многочленами, их нет одинаковых, в таком случае нужно убрать общий множитель за скобки.
Для такого вынесения тоже существуют правила их 4:
- необходимо найти число, на которое можно разделить числа каждого одночлена;
- необходимо также найти буквенный множитель, который повторяется, в каждом одночлене, их может быть несколько;
- выносим буквенный множитель, который был найден, за скобки;
- производим работу с оставшимися многочленами в скобках.
Для того чтобы умножить многочлен на одночлен, необходимо по очереди умножить каждый член многочлена на одночлен.
Приведём пример:
[frac{6 x+42 a}{7 a+x}=frac{6(x+7 a)}{7 a+x}=frac{6}{7}]
Калькулятор сокращения дробей
Подведём итоги. Для того чтобы не возникло трудностей с сокращением, стоит запомнить:
- Сокращая дробь вам необходимо найти общий множитель для числителя и знаменателя, если речь идет об алгебраических дробях, но и НОД обыкновенных;
- Разделить числитель и знаменатель на общий множительделитель;
- Если дробь алгебраическая, при делении многочлена на множитель необходимо вынести общий множитель за скобки;
- Стоит хорошо выучить все формулы и определения, связанные с дробями.
- Всегда проверять результат сокращения.
Общие сведения
Первые упоминания о дробях встречаются в Древнем Египте. Его жители умели делить два предмета на три части. Применяли они для этого специальное обозначение: 1/2, 2/3, 1/3. При этом запись вида 2/3 была единственной, где в верхней части использовалась не единица, а двойка. Египтяне для обозначения, впрочем, как и вавилоняне, использовали формулу: 1/ n. Для записи других дробей использовалась сумма. Например, вместо 8/15 они использовали сложение двух выражений: 1/3 и 1/5.
Работать с такими дробями было сложно. Различные философы и учёные пытались придумать запись, универсальную для любых случаев. Так, были попытки использовать шестидесятеричные дроби, которыми пользовались в Вавилоне и Греции. Но выполнять над ними операции опять же было сложно. В Риме использовали систему, называемую асс. В её основе лежало деление на двенадцать. Долю, которую она составляла, называли унцией.
Современную же систему записи предложили в Индии. Единственным отличием от общепринятой записи была её перевернутость. Сверху писали делимое, а внизу — делитель. Дробную черту не ставили. Запись же, используемая сегодня, была предложена арабами.
Любая дробь состоит из двух частей: верхней, называемой числителем, и нижней — знаменателя. При произношении читается сначала числитель, а после знаменатель. Например, 3/8 — три восьмых. Верхняя часть обозначает, сколько взято долей, а нижняя — каких. В алгебре используется и иная формулировка. Числитель называют делимым, а знаменатель делителем.
Существуют следующие виды дробей:
- Обыкновенные — это числа, образованные одной или несколькими равными частями.
- Правильные — отношения, в которых числитель больше знаменателя.
- Неправильные — выражения, в которых числитель больше либо совпадает по значению со знаменателем.
- Смешанные — представляют собой сумму, состоящую из натурального числа и правильного отношения.
- Десятичные — это дроби, в знаменателе которых стоит десять в натуральной степени.
В любом виде отношений могут стоять определённые числа или неизвестные переменные. Поэтому сократить дробь можно как со степенями, так и буквами или цифрами. На правило упрощения содержание делителя и делимого не влияет.
Свойства дроби
По сути, сократить дробь — значит, её упростить. Можно использовать разный алгоритм, но в любом случае применяется основное свойство отношений. Заключается оно в том, что если делитель или делимое умножить на одно и то же число, то количественное значение в ответе не изменится. Это правило справедливо и при замене операции умножения на деление.
Алгебраически свойство можно записать в виде равенства: (q * c) / (r * c) = q / r. Для объяснения этого правила используется следующее доказательство. Пусть имеется равенство (q * r) * c = (c * r) * q. Оно возможно, так как соответствует закону умножения натуральных чисел. При этом учитывается свойство деления, согласно которому, если число разделить на равное ему значение, то результатом действия будет единица. Например, с / с = 1 или 12к/12k = 1. Последнее правило довольно логичное и интуитивно понятное. Если представить, что есть число вещей, равное x, и их нужно разложить на кучки так, чтобы в каждой оказалось x предметов, то очевидно, что получится лишь одна кучка.
Исходя из этих двух правил, можно утверждать, что выражения q * c / r * c и q : c / r : c равны q / r. То есть эти два выражения равны друг другу. На уроках математики в школе предлагают графическую иллюстрацию основного свойства. Пусть есть квадрат, который набран из девяти других квадратов. Каждый из них, в свою очередь, разделён на четыре части. Можно утверждать, что основная фигура поделена на 9 * 4 = 36 частей.
Если закрасить пять больших квадратов другим цветом, то фактически будет окрашено 20 квадратов меньшего размера (4 * 5). Отмеченная область составляет 5/9 от целого квадрата или 20/36, если считать маленькие фигуры. Но так как окрашенная часть одна, то справедливо будет утверждать о верности равенства 5 / 9 = 20 / 36. Вместо чисел 20 и 36 можно подставить их произведения. В итоге получится выражение: 5 / 9 = 5 * 4 / 9 * 4 = 20 * 4 / 36 * 4 = 20 / 36. Что и следовало доказать.
Свойство дроби используется при поиске наименьшего и наибольшего общего знаменателя, а также позволяет упрощать выражения. Невозможно правильно научиться сокращать дроби, не понимая рассмотренного правила.
Алгоритм сокращения
Существующие дроби можно разделить на сократимые и несократимые. Сократить отношение — значит, разделить верхнюю и нижнюю часть на общий делитель. При этом его значение не должно быть равное единице. В итоге получится новое выражение с меньшим значением делителя и делимого. Например, пусть дана дробь 16 / 24. Числитель и знаменатель выражения можно разделить на восемь. В результате запись упростится до вида 16:8 / 24:8 = 2 / 3. Полученная дробь является уже несократимой и её дальнейшее упрощение невозможно.
Любое упрощение выражения можно представить в виде следующего алгоритма:
- нахождение наибольшего общего делителя числителя и знаменателя;
- деление делимого и делителя на найденное число;
- получение несократимой дроби после выполнения операции.
Таким образом, суть действия сводится к нахождению такого сократителя, после применения которого она превратится в тождественную начальной, но уже станет несократимой. Наибольшим общим делителем (НОД) называют одночлен или многочлен, являющийся самым большим из всевозможных делителей, на которое числитель и знаменатель делится без остатка. Например, для чисел 12a и 24a НОД будет равный 12a.
Чтобы быстро найти НОД, нужно знать таблицу умножения и уметь раскладывать числа на простые множители. Ими называют числа, которые делятся на единицу и сами на себя. Существует даже таблица простых чисел до 997, с которой знакомят на уроках алгебры в 7 классе. Но многие натуральные числовые выражения могут делиться и на другие цифры без остатка. Например, двенадцать можно разделить на 1, 2, 3, 4, 6, и 12. Эти числа называют делителями.
При разложении используется запись в виде столбика с вертикальной чертой. В правой части пишут делимое, а в левой — исходное значение. Начинают пробовать делить на двойку, если действие невозможно, повышают значение делимого на единицу. Например, 45 = 3 * 3 * 5.
При поиске НОД каждый знаменатель раскладывают на простые множители, а затем находят одинаковые цифры и перемножают их. Полученный ответ и будет искомым сокращателем. Например, в числителе стоит число 24, а в знаменателе 42. Согласно правилу, их нужно разложить: 24 = 2 * 2 * 2 * 3 и 42 = 2 * 3 * 7. В одной и другой записи повторяются цифры три и два. Их произведение 2 * 3 = 6 и является НОД, на который и будет сокращаться дробное выражение. То есть 24:6 / 42:6 = 4 / 7. Полученная дробь является уже несократимой.
Сложные выражения
Многочлены, стоящие в числителе или знаменателе, имеющие первую степень, сокращать довольно легко. Но часто в задании попадаются степенные выражения. Для того чтобы их упростить, нужно хорошо знать основные формулы и свойства степеней. Заключаются они в следующем:
- При умножении степеней с одинаковым основанием последнее остаётся без изменения, а показатели складываются: i2 * i4 = i6.
- При делении степеней с равным основанием из показателя числителя вычитается степень, стоящая в знаменателе: i4 / i3 = i1.
- Для возведения степени в степень показатели перемножаются: (i2)4 = i8.
- Для того чтобы выполнить произведение в степени, необходимо каждый член, стоящий в скобках, возвести отдельно в указанный показатель: (i * q)n = in * qn.
- Чтобы раскрыть скобки в степени, при делении нужно возвести в степень отдельно числитель и знаменатель: (i / q) n = sn / qn.
Зная эти свойства, можно приступать непосредственно к решению примеров. Например, пусть дано выражение: 147 * 282 / 79 * 24. Для упрощения дроби следует рассуждать следующим образом. Число четырнадцать можно представить как семь, умноженное на два, а двадцать восемь — как семь, умноженное на четыре. То есть, используя свойства степеней, можно записать равенство: 147 * 282 / 79 * 24 = (27 * 77 * 72 * 42) / (79 * 24).
Можно увидеть, что в числителе находится два одночлена с одинаковым основанием. Это две цифры семь, которые можно объединить: (27 * 79 * 42) / (79 * 24). В делимом и делителе теперь находится одинаковое число 79, на которое можно сократить, то есть исключить из формулы. После преобразования выражение примет вид: 27 * 42 / 24. Два в степени семь разделить на два в степени четыре даст в ответе два в степени три. Таким образом, дробь превращается в простой одночлен: 23 * 42 = 23 * 22 * 22 = 27 = 128.
В заданиях могут встречаться рациональные и простые числа, известные и неизвестные. Решают их таким же образом. Например, нужно сократить дробь со степенями и буквами: ((0,25 ) p +1 * 8p) / (22p+1 * (0,5)p-1) = (0,25p * 0,251 * 8p) / (22p * 21 * 0,5p:0,51) = (1 / 4)p * 0,25 * 8k / 4p * 4 * 0,5p = 2p * 0,25 / 2p * 4 = 0,25 / 4 = (1/4) / 4 = 1 / 4* 4 = 1/16.
Смотря на этот пример, можно понять важность упрощения дробей. Ведь из задания, практически недоступного для решения, получилось простейшее наглядное выражение. Но при этом может случиться так, что исходная формула будет довольно сложна для предварительного анализа, например, содержать квадратный корень, экспоненту или логарифм. Для таких случаев есть резон использовать специализированные сайты-вычислители.
Использование онлайн-калькулятора
Воспользоваться возможностью сократить дробь на онлайн-калькуляторе сможет любой пользователь интернета. Такую услугу бесплатно предоставляют несколько десятков специализированных сайтов. Неоспоримое их преимущество заключается в быстром и правильном упрощении любого дробного выражения. При этом от пользователя не требуется никаких математических знаний.
Всё что необходимо, это подключение к сети и веб-браузер с поддержкой Flash плеера. Пользователю нужно просто зайти на сайт и в предложенную форму ввести упрощаемую формулу, а затем нажать виртуальную кнопку «Рассчитать». Программа сделает все вычисления самостоятельно, используя оптимальный алгоритм.
Кроме того, на этих сайтах содержится теоретический материал. Он часто подкреплён примерами. Причём даётся не просто ответ, а приводится вся цепочка вычислений, по которой можно разобраться в сути действий.
Из доступных сайтов можно выделить несколько, наиболее популярных среди пользователей:
- Kontrolnaya-rabota. Сервис поддерживает введение выражений, содержащих как буквенные части, так и числовые. После вычисления приводятся не только пошаговые действия, но и даются пояснения к каждой операции.
- Calcs. Сайт имеет простой интерфейс, но в то же время содержит всю необходимую для расчёта информацию. Страницы онлайн-калькулятора не загромождены рекламными баннерами и ненужной информацией. Недостаток его в том, что сайт не понимает степени.
- Calc. Онлайн-расчётчик позволяет сокращать любые виды дробей и находить их части. После введения выражения калькулятор выдаёт ответ буквально за несколько секунд и приводит подробное решение. Калькулятор также позволяет рассчитывать и отрицательные дроби.
Применение онлайн-калькуляторов может стать частью учебного процесса. Учащийся, вводя различные дроби, может воочию видеть нюансы сокращения того или иного вида выражений, а также использовать ресурсы для проверки самостоятельного решения.
Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.
Сокращение дробей, определение и формула.
Что такое сокращение дробей? Что значит сократить дробь?
Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.
Формула сокращения дробей основного свойства рациональных чисел.
(frac{p times n}{q times n}=frac{p}{q})
Рассмотрим пример:
Сократите дробь (frac{9}{15})
Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.
(frac{9}{15}=frac{3 times 3}{5 times 3}=frac{3}{5} times color{red} {frac{3}{3}}=frac{3}{5} times 1=frac{3}{5})
Ответ: после сокращения получили дробь (frac{3}{5}). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.
(frac{9}{15}=frac{3}{5})
Как сокращать дроби? Сокращение дроби до несократимого вида.
Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.
Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.
Получите несократимую дробь (frac{48}{136}).
Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6
(frac{48}{136}=frac{color{red} {2 times 2 times 2} times 2 times 3}{color{red} {2 times 2 times 2} times 17}=frac{color{red} {6} times 2 times 3}{color{red} {6} times 17}=frac{2 times 3}{17}=frac{6}{17})
Ответ: (frac{6}{17}) несократимая дробь.
Правило сокращения дроби до несократимого вида.
- Нужно найти наибольший общий делитель для числители и знаменателя.
- Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.
Пример:
Сократите дробь (frac{152}{168}).
Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6
(frac{152}{168}=frac{color{red} {6} times 19}{color{red} {6} times 21}=frac{19}{21})
Ответ: (frac{19}{21}) несократимая дробь.
Сокращение неправильной дроби.
Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.
Рассмотрим пример:
Сократите неправильную дробь (frac{44}{32}).
Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.
(frac{44}{32}=frac{color{red} {2 times 2 } times 11}{color{red} {2 times 2 } times 2 times 2 times 2}=frac{11}{2 times 2 times 2}=frac{11}{8})
Сокращение смешанных дробей.
Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.
Рассмотрим пример:
Сократите смешанную дробь (2frac{30}{45}).
Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.
(2frac{30}{45}=2frac{2 times color{red} {5 times 3}}{3 times color{red} {5 times 3}}=2frac{2}{3})
Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.
(2frac{30}{45}=frac{45 times 2 + 30}{45}=frac{120}{45}=frac{2 times color{red} {5 times 3} times 2 times 2}{3 times color{red} {3 times 5}}=frac{2 times 2 times 2}{3}=frac{8}{3}=2frac{2}{3})
Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:
Вычислите выражение (frac{50+20-10}{20}) .
Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.
(frac{50+color{red} {20}-10}{color{red} {20}}=frac{60}{20}=frac{3 times 20}{20}=frac{3}{1}=3)
На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь (frac{100}{150}).
Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50
(frac{100}{150}=frac{2 times 50}{3 times 50}=frac{2}{3})
Получили несократимую дробь (frac{2}{3}).
Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь (frac{100}{150}) на 2.
(frac{100}{150}=frac{2 times 50}{2 times 75}=frac{50}{75})
Получили сократимую дробь (frac{50}{75}).
Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь (frac{4}{8}). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.
Пример:
Сравните две дроби (frac{2}{3}) и (frac{8}{12}).
Эти две дроби равны. Рассмотрим подробно дробь (frac{8}{12}):
(frac{8}{12}=frac{2 times 4}{3 times 4}=frac{2}{3} times frac{4}{4}=frac{2}{3} times 1=frac{2}{3})
Отсюда получаем, (frac{8}{12}=frac{2}{3})
Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.
Пример:
Сократите если возможно следующие дроби: а) (frac{90}{65}) б) (frac{27}{63}) в) (frac{17}{100}) г) (frac{100}{250})
Решение:
а) (frac{90}{65}=frac{2 times color{red} {5} times 3 times 3}{color{red} {5} times 13}=frac{2 times 3 times 3}{13}=frac{18}{13})
б) (frac{27}{63}=frac{color{red} {3 times 3} times 3}{color{red} {3 times 3} times 7}=frac{3}{7})
в) (frac{17}{100}) несократимая дробь
г) (frac{100}{250}=frac{color{red} {2 times 5 times 5} times 2}{color{red} {2 times 5 times 5} times 5}=frac{2}{5})
В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.
Что означает сократить дробь
Любая обыкновенная дробь может быть сократимой или несократимой. Последние два термина говорят сами за себя. Разность между ними состоит в том, что, несократимую дробь изменить нельзя, а сократимую можно привести к такому виду, когда числитель и знаменатель будут наименьшими, а дробь равна исходной.
Как сокращаются дроби
Чтобы сократить дробь, необходимо разделить числитель и знаменатель на некоторое положительное число, которое больше единицы. Такое число будет называться общим делителем. Например: возьмем дробь frac { 2 } { 8 } и разделим ее числитель и знаменатель на 2. Нетрудно понять, что в итоге получим frac { 1 } { 4 } — дробь, равную исходной:
frac { 2 } { 8 } = frac { 1 } { 4 }
Как привести дробь к несократимому виду
Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):
frac { Ч : НОД ( Ч, З) } { З:НОД ( Ч, З ) } = несократимая дробь.
Практически рассмотрим, используя дробь frac { 6 } { 12 }. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
frac { 6 } { 12 } = frac { 1 } { 2 }
Последняя дробь является несократимой.
Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.
Как сократить большую дробь
Во всех случаях формула сокращения дроби включает в себя два пункта:
- следует найти наибольшее число, на которое делятся одновременно числитель и знаменатель;
- разделить числитель и знаменатель на это число.
В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:
144 : 2 = 72 192 : 2 = 96
72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
9 : 3 = 3 12 : 2 = 6
3 : 3 = 1 6 : 2 = 3
3 : 3 = 1
Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделив исходную дробь на 48 получим несократимую дробь:
frac { 144 } { 192 } = frac { 144 : 48 } { 192 : 48 } = frac { 3 } { 4 }
Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:
frac { 4000 } { 8800 } = 100 ( frac { 40 } {88} ) .
Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь frac { 5 } { 11 } = frac { 4000 } { 8800 }. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.
В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:
frac { 8 } { 64 } = frac { 1 } { 8 } или frac { 14 } { 196 } = frac { 1 } { 14 }

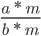
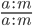
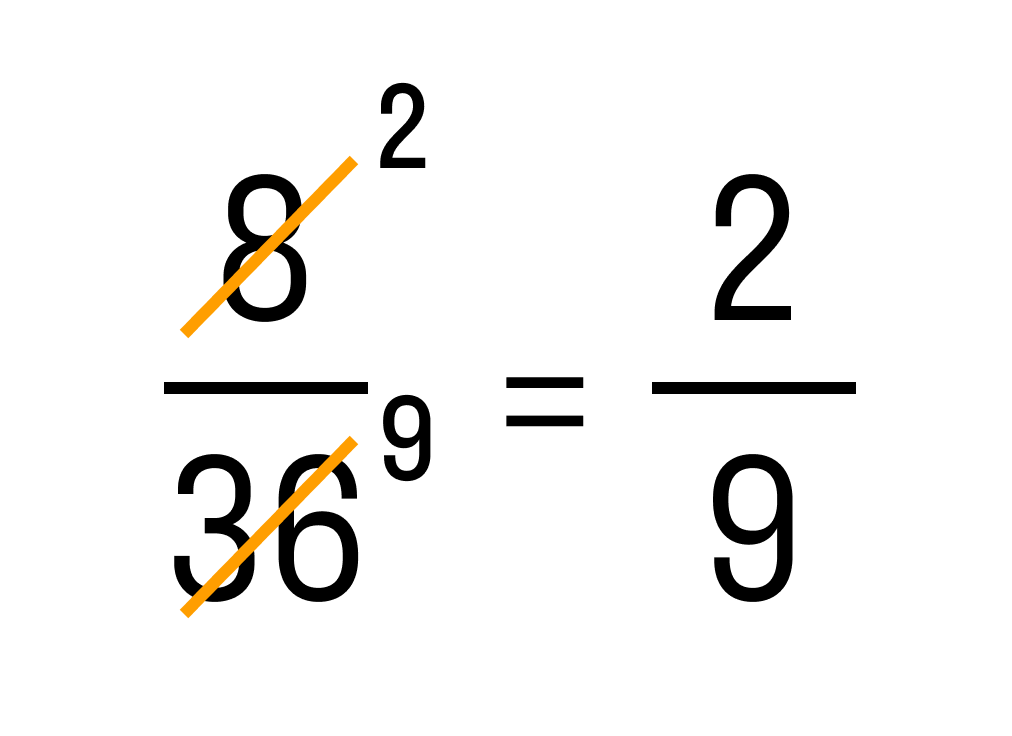
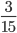
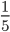
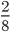

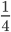
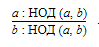 — несократимая дробь, так как по свойствам НОД мы знаем, что:
— несократимая дробь, так как по свойствам НОД мы знаем, что: