This article is about the SI derived unit. For other uses, see Ohm (disambiguation).
| ohm | |
|---|---|

A laboratory one-ohm standard resistor, circa 1917. |
|
| General information | |
| Unit system | SI |
| Unit of | electrical resistance |
| Symbol | Ω |
| Named after | Georg Ohm |
| Conversions | |
| 1 Ω in … | … is equal to … |
| SI base units | kg⋅m2⋅s−3⋅A−2 |
The ohm (symbol: Ω) is the unit of electrical resistance in the International System of Units (SI). It is named after German physicist Georg Simon Ohm. Various empirically derived standard units for electrical resistance were developed in connection with early telegraphy practice, and the British Association for the Advancement of Science proposed a unit derived from existing units of mass, length and time, and of a convenient scale for practical work as early as 1861.
Following the 2019 redefinition of the SI base units, in which the ampere and the kilogram were redefined in terms of fundamental constants, the ohm is now also defined as an exact value in terms of these constants.
Definition[edit]
One of the functions of many types of multimeters is the measurement of resistance in ohms.
The ohm is defined as an electrical resistance between two points of a conductor when a constant potential difference of one volt, applied to these points, produces in the conductor a current of one ampere, the conductor not being the seat of any electromotive force.[1]
in which the following units appear: volt (V), ampere (A), siemens (S), watt (W), second (s), farad (F), henry (H), joule (J), coulomb (C), kilogram (kg), and metre (m).
In many cases the resistance of a conductor is approximately constant within a certain range of voltages, temperatures, and other parameters. These are called linear resistors. In other cases resistance varies, such as in the case of the thermistor, which exhibits a strong dependence of its resistance with temperature.
In the US, a vowel of the prefixed units kiloohm and megaohm is commonly omitted, producing kilohm and megohm.[2][3][4][5]
In alternating current circuits, electrical impedance is also measured in ohms.
Conversions[edit]
The siemens (symbol: S) is the SI derived unit of electric conductance and admittance, historically known as the mho (ohm spelled backwards, symbol is ℧); it is the reciprocal of the ohm (Ω).
Power as a function of resistance[edit]
The power dissipated by a resistor may be calculated from its resistance, and the voltage or current involved. The formula is a combination of Ohm’s law and Joule’s law:
where:
- P is the power
- R is the resistance
- V is the voltage across the resistor
- I is the current through the resistor
A linear resistor has a constant resistance value over all applied voltages or currents; many practical resistors are linear over a useful range of currents. Non-linear resistors have a value that may vary depending on the applied voltage (or current). Where alternating current is applied to the circuit (or where the resistance value is a function of time), the relation above is true at any instant but calculation of average power over an interval of time requires integration of «instantaneous» power over that interval.
Since the ohm belongs to a coherent system of units, when each of these quantities has its corresponding SI unit (watt for P, ohm for R, volt for V and ampere for I, which are related as in § Definition) this formula remains valid numerically when these units are used (and thought of as being cancelled or omitted).
History[edit]
The rapid rise of electrotechnology in the last half of the 19th century created a demand for a rational, coherent, consistent, and international system of units for electrical quantities. Telegraphers and other early users of electricity in the 19th century needed a practical standard unit of measurement for resistance. Resistance was often expressed as a multiple of the resistance of a standard length of telegraph wires; different agencies used different bases for a standard, so units were not readily interchangeable. Electrical units so defined were not a coherent system with the units for energy, mass, length, and time, requiring conversion factors to be used in calculations relating energy or power to resistance.[6]
Two different methods of establishing a system of electrical units can be chosen. Various artifacts, such as a length of wire or a standard electrochemical cell, could be specified as producing defined quantities for resistance, voltage, and so on. Alternatively, the electrical units can be related to the mechanical units by defining, for example, a unit of current that gives a specified force between two wires, or a unit of charge that gives a unit of force between two unit charges. This latter method ensures coherence with the units of energy. Defining a unit for resistance that is coherent with units of energy and time in effect also requires defining units for potential and current. It is desirable that one unit of electrical potential will force one unit of electric current through one unit of electrical resistance, doing one unit of work in one unit of time, otherwise, all electrical calculations will require conversion factors.
Since so-called «absolute» units of charge and current are expressed as combinations of units of mass, length, and time, dimensional analysis of the relations between potential, current, and resistance show that resistance is expressed in units of length per time – a velocity. Some early definitions of a unit of resistance, for example, defined a unit resistance as one quadrant of the Earth per second.
The absolute-unit system related magnetic and electrostatic quantities to metric base units of mass, time, and length. These units had the great advantage of simplifying the equations used in the solution of electromagnetic problems, and eliminated conversion factors in calculations about electrical quantities. However, the centimeter–gram–second, CGS, units turned out to have impractical sizes for practical measurements.
Various artifact standards were proposed as the definition of the unit of resistance. In 1860 Werner Siemens (1816–1892) published a suggestion for a reproducible resistance standard in Poggendorff’s Annalen der Physik und Chemie.[7] He proposed a column of pure mercury, of one square millimeter cross section, one metre long: Siemens mercury unit. However, this unit was not coherent with other units. One proposal was to devise a unit based on a mercury column that would be coherent – in effect, adjusting the length to make the resistance one ohm. Not all users of units had the resources to carry out metrology experiments to the required precision, so working standards notionally based on the physical definition were required.
In 1861, Latimer Clark (1822–1898) and Sir Charles Bright (1832–1888) presented a paper at the British Association for the Advancement of Science meeting [8] suggesting that standards for electrical units be established and suggesting names for these units derived from eminent philosophers, ‘Ohma’, ‘Farad’ and ‘Volt’. The BAAS in 1861 appointed a committee including Maxwell and Thomson to report upon standards of electrical resistance.[9] Their objectives were to devise a unit that was of convenient size, part of a complete system for electrical measurements, coherent with the units for energy, stable, reproducible and based on the French metrical system.[10] In the third report of the committee, 1864, the resistance unit is referred to as «B.A. unit, or Ohmad».[11] By 1867 the unit is referred to as simply ohm.[12]
The B.A. ohm was intended to be 109 CGS units but owing to an error in calculations the definition was 1.3% too small. The error was significant for preparation of working standards.
On 21 September 1881 the Congrès internationale des électriciens (international conference of electricians) defined a practical unit of ohm for the resistance, based on CGS units, using a mercury column 1 mm2 in cross-section, approximately 104.9 cm in length at 0 °C,[13] similar to the apparatus suggested by Siemens.
A legal ohm, a reproducible standard, was defined by the international conference of electricians at Paris in 1884[citation needed] as the resistance of a mercury column of specified weight and 106 cm long; this was a compromise value between the B. A. unit (equivalent to 104.7 cm), the Siemens unit (100 cm by definition), and the CGS unit. Although called «legal», this standard was not adopted by any national legislation. The «international» ohm was recommended by unanimous resolution at the International Electrical Congress 1893 in Chicago.[14] The unit was based upon the ohm equal to 109 units of resistance of the C.G.S. system of electromagnetic units. The international ohm is represented by the resistance offered to an unvarying electric current in a mercury column of constant cross-sectional area 106.3 cm long of mass 14.4521 grams and 0 °C. This definition became the basis for the legal definition of the ohm in several countries. In 1908, this definition was adopted by scientific representatives from several countries at the International Conference on Electric Units and Standards in London.[14] The mercury column standard was maintained until the 1948 General Conference on Weights and Measures, at which the ohm was redefined in absolute terms instead of as an artifact standard.
By the end of the 19th century, units were well understood and consistent. Definitions would change with little effect on commercial uses of the units. Advances in metrology allowed definitions to be formulated with a high degree of precision and repeatability.
Historical units of resistance[edit]
| Unit[15] | Definition | Value in B.A. ohms | Remarks |
|---|---|---|---|
| Absolute foot/second × 107 | using imperial units | 0.3048 | considered obsolete even in 1884 |
| Thomson’s unit | using imperial units | 0.3202 | 100 million ft/s (30,480 km/s), considered obsolete even in 1884 |
| Jacobi copper unit | A specified copper wire 25 ft (7.620 m) long weighing 345 gr (22.36 g) | 0.6367 | Used in 1850s |
| Weber’s absolute unit × 107 | Based on the metre and the second | 0.9191 | |
| Siemens mercury unit | 1860. A column of pure mercury | 0.9537 | 100 cm and 1 mm2 cross section at 0 °C |
| British Association (B.A.) «ohm» | 1863 | 1.000 | Standard coils deposited at Kew Observatory in 1863[16] |
| Digney, Breguet, Swiss | 9.266–10.420 | Iron wire 1 km long and 4 mm2 cross section | |
| Matthiessen | 13.59 | 1 mi (1.609 km) of 1⁄16-inch-diameter (1.588 mm) pure annealed copper wire at 15.5 °C | |
| Varley | 25.61 | One mile of special 1⁄16-inch-diameter copper wire | |
| German mile | 57.44 | A German mile (8,238 yd or 7,533 m) of iron wire 1⁄6 in (4.233 mm) diameter | |
| Abohm | 10−9 | Electromagnetic absolute unit in centimeter–gram–second units | |
| Statohm | 8.987551787×1011 | Electrostatic absolute unit in centimeter–gram–second units |
Realization of standards[edit]
The mercury column method of realizing a physical standard ohm turned out to be difficult to reproduce, owing to the effects of non-constant cross section of the glass tubing. Various resistance coils were constructed by the British Association and others, to serve as physical artifact standards for the unit of resistance. The long-term stability and reproducibility of these artifacts was an ongoing field of research, as the effects of temperature, air pressure, humidity, and time on the standards were detected and analyzed.
Artifact standards are still used, but metrology experiments relating accurately dimensioned inductors and capacitors provided a more fundamental basis for the definition of the ohm. Since 1990 the quantum Hall effect has been used to define the ohm with high precision and repeatability. The quantum Hall experiments are used to check the stability of working standards that have convenient values for comparison.[17]
Following the 2019 redefinition of the SI base units, in which the ampere and the kilogram were redefined in terms of fundamental constants, the ohm is now also defined in terms of these constants.
Symbol[edit]
The symbol Ω was suggested, because of the similar sound of ohm and omega, by William Henry Preece in 1867.[18] In documents printed before WWII the unit symbol often consisted of the raised lowercase omega (ω), such that 56 Ω was written as 56ω.
Historically, some document editing software applications have used the Symbol typeface to render the character Ω.[19] Where the font is not supported, a W is displayed instead («10 W» instead of «10 Ω», for instance). As W represents the watt, the SI unit of power, this can lead to confusion, making the use of the correct Unicode code point preferable.
Where the character set is limited to ASCII, the IEEE 260.1 standard recommends substituting the symbol ohm for Ω.
In the electronics industry it is common to use the character R instead of the Ω symbol, thus, a 10 Ω resistor may be represented as 10R. This is part of the RKM code. It is used in many instances where the value has a decimal place. For example, 5.6 Ω is listed as 5R6, or 2200 Ω is listed as 2K2. This method avoids overlooking the decimal point, which may not be rendered reliably on components or when duplicating documents.
Unicode encodes the symbol as U+2126 Ω OHM SIGN, distinct from Greek omega among letterlike symbols, but it is only included for backward compatibility and the Greek uppercase omega character U+03A9 Ω GREEK CAPITAL LETTER OMEGA (Ω, Ω) is preferred.[20] In MS-DOS and Microsoft Windows, the alt code ALT 234 may produce the Ω symbol. In Mac OS, ⌥ Opt+Z does the same.
See also[edit]
- Electronic color code
- History of measurement
- International Committee for Weights and Measures
- Orders of magnitude (resistance)
- Resistivity
Notes and references[edit]
- ^ BIPM SI Brochure: Appendix 1, p.46 (pdf)
- ^ SASB/SCC14 – SCC14 – Quantities, Units, and Letter Symbols (2002-12-30). IEEE/ASTM SI 10-2002: IEEE/ASTM Standard for Use of the International System of Units (SI): The Modern Metric System.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Thompson, Ambler; Taylor, Barry N. (November 2008) [March 2008]. «Chapter 9.3 Spelling unit names with prefixes». Guide for the Use of the International System of Units (SI) (PDF) (2nd corrected printing, 2008 ed.). Gaithersburg, Maryland, USA: National Institute of Standards and Technology, U.S. Department of Commerce. CODEN NSPUE3. NIST Special Publication 811. Archived (PDF) from the original on 2021-01-31. Retrieved 2021-01-31. p. 31:
Reference [6] points out that there are three cases in which the final vowel of an SI prefix is commonly omitted: megohm (not megaohm), kilohm (not kiloohm), and hectare (not hectoare). In all other cases in which the unit name begins with a vowel, both the final vowel of the prefix and the vowel of the unit name are retained and both are pronounced.
(85 pages) - ^ «NIST Guide to the SI». Gaithersburg, Maryland, USA: National Institute of Standards and Technology (NIST), Physical Measurement Laboratory. 2016-08-25 [2016-01-28]. Chapter 9: Rules and Style Conventions for Spelling Unit Names, 9.3: Spelling unit names with prefixes. Special Publication 811. Archived from the original on 2021-01-31. Retrieved 2021-01-31. [1]
- ^ Aubrecht II, Gordon J.; French, Anthony P.; Iona, Mario (2012-01-20). «About the International System of Units (SI) Part IV. Writing, Spelling, and Mathematics». The Physics Teacher. 50 (2): 77–79. Bibcode:2012PhTea..50…77A. doi:10.1119/1.3677278.
- ^ Hunt, Bruce J. (1994). «The Ohm Is Where the Art Is: British Telegraph Engineers and the Development of Electrical Standards» (PDF). Osiris. 2. 9: 48–63. doi:10.1086/368729. S2CID 145557228. Archived from the original on 2014-03-08. Retrieved 2014-02-27.
- ^ Siemens, Werner (1860). «Vorschlag eines reproducirbaren Widerstandsmaaßes». Annalen der Physik und Chemie (in German). 186 (5): 1–20. Bibcode:1860AnP…186….1S. doi:10.1002/andp.18601860502.
- ^ Clark, Latimer; Bright, Sir Charles (1861-11-09). «Measurement of Electrical Quantities and Resistance». The Electrician. 1 (1): 3–4. Retrieved 2014-02-27.
- ^ Report of the Thirty-First Meeting of the British Association for the Advancement of Science; held at Manchester in September 1861. September 1861. pp. xxxix–xl.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming (September 1862). Provisional Report of the Committee appointed by the British Association on Standards of Electrical Resistance. Thirty-second Meeting of the British Association for the Advancement of Science. London: John Murray. pp. 125–163. Retrieved 2014-02-27.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming; Bright, Charles; Maxwell, James Clerk; Siemens, Carl Wilhelm; Stewart, Balfour; Joule, James Prescott; Varley, C. F. (September 1864). Report of the Committee on Standards of Electrical Resistance. Thirty-fourth Meeting of the British Association for the Advancement of Science. London: John Murray. p. Foldout facing page 349. Retrieved 2014-02-27.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming; Bright, Charles; Maxwell, James Clerk; Siemens, Carl Wilhelm; Stewart, Balfour; Varley, C. F.; Foster, G. C.; Clark, Latimer; Forbes, D.; Hockin, Charles; Joule, James Prescott (September 1867). Report of the Committee on Standards of Electrical Resistance. Thirty-seventh Meeting of the British Association for the Advancement of Science. London: John Murray. p. 488. Retrieved 2014-02-27.
- ^ «System of measurement units». Engineering and Technology History Wiki. 2012-04-24. Retrieved 2018-04-13.
- ^ a b Fleming, John Ambrose (1911). «Units, Physical» . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 27 (11th ed.). Cambridge University Press. pp. 738–745, see page 742.
An Electrical Congress was held in Chicago, U.S.A. in August 1893, to consider……and at the last one held in London in October 1908 were finally adopted
- ^ Gordon Wigan (trans. and ed.), Electrician’s Pocket Book, Cassel and Company, London, 1884
- ^ Historical Studies in International Corporate Business. Teich p34
- ^ R. Dzuiba and others, Stability of Double-Walled Maganin Resistors in NIST Special Publication Proceedings of SPIE, The Institute, 1988 pp. 63–64
- ^ Preece, William Henry (1867), «The B.A. unit for electrical measurements», Philosophical Magazine, vol. 33, p. 397, retrieved 2017-02-26
- ^ E.g. recommended in HTML 4.01: «HTML 4.01 Specification». W3C. 1998. Section 24.1 «Introduction to character entity references». Retrieved 2018-11-22.
- ^ Excerpts from The Unicode Standard, Version 4.0, accessed 11 October 2006
External links[edit]
- Scanned books of Georg Simon Ohm at the library of the University of Applied Sciences Nuernberg
- Official SI brochure
- NIST Special Publication 811
- History of the ohm at sizes.com
- History of the electrical units.
This article is about the SI derived unit. For other uses, see Ohm (disambiguation).
| ohm | |
|---|---|

A laboratory one-ohm standard resistor, circa 1917. |
|
| General information | |
| Unit system | SI |
| Unit of | electrical resistance |
| Symbol | Ω |
| Named after | Georg Ohm |
| Conversions | |
| 1 Ω in … | … is equal to … |
| SI base units | kg⋅m2⋅s−3⋅A−2 |
The ohm (symbol: Ω) is the unit of electrical resistance in the International System of Units (SI). It is named after German physicist Georg Simon Ohm. Various empirically derived standard units for electrical resistance were developed in connection with early telegraphy practice, and the British Association for the Advancement of Science proposed a unit derived from existing units of mass, length and time, and of a convenient scale for practical work as early as 1861.
Following the 2019 redefinition of the SI base units, in which the ampere and the kilogram were redefined in terms of fundamental constants, the ohm is now also defined as an exact value in terms of these constants.
Definition[edit]
One of the functions of many types of multimeters is the measurement of resistance in ohms.
The ohm is defined as an electrical resistance between two points of a conductor when a constant potential difference of one volt, applied to these points, produces in the conductor a current of one ampere, the conductor not being the seat of any electromotive force.[1]
in which the following units appear: volt (V), ampere (A), siemens (S), watt (W), second (s), farad (F), henry (H), joule (J), coulomb (C), kilogram (kg), and metre (m).
In many cases the resistance of a conductor is approximately constant within a certain range of voltages, temperatures, and other parameters. These are called linear resistors. In other cases resistance varies, such as in the case of the thermistor, which exhibits a strong dependence of its resistance with temperature.
In the US, a vowel of the prefixed units kiloohm and megaohm is commonly omitted, producing kilohm and megohm.[2][3][4][5]
In alternating current circuits, electrical impedance is also measured in ohms.
Conversions[edit]
The siemens (symbol: S) is the SI derived unit of electric conductance and admittance, historically known as the mho (ohm spelled backwards, symbol is ℧); it is the reciprocal of the ohm (Ω).
Power as a function of resistance[edit]
The power dissipated by a resistor may be calculated from its resistance, and the voltage or current involved. The formula is a combination of Ohm’s law and Joule’s law:
where:
- P is the power
- R is the resistance
- V is the voltage across the resistor
- I is the current through the resistor
A linear resistor has a constant resistance value over all applied voltages or currents; many practical resistors are linear over a useful range of currents. Non-linear resistors have a value that may vary depending on the applied voltage (or current). Where alternating current is applied to the circuit (or where the resistance value is a function of time), the relation above is true at any instant but calculation of average power over an interval of time requires integration of «instantaneous» power over that interval.
Since the ohm belongs to a coherent system of units, when each of these quantities has its corresponding SI unit (watt for P, ohm for R, volt for V and ampere for I, which are related as in § Definition) this formula remains valid numerically when these units are used (and thought of as being cancelled or omitted).
History[edit]
The rapid rise of electrotechnology in the last half of the 19th century created a demand for a rational, coherent, consistent, and international system of units for electrical quantities. Telegraphers and other early users of electricity in the 19th century needed a practical standard unit of measurement for resistance. Resistance was often expressed as a multiple of the resistance of a standard length of telegraph wires; different agencies used different bases for a standard, so units were not readily interchangeable. Electrical units so defined were not a coherent system with the units for energy, mass, length, and time, requiring conversion factors to be used in calculations relating energy or power to resistance.[6]
Two different methods of establishing a system of electrical units can be chosen. Various artifacts, such as a length of wire or a standard electrochemical cell, could be specified as producing defined quantities for resistance, voltage, and so on. Alternatively, the electrical units can be related to the mechanical units by defining, for example, a unit of current that gives a specified force between two wires, or a unit of charge that gives a unit of force between two unit charges. This latter method ensures coherence with the units of energy. Defining a unit for resistance that is coherent with units of energy and time in effect also requires defining units for potential and current. It is desirable that one unit of electrical potential will force one unit of electric current through one unit of electrical resistance, doing one unit of work in one unit of time, otherwise, all electrical calculations will require conversion factors.
Since so-called «absolute» units of charge and current are expressed as combinations of units of mass, length, and time, dimensional analysis of the relations between potential, current, and resistance show that resistance is expressed in units of length per time – a velocity. Some early definitions of a unit of resistance, for example, defined a unit resistance as one quadrant of the Earth per second.
The absolute-unit system related magnetic and electrostatic quantities to metric base units of mass, time, and length. These units had the great advantage of simplifying the equations used in the solution of electromagnetic problems, and eliminated conversion factors in calculations about electrical quantities. However, the centimeter–gram–second, CGS, units turned out to have impractical sizes for practical measurements.
Various artifact standards were proposed as the definition of the unit of resistance. In 1860 Werner Siemens (1816–1892) published a suggestion for a reproducible resistance standard in Poggendorff’s Annalen der Physik und Chemie.[7] He proposed a column of pure mercury, of one square millimeter cross section, one metre long: Siemens mercury unit. However, this unit was not coherent with other units. One proposal was to devise a unit based on a mercury column that would be coherent – in effect, adjusting the length to make the resistance one ohm. Not all users of units had the resources to carry out metrology experiments to the required precision, so working standards notionally based on the physical definition were required.
In 1861, Latimer Clark (1822–1898) and Sir Charles Bright (1832–1888) presented a paper at the British Association for the Advancement of Science meeting [8] suggesting that standards for electrical units be established and suggesting names for these units derived from eminent philosophers, ‘Ohma’, ‘Farad’ and ‘Volt’. The BAAS in 1861 appointed a committee including Maxwell and Thomson to report upon standards of electrical resistance.[9] Their objectives were to devise a unit that was of convenient size, part of a complete system for electrical measurements, coherent with the units for energy, stable, reproducible and based on the French metrical system.[10] In the third report of the committee, 1864, the resistance unit is referred to as «B.A. unit, or Ohmad».[11] By 1867 the unit is referred to as simply ohm.[12]
The B.A. ohm was intended to be 109 CGS units but owing to an error in calculations the definition was 1.3% too small. The error was significant for preparation of working standards.
On 21 September 1881 the Congrès internationale des électriciens (international conference of electricians) defined a practical unit of ohm for the resistance, based on CGS units, using a mercury column 1 mm2 in cross-section, approximately 104.9 cm in length at 0 °C,[13] similar to the apparatus suggested by Siemens.
A legal ohm, a reproducible standard, was defined by the international conference of electricians at Paris in 1884[citation needed] as the resistance of a mercury column of specified weight and 106 cm long; this was a compromise value between the B. A. unit (equivalent to 104.7 cm), the Siemens unit (100 cm by definition), and the CGS unit. Although called «legal», this standard was not adopted by any national legislation. The «international» ohm was recommended by unanimous resolution at the International Electrical Congress 1893 in Chicago.[14] The unit was based upon the ohm equal to 109 units of resistance of the C.G.S. system of electromagnetic units. The international ohm is represented by the resistance offered to an unvarying electric current in a mercury column of constant cross-sectional area 106.3 cm long of mass 14.4521 grams and 0 °C. This definition became the basis for the legal definition of the ohm in several countries. In 1908, this definition was adopted by scientific representatives from several countries at the International Conference on Electric Units and Standards in London.[14] The mercury column standard was maintained until the 1948 General Conference on Weights and Measures, at which the ohm was redefined in absolute terms instead of as an artifact standard.
By the end of the 19th century, units were well understood and consistent. Definitions would change with little effect on commercial uses of the units. Advances in metrology allowed definitions to be formulated with a high degree of precision and repeatability.
Historical units of resistance[edit]
| Unit[15] | Definition | Value in B.A. ohms | Remarks |
|---|---|---|---|
| Absolute foot/second × 107 | using imperial units | 0.3048 | considered obsolete even in 1884 |
| Thomson’s unit | using imperial units | 0.3202 | 100 million ft/s (30,480 km/s), considered obsolete even in 1884 |
| Jacobi copper unit | A specified copper wire 25 ft (7.620 m) long weighing 345 gr (22.36 g) | 0.6367 | Used in 1850s |
| Weber’s absolute unit × 107 | Based on the metre and the second | 0.9191 | |
| Siemens mercury unit | 1860. A column of pure mercury | 0.9537 | 100 cm and 1 mm2 cross section at 0 °C |
| British Association (B.A.) «ohm» | 1863 | 1.000 | Standard coils deposited at Kew Observatory in 1863[16] |
| Digney, Breguet, Swiss | 9.266–10.420 | Iron wire 1 km long and 4 mm2 cross section | |
| Matthiessen | 13.59 | 1 mi (1.609 km) of 1⁄16-inch-diameter (1.588 mm) pure annealed copper wire at 15.5 °C | |
| Varley | 25.61 | One mile of special 1⁄16-inch-diameter copper wire | |
| German mile | 57.44 | A German mile (8,238 yd or 7,533 m) of iron wire 1⁄6 in (4.233 mm) diameter | |
| Abohm | 10−9 | Electromagnetic absolute unit in centimeter–gram–second units | |
| Statohm | 8.987551787×1011 | Electrostatic absolute unit in centimeter–gram–second units |
Realization of standards[edit]
The mercury column method of realizing a physical standard ohm turned out to be difficult to reproduce, owing to the effects of non-constant cross section of the glass tubing. Various resistance coils were constructed by the British Association and others, to serve as physical artifact standards for the unit of resistance. The long-term stability and reproducibility of these artifacts was an ongoing field of research, as the effects of temperature, air pressure, humidity, and time on the standards were detected and analyzed.
Artifact standards are still used, but metrology experiments relating accurately dimensioned inductors and capacitors provided a more fundamental basis for the definition of the ohm. Since 1990 the quantum Hall effect has been used to define the ohm with high precision and repeatability. The quantum Hall experiments are used to check the stability of working standards that have convenient values for comparison.[17]
Following the 2019 redefinition of the SI base units, in which the ampere and the kilogram were redefined in terms of fundamental constants, the ohm is now also defined in terms of these constants.
Symbol[edit]
The symbol Ω was suggested, because of the similar sound of ohm and omega, by William Henry Preece in 1867.[18] In documents printed before WWII the unit symbol often consisted of the raised lowercase omega (ω), such that 56 Ω was written as 56ω.
Historically, some document editing software applications have used the Symbol typeface to render the character Ω.[19] Where the font is not supported, a W is displayed instead («10 W» instead of «10 Ω», for instance). As W represents the watt, the SI unit of power, this can lead to confusion, making the use of the correct Unicode code point preferable.
Where the character set is limited to ASCII, the IEEE 260.1 standard recommends substituting the symbol ohm for Ω.
In the electronics industry it is common to use the character R instead of the Ω symbol, thus, a 10 Ω resistor may be represented as 10R. This is part of the RKM code. It is used in many instances where the value has a decimal place. For example, 5.6 Ω is listed as 5R6, or 2200 Ω is listed as 2K2. This method avoids overlooking the decimal point, which may not be rendered reliably on components or when duplicating documents.
Unicode encodes the symbol as U+2126 Ω OHM SIGN, distinct from Greek omega among letterlike symbols, but it is only included for backward compatibility and the Greek uppercase omega character U+03A9 Ω GREEK CAPITAL LETTER OMEGA (Ω, Ω) is preferred.[20] In MS-DOS and Microsoft Windows, the alt code ALT 234 may produce the Ω symbol. In Mac OS, ⌥ Opt+Z does the same.
See also[edit]
- Electronic color code
- History of measurement
- International Committee for Weights and Measures
- Orders of magnitude (resistance)
- Resistivity
Notes and references[edit]
- ^ BIPM SI Brochure: Appendix 1, p.46 (pdf)
- ^ SASB/SCC14 – SCC14 – Quantities, Units, and Letter Symbols (2002-12-30). IEEE/ASTM SI 10-2002: IEEE/ASTM Standard for Use of the International System of Units (SI): The Modern Metric System.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Thompson, Ambler; Taylor, Barry N. (November 2008) [March 2008]. «Chapter 9.3 Spelling unit names with prefixes». Guide for the Use of the International System of Units (SI) (PDF) (2nd corrected printing, 2008 ed.). Gaithersburg, Maryland, USA: National Institute of Standards and Technology, U.S. Department of Commerce. CODEN NSPUE3. NIST Special Publication 811. Archived (PDF) from the original on 2021-01-31. Retrieved 2021-01-31. p. 31:
Reference [6] points out that there are three cases in which the final vowel of an SI prefix is commonly omitted: megohm (not megaohm), kilohm (not kiloohm), and hectare (not hectoare). In all other cases in which the unit name begins with a vowel, both the final vowel of the prefix and the vowel of the unit name are retained and both are pronounced.
(85 pages) - ^ «NIST Guide to the SI». Gaithersburg, Maryland, USA: National Institute of Standards and Technology (NIST), Physical Measurement Laboratory. 2016-08-25 [2016-01-28]. Chapter 9: Rules and Style Conventions for Spelling Unit Names, 9.3: Spelling unit names with prefixes. Special Publication 811. Archived from the original on 2021-01-31. Retrieved 2021-01-31. [1]
- ^ Aubrecht II, Gordon J.; French, Anthony P.; Iona, Mario (2012-01-20). «About the International System of Units (SI) Part IV. Writing, Spelling, and Mathematics». The Physics Teacher. 50 (2): 77–79. Bibcode:2012PhTea..50…77A. doi:10.1119/1.3677278.
- ^ Hunt, Bruce J. (1994). «The Ohm Is Where the Art Is: British Telegraph Engineers and the Development of Electrical Standards» (PDF). Osiris. 2. 9: 48–63. doi:10.1086/368729. S2CID 145557228. Archived from the original on 2014-03-08. Retrieved 2014-02-27.
- ^ Siemens, Werner (1860). «Vorschlag eines reproducirbaren Widerstandsmaaßes». Annalen der Physik und Chemie (in German). 186 (5): 1–20. Bibcode:1860AnP…186….1S. doi:10.1002/andp.18601860502.
- ^ Clark, Latimer; Bright, Sir Charles (1861-11-09). «Measurement of Electrical Quantities and Resistance». The Electrician. 1 (1): 3–4. Retrieved 2014-02-27.
- ^ Report of the Thirty-First Meeting of the British Association for the Advancement of Science; held at Manchester in September 1861. September 1861. pp. xxxix–xl.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming (September 1862). Provisional Report of the Committee appointed by the British Association on Standards of Electrical Resistance. Thirty-second Meeting of the British Association for the Advancement of Science. London: John Murray. pp. 125–163. Retrieved 2014-02-27.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming; Bright, Charles; Maxwell, James Clerk; Siemens, Carl Wilhelm; Stewart, Balfour; Joule, James Prescott; Varley, C. F. (September 1864). Report of the Committee on Standards of Electrical Resistance. Thirty-fourth Meeting of the British Association for the Advancement of Science. London: John Murray. p. Foldout facing page 349. Retrieved 2014-02-27.
- ^ Williamson, A.; Wheatstone, C.; Thomson, W.; Miller, W. H.; Matthiessen, A.; Jenkin, Fleeming; Bright, Charles; Maxwell, James Clerk; Siemens, Carl Wilhelm; Stewart, Balfour; Varley, C. F.; Foster, G. C.; Clark, Latimer; Forbes, D.; Hockin, Charles; Joule, James Prescott (September 1867). Report of the Committee on Standards of Electrical Resistance. Thirty-seventh Meeting of the British Association for the Advancement of Science. London: John Murray. p. 488. Retrieved 2014-02-27.
- ^ «System of measurement units». Engineering and Technology History Wiki. 2012-04-24. Retrieved 2018-04-13.
- ^ a b Fleming, John Ambrose (1911). «Units, Physical» . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 27 (11th ed.). Cambridge University Press. pp. 738–745, see page 742.
An Electrical Congress was held in Chicago, U.S.A. in August 1893, to consider……and at the last one held in London in October 1908 were finally adopted
- ^ Gordon Wigan (trans. and ed.), Electrician’s Pocket Book, Cassel and Company, London, 1884
- ^ Historical Studies in International Corporate Business. Teich p34
- ^ R. Dzuiba and others, Stability of Double-Walled Maganin Resistors in NIST Special Publication Proceedings of SPIE, The Institute, 1988 pp. 63–64
- ^ Preece, William Henry (1867), «The B.A. unit for electrical measurements», Philosophical Magazine, vol. 33, p. 397, retrieved 2017-02-26
- ^ E.g. recommended in HTML 4.01: «HTML 4.01 Specification». W3C. 1998. Section 24.1 «Introduction to character entity references». Retrieved 2018-11-22.
- ^ Excerpts from The Unicode Standard, Version 4.0, accessed 11 October 2006
External links[edit]
- Scanned books of Georg Simon Ohm at the library of the University of Applied Sciences Nuernberg
- Official SI brochure
- NIST Special Publication 811
- History of the ohm at sizes.com
- History of the electrical units.
Сопротивление
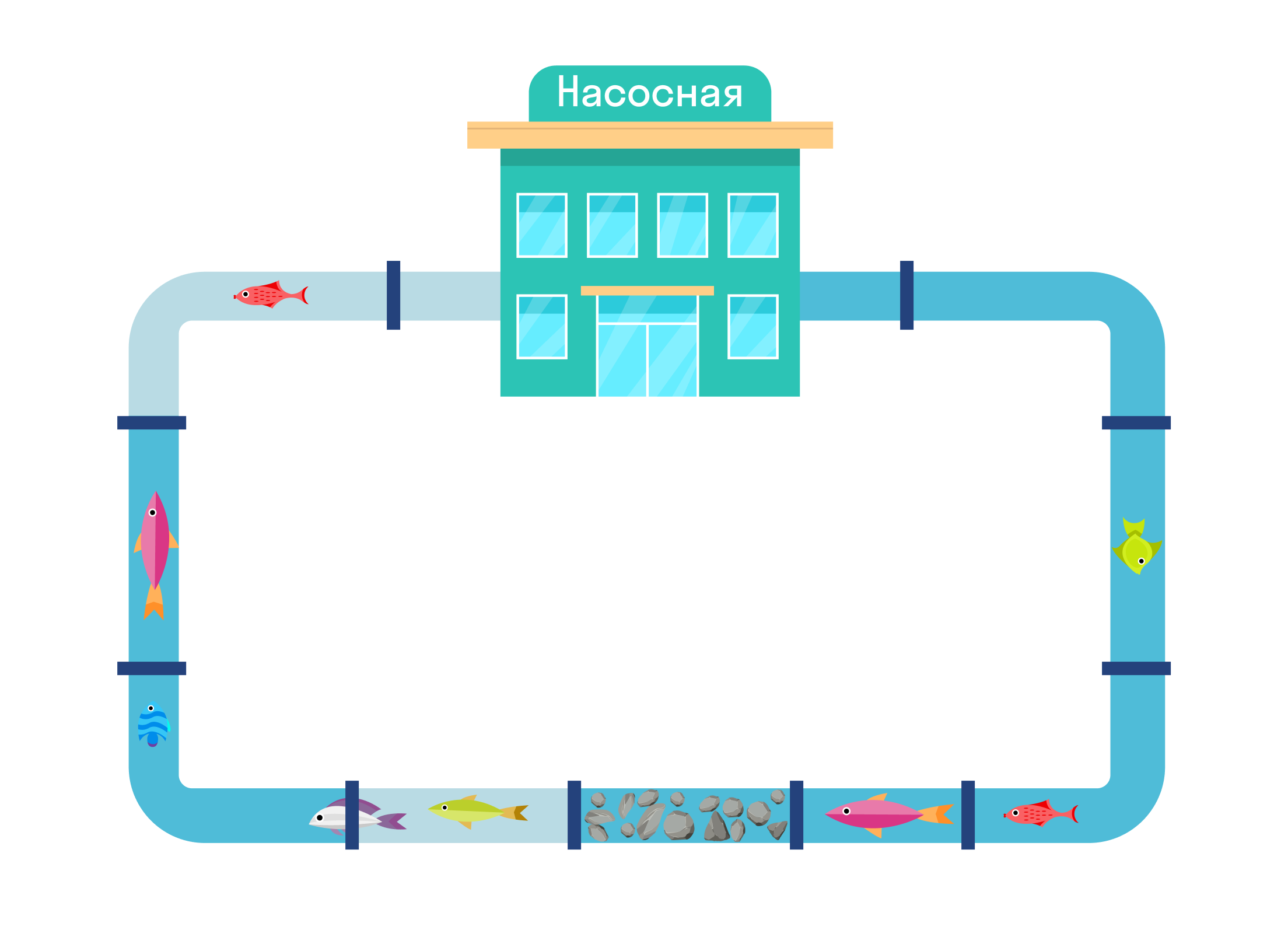
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Таблица удельных сопротивлений различных материалов
|
Материал |
Удельное сопротивление ρ, Ом · мм2/м |
|
Алюминий |
0,028 |
|
Бронза |
0,095–0,1 |
|
Висмут |
1,2 |
|
Вольфрам |
0,05 |
|
Железо |
0,1 |
|
Золото |
0,023 |
|
Иридий |
0,0474 |
|
Константан (сплав NiCu + Mn) |
0,5 |
|
Латунь |
0,025–0,108 |
|
Магний |
0,045 |
|
Манганин (сплав меди марганца и никеля — приборный) |
0,43–0,51 |
|
Медь |
0,0175 |
|
Молибден |
0,059 |
|
Нейзильбер (сплав меди, цинка и никеля) |
0,2 |
|
Натрий |
0,047 |
|
Никелин (сплав меди и никеля) |
0,42 |
|
Никель |
0,087 |
|
Нихром (сплав никеля, хрома, железа и марганца) |
1,05–1,4 |
|
Олово |
0,12 |
|
Платина |
0,107 |
|
Ртуть |
0,94 |
|
Свинец |
0,22 |
|
Серебро |
0,015 |
|
Сталь |
0,103–0,137 |
|
Титан |
0,6 |
|
Хромаль |
1,3–1,5 |
|
Цинк |
0,054 |
|
Чугун |
0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
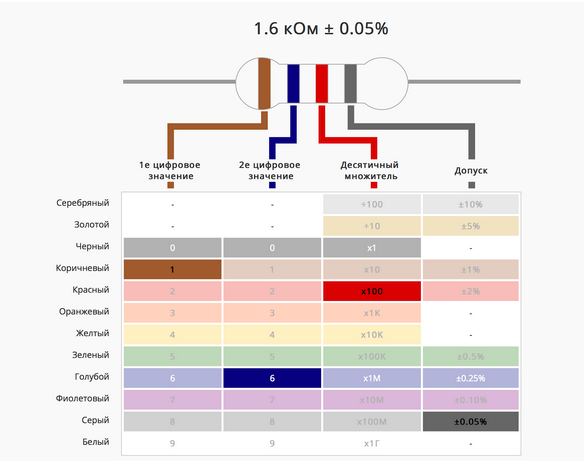
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
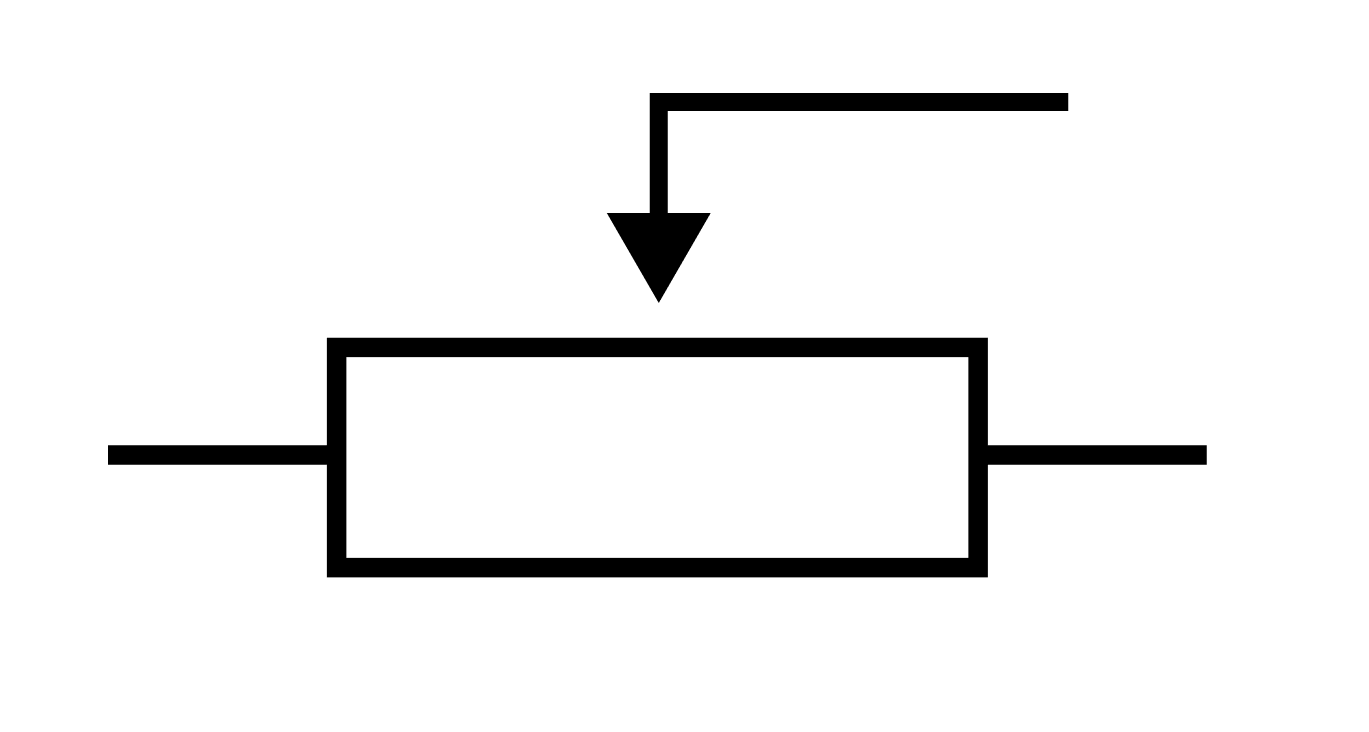
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи
I — сила тока [A]
ε — ЭДС [В]
R — сопротивление нагрузки [Ом]
r — внутреннее сопротивление источника [Ом]
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
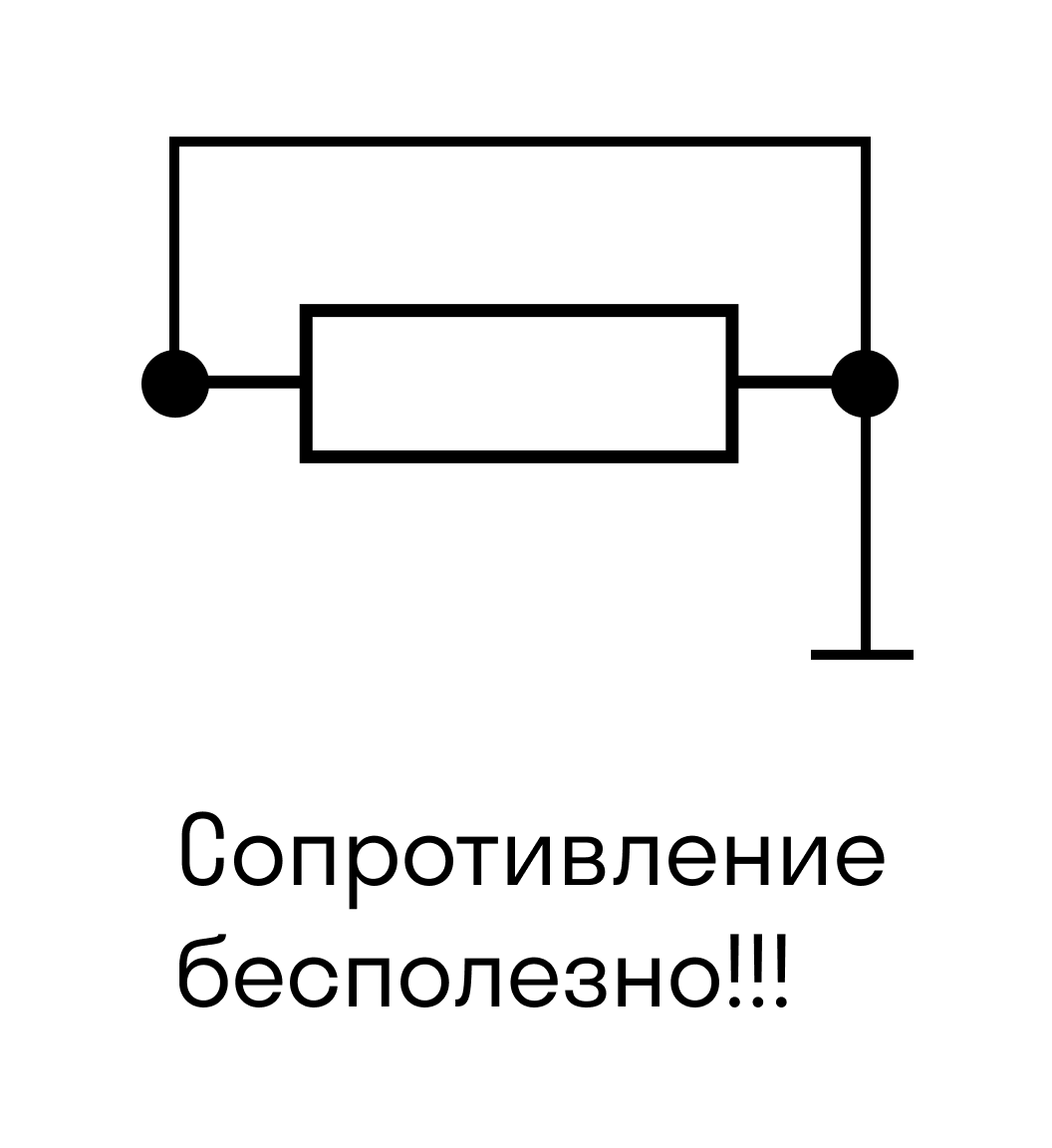
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
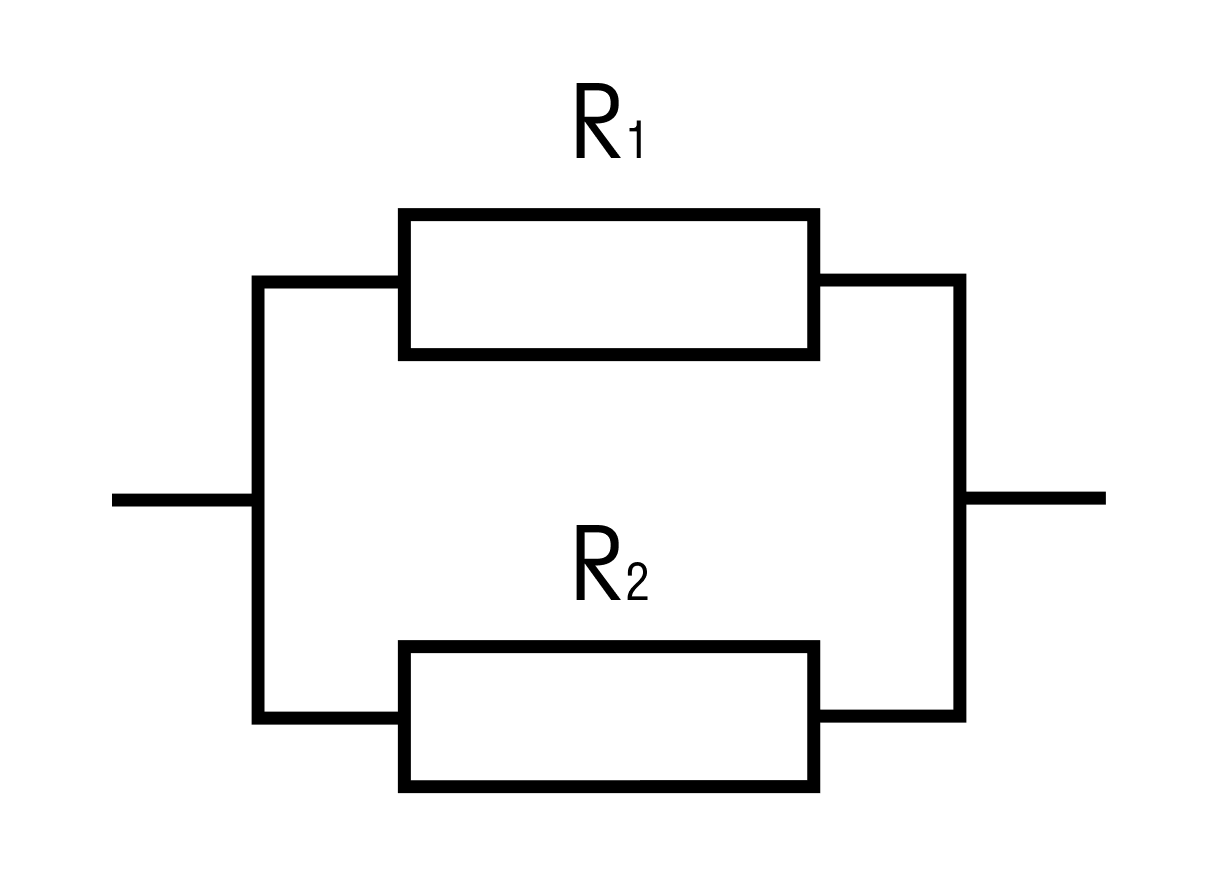
Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Ответ: общее сопротивление цепи равно
Ом
Задачка три
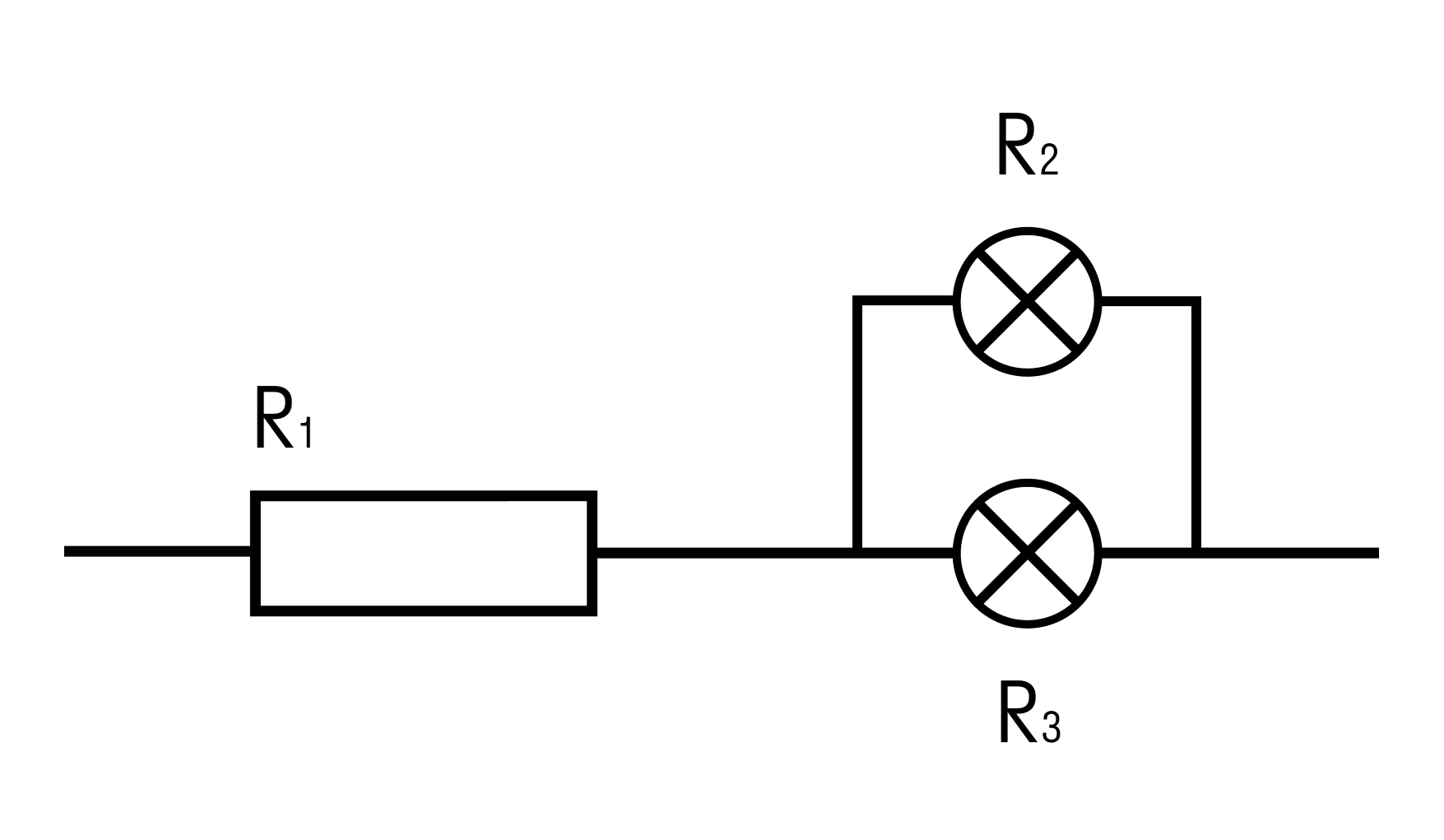
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соединены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
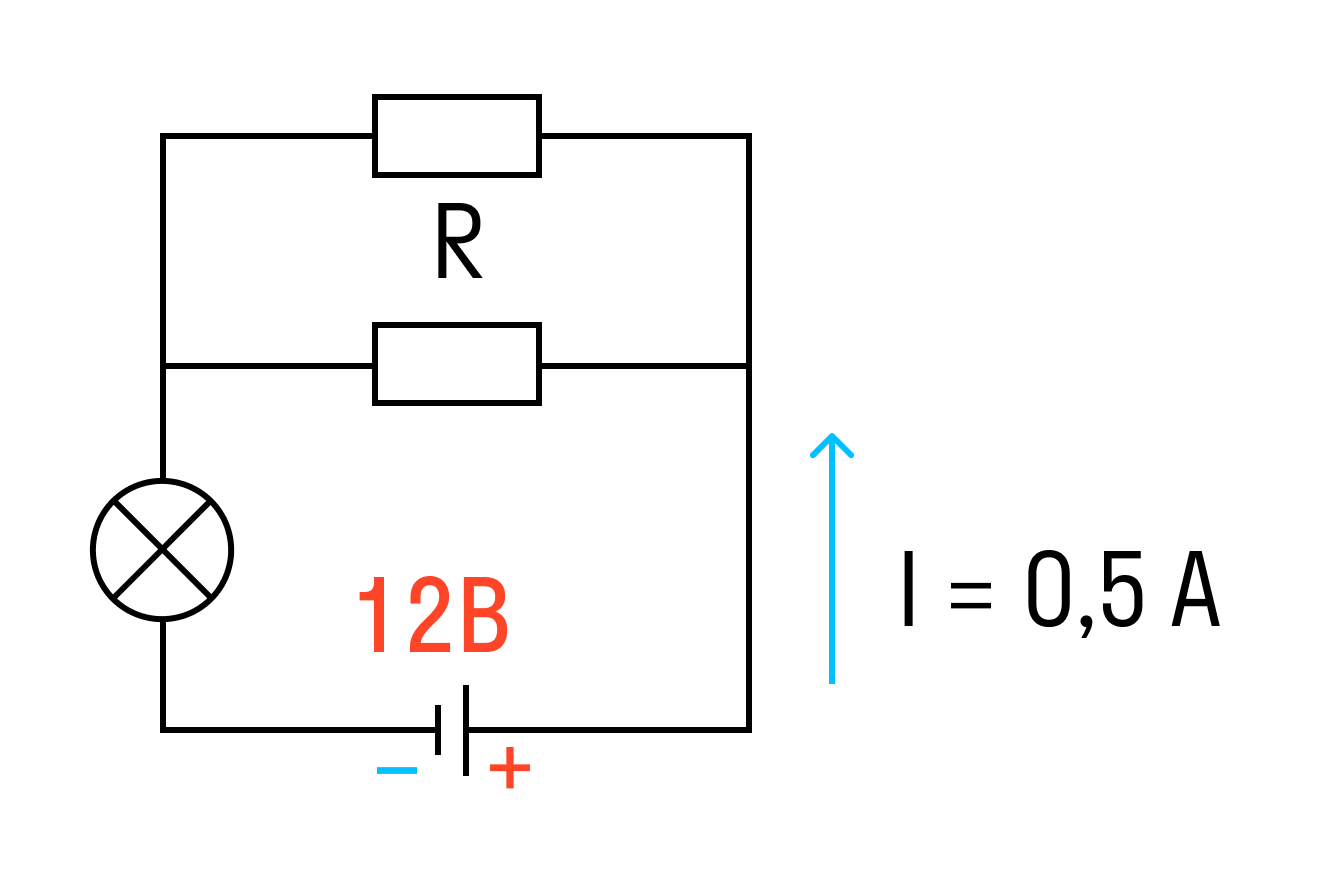
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
R + r = ε/I
r = ε/I − R
Подставим значения:
r = 12/0,5 − 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Электрическое сопротивление характеризует свойство проводника оказывать противодействие направленному движению заряженных частиц.
Влияние электрического сопротивления на электрический ток можно представить следующим образом:
- Движение свободных носителей электрического заряда внутри проводника приводит к тому, что свободные носители заряда сталкиваются с атомами и нарушают их поток.
- Этот эффект называется сопротивлением, которое обладает свойством ограничивать электрический ток в электрической цепи.
- Столкновение носителей электрического заряда с атомами также имеет тепловой эффект. Соответствующий элемент электрической цепи становится теплым или даже горячим. Если он перегреется, он может выйти из строя.
Электрическое сопротивление говорит о том, какое напряжение U необходимо, чтобы заставить электрический ток определенной силы тока I протекать через проводник. В физике для обозначения электрического сопротивления в формуле используется прописная буква R (от английского слова «Resistor» или «Resistance»).
Аналогия с потоком воды
Когда речь идет об электрическом сопротивлении в физике, необходимо различать два случая:
- Электрические сопротивления как элементы электрической цепи (см. пример на рисунке 2). То есть, если вы называете элемент в электротехнике резистором, то вы имеете в виду конкретный элемент, предназначенный для целей ограничения протекания электрического тока в электрической цепи.
- Электрическое сопротивление как физическая величина. Вы также можете спросить, насколько сильно тот или иной элемент препятствует протеканию электрического тока или вообще как можно рассчитать электрическое сопротивление. Здесь вы говорите об электрическом сопротивлении как о физической величине.
Примечание. Резистор — это прибор с постоянным сопротивлением. Если необходимо регулировать силу тока в электрической цепи, то используют для этой цели реостаты — приборы с переменным сопротивлением. В составе реостата имеется подвижный контакт, при помощи которого изменяется длина участка, включённого в цепь. Реостат используется, например, в регуляторах громкости радиоприёмников.
Вы можете проиллюстрировать работу резистора как элемента (т.е. случай 1) с помощью модели протекания воды в трубе.
Если представить поток электрического тока как поток воды через трубу, то резистор, имеющий электрическое сопротивление R, выполняет функцию сужения трубы. Сужение в трубе препятствует потоку воды, подобно тому, как резистор препятствует потоку электрического тока. Если вы сильнее сузите трубу, то сопротивление потоку воды увеличится. Тем самым труба будет больше препятствовать потоку воды.
Формулы для определения электрического сопротивления
Согласно закона Ома для участка электрической цепи следует, что если вы измеряете напряжение U на проводнике и через него течет ток силой I, то проводник имеет электрическое сопротивление R, равное U, деленное на I, т.е. R = U / I. Единицей измерения электрического сопротивления в СИ является Ом, которая названа в честь немецкого физика Георга Симона Ома. То есть, 1 Ом — это сопротивление проводника, в котором при напряжении 1 В проходит ток силой 1 А. Поэтому, иногда, электрическое сопротивление ещё могут называть «омическим сопротивлением».
Для очень малых или очень больших сопротивлений используются такие дополнения, как милли-, кило- или мегаом. Применяются следующие отношения:
- 1 Миллиом = 1 мОм = 1*10-3 Ом;
- 1 Килоом = 1 кОм = 1*103 Ом;
- 1 Мегаом = 1 МОм = 1*106 Ом.
Интересный факт! Электрическое сопротивление человеческого тела может изменяться от 20000 Ом до 1800 Ом.
Также вы можете рассчитать электрическое сопротивление проводников с помощью их геометрических характеристик. Формула для этого следующая (см. также рисунок 3):
R = (ρ * l) / S, где
- R — электрическое сопротивление проводника;
- l — длина проводника;
- S — площадь поперечного сечения проводника;
- ρ — удельное сопротивление вещества проводника (выбирается по таблицам).
Другими словами, чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Весомое значение имеет также материал, из которого изготовлен проводник.
Как измерять электрического сопротивление?
Для измерения электрического сопротивления необходимо придерживаться следующих правил:
- Измерение проводить нужно параллельно элементу электрического цепи;
- Элемент должен быть обесточен;
- Элемент не должен быть подключен к электрической цепи;
- Измерение имеет смысл только для обычного резистора.
Значение омического сопротивления лучше всего определять с помощью цифрового мультиметра, чтобы избежать ошибок и неточностей в показаниях.
При измерении с помощью измерительного прибора измеряемый элемент не должен быть подключен к источнику напряжения во время измерения. Измеряемый элемент должен быть отпаян от электрической цепи, по крайней мере, с одной стороны. В противном случае расположенные параллельно элементы будут влиять на результат измерения.
Всё что нужно знать о сопротивлении
Содержание
- 1 Электрический ток в разных веществах
- 2 Почему «сопротивляется» проводник
- 3 Закон Ома
- 4 Вторая формула
- 5 В чем измеряется
- 6 Зависимость сопротивления от температуры
- 7 Примеры сопротивлений
- 8 Средства измерения
- 9 Видео по теме
Электрический ток — это однонаправленное перемещение заряженных частиц в электрическом поле. Способность проводника ограничивать величину электротока характеризуется физической величиной, именуемой электрическим сопротивлением. Расчёт конкретного сопротивления выполняется либо по формуле закона Ома, либо используются зависимости, в которых в качестве исходных данных выступают физические параметры проводника (геометрические размеры, удельное сопротивление или проводимость).
Электрический ток в разных веществах
На рисунке ниже схематично представлена модель возникновения электрического тока в двух разных случаях:
- Ток вызван перемещением отрицательных зарядов («минусов») в электрическом поле Е.
- Ток образован движением положительных зарядов («плюсов») в электрическом поле Е.
При этом направлением электротока считается в обоих случаях направление, в котором двигаются положительные заряды.
В зависимости от количества (концентрации) заряженных частиц и преимущественного типа проводимости (плюс или минус) вещества и среды делятся на:
- Проводники (металлы, электролиты).
- Диэлектрики.
- Полупроводники.
- Газы, плазму.
- Вакуум.
Далее речь будет идти о том, что такое сопротивление, и как найти его величину на примере металлических проводников.
Почему «сопротивляется» проводник
Структура металлов представляет собой жесткую кристаллическую решётку, в узлах которой расположены массивные, положительно заряженные ионы. В межузловом пространстве имеется большое количество свободных электронов, оторвавшихся с крайних, валентных орбит. В отсутствии электрического поля этот «электронный газ» пребывает в хаотическом движении. Как только к проводнику прикладывается напряжение (разность потенциалов) в металле возникает электрополе, которое создаёт однонаправленный поток электронов.
Электроны, набрав некоторую скорость в электрическом поле, начинают двигаться в одном направлении, но при этом они сталкиваются на своём пути с крупными препятствиями — заряженными и нейтральными атомами, хаотично колеблющимися в узлах решётки. После столкновений электроны теряют часть кинетической энергии, то есть «тормозятся». Такова физика электрического сопротивления проводника, величина которого зависит от массы атомов конкретного вещества, структуры решётки, температуры.
Закон Ома
Выдающийся европейский учёный Георг Ом исследовал на разных металлах зависимость величины электротока от электронапряжения. В 1827 г. он сделал открытие, названное в его честь законом Ома, которое выражается формулой:
Из данной формулы можно вычислить омическое сопротивление:
Единица измерения сопротивления (Ом) была названа также в честь первооткрывателя закона.
Вторая формула
Чтобы воспользоваться формулой, необходимо изначально провести измерения электронапряжения и электротока с помощью небольшой экспериментальной установки, показанной на рисунке.
В ХIХ веке многочисленные измерения исследователей разных стран, пытавшихся понять от чего зависит сопротивление проводника, нашли следующие закономерности:
- R увеличивается, когда возрастает длина экспериментального образца, т. е. R∼ L (прямо пропорционально).
- Сопротивление проводников уменьшается при увеличении поперечной площади S металлического образца, т. е. R∼1/S обратно пропорционально).
- Поскольку сопротивления идентичных по размерам образцов разных металлов существенно отличались друг от друга, учёные ввели дополнительную физическую величину, которая обозначается буквой ρ и называется удельным электрическим сопротивлением.
Полученные в ходе экспериментов данные корректно описывала итоговая формула для вычисления сопротивления:
Ниже приведена таблица удельных сопротивлений широко используемых металлов.
В чем измеряется
Общепринятая в системе СИ единица сопротивления — Ом. Он является производной от единиц напряжения (вольт, В) и тока (ампер, А). Определение единицы измерения электрического сопротивления следующее: сопротивлением 1 Ом обладает проводник, через который протекает ток величиной 1 А, а напряжение при этом равно 1 В:
[1 Ом] = [1 В] / [1 А].
В электро- и радиотехнике чаще используются кратные единицы омического сопротивления.
При решении научных задач более удобной бывает величина обратная электрическому сопротивлению 1/R, названная электропроводностью. Размерности этой единицы присвоено наименование «сименс» (См): [1 См] = [1 Ом-1].
Из второй формулы электрического сопротивления можно найти чему равно ρ:
Проанализировав данное равенство, можно сделать вывод, что единица измерения удельного сопротивления имеет размерность Ом*м, поскольку L и S измеряются в метрах и метрах квадратных соответственно: [ρ] = [Ом * м].
Для практики такая единица, равная сопротивлению провода длиной 1 м и площадью сечения 1 кв. м оказалась не очень востребованной из-за чрезмерно больших значений. Для электротехнических расчётов была введена внесистемная единица Ом*мм2/м, для которой S выражена в квадратных миллиметрах. Удобство такой единицы легко оценить, если учесть, что типичные сечения кабелей и проводов находятся в диапазоне 1.0-15.0 кв. мм.
Зависимость сопротивления от температуры
Удельное сопротивление металлов увеличивается с ростом температуры прямо пропорционально. Такая зависимость хорошо описывается линейной функцией:
В справочниках значение ТКС обычно указывается для комнатной температуры 20 градусов. Сопротивление с ростом тока меняется в связи с выделением джоулева тепла, приводящего к нагреву проводника.
При уменьшении температуры ρ плавно уменьшается, но при достижении сверхнизких показателей < 30°K некоторые металлы и сплавы переходят в сверхпроводящее состояние, то есть, их удельное сопротивление падает до нуля. Качественно физический эффект объясняется тем, что тепловое движение атомов «замораживается», и электроны начинают двигаться беспрепятственно. Теория, объясняющая, что такое нулевое сопротивление проводника, требует привлечения аппарата квантовой физики. На рисунке ниже представлена зависимость ρ(Т). Точка Ткр — переход в сверхпроводимость.
Примеры сопротивлений
При проектировании и тиражировании электронных и электротехнических устройств в качестве пассивных элементов, способных предсказуемо ограничивать рабочий ток и рассеивать излишки электрической энергии, применяются произведённые заранее виды сопротивлений заданной величины, для которых используется термин «резистор» (от англ. resist — сопротивляться).
В качестве резистивной основы используют не чистые металлы, а сплавы, имеющие низкий ТКС, например, нихром — сплав никеля (Ni) и хрома (Cr). Кроме металлических (проволочных) производятся резисторы на базе других материалов:
- Углеродистые — состоят из смеси порошковой керамики с углеродом.
- Металлоплёночные — тонкая плёнка Ni-Cr размещается на керамике.
- Металлооксидные — на керамику наносится оксид олова (SnO2) с добавлением примеси оксида сурьмы (Sb2O5).
- Композиционные — на базе соединения графита с органическими или неорганическими добавками.
- Интегральные — формируются внутри монокристалла интегральной схемы с помощью слабого легирования.
Тип резистора можно узнать из маркировки, нанесённой на его поверхность.
Средства измерения
Найти неизвестное сопротивление цепи можно без применения математических расчётов гораздо быстрее и точнее, если вооружиться современными приборами, на цифровом или стрелочном табло которых отобразится искомое значение R. Существуют омметры и мультиметры. Первые — узкоспециализированные приборы, ориентированные на измерение сопротивления. Имеются аналоговые и цифровые версии омметров. В зависимости от диапазона предполагаемых измерений различают:
- Микроомметры.
- Миллиомметры.
- Мегаоомметры.
- Гигаомметры.
- Тераомметры.
Мультиметры — комбинированные приборы, способные измерять не только электрическое сопротивление проводника, но и величину электронапряжений и электротоков.
Таким образом, с помощью приборов можно без особого труда найти сопротивление проводника и та формула, для которой требуются данные о геометрических размерах проводника и величине удельного сопротивления не понадобится. Можно также снять вольт-амперную характеристику и воспользоваться законом Ома. С помощью современных электро-измерительных приборов (омметров, мультиметров) достаточно просто определяется сопротивление, если его обозначение отсутствует на резисторах или других радиоэлементах.
Видео по теме
| Электрическое сопротивление | |
 |
|
| Размерность |
L2MT −3I −2 (СИ); |
|---|---|
| Единицы измерения | |
| СИ |
Ом |
| СГСЭ |
статом, с/см |
| СГСМ |
абом, см/с |
| |
||||||||||||
 |
||||||||||||
| Электричество · Магнетизм | ||||||||||||
|
||||||||||||
| См. также: Портал:Физика |
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
- R — сопротивление;
- U — разность электрических потенциалов на концах проводника;
- I — сила тока, протекающего между концами проводника под действием разности потенциалов.
Содержание
- 1 Единицы и размерности
- 2 Физика явления
- 3 Сопротивление человека
- 4 Метрологические аспекты
- 4.1 Приборы для измерения сопротивления (постоянного тока)
- 4.2 Средства воспроизведения сопротивления
- 4.3 Государственный эталон сопротивления
- 5 См. также
- 6 Примечания
- 7 Ссылки
Единицы и размерности
Размерность электрического сопротивления в СИ: dim R = L2MT −3I −2. В международной системе единиц (СИ) единицей сопротивления является Ом (Ω, Ohm). В системе СГС как таковой единица сопротивления не имеет специального названия, однако в её расширениях (СГСЭ, СГСМ и гауссова система единиц) используются[2]:
- статом (в СГСЭ и гауссовой системе, 1 statΩ = (109 c−2) с/см = 898 755 178 736,818 Ом (точно) ≈ 8,98755·1011 Ом, равен сопротивлению проводника, через который под напряжением 1 статвольт течёт ток 1 статампер);
- абом (в СГСМ, 1 abΩ = 1·10−9 Ом = 1 наноом, равен сопротивлению проводника, через который под напряжением 1 абвольт течёт ток 1 абампер).
Размерность сопротивления в СГСЭ и гауссовой системе равна TL−1 (то есть совпадает с размерностью обратной скорости, с/см), в СГСМ — LT−1 (то есть совпадает с размерностью скорости, см/с)[3].
Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой в системе СИ служит сименс (1 См = 1 Ом−1), в системе СГСЭ (и гауссовой) статсименс и в СГСМ — абсименс[4].
Физика явления
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:
где ρ — удельное сопротивление вещества проводника, l — длина проводника, а S — площадь сечения.
Сопротивление однородного проводника также зависит от температуры.
Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади.
Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.
Сопротивление человека
- Для расчёта величины силы тока, протекающего через человека при попадании его под электрическое напряжение частотой 50 Гц, сопротивление тела человека условно принимается равным 1 кОм[5]. Эта величина имеет малое отношение к реальному сопротивлению человеческого тела. В реальности сопротивление человека не является омическим, так как эта величина, во-первых, нелинейна по отношению к приложенному напряжению, во-вторых меняется во времени, в третьих, гораздо меньше у человека, который волнуется и, следовательно, потеет и т. д.
- Серьёзные поражения тканей человека наблюдаются обычно при прохождении тока силой около 100 мА. Совершенно безопасным считается ток силой до 1 мА. Удельное сопротивление тела человека весьма значительно (около 15 кОм). Поэтому опасные токи могут быть достигнуты только при значительном напряжении. Однако при наличии сырости сопротивление тела человека резко снижается и безопасным может считаться напряжение только до 12 В.
Метрологические аспекты
Приборы для измерения сопротивления (постоянного тока)
- Омметр
- Измерительный мост
- Комбинированные приборы (мультиметры, универсальные вольтметры и т. д.)
Средства воспроизведения сопротивления
- Магазин сопротивлений — набор резисторов
- Катушки электрического сопротивления
Государственный эталон сопротивления
- ГЭТ 14-91 Государственный первичный эталон единицы электрического сопротивления. Институт-хранитель: ВНИИМ.
См. также
- Сверхпроводимость
- Закон Ома
- Закон Барлоу
- Удельное электрическое сопротивление
- Электрическая проводимость
- Отрицательное сопротивление
- Внутреннее сопротивление
- Импеданс
- Волновое сопротивление
- Активное сопротивление
- Реактивное сопротивление
Примечания
- ↑ Электрическое сопротивление — БСЭ.
- ↑ CRC Handbook of Chemistry and Physics, 92nd Edition. — Ed. William M. Haynes. — 2011. — ISBN 978-1-4398-5511-9
- ↑ Б. М. Яворский, А. А. Детлаф. — Справочник по физике для инженеров и студентов вузов. — М.: Наука, 1968. — 939 с.
- ↑ Иногда в англоязычной литературе сименс называют mho («перевёрнутое» название обратной единицы ohm), соответственно для СГСЭ и СГСМ — statmho (=statsiemens) и abmho (=absiemens).
- ↑ 1 кОм в модели, принятой в стандарте IEEE Std 80
Ссылки
- Электрическое сопротивление проводников
Электрическое сопротивление характеризует способность электрического проводника препятствовать прохождению электрического тока.
Электрическое сопротивление обозначается буквой R. Единицей сопротивления является ом (Ом).
Закон Ома
Сила тока (I) прямо пропорциональна напряжению (U). Это означает следующее: во сколько раз изменяется напряжение, во столько раз изменяется и сила тока.
Сила тока (I) обратно пропорциональна электрическому сопротивлению (R). Поэтому чем больше сопротивление, тем меньше сила тока, протекающего в проводнике.
I=UR
Причиной электрического сопротивления является тепловое движение образующих материал атомов или молекул. Частицы колеблются около своих мест и мешают перемещению электронов. Это можно сравнить с длинным коридором, в котором одновременно перемещается много людей. И насколько быстро можно двигаться вперед, зависит от различных причин.
Электрическое сопротивление характерно для всех веществ и зависит от:
| Материала проводника тока ρ | Длины проводника (l) | Площади поперечного сечения проводника (S) |
| Для каждого материала характерно его удельное сопротивление, которое обозначают буквой ρ и которое можно найти в таблице удельных сопротивлений. | Чем длиннее проводник электричества, тем больше его электрическое сопротивление. | Чем меньше площадь поперечного сечения проводника электричества, тем больше электрическое сопротивление. |
| Пример с коридором: движение вперёд зависит от того, сколько людей в нём находится, как каждый из них двигается, насколько они полные или худые. |
Пример с коридором: чем длиннее коридор, тем дольше и труднее путь. |
Пример с коридором: чем уже коридор, тем труднее пробираться сквозь толпу людей. |
Удельное сопротивление металлов небольшое, а изоляторов — очень большое. В цепях, в которых электрический ток должен производить большую теплоту (например, в обогревателях), используют проводники с большим удельным сопротивлением, например, нихром. Току труднее течь, увеличивается тепловое движение частиц, в результате проводник нагревается. У алюминия низкое удельное сопротивление, поэтому его можно использовать для передачи электроэнергии.
Электрическое сопротивление человеческого тела может изменяться от 20000 Ом до 1800 Ом.
Чтобы электрическая цепь обеспечивала необходимую силу тока, в неё включают резисторы.
Резистор — прибор с постоянным сопротивлением.
Резисторы имеются во всех телевизорах, компьютерах, радиоприёмниках и т.д.
Чтобы изменить силу тока в электрической цепи, используют реостаты.
Реостат — прибор с переменным сопротивлением.
В составе реостата имеется подвижный контакт, при помощи которого изменяется длина участка, включённого в цепь.
Реостат используется, например, в регуляторах громкости радиоприёмников.