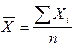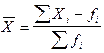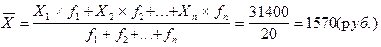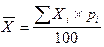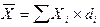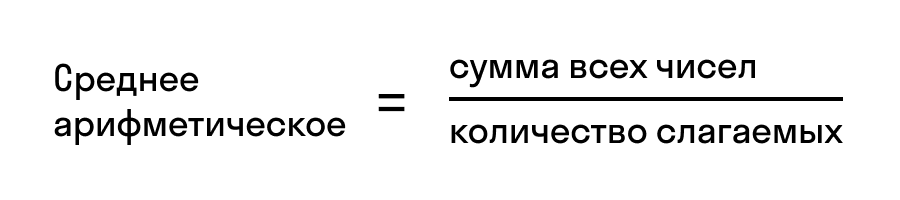For broader coverage of this topic, see Mean.
In mathematics and statistics, the arithmetic mean ( air-ith-MET-ik), arithmetic average, or just the mean or average (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection.[1] The collection is often a set of results from an experiment, an observational study, or a survey. The term «arithmetic mean» is preferred in some mathematics and statistics contexts because it helps distinguish it from other types of means, such as geometric and harmonic.
In addition to mathematics and statistics, the arithmetic mean is frequently used in economics, anthropology, history, and almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation’s population.
While the arithmetic mean is often used to report central tendencies, it is not a robust statistic: it is greatly influenced by outliers (values much larger or smaller than most others). For skewed distributions, such as the distribution of income for which a few people’s incomes are substantially higher than most people’s, the arithmetic mean may not coincide with one’s notion of «middle». In that case, robust statistics, such as the median, may provide a better description of central tendency.
Definition[edit]
Given a data set 




The arithmetic mean is a data set’s most commonly used and readily understood measure of central tendency. In statistics, the term average refers to any measurement of central tendency. The arithmetic mean of a set of observed data is equal to the sum of the numerical values of each observation, divided by the total number of observations. Symbolically, for a data set consisting of the values 

[3]
(For an explanation of the summation operator, see summation.)
For example, if the monthly salaries of 

If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean and denoted by the Greek letter 


The arithmetic mean can be similarly defined for vectors in multiple dimensions, not only scalar values; this is often referred to as a centroid. More generally, because the arithmetic mean is a convex combination (meaning its coefficients sum to 
Motivating properties[edit]
The arithmetic mean has several properties that make it interesting, especially as a measure of central tendency. These include:
Additional properties[edit]
- The arithmetic mean of any amount of equal-sized number groups together is the arithmetic mean of the arithmetic means of each group.
Contrast with median[edit]
The arithmetic mean may be contrasted with the median. The median is defined such that no more than half the values are larger, and no more than half are smaller than it. If elements in the data increase arithmetically when placed in some order, then the median and arithmetic average are equal. For example, consider the data sample 




There are applications of this phenomenon in many fields. For example, since the 1980s, the median income in the United States has increased more slowly than the arithmetic average of income.[4]
Generalizations[edit]
Weighted average[edit]
A weighted average, or weighted mean, is an average in which some data points count more heavily than others in that they are given more weight in the calculation.[5] For example, the arithmetic mean of 









Continuous probability distributions[edit]
If a numerical property, and any sample of data from it, can take on any value from a continuous range instead of, for example, just integers, then the probability of a number falling into some range of possible values can be described by integrating a continuous probability distribution across this range, even when the naive probability for a sample number taking one certain value from infinitely many is zero. In this context, the analog of a weighted average, in which there are infinitely many possibilities for the precise value of the variable in each range, is called the mean of the probability distribution. The most widely encountered probability distribution is called the normal distribution; it has the property that all measures of its central tendency, including not just the mean but also the median mentioned above and the mode (the three Ms[6]), are equal. This equality does not hold for other probability distributions, as illustrated for the log-normal distribution here.
Angles[edit]
Particular care is needed when using cyclic data, such as phases or angles. Taking the arithmetic mean of 1° and 359° yields a result of 180°.
This is incorrect for two reasons:
In general application, such an oversight will lead to the average value artificially moving towards the middle of the numerical range. A solution to this problem is to use the optimization formulation (that is, define the mean as the central point: the point about which one has the lowest dispersion) and redefine the difference as a modular distance (i.e., the distance on the circle: so the modular distance between 1° and 359° is 2°, not 358°).
Symbols and encoding[edit]
The arithmetic mean is often denoted by a bar (vinculum or macron), as in 
Some software (text processors, web browsers) may not display the «x̄» symbol correctly. For example, the HTML symbol «x̄» combines two codes — the base letter «x» plus a code for the line above (̄ or ¯).[7]
In some document formats (such as PDF), the symbol may be replaced by a «¢» (cent) symbol when copied to a text processor such as Microsoft Word.
See also[edit]
- Fréchet mean
- Generalized mean
- Geometric mean
- Harmonic mean
- Inequality of arithmetic and geometric means
- Sample mean and covariance
- Standard deviation
- Standard error of the mean
- Summary statistics
References[edit]
- ^ Jacobs, Harold R. (1994). Mathematics: A Human Endeavor (Third ed.). W. H. Freeman. p. 547. ISBN 0-7167-2426-X.
- ^ a b c Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53–58. ISBN 9788122404197.
- ^ Weisstein, Eric W. «Arithmetic Mean». mathworld.wolfram.com. Retrieved 21 August 2020.
- ^ Krugman, Paul (4 June 2014) [Fall 1992]. «The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate». The American Prospect.
- ^ {{Cite web|title=Mean {{!}tannica.com/science/mean|access-date=2020-08-21|website=Encyclopedia Britannica|language=en}}
- ^ Thinkmap Visual Thesaurus (30 June 2010). «The Three M’s of Statistics: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Retrieved 3 December 2018.
- ^ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Retrieved 14 October 2018.
- ^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.
Further reading[edit]
- Huff, Darrell (1993). How to Lie with Statistics. W. W. Norton. ISBN 978-0-393-31072-6.
External links[edit]
- Calculations and comparisons between arithmetic mean and geometric mean of two numbers
- Calculate the arithmetic mean of a series of numbers on fxSolver
For broader coverage of this topic, see Mean.
In mathematics and statistics, the arithmetic mean ( air-ith-MET-ik), arithmetic average, or just the mean or average (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection.[1] The collection is often a set of results from an experiment, an observational study, or a survey. The term «arithmetic mean» is preferred in some mathematics and statistics contexts because it helps distinguish it from other types of means, such as geometric and harmonic.
In addition to mathematics and statistics, the arithmetic mean is frequently used in economics, anthropology, history, and almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation’s population.
While the arithmetic mean is often used to report central tendencies, it is not a robust statistic: it is greatly influenced by outliers (values much larger or smaller than most others). For skewed distributions, such as the distribution of income for which a few people’s incomes are substantially higher than most people’s, the arithmetic mean may not coincide with one’s notion of «middle». In that case, robust statistics, such as the median, may provide a better description of central tendency.
Definition[edit]
Given a data set 




The arithmetic mean is a data set’s most commonly used and readily understood measure of central tendency. In statistics, the term average refers to any measurement of central tendency. The arithmetic mean of a set of observed data is equal to the sum of the numerical values of each observation, divided by the total number of observations. Symbolically, for a data set consisting of the values 

[3]
(For an explanation of the summation operator, see summation.)
For example, if the monthly salaries of 

If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean and denoted by the Greek letter 


The arithmetic mean can be similarly defined for vectors in multiple dimensions, not only scalar values; this is often referred to as a centroid. More generally, because the arithmetic mean is a convex combination (meaning its coefficients sum to 
Motivating properties[edit]
The arithmetic mean has several properties that make it interesting, especially as a measure of central tendency. These include:
Additional properties[edit]
- The arithmetic mean of any amount of equal-sized number groups together is the arithmetic mean of the arithmetic means of each group.
Contrast with median[edit]
The arithmetic mean may be contrasted with the median. The median is defined such that no more than half the values are larger, and no more than half are smaller than it. If elements in the data increase arithmetically when placed in some order, then the median and arithmetic average are equal. For example, consider the data sample 




There are applications of this phenomenon in many fields. For example, since the 1980s, the median income in the United States has increased more slowly than the arithmetic average of income.[4]
Generalizations[edit]
Weighted average[edit]
A weighted average, or weighted mean, is an average in which some data points count more heavily than others in that they are given more weight in the calculation.[5] For example, the arithmetic mean of 









Continuous probability distributions[edit]
If a numerical property, and any sample of data from it, can take on any value from a continuous range instead of, for example, just integers, then the probability of a number falling into some range of possible values can be described by integrating a continuous probability distribution across this range, even when the naive probability for a sample number taking one certain value from infinitely many is zero. In this context, the analog of a weighted average, in which there are infinitely many possibilities for the precise value of the variable in each range, is called the mean of the probability distribution. The most widely encountered probability distribution is called the normal distribution; it has the property that all measures of its central tendency, including not just the mean but also the median mentioned above and the mode (the three Ms[6]), are equal. This equality does not hold for other probability distributions, as illustrated for the log-normal distribution here.
Angles[edit]
Particular care is needed when using cyclic data, such as phases or angles. Taking the arithmetic mean of 1° and 359° yields a result of 180°.
This is incorrect for two reasons:
In general application, such an oversight will lead to the average value artificially moving towards the middle of the numerical range. A solution to this problem is to use the optimization formulation (that is, define the mean as the central point: the point about which one has the lowest dispersion) and redefine the difference as a modular distance (i.e., the distance on the circle: so the modular distance between 1° and 359° is 2°, not 358°).
Symbols and encoding[edit]
The arithmetic mean is often denoted by a bar (vinculum or macron), as in 
Some software (text processors, web browsers) may not display the «x̄» symbol correctly. For example, the HTML symbol «x̄» combines two codes — the base letter «x» plus a code for the line above (̄ or ¯).[7]
In some document formats (such as PDF), the symbol may be replaced by a «¢» (cent) symbol when copied to a text processor such as Microsoft Word.
See also[edit]
- Fréchet mean
- Generalized mean
- Geometric mean
- Harmonic mean
- Inequality of arithmetic and geometric means
- Sample mean and covariance
- Standard deviation
- Standard error of the mean
- Summary statistics
References[edit]
- ^ Jacobs, Harold R. (1994). Mathematics: A Human Endeavor (Third ed.). W. H. Freeman. p. 547. ISBN 0-7167-2426-X.
- ^ a b c Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53–58. ISBN 9788122404197.
- ^ Weisstein, Eric W. «Arithmetic Mean». mathworld.wolfram.com. Retrieved 21 August 2020.
- ^ Krugman, Paul (4 June 2014) [Fall 1992]. «The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate». The American Prospect.
- ^ {{Cite web|title=Mean {{!}tannica.com/science/mean|access-date=2020-08-21|website=Encyclopedia Britannica|language=en}}
- ^ Thinkmap Visual Thesaurus (30 June 2010). «The Three M’s of Statistics: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Retrieved 3 December 2018.
- ^ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Retrieved 14 October 2018.
- ^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.
Further reading[edit]
- Huff, Darrell (1993). How to Lie with Statistics. W. W. Norton. ISBN 978-0-393-31072-6.
External links[edit]
- Calculations and comparisons between arithmetic mean and geometric mean of two numbers
- Calculate the arithmetic mean of a series of numbers on fxSolver
Определение. Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Примером среднего арифметического служат такие показатели, как урожайность, производительность, посещаемость, скорость движения на определенном участке. Вычисление среднего арифметического и его составляющих производится по следующему простом правилу.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Пример 1. У Васи было 2 яблока, у Кати — 10 яблок, а у Саши — 6. Среднее количество яблок:
Пример 2. Средняя посещаемость зала в столовой за неделю высчитывается из посещаемости в течение 7 дней: 145 человек в 1-й день; 152 человека во 2-й день; 158 человек в 3-й лень; 162 человека в 4-й день; 164 человека в 5-й день; 161 человек в 6-й день и 157 человек в 7-й день.
Найдем среднее арифметическое (посещаемость) за
неделю:
Xсреднее = (145 + 152 + 158 + 162 + 164 + 161 + 157) : 7 = 157.
Можно определить среднюю посещаемость и как 1099 : 7 = 157 человек (1099 человек за 7 дней). Т. с. можно фиксировать общее количество посетителей за неделю без учета посещаемости по дням. Но тогда мы не будем знать, что наибольшее количество посетителей в день — 164 человека, а наименьшее — 145 человек, что в этом примере важно (кухня должна ориентироваться на максимальное посещение, от количества посетителей зависит выручка столовой н т. д.).
Во втором примере мы вели статистический учет, следовательно, среднее арифметическое — показатель и в статистике. Но вычисление среднего арифметического имеет смысл только в определенных пределах (небольших промежутках). Нам ничего не даст, например, среднее-мировое количество жителей в одной стране. Стран в мире более 200, а число жителей Индии и Китая совершенно несоизмеримо с количеством жителей Нидерландов или Люксембурга. Полученная средняя численность проживающих в одной стране не будет объективной характеристикой каждой из стран (из-за большого расхождения в числах).
Запись опубликована в рубрике Математика с метками арифметическое, среднее. Добавьте в закладки постоянную ссылку.
Для выяснения методики расчета средней арифметической используем следующие обозначения:
X — арифметический признак
X (X1, X2, … X3) — варианты определенного признака
n — число единиц совокупности
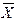
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами:
1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:
2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:
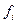
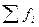
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
| Заработная плата, руб. Xi | Число сотрудников, чел. fi | Произведение вариант на веса (частоты) Xi*fi |
| Итого: |
В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:
pi — относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот.
Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции одной переменной, то среднее арифметическое этой функции на отрезке определяется через определённый интеграл:
Здесь для определения отрезка подразумевается, что причём чтобы знаменатель не был равен 0.
Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35,1. Арифметическое среднее этого роста 10 %, но, поскольку акции выросли за 2 года всего на $5,1, средний рост в 8,2 % даёт конечный результат $35,1:
$30 × (1 – 0,1) (1 + 0,3) = $30 × (1 + 0,082) (1 + 0,082) = $35,1. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: $30 × (1 + 0,1) (1 + 0,1) = $36.3.
Сложный процент в конце 2 года: 90 % * 130 % = 117 %, то есть общий прирост 17 %, а среднегодовой сложный процент , то есть среднегодовой прирост 8,2 %.
Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
Понятие среднего арифметического
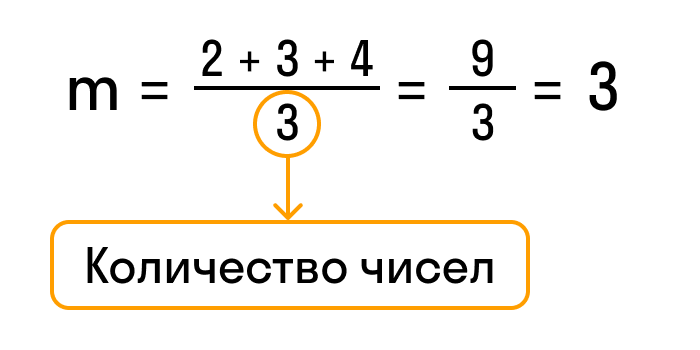
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
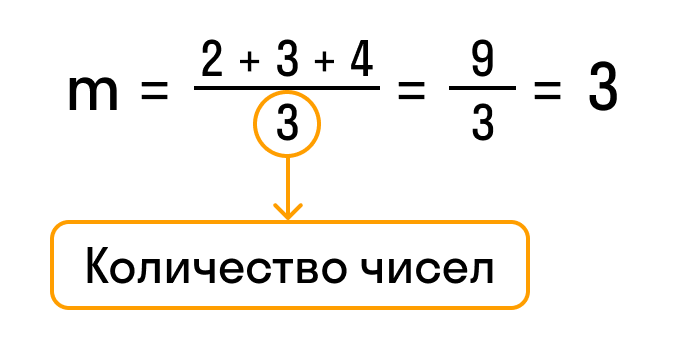
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
- 2 + 3 + 4 = 9
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Как решаем:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Как решаем:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Как решаем:
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Как решаем:
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
- 2 + 3 + 4 = 9
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Как решаем:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Как решаем:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Как решаем:
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Как решаем:
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Как правильно пишется словосочетание «среднее арифметическое»
- Как правильно пишется слово «средний»
- Как правильно пишется слово «арифметический»
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: почто — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «средний»
Синонимы к словосочетанию «среднее арифметическое»
Предложения со словосочетанием «среднее арифметическое»
- В итоге вывожу среднее арифметическое и рассказываю про жизнь в столицах.
- Самый простой способ уменьшения погрешности – провести измерение не один раз, а несколько, затем вычислить среднее арифметическое из результатов каждого замера.
- Соответственно, рейтинг является средним арифметическим курсов акций этих компаний, взвешенным по весам этих акций в рейтинге.
- (все предложения)
Цитаты из русской классики со словосочетанием «среднее арифметическое»
- — Да, милейший математик, к счастью, к счастью, к счастью! Мы — счастливейшее среднее арифметическое… Как это у вас говорится: проинтегрировать от нуля до бесконечности — от кретина до Шекспира… Так!
- (все
цитаты из русской классики)
Значение словосочетания «среднее арифметическое»
-
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — сумма всех чисел, делённая на их количество. Является одной из наиболее распространённых мер центральной тенденции. (Википедия)
Все значения словосочетания СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Афоризмы русских писателей со словом «средний»
- Ни плохих, ни хороших, ни средних…
Все они по своим местам,
Где ни первых нет, ни последних…
Все они опочили там. - У всякого великого писателя свой слог: слога нельзя разделить на три рода — высокий, средний и низкий: слог делится на столько родов, сколько есть на свете великих, по крайней мере, сильнодаровитых писателей.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
среднеарифметический
- среднеарифметический
-
СРЕДНЕАРИФМЕТИ́ЧЕСКИЙ -ая, -ое. Полученный в результате сложения частей и последующего деления на количество этих частей. С. результат.
◁ Среднеарифмети́ческое, -ого;
ср.
Вычислить с.
Энциклопедический словарь.
2009.
Смотреть что такое «среднеарифметический» в других словарях:
-
среднеарифметический — среднеарифметический … Орфографический словарь-справочник
-
Среднеарифметический радиус частиц — Отношение суммарной длины радиусов частиц к количеству этих частиц Источник: ГОСТ 22023 76: Материалы строительные. Метод микроскопического количественного анализа структуры … Словарь-справочник терминов нормативно-технической документации
-
Среднеарифметический частиц на шлифе — радиус Отношение суммарной длины радиусов всех частиц данного компонента на срезе к количеству этих частиц Источник: ГОСТ 22023 76: Материалы строительные. Метод микроскопического количественного анализа структуры … Словарь-справочник терминов нормативно-технической документации
-
Среднеарифметический реверберационный коэффициент звукопоглощения — 5. Среднеарифметический реверберационный коэффициент звукопоглощения Реверберационный коэффициент звукопоглощения, усредняемый по двум или более октавным полосам частот Источник … Словарь-справочник терминов нормативно-технической документации
-
среднеарифметический — среднеарифмет ический … Русский орфографический словарь
-
среднеарифметический — … Орфографический словарь русского языка
-
среднеарифметический — среднеарифмети/ческий … Слитно. Раздельно. Через дефис.
-
среднеарифметический — ая, ое. см. тж. среднеарифметическое Полученный в результате сложения частей и последующего деления на количество этих частей. Среднеарифмети/ческий результат … Словарь многих выражений
-
среднеарифметический — средн/е/арифмет/ич/еск/ий … Морфемно-орфографический словарь
-
среднеарифметический реверберационный коэффициент звукопоглощения — реверберационный коэффициент звукопоглощения, усредняемый по двум или более октавным полосам частот. (Смотри: ГОСТ 23499 79. Материалы и изделия строительные звукопоглощающие и звукоизоляционные. Классификация и общие технические требования.)… … Строительный словарь