Найди верный ответ на вопрос ✅ «Как обозначается или пишется в геометрии понятие «окружность»? …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Геометрия » Как обозначается или пишется в геометрии понятие «окружность»?
кирилл красавчик
Ученик
(1),
на голосовании
10 лет назад
Голосование за лучший ответ
Герман Одинцов
Мастер
(2032)
10 лет назад
Принадлежит
Владимир
Мудрец
(13605)
10 лет назад
Это знак принадлежности, вхождения в множество.
viktor potarev
Знаток
(325)
10 лет назад
Принадлежит
Debero
Просветленный
(24716)
10 лет назад
Знак принадлежности
Пусть число а = 5, а множество А = (2,5,8)
Тогда а «принадлежит» А
Марина Пищикова
Ученик
(135)
6 лет назад
я чет не догоняю
геоме́трия
геоме́трия, -и
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: лихачить — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «геометрия»
Синонимы к слову «геометрия»
Предложения со словом «геометрия»
- Геометрические построения в рамках начертательной геометрии довольно сложные, изучаются в специальных высших и средних учебных заведениях.
- Большое значение имела математика, и преподавалась в старшем классе даже аналитическая геометрия и элементы высшей, математики.
- Термин сакральная геометрия часто используется людьми, чья работа связана с духовной деятельностью.
- (все предложения)
Цитаты из русской классики со словом «геометрия»
- В училище преподавали общеобразовательные предметы, арифметику, немного физики, алгебру и геометрию.
- Большое значение имела математика, и преподавалась в старшем классе даже аналитическая геометрия и элементы высшей математики.
- У этого-то Тиммермана Петр, уже шестнадцатилетний юноша, принялся учиться арифметике, геометрии, фортификации.
- (все
цитаты из русской классики)
Значение слова «геометрия»
-
ГЕОМЕ́ТРИЯ, -и, ж. Раздел математики, изучающий пространственные формы и отношения тел. (Малый академический словарь, МАС)
Все значения слова ГЕОМЕТРИЯ
Афоризмы русских писателей со словом «геометрия»
- Вдохновение есть расположение к живейшему принятию впечатлений и соображению понятий, следственно и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии.
- Вдохновение нужно в геометрии, как в поэзии.
- (все афоризмы русских писателей)
геометрия / Как записывается расстояние между прямыми? [закрыт] / Математика
|
Как записывается «расстояние между прямыми»? Сойдет ли, например, $% rho(AB; CD) $% в записи решения как расстояние между AB и CD?
задан student Я думаю, тут нет единого общепринятого стандарта обозначения. Поэтому в описании, если оно требуется, его можно ввести, предварительно сказав, что символом $%rho$% (или $%d$%) будет обозначаться расстояние между двумя прямыми или фигурами более общего вида. Иногда в таких случаях пишут что-то вроде $%dist$%, но, вообще говоря, всё годится. @falcao, просто мне интересно, как это записать, например, в блоке «Дано» стереометрической задачи на ЕГЭ. Думаю, проверяющие поймут эту запись. Я считаю, что любое обозначение, не являющееся стопроцентно общепринятым и стандартным, нужно пояснять словами. Это как бы «правило хорошего тона». Конечно, при использовании «естественных» обозначений есть надежда, что смысл будет понят и так, но в принципе могут и «придраться». Поэтому я бы «во избежание» всегда придерживался указанного выше принципа. %COMMENT% |
math.hashcode.ru
в геометрии, что обозначается буквами S?H
S — полащадь фигуры, а H — высота
S -площадь, H — высота)
Книгу почитайте по гиометрии)
S -площадь, H — высота)
Все правы. S — площадь, h (обычно маленькой буквой) — высота. А также есть: О — центр окружности (центр вписанной окружности) , М — центроид (центр масс, центр тяжести) , L — точка Лемуана, Н — ортоцентр и др.
Так что, возможно, вы имели ввиду площадь, однозначно, и высоту или ортоцентр. Всё зависит от записи. Так что проверьте её.
touch.otvet.mail.ru
Как выглядит в геометрии значок «скрещивается»?
Нет такого значка.. Это только животные могут)))<br>
Да есть такой значок. Только не знаю как объяснить. Вот крестик, как умножение, но одна палочка прерывается в месте пересечения с другой
Всемирно принятого значка для скрещивающихся прямых нет. Просто некоторые авторы учебников и справочников придумывают свои, для местного использования.
touch.otvet.mail.ru
Многоугольник с тремя сторонами
Прежде чем рассматривать задачу о том, как проверить, существует ли треугольник, следует подробно изучить эту фигуру. Согласно общепринятому определению, любой замкнутый многоугольник на плоскости, который состоит из трех отрезков, пересекающихся своими концами друг с другом, является треугольником. Эта фигура имеет две группы образующих ее элементов:
- стороны;
- вершины.
Сторонами являются три отрезка, длины которых могут быть либо известны по условию задачи, либо их предстоит рассчитать. Касательно вершин следует сказать, что у любого рассматриваемого многоугольника их три. Каждую принято обозначать одной латинской буквой, например, A, B, C и так далее. Поскольку два отрезка пересекаются в вершине, то они образуют некоторый угол. Их у фигуры три, поэтому становится понятным, откуда происходит название «треугольник».
Типы фигуры
Их классификация является достаточно развитой. В ее основу положены принципы взаимоотношения длин сторон друг с другом, а также численные значения углов. В общем случае в геометрии рассматривают следующие типы треугольников:
- Равносторонний или равноугольный. Это самая симметричная фигура рассматриваемого класса, поскольку ее образуют три равные по длине стороны. Все ее углы также являются одинаковыми, каждый из них составляет 60 °. Специальные отрезки в таком треугольнике (медиана, биссектриса, медиатриса или серединный перпендикуляр и высота) совпадают друг с другом независимо от того, через какую сторону или угол они проходят.
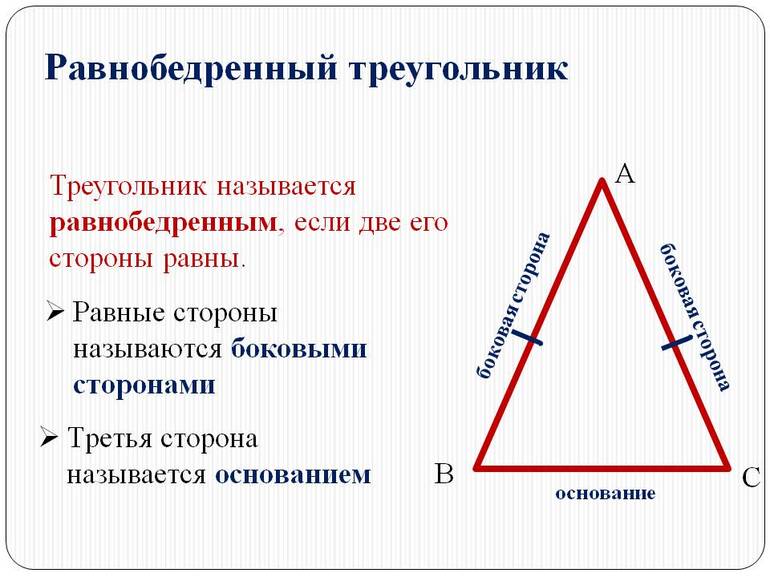
- Равнобедренный. Этот тип многоугольников является менее симметричным, чем равносторонний, однако, некоторая симметрия все же сохраняется. У этой фигуры имеются две одинаковые стороны и, как следствие, два одинаковых угла. Третий угол и сторона имеют отличные значения. Биссектриса, медиана, высота и медиатриса, которые проведены из вершины, где пересекаются одинаковые стороны, совпадают между собой. Равнобедренный треугольник может иметь как тупой, так и острый угол.
- Прямоугольный. Каждому школьнику известна знаменитая теорема Пифагора, которая применима только к данному типу многоугольников. В прямоугольной фигуре имеется один (и только один) угол, мера которого составляет 90 °. Лежащий против него отрезок называется гипотенузой, она имеет самую большую длину. Оставшиеся отрезки называются катетами. Они могут быть как одинаковыми, так и иметь разную длину.
- Общего типа. Именно этот вид фигур встречается чаще всего в задачах, поскольку его углы и стороны могут иметь произвольные значения. По этой причине работать с ним гораздо сложнее, чем с симметричными и прямоугольными многоугольниками. Тем не менее теоремы синусов и косинусов остаются справедливыми всегда.
Два основных свойства
В некоторых геометрических задачах можно встретить проблемы, которые формулируются так: можно ли построить треугольник со сторонами a, b, c, если известны их длины. Либо другой тип задач, которые предполагают знание некоторых сторон и углов, и требуют определить возможность существования такой фигуры.
Ответ на все эти проблемы заключается всего в одном слове: либо «да» и такой треугольник действительно существует, либо «нет» и из заданных элементов его построить не представляется возможным. Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:
- Равенство всех углов 180 °. Если их обозначить буквами A, B и C, тогда будет выполняться следующее выражение: A + B + C = 180 °. Из него можно сделать множество важных выводов. Например, если три угла равностороннего треугольника одинаковые, то мера каждого из них составит 60 ° (A=B=C=180 °/3=60 °). Также это свойство позволяет понять, почему в рассматриваемом многоугольнике может существовать лишь один тупой или прямой угол.
- Длины двух сторон в сумме всегда больше длины третьей стороны. Это второе важное свойство любого типа треугольников. Независимо от того, идет речь о тупоугольной фигуре или о прямоугольной, одна сторона в ней по своей длине будет всегда меньше суммы двух других.
Оба свойства с успехом можно и необходимо применять, чтобы проверить или узнать возможность существования того или иного треугольника. Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.
Вопрос вырождения
В свете изучения возможности существования треугольников важно рассмотреть вопрос их вырождения. В математике придумали универсальную формулу, которая позволяет оценить качество треугольника. Она имеет вид:
CT = (a+b-c)*(b+c-a)*(c+a-b)/(a*b*c).
Каждый из трех множителей числителя является положительным числом, что следует из главного свойства треугольников. Величина качества CT является положительной и лежит в пределах значений 0 и 1. Возможны следующие случаи:
- CT = 1. Такое качество имеют лишь равносторонние треугольники. Это легко проверить, если подставить в формулу a=b=c.
- CT>0,5. Эти фигуры называют высококачественными, все три угла в них являются острыми или один из них прямой. Под качеством имеется в виду более-менее близкое соотношение длин сторон, поэтому фигура выглядит «скругленной».
- CT<0,5. Это треугольники низкого качества, один угол у них является тупым, что говорит о некоторой доле «приплюснутости» таких фигур.
- CT => 0. Абсолютно вырожденный треугольник. В нем тупой угол приближается к 180 °. Это означает, что два других угла должны быть равны нулю. Подобная ситуация возможна лишь в одном случае: вершина тупого угла приближается к противоположной стороне, и вся фигура вырождается в отрезок нулевой толщины («сплющивается»). Важно отметить, что второе главное свойство для этого треугольника будет говорить о том, что длины двух малых сторон в сумме равны третьей.
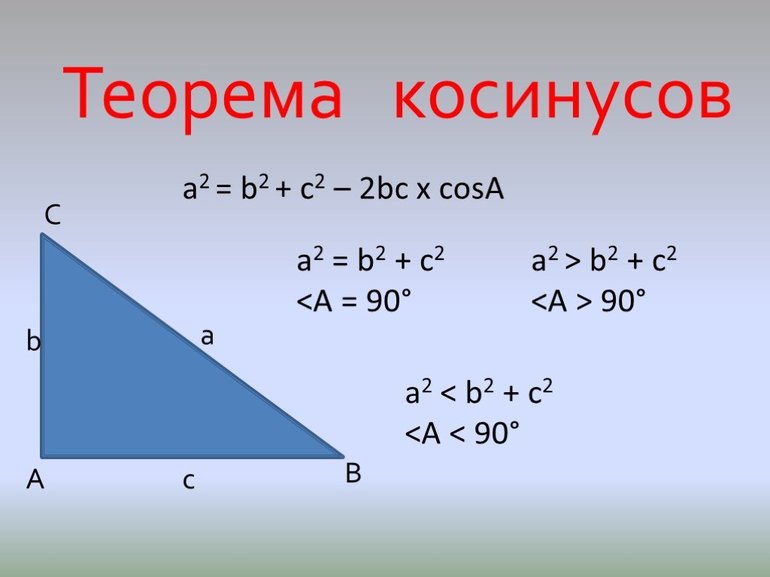
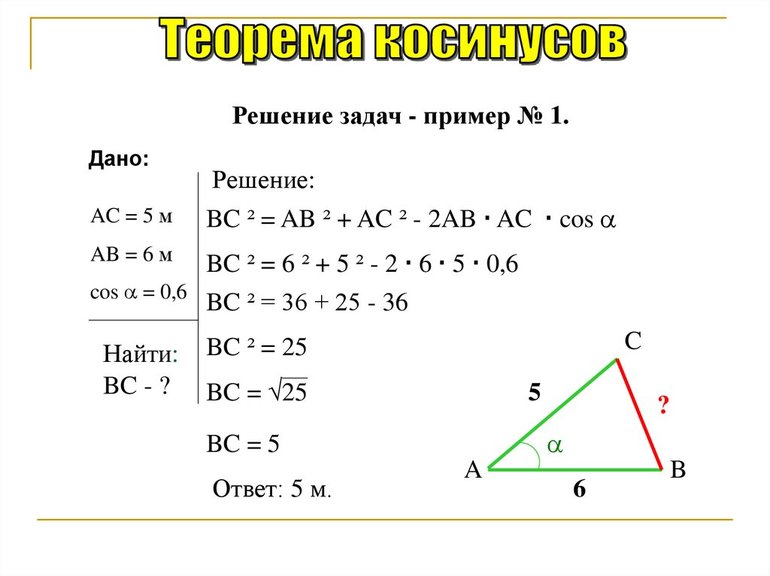
Теорема косинусов
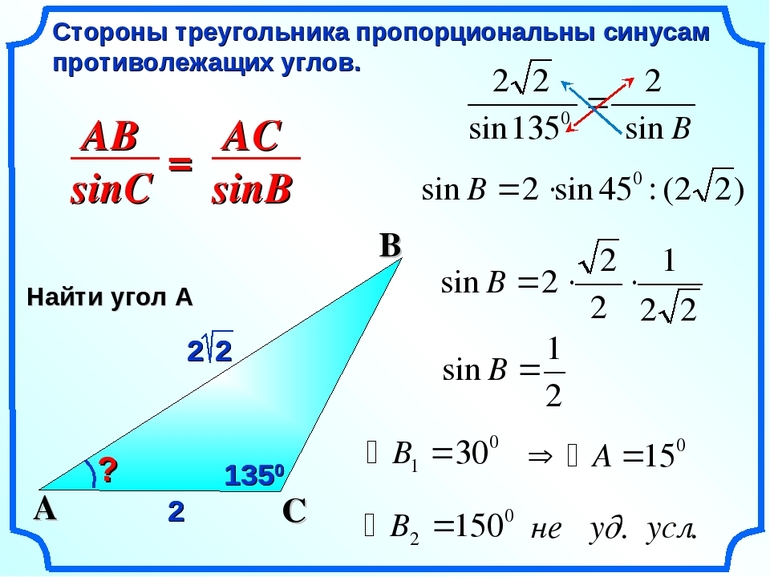
Чтобы решать задачи на треугольники, недостаточно знать лишь главные их свойства. Последние позволяют лишь дать качественный, но не количественный ответ. Теорем и формул для рассматриваемых многоугольников известно много (синусов, Пифагора, медиан, Герона и др.). Однако, теорема косинусов является одной из основополагающих, поскольку позволяет по двум сторонам и углу определить значение длины третьей стороны (справедливости ради следует отметить, что теорема синусов является не менее важной, поскольку она по двум углам и стороне позволяет вычислить неизвестные стороны).
Соответствующее выражение имеет следующий вид:
c 2 = a 2 + b 2 — 2*a*b*cos (α).
Здесь a, b, c — длины сторон фигуры, α — угол между a и b. Нетрудно догадаться, что это выражение является обобщение пифагоровой теоремы для треугольника с прямым углом.
По сути, записанное равенство заключает в себе второе главное свойство треугольников. Действительно, значение угла α может изменяться от 0 ° до 180 °. При этом тригонометрическая функция cos пробегает значения от 1 до -1. Для всех них длина одного отрезка будет меньше суммы двух других. Лишь для значений -1 и +1 получается равенство, что свидетельствует о полном вырождении треугольника в отрезок.
Решение задач
Для закрепления полученных знаний полезно привести пару примеров решения типичных геометрических задач с треугольниками, в которых нужно будет либо дать качественный ответ, либо получить некоторое количественное значение.
Первая задача требует получить качественный ответ. Пусть имеется треугольник со сторонами 1, 2, 4. Существует ли такая фигура, требуется выяснить.
Для решения этой проблемы абсолютно неважно измеряются стороны в метрах, в сантиметрах, в дюймах или в других величинах. Важно лишь взаимоотношение между ними. Для каждой из длин отрезков следует проверить свойство существования рассматриваемой фигуры. Если получится хотя бы одна ложь, то треугольник построить нельзя:
- 1<2+4 — правда;
- 2<1+4 — правда;
- 4<1+2 — ложь.
Таким образом, не существует треугольник со сторонами 1−2-4. Длин сторон 1 и 2 недостаточно даже для построения абсолютно вырожденной фигуры. Следует отметить, что является необязательным проверка всех трех неравенств, если встретилась «ложь», то есть уже по одному неравенству можно сказать о невозможности начертить фигуру.
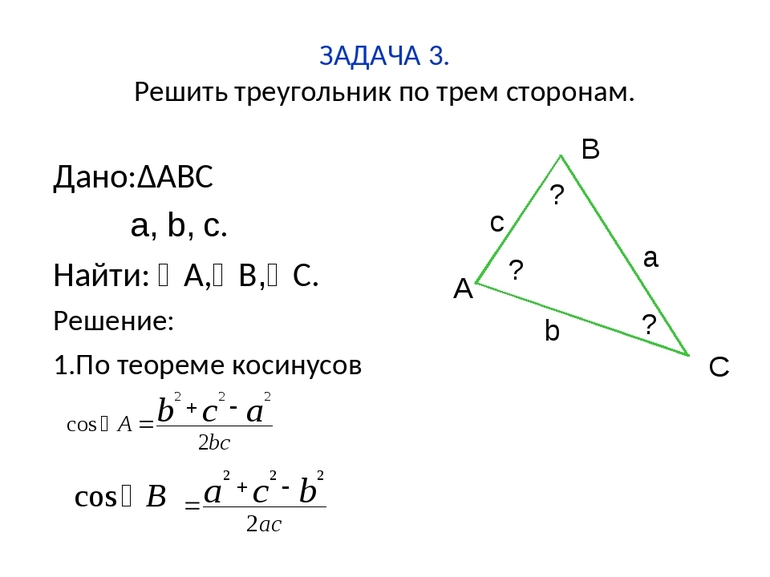
Вторая задача требует дать не только качественный ответ, но и получить количественные характеристики фигуры. Нужно узнать, возможно ли построить треугольник со сторонами 3, 4 и 6, и, если да, то какой должен быть угол между сторонами с длинами 3 и 4.
Сначала следует проверить существующие неравенства:
- 3<4+6 — правда;
- 4<3+6 — правда;
- 6<3+4 — правда.
Все три неравенства являются истинными (править их не нужно), значит, треугольник со сторонами 3, 4 и 6 можно построить. Для определения значения угла между отрезками 3 и 4 следует применить формулу косинусов. Пусть a=3, b=4, c=6, тогда:
α = arccos ((a 2 + b 2 — c 2 )/(2*a*b)) = arccos ((3 2 + 4 2 — 6 2 )/(2*3*4)) ≈ 51,38 °.
Таким образом, для определения возможности существования того или иного треугольника на плоскости необходимо проверить тот факт, что каждая из его сторон имеет меньшую длину, чем сумма двух других отрезков. Теорема косинусов является удобным инструментом для определения количественных характеристик рассматриваемого типа фигур.
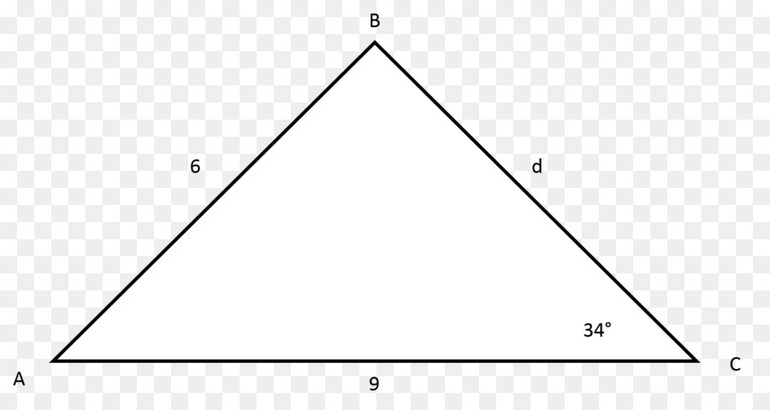
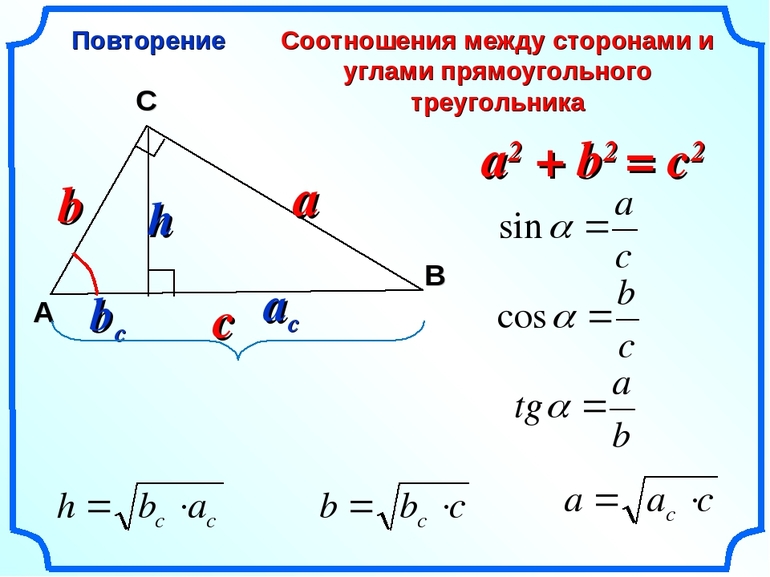
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):