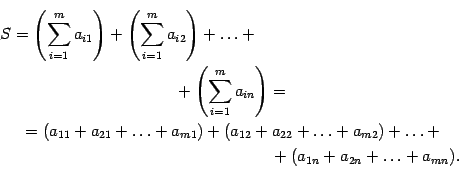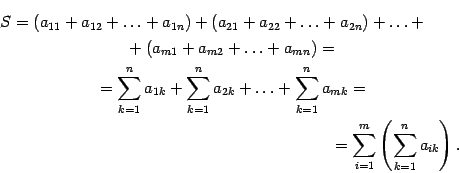Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Вёрстка:
Кирилл Климентьев
In mathematics, summation is the addition of a sequence of any kind of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted «+» is defined.
Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article.
The summation of an explicit sequence is denoted as a succession of additions. For example, summation of [1, 2, 4, 2] is denoted 1 + 2 + 4 + 2, and results in 9, that is, 1 + 2 + 4 + 2 = 9. Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0.
Very often, the elements of a sequence are defined, through a regular pattern, as a function of their place in the sequence. For simple patterns, summation of long sequences may be represented with most summands replaced by ellipses. For example, summation of the first 100 natural numbers may be written as 1 + 2 + 3 + 4 + ⋯ + 99 + 100. Otherwise, summation is denoted by using Σ notation, where 

For long summations, and summations of variable length (defined with ellipses or Σ notation), it is a common problem to find closed-form expressions for the result. For example,[a]
Although such formulas do not always exist, many summation formulas have been discovered—with some of the most common and elementary ones being listed in the remainder of this article.
Notation[edit]
Capital-sigma notation[edit]
Mathematical notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, 
where i is the index of summation; ai is an indexed variable representing each term of the sum; m is the lower bound of summation, and n is the upper bound of summation. The «i = m» under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by one for each successive term, stopping when i = n.[b]
This is read as «sum of ai, from i = m to n«.
Here is an example showing the summation of squares:
In general, while any variable can be used as the index of summation (provided that no ambiguity is incurred), some of the most common ones include letters such as 



Alternatively, index and bounds of summation are sometimes omitted from the definition of summation if the context is sufficiently clear. This applies particularly when the index runs from 1 to n.[1] For example, one might write that:
Generalizations of this notation are often used, in which an arbitrary logical condition is supplied, and the sum is intended to be taken over all values satisfying the condition. For example:
is an alternative notation for 


is the sum of 


is the sum of 


There are also ways to generalize the use of many sigma signs. For example,
is the same as
A similar notation is used for the product of a sequence, where 

Special cases[edit]
It is possible to sum fewer than 2 numbers:
These degenerate cases are usually only used when the summation notation gives a degenerate result in a special case.
For example, if 

Formal definition[edit]
Summation may be defined recursively as follows:
, for b < a;
, for b ≥ a.
Measure theory notation[edit]
In the notation of measure and integration theory, a sum can be expressed as a definite integral,
where ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



Calculus of finite differences[edit]
Given a function f that is defined over the integers in the interval [m, n], the following equation holds:
This is the analogue of the fundamental theorem of calculus in calculus of finite differences, which states that:
where
is the derivative of f.
An example of application of the above equation is the following:
Using binomial theorem, this may be rewritten as:
The above formula is more commonly used for inverting of the difference operator 
where f is a function defined on the nonnegative integers.
Thus, given such a function f, the problem is to compute the antidifference of f, a function 

This function is defined up to the addition of a constant, and may be chosen as[2]
There is not always a closed-form expression for such a summation, but Faulhaber’s formula provides a closed form in the case where 
Approximation by definite integrals[edit]
Many such approximations can be obtained by the following connection between sums and integrals, which holds for any increasing function f:
and for any decreasing function f:
For more general approximations, see the Euler–Maclaurin formula.
For summations in which the summand is given (or can be interpolated) by an integrable function of the index, the summation can be interpreted as a Riemann sum occurring in the definition of the corresponding definite integral. One can therefore expect that for instance
since the right-hand side is by definition the limit for 
Identities[edit]
The formulae below involve finite sums; for infinite summations or finite summations of expressions involving trigonometric functions or other transcendental functions, see list of mathematical series.
General identities[edit]
(distributivity)[3]
(commutativity and associativity)[3]
(index shift)
for a bijection σ from a finite set A onto a set B (index change); this generalizes the preceding formula.
(splitting a sum, using associativity)
(a variant of the preceding formula)
(the sum from the first term up to the last is equal to the sum from the last down to the first)
(a particular case of the formula above)
(commutativity and associativity, again)
(another application of commutativity and associativity)
(splitting a sum into its odd and even parts, for even indexes)
(splitting a sum into its odd and even parts, for odd indexes)
(distributivity)
(distributivity allows factorization)
(the logarithm of a product is the sum of the logarithms of the factors)
(the exponential of a sum is the product of the exponential of the summands)
Powers and logarithm of arithmetic progressions[edit]
for every c that does not depend on i
(Sum of the simplest arithmetic progression, consisting of the first n natural numbers.)[2]: 52
(Sum of first odd natural numbers)
(Sum of first even natural numbers)
(A sum of logarithms is the logarithm of the product)
(Sum of the first squares, see square pyramidal number.) [2]: 52
(Nicomachus’s theorem) [2]: 52
More generally, one has Faulhaber’s formula for 
where 

Summation index in exponents[edit]
In the following summations, a is assumed to be different from 1.
(sum of a geometric progression)
(special case for a = 1/2)
(a times the derivative with respect to a of the geometric progression)
-
- (sum of an arithmetico–geometric sequence)
-
Binomial coefficients and factorials[edit]
There exist very many summation identities involving binomial coefficients (a whole chapter of Concrete Mathematics is devoted to just the basic techniques). Some of the most basic ones are the following.
Involving the binomial theorem[edit]
the binomial theorem
the special case where a = b = 1
, the special case where p = a = 1 − b, which, for
expresses the sum of the binomial distribution
the value at a = b = 1 of the derivative with respect to a of the binomial theorem
the value at a = b = 1 of the antiderivative with respect to a of the binomial theorem
Involving permutation numbers[edit]
In the following summations, 
, where and
denotes the floor function.
Others[edit]
Harmonic numbers[edit]
(that is the nth harmonic number)
(that is a generalized harmonic number)
Growth rates[edit]
The following are useful approximations (using theta notation):
for real c greater than −1
(See Harmonic number)
for real c greater than 1
for non-negative real c
for non-negative real c, d
for non-negative real b > 1, c, d
History[edit]
- In 1675, Gottfried Wilhelm Leibniz, in a letter to Henry Oldenburg, suggests the symbol ∫ to mark the sum of differentials (Latin: calculus summatorius), hence the S-shape.[4][5][6] The renaming of this symbol to integral arose later in exchanges with Johann Bernoulli.[6]
- In 1755, the summation symbol Σ is attested in Leonhard Euler’s Institutiones calculi differentialis.[7][8] Euler uses the symbol in expressions like:
- In 1772, usage of Σ and Σn is attested by Lagrange.[7][9]
- In 1823, the capital letter S is attested as a summation symbol for series. This usage was apparently widespread.[7]
- In 1829, the summation symbol Σ is attested by Fourier and C. G. J. Jacobi.[7] Fourier’s use includes lower and upper bounds, for example:[10][11]
See also[edit]
- Capital-pi notation
- Einstein notation
- Iverson bracket
- Iterated binary operation
- Kahan summation algorithm
- Product (mathematics)
- Summation by parts
- ∑ the summation single glyph (U+2211 N-ARY SUMMATION)
- ⎲ the paired glyph’s beginning (U+23B2 SUMMATION TOP)
- ⎳ the paired glyph’s end (U+23B3 SUMMATION BOTTOM)
Notes[edit]
- ^ For details, see Triangular number.
- ^ For a detailed exposition on summation notation, and arithmetic with sums, see Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). «Chapter 2: Sums». Concrete Mathematics: A Foundation for Computer Science (PDF) (2nd ed.). Addison-Wesley Professional. ISBN 978-0201558029.[permanent dead link]
- ^ in contexts where there is no possibility of confusion with the imaginary unit
- ^ Although the name of the dummy variable does not matter (by definition), one usually uses letters from the middle of the alphabet (
through
) to denote integers, if there is a risk of confusion. For example, even if there should be no doubt about the interpretation, it could look slightly confusing to many mathematicians to see
instead of
in the above formulae involving
. See also typographical conventions in mathematical formulae.
References[edit]
- ^ «Summation Notation». www.columbia.edu. Retrieved 2020-08-16.
- ^ a b c d Handbook of Discrete and Combinatorial Mathematics, Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, ISBN 0-8493-0149-1.
- ^ a b «Calculus I — Summation Notation». tutorial.math.lamar.edu. Retrieved 2020-08-16.
- ^ Burton, David M. (2011). The History of Mathematics: An Introduction (7th ed.). McGraw-Hill. p. 414. ISBN 978-0-07-338315-6.
- ^ Leibniz, Gottfried Wilhelm (1899). Gerhardt, Karl Immanuel (ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller. p. 154.
- ^ a b Cajori (1929), pp. 181-182.
- ^ a b c d Cajori (1929), p. 61.
- ^ Euler, Leonhard (1755). Institutiones Calculi differentialis (in Latin). Petropolis. p. 27.
- ^ Lagrange, Joseph-Louis (1867–1892). Oeuvres de Lagrange. Tome 3 (in French). Paris. p. 451.
- ^ Mémoires de l’Académie royale des sciences de l’Institut de France pour l’année 1825, tome VIII (in French). Paris: Didot. 1829. pp. 581-622.
- ^ Fourier, Jean-Baptiste Joseph (1888–1890). Oeuvres de Fourier. Tome 2 (in French). Paris: Gauthier-Villars. p. 149.
Bibliography[edit]
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. ISBN 978-0-486-67766-8.
External links[edit]
Media related to Summation at Wikimedia Commons
In mathematics, summation is the addition of a sequence of any kind of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted «+» is defined.
Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article.
The summation of an explicit sequence is denoted as a succession of additions. For example, summation of [1, 2, 4, 2] is denoted 1 + 2 + 4 + 2, and results in 9, that is, 1 + 2 + 4 + 2 = 9. Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0.
Very often, the elements of a sequence are defined, through a regular pattern, as a function of their place in the sequence. For simple patterns, summation of long sequences may be represented with most summands replaced by ellipses. For example, summation of the first 100 natural numbers may be written as 1 + 2 + 3 + 4 + ⋯ + 99 + 100. Otherwise, summation is denoted by using Σ notation, where 

For long summations, and summations of variable length (defined with ellipses or Σ notation), it is a common problem to find closed-form expressions for the result. For example,[a]
Although such formulas do not always exist, many summation formulas have been discovered—with some of the most common and elementary ones being listed in the remainder of this article.
Notation[edit]
Capital-sigma notation[edit]
Mathematical notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, 
where i is the index of summation; ai is an indexed variable representing each term of the sum; m is the lower bound of summation, and n is the upper bound of summation. The «i = m» under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by one for each successive term, stopping when i = n.[b]
This is read as «sum of ai, from i = m to n«.
Here is an example showing the summation of squares:
In general, while any variable can be used as the index of summation (provided that no ambiguity is incurred), some of the most common ones include letters such as 



Alternatively, index and bounds of summation are sometimes omitted from the definition of summation if the context is sufficiently clear. This applies particularly when the index runs from 1 to n.[1] For example, one might write that:
Generalizations of this notation are often used, in which an arbitrary logical condition is supplied, and the sum is intended to be taken over all values satisfying the condition. For example:
is an alternative notation for 


is the sum of 


is the sum of 


There are also ways to generalize the use of many sigma signs. For example,
is the same as
A similar notation is used for the product of a sequence, where 

Special cases[edit]
It is possible to sum fewer than 2 numbers:
These degenerate cases are usually only used when the summation notation gives a degenerate result in a special case.
For example, if 

Formal definition[edit]
Summation may be defined recursively as follows:
, for b < a;
, for b ≥ a.
Measure theory notation[edit]
In the notation of measure and integration theory, a sum can be expressed as a definite integral,
where ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



Calculus of finite differences[edit]
Given a function f that is defined over the integers in the interval [m, n], the following equation holds:
This is the analogue of the fundamental theorem of calculus in calculus of finite differences, which states that:
where
is the derivative of f.
An example of application of the above equation is the following:
Using binomial theorem, this may be rewritten as:
The above formula is more commonly used for inverting of the difference operator 
where f is a function defined on the nonnegative integers.
Thus, given such a function f, the problem is to compute the antidifference of f, a function 

This function is defined up to the addition of a constant, and may be chosen as[2]
There is not always a closed-form expression for such a summation, but Faulhaber’s formula provides a closed form in the case where 
Approximation by definite integrals[edit]
Many such approximations can be obtained by the following connection between sums and integrals, which holds for any increasing function f:
and for any decreasing function f:
For more general approximations, see the Euler–Maclaurin formula.
For summations in which the summand is given (or can be interpolated) by an integrable function of the index, the summation can be interpreted as a Riemann sum occurring in the definition of the corresponding definite integral. One can therefore expect that for instance
since the right-hand side is by definition the limit for 
Identities[edit]
The formulae below involve finite sums; for infinite summations or finite summations of expressions involving trigonometric functions or other transcendental functions, see list of mathematical series.
General identities[edit]
(distributivity)[3]
(commutativity and associativity)[3]
(index shift)
for a bijection σ from a finite set A onto a set B (index change); this generalizes the preceding formula.
(splitting a sum, using associativity)
(a variant of the preceding formula)
(the sum from the first term up to the last is equal to the sum from the last down to the first)
(a particular case of the formula above)
(commutativity and associativity, again)
(another application of commutativity and associativity)
(splitting a sum into its odd and even parts, for even indexes)
(splitting a sum into its odd and even parts, for odd indexes)
(distributivity)
(distributivity allows factorization)
(the logarithm of a product is the sum of the logarithms of the factors)
(the exponential of a sum is the product of the exponential of the summands)
Powers and logarithm of arithmetic progressions[edit]
for every c that does not depend on i
(Sum of the simplest arithmetic progression, consisting of the first n natural numbers.)[2]: 52
(Sum of first odd natural numbers)
(Sum of first even natural numbers)
(A sum of logarithms is the logarithm of the product)
(Sum of the first squares, see square pyramidal number.) [2]: 52
(Nicomachus’s theorem) [2]: 52
More generally, one has Faulhaber’s formula for 
where 

Summation index in exponents[edit]
In the following summations, a is assumed to be different from 1.
(sum of a geometric progression)
(special case for a = 1/2)
(a times the derivative with respect to a of the geometric progression)
-
- (sum of an arithmetico–geometric sequence)
-
Binomial coefficients and factorials[edit]
There exist very many summation identities involving binomial coefficients (a whole chapter of Concrete Mathematics is devoted to just the basic techniques). Some of the most basic ones are the following.
Involving the binomial theorem[edit]
the binomial theorem
the special case where a = b = 1
, the special case where p = a = 1 − b, which, for
expresses the sum of the binomial distribution
the value at a = b = 1 of the derivative with respect to a of the binomial theorem
the value at a = b = 1 of the antiderivative with respect to a of the binomial theorem
Involving permutation numbers[edit]
In the following summations, 
, where and
denotes the floor function.
Others[edit]
Harmonic numbers[edit]
(that is the nth harmonic number)
(that is a generalized harmonic number)
Growth rates[edit]
The following are useful approximations (using theta notation):
for real c greater than −1
(See Harmonic number)
for real c greater than 1
for non-negative real c
for non-negative real c, d
for non-negative real b > 1, c, d
History[edit]
- In 1675, Gottfried Wilhelm Leibniz, in a letter to Henry Oldenburg, suggests the symbol ∫ to mark the sum of differentials (Latin: calculus summatorius), hence the S-shape.[4][5][6] The renaming of this symbol to integral arose later in exchanges with Johann Bernoulli.[6]
- In 1755, the summation symbol Σ is attested in Leonhard Euler’s Institutiones calculi differentialis.[7][8] Euler uses the symbol in expressions like:
- In 1772, usage of Σ and Σn is attested by Lagrange.[7][9]
- In 1823, the capital letter S is attested as a summation symbol for series. This usage was apparently widespread.[7]
- In 1829, the summation symbol Σ is attested by Fourier and C. G. J. Jacobi.[7] Fourier’s use includes lower and upper bounds, for example:[10][11]
See also[edit]
- Capital-pi notation
- Einstein notation
- Iverson bracket
- Iterated binary operation
- Kahan summation algorithm
- Product (mathematics)
- Summation by parts
- ∑ the summation single glyph (U+2211 N-ARY SUMMATION)
- ⎲ the paired glyph’s beginning (U+23B2 SUMMATION TOP)
- ⎳ the paired glyph’s end (U+23B3 SUMMATION BOTTOM)
Notes[edit]
- ^ For details, see Triangular number.
- ^ For a detailed exposition on summation notation, and arithmetic with sums, see Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). «Chapter 2: Sums». Concrete Mathematics: A Foundation for Computer Science (PDF) (2nd ed.). Addison-Wesley Professional. ISBN 978-0201558029.[permanent dead link]
- ^ in contexts where there is no possibility of confusion with the imaginary unit
- ^ Although the name of the dummy variable does not matter (by definition), one usually uses letters from the middle of the alphabet (
through
) to denote integers, if there is a risk of confusion. For example, even if there should be no doubt about the interpretation, it could look slightly confusing to many mathematicians to see
instead of
in the above formulae involving
. See also typographical conventions in mathematical formulae.
References[edit]
- ^ «Summation Notation». www.columbia.edu. Retrieved 2020-08-16.
- ^ a b c d Handbook of Discrete and Combinatorial Mathematics, Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, ISBN 0-8493-0149-1.
- ^ a b «Calculus I — Summation Notation». tutorial.math.lamar.edu. Retrieved 2020-08-16.
- ^ Burton, David M. (2011). The History of Mathematics: An Introduction (7th ed.). McGraw-Hill. p. 414. ISBN 978-0-07-338315-6.
- ^ Leibniz, Gottfried Wilhelm (1899). Gerhardt, Karl Immanuel (ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller. p. 154.
- ^ a b Cajori (1929), pp. 181-182.
- ^ a b c d Cajori (1929), p. 61.
- ^ Euler, Leonhard (1755). Institutiones Calculi differentialis (in Latin). Petropolis. p. 27.
- ^ Lagrange, Joseph-Louis (1867–1892). Oeuvres de Lagrange. Tome 3 (in French). Paris. p. 451.
- ^ Mémoires de l’Académie royale des sciences de l’Institut de France pour l’année 1825, tome VIII (in French). Paris: Didot. 1829. pp. 581-622.
- ^ Fourier, Jean-Baptiste Joseph (1888–1890). Oeuvres de Fourier. Tome 2 (in French). Paris: Gauthier-Villars. p. 149.
Bibliography[edit]
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. ISBN 978-0-486-67766-8.
External links[edit]
Media related to Summation at Wikimedia Commons
Знак суммы в математике как считать?
summa — итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. .
Как записать алгебраическую сумму?
Обратите внимание, что запись алгебраической суммы обычно упрощают: положительные числа записываются без предшествующего знака + , а отрицательные числа, стоящие в начале выражения, записываются без скобок: (-5) + (+7) = -5 + 7. заменяют на выражение: 3z — 2x — y.
Что такое слагаемое в математике?
Числа при сложении называются слагаемыми. Результат сложения – сумма. сложение, слагаемые, сумма, результат сложения.
Что такое сумма и ее значение?
(Сумма -это объединение двух или несколько чисел, между ними ставится знак «+»).
Что такое сумма чисел 2 класс?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). . Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Что такое разность и ее значение?
Значение разности: Разность-это то что получается при вычитание чисел. . Уменьшаемое-вычитаемое=разность. Вот оно значение разности .
Что такое алгебраическая сумма 6 класс?
Алгебраическая сумма — это выражение, которое можно представить в виде суммы положительных и отрицательных чисел.
Как найти алгебраическую сумму многочленов?
Для того чтобы найти алгебраическую сумму нескольких многочленов, записанную в стандартном виде, необходимо раскрыть скобки и привести подобные слагаемые. При этом, если перед скобкой стоит знак «плюс», то раскрывая скобки, знаки перед слагаемыми нужно оставить без изменений.
Как найти сумму числового и функционального ряда
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ — математический знак суммы;
- ai — общий аргумент;
- i — переменная, правило для изменения каждого последующего аргумента;
- ∞ — знак бесконечности, «предел», до которого проводится суммирование.
Запись 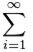
В соответствии с переменной i ряд можно записать развернуто:
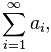
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
Сумма числового ряда – это предел частичных сумм Sn. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
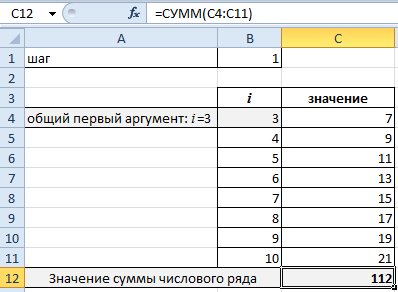
Сначала найдем сумму числового ряда:
Теперь построим в Excel таблицу значений членов ряда:
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.
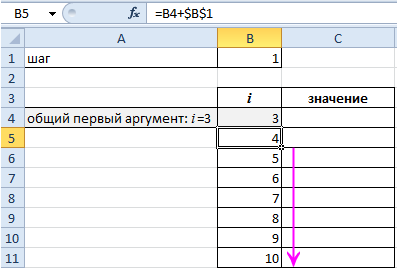
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.
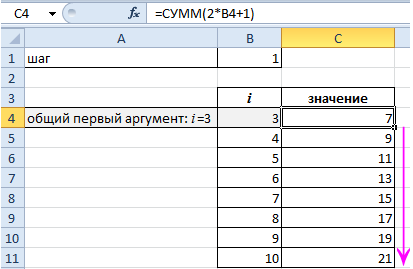
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x) 2 ; S3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
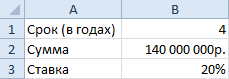
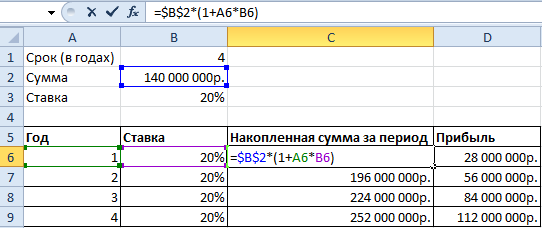
Исходные параметры для учебной задачи:
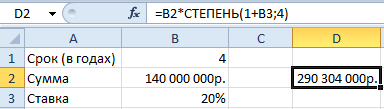
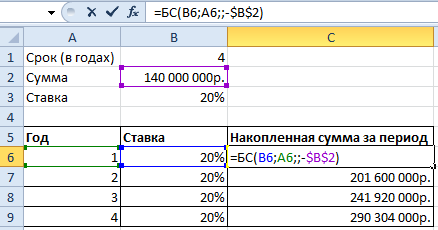
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
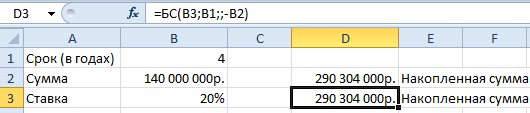
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
Результаты одинаковые, как и должно быть.
Как заполнить аргументы функции БС():
- «Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
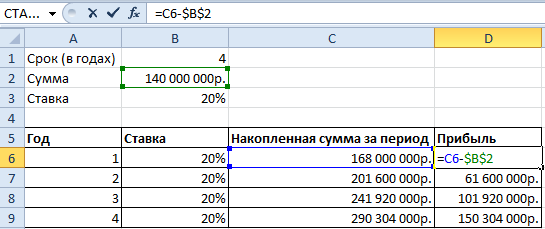
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
Сделаем еще один столбец, в котором отразим прибыль:
Как мы считали – в строке формул.
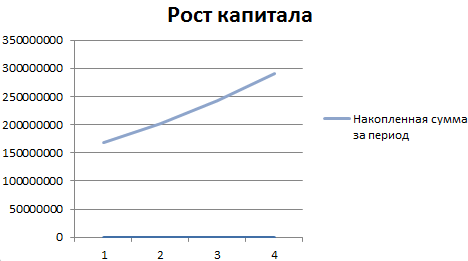
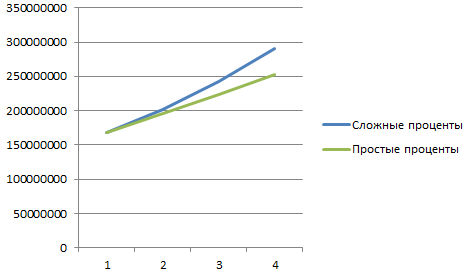
На основании полученных данных построим график функций.
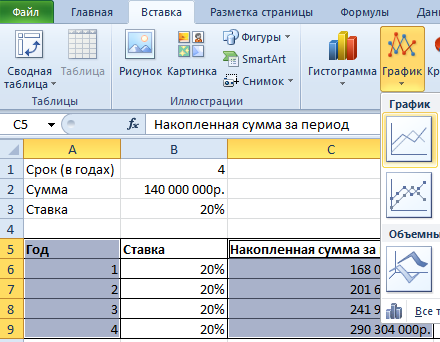
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
Добавим полученные значения в график «Рост капитала».
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Как написать знак суммы (количества) в таблицах Excel.
При написании формул в документах MS Excel или Word зачастую возникает потребность в написании математического знака суммы (он же «знак суммирования» или «знак нахождения суммы»). Некоторые далекие от математических исчислений люди называют его «знак количества».
Выглядит знак суммы, как угловатая растянутая относительно горизонтальной оси симметрии заглавная русская буква «Е» или английская «E».
Вставить знак суммы в ячейку таблицы «эксель» или на лист «вордовского» документа можно двумя методами, которые приведены ниже:
При помощи таблицы символов;
При помощи опций на панели быстрого доступа в самой программе.
Как поставить знак суммы при помощи таблицы символов.
Необходимо последовательно выполнить следующие действия:
- Войти в меню «Пуск» => Программы => Стандартные => Служебные => Таблица символов.
- Выбрать символ суммирования;
- Скопировать символ суммирования;
- Вставить символ в таблицу или документ «Ворда».
Способ нехитрый и не занимает много времени.
Как поставить знак суммы при помощи встроенных возможностей «Эксель».
Необходимо выполнить следующую последовательность действий:
- Выбрать ячейку, в которую поставите знак суммы;
- В меню быстрого доступа выбрать вкладку «Вставка»
- Выбрать пиктограмму «Символ»;
- В появившемся окне выбрать знак суммы и вставить его при помощи кнопки «Вставить»
Подробное пошаговое видео о том, как выполняются описанные выше действия:
У этого термина существуют и другие значения, см. сумма.
Су́мма (лат. summa — итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. д.). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
а + b = b + aа + (b + с) = (а + b) + с(а + b) с = ас + bcс (а + b) = ca + cb
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы слагаемых множеств, взятые без повторений.
Содержание
- 1 Определенная сумма
- 2 Свойства определённой суммы
- 3 Примеры
- 4 Неопределённая сумма
- 5 Формула Ньютона-Лейбница
- 6 Этимология
- 7 Литература
- 8 См. также
Определенная сумма
Часто для краткости сумму n слагаемых ak, ak+1, …, aN обозначают заглавной греческой буквой Σ (сигма):
Это обозначение называют определённой (конечной) суммой 
Для удобства вместо 





Свойства определённой суммы
Примеры
1. Сумма арифметической прогрессии:
2. Сумма геометрической прогрессии:
3.
Почему это так
4.
Почему это так
Доказательство:
5.
-
-
- Стоит заметить, что при
получаем
, а это последовательность равенств следующего вида:
- Стоит заметить, что при
-
Неопределённая сумма
Неопределённой суммой 




Формула Ньютона-Лейбница
Если найдена неопределённая сумма 

Этимология
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (S) первым ввёл Эйлер в 1755 году. Как вариант, использовалась греческая буква Сигма Σ. Позднее ввиду связи понятий суммирования и интегрирования, S также использовали для обозначения операции интегрирования.
Литература
Фихтенгольц Г.М. Курс дифференциального и интегрального исчесления. — седьмое. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
См. также
- Контрольная сумма
‹— Назад
Символ суммирования
В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:
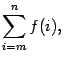
которая расшифровывается так
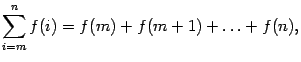 |
(14.1) |
где — функция целочисленного аргумента. Здесь символ
(большая греческая буква «сигма») означает суммирование. Запись
внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой
и что начальное значение этой переменной равно
. Запись вверху обозначает последнее значение, которое принимает переменная
.
Пример 14.2 Вычислим несколько сумм:
1) 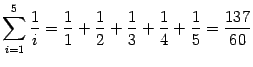
2) 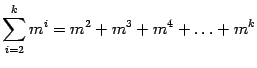
и знаменателем прогрессии равным
, то эту сумму легко найти
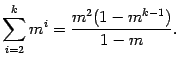
3) 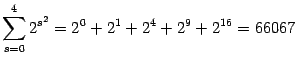
4) 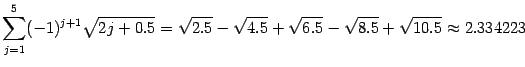
5) 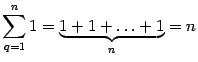
В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
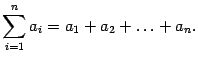
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:
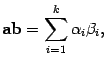 |
(14.2) |
где для трехмерного пространства , для плоскости
.
Для единообразия будем считать, что
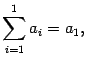
и говорить, что это сумма, содержащая одно слагаемое.
Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,
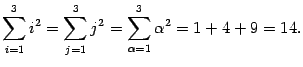
Или
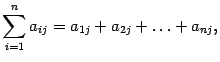
в правой части никакой буквы нет, значит, и результат от
не зависит.
Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:
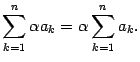
Доказательство этого предложения предоставляется читателю.
Предложение 14.2
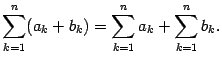 |
(14.3) |
Это предложение является частным случаем следующего утверждения.
Доказательство. Пусть
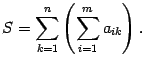
Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).
Замечание 14.2 Двойные суммы из равенства (14.4) можно записывать и без использования скобок
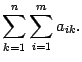
Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
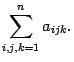
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
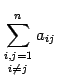
означает, что в сумму не включаются величины ,
,…,
, то есть
с равными индексами.
Иногда в записи суммы не указываются границы изменения индексов, например,
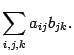
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции


















![sum _{k{mathop {=}}a}^{b}f(k)=int _{[a,b]}f,dmu](https://wikimedia.org/api/rest_v1/media/math/render/svg/3df03fc79c21c319ce553adbbd688204560d2f47)


































































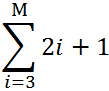
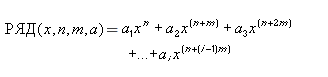

















 получаем
получаем  , а это последовательность равенств следующего вида:
, а это последовательность равенств следующего вида: