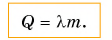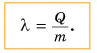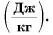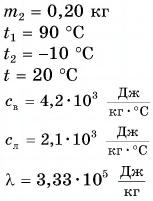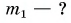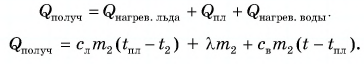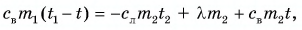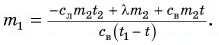Ice cubes put in water will start to melt when they reach their melting point of 0 °C
The melting point (or, rarely, liquefaction point) of a substance is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at a standard pressure such as 1 atmosphere or 100 kPa.
When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point. Because of the ability of substances to supercool, the freezing point can easily appear to be below its actual value. When the «characteristic freezing point» of a substance is determined, in fact, the actual methodology is almost always «the principle of observing the disappearance rather than the formation of ice, that is, the melting point.»[1]
Examples[edit]
Melting points (in blue) and boiling points (in pink) of the first eight carboxylic acids (°C)
For most substances, melting and freezing points are approximately equal. For example, the melting point and freezing point of mercury is 234.32 kelvins (−38.83 °C; −37.89 °F).[2] However, certain substances possess differing solid-liquid transition temperatures. For example, agar melts at 85 °C (185 °F; 358 K) and solidifies from 31 °C (88 °F; 304 K); such direction dependence is known as hysteresis. The melting point of ice at 1 atmosphere of pressure is very close[3] to 0 °C (32 °F; 273 K); this is also known as the ice point. In the presence of nucleating substances, the freezing point of water is not always the same as the melting point. In the absence of nucleators water can exist as a supercooled liquid down to −48.3 °C (−54.9 °F; 224.8 K) before freezing.[citation needed]
The metal with the highest melting point is tungsten, at 3,414 °C (6,177 °F; 3,687 K);[4] this property makes tungsten excellent for use as electrical filaments in incandescent lamps. The often-cited carbon does not melt at ambient pressure but sublimes at about 3,700 °C (6,700 °F; 4,000 K); a liquid phase only exists above pressures of 10 MPa (99 atm) and estimated 4,030–4,430 °C (7,290–8,010 °F; 4,300–4,700 K) (see carbon phase diagram). Hafnium carbonitride (HfCN) is a refractory compound with the highest known melting point of any substance to date and the only one confirmed to have a melting point above 4,273 K (4,000 °C; 7,232 °F) at ambient pressure. Quantum mechanical computer simulations predicted that this alloy (HfN0.38C0.51) would have a melting point of about 4,400 K.[5] This prediction was later confirmed by experiment, though a precise measurement of its exact melting point has yet to be confirmed.[6] At the other end of the scale, helium does not freeze at all at normal pressure even at temperatures arbitrarily close to absolute zero; a pressure of more than twenty times normal atmospheric pressure is necessary.
| List of common chemicals | |||
|---|---|---|---|
| Chemical[I] | Density (g/cm3) | Melt (K)[7] | Boil (K) |
| Water @STP | 1 | 273 | 373 |
| Solder (Pb60Sn40) | 456 | ||
| Cocoa butter | 307.2 | — | |
| Paraffin wax | 0.9 | 310 | 643 |
| Hydrogen | 0.00008988 | 14.01 | 20.28 |
| Helium | 0.0001785 | —[II] | 4.22 |
| Beryllium | 1.85 | 1,560 | 2,742 |
| Carbon | 2.267 | —[III][8] | 4,000[III][8] |
| Nitrogen | 0.0012506 | 63.15 | 77.36 |
| Oxygen | 0.001429 | 54.36 | 90.20 |
| Sodium | 0.971 | 370.87 | 1,156 |
| Magnesium | 1.738 | 923 | 1,363 |
| Aluminium | 2.698 | 933.47 | 2,792 |
| Sulfur | 2.067 | 388.36 | 717.87 |
| Chlorine | 0.003214 | 171.6 | 239.11 |
| Potassium | 0.862 | 336.53 | 1,032 |
| Titanium | 4.54 | 1,941 | 3,560 |
| Iron | 7.874 | 1,811 | 3,134 |
| Nickel | 8.912 | 1,728 | 3,186 |
| Copper | 8.96 | 1,357.77 | 2,835 |
| Zinc | 7.134 | 692.88 | 1,180 |
| Gallium | 5.907 | 302.9146 | 2,673 |
| Silver | 10.501 | 1,234.93 | 2,435 |
| Cadmium | 8.69 | 594.22 | 1,040 |
| Indium | 7.31 | 429.75 | 2,345 |
| Iodine | 4.93 | 386.85 | 457.4 |
| Tantalum | 16.654 | 3,290 | 5,731 |
| Tungsten | 19.25 | 3,695 | 5,828 |
| Platinum | 21.46 | 2,041.4 | 4,098 |
| Gold | 19.282 | 1,337.33 | 3,129 |
| Mercury | 13.5336 | 234.43 | 629.88 |
| Lead | 11.342 | 600.61 | 2,022 |
| Bismuth | 9.807 | 544.7 | 1,837 |
|
Notes
|
Melting point measurements[edit]
Kofler bench with samples for calibration
Many laboratory techniques exist for the determination of melting points.
A Kofler bench is a metal strip with a temperature gradient (range from room temperature to 300 °C). Any substance can be placed on a section of the strip, revealing its thermal behaviour at the temperature at that point. Differential scanning calorimetry gives information on melting point together with its enthalpy of fusion.
Automatic digital melting point meter
A basic melting point apparatus for the analysis of crystalline solids consists of an oil bath with a transparent window (most basic design: a Thiele tube) and a simple magnifier. Several grains of a solid are placed in a thin glass tube and partially immersed in the oil bath. The oil bath is heated (and stirred) and with the aid of the magnifier (and external light source) melting of the individual crystals at a certain temperature can be observed. A metal block might be used instead of an oil bath. Some modern instruments have automatic optical detection.
The measurement can also be made continuously with an operating process. For instance, oil refineries measure the freeze point of diesel fuel «online», meaning that the sample is taken from the process and measured automatically. This allows for more frequent measurements as the sample does not have to be manually collected and taken to a remote laboratory.
Techniques for refractory materials[edit]
For refractory materials (e.g. platinum, tungsten, tantalum, some carbides and nitrides, etc.) the extremely high melting point (typically considered to be above, say, 1,800 °C) may be determined by heating the material in a black body furnace and measuring the black-body temperature with an optical pyrometer. For the highest melting materials, this may require extrapolation by several hundred degrees. The spectral radiance from an incandescent body is known to be a function of its temperature. An optical pyrometer matches the radiance of a body under study to the radiance of a source that has been previously calibrated as a function of temperature. In this way, the measurement of the absolute magnitude of the intensity of radiation is unnecessary. However, known temperatures must be used to determine the calibration of the pyrometer. For temperatures above the calibration range of the source, an extrapolation technique must be employed. This extrapolation is accomplished by using Planck’s law of radiation. The constants in this equation are not known with sufficient accuracy, causing errors in the extrapolation to become larger at higher temperatures. However, standard techniques have been developed to perform this extrapolation.
Consider the case of using gold as the source (mp = 1,063 °C). In this technique, the current through the filament of the pyrometer is adjusted until the light intensity of the filament matches that of a black-body at the melting point of gold. This establishes the primary calibration temperature and can be expressed in terms of current through the pyrometer lamp. With the same current setting, the pyrometer is sighted on another black-body at a higher temperature. An absorbing medium of known transmission is inserted between the pyrometer and this black-body. The temperature of the black-body is then adjusted until a match exists between its intensity and that of the pyrometer filament. The true higher temperature of the black-body is then determined from Planck’s Law. The absorbing medium is then removed and the current through the filament is adjusted to match the filament intensity to that of the black-body. This establishes a second calibration point for the pyrometer. This step is repeated to carry the calibration to higher temperatures. Now, temperatures and their corresponding pyrometer filament currents are known and a curve of temperature versus current can be drawn. This curve can then be extrapolated to very high temperatures.
In determining melting points of a refractory substance by this method, it is necessary to either have black body conditions or to know the emissivity of the material being measured. The containment of the high melting material in the liquid state may introduce experimental difficulties. Melting temperatures of some refractory metals have thus been measured by observing the radiation from a black body cavity in solid metal specimens that were much longer than they were wide. To form such a cavity, a hole is drilled perpendicular to the long axis at the center of a rod of the material. These rods are then heated by passing a very large current through them, and the radiation emitted from the hole is observed with an optical pyrometer. The point of melting is indicated by the darkening of the hole when the liquid phase appears, destroying the black body conditions. Today, containerless laser heating techniques, combined with fast pyrometers and spectro-pyrometers, are employed to allow for precise control of the time for which the sample is kept at extreme temperatures. Such experiments of sub-second duration address several of the challenges associated with more traditional melting point measurements made at very high temperatures, such as sample vaporization and reaction with the container.
Thermodynamics[edit]
Pressure dependence of water melting point.
For a solid to melt, heat is required to raise its temperature to the melting point. However, further heat needs to be supplied for the melting to take place: this is called the heat of fusion, and is an example of latent heat.
From a thermodynamics point of view, at the melting point the change in Gibbs free energy (ΔG) of the material is zero, but the enthalpy (H) and the entropy (S) of the material are increasing (ΔH, ΔS > 0). Melting phenomenon happens when the Gibbs free energy of the liquid becomes lower than the solid for that material. At various pressures this happens at a specific temperature. It can also be shown that:
Here T, ΔS and ΔH are respectively the temperature at the melting point, change of entropy of melting and the change of enthalpy of melting.
The melting point is sensitive to extremely large changes in pressure, but generally this sensitivity is orders of magnitude less than that for the boiling point, because the solid-liquid transition represents only a small change in volume.[9][10] If, as observed in most cases, a substance is more dense in the solid than in the liquid state, the melting point will increase with increases in pressure. Otherwise the reverse behavior occurs. Notably, this is the case of water, as illustrated graphically to the right, but also of Si, Ge, Ga, Bi. With extremely large changes in pressure, substantial changes to the melting point are observed. For example, the melting point of silicon at ambient pressure (0.1 MPa) is 1415 °C, but at pressures in excess of 10 GPa it decreases to 1000 °C.[11]
Melting points are often used to characterize organic and inorganic compounds and to ascertain their purity. The melting point of a pure substance is always higher and has a smaller range than the melting point of an impure substance or, more generally, of mixtures. The higher the quantity of other components, the lower the melting point and the broader will be the melting point range, often referred to as the «pasty range». The temperature at which melting begins for a mixture is known as the solidus while the temperature where melting is complete is called the liquidus. Eutectics are special types of mixtures that behave like single phases. They melt sharply at a constant temperature to form a liquid of the same composition. Alternatively, on cooling a liquid with the eutectic composition will solidify as uniformly dispersed, small (fine-grained) mixed crystals with the same composition.
In contrast to crystalline solids, glasses do not possess a melting point;
on heating they undergo a smooth glass transition into a viscous liquid.
Upon further heating, they gradually soften, which can be characterized by certain softening points.
Freezing-point depression[edit]
The freezing point of a solvent is depressed when another compound is added, meaning that a solution has a lower freezing point than a pure solvent. This phenomenon is used in technical applications to avoid freezing, for instance by adding salt or ethylene glycol to water.
Carnelley’s rule[edit]
In organic chemistry, Carnelley’s rule, established in 1882 by Thomas Carnelley, states that high molecular symmetry is associated with high melting point.[12] Carnelley based his rule on examination of 15,000 chemical compounds. For example, for three structural isomers with molecular formula C5H12 the melting point increases in the series isopentane −160 °C (113 K) n-pentane −129.8 °C (143 K) and neopentane −16.4 °C (256.8 K).[13] Likewise in xylenes and also dichlorobenzenes the melting point increases in the order meta, ortho and then para. Pyridine has a lower symmetry than benzene hence its lower melting point but the melting point again increases with diazine and triazines. Many cage-like compounds like adamantane and cubane with high symmetry have relatively high melting points.
A high melting point results from a high heat of fusion, a low entropy of fusion, or a combination of both. In highly symmetrical molecules the crystal phase is densely packed with many efficient intermolecular interactions resulting in a higher enthalpy change on melting.
Like many high symmetry compounds, tetrakis(trimethylsilyl)silane has a very high melting point (m.p.) of 319-321 °C. It tends to sublime, so the m.p. determination requires that the sample be sealed in a tube.[14]
Predicting the melting point of substances (Lindemann’s criterion)[edit]
An attempt to predict the bulk melting point of crystalline materials was first made in 1910 by Frederick Lindemann.[15] The idea behind the theory was the observation that the average amplitude of thermal vibrations increases with increasing temperature. Melting initiates when the amplitude of vibration becomes large enough for adjacent atoms to partly occupy the same space. The Lindemann criterion states that melting is expected when the vibration root mean square amplitude exceeds a threshold value.
Assuming that all atoms in a crystal vibrate with the same frequency ν, the average thermal energy can be estimated using the equipartition theorem as[16]
where m is the atomic mass, ν is the frequency, u is the average vibration amplitude, kB is the Boltzmann constant, and T is the absolute temperature. If the threshold value of u2 is c2a2 where c is the Lindemann constant and a is the atomic spacing, then the melting point is estimated as
Several other expressions for the estimated melting temperature can be obtained depending on the estimate of the average thermal energy. Another commonly used expression for the Lindemann criterion is[17]
From the expression for the Debye frequency for ν, we have
where θD is the Debye temperature and h is the Planck constant. Values of c range from 0.15 to 0.3 for most materials.[18]
Melting point prediction[edit]
In February 2011, Alfa Aesar released over 10,000 melting points of compounds from their catalog as open data. This dataset has been used to create a random forest model for melting point prediction which is now freely available.[19] Open melting point data are also available from Nature Precedings.[20] High quality data mined from patents and also models[21] developed with these data were published by Tetko et al.[22]
Melting point of the elements[edit]
Melting point of the elements in the periodic table |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group → | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| ↓ Period | |||||||||||||||||||
| 1 | H2 13.99 K (−259.16 °C) |
He0.95 K (−272.20 °C) |
|||||||||||||||||
| 2 | Li453.65 K (180.50 °C) |
Be1560 K (1287 °C) |
B 2349 K (2076 °C) |
C |
N2 63.23 K (−209.86 °C) |
O2 54.36 K (−218.79 °C) |
F2 53.48 K (−219.67 °C) |
Ne24.56 K (−248.59 °C) |
|||||||||||
| 3 | Na370.944 K (97.794 °C) |
Mg923 K (650 °C) |
Al933.47 K (660.32 °C) |
Si1687 K (1414 °C) |
P 317.3 K (44.15 °C) |
S 388.36 K (115.21 °C) |
Cl2171.6 K (−101.5 °C) |
Ar83.81 K (−189.34 °C) |
|||||||||||
| 4 | K 336.7 K (63.5 °C) |
Ca1115 K (842 °C) |
Sc1814 K (1541 °C) |
Ti1941 K (1668 °C) |
V 2183 K (1910 °C) |
Cr2180 K (1907 °C) |
Mn1519 K (1246 °C) |
Fe1811 K (1538 °C) |
Co1768 K (1495 °C) |
Ni1728 K (1455 °C) |
Cu1357.77 K (1084.62 °C) |
Zn692.68 K (419.53 °C) |
Ga302.9146 K (29.7646 °C) |
Ge1211.40 K (938.25 °C) |
As |
Se494 K (221 °C) |
Br2265.8 K (−7.2 °C) |
Kr115.78 K (−157.37 °C) |
|
| 5 | Rb312.45 K (39.30 °C) |
Sr1050 K (777 °C) |
Y 1799 K (1526 °C) |
Zr2128 K (1855 °C) |
Nb2750 K (2477 °C) |
Mo2896 K (2623 °C) |
Tc2430 K (2157 °C) |
Ru2607 K (2334 °C) |
Rh2237 K (1964 °C) |
Pd1828.05 K (1554.9 °C) |
Ag1234.93 K (961.78 °C) |
Cd594.22 K (321.07 °C) |
In429.7485 K (156.5985 °C) |
Sn505.08 K (231.93 °C) |
Sb903.78 K (630.63 °C) |
Te722.66 K (449.51 °C) |
I2 386.85 K (113.7 °C) |
Xe161.40 K (−111.75 °C) |
|
| 6 | Cs301.7 K (28.5 °C) |
Ba1000 K (727 °C) |
Lu1925 K (1652 °C) |
Hf2506 K (2233 °C) |
Ta3290 K (3017 °C) |
W 3695 K (3422 °C) |
Re3459 K (3186 °C) |
Os3306 K (3033 °C) |
Ir2719 K (2446 °C) |
Pt2041.4 K (1768.3 °C) |
Au1337.33 K (1064.18 °C) |
Hg234.3210 K (−38.8290 °C) |
Tl577 K (304 °C) |
Pb600.61 K (327.46 °C) |
Bi544.7 K (271.5 °C) |
Po527 K (254 °C) |
At575 K (302 °C) |
Rn202 K (−71 °C) |
|
| 7 | Fr300 K (27 °C) |
Ra973 K (700 °C) |
Lr1900 K (1627 °C) |
Rf2400 K (2100 °C) |
Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn283±11 K (10±11 °C) |
Nh700 K (430 °C) |
Fl200 K (−73 °C) |
Mc670 K (400 °C) |
Lv637–780 K (364–507 °C) |
Ts623–823 K (350–550 °C) |
Og325±15 K (52±15 °C) |
|
| La1193 K (920 °C) |
Ce1068 K (795 °C)6 |
Pr1208 K (935 °C) |
Nd1297 K (1024 °C) |
Pm1315 K (1042 °C) |
Sm1345 K (1072 °C) |
Eu1099 K (826 °C) |
Gd1585 K (1312 °C) |
Tb1629 K (1356 °C) |
Dy1680 K (1407 °C) |
Ho1734 K (1461 °C) |
Er1802 K (1529 °C) |
Tm1818 K (1545 °C) |
Yb1097 K (824 °C) |
||||||
| Ac1500 K (1227 °C) |
Th2023 K (1750 °C) |
Pa1841 K (1568 °C) |
U 1405.3 K (1132.2 °C) |
Np912±3 K (639±3 °C) |
Pu912.5 K (639.4 °C) |
Am1449 K (1176 °C) |
Cm1613 K (1340 °C) |
Bk1259 K (986 °C) |
Cf1173 K (900 °C) |
Es1133 K (860 °C) |
Fm1800 K (1527 °C) |
Md1100 K (827 °C) |
No1100 K (827 °C) |
||||||
| Legend | |||||||||||||||||||
| Values are in Kelvin K and Celsius °C, rounded | |||||||||||||||||||
| For the equivalent in Fahrenheit °F, see: Melting points of the elements (data page) | |||||||||||||||||||
| Some values are predictions | |||||||||||||||||||
|
Primordial From decay Synthetic Border shows natural occurrence of the element
|
See also[edit]
- Congruent melting
- Hagedorn temperature
- Highest melting point
- List of elements by melting point
- Melting points of the elements (data page)
- Phase diagram
- Simon–Glatzel equation
- Slip melting point
- Triple point
- Zone melting
References[edit]
Citations[edit]
- ^ Ramsay, J. A. (1 May 1949). «A New Method of Freezing-Point Determination for Small Quantities». Journal of Experimental Biology. 26 (1): 57–64. doi:10.1242/jeb.26.1.57. PMID 15406812.
- ^ Haynes, p. 4.122.
- ^ The melting point of purified water has been measured as 0.002519 ± 0.000002 °C, see Feistel, R. & Wagner, W. (2006). «A New Equation of State for H2O Ice Ih». J. Phys. Chem. Ref. Data. 35 (2): 1021–1047. Bibcode:2006JPCRD..35.1021F. doi:10.1063/1.2183324.
- ^ Haynes, p. 4.123.
- ^ Hong, Q.-J.; van de Walle, A. (2015). «Prediction of the material with highest known melting point from ab initio molecular dynamics calculations». Phys. Rev. B. 92 (2): 020104(R). Bibcode:2015PhRvB..92b0104H. doi:10.1103/PhysRevB.92.020104.
- ^ Buinevich, V.S.; Nepapushev, A.A.; Moskovskikh, D.O.; Trusov, G.V.; Kuskov, K.V.; Vadchenko, S.G.; Rogachev, A.S.; Mukasyan, A.S. (March 2020). «Fabrication of ultra-high-temperature nonstoichiometric hafnium carbonitride via combustion synthesis and spark plasma sintering». Ceramics International. 46 (10): 16068–16073. doi:10.1016/j.ceramint.2020.03.158. S2CID 216437833.
- ^ Holman, S. W.; Lawrence, R. R.; Barr, L. (1 January 1895). «Melting Points of Aluminum, Silver, Gold, Copper, and Platinum». Proceedings of the American Academy of Arts and Sciences. 31: 218–233. doi:10.2307/20020628. JSTOR 20020628.
- ^ a b «Carbon». rsc.org.
- ^ The exact relationship is expressed in the Clausius–Clapeyron relation.
- ^ «J10 Heat: Change of aggregate state of substances through change of heat content: Change of aggregate state of substances and the equation of Clapeyron-Clausius». Retrieved 19 February 2008.
- ^ Tonkov, E. Yu. and Ponyatovsky, E. G. (2005) Phase Transformations of Elements Under High Pressure, CRC Press, Boca Raton, p. 98 ISBN 0-8493-3367-9
- ^ Brown, R. J. C. & R. F. C. (2000). «Melting Point and Molecular Symmetry». Journal of Chemical Education. 77 (6): 724. Bibcode:2000JChEd..77..724B. doi:10.1021/ed077p724.
- ^ Haynes, pp. 6.153–155.
- ^ Gilman, H.; Smith, C. L. (1967). «Tetrakis(trimethylsilyl)silane». Journal of Organometallic Chemistry. 8 (2): 245–253. doi:10.1016/S0022-328X(00)91037-4.
- ^ Lindemann FA (1910). «The calculation of molecular vibration frequencies». Phys. Z. 11: 609–612.
- ^ Sorkin, S., (2003), Point defects, lattice structure, and melting Archived 5 October 2016 at the Wayback Machine, Thesis, Technion, Israel.
- ^ Philip Hofmann (2008). Solid state physics: an introduction. Wiley-VCH. p. 67. ISBN 978-3-527-40861-0. Retrieved 13 March 2011.
- ^ Nelson, D. R., (2002), Defects and geometry in condensed matter physics, Cambridge University Press, ISBN 0-521-00400-4
- ^ Predict melting point from SMILES. Qsardb.org. Retrieved on 13 September 2013.
- ^ Bradley, Jean-Claude; Lang, Andrew; Williams, Antony; Curtin, Evan (11 August 2011). «ONS Open Melting Point Collection». Nature Precedings. doi:10.1038/npre.2011.6229.1.
- ^ OCHEM melting point models. ochem.eu. Retrieved on 18 June 2016.
- ^ Tetko, Igor V; m. Lowe, Daniel; Williams, Antony J (2016). «The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS». Journal of Cheminformatics. 8: 2. doi:10.1186/s13321-016-0113-y. PMC 4724158. PMID 26807157.
Sources[edit]
- Works cited
- Haynes, William M., ed. (2011). CRC Handbook of Chemistry and Physics (92nd ed.). CRC Press. ISBN 978-1439855119.
External links[edit]
- Melting and boiling point tables vol. 1 by Thomas Carnelley (Harrison, London, 1885–1887)
- Melting and boiling point tables vol. 2 by Thomas Carnelley (Harrison, London, 1885–1887)
- Patent mined data Over 250,000 freely downloadable melting point data. Also downloadable at figshare
Ice cubes put in water will start to melt when they reach their melting point of 0 °C
The melting point (or, rarely, liquefaction point) of a substance is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at a standard pressure such as 1 atmosphere or 100 kPa.
When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point. Because of the ability of substances to supercool, the freezing point can easily appear to be below its actual value. When the «characteristic freezing point» of a substance is determined, in fact, the actual methodology is almost always «the principle of observing the disappearance rather than the formation of ice, that is, the melting point.»[1]
Examples[edit]
Melting points (in blue) and boiling points (in pink) of the first eight carboxylic acids (°C)
For most substances, melting and freezing points are approximately equal. For example, the melting point and freezing point of mercury is 234.32 kelvins (−38.83 °C; −37.89 °F).[2] However, certain substances possess differing solid-liquid transition temperatures. For example, agar melts at 85 °C (185 °F; 358 K) and solidifies from 31 °C (88 °F; 304 K); such direction dependence is known as hysteresis. The melting point of ice at 1 atmosphere of pressure is very close[3] to 0 °C (32 °F; 273 K); this is also known as the ice point. In the presence of nucleating substances, the freezing point of water is not always the same as the melting point. In the absence of nucleators water can exist as a supercooled liquid down to −48.3 °C (−54.9 °F; 224.8 K) before freezing.[citation needed]
The metal with the highest melting point is tungsten, at 3,414 °C (6,177 °F; 3,687 K);[4] this property makes tungsten excellent for use as electrical filaments in incandescent lamps. The often-cited carbon does not melt at ambient pressure but sublimes at about 3,700 °C (6,700 °F; 4,000 K); a liquid phase only exists above pressures of 10 MPa (99 atm) and estimated 4,030–4,430 °C (7,290–8,010 °F; 4,300–4,700 K) (see carbon phase diagram). Hafnium carbonitride (HfCN) is a refractory compound with the highest known melting point of any substance to date and the only one confirmed to have a melting point above 4,273 K (4,000 °C; 7,232 °F) at ambient pressure. Quantum mechanical computer simulations predicted that this alloy (HfN0.38C0.51) would have a melting point of about 4,400 K.[5] This prediction was later confirmed by experiment, though a precise measurement of its exact melting point has yet to be confirmed.[6] At the other end of the scale, helium does not freeze at all at normal pressure even at temperatures arbitrarily close to absolute zero; a pressure of more than twenty times normal atmospheric pressure is necessary.
| List of common chemicals | |||
|---|---|---|---|
| Chemical[I] | Density (g/cm3) | Melt (K)[7] | Boil (K) |
| Water @STP | 1 | 273 | 373 |
| Solder (Pb60Sn40) | 456 | ||
| Cocoa butter | 307.2 | — | |
| Paraffin wax | 0.9 | 310 | 643 |
| Hydrogen | 0.00008988 | 14.01 | 20.28 |
| Helium | 0.0001785 | —[II] | 4.22 |
| Beryllium | 1.85 | 1,560 | 2,742 |
| Carbon | 2.267 | —[III][8] | 4,000[III][8] |
| Nitrogen | 0.0012506 | 63.15 | 77.36 |
| Oxygen | 0.001429 | 54.36 | 90.20 |
| Sodium | 0.971 | 370.87 | 1,156 |
| Magnesium | 1.738 | 923 | 1,363 |
| Aluminium | 2.698 | 933.47 | 2,792 |
| Sulfur | 2.067 | 388.36 | 717.87 |
| Chlorine | 0.003214 | 171.6 | 239.11 |
| Potassium | 0.862 | 336.53 | 1,032 |
| Titanium | 4.54 | 1,941 | 3,560 |
| Iron | 7.874 | 1,811 | 3,134 |
| Nickel | 8.912 | 1,728 | 3,186 |
| Copper | 8.96 | 1,357.77 | 2,835 |
| Zinc | 7.134 | 692.88 | 1,180 |
| Gallium | 5.907 | 302.9146 | 2,673 |
| Silver | 10.501 | 1,234.93 | 2,435 |
| Cadmium | 8.69 | 594.22 | 1,040 |
| Indium | 7.31 | 429.75 | 2,345 |
| Iodine | 4.93 | 386.85 | 457.4 |
| Tantalum | 16.654 | 3,290 | 5,731 |
| Tungsten | 19.25 | 3,695 | 5,828 |
| Platinum | 21.46 | 2,041.4 | 4,098 |
| Gold | 19.282 | 1,337.33 | 3,129 |
| Mercury | 13.5336 | 234.43 | 629.88 |
| Lead | 11.342 | 600.61 | 2,022 |
| Bismuth | 9.807 | 544.7 | 1,837 |
|
Notes
|
Melting point measurements[edit]
Kofler bench with samples for calibration
Many laboratory techniques exist for the determination of melting points.
A Kofler bench is a metal strip with a temperature gradient (range from room temperature to 300 °C). Any substance can be placed on a section of the strip, revealing its thermal behaviour at the temperature at that point. Differential scanning calorimetry gives information on melting point together with its enthalpy of fusion.
Automatic digital melting point meter
A basic melting point apparatus for the analysis of crystalline solids consists of an oil bath with a transparent window (most basic design: a Thiele tube) and a simple magnifier. Several grains of a solid are placed in a thin glass tube and partially immersed in the oil bath. The oil bath is heated (and stirred) and with the aid of the magnifier (and external light source) melting of the individual crystals at a certain temperature can be observed. A metal block might be used instead of an oil bath. Some modern instruments have automatic optical detection.
The measurement can also be made continuously with an operating process. For instance, oil refineries measure the freeze point of diesel fuel «online», meaning that the sample is taken from the process and measured automatically. This allows for more frequent measurements as the sample does not have to be manually collected and taken to a remote laboratory.
Techniques for refractory materials[edit]
For refractory materials (e.g. platinum, tungsten, tantalum, some carbides and nitrides, etc.) the extremely high melting point (typically considered to be above, say, 1,800 °C) may be determined by heating the material in a black body furnace and measuring the black-body temperature with an optical pyrometer. For the highest melting materials, this may require extrapolation by several hundred degrees. The spectral radiance from an incandescent body is known to be a function of its temperature. An optical pyrometer matches the radiance of a body under study to the radiance of a source that has been previously calibrated as a function of temperature. In this way, the measurement of the absolute magnitude of the intensity of radiation is unnecessary. However, known temperatures must be used to determine the calibration of the pyrometer. For temperatures above the calibration range of the source, an extrapolation technique must be employed. This extrapolation is accomplished by using Planck’s law of radiation. The constants in this equation are not known with sufficient accuracy, causing errors in the extrapolation to become larger at higher temperatures. However, standard techniques have been developed to perform this extrapolation.
Consider the case of using gold as the source (mp = 1,063 °C). In this technique, the current through the filament of the pyrometer is adjusted until the light intensity of the filament matches that of a black-body at the melting point of gold. This establishes the primary calibration temperature and can be expressed in terms of current through the pyrometer lamp. With the same current setting, the pyrometer is sighted on another black-body at a higher temperature. An absorbing medium of known transmission is inserted between the pyrometer and this black-body. The temperature of the black-body is then adjusted until a match exists between its intensity and that of the pyrometer filament. The true higher temperature of the black-body is then determined from Planck’s Law. The absorbing medium is then removed and the current through the filament is adjusted to match the filament intensity to that of the black-body. This establishes a second calibration point for the pyrometer. This step is repeated to carry the calibration to higher temperatures. Now, temperatures and their corresponding pyrometer filament currents are known and a curve of temperature versus current can be drawn. This curve can then be extrapolated to very high temperatures.
In determining melting points of a refractory substance by this method, it is necessary to either have black body conditions or to know the emissivity of the material being measured. The containment of the high melting material in the liquid state may introduce experimental difficulties. Melting temperatures of some refractory metals have thus been measured by observing the radiation from a black body cavity in solid metal specimens that were much longer than they were wide. To form such a cavity, a hole is drilled perpendicular to the long axis at the center of a rod of the material. These rods are then heated by passing a very large current through them, and the radiation emitted from the hole is observed with an optical pyrometer. The point of melting is indicated by the darkening of the hole when the liquid phase appears, destroying the black body conditions. Today, containerless laser heating techniques, combined with fast pyrometers and spectro-pyrometers, are employed to allow for precise control of the time for which the sample is kept at extreme temperatures. Such experiments of sub-second duration address several of the challenges associated with more traditional melting point measurements made at very high temperatures, such as sample vaporization and reaction with the container.
Thermodynamics[edit]
Pressure dependence of water melting point.
For a solid to melt, heat is required to raise its temperature to the melting point. However, further heat needs to be supplied for the melting to take place: this is called the heat of fusion, and is an example of latent heat.
From a thermodynamics point of view, at the melting point the change in Gibbs free energy (ΔG) of the material is zero, but the enthalpy (H) and the entropy (S) of the material are increasing (ΔH, ΔS > 0). Melting phenomenon happens when the Gibbs free energy of the liquid becomes lower than the solid for that material. At various pressures this happens at a specific temperature. It can also be shown that:
Here T, ΔS and ΔH are respectively the temperature at the melting point, change of entropy of melting and the change of enthalpy of melting.
The melting point is sensitive to extremely large changes in pressure, but generally this sensitivity is orders of magnitude less than that for the boiling point, because the solid-liquid transition represents only a small change in volume.[9][10] If, as observed in most cases, a substance is more dense in the solid than in the liquid state, the melting point will increase with increases in pressure. Otherwise the reverse behavior occurs. Notably, this is the case of water, as illustrated graphically to the right, but also of Si, Ge, Ga, Bi. With extremely large changes in pressure, substantial changes to the melting point are observed. For example, the melting point of silicon at ambient pressure (0.1 MPa) is 1415 °C, but at pressures in excess of 10 GPa it decreases to 1000 °C.[11]
Melting points are often used to characterize organic and inorganic compounds and to ascertain their purity. The melting point of a pure substance is always higher and has a smaller range than the melting point of an impure substance or, more generally, of mixtures. The higher the quantity of other components, the lower the melting point and the broader will be the melting point range, often referred to as the «pasty range». The temperature at which melting begins for a mixture is known as the solidus while the temperature where melting is complete is called the liquidus. Eutectics are special types of mixtures that behave like single phases. They melt sharply at a constant temperature to form a liquid of the same composition. Alternatively, on cooling a liquid with the eutectic composition will solidify as uniformly dispersed, small (fine-grained) mixed crystals with the same composition.
In contrast to crystalline solids, glasses do not possess a melting point;
on heating they undergo a smooth glass transition into a viscous liquid.
Upon further heating, they gradually soften, which can be characterized by certain softening points.
Freezing-point depression[edit]
The freezing point of a solvent is depressed when another compound is added, meaning that a solution has a lower freezing point than a pure solvent. This phenomenon is used in technical applications to avoid freezing, for instance by adding salt or ethylene glycol to water.
Carnelley’s rule[edit]
In organic chemistry, Carnelley’s rule, established in 1882 by Thomas Carnelley, states that high molecular symmetry is associated with high melting point.[12] Carnelley based his rule on examination of 15,000 chemical compounds. For example, for three structural isomers with molecular formula C5H12 the melting point increases in the series isopentane −160 °C (113 K) n-pentane −129.8 °C (143 K) and neopentane −16.4 °C (256.8 K).[13] Likewise in xylenes and also dichlorobenzenes the melting point increases in the order meta, ortho and then para. Pyridine has a lower symmetry than benzene hence its lower melting point but the melting point again increases with diazine and triazines. Many cage-like compounds like adamantane and cubane with high symmetry have relatively high melting points.
A high melting point results from a high heat of fusion, a low entropy of fusion, or a combination of both. In highly symmetrical molecules the crystal phase is densely packed with many efficient intermolecular interactions resulting in a higher enthalpy change on melting.
Like many high symmetry compounds, tetrakis(trimethylsilyl)silane has a very high melting point (m.p.) of 319-321 °C. It tends to sublime, so the m.p. determination requires that the sample be sealed in a tube.[14]
Predicting the melting point of substances (Lindemann’s criterion)[edit]
An attempt to predict the bulk melting point of crystalline materials was first made in 1910 by Frederick Lindemann.[15] The idea behind the theory was the observation that the average amplitude of thermal vibrations increases with increasing temperature. Melting initiates when the amplitude of vibration becomes large enough for adjacent atoms to partly occupy the same space. The Lindemann criterion states that melting is expected when the vibration root mean square amplitude exceeds a threshold value.
Assuming that all atoms in a crystal vibrate with the same frequency ν, the average thermal energy can be estimated using the equipartition theorem as[16]
where m is the atomic mass, ν is the frequency, u is the average vibration amplitude, kB is the Boltzmann constant, and T is the absolute temperature. If the threshold value of u2 is c2a2 where c is the Lindemann constant and a is the atomic spacing, then the melting point is estimated as
Several other expressions for the estimated melting temperature can be obtained depending on the estimate of the average thermal energy. Another commonly used expression for the Lindemann criterion is[17]
From the expression for the Debye frequency for ν, we have
where θD is the Debye temperature and h is the Planck constant. Values of c range from 0.15 to 0.3 for most materials.[18]
Melting point prediction[edit]
In February 2011, Alfa Aesar released over 10,000 melting points of compounds from their catalog as open data. This dataset has been used to create a random forest model for melting point prediction which is now freely available.[19] Open melting point data are also available from Nature Precedings.[20] High quality data mined from patents and also models[21] developed with these data were published by Tetko et al.[22]
Melting point of the elements[edit]
Melting point of the elements in the periodic table |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group → | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| ↓ Period | |||||||||||||||||||
| 1 | H2 13.99 K (−259.16 °C) |
He0.95 K (−272.20 °C) |
|||||||||||||||||
| 2 | Li453.65 K (180.50 °C) |
Be1560 K (1287 °C) |
B 2349 K (2076 °C) |
C |
N2 63.23 K (−209.86 °C) |
O2 54.36 K (−218.79 °C) |
F2 53.48 K (−219.67 °C) |
Ne24.56 K (−248.59 °C) |
|||||||||||
| 3 | Na370.944 K (97.794 °C) |
Mg923 K (650 °C) |
Al933.47 K (660.32 °C) |
Si1687 K (1414 °C) |
P 317.3 K (44.15 °C) |
S 388.36 K (115.21 °C) |
Cl2171.6 K (−101.5 °C) |
Ar83.81 K (−189.34 °C) |
|||||||||||
| 4 | K 336.7 K (63.5 °C) |
Ca1115 K (842 °C) |
Sc1814 K (1541 °C) |
Ti1941 K (1668 °C) |
V 2183 K (1910 °C) |
Cr2180 K (1907 °C) |
Mn1519 K (1246 °C) |
Fe1811 K (1538 °C) |
Co1768 K (1495 °C) |
Ni1728 K (1455 °C) |
Cu1357.77 K (1084.62 °C) |
Zn692.68 K (419.53 °C) |
Ga302.9146 K (29.7646 °C) |
Ge1211.40 K (938.25 °C) |
As |
Se494 K (221 °C) |
Br2265.8 K (−7.2 °C) |
Kr115.78 K (−157.37 °C) |
|
| 5 | Rb312.45 K (39.30 °C) |
Sr1050 K (777 °C) |
Y 1799 K (1526 °C) |
Zr2128 K (1855 °C) |
Nb2750 K (2477 °C) |
Mo2896 K (2623 °C) |
Tc2430 K (2157 °C) |
Ru2607 K (2334 °C) |
Rh2237 K (1964 °C) |
Pd1828.05 K (1554.9 °C) |
Ag1234.93 K (961.78 °C) |
Cd594.22 K (321.07 °C) |
In429.7485 K (156.5985 °C) |
Sn505.08 K (231.93 °C) |
Sb903.78 K (630.63 °C) |
Te722.66 K (449.51 °C) |
I2 386.85 K (113.7 °C) |
Xe161.40 K (−111.75 °C) |
|
| 6 | Cs301.7 K (28.5 °C) |
Ba1000 K (727 °C) |
Lu1925 K (1652 °C) |
Hf2506 K (2233 °C) |
Ta3290 K (3017 °C) |
W 3695 K (3422 °C) |
Re3459 K (3186 °C) |
Os3306 K (3033 °C) |
Ir2719 K (2446 °C) |
Pt2041.4 K (1768.3 °C) |
Au1337.33 K (1064.18 °C) |
Hg234.3210 K (−38.8290 °C) |
Tl577 K (304 °C) |
Pb600.61 K (327.46 °C) |
Bi544.7 K (271.5 °C) |
Po527 K (254 °C) |
At575 K (302 °C) |
Rn202 K (−71 °C) |
|
| 7 | Fr300 K (27 °C) |
Ra973 K (700 °C) |
Lr1900 K (1627 °C) |
Rf2400 K (2100 °C) |
Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn283±11 K (10±11 °C) |
Nh700 K (430 °C) |
Fl200 K (−73 °C) |
Mc670 K (400 °C) |
Lv637–780 K (364–507 °C) |
Ts623–823 K (350–550 °C) |
Og325±15 K (52±15 °C) |
|
| La1193 K (920 °C) |
Ce1068 K (795 °C)6 |
Pr1208 K (935 °C) |
Nd1297 K (1024 °C) |
Pm1315 K (1042 °C) |
Sm1345 K (1072 °C) |
Eu1099 K (826 °C) |
Gd1585 K (1312 °C) |
Tb1629 K (1356 °C) |
Dy1680 K (1407 °C) |
Ho1734 K (1461 °C) |
Er1802 K (1529 °C) |
Tm1818 K (1545 °C) |
Yb1097 K (824 °C) |
||||||
| Ac1500 K (1227 °C) |
Th2023 K (1750 °C) |
Pa1841 K (1568 °C) |
U 1405.3 K (1132.2 °C) |
Np912±3 K (639±3 °C) |
Pu912.5 K (639.4 °C) |
Am1449 K (1176 °C) |
Cm1613 K (1340 °C) |
Bk1259 K (986 °C) |
Cf1173 K (900 °C) |
Es1133 K (860 °C) |
Fm1800 K (1527 °C) |
Md1100 K (827 °C) |
No1100 K (827 °C) |
||||||
| Legend | |||||||||||||||||||
| Values are in Kelvin K and Celsius °C, rounded | |||||||||||||||||||
| For the equivalent in Fahrenheit °F, see: Melting points of the elements (data page) | |||||||||||||||||||
| Some values are predictions | |||||||||||||||||||
|
Primordial From decay Synthetic Border shows natural occurrence of the element
|
See also[edit]
- Congruent melting
- Hagedorn temperature
- Highest melting point
- List of elements by melting point
- Melting points of the elements (data page)
- Phase diagram
- Simon–Glatzel equation
- Slip melting point
- Triple point
- Zone melting
References[edit]
Citations[edit]
- ^ Ramsay, J. A. (1 May 1949). «A New Method of Freezing-Point Determination for Small Quantities». Journal of Experimental Biology. 26 (1): 57–64. doi:10.1242/jeb.26.1.57. PMID 15406812.
- ^ Haynes, p. 4.122.
- ^ The melting point of purified water has been measured as 0.002519 ± 0.000002 °C, see Feistel, R. & Wagner, W. (2006). «A New Equation of State for H2O Ice Ih». J. Phys. Chem. Ref. Data. 35 (2): 1021–1047. Bibcode:2006JPCRD..35.1021F. doi:10.1063/1.2183324.
- ^ Haynes, p. 4.123.
- ^ Hong, Q.-J.; van de Walle, A. (2015). «Prediction of the material with highest known melting point from ab initio molecular dynamics calculations». Phys. Rev. B. 92 (2): 020104(R). Bibcode:2015PhRvB..92b0104H. doi:10.1103/PhysRevB.92.020104.
- ^ Buinevich, V.S.; Nepapushev, A.A.; Moskovskikh, D.O.; Trusov, G.V.; Kuskov, K.V.; Vadchenko, S.G.; Rogachev, A.S.; Mukasyan, A.S. (March 2020). «Fabrication of ultra-high-temperature nonstoichiometric hafnium carbonitride via combustion synthesis and spark plasma sintering». Ceramics International. 46 (10): 16068–16073. doi:10.1016/j.ceramint.2020.03.158. S2CID 216437833.
- ^ Holman, S. W.; Lawrence, R. R.; Barr, L. (1 January 1895). «Melting Points of Aluminum, Silver, Gold, Copper, and Platinum». Proceedings of the American Academy of Arts and Sciences. 31: 218–233. doi:10.2307/20020628. JSTOR 20020628.
- ^ a b «Carbon». rsc.org.
- ^ The exact relationship is expressed in the Clausius–Clapeyron relation.
- ^ «J10 Heat: Change of aggregate state of substances through change of heat content: Change of aggregate state of substances and the equation of Clapeyron-Clausius». Retrieved 19 February 2008.
- ^ Tonkov, E. Yu. and Ponyatovsky, E. G. (2005) Phase Transformations of Elements Under High Pressure, CRC Press, Boca Raton, p. 98 ISBN 0-8493-3367-9
- ^ Brown, R. J. C. & R. F. C. (2000). «Melting Point and Molecular Symmetry». Journal of Chemical Education. 77 (6): 724. Bibcode:2000JChEd..77..724B. doi:10.1021/ed077p724.
- ^ Haynes, pp. 6.153–155.
- ^ Gilman, H.; Smith, C. L. (1967). «Tetrakis(trimethylsilyl)silane». Journal of Organometallic Chemistry. 8 (2): 245–253. doi:10.1016/S0022-328X(00)91037-4.
- ^ Lindemann FA (1910). «The calculation of molecular vibration frequencies». Phys. Z. 11: 609–612.
- ^ Sorkin, S., (2003), Point defects, lattice structure, and melting Archived 5 October 2016 at the Wayback Machine, Thesis, Technion, Israel.
- ^ Philip Hofmann (2008). Solid state physics: an introduction. Wiley-VCH. p. 67. ISBN 978-3-527-40861-0. Retrieved 13 March 2011.
- ^ Nelson, D. R., (2002), Defects and geometry in condensed matter physics, Cambridge University Press, ISBN 0-521-00400-4
- ^ Predict melting point from SMILES. Qsardb.org. Retrieved on 13 September 2013.
- ^ Bradley, Jean-Claude; Lang, Andrew; Williams, Antony; Curtin, Evan (11 August 2011). «ONS Open Melting Point Collection». Nature Precedings. doi:10.1038/npre.2011.6229.1.
- ^ OCHEM melting point models. ochem.eu. Retrieved on 18 June 2016.
- ^ Tetko, Igor V; m. Lowe, Daniel; Williams, Antony J (2016). «The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS». Journal of Cheminformatics. 8: 2. doi:10.1186/s13321-016-0113-y. PMC 4724158. PMID 26807157.
Sources[edit]
- Works cited
- Haynes, William M., ed. (2011). CRC Handbook of Chemistry and Physics (92nd ed.). CRC Press. ISBN 978-1439855119.
External links[edit]
- Melting and boiling point tables vol. 1 by Thomas Carnelley (Harrison, London, 1885–1887)
- Melting and boiling point tables vol. 2 by Thomas Carnelley (Harrison, London, 1885–1887)
- Patent mined data Over 250,000 freely downloadable melting point data. Also downloadable at figshare
«Плавление и кристаллизация.
Удельная теплота плавления»
Плавление
Плавление — это процесс превращения вещества из твёрдого состояния в жидкое.
Наблюдения показывают, что если измельчённый лёд, имеющий, например, температуру –10 °С, оставить в тёплой комнате, то его температура будет повышаться. При 0 °С лёд начнет таять, а температура при этом не будет изменяться до тех пор, пока весь лёд не превратится в жидкость. После этого температура образовавшейся изо льда воды будет повышаться.
Это означает, что кристаллические тела, к которым относится и лед, плавятся при определённой температуре, которую называют температурой плавления. Важно, что во время процесса плавления температура кристаллического вещества и образовавшейся в процессе его плавления жидкости остаётся неизменной.
В описанном выше опыте лёд получал некоторое количество теплоты, его внутренняя энергия увеличивалась за счёт увеличения средней кинетической энергии движения молекул. Затем лёд плавился, его температура при этом не менялась, хотя лёд получал некоторое количество теплоты. Следовательно, его внутренняя энергия увеличивалась, но не за счёт кинетической, а за счёт потенциальной энергии взаимодействия молекул. Получаемая извне энергия расходуется на разрушение кристаллической решетки. Подобным образом происходит плавление любого кристаллического тела.
Аморфные тела не имеют определённой температуры плавления. При повышении температуры они постепенно размягчаются, пока не превратятся в жидкость.
Кристаллизация
Кристаллизация — это процесс перехода вещества из жидкого состояния в твёрдое состояние. Охлаждаясь, жидкость будет отдавать некоторое количество теплоты окружающему воздуху. При этом будет уменьшаться её внутренняя энергия за счёт уменьшения средней кинетической энергии его молекул. При определённой температуре начнётся процесс кристаллизации, во время этого процесса температура вещества не будет изменяться, пока всё вещество не перейдет в твёрдое состояние. Этот переход сопровождается выделением определённого количества теплоты и соответственно уменьшением внутренней энергии вещества за счёт уменьшения потенциальной энергии взаимодействия его молекул.
Таким образом, переход вещества из жидкого состояния в твёрдое состояние происходит при определённой температуре, называемой температурой кристаллизации. Эта температура остаётся неизменной в течение всего процесса плавления. Она равна температуре плавления этого вещества.
На рисунке приведён график зависимости температуры твёрдого кристаллического вещества от времени в процессе его нагревания от комнатной температуры до температуры плавления, плавления, нагревания вещества в жидком состоянии, охлаждения жидкого вещества, кристаллизации и последующего охлаждения вещества в твёрдом состоянии.
Удельная теплота плавления
Различные кристаллические вещества имеют разное строение. Соответственно, для того, чтобы разрушить кристаллическую решётку твёрдого тела при температуре его плавления, необходимо ему сообщить разное количество теплоты.
Удельная теплота плавления — это количество теплоты, которое необходимо сообщить 1 кг кристаллического вещества, чтобы превратить его в жидкость при температуре плавления. Опыт показывает, что удельная теплота плавления равна удельной теплоте кристаллизации.
Удельная теплота плавления обозначается буквой λ. Единица удельной теплоты плавления — [λ] = 1 Дж/кг.
Значения удельной теплоты плавления кристаллических веществ приведены в таблице. Удельная теплота плавления алюминия 3,9*105 Дж/кг. Это означает, что для плавления 1 кг алюминия при температуре плавления необходимо затратить количество теплоты 3,9*105 Дж. Этому же значению равно увеличение внутренней энергии 1 кг алюминия.
Чтобы вычислить количество теплоты Q, необходимое для плавления вещества массой m, взятого при температуре плавления, следует удельную теплоту плавления λ умножить на массу вещества: Q = λm.
Эта же формула используется при вычислении количества теплоты, выделяющегося при кристаллизации жидкости.
Конспект урока «Плавление и кристаллизация. Удельная теплота плавления».
Следующая тема: «Тепловые машины. ДВС. Удельная теплота сгорания топлива».
Плавление и кристаллизация:
При теплопередаче внутренняя энергия тела изменяется. Чаще всего это выражается в изменении его температуры. При этом агрегатное состояние вещества остается прежним. Однако существуют процессы, при которых внутренняя энергия вещества при получении теплоты увеличивается, а температура остается постоянной.
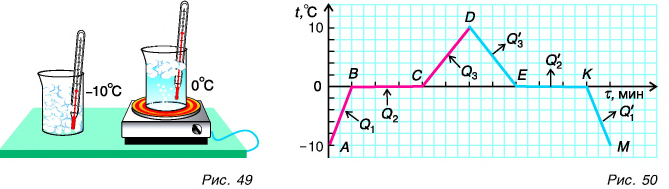
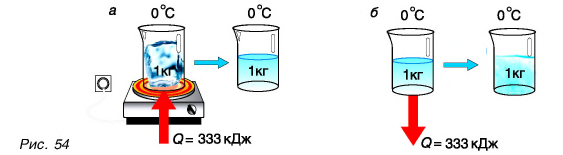
К таким процессам относятся плавление и кристаллизация (отвердевание). Изучим эти процессы с помощью опыта. В стакан поместим кусочки льда из морозильной камеры, охлажденные до температуры, например, -10 °C. Вставим в стакан термометр и начнем нагревать (рис. 49). Температура льда повышается. Он нагревается. Внутренняя энергия льда увеличивается за счет кинетической энергии его молекул. Изменение температуры вещества в стакане с течением времени будем изображать на графике (рис. 50). Участок АВ соответствует нагреванию льда от -10 °C до 0 °C. При дальнейшей передаче льду теплоты его температура остается постоянной, равной 0 °C (участок ВС). На что же уходит получаемая льдом теплота? Наблюдения показывают, что кристаллический лед превращается в воду.
Процесс перехода вещества из твердого состояния в жидкое называется плавлением.
Получаемая от плитки теплота по-прежнему превращается во внутреннюю энергию вещества, увеличивая ее. Это увеличение связано с изменением потенциальной энергии взаимодействия частиц при разрушении кристалла. Кинетическая же энергия не изменяется, так как температура постоянна. Аналогично идет процесс плавления других кристаллических веществ: железа, меди, стали и т. д.
Температура, при которой вещество переходит из твердого состояния в жидкое, т. е. плавится, называется температурой плавления.
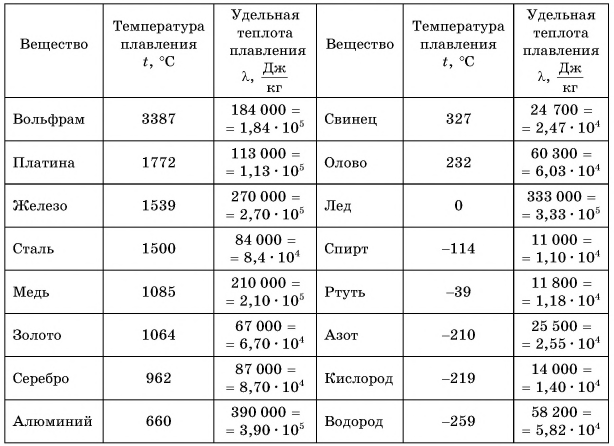
Температура плавления у разных кристаллических веществ неодинакова (табл. 3). Она очень высокая у вольфрама и очень низкая у водорода.
Таблица 3. Температура плавления и удельная теплота плавления некоторых веществ (при нормальном атмосферном давлении)
Продолжим опыт. Как только весь лед расплавится, температура воды в стакане начнет возрастать (участок CD, см. рис. 50). На всех рассмотренных участках теплота веществом (льдом, водой) поглощалась.
А теперь снимем стакан с плитки, поставим в морозильную камеру и будем периодически наблюдать за показаниями термометра и состоянием вещества. Вода сначала охлаждается до 0 °C (участок DE). Ее внутренняя энергия уменьшается, теплота 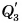
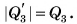
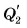
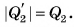
Процесс перехода вещества из жидкого состояния в твердое называется кристаллизацией.
Обратите внимание, что температура плавления и температура кристаллизации одинаковы. Например, если олово плавится при температуре 232 °C (см. табл. 3), то и отвердевать оно будет при температуре 232 °C.
Для любознательных:
В таблице 3 даны температуры плавления веществ при нормальном атмосферном давлении. И это не случайно. Для большинства веществ с увеличением давления температура плавления увеличивается. Но для льда — наоборот: при повышении давления лед может плавиться, например, при температуре -5 °C.
Понятия «температура плавления» и «температура кристаллизации» применимы не ко всем веществам. Согрев рукой кусок холодного твердого пластилина, мы ощутим постепенное уменьшение его твердости. Нагревая пластилин далее, можно перевести его в состояние вязкой жидкости. Но мы не обнаружим определенной температуры плавления. То же самое происходит при нагревании стекла: наблюдается непрерывное уменьшение его твердости (рис. 51) и увеличение текучести. Причина такого поведения указанных веществ (их называют аморфными) в отсутствии в их строении упорядоченного расположения частиц.
Понятия «температура плавления» и «температура кристаллизации» применимы лишь к веществам, имеющим кристаллическое строение.
Температуру плавления приходится учитывать при создании бытовой и промышленной техники. Спирали лампочек, нагревательных элементов (рис. 52) делают из тугоплавких материалов. В самолетостроении, в ракетной и космической промышленности используют материалы с высокой температурой плавления. Объясните причину этого.
Температуру плавления одних веществ можно изменить, смешивая их с другими. Так, добавляя поваренную соль ко льду, можно получить смесь с температурой плавления -21 °C. Это свойство активно используют дорожные службы, посыпая зимой улицы смесью песка и соли.
- Заказать решение задач по физике
Главные выводы:
- Для перехода кристаллического вещества из твердого состояния в жидкое его необходимо нагреть до температуры плавления.
- В процессах плавления и кристаллизации температура вещества не изменяется.
- Температуры плавления и кристаллизации для данного вещества одинаковы.
- При плавлении вещество поглощает энергию, при кристаллизации столько же энергии выделяется.
Удельная теплота плавления и кристаллизации
Как определить количество теплоты, которое должно поглотить твердое кристаллическое тело массой т, чтобы перейти в жидкое состояние, т. е. расплавиться? Еще раз обращаем ваше внимание на то, что температура во время плавления не изменяется (см. рис. 50, участок ВС), но теплота телу сообщается. Значит, она идет на разрушение кристаллической упорядоченной структуры вещества тела.
Физическая величина, численно равная количеству теплоты, которое необходимо передать твердому телу массой 1 кг при температуре плавления для перехода в жидкое состояние, называется удельной теплотой плавления.
Удельная теплота плавления обозначается греческой буквой 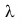
Чтобы расплавить твердое тело массой 2 кг, ему надо передать энергии (теплоты) Q в 2 раза больше. А если масса тела равна m? Очевидно, для перехода в жидкое состояние тело должно получить теплоты Q в m раз больше, т. е.
Из этой формулы следует, что удельная теплота плавления определяется как
В СИ единицей удельной теплоты плавления является 1 джоуль на килограмм
У различных веществ удельная теплота плавления 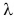
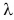
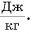
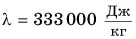
Большая удельная теплота плавления объясняет затяжное таяние льда озер, рек и других водоемов. А так как теплоту лед поглощает из окружающей среды, то погода в это время, как правило, прохладная. И наоборот, при замерзании озер, рек и других водоемов (рис. 55) выделяется большое количество энергии, что делает более теплой позднюю осеннюю погоду, а климат вблизи морей и океанов более умеренным.
Главные выводы:
- При переходе 1 кг вещества из твердого состояния в жидкое поглощается количество теплоты, численно равное удельной теплоте плавления, и ровно столько же теплоты выделяется при его переходе из жидкого состояния в твердое.
- Температуры плавления и кристаллизации для данного вещества одинаковы.
- Удельная теплота плавления у разных веществ различная.
Пример решения задачи
В горячую воду температурой 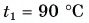
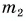
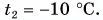
Дано:
Решение:
Составим уравнение теплового баланса: 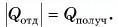
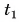
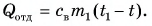
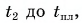
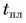
Тогда
откуда
Ответ: 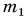
- Испарение жидкостей в физике
- Поверхностное натяжение жидкости
- Свойства паров в физике
- Кипение жидкостей в физике
- Инфракрасные излучения
- Количество теплоты в физике
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
Температу́ра плавле́ния и отвердева́ния — температура, при которой твёрдое кристаллическое тело совершает переход в жидкое состояние и наоборот. При температуре плавления вещество может находиться как в жидком, так и в твёрдом состоянии. При подведении дополнительного тепла вещество перейдёт в жидкое состояние, а температура не будет меняться, пока всё вещество в рассматриваемой системе не расплавится. При отведении лишнего тепла (охлаждении) вещество будет переходить в твёрдое состояние (застывать) и, пока оно не застынет полностью, температура не изменится.
Температура плавления/отвердевания и температура кипения/конденсации считаются важными физическими свойствами вещества. Температура отвердевания совпадает с температурой плавления только для чистого вещества.
На этом свойстве основаны специальные калибраторы термометров для высоких температур. Так как температура застывания чистого вещества, например, олова, стабильна, достаточно расплавить и ждать, пока расплав не начнёт кристаллизоваться. В это время, при условии хорошей теплоизоляции, температура застывающего слитка не меняется и в точности совпадает с эталонной температурой, указанной в справочниках.
Смеси веществ не имеют температуры плавления/отвердевания вовсе, и совершают переход в некотором диапазоне температур (температура появления жидкой фазы называется точкой солидуса, температура полного плавления — точкой ликвидуса). Поскольку точно измерить температуру плавления такого рода веществ нельзя, применяют специальные методы (ГОСТ 20287 и ASTM D 97). Но некоторые смеси (эвтектического состава) обладают определенной температурой плавления, как чистые вещества.
Аморфные (некристаллические) вещества, как правило, не обладают чёткой температурой плавления, с ростом температуры снижается вязкость таких веществ, и чем ниже вязкость, тем более жидким становится материал.
К примеру, обычное оконное стекло — это переохлаждённая жидкость. За несколько столетий становится видно, что при комнатной температуре стекло на окне сползает вниз под действием гравитации и становится внизу толще. При температуре 500—600 этот же эффект можно наблюдать уже в течение нескольких суток.
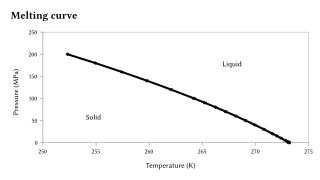
Поскольку при плавлении объём тела меняется незначительно, давление мало влияет на температуру плавления. Зависимость температуры фазового перехода (в том числе и плавления, и кипения) от давления для однокомпонентной системы даётся уравнением Клапейрона-Клаузиуса. Температуру плавления при нормальном атмосферном давлении (101 325 Па, или 760 мм ртутного столба) называют точкой плавления.
Температуры плавления некоторых важных веществ[1]:
| вещество | температура плавления (°C) |
|---|---|
| гелий (при 2,5 МПа) | −272,2 |
| водород | −259,2 |
| кислород | −218,8 |
| азот | −210,0 |
| метан | −182,5 |
| этиловый спирт | −114,5 |
| хлор | −101 |
| аммиак | −77,7 |
| ртуть | −38,87 |
| водяной лёд | 0 |
| бензол | +5,53 |
| цезий | +28,64 |
| сахароза | +185 |
| сахарин | +225 |
| олово | +231,93 |
| свинец | +327,5 |
| алюминий | +660,1 |
| серебро | +960,8 |
| золото | +1063 |
| кремний | +1415 |
| железо | +1539 |
| титан | +1668 |
| платина | +1772 |
| цирконий | +1852 |
| корунд | +2050 |
| рутений | +2334 |
| молибден | +2622 |
| карбид кремния | +2730 |
| осмий | +3054 |
| оксид тория | +3350 |
| вольфрам | +3410 |
| углерод | +3547 |
| карбид гафния | +3960 |
| карбид тантала-гафния | +4216 |
Примечания
- ↑ Дрица М. Е., Будберг П. Б., Бурханов Г. С., Дриц А. М., Пановко В. М. Свойства элементов. — Металлургия, 1985. — С. 672 с.
| |
|
|---|---|
| Твёрдое тело |
Аморфное • Кристаллы • Аэрогель (Температура плавления • Сублимация) |
| Жидкость |
Электролит • Перегретая • Переохлаждённая • Расплав (Критическая точка • Температура кипения) |
| Газ |
Пар |
| Плазма |
Электромагнитная • Кварк-глюонная • Глазма |
| См. также |
Сверхкритическая жидкость • Вырожденный газ • Конденсат Бозе — Эйнштейна • Странная материя • Кривая охлаждения • Твёрдый гелий (λ-точка) • Квантовая жидкость (Сверхтекучесть • Сверхтекучее твёрдое тело) • Дисперсная система (Раствор • Коллоидные • Грубодисперсная • Свободнодисперсная коллоидная (Дым • Золи)) • Термодинамическая фаза • Фазовый переход • Нормальные и стандартные условия • Статистика Ферми — Дирака • Уравнение состояния • Теория катастроф |
Что такое удельная теплота плавления
Содержание
- 1 Процессы плавления и кристаллизации
- 2 Чем отличается удельная теплота плавления от количества теплоты
- 3 Как связаны количество теплоты и удельная теплота плавления — формула
- 4 Выводы
Возьмем предварительно нагретое до температуры плавления вещество массой 1 кг. Будем сообщать ему тепловую энергию, чтобы расплавить это вещество.
Та энергия, которую мы затратим, чтобы расплавить 1 кг вещества, называется удельной теплотой плавления.
Эту теплоту называют удельной величиной, так как она приходится на 1 кг вещества.
Удельная теплота плавления — это энергия, которую мы затратим, чтобы расплавить 1 кг вещества, если это вещество предварительно было нагрето до температуры плавления.
Эту величину обозначают маленькой греческой буквой (large lambda) — лямбда.
(large lambda left( frac{text{Дж}}{text{кг}}right)) – удельная теплота плавления.
Примечания:
- Чтобы твердое кристаллическое тело начало плавиться, его нужно нагреть до температуры плавления.
- Температуру плавления различных веществ можно найти в справочнике физики.
- Если твердое кристаллическое тело плавится при температуре плавления, значит, оно будет затвердевать (кристаллизоваться) при этой же температуре, когда будет терять тепловую энергию.
- В физике применяются и другие удельные величины, например, удельная теплота сгорания топлива.
Перед тем, как расплавить вещество, нужно нагреть его до температуры плавления.
Процессы плавления и кристаллизации
Будем рассматривать такие процессы, как плавление и кристаллизация (затвердевание):
- плавление — тело получает тепловую энергию (количество теплоты);
- кристаллизация – тело отдает тепловую энергию в окружающее пространство.
Благодаря процессам кристаллизации зимой замерзает вода, образуется лед и можно кататься на коньках.
Весной, лед сначала нагреется от минусовой температуры до температуры плавления 0 градусов Цельсия, когда получит количество теплоты (тепловую энергию) от нагревающего его солнца. А затем, будет таять – то есть, плавиться, получая от солнца дополнительную тепловую энергию (теплоту). Покуда весь лед не расплавится, его температура подниматься не будет. Но как только весь лед превратится в воду, ее температура при нагревании начнет повышаться.
Чем отличается удельная теплота плавления от количества теплоты
Запомнить, чем удельная теплота плавления отличается от количества теплоты, можно так (рис. 1):
Рис. 1. Удельная теплота плавления и количество теплоты – это тепловая энергия, приходящаяся на различное количество килограммов
Количество теплоты – это энергия плавления нескольких килограммов вещества, предварительно нагретого до температуры плавления.
Удельная теплота плавления – это энергия плавления 1-го килограмма вещества, предварительно нагретого до температуры плавления.
Как связаны количество теплоты и удельная теплота плавления — формула
Если вещество предварительно нагрето до температуры плавления, и
Если известны:
- удельная теплота плавления вещества;
- количество килограммов вещества;
то легко посчитать общую тепловую энергию – т. е. количество теплоты.
Для этого используем формулу:
[large boxed{ Q = lambda cdot m }]
(large Q left( text{Дж} right) ) – количество теплоты, т. е. общая тепловая энергия;
(large lambda left( frac{text{Дж}}{text{кг}} right) ) – удельная теплота плавления (кристаллизации);
(large m left( text{кг} right) ) – масса вещества;
Примечание: Если умножить удельную теплоту плавления (large lambda ) на количество килограммов m расплавленного вещества, то можно вычислить общее количество теплоты (large Q ), затраченной на плавление.
Выводы
- Переход из твердого в жидкое состояние – это плавление, а из жидкого в твердое состояние – кристаллизация;
- Перед тем, как расплавить твердое кристаллическое вещество, нужно нагреть его до температуры плавления. Температуру плавления различных веществ можно найти в справочнике физики.
- Кристаллическое тело плавится и кристаллизуются при одной и той же температуре. Эту температуру называют температурой плавления (кристаллизации).
- Пока происходят процессы плавления и кристаллизации, температура не меняется.
- Во время плавления тело получает тепловую энергию (количество теплоты), а во время кристаллизации тело отдает тепловую энергию в окружающее пространство.
- Если 1 кг вещества предварительно нагрет до температуры плавления. То удельная теплота плавления – это тепловая энергия, необходимая для того, чтобы расплавить этот 1 килограмм вещества.
- Если вещество предварительно нагрето до температуры плавления, и нам известны его удельная теплота плавления и количество килограммов, то можно посчитать общее затраченное количество теплоты Q. Для этого нужно умножить удельную теплоту плавления (large lambda ) на количество килограммов m расплавленного вещества.
Оценка статьи:
Загрузка…