Основные понятия
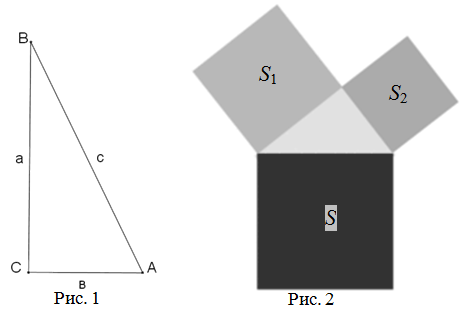
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
a2 + b2 = c2,
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c2 − b2
- b = √c2 − a2
- c = √a2 + b2
Запоминаем
в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
- если c2 < a2 + b2, значит угол, противолежащий стороне c, является острым.
- если c2 = a2 + b2, значит угол, противолежащий стороне c, является прямым.
- если c2 > a2 +b2, значит угол, противолежащий стороне c, является тупым.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a2 + b2 = c2.
Пошаговое доказательство:
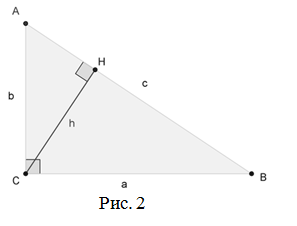
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
∠ACB =∠CHA = 90º,
∠A — общий.
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a2 = c * HB, b2 = c * AH.
- Сложим полученные равенства:
a2 + b2 = c * HB + c * AH
a2 + b2 = c * (HB + AH)
a2 + b2 = c * AB
a2 + b2 = c * c
a2 + b2 = c2
Теорема доказана.
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁2 = A₁C₁2 + B₁C₁2.
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
-
Пусть катеты a = 6 и b = 8.
-
По теореме Пифагора c2 = a2 + b2.
-
Подставим значения a и b в формулу:
c2 = 62 + 82 = 36 + 64 = 100
c = √100 = 10.
Ответ: 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
Как решаем:
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
112 = 82 + 92
121 ≠ 145
Ответ: треугольник не является прямоугольным.
 |
|
| Type | Theorem |
|---|---|
| Field | Euclidean geometry |
| Statement | The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c). |
| Symbolic statement |  |
| Generalizations |
|
| Consequences |
|
In mathematics, the Pythagorean theorem or Pythagoras’ theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, often called the Pythagorean equation:[1]
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points.
The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids. The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power; popular references in literature, plays, musicals, songs, stamps, and cartoons abound.
Other forms of the theorem
If c denotes the length of the hypotenuse and a and b denote the two lengths of the legs of a right triangle, then the Pythagorean theorem can be expressed as the Pythagorean equation:
If only the lengths of the legs of the right triangle are known but not the hypotenuse, then the length of the hypotenuse can be calculated with the equation
If the length of the hypotenuse and of one leg is known, then the length of the other leg can be calculated as
or
A generalization of this theorem is the law of cosines, which allows the computation of the length of any side of any triangle, given the lengths of the other two sides and the angle between them. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.
Proofs using constructed squares
Rearrangement proof of the Pythagorean theorem.
(The area of the white space remains constant throughout the translation rearrangement of the triangles. At all moments in time, the area is always c². And likewise, at all moments in time, the area is always a²+b².)
Rearrangement proofs
In one rearrangement proof, two squares are used whose sides have a measure of 









In another proof rectangles in the second box can also be placed such that both have one corner that correspond to consecutive corners of the square. In this way they also form two boxes, this time in consecutive corners, with areas 


English mathematician Sir Thomas Heath gives this proof in his commentary on Proposition I.47 in Euclid’s Elements, and mentions the proposals of German mathematicians Carl Anton Bretschneider and Hermann Hankel that Pythagoras may have known this proof. Heath himself favors a different proposal for a Pythagorean proof, but acknowledges from the outset of his discussion «that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him.»[3] Recent scholarship has cast increasing doubt on any sort of role for Pythagoras as a creator of mathematics, although debate about this continues.[4]
Algebraic proofs
The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram.[5] This results in a larger square, with side a + b and area (a + b)2. The four triangles and the square side c must have the same area as the larger square,
giving
A similar proof uses four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram.[6] The triangles are similar with area 
But this is a square with side c and area c2, so
Other proofs of the theorem
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.[7]
Proof using similar triangles
Proof using similar triangles
This proof is based on the proportionality of the sides of three similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar triangles is the same regardless of the size of the triangles.
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. Draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle, ACH, is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the triangle postulate: The sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides:
The first result equates the cosines of the angles θ, whereas the second result equates their sines.
These ratios can be written as
Summing these two equalities results in
which, after simplification, demonstrates the Pythagorean theorem:
The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the Elements, and that the theory of proportions needed further development at that time.[8][9]
Euclid’s proof
Proof in Euclid’s Elements
In outline, here is how the proof in Euclid’s Elements proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details follow.
Let A, B, C be the vertices of a right triangle, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.
For the formal proof, we require four elementary lemmata:
- If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
- The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
- The area of a rectangle is equal to the product of two adjacent sides.
- The area of a square is equal to the product of two of its sides (follows from 3).
Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.[10]
Illustration including the new lines
Showing the two congruent triangles of half the area of rectangle BDLK and square BAGF
The proof is as follows:
- Let ACB be a right-angled triangle with right angle CAB.
- On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.[11]
- From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
- Join CF and AD, to form the triangles BCF and BDA.
- Angles CAB and BAG are both right angles; therefore C, A, and G are collinear.
- Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
- Since AB is equal to FB, BD is equal to BC and angle ABD equals angle FBC, triangle ABD must be congruent to triangle FBC.
- Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
- Since C is collinear with A and G, and this line is parallel to FB, then square BAGF must be twice in area to triangle FBC.
- Therefore, rectangle BDLK must have the same area as square BAGF = AB2.
- By applying steps 3 to 10 to the other side of the figure, it can be similarly shown that rectangle CKLE must have the same area as square ACIH = AC2.
- Adding these two results, AB2 + AC2 = BD × BK + KL × KC
- Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Therefore, AB2 + AC2 = BC2, since CBDE is a square.
This proof, which appears in Euclid’s Elements as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares.[12][13]
This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.[9][14]
Proofs by dissection and rearrangement
Another by rearrangement is given by the middle animation. A large square is formed with area c2, from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a2 and b2, which must have the same area as the initial large square.[15]
Diagram of the two algebraic proofs
The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.[16]
|
Animation showing proof by rearrangement of four identical right triangles |
Animation showing another proof by rearrangement |
Proof using an elaborate rearrangement |
Einstein’s proof by dissection without rearrangement
Right triangle on the hypotenuse dissected into two similar right triangles on the legs, according to Einstein’s proof
Albert Einstein gave a proof by dissection in which the pieces do not need to be moved.[17] Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two similar shapes that each include one of two legs instead of the hypotenuse (see Similar figures on the three sides). In Einstein’s proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well.
Proof by area-preserving shearing
Visual proof of the Pythagorean theorem by area-preserving shearing.
As shown in the accompanying animation, area-preserving shear mappings and translations can transform the squares on the sides adjacent to the right-angle onto the square on the hypotenuse, together covering it exactly.[18] Each shear leaves the base and height unchanged, thus leaving the area unchanged too. The translations also leave the area unchanged, as they do not alter the shapes at all. Each square is first sheared into a parallelogram, and then into a rectangle which can be translated onto one section of the square on the hypotenuse.
Algebraic proofs
A related proof was published by future U.S. President James A. Garfield (then a U.S. Representative) (see diagram).[19][20][21] Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is
The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of 
Proof using differentials
One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.[22][23][24]
The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.
Diagram for differential proof
If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore, the ratios of their sides must be the same, that is:
This can be rewritten as 
giving
The constant can be deduced from x = 0, y = a to give the equation
This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.
Converse
The converse of the theorem is also true:[25]
Given a triangle with sides of length a, b, and c, if a2 + b2 = c2, then the angle between sides a and b is a right angle.
For any three positive real numbers a, b, and c such that a2 + b2 = c2, there exists a triangle with sides a, b and c as a consequence of the converse of the triangle inequality.
This converse appears in Euclid’s Elements (Book I, Proposition 48): «If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right.»[26]
It can be proven using the law of cosines or as follows:
Let ABC be a triangle with side lengths a, b, and c, with a2 + b2 = c2. Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length c = √a2 + b2, the same as the hypotenuse of the first triangle. Since both triangles’ sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.
The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proven without assuming the Pythagorean theorem.[27][28]
A corollary of the Pythagorean theorem’s converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:[29]
- If a2 + b2 = c2, then the triangle is right.
- If a2 + b2 > c2, then the triangle is acute.
- If a2 + b2 < c2, then the triangle is obtuse.
Edsger W. Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language:
- sgn(α + β − γ) = sgn(a2 + b2 − c2),
where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.[30]
Consequences and uses of the theorem
Pythagorean triples
A Pythagorean triple has three positive integers a, b, and c, such that a2 + b2 = c2. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.[1] Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).
A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).
The following is a list of primitive Pythagorean triples with values less than 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Inverse Pythagorean theorem
Given a right triangle with sides 


while the inverse Pythagorean theorem relates the two legs 

The equation can be transformed to,
where 



using the smallest Pythagorean triple 
where the denominators are squares and also for a heptagonal triangle whose sides 
Incommensurable lengths
The spiral of Theodorus: A construction for line segments with lengths whose ratios are the square root of a positive integer
One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras’ theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.
The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.[32] Each triangle has a side (labeled «1») that is the chosen unit for measurement. In each right triangle, Pythagoras’ theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.
Incommensurable lengths conflicted with the Pythagorean school’s concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.[33] According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.[34][35]
Complex numbers
The absolute value of a complex number z is the distance r from z to the origin
For any complex number
the absolute value or modulus is given by
So the three quantities, r, x and y are related by the Pythagorean equation,
Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.
This can be generalised to find the distance between two points, z1 and z2 say. The required distance is given by
so again they are related by a version of the Pythagorean equation,
Euclidean distance
The distance formula in Cartesian coordinates is derived from the Pythagorean theorem.[36] If (x1, y1) and (x2, y2) are points in the plane, then the distance between them, also called the Euclidean distance, is given by
More generally, in Euclidean n-space, the Euclidean distance between two points, 

If instead of Euclidean distance, the square of this value (the squared Euclidean distance, or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates:
The squared form is a smooth, convex function of both points, and is widely used in optimization theory and statistics, forming the basis of least squares.
Euclidean distance in other coordinate systems
If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras’ theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:
Then two points with locations (r1, θ1) and (r2, θ2) are separated by a distance s:
Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:
using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem.[37] From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras’ theorem is regained: 
Pythagorean trigonometric identity
Similar right triangles showing sine and cosine of angle θ
In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:
From that it follows:
where the last step applies Pythagoras’ theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.[38] In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.
Relation to the cross product
The area of a parallelogram as a cross product; vectors a and b identify a plane and a × b is normal to this plane.
The Pythagorean theorem relates the cross product and dot product in a similar way:[39]
This can be seen from the definitions of the cross product and dot product, as
with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.
This can also be used to define the cross product. By rearranging the following equation is obtained
This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.[40][41]
Generalizations
Similar figures on the three sides
The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any similar figures. This was known by Hippocrates of Chios in the 5th century BC,[42] and was included by Euclid in his Elements:[43]
If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.
This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c).[44] While Euclid’s proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure’s boundary being the side of the original triangle).[44]
The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:
But, by the Pythagorean theorem, a2 + b2 = c2, so A + B = C.
Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a2 + b2 = c2. (See also Einstein’s proof by dissection without rearrangement)
|
Generalization for similar triangles, |
Pythagoras’ theorem using similar right triangles |
Generalization for regular pentagons |
Law of cosines
The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:[45]
where 


When 


Arbitrary triangle
Generalization of Pythagoras’ theorem by Tâbit ibn Qorra.[46] Lower panel: reflection of triangle CAD (top) to form triangle DAC, similar to triangle ABC (top).
At any selected angle of a general triangle of sides a, b, c, inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled c. Inscribing the isosceles triangle forms triangle CAD with angle θ opposite side b and with side r along c. A second triangle is formed with angle θ opposite side a and a side with length s along c, as shown in the figure. Thābit ibn Qurra stated that the sides of the three triangles were related as:[47][48]
As the angle θ approaches π/2, the base of the isosceles triangle narrows, and lengths r and s overlap less and less. When θ = π/2, ADB becomes a right triangle, r + s = c, and the original Pythagorean theorem is regained.
One proof observes that triangle ABC has the same angles as triangle CAD, but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the triangle postulate.) Consequently, ABC is similar to the reflection of CAD, the triangle DAC in the lower panel. Taking the ratio of sides opposite and adjacent to θ,
Likewise, for the reflection of the other triangle,
Clearing fractions and adding these two relations:
the required result.
The theorem remains valid if the angle 
General triangles using parallelograms
Generalization for arbitrary triangles,
green area = blue area
Construction for proof of parallelogram generalization
Pappus’s area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras’ theorem, and was considered a generalization by Pappus of Alexandria in 4 AD[49][50]
The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.
Solid geometry
Pythagoras’ theorem in three dimensions relates the diagonal AD to the three sides.
A tetrahedron with outward facing right-angle corner
In terms of solid geometry, Pythagoras’ theorem can be applied to three dimensions as follows. Consider a rectangular solid as shown in the figure. The length of diagonal BD is found from Pythagoras’ theorem as:
where these three sides form a right triangle. Using horizontal diagonal BD and the vertical edge AB, the length of diagonal AD then is found by a second application of Pythagoras’ theorem as:
or, doing it all in one step:
This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {vk} (the three mutually perpendicular sides):
This one-step formulation may be viewed as a generalization of Pythagoras’ theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras’ theorem to a succession of right triangles in a sequence of orthogonal planes.
A substantial generalization of the Pythagorean theorem to three dimensions is de Gua’s theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the «n-dimensional Pythagorean theorem»:[51]
Let
be orthogonal vectors in Rn. Consider the n-dimensional simplex S with vertices
. (Think of the (n − 1)-dimensional simplex with vertices
not including the origin as the «hypotenuse» of S and the remaining (n − 1)-dimensional faces of S as its «legs».) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.
This statement is illustrated in three dimensions by the tetrahedron in the figure. The «hypotenuse» is the base of the tetrahedron at the back of the figure, and the «legs» are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the «legs» increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras’ theorem applies. In a different wording:[52]
Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.
Inner product spaces
Vectors involved in the parallelogram law
The Pythagorean theorem can be generalized to inner product spaces,[53] which are generalizations of the familiar 2-dimensional and 3-dimensional Euclidean spaces. For example, a function may be considered as a vector with infinitely many components in an inner product space, as in functional analysis.[54]
In an inner product space, the concept of perpendicularity is replaced by the concept of orthogonality: two vectors v and w are orthogonal if their inner product 
The concept of length is replaced by the concept of the norm ||v|| of a vector v, defined as:[56]
In an inner-product space, the Pythagorean theorem states that for any two orthogonal vectors v and w we have
Here the vectors v and w are akin to the sides of a right triangle with hypotenuse given by the vector sum v + w. This form of the Pythagorean theorem is a consequence of the properties of the inner product:
where 
A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the parallelogram law :[56]
which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is ipso facto a norm corresponding to an inner product.[56]
The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If v1, v2, …, vn are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on solid geometry) results in the equation[57]
Sets of m-dimensional objects in n-dimensional space
Another generalization of the Pythagorean theorem applies to Lebesgue-measurable sets of objects in any number of dimensions. Specifically, the square of the measure of an m-dimensional set of objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space is equal to the sum of the squares of the measures of the orthogonal projections of the object(s) onto all m-dimensional coordinate subspaces.[58]
In mathematical terms:
where:
Non-Euclidean geometry
The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem implies, and is implied by, Euclid’s Parallel (Fifth) Postulate.[59][60] Thus, right triangles in a non-Euclidean geometry[61]
do not satisfy the Pythagorean theorem. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because

Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.
However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A+B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.[62]
Spherical geometry
For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, c, the relation between the sides takes the form:[63]
This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:
By expressing the Maclaurin series for the cosine function as an asymptotic expansion with the remainder term in big O notation,
it can be shown that as the radius R approaches infinity and the arguments a/R, b/R, and c/R tend to zero, the spherical relation between the sides of a right triangle approaches the Euclidean form of the Pythagorean theorem. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields
The constants a4, b4, and c4 have been absorbed into the big O remainder terms since they are independent of the radius R. This asymptotic relationship can be further simplified by multiplying out the bracketed quantities, cancelling the ones, multiplying through by −2, and collecting all the error terms together:
After multiplying through by R2, the Euclidean Pythagorean relationship c2 = a2 + b2 is recovered in the limit as the radius R approaches infinity (since the remainder term tends to zero):
For small right triangles (a, b << R), the cosines can be eliminated to avoid loss of significance, giving
Hyperbolic geometry
In a hyperbolic space with uniform Gaussian curvature −1/R2, for a right triangle with legs a, b, and hypotenuse c, the relation between the sides takes the form:[64]
where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:[65]
with γ the angle at the vertex opposite the side c.
By using the Maclaurin series for the hyperbolic cosine, cosh x ≈ 1 + x2/2, it can be shown that as a hyperbolic triangle becomes very small (that is, as a, b, and c all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras’ theorem.
For small right triangles (a, b << R), the hyperbolic cosines can be eliminated to avoid loss of significance, giving
Very small triangles
For any uniform curvature K (positive, zero, or negative), in very small right triangles (|K|a2, |K|b2 << 1) with hypotenuse c, it can be shown that
Differential geometry
The Pythagorean theorem applies to infinitesimal triangles seen in differential geometry. In three dimensional space, the distance between two infinitesimally separated points satisfies
with ds the element of distance and (dx, dy, dz) the components of the vector separating the two points. Such a space is called a Euclidean space. However, in Riemannian geometry, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:[66]
which is called the metric tensor. (Sometimes, by abuse of language, the same term is applied to the set of coefficients gij.) It may be a function of position, and often describes curved space. A simple example is Euclidean (flat) space expressed in curvilinear coordinates. For example, in polar coordinates:
History
There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras was born.[68][69][70][71] The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system.
Written between 2000 and 1786 BC, the Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. The Mesopotamian tablet Plimpton 322, written between 1790 and 1750 BC during the reign of King Hammurabi the Great, contains many entries closely related to Pythagorean triples.
In India, the Baudhayana Shulba Sutra, the dates of which are given variously as between the 8th and 5th century BC,[72] contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the isosceles right triangle and in the general case, as does the Apastamba Shulba Sutra (c. 600 BC).[a]
Byzantine Neoplatonic philosopher and mathematician Proclus, writing in the fifth century AD, states two arithmetic rules, «one of them attributed to Plato, the other to Pythagoras»,[74] for generating special Pythagorean triples. The rule attributed to Pythagoras (c. 570 – c. 495 BC) starts from an odd number and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to Thomas L. Heath (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived.[75] However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.[76][77] Classicist Kurt von Fritz wrote, «Whether this formula is rightly attributed to Pythagoras personally, but one can safely assume that it belongs to the very oldest period of Pythagorean mathematics.»[35] Around 300 BC, in Euclid’s Elements, the oldest extant axiomatic proof of the theorem is presented.[78]
With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the Chinese text Zhoubi Suanjing (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the «Gougu theorem» (勾股定理).[79][80] During the Han Dynasty (202 BC to 220 AD), Pythagorean triples appear in The Nine Chapters on the Mathematical Art,[81] together with a mention of right triangles.[82] Some believe the theorem arose first in China,[83] where it is alternatively known as the «Shang Gao theorem» (商高定理),[84] named after the Duke of Zhou’s astronomer and mathematician, whose reasoning composed most of what was in the Zhoubi Suanjing.[85]
See also
- Addition in quadrature
- At Dulcarnon
- British flag theorem
- Fermat’s Last Theorem
- Inverse Pythagorean theorem
- Kepler triangle
- Linear algebra
- List of triangle topics
- Lp space
- Nonhypotenuse number
- Parallelogram law
- Parseval’s identity
- Ptolemy’s theorem
- Pythagorean expectation
- Pythagorean tiling
- Rational trigonometry in Pythagoras’ theorem
- Thales theorem
Notes and references
Notes
- ^ Van der Waerden believed that this material «was certainly based on earlier traditions». Carl Boyer states that the Pythagorean theorem in the Śulba-sũtram may have been influenced by ancient Mesopotamian math, but there is no conclusive evidence in favor or opposition of this possibility.[73]
References
- ^ a b Judith D. Sally; Paul Sally (2007). «Chapter 3: Pythagorean triples». Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 978-0-8218-4403-8.
- ^ Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ^ Euclid (1956), pp. 351–352
- ^ Huffman, Carl (23 February 2005). «Pythagoras». In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition)., «It should now be clear that decisions about sources are crucial in addressing the question of whether Pythagoras was a mathematician and scientist. The view of Pythagoras’s cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus.»
- ^ Alexander Bogomolny. «Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4». Cut the Knot. Retrieved 4 November 2010.
- ^
Alexander Bogomolny. «Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3». Cut the Knot. Retrieved 4 November 2010. - ^ (Loomis 1968)
- ^ (Maor 2007, p. 39)
- ^ a b
Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. p. 12. ISBN 0-7624-1922-9.This proof first appeared after a computer program was set to check Euclidean proofs.
- ^ See for example Pythagorean theorem by shear mapping Archived 2016-10-14 at the Wayback Machine, Saint Louis University website Java applet
- ^
Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. p. 435. ISBN 0-393-04002-X.
- ^ Heiberg, J.L. «Euclid’s Elements of Geometry» (PDF). pp. 46–47.
- ^ «Euclid’s Elements, Book I, Proposition 47».
web page version using Java applets from Euclid’s Elements by Prof. David E. Joyce, Clark University
- ^ The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007, p. 25)
- ^ Alexander Bogomolny. «Pythagorean theorem, proof number 10». Cut the Knot. Retrieved 27 February 2010.
- ^ (Loomis 1968, p. 113, Geometric proof 22 and Figure 123)
- ^ Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. pp. 3–4. ISBN 978-0486134789.
- ^ Polster, Burkard (2004). Q.E.D.: Beauty in Mathematical Proof. Walker Publishing Company. p. 49.
- ^
Published in a weekly mathematics column: James A Garfield (1876). «Pons Asinorum». The New England Journal of Education. 3 (14): 161. as noted in William Dunham (1997). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. p. 96. ISBN 0-471-17661-3. and in A calendar of mathematical dates: April 1, 1876 Archived July 14, 2010, at the Wayback Machine by V. Frederick Rickey - ^ Lantz, David. «Garfield’s proof of the Pythagorean Theorem». Math.Colgate.edu. Archived from the original on 2013-08-28. Retrieved 2018-01-14.
- ^ Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: pp. 106-107.
- ^
Mike Staring (1996). «The Pythagorean proposition: A proof by means of calculus». Mathematics Magazine. Mathematical Association of America. 69 (1): 45–46. doi:10.2307/2691395. JSTOR 2691395. - ^
Bogomolny, Alexander. «Pythagorean Theorem». Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Archived from the original on 2010-07-06. Retrieved 2010-05-09. - ^
Bruce C. Berndt (1988). «Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?». The Mathematical Intelligencer. 10 (3): 24–31. doi:10.1007/BF03026638. S2CID 123311054. - ^
Judith D. Sally; Paul J. Sally Jr. (2007-12-21). «Theorem 2.4 (Converse of the Pythagorean theorem).». Roots to Research. American Mathematical Society. pp. 54–55. ISBN 978-0-8218-4403-8. - ^
Euclid’s Elements, Book I, Proposition 48 From D.E. Joyce’s web page at Clark University - ^ Casey, Stephen, «The converse of the theorem of Pythagoras», Mathematical Gazette 92, July 2008, 309–313.
- ^ Mitchell, Douglas W., «Feedback on 92.47», Mathematical Gazette 93, March 2009, 156.
- ^
Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). «Theorem 1 and Theorem 2». Plane trigonometry and applications. Allyn and Bacon. p. 85. - ^ Dijkstra, Edsger W. (September 7, 1986). «On the theorem of Pythagoras». EWD975. E. W. Dijkstra Archive.
- ^ Alexander Bogomolny, Pythagorean Theorem for the Reciprocals,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- ^ Law, Henry (1853). «Corollary 5 of Proposition XLVII (Pythagoras’s Theorem)». The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. p. 49.
- ^
Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. p. 13. ISBN 0-674-92096-1.
- ^
(Heath 1921, Vol I, pp. 65); Hippasus was on a voyage at the time, and his fellows cast him overboard. See James R. Choike (1980). «The pentagram and the discovery of an irrational number». The College Mathematics Journal. 11: 312–316.
- ^ a b
A careful discussion of Hippasus’s contributions is found in
Kurt Von Fritz (Apr 1945). «The Discovery of Incommensurability by Hippasus of Metapontum». Annals of Mathematics. Second Series. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021. - ^ Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). «Euclidean distance». Mastering algorithms with Perl. O’Reilly Media, Inc. p. 426. ISBN 1-56592-398-7.
- ^ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 978-1-103-07998-8., Exercises, page 116
- ^
Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron’s Educational Series. p. 296. ISBN 0-7641-2892-2. - ^
WS Massey (Dec 1983). «Cross products of vectors in higher-dimensional Euclidean spaces» (PDF). The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Archived from the original (PDF) on 2021-02-26. - ^ Pertti Lounesto (2001). «§7.4 Cross product of two vectors». Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 96. ISBN 0-521-00551-5.
- ^
Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover Publications. p. 24. ISBN 0-486-67002-3. - ^ Heath, T. L., A History of Greek Mathematics, Oxford University Press, 1921; reprinted by Dover, 1981.
- ^ Euclid’s Elements: Book VI, Proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.»
- ^ a b Putz, John F. and Sipka, Timothy A. «On generalizing the Pythagorean theorem», The College Mathematics Journal 34 (4), September 2003, pp. 291–295.
- ^
Lawrence S. Leff (2005-05-01). cited work. Barron’s Educational Series. p. 326. ISBN 0-7641-2892-2.
- ^
Howard Whitley Eves (1983). «§4.8:…generalization of Pythagorean theorem». Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0-88385-310-8.
- ^
Aydin Sayili (Mar 1960). «Thâbit ibn Qurra’s Generalization of the Pythagorean Theorem». Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603. S2CID 119868978.
- ^
Judith D. Sally; Paul Sally (2007-12-21). «Exercise 2.10 (ii)». Roots to Research: A Vertical Development of Mathematical Problems. p. 62. ISBN 978-0-8218-4403-8.
- ^ For the details of such a construction, see Jennings, George (1997). «Figure 1.32: The generalized Pythagorean theorem». Modern geometry with applications: with 150 figures (3rd ed.). Springer. p. 23. ISBN 0-387-94222-X.
- ^ Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 77–78 (excerpt, p. 77, at Google Books)
- ^
Rajendra Bhatia (1997). Matrix analysis. Springer. p. 21. ISBN 0-387-94846-5. - ^
For an extended discussion of this generalization, see, for example, Willie W. Wong Archived 2009-12-29 at the Wayback Machine 2002, A generalized n-dimensional Pythagorean theorem. - ^
Ferdinand van der Heijden; Dick de Ridder (2004). Classification, parameter estimation, and state estimation. Wiley. p. 357. ISBN 0-470-09013-8.
- ^
Qun Lin; Jiafu Lin (2006). Finite element methods: accuracy and improvement. Elsevier. p. 23. ISBN 7-03-016656-6.
- ^
Howard Anton; Chris Rorres (2010). Elementary Linear Algebra: Applications Version (10th ed.). Wiley. p. 336. ISBN 978-0-470-43205-1.
- ^ a b c
Karen Saxe (2002). «Theorem 1.2». Beginning functional analysis. Springer. p. 7. ISBN 0-387-95224-1.
- ^ Douglas, Ronald G. (1998). Banach Algebra Techniques in Operator Theory (2nd ed.). New York, New York: Springer-Verlag New York, Inc. pp. 60–61. ISBN 978-0-387-98377-6.
- ^
Donald R Conant & William A Beyer (Mar 1974). «Generalized Pythagorean Theorem». The American Mathematical Monthly. Mathematical Association of America. 81 (3): 262–265. doi:10.2307/2319528. JSTOR 2319528. - ^
Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). p. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ^
Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 0-521-85959-X.
We could include…the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ^
Stephen W. Hawking (2005). cited work. p. 4. ISBN 0-7624-1922-9.
- ^
Victor Pambuccian (December 2010). «Maria Teresa Calapso’s Hyperbolic Pythagorean Theorem». The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ^
Barrett O’Neill (2006). «Exercise 4». Elementary differential geometry (2nd ed.). Academic Press. p. 441. ISBN 0-12-088735-5.
- ^
Saul Stahl (1993). «Theorem 8.3». The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 0-86720-298-X.
- ^
Jane Gilman (1995). «Hyperbolic triangles». Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- ^
Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0-521-65544-7. - ^ Neugebauer 1969, p. 36.
- ^ Neugebauer 1969: p. 36 «In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse.»
- ^ Friberg, Jöran (1981). «Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations». Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.: p. 306 «Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period.»
- ^ Høyrup, Jens. «Pythagorean ‘Rule’ and ‘Theorem’ – Mirror of the Relation Between Babylonian and Greek Mathematics». In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407., p. 406, «To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db2-146, somewhere between 2300 and 1825 BC.» (Db2-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)
- ^ Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.: p. 109 «Many Old Babylonian mathematical practitioners … knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste ‘algebra’ on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia.»
- ^ Kim Plofker (2009). Mathematics in India. Princeton University Press. pp. 17–18. ISBN 978-0-691-12067-6.
- ^ Carl Benjamin Boyer; Uta C. Merzbach (2011). «China and India». A history of mathematics (3rd ed.). Wiley. p. 229. ISBN 978-0470525487.
Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid’s Elements. (…)
- ^ Proclus (1970). A Commentary of the First Book of Euclid’s Elements. Translated by Morrow, Glenn R. Princeton University Press. 428.6.
- ^ (Euclid 1956, p. 351) page 351
- ^ (Heath 1921, Vol I, p. 144): «Though this is the proposition universally associated by tradition with the name of Pythagoras, no really trustworthy evidence exists that it was actually discovered by him. The comparatively late writers who attribute it to him add the story that he sacrificed an ox to celebrate his discovery.»
- ^
An extensive discussion of the historical evidence is provided in (Euclid 1956, p. 351) page=351
- ^
Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. p. 51. ISBN 0-88385-613-1.…it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
- ^
Robert P. Crease (2008). The great equations: breakthroughs in science from Pythagoras to Heisenberg. W W Norton & Co. p. 25. ISBN 978-0-393-06204-5. - ^
A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by Christopher Cullen (2007). Astronomy and Mathematics in Ancient China: The ‘Zhou Bi Suan Jing’. Cambridge University Press. pp. 139 ff. ISBN 978-0-521-03537-8.
- ^
This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. Philip D. Straffin Jr. (2004). «Liu Hui and the first golden age of Chinese mathematics». In Marlow Anderson; Victor J. Katz; Robin J. Wilson (eds.). Sherlock Holmes in Babylon: and other tales of mathematical history. Mathematical Association of America. pp. 69 ff. ISBN 0-88385-546-1. See particularly §3: Nine chapters on the mathematical art, pp. 71 ff.
- ^
Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). The nine chapters on the mathematical art: companion and commentary. Oxford University Press. p. 488. ISBN 0-19-853936-3.
- ^
In particular, Li Jimin; see Centaurus, Volume 39. Copenhagen: Munksgaard. 1997. pp. 193, 205.
- ^
Chen, Cheng-Yih (1996). «§3.3.4 Chén Zǐ’s formula and the Chóng-Chã method; Figure 40». Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. Hong Kong University Press. p. 142. ISBN 962-209-385-X.
- ^
Wen-tsün Wu (2008). «The Gougu theorem». Selected works of Wen-tsün Wu. World Scientific. p. 158. ISBN 978-981-279-107-8.
Works cited
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- Euclid (1956). The Thirteen Books of Euclid’s Elements, Translated from the Text of Heiberg, with Introduction and Commentary. Vol. 1 (Books I and II). Translated by Heath, Thomas L. (Reprint of 2nd (1925) ed.). Dover. On-line text at archive.org
- Heath, Sir Thomas (1921). «The ‘Theorem of Pythagoras’«. A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 ff. ISBN 0-486-24073-8.
- Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 978-0-7637-4366-6. This high-school geometry text covers many of the topics in this WP article.
- Loomis, Elisha Scott (1968). The Pythagorean proposition (2nd ed.). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1. For full text of 2nd edition of 1940, see Elisha Scott Loomis. «The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs» (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Retrieved 2010-05-04. Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, ISBN 0-87353-036-5.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Neugebauer, Otto (1969). The exact sciences in antiquity. Acta Historica Scientiarum Naturalium et Medicinalium. Vol. 9 (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. pp. 1–191. ISBN 0-486-22332-9. PMID 14884919.
- Robson, Eleanor and Jacqueline Stedall, eds., The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, 2009. pp. vii + 918. ISBN 978-0-19-921312-2.
- Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
Pythagorean triples Babylonian scribes van der Waerden.
External links
- Pythagorean theorem at ProofWiki
- Euclid (1997) [c. 300 BC]. David E. Joyce (ed.). Elements. Retrieved 2006-08-30. In HTML with Java-based interactive figures.
- «Pythagorean theorem». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- History topic: Pythagoras’s theorem in Babylonian mathematics
- Interactive links:
- Interactive proof in Java of the Pythagorean theorem
- Another interactive proof in Java of the Pythagorean theorem
- Pythagorean theorem with interactive animation
- Animated, non-algebraic, and user-paced Pythagorean theorem
- Pythagorean theorem water demo on YouTube
- Pythagorean theorem (more than 70 proofs from cut-the-knot)
- Weisstein, Eric W. «Pythagorean theorem». MathWorld.
 |
|
| Type | Theorem |
|---|---|
| Field | Euclidean geometry |
| Statement | The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c). |
| Symbolic statement |  |
| Generalizations |
|
| Consequences |
|
In mathematics, the Pythagorean theorem or Pythagoras’ theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, often called the Pythagorean equation:[1]
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points.
The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids. The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power; popular references in literature, plays, musicals, songs, stamps, and cartoons abound.
Other forms of the theorem
If c denotes the length of the hypotenuse and a and b denote the two lengths of the legs of a right triangle, then the Pythagorean theorem can be expressed as the Pythagorean equation:
If only the lengths of the legs of the right triangle are known but not the hypotenuse, then the length of the hypotenuse can be calculated with the equation
If the length of the hypotenuse and of one leg is known, then the length of the other leg can be calculated as
or
A generalization of this theorem is the law of cosines, which allows the computation of the length of any side of any triangle, given the lengths of the other two sides and the angle between them. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.
Proofs using constructed squares
Rearrangement proof of the Pythagorean theorem.
(The area of the white space remains constant throughout the translation rearrangement of the triangles. At all moments in time, the area is always c². And likewise, at all moments in time, the area is always a²+b².)
Rearrangement proofs
In one rearrangement proof, two squares are used whose sides have a measure of 









In another proof rectangles in the second box can also be placed such that both have one corner that correspond to consecutive corners of the square. In this way they also form two boxes, this time in consecutive corners, with areas 


English mathematician Sir Thomas Heath gives this proof in his commentary on Proposition I.47 in Euclid’s Elements, and mentions the proposals of German mathematicians Carl Anton Bretschneider and Hermann Hankel that Pythagoras may have known this proof. Heath himself favors a different proposal for a Pythagorean proof, but acknowledges from the outset of his discussion «that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him.»[3] Recent scholarship has cast increasing doubt on any sort of role for Pythagoras as a creator of mathematics, although debate about this continues.[4]
Algebraic proofs
The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram.[5] This results in a larger square, with side a + b and area (a + b)2. The four triangles and the square side c must have the same area as the larger square,
giving
A similar proof uses four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram.[6] The triangles are similar with area 
But this is a square with side c and area c2, so
Other proofs of the theorem
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.[7]
Proof using similar triangles
Proof using similar triangles
This proof is based on the proportionality of the sides of three similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar triangles is the same regardless of the size of the triangles.
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. Draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle, ACH, is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the triangle postulate: The sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides:
The first result equates the cosines of the angles θ, whereas the second result equates their sines.
These ratios can be written as
Summing these two equalities results in
which, after simplification, demonstrates the Pythagorean theorem:
The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the Elements, and that the theory of proportions needed further development at that time.[8][9]
Euclid’s proof
Proof in Euclid’s Elements
In outline, here is how the proof in Euclid’s Elements proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details follow.
Let A, B, C be the vertices of a right triangle, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.
For the formal proof, we require four elementary lemmata:
- If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
- The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
- The area of a rectangle is equal to the product of two adjacent sides.
- The area of a square is equal to the product of two of its sides (follows from 3).
Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.[10]
Illustration including the new lines
Showing the two congruent triangles of half the area of rectangle BDLK and square BAGF
The proof is as follows:
- Let ACB be a right-angled triangle with right angle CAB.
- On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.[11]
- From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
- Join CF and AD, to form the triangles BCF and BDA.
- Angles CAB and BAG are both right angles; therefore C, A, and G are collinear.
- Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
- Since AB is equal to FB, BD is equal to BC and angle ABD equals angle FBC, triangle ABD must be congruent to triangle FBC.
- Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
- Since C is collinear with A and G, and this line is parallel to FB, then square BAGF must be twice in area to triangle FBC.
- Therefore, rectangle BDLK must have the same area as square BAGF = AB2.
- By applying steps 3 to 10 to the other side of the figure, it can be similarly shown that rectangle CKLE must have the same area as square ACIH = AC2.
- Adding these two results, AB2 + AC2 = BD × BK + KL × KC
- Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Therefore, AB2 + AC2 = BC2, since CBDE is a square.
This proof, which appears in Euclid’s Elements as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares.[12][13]
This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.[9][14]
Proofs by dissection and rearrangement
Another by rearrangement is given by the middle animation. A large square is formed with area c2, from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a2 and b2, which must have the same area as the initial large square.[15]
Diagram of the two algebraic proofs
The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.[16]
|
Animation showing proof by rearrangement of four identical right triangles |
Animation showing another proof by rearrangement |
Proof using an elaborate rearrangement |
Einstein’s proof by dissection without rearrangement
Right triangle on the hypotenuse dissected into two similar right triangles on the legs, according to Einstein’s proof
Albert Einstein gave a proof by dissection in which the pieces do not need to be moved.[17] Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two similar shapes that each include one of two legs instead of the hypotenuse (see Similar figures on the three sides). In Einstein’s proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well.
Proof by area-preserving shearing
Visual proof of the Pythagorean theorem by area-preserving shearing.
As shown in the accompanying animation, area-preserving shear mappings and translations can transform the squares on the sides adjacent to the right-angle onto the square on the hypotenuse, together covering it exactly.[18] Each shear leaves the base and height unchanged, thus leaving the area unchanged too. The translations also leave the area unchanged, as they do not alter the shapes at all. Each square is first sheared into a parallelogram, and then into a rectangle which can be translated onto one section of the square on the hypotenuse.
Algebraic proofs
A related proof was published by future U.S. President James A. Garfield (then a U.S. Representative) (see diagram).[19][20][21] Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is
The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of 
Proof using differentials
One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.[22][23][24]
The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.
Diagram for differential proof
If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore, the ratios of their sides must be the same, that is:
This can be rewritten as 
giving
The constant can be deduced from x = 0, y = a to give the equation
This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.
Converse
The converse of the theorem is also true:[25]
Given a triangle with sides of length a, b, and c, if a2 + b2 = c2, then the angle between sides a and b is a right angle.
For any three positive real numbers a, b, and c such that a2 + b2 = c2, there exists a triangle with sides a, b and c as a consequence of the converse of the triangle inequality.
This converse appears in Euclid’s Elements (Book I, Proposition 48): «If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right.»[26]
It can be proven using the law of cosines or as follows:
Let ABC be a triangle with side lengths a, b, and c, with a2 + b2 = c2. Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length c = √a2 + b2, the same as the hypotenuse of the first triangle. Since both triangles’ sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.
The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proven without assuming the Pythagorean theorem.[27][28]
A corollary of the Pythagorean theorem’s converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:[29]
- If a2 + b2 = c2, then the triangle is right.
- If a2 + b2 > c2, then the triangle is acute.
- If a2 + b2 < c2, then the triangle is obtuse.
Edsger W. Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language:
- sgn(α + β − γ) = sgn(a2 + b2 − c2),
where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.[30]
Consequences and uses of the theorem
Pythagorean triples
A Pythagorean triple has three positive integers a, b, and c, such that a2 + b2 = c2. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.[1] Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).
A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).
The following is a list of primitive Pythagorean triples with values less than 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Inverse Pythagorean theorem
Given a right triangle with sides 


while the inverse Pythagorean theorem relates the two legs 

The equation can be transformed to,
where 



using the smallest Pythagorean triple 
where the denominators are squares and also for a heptagonal triangle whose sides 
Incommensurable lengths
The spiral of Theodorus: A construction for line segments with lengths whose ratios are the square root of a positive integer
One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras’ theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.
The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.[32] Each triangle has a side (labeled «1») that is the chosen unit for measurement. In each right triangle, Pythagoras’ theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.
Incommensurable lengths conflicted with the Pythagorean school’s concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.[33] According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.[34][35]
Complex numbers
The absolute value of a complex number z is the distance r from z to the origin
For any complex number
the absolute value or modulus is given by
So the three quantities, r, x and y are related by the Pythagorean equation,
Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.
This can be generalised to find the distance between two points, z1 and z2 say. The required distance is given by
so again they are related by a version of the Pythagorean equation,
Euclidean distance
The distance formula in Cartesian coordinates is derived from the Pythagorean theorem.[36] If (x1, y1) and (x2, y2) are points in the plane, then the distance between them, also called the Euclidean distance, is given by
More generally, in Euclidean n-space, the Euclidean distance between two points, 

If instead of Euclidean distance, the square of this value (the squared Euclidean distance, or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates:
The squared form is a smooth, convex function of both points, and is widely used in optimization theory and statistics, forming the basis of least squares.
Euclidean distance in other coordinate systems
If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras’ theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:
Then two points with locations (r1, θ1) and (r2, θ2) are separated by a distance s:
Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:
using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem.[37] From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras’ theorem is regained: 
Pythagorean trigonometric identity
Similar right triangles showing sine and cosine of angle θ
In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:
From that it follows:
where the last step applies Pythagoras’ theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.[38] In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.
Relation to the cross product
The area of a parallelogram as a cross product; vectors a and b identify a plane and a × b is normal to this plane.
The Pythagorean theorem relates the cross product and dot product in a similar way:[39]
This can be seen from the definitions of the cross product and dot product, as
with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.
This can also be used to define the cross product. By rearranging the following equation is obtained
This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.[40][41]
Generalizations
Similar figures on the three sides
The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any similar figures. This was known by Hippocrates of Chios in the 5th century BC,[42] and was included by Euclid in his Elements:[43]
If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.
This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c).[44] While Euclid’s proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure’s boundary being the side of the original triangle).[44]
The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:
But, by the Pythagorean theorem, a2 + b2 = c2, so A + B = C.
Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a2 + b2 = c2. (See also Einstein’s proof by dissection without rearrangement)
|
Generalization for similar triangles, |
Pythagoras’ theorem using similar right triangles |
Generalization for regular pentagons |
Law of cosines
The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:[45]
where 


When 


Arbitrary triangle
Generalization of Pythagoras’ theorem by Tâbit ibn Qorra.[46] Lower panel: reflection of triangle CAD (top) to form triangle DAC, similar to triangle ABC (top).
At any selected angle of a general triangle of sides a, b, c, inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled c. Inscribing the isosceles triangle forms triangle CAD with angle θ opposite side b and with side r along c. A second triangle is formed with angle θ opposite side a and a side with length s along c, as shown in the figure. Thābit ibn Qurra stated that the sides of the three triangles were related as:[47][48]
As the angle θ approaches π/2, the base of the isosceles triangle narrows, and lengths r and s overlap less and less. When θ = π/2, ADB becomes a right triangle, r + s = c, and the original Pythagorean theorem is regained.
One proof observes that triangle ABC has the same angles as triangle CAD, but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the triangle postulate.) Consequently, ABC is similar to the reflection of CAD, the triangle DAC in the lower panel. Taking the ratio of sides opposite and adjacent to θ,
Likewise, for the reflection of the other triangle,
Clearing fractions and adding these two relations:
the required result.
The theorem remains valid if the angle 
General triangles using parallelograms
Generalization for arbitrary triangles,
green area = blue area
Construction for proof of parallelogram generalization
Pappus’s area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras’ theorem, and was considered a generalization by Pappus of Alexandria in 4 AD[49][50]
The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.
Solid geometry
Pythagoras’ theorem in three dimensions relates the diagonal AD to the three sides.
A tetrahedron with outward facing right-angle corner
In terms of solid geometry, Pythagoras’ theorem can be applied to three dimensions as follows. Consider a rectangular solid as shown in the figure. The length of diagonal BD is found from Pythagoras’ theorem as:
where these three sides form a right triangle. Using horizontal diagonal BD and the vertical edge AB, the length of diagonal AD then is found by a second application of Pythagoras’ theorem as:
or, doing it all in one step:
This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {vk} (the three mutually perpendicular sides):
This one-step formulation may be viewed as a generalization of Pythagoras’ theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras’ theorem to a succession of right triangles in a sequence of orthogonal planes.
A substantial generalization of the Pythagorean theorem to three dimensions is de Gua’s theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the «n-dimensional Pythagorean theorem»:[51]
Let
be orthogonal vectors in Rn. Consider the n-dimensional simplex S with vertices
. (Think of the (n − 1)-dimensional simplex with vertices
not including the origin as the «hypotenuse» of S and the remaining (n − 1)-dimensional faces of S as its «legs».) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.
This statement is illustrated in three dimensions by the tetrahedron in the figure. The «hypotenuse» is the base of the tetrahedron at the back of the figure, and the «legs» are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the «legs» increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras’ theorem applies. In a different wording:[52]
Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.
Inner product spaces
Vectors involved in the parallelogram law
The Pythagorean theorem can be generalized to inner product spaces,[53] which are generalizations of the familiar 2-dimensional and 3-dimensional Euclidean spaces. For example, a function may be considered as a vector with infinitely many components in an inner product space, as in functional analysis.[54]
In an inner product space, the concept of perpendicularity is replaced by the concept of orthogonality: two vectors v and w are orthogonal if their inner product 
The concept of length is replaced by the concept of the norm ||v|| of a vector v, defined as:[56]
In an inner-product space, the Pythagorean theorem states that for any two orthogonal vectors v and w we have
Here the vectors v and w are akin to the sides of a right triangle with hypotenuse given by the vector sum v + w. This form of the Pythagorean theorem is a consequence of the properties of the inner product:
where 
A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the parallelogram law :[56]
which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is ipso facto a norm corresponding to an inner product.[56]
The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If v1, v2, …, vn are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on solid geometry) results in the equation[57]
Sets of m-dimensional objects in n-dimensional space
Another generalization of the Pythagorean theorem applies to Lebesgue-measurable sets of objects in any number of dimensions. Specifically, the square of the measure of an m-dimensional set of objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space is equal to the sum of the squares of the measures of the orthogonal projections of the object(s) onto all m-dimensional coordinate subspaces.[58]
In mathematical terms:
where:
Non-Euclidean geometry
The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem implies, and is implied by, Euclid’s Parallel (Fifth) Postulate.[59][60] Thus, right triangles in a non-Euclidean geometry[61]
do not satisfy the Pythagorean theorem. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because

Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.
However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A+B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.[62]
Spherical geometry
For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, c, the relation between the sides takes the form:[63]
This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:
By expressing the Maclaurin series for the cosine function as an asymptotic expansion with the remainder term in big O notation,
it can be shown that as the radius R approaches infinity and the arguments a/R, b/R, and c/R tend to zero, the spherical relation between the sides of a right triangle approaches the Euclidean form of the Pythagorean theorem. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields
The constants a4, b4, and c4 have been absorbed into the big O remainder terms since they are independent of the radius R. This asymptotic relationship can be further simplified by multiplying out the bracketed quantities, cancelling the ones, multiplying through by −2, and collecting all the error terms together:
After multiplying through by R2, the Euclidean Pythagorean relationship c2 = a2 + b2 is recovered in the limit as the radius R approaches infinity (since the remainder term tends to zero):
For small right triangles (a, b << R), the cosines can be eliminated to avoid loss of significance, giving
Hyperbolic geometry
In a hyperbolic space with uniform Gaussian curvature −1/R2, for a right triangle with legs a, b, and hypotenuse c, the relation between the sides takes the form:[64]
where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:[65]
with γ the angle at the vertex opposite the side c.
By using the Maclaurin series for the hyperbolic cosine, cosh x ≈ 1 + x2/2, it can be shown that as a hyperbolic triangle becomes very small (that is, as a, b, and c all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras’ theorem.
For small right triangles (a, b << R), the hyperbolic cosines can be eliminated to avoid loss of significance, giving
Very small triangles
For any uniform curvature K (positive, zero, or negative), in very small right triangles (|K|a2, |K|b2 << 1) with hypotenuse c, it can be shown that
Differential geometry
The Pythagorean theorem applies to infinitesimal triangles seen in differential geometry. In three dimensional space, the distance between two infinitesimally separated points satisfies
with ds the element of distance and (dx, dy, dz) the components of the vector separating the two points. Such a space is called a Euclidean space. However, in Riemannian geometry, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:[66]
which is called the metric tensor. (Sometimes, by abuse of language, the same term is applied to the set of coefficients gij.) It may be a function of position, and often describes curved space. A simple example is Euclidean (flat) space expressed in curvilinear coordinates. For example, in polar coordinates:
History
There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras was born.[68][69][70][71] The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system.
Written between 2000 and 1786 BC, the Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. The Mesopotamian tablet Plimpton 322, written between 1790 and 1750 BC during the reign of King Hammurabi the Great, contains many entries closely related to Pythagorean triples.
In India, the Baudhayana Shulba Sutra, the dates of which are given variously as between the 8th and 5th century BC,[72] contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the isosceles right triangle and in the general case, as does the Apastamba Shulba Sutra (c. 600 BC).[a]
Byzantine Neoplatonic philosopher and mathematician Proclus, writing in the fifth century AD, states two arithmetic rules, «one of them attributed to Plato, the other to Pythagoras»,[74] for generating special Pythagorean triples. The rule attributed to Pythagoras (c. 570 – c. 495 BC) starts from an odd number and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to Thomas L. Heath (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived.[75] However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.[76][77] Classicist Kurt von Fritz wrote, «Whether this formula is rightly attributed to Pythagoras personally, but one can safely assume that it belongs to the very oldest period of Pythagorean mathematics.»[35] Around 300 BC, in Euclid’s Elements, the oldest extant axiomatic proof of the theorem is presented.[78]
With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the Chinese text Zhoubi Suanjing (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the «Gougu theorem» (勾股定理).[79][80] During the Han Dynasty (202 BC to 220 AD), Pythagorean triples appear in The Nine Chapters on the Mathematical Art,[81] together with a mention of right triangles.[82] Some believe the theorem arose first in China,[83] where it is alternatively known as the «Shang Gao theorem» (商高定理),[84] named after the Duke of Zhou’s astronomer and mathematician, whose reasoning composed most of what was in the Zhoubi Suanjing.[85]
See also
- Addition in quadrature
- At Dulcarnon
- British flag theorem
- Fermat’s Last Theorem
- Inverse Pythagorean theorem
- Kepler triangle
- Linear algebra
- List of triangle topics
- Lp space
- Nonhypotenuse number
- Parallelogram law
- Parseval’s identity
- Ptolemy’s theorem
- Pythagorean expectation
- Pythagorean tiling
- Rational trigonometry in Pythagoras’ theorem
- Thales theorem
Notes and references
Notes
- ^ Van der Waerden believed that this material «was certainly based on earlier traditions». Carl Boyer states that the Pythagorean theorem in the Śulba-sũtram may have been influenced by ancient Mesopotamian math, but there is no conclusive evidence in favor or opposition of this possibility.[73]
References
- ^ a b Judith D. Sally; Paul Sally (2007). «Chapter 3: Pythagorean triples». Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 978-0-8218-4403-8.
- ^ Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ^ Euclid (1956), pp. 351–352
- ^ Huffman, Carl (23 February 2005). «Pythagoras». In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition)., «It should now be clear that decisions about sources are crucial in addressing the question of whether Pythagoras was a mathematician and scientist. The view of Pythagoras’s cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus.»
- ^ Alexander Bogomolny. «Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4». Cut the Knot. Retrieved 4 November 2010.
- ^
Alexander Bogomolny. «Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3». Cut the Knot. Retrieved 4 November 2010. - ^ (Loomis 1968)
- ^ (Maor 2007, p. 39)
- ^ a b
Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. p. 12. ISBN 0-7624-1922-9.This proof first appeared after a computer program was set to check Euclidean proofs.
- ^ See for example Pythagorean theorem by shear mapping Archived 2016-10-14 at the Wayback Machine, Saint Louis University website Java applet
- ^
Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. p. 435. ISBN 0-393-04002-X.
- ^ Heiberg, J.L. «Euclid’s Elements of Geometry» (PDF). pp. 46–47.
- ^ «Euclid’s Elements, Book I, Proposition 47».
web page version using Java applets from Euclid’s Elements by Prof. David E. Joyce, Clark University
- ^ The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007, p. 25)
- ^ Alexander Bogomolny. «Pythagorean theorem, proof number 10». Cut the Knot. Retrieved 27 February 2010.
- ^ (Loomis 1968, p. 113, Geometric proof 22 and Figure 123)
- ^ Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. pp. 3–4. ISBN 978-0486134789.
- ^ Polster, Burkard (2004). Q.E.D.: Beauty in Mathematical Proof. Walker Publishing Company. p. 49.
- ^
Published in a weekly mathematics column: James A Garfield (1876). «Pons Asinorum». The New England Journal of Education. 3 (14): 161. as noted in William Dunham (1997). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. p. 96. ISBN 0-471-17661-3. and in A calendar of mathematical dates: April 1, 1876 Archived July 14, 2010, at the Wayback Machine by V. Frederick Rickey - ^ Lantz, David. «Garfield’s proof of the Pythagorean Theorem». Math.Colgate.edu. Archived from the original on 2013-08-28. Retrieved 2018-01-14.
- ^ Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: pp. 106-107.
- ^
Mike Staring (1996). «The Pythagorean proposition: A proof by means of calculus». Mathematics Magazine. Mathematical Association of America. 69 (1): 45–46. doi:10.2307/2691395. JSTOR 2691395. - ^
Bogomolny, Alexander. «Pythagorean Theorem». Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Archived from the original on 2010-07-06. Retrieved 2010-05-09. - ^
Bruce C. Berndt (1988). «Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?». The Mathematical Intelligencer. 10 (3): 24–31. doi:10.1007/BF03026638. S2CID 123311054. - ^
Judith D. Sally; Paul J. Sally Jr. (2007-12-21). «Theorem 2.4 (Converse of the Pythagorean theorem).». Roots to Research. American Mathematical Society. pp. 54–55. ISBN 978-0-8218-4403-8. - ^
Euclid’s Elements, Book I, Proposition 48 From D.E. Joyce’s web page at Clark University - ^ Casey, Stephen, «The converse of the theorem of Pythagoras», Mathematical Gazette 92, July 2008, 309–313.
- ^ Mitchell, Douglas W., «Feedback on 92.47», Mathematical Gazette 93, March 2009, 156.
- ^
Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). «Theorem 1 and Theorem 2». Plane trigonometry and applications. Allyn and Bacon. p. 85. - ^ Dijkstra, Edsger W. (September 7, 1986). «On the theorem of Pythagoras». EWD975. E. W. Dijkstra Archive.
- ^ Alexander Bogomolny, Pythagorean Theorem for the Reciprocals,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- ^ Law, Henry (1853). «Corollary 5 of Proposition XLVII (Pythagoras’s Theorem)». The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. p. 49.
- ^
Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. p. 13. ISBN 0-674-92096-1.
- ^
(Heath 1921, Vol I, pp. 65); Hippasus was on a voyage at the time, and his fellows cast him overboard. See James R. Choike (1980). «The pentagram and the discovery of an irrational number». The College Mathematics Journal. 11: 312–316.
- ^ a b
A careful discussion of Hippasus’s contributions is found in
Kurt Von Fritz (Apr 1945). «The Discovery of Incommensurability by Hippasus of Metapontum». Annals of Mathematics. Second Series. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021. - ^ Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). «Euclidean distance». Mastering algorithms with Perl. O’Reilly Media, Inc. p. 426. ISBN 1-56592-398-7.
- ^ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 978-1-103-07998-8., Exercises, page 116
- ^
Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron’s Educational Series. p. 296. ISBN 0-7641-2892-2. - ^
WS Massey (Dec 1983). «Cross products of vectors in higher-dimensional Euclidean spaces» (PDF). The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Archived from the original (PDF) on 2021-02-26. - ^ Pertti Lounesto (2001). «§7.4 Cross product of two vectors». Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 96. ISBN 0-521-00551-5.
- ^
Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover Publications. p. 24. ISBN 0-486-67002-3. - ^ Heath, T. L., A History of Greek Mathematics, Oxford University Press, 1921; reprinted by Dover, 1981.
- ^ Euclid’s Elements: Book VI, Proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.»
- ^ a b Putz, John F. and Sipka, Timothy A. «On generalizing the Pythagorean theorem», The College Mathematics Journal 34 (4), September 2003, pp. 291–295.
- ^
Lawrence S. Leff (2005-05-01). cited work. Barron’s Educational Series. p. 326. ISBN 0-7641-2892-2.
- ^
Howard Whitley Eves (1983). «§4.8:…generalization of Pythagorean theorem». Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0-88385-310-8.
- ^
Aydin Sayili (Mar 1960). «Thâbit ibn Qurra’s Generalization of the Pythagorean Theorem». Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603. S2CID 119868978.
- ^
Judith D. Sally; Paul Sally (2007-12-21). «Exercise 2.10 (ii)». Roots to Research: A Vertical Development of Mathematical Problems. p. 62. ISBN 978-0-8218-4403-8.
- ^ For the details of such a construction, see Jennings, George (1997). «Figure 1.32: The generalized Pythagorean theorem». Modern geometry with applications: with 150 figures (3rd ed.). Springer. p. 23. ISBN 0-387-94222-X.
- ^ Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 77–78 (excerpt, p. 77, at Google Books)
- ^
Rajendra Bhatia (1997). Matrix analysis. Springer. p. 21. ISBN 0-387-94846-5. - ^
For an extended discussion of this generalization, see, for example, Willie W. Wong Archived 2009-12-29 at the Wayback Machine 2002, A generalized n-dimensional Pythagorean theorem. - ^
Ferdinand van der Heijden; Dick de Ridder (2004). Classification, parameter estimation, and state estimation. Wiley. p. 357. ISBN 0-470-09013-8.
- ^
Qun Lin; Jiafu Lin (2006). Finite element methods: accuracy and improvement. Elsevier. p. 23. ISBN 7-03-016656-6.
- ^
Howard Anton; Chris Rorres (2010). Elementary Linear Algebra: Applications Version (10th ed.). Wiley. p. 336. ISBN 978-0-470-43205-1.
- ^ a b c
Karen Saxe (2002). «Theorem 1.2». Beginning functional analysis. Springer. p. 7. ISBN 0-387-95224-1.
- ^ Douglas, Ronald G. (1998). Banach Algebra Techniques in Operator Theory (2nd ed.). New York, New York: Springer-Verlag New York, Inc. pp. 60–61. ISBN 978-0-387-98377-6.
- ^
Donald R Conant & William A Beyer (Mar 1974). «Generalized Pythagorean Theorem». The American Mathematical Monthly. Mathematical Association of America. 81 (3): 262–265. doi:10.2307/2319528. JSTOR 2319528. - ^
Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). p. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ^
Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 0-521-85959-X.
We could include…the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ^
Stephen W. Hawking (2005). cited work. p. 4. ISBN 0-7624-1922-9.
- ^
Victor Pambuccian (December 2010). «Maria Teresa Calapso’s Hyperbolic Pythagorean Theorem». The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ^
Barrett O’Neill (2006). «Exercise 4». Elementary differential geometry (2nd ed.). Academic Press. p. 441. ISBN 0-12-088735-5.
- ^
Saul Stahl (1993). «Theorem 8.3». The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 0-86720-298-X.
- ^
Jane Gilman (1995). «Hyperbolic triangles». Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- ^
Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0-521-65544-7. - ^ Neugebauer 1969, p. 36.
- ^ Neugebauer 1969: p. 36 «In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse.»
- ^ Friberg, Jöran (1981). «Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations». Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.: p. 306 «Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period.»
- ^ Høyrup, Jens. «Pythagorean ‘Rule’ and ‘Theorem’ – Mirror of the Relation Between Babylonian and Greek Mathematics». In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407., p. 406, «To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db2-146, somewhere between 2300 and 1825 BC.» (Db2-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)
- ^ Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.: p. 109 «Many Old Babylonian mathematical practitioners … knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste ‘algebra’ on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia.»
- ^ Kim Plofker (2009). Mathematics in India. Princeton University Press. pp. 17–18. ISBN 978-0-691-12067-6.
- ^ Carl Benjamin Boyer; Uta C. Merzbach (2011). «China and India». A history of mathematics (3rd ed.). Wiley. p. 229. ISBN 978-0470525487.
Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid’s Elements. (…)
- ^ Proclus (1970). A Commentary of the First Book of Euclid’s Elements. Translated by Morrow, Glenn R. Princeton University Press. 428.6.
- ^ (Euclid 1956, p. 351) page 351
- ^ (Heath 1921, Vol I, p. 144): «Though this is the proposition universally associated by tradition with the name of Pythagoras, no really trustworthy evidence exists that it was actually discovered by him. The comparatively late writers who attribute it to him add the story that he sacrificed an ox to celebrate his discovery.»
- ^
An extensive discussion of the historical evidence is provided in (Euclid 1956, p. 351) page=351
- ^
Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. p. 51. ISBN 0-88385-613-1.…it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
- ^
Robert P. Crease (2008). The great equations: breakthroughs in science from Pythagoras to Heisenberg. W W Norton & Co. p. 25. ISBN 978-0-393-06204-5. - ^
A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by Christopher Cullen (2007). Astronomy and Mathematics in Ancient China: The ‘Zhou Bi Suan Jing’. Cambridge University Press. pp. 139 ff. ISBN 978-0-521-03537-8.
- ^
This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. Philip D. Straffin Jr. (2004). «Liu Hui and the first golden age of Chinese mathematics». In Marlow Anderson; Victor J. Katz; Robin J. Wilson (eds.). Sherlock Holmes in Babylon: and other tales of mathematical history. Mathematical Association of America. pp. 69 ff. ISBN 0-88385-546-1. See particularly §3: Nine chapters on the mathematical art, pp. 71 ff.
- ^
Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). The nine chapters on the mathematical art: companion and commentary. Oxford University Press. p. 488. ISBN 0-19-853936-3.
- ^
In particular, Li Jimin; see Centaurus, Volume 39. Copenhagen: Munksgaard. 1997. pp. 193, 205.
- ^
Chen, Cheng-Yih (1996). «§3.3.4 Chén Zǐ’s formula and the Chóng-Chã method; Figure 40». Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. Hong Kong University Press. p. 142. ISBN 962-209-385-X.
- ^
Wen-tsün Wu (2008). «The Gougu theorem». Selected works of Wen-tsün Wu. World Scientific. p. 158. ISBN 978-981-279-107-8.
Works cited
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- Euclid (1956). The Thirteen Books of Euclid’s Elements, Translated from the Text of Heiberg, with Introduction and Commentary. Vol. 1 (Books I and II). Translated by Heath, Thomas L. (Reprint of 2nd (1925) ed.). Dover. On-line text at archive.org
- Heath, Sir Thomas (1921). «The ‘Theorem of Pythagoras’«. A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 ff. ISBN 0-486-24073-8.
- Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 978-0-7637-4366-6. This high-school geometry text covers many of the topics in this WP article.
- Loomis, Elisha Scott (1968). The Pythagorean proposition (2nd ed.). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1. For full text of 2nd edition of 1940, see Elisha Scott Loomis. «The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs» (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Retrieved 2010-05-04. Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, ISBN 0-87353-036-5.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Neugebauer, Otto (1969). The exact sciences in antiquity. Acta Historica Scientiarum Naturalium et Medicinalium. Vol. 9 (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. pp. 1–191. ISBN 0-486-22332-9. PMID 14884919.
- Robson, Eleanor and Jacqueline Stedall, eds., The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, 2009. pp. vii + 918. ISBN 978-0-19-921312-2.
- Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
Pythagorean triples Babylonian scribes van der Waerden.
External links
- Pythagorean theorem at ProofWiki
- Euclid (1997) [c. 300 BC]. David E. Joyce (ed.). Elements. Retrieved 2006-08-30. In HTML with Java-based interactive figures.
- «Pythagorean theorem». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- History topic: Pythagoras’s theorem in Babylonian mathematics
- Interactive links:
- Interactive proof in Java of the Pythagorean theorem
- Another interactive proof in Java of the Pythagorean theorem
- Pythagorean theorem with interactive animation
- Animated, non-algebraic, and user-paced Pythagorean theorem
- Pythagorean theorem water demo on YouTube
- Pythagorean theorem (more than 70 proofs from cut-the-knot)
- Weisstein, Eric W. «Pythagorean theorem». MathWorld.
Пифагор ((570)–(490) года до н. э.) – древнегреческий математик, мыслитель и философ.
Рис. (1). Пифагор.
Факты биографии Пифагора достоверно не известны. О его жизненном пути можно судить лишь по произведениям других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учёными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.
Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и учёного было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.
Рис. (2). Теорема Пифагора.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами (3), (4) и (5) является прямоугольным.
В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):
Рис. (3). Прямоугольный треугольник.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c2=a2+b2
.
Известны очень многие доказательства теоремы разными математическими методами, но одни из самых наглядных связаны с площадями.
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника
a+b
. Площадь квадрата равна
a+b2
:
Рис. (4). Первое доказательство теоремы Пифагора.
2. Если провести гипотенузы (c), очевидно, что они образовали квадрат внутри построенного квадрата.
Стороны четырёхугольника равны (c), а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают
90°
, то угол четырёхугольника также равен
90°
, потому что вместе все три угла дают
180°
.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.
Рис. (5). Второе доказательство теоремы Пифагора.
3. На двух сторонах квадрата поменяем местами отрезки (a) и (b), при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами (a) и (b), и двух площадей прямоугольников:
Рис. (6). Третье доказательство теоремы Пифагора.
4. Из этого следуют выводы:
и
c2=a2+b2
— что и является одним из доказательств теоремы Пифагора.
Обрати внимание!
Если находим длину гипотенузы (c), то выполняем сложение квадратов длин катетов (a) и (b) и определяем квадратный корень:
c2=a2+b2;c=a2+b2.
Если находим длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:
a2=c2−b2;a=c2−b2.
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
является ли треугольник со сторонами (6) см, (7) см и (9) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник не прямоугольный.
Является ли треугольник со сторонами (5) см, (12) см и (13) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник прямоугольный.
Чтобы не тратить много времени на решение, полезно запомнить наиболее часто используемые числа Пифагора:
катет, катет, гипотенуза
(3), (4), (5);
(6), (8), (10);
(12), (16), (20);
(5), (12), (13).
Посмотри ещё одно своеобразное доказательство теоремы Пифагора:
Рис. (7). Четвёртое доказательство теоремы Пифагора.
Источники:
Рис. 2. Теорема Пифагора. Указание авторства не требуется, 2021-06-05, Наука/Технологии, бесплатно для коммерческого использования, https://clck.ru/VK55r.
Рис. 4, 5, 6. Доказательства теоремы Пифагора, © ЯКласс.
Рис. 7. Четвёртое доказательство теоремы Пифагора, http://linguaggio-macchina.blogspot.com
Содержание:
- Формула теоремы Пифагора
- Доказательство теоремы Пифагора
- Геометрическая формулировка теоремы Пифагора
- Примеры решения задач
- Историческая справка
Формула теоремы Пифагора
Теорема
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):
Доказательство теоремы Пифагора
Пусть треугольник $A B C$ — прямоугольный треугольник с
прямым углом $C$ (рис. 2).
Проведём высоту из вершины $C$ на гипотенузу $A B$, основание высоты обозначим как $H$ .
Прямоугольный треугольник $A C H$ подобен треугольнику $A B C$ по двум углам ( $angle A C B=angle C H A=90^{circ}$,
$angle A$ — общий). Аналогично, треугольник $C B H$ подобен $A B C$ .
Введя обозначения
$$B C=a, A C=b, A B=c$$
из подобия треугольников получаем, что
$$frac{a}{c}=frac{H B}{a}, frac{b}{c}=frac{A H}{b}$$
Отсюда имеем, что
$$a^{2}=c cdot H B, b^{2}=c cdot A H$$
Сложив полученные равенства, получаем
$$a^{2}+b^{2}=c cdot H B+c cdot A H$$
$$a^{2}+b^{2}=c cdot(H B+A H)$$
$$a^{2}+b^{2}=c cdot A B$$
$$a^{2}+b^{2}=c cdot c$$
$$a^{2}+b^{2}=c^{2}$$
Что и требовалось доказать.
Геометрическая формулировка теоремы Пифагора
Теорема
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей
квадратов, построенных на катетах (рис. 2):
Примеры решения задач
Пример
Задание. Задан прямоугольный треугольник $A B C$, катеты которого равны 6 см и 8 см.
Найти гипотенузу этого треугольника.
Решение. Согласно условию катеты $a=6$ см, $b=8$ см. Тогда, согласно теореме
Пифагора, квадрат гипотенузы
$c^{2}=a^{2}+b^{2}=6^{2}+8^{2}=36+64=100$
Отсюда получаем, что искомая гипотенуза
$c=sqrt{100}=10$ (см)
Ответ. 10 см

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти
площадь прямоугольного треугольника, если известно, что один
из его катетов на 5 см больше другого, а гипотенуза равна 25 см.
Решение. Пусть
$x$ см — длина меньшего катета, тогда $(x+5)$ см — длина большего. Тогда согласно теореме Пифагора имеем:
$$x^{2}+(x+5)^{2}=25^{2}$$
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:
$x^{2}+5 x-300=0$
Согласно теореме Виета, получаем, что
$x_{1}=15$ (см) , $x_{2}=-20$ (см)
Значение $x_{2}$ не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший — 20 см.
Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть
$$S=frac{15 cdot 20}{2}=15 cdot 10=150left(mathrm{см}^{2}right)$$
Ответ. $S=150left(mathrm{см}^{2}right)$
Историческая справка
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая
соотношение между сторонами прямоугольного треугольника.
В древнекитайской книге «Чжоу би суань цзин» говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий
историк математики Мориц Кантор (1829 — 1920) считает, что равенство $3^{2}+4^{2}=5^{2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является
единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным
значением теоремы для геометрии.
Остались вопросы?
Здесь вы найдете ответы.
Как выглядит формула, отражающая смысл теоремы Пифагора?
Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с
прямыми углами, возведенное в квадратную степень, является величиной,
равной сумме его катетов (а и b), каждый из которых также возведен в
квадрат. Наглядно и с применением условных обозначений это выглядит так:
a² + b² = c².
О чем гласит теорема Пифагора?
В теореме Пифагора говорится о том, что в треугольнике с прямыми углами
сумма длин катетов, каждая из которых возведена в квадрат, равна длине его
гипотенузы, также возведенной в квадратную степень.
При этом под гипотенузой понимается сторона, которая расположена
противоположно прямому углу. Катетом считается одна из сторон, участвующих
в образовании прямого угла.
Треугольник имеет прямой угол. Как доказать теорему Пифагора, которая
гласит, что сумма квадратов катетов прямоугольного труегольника равна длине
его гипотенузы, которая возведена в квадрат?
Основание прямоугольного треугольника обозначим как Н. Из его вершины С
проведем высоту на гипотенузу АВ. Получившийся в результате этого
треугольник АСН является подобным треугольнику АВС по двум углам, равным
90º (∠ACB =∠CHA).
В обоих треугольниках есть один общий угол — ∠A.
Подобными также являются треугольные фигуры АВС и СВН. Основанием их
подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют
общий угол, которым является ∠B.
Для продолжения доказательства теоремы Пифагора следует ввести
дополнительные обозначения: BC = a, AC = b, AB = c.
На основании полученной ранее информации о подобии треугольников можно
утверждать, что:
a/с = HB/a, b/с = AH/b.
Полученное равенство также позволяет сделать следующий вывод:
a2 = c * HB, b2 = c * AH.
На следующем этапе произведем сложение полученных ранее равенств:
a2 + b2 = c * HB + c * AH
Вынесем за скобки общий множитель во второй части равенства:
a2 + b2 = c * (HB + AH)
Теперь можно сократить Н в левой части равенства, в результате получим:
a2 + b2 = c * AB
В приведенных выше обозначениях указано, что АВ = с. Это позволяет
переписать равенство следующим образом:
a2 + b2 = c * c, или a2 + b2 = c2
Таким образом, теорема Пифагора доказана.
Длина катетов прямоугольного треугольника равна 5 см. Как вычислить длину
его гипотенузы?
Согласно теореме Пифагора, длина гипотенузы прямоугольного треугольника,
которая возведена в квадрат, равна сумме, полученной в результате сложения
квадратов длин его катетов. Из этого следует, что:
х² = 5^2 + 5^2
Извлечем квадрат из обеих частей равенства, в итоге получим:
x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2
Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен
5 см, составляет 5√2, что равно примерно 7,07 см.
Применима ли теорема Пифагора к любому треугольнику?
Теорема Пифагора не может быть применима к треугольнику с тупыми или
острыми углами. Она выполняется только в случае прямоугольного
треугольника.
Для треугольника с углом 90º справедливо утверждение о том, что длина его
гипотенузы, возведенная во вторую степень, равна сумме длин его катетов,
взятых в квадрат.
Дан прямоугольный треугольник, длина гипотенузы которого равна 7 см, а
одного катета – 6 см. Как вычислить длину второго катета, используя теорему
Пифагора?
В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного
треугольника, возведенных во вторую степень, равна квадрату длины его
гипотенузы. В случае с треугольником, некоторые параметры которого
приведены в задании, это утверждение выглядит следующим образом:
х² = 7²-6² = 49-36 = 13.
Для того чтобы найти значение х, нужно извлечь квадратный корень из числа
13:
х =√13.
Ответ: Длина второго катета прямоугольного треугольника равна корню
квадратному из 13.
Длина одного из стоящих рядом домов равна 24 м, высота второго из них
составляет 16 м. Как вычислить расстояние между крышами обоих домов, зная,
что квадрат гипотенузы равен сумме квадратов катетов?
Для решения поставленной задачи следует воспользоваться теоремой Пифагора,
которая говорит о том, что сумма длин катетов треугольника с прямым углом,
возведенных в квадрат, равна длине его гипотенузы, также возведенной во
вторую степень:
a² + b² = c².
Теорема Пифагора может быть применима в данном случае по причине того, что
образованная между двумя домами конструкция является прямоугольным
треугольником. Зная о том, что сумма квадратов катетов в прямоугольном
треугольнике равна длине его катета, возведенной в квадрат, можно
вычислить длину неизвестного катета:
24 м – 16 м = 8 м.
Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это,
можно применить теорему Пифагора для вычисления длины гипотенузы:
(16*16) + (8*8) = 256 + 64 = 320 м.
Осталось только извлечь квадратный корень из 320, для того чтобы узнать
длину расстояния между крышами двух домов.
Ответ: Расстояние между крышами домов равно корню квадратному из 320.
Длина гипотенузы треугольника с прямым углом равна 13 см. Один из его
катетов равен 12 см. Как найти длину его второго катета по теореме Пифагора?
Обозначим длину неизвестного катета как х. Зная то, что по теореме
Пифагора длина гипотенузы прямоугольного треугольника, возведенная во
вторую степень, равна сумме длин его катетов, которые также возведены в
квадрат, можно выразить длину неизвестного катета следующим образом:
х² = 132 – 122 = 169 – 144 = 25
Теперь, для того чтобы узнать длину второго катета, необходимо извлечь
квадратный корень из числа 25:
х = √25 = 5
Ответ: длина второго катета прямоугольного треугольника равна 5 см.
Дан треугольник с прямым углом, к гипотенузе которого проведена медиана
длиной 6,5 м. Длина одного из катетов данного треугольника составляет 5 см.
Как вычислить длину второго катета треугольника по теореме Пифагора?
Известно, что длина медианы (m), которая проведена к гипотенузе
прямоугольного треугольника, равна ½ ее длины. Используя это, можно
высчитать длину гипотенузы прямоугольного треугольника:
с = 2*m = 2*6,5 = 13 см.
Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного
треугольника, можно вычислить, чему равен его второй катет. Для этого
можно использовать теорему Пифагора, согласно которой:
a²+b²=c²
В нашем случае:
5²+b²=13²
Выражаем из записанного выше равенства длину неизвестного катета:
b²=13²-5²= 144
Из полученного числа нужно извлечь квадратный корень, для того чтобы
узнать длину второго катета прямоугольного треугольника:
b = √144 = 12 см.
Ответ: Длина второго катета прямоугольного треугольника равна 12 см.
Как можно вычислить треугольник, для которого по теореме Пифагора,
соблюдается равенство f2=a2+ b2?
Равенство, указанное в задании, применимо к треугольнику с прямым углом,
как гласит теорема Пифагора.
Каждая из сторон треугольника может быть обозначена прописной буквой,
которая соответствует строчной букве, обозначающей угол треугольника,
расположенный противоположно этой стороне. На основании этого можно
сделать вывод о том, что искомый треугольник является прямоугольным и
имеет гипотенузу f и катеты a и b:
∆АDF c ∠F= 90°
Ответ: имеется треугольник АDF с прямым углом F.
Существует ли теорема, которая обратна теореме Пифагора, и что она гласит?
Теорема, которая является обратной теореме Пифагора, существует. Согласно
этой теореме, треугольник считается прямоугольным в том случае, если длина
его большей стороны, возведенная в квадратную степень, равна сумме длин
двух других его сторон, которые также возведены в квадратную степень.
Имеется равнобедренный треугольник, длина двух сторон которого равна 48 см,
а третьей – 51 см. Как можно высчитать площадь данного треугольника по
теореме Пифагора?
Для начала следует провести высоту (h) к основанию равнобедренного
треугольника. Данная высота, проведенная к основанию, в случае с
равнобедренным треугольником является медианой.
Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет
равна:
h = √((48 см)² — (25,5 см)²) = 10,5√15 см.
Площадь (S) треугольника рассчитывается путем деления на число, полученное
в результате умножения длины высоты на длину основания треугольника:
S = ½*10,5√15 см*51 см = 267,75√15 см².
Ответ: Площадь треугольника равна 267,75√15 см².
Каким образом можно вычислить высоту равностороннего треугольника со
стороной а по теореме Пифагора?
В равностороннем треугольнике высота (h), проведенная к его основанию,
является также его биссектрисой и медианой. Она делит равносторонний
треугольник на две части, которые являются равными треугольниками с прямым
углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный
вопрос следует применить теорему Пифагора:
h²=a²-(a/2)²=a²-(a²/4)=3a²/4
h=a√3/2.
Дан треугольник с прямым углом, длина одного из катетов которого вдвое
меньше длины его второго катета. Гипотенуза данного треугольника равна корню
квадратному из 15. Как по теореме Пифагора вычислить длину меньшего из
катетов треугольника?
Обозначим меньший из катетов как х. Тогда другой катет, длина которого в
два раза больше, будет обозначен как 2х. Если в случае с прямоугольным
треугольником, длина гипотенузы которого равна √15, применить теорему
Пифагора, то она будет выглядеть следующим образом:
(2х)²+(x)²=√15
После раскрытия скобок в уравнении получаем следующее равенство:
4х²+x²=15
Складываем слагаемые в первой части и получаем:
5x²=15
Сокращаем обе части уравнения на 5, и в итоге получается, что:
x²=3
Это значит, что:
x=√3
Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.
Известно, что длина одного из катетов прямоугольного треугольника составляет
60 см, а длина его гипотенузы и второго катета в сумме дают 180 см. Можно ли
по теореме Пифагора высчитать длину гипотенузы данного треугольника?
Если обозначить длину неизвестного катета через х, то гипотенуза будет
равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для
данного треугольника:
x²+60²=(180-x)² = x²+3600=32400-360x+x²
После сокращений получается следующее равенство:
360х=32400-3600=28800
Теперь можно найти значение х:
х=28800/360=80
Длина второго катета равна 80 см.
Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180
см, можно вычислить длину гипотенузы:
180-80=100 см.
Ответ: Длина гипотенузы равна 100 см.
Дана прямоугольная трапеция ABCD. Ее углы А и В равны по 90°. Длины боковых
сторон данной трапеции составляют 9 см и 18 см. Диагональ АС составляет 15
см. Как можно вычислить длину основания трапеции по теореме Пифагора?
АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см.
Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются
неизвестными величинами. Длину ВС можно вычислить по следующей формуле:
√15²-9²=√144=12 см.
Произведем перенос высоты:
СС1=АВ=9 см.
Тогда получаем, что:
C1D=√18²-9²=9√3
BC=AC1=12
AD=12+9√3 см.
Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.
Доказательства теоремы Пифагора
Содержание:
- Теорема Пифагора — краткая история
- Формулировка теоремы
- Уравнение
- Доказательство через подобные треугольники
-
Другие способы доказательства теоремы
- Методом площадей
- Методом бесконечных малых
- Следствие из теоремы Пифагора
-
Применение теоремы
- Расстояние между точками
- Евклидова метрика
- Теория чисел
- Примеры решения задач
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
Теорема
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
Теорема
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
a2+b2=c2, где:
- а и b – длины двух катетов,
- с – длина гипотенузы.
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB/AB=HB/CB, AC/AB=AH/AC
Это соответствует:
CB2=ABxHB, AC2=ABxAH
Сложив между собой квадраты катетов, получаем:
AC2+CB2=ABx(HB+AH)=AB2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
- сумму площадей четырех прямоугольных треугольников;
- площадь внутреннего квадрата.
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Значит:
4ab2=2ab ⇒ c2=a2+b2, что и нужно было доказать.
Методом бесконечных малых
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
da/ca = c/a, b = const
Разделяя переменные составляется дифференциальное уравнение:
c x dc = a x da
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
c2 = a2 + const
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c2 = b2 = const
Таким образом мы определяем, что
c2 = a2 + b2
Теорема доказана!
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Определение
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
- c – гипотенуза треугольника;
- a и b – его катеты.
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
( s=sqrt{(a-с)^{2} + (b-d)^{2}}), где:
- s – необходимое расстояние;
- (a; b) и (с; d) – координаты двух точек.
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
(d(p,;q)=sqrt{sum_{i=1}^n{(p_i-q_i)}^2}), где:
- n – число измерений данного пространства;
- d (p, q) – необходимое расстояние;
- p(p1,….,pn) и q(q1,….,qn) – две точки, расстояние между которыми нужно найти.
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Определение
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
По теореме Пифагора ВС2+АС2=АВ2, значит
(АС;=;sqrt{АВ^2;-;АС^2})
Для нахождения ответа подставим в формулу исходные значения:
(АС;=;sqrt{85^2;-;36^2};=;sqrt{7225;-;1296;}={;sqrt{5929};=;77;})
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
- 46²+56²= 5252;
- 76²= 5776;
- 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
По теореме Пифагора:
АО2+BO2=AB2, значит
(АС;=;sqrt{85^2;-;36^2};=;sqrt{7225;-;1296;}={;sqrt{5929};=;77;})
Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру
Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника abc:
- Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
- Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
- Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
- Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
- Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:
(a + b) (a + b) = c² + 2ab
a² + 2ab + b² = c² + 2ab
a² + b² = c²
Что и требовалось доказать.
«Пифагоровы штаны на все стороны равны»
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
- Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
- Делим «Пифагоровы штаны» на 3 похожие фигуры:
- Все 3 треугольника подобны друг другу (A, B, C) и из-за этого «фигуры-домики» также являются подобными.
- Значит соотношение площади A и a² будет одинаковым с площадью B и b², но и с площадью C и c². Т. е.: A/a² = B/b² = C/c² = β (назовём это соотношение греческой буквой бета);
- Площадь каждого треугольника, через площадь каждого из квадратов, равна: A = βa², B = βb², C = βc²;
- Вспомним, что С = А + B, т. е. βc² = βa² + βb², это равно c² = a² + b².
Что и требовалось доказать.
Примеры
Задача 1
На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Решение:
Записать формулу
c² = a² + b²
Подставить известные значения
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Ответ: длина гипотенузы равна 5.
Задача 2
Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Решение:
Записать формулу
c² = a² + b²
Подставить известные значения
13² = 12² + b²
169 = 144 + b²
169 – 144 = b²
25 = b²
√25 = b
5 = b
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
- В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
- Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
- Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
- Любой косинус (cos) острого угла будет меньше 1.
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.






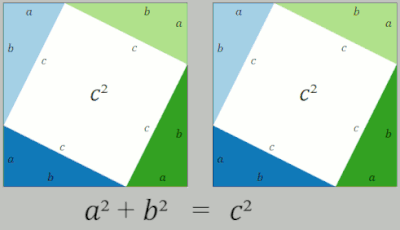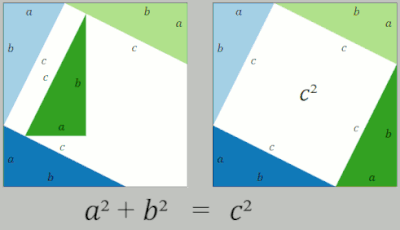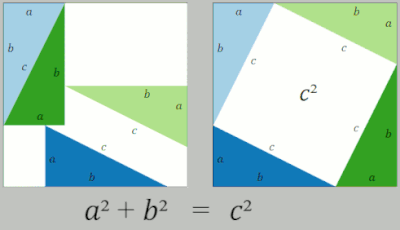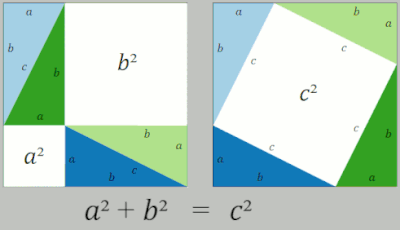











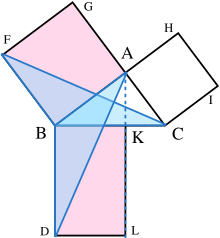




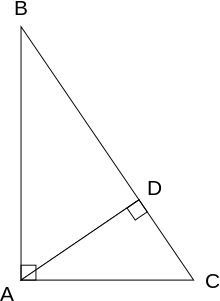


































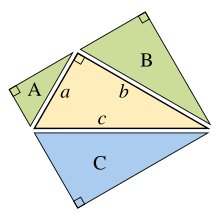
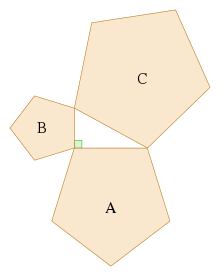







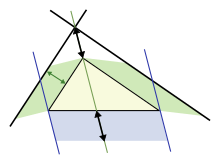

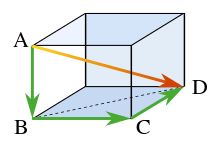











![{displaystyle {begin{aligned}left|mathbf {v} +mathbf {w} right|^{2}&=langle mathbf {v+w} , mathbf {v+w} rangle \[3mu]&=langle mathbf {v} , mathbf {v} rangle +langle mathbf {w} , mathbf {w} rangle +langle mathbf {v, w} rangle +langle mathbf {w, v} rangle \[3mu]&=left|mathbf {v} right|^{2}+left|mathbf {w} right|^{2},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c30b0575230c350ae41528af64dbe6ed55df988)







![1-{frac {1}{2}}left({frac {c}{R}}right)^{2}+Oleft({frac {1}{R^{4}}}right)=left[1-{frac {1}{2}}left({frac {a}{R}}right)^{2}+Oleft({frac {1}{R^{4}}}right)right]left[1-{frac {1}{2}}left({frac {b}{R}}right)^{2}+Oleft({frac {1}{R^{4}}}right)right]{text{ as }}Rto infty .](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab88b5e5c1da838bc94164e6cbdd8f54d6e8035)