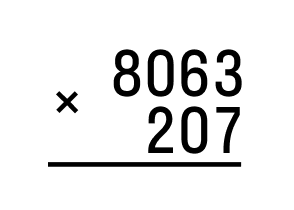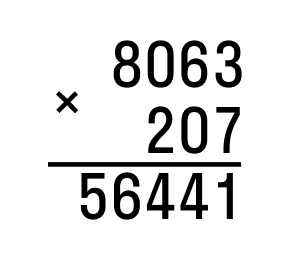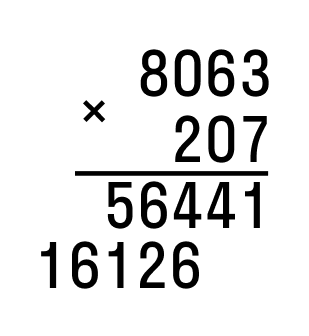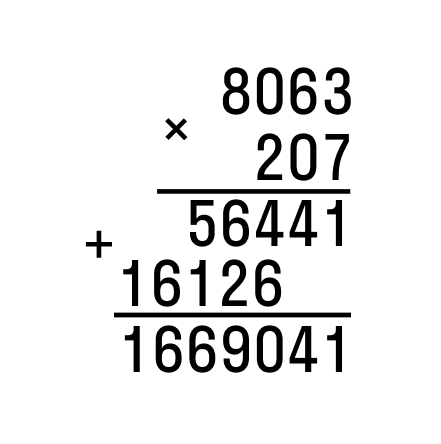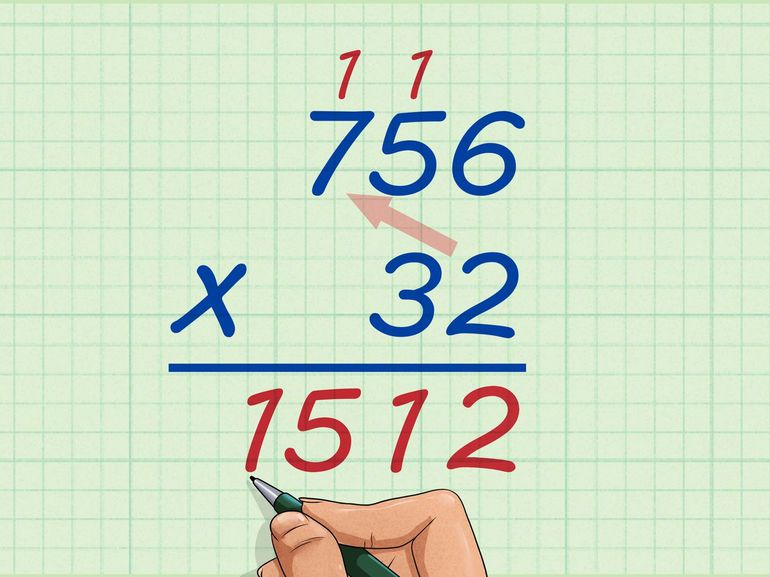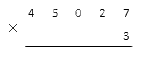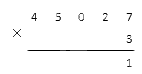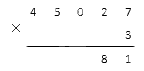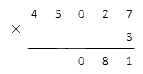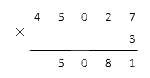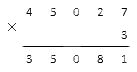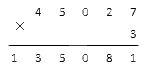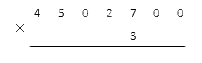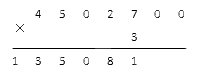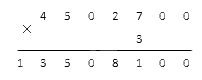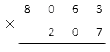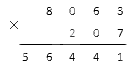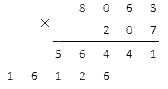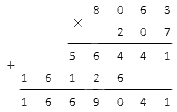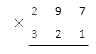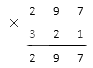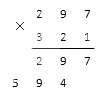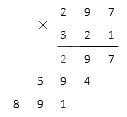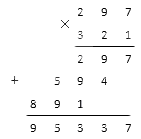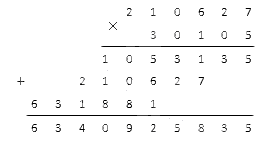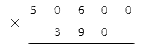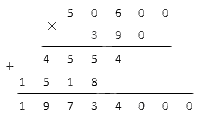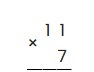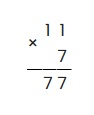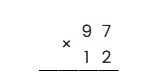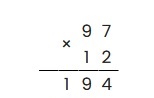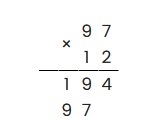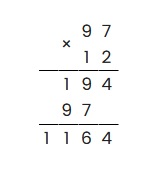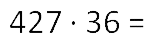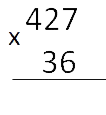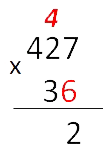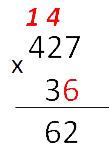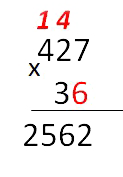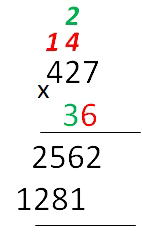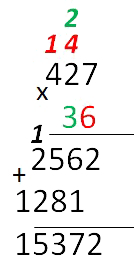Загрузить PDF
Загрузить PDF
На первый взгляд перемножить два многозначных числа весьма непросто. Но вы сможете быстро делать это, если запомните пошаговый процесс умножения.
-
1
Запишите большее число над меньшим. Например, нужно перемножить 756 и 32. Запишите 756 над 32 так, чтобы единицы располагались под единицами (2 под 6), десятки под десятками (3 под 5) и так далее.
- Сначала вы умножите 756 на 2 (из числа 32), а затем на 3 (из того же числа). Но не будем забегать вперед.
-
2
Начните с перемножения чисел, стоящих в разряде единиц. В нашем примере умножьте 2 (из числа 32) на 6 (из числа 756): 6*2 = 12. Запишите 2 в разряд единиц (в промежуточном ответе), а 1 переносите и записываете над разрядом десятков (над 5 из числа 756). В общих случаях единицы записываете в разряд единиц (в промежуточном ответе), а любые десятки переносите и записываете над разрядом десятков (второй столбец справа).
-
3
Теперь перемножьте единицы второго (нижнего) числа и десятки первого (верхнего) числа. В нашем примере перемножьте 5 и 2, что равно 10. Кроме того, к этому результату прибавьте число, написанное над 5 (перенесенное число из предыдущего шага; в нашем случае 1). Получите 11, поэтому запишите 1 в разряд десятков (в промежуточном ответе, слева от 2) и перенесите и запишите другую 1 над разрядом сотен (над 7 из числа 756).
-
4
Теперь перемножьте единицы второго (нижнего) числа и сотни первого (верхнего) числа. В нашем примере перемножьте 7 и 2. Получите 14. К этому результату прибавьте число, перенесенное из предыдущего шага (в нашем случае опять 1): 14+1=15. Так как 7 – последняя цифра первого (верхнего) числа, запишите 15 рядом с 12 (в промежуточном ответе).
-
5
Теперь переходите к умножению первого числа (756) на 3 (стоит в разряде десятков числа 32). Запишите 0 в разряд единиц (во втором промежуточном ответе, под 2 из первого промежуточного ответа). Если бы вы умножали первое число на цифру, стоящую в разряде сотен второго числа, то нужно было бы написать два нуля (и так далее).
-
6
Перемножьте десятки второго числа и единицы первого числа. В нашем примере перемножьте 6 и 3: 6*3=18. Запишите 8 во втором промежуточном ответе, а 1 перенесите и запишите над 5 (из числа 756, как в предыдущих шагах).
-
7
Перемножьте десятки второго числа и десятки первого числа. В нашем примере перемножьте 5 и 3: 5*3=15. Прибавьте к этому результату число, перенесенное из предыдущего шага: 15+1=16. Запишите 6 (во втором промежуточном ответе), а 1 перенесите и запишите над 7 (из числа 756).
-
8
Перемножьте десятки второго числа и сотни первого числа. В нашем примере перемножьте 7 и 3: 7*3=21. Прибавьте к этому результату число, перенесенное из предыдущего шага: 21+1=22. Так как 7 – последняя цифра первого числа, запишите 22 рядом с 680 (во втором промежуточном ответе).
-
9
Сложите два промежуточных ответа. Теперь нужно просто сложить 1512 и 22680. Сложите 2 и 0: 2+0=2. Запишите 2 в разряд единиц ответа.
-
10
Сложите десятки обоих промежуточных ответов. В нашем примере сложите 1 и 8: 1+8=9. Запишите 9 в разряд десятков ответа (слева от 2).
-
11
Сложите сотни обоих промежуточных ответов. В нашем примере сложите 5 и 6: 5+6=11. Запишите 1 разряд сотен ответа (слева от 9), а другую 1 перенесите (запишите ее над разрядом тысяч обоих промежуточных ответов).
-
12
Сложите тысячи обоих промежуточных ответов. В нашем примере сложите 1 и 2: 1+2=3. Прибавьте к этому результату число, перенесенное из предыдущего шага: 3+1=4. Запишите 4 в разряд тысяч ответа.
-
13
Сложите десятки тысяч обоих промежуточных ответов. В нашем примере последнюю двойку (в разряде десятков тысяч второго промежуточного ответа) не с чем складывать, поэтому просто запишите ее самой первой в ответе.
-
14
Проверьте ответ при помощи калькулятора. 756*32=24192.
Реклама
-
1
Запишите задачу. Например, решите 325 * 12 (числа друг под другом записывать не нужно).
-
2
Разложите меньшее число на десятки и единицы. Число 12 разложите на 10 и 2 (10+2=12).
-
3
Умножьте большее число на десятки меньшего числа. В нашем примере умножьте 325 на 10: 325*10 = 3250.
-
4
Умножьте большее число на единицы меньшего числа. В нашем примере умножьте 325 на 2: 325*2 = 650 (300*2 = 600, 25*2 = 50 и 600+50 = 650).
-
5
Сложите два полученных результата. В нашем примере сложите 3250 и 650. Для этого запишите 650 под 3250 и сложите эти два числа. Вы получите 3900. Раскладывая меньшее число на десятки и единицы, вы делаете некоторую часть вычислений в голове, что убыстряет процесс перемножения двух многозначных чисел.
Реклама
Советы
- Записывайте цифры в соответствующих столбцах!
- Не забывайте переносить цифры из разряда десятков (в двузначных числах), иначе ответ будет неверным.
- Сначала практикуйтесь на простых (например, двузначных) числах.
- При перемножении многозначных чисел выполните следующие действия: сначала умножьте верхнее число на единицы нижнего числа, потом добавьте нуль и умножьте на десятки, потом добавьте два нуля и умножьте на сотни, потом добавьте три нуля и умножьте на тысячи и так далее. В конце сложите все цифры.
- Всегда пишите в конце 0 при умножении на десятки (цифру, стоящую в разряде десятков второго числа). При умножении на сотни пишите два 0 и так далее. Кроме того, проверьте Ваш ответ и только потом воспользуйтесь калькулятором.
Реклама
Источники
Об этой статье
Эту страницу просматривали 35 936 раз.
Была ли эта статья полезной?
Умножение натуральных чисел в столбик – это способ, который позволит перемножить без калькулятора любые многозначные числа. Чтобы пользоваться таким методом на практике, нужно знать правила его применения. Рассмотрим подробнее умножение разных чисел в теории и на примерах.
Основные закономерности умножения столбиком
Есть ряд математических правил, которые нужно помнить, чтобы успешно пользоваться таким методом умножения:
- Во-первых, нужно знать наизусть таблицу умножения, и, не задумываясь использовать ее.
- Во-вторых, не стоит забывать правила умножения на нуль. Нуль часто встречается в двух и трехзначных числах, а значит, будет выступать в качестве одного из множителей.
- Помним, что [x times 0=0]
- Под x мы понимаем любое натуральное число.
- Прежде, чем решать примеры на умножение в столбик, стоит вспомнить правила сложения в столбик и потренироваться суммировать числа.
- Повторить понятие разряда и сравнения любых натуральных цифр.
Как записывать множители при решении примеров на умножение столбиком
Залогом правильного решения задачи будет умение правильно записывать выражение столбиком. Здесь придерживаемся следующих правил:
- В качестве первого множителя записывается цифру, которая имеет больший разряд.
- Во второй строке (под первым множителем) записывается второй множитель. Здесь важно строго соблюдать закономерность сопоставления разрядов. Это значит, что десятки пишутся под десятками, единицы под единицами, и никак иначе.
- Записав все множители друг под другом, нужно подвести горизонтальную черту, которая отделит их от ответа.
Рассмотрим на примере, как записать такое выражение.
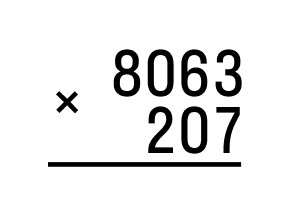
На примере мы видим, как соблюдаются разряды при умножении четырехзначной цифры на трехзначную.
Теперь, чтобы научиться умножать в столбик, потребуется разобраться, как происходит умножение и как записывается результат. Начнем с умножения многозначного множителя на однозначный.
Как происходит умножение двузначных чисел в столбик на однозначные
Если требуется решить пример на умножение многозначного натурального числа на однозначное, легко можем применить данный метод. Процесс решения сразу рассмотрим ниже.
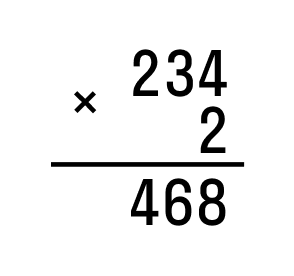
Разберем алгоритм действий:
- Записываем множители в столбик, строго соблюдая разряды. Единицы пишем под единицами, следовательно, 2 под 4.
- Перемножаем их по порядку, так же соблюдая разряд. Сначала перемножаем на 2 единицы, потом десятки, потом сотни. Полученный результат вписываем под чертой.
Здесь стоит отметить, что в образце приведены числа, при перемножении которых результат не превысил 10. В том случае, если при перемножении мы получаем двузначный ответ, то записываем только единицы. Десятки запоминаем и прибавляем к результату, который получится при перемножении следующего разряда. Если количество разрядов закончилось, а остались неучтенные десятки, они просто вписываются крайней левой цифрой.
Умножение в столбик с нулями
Если нам потребуется решить пример по математике, где один из множителей имеет на конце нули, действовать придется несколько иначе. Рассмотрим на конкретном примере.
Условие: нам нужно умножить 5400 на 7.
Первым делом нужно правильно записать выражение:
[begin{array}{r} times begin{array}{r} 5400\ 7\ end{array} \ hline begin{array}{r} end{array} end{array}]
Здесь нужно обратить внимание на то, что под нулями множитель не записывается.
Следующий этап решения примера в столбик – умножение без учета нулей.
[begin{array}{r} times begin{array}{r} 5400\ 7quad\ end{array} \ hline begin{array}{r} 378 quad end{array} end{array}]
Теперь вспоминаем, что у нас осталось два неучтенных нуля. Их просто переносим вниз за черту.
[begin{array}{r} times begin{array}{r} 5400\ 7quad\ end{array} \ hline begin{array}{r} 37800 end{array} end{array}]
В итоге получаем: 5400×7=37800
Нет времени решать самому?
Наши эксперты помогут!
Как умножать столбиком, если в примере два многозначных числа
Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения. Предположим, нам нужно умножить 8063 на 207.
Решение:
- Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
- Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
- Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
- Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат. Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
В итоге мы получили два неполных произведения. Задания на умножение столбиком содержат столько промежуточных результатов, сколько разрядов во втором множителе. У нас получилось два, так как в десятках мы имеем нуль, и его пропускаем. Если бы вместо него была любая другая натуральная цифра, мы бы записали три неполных произведения друг под другом со сдвигом влево. - Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.
Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.
Таким образом, можно записать выражение:
8063×207=1669041
Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.
Под основными терминами понимаются следующие:
- Однозначное число – это число, состоящее из одной цифры (например, 6).
- Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
- Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
- Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.
Например, число 4657.
7 – разряд единиц;
5 – разряд десятков;
6 – разряд сотен;
4 – разряд тысяч.
Определение
Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.
Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.
- Перестановка мест множителей не влияет на результат.
[x times y=y times x] - Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.
[x times y times z=(x times y) times z] - Умножение на нуль всегда дает нуль.
Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули. В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.
Пример умножения чисел столбиком
Пример
Условие: 34500×230
Первым делом нужно записать пример в столбик таким образом, чтобы натуральные числа, отличные от нуля, расположились друг под другом.
[begin{array}{r}timesbegin{array}{r}34500\230\end{array}
\hlinebegin{array}{r}end{array}end{array}]
После того, как мы записали пример в столбик, мы можем просто перемножить множители в соответствие с
правилами перемножения многозначных чисел, без учета нулей.
В ходе вычислений у нас должно получиться два неполных, или промежуточных результата.
[begin{array}{r}timesbegin{array}{r}34500\230\end{array}
\hlinebegin{array}{r}end{array}\+1035\690\hlineend{array}]
Последний этап – сложение двух промежуточных результатов и переписывание справа нулей. Нулей мы напишем столько, сколько имеют оба множителя, а именно, три.
[begin{array}{r}timesbegin{array}{r}34500\230\end{array} \hlinebegin{array}{r}end{array}\+1035\690\hline7935000end{array}]
В итоге получаем, что 34 500×230=7 935 000
Анализируя вышеперечисленный пример, можно сказать, что перемножить в столбик можно любые без исключения числа, если руководствоваться правилами математики. Умножение двузначных чисел в столбик – это школьная программа, освоив которую, примеры научится решать любой ребенок, ученик четвертого класса.
Вычислять же значения дробей и многозначных чисел в строку бывает довольно затруднительно.
удержать промежуточные результаты в голове порой просто невозможно. Как раз для таких случаев придумано умножение в столбик — этот метод значительно упрощает математические вычисления.
Необходимый минимум
Преимущество использования «столбиков» очевидно — пропадает необходимость считать в уме или всегда держать при себе калькулятор. Даже действительно длинные числа с помощью этого метода умножаются без лишних проблем. Достаточно иметь при себе:
- черновик (листок);
- ручку;
- умение складывать числа столбиком;
- хорошее знание таблицы умножения.
Если же с последним пока ещё возникают затруднения, можно положить её рядом с собой и сверять по ходу решения. Правда, при таком раскладе процесс затянется на какое-то время, а полученный результат желательно перепроверить. Ведь одна маленькая ошибка в начале или середине вычисления сделает ответ заведомо неверным.
Регулярное решение примеров столбиком тренирует внимательность и память ребёнка, учит его концентрироваться на отдельно взятой задаче. Это также удобный способ закрепить базовые математические знания.
Как умножать столбиком
Чтобы научиться решать примеры, необходимо понять и отработать базовый алгоритм.
В целом он достаточно прост:
- Записать пример в привычной форме, строкой. Выбрав из двух чисел наименьшее, подчеркнуть его карандашом — при новой записи оно будет стоять внизу, т. к. умножать на меньший множитель всегда проще. Этот пункт можно опустить, если пример уже есть перед глазами (в тетради, учебнике или на доске).
- После этого можно переходить к записи столбиком. Первым пишут больший множитель, а под ним — подчёркнутое число. Слева обязательно ставится знак умножения «х», а пример подводится чертой. Важным моментом являются разряды: единицы должны стоять строго под единицами, десятки под десятками и т. д. Исключением считаются только цифры, на конце которых располагаются нули.
- Далее идёт поэтапное умножение. Каждую из цифр первого множителя нужно умножить на крайнюю цифру второго. Делать это надо справа налево: единицы, десятки, сотни и т. д. Если получаются двухзначные числа, под чертой записывается только последняя. Остальное потребуется перенести в следующий разряд (запомнить или указать над столбиком слева) и сложить со значением, полученным при следующем умножении.
- После умножения на единицу второго множителя с остальными цифрами проводят аналогичные манипуляции. Результат каждого вычисления записывать под чертой, сдвигаясь влево на одну позицию.
- Для получения ответа найденные значения складывают.
Метод столбиков не подходит для решения примеров, содержащих корни или возведённые в степень числа.
Прежде чем приступить к вычислениям, «проблемные» цифры нужно преобразовать до целых или десятичных.
Решение базовых примеров
Для большей наглядности стоит привести примеры умножения двузначных и трёхзначных чисел.
Пример 1 — отыскать произведение чисел 58 и 23. Решение задания:
- Записать числа столбиком. Сначала нужно выполнить умножение верхнего множителя на правое крайнее число нижнего: 8х3=24. Четвёрку записать под черту в разряд единиц, а 2 «запомнить». И второе: (5х3)+2=17 — результат указать перед первым. Получится 174.
- По аналогии с предыдущей операцией нужно умножить первое число на 2: 8х2=16 и (5х2)+1=11. Вычисление даст 116, которое нужно записать под 174, отступив на 1 цифру влево.
- Конечный ответ получить путём сложения умножений: 174+1160=1334.
По такому же принципу происходит умножение трёхзначных чисел. Разве что вычисление потребует чуть больше времени, а количество промежуточных результатов увеличится.
Пример 2 — решить выражение 659х854. Пошаговое решение:
- Для удобства множители необходимо поменять местами и только потом записать столбиком как: 854х659.
- Сначала выполняется умножение на 9: 4х9=36, (5х9)+3=48 и (8х9)+4=76. Последнее число (единицы) записать в столбик, остатки последовательно перенести и суммировать. В итоге получится 7686.
- Последовательно умножить на 5: 4х5=20, (5х5)+2=27 и (8х5)+2=42. После всех манипуляций должно быть 4270.
- Умножение 854 на 6: 4х6=24, (5х6)+2=32 и (8х6)+3=51. Выйдет 5124.
- Сложить результаты, заменяя пустые «соты» в столбцах на 0: 7686+42700+512400=565186.
При затруднениях в процессе решения можно проверить правильность умножения столбиком онлайн-калькулятором. А также существуют специальные генераторы примеров, которые используют как своеобразный тренажёр для закрепления изученного материала.
Целые числа с нулями
В ситуациях с нулями немного сложнее.
Если нолик «потерялся» где-то в середине, то в процессе решения его следует пропустить. Ведь умножение абсолютно любого числа на 0 в итоге даёт этот же 0. Поэтому можно сразу переходить к следующей цифре и заполнить строку под чертой, отступив не на 1, а на 2 единицы.
Что касается таких чисел как 10, 100, 1200, 12030 и т. п. — суть такая же, но алгоритм решения отличается. Вычисления проводят лишь с цифрами, отличными от нуля. А все «0» на конце чисел просто игнорируются. Хотя после сложения их количество надо подсчитать и добавить к ответу:
- 10х10=100 — 1+1=2 нуля;
- 12х2000=24000 — 3 нуля;
- 1000х10000=1000000 — 3+4=7 нулей и т. д.
Задание 1 — найти произведение чисел 202 и 123. Решение таково:
- Важный момент — 202>123, но первый множитель содержит «0», поэтому при вычислении столбиком числа местами не менять не нужно.
- Умножение на 2: 3х2=6, 2х2=4 и 2х1=2. Записать ответы под черту в обратном порядке — 246.
- Так как множитель содержит 0, пропустить его и сразу перейти к следующему этапу.
- Снова на 2. Второй раз можно не вычислять, просто переписать 246, сделав отступ влево на 2 цифры.
- Сложение столбиком даст окончательный ответ: 246+24600=24846.
Задание 2 — вычислить 120х300. Пошаговое решение:
- Отбросить «ненужное». При записи в столбик нули в конце числа пишут только под нулями, а цифры — под цифрами. То есть, потребуется найти произведение 12х3.
- При умножении 2 на 3 будет 6 — указать под тройкой. 1х3=3. Под чертой записать 36.
- Чтобы найти ответ, нужно посчитать «0» в примере: 1+2=3. То есть 120х300=3600.
Операции с десятичными дробями
На самом деле умножение десятичных дробей столбиком не слишком сильно отличается от аналогичного действия с числами, у которых есть нули.
В этом случае примеры решают точно так же, как и обычные — про запятую можно временно забыть. Но, когда ответ уже найден, её обязательно нужно восстановить. А для этого надо узнать, сколько цифр после запятой находится у каждого множителя. Их количество складывают, а потом отсчитывают это число с конца ответа.
Задание 1 — вычислить 2,5х3. Пошаговое решение:
- Запятые на время условно убрать: 25х3.
- Сначала умножить на 3 крайнюю правую цифру первого множителя — 5х3=15. Под черту записать 5, а 1 «запомнить».
- 2х3=6 и оставшаяся единица. Получится 75.
- Чтобы найти конечный ответ, следует посмотреть на количество цифр запятой. Она одна, поэтому 2,5х3=7,5.
Задание 2 — отыскать значение произведения 7,5х2,5. Решение с объяснением:
- Пример записать в столбик, игнорируя запятые: 75х25.
- По общим правилам сначала умножить на 5. При 5х5=25 записать цифру 5 под единицами, а 2 — отправить к десяткам. 7х5=35 и плюс перенос — под чертой должно быть 375.
- Аналогично с числом 2: 5х2=10, где единицу нужно перенести, и (7х2)+1=15.
- Сложение промежуточных результатов: 375+1500=1875.
- В обоих множителях после запятой стоит 1 цифра, а значит 1+1=2. Конечный ответ: 18,75.
Если как следует разобраться в теме, юный математик сможет решать даже сложные примеры. Единственный минус метода — большие числа делают вычисления громоздкими, из-за каждой ошибки придётся проверять и править весь пример.
Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
В этом материале мы расскажем, как считать с помощью данного способа. Все пояснения будут проиллюстрированы примерами решений задач.
Основы умножения столбиком
Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.
Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a·0=0 (a – любое натуральное число).
Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.
Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.
Как записывать множители при подсчете столбиком
Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.
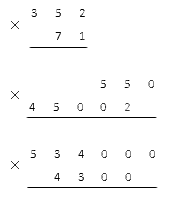
Например, чтобы вычислить и 71, 550·45 002 и 534 000·4 300, запишем такие столбики:
Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.
Как умножить столбиком многозначное число на однозначное
Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Условие: вычислить 45 027·3.
Решение
Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:
Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.
На конкретных числах процесс будет выглядеть так:
1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7·3=21. Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем. Наша запись принимает вид:
2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10, то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2·3, это будет 6. Добавляем оставшиеся с прошлого умножения десятки (от числа 21, как мы помним): 6+2=8. Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:
3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
Здесь нужно умножить 3 на 0. Согласно правилам умножения, результат будет равен 0. Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10. Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.
Осталось умножить 5·3 и получить 15. Результат больше 10, пишем пятерку и запоминаем десяток:
Нам осталось только перемножить 4·3, это будет 12. Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10, пишем 3 на нужное место и сохраняем единицу.
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.
Ответ: 45 027·3 = 135 081.
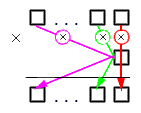
Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.
Условие: подсчитать, сколько будет 4 502 700·3.
Решение
Cначала запишем числа нужным способом.
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.
Ответ: 4 502 700·3 =13 508 100.
Как перемножить столбиком два многозначных натуральных числа
Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.
Условие: вычислить, сколько будет 207·8 063.
Решение
Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063, а под ним 207. Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:
Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.
1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7. Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0, то сразу переходим к следующему этапу.
3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.
Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:
У нас получились все нужные нам неполные произведения. Их количество равно числу разрядов во втором множителе (кроме 0). Последнее, что нам осталось сделать, – это сложить два произведения в столбик, используя ту же запись. Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем этапе). В нашей задаче получится:
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.
Ответ: 8 063·207 = 1 669 041.
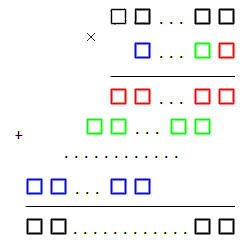
Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:
Чтобы лучше закрепить материал, приведем решение еще одного примера.
Условие: умножьте 297 на 321.
Решение
Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
1. Первый этап – умножаем 297 на 1, которая стоит в разряде единиц второго множителя.
2. Потом умножаем таким же образом первый множитель на 2, что стоит в десятках второго множителя. Получаем второе неполное произведение:
3. Далее умножаем на значения сотен, т.е. 297 на 3:
4. У нас получилось три неполных произведения, которые надо сложить (для этого желательно повторить, как правильно складывать столбиком три числа и более). Считаем:
Ответ: 297·321 = 95 337.
Еще один пример приведем без пояснений.
Условие: вычислите 210 627·30 105.
Решение
Весь процесс вычислений указан в записи ниже.
Ответ: 210 627·30 105 = 6 340 925 835.
В целом можно сказать, что если вы отлично владеете способностью умножать однозначные числа и умеете складывать столбиком, то процесс умножения многозначных натуральных чисел указанным методом не будет представлять для вас никакого труда.
У нас остался еще один момент, который мы хотели бы пояснить. Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.
Условие: вычислите 50 600·390.
Решение
Все, что нам надо сделать, – это записать множители так, чтобы друг под другом оказались цифры, отличные от нуля.
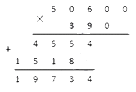
После этого мы можем просто провести все вычисления по указанному выше алгоритму, игнорируя нули. Т.е. в данном примере нам нужно просто умножить 506 на 39. Получаем два неполных произведения и складываем их:
Нам осталось все лишь дописать к результату оставшиеся нули. Мы добавляем их столько, сколько указано справа у обоих множителей. В нашем примере к готовому числу надо написать три нуля:
Это и будет корректный ответ.
Ответ: 50 600·390 = 19 734 000.
Сегодня мы рассмотрим вопрос, касающийся умножению в столбик. Познакомимся с алгоритмом и закрепим материал на конкретных примерах.
Алгоритм умножения в столбик
Для нахождения произведения двух натуральных чисел, воспользуемся следующим правилом:
- Запишем первый множитель (для удобства, возьмем тот, у которого большего разрядов);
- Соблюдая разрядность, с новой строки запишем второй множитель (важно, чтобы десятки были под десятками, сотни под сотнями и т.д.);
- Чертим горизонтальную линию;
- Далее необходимо каждую цифру первого множителя, умножить с каждой цифрой второго:
- Производим умножение справа налево.
- Если ответ оказался двузначным, то в текущем разряде оставляем последнюю цифру, а первую переносим в следующий разряд, сложив со значением, при следующем перемножении.
- Перемножаем все цифры второго множителя, сдвигаясь влево на один разряд;
- Получившиеся цифры складываем.
Примеры
Умножение в столбик двузначного числа на однозначное
Пример: умножить 11 на 7
Выполним умножение исходя из вышеприведенного алгоритма:
-
Запишем первый множитель и поставим знак умножения:
-
Запишем ниже второй множитель — 7, соблюдая разрядность и поставим горизонтальную черту, т.е так:
-
Далее необходимо перемножить каждую цифру второго множителя с каждой цифрой первого. Т.к. во втором множителе всего одна цифра, перемножаем её с с цифрами первого. Получится, что необходимо дважды перемножить 7 с единицей — это и будет ответом. Записываем под чертой.
Умножение в столбик двузначных чисел
Пример: умножить 97 на 12
-
Аналогично предыдущему примеру, запишем множители, поставим знак умножения, проведем черту:
-
Перемножим крайнюю правую цифру второго множителя с каждой цифрой первого, таким образом:
- 2 умножаем на 7 получаем 14, согласно алгоритму, 4 пишем, единицу запоминаем и прибавляем к следующему произведению;
- 2 умножаем на 9 получаем 18, плюс прибавляем единицу, которую запомнили в предыдущем пункте, получаем 19;
- Записываем:
-
Аналогично предыдущему шагу, перемножаем оставшуюся цифру второго множителя (единицу) со всеми цифрами первого (7 и 9). При записи не забываем сдвинуться на разряд влево, т.е:
-
Последним шагом необходимо сложить получившиеся значения, таким образом:
Умножение в столбик трехзначных и более разрядных чисел производится аналогично!
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Умножение в столбик
Поддержать сайт
Решим пример:
- Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее.
Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа.
Сбоку слева между числами ставим знак действия. У нас это «×» (знак умножения).
- Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается
под чертой под самой правой цифрой.Умножаем число сверху по цифре (знаку) справа налево.
7 · 6 = 42
У нас получилось число большее или равное «10».
Поэтому под черту идет только последняя
цифра результата. Это «2».
Количество десятков произведения (у нас «4 десятка»)
ставим над соседом слева от «7».
- Умножаем «2» на «6».
2 · 6 = 12
Не забудем, что над «2» стоит
«4». Это значит, что к результату
умножения (произведению) надо прибавить «4».12 + 4 = 16
«6» записываем под чертой и
«1» записываем над «4».
- Умножаем «4» на «6».
4 · 6 = 24
К произведению добавляем «1»
24 + 1 = 25
- Переходим к умножению числа «427» на
«3». Умножаем по тем же правилам, что и на
«6».
Запомните!
Результат умножения на вторую цифру необходимо записывать под второй
цифрой результата первого действия умножения.
- Полученные числа под чертой складываем по
правилам сложения в столбик.
Теперь освоив умножение столбиком, вы сможете перемножать сколь угодно большие числа.
В данной публикации мы рассмотрим правила и практические примеры того, каким образом можно умножать столбиком натуральные числа (двузначные, трехзначные и многозначные).
- Правила умножения в столбик
- Примеры умножения в столбик
Правила умножения в столбик
Чтобы найти произведение двух натуральных чисел с любым количеством разрядов можно выполнить умножение в столбик. Для этого:
- Пишем первый множитель (начинаем с того, у которого больше разрядов).
- Под ним записываем второй множитель (с новой строки). При этом важно, чтобы одинаковые разряды обоих чисел были расположены строго друг под другом (десятки под десятками, сотни под сотнями и т.д.)
- Под сомножителями чертим горизонтальную линию, которая будет отделять их от результата.
- Начинаем выполнять умножение:
- Крайнюю правую цифру второго множителя (разряд – единицы) поочередно умножаем на каждую цифру первого числа (справа налево). При этом если ответ оказался двузначным, в текущем разряде оставляем последнюю цифру, а первую переносим в следующий, сложив со значением, полученным в результате умножения. Иногда в результате такого переноса в ответе появляется новый разряд.
- Затем переходим к следующей цифре второго множителя (десятки) и выполняем аналогичные действия, записывая результат со сдвигом на один разряд влево.
- Получившиеся числа складываем и получаем ответ. Правила и примеры сложения чисел в столбик мы рассмотрели в отдельной публикации.
Примеры умножения в столбик
Пример 1
Умножим двузначное число на однозначное, например 32 на 7.
Пояснение:
В данном случае второй множитель состоит только из одного разряда – единицы. Поочередно умножаем 7 на каждую цифру первого множителя. При этом произведение чисел 7 и 2 равняется 14, следовательно, в ответе цифру 4 оставляем в текущем разряде (единицы), а один прибавляем к результату умножения 7 на 3 (7⋅3+1=22).
Пример 2
Найдем произведение двузначного и трехзначного чисел: 416 и 23.
Пояснение:
- Записываем множители друг под другом (в верхней строке – 416).
- Поочередно умножаем цифру 3 числа 23 на каждый разряд числа 416, получаем – 1248.
- Теперь умножаем 2 на каждую цифру 416, и полученный результат (832) записываем под числом 1248 со смещением на один разряд влево.
- Остается только сложить числа 832 и 1248, чтобы получить ответ, который равняется 9568.